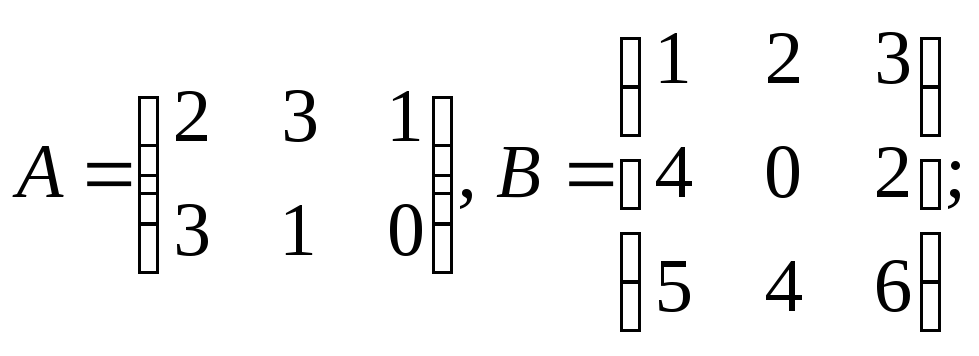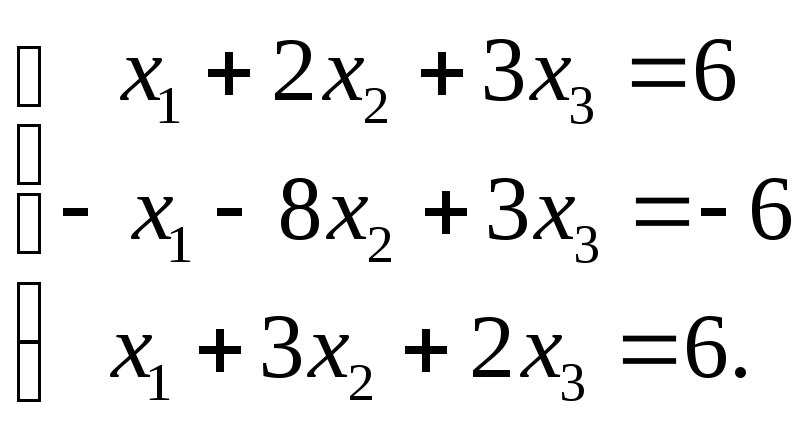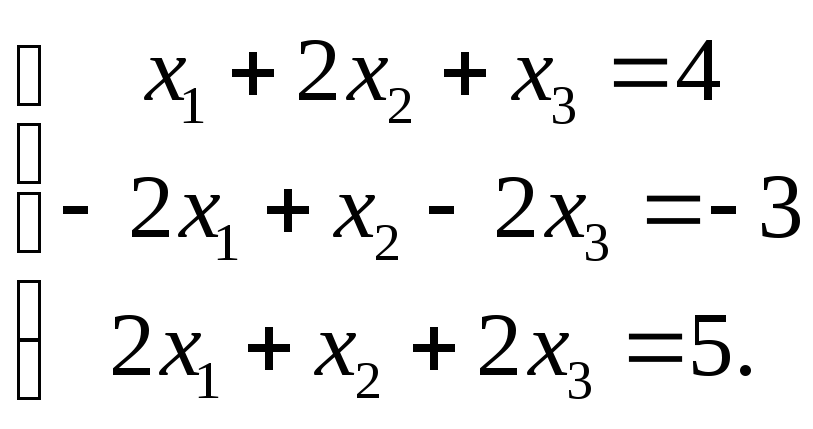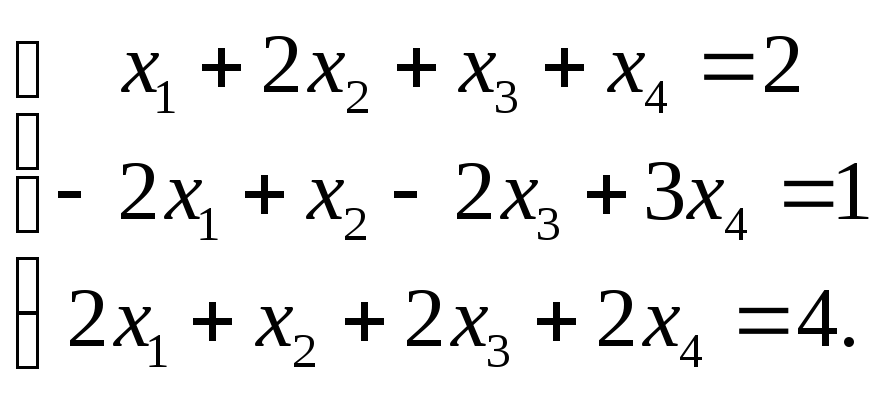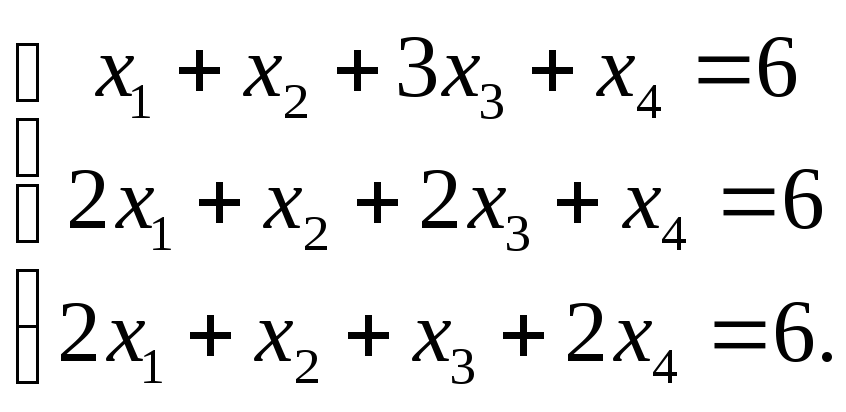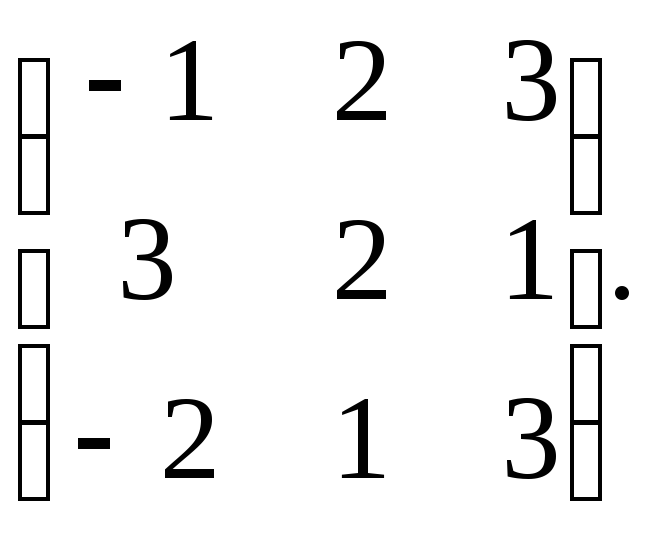Как сдать экзамен по аналитической геометрии



Аналитическая геометрия для «чайников»

Настоящая книга позволит вам в сжатые сроки (2-3 недели) освоить основы аналитической геометрии и научиться решать наиболее распространённые задачи по теме. Материал предназначен для студентов-заочников и других читателей, которые хотят быстро освоить минимум теории и максимум  практики

Сначала немного о предмете…. Наверняка вам сейчас вспомнился курс школьной геометрии с многочисленными теоремами, их доказательствами, чертежами и т.д. Что скрывать, нелюбимый и часто малопонятный предмет для значительной доли учеников. Аналитическая геометрия, как ни странно, может показаться более интересной и доступной. Что означает «аналитическая»? На ум сразу приходят два «штампованных» математических оборота: графический метод решения и аналитический метод решения.

Графический метод связан с построением графиков, чертежей. Аналитический же метод предполагает решение задач преимущественно посредством алгебраических действий. В этой связи алгоритм решения многих задач аналитической геометрии  прост и прозрачен, зачастую достаточно аккуратно применить нужные формулы – и ответ готов! Нет, конечно, совсем без чертежей тут не обойдется, к тому же для лучшего понимания материала я постараюсь приводить их сверх необходимости.

1. Векторы

1.1. Что такое вектор?
1.2. Коллинеарность векторов
1.3. Основные действия с векторами
1.4. Координаты вектора на плоскости и в пространстве
1.5. Простейшие задачи с векторами
1.5.1. Как найти вектор по двум точкам?
1.5.2. Как найти длину отрезка?
1.5.3. Как найти длину вектора?
1.5.4. Действия с векторами в координатах
1.5.5. Как найти единичный вектор
1.5.6. Деление отрезка в данном отношении
1.5.7. Формулы координат середины отрезка
1.6. Скалярное произведение векторов
1.6.1. Определение скалярного произведения
1.6.2. Угол между векторами и знак скалярного произведения
1.6.3. Скалярный квадрат вектора
1.6.4. Свойства скалярного произведения
1.6.5. Как найти угол между векторами?
1.6.6. Скалярное произведение векторов в координатах
1.6.7. Как проверить векторы на ортогональность?
1.6.8. Если векторы заданы суммами векторов с известными координатами
1.6.9. Как найти угол между векторами в координатах?
1.7. Ортогональные проекции векторов
1.7.1. Как найти проекцию вектора на вектор?
1.7.2. Проекции вектора на координатные оси. Направляющие косинусы
1.8. Линейная зависимость и линейная независимость векторов.
Базис векторов. Аффинная система координат.
1.8.1. «Плоский» случай
1.8.2. Как определить коллинеарность векторов плоскости?
1.8.3. Как определить коллинеарность векторов пространства?
1.8.4. Базис и система координат пространства
1.9. Векторное произведение векторов
1.9.1. Определение векторного произведения
1.9.2. Свойства векторного произведения
1.9.3. Векторное произведение в координатах
1.10. Смешанное произведение векторов
1.10.1. Определение смешанного произведения
1.10.2. Как вычислить смешанное произведение?
1.10.3. Как вычислить объём треугольной пирамиды?

2. Прямая на плоскости

2.1. Уравнение прямой с угловым коэффициентом
2.2. Общее уравнение прямой
2.2.1. Общее уравнение и направляющий вектор прямой
2.2.2. Как составить уравнение прямой по точке и направляющему вектору?

2.2.3. Как найти направляющий вектор по общему уравнению прямой?
2.2.4. Как составить уравнение прямой по двум точкам?
2.2.5. Нормальный вектор прямой
2.2.6. Как составить уравнение прямой по точке и вектору нормали?
2.3. Уравнение прямой в отрезках
2.4. Параметрические уравнениЯ прямой
2.5. Простейшие задачи с прямой на плоскости
2.5.1. Взаимное расположение двух прямых
2.5.2. Как найти прямую, параллельную данной?
2.5.3. Как найти точку пересечения прямых?
2.5.4. Как найти прямую, перпендикулярную данной?
2.5.5. Как вычислить расстояние от точки до прямой.
Как найти точку, симметричную относительно прямой?
2.5.6. Как найти расстояние между параллельными прямыми?
2.5.7. Как найти угол между прямыми?
2.5.8. Как найти проекцию вектора на прямую?
2.6. Линейные неравенства
2.7. Системы линейных неравенств
2.8. Как научиться решать задачи по геометрии?
2.9. Типовая задача с треугольником

3. Линии второго порядка

3.1. Алгебраическая линия и её порядок
3.2. Классификация линий второго порядка
3.3. Эллипс
3.3.1. Каноническое уравнение эллипса. Как построить эллипс?
3.3.2. Определение эллипса. Фокусы эллипса
3.3.3. Эксцентриситет эллипса и его геометрический смысл
3.3.4. Поворот и параллельный перенос эллипса
3.4. Гипербола
3.4.1. Каноническое уравнение и построение гиперболы
3.4.2. Определение гиперболы
3.4.3. Фокусы и эксцентриситет гиперболы
3.4.4. Равносторонняя гипербола
3.4.5. Поворот и параллельный перенос гиперболы
3.5. Парабола
3.5.1. Построение, уравнение, определение, фокусы, директриса, эксцентриситет
3.5.2. Поворот и параллельный перенос параболы
3.6. Неравенства с линиями второго порядка
3.7. Задачи с линиями второго порядка
3.7.1. Директрисы эллипса
3.7.2. Директрисы гиперболы
3.8. Приведение уравнения к каноническому виду
3.8.1. Приведение уравнения центральной линии. Метод инвариантов
3.8.2. Приведение уравнения нецентральной линии
3.8.3. Универсальный метод приведения

4. Полярная система координат

4.1. Что такое полярные координаты?

4.2. Порядок и техника построения точек в полярных координатах
4.3. Взаимосвязь прямоугольной и полярной системы координат

4.4. Уравнение линии в полярных координатах
4.5. Полярная роза
4.6. Как построить линию в полярных координатах?

5. Плоскость и прямая в пространстве

5.1. Плоскость и её уравнение

5.1.1. Понятие плоскости
5.1.2. Общее уравнение плоскости

5.1.3. Линейные неравенства в пространстве
5.1.4. Как построить плоскость?
5.1.5. Уравнение плоскости в отрезках
5.2. Как составить уравнение плоскости?
5.2.1. Уравнение плоскости по точке и двум неколлинеарным векторам
5.2.2. Как составить уравнение плоскости по трём точкам?
5.2.3. Вектор нормали плоскости (нормальный вектор)
5.2.4. Как составить уравнение плоскости по точке и вектору нормали?
5.3. Простейшие задачи с плоскостью
5.3.1. Как найти плоскость, параллельную данной?
5.3.2. Как найти расстояние от точки до плоскости?
5.3.3. Как найти расстояние между плоскостями?
5.3.4. Взаимное расположение двух плоскостей
5.3.5. Как найти угол между плоскостями?
5.3.6. Как найти плоскость, перпендикулярную данной?
5.3.7. Взаимное расположение трёх плоскостей
5.4. УравнениЯ прямой в пространстве
5.4.1. Канонические уравнения прямой
5.4.2. Как составить уравнения прямой по двум точкам?
5.4.3. Параметрические уравнения прямой
5.4.4. Прямая, заданная пересечением двух плоскостей
5.5. Задачи с прямой в пространстве
5.5.1. Взаимное расположение прямых
5.5.2. Скрещивающиеся прямые
5.5.3. Как найти прямую, содержащую общий перпендикуляр?
5.5.4. Как найти расстояние между скрещивающимися прямыми?
5.5.5. Пересекающиеся прямые в пространстве
5.5.6. Как найти прямую, перпендикулярную данной?
5.5.7. Как найти расстояние от точки до прямой?
5.5.8. Как найти точку, симметричную относительно прямой?
5.5.9. Как найти угол между прямыми?
5.5.10. Параллельные прямые в пространстве
5.6. Основные задачи с прямой и плоскостью
5.6.1. Взаимное расположение прямой и плоскости
5.6.2. Как найти точку пересечения прямой и плоскости?
5.6.3. Как найти проекцию прямой на плоскость?
5.6.4. Как найти угол между прямой и плоскостью?
5.6.5. Прямая перпендикулярна плоскости
5.6.6. Прямая параллельна плоскости
5.6.7. Добро пожаловать в «реальные боевые условия»!
5.7. Задача с треугольной пирамидой

6. Поверхности второго порядка

6.1. Понятие алгебраической поверхности
6.2. Цилиндрические поверхности
6.3. Эллипсоид

6.4. Коническая поверхность
6.5. Параболоиды
6.6. Гиперболоиды
6.7. Альтернативные системы координат
6.7.1. Цилиндрическая система координат
6.7.2. Сферическая система координат

7. Решения и ответы, а также Приложения доступны в полной версии.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!



Автор: Aлeксaндр Eмeлин

• 1620
• 16 января 2016, 18:51

Вопросы
для подготовки к экзамену по линейной
алгебре и аналитической геометрии

Элементы
линейной алгебры

1. Матрицы, виды матриц (квадратная,
диагональная, единичная, нулевая).

2. Действия с матрицами (сложение,
умножение на число, умножение матриц),
их свойства; перестановочные матрицы,
необходимое условие перестановочности
матриц.

3. Определитель матрицы n–го
порядка, свойства определителей.

4. Миноры и алгебраические дополнения.
Разложение определителя по элементам
произвольной строки или столбца.

5. Ранг матрицы. Ступенчатая матрица.
Элементарные преобразования строк
(столбцов) матрицы, определение. Теорема
о ранге ступенчатой матрицы.

6. Обратная матрица, теорема о единственности
обратной матрицы в случае ее существования.
Способы нахождения обратной матрицы:
с помощью элементарных преобразований,
алгебраических дополнений.

7. Системы линейных уравнений, основная
и расширенная матрицы системы, матричная
форма записи системы линейных уравнений.

8. Системы линейных уравнений и методы
их решения: с помощью обратной матрицы
(обоснование), метод Крамера (обоснование),
метод Гаусса (описание алгоритма).

Элементы векторной алгебры и
аналитической геометрии

1.
Вектор. Операции
с векторами (сложение, умножение на
число, скалярное произведение). Свойства
скалярного произведения векторов.
Коллинеарные векторы, определение.
Необходимое и достаточное условия
коллинеарности двух векторов.

2.
Теорема о разложении вектора по двум
неколлинеарным векторам.

3.
Координаты вектора. Необходимое и
достаточное условие коллинеарности
двух векторов в координатной форме.

4.
Скалярное произведение двух векторов,
заданных координатами. Необходимое и
достаточное условие перпендикулярности
двух векторов, заданных координатами.

5.
Линейная
зависимость и линейная независимость
векторов, определение. Основные теоремы
о линейной зависимости: линейная
зависимость системы векторов, содержащей
нулевой вектор; содержащей два
пропорциональных вектора. Связь между
линейной зависимостью и коллинеарностью
двух векторов. Связь между линейной
зависимостью и компланарностью трех
векторов.

6. Деление отрезка
в данном отношении.

7.
Уравнение линии на плоскости. Вывод
уравнения окружности.

8.
Уравнение прямой линии на плоскости.
Направляющий и нормальный векторы
прямой, определения. Уравнение прямой,
заданной: точкой и направляющим вектором;
точкой и нормальным вектором; точкой и
угловым коэффициентом; двумя точками.

9.
Взаимное расположение прямых на
плоскости: угол между двумя прямыми;
необходимые и достаточные условия
параллельности и перпендикулярности
двух прямых.

10.
Общее уравнение прямой. Теорема о том,
что любое уравнение первой степени
относительно переменных x,
y
определяет прямую линию на плоскости.

11.
Расстояние от точки до прямой.

12.
Геометрический смысл линейных неравенств
с двумя переменными.

13.
Кривые второго порядка: эллипс (вывод
канонического уравнения эллипса),
гипербола (вывод канонического уравнения
гиперболы), парабола (вывод канонического
уравнения параболы).

14.
Уравнение плоскости, заданной: точкой
и нормальным вектором; тремя точками.
Условия параллельности и перпендикулярности
плоскостей. Угол между двумя плоскостями.
Расстояние от точки до плоскости.
Уравнение плоскости, проходящей через
заданную точку параллельно заданной
плоскости.

15.
Уравнение прямой, заданной точкой и
направляющим вектором; параметрические
уравнения прямой. Угол между прямой и
плоскостью. Условия параллельности и
перпендикулярности прямой и плоскости.

16.
Уравнение прямой, проходящей через
заданную точку перпендикулярно заданной
плоскости. Уравнение плоскости, проходящей
через заданную точку перпендикулярно
заданной прямой.

Задания для
подготовки к экзамену по линейной
алгебре и аналитической геометрии

1.
Даны матрицы

и
.
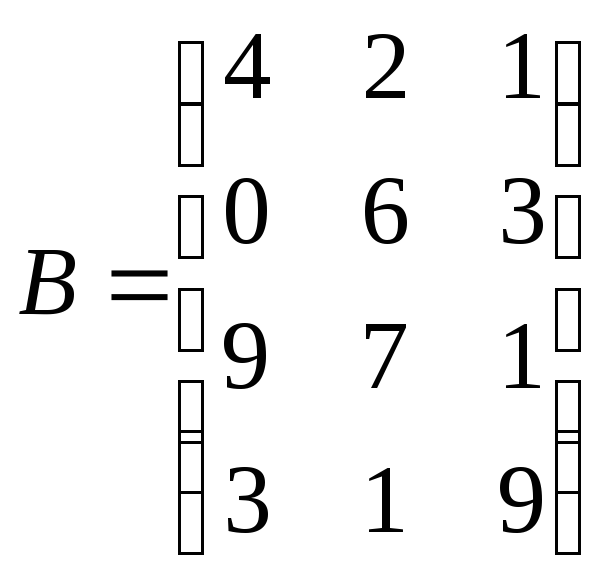
Найдите сумму этих матриц и разность
А
– В.

2.
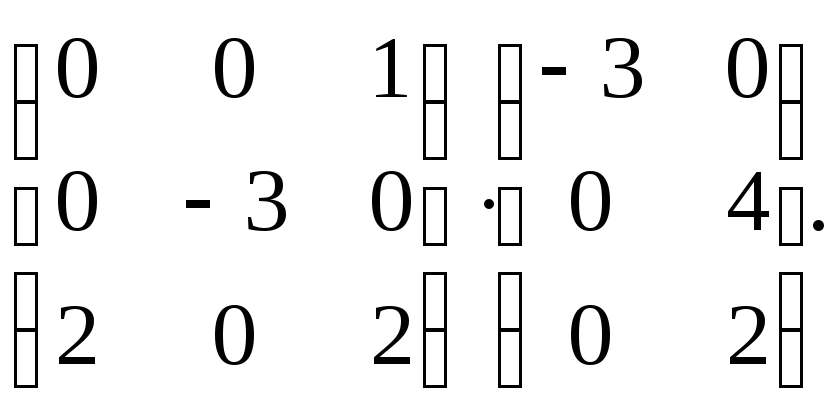
Найдите произведение матриц: а)
б)

3.
Найдите элемент с₂₁
матрицы С = АВ,
если

4.
Решите уравнение
.

5.
Вычислите определитель: а)
;
б)
.

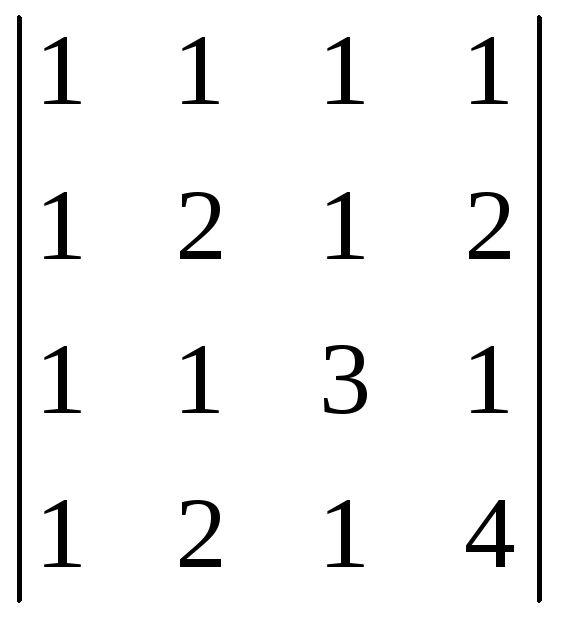
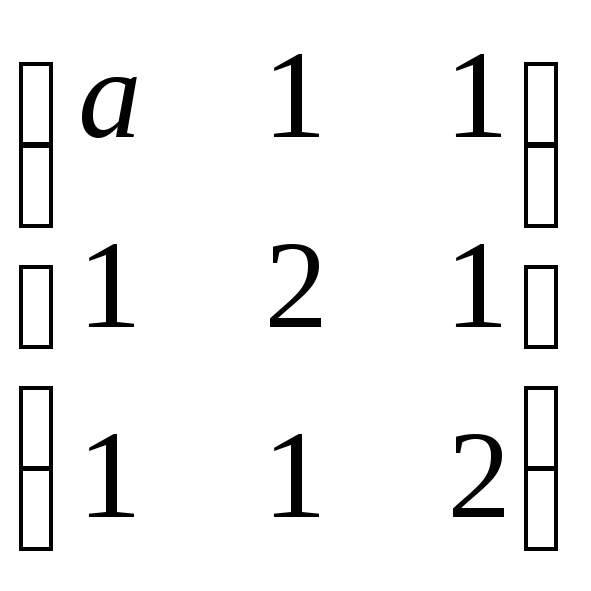
6.
При каких значениях параметра а
матрица

не имеет обратной?

7. Решите систему
уравнений:

а)
б)

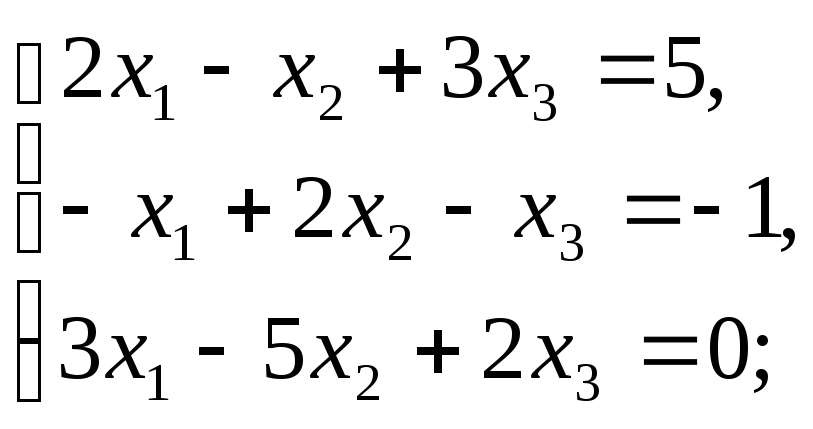
в)
г)

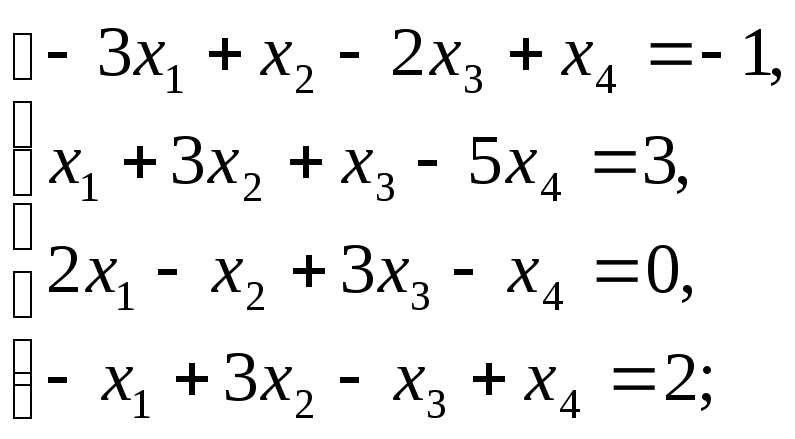
8.
Даны векторы

и
.
Найдите: а)
;
б)
.

9.
Даны векторы
.
Найдите угол между векторами:

а)

и
;
б)

и
;
в)

и
.

10.
Найдите угол между векторами

и
,
если А(2;5;0),
Р(−2;4;8),
М(0;−1;5).

11.
Найдите х,
при котором векторы

и

перпендикулярны.

12.
Даны векторы

и
.
При каком значении m
эти векторы коллинеарны?

13.
На векторах

и

построен параллелограмм. Найдите длины
диагоналей этого параллелограмма и
косинус острого угла между ними, если
.

14.
Найдите вектор
,
cонаправленный
с вектором
,
если известно, что
.

15.
Найдите вектор
,
коллинеарный вектору
,
если известно, что
.

16. Исследуйте на
линейную зависимость векторы:

1)
;
2)
.

17.
Разложите вектор

по векторам
,
если это возможно.

18.
Напишите уравнение прямой, проходящей
через точку М(0;−2)
перпендикулярно прямой x + 2y – 1 = 0.

19.
Прямая проходит через середину отрезка,
соединяющего точки А(−2;−2)
и В(4;0),
перпендикулярно этому отрезку. Составьте
уравнение этой прямой.

20.
Найдите расстояния от точек А(1;−2),
В(0;−1)
и С(2;−2)
до прямой 2x + y
− 2 = 0.

21. Даны вершины
треугольника: А(−2;−4), В(−5;2), С(3;6).

1)
Напишите уравнения прямых, содержащих
стороны треугольника АВС.

2)
Напишите уравнение прямой, содержащей
медиану АМ
и найдите ее длину.

3)
Напишите уравнение прямой, содержащей
высоту ВН
и найдите ее длину.

4)
Напишите уравнение прямой, содержащей
среднюю линию MN
(точка N –
середина стороны СА),
найдите ее длину.

5)
Найдите расстояние от точки В
до медианы АМ.

22.
Изобразите на плоскости множество
точек, координаты которых удовлетворяют
системе линейных неравенств:

1)

2)

23.
Что представляют собой геометрические
места точек плоскости, заданные следующими
уравнениями? Изобразите эти геометрические
места точек.

1)
25x²
+ 9y²
= 225; 2) 36y²
− 9x²=
324;

3)
x²
+ y²
= 25; 4) x²
− 16y²
= 16;

5)
у²
= 5х; 6)
16x²
+ 25y²
+ 64x
− 50y
− 311 = 0.

24.
Напишите уравнение плоскости, проходящей
через точки М₁(−2;3;−5),
М₂(1;2;−4)
и М₃(5;0;−3).

25.
Даны точки М₁(1;−3;5)
и М₂(3;2;0).
Напишите уравнение плоскости, проходящей
через точку М₁
и перпендикулярной вектору
.

26.
Напишите уравнение прямой, проходящей
через точку
М(1;3;−2)
и
параллельной вектору
.

27.
Напишите уравнение прямой, проходящей
через точки
М₁(5;–3;2)
и
М₂(3;1;–2).

28.
Определите взаимное расположение
плоскостей: а) 2x
– 3y
– 4z
+ 11 = 0, –4x
+ 6y
+ 8z
+ 36 = 0;

б)
2x
– 3z
– 12 = 0, 4x
+ 4y
– 6z
+ 7 = 0; в) 3x
– 2y
– 2z
+ 7 = 0, 2x
+ 2y
+ z
+ 4 = 0.

29.
Найдите угол между плоскостями

и
.

30.
Напишите уравнение плоскости, проходящей
через точку М(2;–1;6) параллельно плоскости

x
+ y
– 2z
+ 5 = 0.

31.
Найдите расстояние от точки А(3;9;1)
до плоскости x
– 2y
+ 2z
– 3 = 0.

32. Напишите
уравнение плоскости, проходящей через
точку М(–1;–5;8)
перпендикулярно прямой

.

33. Напишите
уравнение прямой, проходящей через
начало координат перпендикулярно
плоскости, заданной уравнением
3x + 5z – 5 = 0.

Задания для
самостоятельной работы

Вариант 1.1

1) Найдите
произведения (если они существуют) АВ
и ВА, где

2) Решите систему
уравнений

3) Найдите косинус
угла между векторами

и
,
если известно, что

4) Напишите
уравнение прямой, проходящей через
точку М(–3;2)
параллельно прямой 3x + y – 1 = 0.

5) Какую линию
на плоскости задает уравнение x²
+ 4y² = 36? Постройте
эту линию в прямоугольной системе
координат.

Вариант 1.2

1) Найдите произведения
(если они существуют) АВ и ВА,
где

2) Решите систему
уравнений

3) При каком
значении параметра а векторы

и

будут коллинеарны?

4) Напишите
уравнение прямой, проходящей через
точку М(–2;–1)
параллельно прямой 3x – 2y + 7 = 0.

5) Какую линию
на плоскости задает уравнение
?
Постройте эту линию в прямоугольной
системе координат.

Вариант 2.1

1) Найдите матрицу
C = 2AВ
− 3B, если

2) Решите систему
уравнений

3) Найдите длину
вектора
,
если известно, что

4) Напишите
уравнение прямой, проходящей через
точку М(0;–2)
перпендикулярно прямой x – 2y + 5 = 0.

5) Какую линию
на плоскости задает уравнение 6x²
− 4y² = 36? Постройте
эту линию в прямоугольной системе
координат.

Вариант 2.2

1) Найдите матрицу
C = 3AВ
− 2А, если

2) Решите систему
уравнений

3) Найдите длину
вектора
,
если известно, что А(1;0;2), В(–1;0;3),
С(–2;–3;5).

4) Напишите
уравнение прямой, проходящей через
точку М(–1;3)
перпендикулярно прямой x – 2y + 7 = 0.

5) Какую линию
на плоскости задает уравнение
?
Постройте эту линию в прямоугольной
системе координат.

БИЛЕТ
(образец)

1. а) Алгебраическое
дополнение элемента матрицы. Разложение
определителя матрицы по элементам
любого столбца.

б) Вычислите
сумму А₁₃ – А₃₂,
где A_ij − алгебраическое
дополнение соответствующего элемента
матрицы

2. а) Теорема
о том, что координаты точек, лежащих в
одной полуплоскости относительно
прямой, заданной уравнением Ax
+ By
+ C
= 0, удовлетворяют одному из неравенств

Ax
+ By
+ C
> 0, Ax
+ By
+ C
< 0.

б) Не
выполняя построение, выясните, пересекает
ли прямая 3x
– y
+ 5 = 0 отрезок АВ,
где А(5;–1),
В(–3;2).

3. 1)
Найдите матрицу C
= 3AВ
− 2А,
если

2) Решите
систему уравнений

3) Найдите
длину вектора
,
если известно, что А(1;0;2),
В(–1;0;3),
С(–2;–3;5).

4) Напишите
уравнение прямой, проходящей через
точку М(–1;3)
перпендикулярно прямой
x – 2y + 7 = 0.

5) Какую
линию на плоскости задает уравнение
?
Постройте эту линию в прямоугольной
системе координат.