Как сдать начертательную геометрию
Начертательная геометрия — один из самых важных предметов, рассматриваемых в программе технических вузов. Проще говоря, знание начертательной геометрии — фундамент знаний современного инженера. Сдать начертательную геометрию нужно не только для того, чтобы получить зачет, но и для того, чтобы хорошо разобраться в ней.
Вам понадобится
- Список существующих ГОСТов (с их расшифровкой),
- справочник ЕСКД (Единый стандарт конструкторской документации), AutoCAD или Компас
Инструкция
Сначала вам нужно выучить все необходимые линии и правила. Основные линии, которые выделяют в начертательной геометрии: основная (ей обводится сам чертеж), пунктирная (для обозначения невидимых линий) и штрихпунктирная — для осей.
Следующим этапом будет изучение тел вращения. Тут все довольно просто: тело вращения получается при вращении какой-либо фигуры вокруг оси. Наиболее встречающиеся в зачетных работах тела: шар, цилиндр и конус.
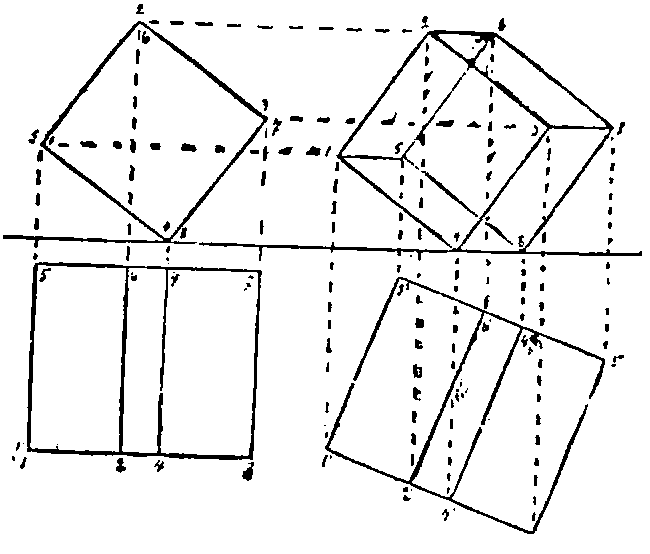
Далее вам нужно научиться выполнять сечение фигуры. Сечение, как правило, выполняется по характерным точкам. Найти характерные точки на чертеже довольно просто — на главном виде это пересечение плоскостей. То есть, если две какие-то части эпюра (не контура, что важно), пересекаются, значит точка их пересечения является характерной.
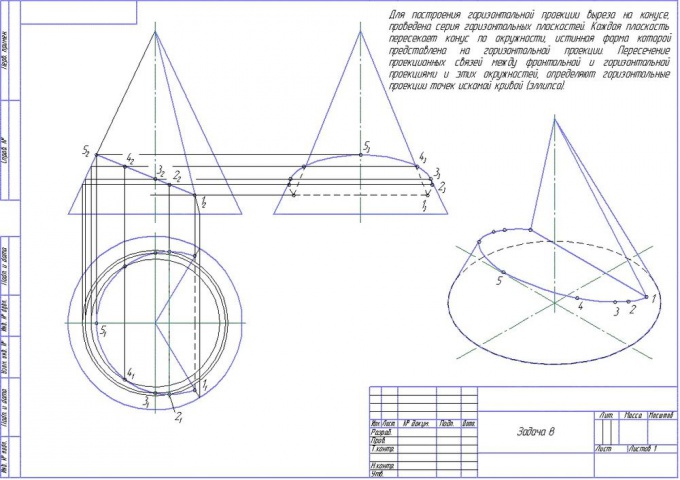
Далее вам нужно научиться выполнять сечение фигур вращения в компьютерной среде. Типовые среды выполнения — Автокад и Компас. Выполнять сечение по характерным точкам в этих средах нужно следующим образом. Переносим характерные точки на все три вида: ведем тонкую линию до пересечения со вспомогательным видом, затем отмеряем на вспомогательном расстояние от оси до очерка, и отмечаем характерную точку на нем. После того, как все характерные точки соединены, остается только соединить их. Сечение готово, работа выполнена, а вы получаете зачет.
Видео по теме
Полезный совет
Нужно выучить сечения основных фигур вращения, это поможет вам не ошибиться при соединении характерных точек.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Что такое зачет? Как бы мы его не воспринимали – экзаменом или контрольной работой, это этап проверки знаний, дающий встряску любому организму. Нет похожих зачетов, у каждого преподавателя метод его приема свой. Но есть некоторые правила для того, чтобы зачет прошел успешно, без излишних волнений.
Как же подготовиться к зачету, особенно если предметом для сдачи является начертательная геометрия? Это зависит от того, какие требования у преподавателя. Иногда встречаются лояльные преподаватели, которые ставят всем автомат и не тратят свои время и нервы на то, чтобы повторно принимать зачет. Есть преподаватели очень требовательные и придирчивые, к зачетам у которых надо готовиться наравне с экзаменами. Даже серьезнее, если учесть, что экзамены проводятся в период сессии, а зачеты надо сдавать по ходу учебы, когда кроме них еще надо готовиться к теоретическим занятиям.
Посещайте лекции, их читают не просто ради удовольствия, практически любой зачет проходит по выявлению знаний, полученных на лекциях. Чем лучше вы законспектируете поданный материал, тем легче вам будет готовиться к зачетам и к самой сессии. Этот совет можно считать основным. Ведь сдать зачет по начертательной геометрии без знаний практически нереально.
Для того, чтобы не оказаться в затруднительной ситуации во время зачетов, необходимо заранее пообщаться со студентами старших курсов. Они всегда готовы поделиться всеми нюансами по сдаче того или иного зачета, об особенностях преподавателя. Никогда не делайте поспешных выводов на основе мнения одного студента, оно может быть субъективным. Поговорите с несколькими людьми. Сейчас почти в каждом учебном заведении есть свой сайт, на котором обязательно найдется форум для студентов. Поищите информацию в интернете, осведомлен – значит, вооружен. Но этот совет годится лишь для тех, кто точно знает, какой преподаватель будет принимать зачет. В этом случае не следует надеяться на лучшее. Наоборот, всегда надо думать о худшем, тогда лучшее будет еще более приятной неожиданностью.
Поинтересуйтесь, как готовятся к зачетам по начертательной геометрии ваши однокурсники, но имейте в виду, не все скажут правду. От знаний, которыми владеют они, может зависеть результат вашей сдачи зачета. Ведь на фоне человека, который совсем не знает материала, ваши средние знания могут показаться фантастическими. Но надеяться на это, все же не стоит, ведь возможен вариант, что перед вами будет отвечать отличник.
Успехов вам в учебе!
Успешная
сдача экзамена обеспечена качеством
учебы в течении семестра. Подготовка к
экзамену осуществляется при наличии
конспекта лекций, блока решенных задач,
которые оформлены в сборнике и альбоме
индивидуальных заданий. Студентам перед
сессией выдаются вопросы для подготовки
к экзамену по начертательной геометрии,
которые содержат также список
рекомендованной литературы используемой
студентами для подготовки к экзамену.
Все это в совокупности позволяет
качественно подготовиться к экзамену
и успешно его сдать.
Экзамен
по начертательной геометрии проводится
в письменной форме. На листах формата
А3 подготовленных как сказано на рис.
1.1 выполняются задачи билета, приводятся
пояснения в краткой алгоритмической
форме. Оформление соответствует
требованиям ГОСТ и СТБ.
Список рекомендуемой литературы основной:
-
Гордон
В.О., Семенцов-Огиевский М.А. Курс
начертательной геометрии: Учебное
пособие для вузов \ Под ред. В.О. Гордона,
Ю.Б. Иванова. – М.: Высш. Шк., 1999.- 272 с.: ил. -
Гордон
В.О. и др. Сборник задач по курсу
начертательной геометрии: Учебное
пособие для вузов \ Под ред. Ю.Б. Иванова.
– М.: Высш. Шк., 1998.- 320 с.: ил. -
Начертательная
геометрия: Учебник для вузов \ Под ред.
Проф. Н.Н. Крылова. — М.: Высшая школа,
2000. – 224 с.: ил. -
Начертательная
геометрия: Учебник для вузов \ Н.Н.
Крылов, Г.С. Иконникова, В.Н. Николаев и
др.; Под ред. Н.Н. Крылова. — М.: Высшая
школа, 2000. – 224 с.: ил. -
Кузнецов
Н.С. Начертательная геометрия. — М.,1981 -
Арустамов
Х.А. Сборник задач по начертательной
геометрии. — М.: Машиностр., 1978 -
Винницкий
Н.Г. Начертательная геометрия. — М.:
Высш. шк., 1975 -
Государственные
стандарты Единой
системы
конструкторской документации (ЕСКД,
СПДС и СТБ) -
Стандарт
университета. Общие требования и правила
оформления / под ред. Т.Н.Базенкова. –
Брест: БГТУ, 2002
Дополнительной:
-
Бубенников
А.В. Начертательная геометрия. – М.,
1985 -
Бубенников
А.В. Начертательная геометрия: Задачи
для упражнений. — М., 1981 -
Држевецкий
В.В. Основы начертательной геометрии
и проекционное черчение. \ Под ред.
Л.С.Шабеки. – Мн.: Дизайн ПРО, 2000. – 112
с.: ил. -
Локтев
О.В. Краткий курс начертательной
геометрии: Учеб. для втузов. – М.: Высш.
Шк., 1999. – 136 с.: ил. -
Локтев
О.В. Задачник по начертательной геометрии:
Учеб. пособие для втузов. – М. – Высш.
шк., 1999. – 104 с.: ил. -
Начертательная
геометрия. Инженерная и машинная
графика: Учебник для строит. спец. вузов
\ К.И. Вальков, Б.И. Дралин, В.Ю. Климентьев,
М.Н.Чукова; Под ред. К.И. Валькова. – М.:
Высш. шк., 1997. – 495 с. : ил. -
Фролов
С.А. Начертательная геометрия .- М,, 1983. -
Фролов
С.А. Сборник задач по начертательной
геометрии. — М.,1980.
52
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Подготовка к экзамену по начертательной геометрии и инженерной графике.
1. Предмет начертательной геометрии. Виды проецирования. Свойства параллельного проецирования. Требования к проекционному чертежу.
Начертательная геометрия – один из разделов геометрии, в котором пространственные фигуры, представляющие совокупность точек, линий и поверхностей, изучаются по их проекционным изображениям.
Виды проецирования:
• Центральное проецирование.
• Параллельное проецирование:
– прямоугольное (ортогональное);
– косоугольное.
Свойства параллельного проецирования:
1. Проекция точки – точка.
2. Проекция прямой в общем случае – прямая.
3. Если точка принадлежит линии, то проекция этой точки принадлежит проекции линии.
4. Точка пересечения проекций пересекающихся прямых является проекцией точки пересечения этих прямых.
5. Проекции взаимно параллельных прямых взаимно параллельны, а отношение отрезков таких прямых равно отношению их параллельных проекций.
6. Плоская фигура, параллельная плоскости проекций, проецируется на эту плоскость без искажения.
Требования к проекционному чертежу:
• Обратимость – чертеж должен единственным образом определять форму и
расположение изображаемого предмета.
• Наглядность – чертеж должен давать пространственное представление о
изображаемом предмете.
• Простота построения.
• Удобство чтения.
2. Эпюр точки в системе трех плоскостей проекций. Ортогональные проекции и система прямоугольных координат. Эпюры точек, расположенных в четвертях и октантах пространства.
Ортогональные проекции геометрических фигур строятся на двух или трех взаимно перпендикулярных плоскостях проекций.
3. Прямая. Задание и изображение на чертеже. Положение прямых относительно плоскостей проекций. Следы прямой. Принадлежность точки прямой.
Положение прямых относительно плоскостей проекций
• Прямые общего положения – прямая, наклоненная ко всем плоскостям проекций;
• Прямые частного положения:
– прямые уровня – прямые, параллельные одной из плоскостей проекций:
a. горизонталь – прямая, параллельная горизонтальной плоскости проекций;
b. фронталь – прямая, параллельная фронтальной плоскости проекций;
c. профильная прямая – прямая, параллельная профильной плоскости проекций;
– проецирующие прямые – прямые, перпендикулярные одной из
плоскостей проекций:
a. горизонтально-проецирующая– прямая, перпендикулярная горизонтальной плоскости проекций;
b. фронтально-проецирующая – прямая, перпендикулярная фронтальной плоскости проекций;
c. профильно-проецирующая– прямая, перпендикулярная профильной плоскости проекций.
Следы прямой
Следом прямой называется точка пересечения прямой с плоскостью проекций.
Принадлежность точки прямой
Если точка принадлежит прямой, то проекции точки принадлежат одноименным проекциям этой прямой.
4. Взаимное положение двух прямых: параллельные, пересекающиеся и скрещивающиеся прямые. Конкурирующие точки. Теорема о проецировании прямого угла.
Взаимное положение прямых
• Параллельные прямые – прямые, лежащие в одной плоскости и не имеющие общей точки.
Одноименные параллельные проекции параллельных прямых взаимно параллельны.
• Пересекающиеся прямые – прямые, лежащие в одной плоскости и имеющие общую точку
Точки пересечения одноименных проекций пересекающихся прямых лежат на одной линии связи.
• Скрещивающиеся прямые – прямые, не лежащие в одной плоскости и не имеющие общих точек.
Точки, лежащие на одном проецирующем луче, называются конкурирующими.
Теорема о проецировании прямого угла
Прямой угол проецируется без искажения, если одна из его сторон параллельна плоскости проекций, а другая – не перпендикулярна ей.
5. Плоскость. Способы задания плоскости на эпюре. Следы плоскости. Положение плоскости относительно плоскостей проекций.
Способы задания плоскости на эпюре:
a. по трем точкам, не лежащим на 1 прямой;
b. по прямой и точке, не лежащей на этой прямой;
c. по двум пересекающимся прямым;
d. по двум параллельным прямым;
e. по плоской фигуре.
Следы плоскости
Следом плоскости называется линия пересечения плоскости с плоскостью проекций.
Положение плоскостей относительно плоскостей проекций
• Плоскости общего положения – плоскость, наклоненная ко всем плоскостям
проекций.
• Плоскости частного положения:
– проецирующие плоскости – плоскости, перпендикулярные одной из плоскостей проекций:
a. горизонтально-проецирующая – плоскость, перпендикулярная горизонтальной плоскости проекций;
b. фронтально-проецирующая – плоскость, перпендикулярная фронтальной плоскости проекций;
c. профильно-проецирующая – плоскость, перпендикулярная профильной плоскости проекций;
– плоскости уровня – плоскости, параллельные одной из плоскостей проекций:
a. горизонтальная плоскость уровня– плоскость, параллельная горизонтальной плоскости проекций;
b. фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций;
c. профильная плоскость уровня– плоскость, параллельная профильной плоскости проекций.
6. Принадлежность точки и линии плоскости. Построение на плоскости прямых общего положения, горизонталей, фронталей и линий ската.
Принадлежность точки и линии плоскости
Точка принадлежит плоскости, если она принадлежит прямой этой плоскости.
Прямая принадлежит плоскости, если она проходит через две точки этой плоскости.
Прямая принадлежит плоскости, если имеет с ней одну общую точку и параллельна
прямой, лежащей в этой плоскости.
Линии особого положения в плоскости
• Горизонталь плоскости – прямая, принадлежащая плоскости и
параллельная горизонтальной плоскости проекций;
• Фронталь плоскости – прямая, принадлежащая плоскости и
параллельная фронтальной плоскости проекций;
• Профильная прямая плоскости – прямая, принадлежащая плоскости и
параллельная профильной плоскости проекций;
• Линия ската плоскости – прямая наибольшего наклона плоскости
к горизонтальной плоскости проекций.
7. Взаимное расположение двух плоскостей. Построение через данную точку плоскости, параллельной данной. Построение линии пересечения плоскостей.
Взаимное расположение двух плоскостей:
• параллельные плоскости;
• пересекающиеся плоскости.
8. Взаимное расположение прямой и плоскости. Построение прямой, принадлежащей плоскости, параллельной плоскости. Построение точки пересечения прямой с плоскостью.
Взаимное расположение прямой и плоскости:
• Прямая параллельна плоскости;
• Прямая пересекает плоскость;
• Прямая принадлежит плоскости.
9. Преобразование комплексного чертежа. Способ замены плоскостей проекций. Сущность способа. Замена одной или двух плоскостей проекций. Основные типы задач, решаемых этим способом.
Преобразование комплексного чертежа
Применяется при решении позиционных и метрических задач для приведения геометрических фигур в частное положение относительно плоскостей проекций.
Способы преобразования комплексного чертежа
• изменением положения плоскостей проекций относительно неподвижных
геометрических фигур;
• изменением положения заданных геометрических фигур относительно
неподвижных плоскостей проекций;
• изменением направления проецирования.
Способ замены плоскостей проекций
Положение геометрической фигуры в пространстве не изменяется. Одна из плоскостей проекций заменяется новой плоскостью, перпендикулярной оставляемой плоскости проекций. Новая плоскость проекций выбирается так, чтобы по отношению к ней геометрическая фигура заняла частное положение.
Основные задачи, решаемые способом замены плоскостей проекций
Задача 1. Преобразовать прямую общего положения в прямую уровня.
Задача 2. Преобразовать прямую общего положения в проецирующую.
3адача 3. Преобразовать плоскость общего положения в проецирующую.
3адача 4. Преобразовать плоскость общего положения в плоскость уровня.
10. Решение метрических задач: определение расстояний; определение углов; построение плоской фигуры по заданным условиям.
11. Кривые линии. Образование, задание и основные свойства проекций плоских и пространственных кривых линий. Образование и построение цилиндрической винтовой линии.
Свойства проекций кривых
1. Если точка принадлежит кривой, то проекции точки принадлежат проекциям кривой.
2. Хорда и касательная кривой проецируются соответственно в хорду и касательную
проекции кривой.
Цилиндрическая винтовая линия – пространственная кривая, описываемая точкой при
равномерном движении по прямой, которая равномерно вращается вокруг параллельной ей оси.
Это линия одинакового уклона – гелиса.
Величина перемещения точки вдоль оси за один оборот – шаг винтовой линии h.
α – угол подъема винтовой линии.
Что нужно, чтобы сдать экзамен? Как получить высокие баллы на экзамене, известно всем. Для этого достаточно просто хорошо подготовиться и выучить предмет. Но студенты — непростой народ. У них всегда находится много дел поважнее и поинтересней, чем сидение над учебниками. Поэтому они часто задают вопрос, как сдать экзамен, если ничего не знаешь?
Главное правило зачётной книжки никто не отменял
«Сначала студент работает на зачётку, потом зачётка работает на студента». Первокурсникам тяжело поверить в то, что зачётка будет работать на них в последние несколько лет обучения, но эта истина подтверждена не один раз. Почти все преподаватели обращают внимание на успеваемость по другим дисциплинам и на прошлых курсах, эта информация прямо влияет на результат экзамена. Это же касается и текущих оценок по предмету. Если журнал украшают двойки и прогулы, то получить хороший балл на экзамене будет непросто.
Старшекурсники знают, как хорошо сдать экзамен – просто нужно быть владельцем «красивой» зачётки. Но есть и небольшая хитрость для тех, у кого зачётная книжка — не повод для гордости. Просто закрепите первые листочки зачётки с помощью скрепки, чтобы преподавателю было неудобно листать её.
Экзамен «автоматом»
Такой способ сдачи экзаменов придется по душе ответственным и старательным студентам. Все знают: чтобы получить «автомат», нужно регулярно посещать лекции и практические занятия, участвовать в олимпиадах и конференциях по предмету, быть активным на уроках и иметь хорошие текущие оценки. Такого студента преподаватель обязательно заметит на протяжении семестра и выставит оценки в зачётку без дополнительной проверки знаний.
Но, как ни крути, этот способ сдачи экзаменов сложный и требует массы усилий. Нас же, наоборот, интересует, как сдать экзамен, если ничего не знаешь и не хочешь учить.
Шпаргалки обязательны!
Также важно вовремя себя спросить: сдам ли я экзамен? Если до «судного» дня остаётся ещё немного времени, то нужно срочно приступать к написанию шпаргалок. Сможете ли вы воспользоваться ими – это уже совсем другой вопрос, но приготовить их обязательно нужно.
Важно не просто скачать с Интернета готовые шпоры, распечатать их и вырезать, а сделать их самостоятельно. Написание записок с подсказками подразумевает чтение, выбор материала и непроизвольное запоминание информации, с которой вы работаете. После этого во время экзамена вам проще будет ориентироваться в тех шпаргалках, которые вы сами составили. Если преподаватель настолько строго контролирует обстановку в аудитории, что списать становится нереально, — поможет память. Гораздо легче вспомнить то, что вы совсем недавно самостоятельно писали на шпаргалку.
Помните, что списывать – это рискованное занятие, и важно знать, сколько раз можно сдавать экзамен конкретно у этого преподавателя. Подумайте, позволят ли вам прийти на пересдачу, если обман будет раскрыт.
Используем современные достижения науки и техники
В советском фильме показывали, как для успешной сдачи экзаменов студенты использовали наушники и радиопередатчик. Современным ученикам в этом плане намного проще. Мобильные телефоны, смартфоны, планшеты, диктофоны намного компактней советской радиоаппаратуры, а связь с Интернетом даёт неограниченный доступ к любой информации. Многие выбирают такой способ, чтобы, ничего не зная по предмету, сдать экзамен. ЕГЭ, скорей всего, не получится осилить, используя гаджеты, ведь там очень строгие проверки наличия телефонов и прочих технических приспособлений, но они вполне могут спасти ситуацию на экзаменах в вузах.
Спасёт хорошая репутация
Как хорошо сдать экзамен, не прилагая особых усилий к изучению предмета, а пользуясь только харизмой и хорошим авторитетом? Задуматься о том, что вам предстоит сдавать экзамен, нужно заранее и с первого знакомства с преподавателем начинать создавать о себе хорошее впечатление.
Это может быть участие в самодеятельности, помощь в организации субботников, написание статей в студенческую газету. Также нужно создавать впечатление любознательного ученика. Почаще задавайте на лекциях вопросы и делитесь информацией, которую вы услышали из телепрограмм и прочитали в журналах, если она касается темы урока. Можно также интересоваться научными трудами преподавателя и его диссертациями.
Как вести себя на экзамене
Итак, наступает день сдачи. Как сдать экзамен, если ничего не знаешь? Важно следовать правилам поведения, которые помогут получить хорошие баллы за сомнительные знания:
- Ведите себя уверенно, не выдавайте отсутствие знаний своим внешним видом.
- Заходите в аудиторию в первой пятёрке. В таком случае, когда вы будете теряться в ответе, можно это будет аргументировать волнением.
- Говорите, не останавливаясь, используйте вводные слова и конструкции, если не знаете точного ответа, постарайтесь плавно перевести тему на знакомый вам вопрос.
- Проявляйте заинтересованность при ответе, приводите примеры из личного опыта, телепередач или фильмов.
- Боритесь до конца, даже если преподаватель хочет поставить неуд. Просите дополнительные вопросы, поплачьте, давите на жалость, списывайте всё на плохое самочувствие или волнение.
Крайние меры
Если, несмотря на все старания сдать экзамен, ничего не зная, вы понимаете, что единственная оценка, которая вам светит, – это неуд, нужно идти на крайние меры.
Можно предложить преподавателю решить вопрос полюбовно. Некоторые из них согласны повысить балл, если вы сможете быть ему чем-то полезным. Например, сделаете уборку в аудитории, или купите новый набор колб для опытов по химии. Иные преподаватели способны поменять гнев на милость, если вы заявитесь к ним с бутылочкой хорошего коньяка. В этом деле важно быть очень осторожным, и попытаться найти персональный подход к каждому. Помните, что в случае отказа преподавателя от такого варианта решения вопроса, сдать экзамен на свои знания вам будет сложнее. Возможно, вас ждут завышенные требования к качеству ответов и дополнительные каверзные вопросы.
Полезные советы для тех, кто хочет хорошо сдать экзамен
- Перед тем как зайти в аудиторию, съешьте кусочек шоколадки или несколько шоколадных конфет. Сладкое стимулирует работу мозга и помогает концентрации.
- За день до экзамена почитайте или посмотрите последние новости, которые могут касаться изучаемого предмета. Если сдаёте экономику – изучите экономические новости, политологию – ознакомьтесь с политической ситуацией. Показав, что вы ориентируетесь в современной обстановке относительно изучаемого материала, можно произвести самое положительное впечатление на преподавателя.
- Не переусердствуйте с энергетиками. Во время подготовки к экзамену студенты часто употребляют энергетические напитки. Помните, что, как бы усердно вы ни готовились, ночь накануне сдачи нужно провести в спокойствии, забыть о кофе и прочих энергетиках и просто выспаться.
Вы узнали, как сдать экзамен, если ничего не знаешь, и увидели, что, применяя определенную стратегию, получить высокий балл, обладая низкими знаниями, не составит особого труда. Но следует помнить, что отсутствие знаний за пределами учебных аудиторий может обернуться более серьёзной проблемой, чем «кол» на экзамене.
Для студентов МГТУ им. Н.Э.Баумана по предмету Начертательная геометрияПОДГОТОВКА К ЭКЗАМЕНУ ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИПОДГОТОВКА К ЭКЗАМЕНУ ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ
2022-08-092022-08-09СтудИзба
Ответы: ПОДГОТОВКА К ЭКЗАМЕНУ ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ
Описание
- ПОДГОТОВКА К ЭКЗАМЕНУ ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ:
- Краткое объяснение как решить задачи в билете.
Характеристики ответов (шпаргалок)
Качество
Идеальное компьютерное
Список файлов
- 1.jpg 885,35 Kb
- 2.jpg 837,47 Kb
- 3.jpg 928,61 Kb
- 4.jpg 881,1 Kb
Если работа Вам была полезна, Пожалуйста, потратьте несколько секунд, чтобы оставить нам 5 ЗВЁЗД и положительный отзывы. Мы Вам глубоко признателены!
Комментарии
Сопутствующие материалы
Свежие статьи
Популярно сейчас
Ответы на популярные вопросы
То есть уже всё готово?
Да! Наши авторы собирают и выкладывают те работы, которые сдаются в Вашем учебном заведении ежегодно и уже проверены преподавателями.
А я могу что-то выложить?
Да! У нас любой человек может выложить любую учебную работу и зарабатывать на её продажах! Но каждый учебный материал публикуется только после тщательной проверки администрацией.
А если в купленном файле ошибка?
Вернём деньги! А если быть более точными, то автору даётся немного времени на исправление, а если не исправит или выйдет время, то вернём деньги в полном объёме!
Отзывы студентов
Добавляйте материалы
и зарабатывайте!
Продажи идут автоматически
652
Средний доход
с одного платного файла
Обучение Подробнее









