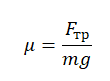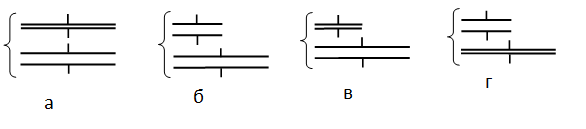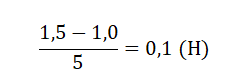Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Объём жидкости измерили при помощи мензурки (см. рис.). Погрешность измерения объёма при помощи данной мензурки равна её цене деления. Укажите объём воды (в мл) с учётом погрешности измерения. В ответе запишите значение и погрешность слитно без пробела.
Источник: Демонстрационная версия ЕГЭ—2015 по физике.
2
Чему равно напряжение на лампочке (см. рис.), если погрешность прямого измерения напряжения составляет половину цены деления вольтметра? В ответе запишите значение и погрешность слитно без пробела.
Источник: Демонстрационная версия ЕГЭ−2017 по физике
3
При помощи миллиамперметра измеряется ток в некоторой электрической цепи. Миллиамперметр изображён на рисунке. Чему равен ток в цепи, если погрешность прямого измерения тока составляет половину цены деления миллиамперметра? Ответ приведите в миллиамперах. В ответе запишите значение и погрешность слитно без пробела.
Источник: РЕШУ ЕГЭ
4
При помощи вольтметра измеряется напряжение в некоторой электрической цепи. Вольтметр изображён на рисунке. Чему равно напряжение в цепи, если погрешность прямого измерения напряжения составляет половину цены деления вольтметра? Ответ приведите в вольтах. В ответе запишите значение и погрешность слитно без пробела.
Источник: РЕШУ ЕГЭ
5
Длину бруска измеряют с помощью сантиметровой линейки. Запишите результат измерения, учитывая, что погрешность измерения равна половине цены деления. Ответ приведите в сантиметрах. В ответе запишите значение и погрешность слитно без пробела.
Источник: РЕШУ ЕГЭ
Пройти тестирование по этим заданиям
Механика — квантовая физика, методы научного познания
В. З. Шапиро
В задании 22 ЕГЭ по физике проверяется, как вы применяете знание физики в практической деятельности и повседневной жизни. В задании дается изображение какого-либо школьного физического прибора, по которому надо определить показания с учетом погрешности измерения.
Что необходимо знать и уметь?
- Вычислять цену деления измерительного прибора. Для этого надо найти два ближайших штриха, обозначенных числами, из большего вычесть меньшее и поделить на число делений.
- Определить границы измерения для приборов, имеющих две шкалы измерения, например, вольтметра, амперметра, барометра. Соответственно, надо выбрать необходимую шкалу для определения показаний прибора.
- Определить погрешность измерения в соответствии с ее описанием в условии. Погрешность измерения может быть равна цене деления или половине цены деления измерительного прибора. Расчет в соответствии с условием задачи.
- В некоторых задачах погрешности измерений могут быть приведены в условии для разных шкал. При выборе определенной шкалы измерений выбирается соответствующая ей погрешность.
- Запись ответа в бланк с учетом требований: каждая цифра и запятая в отдельной клеточке. Если погрешность указана до десятых (или сотых), то показания прибора точно также должны быть указаны до десятых (или сотых).
- Чему равна сила тока в лампочке (см. рисунок), если погрешность прямого измерения силы тока амперметром на пределе измерения 3 А равна 0,15 А, а на пределе измерения 0,6 А равна 0,03 А?
Ответ: ( ± ) А.
Согласно рисунку, амперметр подключен к зажимам 0 и 0,6 А. Поэтому определять показания необходимо по нижней шкале. Цена деления этой шкалы равна (0,4 — 0,2):5 = 0,02 (А). Показания амперметра равны 0,28 А. Для выбранной шкалы погрешность измерений указана в условии задачи. Она равна 0,03 А.
Ответ: (0,28 ± 0,03) А.
В бланк надо записать ответ в следующем виде:
| 0 | , | 2 | 8 | 0 | , | 0 | 3 |
Секрет решения. Задание является достаточно простым, но требует внимательного чтения условия. Если в задаче приводится в качестве измерительного прибора термометр со шкалой, проградуированной в градусах Цельсия, а ответ требуется дать по шкале Кельвина, то надо учесть, что погрешности по этим двум шкалам одинаковые. Добавление к погрешности +273 является грубой ошибкой.
+273 требуется только для перевода температуры из шкалы Цельсия в шкалу Кельвина.
2. Погрешность прямого измерения силы динамометром, на котором висит груз, равна цене деления. Каков вес груза?
Ответ: ( ± ) Н.
Цена деления динамометра определяется следующим расчетом:
(1,5 – 1) : 5 = 0,1 (Н).
Показания динамометра равны 1,1 Н.
Погрешность измерения, согласно условию задачи, равна цене деления, т.е. 0,1 Н.
Ответ: (1,1 ± 0,1) Н.
В бланк надо записать ответ в следующем виде:
| 1 | , | 1 | 0 | , | 1 |
Секрет решения. Задание достаточно простое, но требует внимательного проведения простых расчетов. Главное – правильная запись в бланк ответов №1 показаний динамометра с учетом погрешности измерений.
- Определите показания вольтметра (см. рисунок), если погрешность прямого измерения напряжения составляет половину цены деления вольтметра.
Ответ: ( ___________ ± ___________) В.
Цена деления вольтметра определяется следующим расчетом:
(2 – 1) : 5 = 0,2 (Н).
Показания вольтметра равны 2 В.
Погрешность измерения, согласно условию задачи, составляет половину цены деления, т.е. 0,1 В.
Ответ: (2,0 ± 0,1) В.
| 2 | , | 0 | 0 | , | 1 |
Секрет решения. В этой задаче надо обратить внимание на то, что погрешность измерений равна половине цены деления. При заполнении бланка ответов №1 показания вольтметра необходимо указать с учетом десятичной записи числа (2,0).
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Задание 22 ЕГЭ по физике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.03.2023
Чтобы успешно справиться с решением задания № 22, требуется ориентироваться в комплексе устройств, используемых для различных физических величин. На основании показаний прибора нужно уметь вычислить цену деления его шкалы. Кроме этого, следует понимать, что представляет собой понятие погрешности.
Задание EF18915
Необходимо собрать экспериментальную установку, с помощью которой можно определить коэффициент трения скольжения стали по дереву. Для этого школьник взял стальной брусок с крючком. Какие два предмета из приведённого ниже перечня оборудования необходимо дополнительно использовать для проведения этого эксперимента?
а) деревянная рейка
б) динамометр
в) мензурка
г) пластмассовая рейка
д) линейка
Алгоритм решения
1.Проанализировать задачу. Выяснить, какие предметы необходимы для проведения опыта.
2.Вывести формулу для коэффициента трения.
3.Определить, какую величину нужно измерить, чтобы рассчитать коэффициент трения, и какой прибор для этого нужен.
Решение
Для определения коэффициента трения стали по дереву, нужен не только стальной груз, но и деревянная поверхность. То есть, понадобится деревянная рейка.
Сила трения определяется формулой:
Отсюда коэффициент трения равен:
Ускорение свободного падения известно. Массу можно измерить на весах, но весов в вариантах ответа нет. Силу трения можно измерить динамометром. Следовательно, для опыта нужны только динамометр и деревянная рейка. Рейка из пластика не понадобится, так как цели расчета коэффициента трения стали по пластику нет. Мензурка используется для определения объема жидкости. В данном опыте она тоже не нужна.
Ответ: аб
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18477
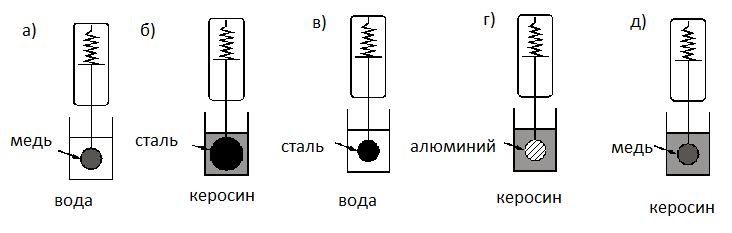
Ученик изучает силу Архимеда, действующую на тела, полностью погружённые в жидкость. В его распоряжении имеется установка, состоящая из ёмкости с водой и сплошного деревянного шарика объёмом 30 см3. Какая из следующих установок необходима ещё ученику для того, чтобы на опыте обнаружить зависимость силы Архимеда от объёма тела?
| № установки | Жидкость, налитая в ёмкость | Объём шарика | Материал, из которого сделан шарик |
| 1 | вода | 30 см3 | сталь |
| 2 | вода | 20 см3 | дерево |
| 3 | керосин | 20 см3 | дерево |
| 4 | подсолнечное масло | 30 см3 | сталь |
Ответ:
а) установка № 1
б) установка № 2
в) установка № 3
г) установка № 4
Алгоритм решения
- Сделать анализ задачи. Определить, какие величины в опыте остаются постоянными.
- Определить, какие величины должны быть в опыте переменными.
Решение
Ученик изучает силу Архимеда, действующую на тела, полностью погружённые в жидкость. В формулировке слово «жидкость» используется в единственном числе. Следовательно, жидкость во всех опытах будет одной и той же (плотность жидкости будет постоянной). У ученика уже есть установка, в которую входит емкость с водой. Поэтому во второй установке в качестве жидкости тоже должна использоваться вода. Варианты 3 и 4 исключаются.
В формулировки задачи также говорится о «телах». Они могут быть выполнены из разных материалов, и они могут иметь разный объем. Но известно, что архимедова сила зависит только от объема тела. Поэтому во второй установке нужно использовать тело другого объема. В вариантах 1 и 2 этому условию соответствует деревянный шарик объемом 20 куб. см (так как в первой установке используется шарик объемом 30 куб. см).
Отсюда верный ответ: б.
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF22696
Необходимо экспериментально изучить зависимость силы Архимеда, действующей на тело, погружённое в жидкость, от плотности жидкости.
Какие две установки следует использовать для проведения такого исследования?
Алгоритм решения
- Установить цели опыта.
- Сделать вывод о том, какие величины в опыте должны быть постоянными, а какие — переменными.
- Выбрать установки, соответствующие выводу.
Решение
В опыте нужно изучить зависимость силы Архимеда, действующей на тело, погружённое в жидкость, от плотности жидкости. Это значит, что плотность жидкости — величина переменная. Все остальные величины при этом должны оставаться постоянным. Поэтому нам нужны установки с разными жидкостями, но одинаковыми телами. Этому условию соответствуют две установки: «а» и «д».
Ответ: ад
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18695
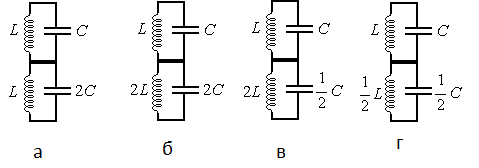
Ученик изучает свойства плоского конденсатора. Какую пару конденсаторов (см. рисунок) он должен выбрать, чтобы на опыте обнаружить зависимость ёмкости конденсатора от расстояния между его обкладками?
Алгоритм решения
- Установить, какие величины в данном эксперименте должны быть переменными, а какие — постоянными.
- Найти рисунок с парой конденсаторов, удовлетворяющий требованиям, выявленным в шаге 1.
Решение
Чтобы на опыте обнаружить зависимость ёмкости конденсатора от расстояния между его обкладками, нужно сохранить все величины постоянными, кроме самого расстояния. Поэтому площади обкладок должны быть одинаковыми, но расстояние между ними разными, как на рисунке 1.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18445
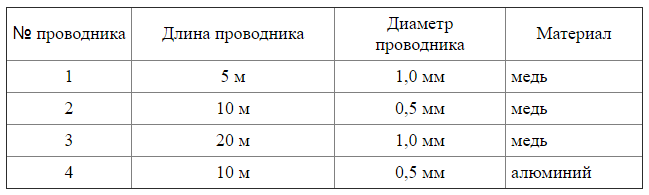
Для проведения лабораторной работы по обнаружению зависимости сопротивления проводника от его диаметра ученику выдали медный проводник длиной 10 м и диаметром 1,0 мм. Какой ещё проводник из предложенных ниже необходимо взять ученику, чтобы провести данное исследование?
Ответ:
а) проводник № 1
б) проводник № 2
в) проводник № 3
г) проводник № 4
Алгоритм решения
- Определить задачу лабораторных испытаний.
- Определить, какие величины в эксперименте должны оставаться постоянными, а какие переменными.
- Выбрать подходящий проводник.
Решение
Учение проводит лабораторную работу по обнаружению зависимости сопротивления проводника от его диаметра. Следовательно, материал проводника и его длина должны оставаться постоянными. Меняться должен только его диаметр. Поскольку в первом опыте берется медный длиной 10 м, диаметром 1,0 мм, то в следующем опыте он тоже должен быть медным, и длина его должна составлять 10 м, но диаметр должен быть другим. Этому условия удовлетворяет второй проводник.
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF22760
Необходимо сделать нитяной маятник и с его помощью экспериментально определить ускорение свободного падения. Для этого школьник уже взял штатив с муфтой и лапкой, линейку и нить. Какие два предмета из приведённого ниже перечня оборудования необходимо дополнительно использовать для проведения этого эксперимента?
Ответ:
а) секундомер
б) динамометр
в) мензурка
г) электронные весы
д) алюминиевый шарик
Алгоритм решения
1.Записать формулу, которая связывает ускорение свободного падения с периодом колебаний маятника.
2.Определить, что не хватает для проведения эксперимента и выбрать недостающие предметы из списка.
Решение
Ускорение свободного падения с периодом колебаний маятника связывает формула:
T=2π√lg
Следовательно, нужно значит не только длину нити маятника, но и период колебаний. Измерить его можно с помощью секундомера. А чтобы получить сам маятник, к нити нужно будет привязать массивный шарик. Например, алюминиевый.
Ответ: а, д
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18116
Ученик изучает зависимость периода электромагнитных колебаний в контуре от ёмкости конденсатора. Какие два контура он должен выбрать для этого исследования?
Алгоритм решения
- Выделить цель эксперимента.
- Установить, какие величины для достижения цели эксперимента должны меняться, а какие — оставаться постоянными.
- Выбрать верную пару контуров
Решение
Цель эксперимента — изучить зависимость периода электромагнитных колебаний в контуре от ёмкости конденсатора. Следовательно, емкости конденсатора должна быть единственной меняющейся величиной. При этом все другие величины должны оставаться постоянными. Поэтому катушки индуктивности должны быть одинаковыми, но конденсаторы — разные. Этому условию соответствует рисунок «а».
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17607

Алгоритм решения
- Установить, какие условия проведения эксперимента должны менять, а какие — оставаться постоянными, чтобы проверить данную гипотезу.
- Выбрать 2 картинки, удовлетворяющие этим условиям.
Решение
Если нужно проверить, зависит ширина пучка на экране за призмой от угла при вершине призмы, нужно поставить эксперименты с разными углами при вершине призмы. Угол падения на призму при этом должен быть одним и тем же. Этим условиям удовлетворяют призмы, изображенные на картинках А и В.
Ответ: АВ
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF22791

Ответ: ( ± ) Н.
Внимание! Записывать ответ следует последовательностью цифр без запятых.
Алгоритм решения
1.Записать исходные данные.
2.Определить цену деления шкалы.
3.Записать значение измерения с учетом погрешности.
Решение
Из условий задачи известно, что погрешность равна цене деления шкалы. Цена деления шкалы определяется отношением разности двух ближайших числовых обозначений на шкале и количеству делений между ними. Возьмем ближайшие значения 1,0 и 1,5. Между ними 5 делений. Следовательно, цена деления шкалы динамометра равна:
Так как погрешность равна цене деления, она также равна 0,1 Н.
Стрелка динамометра показывает 1,1 Н. Следовательно, вес груза равен: 1,1±0,1. Но по условию задачи ответ нужно записать без запятых и прочих знаков. Следовательно, верный ответ: 1101.
Ответ: 1101
pазбирался: Алиса Никитина | обсудить разбор | оценить
За это задание ты можешь получить 1 балл. Уровень сложности: базовый.
Средний процент выполнения: 42.8%
Ответом к заданию 22 по физике может быть последовательность цифр, чисел или слов. Порядок записи имеет значение.
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
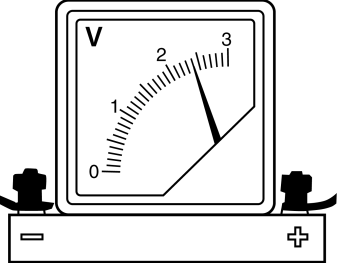
Что показывает вольтметр с учётом абсолютной погрешности? Принять абсолютную погрешность равной половине цены деления шкалы прибора.
В ответе запишите результат измерения с погрешностью без пробелов и других разделителей .
Решение
Цена деления$={3-2}/{10}={1}/{10}=0.1B; {ц.д.}/{2}={0.1}/{2}=0.05B$. Тогда имеем: $(2.40±0.05)B$. Согласно правилу записи ответа с погрешностью, результат измерения и погрешность должны иметь одинаковое количество знаков после запятой.
Ответ: 2.400.05
Задача 2
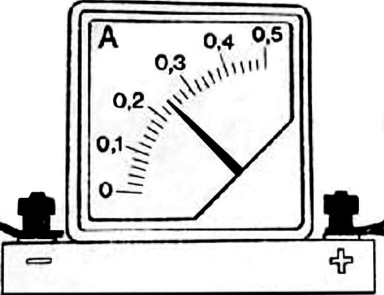
Что показывает амперметр с учётом абсолютной погрешности? Абсолютную погрешность принять равной половине цены деления прибора. Формат ответа: результат измерения и погрешность без пробелов и других разделительных знаков.
Решение
Цена деления$={0.3-0.2}/{5}={0.1}/{5}=0.02A; {ц.д.}/{2}={0.02}/{2}=0.01A$. Тогда имеем: $(0.24±0.01)A$
Ответ: 0.240.01
Задача 3

С помощью амперметра проводились измерения силы тока на участке электрической цепи. Чему равна сила тока с учётом погрешностей измерений, если погрешность прямого измерения составляет половину цены деления прибора, а его класс точности равен 0,5 (т.е. инструментальная погрешность составляет 0,5% от верхнего предела измерений данной шкалы амперметра)? Ответ: (_ ± _) А.
Решение
Определим погрешность прибора: если верхняя граница равна 10А, то инструментальная равна: $∆x_{пр}={10·0,5}/100=0,05$.
Погрешность измерения равна половина цены деления $∆x_{изм}=0,25$.
$∆x=∆x_{изм}+∆x_{пр}=0,05+0,25=0,3$.
$x=7.5±0.3$
Ответ: 7.50.3
Задача 4
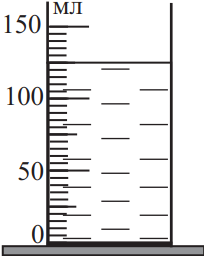
При определении массы воды, налитой в мензурку, ученик при помощи мензурки измерил объём воды. Запишите в ответ массу воды в граммах с учётом погрешности измерений (без пробелов). Погрешность измерения объёма равна половине цены деления мензурки. Ответ: (_ ± _) г.
Решение
Определим значение погрешности прямого измерения $∆V={V’}/{2}={5}/{2}=2.5г$. Тогда: $125±2.5г$. Количество знаков после запятой в измеренной величине должно совпадать с количеством знаков после запятой в значении погрешности. Поэтому $125.0±2.5г$
Ответ: 125.02.5
Задача 5
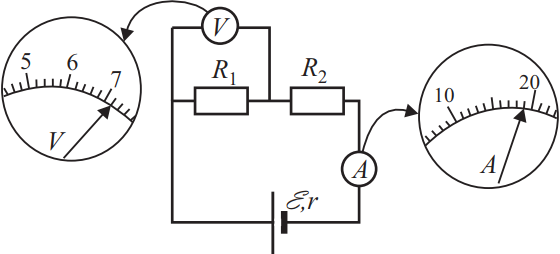
Ученик собрал электрическую цепь, состоящую из батарейки, двух резисторов, амперметра и вольтметра. После этого он провёл измерения напряжения на одном из резисторов и силы тока в цепи. Погрешности измерения силы тока в цепи и напряжения на источнике равны половине цены деления шкал приборов. Чему равно по результатам этих измерений значение напряжения на резисторе R1? Ответ: (_ ± _) В.
Решение
$U=U’+∆U; ∆U={0.2}/{2}=0.1$(половина угла деления). Запишем ответ $U’=7.2B$ как сумму, действующего измерения и погрешности: $7.2±0.1$.
Ответ: 7.20.1
Задача 6

Найдите длину проволоки, если погрешность прямого измерения составляет половину цены деления линейки, изображённой на рисунке. Ответ: (_ ± _) см.
Решение
Погрешность измерения равна половине цены деления ${0.5}/{2}-0.25$, тогда длина проволоки $23.00±0.25$см.
Ответ: 23.000.25
Задача 7
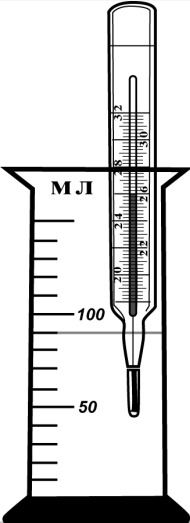
Запишите величину объёма с учётом погрешности, если погрешность равна половине цены деления. Ответ: (_ ± _) мл.
Решение
$∆V={V_1}/{2}={10}/{2}=5$мл (погрешность измерения половина цены деления). Запишем ответ исходя из рисунка $V=90$мл.
Ответ: 905
Задача 8
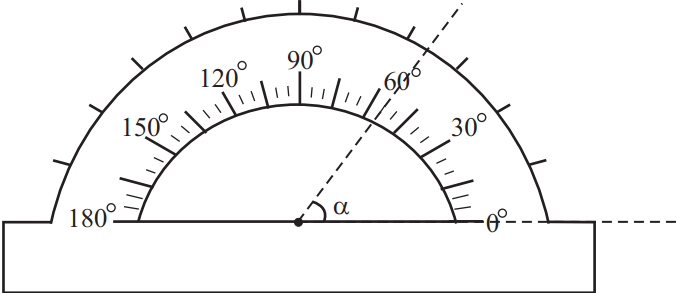
Запишите величину угла с учётом погрешности. С точностью до десятых. Ответ: (_ ± _)◦ .
Решение
Найдем погрешность, как половину цены деления ${5}/{2}=2.5°$. Тогда, исходя из графика получим: $55±2.5$.
Ответ: 55.02.5
Задача 9
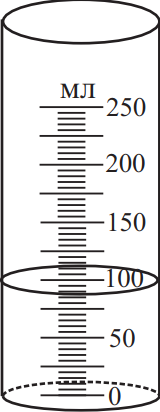
По рисунку определите объём жидкости с учётом погрешности измерения. Ответ: (_ ± _) мл.
Решение
По измерению проведенному измерим погрешность половины угла деления 2.5: $87.5±2.5$мл.
Ответ: 87.52.5
Задача 10
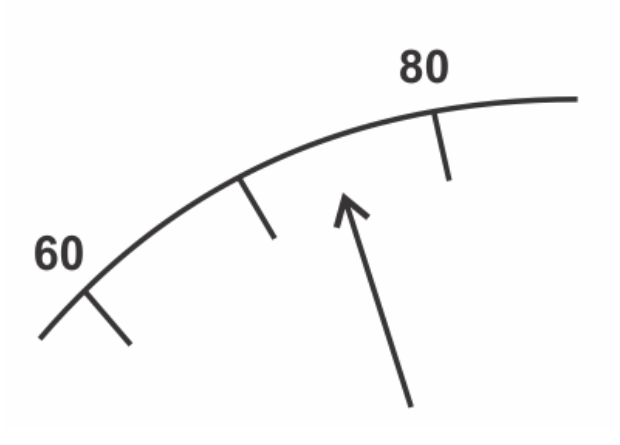
Запишите показания спидометра с учётом его погрешности, равной половине цены деления. Ответ: (_ ± _) км/ч. Значение величины и погрешность запишите слитно (без ±)
Решение
По рисунку видно, что стрелка ближе к 70, чем к 80 км/ч.
Погрешность измерения принимается за половину цены деления, а так как цена деления 10 км/ч, то показания спидометра (70 ± 5) км/ч.
Ответ: 705
Задача 11
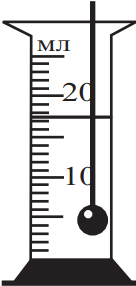
Запишите величину объёма, которая измеряется в данном эксперименте. Ответ: (_ ± _) мл.
Решение
Как известно, погрешность — это половина цены деления, где $V={V’}/{2}={1}/{2}=0.5$. Исходя из рисунка, определим объем и запишем ответ: $17.5±0.5$мл.
Ответ: 17.50.5
Задача 12
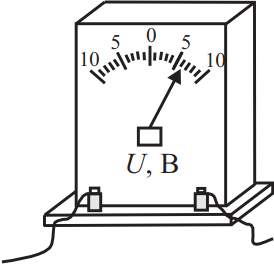
Запишите результат измерения электрического напряжения, учитывая, что погрешность равна половине цены деления. Укажите показание и погрешность. Ответ: (_ ± _) В.
Решение
Учитывая, что погрешность половины цены деления, определим ее: $∆U={1}/{2}=0.5B$. Запишем ответ, исходя из того, что прибор регестрирует $6В$: $6±0.5$.
Ответ: 6.00.5
Задача 13
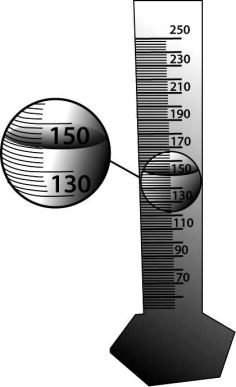
Для проведения опыта ученик налил воду в мензурку. Шкала мензурки проградуирована в миллилитрах (мл). Погрешность измерений объёма равна цене деления шкалы мензурки. Чему равен объём налитой учеником воды? Ответ: (__ ± __) мл.
Решение
Цена деления мензурки$={150-130}/{10}={20}/{10}=2мл$
Значит, объем налитой учеником воды равен: $V=(150±2)мл$
Ответ: 1502
Задача 14

На рисунке показана шкала универсального прибора, измеряющего величину атмосферного давления, температуру и влажность. Какова относительная погрешность показания шкалы барометра, проградуированной в гПа, если абсолютная погрешность равна цене деления шкалы. Ответ выразите в (%) и округлите до десятых.
Решение
Относительная погрешность $ε={∆p}/{p_{пр}}·100%$, где $∆p={ц.д.}={{(1000-950)}/{10}}={5}гПа$.
Показания прибора барометра равны: $p_{пр}=1050гПа$, тогда $ε={5·100%}/{1050}≈0.5%$
Ответ: 0.5
Задача 15

На фотографии представлена электрическая схема для определения сопротивления резистора. По показаниям приборов определите показания вольтметра с учётом погрешности, равной цене деления прибора. Ответ: (__ ± __) В.
Решение
Цена деления$={4-3}/{5}={1}/{5}=0.2B$
Тогда показания вольтметра равны: $(3.2±0.2)В$
Ответ: 3.20.2
Задача 16

Какую температуру показывает термометр, если погрешность прямого измерения равна половине цены деления прибора? Ответ: ( ± ) ◦ C, использовать точку, но не запятую как знак-разделитель, например 9.90.1 .
Решение
Цена деления$={40°С-30°С}/{10}={10°С}/{10}=1°С; {ц.д.}/{2}={1°С}/{2}=0.5°С$
Тогда показания термометра равны: $(26±0.5)°С$
Ответ: 26.00.5
Задача 17
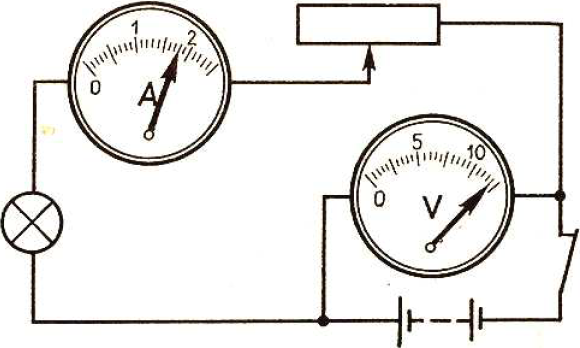
Каковы показания амперметра, если погрешность прямого измерения равна половине цены деления прибора? Ответ выразите в(___ ± ___) А.
Решение
Цена деления$={2A-1A}/{10}=0.1A; {ц.д.}/{2}={0.1A}/{2}=0.05A$
Тогда показания алтерметра равны: $(1.80±0.05)А$
Ответ: 1,800,05
Задача 18
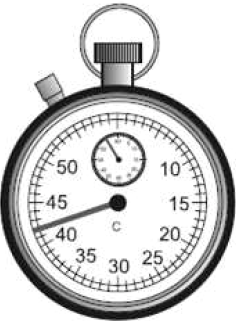
Каковы показания секундомера, если погрешность прямого измерения равна половине цены деления прибора? Ответ выразите в (___ ± ___) с.
Решение
Цена деления$={50-45}/{5}=1; {ц.д.}/{2}={1}/{2}=0.5c$
Тогда показания прибора: $t=(42±0.5)c$
Ответ: 42.00.5
Задача 19
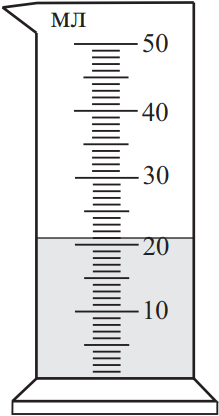
Каков объём воды в измерительном цилиндре, если погрешность прямого измерения равна половине цены деления прибора? Ответ выразите в (___ ± ____) мл.
Решение
Находим погрешность как половину цены деления и получаем 0.5. Соответственно записываем показание прибора с одной цифрой после запятой, чтобы это совпадало с записью погрешности.
Ответ: 21.00.5
Рекомендуемые курсы подготовки
В задании 22 ЕГЭ по физике (2017) нужно уметь определять погрешности вычислений различных величин. Теория вычисления различных погрешностей — сложная самостоятельная наука, которую преподают обычно в вузах. Для школы и для успешной сдачи экзамена нам потребуются базовые знания, которые я и собрала в этой статье.
В практической деятельности человеку приходится измерять различные величины, производить различные вычисления. Результатами измерений, подсчетов и вычислений являются числа. Однако точные измерения невозможны ввиду несовершенства наших органов зрения, неточности измерительных приборов и некоторых свойств самих измеряемых объектов.
При различных измерениях одной и той же величины получают различные приближенные значения. Каждое из этих приближений отличается от истинного значения на некоторую величину, называемую погрешностью.
Абсолютной погрешностью называется модуль разности истинного и приближенного значения некоторой величины, обозначается она буквой и измеряется в тех же единицах, что и вычисляемая величина:
Где — истинное значение,
— приближенное.
Из этого определения следует, что истинное значение величины равно приближенному значению плюс-минус абсолютная погрешность :
Абсолютная погрешность приближения не характеризует качества измерений, т.к., например, точность 1 см для определения ширины стадиона является высокой, а для определения длины листа бумаги — низкой. Поэтому для характеристики точности измерения вводится понятие относительной погрешности.
Относительной погрешностью приближения называется отношение абсолютной погрешности приближения к модулю числа приближенного значения. Обозначается относительная погрешность буквой (эпсилон) и выражается в процентах:
Далее я приведу таблицу правил определения погрешностей сумм, разностей, произведений и т.п.
Погрешности
Ну и теперь порешаем задачи, чтобы окончательно разобраться.
Задача 1.
Чтобы оценить, каков будет период малых колебаний математического маятника, используем для вычислений на калькуляторе формулу . По оценке «на глазок» длина нити равна
м. Калькулятор показывает на экране число 2,4322335. Чему равен, с учётом погрешности оценки длины нити, период колебаний маятника? (Ответ дайте в секундах, значение и погрешность запишите через точку с запятой без пробелов.)
Относительная погрешность определения периода равна
С другой стороны, по таблице находим, что
Тогда
Тогда
Так как по правилам вычисления погрешностей мы должны оставить одну значащую цифру, то получим c, так как погрешность определена с точностью до сотых, то период тоже округляем до сотых:
. Имеем:
Ответ: 2,43;0,08
Задача 2.
При определении массы масла плотностью 0,9 г/см ученик измерил объём масла с использованием мерного цилиндра:
см
. Запишите в ответ массу масла в граммах с учётом погрешности измерений через точку с запятой без пробелов.
Определяем массу масла:
Определим погрешность вычисления:
Оставляя одну значащую цифру, имеем: г — тогда с такой же точностью и саму величину запишем:
Ответ: 16,2;0,5
Теория по физике на тему «Погрешность»
- 14.12.2016
Теория по физике на тему «Погрешность»
- определение понятия «погрешность»
- правило определения погрешности
- правила округления
- погрешность при измерении большого количества элементов
- погрешность измерительных приборов
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.
Сохранить ссылку:
Комментарии (0)
Добавить комментарий
Добавить комментарий
Комментарии без регистрации. Несодержательные сообщения удаляются.
Имя (обязательное)
E-Mail
Подписаться на уведомления о новых комментариях
Отправить
Содержание:
При измерении разных физических величин мы получаем их числовые значения с определенной точностью. Например, при определении размеров листа бумаги (длины, ширины) мы можем указать их с точностью до миллиметра; размеры стола – с точностью до сантиметра, размеры дома, стадиона – с точностью до метра.
Нет необходимости указывать размеры стола с точностью до миллиметра, а размеры стадиона с точностью до сантиметра или миллиметра. Мы сами в каждой ситуации, опыте и эксперименте определяем, с какой точностью нам нужны данные физические величины. Однако очень важно оценивать, насколько точно мы определяем физическую величину, какую ошибку (погрешность) в ее измерении допускаем.
При измерении мы не можем определить истинное значение измеряемой величины, а только пределы, в которых она находится.
Пример:
Измерим ширину стола рулеткой с сантиметровыми и миллиметровыми делениями на ней (рис. 5.1). Значение наименьшего деления шкалы называют ценой деления и обозначают буквой С. Видно, что цена деления рулетки С = 1 мм (или 0,1 см).
Совместим нулевое деление рулетки с краем стола и посмотрим, с каким значением
шкалы линейки совпадает второй край стола (рис. 5.1). Видно, что ширина стола составляет чуть больше 70 см и 6 мм, или 706 мм. Но результат наших измерений мы запишем с точностью до 1 мм, то есть L = 706 мм.
Абсолютная погрешность измерения ∆ (ДЕЛЬТА)
Из рис. 5.1 видно, что мы допускаем определенную погрешность и определить ее «на глаз» достаточно трудно. Эта погрешность составляет не более половины цены деления шкалы рулетки. Эту погрешность называют погрешностью измерения и помечают ∆L («дельта эль»). В данном эксперименте ее можно записать
Сам результат измерения принято записывать таким образом: ширина стола L = (706,0 ± 0,5) мм, читают: 706 плюс-минус 0,5 мм. Эти 0,5 мм в нашем примере называют абсолютной погрешностью. Значения измеряемой величины (706,0 мм) и абсолютной погрешности (0,5 мм) должны иметь одинаковое количество цифр после запятой, то есть нельзя записывать 706 мм ± 0,5 мм.
Такая запись результата измерения означает, что истинное значение измеряемой величины находится между 705,5 мм и 706,5 мм, то есть 705,5 мм ≤ L ≤ 706,5 мм.
Относительная погрешность измерения ε (ЭПСИЛОН)
Иногда важно знать, какую часть составляет наша погрешность от значения
измеряемой величины. Для этого разделим 0,5 мм на 706 мм. В результате получим: 

Относительная погрешность измерения свидетельствует о качестве измерения. Если длина какогото предмета равна 5 мм, а точность измерения – плюс-минус 0,5 мм, то относительная погрешность будет составлять уже 10%.
Стандартная запись результата измерений и выводы
Таким образом, абсолютная погрешность в примере 5.1. составляет ∆L = 0,5 мм, а результат измерений следует записать в стандартном виде: L = (706,0 
На точность измерения влияет много факторов, в частности:
- При совмещении края стола с делением шкалы рулетки мы неминуемо допускаем погрешность, поскольку делаем это «на глаз» — смотреть можно под разными углами.
- Не вполне ровно установили рулетку.
- Наша рулетка является копией эталона и может несколько отличаться от оригинала.
Все это необходимо учитывать при проведении измерений.
Итоги:
- Измерения в физике всегда неточны, и надо знать пределы погрешности измерений, чтобы понимать, насколько можно доверять результатам.
- Абсолютную погрешность измерения можно определить как половину цены деления шкалы измерительного прибора.
- Относительная погрешность есть частное от деления абсолютной погрешности на значение измеряемой величины:
и указывает на качество измерения. Ее можно выразить в процентах.
Измерительные приборы
Устройства, с помощью которых измеряют физические величины, называют измерительными приборами.
Простейший и хорошо известный вам измерительный прибор — линейка с делениями. На ее примере вы видите, что у измерительного прибора есть шкала, на которой нанесены деления, причем возле некоторых делений написано соответствующее значение физической величины. Так, значения длины в сантиметрах нанесены на линейке возле каждого десятого деления (рис. 3.11). Значения же, соответствующие «промежуточным» делениям шкалы, можно найти с помощью простого подсчета.
Разность значений физической величины, которые соответствуютближайшим делениям шкалы, называют ценой деления прибора. Ёе находят так: берут ближайшие деления, возле которых написаны значения величины, и делят разность этих значений на количество промежутков между делениями, расположенными между ними.
Например, ближайшие сантиметровые деления на линейке разделены на десять промежутков. Значит, цена деления линейки равна 0,1 см = 1 мм.
Как определяют единицы длины и времени
В старину мерами длины служили большей частью размеры человеческого тела и его частей. Дело в том, что собственное тело очень удобно как «измерительный прибор», так как оно всегда «рядом». И вдобавок «человек есть мера всех вещей»: мы считаем предмет большим или малым, сравнивая его с собой.
Так, длину куска ткани измеряли «локтями», а мелкие предметы — «дюймами» (это слово происходит от голландского слова, которое означает «большой палец»).
Однако человеческое тело в качестве измерительного прибора имеет существенный недостаток: размеры тела и его частей у разных людей заметно отличаются. Поэтому ученые решили определить единицу длины однозначно и точно. Международным соглашением было принято, что один метр равен пути, который проходит свет в вакууме за 1/299792458 с. А секунду определяют с помощью атомных часов, которые сегодня являются самыми точными.
Можно ли расстояние измерять годами
Именно так и измеряют очень большие расстояния — например, расстояния между звездами! Но при этом речь идет не о годах как промежутках времени, а о «световых годах». А один световой год — это расстояние, которое проходит свет за один земной год. По нашим земным меркам это очень большое расстояние — чтобы убедиться в этом, попробуйте выразить его в километрах! А теперь вообразите себе, что расстояние от Солнца до ближайшей к нему звезды составляет больше четырех световых лет! И по астрономическим масштабам это совсем небольшое расстояние: ведь с помощью современных телескопов астрономы тщательно изучают звезды, расстояние до которых составляет много тысяч световых лет!
Что надо знать об измерительных приборах
Приступая к измерениям, необходимо, прежде всего, подобрать приборы. Что надо знать об измерительных приборах?
Минимальное (нижний предел) и максимальное (верхний предел) значения шкалы прибора — это пределы измерения. Чаще всего предел измерения один, но может быть и два. Например, линейка имеет один предел — верхний. У линейки на рисунке 32 он равен 25 см. У термометра на рисунке 33 два предела: верхний предел измерения температуры равен +50 °С; нижний -40 °С.
На рисунке 34 изображены три линейки с одинаковыми верхними пределами (25 см). По эти линейки измеряют длину с различной точностью. Наиболее точные результаты измерений дает линейка 7, наименее точные — линейка 3. Что же такое точность измерений и от чего она зависит? Для ответа на эти вопросы рассмотрим сначала понятие цена деления шкалы прибора.
Цена деления — это значение наименьшего деления шкалы прибора.
Как определить цену деления шкалы? Для этого необходимо:
- выбрать на шкале линейки два соседних значения, например 3 см и 4 см;
- подсчитать число делений (не штрихов!) между этими значениями; например, на линейке 1 (см. рис. 34) число делений между значениями 3 см и 4 см равно 10;
- вычесть из большего значения меньшее (4 см — 3 см = 1 см) и результат разделить на число делений.
Полученное значение и будет ценой деления шкалы прибора. Обозначим ее буквой С.
Точно так же можно определить и цену деления шкалы мензурок 1 и 2 (рис. 35). Цена деления шкалы мензурки 1:
Цена деления шкалы мензурки 2:
А какими линейкой и мензуркой можно измерить точнее?
Измерим один и тот же объем мензуркой 1 и мензуркой 2. Но показаниям шкал в мензурке 1 объем воды V = 35 мл; в мензурке 2 — V = 37 мл.
Понятно, что точнее измерен объем воды мензуркой 2, цена деления которой меньше 


Итак, любым прибором, имеющим шкалу, измерить физическую величину можно с точностью, не превышающей цены деления шкалы.
Линейкой 1 (см. рис. 34) можно измерить длину с точностью до 1 мм. Точность измерения длины линейками 2 и 3 определите самостоятельно.
Главные выводы:
- Верхний и нижний пределы измерения — это максимальное и минимальное значения шкалы прибора.
- Цена деления шкалы равна значению наименьшего деления шкалы.
- Чем меньше цена деления шкалы, тем точнее будут проведены измерения данным прибором.
Для любознательных:
В истории науки есть немало случаев, когда повышение точности измерений давало толчок к новым открытиям. Более точные измерения плотности азота, выделенного из воздуха, позволили в 1894 г. открыть новый инертный газ — аргон. Повышение точности измерений плотности воды привело к открытию в 1932 г. одной из разновидностей тяжелых атомов водорода — дейтерия. Позже дейтерий вошел в состав ядерного горючего. Оценить расстояния до звезд и создать их точные каталоги ученые смогли благодаря повышению точности при измерении положения ярких звезд на небе.
- Заказать решение задач по физике
Пример решения задачи
Для измерения величины угла используют транспортир. Определите: 1) цену деления каждой шкалы транспортира, изображенного на рисунке 38; 2) значение угла BАС, используя каждую шкалу; укажите точность измерения угла ВАС в каждом случае.
Решение:
1) Цена деления нижней шкалы:
Цена деления средней шкалы:
Цена деления верхней шкалы:
2) Определенный но нижней шкале с точностью до 10° 

- Определение площади и объема
- Связь физики с другими науками
- Макромир, мегамир и микромир в физике
- Пространство и время
- Как зарождалась физика
- Единая физическая картина мира
- Физика и научно-технический прогресс
- Физические величины и их единицы измерения