Топ сложных заданий ЕГЭ по математике, в которых ошибается каждый третий
Математика — царица наук, а ты в её королевстве даже не холоп, а пятое дерево в седьмом ряду? У тебя ещё есть возможность это исправить, ведь мы собрали для тебя самые сложные задания в ЕГЭ по математике, чтобы знал, на что обратить внимание и не допускал в них ошибок.
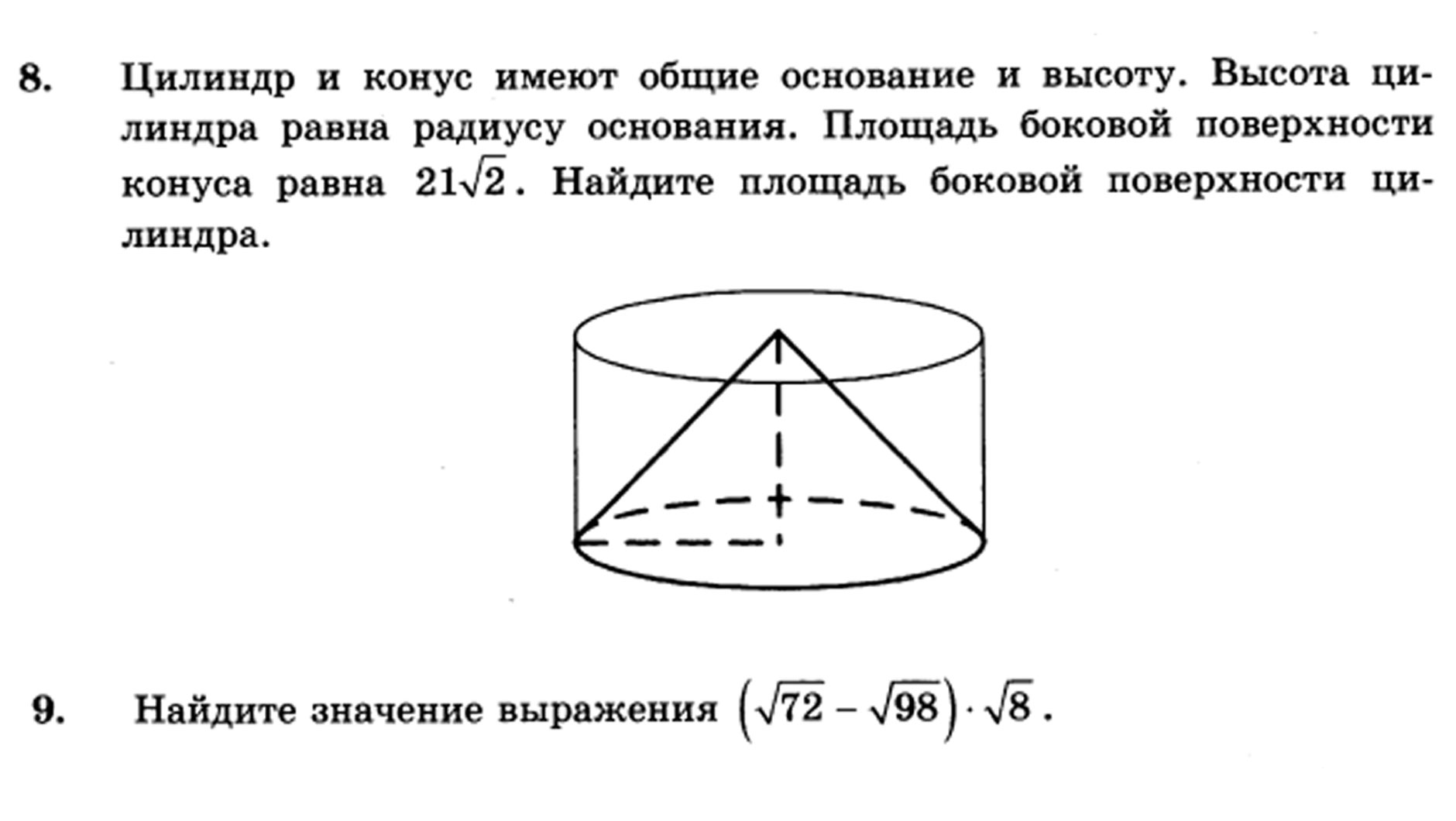
Задание 8
Для того, чтобы решить это задание, тебе нужно научиться представлять объёмную фигуру в пространстве, а также уметь соотносить размеры одной фигуры с другой. Для более чёткого понимания этой темы можешь склеить модели фигур из бумаги и использовать их при подготовке.
Задание 9
Чтобы получить максимальный балл за это задание, тебе нужно уделить особое внимание преобразованию тригонометрических выражений и их вычислению. В учебнике этому посвящён целый раздел, не поленись его изучить, если рассчитываешь на хороший результат.
Задание 14
В любой геометрической задаче важно знать свойства фигуры, которая в ней дана. Именно из-за недостаточных теоретических знаний выпускники путаются в последовательности решения, неправильно строят чертёж и пытаются самостоятельно вывести формулу вместо того, чтобы использовать уже существующую и не тратить время на долгие логические рассуждения.
Демоварианты ЕГЭ 2021: как сделать подготовку с их помощью эффективнее
Задание 16
Больше всего сложностей в этом задании возникает на этапе построения чертежа, поэтому важно быть внимательным. Неправильный рисунок разрушит твои шансы на успех ещё до того, как приступишь к расчётам. Баллы теряют также из-за неправильного построения доказательств, поэтому внимательно изучи теоремы, которые даются в учебнике, чтобы понять логику и не ошибиться.
Задание 17
Это пункт лучше всего показывает, как математика может помочь тебе в обычной жизни. Чаще всего ошибки в нём допускаются при вычислении и составлении модели задачи — выпускники не видят взаимосвязи между величинами и из-за этого путаются в них. И не забывай писать пояснения к своим действиям, так ты не запутаешься и не потеряешь драгоценные баллы.
Задание 19
Многие абитуриенты надеются на удачу и в этом задании пишут ответ да или нет наугад. Но даже в случае угадывания, этого недостаточно. Комиссии необходимо видеть аргументированное решение с пояснениями. Поэтому обрати внимание на раздел, который посвящён вероятности.
Решай как можно больше заданий из демовариантов и не забывай, что в борьбе за высокий балл на ЕГЭ у тебя всегда есть помощники. Заглядывай на наш канал, там много полезной информации для подготовки. Спасибо, что дочитал до конца. Мы рады, что были полезны. Чтобы получить больше информации, посмотри ещё:
Курсы подготовки к ЦТ 2021 в образовательном центре Адукар
Курсы подготовки к ЕГЭ 2021 в образовательном центре Адукар
Каталог учебных заведений Адукар
Не пропускай важные новости и подписывайся на наш YouTube, ВК, Instagram, Telegram, Facebook и уведомления на adukar.by.
***
Если хотите разместить этот текст на своём сайте или в социальной сети, свяжись с нами по адресу info@adukar.by. Перепечатка материалов возможна только с письменного согласия редакции.
Хочешь быть в курсе новостей ЦТ?
Подписывайся на Адукар в соцсетях!
Начни подготовку к ЦТ и ЦЭ прямо сейчас!

Адукар обещает крутых преподавателей и много полезной практики.
итоговые занятия перед ЦТ? Такие занятия мы проводим уже четвёртый год, и преподаватели нашего учебного центра
научились достаточно точно предсказывать, какие вопросы будут на ЦТ. На этом занятии мы прорешаем их вместе с тобой!
Регистрируйся,
если еще не сделал этого — и увеличь свои шансы на поступление!
Выпускные экзамены по математике относятся к категории сложных. Поэтому требуют хороших знаний и предварительной подготовки, желательно с репетитором. Что нужно знать о самых сложных заданиях в математике по ЕГЭ 2023 г., есть ли изменения к КИМ, рекомендованные ФИПИ по предмету, и на какие нюансы стоит обратить детальное внимание, предлагаем узнать из нашей статьи.
Нововведения 2023 г.
ЕГЭ по математике имеет свои особенности, и будет оцениваться по пятибалльной (для базовой части) и четырехбальной (профильной) системе. Особенность сдачи предмета состоит в том, что учащийся должен заранее определиться, какой именно он будет сдавать экзамен – базовый или профильный.
Базовый после 11 класса сдается всеми выпускниками, относится к части №1 в ЕГЭ, и не подходит для поступления в ВУЗы и колледжи на такие специальности, как: инженерия, экономика, ИТ-сфера, физика, экономика, техника и т.д. Для его успешной сдачи достаточно школьной программы и основной теории.
Профильный экзамен, напротив, считается более углубленным, нужен для ВУЗа, требует основательной подготовки и хороших знаний. Важным нововведением части №1 (базовой) ЕГЭ по математике в 2023 г., для профильного экзамена, является требование к оцифровке ответов техническими средствами. Часть №2 будут проверять эксперты.
Для упрощенного базового ЕГЭ по математике в 2023 г. предложено 21 задание, каждое из них будет оцениваться по 1 ПБ (первичному баллу). Для получения положительного ответа школьнику достаточно выполнить всего 7 заданий. Наглядно оценивание выглядит таким образом:
Тематические разделы
|
Тематические разделы |
Количество заданий по ЕГЭ |
Процент общего оценивания |
|
Алгебра |
10 |
47% |
|
Геометрия |
5 |
24% |
|
Неравенства, уравнения, системы |
3 |
14% |
|
Начала математического анализа |
1 |
5% |
|
Функции |
1 |
5% |
|
Теория вероятности, статистика |
1 |
5% |
Из таблицы видно, что большинство баллов могут быть получены при решении стандартных заданий по базовой основе курса алгебры + геометрии + неравенств, уравнений и систем. Поэтому при подготовке к экзамену на них стоит обратить самое пристальное внимание.
Выставление баллов за задания по профильному экзамену осуществляется в 4 балла:
- 1 ПБ – № 1-11.
- 2 ПБ – № 12, 14, 15.
- 3 ПБ – № 13, 16.
- 4 ПБ – № 17, 18.
Полученные первичные баллы переводятся в 100-бальную систему:
Перевод баллов по ЕГЭ (математика) в 2023 г.
|
Перевод баллов по ЕГЭ (математика) в 2023 г. |
|
|
Первичный балл |
Тестовый балл |
|
1 |
5 |
|
2 |
9 |
|
3 |
14 |
|
4 |
18 |
|
5 |
23 |
|
6 |
27 |
|
7 |
33 |
|
8 |
39 |
|
9 |
45 |
|
10 |
50 |
|
11 |
56 |
|
12 |
62 |
|
13 |
68 |
|
14 |
70 |
|
15 |
72 |
|
16 |
74 |
|
17 |
76 |
|
18 |
78 |
|
19 |
80 |
|
20 |
82 |
|
21 |
84 |
|
22 |
86 |
|
23 |
88 |
|
24 |
90 |
|
25 |
92 |
|
26 |
94 |
|
27 |
96 |
|
28 |
98 |
|
29 |
99 |
|
30 |
100 |
|
31 |
100 |
В новом ЕГЭ 2023 г. все задания, кроме № 11, поменяли нумерацию. Задания с векторами и комплексными числами в экзамен включены не были.
Разбор демоверсии
По сложным заданиям, встречающимся в профильном ЕГЭ, желательно поработать заранее. Они требуют детального расписывания решения, которое должно соответствовать критериям оценивания.
Первые вопросы по математике – стандартные, по геометрии и стереометрии.
- 3, 4 – теория вероятности, в четвертом предлагается вариант с %.
- 5, 6 –уравнения и выражения, тригонометрия и степени.
- 7 – задание по графикам и производным.
- 8 – задача по формуле величин с подстановкой.
- 9 – вторая задача по теме динамики движений по прямой, окружности или молекул в составах.
- 10 – построение графика.
- 11 – вычисление графических производных, точек максимума/минимума
- 12 – требуется решение тригонометрического уравнения.
- 13 – задание по стереометрии с треугольной призмой.
- 14 – неравенства с логарифмами.
- 15 – экономическая задача про клиента банка, которому нужен расчет % и сумм выплат за взятый займ.
- 16 – задача по планиметрии про две окружности.
- 17 – требуется решение задания на параметры.
- 18 – сложная задача на целые числа.
Демоверсия доступна на официальном сайте ФИПИ. Можно посмотреть, как задания примерно будут выглядеть в бумажном файле. Если у учащегося возникают трудности с предметом, подготовиться к ЕГЭ по математике он может с репетитором.
Подводя итоги
Чтобы лучше разбираться в деталях экзамена, желательно скачать демоверсию КИМ, спецификации и кодификатор с сайта ФИПИ. При подготовке необходимо повторить функции тригонометрии, уметь решать обычные и квадратные уравнения, а также задания на поиск %.
ЕГЭ по математике 2023 г. состоит из 2-х частей:
- 1 часть – 35%, 11 ПБ по 11 заданиям с кратким ответом.
- 2 часть – 65%, 20 ПБ по 7 заданиям развернутого характера.
Для получения более 80 ТБ за профильный экзамен, необходимо решить 1 часть без ошибок, и обязательно выполнить задания № 12, 14, 15, 18 (а, б). Получить 100 ТБ помогут задачи по стереометрии и планиметрии. Длится профильный ЕГЭ по математике в 2023 г. 235 минут.
Каким был ЕГЭ-2020 по математике?
Когда я увидела московский вариант ЕГЭ – он мне сразу понравился.
Вот разбор этого варианта на Ютьюбе:
Я сказала ученикам, что вариант простой. И что я решила его за максимально короткое время.
Смотрите сами. В этом варианте:
Стандартная задача № 13 (Тригонометрия).
Простые задачи № 14 (Стереометрия) и 15 (Неравенство).
Задача по планиметрии (№16) вызывает ощущение, что мы ее где-то видели. Стандартная, решается быстро.
«Экономическая» задача (№17) – обыкновенная.
Задача с параметром (№18) – новая. Уровень сложности – обычный.
И наконец, задача 19 на числа и их свойства – просто подарок. Легко, приятно, один за другим решаются все пункты – (а), (б) и (в).
Но оказалось, что я рано обрадовалась. И легким был только московский вариант.
Очень странно, что в разных городах на ЕГЭ дали разные по сложности варианты. Например, в краснодарском варианте более сложная, чем в московском, задача с параметром (№18). В варианте, который дали в Санкт-Петербурге, задача 16 более замысловатая, чем в московском. Что касается задачи 19 из питерского варианта – первые два пункта решаются легко, а пункт (в) невозможно решить обычными школьными методами. Скорее всего, составители варианта некорректно сформулировали условие.
Это не всё. Дмитрий Гущин, автор сайта РешуЕГЭ, отметил, что задание 15 (неравенство) оказалось одинаковым во всех регионах нашей большой страны. Неужели составители забыли, что в России одиннадцать часовых поясов? Когда выпускники в Магадане уже написали ЕГЭ, московские школьники еще не проснулись. А проснувшись, заглянули в соцсети и увидели, какие задачи были в других городах.
Так не должно быть. Не должно быть одинаковых заданий в разных регионах. Не должно быть вариантов, значительно отличающихся по уровню сложности. И тем не менее, они были!
Борис Трушин даже записал на эту тему видео: «ЕГЭ сломался, несите новый!» Но может быть, все-таки этот починить?
Давайте разберемся, что же там было, на ЕГЭ-2020. Какие сложные и необычные задачи достались выпускникам.
Санкт-Петербург, №14
В правильной четырёхугольной пирамиде SABCD сторона основания AB = 4, а боковое ребро SA = 7. На рёбрах AB и SB отмечены точки M и K соответственно, причём AM = SK = 1.
а) Докажите, что плоскость CKM перпендикулярна плоскости ABC.
б) Найдите объём пирамиды BCKM.
Посмотреть решение
Санкт-Петербург, №16
На сторонах AB, BC и AC треугольника ABC отмечены точки C1, A1 и B1 соответственно, причём AC1 : C1B = 8 : 3, BA1 : A1C = 1 : 2, CB1 : B1A = 3 : 1. Отрезки BB1 и CC1 пересекаются в точке D.
а) Докажите, что ADA1B1 — параллелограмм.
б) Найдите CD, если отрезки AD и BC перпендикулярны, AC = 28, BC = 18.
Посмотреть решение
Разберем несколько задач из варианта, который получили выпускники Краснодара. Задачи 16 и 17 – стандартные, задача 18 – сложная, задача 19 – обычный уровень сложности.
Краснодар, №16
Дан прямоугольный треугольник ABC. На катете AC отмечена точка M, а на продолжении катета BC за точку C — точка N так, что CM = CB и CA = CN.
а) Пусть CH и CF — высоты треугольников ABC и NMC соответственно. Докажите, что CF и CH перпендикулярны.
б) Пусть L — это точка пересечения BM и AN, BC = 2, AC = 5. Найдите ML.
Посмотреть решение
Краснодар, №17
В кредит взяли 220 тыс. рублей на 5 лет под r% годовых. По условиям кредита, на конец первых трех лет задолженность остается неизменной и равной 220 тысячам рублей, а выплаты последних двух лет равны. На конец пятого года кредит должен быть погашен. Найдите r если известно, что сумма всех выплат составит 420 тысяч рублей.
Посмотреть решение
Краснодар, №18
При каких значениях a система
имеет ровно два решения?
Посмотреть решение
Краснодар, №19
На доске написано несколько различных натуральных чисел, которые делятся на 3 и оканчиваются на 4.
а) Может ли сумма составлять 282?
б) Может ли их сумма составлять 390?
в) Какое наибольшее количество чисел могло быть на доске, если их сумма равна 2226?
Посмотреть решение
И наконец, та самая задача.
Санкт-Петербург, №19
На доске написано несколько различных натуральных чисел. Эти числа разбили на три группы, в каждой из которых оказалось хотя бы одно число. К каждому числу из первой группы приписали справа цифру 6, к каждому числу из второй группы приписали справа цифру 9, а числа третьей группы оставили без изменений.
а) Могла ли сумма всех этих чисел увеличиться в 9 раз?
б) Могла ли сумма всех этих чисел увеличиться в 19 раз?
в) В какое наибольшее число раз могла увеличиться сумма всех этих чисел?
Посмотреть решение
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «ЕГЭ-2020 по математике. Сложные задачи, неравноценные варианты и одно неравенство для всей страны» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
09.03.2023
2 апреля 2018
В закладки
Обсудить
Жалоба
Самые сложные задания из первой части. Математика
Обзор наиболее сложных задач первой части профильного ЕГЭ по математике.
Задачи для закрепления: zadanie-k-pervoy-chasti.docx.pdf
Ещё одна подборка трудных заданий: 4ege.ru/video-matematika/54886-top-10-samyh-slozhnyh-zadaniy-chasti-1-ege-po-matematike.html
Таймкоды:
0:19 В книге елены молоховец для пирога на 10 человек 1/10…
1:05 На рисунке показано изменение биржевой стоимости акций…
2:39 Найдите площадь четырехугольника…
3:52 При артиллерийской стрельбе автоматическая система делает выстрел по цели…
6:02 Решите уравнения. В ответе напишите наименьший положительный корень.
8:22 В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна…
9:37 Прямая является касательной к графику функции найдите b…
10:35 В сосуде имеющем форму конуса уровень жидкости достигает…
13:25 Найдите значения выражения…
16:04 Установка для демонстрации адиабатического сжатия представляет собой сосуд с поршнем, резко сжимающим газ…
17:37 Из пункта а круговой трассы выехал велосипедист…
19:56 Найдите точку максимума функций…
Математика — обязательный для сдачи на ЕГЭ предмет, без которого не получишь аттестат. Это также один из самых сложных экзаменов для выпускников. Почти 8% сдающих в 2021 году не прошли минимальный порог, а количество высокобалльников составило лишь 2,4%.
Как повысить свои шансы на успешную сдачу ЕГЭ по математике и на каких заданиях легче набрать баллы, разбираем в этой статье вместе с преподавателем онлайн-школы Вебиум.
ЕГЭ по математике — обязательный предмет
ЕГЭ по математике — обязательный для сдачи предмет. В 2015 году его разделили на два уровня сложности — базовый и профильный. Это упростило жизнь выпускникам, которым не нужна математика для поступления в вуз. В основном, ЕГЭ по базовой математике сдают те, кто идёт в медицинские вузы или на некоторые гуманитарные специальности: рекламу, юриспруденцию, издательское дело, остальные сдают профиль.
Чтобы получить аттестат, нужно успешно сдать ЕГЭ либо по профильной математике, либо по базовой. Но выбрать профиль и базу «для подстраховки» нельзя: с 2018 года запретили сдавать оба уровня.
В 2022 году в ЕГЭ по математике также появились изменения, о них подробно рассказали в нашей статье.
Базовая математика: структура экзамена
В базовой математике всего 21 задание, из них 16 — по алгебре и началам анализа, пять — по геометрии. За каждое можно получить 1 балл. Этот ЕГЭ пишут 3 часа.
Это единственный экзамен, результат которого переводится не в 100-балльную систему, а в оценки по 5-балльной шкале. Для получения аттестата нужно набрать семь баллов.
Подготовьтесь к базовой математике на 5 за шесть недель с нашим спецкурсом.
Профильная математика: структура экзамена
Количество заданий в ЕГЭ по профильной математике — 18. Их делят на три блока: восемь заданий по алгебре и началам анализа, четыре — по геометрии и шесть — по реальной математике.
При этом номеров базового уровня сложности шесть, повышенного — десять, высокого — два. Время на их выполнение — 3 часа 55 минут.
Список тем, которые нужно знать для экзамена, собрали в нашей шпаргалке. Также рекомендуем посмотреть разбор демоверсии ЕГЭ 2022 по профильной математике.
Для получения аттестата нужно преодолеть минимальный порог в 27 вторичных баллов — то есть решить шесть заданий тестовой части.
Есть и особенности: сдать ЕГЭ по профильной математике на 100 баллов вы можете, даже если допустите ошибку. Дело в том, что первичный балл, которому соответствуют 100 вторичных баллов, — 30. Но максимальное количество вторичных баллов, которое вы можете получить, — 31, то есть у вас есть запас в 1 балл.
Перевод баллов: сколько я получу, если решу N заданий
Если вы решите всю первую часть без единой ошибки, то получите 11 первичных баллов. Согласно шкале перевода, это соответствует 56 вторичным баллам по 100-балльной системе.
Чтобы получить 60+ баллов (62–68), вам нужно суммарно с верно решённой тестовой частью набрать ещё 1–2 первичных балла соответственно. Набор задач может быть таким: вся первая часть + 12 или 14 задание.
Вы можете решить первую часть с двумя ошибками — тогда нужно будет выполнить 12 и 14 номер на максимальный балл или суммарно потерять в них не более одного балла.
Если вы решите верно всю первую часть, а также 12 и 14 задания, то сдадите ЕГЭ по профилю на 72 вторичных балла. Добавив к этому набору задачу по финансовой математике, вы получите 76 вторичных баллов.
Решив верно тестовую часть, 12,14,15 задания и задачу с параметром вы получите 80+ баллов. Вместо полностью правильной 17 задачи можно решить пункты а) и б) в 13 задании и пункт а) в 18 задании.
Простые задания в ЕГЭ по профильной математике
Несмотря на то, что профиль — достаточно сложный экзамен, к которому нужно долго и упорно готовиться, в нём есть лёгкие задания. Это задачи из первой части КИМа.
Задание 1
Это задание на решение простейших уравнений. Здесь нужны базовые знания в работе с линейными, квадратными, показательными, логарифмическими уравнениями. Если повезёт, то нужно будет всего лишь разделить одно число на другое.
Задание 2
Здесь встречаются простейшие задачи на теорию вероятности, для решения которых нужна одна формула: число благоприятных событий разделить на количество всех событий. Подробнее об этом — в шпаргалке по теории вероятности. Также можно пройти бесплатный курс по этой теме.
Задание 4
Задача проверяет ваше умение выполнять простейшие вычисления и преобразования. Вы должны понимать, как работать с дробями, иррациональными, степенными, логарифмическими, тригонометрическими выражениями, а потом вычислять их значение, подставив числа.
Освежить в памяти тему логарифмов и степеней поможет наша шпаргалка, а тему тригонометрических преобразований — статья с основными формулами.
Задание 7
Это задача с прикладным содержанием. Здесь от вас требуется лишь умение верно считать и подставлять значение в формулу, которая даётся в условии.
Задания по геометрии из первой части
Планиметрия и стереометрия — достаточно пугающие разделы для большинства выпускников, но подождите паниковать: справиться с задачами первой части под силу каждому. Вы должны знать лишь основные свойства и формулы площадей плоских фигур — треугольников, параллелограммов, трапеций, разбираться в центральных и вписанных углах и знать основные свойства и формулы площадей объёмных тел — параллелепипедов, призм, конусов, шаров, цилиндров, пирамид.
Основные лайфхаки по решению тестовой части мы собрали в этой статье.
Самые сложные задания в ЕГЭ по профильной математике
Чтобы гарантированно сдать ЕГЭ по профильной математике на 80+ баллов, необходимо решать не только первую часть, уравнение из 12 задания и неравенство из 14, но и более сложные задания: стереометрию, планиметрию, задачу с параметром и олимпиадную задачу на свойства чисел.
Забудьте про «Либо всё, либо ничего» — на ЕГЭ по математике так не работает. Вы должны бороться за каждый балл: записать половину решения с идеей, которая пришла вам в голову за пять минут до конца и кажется вам глупой, или сделать только пункт А) в задаче. Возможно, именно эти драгоценные баллы помогут вам с поступлением.
Сложная стереометрия (13 задание)
Это задача даётся, как правило, легче, чем задание на сложную планиметрию, но не всё так просто. Не стоит сразу решать задания ЕГЭ, если у вас есть пробелы в стереометрии. Перед этим повторите необходимый объём теоретического материала — свойства объёмных фигур, теоремы, научитесь строить сечения, находить расстояние между прямыми и плоскостями или от точки до прямой и до плоскости, находить углы: между плоскостями, между прямой и плоскостью, между скрещивающимися прямыми. И только потом приступайте к задачам, начиная с самых простых. Постепенно вы научитесь применять теорию и будете видеть случаи, когда можно использовать ту или иную теорему.
Ключ к успеху в том, чтобы перестать думать, что геометрия вам не по силам. Начните с простых заданий, дайте себе время, чтобы подумать над задачей — вы можете вернуться к ней даже через день. Поверьте, регулярный труд даст свои плоды через некоторое время.
Сложная планиметрия (16 задание)
В этой задаче, как и в предыдущей, не стоит сразу открывать типовые варианты — скорее всего, вы подумаете, что это очень сложно, и запал пропадёт. Помимо базовых свойств и теорем, обратите внимания на «экзотику» — теоремы, которые вы, скорее всего, не встречали в школьных учебниках. Это, например, теоремы Менелая или Чевы. Больше теорем вы найдёте в нашей шпаргалке.
Не игнорируйте пункт на доказательство: он может быть простым и подарить драгоценный балл. Однако если вы решили пункт б), но не притронулись к а) — вы все равно получите балл за него.
Задача с параметром (17 задание)
То, что пугает выпускников больше, чем геометрия. За это задание дают четыре первичных балла — столько же вы получите только за последнюю олимпиадную задачу, но решают его только 2% сдающих ЕГЭ по профильной математике.
К сожалению, в школе это задание зачастую не объясняют, поэтому вам придётся изучать это самому или на курсах.
Начните с повторения элементарных функций, далее — с равносильных преобразований неравенств и их систем. Поймите, при каких ограничениях параметра вы можете выполнить определённое преобразование. Идеальный вариант для практики — начать с заданий вида «Для каждого значения параметра решить…»
После этого начните подробнее знакомиться с аналитическим методом решения задач с параметром: познакомьтесь с заданиями вида, например, «При каких значениях параметра уравнение (неравенство, система) имеет N решений».
Теперь приступайте к изучению графического метода решения. Для этого обязательно повторите графики, уравнение прямой и окружности, области определения и значения функции, чётность, периодичность, параллельный перенос.
Пройдите спецкурс по параметрам от Вебиума, чтобы разложить эту тему по полочкам
Олимпиадная задача на свойства чисел (18 задание)
За верное решение этого номера вы получите четыре первичных балла. Но здесь нужно пробовать ухватить и один балл — иногда это может быть достаточно легко.
Что нужно знать? Теорию чисел, их свойства, признаки делимости чисел, прогрессии — арифметическую и геометрическую, среднее арифметическое. Когда вы освоите более простые задания, можно изучить метод кругов Эйлера, метод математической индукции и принцип Дирихле.
Как получить 1 балл? Традиционно этот номер содержит в себе три пункта — а), б) и в). В первом пункте обычно предлагается решить несложную задачу, где вы должны привести пример. Обычно их существует несколько, но вы можете привести только один. Если пример будет верным, то вы получите желанный балл. Вот, как может выглядеть задание:
На доске написано несколько различных натуральных чисел, каждое из которых делится на 3 и оканчивается на 7.
а) Может ли сумма этих чисел быть равна 231?
Решение:
а) Да, может. Числа 27, 57 и 147 дают в сумме 231.
Как видите, ничего сверхъестественного от вас в первом пункте не требуют, и получить 1 первичный балл достаточно легко.
Пункт б) тоже стоит 1 первичный балл, но решить его будет немного сложнее. Зачастую вопрос этого пункта очень похож на вопрос пункта а), но есть исключение: чаще всего пример привести невозможно, и это нужно доказать. Делают это обычно «от противного»
За верное решение пункта в) вы получите 2 первичных балла, но это уже достаточно высокий уровень сложности. Чаще всего в задании требуют найти минимальное значение какой-нибудь величины. К решению пункта в) стоит приступать, когда предыдущие начнут стабильно получаться.
Как готовиться, если осталось два месяца
Начинать подготовку нужно с составления плана занятий. Самостоятельно сделать это достаточно сложно, но вот основные рекомендации:
- Нарешайте тестовую часть так, чтобы стабильно не допускать в ней ошибок. Её верное решение даст вам 56 вторичных баллов, в то время как потерю придётся компенсировать сложными заданиями второй части.
- Вы должны уметь решать все виды 12 и 14 заданий, а также задачи на финансовую математику. Не стоит забывать про 2018 год: составители добавили новую задачу на кредиты, и её смогли решить только те, кто понимал суть, а не следовал алгоритму.
- Когда вы перейдёте к подготовке ко второй части, рекомендуем раз в 3–5 дней прорешивать полный вариант. Иначе вы рискуете забыть что-нибудь простое, уделяя время только сложному.
- Используйте сборники и пособия для подготовки к ЕГЭ по профильной математике. Анализ ресурсов и подборку лучших мы сделали в этой статье.
- Изучите типичные ошибки, которые допускают участники ЕГЭ, — вы научитесь видеть недочёты и совершите их с меньшей вероятностью.
Подготовка будет эффективной, если ваши работы будет проверять человек с опытом — иногда верный ответ не даёт максимальный балл за задание. Именно поэтому мы запустили спецкурсы с проверкой от наставников по заданию 14 и по заданию 12.
На курсах Вебиума мы поможем вам подготовиться к ЕГЭ на максимальный балл: разберём актуальные задания, ты получишь обратную связь и ответы на вопросы по домашкам и закроешь пробелы во всех темах.
Какие задания реже всего выполняют на ЕГЭ по профилю
Мы проанализировали статистику с официального сайта ФИПИ за 2021 год и составили рейтинг заданий в соответствии со средним процентов выполнения. Номера заданий приведены согласно новой демоверсии ЕГЭ по профильной математике.
| Номер задания | Тема | Средний процент выполнения, % |
| 1 | Простейшие уравнения и неравенства | 95,0% |
| 2 | Теория вероятности | 92,9% |
| 7 | Задачи с прикладным содержанием | 78,3% |
| 3 | Планиметрия | 70,6% |
| 4 | Вычисления и преобразования | 68,8% |
| 5 | Стереометрия | 66,3% |
| 6 | Производная и первообразная | 58,8% |
| 11 | Наибольшее и наименьшее значение функции | 55,5% |
| 8 | Текстовые задачи | 53,8% |
| 12 | Уравнения | 36,1% |
| 14 | Неравенства | 22,3% |
| 16 | Экономическая задача | 19,0% |
| 18 | Задача на теорию чисел | 11,4% |
| 13 | Сложная стереометрия | 7,20% |
| 15 | Сложная планиметрия | 3,50% |
| 17 | Задача с параметром | 2,00% |
Как сдать ЕГЭ по математике на 80+ баллов: советы от Эйджея Гаусса
Преподаватель математики в Вебиуме Эйджей Гаусс поделился советами, как правильно готовиться к ЕГЭ по профилю.
- Внимательно изучите критерии заданий второй части, особенно связанные с оформлением! Даже если вам кто-то сказал, что именно в вашей области «вот это можно не писать», — это не гарантия того, что эксперт, проверяющий вашу работу, закроет глаза на мелкие нарушения.
- Запаситесь терпением и готовьте свои нервы к атмосфере экзамена. Советую заранее спланировать, в каком порядке вы будете решать задания: это поможет избежать паники в стрессовой ситуации.
- Не забывайте решать пробники. Так вы поймёте, сколько времени вам требуется для решения определённого типа заданий, что вызывает наибольшие трудности и какие номера вы точно должны успеть решить. В стрессовых ситуациях время течёт иначе, поэтому будьте готовы к любому развитию событий — в этом поможет регулярная практика.
Решайте бесплатные варианты ЕГЭ по профильной математике на сайте Вебиума, чтобы набить руку.
- Осознайте важную вещь: прорешать все задания, пробники, просмотреть все видео-разборы, которые вы сохранили на будущее, не получится! Сколько бы вы ни готовились, не опирайтесь на паттерны заданий и внимательно читайте условия. Даже в таком экзамене, как ЕГЭ, важна изворотливость ума и умение применять все свои знания. Шаблонно решать номера не получится, и пытаться не стоит — кто знает, что взбредёт составителям в голову. Именно поэтому нужно понимать логику решения, а не заучивать алгоритм.
- Сохраните здравомыслие. Можно каждый месяц говорить себе: «О ужас! Осталось N дней до экзамена, а я ничего не знаю и ничего не сдам!» Однако задайте себе вопрос: чем паника и необоснованное недовольство собой помогут вам сдать ЕГЭ по профильной математике? Каждый день времени становится меньше, но ведь в сутках целых 24 часа! Стоит ли расстраиваться и накручивать себя из-за потерянной минуты? Конечно же, нет. Подготовиться с нуля можно, даже начав в апреле. Главное — верить в себя, в свои силы и прилагать усилия, чтобы достичь результата.
- Не доводите себя до изнеможения! Находясь в постоянном напряжении, ваш мозг будет перегружаться. Это может привести к сильной усталости, нежеланию что-либо делать и даже к эмоциональному выгоранию. О том, как с этим справиться, рассказывали в этой статье.
- Когда вы находитесь на пике стрессовой активности, у вас снижаются концентрация и внимание: даже простые задания перестанут получаться. А это ещё больше способствует самобичеванию. Так что не забывайте отдыхать и проводить время не только с учебниками.
Для тех, кто сдаёт ЕГЭ по профильной математике и не знает, куда поступать, мы сделали подборки из десяти топовых технических вузов России и пяти лучших социально-экономических вузов России.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!
!!! Экзамен приближается, осталось совсем немного времени. Рекомендую акцентировать внимание на некоторых сложных заданиях 1-14 (в прошлом часть В). Вернее, понятие сложность здесь весьма относительно, оно вполне применимо к задачам с развёрнутым ответом (15-21).
К вам большая просьба, дайте ссылку на статью в социальных сетях, чтобы как можно больше ребят посмотрели информацию, многим она будет полезна. Все перечисленные ниже задачи вы можете посмотреть кликнув на ссылку (если какая-то не работает, напишите в комментариях).
Если по какой-то задаче хотите больше информации, то введите номер задачи в строку поиска. Если соответствующая статья имеется на блоге, то она будет в выдаче.
Также к вашим услугам карта блога.
Итак, речь пойдёт о задачах, которые чуть сложнее других в этой же части. Например, посмотрите примеры – 26623 и 26631, 27545 и 245000, 282855 и 320199, 26646 и 26669, 27220 и 27261, можно ещё перечислять… Каждая пара относится к одной группе, но разницу вы видите – одну можно решить практически устно, на решение другой времени уходит гораздо больше. Итак, советую обратить внимание на следующие задания:
Задачи 1. Задачи на проценты 26631, 26644, 77341, 77347, 77348, 77349, 77352. На блоге они решены через составление пропорции, в решении это помогает, но с процентами так «поступать» не совсем математически корректно. Если вы решаете такие задания без пропорции, то это хорошо. Важно чтобы у вас было понимание понятия «процент» и ответ в итоге был верен.
Задачи 2. Требуется внимательность 26866 и 263866.
Задачи 3. Обратите внимание на задачи 26682 и 77363.
Задачи 4. Задания довольно разнообразны. По площадям фигур посмотрите 244999, 245000, 245008, есть статья на блоге, излагаются оба способа решения. По остальным заданиям планиметрии посмотрите разделы на блоге, кому что необходимо и с чем возникают затруднения – задачи с векторами, задачи на координатную плоскость, вычисление углов в треугольнике, угол на листе в клетку. Обратите внимание на 27780, 27821, 27825, 27826.
Задачи 5. Теория вероятности 285925, 320177, 320187, 320188, 320196, 320199, 320200, 320206, 320212, 500998, 500997.
Задачи 6. Уравнения 26669, 77368, 77376, 77377, 77382. Самые времязатратные из уравнений это тригонометрические.
Задачи 7. Если есть трудности с прямоугольным треугольником, есть рубрика на блоге — в ней можете выбрать необходимые статьи и повторить. Посмотрите задачи 27827, 27842, 27843. Задачи этой части примерно все одного уровня. Требуется хорошие твёрдые знания формул, свойств фигур и нескольких теорем.
Задачи 8. Посмотрите 27486, 119972, 119973, 323078, 323079, 323080. Все задачи этой группы есть на блоге.
Задачи 9 и Задачи 12 (стереометрия). Не смотря на всё разнообразие заданий, решаются они в одно-два действия. Если есть вопросы и трудности с какими-то конкретными заданиями, например, на вычисление объёма или площади поверхности, то посмотрите соответствующие статьи в рубриках стереометрия, а также в карте блога есть вкладка «Стереометрия» с задачами. Задачи с жидкостями 27045, 27047, 27048, по ним как-то было много вопросов, написал статью.
Задачи 10. Типы примеров с выражениями на блоге рассмотрены все. Посмотрите, интересующие вас в соответствующих статьях. Отмечу некоторые алгебраические 26803, 26819, 26820, 26823, 26829, 26830, 26840.
Задачи 11. Есть прикладные задачи, которые решаются через составление неравенств, как и должно быть. Их можно решать и уравнением, это – 27956, 27957, 27961, 27962, 27963, 27966, 27989, но есть одно большое НО! Вы должны чётко понимать что за два значения переменной у вас получится при решении и как с ними поступать далее. Стоит отметить задачи 27970 и 27974 (решение расписано подробно). Задания с тригонометрическими функциями рекомендую решать именно через неравенство, например 28010, 28013, 28014 и другие, все задания этой части есть на моём втором сайте.
Задачи 13. Посмотрите задачу на параллельное движение двух объектов 99610, прогрессии 99587, задачи на среднюю скорость 99603 и 99606, на проценты 99566, 99568, задачи на смеси-сплавы-растворы.
Задачи 14. Все задания решаются по стандартному алгоритму, на блоге рассмотрены практически все типы. Отмечу задания, которые решаются без использования этого алгоритма 245173, 245175, 245177, 245179, 245181, 245183, посмотрите статью.
Рекомендую вам книгу «Самые хитрые задачи на ЕГЭ по математике». Там собраны все задачки с нюансами.
Кратко по Задачам 15 – при решении тригонометрических уравнений сразу рекомендую найти область определения. После решения самого уравнения (системы) внимательно произведите отбор корней принадлежащих этой области. При вычислении корней принадлежащих отрезку будьте предельно внимательны. При решении логарифмических уравнений также не забывайте, что выражение стоящее по знаком логарифма и основание логарифма больше нуля.
По остальным задачам с развёрнутым ответом общие краткие рекомендации дать не просто, для решения требуется основательная подготовка и хорошая практика. Задачи 16 и 18 (геометрия) не редко бывают довольно просты, но проблема в одном – как сразу увидеть ту теорему, свойство или применить их «комбинацию»? Поэтому и крайне важны отработанные практические навыки и логика, которые и дают видение путей решения, надеюсь у вас есть и то и другое.
К сожалению, я до рассмотрения этих заданий ещё не добрался, так как не все ещё сделано по задачам 1-14, а блог веду по строгому плану и стремлюсь закончить, в первую очередь, именно эти части. Рекомендую вам два сайта, где имеются задания 15-21:
www.ege-ok.ru блог Инны Фельдман
www.egemaximum.ru блог Елены Репиной
На этом всё. Буду рад, если информация была для вас полезна, обязательно порекомендуйте её в социальных сетях, кнопки имеются ниже. До экзамена обязательно ожидайте статью с моим напутствием, удачи вам и ХОРОШИХ ЗНАНИЙ!
С уважением, Александр Крутицких.
4. Введение в теорию вероятностей
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Сложные задачи по теории вероятности
Общая памятка по всем разделам теории вероятностей:
Задание
1
#3858
Уровень задания: Равен ЕГЭ
Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы (4) очка в двух играх. Если команда выигрывает, она получает (3) очка, в случае ничьей — (1) очко, если проигрывает — (0) очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны (0,3).
Чтобы команда в двух играх набрала не менее (4) очков, ей нужно: либо 1) выиграть обе игры, либо 2) выиграть в одной из игр и сыграть вничью в другой игре.
Так как вероятности выиграть и проиграть одинакова и равна (0,3), то вероятность сыграть вничью равна (1-0,3-0,3=0,4).
Следовательно, вероятности в этих случаях равны соответственно:
1) (0,3cdot 0,3)
2) (0,3cdot 0,4+0,4cdot 0,3) (выиграть в первой игре и сыграть вничью во второй или сыграть вничью в первой и выиграть во второй).
Следовательно, вероятность того, что команда выйдет в следующий круг соревнований, равна [0,3cdot 0,3+0,3cdot 0,4+0,4cdot 0,3=0,33]
Ответ: 0,33
Задание
2
#2739
Уровень задания: Сложнее ЕГЭ
Илья решает задачу по геометрии, в которой дан четырёхугольник (ABCD), причём (AB = 5), (BC = 6), (CD = 4), (AD = 10). В условии задачи сказано, что одна из вершин является центром некоторой окружности и Илья думает, какую вершину ему выбрать в качестве центра этой самой окружности.
Известно, что вероятность выбора каждой конкретной вершины пропорциональна сумме длин сторон четырёхугольника (ABCD), проходящих через эту вершину. Какова вероятность того, что Илья выберет вершину (B)?
Через вершину (A) проходят стороны (AB) и (AD), их сумма: (AB + AD = 15).
Через вершину (B) проходят стороны (AB) и (BC), их сумма: (AB + BC = 11).
Через вершину (C) проходят стороны (BC) и (CD), их сумма: (BC + CD = 10).
Через вершину (D) проходят стороны (CD) и (DA), их сумма: (CD + DA = 14).
Обозначим вероятность выбора вершины (A) через (P(A)) (для остальных вершин аналогично). Тогда по условию имеем: [P(A) = 15k,qquad P(B) = 11k,qquad P(C) = 10k,qquad P(D) = 14k,,] но (P(A) + P(B) + P(C) + P(D) = 1), тогда (k = 0,02), откуда находим: (P(B) = 0,22).
Ответ: 0,22
Задание
3
#191
Уровень задания: Сложнее ЕГЭ
Монетку подбросили 10 раз. Какова вероятность того, что выпало не менее 9 орлов? Ответ округлите до тысячных.
Условие того, что выпало не менее 9 орлов эквивалентно тому, что выпало не более 1 решки, то есть либо ровно 1 решка, либо 0 решек.
Количество всевозможных различных исходов в серии из 10 испытаний равно (2^{10} = 1024).
Среди них есть 11 исходов, подходящих под условие: (Орёл; Орёл; …; Орёл), (Орёл; Орёл; …; Орёл; Решка), (Орёл; Орёл; …; Решка; Орёл), …, (Решка; Орёл; …; Орёл), следовательно, искомая вероятность равна [dfrac{11}{1024}.] После округления получим (0,011).
Ответ: 0,011
Задание
4
#190
Уровень задания: Сложнее ЕГЭ
Монетку подбросили 3 раза. Какова вероятность того, что выпало не менее 3 орлов? Ответ округлите до тысячных.
Условие того, что выпало не менее 3 орлов эквивалентно тому, что выпали только орлы.
Количество всевозможных различных исходов в серии из 3 испытаний равно (2^3 = 
Ответ: 0,125
Задание
5
#189
Уровень задания: Сложнее ЕГЭ
Монетку подбросили 2 раза. Какова вероятность того, что выпало не менее 1 орла? Ответ округлите до тысячных.
Всевозможных исходов в серии из 2 подбрасываний может быть (2^2 = 4): (Орёл; Орёл), (Орёл; Решка), (Решка; Орёл), (Решка; Решка).
Среди выписанных (всевозможных) исходов под условие задачи подходят первые 3, следовательно, искомая вероятность равна [dfrac{3}{4} = 0,75.]
Ответ: 0,75
Задание
6
#2658
Уровень задания: Сложнее ЕГЭ
Игорь трижды подбрасывает правильную игральную кость. Какова вероятность того, что за эти три подбрасывания ровно один раз выпадет число, кратное трём, а сумма результатов подбрасываний не будет делиться на (3)? Ответ округлите до сотых.
Так как игральная кость правильная, то вероятность выпадения каждой грани равна (dfrac{1}{6}). Среди чисел на гранях есть два числа, дающих при делении на (3) остаток (0), два числа, дающих при делении на (3) остаток (1) и два числа, дающих при делении на (3) остаток (2).
Тогда вероятность за одно подбрасывание получить, например, число, дающее при делении на (3) остаток (1), равна (dfrac{1}{3}). С другими остатками аналогично.
Условие задачи можно переформулировать в следующем виде: какова вероятность за три подбрасывания получить результаты, остатки от деления на (3) которых будут содержать единственный (0) и два одинаковых числа?
Таким образом, нас устраивают исходы, остатки от деления на (3) которых будут иметь вид:
[begin{aligned}
&0,quad 1,quad 1\
&1,quad 0,quad 1\
&1,quad 1,quad 0\
&0,quad 2,quad 2\
&2,quad 0,quad 2\
&2,quad 2,quad 0,.
end{aligned}]
Вероятность любого из выписанных исходов равна [dfrac{1}{3}cdot dfrac{1}{3}cdot dfrac{1}{3},.] При этом различных исходов здесь шесть, следовательно, вероятность получения подходящего исхода равна [6cdot dfrac{1}{3}cdot dfrac{1}{3}cdot dfrac{1}{3} = dfrac{2}{9},.] После округления получим ответ (0,22).
Ответ: 0,22
Задание
7
#2765
Уровень задания: Сложнее ЕГЭ
Таня заметила, что в казино “Подкинем” используют неправильную игральную кость (т.е. не у всех граней вероятности выпадения одинаковы). При этом она установила, что вероятность выпадения чётного числа равна (0,6); вероятность выпадения числа, делящегося на (3), равна (0,3); вероятность того, что выпадет (1) или (5), равна (0,22). Найдите вероятность того, что на этой игральной кости выпадет число (3). Ответ округлите до сотых.
Вероятность выпадения числа (n) обозначим через (P({n})), вероятность выпадения одного из чисел (m) и (n) обозначим через (P({m; n})), а вероятность выпадения одного из чисел (m), (n) и (k) обозначим через (P({m; n; k})). Тогда [P({2; 4; 6}) = 0,6qquadLeftrightarrowqquad P({1; 3; 5}) = 1 — 0,6 = 0,4]
При этом (P({1; 5}) = 0,22), но ведь (P({1; 3; 5}) — P({1; 5}) = P({3})), следовательно, [P({3}) = 0,4 — 0,22 = 0,18,.]
Ответ: 0,18
Если выпускник готовится к сдаче ЕГЭ по математике профильного уровня, ему необходимо научиться решать задачи на применение теории вероятности повышенной сложности. Как показывает практика многих лет, такие задания являются обязательной частью программы аттестационного испытания. Поэтому если учащийся не до конца понимает принцип решения сложных задач на теорию вероятности, ему обязательно стоит вновь разобраться в данной теме.
Вместе с образовательным порталом «Школково» старшеклассники смогут качественно подготовиться к прохождению аттестационного испытания. Наш сайт позволит определить наиболее сложные темы и восполнить пробелы в знаниях. Опытные специалисты «Школково» подготовили весь необходимый материал, изложив его таким образом, чтобы школьники с любым уровнем подготовки смогли легко справиться с решением сложных задач ЕГЭ на теорию вероятности. Базовая информация по данной теме представлена в разделе «Теоретическая справка».
Чтобы попрактиковаться в выполнении сложных задач ЕГЭ по теории вероятности, школьники могут выполнить соответствующие упражнения. Простые и сложные задания, подобранные нашими специалистами, содержат подробные алгоритмы решения и правильные ответы. База заданий регулярно обновляется и дополняется.
Выполнять упражнения школьники из Москвы и других российских городов могут в онлайн-режиме. При необходимости задания по теории вероятности в ЕГЭ можно сохранить в разделе «Избранное». Благодаря этому вы сможете быстро найти интересующие примеры и обсудить алгоритмы нахождения правильного ответа с преподавателем.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ