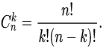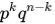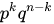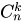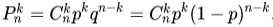Вопросы »
Комбинаторика,вероятность » Какова вероятность, отвечая наудачу на вопросы экзамена правильно ответить:
Какова вероятность, отвечая наудачу на вопросы экзамена правильно ответить:
создана: 09.01.2012 в 15:16
…………………………………………
|
|
 ( +229 ) |
Nikit :
Какова вероятность, отвечая наудачу на вопросы экзамена правильно ответить:
а) на первое задание
б) на первые два задания
в) только на первое задание
г) только на первые два задания?
В части А ЕГЭ по математики в 2003 году было 16 заданий. К Каждому из них предлагается 4 варианта ответа, из которых ровно один-верный.
Хочу написать ответ
Предмет: Другие предметы,
автор: vladiimj
Ответы
Автор ответа: kibuzz
2
Ответ:
На первое — 0.25
На первые два — 0.0625
Последние два вопроса это тоже самое
Объяснение:
vladiimj:
чел, ты опоздал, дня на три…
Предыдущий вопрос
Следующий вопрос
Интересные вопросы
Предмет: Геометрия,
автор: yaroslavdrigoola
В треугольнике ABC AB = 4 см, BC = 7 см, AC = 6 см, а в треугольнике MNK MK = 8 см, MN = 12 см , KN = 14 см.
Найдите углы треугольника MNK, если °, °.
Помогите пж
4 года назад
Предмет: Биология,
автор: maksimsinavin1
1. Наличие чего является основным признаком покрытосеменных растений? 2. Чем обусловлено разнообразие покрытосеменных? 3. Какие отличия между голосеменными и покрытосеменными растениями?
4 года назад
Предмет: Қазақ тiлi,
автор: raveraze1
Қадыр Мырза Әлі
1. Өлеңді қалай атауға болады? Авторы кім?
2. Мәтіннен 3- тірек сөзді табыңыз.
3. Мәтін бойынша дұрыс, бұрыстығын анықта.
1. Домбыраның төрт шегі болады
2. Нағыз қазақ- домбыра
3. Домбырадан асқан шежіре, дана жоқ –
4. Домбыра мылқауды сөйлетпейді, жылатпайды –
5. Домбыра жалған сөйлемейді
2-тапсырма
«Ғаламтордың пайдасы мен зияны» тақырыбына диалог құрастыр.
ПОМОГИТЕ ПОЖАЛУЙСТА, СРОЧНО, ССОР
4 года назад
Предмет: Физика,
автор: kudaybergenova
Помогите написать физическое значение пословиц(по теме «Сила трения «). Очень сроооочно!!!! Отвечаете на то, что знаете. Не обязательно на все.
из навощенной нити сеть не сплетешь;
* колодезная веревка сруб перетирает;
* ржавый плуг только на пахоте очищается;
.Задумал муравей
Фудзияму-гору сдвинуть. (японская)
.На льду не строятся. (русская)
.Лопату не покрывают позолотой. (корейская)
.Не подмазанная арба не поедет. (таджикская)
.Сухая ложка рот дерет. (русская)
.Из навощенной нити трудно плести сети. (корейская)
6 лет назад
Предмет: Физика,
автор: Tutt2atylikaks
Космонавт на Международной космической станции, выполняющий наблюдения, находится в покое относительно …
а) .. .прибора, с которыми он работает.
б) …звезд.
в) …Земли.
г) …Солнца.
6 лет назад
Библиографическое описание:
Петров, Р. С. Вероятность сдачи ЕГЭ методом угадывания правильного ответа / Р. С. Петров, Б. З. Назримадов, Н. Н. Романова. — Текст : непосредственный // Юный ученый. — 2020. — № 4 (34). — С. 67-70. — URL: https://moluch.ru/young/archive/34/1985/ (дата обращения: 11.03.2023).
Единый государственный экзамен (ЕГЭ) — это один из видов государственной итоговой аттестации по образовательным программам среднего общего образования (ГИА), которую пишут все без исключения выпускники одиннадцатых классов российских средних учебных заведений. Первая часть экзамена — это тест, т. е. выбор правильного(-ых) варианта(-ов) ответа(-ов) из нескольких предложенных. Если вы не знаете ответа, вам остаётся положиться на свою интуицию… Однако реально ли получить высокий балл, попросту расставляя ответы наобум?
Ключевые слова:
ЕГЭ, теория вероятностей, вероятность сдачи ЕГЭ, экзамен, тест.
Актуальность исследования:
данное исследование будет актуально в основном для учащихся 11-х классов, так как оно даст ответ на довольно важный вопрос: насколько хорошо можно написать ЕГЭ, не готовясь к нему? Кажется, как можно «предвидеть» наступление такого случайного события, как правильно данный ответ? Оно ведь может произойти, а может и нет… Но математика нашла способы оценивать вероятность наступления таких событий.
Цель
: определить вероятность сдачи ЕГЭ при помощи угадывания правильного ответа, применяя теорию вероятностей
Объект исследования:
теория вероятностей
Предмет исследования
: практическое применение теории вероятностей
Задачи
:
- Изучить задания первой части (теста) из ЕГЭ
- Выявить вероятность сдачи ЕГЭ методом угадывания ответов
Гипотеза
: предположим, что невозможно сдать ЕГЭ, просто расставляя ответы в первой части «наугад»
Методы исследования
:
- Изучение литературы и других источников информации
- Анализ и синтез
- Идеализация
- Изучение и обобщение
Единый государственный экзамен
Основные сведения о
ЕГЭ
Единый государственный экзамен (ЕГЭ) является одним из видов государственной итоговой аттестации (ГИА) по образовательным программам среднего общего образования.
При проведении ЕГЭ используются контрольные измерительные материалы (КИМ), представляющие собой наборы из заданий стандартизированной формы, а также специальные бланки для оформления ответов на задания.
Чтобы получить аттестат, выпускникам необходимо сдать ЕГЭ по двум обязательным предметам — русскому языку и математике (базового или профильного уровня). ЕГЭ по остальным учебным предметам они сдают по своему выбору.
Структура ЕГЭ
Задания ЕГЭ (КИМы) разрабатываются
Федеральным институтом педагогических измерений
[6].
Примерная структура, форма и содержание КИМов предопределены и не могут быть изменены произвольным образом, а регламентируется они тремя документами, утверждаемыми Рособрнадзором каждую осень: кодификаторами, спецификациями и демоверсиями экзаменов. КИМы включают в себя задания с кратким и развернутым ответами.
В экзаменах по математике базового и профильного уровней нет заданий с выбором ответа: следовательно, для сдачи данных экзаменов способ расстановки ответов «наугад» не подходит меньше всего.
При проведении ЕГЭ по иностранным языкам в состав экзамена входит раздел «говорение», устные ответы на задания которого записываются на аудионосители.
Теория вероятностей
Теория вероятностей — это раздел математики, который изучает числовые характеристики вероятности появления некоторого случайного события в конкретных условиях, которые могут быть многократно воссозданы (как, например, сдача ЕГЭ).
Для событий, вероятность которых находиться по формуле классической вероятности, может быть применён статистический подход. Это было обосновано ещё швейцарским математиком Якобом Бернулли (1655–1705).
Являясь математической основой статистики, теория вероятностей имеет большое значение для множества видов деятельности человека, включающих количественный анализ данных, таких как: социологические исследования, экономический анализ и др.
За последние десятилетия теория вероятностей стала развивающейся наукой со множеством возможных направлений применения.
Вероятность события
В так называемых
случайных
[1]
явлениях существуют определённые закономерности. Задачей теории вероятности является установление таких закономерностей.
Классическое определение вероятности: вероятность события А (обозначается Р(А)) равна отношению числа благоприятствующих исходов к числу всех возможных исходов. Т. е. вероятность события А вычисляется по формуле: Р(А)=n/m, где n ≤ m и n, m є N, из чего следует, что 0 ≤ Р(А) ≤ 1. В данной формуле: n — число благоприятствующих исходов, m — число всех исходов испытания.
Однако в нашей жизни встречаются ситуации, где без практики определить число благоприятных исходов очень трудно, а то и вовсе невозможно.
Например, не подбрасывая кнопку много раз, трудно определить, равновозможны ли ее падения на плоскую часть или на иглу. В подобных случаях и используется статистическое определение вероятности.
Статистическая вероятность
Статистическая вероятность — это числовое выражение степени возможности наступления некоторого события (или того, что данное событие не наступит). Одним из способов, помогающих её рассчитать, является использование формулы Бернулли, позволяющей найти вероятность появления события A при нескольких независимых испытаниях.
Чтобы найти, каков шанс наступления события А при помощи формулы Бернулли, нам надо:
– найти общее количество исходов рассматриваемой ситуации;
– найти количество всех возможных исходов, при которых произойдёт событие А;
– найти, какую часть составляют возможные исходы, при которых произойдёт событие А, от общего количества исходов
Определение вероятности сдачи ЕГЭ
Вероятность сдачи ЕГЭ
Согласно нашим наблюдениям, у учащихся старших классов часто возникают мысли, что можно выбрать ответ наугад и при этом получить высокий балл за экзамен. Но так ли это?
Ответить на этот вопрос мы планируем, используя методы из теории вероятностей. А в качестве объекта для анализа мы решили выбрать ЕГЭ по истории, который сдаём сами.
По данному предмету экзамен включает 14 заданий с выбором ответа. Чтобы сдать экзамен, нужно набрать больше или ровно 32 балла.
Определить вероятность сдачи экзамена (о получении «высокого балла» для поступления в вуз, как мы понимаем, речи не идёт) можно по формуле Бернулли.
Если проводится n независимых испытаний, в результате каждого из которых событие A наступает с вероятностью P(A)=p и не наступает с вероятностью q (q=P(А)=1-p). Вероятность того, что в результате n независимых испытаний событие A наступит ровно k раз равна количеству сочетаний из n по k:
При этом все испытания независимы, а их исходы несовместимы (событие A либо наступает, либо нет). Из этого следует, что вероятность получения удовлетворяющей комбинации будет равна:
Чтобы найти вероятность того, что в n испытаниях событие A наступит k раз, нужно сложить вероятности получения всех удовлетворяющих комбинаций
(они одинаковы и равны).
Тогда количество комбинаций равно
. Получим, что:
— это и есть формула Бернулли.
В итоге мы имеем 14 вопросов. Вероятность угадывания правильного ответа на отдельный вопрос одинакова и равна 1/4 = 0.25 (количество удовлетворяющих исходов (дан правильный ответ) ко всем возможным (всего 4 варианта ответа)). Получаем:
P = P(14) = C
14
14
*0.25
14
*0.75
0
= 0,0000000037252902984619140625 — данное число и является числовым выражением вероятности сдачи ЕГЭ методом угадывания правильного ответа.
Заключение
Как мы можем видеть, вероятность сдать ЕГЭ по истории методом случайной расстановки ответов практически равна нулю. Судя по количеству тестовых заданий в ЕГЭ по другим предметам, утверждение, что сдать его методом угадывания правильного ответа невозможно, справедливо для всех предметов, которые доступны для сдачи выпускниками 11-х классов.
Литература:
- Аджиева А. А., Кибишева А. Р. Формула Бернулли // Вестник научных конференций. — ООО Консалтинговая компания Юком, 2016. — №. 4–3. — С. 17–18.
-
Википедия [электронный ресурс] // Единый государственный экзамен URL:
https
://
ru
.
wikipedia
.
org
/
wiki
/
Единый
_
государственный
_
экзамен
-
Википедия [электронный ресурс] // Формула Бернулли URL:
https
://
ru
.
wikipedia
.
org
/
wiki
/
Формула
_
Бернулли
-
Википедия [электронный ресурс] // Бернулли, Якоб URL:
https
://
ru
.
wikipedia
.
org
/
wiki
/
Бернулли
,_
Якоб
-
4ege [электронный ресурс] // Шкала перевода баллов ЕГЭ 2020 URL:
https
://4
ege
.
ru
/
novosti
—
ege
/4023-
shkala
—
perevoda
—
ballov
—
ege
.
html
- О нас // Федеральный институт педагогических измерений. URL: http://www.fipi.ru/about (дата обращения: 21.03.2020).
[1]
Событие называют случайным, если оно либо происходит, либо не происходит
Основные термины (генерируются автоматически): теория вероятностей, правильный ответ, вероятность сдачи ЕГЭ, ЕГЭ, единый государственный экзамен, вероятность, задание, исход, ответ, событие.
Похожие статьи
Взаимосвязь теории вероятности и случайных событий
Когда студент идет на экзамен, вероятность получения им хорошей оценки зависит от
Зарождение теории вероятностей и формирование первых понятий этой ветви математики
При этом вероятности до проведения опыта и после проведения должны совпадать.
Особенности решения текстовых задач в вариантах ЕГЭ по…
Выполнение вариантов единого государственного экзамена предполагает умение сконцентрироваться на полученном задании, внимательность к его выполнению, способность определять главное в большом потоке полученной информации…
Конструирование электронных учебных материалов по…
‒ степень поддержки: исправляются неверные ответы в заданиях или добавляются новые задания по требованию; ‒ интерфейс системы и условия генерируемых заданий могут быть русскими или иностранными; ‒ наличие возможности создания собственных заданий или…
Типология текстовых задач в Едином государственном экзамене…
Решение текстовых задач — одно из базовых умений, необходимое для успешной сдачи единого государственного экзамена. Чаще всего сложности при их решении возникают при составлении уравнения из данных задачи.
Об автоматизации процедуры проведения единого…
Аннотация. В статье проанализирована процедура проведения Единого государственного экзамена (ЕГЭ). Неэффективность использования современных информационных технологий в процедуре ЕГЭ в настоящее время приводит к большим затратам времени и средств…
Единый государственный экзамен: достоинства и недостатки
Про достоинства и недостатки ЕГЭ говорилось и говорится много. К достоинствам относят равные возможности для поступления учащихся в любые
Преимуществом Единого экзамена являются также одновременное его проведение и задания, одинаковые для всех выпускников.
Некоторые факты об успешной подготовке к ЕГЭ
Итоговой аттестацией школьного курса математики является сдача единого государственного экзамена (ЕГЭ).
Проанализировав задания варианта ЕГЭ можно отметить следующие темы курса школьной математики, затронутые в проверке знаний: решение текстовых задач на…
Внеклассное мероприятие «Акция «100 баллов для Победы»
ЕГЭ — это сложно, но можно», который добавил выпускникам заряд позитивной энергии и сил
Проанализировав задания варианта ЕГЭ можно отметить следующие темы курса школьной
Единый государственный экзамен можно считать особым тестом достижений школьников…
Три основных действия с процентами. Математика вокруг нас
— получить представление об экзаменационных заданиях на проценты
Чтобы правильно сориентироваться в этих жизненных ситуациях, нужно хорошо уметь решать задачи на проценты.
Математика с теорией вероятностей и статистикой. ЕГЭ-2014.
Я вообще сильно слаб в таких задачках, по этому попытался найти ответ в интернете, но оказалось, что все в разных местах сообщаются разные ответы. Давайте мы с вами попробуем выяснить, какой правильны то. Вот собственно задачка:
Этот необычный вопрос придумал математик Рэймонд Джонсон:
Если вы выберете ответ случайным образом, какова вероятность, что он будет правильным?
а) 25%
b) 50%
c) 60%
d) 25%
Вот какие объяснения и варианты ответов есть в интернете:
Вариант ответа — 0%
Правильный ответ — 0%, т. е. он не предложен среди результатов.
Поясняем: возможное количество правильных ответов — от 0 до 4, значит, вероятность случайно выбрать правильный должна составлять 0, 25, 50, 75 или 100%. Это автоматически исключает вариант в) (вероятности 60% быть не может).
Далее, поскольку, а) и г) одинаковы, они либо оба верны, либо оба ошибочны.
Итак, у нас есть 4 взаимоисключающих варианта ответа:
1: а), б) и г) — верные ответы.
2: а) и г) — верные ответы.
3: б) — верный ответ.
4: верного ответа нет.
Первый вариант невозможен, поскольку вероятность не может одновременно составлять и 25%, и 50%.
Второй вариант невозможен, поскольку, если 2 ответа верны, то вероятность выбора должна составлять 50%, а не 25%.
То же самое с третьим вариантом: если только 1 вариант верен, то вероятность выбрать его составляет 25%, а не 50% (как сказано в ответе б)).
Итак, остаётся вариант 4: верного ответа нет. Следовательно, вероятность выбрать правильный ответ составляет 0%.
Вариант ответа 37,5%:
Возможны 3 случая при угадывании ответа. 1 — выбрал 25% и угадал. 2 — выбрал 50% и угадал. 3 — выбрал 60% и угадал.
1) Шанс что ты выберешь 25% = 1/2. При этом шанс, что ты угадаешь эти 25% тоже 1/2.
Итоговая вероятность случая 1/2 * 1/2 = 1/4.
2) Шанс что ты выберешь 50% = 1/4. При этом шанс, что ты угадаешь эти 50% тоже 1/4.
Итоговая вероятность случая 1/4 * 1/4 = 1/16.
3) Шанс что ты выберешь 60% = 1/4. При этом шанс, что ты угадаешь эти 60% тоже 1/4.
Итоговая вероятность случая 1/4 * 1/4 = 1/16.
Суммируем итоговые вероятности для всех 3 случаев, получаем 3/8, или 37,5%.
Вариант ответа — 50%
Получится одна вторая
1) Сначала определим какова вероятность каждого ответа. Тут все просто — по логике вероятность того что мы выберем один из четырех вариантов ответа будет 1/4, то есть 0,25
2) Теперь посчитаем вероятность попадания на варианты ответа с числом 25%. Если учесть что события не совместны, то есть появление одного исключает появление другого, то можно воспользоваться суммой вероятностей ( вероятность того, что мы ответим 1 или 4, т.к. он содержат нужное нам 25%), то есть 25% + 25% = 50% процентов.
В итоге правильный ответ b)
Вариант ответа — рекурсия
объясняю: из 4 вариантов 1 наугад,то-есть 25%,но таких вариантов 2,значит умножаем на 2,стало 50%,но такой вариант 1,значит делим на 2 и получаем 25%,но таких вариантов 2,значит умножаем на 2,стало 50%,но такой вариант 1,значит делим на 2 и получаем 25%,но таких вариантов 2,значит умножаем на 2,стало 50%,но такой вариант 1,значит делим на 2 и получаем 25%,но таких вариантов 2,значит умножаем на 2,стало 50%,но такой вариант 1,значит делим на 2 и получаем 25%,но таких вариантов 2,значит умножаем на 2,стало 50%,но такой вариант 1,значит делим на 2 и получаем 25%,но таких вариантов 2,значит умножаем на 2,стало 50%,но такой вариант 1,значит делим на 2 и получаем 25%…
Какой вариант ответа получился у вас?
А вот еще несколько интересных задачек: вот например Простая логическая загадка, демонстрирующая нелогичность людей, а вот про задачку с шариками и водой и в какую сторону поедет велосипед ? . Можете посмотреть на задачку с которой по статистике справляются всего 10% людей, а можете решить загадку Льва Толстого
Муниципальное бюджетное общеобразовательное учреждение «Раздольненская средняя общеобразовательная школа имени Г.П. Котенко»
Исследовательская работа по теме:
«Вероятность получения положительной отметки при написании тестовой контрольной работы
путем угадывания правильного ответа»
предмет: математика
Выполнил:
Ученик 9 «Б» класса
Саркисян Артём
Учитель:
Александрова Алёна Сергеевна
с. Раздольное, 2020 г.
Содержание:
ВВЕДЕНИЕ 3
1 ТЕОРЕТИЧЕСКАЯ ЧАСТЬ 5
1.1 История возникновения теории вероятностей как науки 5
1.2 Научное обоснование и применение теории вероятностей 7
1.3 Основные формулы 12
1.4 Вероятности в жизни 14
2 ПРАКТИЧЕСКАЯ ЧАСТЬ 15
ЗАКЛЮЧЕНИЕ 19
Список использованных источников 20
ПРИЛОЖЕНИЯ 21
ВВЕДЕНИЕ
Процесс обучения невозможен без диагностики контроля знаний и умений учащихся. Существуют различные системы контроля, их разработкой занимаются не только учёные, но и сами учителя-предметники.
Среди форм и методов контроля знаний выделяют опросы и письменные работы. Считается, что более объективную оценку уровню знаний учащегося можно дать по результатам индивидуальной письменной работы. В связи с введением ОГЭ и ЕГЭ, учителя стали чаще проводить контрольные и самостоятельные работы в виде тестов, особенно по математике, информатике и физике. Тестовым заданиям в последнее время уделяют достаточно много внимания в образовании. Контроль знаний в виде теста требует обобщения знаний по конкретной теме, главе или предмету в целом.
Понятно, что всего знать невозможно. А часто встречаются такие ученики, которые и не думают включаться в учебу. Поэтому, у некоторых учеников возникает вопрос: «Нельзя ли выбрать наугад ответы и при этом получить положительную отметку за тест?». Мы тоже заинтересовались этим вопросом и возможными ответами на него. А обязательно ли знать многое, или достаточно быть удачливым?
Известно, что объем теста может быть различным, как и количество вариантов ответа на каждый вопрос. Мы решили провести исследование и выяснить вероятность получения хорошей отметки для разных видов тестов. Таким образом мы выдвинули предположение о том, что выбор ответов наугад не может обеспечить положительную отметку за контрольную работу в тестовой форме.
Цель исследования: определение вероятности получения положительной отметки при написании тестовой контрольной работы учащимися 9-х классов путем угадывания правильного ответа.
Задачи исследования:
- найти и изучить теоретический материал по данной теме, используя справочную литературу и ресурсы интернета;
- разработать тесты разного уровня сложности по математике для учащихся 9-х классов;
- апробировать тесты на уроке математики;
- проанализировать и обобщить результаты тестирования;
- выявить наиболее оптимальный вариант содержания тестов.
Объект исследования: тестовые контрольные работы.
Предмет исследования: результаты тестовых заданий по алгебре и геометрии, составленных на основе школьной программы.
Методы исследования: анкетирование, сбор информации, эксперимент, анализ полученных результатов.
Практическая значимость данной работы состоит в том, чтобы помочь обучающимся осознать важность учения, так как согласно проведенному исследованию, получить положительную отметку за тестовую контрольную работу путем угадывания маловероятна.
1 ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
- История возникновения теории вероятностей как науки
Опр. Теория вероятностей – это раздел математики, изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними.
Долгое время теория вероятностей не имела четкого определения. Оно было сформулировано лишь в 1929 году. Теория вероятностей возникла как наука из убеждения, что в основе массовых случайных событий лежат определенные закономерности. Теория вероятностей занимается изучением этих закономерностей, различных событий, наступление которых достоверно неизвестно. Она позволяет судить о степени вероятности наступления одних событий по сравнению с другими.
Возникновение этой науки относят к средним векам и первым попыткам математического анализа азартных игр (орлянка, кости, рулетка). Французские математики XVII века Блез Паскаль и Пьер Ферма, исследуя прогнозирование выигрыша в азартных играх, открыли первые вероятностные закономерности, возникающие при бросании костей.
Вклад Паскаля и Ферма в развитие теории вероятностей
Считается, что идея теории вероятностей зародилась в переписке двух великих ученых Блез Паскаля (1623–1662) и Пьера Ферма (1601–1665). От этой переписки сохранились лишь семь писем. В этой переписке оба ученых ограничиваются рассмотрением числа благоприятствующих событию шансов. У этих авторов впервые в истории имеется правильное решение задачи о разделе ставки, которая отняла много усилий у исследователей в течение длительного времени.
Основное содержание писем Паскаля и Ферма посвящено разделу ставки. Решение Паскаля подробно излагается в письме:
«Вот примерно, что я делаю для определения стоимости каждой партии, когда два игрока играют, например, на три партии и каждым вложено по 32 пистоля.
Предположим, что один выиграл две партии, а другой одну. Они играют еще одну партию, и если выигрывает первый, то он получает всю сумму в 64 пистоля, вложенную в игру; если же эту партию выигрывает второй, то каждый игрок будет иметь по две выигранных партии и, следовательно, если они намерены произвести раздел, то каждый должен получить обратно свой вклад в 32 пистоля.
Примите же во внимание, монсеньер, что если первый выиграет, то ему причитается 64; если он проигрывает, то ему причитается 32. Если же игроки не намерены рисковать на эту партию, и хотят произвести раздел, то первый должен сказать: «Я имею 32 пистоля верных, ибо в случае проигрыша я их все равно получил бы, но остальные 32 пистоля могут быть получены либо мной, либо Вами, случайности равны. Разделим же эти 32 пистоля пополам, и дайте мне, кроме того, бесспорную сумму в 32 пистоля».
Далее Паскаль рассмотрел другой случай, когда первый игрок выиграл две партии, а второй ни одной и третий, когда первый игрок выиграл одну партию, а второй ни одной. В обоих случаях рассуждения те же, что были приведены выше.
Ферма предложил следующее решение этой задачи:
Пусть до выигрыша игроку А недостает двух партий, а игроку В трех. Тогда для завершения игры достаточно сыграть максимум четыре партии. Возможные исходы представлены в виде таблицы. В первых одиннадцати исходах выигрывает А, в последних пяти В. Таким образом, ставка между игроками должна быть разделена в отношении . Т.е. игрок А получит
, а В получит
ставки.
Очевидно, что Ферма, как и Паскаль, делит ставку пропорционально вероятностям выигрыша каждым из игроков всей игры. Однако, они и сами не замечают, что их исходные позиции одинаковы.
Паскаль одновременно с размышлениями над проблемами, составившими содержание его переписки с Ферма, разрабатывал вопросы комбинаторики. Результатом этого явился «Трактат об арифметическом треугольнике», внесший серьезный вклад в развитие комбинаторики. В этом трактате есть параграф, в котором изложены правила использования комбинаторных результатов в задаче о разделе ставки. Правило, предложенное Паскалем, состоит в следующем: пусть игроку до выигрыша всей игры не хватает
партий, а игроку
—
партий, тогда ставка должна делиться между игроками в следующем отношении:
Оба они исходили из одной и той же идеи: раздела ставки в отношении, пропорциональном вероятностям окончательного выигрыша каждого игрока. В предложенных ими решениях можно увидеть зачатки использования математического ожидания и теорем о сложении и умножении вероятностей. Это был серьезный шаг в создании предпосылок и интересов к задачам теоретико-вероятностного характера. Второй шаг был сделан также Паскалем, когда он существенно продвинул развитие комбинаторики и указал на ее значение для зарождающейся теории вероятностей.
1.2 Научное обоснование и применение теории вероятностей
С вероятностными представлениями люди сталкивались уже в античности. У Демокрита, Лукреция Кара и других античных ученых можно найти рассуждения о равновозможных исходах.
Развитие теории вероятностей с момента зарождения этой науки и до настоящего времени было необычным. Все дело в том, что в самом начале она рассматривалась как нечто несерьезное, занимательное, как собрание курьезных задач, связанных в первую очередь с азартными играми в кости и карты, для переписи населения, и даже определения численности войска неприятеля. Такие элементарные задачи ставились и решались на начальном этапе, к теории вероятностей они будут отнесены позже. В этот период становятся известными работы Джероламо Кардано, Лука Пачоли и Никколо Тарталья, но никаких специальных методов они не создают.
К середине, XVII века вероятностные вопросы и проблемы, возникающие в статистической практике, в практике страховых обществ, при обработке результатов наблюдений и в других областях, привлекли внимание ученых своей актуальностью. Учёными, решившими найти разрешение данных вопросов были Блез Паскаль, Пьер Ферма и Христиан Гюйгенс. Именно они создали первые специфические понятия: математическое ожидание, вероятность; разработали первые свойства: теоремы сложения и умножения вероятностей. Тогда теория вероятностей начала использоваться в страховом деле, демографии, в оценке ошибок наблюдения.
Получив уже небольшое начало в обосновании и применении, теория вероятностей стала заинтересовывать все большее число ученых математиков. Швейцарский математик Якоб Бернулли, установил закон больших чисел для схемы независимых испытаний с двумя исходами и продолжил работать в этом направлении. Считается, что теория вероятностей как наука начинается с работы Якоба Бернулли (1654–1705) «Искусство предположений», опубликованной в 1716 году. В этом произведении уже введено и широко использовано понятие вероятности случайного события, доказаны некоторые общие теоремы и сделаны полезные примечания к работе Х. Гюйгенса.
В этот период становления науки, который продолжался до середины XIX века в центре внимания находятся предельные теоремы Муавра, Лапласа, Гаусса и др. теория вероятностей начинает широко применяться в различных областях естествознания. Вводятся понятия геометрическая вероятность, статистическая вероятность, но во главу изучения становится классическое определение вероятности.
Строгое логическое обоснование теории вероятностей произошло в XX в. и связано с именами советских математиков С. Н. Бернштейна и А. Н. Колмогорова. Попыток изменить ситуацию и поставить теорию вероятностей на заслуженное место было много, однако лишь в 1933 году Колмогорову удалось это сделать. Современный период начался с установления аксиоматики, правил, т.к. применение теории вероятностей в физике, биологии, технике, военном деле и других областях требовало уточнения и приведения к стройной системе её основных понятий. До Андрея Николаевича все классические, статистические данные, философские мысли и теории для азартных игр были лишь «интуитивными предпосылками», «кирпичиками» современной теории вероятностей. Ученый наделил теорию всеми необходимыми элементами, чтобы ее можно было назвать математической дисциплиной. Благодаря аксиоматике наука стала абстрактно-дедуктивной математической дисциплиной, тесно связанной с другими математическими дисциплинами. Такой шаг обусловил небывалую широту исследований и её применения начиная от хозяйственно-прикладных вопросов и заканчивая самыми тонкими теоретическими вопросами теории информации и теории случайных процессов.
Заслуга А.Н. Колмогорова не только в том, что он внес полную ясность в формальное строение теории вероятностей, но и в том, что сделал это с минимальными изменениями. Ученый сумел применить уже готовый мощный инструмент — так называемую теорию меры. Однако все равно это оказалось делом нелегким. Историю открытия теории вероятностей можно сравнить с открытием Эйнштейном теории относительности.
Рассмотрим несколько направлений где применяется теория вероятностей. Вообще, современная математическая статистика, пригодная для широкого применения в практике, была развита в Англии Карлом Пирсоном, Стьюдентом, Робертом Джеймсом Фишером.
- Астрономия. В то время (конец XVIII – начало XIX века) главным вопросом для ученых было расчет движения орбит комет. Тогда ограничивались лишь малым числом наблюдений, но ясно, что надежное определение типа орбиты (эллипс или гипербола) и точный расчет ее параметров оказывается трудным, так как орбита наблюдается лишь на небольшом участке. Тогда специально для этого был разработан знаменитый “метод наименьших квадратов” (Лежандр 1805, Гаусс 1815). Метод оказался эффективным, универсальным, его стали использовать в геодезии и картографии.
- Физика. Во второй половине XIX века теория вероятностей была применена в работах Максвелла, Больцмана и Гиббса. Ими была развита статистическая механика, которая описывала состояние разряженных систем, содержащих огромное число частиц (порядка числа Авогадро =
). Если раньше понятие распределения случайной величины было преимущественно связано с распределением ошибок измерения, то теперь распределенными оказались самые разные величины: скорости, энергии, длины свободного пробега.
- Биометрия. В конце XIX века в 70х-00х годах, бельгиец Адольф Кетле и англичане Френсис Гальтон и Карл Пирсон основали новое научное направление – биометрию, в которой впервые стала систематически и количественно изучаться неопределенная изменчивость живых организмов и наследование количественных признаков. В научный оборот были введены новые понятия – регрессии и корреляции.
- Сельское хозяйство. В начале 20 века в Англии была поставлена задача количественного сравнения эффективности различных методов ведения сельского хозяйства. Для её решения была развита теория планирования экспериментов, дисперсионный анализ. Основная заслуга принадлежит сэру Рональду Фишеру, астроному по образованию, а в дальнейшем фермеру, статистику, генетику, президенту английского Королевского общества.
- Промышленность. Здесь были введены методы статистического контроля на производстве (контрольные карты Шухарта), что позволило сократить количество испытаний качества продукции. Постепенно математические методы становились настолько важными, что их стали засекречивать. Так книга с описанием новой методики, позволявшей сократить количество испытаний (“Последовательный анализ” Вальда), была издана только после окончания второй мировой войны в 1947 году.
- Медицина. Широкое применение статистических методов в медицине началось сравнительно недавно (вторая половина 20 века). Развитие эффективных методов лечения (антибиотики, инсулин, эффективная анестезия, искусственное кровообращение) потребовало достоверных методов оценки их эффективности. Возникло новое понятие “Доказательная медицина”. Начал развиваться более формальный, количественный подход к терапии многих заболевании – введение протоколов.
- Биоинформатика. К 1968му году уже были осуществлены проекты, связанные со строительством атомных электростанций, полетами на Луну, созданием термоядерной бомбы. Начиная с 1980-х годов количество известных последовательностей белков и нуклеиновых кислот стремительно возросло. Объем накопленной информации таков, что только компьютерный анализ этих данных может решать задачи по извлечению информации. С середины 1980-х годов появилась возможность широкого использования быстрых и доступных компьютеров.
- Основные формулы
Основное понятие теории вероятностей – вероятность. Это слово достаточно часто применяется в повседневной жизни. Наверняка, каждому знакомы фразы: «завтра, вероятно, выпадет снег», или «вероятнее всего в выходные я поеду на природу». С.И. Ожегов словаре дает такое толкование слова вероятность: «возможности осуществления чего-нибудь». Там же дает определение понятию теории вероятностей: «раздел математики, изучающий закономерности, основанные на взаимодействии большого числа случайных явлений».
При изучении явлений, мы проводим эксперименты, в ходе которых происходят различные события, среди которых различают: достоверные, невозможные, равновероятные, случайные.
Опр. Событие В называют достоверным в некотором испытании, если в ходе этого испытания оно обязательно произойдет.
Пример: событие В: при одном бросании игральной кости, выпадет одно из шести чисел 1,2,3,4,5,6.
Опр. Событие С называют невозможным в некотором испытании, если в ходе этого испытания оно никогда не произойдет.
Пример: событие С: при однократном бросании игральной кости, выпадет число большее 6. Понятно, что это невозможно.
Опр. Равновероятными называют события, которые при данных условиях в некотором испытании имеют одинаковые шансы для наступления.
Пример: событие D: при однократном бросании симметричной монеты выпадет орёл. Монета имеет две стороны и всего два исхода, поэтому вероятности выпадения орла или решки равны.
Опр. Событие А называют случайным в некотором испытании, если в ходе этого испытания оно может произойти или не произойти.
Пример: событие А: при однократном бросании игральной кости выпадет четное число. Четное число может выпасть, а может выпасть нечетное число.
Особое место в теории вероятностей занимают случайные события, ведь если событие случайное, значит, не подчиняется закономерностям, алгоритмам. Оказывается, и в мире случайного действуют определенные законы, позволяющие вычислять вероятности.
Как уже было сказано, существуют разные вероятности: классическая, статистическая, так же в экзамен ЕГЭ включены задачи, решаемые с помощью теорем теории вероятностей. В школе изучают классическое определение вероятности. Рассмотрим классическое определение вероятности.
Принято вероятность события А обозначать так: Р(А), тогда формула для вычисления вероятности записывается так:
Опр. Вероятностью Р(А) события А в испытании с равновозможными элементарными исходами называется отношение числа исходов , благоприятствующих событию
, к числу исходов
всех исходов испытания. Из формулы (1) следует, что
При решении вероятностных задач часто приходится сталкиваться с многократными повторами испытаний и исход каждого испытания независим от исходов других. Такой эксперимент называется схемой повторных независимых испытаний или схемой Бернулли. Данная схема названа в честь выдающегося швейцарского математика Якоба Бернулли, выведшего формулу для нахождения вероятности появления случайного события:
(2),
где – вероятность, что событие
появится ровно m раз в n испытаниях,
– число испытаний,
– вероятность появления события
в одном испытании,
– вероятность не появления события
в одном испытании.
Из комбинаторики мы знаем, что число сочетаний выражается формулой: . Тогда заменим в (2):
Данную формулу будем применять при расчете вероятности получения положительной отметки при выполнении теста.
- Вероятности в жизни
В жизни мы каждый день встречаемся с задачами из теории вероятностей, но мало кто сможет такую задачу решить. В школе на уроках математики нас знакомят и учат решат простейшие вероятностные и комбинаторные задачи начиная с пятого класса. Ниже представлены некоторые виды таких задач, встречающихся в жизни.
1. Игры в кости
Кости – одна из древнейших игр. Инструментом для игры являются кубики (кости) в количестве от одного до пяти в зависимости от вида игры. Суть игры состоит в выбрасывании кубиков и дальнейшем подсчёте очков, количество которых и определяет победителя. Разновидности игры предполагают разный подсчёт очков.
2. Коды на ….
– сейфах
– телефонные номера
– пароль в социальных сетях (агент, одноклассники и т.д.)
3. Лотереи
Лотерея – организованная игра, при которой распределение выгод и убытков зависит от случайного извлечения того или иного билета или номера (жребия, лота). Кто из нас не мечтал выиграть в лотерею миллион! Но все мы реалисты, и понимаем, что вероятность такого выигрыша очень мала. Ведь игра в лотерею – это игра с судьбой, попытка поймать удачу; и чем больше выигрыш стоит на кону – тем сильнее ощущения!
4. Карточные игры
Карточная игра — игра с применением игральных карт, характеризуется случайным начальным состоянием, для определения которого используется набор (колода).
Важным принципом практически всех карточных игр является случайность порядка карт в колоде. Перед использовании той же колоды в следующей игре карты в ней перемешиваются (перетасовываются).
5. Игровые автоматы
Известно, что в игровых автоматах скорость вращения барабанов зависит от работы микропроцессора, повлиять на который нельзя. Но можно вычислить вероятность выигрыша на игровом автомате, в зависимости от количества символов на нем, числа барабанов и других условий. Однако выиграть это знание вряд ли поможет. Тут все решает Её величество фортуна.
- ПРАКТИЧЕСКАЯ ЧАСТЬ
В эксперименте принимали участие 27 девятиклассников и 15 десятиклассников.
Всё исследование мы разбили на несколько этапов:
1) анкетирование учащихся 9х-10го классов и анализ результатов;
2) составление тестов разного уровня сложности;
3) апробация тестов, анализ результатов;
4) общий вывод.
На первом этапе мы провели анкетирование (приложение 1) среди учащихся 9х-10го класса нашей школы, в котором им нужно было ответить на вопрос «Возможно ли пройти тест на «хорошо» и «отлично», выбирая вариант ответа наугад?».
В результате анкетирования выяснилось, что 69% учащихся предложенной группы считают, что возможно получить отметку «хорошо» или «отлично» путем угадывания правильного ответа в тесте.
Второй этап исследования.
На этом этапе мы занялись составлением тестов разной структуры. Мы решили проверить, как будет отличаться вероятность получения положительной отметки в зависимости от количества вариантов ответа. Понятно, что вероятность уменьшится, если правильных вариантов будет несколько как, например, в 20м задании ОГЭ по математике, поэтому решили ограничиться одним верным вариантом.
Решили составить три типа тестов с двумя, тремя и четырьмя вариантами ответа, из которых только один верный. Мы решили составить комбинированные тесты по математике (алгебра и геометрия вместе) из 10 вопросов. Вопросы взяты из открытого банка заданий ОГЭ сайта ФИПИ. Тесты представлены в приложении 2.
Так как тест состоит из 10 вопросов, то, чтобы получить отметку «хорошо» или «отлично», учащемуся необходимо набрать от 7 до 10 баллов.
Третий этап исследования.
Для подтверждения гипотезы исследования, учащимся на уроках математики были предложены контрольные работы в тестовой форме разного уровня структуры. Их задачей было наугад выбрать правильный ответ. Далее сравним теоретические подсчеты с реальными данными.
Наше исследование является задачей случайных событий в независимых испытаниях, поэтому для обработки данных мы использовали формулу Бернулли, она позволила нам вычислить вероятность получения положительной отметки при написании тестовой контрольной работы путем угадывания правильного ответа.
Вспомним формулу и её компоненты:
где – вероятность, что событие
появится ровно
раз в
испытаниях,
– число испытаний,
– вероятность появления события
в одном испытании,
– вероятность не появления события
в одном испытании.
Согласно этой формуле, мы должны выбрать событие A. Рассчитаем вероятность для каждого отдельного теста.
- Тест с двумя вариантами ответа.
Событие : верный ответ в одном вопросе. Тогда
, тогда
. Чтобы получить положительную отметку, необходимо набрать минимум 7 баллов, значит
.
Теоретически, отметку «хорошо» и «отлично», выбирая ответ наугад можно получить с вероятностью всего лишь 0,12. А эксперимент с учащимися показал следующий результат: из сорока двух тестируемых только у девяти получилось набрать 7 и более баллов. Таким образом экспериментально вероятность составила – это 21%.
- Тест с тремя вариантами ответа.
Событие : верный ответ в одном вопросе. Тогда
, тогда
. Чтобы получить положительную отметку, необходимо набрать минимум 7 баллов, значит
.
Добавлением еще одного варианта ответа, мы уменьшили вероятность получения положительной отметки почти в 8 раз. Даже с тремя вариантами ответа мы получаем практически нулевую вероятность. Результат практического эксперимента: только одному тестируемому удалось получить отметку «хорошо». Вероятность 0,023 – 2%.
- Тест с четырьмя вариантами ответа.
Событие : верный ответ в одном вопросе. Тогда
, тогда
. Чтобы получить положительную отметку, необходимо набрать минимум 7 баллов, значит
.
Экспериментально ни один тестируемый не смог получить отметку 4 или 5.
Вывод: угадать на хорошую отметку можно, особенно в тестах с малым выбором вариантов ответа. Вероятность получения хорошей отметки в тесте с четырьмя вариантами очень мала – практически нулевая. Мы проводили эксперимент с тестами, считая, что учащиеся не знают ответ ни на один вопрос теста, но что если ученик знает половину и больше? Тогда угадать правильный ответ всего на 5 и менее вопросов из двух вариантов не сложно. Поэтому данный вид теста не будет на 100% отражать уровень знаний учащегося. Поэтому, мы считаем, что наиболее оптимальным (нелегким для учащегося и не сложным в проверке для учителя) будет тест, содержащий 4 варианта ответа.
Результаты практических экспериментов и их теоретическое обоснование подтверждают правильность выдвинутой гипотезы.
ЗАКЛЮЧЕНИЕ
Проведя данное исследование, мы можем сделать вывод о том, что только планомерная, вдумчивая и добросовестная учеба в школе позволит обучающимся успешно писать тестовые контрольные работы, хорошо подготовиться к государственной итоговой аттестации в среднем и старшем звене. Ведь, не научившись учиться в школе, будет очень трудно обучаться на более высоких ступенях.
Таким образом, гипотеза исследования подтверждена, цель работы достигнута и задачи выполнены.
Список использованных источников
1. Алтынов П.И. Алгебра. Тесты. 7-9 классы: Учебно- методическое пособие. – 3-е изд. – М.: Дрофа, 1999. – 128 с.
2. Алтынов П.И. Геометрия. Тесты. 7-9 классы: Учебно- методическое пособие. – 3-е изд. – М.: Дрофа, 1999. – 122 с.
3. Лоэв М. Теория вероятностей. М.: ИЛ, 1962
4. Митропольский А.К. Техника статистических вычислений (2-е изд.). М.: Наука, 1971
5. Невё Ж. Математические основы теории вероятностей. М.: Мир, 1982
6. Новейший справочник школьника. Г.П.Шалаева — М.: СЛОВО; Эксмо, 2005. — 736с.
7. Энциклопедический словарь юного математика./Сост. А.П.Савин. — М.: Педагогика, 1985. — 352с., ил.
8. http://ru.wikipedia.org/
9. http://www.teorver.ru/vvedenie-v-teoriyu-veroyatnostej/
10. http://www.fmclass.ru/
11.https://ru.wikipedia.org/wiki
12. http://www.nsu.ru/mmf/tvims/chernova/tv/lec/node4.html
13. http://www.grandars.ru/student/vysshaya-matematika/veroyatnost-sobytiya.html
14. http://sins.xaoc.ru/pdf/articles/articles_r038.pdf
15. http://www.ofim.oscsbras.ru/~klokov/probability/download/essay.pdf
ПРИЛОЖЕНИЯ
Приложение 1
Анкета
Ответьте на вопрос:
Возможно ли пройти тест на «хорошо» и «отлично», выбирая вариант ответа наугад?
Да Нет
Приложение 2
Итоговый контрольный тест
Выберите вариант ответа. Примечание: только один вариант является верным.
- Найдите значение выражения 4,6 · 3,9 + 1,74.
А) 19,8
Б) 19,68
В) 1620
Г) 16,20
2. На координатной прямой точки A, B, C и D соответствуют числам 0,0137; 0,103; 0,03; 0,021.
Какой точке соответствует число 0,03?
А) A
Б) B
В) C
Г) D
3. Какое из чисел больше: или
А)
Б)
В)
Г) Никакое
4. Найдите корни уравнения .
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
А) 50
Б) 5
В) 05
Г) 210
5. На экзамене 60 билетов, Олег не выучил 12 из них. Найдите вероятность того, что ему попадется выученный билет.
А) 48
Б) 12
В) 0,48
Г) 0,8
6. — правильный восьмиугольник. Найдите угол
. Ответ дайте в градусах.
А) 45
Б) 22,5
В) 8
Г) 90
7. Величина центрального угла AOD равна 110°. Найдите величину вписанного угла ACB. Ответ дайте в градусах.
А) 55
Б) 110
В) 125
Г) 70
- В трапеции ABCD известно, что AD=6, BC=5, а её площадь равна 22. Найдите площадь треугольника ABC.
А) 12
Б) 11
В) 10
Г) 22
9. На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
А) 4
Б) 9
В)10
Г) 2,5
10. Какие из следующих утверждений верны?
1) Треугольника со сторонами 1, 2, 4 не существует.
2) Смежные углы равны.
3) Все диаметры окружности равны между собой.
А) только 1
Б) 1 и 2
В) все верны
Г) 2 и 3
На чтение 16 мин Просмотров 105к. Опубликовано 25 мая, 2018
Вероятность — очень лёгкая тема, если концентрироваться на смысле задач, а не на формулах. Найти вероятность того что — не просто. И как решать задачи на вероятность?. Во-первых, что такое вероятность? Это шанс, что какое-то событие произойдёт. Если мы говорим, что вероятность некоторого события 50%, что это значит? Что оно либо произойдет, либо не произойдет — одно из двух. Таким образом подсчитать значение вероятности очень просто — нужно взять количество подходящих нам вариантов и разделить на количество всех возможных вариантов. Например, шанс получить решку при подбрасывании монеты это ½. Как мы получаем ½? Всего у нас два возможных варианта (орёл и решка), из них нам подходит один (решка), так мы и получаем вероятность ½.
Как мы уже с вами увидели, вероятность может быть выражена как в процентах, так и в обычных числах. Важно: на ЕГЭ вам нужно будет записать ответ в числах, не в процентах. Принято, что вероятность изменяется от 0 (никогда не произойдет) до 1 (абсолютно точно произойдет). Также можно сказать, что всегда
Вероятность подходящих событий + вероятность неподходящих событий = 1
Теперь мы точно понимаем, как считать вероятность отдельного события, и даже такие задачи есть в банке ФИПИ, но понятно, что на этом всё не заканчивается. Чтобы жизнь была веселее, в задачах на вероятность обычно происходят как минимум два события, и надо посчитать вероятность с учетом каждого из них.
Содержание
- Вероятность нескольких событий
- Задачи и решения задач на вероятность
- Вероятность нескольких событий
- Дополняющая вероятность
Вероятность нескольких событий
Подсчитываем вероятность каждого события в отдельности, затем между дробями ставим знаки:
1. Если нужно первое И второе событие, то умножаем.
2. Если нужно первое ИЛИ второе событие, то складываем.
Задачи и решения задач на вероятность
Задача 1. Среди натуральных чисел от 23 до 37 случайно выбирают одно число. Найдите вероятность того, что оно не делится на 5.
Решение:
Вероятность, это отношение благоприятных вариантов к общему их количеству.
Всего в этом промежутке 15 чисел. Из них на 5 делится всего 3, значит не делится 12.
Вероятность тогда:
Ответ: 0,8.
Задача 2. Для дежурства в столовой случайно выбирают двух учащихся класса. Какова вероятность того, что дежурить будут два мальчика, если в классе обучается 7 мальчиков и 8 девочек?
Решение: Вероятность, это отношение благоприятных вариантов к общему их количеству. В классе 7 мальчиков, это благоприятные варианты. А всего 15 учеников.
Вероятность что первый дежурный мальчик:
Вероятность что второй дежурный мальчик:
Раз оба должны быть мальчики, вероятности перемножим:
Ответ: 0,2.
Задача 3. На борту самолёта 12 мест рядом с запасными выходами и 18 мест за перегородками, разделяющими салоны. Остальные места неудобны для пассажира высокого роста. Пассажир В. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру В. достанется удобное место, если всего в самолёте 300 мест.
Решение: Пассажиру В. удобны 30 мест (12 + 18 = 30), а всего в самолете 300 мест. Поэтому вероятность того, что пассажиру В. достанется удобное место равна 30/300, т. е. 0,1.
Задача 4. В сборнике билетов по математике всего 25 билетов, в 10 из них встречается вопрос по неравенствам.
Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по неравенствам.
Решение: Из 25 билетов 15 не содержат вопроса по неравенствам, поэтому вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по неравенствам, равна 15/25, т. е. 0,6.
Задача 5. В сборнике билетов по химии всего 35 билетов, в 7 из них встречается вопрос по кислотам.
Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по кислотам.
Решение: Из 35 билетов 28 не содержат вопроса по кислотам, поэтому вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по кислотам, равна 28/35, т. е. 0,8.
Задача 6. В среднем из 500 садовых насосов, поступивших в продажу, 2 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
Решение: Если из 500 насосов 2 подтекают, то 498 не подтекают. Следовательно, вероятность выбора хорошего насоса — 498/500, т. е. 0,996.
Задача 7. Вероятность того, что новый пылесос в течение года поступит в гарантийный ремонт, равна 0,065. В некотором городе из 1000 проданных пылесосов в течение года в гарантийную мастерскую поступило 70 штук.
На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?
Решение: Частота события «гарантийный ремонт» равна 70/1000, т. е. 0,07. Она отличается от предсказанной вероятности на 0,005 (0,07 – 0,065 = 0,005).
Задача 8. В чемпионате по гимнастике участвуют 50 спортсменок: 18 из России, 14 из Украины, остальные — из Белоруссии. Порядок, в котором выступают гимнастки, определяется жребием.
Найдите вероятность того, что спортсменка, выступающая первой, окажется из Белоруссии.
Решение: Всего участниц на чемпионате 50, а спортсменок из Белоруссии — 18 (50 – 18 – 14 = 18).
Вероятность того, что первой будет выступать спортсменка из Белоруссии — 18 из 50, т. е. 18/50, или 0,36.
Задача 9. Научная конференция проводится в 5 дней. Всего запланировано 80 докладов — первые три дня по 12 докладов, остальные распределены поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой.
Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
Решение: За первые три дня будут прочитаны 36 докладов (12 ∙ 3 = 36), на последние два дня планируется 44 доклада. Поэтому на последний день запланировано 22 докладов (44 : 2 = 22). Значит, вероятность того, что доклад профессора М. окажется запланированным на последний день конференции, равна 22/80, т. е. 0,275.
Задача 10.
Перед началом первого тура чемпионата по шахматам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 шахматистов, среди которых 14 участников из России, в том числе Егор Косов.
Найдите вероятность того, что в первом туре Егор Косов будет играть с каким-либо шахматистом из России?
Решение: В первом туре Егор Косов может сыграть с 25 шахматистами (26 – 1 = 25), из которых 13 ― из России. Значит, вероятность того, что в первом туре Егор Косов будет играть с каким-либо шахматистом из России, равна 13/25, или 0,52.
Задача 11.
В чемпионате мира участвуют 16 команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп: 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4.
Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе?
Решение: Вероятность того, что команда России окажется во второй группе, равна отношению количества карточек с номером 2, к общему числу карточек, т. е. 4/16, или 0,25.
Задача 12. В группе туристов 5 человек. С помощью жребия они выбирают двух человек, которые должны идти в село за продуктами. Турист А. хотел бы сходить в магазин, но он подчиняется жребию. Какова вероятность того, что А. пойдёт в магазин?
Решение: Выбирают двоих туристов из пяти. Следовательно, вероятность быть выбранным равна 2/5, т. е. 0,4.
Задача 13. В группе туристов 30 человек. Их вертолётом в несколько приёмов забрасывают в труднодоступный район по 6 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист П. полетит первым рейсом вертолёта.
Решение: На первом рейсе 6 мест, всего мест 30. Тогда вероятность того, что турист полетит первым рейсом вертолёта, равна 6/30, или 0,2.
Задача 14. Какова вероятность того, что случайно выбранное натуральное число от 10 до 19 делится на три?
Решение: Натуральных чисел от 10 до 19 десять, из них на 3 делятся три числа: 12, 15 и 18. Следовательно, искомая вероятность равна 3/10, т. е. 0,3.
Вероятность нескольких событий
Задача 1. Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Стартер» по очереди играет с командами «Ротор», «Мотор» и «Стратор». Найдите вероятность того, что «Стартер» будет начинать только вторую игру.
Решение:
Тип вопроса: совмещение событий.
Нас устроит следующий вариант: «Статор» не начинает первую игру, начинает вторую игру, не начинает третью игру. Вероятность такого развития событий равна произведению вероятностей каждого из этих событий. Вероятность каждого из них равна 0,5, следовательно: 0,5 · 0,5 · 0,5 = 0,125.
Задача 2. Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей ― 1 очко, если проигрывает ― 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,4.
Решение:
Тип вопроса: совмещение событий.
Задачу выполняют несколько вариантов:
| Игра №1 | Игра №2 | Вероятность данного варианта |
| 3 | 1 | 0,4 · 0,2 = 0,08 |
| 1 | 3 | 0,2 · 0,4 = 0,08 |
| 3 | 3 | 0,4 · 0,4 = 0,16 |
Вероятность происхождения какого-либо их этих 3-х вариантов равна сумме вероятностей каждого из вариантов: 0,08 + 0,08 + 0,16 = 0,32.
Задача 3. В классе учится 21 человек. Среди них две подруги: Аня и Нина. Класс случайным образом делят на 7 групп, по 3 человека в каждой. Найти вероятность того что Аня и Нина окажутся в одной группе.
Решение:
Тип вопроса: уменьшение групп.
Вероятность попадания Ани в одну из групп равна 1. Вероятность попадания Нины в ту же группу равна 2 из 20 (2 оставшихся места в группе, а человек осталось 20). 2/20 = 1/10 = 0,1.
Задача 4. В кармане у Пети было 4 монеты по рублю и 2 монеты по два рубля. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что обе двухрублёвые монеты лежат в одном кармане.
Решение:
Способ №1
Тип задачи: уменьшение групп.
Представим, что шесть монет делят на две группы по три монеты. Вероятность, что первая однорублевая монета попадет в один из карманов (групп) = 1.
Вероятность, что две двухрублевые монеты попадут в этот же карман = количество оставшихся мест в этом кармане/на количество оставшихся мест в обоих карманах = 2/5 = 0,4.
Способ №2
Тип вопроса: совмещение событий.
Задачу выполняют в несколько вариантов:
Если Петя переложил в другой карман три из четырех рублевых монет (а двухрублевые не перекладывал), или если переложил в другой карман обе двухрублевые монеты и одну рублевую одним из трех способов: 1, 2, 2; 2, 1, 2; 2, 2, 1. Можно изобразить это на схеме (перекладывает Петя в карман 2, поэтому будем высчитывать вероятности в колонке «карман 2»):
Вероятность происхождения какого-либо их этих 4-х вариантов равна сумме вероятностей каждого из вариантов:
Задача 5. В кармане у Пети было 2 монеты по 5 рублей и 4 монеты по 10 рублей. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных карманах.
Решение:
Тип задачи: уменьшение групп.
Способ №1
Представим, что шесть монет делят на две группы по три монеты. Вероятность, что первая двухрублевая монета попадет в один из карманов (групп) = 1. Вероятность, что вторая монета попадет в другой карман = количество оставшихся мест в другом/ на количество оставшихся мест в обоих карманах = 3/5 = 0,6.
Способ №2
Тип вопроса: совмещение событий.
Задачу выполняют несколько вариантов:
Чтобы пятирублевые монеты оказались в разных карманах, Петя должен взять из кармана одну пятирублевую и две десятирублевые монеты. Это можно сделать тремя способами: 5, 10, 10; 10, 5, 10 или 10, 10, 5. Можно изобразить это на схеме (перекладывает Петя в карман 2, поэтому будем высчитывать вероятности в колонке «карман 2»):
Вероятность происхождения какого-либо их этих 4-х вариантов равна сумме вероятностей каждого из вариантов:
Задача 6. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орёл выпадет ровно два раза.
Решение: Тип вопроса: нахождение желаемого и действительного совмещение событий Нас устраивают три варианта:
Орёл ― решка ― орёл;
Орёл ― орёл ― решка;
Решка ― орёл ― орёл;
Вероятность каждого случая ― 1/2, а каждого варианта ― 1/8 (1/2 ∙ 1/2 ∙ 1/2 = 1/8)
Нас устроит либо первый, либо второй, либо третий вариант. Следовательно, складываем их вероятности и получаем 3/8 (1/8 + 1/8 + 1/8 = 3/8), т. е. 0,375.
Задача 7. Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,5. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,34. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
Решение:
Тип вопроса: совмещение событий.
В любом случае А. будет играть как белыми, так и черными, поэтому нас устроит вариант, когда гроссмейстер А. выиграет, играя белыми (вероятность ― 0,5), а также играя чёрными (вероятность ― 0,34). Поэтому надо перемножить вероятности этих двух событий: 0,5 ∙ 0,34 = 0,17.
Задача 8. Вероятность того, что батарейка бракованная, равна 0,02. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.
Решение:
Тип вопроса: совмещение событий.
Вероятность того, что батарейка исправна, равна 0,98. Покупателю надо, чтобы и первая, и вторая батарейка были исправны: 0,98 · 0,98 = 0,9604.
Задача 9. На рок-фестивале выступают группы ― по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из США будет выступать после группы из Канады и после группы из Китая? Результат округлите до сотых.
Решение:
Тип вопроса: совмещение событий.
Общее количество выступающих на фестивале групп для ответа на вопрос неважно. Сколько бы их ни было, для указанных стран есть 6 способов взаимного расположения среди выступающих (КИТ — Китай, КАН = Канада):
… США, КАН, КИТ …
… США, КИТ, КАН …
… КИТ, США, КАН …
… КАН, США, КИТ …
… КАН, КИТ, США …
… КИТ, КАН, США …
США находится после Китая и Канады в двух последних случаях. Поэтому вероятность того, что группы случайным образом будут распределены именно так, равна:
≈ 0,33.
Дополняющая вероятность
Задача 1.
Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,02. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,97. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,05.
Найдите вероятность того, что случайно выбранная батарейка будет забракована.
Решение:
Существуют 2 варианта, которые нам подходят:
Вариант А: батарейка забракована, она неисправна;
Вариант Б: батарейка забракована, она исправна.
Вероятность варианта А: 0,02 ∙ 0,97 = 0,0194;
Вероятность варианта Б: 0,05 ∙ 0,98 = 0,049;
Нас устроит либо первый, либо второй вариант: 0,0194 + 0,049 = 0,0684.
Задача 2. Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 60% этих стекол, вторая — 40%. Первая фабрика выпускает 3% бракованных стекол, а вторая — 5%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Решение:
Вероятность того, что стекло куплено на первой фабрике и оно бракованное: 0,6 · 0,03 = 0,018.
Вероятность того, что стекло куплено на второй фабрике и оно бракованное: 0,4 · 0,05 = 0,02.
Вероятность того, что случайно купленное в магазине стекло окажется бракованным, равна 0,018 + 0,02 = 0,038.
Задача 3. На фабрике керамической посуды 10% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 80% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Результат округлите до тысячных.
Решение:
Предположим, у нас х тарелок изначально (ведь мы постоянно имеем дело с процентами, поэтому нам ничего не мешает оперировать конкретными величинами).
Тогда 0,1х — дефектные тарелки, а 0,9х — нормальные, которые поступят в магазин сразу. Из дефектных убирается 80%, то есть 0,08х, и остаётся 0,02х, которые тоже пойдут в магазин. Таким образом, общее количество тарелок на полках в магазине окажется: 0,9х + 0,02х = 0,92х. Из них нормальными будет 0,9х. Соответственно, по формуле вероятность будет 0,9х/0,92х ≈ 0,978.
Задача 4. По отзывам покупателей Игорь Игоревич оценил надёжность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,91. Вероятность того, что этот товар доставят из магазина Б, равна 0,89. Игорь Игоревич заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар.
Решение. Вероятность того, что первый магазин не доставит товар, равна 1 − 0,91 = 0,09. Вероятность того, что второй магазин не доставит товар, равна 1 − 0,89 = 0,11. Вероятность происхождения двух этих событий одновременно равна произведению вероятностей каждого из них: 0,09 · 0,11 = 0,0099.
Задача 5. При изготовлении подшипников диаметром 70 мм вероятность того, что диаметр будет отличаться от заданного меньше чем на 0,01 мм, равна 0,961. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше чем 69,99 мм или больше чем 70,01 мм.
Решение: Нам дана вероятность события, при котором диаметр будет в пределах между 69,99 мм и 70,01 мм, и она равна 0,961. Вероятность всех остальных вариантов мы можем найти по принципу дополняющей вероятности: 1 − 0,961 = 0,039.
Задача 6. Вероятность того, что на тесте по истории учащийся верно решит больше 9 задач, равна 0,68. Вероятность того, что верно решит больше 8 задач, равна 0,78. Найдите вероятность того, что верно решит ровно 9 задач.
Решение: Вероятность того, что Т. верно решит более 8 задач, включает в себя вероятность решения ровно 9 задач. При этом, события, при которых О. решит больше 9 задач, нам не подходят. Следовательно, отняв от вероятности решения более 9 задач вероятность решения более 8 задач, мы и найдём вероятность решения только 9 задач: 0,78 – 0,68 = 0,1.
Задача 7. Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 21 пассажира, равна 0,88. Вероятность того, что окажется меньше 12 пассажиров, равна 0,66. Найдите вероятность того, что число пассажиров будет от 12 до 20.
Решение. Вероятность того, что в автобусе окажется меньше 21 пассажира, включает в себя вероятность, что в нём окажутся от 12 до 20 пассажиров. При этом события, при которых пассажиров будет меньше 12, нам не подходят. Следовательно, отняв от первой вероятности (менее 21) вторую вероятность (менее 12), мы и найдём вероятность того, что пассажиров будет от 12 до 20 : 0,88 – 0,66 = 0,22.
Задача 8. В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,9 погода завтра будет такой же, как и сегодня. 10 апреля погода в Волшебной стране хорошая. Найдите вероятность того, что 13 апреля в Волшебной стране будет отличная погода.
Решение:
Задачу выполняют несколько вариантов («Х» — хорошая погода, «О» — отличная погода):
| 11 апреля | 12 апреля | 13 апреля | Вероятность данного варианта |
| X – 0,9 | X – 0,9 | O – 0,1 | 0,9 ·0,9 ·0,1 = 0,081 |
| X – 0,9 | O – 0,1 | O – 0,9 | 0,9 ·0,1 ·0,9 = 0,081 |
| O – 0,1 | O – 0,9 | O – 0,9 | 0,1 ·0,9 ·0,9 = 0,081 |
| O – 0,1 | X – 0,1 | O – 0,1 | 0,1 ·0,1 ·0,1 = 0,001 |
Вероятность происхождения какого-либо их этих 4-х вариантов равна сумме вероятностей каждого из вариантов: 0,081 + 0,081 + 0,081 + 0,001 = 0,244.
Задача 9. В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода.
Решение:
Задачу выполняют несколько вариантов («Х» ― хорошая погода, «О» ― отличная погода):
| 4 июля | 5 июля | 6 июля | Вероятность данного варианта |
| X – 0,8 | X – 0,8 | O – 0,2 | 0,8 · 0,8 · 0,2 = 0,128 |
| X – 0,8 | O – 0,2 | O – 0,8 | 0,8 · 0,2 · 0,8 = 0,128 |
| O – 0,2 | O − 0,8 | O − 0,8 | 0,2 · 0,8 · 0,8 = 0,128 |
| O – 0,2 | X – 0,2 | O – 0,2 | 0,2 · 0,2 · 0,2 = 0,008 |
Вероятность происхождения какого-либо их этих 4 ― х вариантов равна сумме вероятностей каждого из вариантов: 0,128 + 0,128 + 0,128 + 0,008 = 0,392.
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Каждый человек в той или иной мере применяет теорию вероятности для анализа произошедших в его жизни событий. Люди обращают внимание на вероятность вещей и прогнозируют свое дальнейшие поведение. Но к большому сожалению, не всегда возможны точно определить вероятность того или иного события. [1,3]
Примеров реального использования теории вероятности в жизни огромное множество. Так, практически вся современная экономика базируется на ней. В общем, можно сказать, что теория вероятности будет иметь большое значение в начале практически любой деятельности, а так же в её регулировании. Она дает возможность оценить шансы той или иной неполадки, позволяет нам понять, что нужно проверить и какие усилия необходимо предпринять, исходя из полученных данных. [5]
Любую деятельность любой сферы можно проанализировать, используя статистику, рассчитать благодаря теории вероятности и заметно улучшить.
Попробуем составить собственный алгоритм для решения задач по теории вероятности: [2,4]
Необходимо ознакомится с условием задачи и понять какие действия, с какими предметами выполняются.
Определить ключевой вопрос задачи и обозначить событие, вероятность которого необходимо вычислить.
Чтобы выбрать дальнейшую последовательность действий следует конкретизировать тип задачи и выяснить, какие формулы будут использоваться в дальнейшем для её решения.
Исходя из ответов на приведенные вопросы, выбрать формулы и подставить в них данные задачи.
Готово, вероятность найдена.
Одно из важных событий в жизни любого студента – это сессия. Это то время, когда нервничают все, включая отличников. Ведь всегда существует вероятность не сдать экзамен. Чтобы этого не произошло необходимо соблюдать десятки различных примет, можно даже обратиться к нумерологии. Но один из простых способов вытянуть счастливый билет – рассчитать вероятность его выпадения.
Составим и решим несколько простыхзадач, на примере которых каждый студент может вычислить вероятность выпадения счастливого билета на экзамене. [6]
Задача 1. «На экзамене по математике шесть студентов второго курса факультета агробиологии и земельных ресурсов друг за другом вытягивают билеты. Тридцать билетов включают в себя четыре простых вопроса. Необходимо вычислить вероятность, что хотя бы одному студенту попадется билет с простыми вопросами».
Решение: В первую очередь, определим ключевой вопрос задачи — вычислить вероятность, что хотя бы одному студенту попадется билет с простыми вопросами.
Далее пойдем от обратного, найдем вероятность того, что никому из студентов не попадется простой билет.
Эта вероятность будет равна
Первая дробь показывает вероятность того, что билет со сложным вопросом достался первому студенту.
Вторая дробь показывает вероятность того, что билет со сложным вопросом достался второму студенту. Третья дробь показывает вероятность того, что билет со сложным вопрос достался третьему студенту и так далее до шестого студента. Так как в задаче требуется одновременное выполнение условий, то вероятности следует перемножить.
Для того, чтобы найти искомую вероятность, надо вычесть полученную выше вероятность из единицы.
Задача 2. Леша, студент второго курса факультета механизации сельского хозяйства, сдаёт экзамен по теоретической механике, при этом из 50 билетов 35 он знает хорошо, а 15 плохо. Допустим, группа сдаёт экзамен по частям. В первый день 15 человек, включая Алексея. В каком случае Леше достанется с большей вероятностью «счастливый» билет — если он пойдет на экзамен в числе первых, в середине или же будет тянуть билет последним? Когда ему лучше зайти в кабинет?
Для начала рассмотрим случай, при котором Леша сохраняет свои шансы постоянными, то есть он не знает какие билеты вытянули однокурсники и не учит вопросы, которые знает плохо.
Пусть Алексей зайдет в аудиторию первым и вытянет «счастливый» билет, обозначим это событие . По классическому определению вероятности:
Может ли измениться вероятность извлечения нужного билета, если пропустить вперед отличника Жору? В этом случае станут возможными две несовместимые гипотезы:
— Жора вытянет «счастливый» (для Леши) билет;
— Жора вытянет «несчастливый» билет, таким образом, увеличивая шансы Леши.
Событие, при котором Леша зайдет вторым и вытянет «счастливый» билет становится зависимым.
1) Можно предположить, что Жора с вероятностью забрал у Леши «удачный» билет. Тогда останется всего 49 билетов, среди которых 34 «Счастливых». По классическому определению вероятности:
2) Допустим, что Жора с вероятностью «спас» Лешу от одного сложного билета. В этом случае останется 49 билетов, 35 из которых «счастливые». Тогда по классическому определению вероятности:
Воспользовавшись теоремами сложения вероятностей несовместных и умножение вероятностей зависимых событий, определим вероятность, что Леша вытянет «счастливый» билет, будучи вторым в очереди:
Вероятность не изменилась.
Рассмотрим следующее событие , при котором Леша пойдет третьим, пропустив перед собой Жору и Леру, и вытянет «счастливый» билет.
В данном событии гипотез будет больше: однокурсники могут забрать два удачных билета или же два неудачных, так же вытянуть один «счастливый» билет и один «несчастливый» билет. Проведем аналогичные рассуждения, воспользуемся теми же теоремами и получим значение вероятности . И так далее.
Следовательно, не важно, когда идти – первоначальные вероятности останутся неизменными. Но нужно помнить, что это лишь усредненная теоретическая оценка. Если Леша пойдет последним на экзамен, то это не значит, что ему достанутся на выбор 17 «счастливых» билетов и 19 «несчастливых» билетов в соответствии с его изначальными шансами. Это соотношение может изменяться, как в лучшую, так и в худшую сторону. Однако, маловероятно, что среди билетов останутся одни «счастливые» или же наоборот — «несчастливые».
Математика и «чистый эксперимент» — это хорошо, но чего следует придерживаться в реальных условиях? Нужно принять во внимание субъективные факторы, такие как дополнительный балл для «храбрецов» или же усталость преподавателя в конце экзамена. Часто они могут решающими факторами.
В случае, если вы хорошо подготовились к экзамену, то лучше идти в числе первых, так как есть полный комплект билетов, постулат «мало возможные события не происходят» работает в большей степени.
Если же студент готов к экзамену достаточно хорошо, но пробелы в знаниях всё-таки есть, то будет целесообразно пропустить вперед несколько человек и ожидать подходящего момента вне аудитории. Здесь нужно действовать по ситуации, когда начнет поступать информация о вытянутых билетах, и можно будет учить и повторять оставшиеся билеты, повышая первоначальную вероятность своего успеха.
В случае, если вы готовы неважно или плохо, то лучше идти в последнюю очередь. Существует небольшая вероятность, что останутся «счастливые» для вас билеты, вы можете изучить материал за время экзамена или же (в крайнем случае) сделать «шпаргалку».
Никогда невозможно точно предугадать, что произойдет с нами через день, два. Ведь событий связанных с нами в каждый момент невероятно много. Безусловно, мало кто будет высчитывать по формулам вероятность появления событий, но иногда бывает интересно проверить совпадает ли «эмпирический анализ» с математическим. Теория вероятности позволяет предугадать лишь однотипные события. Именно поэтому её применение связанно с большим количеством условий и ограничений, существуют такие задачи, вычисления в которых можно провести лишь с использованием компьютера.
Список литературы
Бондаренко В.А., Цыплакова О.Н. Задачи с экономическим содержанием на занятиях по дифференциальному исчислению / Актуальные вопросы теории и практики бухгалтерского учета, анализа и аудита: ежегодная 75-я научно-практическая конференция. Редколлегия: В.З. Мазлоев, А.В. Ткач, И.С. Санду, И.Ю. Скляров, Е.И. Костюкова, ответственный за выпуск А.Н. Бобрышев. — 2011. — С. 124-127.
Гулай Т.А., Жукова В.А., Мелешко С.В., Невидомская И.А. Математика / рабочая тетрадь / Ставрополь, 2015.
Литвин Д.Б., Гулай Т.А., Жукова В.А., Мамаев И.И. Модель экономического роста с распределенным запаздыванием в инвестиционной сфере / Вестник АПК Ставрополья. 2017. № 2 (26). С. 225-228.
Математика. Теория вероятностей и случайные величины: рабочая тетр.; учеб. пособие для студентов вузов по направлениям: 38.03.04 – «Гос. муницип. упр.», 38.03.05 – «Бизнес-информатика»/Т.А.Гулай, В.А.Жукова, С.В.Мелешко, И.А. Невидомская; СтГАУ. –Ставрополь: Сервисшкола, 2016.
Элементы теории вероятностей случайных событий. Рабочая тетрадь/ И.А. Невидомская, С.В. Мелешко,Т.А. Гулай. — Ставрополь.: Сервисшкола, — 2015.
Теория вероятностей для экономических специальностей на базе Excel (практикум)/Долгополова А.Ф., Морозова О.В., Долгих Е.В., Крон Р.В., Тынянко Н.Н., Попова С.В., Смирнова Н.Б.//Международный журнал экспериментального образования. 2009. № S4. С. 19