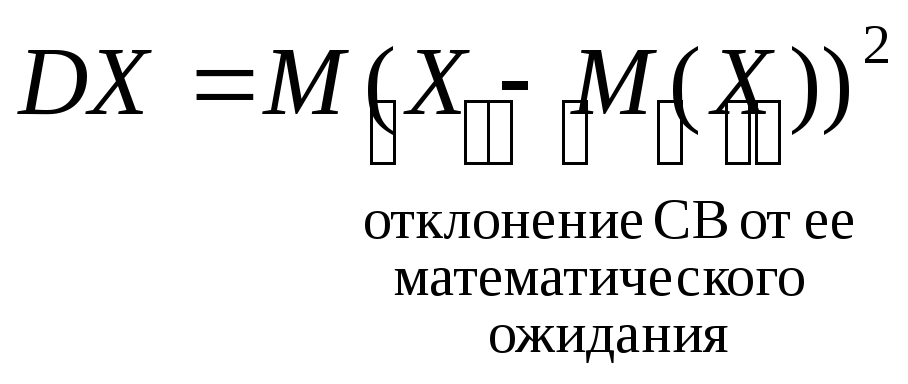1. Пусть Х – число сданных экзаменов. Составим ряд распределения Х. Возможные значения Х: 0, 1, 2, 3. Вычислим вероятности этих значений: Р(Х=0) = 0.1, Р(Х=1) = 0.9*0.2 = 0.18, Р(Х=2) = 0.9*0.8*0.3=0.216, Р(Х=3) = 0.9*0.8*0.7=0.504.
Математическое ожидание. М[X] = 0*0.1 + 1*0.18 2*0.216 + 3*0.504 = 2.124
2. Пусть Х – прибыль от инвестиций. Далее, решение можно оформить различными способами. Сначала находим все значения Х и их вероятности, а потом математическое ожидание Х. Можно немного ” повеселее”. Введём две случайные величины: Y – доход от инвестиций в фирму А, Z – доход от инвестиций в фирму В.
Значения Y: 0 , 0.5 с вероятностями 0.2 и 0.8 соответственно. M[Y] = 0.5*0.8 = 0.4.
Значения Z: 0 , 0.4 с вероятностями 0.15 и 0.85 соответственно. M[Y] = 0.4*0.85 = 0.34.
Тогда X = 10*Y + 15*Z. Поэтому М[X] = 10*M[Y] + 15*M[Z] = 9.1
Однако закон распределения Х надо найти.
Значения Х: 0, 5, 6, 11, с вероятностями 0.03, 0.12, 0.17, 0.68.






Чтобы получить решение, напишите мне в WhatsApp, оплатите, и я Вам вышлю файлы.
Кстати, если эта работа не по вашей теме или не по вашим данным, не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу, я смогу выполнить её в срок 1-3 дня!
Описание и исходные данные задания, 50% решения + фотография:
Каждый поступающий в институт должен сдать 4 экзамена. Вероятность успешной сдачи первого экзамена равна 0,9, второго – 0,8, третьего – 0,7 и четвёртого – 0,8. Следующий экзамен поступающий сдаёт только в случае успешной сдачи предыдущего. Составить закон распределения числа экзаменов, сдававшихся поступающим в институт. Найти числовые характеристики: моду, математическое ожидание, дисперсию и среднее квадратическое отклонение. Составить функцию распределения и построить её график. Найти P(X Є (0,5;2)), P(X > 1).
Решение.
Случайная величина Х – число экзаменов, сдававшихся поступающим в институт. Очевидно, что это дискретная случайная величина, которая может принимать значения 1, 2, 3 или 4.
Случайная величина Х примет значение 1, если поступающий не сдаст первый экзамен. Вероятность этого:.
Случайная величина Х примет значение 2, если поступающий сдаст первый экзамен (вероятность этого 0,9) и не сдаст второй (вероятность этого 1 – 0,8 = 0,2). Следовательно:.
Случайная величина Х примет значение 3, если поступающий сдаст первый экзамен (вероятность 0,9), сдаст второй экзамен (вероятность 0,8) и не сдаст третий (вероятность 1 – 0,7 = 0,3). Следовательно:.
Случайная величина Х примет значение 4, если поступающий сдаст первый экзамен (вероятность 0,9), сдаст второй экзамен (вероятность 0,8) и сдаст третий (вероятность 0,7). В этом случае поступающий будет сдавать четвёртый экзамен, а результат сдачи на вероятности значений случайной величины Х не повлияет. Следовательно:
- Вероятность события A – 0,7. Построить ряд распределения числа наступлений события A при одном опыте.
- 5 % лотерейных билетов – выигрышные. X – число выигрышных билетов среди двух выбранных. Найти дисперсию случайной величины X.
- Батарея состоит из трёх орудий. Вероятности попадания из первого, второго и третьего орудия равны соответственно 0,6; 0,7 и 0,9. Каждое орудие стреляет по цели один раз.
- Вероятности попадания в цель при одном выстреле для стрелков A, B, C равны соответственно 0,9; 0,7; 0,6. Каждый стрелок произвёл по одному выстрелу.
7.1. Среди 10 изготовленных приборов 3 неточных. Составить закон распределения числа неточных приборов среди взятых наудачу 4 приборов. Найти математическое ожидание и дисперсию этой случайной величины. Составить функцию распределения случайной величины и построить ее график.
Ответ:
|
X |
0 |
1 |
2 |
3 |
|
P |
|
|
|
|
;
.
7.2. В магазине продаются 5 отечественных и 3 импортных телевизора. Составить закон распределения случайной величины — числа импортных из 4 наудачу взятых телевизоров. Найти функцию распределения и построить ее график.
Ответ:
|
X |
0 |
1 |
2 |
3 |
|
P |
|
|
|
|
7.3. В билете три задачи. Вероятность правильного решения первой задачи равна 0,9, второй — 0,8, третьей — 0,7. Составить закон распределения числа правильно решенных задач в билете и вычислить математическое ожидание и дисперсию.
Ответ:
|
X |
0 |
1 |
2 |
3 |
|
P |
0,006 |
0,092 |
0,398 |
0,504 |
;
.
7.4. Поступающий в институт должен сдать 3 экзамена. Вероятность сдачи первого экзамена 0,9, второго — 0,8, третьего — 0,7. Следующий экзамен поступающий сдает только в случае успешной сдачи предыдущего. Составить закон распределения числа приходов на экзамен для лица, поступающего в институт. Найти математическое ожидание случайной величины.
Ответ:
.
7.5. В городе 4 коммерческих банка. У каждого риск банкротства в течение года составляет 10 %. Составить закон распределения числа банков, которые могут обанкротиться в течение следующего года и найти числовые характеристики этого распределения.
Ответ:
|
X |
0 |
1 |
2 |
3 |
4 |
|
P |
0,6561 |
0,2916 |
0,0486 |
0,0036 |
0,0001 |
;
;
.
7.6. Вероятность поражения земляники вирусным заболеванием равна 0,2. Составить закон распределения числа кустов земляники, зараженных вирусом, из четырех посаженных кустов. Найти математическое ожидание и дисперсию этой случайной величины.
Ответ:
|
X |
0 |
1 |
2 |
3 |
4 |
|
P |
0,4096 |
0,4096 |
0,1536 |
0,0256 |
0,0016 |
;
.
7.7. В урне находятся шары трех весов 3, 4 и 5 кг с соответствующими вероятностями 0,2; 0,3; 0,5. Извлекаются два шара с возвращением обратно. Составить закон распределения суммарного веса двух извлеченных шаров. Найти математическое ожидание и дисперсию этой случайной величины.
Ответ:
|
X |
6 |
7 |
8 |
9 |
10 |
|
P |
0,04 |
0,12 |
0,29 |
0,30 |
0,25 |
;
.
7.8. Производится стрельба из орудия по удаляющейся цели. При первом выстреле вероятность попадания равна 0,8, при каждом следующем выстреле вероятность попадания уменьшается в 2 раза. Случайная величина Х — число попаданий в цель при трех выстрелах. Составить закон распределения случайной величины Х.
Ответ:
|
X |
0 |
1 |
2 |
3 |
|
P |
0,096 |
0,472 |
0,368 |
0,064 |
7.9. Найти закон распределения числа пакетов трех акций, по которым владельцем будет получен доход, если вероятность получения дохода по каждому из них равна соответственно 0,5; 0,6; 0,7. Найти математическое ожидание и дисперсию этой случайной величины.
Ответ:
|
X |
0 |
1 |
2 |
3 |
|
P |
0,06 |
0,29 |
0,44 |
0,21 |
;
.
7.10. В лотерее разыгрывается один автомобиль стоимостью 5000 ден. ед., четыре телевизора – стоимостью 250 ден. ед. каждый, пять магнитофонов – стоимостью 200 ден. ед. каждый. Продано 1000 билетов стоимостью 7 ден. ед. каждый. Составить закон распределения случайной величины Х – чистого выигрыша, полученного участником лотереи, купившим один билет.
Ответ:
|
X |
– 7 |
193 |
243 |
4993 |
|
P |
0,990 |
0,005 |
0,004 |
0,001 |
7.11. В карточной игре игрок, который извлекает из колоды карт (52 карты) валет или даму, выигрывает 15 очков; тот, кто вытащит короля или козырного туза, выигрывает 5 очков. Игрок, который достанет любую другую карту, проигрывает 4 очка. Если вы решили участвовать в этой игре, определите сумму очков ожидаемого выигрыша.
Ответ:
.
7.12. Дискретная случайная величина Х может принимать только два значения и
, причем
. Известны вероятность
возможного значения
, математическое ожидание
И дисперсия
. Найти закон распределения этой случайной величины.
Ответ:
7.13. Два стрелка стреляют по одной мишени, делая независимо друг от друга по два выстрела. Вероятность попадания в мишень для первого стрелка равна 0,4, для второго – 0,5. Пусть Х – число попаданий в мишень первым стрелком, Y– число попаданий в мишень вторым стрелком. Построить закон распределения случайной величины Z = X – Y и найти M(Z), D(Z).
Ответ: M(Z) = –0,2; D(Z) = 0,98.
7.14. Имеется шесть ключей, из которых только один подходит к замку. Составить закон распределения числа попыток при открывании замка, если испробованный ключ в последующих опробованиях не участвует. Найти математическое ожидание и дисперсию этой случайной величины.
Ответ: M(Х) =; D(Х) =
7.15. В магазин поступила обувь с двух фабрик в соотношении 2 : 3. Куплено четыре пары обуви. Построить закон распределения числа купленных пар обуви, изготовленных первой фабрикой. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины.
Ответ: M(Х) = 1,6; D(Х) = 0,96; .
7.16. В партии из десяти изделий имеется одно бракованное. Чтобы его обнаружить вынимают наугад одно изделие за другим и каждое вынутое изделие проверяют. Построить закон распределения и найти математическое ожидание числа проверенных изделий.
Ответ: M(Х) = 5,5.
7.17. Проводится проверка большой партии деталей до обнаружения бракованной (без ограничения числа проверенных деталей). Составить закон распределения числа проверенных деталей. Найти M(Х) и D(Х) случайной величины, если известно, что вероятность брака для каждой детали равна 0,1.
Ответ: M(Х) = 10;D(X)= 90.
7.18. Независимые случайные величины Х и Y заданы следующими законами распределения:
|
X |
5 |
2 |
4 |
Y |
7 |
9 |
|
|
P |
0,6 |
0,1 |
0,3 |
Р |
0,8 |
0,2 |
Найти ,
и проверить, что
=
,
.
Ответ: =11,8;
= 32,56.
7.19. Дискретная случайная величина задана законом распределения
|
|
0 |
1 |
2 |
3 |
|
|
|
0,2 |
|
0,5 |
Найти вероятность если известно, что
в 2 раза больше, чем вероятность
Ответ: .
7.20. Найти дисперсию случайной величины если известно, что
Ответ: .
7.21. Найти дисперсию случайной величины если известно, что
Ответ: .
7.22. Даны две независимые случайные величины Х и Y; дисперсии которых равны Найти дисперсию
Ответ: .
7.23. Даны две независимые случайные величины Х и Y; дисперсии которых равны Найти дисперсию
Ответ: .
7.24. Даны законы распределения двух независимых случайных величин Х и Y.
|
|
1 |
2 |
|
0 |
2 |
3 |
|||
|
|
0,6 |
0,4 |
|
0,1 |
0,2 |
0,7 |
Найти вероятность того, что случайная величина Примет значение, равное 4.
Ответ: .
7.25. Даны все возможные значения дискретной случайной величины Х: и
Найти
Ответ: .
7.26. Даны все возможные значения дискретной случайной величины Х: и
Найти
Ответ: .
7.27. Случайную величину умножили на постоянный множитель K. Как от этого изменится среднее квадратическое отклонение?
Ответ: Увеличится в раз.
| < Предыдущая | Следующая > |
|---|
Главная » Учебные материалы » Математика » Решения задач » Несколько классов/семестров » Каждый поступающий в университет должен сдать 3 экзамена. Вероятность успешной сдачи первого экзамена 0,9, второго-0,8, третьего-0,7. Следующий экзамен поступающий сдает только в случае успешной сдачи предыдущего. Составить закон распределения СВ-чис
Для студентов по предмету МатематикаКаждый поступающий в университет должен сдать 3 экзамена. Вероятность успешной сдачи первого экзамена 0,9, второго-0,8, третьего-0,7. Следующий экзамеКаждый поступающий в университет должен сдать 3 экзамена. Вероятность успешной сдачи первого экзамена 0,9, второго-0,8, третьего-0,7. Следующий экзаме
2022-01-242022-01-24СтудИзба
Описание
Каждый поступающий в университет должен сдать 3 экзамена. Вероятность успешной сдачи первого экзамена 0,9, второго-0,8, третьего-0,7. Следующий экзамен поступающий сдает только в случае успешной сдачи предыдущего. Составить закон распределения СВ-числа экзаменов, сдавших поступающим в университет. Найти F(x), M(x), D(x).
Характеристики решённой задачи
Учебное заведение
Неизвестно
Качество
Идеальное компьютерное
Список файлов
-
Задача.docx 35,18 Kb
Комментарии
Сопутствующие материалы
Даны графы G1 и G2. Найти G1UG2, G1∩G2, G1+G2, G1∙G2. Для графа G1UG2 найти матрицы смежности, инцидентности, сильных компонент, маршрутов длины 2 и все маршруты длины 2, исходящие из вершины 1.
Портфель состоит из двух бумаг А и В. Ожидаемые доходности равны 0,35 и 0,75, а риски 0,2 и 0,6. Коэффициент корреляции равен ½. Риск портфеля равен 0,55. Найти портфель и его доходность.
Необходимо принять решение о вложении денежных средств в строительство предприятия, которое предполагается эксплуатировать 18 лет. Инвестиции, общей суммой 10 000 тыс. р., решено вкладывать поэтапно в начале каждого года строительства предприятия в т
В цехе имеются 1 станок с ЧПУ и 9 станков без ЧПУ. Вероятность того, что за время выполнения некоторой задачи станок с ЧПУ не выйдет из строя равна 0,9, для станков без ЧПУ – 0,6. Во время выполнения рабочим задания, станок из строя не вышел. Найти в
Телевизионный канал рекламирует новый вид детского питания. Вероятность того, что телезритель увидит эту рекламу, оценивается в 0,2. В случайном порядке выбраны четыре телезрителя, случайная величина ξ – число лиц, видевших рекламу. Составить закон р
FREE
Сформулировать свойства определённого интеграла. Доказать теорему об оценке модуля определённого
Свежие статьи
Популярно сейчас
Ответы на популярные вопросы
То есть уже всё готово?
Да! Наши авторы собирают и выкладывают те работы, которые сдаются в Вашем учебном заведении ежегодно и уже проверены преподавателями.
А я могу что-то выложить?
Да! У нас любой человек может выложить любую учебную работу и зарабатывать на её продажах! Но каждый учебный материал публикуется только после тщательной проверки администрацией.
А если в купленном файле ошибка?
Вернём деньги! А если быть более точными, то автору даётся немного времени на исправление, а если не исправит или выйдет время, то вернём деньги в полном объёме!
Отзывы студентов
Добавляйте материалы
и зарабатывайте!
Продажи идут автоматически
652
Средний доход
с одного платного файла
Обучение Подробнее
СВ является непрерывной, если
ее функция распределения непрерывна.
Для НСВ наряду с функцией распределения
вводится еще 1 закон распределения –
плотность вероятности.
Определение 4.6:
Плотностью вероятностей хназывается производная ее функции
распределения, т.е.
(плотность вероятностей может быть
обозначена
)
Свойства плотностей вероятности:
1.
2.
3.
4.
— условие нормировки
4.5. Числовые характеристики cb
Определение 4.7:
Математическим ожиданием ДСВназывается число.
Определение 4.8:
Математическим ожиданием НСВназывается число.
математическое
ожидание
Свойства математического ожидания:
1. X = с
= const,
M(C) = C
2. Постоянный множитель выносится за
знак математического ожидания, т.е.:
3. Математическое ожидание суммы СВ
равно сумме математических ожиданий
4.6. Дисперсия случайной величины
Определение 4.9:
Дисперсией СВназывается число:
Свойства дисперсии:
1. Дисперсию можно найти по формуле:
2.
3. Если X = с=const,
тоD(C)
= 0
4. Если
,
то
Формулы:
для ДСВ:
1.
2.
для НСВ:
1.
2.
Средним квадратичным отклонением
СВ Хназывается число:.
Законы распределения СВ (стр.19):
-
Биноминальное распределение.
-
Распределение Пуассона
-
Равномерное распределение
-
Показательное распределение
-
Нормальное распределение
Практическая работа № 2
№ 1.
Для данного студента вероятность
успешной сдачи первого экзамена равна
0,9, второго – 0,8, третьего – 0,7. Случайная
величина х – число успешно
сданных экзаменов. Найти: ряд распределения
ДСВ, математическое ожидание М(Х);
дисперсию D(X);
среднеквадратичное отклонение
.
Решение:
Случайная величина принимает значения:
0, 1, 2, 3
Пусть р1– вероятность
сдачи первого экзамена.
р2– вероятность сдачи
второго экзамена.
р3– вероятность сдачи
третьего экзамена.
q1– вероятность
несдачи первого экзамена.
q2– вероятность
несдачи второго экзамена.
q3– вероятность
несдачи третьего экзамена.
-
Х
0
1
2
3
Р
0,006
0,092
0,398
0,504
(методичка, стр.25, формула для доверительного
интервала)
Нормальное распределение – стр.21
П.6 зад.7 для решения к.р.
№ 2.
На сборку поступили детали с 3 конвейеров.
Первый дает 25%, второй – 30%, третий – 45%
деталей, поступающих на сборку. С первого
конвейера в среднем поступает 2% брака,
со второго – 3%, с третьего – 1%. Найти
вероятность того, что:
-
На сборку поступила бракованная
деталь. -
Поступившая бракованная деталь со
второго конвейера.
Решение:
Пункт 1.
Пусть событие А– поступившая деталь
на сборку – бракованная.
Н1– деталь с первого конвейера.
Н2– деталь со второго конвейера.
Н1– деталь с третьего конвейера.
Пункт 2.
№ 3.
Монету бросают 10 раз. Найти вероятность
того, что герб выпадет:
-
2 Раза.
-
Менее 2 раз.
-
Не менее 2 раз.
Решение:
1:
Вероятность того, что выпадет герб,
;n = 10, k
= 2
Формула Бернулли:
2:
По формуле Бернулли:
3:
Тел. кафедры – 60-27-71
Надежда Николаевна
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,622 -
гуманитарные
33,648 -
юридические
17,917 -
школьный раздел
611,562 -
разное
16,897
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
1. Вероятность сдачи первого экзамена 0,6, тогда вероятность его не сдать 1 — 0,6 = 0,4.
Вероятность сдачи второго экзамена равна 0,8, а неуспеха 1 — 0,8 = 0,2.
Известно, что вероятность сдать третий экзамен составляет 0,7.
Тогда вероятность его не сдать 1 — 0,7 = 0,3.
2. Вычислим вероятность сдачи одного экзамена.
Это событие происходит в случае, когда один предмет сдан, а два других нет.
Р1 = 0,6 * 0,2 * 0,3 + 0,4 * 0,8 * 0,3 + 0,4 * 0,2 * 0,7 = 0,036 + 0,096 + 0,056 = 0,188.
2. Найдем вероятность сдачи двух предметов.
Р2 = 0,6 * 0,8 * 0,3 + 0,4 * 0,8 * 0,7 + 0,6 * 0,2 * 0,7 = 0,144 + 0,224 + 0,084 = 0,452.
3. Определим вероятность сдачи трех экзаменов.
Р3 = 0,6 * 0,8 * 0,7 = 0,336.
4. Вычислим вероятность сдать хотя бы один экзамен.
Обратное этому событию — ничего не сдать.
Р = 0,4 * 0,2 * 0,3 = 0,024.
Р4 = 1 — 0,024 = 0,976.
Ответ: 0,188; 0,452; 0,336; 0,976.