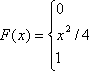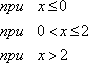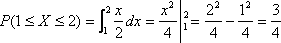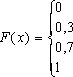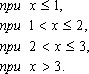Каждый поступающий в институт должен сдать 3 экзамена вероятность успешной сдачи первого

1. Пусть Х – число сданных экзаменов. Составим ряд распределения Х. Возможные значения Х: 0, 1, 2, 3. Вычислим вероятности этих значений: Р(Х=0) = 0.1, Р(Х=1) = 0.9*0.2 = 0.18, Р(Х=2) = 0.9*0.8*0.3=0.216, Р(Х=3) = 0.9*0.8*0.7=0.504.
Математическое ожидание. М[X] = 0*0.1 + 1*0.18 2*0.216 + 3*0.504 = 2.124

2. Пусть Х – прибыль от инвестиций. Далее, решение можно оформить различными способами. Сначала находим все значения Х и их вероятности, а потом математическое ожидание Х. Можно немного ” повеселее”. Введём две случайные величины: Y – доход от инвестиций в фирму А, Z – доход от инвестиций в фирму В.
Значения Y: 0 , 0.5 с вероятностями 0.2 и 0.8 соответственно. M[Y] = 0.5*0.8 = 0.4.
Значения Z: 0 , 0.4 с вероятностями 0.15 и 0.85 соответственно. M[Y] = 0.4*0.85 = 0.34.
Тогда X = 10*Y + 15*Z. Поэтому М[X] = 10*M[Y] + 15*M[Z] = 9.1
Однако закон распределения Х надо найти.
Значения Х: 0, 5, 6, 11, с вероятностями 0.03, 0.12, 0.17, 0.68.

7.1. Среди 10 изготовленных приборов 3 неточных. Составить закон распределения числа неточных приборов среди взятых наудачу 4 приборов. Найти математическое ожидание и дисперсию этой случайной величины. Составить функцию распределения случайной величины и построить ее график.

Ответ:

X	0	1	2	3
P

; .

7.2. В магазине продаются 5 отечественных и 3 импортных телевизора. Составить закон распределения случайной величины — числа импортных из 4 наудачу взятых телевизоров. Найти функцию распределения и построить ее график.

Ответ:

X	0	1	2	3
P

7.3. В билете три задачи. Вероятность правильного решения первой задачи равна 0,9, второй — 0,8, третьей — 0,7. Составить закон распределения числа правильно решенных задач в билете и вычислить математическое ожидание и дисперсию.

Ответ:

X	0	1	2	3
P	0,006	0,092	0,398	0,504

;

.

7.4. Поступающий в институт должен сдать 3 экзамена. Вероятность сдачи первого экзамена 0,9, второго — 0,8, третьего — 0,7. Следующий экзамен поступающий сдает только в случае успешной сдачи предыдущего. Составить закон распределения числа приходов на экзамен для лица, поступающего в институт. Найти математическое ожидание случайной величины.

Ответ:

.

7.5. В городе 4 коммерческих банка. У каждого риск банкротства в течение года составляет 10 %. Составить закон распределения числа банков, которые могут обанкротиться в течение следующего года и найти числовые характеристики этого распределения.

Ответ:

X	0	1	2	3	4
P	0,6561	0,2916	0,0486	0,0036	0,0001

;

;

.

7.6. Вероятность поражения земляники вирусным заболеванием равна 0,2. Составить закон распределения числа кустов земляники, зараженных вирусом, из четырех посаженных кустов. Найти математическое ожидание и дисперсию этой случайной величины.

Ответ:

X	0	1	2	3	4
P	0,4096	0,4096	0,1536	0,0256	0,0016

;

.

7.7. В урне находятся шары трех весов 3, 4 и 5 кг с соответствующими вероятностями 0,2; 0,3; 0,5. Извлекаются два шара с возвращением обратно. Составить закон распределения суммарного веса двух извлеченных шаров. Найти математическое ожидание и дисперсию этой случайной величины.

Ответ:

X	6	7	8	9	10
P	0,04	0,12	0,29	0,30	0,25

;

.

7.8. Производится стрельба из орудия по удаляющейся цели. При первом выстреле вероятность попадания равна 0,8, при каждом следующем выстреле вероятность попадания уменьшается в 2 раза. Случайная величина Х — число попаданий в цель при трех выстрелах. Составить закон распределения случайной величины Х.

Ответ:

X	0	1	2	3
P	0,096	0,472	0,368	0,064

7.9. Найти закон распределения числа пакетов трех акций, по которым владельцем будет получен доход, если вероятность получения дохода по каждому из них равна соответственно 0,5; 0,6; 0,7. Найти математическое ожидание и дисперсию этой случайной величины.

Ответ:

X	0	1	2	3
P	0,06	0,29	0,44	0,21

;

.

7.10. В лотерее разыгрывается один автомобиль стоимостью 5000 ден. ед., четыре телевизора – стоимостью 250 ден. ед. каждый, пять магнитофонов – стоимостью 200 ден. ед. каждый. Продано 1000 билетов стоимостью 7 ден. ед. каждый. Составить закон распределения случайной величины Х – чистого выигрыша, полученного участником лотереи, купившим один билет.

Ответ:

X	– 7	193	243	4993
P	0,990	0,005	0,004	0,001

7.11. В карточной игре игрок, который извлекает из колоды карт (52 карты) валет или даму, выигрывает 15 очков; тот, кто вытащит короля или козырного туза, выигрывает 5 очков. Игрок, который достанет любую другую карту, проигрывает 4 очка. Если вы решили участвовать в этой игре, определите сумму очков ожидаемого выигрыша.

Ответ:

.

7.12. Дискретная случайная величина Х может принимать только два значения и , причем . Известны вероятность возможного значения , математическое ожидание И дисперсия . Найти закон распределения этой случайной величины.

Ответ:

7.13. Два стрелка стреляют по одной мишени, делая независимо друг от друга по два выстрела. Вероятность попадания в мишень для первого стрелка равна 0,4, для второго – 0,5. Пусть Х – число попаданий в мишень первым стрелком, Y– число попаданий в мишень вторым стрелком. Построить закон распределения случайной величины Z = X – Y и найти M(Z), D(Z).

Ответ: M(Z) = –0,2; D(Z) = 0,98.

7.14. Имеется шесть ключей, из которых только один подходит к замку. Составить закон распределения числа попыток при открывании замка, если испробованный ключ в последующих опробованиях не участвует. Найти математическое ожидание и дисперсию этой случайной величины.

Ответ: M(Х) =; D(Х) =

7.15. В магазин поступила обувь с двух фабрик в соотношении 2 : 3. Куплено четыре пары обуви. Построить закон распределения числа купленных пар обуви, изготовленных первой фабрикой. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины.

Ответ: M(Х) = 1,6; D(Х) = 0,96; .

7.16. В партии из десяти изделий имеется одно бракованное. Чтобы его обнаружить вынимают наугад одно изделие за другим и каждое вынутое изделие проверяют. Построить закон распределения и найти математическое ожидание числа проверенных изделий.

Ответ: M(Х) = 5,5.

7.17. Проводится проверка большой партии деталей до обнаружения бракованной (без ограничения числа проверенных деталей). Составить закон распределения числа проверенных деталей. Найти M(Х) и D(Х) случайной величины, если известно, что вероятность брака для каждой детали равна 0,1.

Ответ: M(Х) = 10;D(X)= 90.

7.18. Независимые случайные величины Х и Y заданы следующими законами распределения:

X	5	2	4		Y	7	9
P	0,6	0,1	0,3		Р	0,8	0,2

Найти , и проверить, что =, .

Ответ: =11,8; = 32,56.

7.19. Дискретная случайная величина задана законом распределения

	0	1	2	3
		0,2		0,5

Найти вероятность если известно, что в 2 раза больше, чем вероятность

Ответ: .

7.20. Найти дисперсию случайной величины если известно, что

Ответ: .

7.21. Найти дисперсию случайной величины если известно, что

Ответ: .

7.22. Даны две независимые случайные величины Х и Y; дисперсии которых равны Найти дисперсию

Ответ: .

7.23. Даны две независимые случайные величины Х и Y; дисперсии которых равны Найти дисперсию

Ответ: .

7.24. Даны законы распределения двух независимых случайных величин Х и Y.

	1	2					0	2	3
	0,6	0,4					0,1	0,2	0,7

Найти вероятность того, что случайная величина Примет значение, равное 4.

Ответ: .

7.25. Даны все возможные значения дискретной случайной величины Х: и Найти

Ответ: .

7.26. Даны все возможные значения дискретной случайной величины Х: и Найти

Ответ: .

7.27. Случайную величину умножили на постоянный множитель K. Как от этого изменится среднее квадратическое отклонение?

Ответ: Увеличится в раз.

< Предыдущая		Следующая >

 Готовое решение: Заказ №8392

 Тип работы: Задача

Статус:  Выполнен (Зачтена преподавателем ВУЗа)

 Предмет: Теория вероятности

 Дата выполнения: 30.09.2020

 Цена: 226 руб.

Чтобы получить решение, напишите мне в WhatsApp, оплатите, и я Вам вышлю файлы.

Кстати, если эта работа не по вашей теме или не по вашим данным, не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу, я смогу выполнить её в срок 1-3 дня!

Описание и исходные данные задания, 50% решения + фотография:

Каждый поступающий в институт должен сдать 4 экзамена. Вероятность успешной сдачи первого экзамена равна 0,9, второго – 0,8, третьего – 0,7 и четвёртого – 0,8. Следующий экзамен поступающий сдаёт только в случае успешной сдачи предыдущего. Составить закон распределения числа экзаменов, сдававшихся поступающим в институт. Найти числовые характеристики: моду, математическое ожидание, дисперсию и среднее квадратическое отклонение. Составить функцию распределения и построить её график. Найти P(X Є (0,5;2)),  P(X > 1).

Решение.

Случайная величина Х – число экзаменов, сдававшихся поступающим в институт. Очевидно, что это дискретная случайная величина, которая может принимать значения 1, 2, 3 или 4.

Случайная величина Х примет значение 1, если поступающий не сдаст первый экзамен. Вероятность этого:.

Случайная величина Х примет значение 2, если поступающий сдаст первый экзамен (вероятность этого 0,9) и не сдаст второй (вероятность этого 1 – 0,8 = 0,2). Следовательно:.

Случайная величина Х примет значение 3, если поступающий сдаст первый экзамен (вероятность 0,9), сдаст второй экзамен (вероятность 0,8) и не сдаст третий (вероятность 1 – 0,7 = 0,3). Следовательно:.

Случайная величина Х примет значение 4, если поступающий сдаст первый экзамен (вероятность 0,9), сдаст второй экзамен (вероятность 0,8) и сдаст третий (вероятность 0,7). В этом случае поступающий будет сдавать четвёртый экзамен, а результат сдачи на вероятности значений случайной величины Х не повлияет. Следовательно:

Ответы на популярные вопросы

Отзывы студентов

Добавляйте материалы
и зарабатывайте!

Продажи идут автоматически

Обучение Подробнее

                        (3.38)
Второй
способ состоит
в том, что заданы законы (ряды) распределения
альтернативных случайных
величин X_k (
k=1,2,3,4),
выражающих число станков, не потребующих
внимания рабочего в течение часа (это
число для каждого станка равно 1, если
этот станок не потребует внимания
рабочего, и равно 0, если
потребует):

X₁:                                          X₂:                                           X₃:                                          X₄:

xi	0	1		xi	0	1		xi	0	1		xi	0	1
pi1	0,1	0,9	pi2	0,2	0,8	pi3	0,25	0,75	pi4	0,3	0,7

Необходимо
найти закон распределения суммы этих
случайных величин, т.е. Х = Х₁ +
Х₂ +
Х₃ +
Х₄.
Суммируя последовательно Х₁ +
Х₂ =Z,
Х₁ +
Х₂ +
Х₃ = Z + X₃ = U,
Х₁ +
Х₂ +
Х₃ +
Х₄ = U + X₄ = X,
получим

Z =
Х₁ +
Х₂:

zi	0	1	2
pi	0,02	0,26	0,2

U = Z + X₃:

um	0	1	2	3
pm	0,005	0,08	0,375	0,54

и,
наконец, распределение X = U + X₄,
т.е. получили (3.38).

Третий
способ: Распределение
Х можно получить чисто механически,
перемножив биномы
(двучлены):

,                             (3.39)

причем
каждый из пяти полученных коэффициентов
при z^k (k =
0, 1, 2, 3, 4) в функции φ₄(
z) будет
выражать соответствующие
вероятности P(
X = 
k). Действительно,
преобразовав (3.39), получим 

,

где
коэффициенты – это вероятности значений
случайной величины Х (3.38).

Пример
3.6

В
1-й урне содержится 6 белых и 4 черных
шара, а во 2-й –3 белых и 7 черных шаров.
Из 1-й урны берут на удачу два шара и
перекладывают во 2-ю урну, а затем из 2-й
урны берут наудачу один шар и перекладывают
в 1-ю урну. Составить законы распределения
числа белых шаров в 1-й и 2-й
урнах.

Решение

Найдем
закон распределения случайной величины X –
числа белых шаров в 1-й урне. 

Пусть Ai()
– событие,
состоящее в извлечении из первой
урны i-го
белого (черного) шара (i =
1, 2), а В()
— извлечение
из 2-й урны белого (черного) шара после
того, как в нее из 1-й урны переложили
два извлеченных шара. В соответствии с
условием число X белых
шаров в 1-й урне может быть равным 4, 5, 6
или 7. Вероятность того, что в 1-й урне
останется 4 белых шара, будет равна
вероятности совместного осуществления
трех событий: из 1-й урны извлечены первый
шар -белый, второй шар – белый, из 2-й
урны извлечен черный шар (после того
как в нее переложили два белых шара),
т.е.

Рассуждая
аналогично, получим

;

;

.

Итак,
закон распределения 

X:	xi	4	5	6	7
pi	7/36	89/180	5/18	1/30

Убеждаемся
в том, что

Распределение
числа Y белых
шаров во 2-й урне можно найти аналогично,
но проще это сделать, если учесть,
что X+
Y=9 (при
любых значениях x_i и y_j). Поэтому
закон распределения случайной величины Y =
9-
X есть

Y:	yj	2	3	4	5
pj	1/30	5/18	89/180	7/36

Пример
3.7

Дана
функция распределения случайной
величины X:

а)      найти
плотность вероятности φ(х);

б)      построить
графики φ(х)
и F(x);

в)      убедится
в том, что Х –
непрерывная случайная величина;

г)       найти
вероятности P(X =
1), P(X <
1), P(1
≤ X <
2) (две последние вероятности показать
на графиках φ(х)
и F(x));

д)      вычислить
математическое ожидание М(Х),
дисперсию D(X),
моду M₀(X)
и медиану M_e(X).

Решение

а)
Плотность вероятности

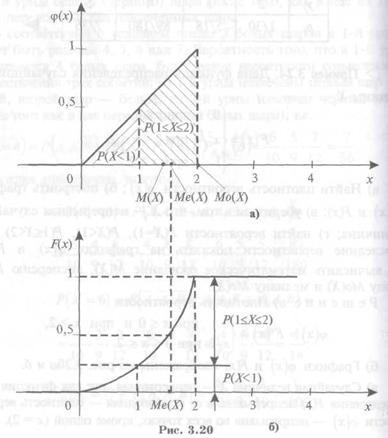
б) Графики φ(x)
и F(
x) изображены
на рис.3.20 a и б.

в)
Случайная величина X – непрерывная,
так как функция распределения F(x)
непрерывна, а ее производная – плотность
вероятностиφ(x) –
непрерывна во всех точках, кроме одной (х
= 2).

г) Р(Х
= 1)
= 0 как вероятность отдельно взятого
значения непрерывной случайной
величины.

Р(Х
< 1)
можно найти либо по определению функции
распределения, либо по формуле (3.21) через
плотность вероятности φ(x):

 (ордината
графика F(1)
– см. рис. 3.20б)

или

(площадь
под кривой распределения φ(x)
на отрезке [0,1] – см.рис.3.20а).

Р(1≤ X ≤ 2)
можно найти либо как приращение функции
распределения по формуле (3.20), либо по
формуле (3.22) через

(приращение
ординаты графика F(x)
на отрезке [1,2] – рис.3.20б) – или

(площадь
под кривой распределения φ(x)
на отрезке [1,2] – рис. 3.20а)

д)
По формуле (3.25) математическое
ожидание

плотность
вероятности φ(x).

Если
представить распределение случайной
величины Х
в виде
единичной массы, распределенной по
треугольнику (рис. 3.20а), то
значение М(Х)=4/3 означает
абсциссу центра массы треугольника.

По
формуле (3.27) дисперсия D(X) = M(X²)
– a2.

Теперь 

Плотность
вероятности φ(x)
максимальна при х = 2 (см. рис. 3.20а),
следовательно, М₀(Х)
= 2.

Медиану
М_е(Х)
= b найдем
из условия F(b)
= ,
т.е. ,
откуда b = M_e(X)
= ,
или через плотность вероятности

,
т.е. ,
откуда b = M_e(X)
= 

Задания
3.1.      Вероятность
поражения вирусным заболеванием куста
земляники равна 0,2. Составить закон
распределения числа кустов земляники,
зараженных вирусом, из четырех посаженных
кустов.

3.2.      Стрелок
ведет стрельбу по цели с вероятностью
попадания при каждом выстреле 0,2. За
каждое попадание он получает 5 очков, а
в случае промаха очков ему не начисляют.
Составить закон распределения числа
очков, полученных стрелком за 3 выстрела,
и вычислить математическое ожидание
этой случайной величины.

3.3.      В
рекламных целях торговая фирма вкладывает
в каждую десятую единицу товара денежный
приз размером 1 тыс. руб. Составить закон
распределения случайной величины –
размера выигрыша при пяти сделанных
покупках. Найти математическое ожидание
и дисперсию этой случайной
величины.

3.4.      Клиенты
банка, не связанные друг с другом, не
возвращают кредиты в срок с вероятностью
0,1. Составить закон распределения числа
возвращенных в срок кредитов из 5
выданных. Найти математическое ожидание,
дисперсию и среднее квадратическое
отклонение этой случайной
величины.

3.5.      Контрольная
работа состоит из трех вопросов. На
каждый вопрос приведено 4 ответа, один
из которых правильный. Составить закон
распределения числа правильных ответов
при простом угадывании. Найти математическое
ожидание и дисперсию этой случайной
величины.

3.6.      В
среднем по 10% договоров страховая
компания выплачивает страховые суммы
в связи с наступлением страхового
случая. Составить закон распределения
числа таких договоров среди наудачу
выбранных четырех. Вычислить математическое
ожидание и дисперсию этой
случайной величины.

3.7.      В
билете три задачи. Вероятность правильного
решения первой задачи равна 0,9, второй
– 0,8, третьей – 0,7. Составить закон
распределения числа правильно решенных
задач в билете и вычислить математическое
ожидание и дисперсию этой случайной
величины.

3.8.      Вероятность
попадания в цель при одном выстреле
равна 0,8 и уменьшается с каждым выстрелом
на 0,1. Составить закон распределения
числа попаданий в цель, если сделано
три выстрела. Найти математическое
ожидание, дисперсию и среднее квадратическое
отклонение этой случайной
величины.

3.9.      Произведено
два выстрела в мишень. Вероятность
попадания в мишень первым стрелком
равна 0,8, вторым – 0,7, Составить закон
распределения числа попаданий в мишень.
Найти математическое ожидание, дисперсию
и функцию распределения этой случайной
величины и построить ее график. (Каждый
стрелок делает по одному выстрелу.)

3.10. Найти
закон распределения числа пакетов трех
акций, по которым владельцем будет
получен доход, если вероятность получения
дохода по каждому из них равна
соответственно 0,5, 0,6, 0,7. Найти математическое
ожидание и дисперсию данной случайной
величины, построить функцию
распределения.

3.11. Дан
ряд распределения случайной величины:

X:	xi	2	4
pi	p1	p2

Найти
функцию распределения этой случайной
величины, если ее математическое ожидание
равно 3,4, а дисперсия равна 0,84.

3.12. Из
пяти гвоздик две белые. Составить закон
распределения и найти функцию распределения
случайной величины, выражающей число
белых гвоздик среди двух одновременно
взятых.

3.13. Из
10 телевизоров на выставке 4 оказались
фирмы «Сони». Наудачу для осмотра выбрано
3. Составить закон распределения числа
телевизоров фирмы «Сони» среди 3
отобранных.

3.14. Среди
15 собранных агрегатов 6 нуждаются в
дополнительной смазке. Составить закон
распределения числа агрегатов, нуждающихся
в дополнительной смазке, среди пяти
наудачу отобранных из общего числа.

3.15. В
магазине продаются 5 отечественных и 3
импортных телевизора. Составить закон
распределения случайной величины –
числа импортных из четырех наудачу
выбранных телевизоров. Найти функцию
распределения этой случайной величины
и построить ее график.

3.16.  Вероятность
того, что в библиотеке необходимая
студенту книга свободна, равна 0,3.
Составить закон распределения числа
библиотек, которые посетит студент,
если в городе 4 библиотеки.  Найти
математическое ожидание
и дисперсию этой случайной
величины.

3.17.  Экзаменатор
задает студенту вопросы, пока тот
правильно отвечает. Как только число
правильных ответов достигнет четырех
либо студент ответит неправильно,
экзаменатор прекращает задавать вопросы.
Вероятность правильного ответа на один
вопрос равна 2/3. Составить закон
распределения числа заданных студенту
вопросов.

3.18.  Торговый
агент имеет 5 телефонных номеров
потенциальных покупателей и звонит им
до тех пор, пока не получит заказ на
покупку товара. Вероятность того, что
потенциальный покупатель сделает заказ,
равна 0,4. Составить закон распределения
числа телефонных разговоров, которые
предстоит провести агенту. Найти
математическое ожидание и дисперсию
этой случайной величины.

3.19.  Каждый
поступающий в институт должен сдать 3
экзамена. Вероятность успешной сдачи
первого экзамена 0,9, второго – 0,8, третьего
– 0,7. Следующий экзамен поступающий
сдает только в случае успешной сдачи
предыдущего. Составить закон распределения
числа экзаменов, сдававшихся поступающим
в институт. Найти математическое ожидание
этой случайной величины.

3.20.  Охотник,
имеющий 4 патрона, стреляет по дичи до
первого попадания или до израсходования
всех патронов. Вероятность попадания
при первом выстреле равна 0,6, при каждом
последующем – уменьшается на 0,1.
Необходимо:

а)
составить закон распределения числа
патронов, израсходованных охотником;

б)
найти математическое ожидание и дисперсию
этой случайной величины.

3.21.  Из
поступивших в ремонт 10 часов 7 нуждаются
в общей чистке механизма. Часы не
рассортированы по виду ремонта. Мастер,
желая найти часы, нуждающиеся в чистке,
рассматривает их поочередно и, найдя
такие часы, прекращает дальнейший
просмотр. Составить закон распределения
числа просмотренных часов. Найти
математическое ожидание и дисперсию
этой случайной величины.

3.22.  Имеются
4 ключа, из которых только один подходит
к замку. Составить закон распределения
числа попыток открывания замка, если
испробованный ключ в последующих
попытках не участвует. Найти математическое
ожидание, дисперсию и среднее квадратическое
отклонение этой случайной
величины.

3.23. Абонент
забыл последнюю цифру нужного ему номера
телефона, однако помнит, что она нечетная.
Составить закон распределения числа
сделанных им наборов номера телефона
до попадания на нужный номер, если
последнюю цифру он набирает наудачу, а
набранную цифру в дальнейшем не набирает.
Найти математическое ожидание и функцию
распределения этой случайной
величины.

3.24. Дана
функция распределения случайной
величины X

Найти:

а)
ряд распределения;

б) М(Х) и D(X);

в)
построить многоугольник распределения
и график F(
x).

3.25.  Даны
законы распределения двух независимых
случайных величин

X:	xi	0	1	3
pi	0,2	0,5	?

и

Y:	xi	2	3
pi	0,4	?

Найти
вероятности, с которыми случайные
величины принимают значение 3, а затем
составить закон распределения случайной
величины ЗХ–
2
Y и
проверить выполнение свойств математических
ожиданий и дисперсий: M(ЗХ- 2Y)
= 3М(Х)
— 2
M(
Y),
D(ЗХ- 2
Y) =
9D(X) + 4D(Y).

3.26.  На
двух автоматических станках производятся
одинаковые изделия. Даны законы
распределения числа бракованных изделий,
производимых в течение смены на каждом
из них:

а)
для первого

X:	xi	0	1	2
pi	0,1	0,6	0,3

б)
для второго

Y:	xj	0	2
pj	0,5	0,3

Необходимо:

а)
составить закон распределения числа
производимых в течение смены бракованных
изделий обоими станками;

б)
проверить свойство математического
ожидания суммы случайных величин.

3.27.  Одна
из случайных величин задана законом
распределения

xi	-1	0	1
pi	0,1	0,8	0,1

а
другая имеет биномиальное распределение
с параметрами п
= 2, р =
0,6. Составить закон распределения их
суммы и найти математическое ожидание
этой случайной величины.

3.28.  Случайные
величины X и Y независимы
и имеют один и тот же закон распределения:

Значение	1	2	4
Вероятность	0,2	0,3	0,5

Составить
закон распределения случайных
величин 2
X и X+
Y. Убедиться
в том, что 2
X ≠
X+
Y, но М(2Х)
= 
M(
X+
Y).

3.29.  По
данным примера 3.52 убедиться в том,
что X² ≠ XY . Проверить
равенство M(XY) =[М(Х)]².

3.30.  Два
стрелка сделали по два выстрела по
мишени. Вероятность попадания в мишень
для первого стрелка равна 0,6, для второго
– 0,7. Необходимо:

а)
составить закон распределения общего
числа попаданий;

б)
найти математическое ожидание и дисперсию
этой случайной
величины.

3.31.  Пусть X, 
Y, 
Z – случайные
величины: X – выручка фирмы, Y –
ее затраты, Z =
Х — 
Y –
прибыль. Найти распределение прибыли Z,
если затраты и выручка независимы и
заданы распределениями:

X:	xi	3	4	5
pi	1/3	1/3	1/3

Y:	yj	1	2
pj	1/2	1/2

3.32.  Пусть X –
выручка фирмы в долларах. Найти
распределение выручки в рублях Z=
X*
Y в
пересчете по курсу доллара Y, если
выручка X не
зависит от курса Y,
а распределения X и Y имеют
вид

X:	xi	1000	2000
pi	0,7	0,3

Y:	yj	25	27
pj	0,4	0,6

3.33.  Сделано
два высокорисковых вклада: 10 тыс. руб.
в компанию А и
15 тыс. руб. – в компанию В. Компания А обещает
50% годовых, но может «лопнуть» с
вероятностью 0,2. Компания В обещает
40% годовых, но может «лопнуть» с
вероятностью 0,15. Составить закон
распределения случайной величины –
общей суммы прибыли (убытка), полученной
от двух компаний через год, и найти ее
математическое ожидание.

3.34.  Дискретная
случайная величина X задана
рядом распределения

X:	xi	1	2	3	4	5
pi	0,2	0,3	0,3	0,1	0,1

Найти
условную вероятность события X<5
при условии, что Х>2.

3.35.  Случайные
величины Х₁,
Х₂ независимы
и имеют одинаковое распределение

xi	0	1	2	3
pi	1/4	1/4	1/4	1/4

а) Найти
вероятность события X₁+
X₂>
2.

б) Найти
условную вероятность P_X1=1[(X₁ +
X₂) >
2].

3.36.  Распределение
дискретной случайной величины X задано
формулой р(Х
= к) = Ск², где к
= 1,
2, 3, 4, 5. Найти:

а)
константу С;

б)
вероятность события |Х– 2|<1.

4
ГЛАВА

Основные
законы распределения

В
главе рассматриваются:

— биноминальный,
равномерный, показательный и нормальный
законы распределения;

— закон
распределения Пуассона;

— геометрическое
и гипергеометрическое
распределения;

— логарифмически-нормальное
распределение.
Типовые
задачи
Пример
4.1

В магазин
поступила обувь с двух фабрик в соотношении
2:3. Куплено 4 пары обуви. Найти закон
распределения числа купленных пар
обуви, изготовленной первой фабрикой.
Найти математическое ожидание и среднее
квадратическое отклонение этой случайной
величины.

Решение

Вероятность
того, что случайно выбранная пара обуви
изготовлена первой фабрикой,
равна

p=2/(2+3)=0,4.

Случайная
величина X –
число пар обуви среди четырех, изготовленных
первой фабрикой, имеет биномиальный
закон распределения с параметрами п
= 4, р
= 0,4.
Ряд распределения X имеет
вид:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

1. Вероятность сдачи первого экзамена 0,6, тогда вероятность его не сдать 1 — 0,6 = 0,4.

Вероятность сдачи  второго экзамена равна 0,8, а неуспеха  1 — 0,8 = 0,2.

Известно, что вероятность сдать третий экзамен составляет 0,7.

Тогда вероятность его не сдать 1 — 0,7 = 0,3.

2. Вычислим вероятность сдачи одного экзамена.

Это событие происходит в случае, когда один предмет сдан, а два других нет.

Р1 = 0,6 * 0,2 * 0,3 + 0,4 * 0,8 * 0,3 + 0,4 * 0,2 * 0,7 = 0,036 + 0,096 + 0,056 = 0,188.

2. Найдем вероятность сдачи двух предметов.

Р2 = 0,6 * 0,8 * 0,3 + 0,4 * 0,8 * 0,7 + 0,6 * 0,2 * 0,7 = 0,144 + 0,224 + 0,084 = 0,452.

3. Определим вероятность сдачи трех экзаменов.

Р3 = 0,6 * 0,8 * 0,7 = 0,336.

4. Вычислим вероятность сдать хотя бы один экзамен.

Обратное этому событию — ничего не сдать.

Р = 0,4 * 0,2 * 0,3 = 0,024.

Р4 = 1 — 0,024 = 0,976.

Ответ: 0,188; 0,452; 0,336; 0,976.