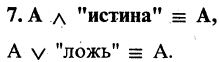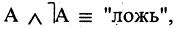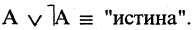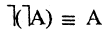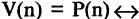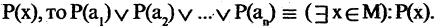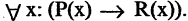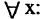Решение задач с помощью диаграмм Венна.
Объединением (суммой) двух множеств А и В называется множество вида:
A∪B ={a a∈ A или a∈ B}(рис. 1.2, а).
Пересечением двух множеств А и В называется множество вида:
A∩B={a a∈ A и a∈ B} (рис. 1.2, б).
Если множества А и В не имеют общих элементов, то A∩B=∅.
Правило сложения. Из двух множеств, содержащих n и m элементов соответственно, выбрать один элемент можно n+m способами, если множества не пересекаются и n+m-k способами, если эти множества имеют k общих элементов.
Число элементов объединения множеств А и В, содержащих nи m элементов соответственно, равно n+m-k, где k- количество общих элементов. Если множества не пересекаются, то k=0.
Если число элементов множества обозначить
, то кол-во элементов объединения (суммы) можно найти по формуле
, где
— количество общих элементов.
Если множеств три, то =
, где
-универсальное множество.
Если число элементов множества обозначить
, то кол-во элементов объединения (суммы) можно найти по формуле
, где
— количество общих элементов.
Если множеств три, то =
, где
-универсальное множество.
Задача. В группе из 29 человек по результатам опроса оказалось, что 20 человек увлекаются музыкой, а 15 человек увлекаются танцами. Сколько человек увлекаются музыкой и танцами, если 6 человек ответили, что не увлекаются ничем?
Решение.
В данной задаче универсальное множество U – это все, кто состоит в группе. По условию задачи его мощность равна 25.
Пусть – множество людей из данной группы, увлекающихся музыкой. Тогда по условию задачи его мощность равна 20.
– множество тех, кто увлекается танцами. Тогда по условию его мощность равна 15.
Тогда — множество тех, кто увлекается музыкой и танцами одновременно,
а — это множество тех, кто увлекается танцами или музыкой, или и тем, и другим одновременно.
Тогда множество — это те люди, которые не увлекаются ничем, по условию задачи мощность этого множества равна 6.
Изобразим эти множества на диаграмме Венна:
U
М
Заштриховано множество — множество тех, кто увлекается музыкой и танцами.
Что бы найти количество элементов множества нужно из суммы мощностей множеств М и Т вычесть мощность их пересечения
. Мощность универсального множества U равна сумме мощностей множества
и множества
. Пусть множество
содержит х элементов, тогда 29 = 6 + 20+15 — х.
Отсюда х=12. Следовательно, множество должно содержать 12 элементов.
Количество увлекающихся музыкой и танцами одновременно 12 человек.
Решить задачи и изобразить на диаграмме Венна.
- На 20 % компьютеров компании установлена операционная система Microsoft Windows XP , на 85 % компьютеров установлена Microsoft Windows 7, на 10 % установлена операционная система Linux. Одновременно Linux и Microsoft Windows 7 установлены на 6% компьютеров, Microsoft Windows XP и Linux на 4% , все три программы установлены на 2% компьютеров. На скольких процентах компьютеров установлена операционная система Microsoft?
- Каждый студент в группе сдает экзамен либо по высшей математике, либо по математической логике, либо по обоим предметам. По высшей математике сдают экзамен 15 человек, а по мат. логике — 19, а тот и другой предмет – 7 студентов. Сколько студентов в группе?
- В торговый центр “Форум” пришло 100 покупателей. Диск Николая Баскова купило 20 человек, диск Стаса Михайлова купило 64 человек, причем 11 человек купило диски этих двух исполнителей. Сколько человек не купило диски этих исполнителей?
- Несколько футбольных болельщиков соседнего дома выписывают журнал “Наш футбол”, часть жителей этого дома выписывают известный автомобильный журнал “Top Gear”, а часть тот, и тот журнал. Сколько жителей соседнего дома выписывают оба журнала, если на “Наш Футбол” подписано 64 процента, а на “Top Gear” – 84 процента?
- Первый и второй зачет по Русскому языку сдали 9 школьников, первый и третий зачет – 6 школьников, второй и третий — 7 школьников. Не менее двух зачетов выполнили 10 школьников. Сколько школьников успешно сдали все три зачета?
- В кондитерском отделе супермаркета посетители обычно покупают либо один торт, либо одну коробку конфет, либо один торт и одну коробку конфет. В один из дней было продано 57 тортов и 36 коробок конфет. Сколько было покупателей, если 12 человек купили и торт, и коробку конфет?
- В Хоккейной команде “Звезда” 24 игрока. Среди них 13 нападающих. 7 полузащитников, 10 защитники и вратари. Известно, что 4 из игроков могут быть нападающими и защитниками, 5 защитниками и полузащитниками, 7 нападающими и защитниками, а 2 и нападающими и защитником, и полузащитником. Вратари не заменимы. Сколько в команде “Звезда” вратарей?
- В магазин «Мир музыки» пришло 35 покупателей. Из них 20 человек купили новый диск певицы Максим, 11 – диск Земфиры, 10 человек не купили ни одного диска. Сколько человек купили диски и Максим, и Земфиры?
- На полке стояло 42 волшебные книги по заклинаниям, все они были прочитаны. Из них 5 прочитали и Гарри Поттер, и Рон. Гермиона прочитала 27 книг, которых не читали ни Гарри Поттер, ни Рон, и 6 книг, которые читал Гарри Поттер. 4 книги прочитали и Рон, и Гермиона. 2 книги прочитали все трое. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал только Рон?
- В магазине побывало 36 человек. Известно, что они купил 10 планшетов, 15 смартфонов, 23 телевизора. 7 из них купило и планшет, и смартфон, 15 человек купили и смартфон, и телевизор, 6 человек – и планшет, и телевизор. И 5 человек совершили все три покупки. Был ли среди них посетитель, который ничего не купил?
- В офисе работает 119 человек. 25 человек приезжает только на личном авто. Автобусом пользуется 27 человек, троллейбусом 43, метро 36, причем, четверо из них пользуются и метро и автобусом, 5 человек — троллейбусом и метро, 6 человек — автобусом и троллейбусом. Часть из них пользуются троллейбусом, метро и автобусом. Сколько человек пользуется не одним видом транспорта?
- Из 100 туристов отправляющихся на зимний курорт, на сноуборде умеют кататься 30 человек, на лыжах – 28 и на коньках – 42 человека. На сноуборде и лыжах умеют кататься 8 человек, на лыжах и на коньках – 5 человек, на сноуборде и коньках 4 человека. На всех трех – трое. Сколько человек вообще не умеет кататься?
- Каждый из 35 шестиклассников является читателем, по крайней мере, одной из двух библиотек: школьной и районной. Причем, 25 человек из них берут книги в школьной библиотеке, 20 человек берут книги в районной библиотеке. Сколько шестиклассников: 1)не являются читателями районной библиотеки; 2) не являются читателями школьной библиотеки; 3) являются читателями только районной библиотеки; 3) являются читателями только школьной библиотеки? 4) являются читателями обеих библиотек?
- Из сотрудников фирмы 16 побывали во Франции, 10-в Италии, 6-в Англии; в Англии и Италии -5; в Англии и Франции — 6; во всех трех странах — 5 сотрудников. Сколько человек посетили и Италию, и Францию, если всего в фирме работают 19 человек, и каждый из них побывал хотя бы в одной из названных стран?
- В трёх группах 70 студентов. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 студентов из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько студентов не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько студентов заняты только спортом?
Решение задач с помощью диаграмм Эйлера-Венна.
Решение задач с помощью диаграмм Венна.
Объединением (суммой) двух множеств А и В называется множество вида:
A∪B ={a a∈ A или a∈ B}(рис. 1.2, а).
Пересечением двух множеств А и В называется множество вида:
A∩B={a a∈ A и a∈ B} (рис. 1.2, б).
Если множества А и В не имеют общих элементов, то A∩B=∅.
Правило сложения. Из двух множеств, содержащих n и m элементов соответственно, выбрать один элемент можно n+m способами, если множества не пересекаются и n+m-k способами, если эти множества имеют k общих элементов.
Число элементов объединения множеств А и В, содержащих nи m элементов соответственно, равно n+m-k, где k- количество общих элементов. Если множества не пересекаются, то k=0.
Если число элементов множества обозначить , то кол-во элементов объединения (суммы) можно найти по формуле , где — количество общих элементов.
Если множеств три, то =
, где -универсальное множество.
Если число элементов множества обозначить , то кол-во элементов объединения (суммы) можно найти по формуле , где — количество общих элементов.
Если множеств три, то =
, где -универсальное множество.
Задача. В группе из 29 человек по результатам опроса оказалось, что 20 человек увлекаются музыкой, а 15 человек увлекаются танцами. Сколько человек увлекаются музыкой и танцами, если 6 человек ответили, что не увлекаются ничем?
Решение.
В данной задаче универсальное множество U – это все, кто состоит в группе. По условию задачи его мощность равна 25.
Пусть – множество людей из данной группы, увлекающихся музыкой. Тогда по условию задачи его мощность равна 20.
– множество тех, кто увлекается танцами. Тогда по условию его мощность равна 15.
Тогда — множество тех, кто увлекается музыкой и танцами одновременно,
а — это множество тех, кто увлекается танцами или музыкой, или и тем, и другим одновременно.
Тогда множество — это те люди, которые не увлекаются ничем, по условию задачи мощность этого множества равна 6.
Изобразим эти множества на диаграмме Венна:
U
М
Заштриховано множество — множество тех, кто увлекается музыкой и танцами.
Что бы найти количество элементов множества нужно из суммы мощностей множеств М и Т вычесть мощность их пересечения . Мощность универсального множества U равна сумме мощностей множества и множества . Пусть множество содержит х элементов, тогда 29 = 6 + 20+15 — х.
Отсюда х=12. Следовательно, множество должно содержать 12 элементов.
Количество увлекающихся музыкой и танцами одновременно 12 человек.
Решить задачи и изобразить на диаграмме Венна.
- На 20 % компьютеров компании установлена операционная система Microsoft Windows XP , на 85 % компьютеров установлена Microsoft Windows 7, на 10 % установлена операционная система Linux. Одновременно Linux и Microsoft Windows 7 установлены на 6% компьютеров, Microsoft Windows XP и Linux на 4% , все три программы установлены на 2% компьютеров. На скольких процентах компьютеров установлена операционная система Microsoft?
- Каждый студент в группе сдает экзамен либо по высшей математике, либо по математической логике, либо по обоим предметам. По высшей математике сдают экзамен 15 человек, а по мат. логике — 19, а тот и другой предмет – 7 студентов. Сколько студентов в группе?
- В торговый центр “Форум” пришло 100 покупателей. Диск Николая Баскова купило 20 человек, диск Стаса Михайлова купило 64 человек, причем 11 человек купило диски этих двух исполнителей. Сколько человек не купило диски этих исполнителей?
- Несколько футбольных болельщиков соседнего дома выписывают журнал “Наш футбол”, часть жителей этого дома выписывают известный автомобильный журнал “Top Gear”, а часть тот, и тот журнал. Сколько жителей соседнего дома выписывают оба журнала, если на “Наш Футбол” подписано 64 процента, а на “Top Gear” – 84 процента?
- Первый и второй зачет по Русскому языку сдали 9 школьников, первый и третий зачет – 6 школьников, второй и третий — 7 школьников. Не менее двух зачетов выполнили 10 школьников. Сколько школьников успешно сдали все три зачета?
- В кондитерском отделе супермаркета посетители обычно покупают либо один торт, либо одну коробку конфет, либо один торт и одну коробку конфет. В один из дней было продано 57 тортов и 36 коробок конфет. Сколько было покупателей, если 12 человек купили и торт, и коробку конфет?
- В Хоккейной команде “Звезда” 24 игрока. Среди них 13 нападающих. 7 полузащитников, 10 защитники и вратари. Известно, что 4 из игроков могут быть нападающими и защитниками, 5 защитниками и полузащитниками, 7 нападающими и защитниками, а 2 и нападающими и защитником, и полузащитником. Вратари не заменимы. Сколько в команде “Звезда” вратарей?
- В магазин «Мир музыки» пришло 35 покупателей. Из них 20 человек купили новый диск певицы Максим, 11 – диск Земфиры, 10 человек не купили ни одного диска. Сколько человек купили диски и Максим, и Земфиры?
- На полке стояло 42 волшебные книги по заклинаниям, все они были прочитаны. Из них 5 прочитали и Гарри Поттер, и Рон. Гермиона прочитала 27 книг, которых не читали ни Гарри Поттер, ни Рон, и 6 книг, которые читал Гарри Поттер. 4 книги прочитали и Рон, и Гермиона. 2 книги прочитали все трое. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал только Рон?
- В магазине побывало 36 человек. Известно, что они купил 10 планшетов, 15 смартфонов, 23 телевизора. 7 из них купило и планшет, и смартфон, 15 человек купили и смартфон, и телевизор, 6 человек – и планшет, и телевизор. И 5 человек совершили все три покупки. Был ли среди них посетитель, который ничего не купил?
- В офисе работает 119 человек. 25 человек приезжает только на личном авто. Автобусом пользуется 27 человек, троллейбусом 43, метро 36, причем, четверо из них пользуются и метро и автобусом, 5 человек — троллейбусом и метро, 6 человек — автобусом и троллейбусом. Часть из них пользуются троллейбусом, метро и автобусом. Сколько человек пользуется не одним видом транспорта?
- Из 100 туристов отправляющихся на зимний курорт, на сноуборде умеют кататься 30 человек, на лыжах – 28 и на коньках – 42 человека. На сноуборде и лыжах умеют кататься 8 человек, на лыжах и на коньках – 5 человек, на сноуборде и коньках 4 человека. На всех трех – трое. Сколько человек вообще не умеет кататься?
- Каждый из 35 шестиклассников является читателем, по крайней мере, одной из двух библиотек: школьной и районной. Причем, 25 человек из них берут книги в школьной библиотеке, 20 человек берут книги в районной библиотеке. Сколько шестиклассников: 1)не являются читателями районной библиотеки; 2) не являются читателями школьной библиотеки; 3) являются читателями только районной библиотеки; 3) являются читателями только школьной библиотеки? 4) являются читателями обеих библиотек?
- Из сотрудников фирмы 16 побывали во Франции, 10-в Италии, 6-в Англии; в Англии и Италии -5; в Англии и Франции — 6; во всех трех странах — 5 сотрудников. Сколько человек посетили и Италию, и Францию, если всего в фирме работают 19 человек, и каждый из них побывал хотя бы в одной из названных стран?
- В трёх группах 70 студентов. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 студентов из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько студентов не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько студентов заняты только спортом?
Использование диаграмм Эйлера-Венна при решении логических задач | Методическая разработка по информатике и икт (10 класс) на тему:
Самостоятельная работа «Использование диаграмм Эйлера-Венна при решении логических задач»
Вариант №1
- В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет
|
Запрос |
Найдено страниц |
|
Польша |
4200 |
|
Польша & Украина |
1230 |
|
Украина |
3990 |
Какое количество страниц (в тысячах) будет найдено по запросу Польша | Украина?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
- В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
|
Запрос |
Найдено страниц |
|
Байрон & Пушкин |
1310 |
|
Байрон & Лермонтов |
1220 |
|
Байрон & (Пушкин | Лермонтов) |
1750 |
Какое количество страниц (в тысячах) будет найдено по запросу
Байрон & Пушкин & Лермонтов?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
- В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
|
Запрос |
Найдено страниц |
|
Амур |
1100 |
|
Днепр |
1600 |
|
Амур | Днепр |
2700 |
|
Амур | Волга | Днепр |
3800 |
|
Волга & Днепр |
550 |
|
Амур & Волга |
670 |
Какое количество страниц (в тысячах) будет найдено по запросу Волга?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Критерий оценивания:
- оценка «5» – правильно решены задачи №2 и №3.
- оценка «4» – правильно решены две задачи: №1 и №2 или №1 и №3.
- оценка «3» – правильно решена только одна задача.
- оценка «2» – ни одна задача не решена правильно.
Вариант №2
- В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет
|
Запрос |
Найдено страниц |
|
Польша | Украина |
7500 |
|
Польша |
4200 |
|
Украина |
3990 |
Какое количество страниц (в тысячах) будет найдено по запросу Польша & Украина? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
- В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
|
Запрос |
Найдено страниц |
|
хоккей & футбол & волейбол |
780 |
|
футбол & волейбол |
1260 |
|
хоккей & волейбол |
1230 |
Какое количество страниц (в тысячах) будет найдено по запросу
(хоккей | футбол) & волейбол?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
- В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
|
Запрос |
Найдено страниц |
|
Вильнюс |
2800 |
|
Таллин |
2400 |
|
Рига |
2100 |
|
Вильнюс | Таллин |
5200 |
|
Рига & Таллин |
850 |
|
Вильнюс & Рига |
870 |
Какое количество страниц (в тысячах) будет найдено по запросу
Вильнюс | Рига | Таллин?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Критерий оценивания:
- оценка «5» – правильно две решены задачи №2 и №3.
- оценка «4» – правильно две решены задачи: №1 и №2 или №1 и №3.
- оценка «3» – правильно решена только одна задача.
- оценка «2» – ни одна задача не решена правильно.
Вариант №3
- В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет
|
Запрос |
Найдено страниц |
|
Польша & Украина |
1230 |
|
Польша | Украина |
7270 |
|
Украина |
3990 |
Какое количество страниц (в тысячах) будет найдено по запросу Польша?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
- В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
|
Запрос |
Найдено страниц |
|
Курск & (Орел | Белгород) |
370 |
|
Курск & Белгород |
204 |
|
Курск & Орел & Белгород |
68 |
Какое количество страниц (в тысячах) будет найдено по запросу Курск & Орел?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
- В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
|
Запрос |
Найдено страниц (тыс.) |
|
белки |
1930 |
|
жиры |
1860 |
|
углеводы |
2340 |
|
жиры | углеводы |
4200 |
|
жиры & белки |
850 |
|
белки | жиры | углеводы |
4870 |
Какое количество страниц (в тысячах) будет найдено по запросу белки & углеводы?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Критерий оценивания:
- оценка «5» – правильно две решены задачи №2 и №3.
- оценка «4» – правильно две решены задачи: №1 и №2 или №1 и №3.
- оценка «3» – правильно решена только одна задача.
- оценка «2» – ни одна задача не решена правильно.
Вариант №4
- В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет
|
Запрос |
Найдено страниц |
|
Чехия |
5150 |
|
Словакия |
5080 |
|
Чехия & Словакия |
3290 |
Какое количество страниц (в тысячах) будет найдено по запросу Чехия | Словакия?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
- В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
|
Запрос |
Найдено страниц |
|
(Суворов & Альпы) | (Суворов & Варшава) |
1300 |
|
Суворов & Варшава |
600 |
|
Суворов & Варшава & Альпы |
50 |
Сколько страниц (в тысячах) будет найдено по запросу Суворов & Альпы? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
- В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
|
Запрос |
Найдено страниц |
|
Сочи |
3100 |
|
Ванкувер |
3600 |
|
Сочи | Ванкувер |
6700 |
|
Сочи | Турин | Ванкувер |
8200 |
|
Турин & Ванкувер |
790 |
|
Сочи & Турин |
720 |
Какое количество страниц (в тысячах) будет найдено по запросу Турин?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Критерий оценивания:
- оценка «5» – правильно решены задачи №2 и №3.
- оценка «4» – правильно решены две задачи: №1 и №2 или №1 и №3.
- оценка «3» – правильно решена только одна задача.
- оценка «2» – ни одна задача не решена правильно.
Вариант №5
- В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет
|
Запрос |
Найдено страниц |
|
Волга | Амур |
8280 |
|
Волга |
5250 |
|
Амур |
4990 |
Какое количество страниц (в тысячах) будет найдено по запросу Волга & Амур ?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
- В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
|
Запрос |
Найдено страниц (в тысячах) |
|
Таллин & Киев |
340 |
|
Киев & Минск |
160 |
|
Таллин & Киев & Минск |
120 |
Какое количество страниц (в тысячах) будет найдено по запросу
(Таллин & Киев) | (Минск & Киев) ?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
- Некоторый сегмент сети Интернет состоит из 1000 сайтов. Поисковый сервер в автоматическом режиме составил таблицу ключевых слов для сайтов этого сегмента. Вот ее фрагмент:
|
Ключевое слово |
Количество сайтов, |
|
сканер |
200 |
|
принтер |
250 |
|
монитор |
410 |
Сколько сайтов будет найдено по запросу «(принтер | сканер) & монитор», если по запросу «принтер | сканер» было найдено 450 сайтов, по запросу «принтер & монитор» — 40, а по запросу «сканер & монитор» — 50.
Критерий оценивания:
- оценка «5» – правильно решены задачи №2 и №3.
- оценка «4» – правильно решены две задачи: №1 и №2 или №1 и №3.
- оценка «3» – правильно решена только одна задача.
- оценка «2» – ни одна задача не решена правильно.
Вариант №6
- В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет
|
Запрос |
Найдено страниц |
|
Латвия & Литва |
2170 |
|
Латвия | Литва |
9350 |
|
Литва |
5640 |
Какое количество страниц (в тысячах) будет найдено по запросу Латвия?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
- В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет. В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
|
Запрос |
Найдено страниц (в тысячах) |
|
(Испания & Америка) | (Испания & Индия) |
2800 |
|
Испания & Америка |
1600 |
|
Испания & Индия & Америка |
150 |
Сколько страниц (в тысячах) будет найдено по запросу Испания & Индия ?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
- В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
|
Запрос |
Найдено страниц |
|
Мерседес |
4700 |
|
Ауди |
4200 |
|
Опель |
3900 |
|
Мерседес | Ауди |
8900 |
|
Опель & Ауди |
1190 |
|
Мерседес & Опель |
1010 |
Какое количество страниц (в тысячах) будет найдено по запросу
Мерседес | Опель | Ауди?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Критерий оценивания:
- оценка «5» – правильно две решены задачи №2 и №3.
- оценка «4» – правильно две решены задачи: №1 и №2 или №1 и №3.
- оценка «3» – правильно решена только одна задача.
- оценка «2» – ни одна задача не решена правильно.
Решение логических задач кругами Эйлера-Венна | Презентация к уроку по информатике и икт (10 класс) по теме:
Слайд 1
Решение логических задач при помощи кругов Эйлера — Венна
Слайд 2
Все мои подруги выращивают в своих квартирах какие-нибудь растения. Шестеро из них разводят лилии, а пятеро — фиалки. И только у двоих есть и лилии и фиалки. Угадайте, сколько у меня подруг? Л — 6 Ф — 5 2 6-2= 4 4 5-2= 3 3 Всего 4+2+3=9
Слайд 3
Каждая семья из нашего дома выписывает газету или журнал, или и то и другое. 75 семей выписывают газеты, 27 семей – журналы. Лишь 13 семей и журналы, и газеты. Сколько семей в доме? Г-75 Ж-27 13 75-13= 62 62 27-13= 14 14 62+13+14= 89 семей
Слайд 4
В классе 30 учащихся. Из них 18 человек занимаются в секции легкой атлетики, 10 – плаванием, 3 – и тем, и другим. Сколько человек не занимается ничем? Плавание – 10 чел. 30 7 3 15 легкая атлетика – 18 чел 30 — (7 + 3 + 15) = 5
Слайд 5
12 учащихся класса любят детектив, 18 – фантастику, 3 и то , и другое, 1 ничего не читает. Сколько человек в классе? Д-12 Ф-18 3 0 9 0 15 0 1 12-3=9 18-3=15 15+3+9+1=28 чел. Не читают — 1
Слайд 6
Ребята посещают три кружка: математики, физики и химии. Решено было организовать кружок юных техников и пригласить тех ребят, которые не занимаются ни в одном из трех перечисленных. Сколько таких ребят, если всего в классе 36 человек , занимаются математикой- 18 , физикой – 14 , химией – 10 . 2 посещают все три кружка, 8 – математику и физику, 5 – математику и химию, 3 – химию и физику. 2 1 3 6 36 4 5 7 математика физика химия 7+3+4+1+5+6+2=28 36-28=8
Слайд 7
На турбазу приехала отдыхать группа студентов. Оказалось 12 человек привезли с собой бутерброды с колбасой, 5 — с сыром, 9 с маслом. 1 сделал бутерброд с маслом и с сыром. 3 сделали бутерброды с маслом и бутерброды с колбасой , не оказалось ни одного, который бы сделал бутерброды с колбасой и с сыром . Сколько человек отдыхало? К-12 М-9 С-5 К М С 3 0 9 12-3=9 0 5 1 5-1=4 4 9-1-3=5 Ответ: 9+3+5+1+4= 22 человека
Слайд 8
В детском саду 11 деток любят манную кашу, 13 — гречневую, 7 – перловую, 4 – манную и гречневую, 3 – манную и перловую, 6 – гречневую и перловую, 2 – уплетают все три вида. Сколько детей в группе, если в ней нет ни одного кто не любит кашу? М-11 Г-13 П-7 2 4 2 1 6 5 0 6+2+5+4+2+1=20 человек
Слайд 9
Самостоятельная работа Из 220 школьников 16 играют в баскетбол, 175 в футбол, 24 не играют в эти игры. Сколько человек одновременно играет в баскетбол и в футбол?
Слайд 10
Из 220 школьников 16 играют в баскетбол, 175 в футбол, 24 не играют в эти игры. Сколько человек одновременно играет в баскетбол и в футбол? Б-16 Ф-175 НЕ ИГР-24 220 220-24=196 175+16=191 196-191=5 5
Слайд 11
2. В классе 35 учеников. 20 из них занимаются в математическом кружке, 11 — в биологическом, а 1 ничем не занимаются. Сколько ребят занимаются и математикой, и биологией?
Слайд 12
2. В классе 35 учеников. 20 из них занимаются в математическом кружке, 11 — в биологическом, а 1 ничем не занимаются. Сколько ребят занимаются и математикой, и биологией? 35 М-20 Б-11 НЕ ЗАНИМ- 1 3 35-1=34 20+11=31 34-1=3
Слайд 13
3. Большая группа туристов выехала в заграничное турне. Из них владеет английским языком 28 человек, французским — 15, немецким — 10, английским и французским — 8, французским и немецким — 5, английским и немецким — 6, всеми тремя языками — двое, а 41 человек не владеет ни одним из трёх языков. Сколько всего туристов?
Слайд 14
3. Большая группа туристов выехала в заграничное турне. Из них владеет английским языком 28 человек, французским — 15, немецким — 10, английским и французским — 8, французским и немецким — 5, английским и немецким — 6, всеми тремя языками — двое, а 41 человек не владеет ни одним из трёх языков. Сколько всего туристов? А-28 Ф-15 Н-10 НВ-41 4 3 6 2 (16+4+1+41)+6+2+4+3=77 (28+10+15) — 6-5-8 +2 =36 36+41=77 1 4 16
Слайд 15
4. В футбольной команде «Спартак» 30 игроков, среди них 18 нападающих. 11 полузащитников, 17 защитников и вратари. Известно, что 3 могут быть нападающими и защитниками, 10 защитниками и полузащитниками, 6 нападающими и полузащитниками , а 1 и нападающим, и защитником, и полузащитником. Вратари не заменимы. Сколько в команде «Спартак» вратарей?
Слайд 16
4. В футбольной команде «Спартак» 30 игроков, среди них 18 нападающих. 11 полузащитников, 17 защитников и вратари. Известно, что 3 могут быть нападающими и защитниками, 10 защитниками и полузащитниками, 6 нападающими и полузащитниками , а 1 и нападающим, и защитником, и полузащитником. Вратари не заменимы. Сколько в команде «Спартак» вратарей? (18+11+17)-3-10-6 +1=28 (игроков) на этой диаграмме. Но в команде всего 30 футболистов. Значит вратарей будет 30-28=2 Ответ: 2 вратаря. Нападающие-18 Полузащитн-11 Защитники-17
Слайд 17
5. Миша, Коля, Лева вместе прочитали 3 книги. Миша и Коля вместе прочитали 5 книг; Миша и Лева вместе – 4 кн.; Коля и Лева вместе – 3 книги. Миша прочитал 8 книг; Коля – 6 книг; Лева – 5 книг. Сколько книг прочитали дети?
Слайд 18
5. Миша, Коля, Лева вместе прочитали 3 книги. Миша и Коля вместе прочитали 5 книг; Миша и Лева вместе – 4 кн.; Коля и Лева вместе – 3 книги. Миша прочитал 8 книг; Коля – 6 книг; Лева – 5 книг. Сколько книг прочитали дети?
Слайд 19
6. В классе 36 человек. Ученики этого класса посещают математический (М), физический (Ф) и химический (Х) кружки, причём посещают М — 18 человек, Ф – 14 человек, Х – 10 человек. Кроме того известно, что 2 человека посещают все три кружка , 8 человек – и математический и физический, 5 – и математический и химический, 3 – и физический и химический. Сколько учеников класса не посещают никаких кружков?
Слайд 20
6. В классе 36 человек. Ученики этого класса посещают математический (М), физический (Ф) и химический (Х) кружки, причём М посещают 18 человек, ф – 14 , х – 10 . Кроме того известно, что 2 человека посещают все три кружка, 8 человек – и математический и физический, 5 – и математический и химический, 3 – и физический и химический. Сколько учеников класса не посещают никаких кружков? Ф-40 Х-40 М-18 2 6 8 ( МФ ) -2= 6 5 (МФ) -2= 3 3 18-(2+6+3)= 7 7 3-2= 1 1 14-(6+2+1)= 5 5 10-(1+2+3)= 4 4
Слайд 21
В классе 36 человек. Ученики этого класса посещают математический (М), физический (Ф) и химический (Х) кружки, причём посещают М — 18 человек, Ф – 14 человек, Х – 10 человек. Кроме того известно, что 2 человека посещают все три кружка , 8 человек – и математический и физический, 5 – и математический и химический, 3 – и физический и химический. Сколько учеников класса не посещают никаких кружков? Ф14 Х-10 М-18 2 7 4 5 1 3 6 Всего посещают кружки: 7+6+2+3+5+1+4=28 36-28=8 человек
Слайд 22
Домашнее задание 1. В классе 30 человек. 20 из них каждый день пользуются метро, 15 — автобусом, 23 — троллейбусом, 10 — и метро, и троллейбусом, 12 — и метро, и автобусом, 9 — и троллейбусом, и автобусом. Сколько человек ежедневно пользуются всеми тремя видами транспорта?
Слайд 23
М-20 А-15 Т-23 МТ-10 -x МА-12 -x ТА-9 -x X — ? 20+15+23-10-12-9+х=30 27+х=30 х=3 Х + (12 − х) + (9 − х) + (10 − х) + (х + 4) + (х − 2) + (х − 6) = 30 тогда х = 3
Слайд 24
2. В восьмом классе учится 40 человек. Каждый из них изучает не менее одного иностранного языка: английский, немецкий, французский. 34 человека изучают хотя бы один из двух языков: английский, немецкий. 25 человек — хотя бы один из языков: немецкий, французский. 6 человек только немецкий. Одновременно английский и немецкий — изучают на 3 человека больше, чем французский и немецкий языки. Сколько человек изучает каждый из языков и сколько изучает одновременно каждую пару языков?
Слайд 25
2. В восьмом классе учится 40 человек. Каждый из них изучает не менее одного иностранного языка: английский, немецкий, французский. 34 человека изучают хотя бы один из двух языков: английский, немецкий. 25 человек — хотя бы один из языков: немецкий, французский. 6 человек только немецкий. Одновременно английский и немецкий — изучают на 3 человека больше, чем французский и немецкий языки. Сколько человек изучает каждый из языков и сколько изучает одновременно каждую пару языков?
Слайд 26
3. В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 — и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?
Слайд 27
17 3. В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 купили холодильник и микроволновку, 19 — микроволновку и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего? Х-35 М-36 Т-37 Купили только холодильники: 35- (17+12+3) = 3 Купили только микроволновки: 36-(17+16+3) = 0 Купили только телевизоры: 37-(12+3+16) = 6 Тогда всего покупателей было: 3+17+3+16+12+6=57 65-57= 8 посетителей магазина не купили ничего. 3 Не купили
Слайд 29
Задание Миша, Коля и Лева прочитали вместе 3 книги. Только Миша и Коля вместе прочитали 1 книгу; только Миша и Лева вместе не прочитали ни одной книги; только Коля и Лева вместе прочитали 3 книги. Миша в одиночку книг не читал; Коля в одиночку прочитал лишь одну книгу, а Лева – 2. Кто из трех мальчиков прочитал книг меньше всех; кто больше всех?
Слайд 30
Миша, Коля и Лева прочитали вместе 3 книги. Только Миша и Коля вместе прочитали 1 книгу; только Миша и Лева вместе не прочитали ни одной книги; только Коля и Лева вместе прочитали 3 книги. Миша в одиночку книг не читал; Коля в одиночку прочитал лишь одну книгу, а Лева – 2. Кто из трех мальчиков прочитал книг меньше всех; кто больше всех?
Слайд 31
Из 110 студентов английский язык изучают 44 человека, немецкий – 50 человек, французский – 49 человек, английский и немецкий – 13, английский и французский – 14, немецкий и французский – 12, все три языка изучают 5 человек. Сколько студентов изучают только один язык? Сколько студентов не изучают ни одного языка?
Слайд 32
Из 110 студентов английский язык изучают 44 человека, немецкий – 50 человек, французский – 49 человек, английский и немецкий – 13, английский и французский – 14, немецкий и французский – 12, все три языка изучают 5 человек. Сколько студентов изучают только один язык? Сколько студентов не изучают ни одного языка? Заполняется постепенно с рассуждениями. Только один язык 22 + 28 +30 = 80 Ни одного 110 – 80 – 29 =1
Слайд 33
В футбольной команде «Спартак» 30 игроков, среди них 18 нападающих, 11 полузащитников, 17 защитников и вратари. Известно, что 3 могут быть нападающими и защитниками, 10 защитниками и полузащитниками, 6 нападающими и защитниками, а 1 и нападающим, и защитником, и полузащитником. Вратари не заменимы. Сколько в команде «Спартак» вратарей? Н-18 П-11 З-17 3 3 1 11 3 18 + 11 + 17 — 3 — 10 — 6 + 1 = 28 30- 28 = 2 18 -3-3-1=11
Подборка задач по теме «Решение логических задач с помщью кругов Эйлера»
§2.Решение логических задач
с помощью кругов Эйлера-Венна.
Один из первых математиков, кто пользовался методом решения логических с помощью кругов Эйлера, был выдающийся немецкий математик и философ Готфрид Вильгельм Лейбниц (1646-1716гг). В его черновых набросках были обнаружены рисунки с такими кругами.
Затем, распространению этого метода во многом способствовал знаменитый швейцарский математик Леонард Эйлер (1707-1783гг). Он долгие годы работал в Петербургской Академии наук. К этому времени относятся его знаменитые «письма к немецкой принцессе», написанные в период с 17 61 по 1768 год. В некоторых из этих «Писем…» Эйлер как раз и рассказал о своём методе.
После Эйлера этот же метод разрабатывал чешский математик Бернард Больцано (1781-1848гг). Только в отличие от Эйлера он рисовал не круговые, а прямоугольные схемы. Методом кругов Эйлера пользовался и немецкий математик Эрнест Шредер (1841-1902гг). Этот метод широко используется в его книге «Алгебра логики».
Но наибольшего расцвета графические методы достигли в сочинениях английского логика Джона Венна (1843-1923). С наибольшей полнотой этот метод изложен им в книге «Символическая логика», изданной в Лондоне в 1881 году. В честь Венна вместо кругов Эйлера соответствующие рисунки называют иногда диаграммами Венна; в некоторых книгах их называют также диаграммами (или кругами) Эйлера-Венна.. Эти диаграммы могут быть построены по-разному. Рассмотрим четыре случая.
1. Дано некоторое множество и указано свойство А. Очевидно, элементы данного множества могут обладать или не обладать свойством А. Поэтому данное множество распадается на две части, которые мы обозначим через А и А. Эту ситуацию можно изобразить двумя способами (рис 1 ,2).
Рис 1. Рис 2.
На рис 1 большой круг изображает данное множество. Маленький круг А изображает ту часть элементов данного множества (подмножества), которые обладают свойством А, а кольцеобразная область, обозначенная через А, изображает ту часть элементов данного множества (подмножества), которые не обладают свойствам А.
На рис 2 те же подмножества А и А изображены по-другому.
2. Дано некоторое множество и указаны два свойства: А, В. Т.к. элементы данного множества могут обладать или не обладать каждый из этих свойств, то возможны четыре случая: АВ, АВ, АВ,АВ. Следовательно, данное множество распадается на четыре подмножества. Соответствующую диаграмму снова можно изобразить двумя способами, как на рис 3,4.
Рис 3. Рис 4.
На рис. 3 круг А — это подмножество тех элементов данного множества, которые обладают свойством А, а область вне круга, т.е. область А — это подмножество тех элементов, которые свойством А не обладают. Аналогично круг В и область вне его.
На рис. 4 подмножества А, А, В, В изображены по-другому. Подмножество А – это область слева от вертикальной черты (красная горизонтальная штриховка), а подмножество А – это область справа от этой черты. Аналогично изображены В иВ: область В – это верхний полукруг (зелёная вертикальная штриховка), а область В – это нижний полукруг.
3. Дано некоторое множество и указаны три свойства: А, В, С. В этом случае множество распадается на восемь частей. Это можно изобразить двумя способами (рис. 5,6).
Рис.5. Рис.6.
На рис5 объяснение аналогично сл2.рис3. На рис 6 подмножества А и В заштрихованы: А – горизонтально, В вертикально, а подмножество С – это маленький круг.
4. Дано некоторое множество и указаны четыре свойства: А, В, С, D. В этом случае множество распадается на 16 частей. Это можно изобразить с помощью диаграммы двумя способами (рис 7,8).
Рис 7. Рис 8.
Если будет указано пять свойств, то множество распадается на 32 частей, диаграммы станут ещё более сложными.
Итак, увеличением свойств число частей каждый раз удваивается. Некоторые части могут оказаться пустыми: в них не попадает ни один элемент множества. Такие части называются пустыми множествами.
Решим несколько задач данным методом.
Задача 16. Кружки.
Ребята из класса посещают три кружка: математический, физический и химический.
Все списки членов кружков хранились у секретаря. Однажды завуч школы решила открыть ещё и кружок юных математиков. В этот кружок она решила пригласить только тех ребят, которые пока ни в какие кружки ещё не записаны.
Чтобы узнать, сколько таких ребят, завуч решила обратиться к секретарю.
Секретарь сказал, что всего в классе 36 человек, а кружки посещают: математический – 18 человек, физический – 14 человек, химический – 10 человек.
Завуч удивилась: «Как же это так? Ведь 18+14+10=42, а в классе только 36 человек». Ей объяснили, что некоторое ребята ходят в два, а возможно, и в три кружка. В три кружка ходят 2 человека, математический и физический – 8, математический и химический – 5, физический и химический – 3.
Сколько человек из класса не ходят ни в один из кружков?
Решение:
Изобразим кругами Эйлера-Венна то, что нам дано.
Большой круг изображает множество всех учеников класса. Внутри этого круга расположены три круга меньшего диаметра: эти круги изображают соответственно множества членов математического, физического и химического кружков. Для ясности эти круги обозначены буквами М, Ф, Х.
О
МФХ
бщей частью всех трёх кругов соответствует множество ребят, посещающих все три кружка. Поэтому эту часть обозначим через МФХ.
Рис 9.
Через МФХ обозначим ту область, которая изображает множество ребят посещающих математический и физический кружки, но не посещающих химический кружок. Аналогичным образом обозначены и все остальные области (рис 9). Теперь обратимся к числовым данным и перейдём к рис 10.
В области МФХ впишем число 2, т.к. все три кружка посещают 2 человека. Далее известно, что ребят посещающих математический и физический кружки было 8. Значит, в область МФ надо вписать число 8. Но область МФ состоит из двух
частей: МФХ и МФХ, причём в МФХ входят 2 человека. Значит, на долю МФХ остаётся 6. Теперь рассмотрим область МХ, на которую приходится 5
человек. Эта область тоже состоит из двух частей. На МФХ приходится 2,значит на МФХ приходится 3.
Рассмотрим теперь область М, на которую приходится 18 человек. Эта область состоит из четырёх частей. Количественный состав трёх частей мы уже нашли: это соответственно 6,2 и 3. Значит, на четвёртую часть приходится 18-(6+2+3)=7 человек.
Аналогичным образом можно вычислить количественный состав всех остальных областей. Выполнив эти вычисления, получим рис 10. Теперь можно подсчитать число ребят, посещающих хотя бы один кружок. Для этого надо просто сложить все числа записанные внутри кругов М, Ф, Х. Получится 28. А всего ребят в нашем классе 36. Значит, на долю области МФХ приходится 8 человек. Следовательно, ребят, не посещающих никаких кружков, будет 8.
Задача 17. Кубики.
Дети изготовляли кубики для игры. Несколько кубиков они склеили из картона, а остальные сделали из дерева. Кубики были только двух размеров: большие и маленькие. Когда кубики были изготовлены, их покрасили: несколько кубиков — в зелёный цвет, а остальные – в красный. Получилось 16 зелёных кубиков. Зелёных кубиков большого размера было 6. Больших зелёных кубиков из картона было 4. Красных кубиков из картона было 8, а красных кубиков из дерева 9. Больших деревянных кубиков было 7, а маленьких деревянных кубиков было 11.
Сколько же всего получилось кубиков?
Решение:
Построим диаграмму Эйлера-Венна рис11.
Маленький круг – это красные кубики, кольцеобразная область – это зелёные. Левый большой полукруг – это деревянные, а правый – это картонные. Верхний большой полукруг – это большие кубики, А нижний – маленькие.
Каждая пара свойств: большие – маленькие, красные – зелёные, деревянные – картонные – представляет собой пару взаимно противоположных свойств, поэтому можно было бы
описать кубики и с помощью всего трёх свойств: быть или не быть красным (зелёные – это не красные), быть или не быть большим (маленькие — это не большие), быть или не быть деревянными (картонные – это не деревянные). Заполнение диаграммы следует начинать с того подмножества, для которого указаны все три свойства. Такое подмножество есть: это больших зелёных кубиков из картона – таких кубиков 4.
Теперь ищем подмножество, для которого указаны два свойства из перечисленных трёх. Это подмножество больших зелёных кубиков – таких кубиков 6. Но это подмножество состоит из картонных и деревянных кубиков. Картонных было 4. Значит, деревянных будет 6-4=2. Записываем в соответствующую клетку диаграммы цифру 2.
Больших деревянных кубиков 7 (это левая верхняя часть нашей диаграммы). Значит, красных будет 7-2=5. Записываем цифру 5 в соответствующую клетку.
Красных деревянных кубиков 9. А мы узнали, что из них 5 – это большие. Значит, маленьких красных кубиков из дерева будет 9-5=4. Записываем цифру 4 в соответствующую клетку.
Маленьких деревянных кубиков 11. Из них красных – 4, следовательно, маленьких зелёных кубиков из дерева будет 11-4=7. Записываем 7 в соответствующую клетку. Всего зелёных кубиков 16. Зелёные кубики помещены в кольцеобразную область, состоящую из четырёх частей. В трёх частях записаны цифры 4,2 и 7. Значит, на долю последней, четвёртой части приходится 16-(4+2+7)=3 следовательно, маленьких зелёных кубиков из картона было 3.
Осталось последнее условие: красных кубиков из картона было 8. Сколько из них больших и сколько маленьких, мы не знаем. Поэтому цифру 8 записываем так, чтобы было видно, что она обозначает те и другие вместе.
Теперь все клетки диаграммы заполнены, и мы можем сказать, сколько сортов кубиков получилось, и сколько было кубиков каждого сорта.
Всего же было изготовлено 33 кубика.
Задача 18. Спор, возникший после субботника.
Во дворе дома состоялся субботник. Собралось 29 человек. Их разделили на три бригады, которые должны были соответственно убрать двор, поливать сад и мыть подъезд дома. На уборку двора отправили только одних мужчин, а в саду и подъезде женщин было в два раза больше, чем мужчин. Получилось так, что женщин в саду было столько же, сколько было мужчин во дворе, а всего во дворе и в саду было 20 человек.
Н а следующий день между женщинами и мужчинами разгорелся спор. Мужчины утверждали, что на субботнике их было больше, чем женщин, и потому большую часть работы выполнили они — мужчины. Женщины же утверждали обратное: они были уверенны, что на субботнике их было больше, чем мужчин, и поэтому мужчины просто не могли сделать больше, чем они — женщины.
Кого же было больше?
Решение:
Составим диаграмму. Она получится несколько необычная. Особенность диаграммы состоит в том, что свойства – работать во дворе, работать в саду, работать в подъезде – разбивают множество всех ребят на три части, а не на две.
С остальными свойствами – быть мужчиной и быть женщиной – всё обстоит так, как это обычно бывает на диаграммах Эйлера–Венна, эти свойства взаимно противоположны, и поэтому множество, людей распадается на две части.
Начнём заполнять диаграмму.
Известно, что в саду женщин было в два раза больше чем мужчин. Поэтому мы можем обозначить число мужчин, работавших в саду за х, а женщин за 2х. Известно также, что в подъезде женщин тоже было в два раза больше, чем мужчин. Значит, число мужчин, работающих в подъезде можно обозначить через у, а женщин – через 2у. Известно ещё, что женщин в саду было столько же, сколько было мужчин во дворе. Но женщин в саду было 2х. Значит, мальчиков во дворе тоже было 2х.
Все эти данные запишем в соответствующих клетках диаграммы. Наконец, заметим, что во дворе работали только мужчины. Поэтому в клетке, обозначающей женщин, работающих во дворе, запишем нуль.
Всего во дворе и в саду было 20 человек. С помощью диаграммы составим ещё одно уравнение 2х+х+2х=20 следовательно х=4.
Всего на субботнике было 29 человек. С помощью диаграммы составим ещё одно уравнение 5х+5у=29. Т.к. х=4, то у=3.
Теперь подсчитаем, сколько было женщин. Их было 2х+2у т.е. 8+6=14.
А мужчин было 29-14=15. Значит, мужчин было больше.
Задача 19. История со сведениями о количестве выписываемых журналов.
На занятиях физического кружка, состоящего из 10 человек, учитель спросил, выписывают ли члены кружка такие специальные журналы, как «Квант» (К), «Техника молодёжи» (Т), « Юный техник» (Ю). Выяснилось, что 6 человек выписывают К, 5 человек –Т и Ю, 3 человека – К и Ю, а один человек не выписывает ни одного журнала, но читает все эти журналы в библиотеке. Учитель попросил старосту составить справку.
Староста составил справку со всеми этими сведениями. Но учитель был недоволен, так как в записке не было указано, сколько членов кружка выписывают все три журнала, сколько — два, а сколько – только один. Узнать это у самих членов кружка староста не мог, так как все ребята уже разошлись по домам.
Помогите старосте узнать интересующие его сведения.
Решение:
Изобразим данные задачи с помощью кругов Эйлера-Венна (рис 13).
Большой круг – это множество всех членов физического кружка. Он состоит из 10 человек. Внутри большого круга нарисуем три маленьких круга: К, Т, Ю, которые изображают ребят, подписавшихся на соответствующие журналы. Известно, что один человек не выписывает ни одно журнала. Значит, в области расположенной вне кругов К, Т, Ю запишем 1. В остальных ячейках, получившегося рисунка запишем буквы a, b, c, x, y, z, t, которые будут обозначать число рябят, подписавшихся на соответствующие наборы этих журналов.
С помощью этого рис. 13 исходные данные можно теперь записать следующим образом:
(1) (2)
Т. к. членов кружка было 10, то запишем ещё одно уравнение:
(x+y+z)+(a+b+c)+t+1=10 (3)
Сложив уравнения каждой из систем (1) и (2) и присоединив к ним уравнение (3), получим следующую систему:
Отсюда получим: x+y+z=3, a+b+c=5, t=1.
Заметим теперь, что x+y+z это число ребят подписавшихся только на один журнал, a+b+c – это число ребят, подписавшихся ровно на два журнала, а t=1 – это число ребят, подписавшихся на все три журнала.
Значит сведения, необходимые учителю, получены: на один журнал подписалось 3 человека, на два – 5 человек, на три – 1.
Задача 20. Спортивная команда.
На соревнования должна приехать спортивная команда. О составе команды известно следующее. В неё входят волейболисты, бегуны, прыгуны и метатели. Команда сильная. Все бегуны являются и прыгунами, а все прыгуны являются метателями, или бегунами. Одна из особенностей команды состоит в том, что среди тех метателей, которые являются ещё и прыгунами, нет бегунов. Метателей у нас в два раза меньше, чем прыгунов, и на два меньше, чем бегунов. Бегуны составляют третью часть всей команды, а волейболистов в два раза больше, чем тех ребят, которые являются одновременно и прыгунами, и метателями.
Сколько же человек в команде?
Решение:
Воспользуемся методом кругов Эйлера-Венна, и сделаем рис 14.
На этом рисунке круги Б, П, М изображают соответственно множество бегунов, прыгунов и метателей, а область вне кругов представляет множество волейболистов, обозначенных буквой В. Известно, что все бегуны являются прыгунами. Это значит, что область Б должна целиком находиться внутри круга П: никакая часть Б не должна выходить за пределы П. Следовательно, те части области Б, которые на нашем рисунке все же выходят за пределы П, должны быть пустыми. Чтобы это отметить, покроем эти части области Б штриховкой.
Известно также, что все прыгуны являются или метателями, или бегунами. Значит, круг П должен целиком находиться внутри области, состоящей из Б и М. Следовательно, ту часть области П, которая не входит в фигуру, состоящую из Б и М, надо заштриховать. (Штриховка означает, что там никаких элементов нет: это часть пустая).
Известно также, что среди тех метателей, которые были ещё и прыгунами, нет бегунов. Значит, общая часть кругов М и П, не должна находиться внутри круга Б. Поэтому ту частичку общей части М и П, которая на нашем рисунке все же находиться внутри Б, мы тоже покроем штриховкой.
Все заштрихованные ячейки пустые. В оставшихся, не заштрихованных ячейках запишем буквы x, y, z, t. Этими буквами мы обозначили число ребят, занимающихся соответствующими видами спорта.
Обратимся теперь к остальным условиям, указанным в письме. Число метателей в два раза меньше числа прыгунов. Из рисунка видно, что это условие можно записать так: 2(x+y)=y+x.
Число метателей на два меньше числа бегунов. Значит, x+y+2=z.
Бегуны составляют 1/3 всей команды. Значит, 3z=x+y+z+t.
Число волейболистов в два раза больше числа тех ребят, которые одновременно являются прыгунами и метателями. Значит: t=2y.
Итак, получилась система из четырёх уравнений с четырьмя неизвестными:
Решив эту систему найдём: x=2, y=6, z=10, t=12. Значит, всех ребят было: x+y+z+t=2+6+10+12=30 человек.
Задача 21. Олимпиадная задача.
В ящике лежат шары. Некоторые из них тяжёлые, металлические. Все остальные — лёгкие. Лёгкие шары отличаются друг от друга по целому ряду признаков, а все металлические шары одинаковые. Часть лёгких шаров изготовлена из дерева, а остальные из пластмассы. Некоторые из лёгких шаров покрашены в красный цвет, остальные в зелёный. Среди лёгких шаров есть большие и маленькие: все большие одинакового размера, все маленькие тоже одинакового размера. Больших красных шаров нет, нети больших деревянных шаров. Кроме того, известно следующее:
-
Всего шаров 11.
-
Маленьких зелёных шаров столько же, сколько деревянных.
-
Деревянных и красных шаров вместе на 5 больше, чем всех остальных шаров (включая и металлические).
-
Маленьких красных пластмассовых шаров и больших зелёных пластмассовых шаров, взятых вместе, в два раза больше, чем маленьких зелёных деревянных шаров.
-
Сколько было деревянных шаров?
Решение:
Решим эту задачу с помощью кругов Эйлера-Венна (рис15).
Т.к. больших красных шаров не было и не было больших деревянных шаров, то соответствующие области заштриховываем. Число шаров в остальных ячейках обозначим буквами a, b, c, d, t. Теперь обратимся к остальным условиям задачи:
1. Всего шаров было 11. Значит a+b+c+d+t=11.
2. Маленьких зелёных шаров было столько же, сколько деревянных.
Но маленькие зелёные шары — это шары не красные и не большие. Значит, маленькие зелёные шары — это те шары, которые находятся вне кругов К и Б. Из рисунка видно, что таких шаров равно: a+t.
Число деревянных шаров равно a+b. Следовательно, a+t= a+b.
3. Деревянных и красных шаров в месте было a+b+c, всех остальных было d+t. Но деревянных и красных было на 5 больше, чем остальных. Значит, a+b+c= d+t+5.
4. Маленькие красные пластмассовые шары — это те шары из круга К, которые находятся вне кругов Д и Б. Число таких шаров равно с. Большие зелёные пластмассовые шары — это те шары из круга Б, которые находятся вне кругов К и Д. Число таких шаров равно d. Маленькие зелёные деревянные шары – это те шары из круга Д, которые находятся вне кругов Б и К. Число таких шаров равно а. Значит, последнее условие запишется так: c+d=2a.
Т.о., получилась система четырёх уравнений с пятью неизвестными. Чтобы решить эту неопределённую систему уравнений, поступим следующим образом. Примем неизвестное а за параметр, т.е. будем временно считать, что а -это какое-то конкретное число, и выразим все остальные неизвестные через этот параметр. Но сначала упростим систему: заметим, что из второго уравнения следует t=b. Поэтому, заменив в остальных уравнениях t через b, получим:
Из последних двух уравнений этой системы найдём:
с=(a+5)/2; d=(3a-5)/2.
Теперь, подставляя значения с и d во второе уравнение системы, найдём:
b=(11-3a)/2. А т.к. t=b, то t=(11-3a)/2.
Найденные значения для b, c, d, t представляют собой выражения, зависящие от параметра а. Поэтому, придавая а всевозможные значения, мы получим соответствующие различные значения для b, c, d, t.
Т.о., задача, вообще говоря, имеет бесчисленное множество решений. Но из этого бесконечного множества решений приемлемыми будут только те значения b, c, d, t, которые являются натуральными числами. (Число шаров не мажет быть ни отрицательным, ни дробным).
Значит, должны выполняться следующие условия:
Решив эту систему, получим 5/3<a<11/3
a— нечётное число.
Но в промежутке от 53 до 11/3 находится только одно нечетное натуральное число. Значит: а=3.Для остальных неизвестных получатся следующие значения: b=1, c=4, d=2, t=1.
Теперь мы можем ответить на вопрос задачи: деревянных шаров было a+b. Значит, таких шаров было 4.
Задача 22. Дежурство.
На пришкольном участке дежурили ученики одного из классов. В одно из дежурств им пришлось ремонтировать теплицу и поливать огурцы, помидоры и капусту. Через несколько дней ребят попросили предоставить сведения и том, сколько ребят было на дежурстве, но они этого сказать не смогли.
Удалось установить следующее. Ребята, ремонтировавшие теплицу, не занимались поливкой, а ребята, поливавшие овощи, не участвовали в ремонте теплицы. Никто из ребят не поливал одновременно огурцы и капусту. Не было и таких ребят, которые поливали бы только помидоры. Огурцы поливали 7 человек, а помидоры – 4. Число ребят, ремонтировавших теплицу, было на 2 меньше числа ребят, поливавших только огурцы. Удвоенное число ребят, поливавших капусту, было на 1 больше утроенного числа тех ребят, которые поливали только огурцы.
Сколько ребят было на дежурстве?
Решение:
Решим задачу с использованием кругов Эйлера-Венна (рис16).
Итак, никто из ребят не поливал одновременно огурцы и капусту. Поэтому общую часть кругов О и К можно заштриховать. Никто из ребят не поливал только помидоры. Значит, ту часть круга П, которая находится вне круга О и вне круг К, тоже нужно заштриховать. Численный состав остальных ячеек обозначим буквами a, b, c, d, t. Буква а, например, означает число ребят, поливавших только огурцы. Буква b означает число ребят, поливавших и огурцы, и помидоры. Смысл остальных букв тоже ясен из рисунка.
Теперь, по известным нам данным, можно составить следующую систему уравнений:
Получилась система четырёх уравнений с пятью неизвестными. Чтобы решить эту систему, примем а за параметр. Тогда нашу систему можно решить относительно оставшихся четырёх неизвестных. Выполнив соответствующие вычисления, получим:
b=7-a, c=a-3,
d=(3a+1)/2, t=a-2.
Так как значениями a, b, c, d, t должны быть только натуральные числа, то должны выполняться следующие условия:
Откуда 3<a<7, a – нечетное число.
Но между числами 3 и 7 находится только одно нечетное число, а именно 5. Значит, a=5. Для остальных получается теперь следующие значения: b=2, c=2, d=8, t=3. Осталось подсчитать общее число ребят, работавших на участке. Это число равно a+b+c+d+t=5+2+2+8+3=20.
Задача 23. Трудная задача.
Бригада строителей, ремонтировавшая школу, состояла из рабочих и учащихся ПТУ. В этой бригаде были штукатуры, маляры и разнорабочие (т.е. рабочие, выполнявшие подсобные работы). Некоторые члены бригады владели двумя специальностями, а некоторые владели только одной из этих профессий. Те же члены бригады, которые не были ни штукатурами, ни малярами, выполняли подсобные работы. Все подсобные работы выполняли учащиеся ПТУ. Среди учащихся ПТУ не было штукатуров. Все штукатуры были малярами.
Во время обеденного перерыва некоторые члены бригады питались в столовой, а остальные уходили обедать домой. Дома обедали только те члены бригады, которые являлись и штукатурами, и малярами. Кроме того, известно следующее:
-
Число членов бригады, владевших двумя профессиями, было на 1 больше числа рабочих, владевших только одной из профессий.
-
Рабочих было столько же, сколько было учащихся ПТУ.
-
Рабочих, владевших двумя профессиями, было столько же, сколько было маляров среди учащихся ПТУ.
-
Разность между числом 18 и учетверенным числом тех рабочих, которые владели только одной профессией, была такая же как разность между числом рабочих, обедавших дома, и числом тех членов бригады, которые владели двумя профессиями и обедали в столовой.
Сколько членов было в бригаде?
Решение:
Чтобы решить эту задачу, воспользуемся методом кругов Эйлера-Венна. Нарисуем соответствующую диаграмму (рис17).
На этом рисунке круг М изображает множество маляров. Эллипсовидный овал Ш изображает множество штукатуров. Общая часть фигур М и Ш изображает множество членов бригады, владевших обеими специальностями. Кольцеобразная область, находящаяся вне фигур М и Ш, изображает множество членов бригады, не являвшихся ни штукатурами, ни малярами. Эта область обозначена буквой П, так как по условию задачи соответствующее множество состояло только из людей, выполнявших подсобные работы.
Вертикальная черта делит множество всех членов бригады на рабочих и на учащихся ПТУ. Горизонтальная черта делит это же множество на людей, обедавших в столовой, и на людей, обедавших дома. По условию задачи все подсобные работы выполняли учащиеся ПТУ. Значит, кольцеобразной области П надо оставить только правую часть. Поэтому левую часть области П надо заштриховать, отмечая этим, что эта часть области П пустая.
Среди учащихся ПТУ не было штукатуров. Значит, правую часть фигуры Ш надо заштриховать. Все штукатуры были малярами. Значит, те части фигуры Ш, которые выходят за пределы круга М. Надо заштриховать.
Дома обедали только члены бригады, которые являлись и штукатурами, и малярами. Значит, из нижней части нашей диаграммы должна остаться только та часть, которая находится внутри общей части фигур М и Ш; остальные надо заштриховать.
Теперь все пустые области заштрихованы. Обозначив численный состав остальных, не заштрихованных областей буквами a, b, c, x, y, мы можем приступить к составлению системы уравнений. Система этих уравнений получится из условий 1-4:
Из первого и третьего уравнений следует, что x=c+1. Из второго и третьего уравнений следует, что c=y. Первое и четвёртое уравнения перепишем без изменения. Таким образом, мы получим более простую систему:
Приняв за параметр с, получим следующее решение:
a=(19-3c)/2, b=(5c-17)/2, x=c+1, y=c.
Так как a, b, c, x, y должны быть натуральные числа, то запишем:
17/5
с – нечетное число
Это условия можно записать и так: 4с 6, с — нечетное число.
Очевидно, этим условиям удовлетворяет только число 5. Значит с=5. Вычислив значения остальных неизвестных, получим a=2, b=4, x=6, y=5.
Теперь можно ответить на вопрос задачи: число членов бригады равно a+b+c+x+y=2+4+5+6+5=22.
Задача решена. Но в заключение надо сделать одно замечание, касающееся выбора параметра. Этот выбор может быть осуществлён произвольно. Я, например, выбрала в качестве параметра неизвестное с. Я поступила так только потому, что такой выбор казался мне наиболее удобным, наиболее естественным. Но можно было выбрать параметр по-другому.
Рассмотрим, например, случай, когда в качестве параметра выбрано неизвестное а. Тогда мы получим следующее решение:
b=(22-5a)3, c=(19-2a)/3, x=(22-2a)/3, y=(19-2a)/3.
Так как значениями неизвестных должны быть натуральные числа, то должны выполняться ещё следующие условия:
Числа 22-a, 19-2a, 22-2a должны быть кратны 3.
Первые три неравенства сводятся к условию а4. Значит, из четырех чисел 1,2, 3, 4(которые могут быть значениями а) надо выбрать то, при котором будет выполнено и четвертое из вышеуказанных условий. Проверка показывает, что подходит только число 2. Значит, а=2; и теперь нетрудно вычислить значения всех остальных неизвестных. Ответ, конечно, получится такой же, как и в первоначальном решении.
На примерах этих задач, можно убедиться в эффективности метода кругов Эйлера-Венна.
как выглядит, как изобразить множества, примеры решения задач
Диаграмма Эйлера-Венна — что из себя представляет, где используется
Определение
Диаграмма Эйлера-Венна представляет собой геометрическую схему, предназначенную для представления моделей множеств и схем их взаимосвязей.
Благодаря данной диаграмме, приводят наглядное объяснение разных фактов о множествах. При таком методе универсальное множество представляют в виде прямоугольника, а для изображения подмножества используют круги. Широкое применение диаграммы Эйлера-Венна нашли в таких дисциплинах, как математика, логика, менеджмент, финансы и другие прикладные направления.
Примечание
Способы отражения отношений между множествами ранее отличались. Джон Венн применял в качестве обозначения множеств замкнутые фигуры, а Эйлер – круги.
Диаграммы Эйлера-Венна представляют собой важный частный случай кругов, которые изображал Эйлер. На диаграммах представлены все 2n комбинаций n свойств, что является конечной булевой алгеброй. Если n = 3, на диаграмме, как правило, изображают три круга с центрами, которые расположены в углах равностороннего треугольника, и совпадающими радиусами, ориентировочно равными длине сторон этого многоугольника.
Принципы построения, как изобразить множества
Определение
Построить диаграмму Эйлера-Венна – значит, составить большой прямоугольник, представляющий универсальное множество U, и разместить внутри него замкнутые фигуры в качестве обозначения множеств.
В том случае, когда требуется строить на диаграмме не более трех множеств, целесообразно использовать круги. Для изображения свыше четырех множеств применяют эллипсы. Пересечение фигур соответствует максимально общему случаю, согласно условиям задачи, и изображается должным образом на диаграмме.
Если предположить, что диаграмма содержит круг, обозначающий множество А, его центральная часть будет отражать истинность выражения А, а область вне круга – обозначать ложь. Те области, которые соответствуют истинным значениям, заштриховывают, что является отражением логической операции на диаграмме.
Согласно алгебре логики, конъюнкция множеств А и В соответствует истине в том случае, когда истинны оба эти множества. При этом на диаграмме отмечают участок пересечения множеств.
Применяя диаграммы Эйлера-Венна, доказывают любые алгебраические законы с помощью их графического изображения. Алгоритм построения:
- изображение диаграммы с заштрихованными множествами, которые представлены в левой части выражения;
- чертеж другой диаграммы с заштрихованными множествами, расположенными в правой части уравнения;
- сравнение заштрихованных областей на диаграммах: если это одна и та же область, то можно говорить об истинности тождества.
Данные диаграммы являются эффективным методом визуализации операций с множествами. Отдельные множества изображают в виде кругов, а универсальное множество представляют прямоугольником.
Дополнение множества
Источник: avatars.mds.yandex.net
Источник: avatars.mds.yandex.net
Объединение множеств
Источник: avatars.mds.yandex.net
Источник: avatars.mds.yandex.net
Пересечение множеств
Источник: avatars.mds.yandex.net
Источник: avatars.mds.yandex.net
Разность множеств
Источник: avatars.mds.yandex.net
Источник: avatars.mds.yandex.net
Симметричная разность множеств
Источник: avatars.mds.yandex.net
Источник: avatars.mds.yandex.net
Использование диаграмм Эйлера-Венна для доказательства логических равенств
В качестве доказательства логического равенства подходит способ построения диаграмм Эйлера-Венна. Для примера можно представить доказательства следующего выражения: ¬(АvВ) = ¬А&¬В. Равенство демонстрирует запись закона де Моргана. В первую очередь следует наглядно изобразить левую часть уравнения. Для этого необходимо последовательно заштриховать серым цветом все круги, то есть применить дизъюнкцию. Отобразить инверсию можно с помощью закрашивания черным цветом области вне этих кругов.
Источник: urok.1sept.ru
Источник: urok.1sept.ru
Далее следует визуально представить правую часть выражения. Последовательность действий в этом случае такова: необходимо заштриховать область, в которой отображается инверсия (¬А), с использованием серого цвета и аналогично закрасить область ¬В; отобразить конъюнкцию в виде пересечения этих серых областей. Результат такого наложения будет окрашен черным цветом.
Источник: urok.1sept.ru
Источник: urok.1sept.ru
Источник: urok.1sept.ru
На рисунке видно, что области, в которых отображены левая и правая части уравнения, равны друг другу. Таким образом, закономерность доказана.
Решение задачи поиска информации в Интернет с помощью диаграмм Эйлера-Венна
Изучая тему поиска информации в глобальной сети Интернет, нельзя обойтись без примеров поисковых запросов, в которых использованы логические связки. Как правило, их смысл аналогичен союзам «и», «или» из русского языка. Принцип действия можно понять, если изобразить логические связи с помощью графической схемы или диаграммы Эйлера-Венна.
Источник: urok.1sept.ru
Как логические операции связаны с теорией множеств
Используя диаграммы Эйлера-Венна, принято наглядно демонстрировать связь логических действий и теории множеств. Операции логики можно задать с помощью таблиц истинности. В этом случае следует руководствоваться общим принципом.
На диаграмме в виде области круга под названием А отображают истинность определения А, то есть теоретически круг А обозначает все элементы, которые включены в данное множество. Таким образом, область за пределами круга А будет обозначать ложь соответствующего утверждения.
Понимание, какая область диаграммы отражает логическую операцию, возникает после того, как будут заштрихованы только те области, в которых значения логической операции на наборах А и В соответствуют истине. К примеру, импликация истинна при (00, 01 и 11).
Необходимо заштриховать сначала область за пределами пары пересекающихся кругов в соответствии со значениями А=0, В=0. Затем закрасить область в круге В, которая относится к значениям А=0, В=1, и область, соответствующую и кругу А, и кругу В, то есть участок пересечения, отображающий значения А=1, В=1. Эти три области в комплексе являются графическим представлением логической импликации.
Примеры задач с решением
Диаграммы Эйлера-Венна могут содержать три и более круга. Преимуществом данного графического способа представления выражений является его высокая эффективность и наглядность. К примеру, можно изобразить диаграмму пересечений букв из русского, латинского и греческого алфавита:
Источник: avatars.mds.yandex.net
Понять суть методики удобно на практике. Можно решить несколько задач с применением диаграмм Эйлера-Венна.
Задача 1
По условию есть таблица поисковых запросов. В ней представлены страницы по некоторому сегменту. Требуется определить, сколько страниц в тысячах будет отображаться по запросу «Эсминец». Следует отметить, что запросы выполнялись практически в одно время, поэтому набор страниц с искомыми словами не менялся в процессе выполнения запросов.
Источник: urok.1sept.ru
Решение
Допустим, что:
Ф – является числом страниц (в тысячах) в соответствии с запросом «Фрегат»;
Э – является числом страниц (в тысячах) в соответствии с запросом «Эсминец»;
Х – представляет собой число страниц (в тысячах) по запросу, в котором присутствует «Фрегат» и отсутствует «Эсминец»;
У – определяет число страниц (в тысячах) по запросу, в котором указано слово «Эсминец» и отсутствует слово «Фрегат».
Диаграмма для каждого поискового запроса будет иметь следующий вид:
Источник: urok.1sept.ru
Исходя из информации по диаграммам, получим:
Х+900+У = Ф+У = 2100+У = 3400
Таким образом:
У = 3400-2100 = 1300
Э = 900+У = 900+1300= 2200
Ответ: по запросу «Эсминец» будет найдено 2200 страниц
Задача 2
Класс состоит из 36 учеников. Дети ходят на занятия в рамках математического, физического, химического кружка. Факультатив по математике посещают 18 учащихся, по физике – 14, по химии – 10. Также известно, что 2 ученика ходят на все три кружка, 8 – на математику и физику, 5 – на математику и химию, 3 – на физику и химию. Необходимо определить количество учеников, которые не посещают ни одного кружка.
Решение
Решить данную задачу можно с помощью удобного и наглядного метода в виде кругов Эйлера. Наибольшим кругом следует обозначить множество всех учащихся класса. Внутри этой окружности необходимо изобразить пересекающиеся множества в виде учащихся на факультативе по математике (М), физике (Ф), химии (Х).
Допустим, что:
МФХ – является множеством учеников, каждый из которых ходит на занятия во все три кружка;
МФ¬Х – определяет множество учащихся, которые посещают факультативы по математике и физике, но не ходят на занятия по химии.
¬М¬ФХ – представляет собой множество людей, каждый из которых посещает химический факультатив, но отказался от дополнительных занятий по физике и математике.
По аналогичному принципу можно ввести множества: ¬МФХ, М¬ФХ, М¬Ф¬Х, ¬МФ¬Х, ¬М¬Ф¬Х.
Согласно условиям задачи, пара учеников записаны во все три кружка. Поэтому в область МФХ требуется вписать число 2. Исходя из того, что 8 учащихся посещают факультативы по математике и физике, а из них двое школьников ходят во все кружки, то в области МФ¬Х следует отметить 6 человек (8-2). Аналогичным способом можно определить число учеников в остальных множествах:
Источник: urok.1sept.ru
Далее требуется определить сумму учеников по всем областям:
7+6+3+2+4+1+5=28
Таким образом, всего 28 учащихся посещают факультативные занятия.
Поэтому:
36 – 28 = 8
Ответ: 8 учеников из класса не посещают ни одного кружка.
Задача 3
Когда закончились зимние каникулы, преподаватель поинтересовался у учеников, кто из них посещал театр, кино или цирк. Всего в классе 36 человек. По полученной информации, два ребенка не были ни в кино, ни в театре, ни в цирке. Кино посетили 25 школьников, театр – 11, цирк – 17. И в кино, и в театр сходили 6 человек, и в кино, и в цирк – 10, и в театр, и в цирк – 4. Необходимо посчитать, какое количество учащихся из класса посетили и кино, и театр, и цирк.
Решение
Предположим, что х представляет собой число учеников, которые посетили и кино, и театр, и цирк. В таком случае, можно изобразить диаграмму и определить число школьников для каждой области:
Источник: urok.1sept.ru
Ответ: 1 ученик побывал и в кино, и в театре, и в цирке.
Круги Эйлера онлайн — 4 Июля 2016 — Примеры решений задач
Круги Эйлера, диаграммы Венна
Геометрическое моделирование множеств. Калькулятор.
Для наглядного представления множеств и отношений между ними используется диаграммы Венна (иногда их называют кругами Эйлера или диаграммами Эйлера – Венна).
Универсальное множество изображают в виде прямоугольника, а множества, входящие в универсальное множество, – в виде кругов внутри прямоугольника; элементу множества соответствует точка внутри круга.
С помощью диаграмм Венна удобно иллюстрировать операции над множествами.
Калькулятор для построения кругов Эйлера.
Правила вввода основных обозначений операций над множествами:
| Операция | Обозначение | |
| математическое | в калькуляторе | |
| Дополнение | $bar{A}$ | A’ |
| Пересечение | (A∩B) | (A intersection B) |
| Объединение | (А⋃B) | (A union B) |
| Симметрическая разность | (A∆B) | (symmetric difference of A and B) |
| Относительное дополнение | (AB) | (AB) |
| Правильно | Не правильно |
|---|---|
| (A union B) intersection (A union C) | (AunionB)intersection(AunionC) |
Пример. Изобразить множество D с помощью кругов Эйлера (нарисовать диаграмму Эйлера-Венна):
|
№ |
Множество D |
Вводим в калькулятор |
|
1 |
$(Acap B) cup C$ |
(A intersection B) union C |
|
2 |
$(Acap B) cup bar{C}$ |
(A intersection B) union C’ |
|
3 |
$(Acap bar{B}) cup C$ |
(A union B’) intersection C |
|
4 |
$(Аcap B) cup (Аcap C)$ |
(A intersection B) union (A intersection C) |
В таблице показано: как правильно вводить в калькулятор выражения для операций над множествами.
Решение проблем с диаграммами Венна | Объясняется примерами
Что такое диаграммы Венна?
Диаграммы
Венна определяют все возможные отношения между коллекциями множеств. Самые простые диаграммы Венна просто состоят из множества круговых границ, описывающих диапазон множеств.
Простая диаграмма Венна
Перекрывающиеся области между двумя границами описывают общие для них элементы, в то время как области, которые не перекрываются, содержат разные элементы.Диаграммы Венна часто используются в математике, поскольку люди склонны предполагать, что они используются только для решения математических задач. Но, как показывает трехкружная диаграмма Венна ниже, ее можно использовать для решения многих других проблем.
Использование 3-круговой диаграммы Венна для решения задач
Хотя приведенная выше диаграмма может показаться сложной, на самом деле ее очень легко понять. Хотя диаграммы Венна могут выглядеть сложными при решении бизнес-процессов, понимание значения границ и их обозначения может в значительной степени упростить процесс.Давайте посмотрим на несколько примеров, которые демонстрируют, как диаграммы Венна могут значительно облегчить решение проблем.
Пример 1. Процесс найма в компании
Первый пример демонстрирует процесс составления короткого списка сотрудников компании. При составлении короткого списка кандидатов на должность отдел кадров учитывает несколько факторов, таких как опыт, профессиональные навыки и лидерские качества. Все эти качества отличаются друг от друга и могут присутствовать или отсутствовать в некоторых кандидатах.Однако лучшими кандидатами будут те, кто сочетал бы все эти качества.
Как использовать диаграммы Венна для найма людей
Кандидат, обладающий всеми тремя качествами, идеально подходит для вашей организации. Таким образом, используя простые диаграммы Венна, подобные приведенной выше, компания может легко продемонстрировать свои процессы найма и значительно упростить процесс отбора.
Красочную и точную диаграмму Венна, подобную приведенной выше, можно легко создать с помощью нашего программного обеспечения диаграмм Венна, и мы профессионально разработали шаблоны диаграмм Венна, чтобы вы тоже могли быстро приступить к работе.
Пример 2: Инвестиции в местоположение
Второй пример идет дальше и показывает, как компания может использовать диаграмму Венна для выбора подходящего местоположения офиса. Решение будет основано на экономических, социальных и экологических факторах.
Выбор местоположения офиса с помощью диаграммы Венна
В идеальном сценарии вы найдете место, в котором в равной мере учитываются все вышеперечисленные факторы. Но если вам не удается найти такое место, вы можете решить, какой фактор для вас наиболее важен.Независимо от приоритета, поскольку вы уже перечислили места, принятие решения становится проще.
Пример 3: Выбор работы мечты
В последнем примере будет показано, как можно легко ответить на один из самых сложных вопросов жизни с помощью диаграммы Венна. Выбор работы мечты — это то, что ставит в тупик большинство выпускников колледжей, но с помощью единственной диаграммы Венна этот мыслительный процесс можно значительно упростить.
Во-первых, выделите факторы, которые имеют значение при выборе работы мечты, например, то, что вы любите делать, что у вас хорошо получается и, наконец, потенциальный заработок.Хотя большинство из нас мечтают стать знаменитостями и появиться на телевидении, не все наделены актерскими способностями, и этот карьерный путь может быть не самым жизнеспособным. Вместо этого выбор того, что у вас хорошо получается, чем вы любите заниматься, и того, что имеет хороший потенциал заработка, будет наиболее практичным выбором.
Работа мечты Диаграмма Венна
Таким образом, работа, отвечающая всем этим трем критериям, стала бы работой мечты. Эти три критерия не обязательно должны быть одинаковыми и могут быть изменены в соответствии с индивидуальными требованиями.
Итак, вы видите, что даже самые сложные процессы можно упростить, используя эти простые диаграммы Венна.
Диаграмм Венна и диаграмм Эйлера, объясненных на примерах
Диаграммы
Венна и диаграммы Эйлера выглядят очень похоже, поэтому понятно, что многих людей смущает понимание разницы. Хотя оба типа диаграмм основаны на теории множеств, есть некоторые тонкие различия, которые делают их уникальными. Надеюсь, эта статья развеет ваши сомнения относительно диаграмм Венна и диаграмм Эйлера, и я приведу несколько примеров, чтобы сделать ее более понятной.
Венн против Эйлера: Определение
Как я упоминал ранее, оба набора диаграмм основаны на теории множеств. Диаграмма Венна показывает все возможные логические отношения между набором наборов. Но диаграмма Эйлера показывает только отношения, существующие в реальном мире.
Диаграммы Венна и Диаграммы Эйлера Примеры
Начнем с очень простого примера. Давайте рассмотрим надмножество животных с млекопитающими и птицами как подмножества.Диаграмма Венна показывает пересечение двух множеств, даже если такой возможности не существует в реальном мире. Диаграмма Эйлера, с другой стороны, не показывает пересечения.
Диаграммы Венна показывают все возможные комбинации, даже если они не существуют в реальном сценарии.
А теперь рассмотрим более сложный пример с колодой карт. Опять же, важно помнить о различии между двумя типами диаграмм: все возможные комбинации и реальные комбинации .Давайте возьмем карты как расширенный набор, а черные карты, красные карты и ромбы как подмножества.
Как одни и те же данные представлены по-разному с помощью диаграмм Венна и диаграмм Эйлера
Как показано в приведенном выше примере, диаграммы Венна показывают четыре пересечения, для которых нет данных, потому что они должны отображать все возможные комбинации.
Существуют различные методы преобразования диаграмм Венна в диаграммы Эйлера и наоборот. Ознакомьтесь с этой замечательной вики-статьей о диаграммах Эйлера, в которой объясняются некоторые методы, которые вы можете использовать для преобразования диаграмм Венна в диаграммы Эйлера.Я надеюсь, что приведенные выше примеры помогли вам развеять ваши сомнения относительно диаграмм Венна и диаграмм Эйлера. Если у вас есть какие-либо вопросы, не стесняйтесь задавать их в разделе комментариев.
Независимо от того, рисуете ли вы диаграммы Венна или диаграммы Эйлера, Creately предоставит вам все необходимые инструменты. Вы можете быстро начать работу, используя шаблоны диаграмм Венна, доступные нашим пользователям, или начать с нуля в области рисования. Если вы хотите добавить значки и изображения на диаграмму Венна, это можно легко сделать с помощью встроенного поиска изображений Google, доступного на левой боковой панели.Благодаря такому количеству крутых функций вы не ошибетесь с Creately.
Забавы с диаграммами Венна и Эйлера
Диаграмма Венна — это математическая иллюстрация, которая показывает все возможные математические или логические отношения между множествами. Диаграмма Эйлера похожа на диаграмму Венна, но не обязательно показывает все возможных пересечений множеств. Диаграмма Эйлера часто более полезна для отображения данных реального мира, потому что не все наборы частично перекрываются со всеми другими наборами.
Я использовал апплет «Трехкружная диаграмма Венна», чтобы составить диаграмму пищевых предпочтений в моей семье. У меня есть один ребенок, который не ест много мяса или овощей, а другой не любит углеводы. Это классическая диаграмма Венна, которая объясняет, почему я не готовлю так часто, как раньше.
Этот рисунок обозначен как диаграмма Венна, но на самом деле это диаграмма Эйлера, потому что истинное счастье нигде не пересекается с ношением брюк. По крайней мере, для человека, который составил схему.
Больше диаграмм после прыжка.
Если круги не пересекаются, это не диаграмма Венна. Что может быть очень печально, если вы — круг. Этот дизайн был найден в футболках без резьбы. Однако диаграммы Эйлера могут перекрываться или нет. Но Эйлер не то, что имел в виду синий круг.
На прошлой неделе я наткнулся на это очень полезное изображение, с которого я начал поиски различий между диаграммой Венна и диаграммой Эйлера. Он объясняет географическую терминологию, используемую в той области восточной Атлантики, которая сбивает американцев с толку.Автор обозначил этот предмет как «Великая британская диаграмма Венна», а затем пояснил, что на самом деле это диаграмма Эйлера. Без сомнения, люди более знакомы с Венном. Но независимо от того, насколько географически точны названия мест, ирландские комментаторы предсказуемо возражали против включения во все, что помечено словом «британский». Еще одну такую диаграмму, которая включает больше островов, можно найти здесь.
Эти кисло-сладкие каракули представляют собой настоящие диаграммы Венна. Их подготовила Джессика Хэги из Indexed, блога, полного замечательных диаграмм и графиков, сделанных на учетных карточках.
Роб Харвилла использовал диаграммы Венна и другие диаграммы, чтобы деконструировать песню «This Is Why I’m Hot» Мимса из The Villlage Voice. Диаграммы ясно показывают, что тексты вообще не имеют смысла. Тем не менее, на момент написания песня была номером один.
Кстати о музыке. Вот футболка для музыкальных снобов с двухкомпонентной диаграммой Венна. Со страницы товара:
Нет ничего хорошего, если это нравится другим. Мы только что доказали это математически.У меня есть теория, что карикатуристы удосужились изучать на уроках математики только диаграммы Венна.
У Рэндалла Манро из xkcd самые странные любовные записки. Эта классическая диаграмма Венна настолько мила и проста, что с по он начал заполнять зоны.
Диаграммы Венна и диаграммы Эйлера — это еще два из множества удобных обучающих устройств, которые используются для странных или комедийных целей. См. Также Посуда периодического действия, Другая посуда периодического действия и Развлечение с блок-схемами.
Задачи на
слов на множествах и диаграммах Венна
Основной материал
Чтобы понять, как решать задачи со словами на диаграмме Венна с 3 кругами, мы должны знать следующие основные вещи.
u ———> объединение (или)
n ———> пересечение (и)
Теорема сложения на множествах
Теорема 1:
n (AuB) = n (A) + n (B) — n (AnB)
Теорема 2:
n (AuBuC):
= n (A) + n (B) + n (C) — n (AnB) — n (BnC) — n (AnC) + n (AnBnC)
Пояснение:
Позвольте нам узнать подробнее о следующих терминах.
n (AuB) = общее количество элементов, связанных с любым из двух событий A и B.
n (AuBuC) = общее количество элементов, связанных с любым из трех событий A, B и C.
n ( A) = Общее количество элементов, связанных с A.
n (B) = Общее количество элементов, связанных с B.
n (C) = Общее количество элементов, связанных с C.
Для трех событий A, B и C, мы имеем
n (A) — [n (AnB) + n (AnC) — n (AnBnC)]:
Общее количество элементов, относящихся только к A.
n (B) — [n (AnB) + n (BnC) — n (AnBnC)]:
Общее количество элементов, относящихся только к B.
n (C) — [n (BnC) + n (AnC) + n (AnBnC)]:
Общее количество элементов, относящихся только к C.
n (AnB):
Общее количество элементов, связанных как с A, так и с B
n (AnB) — n (AnBnC):
Общее количество элементов, относящихся только к обоим (A и B).
n (BnC):
Общее количество элементов, относящихся к обоим B и C
n (BnC) — n (AnBnC):
Общее количество элементов, относящихся только к обоим (B и C).
n (AnC):
Общее количество элементов, относящихся к обоим A и C
n (AnC) — n (AnBnC):
Общее количество элементов, относящихся только к обоим (A и C).
Для двух событий A и B мы имеем
n (A) — n (AnB):
Общее количество элементов, относящихся только к A.
n (B) — n (AnB):
Общее количество элементов, относящихся только к B.
Практические задачи
Задача 1:
В опросе студентов университетов 64 изучали курс математики, 94 — курс химии, 58 — курс физики, 28 — математику и физику, 26 — математику и химию, 22 — прошли химию, и курс физики, а 14 прошли все три курса. Узнайте, сколько человек прошли только один курс.
Решение:
Шаг 1:
Пусть M, C, P представляют группы студентов, которые изучали математику, химию и физику соответственно
Шаг 2:
Из данной информации мы имеем
n (M) = 64, n (C) = 94, n (P) = 58,
n (MnP) = 28, n (MnC) = 26, n (CnP) = 22
n (MnCnP ) = 14
Шаг 3:
Исходя из основного, у нас есть
No.студентов, изучавших только математику
= n (M) — [n (MnP) + n (MnC) — n (MnCnP)]
= 64 — [28 + 26 — 14]
= 64 — 40
= 24
Шаг 4:
Количество студентов, которые изучали только химию:
= n (C) — [n (MnC) + n (CnP) — n (MnCnP)]
= 94 — [26 + 22-14]
= 94-34
= 60
Шаг 5:
No.студентов, изучавших только физику:
= n (P) — [n (MnP) + n (CnP) — n (MnCnP)]
= 58 — [28 + 22 — 14]
= 58 — 36
= 22
Шаг 6:
Итого студентов, которые прошли только один курс:
= 24 + 60 + 22
= 106
Таким образом, общее количество студентов, которые прошли только один курс, составляет 106 человек.
Альтернативный метод (с использованием диаграммы Венна):
Шаг 1:
Диаграмма Венна, связанная с информацией, приведенной в вопросе:
Шаг 2:
Из диаграммы Венна выше у нас есть
No.студентов, изучавших только математику = 24
Число студентов, изучавших только химию = 60
Число студентов, изучавших только физику = 22
Шаг 3:
Всего студентов, которые прошли только один курс:
= 24 + 60 + 22
= 106
Следовательно, общее количество студентов, которые прошли только один курс, составляет 106.
Задача 2:
группа студентов: 65 играют в фут-мяч, 45 играют в хоккей, 42 играют в крикет, 20 играют в фут-мяч и в хоккей, 25 играют в фут-мяч и в крикет, 15 играют в хоккей и крикет и 8 играют во все три игры.Найдите общее количество учеников в группе (предположим, что каждый ученик в группе играет хотя бы одну игру).
Решение:
Шаг 1:
Пусть F, H и C представляют группу студентов, которые играют в футбол, хоккей и крикет соответственно.
Шаг 2:
Из данной информации имеем
n (F) = 65, n (H) = 45, n (C) = 42,
n (FnH) = 20, n ( FnC) = 25, n (HnC) = 15
n (FnHnC) = 8
Шаг 3:
Исходя из базовых данных, у нас
Общее количество студентов в группе n (FuHuC ).
n (FuHuC) равно
= n (F) + n (H) + n (C) — n (FnH) — n (FnC) — n (HnC) + n (FnHnC)
Тогда , имеем
n (FuHuC) = 65 + 45 + 42-20 — 25-15 + 8
n (FuHuC) = 100
Следовательно, общее количество студентов в группе равно 100.
Альтернатива Метод (с использованием диаграммы Венна):
Шаг 1:
Диаграмма Венна, связанная с информацией, приведенной в вопросе:
Шаг 2:
Общее количество студентов в группе:
= 28 + 12 + 18 + 7 + 10 + 17 + 8
= 100
Таким образом, общее количество студентов в группе составляет 100.
Задача 3:
В колледже 60 студентов обучаются по химии, 40 — по физике, 30 — по биологии, 15 — по химии и физике, 10 — по физике и биологии, 5 — по биологии и химии. На всех троих никто не записался. Узнайте, сколько человек обучается хотя бы по одному из предметов.
Решение:
Пусть C, P и B представляют предметы химии, физики и биологии соответственно.
Число студентов, обучающихся по химии:
n (C) = 60
Число студентов, обучающихся по физике:
n (P) = 40
Число студентов, обучающихся по биологии:
n (B) = 30
№студентов, обучающихся по химии и физике:
n (CnP) = 15
Число студентов, обучающихся по физике и биологии:
n (PnB) = 10
Число студентов, обучающихся по биологии и химии:
n (BnC) = 5
Никто не участвовал во всех трех. Итак, у нас есть
n (CnPnB) = 0
Приведенную выше информацию можно поместить на диаграмму Венна, как показано ниже.
Из приведенной выше диаграммы Венна количество студентов, обучающихся хотя бы по одному из предметов:
= 40 + 15 + 15 + 15 + 5 + 10 + 0
= 100
Итак, количество студентов, обучающихся по хотя бы одному из испытуемых 100 лет.
Задача 4:
В городе 85% людей говорят на тамильском, 40% — на английском и 20% — на хинди. Кроме того, 32% говорят на тамильском и английском языках, 13% говорят на тамильском и хинди и 10% говорят на английском и хинди. Определите процент людей, которые могут говорить на всех трех языках.
Решение:
Пусть T, E и H представляют людей, говорящих на тамильском, английском и хинди соответственно.
Процент людей, говорящих на тамильском:
n (T) = 85
Процент людей, говорящих по-английски:
n (E) = 40
Процент людей, говорящих на хинди:
n (H) = 20
Процент людей, говорящих на английском и тамильском языках:
n (TnE) = 32
Процент людей, говорящих на тамильском и хинди:
n (TnH) = 13
Процент людей, говорящих на английском и хинди :
n (EnH) = 10
Пусть x будет процентным соотношением людей, говорящих на всех трех языках.
Из приведенной выше диаграммы Венна мы можем иметь
100 = 40 + x + 32 — x + x + 13 — x + 10 — x — 2 + x — 3 + x
100 = 40 + 32 + 13 + 10 — 2 — 3 + x
100 = 95 — 5 + x
100 = 90 + x
x = 100 — 90
x = 10%
Таким образом, процент людей, говорящих на всех трех языках, составляет 10%.
Задача 5:
Рекламное агентство обнаружило, что из его 170 клиентов 115 используют телевидение, 110 используют радио и 130 используют журналы.Также 85 используют телевидение и журналы, 75 используют телевидение и радио, 95 используют радио и журналы, 70 используют все три. Нарисуйте диаграмму Венна, чтобы представить эти данные. Найдите
(i) сколько людей используют только радио?
(ii) сколько людей используют только телевидение?
(iii) сколько из них пользуются телевидением и журналами, но не радио?
Решение:
Пусть T, R и M представляют людей, которые используют телевидение, радио и журналы соответственно.
Количество людей, использующих телевидение:
n (T) = 115
Количество людей, использующих радио:
n (R) = 110
Количество людей, использующих журнал:
n (M ) = 130
Количество людей, использующих телевидение и журналы
n (TnM) = 85
Количество людей, использующих телевидение и радио:
n (TnR) = 75
Количество людей, использующих радио и Журнал:
n (RnM) = 95
Количество людей, использующих все три:
n (TnRnM) = 70
Из приведенной выше диаграммы Венна имеем
(i) Количество людей, которые используют только радио, составляет 10
(ii) Количество людей, которые используют только телевидение, составляет 25
(iii) Количество людей, использующих телевидение а журнал, но не радио — 15.
Задача 6:
В классе из 60 учеников 40 учеников любят математику, 36 учеников — естественные науки,
24 нравятся обеим испытуемым. Найдите количество студентов, которым нравится
(i)
Только математика, (ii) Только наука (iii) Математика или естественные науки (iv) Ни то, ни другое
Математика и наука.
Решение:
Шаг 1:
Пусть M и S представляют группу студентов, которые любят математику и
наука соответственно.
Шаг 2:
Из информации, представленной в вопросе, мы имеем
n (M) = 40, n (S) = 36, n (MnS) = 24
Step
3:
Ответ
(i):
No.студентов, которые любят только математику:
= n (M) — n (MnS)
= 40-24
= 16
Step
4:
Ответ
(ii):
No.
студентов, любящих только науку:
= n (S) — n (MnS)
= 36-24
= 12
Step
5:
Ответ
(iii):
No.
студентов, которые любят математику или естественные науки:
= n (M или S)
= n (MuS)
= n (M) + n (S) — n (MnS)
= 40 + 36 — 24
= 52
Шаг
6:
Ответ
(iv):
Итого
нет.студенты, которые любят математику или естественные науки:
n (MuS) = 52
No.
студентов, которые не любят ни математику, ни естественные науки
= 60 — 52
= 8
Задача 7:
На одной конференции из 100 человек 29 индийских женщин
и 23 индийских мужчины. Из этих индийцев 4 доктора и 24 либо
мужчины или врачи. Нет иностранных врачей. Найдите количество женщин-врачей
посещение конференции.
Решение:
Шаг 1:
Пусть M и D представляют группу индийских мужчин и врачей.
соответственно.
Шаг 2:
Исходя из информации, представленной в вопросе, мы имеем
n (M) = 23, n (D) = 4,
n (MuD) = 24
Шаг 3:
Исходя из основного, мы имеем
n (MuD) = n (M) + n (D) — n (MnD)
24 = 23 + 4 — n (MnD)
n (MnD) = 3
n (индийские мужчины и врачи) = 3
Шаг 4:
Итак, из 4 индийских врачей есть 3 мужчины.
И еще одна — индийская женщина-врач.
Итак, число женщин-врачей на конференции — 1.
Помимо вышеперечисленного, если вам нужны еще какие-либо сведения по математике, воспользуйтесь нашим пользовательским поиском Google здесь.
Если у вас есть какие-либо отзывы о наших математических материалах, напишите нам:
[email protected]
Мы всегда ценим ваши отзывы.
Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.
ЗАДАЧИ СО СЛОВАМИ
Задачи со словами HCF и LCM
Задачи со словами на простых уравнениях
Задачи со словами на линейных уравнениях
Задачи со словами на квадратных уравнениях
Задачи на слова
Проблемы со словами в поездах
Проблемы со словами по площади и периметру
Проблемы со словами по прямому и обратному изменению
Проблемы со словами по цене за единицу
Проблемы со словами по количеству слов
Задачи по сравнению ставок
Преобразование обычных единиц в текстовые задачи
Преобразование в метрические единицы в словесных задачах
Текстовые задачи по простому проценту
Словесные задачи по сложным процентам
ngles
Проблемы с дополнительными и дополнительными углами в словах
Проблемы со словами с двойными фактами
Проблемы со словами в тригонометрии
Проблемы со словами в процентах
Проблемы со словами для разметки 9137
задачи
задачи с десятичными числами
задачи со словами на дроби
задачи со словами на смешанные фракции
задачи со словами с одношаговым уравнением
задачи с линейным неравенством и соотношением слов 37
задачи
задачи со временем и работой со словами
задачи со словами на множествах и диаграммах Венна
задачи со словами на возрастах
задачи со словами из теоремы Пифагора
в процентах от числового слова проблемы
Проблемы со словами при постоянной скорости
Проблемы со словами при средней скорости
Проблемы со словами при сумме углов треугольника 180 градусов
ДРУГИЕ ТЕМЫ
Сокращения прибыли и убытков
Сокращения в процентах
Сокращения в таблице времен
Сокращения времени, скорости и расстояния
Сокращения соотношения и пропорции
000 Домен и диапазон рациональных функций 9137 функции с отверстиями
График рациональных функций
График рациональных функций с отверстиями
Преобразование повторяющихся десятичных знаков в дроби
Десятичное представление рациональных чисел
Поиск корня из длинного квадрата видение
Л.Метод CM для решения задач времени и работы
Преобразование словесных задач в алгебраические выражения
Остаток при делении 2 в степени 256 на 17
Остаток при делении степени 17 на 16
Сумма всех трехзначных чисел, делимых на 6
Сумма всех трехзначных чисел, делимых на 7
Сумма всех трехзначных чисел, делящихся на 8
Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4
Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами
Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3
Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6
Задачи со словами на диаграмме Венна с 3 кругами
Рассмотрим три набора A, B и C.
Набор A содержит a элементов, B содержит b элементов и C содержит c элементов.
И A, и B содержат w элементов, B и C содержат x элементов, A и C содержат y элементов, все три набора A, B и C содержат z элементов.
Мы можем использовать диаграмму Венна с 3 кругами, чтобы представить вышеуказанную информацию, как показано ниже.
Сделаем следующие изменения в диаграмме Венна.
Мы можем получить следующие результаты из диаграммы Венна, показанной выше.
Количество элементов, относящихся только к A, равно
= a — (w + y — z)
Количество элементов, относящихся только к B, равно
= b — (w + x — z)
Количество связанных элементов только для C
= c — (y + x — z)
Количество элементов, относящихся только к (A и B), равно
= w — z
Количество элементов, связанных только с (B и C), равно
= x — z
Количество элементов, относящихся только к (A и C), равно
= y — z
Количество элементов, связанных со всеми тремя наборами A, B и C, равно
= z
Всего количество элементов, связанных со всеми тремя наборами A, B и C, равно
= [a- (w + yz)] + [b- (w + xz)] + [c- (y + xz)] + (wz ) + (xz) + (yz) + z
Примеры
Пример 1:
При опросе студентов университетов 64 изучали курс математики, 94 — курс химии, 58 — курс физики, 28 — математику и физику, 26 — математику и химию, 22 прошли химию и курс физики, а 14 прошли все три курса. Узнайте, сколько человек прошли только один курс.
Решение:
Шаг 1:
Пусть M, C и P представляют курсы математики, химии и физики соответственно.
Диаграмма Венна, относящаяся к информации, указанной в вопросе:
Шаг 2:
Из приведенной выше диаграммы Венна имеем
Количество студентов, изучавших только математику = 24
Количество студентов, изучавших только химию = 60
No.студентов, изучавших только физику = 22
Шаг 3:
Всего кол. студентов, которые прошли только один курс:
= 24 + 60 + 22
= 106
Таким образом, общее количество студентов, прошедших только один курс, составляет 106.
Пример 2:
In a группа студентов: 65 играют в фут-мяч, 45 играют в хоккей, 42 играют в крикет, 20 играют в фут-мяч и в хоккей, 25 играют в фут-мяч и в крикет, 15 играют в хоккей и крикет и 8 играют во все три игры.Найдите общее количество учеников в группе (предположим, что каждый ученик в группе играет хотя бы в одну игру.)
Решение:
Шаг 1:
Пусть F, H и C представляют игры в футбол. , хоккей и крикет соответственно.
Диаграмма Венна, относящаяся к информации, указанной в вопросе:
Шаг 2:
Общее количество студентов в группе:
= 28 + 12 + 18 + 7 + 10 + 17 + 8
= 100
Таким образом, общее количество студентов в группе составляет 100.
Пример 3:
В колледже 60 студентов учатся на химию, 40 — на физику, 30 — на биологию, 15 — на химию и физику, 10 — на физику и биологию, 5 — на биологию и химию. На всех троих никто не записался. Узнайте, сколько человек обучается хотя бы по одному из предметов.
Решение:
Пусть C, P и B представляют предметы химии, физики и биологии соответственно.
Диаграмма Венна, относящаяся к информации, указанной в вопросе:
Из приведенной выше диаграммы Венна количество студентов, обучающихся хотя бы по одному из предметов:
= 40 + 15 + 15 + 15 + 5 + 10 + 0
= 100
Итак, количество студентов, обучающихся по хотя бы одному из испытуемых 100.
Пример 4:
В городе 85% жителей говорят на тамильском, 40% — на английском и 20% — на хинди. Кроме того, 32% говорят на тамильском и английском языках, 13% говорят на тамильском и хинди и 10% говорят на английском и хинди. Определите процент людей, которые могут говорить на всех трех языках.
Решение:
Пусть T, E и H представляют людей, говорящих на языках тамильский, английский и хинди соответственно.
Пусть x будет процентной долей людей, говорящих на всех трех языках.
Диаграмма Венна, относящаяся к информации, указанной в вопросе:
Из приведенной выше диаграммы Венна мы можем иметь
100 = 40 + x + 32 — x + x + 13 — x + 10 — x — 2 + x — 3 + x
100 = 40 + 32 + 13 + 10 — 2 — 3 + x
100 = 95 — 5 + x
100 = 90 + x
x = 100 — 90
x = 10%
Итак, процент людей, говорящих на всех трех языках, составляет 10%.
Пример 5:
Рекламное агентство обнаружило, что из его 170 клиентов 115 используют телевидение, 110 используют радио и 130 используют журналы.Также 85 используют телевидение и журналы, 75 используют телевидение и радио, 95 используют радио и журналы, 70 используют все три. Нарисуйте диаграмму Венна, чтобы представить эти данные. Найдите
(i) сколько людей используют только радио?
(ii) сколько людей используют только телевидение?
(iii) сколько из них пользуются телевидением и журналами, но не радио?
Решение:
Пусть T, R и M представляют людей, которые используют телевидение, радио и журналы соответственно.
Диаграмма Венна, относящаяся к информации, указанной в вопросе:
Из приведенной выше диаграммы Венна имеем
(i) Количество людей, использующих только радио, составляет 10
(ii) Количество людей, использующих только телевидение, составляет 25
(iii) Количество людей, использующих телевидение а журнал, но не радио — 15.
Помимо вышеперечисленного, если вам нужны еще какие-либо сведения по математике, воспользуйтесь нашим пользовательским поиском Google здесь.
Если у вас есть какие-либо отзывы о наших математических материалах, напишите нам:
[email protected]
Мы всегда ценим ваши отзывы.
Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.
ЗАДАЧИ СО СЛОВАМИ
Задачи со словами HCF и LCM
Задачи со словами на простых уравнениях
Задачи со словами на линейных уравнениях
Задачи со словами на квадратных уравнениях
Задачи на слова
Проблемы со словами в поездах
Проблемы со словами по площади и периметру
Проблемы со словами по прямому и обратному изменению
Проблемы со словами по цене за единицу
Проблемы со словами по количеству слов
Задачи по сравнению ставок
Преобразование обычных единиц в текстовые задачи
Преобразование в метрические единицы в словесных задачах
Текстовые задачи по простому проценту
Словесные задачи по сложным процентам
ngles
Проблемы с дополнительными и дополнительными углами в словах
Проблемы со словами с двойными фактами
Проблемы со словами в тригонометрии
Проблемы со словами в процентах
Проблемы со словами для разметки 9137
задачи
задачи с десятичными числами
задачи со словами на дроби
задачи со словами на смешанные фракции
задачи со словами с одношаговым уравнением
задачи с линейным неравенством и соотношением слов 37
задачи
задачи со временем и работой со словами
задачи со словами на множествах и диаграммах Венна
задачи со словами на возрастах
задачи со словами из теоремы Пифагора
в процентах от числового слова проблемы
Проблемы со словами при постоянной скорости
Проблемы со словами при средней скорости
Проблемы со словами при сумме углов треугольника 180 градусов
ДРУГИЕ ТЕМЫ
Сокращения прибыли и убытков
Сокращения в процентах
Сокращения в таблице времен
Сокращения времени, скорости и расстояния
Сокращения соотношения и пропорции
000 Домен и диапазон рациональных функций 9137 функции с отверстиями
График рациональных функций
График рациональных функций с отверстиями
Преобразование повторяющихся десятичных знаков в дроби
Десятичное представление рациональных чисел
Поиск корня из длинного квадрата видение
Л.Метод CM для решения задач времени и работы
Преобразование словесных задач в алгебраические выражения
Остаток при делении 2 в степени 256 на 17
Остаток при делении степени 17 на 16
Сумма всех трехзначных чисел, делимых на 6
Сумма всех трехзначных чисел, делимых на 7
Сумма всех трехзначных чисел, делящихся на 8
Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4
Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами
Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3
Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6
Задачи со словами на диаграмме Венна с двумя кругами
ПРОБЛЕМЫ СЛОВА НА ДИАГРАММЕ ВЕННА С 2 КРУГАМИ
Пример 1:
В классе из 50 студентов каждый из них сдал экзамены либо по математике, либо по естественным наукам, либо по обоим предметам.По 10 студентов сдали по обоим и 28 по естествознанию. Узнайте, сколько учеников сдали по математике?
Решение:
Пусть M = Набор студентов, сдавших математику
S = Набор студентов, сдавших естественные науки
Мы можем решить данную задачу двумя способами.
(i) Используя формулу
(ii) Используя диаграмму Венна
Метод 1:
Общее количество студентов n (MUS) = 50
Количество студентов, сданных по обоим предметам n (MnS) = 10
Число студентов, сдавших естественные науки n (S) = 28
Отсюда мы должны найти число студентов, сдавших экзамен по математике.
n (MUS) = n (M) + n (S) — n (M n S)
50 = n (M) + 28-10
50 = n (M) + 18
Вычесть 18 на обе стороны
50 — 18 = n (M) + 18 — 18
n (M) = 32
Итак, количество студентов, сдавших математику, равно 32.
Метод 2:
Пусть «x» быть количеством студентов, сдавших экзамен по математике.
Представляя данные детали на диаграмме Венна, получаем
Из диаграммы Венна
x + 10 + 18 = 50
x = 50 — 28 = 22
Количество студентов, сдавших экзамен по математике
= x + 10 = 22 + 10 = 32
Пример 2:
Население города 10 000 человек.Из них 5400 человек читают газету А и 4700 читают газету Б. 1500 человек читают обе газеты. Найдите количество людей, которые не читают ни одну из двух газет.
Решение:
Пусть A = Набор лиц, читающих газету A
B = Набор лиц, читающих газету B
Количество людей, которые читают хотя бы одну газету
= 3900 + 1500 + 3200
= 8600
Общая численность населения = 10000
Чтобы найти количество людей, которые не читают ни одну из двух газет, мы должны вычтите количество людей, которые прочитали хотя бы одного из всего населения.
= 10000 — 8600
= 1400
Таким образом, количество людей, которые не читают ни одну из двух работ, равно 1400.
Пример 3:
В школе все ученики играют либо в футбол или волейбол, или и то, и другое. 300 студентов играют в футбольный мяч, 270 студентов играют в волейбол и 120 студентов играют в обе игры. Найдите
(i) количество учеников, которые играют только в футбол
(ii) количество учеников, которые играют только в волейбол
(iii) общее количество учеников в школе
Решение:
Пусть A = группа студентов, играющих в мяч
B = группа студентов, играющих в волейбол
(i) Количество учеников, которые играют только в футбол, составляет 180
(ii) Количество учеников, которые играют только в волейбол, составляет 150
(iii) Общее количество учеников в школе
= 180 + 120 + 150
= 450
Пример 4:
В школе 150 учеников сдали X стандартный экзамен.95 студентов подали заявку в I группу, 82 студента — во II группу в старших классах средней школы. Если 20 студентов не подали заявку ни на один из двух, сколько студентов подали заявки в обе группы?
Решение:
A = Набор студентов, подавших заявки на Группу I
B = Набор студентов, подавших заявки на Группу II
Количество студентов, подавших заявки хотя бы на одну группу
= 150-20
= 130
n (A) = 95, n (B) = 82 и n (AUB) = 130
n (AUB) = n (A) + n (B) — n (A n B)
130 = 95 + 82 — n (A n B)
130 = 177 — n (A n B)
n (A n B) = 177-130 ==> 47
Итак, количество студентов, подавших заявки на обе группы 47 лет.
Помимо вышеперечисленного, если вам нужны еще какие-либо сведения по математике, воспользуйтесь нашим пользовательским поиском Google здесь.
Если у вас есть какие-либо отзывы о наших математических материалах, напишите нам:
[email protected]
Мы всегда ценим ваши отзывы.
Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.
ЗАДАЧИ СО СЛОВАМИ
Задачи со словами HCF и LCM
Задачи со словами на простых уравнениях
Задачи со словами на линейных уравнениях
Задачи со словами на квадратных уравнениях
Задачи на слова
Проблемы со словами в поездах
Проблемы со словами по площади и периметру
Проблемы со словами по прямому и обратному изменению
Проблемы со словами по цене за единицу
Проблемы со словами по количеству слов
Задачи по сравнению ставок
Преобразование обычных единиц в текстовые задачи
Преобразование в метрические единицы в словесных задачах
Текстовые задачи по простому проценту
Словесные задачи по сложным процентам
ngles
Проблемы с дополнительными и дополнительными углами в словах
Проблемы со словами с двойными фактами
Проблемы со словами в тригонометрии
Проблемы со словами в процентах
Проблемы со словами для разметки 9137
задачи
задачи с десятичными числами
задачи со словами на дроби
задачи со словами на смешанные фракции
задачи со словами с одношаговым уравнением
задачи с линейным неравенством и соотношением слов 37
задачи
задачи со временем и работой со словами
задачи со словами на множествах и диаграммах Венна
задачи со словами на возрастах
задачи со словами из теоремы Пифагора
в процентах от числового слова проблемы
Проблемы со словами при постоянной скорости
Проблемы со словами при средней скорости
Проблемы со словами при сумме углов треугольника 180 градусов
ДРУГИЕ ТЕМЫ
Сокращения прибыли и убытков
Сокращения в процентах
Сокращения в таблице времен
Сокращения времени, скорости и расстояния
Сокращения соотношения и пропорции
000 Домен и диапазон рациональных функций 9137 функции с отверстиями
График рациональных функций
График рациональных функций с отверстиями
Преобразование повторяющихся десятичных знаков в дроби
Десятичное представление рациональных чисел
Поиск корня из длинного квадрата видение
Л.Метод CM для решения задач времени и работы
Преобразование словесных задач в алгебраические выражения
Остаток при делении 2 в степени 256 на 17
Остаток при делении степени 17 на 16
Сумма всех трехзначных чисел, делимых на 6
Сумма всех трехзначных чисел, делимых на 7
Сумма всех трехзначных чисел, делящихся на 8
Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4
Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами
Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3
Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6
.
No related posts.
Помогаю со студенческими работами здесь

Подскажите пожалуйста, есть ли различие между знаками (4) (четверка в кружке) и vdash в мат логике?
Задания по Мат.логике

Задание по мат. логике
люди добрые помогите решить задание никто ладу дать не может не нашел ничего подобного
—найти…
Литература по мат. логике
Посоветуйте какую нибудь хорошую электронную книжку или сайт по данному предмету, а то вообще на…
Искать еще темы с ответами
Или воспользуйтесь поиском по форуму:
Контрольная работа №1
1. Решить задачу, используя диаграмму ЭйлераВенна.
В одной из студенческих групп все студенты умеют программировать. 10 человек умеют
программировать на Бейсике, 10 – на Паскале, 6 – на Си. Два языка знают: 6 человек Бейсик и
Паскаль, 4 – Паскаль и Си, 3 – Бейсик и Си. Один человек знает все три языка. Сколько
студентов в группе?
1)
Задачу удобнее решать с конца. Т.е. обозначим на диаграмме тех студентов, которые
знают все три языка. А затем, вычитая из общего числа студентов, знающих тот или иной
язык, будем вычитать полученные данные.
Обозначим на диаграмме за В – множество студентов, умеющих программировать на языке
Бейсик, Р – умеющих программировать на Паскале, и, соответственно, С – на Си.
2)
Так как Бейсик и Паскаль знают 6 студентов, а все три языка знает 1 человек (так же
Паскаль и Си знают 4 человека и Бейсик и Си – 3 студента), значит получаем:
3)
Используя данные о том, что 10 человек умеют программировать на Бейсике, 10 – на
Паскале, 6 – на Си, вычтем имеющиеся данных из этих и отобразим результат на
диаграмме:
Общее число студентов в группе получается путём сложения всех получившихся чисел:
2+5+1+2+1+3=14
Ответ: в группе 14 студентов 2. Задано универсальное множество U={1,2,3,4,5,6,7,8} и множества X={1,2,4,6,7},
Y={2,3,5,7,8}, Z={1,4,7,8}. Найти булеан множества Z и какоелибо разбиение множества Y.
Выполнить действия
.
Z
X Y
1) Булеан множества Z
B Z
(
)
,{1}, 4 ,{7},{8},{1, 4},{1,7},{1,8},{4,7},{4,8},{7,8},{1, 4,7},{1, 4,8},{4,7,8},{1, 7,8}
2)
2)
Разбиения множества Y
( )
R Y
1
( )
R Y
2
( )
R Y
3
2 ,{3},{5,7},{8}
{2,3,5},{7,8}
{2,3,5},{7},{8}
3)
X Y
Z
Y
{1,4,6}
X Y
X Y
Z
{1, 2, 4,6,7}
{1, 4,7}
3. Упростить, используя законы и тождества алгебры множеств (перечислить
используемые законы):
№
1
2
3
4
5
6
7
8
9
Свойства универсального множества
Закон коммутативности
Название
Формулы
Свойства пустого множества
A A A
A
;
;
A
A U A A U U A A U
;
;
;
A B B A A B B A
B C
C A
A B
A B
B C
C A
A
A
A A
A A A A A A
A B A B A B A B
A B
A
Закон двойного дополнения
Закон идемпотентности
Законы де Моргана
Законы поглощения
;
A C
A C
A B
B C
B C
Закон дистрибутивности
Закон ассоциативности
;
;
A A
A B
A B
A
;
;
1
B A
5
3
A B
B A
B
B A
B
9
A B
B
4, 9
B B
7
A B
A
B
B B
5
A B
B
A A
B A
B
B
4. Пусть X={1,2,3,4}. Бинарное отношение R
свойством:
способами. Выяснить, какими свойствами оно обладает.
,
a b a b
,
a b X
4,
R
задано характеристическим
. Представить отношение R другими возможными
X X
X X
1,1 , 1, 2 , 1,3 , 1,4 , 2,1 , 2,2 , 2,3 , 2, 4 , 3,1 , 3,2 , 3,3 , 3, 4 , 4,1 , 4, 2 , 4,3 , 4, 4
R
1, 2,3,4
1,1 , 1,2 , 2,1
1,2,3, 4
1) Рефлексивность
Т.к. условие рефлексивности выполняется только при X<2, значит, отношение R не обладает
свойством рефлексивности
2) Антирефлексивность
Антирефлексивным множество R назвать нельзя, т.к. при x=1 выполняется условие (x,x)R
3) Симметричность
Если a+b<4, то b+a<4 – верно
4) Несимметричность
Не является несимметричным (из предыдущего пункта)
5) Антисимметричность
Не является антисимметричным, т.к. из (a+b<4) и (b+a<4) не следует, что a=b.
6) Транзитивность
Не является транзитивным
Rсимметрично
,a b
5. Заданы отношения:
Записать обозначения операций реляционной алгебры и выполнить их:
А) проекция на список (2,1) отношения S
Б) соединение отношений R и S по условию “A1 < B2” проекция на список (2,1) отношения S
(2,1)s
соединение отношений R и S по условию “A1 < B2”
R S
B2
T
Z
Z
T
Z
Z
T
Z
Z
A2
A1
Y
X
Y
X
Y
X
Z
Y
Z
Y
Z
Y
T
X
T
X
T
X
3n
5
n N
A B A B A B
;
B1
U
X
Y
U
X
Y
U
X
Y
.
;
Какова
?
B3
V
Y
V
V
Y
V
V
Y
V
TUVWXYZ – X
Математическая логика — это раздел математики, изучающий математические обозначения, формальные системы, доказуемость математических суждений, природу математического доказательства в целом, вычислимость и прочие аспекты оснований математики.
Алгебра высказываний
Под высказыванием понимаем всякое утверждение (повествовательное предложение), про которое всегда определенно и объективно можно сказать, является оно истинным или ложным. Например, «5-3 = 2» или «В неделе семь дней» — истинные высказывания, а «5 > 8» или «В русском языке 35 букв» — ложные высказывания. Синонимами слова «высказывания» можно считать: логическое высказывание, булевское выражение, суждение, утверждение и т.п. Фразы: «Ура!», «Который час?» — не являются высказываниями.
Если высказывание истинное, то ему предписывается значение «истина» (другие обозначения: «1», «ДА» , «И», «+», «true»). Ложному высказыванию предписывается значение «ложь» (другие обозначения: «О», «НЕТ», «Л», «-«, «false»). Совокупность возможных значений высказывания образует множество истинности {0,1} и {И,Л}.
Есть два вида высказываний: простые и составные (сложные). Под простым будем понимать высказывание, которое не может быть разбито на более простые высказывания. Про него всегда однозначно можно сказать, что оно истинно или ложно, не интересуясь его структурой. Из простых высказываний при помощи логических операций можно строить сложные высказывания, которые всегда только истинны или только ложные. Высказывания обозначаются заглавными латинскими буквами: 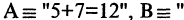
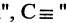
Логические операции
Операции над высказываниями задают в виде таблиц, называемых таблицами истинности.
Отрицание высказывания
Для каждого высказывания А может быть сформировано новое высказывание 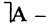
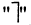
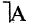
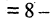
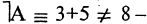
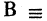
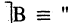
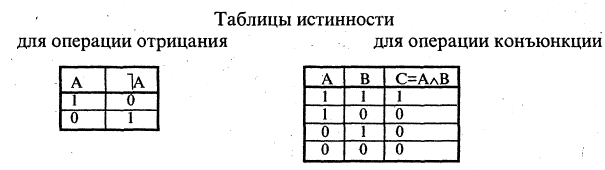
Конъюнкция высказываний
Конъюнкцией высказываний А и В называется высказывание 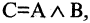

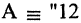
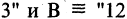

Операцию конъюнкции можно определить и для нескольких высказываний как связку высказываний, объединенных союзом «и». Конъюнкция из п высказываний — новое высказывание, причем высказывание
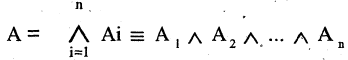
имеет значение «истина», если 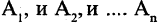
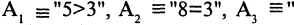
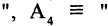
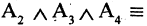
Мурманск севернее Смоленска») — ложное высказывание. В то время как 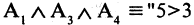
Дизъюнкция высказываний
Дизъюнкцией высказываний А и В называется высказывание 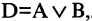

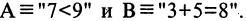
Операцию дизъюнкции можно определить для нескольких высказываний как связку высказываний, объединенных союзом «или»,
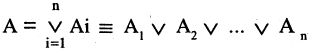
В этом случае высказывание А истинно, если истинно хотя бы одно из высказываний, входящих в связку.
Импликация высказываний
Импликацией высказываний А и В называется высказывание 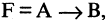
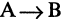
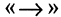


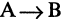

Пусть А и В истинны. Тогда папа, получив премию, покупает сыну велосипед. Естественно считать это истинным высказыванием. Когда же папа не купит сыну велосипед (В — ложно), получив премию (А — истинно), то это, мягко говоря, не логичный поступок, а импликация имеет значение «ложь». Если же папа не получит премию (А — ложно), но купит велосипед (В -истинно), то результат положителен. В том случае, если, не получив премии (А ложно), папа не купит велосипед (В — ложно) -обещание не нарушено, результат можно считать истинным.
Эквивалентность высказываний
Эквивалентностью высказываний А и В называется высказывание 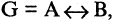
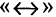






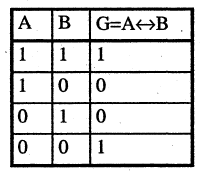
Замечание. Характерной особенностью операций над высказываниями является введение логических союзов с точно определенным смыслом, не допускающим никакой двусмысленности в толковании этих символов. Таким образом, математическая логика применима не для любых высказываний, а только для таких, которые допуск кают четкую оценку в двоичной системе «истина — ложь». Для преодоления такого рода ограничений в рамках нечеткой математики разрабатывается нечеткая логика.
Если в выражении встречаются различные логические операции, то в качестве естественного порядка (выполняемого поочередно слева направо) используется следующая последовательность: 
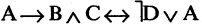
Введя скобки, получим формулу 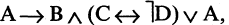
Если в выражении присутствуют арифметические операции, операции сравнения и логические операции, то порядок старшинства операций следующий:
Использование различных операций позволяет в удобной аналитической форме задавать различные множества.
Например, множество точек А, заштрихованное на рис. 1.16, может быть задано следующей формулой:
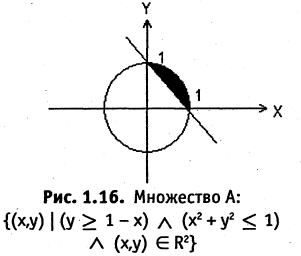
Система операций 
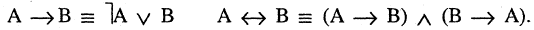
Булевы функции
Всякую формулу логики высказываний можно рассматривать как некоторую функцию: каждая буква (высказывание) может принимать одно из двух значений — «истина» или «ложь», при этом сложное высказывание, заданное этой формулой, также может быть истинным или ложным. Так формула
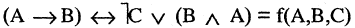
выражает функцию от переменных А, В и С.
Такого рода функции называются булевыми, а их аргументы — булевыми переменными. Аргументы булевых функций могут представлять собой, сокращенные обозначения некоторых конкретных высказываний. Тогда функция обозначает сокращенную запись некоторого сложного высказывания. Например, 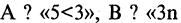
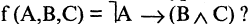
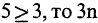
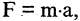
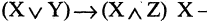
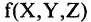
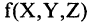
Целый ряд булевых функций обладает тем свойством, что они принимают одни и те же значения при любых значениях истинности аргументов. Такие формулы называются тождественно истинными. Например, при любых X и Y истинны формулы 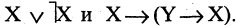
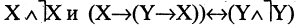
Наиболее важные тождественно истинные формулы получили название Основные законы математической логики.
Основные законы математической логики
1.Коммутативность
2.Ассоциативность
3.Дистрибутивность
4.Законы де Моргана
5.Закон поглощения
6.Закон идемпотентности
8.Закон противоречия
9.Закон исключения третьего
10.Закон двойного отрицания
Пример:
Упростить выражение, используя тождественны преобразования
Существует бесконечное множество тавтологий. Некоторы из них легли в основу методов доказательства.
Основные методы доказательств
При построении любой теории выделяется некоторый набор высказываний, так называемых аксиом, истинность которых постулируется. Из аксиом чисто логическим путем может был установлена истинность некоторых других высказываний называемых теоремами. Последовательность высказываний рассматриваемой теории, каждое из которых либо является аксиомой, либо выводится из одного или более предыдущих высказываний этой последовательности по логическим правилам вывода, называется доказательством. Высказывание, которое можно доказать, называется теоремой.
Формально каждая теорема может быть выражена в форме импликации 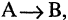
Метод цепочек импликаций
Метод цепочек импликаций состоит в том, что из посылки А страивается цепочка из 
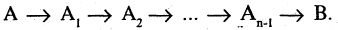
В основе этого метода лежит закон цепного высказывания или закон силлогизма
Метод от противного
Метод от противного. Используя этот метод, вместо доказательства прямого следствия «из А следует В» доказывают, что из «не В» следует «не А». Этот метод основан на законе контрапозиций, имеющем следующий вид:
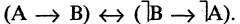
Метод необходимого и достаточного
Метод необходимого и достаточного. Теорема формулируется так: «Чтобы имело место А, необходимо и достаточно выполнение В». Доказательство такого вида теоремы распадается на две части:
а) доказывается, что если имеет место А, то справедливо В (В необходимо для А);
б) если имеет место В, то имеет место и А (В достаточно для А).
Доказательство таким методом базируется на законе тавтологии:
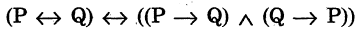
Алгебра предикатов
Предикатом 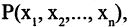
называется функция Р, отображающая их прямое произведение на двоичное множество, т. е. 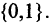
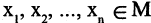
Рассмотрим примеры, 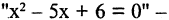
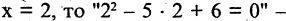
положив 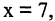
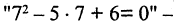
Всякий предикат 
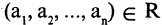
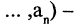

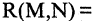
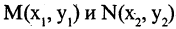
Если в 
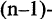
Логические операции над предикатами
Отрицание предиката
Пусть предикат 
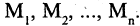


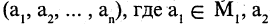
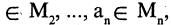
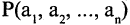
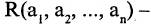
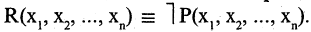
Например, предикат «

Конъюнкция предикатов
Пусть на множествах 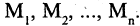

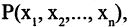

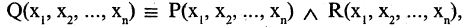
который истинен для одних и тех же кортежей только тогда, когда оба предиката — и 
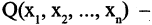
Например, конъюнкция предикатов 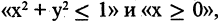
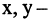
Дизъюнкция предикатов
Дизъюнкция предикатов 


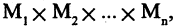


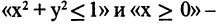
Импликация предикатов
Импликация предикатов 

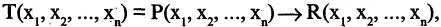
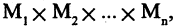


Например, импликация «



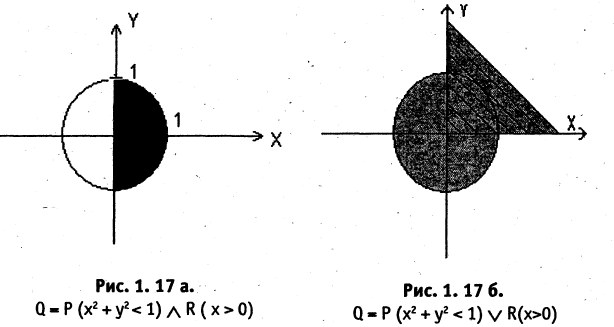
Эквивалентность предикатов
Эквивалентность предикатов 

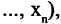



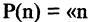
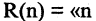

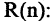


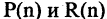
Наряду с логическими операциями важную роль играют операции, называемые кванторами. Квантор всеобщности есть операция, которая предикат 


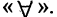



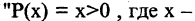



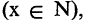

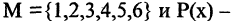

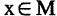
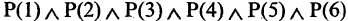
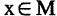
Квантор существования
Квантор существования есть операция, которая предикат 
из М, обладающий свойством 
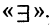







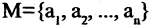
Кванторы обладают свойствами, являющимися аналогами законов де Моргана:
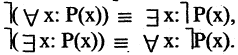
С помощью кванторов можно выражать ряд часто используемых на практике отношений между множествами. Например, высказывание «все объекты 

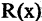
Переход от 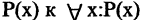



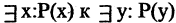
Рассмотрим пример. На множестве чисел задан двухместный предикат 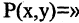


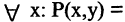

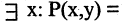

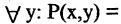

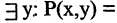

Связывая обе переменные данного предиката, получим высказывания:
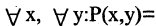
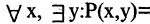
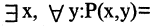
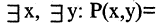
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат