На уроке рассматривается 14 задание, решение и объяснение ЕГЭ по информатике
Содержание:
- Объяснение заданий 14 ЕГЭ по информатике
- Перевод числа из любой системы счисления в десятичную
- Особенности при переводах в разные системы счисления
- Решение заданий 14 ЕГЭ по информатике
- Определите наибольшее/наименьшее значение x, y
- Сколько цифр или сумма цифр
- Найти основание системы счисления и уравнения
14-е задание: «Операции в системах счисления»
Уровень сложности
— повышенный,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 5 минут.
Проверяемые элементы содержания: Знание позиционных систем счисления
До ЕГЭ 2021 года — это было задание № 16 ЕГЭ
Типичные ошибки и рекомендации по их предотвращению:
«Основные ошибки связаны с невнимательностью при выполнении арифметических действий
в недесятичных системах счисления. Например, вычитания единицы в ситуации типа: 10100002 – 1»
ФГБНУ «Федеральный институт педагогических измерений»
С основами темы можно ознакомиться в теории к заданию 1.
Перевод числа из любой системы счисления в десятичную
Чтобы перевести, например, 10045N, из системы счисления с основанием N в десятичную систему, нужно умножить значение каждой цифры на N в степени, равной разряду этой цифры:
Особенности при переводах в разные системы счисления
Некоторые правила, которые нужно знать, при работе с системами счисления:
- последняя цифра (крайняя справа) в записи числа в системе счисления с основанием
N– представляет собой остаток от деления этого числа наN:
710 = 1112 7/2 = остаток 1
N – это остаток от деления этого числа на N², и так далее:710 = 1112 112=310 7/22 = остаток 310 (112)
10N записывается как единица и N нулей:
2N в двоичной системе записывается как единица и N нулей:3N записывается в троичной системе в виде единицы и N нулей:a; общее правило:10N-1 записывается как N девяток:2N-1 в двоичной системе записывается как N единиц:3N-1 записывается в троичной системе как N двоек:aN-1 в системе счисления с основанием a записывается как N старших цифр этой системы, то есть, цифр (a-1)10N-10M = 10M * (10N-M – 1) записывается как N-M девяток, за которыми стоят M нулей:2N – 2K при K < N в двоичной системе записывается как N – K единиц и K нулей:
Решение заданий 14 ЕГЭ по информатике
Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ
Определите наибольшее/наименьшее значение x, y
14_14:
Операнды арифметического выражения записаны в системе счисления с основанием 15.
82x19₁₅ – 6x073₁₅
В записи чисел переменной x обозначена неизвестная цифра из алфавита 15-ричной системы счисления. Определите наименьшее значение x, при котором значение данного арифметического выражения кратно 11. Для найденного значения x вычислите частное от деления значения арифметического выражения на 11 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.
✍ Решение:
-
✎ Решение с использованием программирования:
PascalABC.net:
|
||
|
Python:
|
||
| С++: |
Ответ: 7806
Сколько цифр или сумма цифр
14_12:
Значение арифметического выражения
43∙7103 – 21∙757 + 98
записали в системе счисления с основанием 7.
Найдите сумму цифр получившегося числа и запишите её в ответе в десятичной системе счисления.
✍Решение:
✎ Решение с использованием программирования:
PascalABC.net, Решение 1:
|
||
PascalABC.net, Решение 2:
|
||
Python:
|
||
| С++: |
Результат: 276
14_1:
Значение арифметического выражения:
21024 + 464 — 64
записали в системе счисления с основанием 2.
Сколько цифр «1» содержится в этой записи?
Типовые задания для тренировки
✍Решение:
✎ Решение с использованием программирования:
PascalABC.net, Решение 1:
|
||
PascalABC.net, Решение 2:
|
||
Python:
|
||
| С++: |
✎ Решение теоретическое:
- Существует правило:
- Чтобы воспользоваться этим правилом, преобразуем общее выражение к степеням двойки:
2N = 10..02(1 единица и N нулей)
21024 + (22)64 - 26 = 21024 + 2128 - 26
10...0 (1024 нуля) + 10...0 (128 нулей) - 10...0 (6 нулей)
10....00000 - 1024 нуля + 10..0 - 128 нулей _________________________ 10....10..0
10....00000 - 1024 нуля + 10..0 - 128 нулей _________________________ 10....10..0 - запомним единицу
2N — 2K = 1…1 (N - K единиц)0…0(K нулей)
10..0000000 - 128 нулей - 1000000 _________________________ 11..1000000 - 122 единицы и 6 нулей
122 + 1 = 123 единицы
Результат: 123
Также можно посмотреть видео решения 14 задания ЕГЭ по информатике (аналитическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
14_3: 14 задание. Демоверсия ЕГЭ 2018 информатика:
Значение арифметического выражения:
4910 + 730 – 49
записали в системе счисления с основанием 7.
Сколько цифр «6» содержится в этой записи?
Типовые задания для тренировки
✍ Решение:
✎ Решение с использованием программирования:
PascalABC.net, решение 1:
|
||
PascalABC.net, решение 2:
|
||
Python:
|
||
| С++: |
✎ Решение теоретическое:
- Приведем все числа к степеням 7:
720 + 730 - 72
730 + 720 - 72
1. an = 10..0a n 2. an - am = (a-1)..(a-1)0..0a n-m m
730 = 10..0
30
0 + (20 - 2) = 18
Результат: 18
Подробное решение 14 задания демоверсии ЕГЭ смотрите на видео (аналитическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
14_2:
Значение арифметического выражения:
4500 + 3*42500 + 16500 — 1024
записали в системе счисления с основанием 4.
Сколько цифр «3» содержится в этой записи?
Типовые задания для тренировки
✍ Решение:
✎ Решение с использованием программирования:
PascalABC.net:
|
||
Python:
|
||
| С++: |
Результат: 496
Подробное решение данного 14 задания ЕГЭ по информатике можно посмотреть на видео (аналитическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
14_5:
Значение арифметического выражения: 81024 + 832 – 65 – записали в системе счисления с основанием 8. Сколько цифр «7» содержится в этой записи?
Типовые задания для тренировки
✍ Решение:
✎ Решение с использованием программирования:
PascalABC.net:
|
||
Python:
|
||
| С++: |
✎ Решение теоретическое:
- Приведем все числа к степеням восьмерки:
65 = 64 + 1 = 82 + 80;
81024 + 832 - (82 + 80); 81024 + 832 - 82 - 80
1. an = 10..0a n 2. an - am = (a-1)..(a-1)0..0a n-m m
81024 = 10..0
1024
3.-2n = -2n+1 + 2n
! Формула предназначена для чисел в двоичной системе счисления, но для подсчета цифр "7" в 8-й (или "6" в 7-й и т.п.) ее можно использовать (для поиска единиц или нулей она не подходит!!!)
-82 = -83 + 82
! обратите внимание, что тождество неверно, но
при поиске количества "7" этой формулой можно воспользоваться
(для поиска единиц или нулей она не подходит!)
Получаем:
81024 + 832 - 83 + 82- 80
0 + (32 - 3) + (2 - 0) = 31
Результат: 31
14_13:
Сколько значащих нулей в двоичной записи числа 4350 + 8340 – 2320 – 12?
✍ Решение:
✎ Решение с использованием программирования:
PascalABC.net, решение 1:
|
||
PascalABC.net, решение 2:
|
||
Python:
|
||
| С++: |
✎ Решение теоретическое:
- По возможности приведем каждое слагаемое к степеням 2. Получим:
4350 + 8340 – 2320 – 12
(22)350 + (23)340 - 2320 - 3*22 = (22)350 + (23)340 - 2320 - 12 = 2700 + 21020 - 2320 - (23 + 22)
21020 + 2700 - 2320 - 23 - 22
-2n = -2n+1+2n и преобразуем выражение:21020 + 2700 - 2321+ 2320- 24 + 23 - 22
21020 -> один не ноль 2700 - 2321 -> 379 не нулей 2320- 24 -> 316 не нулей 23 - 22 -> один не ноль Итого: 1+ 379+316 +1 = 697
1021 - 697 = 324
Результат: 324
Найти основание системы счисления и уравнения
14_7:
Укажите, сколько всего раз встречается цифра 2 в записи чисел 13, 14, 15, …, 23 в системе счисления с основанием 3.
Типовые задания для тренировки
✍ Решение:
- Для начала достаточно перевести первое и последнее число предложенного интервала в троичную систему счисления. Сделаем это:
1.
13 | 3
12 4 | 3
1 3 1
1
1310 = 1113
2.
23 | 3
21 7 | 3
2 6 2
1
2310 = 2123
111, 112, 120, 121, 122, 200, 201, 202, 210, 211, 212
111, 112, 120, 121, 122, 200, 201, 202, 210, 211, 212
Ответ: 13
✍ Решение:
- Разделим уравнение на три части и вычислим каждую часть отдельно (выделим части разным цветом):
204N+1 = 204N + 2616 1 2 3
1.
210
204N+1
По формуле получаем:
2*(N+1)2 + 0*(N+1)1 + 4*(N+1)0 =
= 2*(N2 + 2N + 1) + 0 + 4 = 2N2 + 4N + 6
2.
210
204N
По формуле получаем:
2*N2 + 0*N1 + 4*N0 =
= 2N2 + 4
3. 2616 = 3810
2N2 + 4N + 6 = 2N2 + 4 + 38; 4N = 36; N = 9
Результат: 9
✍ Решение:
- Вместо обозначения искомой системы счисления введем неизвестное x:
144x + 24x = 201x
144 + 24 = 201 1*x2 + 4*x1 + 4*x0 + 2*x1 + 4*x0 = 2*x2 + 0*x1 + 1*x0
x2 - 6x - 7 = 0
D = b2 - 4ac = 36 - 4*1*(-7) = 64
x = (-b ± √D)/2a
x1 = (6 + 8)/2 = 7
x2 = (6 - 8)/2 - не подходит
x = 7
Ответ: 7
14_9:
В некоторой системе счисления записи десятичных чисел 68 и 94 заканчиваются на 3. Определите основание системы счисления.
Типовые задания для тренировки
✍ Решение:
- Вспомним правило:
- Примем искомую систему счисления за x. Тогда, исходя из приведенного правила имеем:
Последняя цифра записи числа в системе счисления с основанием X — это остаток от деления этого числа на X
94 / x = некоторое число и остаток 3 и 68 / x = некоторое число и остаток 3
91/x 65/x
91 - 65 = 26 65 - 26 = 39 39 - 26 = 13 26 - 13 = 13
Ответ: 13
14_10:
Некоторое число X из десятичной системы счисления перевели в системы счисления с основаниями 16, 8. Часть символов при записи утеряна. Позиции утерянных символов обозначены *:
X = *516 = *0*8
Сколько чисел соответствуют условию задачи?
Типовые задания для тренировки
✍ Решение:
- Данные числа с утерянными символами переведем из 16-й и из 8-й системы счисления в двоичную. Перевод будем делать триадами и тетрадами, неизвестные позиции оставим пустыми:
1. *516
* | 5 16
* * * * | 0 1 0 1 2
2. *0*8
* | 0 | * 8
* * *|0 0 0|* * * 2
* * 0 0 0 1 0 1
1. 01000101 2. 10000101 3. 11000101
Ответ: 3
Предлагаем посмотреть видео решения данного 14 задания ЕГЭ (аналитическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
14_4:
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 75 оканчивается на 13.
Типовые задания для тренировки
✍ Решение:
- Так как 75 должно оканчиваться на 13, то имеем два общих случая:
1. 7510 = 13N 2. 7510 = ...13N (число оканчивается на 13)
1 случай:
75|N N|1 отсюда имеем => 75 - N = 3; т.е. N = 72 3
2 случай:
75|N 72|y отсюда имеем => 75 = Ny + 3, где N - целое, неотриц. 3
75|N 72| y |N => y = Nz + 1, где z - целое, неотриц. 3 y-1|z 1
75 = Ny + 3 y = Nz + 1
75 = N (Nz + 1) + 3; 75 = N2z + N + 3; 75 = N2z + N
z = (72 - N)/N2
72 - 5 / 52 = 67 / 25 не делится, - не подходит!
75 | 4
72 | 18| 4
3 16| 2
2 => не подходит! должна быть единица
75 | 6
72 | 12| 6
3 12| 1
0 => не подходит! должна быть единица
75 | 7
70
5 => не подходит! должна быть 3
75 | 8
72 | 9| 8
3 8| 1
1 => подходит!
Результат: 8,72
Видеоразбор решения (аналитический способ):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
14_11:
Выражение 25*325 записано в троичной системе счисления. Определите, сколько в этой записи цифр 0, 1 и 2.
✍ Решение:
-
Рассмотрим каждый сомножитель отдельно.
- Первый сомножитель:
25 = 32 Переведем в троичную систему счисления (делением на 3, переписываем остатки). Результат: 3210 = 10123
325 = 10..0{25 нулей}3
1000 x 1012 = ---- 2000 1000 0000 1000 ------- 1012000
Ответ: «0»=26, «1»=2, «2»=1
Смотрите видео разбора на нашем канале (аналитическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Пройти тестирование по 10 заданиям
Пройти тестирование по всем заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Операнды арифметического выражения записаны в системах счисления с основаниями 9 и 11:
88x4y9 + 7x44y11
В записи чисел переменными x и y обозначены допустимые в данных системах счисления неизвестные цифры. Определите значения x и y, при которых значение данного арифметического выражения будет наименьшим и кратно 61. Для найденных значений x и y вычислите частное от деления значения арифметического выражения на 61 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.
2
Операнды арифметического выражения записаны в системах счисления с основаниями 13 и 18:
8x78y13 + 79xy718
В записи чисел переменными x и y обозначены допустимые в данных системах счисления неизвестные цифры. Определите значения x и y, при которых значение данного арифметического выражения будет наименьшим и кратно 9. Для найденных значений x и y вычислите частное от деления значения арифметического выражения на 9 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.
3
Операнды арифметического выражения записаны в системах счисления с основаниями 15 и 16:
90x4y15 + 91xy216
В записи чисел переменными x и y обозначены допустимые в данных системах счисления неизвестные цифры. Определите значения x и y, при которых значение данного арифметического выражения будет наименьшим и кратно 56. Для найденных значений x и y вычислите частное от деления значения арифметического выражения на 56 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.
4
Операнды арифметического выражения записаны в системах счисления с основаниями 11 и 19:
x341y11 + 56x1y19
В записи чисел переменными x и y обозначены допустимые в данных системах счисления неизвестные цифры. Определите значения x и y, при которых значение данного арифметического выражения будет наименьшим и кратно 305. Для найденных значений x и y вычислите частное от деления значения арифметического выражения на 305 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.
5
Операнды арифметического выражения записаны в системах счисления с основаниями 12 и 14:
x231y12 + 78x98y14
В записи чисел переменными x и y обозначены допустимые в данных системах счисления неизвестные цифры. Определите значения x и y, при которых значение данного арифметического выражения будет наименьшим и кратно 99. Для найденных значений x и y вычислите частное от деления значения арифметического выражения на 99 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.
Пройти тестирование по этим заданиям
Мы подошли к 14 заданию из ЕГЭ по информатике 2022. Оно связано с различными системами счисления. Что такое различные системы счисления, мы рассматривали в этой статье. Так же будет полезно посмотреть эту статью.
Переходим к первому тренировочному 14-ому заданию из ЕГЭ по информатике. Раньше это задание было под номером 16.
Задача (ЕГЭ по информатике, 2019, Москва)
Значение выражения 536 + 524 — 25 записали в системе счисления с основанием 5. Сколько цифр «4» содержится в этой записи?
Решение:
Первый способ. (С помощью Питона)
f = 5**36 + 5**24 - 25 s='' while f>0: s = s + str(f%5) f = f // 5 print(s.count('4'))
В переменную f записываем функцию. Две звёздочки подряд обозначают возведение в степень. Заводим строчку s, где и будет сформировано число в пятеричной системе.
Сам перевод числа f в пятеричную систему происходит в цикле WHILE.
Записываем остатки от деления на 5 в строку s. Делаем так же, как если бы переводили в ручную. И так же производим само целочисленное деление. Это мы тоже делаем, когда переводим на листке бумаги.
В строке s получается число в пятеричной системе, но в цифры в этой записи стоят в обратном порядке. Ведь, когда мы переводим в ручную, остатки должны записать задом наперёд.
Здесь и не важен порядок цифр, важно количество четвёрок!
С помощью функции count находим количество четвёрок в строке s.
В ответе напишем 22.
Второй способ. (Классический)
Сформулируем главное правило, на которое будем опираться при решении подобного типа задач.
Примеры:
54 (в десятичной системе) — это 100005 (в пятеричной системе)
72 (в десятичной системе) — это 1007 (в семеричной системе)
29 (в десятичной системе) — это 10000000002 (в двоичной системе)
Перепишем наше выражение, чтобы все числа были в виде степени представлены.
536 + 524 — 52
Посчитаем 536 + 524 в пятеричной системе столбиком, используя основное правило.
Здесь всё просто: ноль прибавить ноль, будет ноль. Единица плюс ноль, будет один.
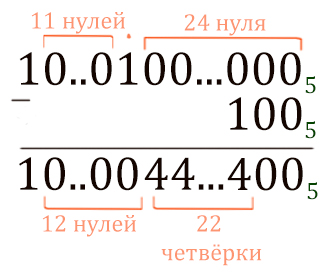
Теперь от получившегося числа нужно отнять 52 (1005).
Первые два разряда посчитать легко. Ноль минус ноль, будет ноль.
Третий разряд: из нуля отнять единицу мы не можем, поэтому занимаем у более старших разрядов.
В более старших разрядах тоже нули, поэтому идём до единицы, у которой можно занять. Получается 22 четвёрки.
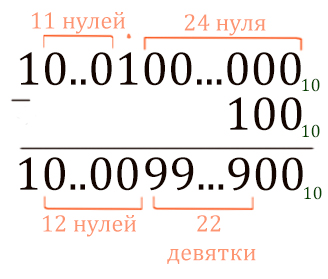
Вот как было бы, если бы считали в нашей родной десятичной системе счисления в аналогичной ситуации.
Здесь мы считаем в десятичной системе, поэтому получаются девятки. В нашей задаче считали в пятеричной системе, поэтому получаются четвёрки.
В ответе напишем 22 четвёрки.
Ответ: 22
Задача (ЕГЭ по информатике, 2020, Москва)
Значение выражения 168 × 420 — 45 — 64 записали в системе счисления с основанием 4. Сколько цифр «3» содержится в этой записи?
Решение:
Первый способ. (С помощью Питона)
f = 16**8 * 4**20 - 4**5 - 64 s='' while f>0: s = s + str(f%4) f = f // 4 print(s.count('3'))
Второй способ. (Классический)
Преобразуем наше выражение. Приведём всё к 4-ам.
168 × 420 — 45 — 64 =
= (42)8 × 420 — 45 — 43 =
= 416 × 420 — 45 — 43 =
= 436 — 45 — 43
Здесь не можем применить технику устного счёта, потому что стоят два минуса. Значит, будем решать с помощью столбиков.
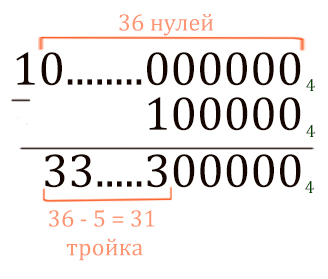
Сначала посчитаем 436 — 45.
Теперь от этого числа нужно отнять 43 (10004)
Получается 32 тройки.
В последнем вычислении нет ничего сложно. В десятичной системе вы бы легко вычислили в аналогичной ситуации.
Ответ: 32
Задача (Тренировочная)
Укажите через запятую в порядке возрастания все десятичные натуральные числа, не превосходящие 17, запись которых в троичной системе счисления оканчивается на две одинаковые цифры.
Решение:
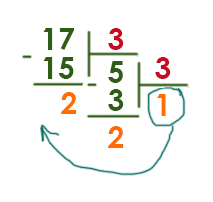
1) Переведём число 17 в троичную систему.
Получилось 1223.
2) Теперь выпишем все числа, которые не превосходят 1223 (Т.е. 1223 тоже подходит!), запись которых в троичной системе счисления оканчивается на две одинаковые цифры. В троичной системе могут применяться цифры 0, 1, 2.
1223
1223
1113
1003
223
113
Теперь переведём эти числа в десятичную систему.
1223 = 2 × 30 + 2 × 31 + 1 × 32 = 1710
1113 = 1 × 30 + 1 × 31 + 1 × 32 = 1310
1003 = 0 × 30 + 0 × 31 + 1 × 32 = 910
223 = 2 × 30 + 2 × 31 = 810
113 = 1 × 30 + 1 × 31 = 410
Ответ: 4, 8, 9, 13, 17
Ещё один интересный тип задания номер 14, который вполне может быть на реальном ЕГЭ по информатике 2022.
Задача (Уравнение)
Чему равно наименьшее основание позиционной системы счисления x, при котором 225x = 405y?
Ответ записать в виде целого числа.
Решение:
Переведём каждое из чисел 225x и 405y в десятичную систему счисления и приравняем, т.к. эти числа равны.
5 × x0 + 2 × x1 + 2 × x2 = 5 × y0 + 0 × y1 + 4 × y2
Любое число в нулевой степени — это 1. Значит, 5 × x0 = 5 × y0 = 5. Эти два выражения равны одному и тому же значению, следовательно, их можно убрать и слева, и справа.
2x + 2x2 = 4y2
x + x2 = 2y2
x(1 + x) = 2y2
Получили уравнение в целых числах. Слева умножение двух последовательных чисел. Нужно начать подбирать целые числа.
При y = 6 :
x (1 + x) = 2 × 62 = 72 ; Произведение двух последовательных чисел 8 * 9 = 72. Значит, x = 8.
Мы начали проверку с числа 6, потому что у нас в уравнении присутствуют цифра 5. Значит, система счисления может быть минимум с основанием 6.
Получается, что наименьшее значение x равно 8.
В подобных задач нужно знать, что числа обязательно найдутся, нужно их просто хорошо поискать.
Для качественной проработки 14 задания из ЕГЭ по информатике 2022 разберём ещё некоторые задачи.
Задача (Основание системы)
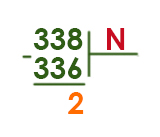
Запись числа 338 в системе счисления с основанием N содержит 3 цифры и оканчивается на 2. Чему равно максимально возможное основание системы счисления?
Решение:
В этой задаче применим формулу:
Примером для данной формулы можно взять два разряда в двоичной системе. Максимальное число в двоичной системе равно 112. А в десятичной системе это число равно 310. Т.е. 22 — 1.
338 число будет точно больше, чем двухзначное число с основанием N.
Получается неравенство:
338 > N2 — 1
N2 < 339
N — положительное целое число. Тогда:
N < √339 ≈ 18
N ≤ 18
Сказано, что число в системе с основанием N оканчивается на 2. Поэтому первый остаток должен быть равен 2!
Будем идти вниз от числа 18 и проверять, на что делится 336.
Число 336 должно делится на N.
Подошло число 16 (16 * 21 = 336!)
Ответ: 16
Продолжаем подготовку к 14 заданию из ЕГЭ по информатике 2022
Задача (На понимание)
Запись числа в девятеричной системе счисления заканчивается цифрой 4. Какой будет последняя цифра в записи этого числа в троичной системе счисления?
Решение:
Подберём такие числа в десятичной системе, которые в остатке при первом делении на 9 дадут 4!
Посмотрим, какой остаток будет при делении этого же числа на 3 при первом делении. Получается 1. Это и будет ответ.
Ответ: 1
Задача (Закрепление материала)
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 23 оканчивается на 2.
Решение:
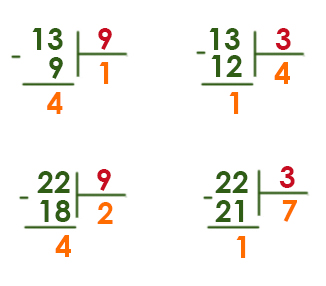
Нужно перебрать все числа от 3 до 23 и определить, какие из них при делении числа 23 дадут остаток 2.
23 : 3 = 7 (ост. 2) +
23 : 4 = 5 (ост. 3) —
23 : 5 = 4 (ост. 3) —
23 : 6 = 3 (ост. 5) —
23 : 7 = 3 (ост. 2) +
23 : 8 = 2 (ост. 7) —
23 : 9 = 2 (ост. 5) —
23 : 10 = 2 (ост. 3) —
23 : 11 = 2 (ост. 1) —
23 : 12 = 1 (ост. 11) —
23 : 13 = 1 (ост. 10) —
23 : 14 = 1 (ост. 9) —
23 : 15 = 1 (ост. 
23 : 16 = 1 (ост. 7) —
23 : 17 = 1 (ост. 6) —
23 : 18 = 1 (ост. 5) —
23 : 19 = 1 (ост. 4) —
23 : 20 = 1 (ост. 3) —
23 : 21 = 1 (ост. 2) +
23 : 22 = 1 (ост. 1) —
23 : 23 = 1 (ост. 0) —
Подходят числа 3, 7, 21.
Здесь можно и написать программу:
for i in range(3, 24): if 23%i==2: print(i)
Ответ: 3, 7, 21
Задача (Добьём 14 задание из ЕГЭ по информатике 2022)
В некоторой системе счисления записи десятичных чисел 66 и 40 заканчиваются на 1. Определите основание системы счисления.
Решение:
Нужно найти такое число, чтобы числа 66 и 40 при делении на это число давали остаток 1.
Т.е. искомое число должно быть делителем чисел 65 (66-1) и 39 (40-1). У числа 39 не так много делителей: 1, 3, 13, 39
Видим, что число 65 делится на 13 (65 : 13 = 5). Поэтому искомое число равно 13.
Ответ: 13
Задача (Для чемпионов!)
В какой системе счисления выполняется равенство 12 · 13 = 222?
В ответе укажите число – основание системы счисления.
Решение:
Если бы мы находились в десятичной системе, то последней цифрой была бы 6 (2 * 3). Но у нас 2! Т.е. Система счисления меньше или равна 6, т.к. если бы система счисления была больше 6, то у нас была бы 6 последняя цифра.
Шестёрка не «поместилась» в младший разряд, от неё осталось только 2. Остальные 4 единицы ушли в более старший разряд. Если 4 единицы составляют единицу более старшего разряда, то значит, мы находимся в четверичной системе.
Ответ: 4
Задача (Новый тип, Статград окт 2022)
В выражении 1xBAD16 + 2CxFE16 x обозначает некоторую цифру из алфавита шестнадцатеричной системы счисления. Определите наименьшее значение x, при котором значение данного выражения кратно 15. Для найденного x вычислите частное от деления данного выражения на 15 и запишите его в ответе в десятичной системе счисления.
Решение:
Здесь дана сумма чисел, которые написаны в шестнадцатеричной системе счисления.
Мы будем перебирать каждую цифру из шестнадцатеричной системы (0-15) с помощью цикла. Нас будут интересовать те значения x, при котором сумма этих чисел будет делится на 15.
for x in range(0, 16): a=13*16**0 + 10*16**1 + 11*16**2 + x*16**3 + 1*16**4 b=14*16**0 + 15*16**1 + x*16**2 + 12*16**3 + 2*16**4 if (a+b)%15==0: print(x, (a+b)//15)
Чтобы проверить, делится ли данное выражение на 15, переводим оба слагаемых в нашу родную десятичную систему. Переводим стандартным образом, об этом можно прочитать здесь.
В задаче нужно написать для наименьшего найденного значения x результат от деления данной суммы на 15.
Получается 18341
Ответ: 18341
Задача(Новый тип, закрепление)
(Богданов) Операнды арифметического выражения записаны в системе счисления с основанием 17:
9759x17 + 3×10817
В записи чисел переменной x обозначена неизвестная цифра из алфавита 17-ричной системы счисления. Определите наименьшее значение x, при котором значение данного арифметического выражения кратного 11. Для найденного значения x вычислите частное от деления значения арифметического выражения на 11 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.
Решение:
Решим задание с помощью предыдущего шаблона на языке Python.
for x in range(0, 17): a=x*17**0 + 9*17**1 + 5*17**2 + 7*17**3 + 9*17**4 b=8*17**0 + 0*17**1 + 1*17**2 + x*17**3 + 3*17**4 if (a+b)%11==0: print(x, (a+b)//11)
Ответ: 95306
Задача (Новый тип, две переменные)
(В. Шубинкин) Числа M и N записаны в системах счисления с основаниями 15 и 13 соответственно.
M = 2y23x515, N = 67x9y13
В записи чисел переменными x и y обозначены допустимые в данных системах счисления неизвестные цифры. Определите наименьшее значение натурального числа A, при котором существуют такие x, y, что M + A кратно N.
Решение:
Принцип решения данной задачи похож на решение 15 задания из ЕГЭ по информатике.
for A in range(1, 5000): for x in range(0, 13): for y in range(0, 13): M=5*15**0 + x*15**1 + 3*15**2 + 2*15**3 + y*15**4 + 2*15**5 N=y*13**0 + 9*13**1 + x*13**2 + 7*13**3 + 6*13**4 if (M+A)%N==0: print(A)
Нужно найти A, значит, начинаем перебирать A. Идём от 1, т.к. речь идёт о натуральных числах. Перебираем x и y. Они могут принимать значения из алфавита в 13-ой системе. Берём меньшую, т.к. эти переменные и в первом числе, и во втором одинаковые.
Если выполняется условие задачи, то нам интересно такое A при котором это произошло.
В этой задаче A получается достаточно большим, поэтому перебираем эту переменную до 5000.
Ответ: 1535
На этом всё! Вы прошли чемпионскую тренировку по подготовке 14 задания из ЕГЭ по информатике 2022. Успехов на экзамене!
«В переменную f записываем функцию». В переменную f мы записываем не функцию, а выражение
Господа, вот это я понимаю, по-настоящему чемпионская подготовка. Тут же и язык свой придумали, и решение на нём сделали. Скажите, зачем над змеёй то издеваться? Очень уж режет слух неправильное произношение. «Пайтон» — вот как должно быть. Я бы промолчал, увидев это раз, но видя подобное насилие над словом постоянно — молчать более не могу
Для ласт задачи модно сделать код куда проще и короче
for a in range(1, 10000):
for x in ‘0123456789ABC’:
for y in ‘0123456789ABC’:
M = int(f’2{y}23{x}5′, 15)
N = int(f’67{x}9{y}’, 13)
if (M + a) % N == 0:
print(a)
break
Первое задание, первое решение, очепятка: «В ответе напишем 4»,
вместо: «В ответе напишем 22».
И спасибо Вам за этот сайт!)
Слайд 1
Подготовка к ЕГЭ по информатике. Задание 14 . Кодирование чисел. Системы счисления. Подготовила: А.С. Безделина, у читель математики и информатики МБОУ «СОШ №9»
Слайд 2
Что проверяется: Знание позиционных систем счисления. Позиционные системы счисления. Умение строить информационные модели объектов, систем и процессов в виде алгоритмов.
Слайд 3
В презентации использованы материалы: http://kpolyakov. spb . ru https://code-enjoy.ru/ege_po_informatike_2021_zadanie_14_chempionskaya_podgotoka /
Слайд 4
Что нужно знать :
Слайд 7
Рассмотрим два вида заданий: Прямое сложение в системе счисления; Определение основания.
Слайд 8
Прямое сложение в СС Примеры заданий: 1 . Сколько единиц содержится в двоичной записи значения выражения: 4 2020 + 2 2017 – 15? 2. Значение арифметического выражения: 9 8 + 3 5 – 9 – записали в системе счисления с основанием 3. Сколько цифр «2» содержится в этой записи? 3. Сколько единиц содержится в двоичной записи значения выражения: 4 255 + 2 255 − 255 ? 4. Значение выражения 25 5 + 5 14 − 5? записали в системе счисления с основанием 5. Сколько цифр 4 содержится в этой записи ?
Слайд 9
Математический способ решения
Слайд 14
Программный способ решения. ЗАДАЧА 1. Р-25 . ( демо-2021 ) Значение арифметического выражения: 49 7 + 7 21 – 7 – записали в системе счисления с основанием 7. Сколько цифр 6 содержится в этой записи ? Решение ( использование программы ) : язык Python позволяет работать с большими числами, не задумываясь о том, что для их хранения требуется больше памяти, чем для «обычного» целого числа (когда значение не помещается в 4 байта, интерпретатор автоматически переходит на представление числа в виде массива с «длинной арифметикой») поэтому может быть написана программа, которая вычисляет нужное значение и методом деления в столбик определяет все цифры его записи в семеричной системе счисления; шестёрки считаем с помощью счётчика count6 : x = 49**7 + 7**21 — 7 count6 = 0 while x: if x % 7 == 6: count6 += 1 x //= 7 print (count6) Ответ: 13 .
Слайд 15
ЗАДАЧА 2. Р-24 . ( М.В. Кузнецова ). Значение арифметического выражения: 64 10 + 2 90 — 16 записали в системе счисления с основанием 8. Сколько цифр «7» содержится в этой записи ? Решение (программа на Python , Б.С. Михлин ): если доступна среда программирования на Python , можно написать программу, которая использует встроенную арифметику длинных чисел: x = 64**10 + 2**90 — 16 print( oct (x).count(‘7’) ) ответ: 1 8 .
Слайд 16
Определение основания . Примеры заданий: 1 . В системе счисления с некоторым основанием десятичное число 18 записывается в виде 30. Укажите это основание. 2. Решите уравнение: 121 x + 1 10 = 101 7. Ответ запишите в троичной системе (основание системы счисления в ответе писать не нужно). 3. Чему равно наименьшее основание позиционной системы счисления x, при котором 225 x = 405 y ? Ответ записать в виде целого числа. 4 . Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 31 оканчивается на 4. 5. Найдите основание системы счисления, в которой выполнено сложение : 144 + 24 = 201.
Слайд 17
ЗАДАЧА 1.
Слайд 18
Задача 2. (уравнение)
Слайд 19
Задача 3.
Слайд 20
Спасибо за внимание!
ЕГЭ-2023 по информатике. Разбор задания №14
Составил:
учитель информатики
МОУ Подосинковской СОШ
Казаров С.Р.
Кодирование чисел. Системы счисления
- Прямое сложение в системах счисления
- Операции в одной системе счисления
- Операции в разных системах счисления с одной переменной
- Операции в разных системах счисления с двумя переменными
Прямое сложение в системах счисления
Сколько единиц содержится в двоичной записи значения выражения: 8 2020 + 4 2017 + 26 – 1?
Прямое сложение в системах счисления
Решение.
Преобразуем немного выражение, получим:
2 6060 + 2 4034 + 25
2 6060 = 100..(всего 6060 нулей)..00 2
2 4034 = 100..(всего 4034 нулей)..00 2
25 10 = 11001 2
В двоичной записи результат будет выглядеть так:
100..(всего 2025 нулей)..00100..(всего 4029 нулей)..0011001
Всего 5 единиц.
Прямое сложение в системах счисления
Решение на языке Python
x = 8**2020 + 4**2017 + 26 — 1
s = ‘ ‘
while x != 0:
s += str(x % 2)
x //= 2
s = s[::-1]
print(s.count(«1»))
Прямое сложение в системах счисления
Значение арифметического выражения: 125 + 25 3 + 5 9 – записали в системе счисления с основанием 5. Сколько значащих нулей содержит эта запись?
Прямое сложение в системах счисления
Решение.
Последовательно рассмотрим данное выражение.
Рассмотрим первое слагаемое 125=5 в кубе =1000_5 .
Рассмотрим второе слагаемое: 25 в кубе = 5 в степени левая круглая скобка 6 правая круглая скобка = 1000000_5..
Рассмотрим третье слагаемое: 5 в степени левая круглая скобка 9 правая круглая скобка = 100…00_5 — на конце 9 нулей.
Результат сложения первых двух чисел: 5 в кубе плюс 5 в степени левая круглая скобка 6 правая круглая скобка = 1001000_5.
На последнем шаге получаем: 1000000000 плюс 1001000=1001001000 .
Нетрудно увидеть, что всего 7 значащих нулей.
Ответ: 7
Прямое сложение в системах счисления
Решение на языке Python
x = 125 + 25**3 + 5**9
s = ‘ ‘
while x != 0:
s += str(x % 5)
x //= 5
s = s[::-1]
print(s.count(«0»))
Операции в одной системе счисления
Операнды арифметического выражения записаны в системе счисления с основанием 19:
321×419 + 498×919
В записи чисел переменной x обозначена неизвестная цифра из алфавита девятнадцатеричной системы счисления. Определите наименьшее значение x, при котором значение данного арифметического выражения кратно 23. Для найденного значения x вычислите частное от деления значения арифметического выражения на 23 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.
Операции в одной системе счисления
При помощи цикла for будем перебирать x в соответствии в заданной системой счисления. Затем переведём все числа в десятичную систему счисления и найдём их сумму, записав полученное значение в переменную. Проверим кратность переменной на 23 и выведем частное от деления значения арифметического выражения.
Решение на языке Python
for x in ‘0123456789ABCDEFGHI’:
t = int(‘321’ + x + ‘4’, 19) + int(‘498’ + x + ‘9’, 19)
if t % 23 == 0:
print(t // 23)
exit
Ответ: 43100.
Операции в одной системе счисления
Числа M и N записаны в системе счисления с основанием 9 соответственно.
M = 842×59, N = 8×7259
В записи чисел переменной x обозначена неизвестная цифра из алфавита девятеричной системы счисления. Определите наименьшее значение натурального числа A, при котором существует такой x, что M + A кратно N.
Операции в одной системе счисления
При помощи цикла for будем перебирать числа A и x (в соответствии в заданной системой счисления). Затем переведём числа M и N в десятичную систему счисления. Проверим кратность суммы M и A на N и выведем наименьшее A на экран.
Решение на языке Python
for A in range(1, 1000):
for x in ‘012345678’:
M = int(‘842’ + x + ‘5’, 9)
N = int(‘8’ + x + ‘725’, 9)
if (M + A) % N == 0:
print(A)
exit
Ответ: 387.
Операции в разных системах счисления с одной переменной
Операнды арифметического выражения записаны в системе счисления с основаниями 18 и 12:
28×218 + 93×512
В записи чисел переменной x обозначена неизвестная цифра из алфавита десятичной системы счисления. Определите наименьшее значение x, при котором значение данного арифметического выражения кратно 133. Для найденного значения x вычислите частное от деления значения арифметического выражения на 133 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.
Операции в разных системах счисления с одной переменной
При помощи цикла for будем перебирать x в соответствии в заданной системой счисления. Затем переведём все числа в десятичную систему счисления и найдём их сумму, записав полученное значение в переменную. Проверим кратность переменной на 133 и выведем частное от деления значения арифметического выражения.
Решение на языке Python
for x in ‘0123456789’:
t = int(’28’ + x + ‘2’, 18) + int(’93’ + x + ‘5’, 12)
if t % 133 == 0:
print(t // 133)
break
Ответ: 229.
Операции в разных системах счисления с одной переменной
Операнды арифметического выражения записаны в системе счисления с основаниями 13 и 18:
xA0413 + 1Dx318
В записи чисел переменной x обозначена неизвестная цифра из алфавита десятичной системы счисления. Определите наименьшее значение x, при котором значение данного арифметического выражения кратно 184. Для найденного значения x вычислите частное от деления значения арифметического выражения на 184 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.
Операции в разных системах счисления с одной переменной
При помощи цикла for будем перебирать x в соответствии в заданной системой счисления. Затем переведём все числа в десятичную систему счисления и найдём их сумму, записав полученное значение в переменную. Проверим кратность переменной на 184 и выведем частное от деления значения арифметического выражения.
Решение на языке Python
for x in ‘0123456789A’:
t = int(‘ ‘ + x + ‘A04’, 13) + int(‘1D’ + x + ‘3’, 18)
if t % 184 == 0:
print(t // 184)
break
Ответ: 124.
Операции в разных системах счисления с двумя переменными
Операнды арифметического выражения записаны в системах счисления с основаниями 15 и 16:
90x4y15 + 91xy216
В записи чисел переменными x и y обозначены допустимые в данных системах счисления неизвестные цифры. Определите значения x и y, при которых значение данного арифметического выражения будет наименьшим и кратно 56. Для найденных значений x и y вычислите частное от деления значения арифметического выражения на 56 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.
Операции в разных системах счисления с двумя переменными
При помощи цикла for будем перебирать x и y в соответствии в заданными системами счислений. Затем переведём все числа в десятичную систему счисления и найдём их сумму, записав полученное значение в переменную. Проверим кратность переменной на 56 и выведем частное от деления значения арифметического выражения.
Решение на языке Python
result_search = [ ]
for x in ‘0123456789ABCDE’:
for y in ‘0123456789ABCDE’:
t = int(’90’ + x + ‘4’ + y, 15) + int(’91’ + x + y + ‘2’, 16)
if t % 56 == 0:
result_search.append(t)
if result_search:
print(min(result_search) // 56)
Операции в разных системах счисления с двумя переменными
Операнды арифметического выражения записаны в системах счисления с основаниями 7 и 9:
yx3207 + 1x3y39
В записи чисел переменными x и y обозначены допустимые в данных системах счисления неизвестные цифры. Определите значения x и y, при которых значение данного арифметического выражения будет наименьшим и кратно 181. Для найденных значений x и y вычислите частное от деления значения арифметического выражения на 181 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.
Операции в разных системах счисления с двумя переменными
При помощи цикла for будем перебирать x и y в соответствии в заданными системами счислений. Затем переведём все числа в десятичную систему счисления и найдём их сумму, записав полученное значение в переменную. Проверим кратность переменной на 181 и выведем частное от деления значения арифметического выражения.
Решение на языке Python
result_search = [ ]
for x in ‘0123456’:
for y in ‘0123456’:
t = int(y + x + ‘320’, 7) + int(‘1’ + x + ‘3’ + y + ‘3’, 9)
if t % 181 == 0:
result_search.append(t)
if result_search:
print(min(result_search) // 181)
Ответ: 148.
В презентации использовались материалы с сайтов
https://inf-ege.sdamgia.ru/
https://kpolyakov.spb.ru/
https://fipi.ru/
ЕГЭ информатика 14 задание разбор, теория, как решать.
Позиционные системы счисления. Кодирование чисел. Системы счисления, (П) — 1 балл
Е14.55 неизвестная цифра из алфавита 15-ричной системы счисления
Операнды арифметического выражения записаны в системе счисления с основанием 15. 123×515 + 1×23315 В записи чисел переменной x обозначена неизвестная цифра из алфавита 15-ричной системы счисления. Определите наименьшее значение x, при котором значение данного арифметического выражения кратно 14. Для найденного значения x вычислите частное от деления значения арифметического выражения на 14 и укажите его в …
Читать далее
Е14.54 Сколько чётных цифр встречается в этой записи
Значение выражения 5 ∙ 7298 + 7 ∙ 8112 + 316 — 171 записали в системе счисления с основанием 9 без незначащих нулей. Сколько чётных цифр встречается в этой записи? Ответ: СтатГрад Вариант ИН2110402 30.03.2022 – задание №14
Читать далее
Е14.53 Значение арифметического выражения 6*512^180+7*64^181+3*8^184+5*8^125-65 записали
Значение арифметического выражения 6*512180+7*64181+3*8184+5*8125-65 записали в системе счисления с основанием 64. Сколько значащих нулей содержится в этой записи? Ответ: Апробация ЕГЭ по информатике 19 февраля 2022 – задание №14 Тренировочный экзамен по информатике и ИКТ (КЕГЭ) в компьютерной форме
Читать далее
Е14.52 Какая цифра чаще всего встречается в этой записи?
Значение выражения 5 ∙ 3438 + 4 ∙ 4912 + 714 – 98 записали в системе счисления с основанием 7 без незначащих нулей. Какая цифра чаще всего встречается в этой записи? Ответ: СтатГрад Вариант ИН2110301 08.02.2022 – задание №14
Читать далее
Е14.51 N^25 — 2N^13 + 10 записали в системе счисления с основанием N
Значение арифметического выражения: N25 — 2N13 + 10 записали в системе счисления с основанием N. Определите основание системы счисления, если известно, что сумма разрядов в числе, представленном в этой системе счисления, равна 75? Ответ: «Некрыловские варианты» от Евгения Джобса — Вариант 6
Читать далее
Е14.50 125^200 — 5^x + 74 содержит ровно 100 цифр «4» в пятеричной записи числа
При каком наименьшем введённом значении x запись выражения 125200 — 5x + 74 содержит ровно 100 цифр «4» в пятеричной записи числа? «Некрыловские варианты» от Евгения Джобса — Вариант 5
Читать далее
Е14.49 Сколько разных цифр встречается в этой записи?
Значение выражения 436 + 3 ∙ 420 + 415 + 2 ∙ 47 + 49 записали в системе счисления с основанием 16. Сколько разных цифр встречается в этой записи? СтатГрад Вариант ИН2110101 27.10.2021– задание №14
Читать далее
Е14.48 3*4^38+2*4^23+4^20+3*4^5+2*4^4+1 записали в системе счисления с основанием 16
Значение арифметического выражения 3*438+2*423+420+3*45+2*44+1 записали в системе счисления с основанием 16. Сколько значащих нулей содержится в этой записи? Источник: Демонстрационный вариант ЕГЭ по информатике 2022 г. задания №14
Читать далее
Е14.47 4^14+64^16–81 записали в системе счисления с основанием 4
Значение арифметического выражения: 414 + 6416 — 81 записали в системе счисления с основанием 4. Сколько цифр «0» содержится в этой записи? Ответы: Источник: «05.04.2021 ЕГЭ 100БАЛЛОВ, Иосиф Дзеранов»
Читать далее
Е14.46 Значение арифметического выражения: 97 + 321 – 8 записали
Значение арифметического выражения: 97 + 321 – 8 записали в системе счисления с основанием 3. Найдите сумму цифр в этой записи. Ответ запишите в десятичной системе. Ответ: Тренировочный вариант от 16.11.2020 «Евгений Джобс»
Читать далее
Кодирование чисел системы счисления егэ задание 14
За правильное выполненное задание получишь 1 балл. На решение отводится примерно 5 минуты.
Для выполнения задания 16 по информатике необходимо знать:
Для любой системы счисления с основанием
- Число a N в системе счисления с основанием a записывается как единица и N нулей: Число a N -1 в системе счисления с основанием a записывается как N старших цифр этой системы счисления, то есть, цифр (a-1): Число a N – a M = a M · (a N-M – 1) записывается в системе счисления с основанием a как N-M старших цифр этой системы счисления, за которыми стоят M нулей:
Чтобы перевести число, скажем, 56720N, из системы счисления с основанием в десятичную систему, нужно умножить значение каждой цифры на в степени, равной ее разряду:
Задание 14. Кодирование чисел. Системы счисления
За правильное выполненное задание получишь 1 балл. На решение отводится примерно 5 минуты.
Для любой системы счисления с основанием
- Число a N в системе счисления с основанием a записывается как единица и N нулей: Число a N -1 в системе счисления с основанием a записывается как N старших цифр этой системы счисления, то есть, цифр (a-1): Число a N – a M = a M · (a N-M – 1) записывается в системе счисления с основанием a как N-M старших цифр этой системы счисления, за которыми стоят M нулей:
Чтобы перевести число, скажем, 56720N, из системы счисления с основанием в десятичную систему, нужно умножить значение каждой цифры на в степени, равной ее разряду:
Для любой системы счисления с основанием.
Bingoschool. ru
12.05.2019 22:05:58
2019-05-12 22:05:58
Источники:
Https://bingoschool. ru/ege/informatics/tasks/14/
Подготовка к ЕГЭ. Задание 14. Кодирование чисел. Системы счисления. | Презентация к уроку по информатике и икт (11 класс): | Образовательная социальная сеть » /> » /> .keyword { color: red; } Кодирование чисел системы счисления егэ задание 14
Подготовка к ЕГЭ. Задание 14. Кодирование чисел. Системы нтация к уроку по информатике и икт (11 класс)
Подготовка к ЕГЭ. Задание 14. Кодирование чисел. Системы счисления.
Презентация к уроку по информатике и икт (11 класс)
Что проверяется: Знание позиционных систем счисления. Позиционные системы счисления. Умение строить информационные модели объектов, систем и процессов в виде алгоритмов.
В презентации использованы материалы: http://kpolyakov. spb. ru https://code-enjoy. ru/ege_po_informatike_2021_zadanie_14_chempionskaya_podgotoka /
Что нужно знать :
Рассмотрим два вида заданий: Прямое сложение в системе счисления; Определение основания.
Прямое сложение в СС Примеры заданий: 1 . Сколько единиц содержится в двоичной записи значения выражения: 4 2020 + 2 2017 – 15? 2. Значение арифметического выражения: 9 8 + 3 5 – 9 – записали в системе счисления с основанием 3. Сколько цифр «2» содержится в этой записи? 3. Сколько единиц содержится в двоичной записи значения выражения: 4 255 + 2 255 − 255 ? 4. Значение выражения 25 5 + 5 14 − 5? записали в системе счисления с основанием 5. Сколько цифр 4 содержится в этой записи?
Математический способ решения
Программный способ решения. ЗАДАЧА 1. Р-25 . ( демо-2021 ) Значение арифметического выражения: 49 7 + 7 21 – 7 – записали в системе счисления с основанием 7. Сколько цифр 6 содержится в этой записи? Решение ( использование программы ) : язык Python позволяет работать с большими числами, не задумываясь о том, что для их хранения требуется больше памяти, чем для «обычного» целого числа (когда значение не помещается в 4 байта, интерпретатор автоматически переходит на представление числа в виде массива с «длинной арифметикой») поэтому может быть написана программа, которая вычисляет нужное значение и методом деления в столбик определяет все цифры его записи в семеричной системе счисления; шестёрки считаем с помощью счётчика count6 : x = 49**7 + 7**21 — 7 count6 = 0 while x: if x % 7 == 6: count6 += 1 x //= 7 print (count6) Ответ: 13 .
ЗАДАЧА 2. Р-24 . ( М. В. Кузнецова ). Значение арифметического выражения: 64 10 + 2 90 — 16 записали в системе счисления с основанием 8. Сколько цифр «7» содержится в этой записи? Решение (программа на Python, Б. С. Михлин ): если доступна среда программирования на Python, можно написать программу, которая использует встроенную арифметику длинных чисел: x = 64**10 + 2**90 — 16 print( oct (x).count(‘7’) ) ответ: 1 8 .
Определение основания. Примеры заданий: 1 . В системе счисления с некоторым основанием десятичное число 18 записывается в виде 30. Укажите это основание. 2. Решите уравнение: 121 x + 1 10 = 101 7. Ответ запишите в троичной системе (основание системы счисления в ответе писать не нужно). 3. Чему равно наименьшее основание позиционной системы счисления x, при котором 225 x = 405 y? Ответ записать в виде целого числа. 4 . Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 31 оканчивается на 4. 5. Найдите основание системы счисления, в которой выполнено сложение : 144 + 24 = 201.
Прямое сложение в СС Примеры заданий 1.
Nsportal. ru
07.08.2017 18:34:38
2017-08-07 18:34:38
Источники:
Https://nsportal. ru/shkola/informatika-i-ikt/library/2021/02/12/podgotovka-k-ege-zadanie-14-kodirovanie-chisel-sistemy
Кодирование чисел. Системы счисления » /> » /> .keyword { color: red; } Кодирование чисел системы счисления егэ задание 14
ЕГЭ-2015 задание 16
ЕГЭ-2015 задание 16.
Чтобы перевести число 12345N, из системы счисления с основанием N в десятичную систему, нужно умножить значение каждой цифры на N в степени, равной ее разряду:
4 3 2 1 0 ← разряды
1 2 3 4 5N = 1•N 4 + 2•N 3 + 3•N 2 + 4•N 1 + 5•N 0 (где N 0 = 1)
Последняя цифра записи числа в системе счисления с основанием N – это остаток от деления этого числа на N. Две последние цифры – это остаток от деления на N 2 , и т. д.
Число 2 N в двоичной системе записывается как единица и N нулей:
Число 2 N -1 в двоичной системе записывается как N единиц:
Так как 2 N + 2 N = 2 • 2 N = 2 N+1 , получаем 2 N = 2 N+1 — 2 N , откуда следует, что -2 N = -2 N+1 + 2 N
Задача
Сколько единиц содержится в двоичной записи значения выражения:
4 2020 + 2 2017 — 15?
Решение
Приведём все числа к степеням двойки, учитывая, что 15 = 16 – 1 = 2 4 – 1.
4 2020 + 2 2017 – 15 = (2 2 ) 2020 + 2 2017 – 2 4 + 1 = 2 4040 + 2 2017 — 2 4 + 2 0
Задача
Сколько единиц содержится в двоичной записи значения выражения:
4 2020 + 2 2017 — 15?
Приведём все числа к степеням двойки, учитывая, что 15 = 16 – 1 = 2 4 – 1.
4 2020 + 2 2017 – 15 = (2 2 ) 2020 + 2 2017 – 2 4 + 1 = 2 4040 + 2 2017 — 2 4 + 2 0
Так как 2 N 2 N 2 2 N 2 N 1 , получаем 2 N 2 N 1 — 2 N, откуда следует, что -2 N -2 N 1 2 N.
Kursypk. ru
15.10.2019 15:03:19
2019-10-15 15:03:19
Источники:
Http://kursypk. ru/index. php/egeinformatics/16zadanie-ege-2015
























![Прямое сложение в системах счисления Решение на языке Python x = 8**2020 + 4**2017 + 26 - 1 s = ‘ ' while x != 0: s += str(x % 2) x //= 2 s = s[::-1] print(s.count(](https://fsd.multiurok.ru/html/2023/01/11/s_63be65aaa3546/img4.jpg)


![Прямое сложение в системах счисления Решение на языке Python x = 125 + 25**3 + 5**9 s = ‘ ' while x != 0: s += str(x % 5) x //= 5 s = s[::-1] print(s.count(](https://fsd.multiurok.ru/html/2023/01/11/s_63be65aaa3546/img7.jpg)









![Операции в разных системах счисления с двумя переменными При помощи цикла for будем перебирать x и y в соответствии в заданными системами счислений. Затем переведём все числа в десятичную систему счисления и найдём их сумму, записав полученное значение в переменную. Проверим кратность переменной на 56 и выведем частное от деления значения арифметического выражения. Решение на языке Python result_search = [ ] for x in '0123456789ABCDE': for y in '0123456789ABCDE': t = int('90' + x + '4' + y, 15) + int('91' + x + y + '2', 16) if t % 56 == 0: result_search.append(t) if result_search: print(min(result_search) // 56)](https://fsd.multiurok.ru/html/2023/01/11/s_63be65aaa3546/img17.jpg)

![Операции в разных системах счисления с двумя переменными При помощи цикла for будем перебирать x и y в соответствии в заданными системами счислений. Затем переведём все числа в десятичную систему счисления и найдём их сумму, записав полученное значение в переменную. Проверим кратность переменной на 181 и выведем частное от деления значения арифметического выражения. Решение на языке Python result_search = [ ] for x in '0123456': for y in '0123456': t = int(y + x + '320', 7) + int('1' + x + '3' + y + '3', 9) if t % 181 == 0: result_search.append(t) if result_search: print(min(result_search) // 181) Ответ: 148.](https://fsd.multiurok.ru/html/2023/01/11/s_63be65aaa3546/img19.jpg)
