Коэффициент полезного действия егэ

Версия для печати и копирования в MS Word

Коэффициент полезного действия (КПД) некоторого двигателя вычисляется по формуле , где T₁ – температура нагревателя (в кельвинах), T₂ – температура холодильника (в кельвинах). При какой температуре нагревателя T₁ КПД этого двигателя будет 20%, если температура холодильника T₂ = 336 К? Ответ дайте в кельвинах.

Источник: Пробный ЕГЭ 2019

Решение:

  η = 20%
  T₂ = 336 К
  Т₁ – ?

0,2T₁ = T₁ – 336
0,2T₁ – T₁ = – 336
–0,8T₁ = –336
T₁ = –336/(–0,8) = 420

Ответ: 420.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 5 / 5. Количество оценок: 1

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

• Запись опубликована:02.05.2021
• Рубрика записи8. Прототипы темы: «Задачи с прикладным содержанием»
• Автор записи:Andrei Maniakin

Тепловые машины

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: принципы действия тепловых машин, КПД тепловой машины, тепловые двигатели и охрана окружающей среды.

Коротко говоря, тепловые машины преобразуют теплоту в работу или, наоборот, работу в теплоту.
Тепловые машины бывают двух видов — в зависимости от направления протекающих в них процессов.

1. Тепловые двигатели преобразуют теплоту, поступающую от внешнего источника, в механическую работу.

2. Холодильные машины передают тепло от менее нагретого тела к более нагретому за счёт механической работы внешнего источника.

Рассмотрим эти виды тепловых машин более подробно.

к оглавлению ▴

Тепловые двигатели

Мы знаем, что совершение над телом работы есть один из способов изменения его внутренней энергии: совершённая работа как бы растворяется в теле, переходя в энергию беспорядочного движения и взаимодействия его частиц.

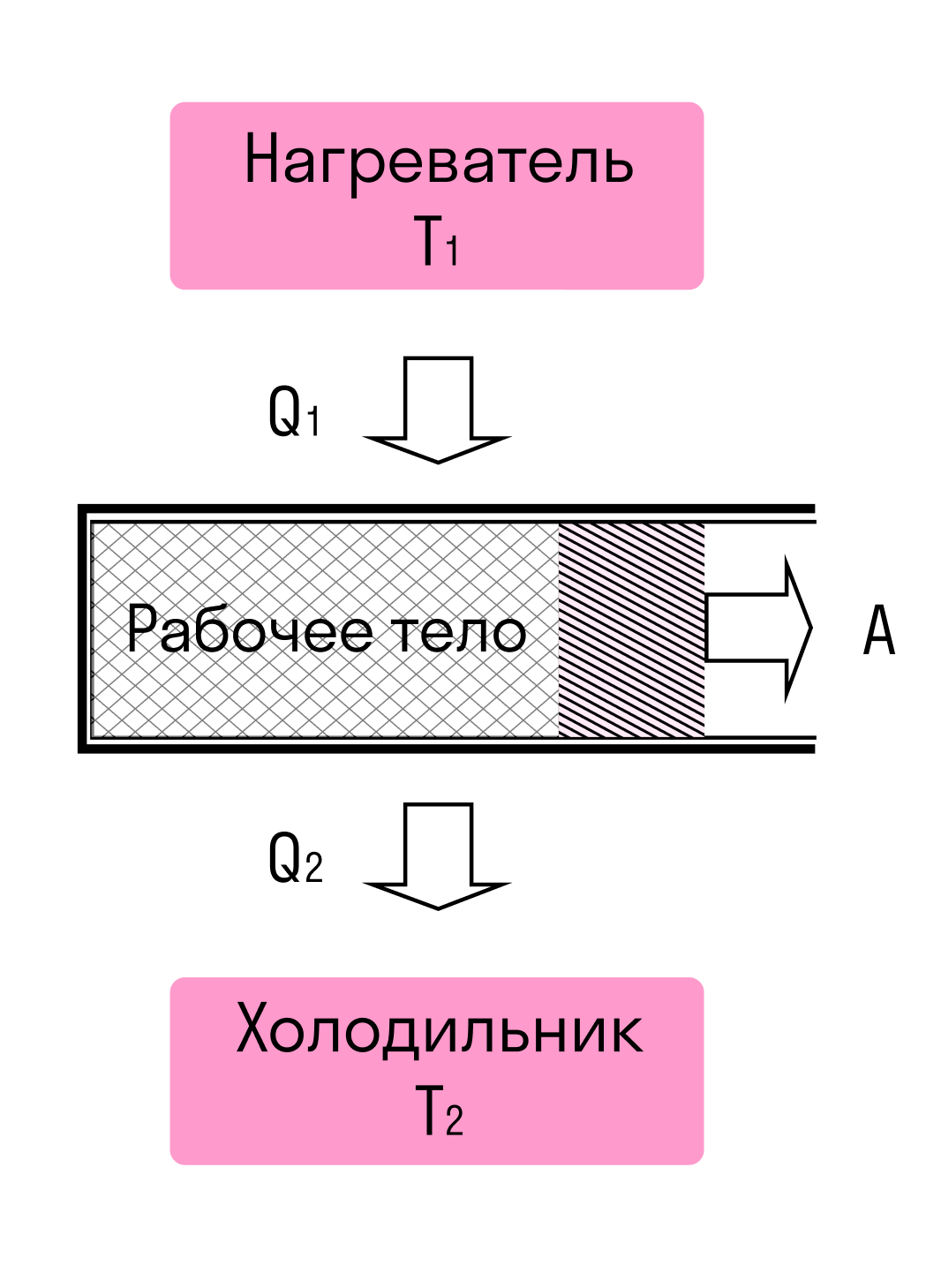
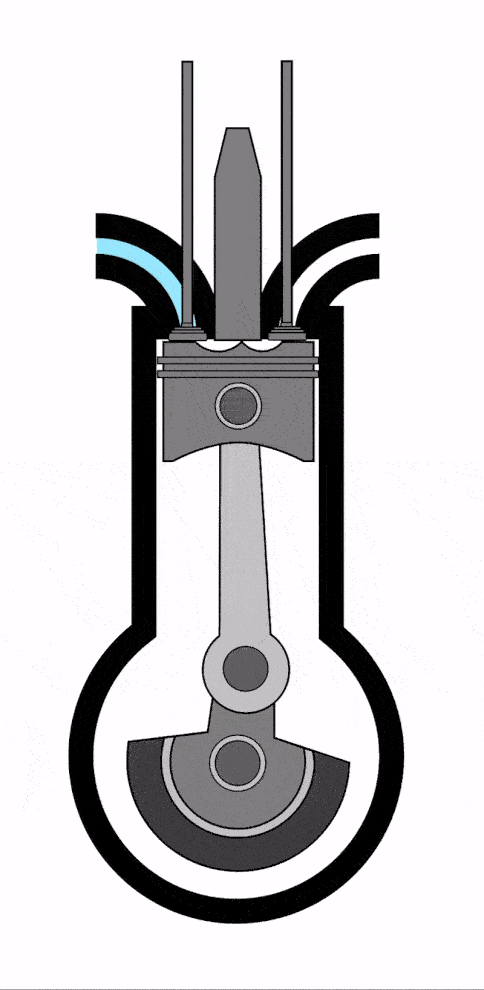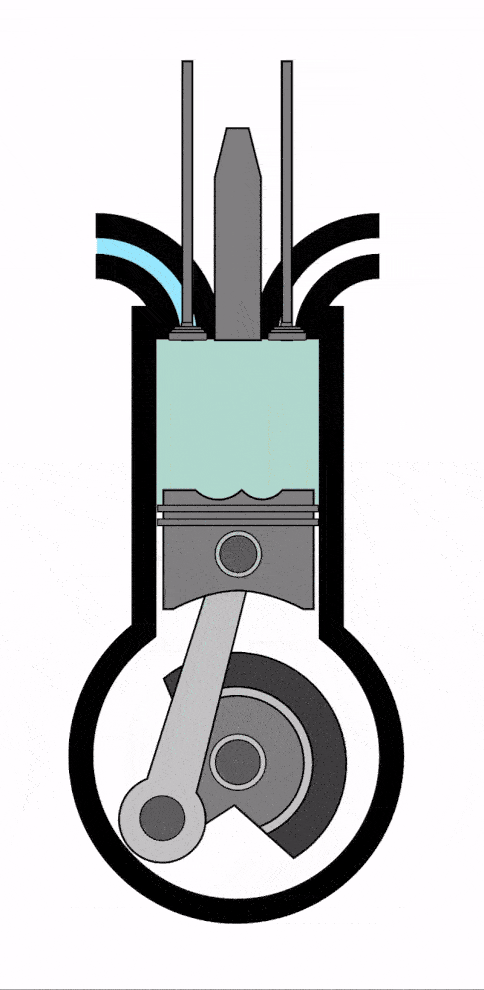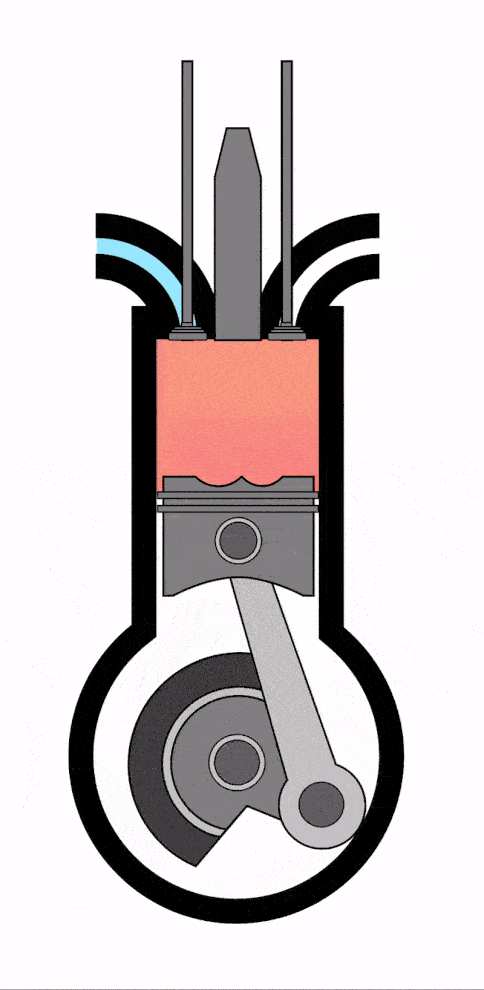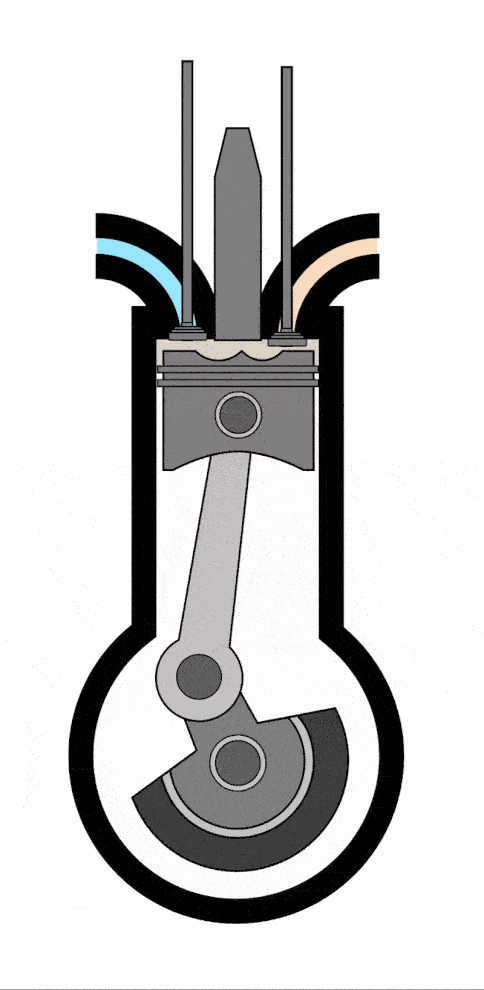
Рис. 1. Тепловой двигатель

Тепловой двигатель — это устройство, которое, наоборот, извлекает полезную работу из «хаотической» внутренней энергии тела. Изобретение теплового двигателя радикально изменило облик человеческой цивилизации.

Принципиальную схему теплового двигателя можно изобразить следующим образом (рис. 1). Давайте разбираться, что означают элементы данной схемы.

Рабочее тело двигателя — это газ. Он расширяется, двигает поршень и совершает тем самым полезную механическую работу.

Но чтобы заставить газ расширяться, преодолевая внешние силы, нужно нагреть его до температуры, которая существенно выше температуры окружающей среды. Для этого газ приводится в контакт с нагревателем — сгорающим топливом.

В процессе сгорания топлива выделяется значительная энергия, часть которой идёт на нагревание газа. Газ получает от нагревателя количество теплоты . Именно за счёт этого тепла двигатель совершает полезную работу .

Это всё понятно. Что такое холодильник и зачем он нужен?

При однократном расширении газа мы можем использовать поступающее тепло максимально эффективно и целиком превратить его в работу. Для этого надо расширять газ изотермически: первый закон термодинамики, как мы знаем, даёт нам в этом случае .

Но однократное расширение никому не нужно. Двигатель должен работать циклически, обеспечивая периодическую повторяемость движений поршня. Следовательно, по окончании расширения газ нужно сжимать, возвращая его в исходное состояние.

В процессе расширения газ совершает некоторую положительную работу . В процессе сжатия над газом совершается положительная работа (а сам газ совершает отрицательную работу ). В итоге полезная работа газа за цикл: .

Разумеется, должно быть , или (иначе никакого смысла в двигателе нет).

Сжимая газ, мы должны совершить меньшую работу, чем совершил газ при расширении.

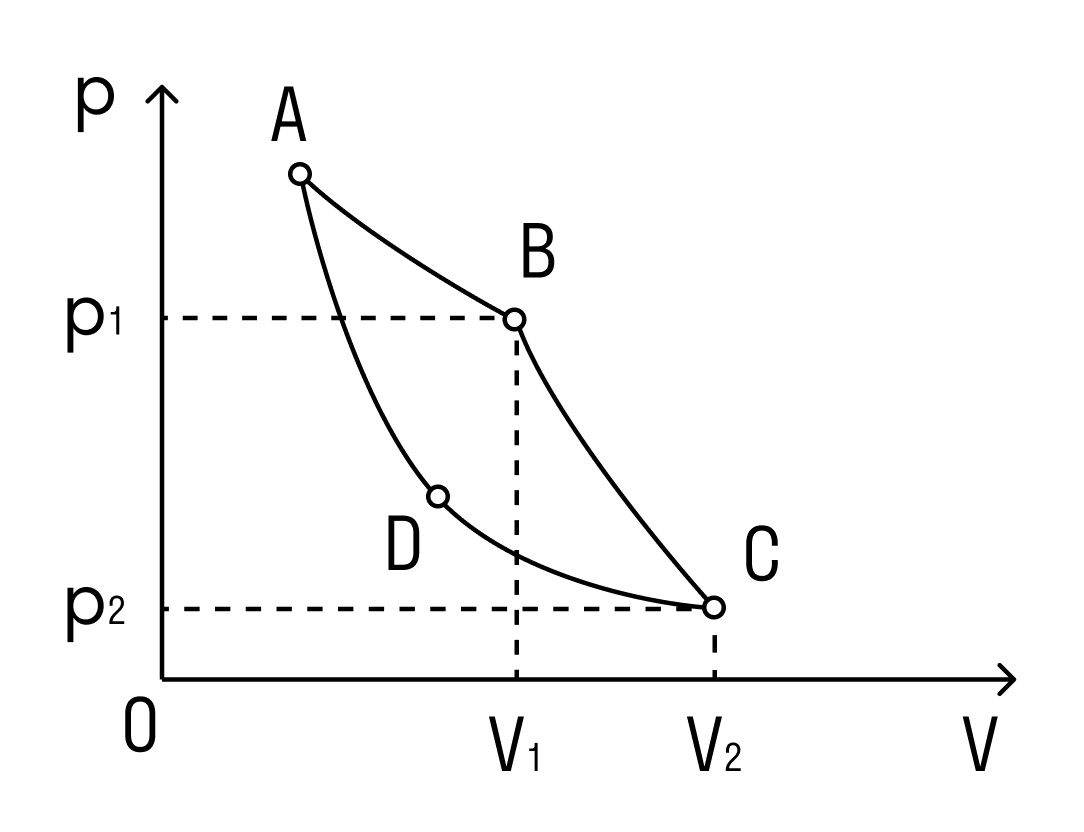
Как этого достичь? Ответ: сжимать газ под меньшими давлениями, чем были в ходе расширения. Иными словами, на -диаграмме процесс сжатия должен идти ниже процесса расширения, т. е. цикл должен проходиться по часовой стрелке (рис. 2).

Рис. 2. Цикл теплового двигателя

Например, в цикле на рисунке работа газа при расширении равна площади криволинейной трапеции . Аналогично, работа газа при сжатии равна площади криволинейной трапеции со знаком минус. В результате работа газа за цикл оказывается положительной и равной площади цикла .

Хорошо, но как заставить газ возвращаться в исходное состояние по более низкой кривой, т. е. через состояния с меньшими давлениями? Вспомним, что при данном объёме давление газа тем меньше, чем ниже температура. Стало быть, при сжатии газ должен проходить состояния с меньшими температурами.

Вот именно для этого и нужен холодильник: чтобы охлаждать газ в процессе сжатия.

Холодильником может служить атмосфера (для двигателей внутреннего сгорания) или охлаждающая проточная вода (для паровых турбин). При охлаждении газ отдаёт холодильнику некоторое количество теплоты .

Суммарное количество теплоты, полученное газом за цикл, оказывается равным . Согласно первому закону термодинамики:

где — изменение внутренней энергии газа за цикл. Оно равно нулю: , так как газ вернулся в исходное состояние (а внутренняя энергия, как мы помним, является функцией состояния). В итоге работа газа за цикл получается равна:

(1)

Как видите, : не удаётся полностью превратить в работу поступающее от нагревателя тепло. Часть теплоты приходится отдавать холодильнику — для обеспечения цикличности процесса.

Показателем эффективности превращения энергии сгорающего топлива в механическую работу служит коэффициент полезного действия теплового двигателя.

КПД теплового двигателя — это отношение механической работы к количеству теплоты , поступившему от нагревателя:

С учётом соотношения (1) имеем также

(2)

КПД теплового двигателя, как видим, всегда меньше единицы. Например, КПД паровых турбин приблизительно , а КПД двигателей внутреннего сгорания около .

к оглавлению ▴

Холодильные машины

Житейский опыт и физические эксперименты говорят нам о том, что в процессе теплообмена теплота передаётся от более нагретого тела к менее нагретому, но не наоборот. Никогда не наблюдаются процессы, в которых за счёт теплообмена энергия самопроизвольно переходит от холодного тела к горячему, в результате чего холодное тело ещё больше остывало бы, а горячее тело — ещё больше нагревалось.

Рис. 3. Холодильная машина

Ключевое слово здесь — «самопроизвольно». Если использовать внешний источник энергии, то осуществить процесс передачи тепла от холодного тела к горячему оказывается вполне возможным. Это и делают холодильные
машины.

По сравнению с тепловым двигателем процессы в холодильной машине имеют противоположное направление (рис. 3).

Рабочее тело холодильной машины называют также хладагентом. Мы для простоты будем считать его газом, который поглощает теплоту при расширении и отдаёт при сжатии (в реальных холодильных установках хладагент — это летучий раствор с низкой температурой кипения, который забирает теплоту в процессе испарения и отдаёт при конденсации).

Холодильник в холодильной машине — это тело, от которого отводится теплота. Холодильник передаёт рабочему телу (газу) количество теплоты , в результате чего газ расширяется.

В ходе сжатия газ отдаёт теплоту более нагретому телу — нагревателю. Чтобы такая теплопередача осуществлялась, надо сжимать газ при более высоких температурах, чем были при расширении. Это возможно лишь за счёт работы , совершаемой внешним источником (например, электродвигателем (в реальных холодильных агрегатах электродвигатель создаёт в испарителе низкое давление, в результате чего хладагент вскипает и забирает тепло; наоборот, в конденсаторе электродвигатель создаёт высокое давление, под которым хладагент конденсируется и отдаёт тепло)). Поэтому количество теплоты, передаваемое нагревателю, оказывается больше количества теплоты, забираемого от холодильника, как раз на величину :

Таким образом, на -диаграмме рабочий цикл холодильной машины идёт против часовой стрелки. Площадь цикла — это работа , совершаемая внешним источником (рис. 4).

Рис. 4. Цикл холодильной машины

Основное назначение холодильной машины — охлаждение некоторого резервуара (например, морозильной камеры). В таком случае данный резервуар играет роль холодильника, а нагревателем служит окружающая среда — в неё рассеивается отводимое от резервуара тепло.

Показателем эффективности работы холодильной машины является холодильный коэффициент, равный отношению отведённого от холодильника тепла к работе внешнего источника:

Холодильный коэффициент может быть и больше единицы. В реальных холодильниках он принимает значения приблизительно от 1 до 3.

Имеется ещё одно интересное применение: холодильная машина может работать как тепловой насос. Тогда её назначение — нагревание некоторого резервуара (например, обогрев помещения) за счёт тепла, отводимого от окружающей среды. В данном случае этот резервуар будет нагревателем, а окружающая среда — холодильником.

Показателем эффективности работы теплового насоса служит отопительный коэффициент, равный отношению количества теплоты, переданного обогреваемому резервуару, к работе внешнего источника:

Значения отопительного коэффициента реальных тепловых насосов находятся обычно в диапазоне от 3 до 5.

к оглавлению ▴

Тепловая машина Карно

Важными характеристиками тепловой машины являются наибольшее и наименьшее значения температуры рабочего тела в ходе цикла. Эти значения называются соответственно температурой нагревателя и температурой холодильника.

Мы видели, что КПД теплового двигателя строго меньше единицы. Возникает естественный вопрос: каков наибольший возможный КПД теплового двигателя с фиксированными значениями температуры нагревателя и температуры холодильника ?

Пусть, например, максимальная температура рабочего тела двигателя равна , а минимальная — . Каков теоретический предел КПД такого двигателя?

Ответ на поставленный вопрос дал французский физик и инженер Сади Карно в 1824 году.

Он придумал и исследовал замечательную тепловую машину с идеальным газом в качестве рабочего тела. Эта машина работает по циклу Карно, состоящему из двух изотерм и двух адиабат.

Рассмотрим прямой цикл машины Карно, идущий по часовой стрелке (рис. 5). В этом случае машина функционирует как тепловой двигатель.

Рис. 5. Цикл Карно

Изотерма . На участке газ приводится в тепловой контакт с нагревателем температуры и расширяется изотермически. От нагревателя поступает количество теплоты и целиком превращается в работу на этом участке: .

Адиабата . В целях последующего сжатия нужно перевести газ в зону более низких температур. Для этого газ теплоизолируется, а затем расширяется адиабатно на учатке .

При расширении газ совершает положительную работу , и за счёт этого уменьшается его внутренняя энергия: .

Изотерма . Теплоизоляция снимается, газ приводится в тепловой контакт с холодильником температуры . Происходит изотермическое сжатие. Газ отдаёт холодильнику количество теплоты и совершает отрицательную работу .

Адиабата . Этот участок необходим для возврата газа в исходное состояние. В ходе адиабатного сжатия газ совершает отрицательную работу , а изменение внутренней энергии положительно: . Газ нагревается до исходной температуры .

Карно нашёл КПД этого цикла (вычисления, к сожалению, выходят за рамки школьной программы):

(3)

Кроме того, он доказал, что КПД цикла Карно является максимально возможным для всех тепловых двигателей с температурой нагревателя и температурой холодильника .

Так, в приведённом выше примере имеем:

В чём смысл использования именно изотерм и адиабат, а не каких-то других процессов?

Оказывается, изотермические и адиабатные процессы делают машину Карно обратимой. Её можно запустить по обратному циклу (против часовой стрелки) между теми же нагревателем и холодильником, не привлекая другие устройства. В таком случае машина Карно будет функционировать как холодильная машина.

Возможность запуска машины Карно в обоих направлениях играет очень большую роль в термодинамике. Например, данный факт служит звеном доказательства максимальности КПД цикла Карно. Мы ещё вернёмся к этому в следующей статье, посвящённой второму закону термодинамики.

к оглавлению ▴

Тепловые двигатели и охрана окружающей среды

Тепловые двигатели наносят серьёзный ущерб окружающей среде. Их повсеместное использование приводит к целому ряду негативных эффектов.

• Рассеяние в атмосферу огромного количества тепловой энергии приводит к повышению температуры на планете. Потепление климата грозит обернуться таянием ледников и катастрофическими бедствиями.
• К потеплению климата ведёт также накопление в атмосфере углекислого газа, который замедляет уход теплового излучения Земли в космос (парниковый эффект).
• Из-за высокой концентрации продуктов сгорания топлива ухудшается экологическая ситуация.

Это — проблемы в масштабе всей цивилизации. Для борьбы с вредными последствиями работы тепловых двигателей следует повышать их КПД, снижать выбросы токсичных веществ, разрабатывать новые виды топлива и экономно расходовать энергию.

22 ноября 2011

Рассмотрим очередные 8 задач B12 из ЕГЭ по математике. Здесь встречаются 2 темы: температура прибора и КПД теплового двигателя. Для разнообразия часть задач, в которых встречаются квадратные уравнения, будем решать через дискриминант (см. урок «Решение квадратных уравнений»), а часть — через формулы Виета (см. урок «Теорема Виета»).

Задача. Зависимость температуры (в градусах Кельвина) от времени (в минутах) для нагревательного элемента некоторого прибора была получении экспериментально и на исследуемом интервале температур дается выражением T(t) = T₀ + at + bt², где T₀ = 340 K, a = 28 К/мин, b = −0,2 К/мин. Известно, что при температурах нагревателя свыше 1000 К прибор может испортиться, поэтому его надо отключать. Определите (в минутах), через какое наибольшее время после начала работы надо отключать прибор.

Все вертится вокруг температуры, которая меняется по закону: T(t) = T₀ + at + bt². Требуется выяснить, в какой момент эта температура пересечет отметку в 1000 К. Поскольку температура T₀, а также коэффициенты a и b нам известны, составим и решим уравнение:

1000 = 340 + 28t − 0,2t²;
0,2t² −28t + 660 = 0 — перенесли все слагаемые влево;
t² − 140t + 3300 = 0 — умножили обе стороны на 5.

Дискриминант: D = 140² − 4 · 1 · 3300 = 6400 = 64 · 100. Очевидно, что корень из дискриминанта равен 80. Корни квадратного уравнения:
t₁ = (140 + 80) : 2 = 110;
t₂ = (140 − 80) : 2 = 30.

Получается, что у нас есть два кандидата на ответ: числа 110 и 30. Требуется найти наибольшее время, и поэтому многие выбирают ответ 110.

Но давайте вспомним, что означают эти числа. Итак, в момент времени t = 30 минут, а также в момент времени t = 110 минут температура пересекает критическую отметку в 1000 К — ту самую, после которой прибор может испортиться. Грубо говоря, прибор испортится через 30 минут и через 110.

Вывод: прибор надо отключить уже через 30 минут, поскольку к 110 минутам он будет давно испорчен.

Задача. Зависимость температуры (в градусах Кельвина) от времени (в минутах) для нагревательного элемента некоторого прибора была получении экспериментально и на исследуемом интервале температур дается выражением T(t) = T₀ + at + bt², где T₀ = 520 K, a = 22 К/мин, b = −0,2 К/мин. Известно, что при температурах нагревателя свыше 1000 К прибор может испортиться, поэтому его надо отключать. Определите (в минутах), через какое наибольшее время после начала работы надо отключать прибор.

Задача полностью аналогична предыдущей — только коэффициенты другие. Предельно допустимую температуру мы знаем, поэтому составим и решим уравнение:

1000 = 520 + 22t − 0,2t²;
0,2t² − 22t + 480 = 0 — собрали все слева;
t² − 110t + 2400 = 0 — умножили обе стороны на 5.

Задача свелась к приведенному квадратному уравнению. По теореме Виета:
t1 + t₂ = −(−110) = 110;
t1 · t₂ = 2400.

Очевидно, корни: 80 и 30, т.к. 80 + 30 = 110; 80 · 30 = 2400. Получаем, что предельная температура будет достигнута через 30 минут и через 80. Следовательно, прибор надо отключить уже через 30 минут.

Задача. Зависимость температуры (в градусах Кельвина) от времени (в минутах) для нагревательного элемента некоторого прибора была получении экспериментально и на исследуемом интервале температур дается выражением T(t) = T₀ + at + bt², где T₀ = 800 K, a = 52 К/мин, b = −0,4 К/мин. Известно, что при температурах нагревателя свыше 2000 К прибор может испортиться, поэтому его надо отключать. Определите (в минутах), через какое наибольшее время после начала работы надо отключать прибор.

Задача аналогична предыдущей, поэтому рассмотрим краткое решение. Именно такой объем вычислений будет достаточным обоснованием ответа в настоящем ЕГЭ по математике.

2000 = 800 + 52t − 0,4t²;
0,4t² − 52t + 1200 = 0;
t² − 130t + 3000 = 0 — разделили все на коэффициент 0,4.

Решаем через дискриминант: D = 130² − 4 · 1 · 3000 = 4900. Корень из дискриминанта: 70. Найдем корни уравнения:
t₁ = (130 + 70) : 2 = 100;
t₂ = (130 − 70) : 2 = 30.

Из двух чисел выбираем наименьшее — это снова число 30.

Задача. Зависимость температуры (в градусах Кельвина) от времени (в минутах) для нагревательного элемента некоторого прибора была получении экспериментально и на исследуемом интервале температур дается выражением T(t) = T₀ + at + bt², где T₀ = 280 K, a = 26 К/мин, b = −0,2 К/мин. Известно, что при температурах нагревателя свыше 1000 К прибор может испортиться, поэтому его надо отключать. Определите (в минутах), через какое наибольшее время после начала работы надо отключать прибор.

Все так же − составляем и решаем уравнение:

1000 = 280 + 26t − 0,2t²;
0,2t² − 26t + 720 = 0 — перенесли все слагаемые в одну сторону;
t² − 130t + 3600 = 0 — умножили каждое слагаемое на 5.

Это приведенное квадратное уравнение, которое хорошо решается по теореме Виета:
t1 + t₂ = −(−130) = 130 = 90 + 40;
t1 · t₂ = 3600 = 90 · 40.

Из приведенных формул очевидно, что корни: 90 и 40. Как и прежде, придется выбрать наименьшей корень — число 40. Потому что до 90 минут прибор уже «не доживет».

Задача. Зависимость температуры (в градусах Кельвина) от времени (в минутах) для нагревательного элемента некоторого прибора была получении экспериментально и на исследуемом интервале температур дается выражением T(t) = T₀ + at + bt², где T₀ = 1100 K, a = 36 К/мин, b = −0,2 К/мин. Известно, что при температурах нагревателя свыше 2000 К прибор может испортиться, поэтому его надо отключать. Определите (в минутах), через какое наибольшее время после начала работы надо отключать прибор.

Снова задача-клон, которая сводится к уравнению:

2000 = 1100 + 36t − 0,2t²;
0,2t² − 36t + 900 = 0;
t² − 180t + 4500 = 0.

Перед нами снова приведенное уравнение. По теореме Виета:
t1 + t₂ = −(−180) = 180 = 150 + 30;
t1 · t₂ = 4500 = 150 · 30.

Теперь корни очевидны — это числа 150 и 30. В ответ пойдет наименьшее число, т.е. прибор надо выключить через 30 минут.

Задача. Коэффициент полезного действия некоторого двигателя определяется формулой:

При каком минимальном значении температуры нагревателя T₁ КПД этого двигателя будет не меньше 60%, если температура холодильника T₂ = 200? Ответ дайте в градусах Кельвина.

Для начала упростим исходную формулу. Умножим обе стороны равенства на переменную T₁, получим:
η · T₁ = (T₁ − T₂) · 100.

Знак процентов мы специально убрали, поскольку в конечном уравнении никаких процентов не может быть — есть только числа. По условию задачи, нам известны КПД η = 60% и температура холодильника T₁ = 200. Подставим эти числа в формулу — получим уравнение:
60 · T₁ = (T₁ − 200) · 100.

Обратите внимание: единицы измерения снова не пишутся. Никаких процентов, никаких градусов Кельвина — только обычные числа. В принципе, аналогично следует поступать во всех задачах B12. Просто до сих пор мы не акцентировали внимание на этом моменте, но с процентами надо работать аккуратно.

Итак, решаем уравнение:
60 · T₁ = (T₁ − 200) · 100;
60T₁ = 100T₁ − 20 000 — раскрыли скобки;
60T₁ − 100T₁ = −20 000 — собрали все слагаемые с T₁ слева;
−40T₁ = −20 000;
T₁ = 500 — разделили все на −40.

Как видим, задача свелась к простому линейному уравнению, которое имеет один корень. Это очень хорошо, поскольку, в отличие от квадратных уравнений, здесь не придется размышлять, какой из корней записать в ответ.

Задача. Коэффициент полезного действия некоторого двигателя определяется формулой:

При каком минимальном значении температуры нагревателя T₁ КПД этого двигателя будет не меньше 60%, если температура холодильника T₂ = 400? Ответ дайте в градусах Кельвина.

Задача полностью аналогична предыдущей. Преобразуем исходную формулу, а затем подставим в нее известные переменные:

η · T₁ = (T₁ − T₂) · 100 — преобразовали формулу;
60 · T₁ = (T₁ − 400) · 100 — подставили числа;
60T₁ − 100T₁ = −40 000 — группируем слагаемые, содержащие переменную T₁;
−40T₁ = −40 000;
T₁ = 1000 — разделили обе стороны на коэффициент −40.

Задача. Коэффициент полезного действия некоторого двигателя определяется формулой:

При каком минимальном значении температуры нагревателя T₁ КПД этого двигателя будет больше 80%, если температура холодильника T₂ = 100? Ответ дайте в градусах Кельвина.

Еще одна задача-клон. Приведу лишь краткое решение:

η · T₁ = (T₁ − T₂) · 100 — преобразованная формула;
80 · T₁ = (T₁ − 100) · 100 — подставили числа;
80T₁ − 100T₁ = −10 000;
−20T₁ = −10 000;
T₁ = 500 — это и есть ответ.

Смотрите также:

1. Упрощаем решение задач с помощью замены переменной
2. Решение задач B12: №440—447
3. Тест к уроку «Что такое логарифм» (тяжелый)
4. Сводный тест по задачам B12 (2 вариант)
5. Как быстро запомнить таблицу синусов и косинусов
6. ЕГЭ 2022, задание 6. Касательная к графику функции

КПД: понятие коэффициента полезного действия

Представьте, что вы пришли на работу в офис, выпили кофе, поболтали с коллегами, посмотрели в окно, пообедали, еще посмотрели в окно — вот и день прошел. Если вы не сделали ни одного дела по работе, то можно считать, что ваш коэффициент полезного действия равен нулю.

В обратной ситуации, когда вы сделали все запланированное — КПД равен 100%.

По сути, КПД — это процент полезной работы от работы затраченной.

Вычисляется по формуле:

Есть такое философское эссе Альбера Камю «Миф о Сизифе». Оно основано на легенде о неком Сизифе, который был наказан за обман. Его приговорили после смерти вечно таскать огромный булыжник вверх на гору, откуда этот булыжник скатывался, после чего Сизиф тащил его обратно в гору. То есть он делал совершенно бесполезное дело с нулевым КПД. Есть даже выражение «Сизифов труд», которое описывает какое-либо бесполезное действие.

Давайте пофантазируем и представим, что Сизифа помиловали и камень с горы не скатился. Тогда, во-первых, Камю бы не написал об этом эссе, потому что никакого бесполезного труда не было. А во-вторых, КПД в таком случае был бы не нулевым.

Полезная работа в этом случае равна приобретенной булыжником потенциальной энергии. Потенциальная энергия прямо пропорционально зависит от высоты: чем выше расположено тело, тем больше его потенциальная энергия. То есть, чем выше Сизиф прикатил камень, тем больше потенциальная энергия, а значит и полезная работа.

Затраченная работа здесь — это механическая работа Сизифа. Механическая работа зависит от приложенной силы и пути, на протяжении которого эта сила была приложена.

Дальше мы просто заменяем полезную и затраченную работы на те величины, которые ими являются.

Давайте разберемся на примере задачи.

Задача

Чтобы вкатить санки массой 4 кг в горку длиной 12 метров, мальчик приложил силу в 15 Н. Высота горки равна 2 м. Найти КПД этого процесса. Ускорение свободного падения принять равным g ≃9,8 м/с²

Запишем формулу КПД.

η = (A_{полезная}/A_{затраченная}) · 100%

Теперь задаем два главных вопроса:

Ради чего все это затеяли?

Чтобы санки в горку поднять — то есть ради приобретения телом потенциальной энергии. Значит в данном процессе полезная работа равна потенциальной энергии санок.

За счет чего процесс происходит?

За счет мальчика, он же тянет санки. Значит затраченная работа равна механической работе

Заменим формуле КПД полезную работу на потенциальную энергию, а затраченную — на механическую работу:

η = E_п/A · 100% = mgh/FS · 100%

Подставим значения:

η = 4 · 9,8 · 2/15 · 12 · 100% = 78,4/180 · 100% ≃ 43,6 %

Ответ: КПД процесса приблизительно равен 43,6%

Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!

КПД в термодинамике

В термодинамике КПД — очень важная величина. Она полностью определяет эффективность такой штуки, как тепловая машина.

• Тепловой двигатель (машина) — это устройство, которое совершает механическую работу циклически за счет энергии, поступающей к нему в ходе теплопередачи.

Схема теплового двигателя выглядит так:

У теплового двигателя обязательно есть нагреватель, который (не может быть!) нагревает рабочее тело, передавая ему количество теплоты Q₁ или Q_{нагревателя} (оба варианта верны, это зависит лишь от учебника, в котором вы нашли формулу).

• Рабочее тело — это тело, на котором завязан процесс (чаще всего это газ или топливо). Оно расширяется при подводе к нему теплоты и сжимается при охлаждении. Часть переданного Q₁ уходит на механическую работу A. Из-за этого производится движение.

Оставшееся количество теплоты Q₂ или Q_{холодильника} отводится к холодильнику, после чего возвращается к нагревателю и процесс повторяется.

КПД такой тепловой машины будет равен:

Если мы выразим полезную (механическую) работу через Q_{нагревателя} и Q_{холодильника}, мы получим:

A = Q_{нагревателя} — Q_{холодильника}.

Подставим в числитель и получим такой вариант формулы.

А возможно ли создать тепловую машину, которая будет работать только за счет охлаждения одного тела?

Точно нет! Если у нас не будет нагревателя, то просто нечего будет передавать на механическую работу. Любой такой процесс — когда энергия не приходит из ниоткуда — означал бы возможность существования вечного двигателя.

Поскольку свидетельств такого процесса в мире не существует, то мы можем сделать вывод: вечный двигатель невозможен. Это второе начало термодинамики.

Запишем его, чтобы не забыть:

Невозможно создать периодическую тепловую машину за счет охлаждения одного тела без изменений в других телах.

Задача

Найти КПД тепловой машины, если рабочее тело получило от нагревателя 20кДж, а отдало холодильнику 10 кДж.

Решение:

Возьмем формулу для расчета КПД:

η = Q_{нагревателя} − Q_{холодильника}/Q_{нагревателя} · 100%

Решать будем в системе СИ, поэтому переведем значения из килоджоулей в джоули и затем подставим в формулу:

η = 20 000 − 10 000/20 000 · 100% = 50%

Ответ: КПД тепловой машины равен 50%.

Идеальная тепловая машина: цикл Карно

Давайте еще чуть-чуть пофантазируем: какая она — идеальная тепловая машина. Кажется, что это та, у которой КПД равен 100%.

На самом деле понятие «идеальная тепловая машина» уже существует. Это тепловая машина, у которой в качестве рабочего тела взят идеальный газ. Такая тепловая машина работает по циклу Карно. Зависимость давления от объема в этом цикле выглядит следующим образом

А КПД для цикла Карно можно найти через температуры нагревателя и холодильника.

КПД в электродинамике

Мы каждый день пользуемся различными электронными устройствами: от чайника до смартфона, от компьютера до робота-пылесоса — и у каждого устройства можно определить, насколько оно эффективно выполняет задачу, для которой оно предназначено, просто посчитав КПД.

Вспомним формулу:

Для электрических цепей тоже есть нюансы. Давайте разбираться на примере задачи.

Задачка, чтобы разобраться

Найти КПД электрического чайника, если вода в нем приобрела 22176 Дж тепла за 2 минуты, напряжение в сети — 220 В, а сила тока в чайнике 1,4 А.

Решение:

Цель электрического чайника — вскипятить воду. То есть его полезная работа — это количество теплоты, которое пошло на нагревание воды. Оно нам известно, но формулу вспомнить все равно полезно 😉

Работает чайник, потому что в розетку подключен. Затраченная работа в данном случае — это работа электрического тока.

То есть в данном случае формула КПД будет иметь вид:

η = Q/A · 100% = Q/UIt · 100%

Переводим минуты в секунды — 2 минуты = 120 секунд. Теперь нам известны все значения, поэтому подставим их:

η = 22176/220 · 1,4 · 120 · 100% = 60%

Ответ: КПД чайника равен 60%.

Давайте выведем еще одну формулу для КПД, которая часто пригождается для электрических цепей, но применима ко всему. Для этого нужна формула работы через мощность:

Подставим эту формулу в числитель и в знаменатель, учитывая, что мощность разная — полезная и затраченная. Поскольку мы всегда говорим об одном процессе, то есть полезная и затраченная работа ограничены одним и тем же промежутком времени, можно сократить время и получить формулу КПД через мощность.

---

---

Коэффициент полезного действия (КПД)

Дата: 2014-10-26

11140

Категория: Физические задачи

Метка: ЕГЭ-№8

27977. Коэффициент полезного действия (КПД) кормозапарника равен отношению количества теплоты, затраченного на нагревание воды массой m_в (в килограммах) от температуры t₁ до температуры t₂ (в градусах Цельсия) к количеству теплоты, полученному от сжигания дров массы m_др кг.  Он определяется формулой               

с_в = 4,2∙10³ (Дж∙К/кг) — теплоёмкость воды

q_др = 8,3∙10⁶ Дж/кг — удельная теплота сгорания дров.

Определите наименьшее количество дров, которое понадобится сжечь в кормозапарнике, чтобы нагреть m_в = 83  воды от 10⁰C до  кипения, если известно, что КПД кормозапарника не больше 21%. Ответ в килограммах.

Необходимо определить наименьшее количество дров m_др. Известно, что КПД не больше 21%, то есть η≤21%. Значит необходимо решить неравенство:

Перечислим известные величины:

t₂ – температура кипения воды 100⁰C

t₁ – начальная температура воды 10⁰C

Подставим их в формулу и найдём m_д:

Масса дров величина положительная, поэтому знак неравенства неизменится:

Наименьшее количество дров, которое понадобится 18 кг.

Ответ: 18

27976. Коэффициент полезного действия (КПД) некоторого двигателя определяется формулой

Т₁ — температура нагревателя (в градусах Кельвина),

Т₂ — температура холодильника (в градусах Кельвина).

При какой минимальной температуре нагревателя Т₁  КПД этого двигателя будет не меньше 15%, если температура холодильника Т₁ = 340 К? Ответ выразите в градусах Кельвина.

По условию необходимо, чтобы КПД  был равен или больше 15%, то есть η ≥ 15%, так как сказано «не меньше 15%». Решение задачи сводится к решению неравенства:

Т₁ величина положительная, поэтому знак неравенства не изменится:

Таким образом, минимальная температура для данных условий работы двигателя 400 градусов Кельвина.

Ответ: 400

Используя этот сайт, Вы соглашаетесь с тем, что мы сохраняем и используем файлы cookies, а также используем похожие технологии для улучшения работы сайта.

Ok