Кофейные аппараты егэ математика - Помощь в подготовке к экзаменам и поступлению

В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

Спрятать решение

Решение.

Рассмотрим события

А = кофе закончится в первом автомате,

В = кофе закончится во втором автомате.

Тогда

A·B = кофе закончится в обоих автоматах,

A + B = кофе закончится хотя бы в одном автомате.

По условию P(A)  =  P(B)  =  0,3; P(A·B)  =  0,12.

События A и B совместные, вероятность суммы двух совместных событий равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения:

P(A + B)  =  P(A) + P(B) − P(A·B)  =  0,3 + 0,3 − 0,12  =  0,48.

Следовательно, вероятность противоположного события, состоящего в том, что кофе останется в обоих автоматах, равна 1 − 0,48  =  0,52.

Ответ: 0,52.

Приведем другое решение.

Вероятность того, что кофе останется в первом автомате, равна 1 − 0,3  =  0,7. Вероятность того, что кофе останется во втором автомате, равна 1 − 0,3  =  0,7. Вероятность того, что кофе останется хотя бы в одном автомате равна 1 − 0,12  =  0,88. Поскольку P(A + B)  =  P(A) + P(B) − P(A·B), имеем: 0,88  =  0,7 + 0,7 − х, откуда искомая вероятность х  =  0,52.

Примечание.

Заметим, что события А и В не являются независимыми. Действительно, вероятность произведения независимых событий была бы равна произведению вероятностей этих событий: P(A·B)  =  0,3·0,3  =  0,09, однако, по условию, эта вероятность равна 0,12.

Источник

В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,25. Вероятность того, что кофе закончится в обоих автоматах, равна 0,1. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

Источники: fipi, Ященко ЕГЭ 2022 (36 вар)

Решение:

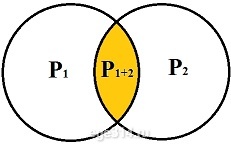
Р₁ = 0,25 кончится в 1-м автомате
Р₂ = 0,25 кончится во 2-м автомате
Р₁₊₂ = 0,1 кончатся и в 1-м и во 2-м автомате

Найдём вероятность того, что кофе закончится или в 1-м автомате, или во 2-м автомате, или в обоих сразу автоматах с учетом совместных событий (вся область внутри двух кругов):

Если сложим Р₁ + Р₂ вероятность Р₁₊₂ посчитается дважды от каждого из автоматов, поэтому один раз её вычитаем:

Р₁ + Р₂ – Р₁₊₂ = 0,25 + 0,25 – 0,1 = 0,4

Полная вероятность, всегда равна 1. Вероятность того, что кофе останется в обоих автоматах обратная тому, что кофе закончится хотя бы в одном автомате:

1 – 0,4 = 0,6

Ответ: 0,6.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 3.5 / 5. Количество оценок: 240

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Источник

Кофейные автоматы егэ математика

Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!

—>

Задание 10 № 320172

А = кофе закончится в первом автомате,

В = кофе закончится во втором автомате.

A·B = кофе закончится в обоих автоматах,

A + B = кофе закончится хотя бы в одном автомате.

По условию P(A) = P(B) = 0,3; P(A·B) = 0,12.

P(A + B) = P(A) + P(B) − P(A·B) = 0,3 + 0,3 − 0,12 = 0,48.

Приведем другое решение.

Вероятность того, что кофе останется в первом автомате, равна 1 − 0,3 = 0,7. Вероятность того, что кофе останется во втором автомате, равна 1 − 0,3 = 0,7. Вероятность того, что кофе останется в первом или втором автомате равна 1 − 0,12 = 0,88. Поскольку P(A + B) = P(A) + P(B) − P(A·B), имеем: 0,88 = 0,7 + 0,7 − Х, откуда искомая вероятность Х = 0,52.

Заметим, что события А и В не являются независимыми. Действительно, вероятность произведения независимых событий была бы равна произведению вероятностей этих событий: P(A·B) = 0,3·0,3 = 0,09, однако, по условию, эта вероятность равна 0,12.

Задание 10 № 320172

—>

А кофе закончится в первом автомате,.

Math-ege. sdamgia. ru

22.08.2018 10:10:05

2018-08-22 10:10:05

Источники:

Https://math-ege. sdamgia. ru/problem? id=320172

Теория вероятности. Готовимся к егэ по математике | Подготовка к ЕГЭ по математике » /> » /> .keyword { color: red; } Кофейные автоматы егэ математика

Теория вероятности. Часть 2

В заданиях ЕГЭ по математике встречаются и более сложные задачи на вероятность (нежели мы рассматривали в части 1), где приходится применять правило сложения, умножения вероятностей, различать совместные и несовместные события.

Совместные и несовместные события

События называются несовместными, если появление одного из них исключает появление других. То есть, может произойти только одно определённое событие, либо другое.

Например, бросая игральную кость, можно выделить такие события, как выпадение четного числа очков и выпадение нечетного числа очков. Эти события несовместны.

События называются совместными, если наступление одного из них не исключает наступления другого.

Например, бросая игральную кость, можно выделить такие события, как выпадение нечетного числа очков и выпадение числа очков, кратных трем. Когда выпадает три, реализуются оба события.

Сумма событий

Суммой (или объединением) нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий.

При этом Сумма двух несовместных событий есть сумма вероятностей этих событий:

Например, вероятность выпадения 5 или 6 очков на игральном кубике при одном броске, будет, потому что оба события (выпадение 5, выпадение 6) неовместны и вероятность реализации одного или второго события вычисляется следующим образом:

Вероятность же Суммы двух совместных событий равна сумме вероятностей этих событий без учета их совместного появления:

Например, в торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдем вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов (то есть или в одном, или в другом, или в обоих сразу).

Вероятность первого события «кофе закончится в первом автомате» также как и вероятность второго события «кофе закончится во втором автомате» по условию равна 0,3. События являются совместными.

Вероятность совместной реализации первых двух событий по условию равна 0,12.

Значит, вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов есть

Зависимые и независимые события

Два случайных события А и В называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. В противном случае события А и В называют зависимыми.

Например, при одновременном броске двух кубиков выпадение на одном из них, скажем 1, и на втором 5, – независимые события.

Произведение вероятностей

Произведением (или пересечением) нескольких событий называется событие, состоящее в совместном появлении всех этих событий.

Если происходят два Независимых события А и В с вероятностями соответственно Р(А) и Р(В), то вероятность реализации событий А и В одновременно равна произведению вероятностей:

Например, нас интересует выпадение на игральном кубике два раза подряд шестерки. Оба события независимы и вероятность реализации каждого из них по отдельности – . Вероятность того, что произойдут оба эти события будет вычисляться по указанной выше формуле: .

Теория вероятности. Часть 2

События называются совместными, если наступление одного из них не исключает наступления другого.

Сумма событий.

Egemaximum. ru

18.04.2018 16:10:13

2018-04-18 16:10:13

Источники:

Https://egemaximum. ru/teoriya-veroyatnosti-chast-2/

Информатика — Задачи на вероятность из ЕГЭ по математике. » /> » /> .keyword { color: red; } Кофейные автоматы егэ математика

Задачи на вероятность из ЕГЭ по математике

Задачи на вероятность из ЕГЭ по математике.

А. В корзине лежат елочные игрушки – 4 шарика разных цветов, красный, синий, зеленый и золотой. Вера наугад достает шарик из корзины. С какой вероятностью она достанет золотой шарик?

Б. В мешке лежат теннисные мячи разных сортов: 45 белых, 35 жёлтых и 20 светло-голубых. С какой вероятностью случайно вынутый из мешка мяч окажется желтым?

В. Для экзамена по информатике есть 30 билетов, в 27 из них встречается вопрос по алгоритмам. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по алгоритмам.

Во всех этих задачах описаны однотипные ситуации. А именно.

1. Совершается определенное действие (можно сказать и так: происходит событие):

А) Вера достает шарик из корзины.
Б) Кто-то достает мячик из мешка.
В) Школьник тащит билет.

2. У событие может быть несколько исходов.

. Все исходы – равно возможны (можно сказать – «равновероятны»).

А) Исход – какой шарик достала Вера. Количество исходов – 4.
Б) Исход – какой мячик достали. Количество исходов – 45+35+20 = 100.
В) Исход – какому билет вытянул школьник. Количество исходов – 30.

3. Некоторые исходы считаются «успешными» (в смысле задачи :), по жизни в таком «успехе» может ничего особенного не быть). Нам важно, сколько есть «успешных» исходов.

А) Успешный исход –Вера достала золотой шарик.
Количество успешных исходов – 1.

Б) Успешный исход – достали желтый мячик.
Количество успешных исходов – 35.

В) Успешный исход – школьник вытянул билет без вопроса по алгоритмам.
Количество успешных исходов – 30-27 = 3.

Вероятность успеха (иными словами – вероятность того, что произойдет один из исходов, которые мы считаем успешными) – это отношение числа успешных исходов к общему числу возможных исходов.

Схематично это можно записать так (знак # заменяет слово «количество»):

Понятно, что вероятность не может быть меньше 0 или больше 1.

4. Таким образом, в задачах получаем такие ответы:

Вот, собственно говоря, и все. В заключение – два важных замечания.

Замечание 1: В основе определения вероятности – предположение о том, что все исходы равноправны (равно возможны). Например, в задаче В школьник не должен знать, что написано в билетах, а Вера не должна подсматривать. В условиях задач на это указывают слова «наугад», «по жребию», и т. п. Иногда таких слов в условии нет, равноправность исходов подразумевается по смыслу (например, в задаче В).

Замечание 2. Разбираясь, что считать исходом в конкретной задаче, нужно следить за тем, чтобы исходы было (по смыслу задачи) равноправны (равновероятны). Например, некто мог бы в задаче Б считать исходом цвет вытащенного мячика. Тогда исходов было бы 3 (белый, желтый, светло-зеленый), из них один успешный. Но эти исходы не равноправны – ведь мячиков разное число.

Упражнение. Вот известный анекдот.

Какова вероятность того, что первый человек, которого ты встретишь, выйдя из дома, будет королева Великобритании

Ответ. Есть 2 исхода – либо королева, либо не королева. Успешный исход – 1. Значит вероятность равна ½ = 0,5 = 50%.

Разберитесь – где в рассуждении ошибка.

2. Как решать задачи

Вероятность находим так.

Разбираемся, что в задаче является исходом и сколько их.

. Следим за тем, чтобы исходы были равновероятными.

2. Разбираемся в том, какие исходы считаются успешными. Находим количество успешных исходов.

3. Находим вероятность – делим количество успехов на количество всех возможных исходов.

При этом не ошибаемся в арифметике и записываем ответ ДЕСЯТИЧНОЙ дробью.

4. Радуемся, что решили задачу 🙂

3. Еще два примера

3.1. На чемпионате по гимнастике выступают 50 спортсменов, среди них 6 спортсменов из Китая. Спортсменам по жребию дали номера – от 1-го до 50-го. Найдите вероятность того, что под номером 37 будет выступать гимнаст из прыгун из Китая.

В этой задаче исход – это спортсмен, которому достался 37-й номер. Всего исходов – 50. То, что говорится о 37-м номере, а не о, скажем, первом нас не смущает. У всех спортсменов равные шансы получить этот номер! Успешных исходов – 6 (спортсмены из Китая). Дальше – сами 🙂

3.2. Завод выпускает часы. В среднем на 1800 качественных часов приходится 200 часов со скрытыми дефектами. Найдите вероятность того, что купленные часы, сделанные на этом заводе, окажутся с дефектом.

В этой задаче – одна тонкость и одна ловушка (несложная).

Тонкость связана со словами «в среднем». По-хорошему, количество исходов, — это количество доступных покупателю часов этого завода. Количество «успехов» — количество доступных ему дефектных часов. Ни того, ни другого мы не знаем. Так в жизни бывает часто.

И часто поступают так.

1) Выбирают наугад достаточно большую группу часов, обозначим ее размер N.

2) Считают количество дефектных часов (т. е. успешных исходов) в этой группе, обозначим его G.

3) Вычисляем вероятность успеха по формуле (P – вероятность):

То есть, мы считаем, что вероятность успеха среди всех исходов (примерно) такая же, как и в выбранном наугад подмножестве всех исходов. Такое предположение выглядит разумно и может быть обосновано (если аккуратно разбираться, что значит «наугад», насколько большое подмножество нужно выбирать и насколько вероятность успеха для множества всех исходов может отличаться от вероятности, подсчитанной по подмножеству).

Слова «в среднем» и означают, что нужно применить такой подход. При этом в выбранном множестве исходов будет 1800 «неуспехов» (качественных часов 🙂 ) и 200 «успехов (дефектных часов). Ловушка в том, что общее количество исходов N здесь не указано. Его нужно подсчитать: N = 1800+200 = 2000. Таким образом, вероятность здесь считается по формуле P = G/N = 200/2000 = 0,1 = 10%/

4. СОбытия, их пересечения, объединения и дополнения.

Вот письмо посетителя сайта http://ege-go. ru/math-ege/b10math/comment-page-1/#comment-1262 : «Помогите, пожалуйста, решить такую задачу.

Задача. В торговом центре два одинаковых автомата продают чай. Вероятность того, что к концу дня в автомате чай закончится, равна 0,4. Вероятность того, что к концу дня чай закончится в обоих автоматах, равна 0,2. Найдите вероятность того, что к концу дня чай останется в обоих автоматах.

Я рассуждаю, что исходя из того, что вероятность не может превышать 1:

1-0,2=0,8 — вероятность, того что чай останется в обоих автоматах. А в ответе 0,4. Не могу понять, где я ошибаюсь.»

Комментарий. Спасибо за письмо! Задача действительно трудная. А трудность в том, чтобы разобраться, что означают слова «вероятность того, что к концу дня в автомате чай закончится»; «вероятность того, что к концу дня чай закончится в обоих автоматах»; «вероятность того, что к концу дня чай останется в обоих автоматах». Я чуть позже разберу задачу на сайте подробно Пока пишу коротко.

Ты ошибаешься вот в чем. Формула 1-0,2=0,8 означает, что события «к концу дня чай закончился в обоих автоматах» и «к концу дня чай остался в обоих автоматах» являются Взаимно дополнительными, то есть в любой день происходит ровно одно из этих событий и они никогда не происходят одновременно. На самом деле, одновременно эти события, конечно произойти не могут, но может не произойти ни одно из них: в одном автомате чай может закончиться, а в другом – нет. Поэтому вероятность того, что к концу дня чай останется в обоих автоматах, заведомо меньше, чем 1-0,2=0,8. Насколько меньше – нужно разбираться.

Решение. Возьмем какой-то день. Для удобства, присвоим автоматам имена A и В. К концу дня может случиться ровно одно из четырех событий (говорят: эти события образуют Полную систему)

1) Чай закончился в обоих автоматах (обозначение: А+В+)

2) Чай закончился в автомате А, но остался в автомате В (обозначение: А+В-)

3) Чай закончился в автомате В, но остался в автомате А (обозначение: А-В+)

4) Чай остался в обоих автоматах (обозначение: А-В-).

Обозначим вероятности этих событий соответственно: Р(А+В+), Р(А+В-), Р(А-В+), Р(А-В-).

Так, как перечисленные события образуют полную систему, то

Р(А+В+) + Р(А+В-) + Р(А-В+) + Р(А-В-) = 1 (1)

Событие «чай закончился в автомате А» — это объединение двух дополнительных событий Р(А+В+) и Р(А+В-). Поэтому

Аналогично, для автомата В получаем:

Наконец, по условию,

Нужную нам вероятность Р(А-В-) находим, решая систему (1)-(4).

Замечание. Чтобы решать такие задачи, нужно уметь свободно рассуждать о Событиях – множествах возможных элементарных исходов. В нашей задаче элементарные исходы – это дни. Например, событие А+В — — это множество всех дней, в которые чай в автомате А закончился, а в автомате В – нет. Про подсчет количества элементов в объединении и пересечении множеств – см. http://ege-go. ru/temy/sets/ .

6 комментариев

Статься очень полезная и помогла мне разобраться с простыми задачами. Но всё равно остались пробелы. Например, я не могу понять как решить такую задачу:
«В двух соседних магазинах «Перекрёсток» и «Пятёрочка» подаются ватрушки с сыром. Вероятность того, что каком-либо магазине закончились ватрушки, — 0,2. Найдите вероятность того, что в «Пятёрочке» ватрушки закончились, а в «Перекрёстке» — ещё нет.
Это задача из пробника по алгебре.
Получается, что вероятность того, что в каком-то магазине ватрушки НЕ закончились равно 0,8 (1-0,2). Или я ошибаюсь?
Большое спасибо, если поможете.

Найдите вероятность того, что под номером 37 будет выступать гимнаст из прыгун из Китая.

Ege-go. ru

05.11.2018 21:30:30

2018-11-05 21:30:30

Источники:

Http://ege-go. ru/b10math-theory/

Источник

В торговом центре два одинаковых автомата

Дата: 2015-03-04

13175

Категория: Вероятность

Метка: ЕГЭ-№3

320172. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

Рассмотрим события. Пусть

А — кофе закончится в первом автомате.

В — кофе закончится во втором автомате.

Обратите внимание, что события А и В не являются несовместными (независимыми). Если бы они были несовместными, то вероятность того, что кофе закончился в обоих автоматах была бы равна 0,03∙0,03 = 0,09. Тогда

А∙В ― кофе закончится в обоих автоматах,

А+В ― кофе закончится хотя бы в одном автомате.

По условию Р(А) = Р (В) = 0,3 Р(А∙В) = 0,12.

Р(А + В) = Р(А) + Р (В) – Р(А∙В) = 0,3 + 0,3 – 0,12 = 0,48.

Все варианты событий, которые могут быть:

НЕ ЗАКОНЧИЛСЯ В ПЕРВОМ ― НЕ ЗАКОНЧИЛСЯ ВО ВТОРОМ

ЗАКОНЧИЛСЯ В ПЕРВОМ ― НЕ ЗАКОНЧИЛСЯ ВО ВТОРОМ

НЕ ЗАКОНЧИЛСЯ В ПЕРВОМ ― ЗАКОНЧИЛСЯ ВО ВТОРОМ

ЗАКОНЧИЛСЯ В ПЕРВОМ ― ЗАКОНЧИЛСЯ ВО ВТОРОМ

Выражению – «кофе закончится хотя бы в одном» соответствуют три события из представленных. Значит, событие «кофе останется в обоих автоматах» противоположно событию «кофе закончится хотя бы в одном». И его вероятность равна 1 – 0,48 = 0,52.

Ответ: 0,52

Используя этот сайт, Вы соглашаетесь с тем, что мы сохраняем и используем файлы cookies, а также используем похожие технологии для улучшения работы сайта.

Источник

Пошаговое объяснение:

цифры дадут 9999 варианто + 1 вариант (0000), т. е. 10000 вариантов.

Теперь разберемся с 32 буквами. Представим их трехзначные сочетания, как число, записанное в 32 ричной системе, где А соответствует цифре 0, а Я соответствует цифре 31 (да, да в 32-ричной системе может есть цифра 31!)

Тогда максимальное число из трех цифр в этой системе будет записано как ЯЯЯ.

Переведем это число в привычную нам десятичную систему счисления:

ЯЯЯ(32) = 31×32² + 31×32¹+31 = 31×(32²+32+1)=32767. По аналогии с 4 цифрами прибавим еще один вариант (ААА), соответствующий нулю в этой системе и получим, сочетание из 3-х букв 32 буквенного алфавита дает нам 32767+1=32768 вариантов. Каждому этому варианту может соответствовать любой из 10000 вариантов из 4 цифр. Поэтому для нахождения общего количества возможных вариантов их надо перемножить:

32768×10000=327680000 возможных вариантов номеров

Введем два события:

А: выбор вопроса по теме «Вписанная окружность»;

B: выбор вопроса по теме «Параллелограмм».

Так как нет вопросов, относящихся одновременно к этим двум темам, то события A и B несовместные. Вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем – это сумма вероятности событий A и B, имеем:

ответ: 0,35.

Т.к. 0,3*0,3 ≠ 0,12, то события «кофе закончится в первом автомате» и «кофе закончится во втором автомате» совместны (т.е. зависимы).

Обозначим событие А = «кофе останется в первом автомате», событие В = «кофе останется во втором автомате». Р(А)=Р(В)= 1-0,3=0,7.

Событие «кофе остался хотя бы в одном автомате» — это объединение событий А U B -событие, противоположное событию «кофе закончится в обоих автоматах).

Р(АUB) = 1-0,12=0,88

С другой стороны » кофе остался хотя бы в одном автомате» означает, что кофе остался или в первом или во втором или в обоих вместе .

Т.е. AUB = AUB U A∩B , тогда Р(AUB) = Р(А) + Р(B) — Р(A∩B)

Р(A∩B) = Р(А) + Р(B) — Р(AUB) = 0,7+0,7 — 0,88 = 0,52

ответ: 0,52

Общаться в чате

1) сдаст оба 0,7*0,3=0,21

2) не сдаст ни одного =такая же вероятность 0,3*0,7=0,21

3)сдаст хотя бы один — это противоположное событию, не сдаст не одного: р(А)=1-0,21=0,79

Поскольку в условии задачи не менее 2 вопросов, то задача распадается на две:

1) студенту попадётся билет с 3-мя вопросами, которые он знает;

2) студенту попадётся билет с 2-мя вопросами, которые он знает.

Решаем 1-ую задачу:

События зависимые:

а — он знает 1 вопрос, благоприятных событий 20 из 25, т.е. Р(а) = 20/25.

в — он знает 2-й вопрос (а известных ему осталось 19 из оставшихся всех 24), т.е Р(в) = 19/24

с — он знает 3-й вопрос (а известных ему осталось 18 из оставшихся всех 23), т.е Р(с) = 18/23

Итак, вероятность того, что студенту достанутся три выученных вопроса) равна

Р(а×в×с) = Р(а)·Р(в)·Р(с) = 20/25 · 19/24 · 18/23 = 57/115.

inghethawh207

Вопрос по алгебре:

В торговом центре два одинаковых автомата продают кофе.Вероятность того, что к концу дня в каком-либо автомате закончится кофе, равна 0.2 независимо от другого автомата. Найдтевеочтноть того,что к концу дня кофе останется в обоих томатах.Помогите пожалуйста!

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

mincant235

1-0.2=0.8 — вероятность что кофе останется в 1 из автоматов.
0.8*0.8=0.64 — вероятность что кофе останется в двух автоматах.

Знаете ответ? Поделитесь им!

Гость ?

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
Использовать мат — это неуважительно по отношению к пользователям;
Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Алгебра.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

4:25ЕГЭ 2017 | Задание 4 | В торговом центре два одинаковых автомата продают кофе … ✘ Школа ПифагораШкола Пифагора ОГЭ и БАЗА

lượt xem 4,6 N6 năm trước

ЕГЭ 2015 (Профильный уровень) Задача #63 из списка пятых заданий Школы Пифагора …

7:15Задание 4 ЕГЭ по математике. Урок 19Valery Volkov

lượt xem 22 N7 năm trước

… ВКонтакте: volkovvalery В торговом центре два одинаковых автомата продают кофе. Вероятность того, что …

2:26В торговом центре два одинаковых автомата продают кофе.Екатерина Игоревна

lượt xem 202Năm trước

В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе …

1:2728.В торговом центре два одинаковых автомата продают кофе.Вероятность того,что к концу дняТамара Остроушко

lượt xem 1,6 N2 năm trước

В торговом центре два одинаковых автомата продают кофе.Вероятность того,что к концу дня в каком либо автомате …

2:22В торговом центре два автомата продают кофе. Вероятность, что в автомате закончится кофе, равна 0,3.Патрик Физматик

lượt xem 346Năm trước

Поддержать автора www.donationalerts.com/r/patrickey В торговом центре два одинаковых автомата продают кофе.

11:00Вероятность на ЕГЭ! Задача на кофеавтоматы???100балльный репетитор

lượt xem 63 N3 năm trước

Узнать подробности и записаться на мои курсы можно тут — vk.cc/cbpGk9 Ищешь крутой контент по другим …

5:24ЕГЭ 4 номер (Теория вероятностей). Разбор задачи про кофейные автоматыИван Абрамов

lượt xem 61010 tháng trước

В торговом центре два одинаковых автомата продают кофе. Обслуживание автоматов происходит по вечерам после …

1:00:08✓ Новая задача на вероятность в ЕГЭ | Задание 10. ЕГЭ-2022. Профильный уровень | Борис ТрушинБорис Трушин

lượt xem 108 N4 tháng trước

0:30:00 В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате …

3:40Теория Вероятностей| Задача на кофеавтоматы с помощью таблицыТатьяна Нарушева

lượt xem 1,4 N2 năm trước

Универсальный метод решения задачи про автоматы с кофе с ПОМОЩЬЮ ТАБЛИЦЫ. еще больше задач на моем …

3:25Теория вероятностей Два одинаковых автомата продают чай 4 вариант Ященко 36 вариантов ФИПИ ЕГЭ 2022Татьяна Нарушева

lượt xem 2184 tháng trước

Задача по теории вероятностей : В торговом центре два одинаковых автомата продают чай. Вероятность, что в автомате …

4:20ЕГЭ 2017 | Задание 4 | В торговом центре … ✘ Школа ПифагораШкола Пифагора ОГЭ и БАЗА

lượt xem 2,4 N7 năm trước

Подпишись! ¯¯/¯¯¯¯¯¯ ☻/ /· / Задача #321 из Списка Пифагора Условие: В торговом центре два одинаковых автомата …

3:44Сложная задача из ЕГЭ 2019 ( Теория вероятностей #11)Данил Лебедев

lượt xem 1,9 N3 năm trước

… обращайтесь Я Вконтакте — d_lebedev0 В торговом центре два одинаковых автомата продают кофе.

12:36Задача 4 ЕГЭ по математике. Урок 25Valery Volkov

lượt xem 13 N8 năm trước

… В торговом центре два одинаковых автомата продают чай. Вероятность того, что к концу дня в автомате закончится чай, …

17:36ЕГЭ задание 4 Задачи на вероятность Что надо знатьСавченко Елена

lượt xem 66310 tháng trước

9:27Совместные и несовместные, зависимые и независимые событияУчиться легко со Славой

lượt xem 7274 tháng trước

7:15Задача про кофейные аппаратыИван Абрамов

lượt xem 52Tháng trước

Решение проблемной задачи на теорию вероятностей В торговом центре два одинаковых автомата продают кофе.

17:34ЕГЭ задание 4 Разные типы задач на вероятностьСавченко Елена

lượt xem 50310 tháng trước

6:37«Вероятность». Задача на Зависимые События. ЕГЭ, Профиль. Математика для гуманитариевegeDoktor

lượt xem 42 tháng trước

В этом видео мы разберем задачу с таким УСЛОВИЕМ: В торговом центре два одинаковых автомата продают кофе.

4:06ЕГЭ 2017. Задание 4. Теория вероятностей. Автоматы в торговом центре. Совместные события.Математика для всех

lượt xem 4,8 N5 năm trước

В торговом центре два одинаковых автомата продают чай. Вероятность того, что к концу дня в автомате закончится чай, …

14:43Задание 4 профильного ЕГЭ по математике. Задача по теории вероятностей про автоматы с кофеРепетитор по математике Инна Леонидовна

lượt xem 2549 tháng trước

0:31Как продают кофе в супермаркетах на МанхеттенеSTUDIO413

lượt xem 2,2 N7 năm trước

8:24Кофейные автоматы (ЕГЭ. Профиль. Задача 4)Сергей Кузин

lượt xem 1602 năm trước

Классическая задача с ЕГЭ, по которой обычно много вопросов. Vk: zormex.

1:01:02ЕГЭ 2022 Ященко 3 вариант ФИПИ школе полный разбор!mrMathlesson Виктор Осипов

lượt xem 20 N3 tháng trước

00:14:03 — В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате …

2:12Теория вероятностей в задачах ОГЭ и ЕГЭ задача №24 #26Андрей Никитин

lượt xem 1,1 N2 năm trước

2:48ЕГЭ Математика профиль Задание 4 #510117Данил Лебедев / Нарезки математики

lượt xem 147Năm trước

2:52ЕГЭ математика Задание 4 #510117Лебедев Данил

lượt xem 80Năm trước

3:03:32Вариант ФИПИ на 100 баллов #20 (математика ЕГЭ профиль)Школа Пифагора ЕГЭ по математике

lượt xem 24 N2 năm trước

Задача 4 — 09:57 В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате …

1:18ЕГЭ математика Задание 4 #320172Лебедев Данил

lượt xem 118Năm trước

25:40РАЗБОР ЕГЭ ПО МАТЕМАТИКЕ 359 ВАРИАНТ ЛАРИН. ЕГЭ ПО МАТЕМАТИКЕ 2022. ПЕРВАЯ ЧАСТЬ 1- 11 ЗАДАНИЯЮлия Гиперболическая

lượt xem 1,4 N5 tháng trước

Разбираю 1- 11 задания 359 варианта ЕГЭ Ларина. задания 12, 14, 15 vnclip.net/video/VUf2RZP7uXo/video.html задание 17 …

5:10Задача про кофейные автоматыГрани

lượt xem 1,1 N5 năm trước

Готовимся к ЕГЭ по математике. Разбор задачи из теории вероятностей про кофейные автоматы.

1:15ЕГЭ Математика профиль Задание 4 #320172Данил Лебедев / Нарезки математики

lượt xem 7Năm trước

36:44урок 3. вероятность,сложнее обычного. задание 10 ЕГЭ 2022Вера Волыхина математика просто

lượt xem 2303 tháng trước

Ященко 36 вариантов ЕГЭ вероятность задание 10 все получится.

1:27ОГЭ Ященко 2015. Вариант 34, задача №19. Ответselfedu

lượt xem 1796 năm trước

В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в каком-либо автомате …

Kế tiếp

Источник