Вероятность того, что новая электрическая кофемашина прослужит больше года, равна $0{,}92$. Вероятность того, что она прослужит больше двух лет, равна $0{,}85$. Найдите вероятность того, что она прослужит меньше двух лет, но больше года.
Заметим, что из событий «кофемашина прослужит меньше года», «кофемашина прослужит от 1 до 2 лет» и «кофемашина прослужит больше двух лет» произойдёт обязательно ровно одно, то есть, говоря математическим языком, они попарно несовместны, а их объединение — достоверное событие. Следовательно, сумма вероятностей этих событий равна 1.
При этом события «кофемашина прослужит меньше года» и «кофемашина прослужит больше года» противоположны, поэтому вероятность события «кофемашина прослужит меньше года» равна 1 — 0.92 = 0.08. Заполним таблицу.
| Событие | Прослужит меньше года | Прослужит от 1 до 2 лет | Прослужит больше двух лет |
| Вероятность | 0.08 | ? | 0.85 |
Отсюда искомая вероятность равна 1 — 0.08 — 0.85 = 0.07.
Ответ: 0.07
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Спрятать решение
Решение.
Рассмотрим события
А = кофе закончится в первом автомате,
В = кофе закончится во втором автомате.
Тогда
A·B = кофе закончится в обоих автоматах,
A + B = кофе закончится хотя бы в одном автомате.
По условию P(A) = P(B) = 0,3; P(A·B) = 0,12.
События A и B совместные, вероятность суммы двух совместных событий равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения:
P(A + B) = P(A) + P(B) − P(A·B) = 0,3 + 0,3 − 0,12 = 0,48.
Следовательно, вероятность противоположного события, состоящего в том, что кофе останется в обоих автоматах, равна 1 − 0,48 = 0,52.
Ответ: 0,52.
Приведем другое решение.
Вероятность того, что кофе останется в первом автомате, равна 1 − 0,3 = 0,7. Вероятность того, что кофе останется во втором автомате, равна 1 − 0,3 = 0,7. Вероятность того, что кофе останется хотя бы в одном автомате равна 1 − 0,12 = 0,88. Поскольку P(A + B) = P(A) + P(B) − P(A·B), имеем: 0,88 = 0,7 + 0,7 − х, откуда искомая вероятность х = 0,52.
Примечание.
Заметим, что события А и В не являются независимыми. Действительно, вероятность произведения независимых событий была бы равна произведению вероятностей этих событий: P(A·B) = 0,3·0,3 = 0,09, однако, по условию, эта вероятность равна 0,12.
Тема 3.
Введение в теорию вероятностей
3
.
03
Сумма вероятностей совместных событий
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
введение в теорию вероятностей
3.01Вероятность как отношение «подходящих» исходов ко всем исходам
3.02Сумма вероятностей несовместных событий
3.03Сумма вероятностей совместных событий
3.04Произведение вероятностей независимых событий
Решаем задачу:
В торговом центре есть три одинаковых кофейных автомата. Вероятность того, что к концу дня в кофейном автомате закончится
кофе, равна Вероятность того, что к концу дня кофе закончится во всех трех кофейных автоматах, равна
Какова
вероятность того, что к концу дня в торговом центре еще можно выпить кофе, но в первом автомате весь кофе
закончился?
Показать ответ и решение
У каждого автомата есть два исхода: кофе в нем закончился (будем обозначать «»), и кофе в нем остался (будем обозначать
«»). По условию вероятность того, что в первом автомате кофе закончился, равна 0,3. Заметим, что в событие «в первом
автомате закончился кофе» входят следующие элементарные исходы:
1) когда во втором и в третьем автоматах тоже нет кофе
2) когда во втором и третьем автоматах есть кофе
3) когда только во втором автомате остался кофе
4) когда толька в третьем автомате остался кофе
Также по условию вероятность того, что во всех автоматах нет кофе равна 0,05.
Тогда вероятность того, что в первом автомате кофе закончился, а во втором или в третьем еще есть кофе, то есть
вероятность события равна
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,25. Вероятность того, что кофе закончится в обоих автоматах, равна 0,1. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Источники: fipi, Ященко ЕГЭ 2022 (36 вар)
Решение:
Р1 = 0,25 кончится в 1-м автомате
Р2 = 0,25 кончится во 2-м автомате
Р1+2 = 0,1 кончатся и в 1-м и во 2-м автомате
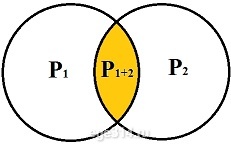
Найдём вероятность того, что кофе закончится или в 1-м автомате, или во 2-м автомате, или в обоих сразу автоматах с учетом совместных событий (вся область внутри двух кругов):
Если сложим Р1 + Р2 вероятность Р1+2 посчитается дважды от каждого из автоматов, поэтому один раз её вычитаем:
Р1 + Р2 – Р1+2 = 0,25 + 0,25 – 0,1 = 0,4
Полная вероятность, всегда равна 1. Вероятность того, что кофе останется в обоих автоматах обратная тому, что кофе закончится хотя бы в одном автомате:
1 – 0,4 = 0,6
Ответ: 0,6.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 3.5 / 5. Количество оценок: 240
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Задачи про кофе в автоматах. Совместные (зависимые) события в теории вероятностей..
создана: 16.04.2020 в 21:46
…………………………………………
liliana :
В торговом центре два разных автомата продают кофе. Вероятность того, что к концу дня
закончится кофе в первом автомате, равна 0,32, что закончится кофе во втором
автомате — 0,24. Вероятность того, что закончится кофе в обоих автоматах, равна 0,133.
Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Решение.
Т.к. 0,32*0,24 ≠ 0,133, то события А=»кофе закончится в первом автомате»
и В=»кофе закончится во втором автомате» совместны (зависимы).
Событие А*В =»Кофе закончится в обоих автоматах»
Р(А)*Р(В) ≠ Р(А*В)
В этом случае Р = Р(не А) + Р(не В) — Р(не А*В)
P= (1-0,32)+(1-0,24) — (1-0,133) = 0,68 + 0,76 — 0,867 = 0,573
Ответ: 0,573

Современная техника все знает, все умеет и многие действия выполняет практически или полностью без участия пользователя. Вы наверняка много слышали о кофейных машинах, которые автоматически не только варят кофе, но и подбирают программы, чистятся, моются, оповещают о том, что вода практически закончилась или нужно добавить зерен. Это общие моменты, поэтому мы предлагаем вам рассмотреть возможности современных кофейных аппаратов на примере техники производства концерна Bosch.
Вкусный эспрессо? Проще простого!
Кофейный автомат TCA5309 производства Бош в очередной раз доказывает, что с прогрессивной техникой не бывает ничего сложного – приготовление эспрессо с использованием данного агрегата не создаст лишних проблем. Насыщенный, богатый вкус напитка обеспечивается благодаря предварительному смачиванию кофейного порошка – данная система носит название Aroma Whirl и позволяет по максимуму извлекать из зерен полезные экстрактивные вещества. Хочется капучино? В модели есть капучинатор, который позволяет использовать теплое молоко для создания любых кофейных напитков и взбивать пенку для капучино буквально в два счета. Что еще хорошего есть в данной машине? Ну, конечно же, простое управление – всего 4 кнопки, вот и все настройки, а также исключительная надежность – ремонт Бош на практике требуется крайне редко.
Стиль, шик и простое использование
Отдельного внимания заслуживает модель БОШ TES50129RW. Выполненная в корпусе черного цвета, она имеет привлекательный лаконичный дизайн и, конечно, потрясающий функционал. Приобретая данное устройство, вы можете рассчитывать на:
- — полуавтоматический капучинатор – простой, удобный в использовании и позволяющий контролировать уровень получаемой молочной пены;
- — особую систему нагрева воды, которую еще можно назвать «умной» — она обеспечивает полноценный аромат готового напитка благодаря подбору идеальной температуры заваривания;
- — полуавтоматический капучинатор MilkMagic – он допускает взбивание пенки прямо в чашке;
- — керамическую мельницу – это и шик, и безупречное качество помола.
Дополнительное преимущество – модель не только красиво выглядит и является исключительно функциональной, но и проста в управлении, а значит, долго осваивать ее вам не придется.
Что еще? На рынке представлено огромное множество разных моделей известного бренда. Широкий ценовой диапазон позволит вам подобрать решение по душе и карману.
21.02.2015
Задание:
В торговом центре два одинаковых автомата продают чай. Вероятность того, что к концу дня в автомате закончится чай, равна 0,4. Вероятность того, что чай закончится в обоих автоматах, равна 0,2. Найдите вероятность того, что к концу дня чай останется в обоих автоматах.
Решение:
Пусть A — событие, что в первом автомате закончился чай.
Пусть B — событие, что во втором автомате закончился чай.Соответственно:
P(A) — вероятность того, что в первом автомате закончится чай. P(A) = 0.4 — по условию задачи.
P(B) — вероятность того, что во втором автомате закончится чай. P(B) = 0.4 — по условию задачи.
P(AB) — вероятность того, что чай закончится в обоих автоматах. P(AB) = 0.2 — по условию.
События A и B являются совместными, то есть появление одного из них не исключает появления другого в одном и том же испытании. Следовательно воспользуемся формулой сложения вероятностей:
P(A + B) = P(A) + P(B) — P(AB)
Подставляем:
P(A + B) = 0.4 + 0.4 — 0.2 = 0.6 (вероятность того, что к концу дня чая не останется в обоих автоматах)
А значит вероятность того, что
к концу дня чай останется в обоих автоматах равна:
1 — P(A + B) = 1 — 0.6 = 0.4
Ответ: 0.4
ЕГЭ Профиль №9. Задачи на работу
Скачать файл в формате pdf.
ЕГЭ Профиль №9. Задачи на работу
| Задача 1. Заказ на 110 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 1 деталь больше?
Пусть x дет/ч делает второй рабочий, тогда (x + 1) дет/ч делает первый рабочий.
Первый рабочий на изготовление 110 деталей тратит на 1 час меньше. Следовательно: (frac{{110}}{x} — frac{{110}}{{x + 1}} = 1,,,, Leftrightarrow ,,,,frac{{110left( {x + 1} right) — 110x}}{{xleft( {x + 1} right)}} = 1,,,, Leftrightarrow ,,,,frac{{110}}{{xleft( {x + 1} right)}} = 1,,,, Leftrightarrow ,,,,,xleft( {x + 1} right) = 110,,,, Leftrightarrow ) ( Leftrightarrow ,,,,{x^2} + x — 110 = 0,;,,,,,,,,,D = 1 + 4 cdot 110 = 441;) ({x_1} = frac{{ — 1 + 21}}{2} = 10;,,,,{x_2} = frac{{ — 1 — 21}}{2} = — 11.) Так как (x > 0), то второй рабочий делает 10 деталей в час. Ответ: 10. |
||||||||||||
| Задача 2. На изготовление 475 деталей первый рабочий тратит на 6 часов меньше, чем второй рабочий на изготовление 550 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей в час делает первый рабочий?
Пусть x дет/ч делает первый рабочий, тогда (x — 3) дет/ч делает второй рабочий.
Первый рабочий тратит на 6 часов меньше. Следовательно: (frac{{550}}{{x — 3}} — frac{{475}}{x} = 6,,,, Leftrightarrow ,,,,frac{{550x — 475left( {x — 3} right)}}{{xleft( {x — 3} right)}} = 6,,,, Leftrightarrow ,,,,frac{{550x — 475x + 475 cdot 3}}{{xleft( {x — 3} right)}} = 6,,,, Leftrightarrow ,,,,) (6xleft( {x — 3} right) = 75x + 475 cdot 3,,left| {,:,} right.3,,,, Leftrightarrow ,,,,2{x^2} — 6x = 25x + 475,,,, Leftrightarrow ,,,,2{x^2} — 31x — 475 = 0;) (D = 961 + 8 cdot 475 = 4761;,,,,,,,,sqrt D = 69;) ({x_1} = frac{{31 + 69}}{4} = 25;,,,,{x_2} = frac{{31 — 69}}{4} = — frac{{19}}{2}.) Так как (x > 3), то первый рабочий делает 25 деталей за час. Ответ: 25. |
||||||||||||
| Задача 3. Двое рабочих, работая вместе, могут выполнить работу за 12 дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за два дня выполняет такую же часть работы, какую второй — за три дня?
Пусть первый рабочий, работая отдельно, выполнил работу за х дней. Так как второй рабочий за 3 дня выполняет такую часть работы, которую первый за 2 дня, то он выполнит всю работу за (frac{3}{2}x) дней. Пусть объём равен А:
Работая вместе, то есть с общей производительностью (frac{A}{x} + frac{{2A}}{{3x}}), рабочие выполняют всю работу (А) за 12 дней. Следовательно: (left( {frac{A}{x} + frac{{2A}}{{3x}}} right) cdot 12 = A,,,, Leftrightarrow ,,,,frac{{3A + 2A}}{{3x}} cdot 12 = A,,,, Leftrightarrow ,,,,frac{{5A cdot 4}}{x} = A,,,left| {:A} right.,,,,,, Leftrightarrow ,,,,,,,frac{{20}}{x} = 1,,,, Leftrightarrow ,,,,x = 20.) Таким образом, первый рабочий, работая отдельно, выполнит работу за 20 дней. Ответ: 20. |
||||||||||||
| Задача 4. Первая труба пропускает на 1 литр воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 110 литров она заполняет на 1 минуту дольше, чем вторая труба?
Пусть первая труба пропускает x литров в минуту, тогда вторая пропускает (x + 1) литр в минуту.
Первая труба тратит на 1 мин больше чем вторая. Следовательно: (frac{{110}}{x} — frac{{110}}{{x + 1}} = 1,,,, Leftrightarrow ,,,,frac{{110left( {x + 1} right) — 110x}}{{xleft( {x + 1} right)}} = 1,,,, Leftrightarrow ,,,,frac{{110}}{{xleft( {x + 1} right)}} = 1,,,, Leftrightarrow ,,,,,xleft( {x + 1} right) = 110,,,, Leftrightarrow ) ( Leftrightarrow ,,,,{x^2} + x — 110 = 0,,,,,,,,,,D = 1 + 4 cdot 110 = 441;) ({x_1} = frac{{ — 1 + 21}}{2} = 10;,,,,{x_2} = frac{{ — 1 — 21}}{2} = — 11.) Так как (x > 0), то первая труба пропускает 10 литров в минуту. Ответ: 10. |
||||||||||||
| Задача 5. Первая труба пропускает на 1 литр воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 110 литров она заполняет на 2 минуты дольше, чем вторая труба заполняет резервуар объемом 99 литров?
Пусть первая труба пропускает x литров в минуту, тогда вторая пропускает (x + 1) литр в минуту.
Первая труба тратит на 2 минуты больше чем вторая. Следовательно: (frac{{110}}{x} — frac{{99}}{{x + 1}} = 2,,,, Leftrightarrow ,,,,frac{{110left( {x + 1} right) — 99x}}{{xleft( {x + 1} right)}} = 2,,,, Leftrightarrow ,,,,frac{{110x + 110 — 99x}}{{xleft( {x + 1} right)}} = 2,,,, Leftrightarrow ,,,,,) ( Leftrightarrow ,,,,2xleft( {x + 1} right) = 11x + 110,,,, Leftrightarrow ,,,,2{x^2} + 2x = 11x + 110,,,,, Leftrightarrow ,,,,2{x^2} — 9x — 110 = 0) (D = 81 + 8 cdot 110 = 961;,,,,,,,{x_1} = frac{{9 + 31}}{4}, = 10;,,,,,{x_2} = frac{{9 — 31}}{4} = — frac{{11}}{2}.) Так как (x > 0), то первая труба пропускает 10 литров в минуту. Ответ: 10. |
||||||||||||
| Задача 6. Первая труба пропускает на 5 литров воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объемом 375 литров она заполняет на 10 минут быстрее, чем первая труба заполняет резервуар объемом 500 литров?
Пусть вторая труба пропускает x литров в минуту, тогда первая пропускает (x — 5) литров в минуту.
Первая труба тратит на 10 минут больше чем вторая. Следовательно: (frac{{500}}{{x — 5}} — frac{{375}}{x} = 10,,,, Leftrightarrow ,,,,frac{{500x — 375left( {x — 5} right)}}{{xleft( {x — 5} right)}} = 10,,,, Leftrightarrow ,,,,frac{{500x — 375x + 375 cdot 5}}{{xleft( {x — 5} right)}} = 10,,,, Leftrightarrow ) ( Leftrightarrow ,,,,,10xleft( {x — 5} right) = 125x + 375 cdot 5,,left| {,:} right.,5,,,, Leftrightarrow ,,,,2{x^2} — 10x = 25x + 375,,,, Leftrightarrow ,,,,2{x^2} — 35x — 375 = 0;) (D = {35^2} + 8 cdot 375 = {5^2} cdot {7^2} + 8 cdot {5^2} cdot 15 = {5^2}left( {49 + 120} right) = {5^2} cdot 169;,,,,,,,,,,sqrt D = 5 cdot 13 = 65;) ({x_1} = frac{{35 + 65}}{4}, = 25;,,,,,{x_2} = frac{{35 — 65}}{4} = — frac{{15}}{2}.) Так как (x > 0), то вторая труба пропускает 25 литров в минуту. Ответ: 25. |
||||||||||||
| Задача 7. Каждый из двух рабочих одинаковой квалификации может выполнить заказ за 15 часов. Через 3 часа после того, как один из них приступил к выполнению заказа, к нему присоединился второй рабочий, и работу над заказом они довели до конца уже вместе. Сколько часов потребовалось на выполнение всего заказа?
После 3 часов работы первому на выполнение заказа осталось работать ещё 12 часов, но так как к нему присоединился второй рабочий, и они стали работать вместе, то им на завершение заказа потребуется 6 часов. Следовательно, заказ будет выполнен за 3 + 6 = 9 часов. Ответ: 9. |
||||||||||||
| Задача 8. Один мастер может выполнить заказ за 12 часов, а другой — за 6 часов. За сколько часов выполнят заказ оба мастера, работая вместе?
Первый мастер за 1 час выполняет (frac{1}{{12}}) часть работы, а второй (frac{1}{6}). Следовательно, работая вместе, два мастера выполняют (frac{1}{{12}} + frac{1}{6} = frac{1}{4}) часть работы. Поэтому всю работу мастера выполнят за 4 часа. Ответ: 4. Замечание: Выведем формулу для совместной работы двух рабочих. Пусть первый рабочий может выполнить работу А за время ({t_1}), а второй за время ({t_2}). Тогда производительность первого рабочего ({W_1} = frac{A}{{{t_1}}}), второго ({W_2} = frac{A}{{{t_2}}}). Следовательно, при совместной работе их общая производительность будет равна: (frac{A}{{{t_1}}} + frac{A}{{{t_2}}}). Пусть ({t_{совм}}) — время за которое будет выполнена работа А при совместной работе. Тогда (frac{A}{{{t_{совм}}}}) будет общая производительность двух рабочих, которая равна (frac{A}{{{t_1}}} + frac{A}{{{t_2}}}), то есть: (frac{A}{{{t_1}}} + frac{A}{{{t_2}}} = frac{A}{{{t_{совм}}}}). Сократив на А, получим: (frac{1}{{{t_1}}} + frac{1}{{{t_2}}} = frac{1}{{{t_{совм}}}}). Если работа выполняется тремя субъектами за время ({t_1}), ({t_2}) и ({t_3}) соответственно, то время совместного выполнения того же объёма работы равно: (frac{1}{{{t_1}}} + frac{1}{{{t_2}}} + frac{1}{{{t_3}}} = frac{1}{{{t_{совм}}}}). Так как первый рабочий выполняет заказ за 12 часов, а второй за 6 часов, то ({t_1} = 12), ({t_2} = 6). Тогда: (frac{1}{{12}} + frac{1}{6} = frac{1}{{{t_{совм}}}},,,,,, Leftrightarrow ,,,,,frac{1}{4} = frac{1}{{{t_{совм}}}},,,,,, Leftrightarrow ,,,,,,{t_{совм}} = 4). |
||||||||||||
| Задача 9. Первый насос наполняет бак за 20 минут, второй — за 30 минут, а третий — за 1 час. За сколько минут наполнят бак три насоса, работая одновременно?
Воспользуемся формулой: (frac{1}{{{t_1}}} + frac{1}{{{t_2}}} + frac{1}{{{t_3}}} = frac{1}{{{t_{совм}}}}) (смотри замечание к задаче 8). В данном случае ({t_1} = 20) минут, ({t_2} = 30) минут, ({t_3} = 1) час = 60 минут: (frac{1}{{20}} + frac{1}{{30}} + frac{1}{{60}} = frac{1}{{{t_{совм}}}},,,,, Leftrightarrow ,,,,,frac{{3 + 2 + 1}}{{60}} = frac{1}{{{t_{совм}}}},,,,,, Leftrightarrow ,,,,,frac{6}{{60}} = frac{1}{{{t_{совм}}}},,,,, Leftrightarrow ,,,,,,{t_{совм}} = 10). Ответ: 10. |
| Задача 10. Игорь и Паша красят забор за 9 часов. Паша и Володя красят этот же забор за 12 часов, а Володя и Игорь — за 18 часов. За сколько часов мальчики покрасят забор, работая втроем?
Пусть Игорь, Паша и Володя каждый покрасят забор за время ({t_1}), ({t_2}) и ({t_3})соответственно. Воспользуемся формулой: (frac{1}{{{t_1}}} + frac{1}{{{t_2}}} = frac{1}{{{t_{совм}}}}) (смотри замечание к задаче 8). Тогда получим систему уравнений: (left{ {begin{array}{*{20}{c}} {frac{1}{{{t_1}}} + frac{1}{{{t_2}}} = frac{1}{9};} \ {frac{1}{{{t_2}}} + frac{1}{{{t_3}}} = frac{1}{{12}};} \ {frac{1}{{{t_1}}} + frac{1}{{{t_3}}} = frac{1}{{18.}}} end{array}} right.) Прибавим к первому уравнению второе и третье: (frac{2}{{{t_1}}} + frac{2}{{{t_2}}} + frac{2}{{{t_3}}} = frac{1}{9} + frac{1}{{12}} + frac{1}{{18}},,,,, Leftrightarrow ,,,,,frac{2}{{{t_1}}} + frac{2}{{{t_2}}} + frac{2}{{{t_3}}} = frac{1}{4},left| {,:2,,,,, Leftrightarrow } right.,,,,,frac{1}{{{t_1}}} + frac{1}{{{t_2}}} + frac{1}{{{t_3}}} = frac{1}{8}.) Так как спрашивают, за сколько часов мальчики покрасят забор, работая втроем, то: (frac{1}{{{t_1}}} + frac{1}{{{t_2}}} + frac{1}{{{t_3}}} = frac{1}{{{t_{совм}}}}). Следовательно: (frac{1}{{{t_{совм}}}} = frac{1}{8},,,,, Leftrightarrow ,,,,,,{t_{совм}} = 8.) Ответ: 8. |
||||||||||||
| Задача 11. Даша и Маша пропалывают грядку за 12 минут, а одна Маша — за 20 минут. За сколько минут пропалывает грядку одна Даша?
Воспользуемся формулой: (frac{1}{{{t_1}}} + frac{1}{{{t_2}}} = frac{1}{{{t_{совм}}}}) (смотри замечание к задаче 8). Пусть ({t_1} = 20) минут время, за которое Маша пропалывает грядку, а ({t_2}) – время за которое Даша. При этом ({t_{совм}} = 12) минут. (frac{1}{{20}} + frac{1}{{{t_2}}} = frac{1}{{12}},,,,, Leftrightarrow ,,,,,frac{1}{{{t_2}}} = frac{1}{{12}} — frac{1}{{20}},,,,, Leftrightarrow ,,,,frac{1}{{{t_2}}} = frac{1}{{30}},,,,,, Leftrightarrow ,,,,,{t_2} = 30) минут. Ответ: 30. |
||||||||||||
| Задача 12. Две трубы наполняют бассейн за 3 часа 36 минут, а одна первая труба наполняет бассейн за 6 часов. За сколько часов наполняет бассейн одна вторая труба?
Воспользуемся формулой: (frac{1}{{{t_1}}} + frac{1}{{{t_2}}} = frac{1}{{{t_{совм}}}}) (смотри замечание к задаче 8). Пусть ({t_1} = 6) часов время, за которое первая труба наполняет бассейн, а ({t_2}) – время второй трубы. При этом ({t_{совм}} = 3) часа 36 минут = (3frac{{36}}{{60}}) часа = (frac{{18}}{5}) часа. (frac{1}{6} + frac{1}{{{t_2}}} = frac{5}{{18}},,,, Leftrightarrow ,,,,frac{1}{{{t_2}}} = frac{5}{{18}} — frac{1}{6},,,,, Leftrightarrow ,,,,frac{1}{{{t_2}}} = frac{1}{9},,,,, Leftrightarrow ,,,,{t_2} = 9) часов. Ответ: 9. |
||||||||||||
| Задача 13. Первая труба наполняет резервуар на 6 минут дольше, чем вторая. Обе трубы наполняют этот же резервуар за 4 минуты. За сколько минут наполняет этот резервуар одна вторая труба?
Воспользуемся формулой: (frac{1}{{{t_1}}} + frac{1}{{{t_2}}} = frac{1}{{{t_{совм}}}}) (смотри замечание к задаче 8). Пусть x – минут время, за которое вторая труба наполняет резервуар, а x + 6 минут время первой трубы. При этом ({t_{совм}} = 4) минуты: (frac{1}{{x + 6}} + frac{1}{x} = frac{1}{4},,,,, Leftrightarrow ,,,,,,frac{{x + x + 6}}{{xleft( {x + 6} right)}} = frac{1}{4},,,,, Leftrightarrow ,,,,{x^2} + 6x = 4left( {2x + 6} right),,,, Leftrightarrow ,,,,,{x^2} — 2x — 24 = 0;) (D = 4 + 4 cdot 24 = 100;,,,,,,{x_1} = frac{{2 + 10}}{2} = 6;,,,,,{x_2} = frac{{2 — 10}}{2} = — 4.) Так как (x > 0), то вторая труба наполнит резервуар за 6 минут. Ответ: 6. |
||||||||||||
| Задача 14. В помощь садовому насосу, перекачивающему 5 литров воды за 2 минуты, подключили второй насос, перекачивающий тот же объем воды за 3 минуты. Сколько минут эти два насоса должны работать совместно, чтобы перекачать 25 литров воды?
Первый нанос перекачивает (frac{5}{2}) л/мин, а второй (frac{5}{3}) л/мин. Тогда вместе они перекачивают (frac{5}{2} + frac{5}{3} = frac{{25}}{6}) л/мин. Следовательно, 25 литров они перекачают за (25:frac{{25}}{6} = 6) минут. Ответ: 6. |
||||||||||||
| Задача 15. Петя и Ваня выполняют одинаковый тест. Петя отвечает за час на 8 вопросов текста, а Ваня — на 9. Они одновременно начали отвечать на вопросы теста, и Петя закончил свой тест позже Вани на 20 минут. Сколько вопросов содержит тест?
Пусть тест содержит х вопросов.
Так как Петя закончил свой тест на 20 минут ((frac{1}{3}) часа) позже Вани, то: (frac{x}{8} — frac{x}{9} = frac{1}{3},,,, Leftrightarrow ,,,,frac{x}{{72}} = frac{1}{3},,,,, Leftrightarrow ,,,,x = 24.) Следовательно, тест содержит 24 вопроса. Ответ: 24. |
||||||||||||
| Задача 16. Плиточник должен уложить 175 м2 плитки. Если он будет укладывать на 10 м2 в день больше, чем запланировал, то закончит работу на 2 дня раньше. Сколько квадратных метров плитки в день планирует укладывать плиточник?
Пусть плиточник планирует укладывать х м2 плитки в день.
Следовательно: (frac{{175}}{x} — frac{{175}}{{x + 10}} = 2,,,, Leftrightarrow ,,,,frac{{175left( {x + 10} right) — 175x}}{{xleft( {x + 10} right)}} = 2,,,, Leftrightarrow ,,,,frac{{175 cdot 10}}{{xleft( {x + 10} right)}} = 2,,,, Leftrightarrow ) ( Leftrightarrow ,,,,2xleft( {x + 10} right) = 175 cdot 10,,left| {,:} right.2,,,, Leftrightarrow ,,,,{x^2} + 10x — 875 = 0) (D = 100 + 4 cdot 875 = 3600;,,,,,{x_1} = frac{{ — 10 + 60}}{2} = 25;,,,,,{x_2} = frac{{ — 10 — 60}}{2} = — 35.) Так как (x > 0), то плиточник планировал укладывать 25 м2 плитки в день. Ответ: 25. |
||||||||||||
| Задача 17. Первый и второй насосы наполняют бассейн за 9 минут, второй и третий — за 14 минут, а первый и третий — за 18 минут. За сколько минут эти три насоса заполнят бассейн, работая вместе?
Пусть первый, второй и третий насосы заполняют бассейн за время ({t_1}), ({t_2}) и ({t_3}) соответственно. Воспользуемся формулой: (frac{1}{{{t_1}}} + frac{1}{{{t_2}}} = frac{1}{{{t_{совм}}}}) (смотри замечание к задаче 8). Тогда получим систему уравнений: ()(left{ {begin{array}{*{20}{c}} {frac{1}{{{t_1}}} + frac{1}{{{t_2}}} = frac{1}{9};} \ {frac{1}{{{t_2}}} + frac{1}{{{t_3}}} = frac{1}{{14}};} \ {frac{1}{{{t_1}}} + frac{1}{{{t_3}}} = frac{1}{{18.}}} end{array}} right.) Прибавим к первому уравнению второе и третье: (frac{2}{{{t_1}}} + frac{2}{{{t_2}}} + frac{2}{{{t_3}}} = frac{1}{9} + frac{1}{{14}} + frac{1}{{18}},,,,, Leftrightarrow ,,,,,frac{2}{{{t_1}}} + frac{2}{{{t_2}}} + frac{2}{{{t_3}}} = frac{5}{{21}},left| {,:2,,,,, Leftrightarrow } right.,,,,,,frac{1}{{{t_1}}} + frac{1}{{{t_2}}} + frac{1}{{{t_3}}} = frac{5}{{42}}.) Так как спрашивается, за сколько минут три насоса заполнят бассейн, работая вместе, то: (frac{1}{{{t_{совм}}}} = frac{5}{{42}},,,,, Leftrightarrow ,,,,,,{t_{совм}} = 8,4) минуты. Ответ: 8,4. |
||||||||||||
| Задача 18. Две бригады, состоящие из рабочих одинаковой квалификации, одновременно начали строить два одинаковых дома. В первой бригаде было 16 рабочих, а во второй — 25 рабочих. Через 7 дней после начала работы в первую бригаду перешли 8 рабочих из второй бригады, в результате чего оба дома были построены одновременно. Сколько дней потребовалось бригадам, чтобы закончить работу в новом составе?
Количество рабочих будем считать производительностью. Пусть в новом составе рабочие доделывали дома t дней. В сумме до и после перехода рабочих каждая из бригад выполнила всю работу. Тогда: (16 cdot 7 + 24 cdot t = 25 cdot 7 + 17t,,,, Leftrightarrow ,,,,7t = 25 cdot 7 — 16 cdot 7,,,, Leftrightarrow ,,,,t = 9.) Следовательно, рабочим понадобилось 9 дней, чтобы закончить работу в новом составе. Ответ: 9. |
В торговом центре два одинаковых автомата
Дата: 2015-03-04
13173
Категория: Вероятность
Метка: ЕГЭ-№3
320172. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Рассмотрим события. Пусть
А — кофе закончится в первом автомате.
В — кофе закончится во втором автомате.
Обратите внимание, что события А и В не являются несовместными (независимыми). Если бы они были несовместными, то вероятность того, что кофе закончился в обоих автоматах была бы равна 0,03∙0,03 = 0,09. Тогда
А∙В ― кофе закончится в обоих автоматах,
А+В ― кофе закончится хотя бы в одном автомате.
По условию Р(А) = Р (В) = 0,3 Р(А∙В) = 0,12.
События A и B совместные, вероятность суммы двух совместных событий равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения:
Р(А + В) = Р(А) + Р (В) – Р(А∙В) = 0,3 + 0,3 – 0,12 = 0,48.
Все варианты событий, которые могут быть:
НЕ ЗАКОНЧИЛСЯ В ПЕРВОМ ― НЕ ЗАКОНЧИЛСЯ ВО ВТОРОМ
ЗАКОНЧИЛСЯ В ПЕРВОМ ― НЕ ЗАКОНЧИЛСЯ ВО ВТОРОМ
НЕ ЗАКОНЧИЛСЯ В ПЕРВОМ ― ЗАКОНЧИЛСЯ ВО ВТОРОМ
ЗАКОНЧИЛСЯ В ПЕРВОМ ― ЗАКОНЧИЛСЯ ВО ВТОРОМ
Выражению – «кофе закончится хотя бы в одном» соответствуют три события из представленных. Значит, событие «кофе останется в обоих автоматах» противоположно событию «кофе закончится хотя бы в одном». И его вероятность равна 1 – 0,48 = 0,52.
Ответ: 0,52
Используя этот сайт, Вы соглашаетесь с тем, что мы сохраняем и используем файлы cookies, а также используем похожие технологии для улучшения работы сайта.
Ok