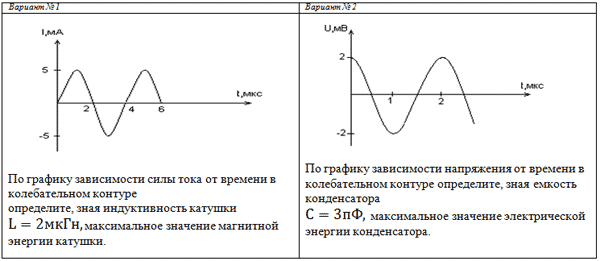
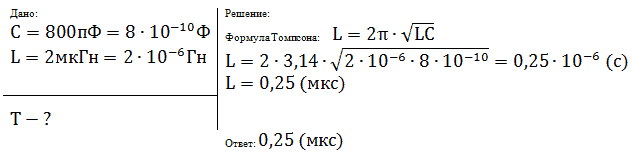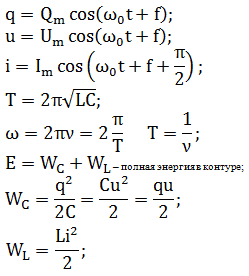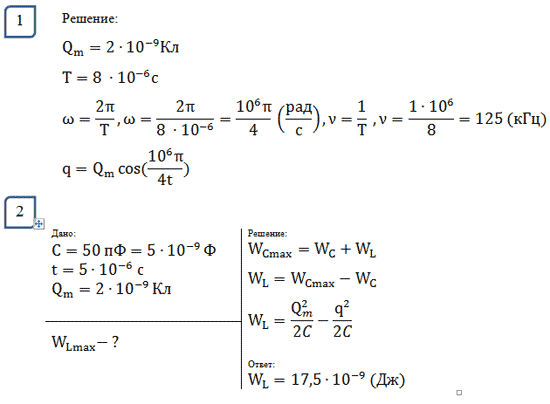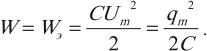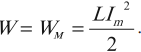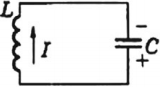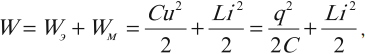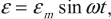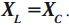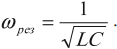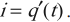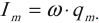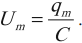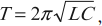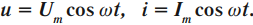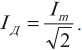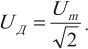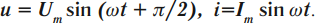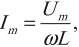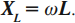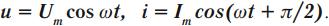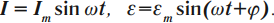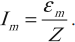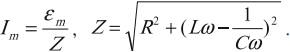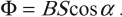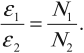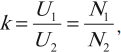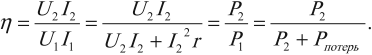Колебательный контур графики егэ - Помощь в подготовке к экзаменам и поступлению

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

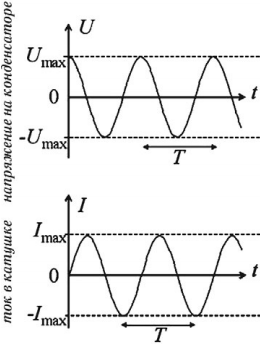
На рисунке приведен график гармонических колебаний тока в колебательном контуре.

Если катушку в этом контуре заменить на другую катушку, индуктивность которой в 4 раза больше, то каков будет период колебаний? (Ответ дать в мкс.)

На рисунке приведен график гармонических колебаний тока в колебательном контуре.

Если катушку в этом контуре заменить на другую катушку, индуктивность которой в 9 раз больше, то каков будет период колебаний? (Ответ дать в мкс.)

На рисунке приведен график гармонических колебаний тока в колебательном контуре.

Если конденсатор в этом контуре заменить на другой конденсатор, емкость которого в 4 раза больше, то каков будет период колебаний? (Ответ дать в мкс.)

На рисунке приведен график гармонических колебаний тока в колебательном контуре.

Если конденсатор в этом контуре заменить на другой конденсатор, емкость которого в 4 раза меньше, то каков будет период колебаний? (Ответ дать в мкс.)

На рисунке приведен график гармонических колебаний тока в колебательном контуре.

Если конденсатор в этом контуре заменить на другой конденсатор, емкость которого в 9 раз больше, то каков будет период колебаний? (Ответ дать в мкс.)

Пройти тестирование по этим заданиям

Источник

Электромагнитные колебания

Темы кодификатора ЕГЭ: свободные электромагнитные колебания, колебательный контур, вынужденные электромагнитные колебания, резонанс, гармонические электромагнитные колебания.
Колебательный контур
Энергетические превращения в колебательном контуре
Электромеханические аналогии
Гармонический закон колебаний в контуре
Вынужденные электромагнитные колебания

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: свободные электромагнитные колебания, колебательный контур, вынужденные электромагнитные колебания, резонанс, гармонические электромагнитные колебания.

Электромагнитные колебания — это периодические изменения заряда, силы тока и напряжения, происходящие в электрической цепи. Простейшей системой для наблюдения электромагнитных колебаний служит колебательный контур.

Колебательный контур

Колебательный контур — это замкнутый контур, образованный последовательно соединёнными конденсатором и катушкой.

Зарядим конденсатор, подключим к нему катушку и замкнём цепь. Начнут происходить свободные электромагнитные колебания — периодические изменения заряда на конденсаторе и тока в катушке. Свободными, напомним, эти колебания называются потому, что они совершаются без какого-либо внешнего воздействия — только за счёт энергии, запасённой в контуре.

Период колебаний в контуре обозначим, как всегда, через . Сопротивление катушки будем считать равным нулю.

Рассмотрим подробно все важные стадии процесса колебаний. Для большей наглядности будем проводить аналогию с колебаниями горизонтального пружинного маятника.

Начальный момент: t=0 . Заряд конденсатора равен q_0 , ток через катушку отсутствует (рис. 1). Конденсатор сейчас начнёт разряжаться.

Рис. 1. t=0

Несмотря на то, что сопротивление катушки равно нулю, ток не возрастёт мгновенно. Как только ток начнёт увеличиваться, в катушке возникнет ЭДС самоиндукции, препятствующая возрастанию тока.

Аналогия. Маятник оттянут вправо на величину x_0 и в начальный момент отпущен. Начальная скорость маятника равна нулю.

Первая четверть периода : . Конденсатор разряжается, его заряд в данный момент равен . Ток через катушку нарастает (рис. 2).

Рис. 2.

Увеличение тока происходит постепенно: вихревое электрическое поле катушки препятствует нарастанию тока и направлено против тока.

Аналогия . Маятник движется влево к положению равновесия; скорость маятника постепенно увеличивается. Деформация пружины (она же — координата маятника) уменьшается.

Конец первой четверти : t = T/4 . Конденсатор полностью разрядился. Сила тока достигла максимального значения I_0 (рис. 3). Сейчас начнётся перезарядка конденсатора.

Рис. 3. t = T/4

Напряжение на катушке равно нулю, но ток не исчезнет мгновенно. Как только ток начнёт уменьшаться, в катушке возникнет ЭДС самоиндукции, препятствующая убыванию тока.

Аналогия. Маятник проходит положение равновесия. Его скорость достигает максимального значения v_0 . Деформация пружины равна нулю.

Вторая четверть: . Конденсатор перезаряжается — на его обкладках появляется заряд противоположного знака по сравнению с тем, что был вначале (рис. 4).

Рис. 4.

Сила тока убывает постепенно: вихревое электрическое поле катушки, поддерживая убывающий ток, сонаправлено с током.

Аналогия. Маятник продолжает двигаться влево — от положения равновесия к правой крайней точке. Скорость его постепенно убывает, деформация пружины увеличивается.

Конец второй четверти t = T/2 . Конденсатор полностью перезарядился, его заряд опять равен q_0 (но полярность другая). Сила тока равна нулю (рис. 5). Сейчас начнётся обратная перезарядка конденсатора.

Рис. 5. t = T/2

Аналогия. Маятник достиг крайней правой точки. Скорость маятника равна нулю. Деформация пружины максимальна и равна x_0 .

Третья четверть: . Началась вторая половина периода колебаний; процессы пошли в обратном направлении. Конденсатор разряжается (рис. 6).

Рис. 6.

Аналогия. Маятник двигается обратно: от правой крайней точки к положению равновесия.

Конец третьей четверти: . Конденсатор полностью разрядился. Ток максимален и снова равен I_0 , но на сей раз имеет другое направление (рис. 7).

Рис. 7.

Аналогия. Маятник снова проходит положение равновесия с максимальной скоростью v_0 , но на сей раз в обратном направлении.

Четвёртая четверть: . Ток убывает, конденсатор заряжается (рис. 8).

Рис. 8.

Аналогия. Маятник продолжает двигаться вправо — от положения равновесия к крайней левой точке.

Конец четвёртой четверти и всего периода: t = T . Обратная перезарядка конденсатора завершена, ток равен нулю (рис. 9).

Рис. 9. t = T

Данный момент идентичен моменту t = 0 , а данный рисунок — рисунку 1. Совершилось одно полное колебание. Сейчас начнётся следующее колебание, в течение которого процессы будут происходить точно так же, как описано выше.

Аналогия. Маятник вернулся в исходное положение.

Рассмотренные электромагнитные колебания являются незатухающими — они будут продолжаться бесконечно долго. Ведь мы предположили, что сопротивление катушки равно нулю!

Точно так же будут незатухающими колебания пружинного маятника при отсутствии трения.

В реальности катушка обладает некоторым сопротивлением. Поэтому колебания в реальном колебательном контуре будут затухающими. Так, спустя одно полное колебание заряд на конденсаторе окажется меньше исходного значения. Со временем колебания и вовсе исчезнут: вся энергия, запасённая изначально в контуре, выделится в виде тепла на сопротивлении катушки и соединительных проводов.

Точно так же будут затухающими колебания реального пружинного маятника: вся энергия маятника постепенно превратится в тепло из-за неизбежного наличия трения.

к оглавлению ▴

Энергетические превращения в колебательном контуре

Продолжаем рассматривать незатухающие колебания в контуре, считая сопротивление катушки нулевым. Конденсатор имеет ёмкость , индуктивность катушки равна .

Поскольку тепловых потерь нет, энергия из контура не уходит: она постоянно перераспределяется между конденсатором и катушкой.

Возьмём момент времени, когда заряд конденсатора максимален и равен q_0 , а ток отсутствует. Энергия магнитного поля катушки в этот момент равна нулю. Вся энергия контура сосредоточена в конденсаторе:

$W = frac{displaystyle q_0^2}{displaystyle 2C vphantom{1^a}}.$

Теперь, наоборот, рассмотрим момент, когда ток максимален и равен I_0 , а конденсатор разряжен. Энергия конденсатора равна нулю. Вся энергия контура запасена в катушке:

$W = frac{displaystyle LI_0^2}{displaystyle 2 vphantom{1^a}}.$

В произвольный момент времени, когда заряд конденсатора равен и через катушку течёт ток , энергия контура равна:

$W = frac{displaystyle q^2}{displaystyle 2C vphantom{1^a}} + frac{displaystyle LI^2}{displaystyle 2 vphantom{1^a}}.$

Таким образом,

$frac{displaystyle q^2}{displaystyle 2C vphantom{1^a}} + frac{displaystyle LI^2}{displaystyle 2 vphantom{1^a}} = frac{displaystyle q_0^2}{displaystyle 2C vphantom{1^a}} = frac{displaystyle LI_0^2}{displaystyle 2 vphantom{1^a}}.$ (1)

Соотношение (1) применяется при решении многих задач.

к оглавлению ▴

Электромеханические аналогии

В предыдущем листке про самоиндукцию мы отметили аналогию между индуктивностью и массой. Теперь мы можем установить ещё несколько соответствий между электродинамическими и механическими величинами.

Для пружинного маятника мы имеем соотношение, аналогичное (1):

$frac{displaystyle kx^2}{displaystyle 2 vphantom{1^a}} + frac{displaystyle mv^2}{displaystyle 2 vphantom{1^a}}=frac{displaystyle kx_0^2}{displaystyle 2 vphantom{1^a}} = frac{displaystyle mv_0^2}{displaystyle 2 vphantom{1^a}}.$ (2)

Здесь, как вы уже поняли, — жёсткость пружины, — масса маятника, и — текущие значения координаты и скорости маятника, x_0 и v_0 — их наибольшие значения.

Сопоставляя друг с другом равенства (1) и (2), мы видим следующие соответствия:

(3)

(4)

(5)

(6)

Опираясь на эти электромеханические аналогии, мы можем предвидеть формулу для периода электромагнитных колебаний в колебательном контуре.

В самом деле, период колебаний пружинного маятника, как мы знаем, равен:

$T = 2 pi sqrt{frac{displaystyle m}{displaystyle k}}.$

B соответствии с аналогиями (5) и (6) заменяем здесь массу на индуктивность , а жёсткость на обратную ёмкость 1/c . Получим:

(7)

Электромеханические аналогии не подводят: формула (7) даёт верное выражение для периода колебаний в колебательном контуре. Она называется формулой Томсона. Мы вскоре приведём её более строгий вывод.

к оглавлению ▴

Гармонический закон колебаний в контуре

Напомним, что колебания называются гармоническими, если колеблющаяся величина меняется со временем по закону синуса или косинуса. Если вы успели забыть эти вещи, обязательно повторите листок «Механические колебания».

Колебания заряда на конденсаторе и силы тока в контуре оказываются гармоническими. Мы сейчас это докажем. Но прежде нам надо установить правила выбора знака для заряда конденсатора и для силы тока — ведь при колебаниях эти величины будут принимать как положительные, так и отрицательные значения.

Сначала мы выбираем положительное направление обхода контура. Выбор роли не играет; пусть это будет направление против часовой стрелки (рис. 10).

Рис. 10. Положительное направление обхода

Сила тока считается положительной (I > 0) , если ток течёт в положительном направлении. В противном случае сила тока будет отрицательной (I < 0) .

Заряд конденсатора — это заряд той его пластины, на которую течёт положительный ток (т. е. той пластины, на которую указывает стрелка направления обхода). В данном случае — заряд левой пластины конденсатора.

При таком выборе знаков тока и заряда справедливо соотношение: (при ином выборе знаков могло случиться ). Действительно, знаки обеих частей совпадают: если I > 0 , то заряд левой пластины возрастает, и потому .

Величины и меняются со временем, но энергия контура остаётся неизменной:

$frac{displaystyle q^2}{displaystyle 2C vphantom{1^a}} + frac{displaystyle LI^2}{displaystyle 2 vphantom{1^a}} = W = const.$ (8)

Стало быть, производная энергии по времени обращается в нуль: . Берём производную по времени от обеих частей соотношения (8); не забываем, что слева дифференцируются сложные функции (Если — функция от , то по правилу дифференцирования сложной функции производная от квадрата нашей функции будет равна: ${(y^2)}$ ):

$frac{displaystyle 2q dot{q}}{displaystyle 2C vphantom{1^a}}+frac{displaystyle L cdot 2I dot{I}}{displaystyle 2 vphantom{1^a}} = W =0.$

Подставляя сюда и , получим:

$frac{displaystyle qI}{displaystyle C vphantom{1^a}} + LI ddot{q} = 0,$

$Ileft ( frac{displaystyle q}{displaystyle C vphantom{1^a}} + L ddot{q} right ) = 0.$

Но сила тока не является функцией, тождественно равной нулю; поэтому

$frac{displaystyle q}{displaystyle C vphantom{1^a}} + L ddot{q} = 0.$

Перепишем это в виде:

$ddot{q} + frac{displaystyle 1}{displaystyle LC vphantom{1^a}}q = 0.$ (9)

Мы получили дифференциальное уравнение гармонических колебаний вида $ddot{q} + omega^2_0 q = 0$ , где . Это доказывает, что заряд конденсатора колеблется по гармоническому закону (т.е. по закону синуса или косинуса). Циклическая частота этих колебаний равна:

$omega_0 = frac{displaystyle 1}{displaystyle sqrt{LC} vphantom{1^a}}.$ (10)

Эта величина называется ещё собственной частотой контура; именно с этой частотой в контуре совершаются свободные (или, как ещё говорят, собственные колебания). Период колебаний равен:

$T = frac{displaystyle 2 pi}{displaystyle omega_0 vphantom{1^a}}= 2 pisqrt{LC}.$

Мы снова пришли к формуле Томсона.

Гармоническая зависимость заряда от времени в общем случае имеет вид:

(11)

Циклическая частота omega_0 находится по формуле (10); амплитуда q_0 и начальная фаза alpha определяются из начальных условий.

Мы рассмотрим ситуацию, подробно изученную в начале этого листка. Пусть при t = 0 заряд конденсатора максимален и равен q_0 (как на рис. 1); ток в контуре отсутствует. Тогда начальная фаза , так что заряд меняется по закону косинуса с амплитудой q_0 :

$q = q_0 cos omega_0t = q_0 cos left ( frac{displaystyle t}{displaystyle sqrt{LC} vphantom{1^a}} right ).$ (12)

Найдём закон изменения силы тока. Для этого дифференцируем по времени соотношение (12), опять-таки не забывая о правиле нахождения производной сложной функции:

$I = dot{q} = -q_0 omega_0 sin omega_0t.$

Мы видим, что и сила тока меняется по гармоническому закону, на сей раз — по закону синуса:

$I = -I_0 sin omega_0t = -I_0 sin left ( frac{displaystyle t}{displaystyle sqrt{LC} vphantom{1^a}} right ).$ (13)

Амплитуда силы тока равна:

$I_0 = q_0 omega_0 = frac{displaystyle q_0}{displaystyle sqrt{LC} vphantom{1^a}}.$

Наличие «минуса» в законе изменения тока (13) понять не сложно. Возьмём, к примеру, интервал времени (рис. 2).

Ток течёт в отрицательном направлении: I < 0 . Поскольку , фаза колебаний находится в первой четверти: . Синус в первой четверти положителен; стало быть, синус в (13) будет положительным на рассматриваемом интервале времени. Поэтому для обеспечения отрицательности тока действительно необходим знак «минус» в формуле (13).

А теперь посмотрите на рис. 8. Ток течёт в положительном направлении. Как же работает наш «минус» в этом случае? Разберитесь-ка, в чём тут дело!

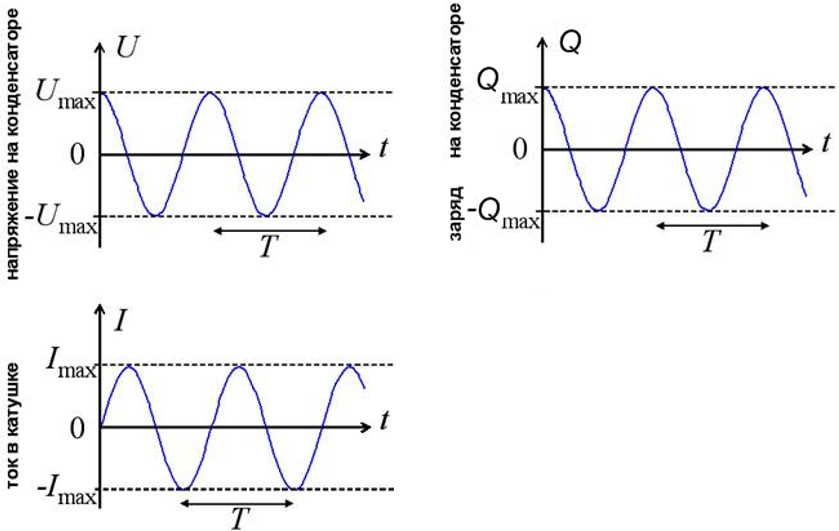
Изобразим графики колебаний заряда и тока, т.е. графики функций (12) и (13). Для наглядности представим эти графики в одних координатных осях (рис. 11).

Рис. 11. Графики колебаний заряда и тока

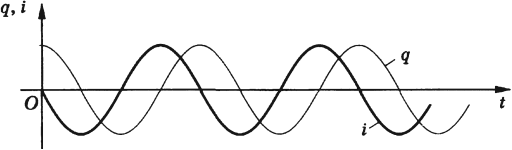
Обратите внимание: нули заряда приходятся на максимумы или минимумы тока; и наоборот, нули тока соответствуют максимумам или минимумам заряда.

Используя формулу приведения

$cos left ( varphi + frac{displaystyle pi}{displaystyle 2 vphantom{1^a}} right ) = - sin varphi,$

запишем закон изменения тока (13) в виде:

$I = -I_0 sin omega_0 t = I_0 cos left ( omega_0 t + frac{displaystyle pi}{displaystyle 2 vphantom{1^a}} right ).$

Сопоставляя это выражение с законом изменения заряда , мы видим, что фаза тока, равная $omega_0 t + frac{displaystyle pi}{displaystyle 2 vphantom{1^a}}$ , больше фазы заряда на величину pi/2 . В таком случае говорят, что ток опережает по фазе заряд на pi/2 ; или сдвиг фаз между током и зарядом равен pi/2 ; или разность фаз между током и зарядом равна pi/2 .

Опережение током заряда по фазе на pi/2 графически проявляется в том, что график тока сдвинут влево на pi/2 относительно графика заряда. Сила тока достигает, например, своего максимума на четверть периода раньше, чем достигает максимума заряд (а четверть периода как раз и соответствует разности фаз pi/2 ).

к оглавлению ▴

Вынужденные электромагнитные колебания

Как вы помните, вынужденные колебания возникают в системе под действием периодической вынуждающей силы. Частота вынужденных колебаний совпадает с частотой вынуждающей силы.

Вынужденные электромагнитные колебания будут совершаться в контуре, поключённом к источнику синусоидального напряжения (рис. 12).

Рис. 12. Вынужденные колебания

Если напряжение источника меняется по закону:

то в контуре происходят колебания заряда и тока с циклической частотой omega (и с периодом, соответственно, ). Источник переменного напряжения как бы «навязывает» контуру свою частоту колебаний, заставляя забыть о собственной частоте $omega_0 = 1/sqrt{LC}$ .

Амплитуда вынужденных колебаний заряда и тока зависит от частоты omega : амплитуда тем больше,чем ближе omega к собственной частоте контура omega_0 .При наступает резонанс — резкое возрастание амплитуды колебаний. Мы поговорим о резонансе более подробно в следующем листке, посвящённом переменному току.

Если вам нравятся наши материалы — записывайтесь на курсы подготовки к ЕГЭ по физике онлайн

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Электромагнитные колебания» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

15. Магнитное поле. Оптика

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Колебательный контур

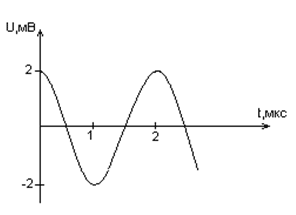
На рисунке приведен график гармонических колебаний тока в колебательном контуре.
Если катушку в этом контуре заменили на другую катушку, индуктивность которой в 9 раз больше. Чему равен период колебаний? (Ответ дать в мкс.)

Из графика видно, что период колебаний равен [T=20 text{ мкс}].
Период колебаний электромагнитного контура вычисляется по формуле Томсона: [T=2pisqrt{LC}] Если катушку заменить на другую катушку, индуктивность которой в 9 раз больше, то период увеличится в 3 раза, следовательно, станет равным 60 мкс.

Ответ: 60

В наборе радиодеталей для изготовления простого колебательного контура имеются две катушки с индуктивностями (L_1=1) мкГн и (L_2=2) мкГн, а также два конденсатора, ёмкости которых (C_1=30) пФ и (C_2=40) пФ. С какой наименьшей собственной частотой (nu) можно составить колебательный контур из двух элементов этого набора? (Ответ выразите в МГц и округлите до целого числа.)

Период колебаний электромагнитного контура вычисляется по формуле Томсона: [T=2pisqrt{LC}] Чтобы частота была наименьшей, период должен быть наибольшим Значит надо взять катушку с индуктивностью (L_2=2) мкГн, конденсатор (C_2=40) пФ.
Найдем частоту: [nu=frac{1}{2pisqrt{LC}}=frac{1}{2cdot3,14cdotsqrt{2cdot10^{-6}text{ Гн}cdot40cdot10^{-12}}text{ Ф}}=18text{ МГц}]

Ответ: 18

Во сколько раз уменьшится частота собственных колебаний контура, если его индуктивность увеличить в 10 раз, а емкость уменьшить в 2,5 раза?

Период колебаний электромагнитного контура вычисляется по формуле Томсона: [T=2pisqrt{LC},] где (L) – индуктивность катушки, (C) – ёмкость конденсатора. Частота: [nu=frac{1}{2pisqrt{LC}}] Если индуктивность увеличить в 10 раз, а емкость уменьшить в 2,5 раза, то корень увеличится в 4 раза, следовательно, частота уменьшится в 2 раза

Ответ: 2

Колебательный контур с конденсатором емкостью 1 мкФ настроен на частоту 400 Гц. Если подключить к нему параллельно второй конденсатор, то частота колебаний в контуре становится равной 200 Гц. Определите емкость (в мкФ) второго конденсатора.

Период колебаний электромагнитного контура вычисляется по формуле Томсона: [T=2pisqrt{LC},] где (L) – индуктивность катушки, (C) – ёмкость конденсатора. Частота: [nu=frac{1}{2pisqrt{LC}}] Частота уменьшилась в 2 раза, следовательно, емкость батареи конденсаторов в 4 раза больше изначальной. При параллельном соединении конденсаторов общая ёмкость равна [C_{text{общ}}=C_2+C_1=4C_1 text{ мкФ}] [C_2=3C_1=3 text{ мкФ}]

Ответ: 3

В колебательном контуре к конденсатору параллельно присоединили другой конденсатор, втрое большей емкости, после чего частота колебаний контура уменьшилась на 300 Гц. Найдите первоначальную частоту колебаний контура.

Ответ: 600

Колебательный контур состоит из катушки и конденсатора. Во сколько раз увеличится частота собственных колебаний в контуре, если в контур последовательно включить второй конденсатор, емкость которого в 3 раза меньше емкости первого?

Период колебаний электромагнитного контура вычисляется по формуле Томсона: [T=2pisqrt{LC},] где (L) – индуктивность катушки, (C) – ёмкость конденсатора. Частота: [nu=frac{1}{2pisqrt{LC}}] При последовательном соединении конденсаторов: [frac{1}{C_{text{общ}}}=frac{1}{C_1}+frac{3}{C_1}] [C_{text{общ}}=frac{C_1}{4}] Емкость уменьшилась в 4 раза, следовательно, частота увеличилась в 2 раза.

Ответ: 2

На какую длину волны настроен радиоприемник, если его колебательный контур обладает индуктивностью 3 мГн и емкостью 3 нФ?

Период колебаний электромагнитного контура вычисляется по формуле Томсона: [T=2pisqrt{LC}] Длина волны: [lambda=cT=3cdot10^8cdot2cdot pi sqrt{3cdot10^{-3}cdot3cdot10^{-9}}=5652text{ м}]

Ответ: 5652

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Слайд 1

Цели урока:

Образовательные: обобщение и
систематизация знаний по теме, проверка знаний,
умений, навыков. В целях повышения интереса к
теме работу вести с помощью опорных конспектов.
Воспитательные: воспитание
мировоззренческого понятия
(причинно-следственных связей в окружающем мире),
развитие у школьников коммуникативной культуры.
Развивающие: развитие самостоятельности
мышления и интеллекта, умение формулировать
выводы по изученному материалу, развитие
логического мышления, развитие грамотной устной
речи, содержащей физическую терминологию.

Тип урока:систематизация и обобщение
знаний.

Слайд 2

Техническая поддержка урока:

Демонстрации:
Плакаты.
Показ слайдов с помощью информационно –
компьютерных технологий.
Дидактический материал:
Опорные конспекты с подробными записями на
столах.
Оформление доски:
Плакат с кратким содержанием опорных
конспектов (ОК);
Плакат – рисунок с изображением колебательного
контура;
Плакат – график зависимости колебаний заряда
конденсатора, напряжения между обкладками
конденсатора, силы тока в катушке от времени,
электрической энергии конденсатора, магнитной
энергии катушки от времени.

Слайд 3

План урока:

1. Этап повторения пройденного материала.
Проверка домашнего задания.
Четыре группы задач по теме:

Электромагнитные колебания.
Колебательный контур.
Свободные колебания. Свободные колебания –
затухающие колебания
Характеристика колебаний.

2. Этап применения теории к решению задач.
3. Закрепление. Самостоятельная работа.
4. Подведение итогов.

ХОД УРОКА

Учитель: Темой урока является
«Решение задач по теме: «Электромагнитные
колебания и волны» на примере разбора задач ЕГЭ»

К доске вызываются 3 ученика для проверки
домашнего задания.

– Задания по этой теме можно разделить на
четыре группы.

Слайд 4

Четыре группы задач по теме:

1. Задачи с использованием общих законов
гармонических колебаний.
2. Задачи о свободных колебаниях конкретных
колебательных систем.
3. Задачи о вынужденных колебаниях.
4. Задачи о волнах различной природы.

– Мы остановимся на решении задач 1 и 2 групп.

Урок начнем с повторения необходимых понятий
для данной группы задач.

Слайд 5

Электромагнитные колебания – это
периодические и почти периодические изменения
заряда, силы тока и напряжения.

Колебательный контур – цепь,
состоящая из соединительных проводов, катушки
индуктивности и конденсатора.

Свободные колебания – это колебания,
происходящие в системе благодаря начальному
запасу энергии с частотой, определяемой
параметрами самой системы: L, C.

Скорость распространения электромагнитных
колебаний равна скорости света: С = 3^.10⁸(м/с)

Основные характеристики колебаний

Амплитуда (силы тока, заряда, напряжения) –
максимальное значение (силы тока, заряда,
напряжения): Im, Qm, Um
Мгновенные значения (силы тока, заряда,
напряжения) – i, q, u

Слайд 6

Схема колебательного контура

Учитель: Что представляют
электромагнитные колебания в контуре?

Слайд 7

Электромагнитные колебания представляют
периодический переход электрической энергии
конденсатора в магнитную энергию катушки и
наоборот согласно закону сохранения энергии.

Слайд 8

Задача №1 (д/з)

Колебательный контур содержит конденсатор
емкостью 800 пФ и катушку индуктивности
индуктивностью 2 мкГн. Каков период собственных
колебаний контура?

Слайд 9

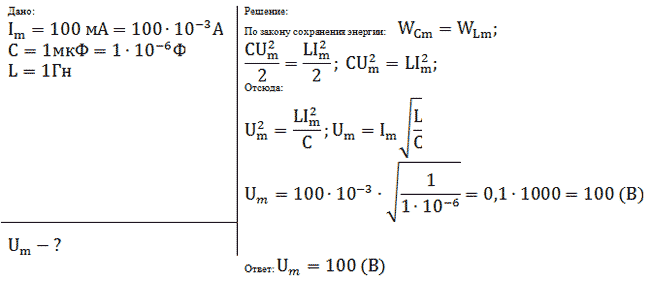
Задача № 2 (д/з)

Колебательный контур состоит из конденсатора
емкостью С и катушки индуктивности
индуктивностью L. Как изменится период свободных
электромагнитных колебаний в этом контуре, если
электроемкость конденсатора и индуктивность
катушки увеличить в 3р.

Слайд 10

Задача № 3 (д/з)

Амплитуда силы тока при свободных колебаниях в
колебательном контуре 100 мА. Какова амплитуда
напряжения на конденсаторе колебательного
контура, если емкость этого конденсатора 1 мкФ, а
индуктивность катушки 1 Гн? Активным
сопротивлением пренебречь.

Слайд 11

Схема электромагнитных колебаний

Ученик 1 наглядно описывает процессы в
колебательном контуре.

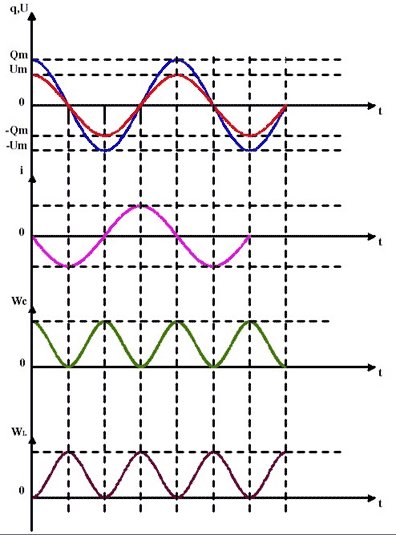
Слайд 12

Ученик 2 комментирует электромагнитные
колебания в контуре, используя графическую
зависимость заряда, напряжения. Силы тока,
электрической энергии конденсатора, магнитной
энергии катушки индуктивности от времени.

Слайд 13

Уравнения, описывающие колебательные процессы
в контуре:

Обращаем внимание, что колебания силы тока в
цепи опережают колебания напряжения между
обкладками конденсатора на π/2.
Описывая изменения заряда, напряжения и силы
тока по гармоническому закону, необходимо
учитывать связь между функциями синуса и
косинуса.

Слайд 14

Задача № 1.

По графику зависимости силы тока от времени в
колебательном контуре определите, какие
преобразования энергии происходят в
колебательном контуре в интервале времени от
1мкс до 2мкс?

1. Энергия магнитного поля катушки
увеличивается до максимального значения;
2. Энергия магнитного поля катушки преобразуется
в энергию электрического поля конденсатора;
3. Энергия электрического поля конденсатора
уменьшается от максимального значения до «о»;
4. Энергия электрического поля конденсатора
преобразуется в энергию магнитного поля катушки.

Слайд 15

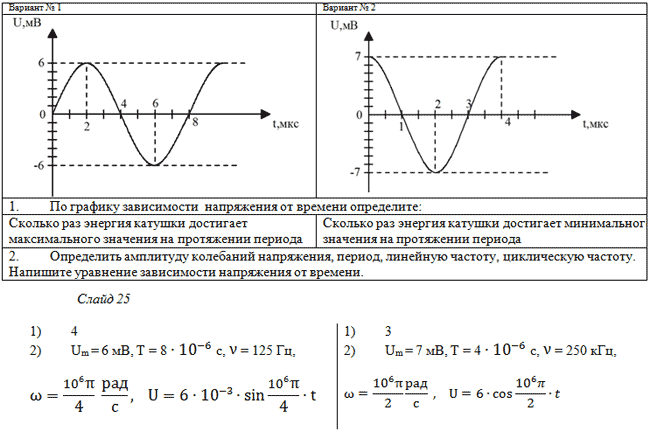
Задача № 2.

По графику зависимости силы тока от времени в
колебательном контуре определите:

а) Сколько раз энергия катушки достигает
максимального значения в течение первых 6 мкс
после начала отсчета?
б) Сколько раз энергия конденсатора достигает
максимального значения в течение первых 6 мкс
после начала отсчета?
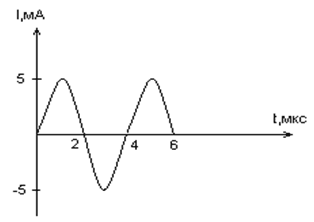
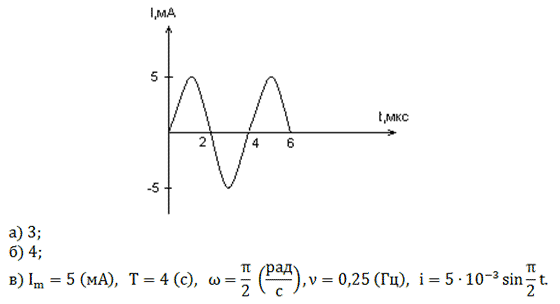
в) Определите по графику амплитудное значение
силы тока, период, циклическую частоту, линейную
частоту и напишите уравнение зависимости силы
тока от времени.

Слайд 16

Задача № 3 (д/з)

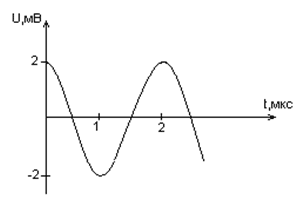
Дана графическая зависимость напряжения между
обкладками конденсатора от времени. По графику
определите, какое преобразование энергии
происходит в интервале времени от 0 до 2 мкс?

Слайд 17

Задача № 4 (д/з)

Дана графическая зависимость напряжения между
обкладками конденсатора от времени. По графику
определите: сколько раз энергия конденсатора
достигает максимального значения в период от
нуля до 2мкс? Сколько раз энергия катушки
достигает наибольшего значения от нуля до 2 мкс?
По графику определите амплитуду колебаний
напряжений, период колебаний, циклическую
частоту, линейную частоту. Напишите уравнение
зависимости напряжения от времени.

Слайд № 18

К доске вызываются 2 ученика

Задача № 5, 6

Слайд 19

Слайд 20

Задача № 7

Заряд на обкладках конденсатора
колебательного контура изменяется по закону
q = 3·10^–7cos800πt. Индуктивность контура 2Гн.
Пренебрегая активным сопротивлением, найдите
электроемкость конденсатора и максимальное
значение энергии электрического поля
конденсатора и магнитного поля катушки
индуктивности.

Слайд 21

Слайд 22

Задача № 8

В идеальном колебательном контуре происходят
свободные электромагнитные колебания. В таблице
показано, как изменяется заряд конденсатора в
колебательном контуре с течением времени.

t, 10^–6(C)	0	1	2	3	4	5	6	7	8	9
q, 10^–9(Кл)	2	1,5	0	–1,5	–2	–1,5	0	1,5	2	1,5

1. Напишите уравнение зависимости заряда от
времени. Найдите амплитуду колебаний заряда,
период, циклическую частоту, линейную частоту.

2. Какова энергия магнитного поля катушки в
момент времени t = 5 мкс, если емкость конденсатора
50 пФ.

Домашнее задание. Напишите уравнение
зависимости силы тока от времени. Найдите
амплитуду колебаний силы тока. Постройте
графическую зависимость силы тока от времени.

Слайд 23

Слайд 24

Самостоятельная работа:

Приложение 1

Источник

За это задание ты можешь получить 2 балла. Уровень сложности: повышенный.
Средний процент выполнения: 55.3%
Ответом к заданию 17 по физике может быть последовательность цифр, чисел или слов. Порядок записи имеет значение.

Разбор сложных заданий в тг-канале

Задачи для практики

Задача 1

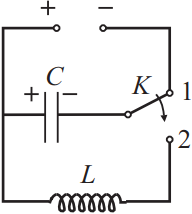
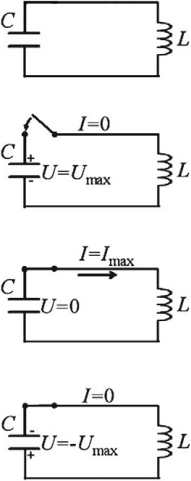
В колебательном контуре конденсатор подключён к источнику постоянного напряжения. В момент t = 0 переключатель K переводят из положения 1 в положение 2. Графики А и Б представляют изменения физических величин, характеризующих колебания в контуре после этого. T — период колебаний. Установите соответствие между графиками и физическими величинами, зависимости которых от времени изображены на этих графиках.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите выбранные цифры под соответствующими буквами.

Решение

Для данного колебательного контура справедливо, что А) заряд левой «+» обкладки конденсатора Б). Энергия магнитного поля катушки $W_L={LI^2}/{2}$, т.к. идеальный колебательный контур за период $W_L$ максимальна 2 раза.

Ответ: 13

Задача 2

Установите соответствие между графиками, изображёнными на рисунках, и законами (зависимостями), которые они могут представлять.

Решение

А) Соответствует зависимости силы фототока от предложенного напряжения, где $U_{max}=U_{напряжения}$.

Б) Соответствует зависимость максимальной $E_к$ энергии фотоэлектронов от частоты света, где $hυ_{min}=A_{вых}$, а остальная энергия идет на $E_к$.

Ответ: 23

Задача 3

Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.

Физические величины	Формулы
А) напряжение на внешней цепи Б) мощность тока на внутренней цепи	1) $ε − Ir$ 2) $I(R+r)$ 3) ${ε^2}/{R+r}$ 4) $({ε}/{R+r})^2r$

Решение

1) Напряжение на внешней цепи по 2 закону Кирхгофа $U=ε-I·r$.

2) Мощность тока на внутренней цепи $P=I^2·r=({ε}/{R+r})^2·r$.

Ответ: 14

Задача 4

Установите соответствие между графиками, представленными на рисунках, и законами (зависимостями), которые они могут выражать.

Решение

Дано:

Решение:

Закон радиоактивного распада имеет такую форму, т.к. $N=N_0·2^{-t/{T_{полураспада}}}$

Зависимость энергии фотона от частоты света зависит $E=hυ$.

Ответ: 14

Задача 5

Идеальный колебательный контур состоит из конденсатора ёмкостью 400 мкФ и катушки индуктивностью 50 мГн. Заряд на пластинах конденсатора изменяется во времени в соответствии с формулой q(t) = 4 · 10⁻⁴ cos(2000 · t) (все величины выражены в СИ). Установите соответствие между физическими величинами и формулами, выражающими их зависимость от времени в условиях данной задачи.

К каждой позиции первого столбца подберите соответствующую позицию второго и запишите выбранные цифры под соответствующими буквами.

Физические величины	Формулы
А) сила тока в колебательном контуре Б) напряжение на конденсаторе	1) −0,8 sin(2000 · t + π/2) 2) −0,8 sin(2000 · t) 3) cos(2000 · t) 4) 100 cos(2000 · t)

Решение

Дано:

$С=400$мкФ

$L=50$мГн

$g(t)=4·10^{-4}·cos(2000·t)$

Решение:

А) Сила тока в колебательном контуре $I(t)=q'(t)=-0.8·sin(2000·t)$.

Б) Напряжение в конденсаторе $U(t)=I'(t)=cos(2000·t)$

Ответ: 23

Задача 6

Частица массой m движется со скоростью v = 0,9c, где c — скорость света в вакууме. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.

Физические величины	Формулы
А) энергия частицы (E) Б) импульс частицы (p)	1) $mc^2$ 2) ${mc^2}/{√{1-{v^2}/{c^2}}}$ 3) ${mv}/{√{1-{v^2}/{c^2}}}$ 4) ${mc}/{√{1-{v^2}/{c^2}}}$

Решение

Из теории о релятивистском движении частиц, очевидно: $E={mc^2}/{√{1-{υ^2}/{c^2}}}$, а импульс частицы $p↖{→}={mυ}/{√{1-{υ^2}/{c^2}}}$.

Ответ: 23

Задача 7

Источник тока, ЭДС которого ε, а внутреннее сопротивление r, замкнут на реостат. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите выбранные цифры под сооветствующими буквами.

Физические величины	Формулы
А) мощность, развиваемая во внешней цепи Б) КПД при изменении сопротивления R реостата	1) ${ε^2}/{(R +r)^2}R$ 2) ${ε^2}/{R+r}$ 3) ${R}/{R+r}$ 4) ${εR}/{R+r}$

Решение

Из теории о постоянном токе:

А) $P=U·I={ε^2}/{(R+r)^2}R$, где ${ε^2}/{(R+r)^2}=I^2$ — квадрат тока.

Б) $η={R}/{R+r}$, где $r$ — внутреннее сопротивление источника.

Ответ: 13

Задача 8

В катушке с индуктивностью L при равномерном увеличении силы тока на ∆I возникла ЭДС самоиндукции E. Графики А и Б представляют изменения физических величин во время изменения силы тока в катушке. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.

Решение

А) Данному графику соответствует сила тока, т.к. ток равномерно увеличивают по условию.

Б) Данному графику соответствует энергия магнитного поля в катушке, $E_L={LI^2}/{2}$ зависимость тока квадратичная.

Ответ: 13

Задача 9

В цепь переменного тока включена катушка индуктивностью L. Частоту тока равномерно увеличивают. Графики А и Б представляют зависимости физических величин от частоты переменного тока. Установите соответствие между графиками и физическими величинами, зависимости которых от частоты они могут представлять.

Решение

Дано:

$υ_2 > υ_1$

Решение:

Для графика А) соответствует индуктивное сопротивление $x_L=ω·L=2nυ·{h}/{2}$, а для графика Б) сила тока зависит квадратичную зависимость от частоты 3.

Ответ: 23

Задача 10

Как определяется направление следующих физических величин? К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите выбранные цифры под соответствующими буквами.

Физическая величина	Правило определения направления
А) вектор магнитной индукции Б) индукционный ток	1) правило левой руки 2) правило буравчика 3) правило Ленца

Решение

Из основ магнетизма известно, что $B↖{→}$ (магн.индукция) по Буравчику определяется, а индукционный ток по правилу Ленца.

Ответ: 23

Задача 11

Конденсатор колебательного контура заряжен некоторым зарядом, после чего контур предоставлен сам себе. Графики А и Б представляют изменения физических величин, характеризующих колебания в контуре после того, как ток в катушке индуктивности в очередной раз достиг максимальной силы. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.

Решение

В начальный момент времени графиков по условию сила тока в катушке имела максимальное значение. Следовательно, график А отражает изменение силы тока на катушке, а Б — заряд на конденсаторе (заряд на конденсаторе равен нулю в тот момент, когда сила тока максимальна). Графиком зависимости энергии от времени здесь нет, так как энергия успевает совершить два колебания за время одного колебания контура.

Ответ: 21

Задача 12

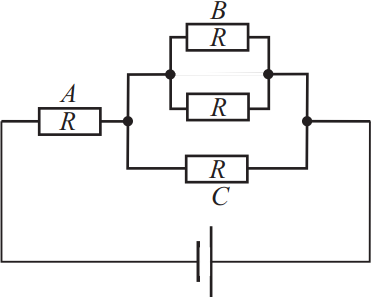
В электрической цепи, схема которой показана на рисунке, через резистор B течёт ток силой I₀. Чему равна сила тока, текущего через резистор A и через резистор C? Установите соответствие между физическими величинами и их значениями. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите выбранные цифры под соответствующими буквами.

Физические величины	Их значение
А) сила тока, текущего через резистор A Б) сила тока, текущего через резистор C	1) I₀ 2) 2I₀ 3) 3I₀ 4) 2I₀/3

Решение

Для решения задачи необходимо вспомнить законы постоянного тока для последовательного и параллельного соединения. При параллельном соединении одинаково и в ветвях, а при последовательном, тогда в резисторе протекает ток $I_0$, а в резисторе $3I_0$.

Ответ: 31

Задача 13

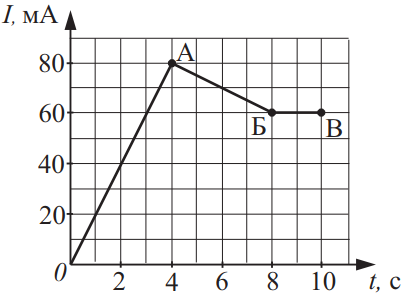
На рисунке представлен график зависимости силы тока I в катушке индуктивностью 100 мГн от времени t. Установите соответствие между участками графика и значениями модуля ЭДС самоиндукции. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите выбранные цифры под соответствующими буквами.

Участок графика	Модуль ЭДС самоиндукции
А) АБ Б) БВ	1) 0 В 2) 0,075 В 3) 0,5 мВ 4) 0,025 В 5) 2 мВ

Решение

Согласно закону электромагнитной индукции, ЭДС самоиндукции равна $|ε_i|=L{dI}/{dt}$. На участке БВ сила тока постоянна, поэтому $ε_i=0$, но на участке АБ $|ε_i|=|100·10^{-3}·{60-80}/{8-4}|=0.5$мВ.

Ответ: 31

Задача 14

Пучок света переходит из воздуха в стекло. Частота световой волны ν, скорость света в воздухе c, показатель преломления стекла относительно воздуха n. Чему равны длина волны и скорость света в стекле? Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите выбранные цифры под соответствующими буквами.

Физические величины	Формулы
А) скорость света в стекле Б) длина волны света в стекле	1) $c · n$ 2) $c · n · ν$ 3) ${c}/{n}$ 4) ${c}/{n · ν}$

Решение

Показатель преломления $n$ показывает во сколько раз скорость света в воздухе больше скорости света в стекле для нашего случая, т.е. $n={c}/{υ}$, откуда $υ={c}/{n}$. Длина волны света в стекле: $λ=υ·T={cT}/{n}={c}/{n·v}$, где $T$ — период колебаний, $v$ — частота света.

Ответ: 34

Задача 15

В катушке с индуктивностью L ток равномерно нарастает от нуля до величины I за время ∆t. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите выбранные цифры под соответствующими буквами.

Физические величины	Формулы
А) модуль ЭДС самоиндукции в катушке Б) энергия магнитного поля катушки в конце промежутка ∆t	1) $LI ∆t$ 2) ${LI}/{∆t}$ 3) ${LI^2}/{2}$ 4) $LI$

Решение

Дано:

$L, ∆t, J$

$ε-?W_м-?$

Решение:

А) Запишем закон электромагнитной индукции: $ε=|-{∆Ф}/{∆t}|=|-{LJ}/{∆t}|={LJ}/{∆t}$

Б) Запишем выражение энергии магнитного поля катушки в конце промежутка $∆t$: $W_м={LJ^2}/{2}$

Ответ: 23

Задача 16

Колебательный контур радиоприёмника, состоящий из катушки с индуктивностью L и конденсатора ёмкостью C, настроен на некоторую длину волны λ (c — скорость света). Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите выбранные цифры под соответствующими буквами.

Физические величины	Формулы
А) резонансная частота контура ν Б) длина волны λ, на которую настроен контур	1) ${c}/{2π√{LC}}$ 2) $2πc√{LC}$ 3) $√{LC}$ 4) ${1}/{2π√{LC}}$

Решение

Дано:

$L, C, λ, c, π$

$v-?λ-?$

Решение:

Период колебаний колебательного контура рассчитывается по формуле Томсона $T=2π√{LC}$. Учитывая, что резонансная частота контура $v={1}/{T}={1}/{2π√{LC}}$

Длина волны $λ={c}{T}=c·2π√{LC}$

Ответ: 42

Задача 17

Собирающая линза даёт на экране увеличенное в Γ раз изображение предмета, находящегося на расстоянии d от линзы. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите выбранные цифры под соответствующими буквами.

Физические величины	Формулы
А) расстояние от изображения предмета до линзы Б) оптическая сила линзы	1) $Γ · d$ 2) ${Γ}/{(Γ + 1) · d}$ 3) ${Γ + 1}/{Γ · d}$ 4) ${d}/{Γ}$

Решение

Учитывая, что $Г={f}/{d}$, где $f$ — расстояние от изображения предмета до линзы; имеем $f=Г·d$. Оптическая сила линзы $D={1}/{F}$, где $F$ — фокус линзы. Увеличение $Г$ равно: $Г={f-F}/{F}⇒Г·F=f-F⇒{Г·1}/{D}=f-{1}/{D}|·D⇒Г=f·D⇒fD=Г+1⇒D={Г+1}/{f}={Г+1}/{Г·d}$

Ответ: 13

Задача 18

В идеальном колебательном контуре происходят гармонические колебания с циклической частотой ω. Максимальное напряжение между обкладками конденсатора ёмкостью C равно U_m . Каковы период колебаний в контуре и максимальное значение силы тока в катушке индуктивности? Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.

Физические величины	Формулы
А) период колебаний Б) амплитуда силы тока	1) ${1}/{ω}$ 2) ${2π}/{ω}$ 3) $U_{m}ωC$ 4) ${U_m}/{ωC}$

Решение

Дано:

$ω, С, U_m$

$T-?J_m-?$

Решение:

Циклическая частота $ω$ связана с периодом колебаний соотношением: $ω={2π}/{T}$, откуда $T={2π}/{ω}$(1). Амплитуда силы тока по закону Ома равна: $J_m={U_m}/{x_c}$(2), где $x_c={1}/{ωc}$ — емкостное сопротивление, тогда имеем $J_m=U_m·ωc$(3)

Ответ: 23

Задача 19

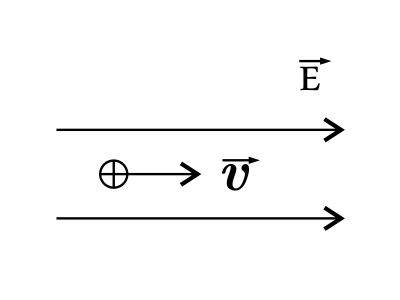
Положительно заряженная пылинка (q > 0) массой m влетела со скоростью v в однородное электрическое поле напряжённостью E вдоль его силовых линий. Установите соответствие между величинами и формулами, по которым их можно рассчитать.

Физические величины	Формулы
А) сила, действующая на пылинку со стороны поля Б) скорость пылинки в момент времени t	1) $qE$ 2) $mE$ 3) $υ + {qE}/{m}t$ 4) ${qE}/{m}t$

Решение

Дано:

$q > 0, m, E$

$υ, t$

$F-?υ_к-?$

Решение:

Пылинка ускоряется под действием силы Кулона $F=qE$(1), тогда $ma=qE$ или $a={qE}/{m}$(2)

Скорость пылинки при равноускоренном движении определяется выражением: $υ_к=υ_0+at=υ+{qEt}/{m}$(3)

Ответ: 13

Задача 20

Положительно заряженная пылинка (q > 0) массой m влетела со скоростью v в однородное электрическое поле напряжённостью E вдоль его силовых линий. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.

Физические величины	Формулы
А) ускорение пылинки Б) кинетическая энергия пылинки в момент времени t	1) ${qE}/{m}$ 2) ${mE}/{q}$ 3) ${m(v + {qE}/{m}t)^2}/{2}$ 4) ${qEt^2}/{2m}$

Решение

Дано:

$q > 0, m$

$υ, E, t$

$a-?E_k-?$

Решение:

Пылинка ускоряется под действием силы Кулона $F=qE$(1), тогда $ma=qE$ или $a={qE}/{m}$(2)

Кинетическая энергия пылинки определяется выражением: $E_k={mυ_k^2}/{2}$(3), учитывая, что скорость пылинки при равноускоренном движении определяется выражением: $υ_k=υ_0+at=υ+{qEt}/{m}$(4)

Подставим числовые значения (4) в (3): $E_k={mυ_k^2}/{2}={m(υ+{qEt}/{m})^2}/{2}$(5)

Ответ: 13

Электромагнитные колебания и волны

Содержание

Свободные электромагнитные колебания. Колебательный контур
Вынужденные электромагнитные колебания. Резонанс
Гармонические электромагнитные колебания
Переменный ток. Производство, передача и потребление электрической энергии
Емкостное сопротивление
Электромагнитное поле
Свойства электромагнитных волн
Различные виды электромагнитных излучений и их применение
Основные формулы раздела «Электромагнитные колебания и волны»

Свободные электромагнитные колебания. Колебательный контур

Электромагнитные колебания — это периодические изменения заряда, силы тока и напряжения, происходящие в электрической цепи. Простейшей системой для наблюдения электромагнитных колебаний служит колебательный контур.

Колебательный контур — это замкнутый контур, образованный последовательно соединенными конденсатором и катушкой.

Сопротивление катушки ( R ) равно нулю.

Если зарядить конденсатор до напряжения ( U_m ), то в начальный момент времени ( t_1=0 ), напряжение на конденсаторе будет равно ( U_m ). Заряд конденсатора в этот момент времени будет равен ( q_m=CU_m ). Сила тока равна нулю.

Полная энергия системы будет равна энергии электрического поля:

Конденсатор начинает разряжаться, по катушке начинает течь ток. Вследствие самоиндукции в катушке конденсатор разряжается постепенно.

Ток достигает своего максимального значения ( I_m ) в момент времени ( t_2=T/4 ). Заряд конденсатора в этот момент равен нулю, напряжение на конденсаторе равно нулю.

Полная энергия системы в этот момент времени равна энергии магнитного поля:

В следующий момент времени ток течет в том же направлении, постепенно (вследствие явления самоиндукции) уменьшаясь до нуля. Конденсатор перезаряжается. Заряды обкладок имеют заряды, по знаку противоположные первоначальным.

В момент времени ( t_3=T/2 ) заряд конденсатора равен ( q_m ), напряжение равно ( U_m ), сила тока равна нулю.

Полная энергия системы равна энергии электрического поля конденсатора.

Затем конденсатор снова разряжается, но ток через катушку течет в обратном направлении.

В момент времени ( t_4=3T/4 ) сила тока в катушке достигает максимального значения, напряжение на конденсаторе и его заряд равны нулю. С этого момента ток в катушке начинает убывать, но не сразу (явление самоиндукции). Энергия магнитного поля переходит в энергию электрического поля. Конденсатор начинает заряжаться, и через некоторое время его заряд равен первоначальному, а сила тока станет равной нулю.

Через время, равное периоду ( T ), система возвращается в начальное состояние. Совершилось одно полное колебание, дальше процесс повторяется.

Важно!
Колебания, происходящие в колебательном контуре, – свободные. Они совершаются без какого-либо внешнего воздействия — только за счет энергии, запасенной в контуре.

В контуре происходят превращения энергии электрического поля конденсатора в энергию магнитного поля катушки и обратно. В любой произвольный момент времени полная энергия в контуре равна:

где ( i, u, q ) – мгновенные значения силы тока, напряжения, заряда в любой момент времени.

Эти колебания являются затухающими. Амплитуда колебаний постепенно уменьшается из-за электрического сопротивления проводников.

Вынужденные электромагнитные колебания. Резонанс

Вынужденными электромагнитными колебаниями называют периодические изменения заряда, силы тока и напряжения в колебательном контуре, происходящие под действием периодически изменяющейся синусоидальной (переменной) ЭДС от внешнего источника:

где ( varepsilon ) – мгновенное значение ЭДС, ( varepsilon_m ) – амплитудное значение ЭДС.

При этом к контуру подводится энергия, необходимая для компенсации потерь энергии в контуре из-за наличия сопротивления.

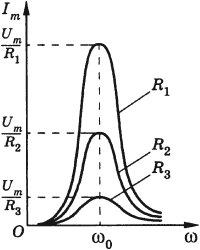
Резонанс в электрической цепи – явление резкого возрастания амплитуды вынужденных колебаний силы тока в колебательном контуре с малым активным сопротивлением при совпадении частоты вынужденных колебаний внешней ЭДС с частотой собственных колебаний в контуре.

Емкостное и индуктивное сопротивления по-разному изменяются в зависимости от частоты. С увеличением частоты растет индуктивное сопротивление, а емкостное уменьшается. С уменьшением частоты растет емкостное сопротивление и уменьшается индуктивное сопротивление. Кроме того, колебания напряжения на конденсаторе и катушке имеют разный сдвиг фаз по отношению к колебаниям силы тока: для катушки колебания напряжения и силы тока имеют сдвиг фаз ( varphi_L=-pi/2 ), а на конденсаторе ( varphi_C=pi/2 ). Это означает, что когда растет энергия магнитного поля катушки, то энергия электрического поля конденсатора убывает, и наоборот. При резонансной частоте индуктивное и емкостное сопротивления компенсируют друг друга и цепь обладает только активным сопротивлением. При резонансе выполняется условие:

Резонансная частота вычисляется по формуле:

Важно!
Резонансная частота не зависит от активного сопротивления ( R ). Но чем меньше активное сопротивление цепи, тем ярче выражен резонанс.

Чем меньше потери энергии в цепи, тем сильнее выражен резонанс. Если активное сопротивление очень мало ( (Rto0) ), то резонансное значение силы тока неограниченно возрастает. С увеличением сопротивления максимальное значение силы тока уменьшается, и при больших значениях сопротивления резонанс не наблюдается.

График зависимости амплитуды силы тока от частоты называется резонансной кривой. Резонансная кривая имеет больший максимум в цепи с меньшим активным сопротивлением.

Одновременно с ростом силы тока при резонансе резко возрастают напряжения на конденсаторе и катушке. Эти напряжения становятся одинаковыми и во много раз больше внешнего напряжения. Колебания напряжения на катушке индуктивности и конденсаторе всегда происходят в противофазе. При резонансе амплитуды этих напряжений одинаковы и они компенсируют друг друга. Падение напряжения происходит только на активном сопротивлении.

При резонансе возникают наилучшие условия для поступления энергии от источника напряжения в цепь: при резонансе колебания напряжения в цепи совпадают по фазе с колебаниями силы тока. Установление колебаний происходит постепенно. Чем меньше сопротивление, тем больше времени требуется для достижения максимального значения силы тока за счет энергии, поступающей от источника.

Явление резонанса используется в радиосвязи. Каждая передающая станция работает на определенной частоте. С приемной антенной индуктивно связан колебательный контур. При приеме сигнала в катушке возникают переменные ЭДС. С помощью конденсатора переменной емкости добиваются совпадения частоты контура с частотой принимаемых колебаний. Из колебаний всевозможных частот, возбужденных в антенне, контур выделяет колебания, равные его собственной частоте.

Резонанс может привести к перегреву проводов и аварии, если цепь не рассчитана на работу в условиях резонанса.

Гармонические электромагнитные колебания

Гармоническими электромагнитными колебаниями называются периодические изменения заряда, силы тока и напряжения, происходящие по гармоническому – синусоидальному или косинусоидальному – закону.

В электрических цепях это могут быть колебания:

силы тока – ( i=I_mcos(omega t+varphi+frac{pi}{2}); )
напряжения – ( u=U_mcos(omega t+varphi); )
заряда – ( q=q_mcos(omega t+varphi); )
ЭДС – ( varepsilon=varepsilon_msinomega t. )

В этих уравнениях ( omega ) –циклическая частота, ( varphi ) – начальная фаза колебаний, амплитудные значения: силы тока – ( I_m ), напряжения – ( U_m ) и заряда – ( q_m ).

Важно!
Если в начальный момент времени заряд имеет максимальное значение, а сила тока равна нулю, то колебания заряда совершаются по закону косинуса с начальной фазой, равной нулю. Если в начальный момент времени заряд равен нулю, а сила тока максимальна, то колебания заряда совершаются по закону синуса.

Сила тока равна первой производной заряда от времени:

Амплитуда колебаний силы тока равна:

Колебания заряда и напряжения в колебательном контуре происходят в одинаковых фазах. Амплитуда напряжения равна:

Колебания силы тока смещены по фазе относительно колебаний заряда на ( pi/2 ).

Период свободных электромагнитных колебаний

Период свободных электромагнитных колебаний находится по формуле Томсона:

где ( L ) – индуктивность катушки, ( C ) – электроемкость конденсатора.

Циклическая частота: ( omega=frac{2pi}{T}=frac{1}{sqrt{LC}} )

Важно!
Период и циклическая частота не зависят от начальных условий, а определяются только индуктивностью катушки и электроемкостью конденсатора. Амплитуда колебаний заряда и силы тока определяются начальным запасом энергии в контуре.

При свободных гармонических колебаниях происходит периодическое преобразование энергии. Период колебаний энергии в два раза меньше, чем период колебаний заряда, силы тока и напряжения. Частота колебаний энергии в два раза больше частоты колебаний заряда, силы тока и напряжения.

Переменный ток. Производство, передача и потребление электрической энергии

Переменным называется ток, изменяющийся по величине и направлению по гармоническому закону.

Переменный ток представляет пример вынужденных электромагнитных колебаний. Для описания переменного электрического тока используют следующие величины:

• мгновенное значение силы тока – i;

• мгновенное значение напряжения – u;

• амплитудное значение силы тока – Im;

• амплитудное значение напряжения –Um.

Цепь переменного тока представляет собой колебательный контур, к которому приложена внешняя синусоидальная ЭДС. В цепь переменного тока могут включаться различные нагрузки: резистор, катушка, конденсатор.

Активное сопротивление

Проводник, преобразующий всю энергию электрического тока во внутреннюю, называется активным сопротивлением ( R ). (Эту величину мы раньше называли сопротивлением.) Активное сопротивление зависит от материала проводника, его длины и площади поперечного сечения и не зависит от частоты переменного тока.

В проводнике с активным сопротивлением колебания силы тока и напряжения совпадают по фазе:

Мгновенное значение мощности: ( p=i^2R, )

среднее значение мощности за период: ( overline{p}=frac{I_m^2R}{2}. )

Действующим значением силы переменного тока ( I_Д ) называют значение силы постоянного тока, который в том же проводнике выделяет то же количество теплоты , что и переменный ток за то же время:

Действующим значением напряжения переменного тока ( U_Д ) называют значение напряжения постоянного тока, который в том же проводнике выделяет то же количество теплоты, что и переменный ток за то же время:

Для цепи с активным сопротивлением выполняется закон Ома для мгновенных, амплитудных и действующих значений.

Индуктивное сопротивление

Катушка в цепи переменного тока имеет большее сопротивление, чем в цепи постоянного тока. В такой цепи колебания напряжения опережают колебания силы тока по фазе на ( pi/2 ). Колебания силы тока и напряжения происходят по закону:

Амплитуда силы тока в катушке:

где ( L ) – индуктивность катушки.

Индуктивным сопротивлением ( X_L ) называют физическую величину, равную произведению циклической частоты на индуктивность катушки:

Индуктивное сопротивление прямо пропорционально частоте. Физический смысл индуктивного сопротивления: ЭДС самоиндукции препятствует изменению в ней силы тока. Это приводит к существованию индуктивного сопротивления, уменьшающего силу тока.

Для цепи с индуктивным сопротивлением выполняется закон Ома.

Емкостное сопротивление

В цепи постоянного тока через конденсатор ток не идет. Для переменного тока конденсатор обладает конечным сопротивлением, обратно пропорциональным его емкости. В цепи переменного тока сопротивление конденсатора меньше, чем в цепи постоянного тока.

В такой цепи колебания напряжения отстают от колебаний силы тока по фазе на ( pi/2 ). Колебания силы тока и напряжения происходят по закону:

Амплитуда силы тока в катушке: ( I_m=Comega U_m. ).

Если ввести обозначение ( X_C=frac{1}{omega C} ), то получим соотношение между амплитудными значениями силы тока и напряжения, аналогичное закону Ома: ( I_m=frac{U_m}{X_C}. )

Емкостным сопротивлением ( X_C ) называют величину, обратную произведению циклической частоты на электроемкость конденсатора. Емкостное сопротивление обратно пропорционально частоте.

Физический смысл емкостного сопротивления: изменению переменного тока в любой момент времени противодействует электрическое поле между обкладками конденсатора.

В цепи переменного тока колебания силы тока и ЭДС происходят по синусоидальному закону с одинаковой циклической частотой ( omega ) и разностью фаз ( varphi ):

Соотношения амплитудных значений силы тока ( I_m ) и ЭДС ( varepsilon_m ) в цепи переменного тока связаны между собой законом Ома для цепи переменного тока:

Он гласит: амплитуда силы переменного тока прямо пропорциональна амплитуде ЭДС и обратно пропорциональна полному сопротивлению цепи:

Величина ( Z ) называется полным сопротивлением цепи переменного тока.

Электрическая энергия имеет перед другими видами энергии следующие преимущества:

можно передавать на большие расстояния с малыми потерями;
удобно распределять между потребителями;
легко превращать в другие виды энергии.

В настоящее время производится и используется энергия переменного тока. Это связано с возможностью преобразовывать его напряжение и силу тока с малыми потерями энергии, что особенно важно при передаче электроэнергии на большие расстояния.

Различают следующие типы электростанций:

тепловые;
гидроэлектростанции;
атомные.

Получение переменного тока

Переменный ток получают с помощью генератора переменного тока.

Генератор переменного тока (электромеханический генератор переменного тока) – это устройство, преобразующее механическую энергию в электрическую. В основе работы генератора переменного тока лежит явление электромагнитной индукции.

Процесс получения переменного тока можно рассмотреть на примере вращения витка провода в однородном магнитном поле. Магнитный поток через площадь витка равен:

Если период вращения витка ( T ), то угол ( alpha=frac{2pi t}{T}=omega t ).

Тогда ( Phi=BScosomega t. )

ЭДС индукции изменяется по закону ( e=-Phi’=BSomegasinomega t=varepsilon_msinomega t. )

Амплитуда ЭДС ( varepsilon_m=BSomega. )

Если рамка содержит ( N ) витков, то ( varepsilon_m=NBSomega. )

Основные части генератора переменного тока:

обмотка статора с большим числом витков, в ней индуцируется ЭДС. Статор состоит из отдельных пластин из электротехнической стали для уменьшения нагрева от вихревых токов;
ротор (вращающаяся часть генератора) создает магнитное поле. Для получения нужной частоты переменного тока может иметь несколько пар полюсов. На гидроэлектростанциях в генераторе число пар полюсов равно 40–50, на тепловых электростанциях – 10^-16;
клеммы для снятия напряжения.

Промышленные генераторы вырабатывают напряжение порядка 10⁴ В. Промышленная частота переменного тока в нашей стране 50 Гц.

Передача электроэнергии

Электроэнергия производится в основном вдалеке от основных потребителей энергии, там, где есть топливные ресурсы.

С электростанции переменный ток по проводам линии электропередач (ЛЭП) поступает к различным потребителям электрической энергии. Для уменьшения потерь при передаче переменного тока необходимо использовать высокое напряжение. Чем длиннее линия, тем выше должно быть напряжение. В высоковольтных ЛЭП оно может достигать 500 кВ. Генераторы на электростанциях вырабатывают напряжение 16–20 кВ. Потребителям не нужно высокое напряжение. Возникает необходимость преобразования напряжения. С электростанции электрический ток поступает на повышающую подстанцию, затем передается по линии электропередач на понижающую подстанцию, где напряжение понижается до 6–10 кВ, а затем до 220–380 В. Для преобразования напряжения используют трансформатор.

Трансформатор – устройство, преобразующее переменное напряжение без изменения его частоты.

На схемах трансформатор обозначается:

Основные части трансформатора:

замкнутый сердечник из электротехнической стали;
две катушки-обмотки.

Катушка, подключаемая к источнику переменного напряжения, называется первичной обмоткой; катушка, к которой подключается нагрузка, – вторичной обмоткой.

Сердечник набирается из отдельных пластин для уменьшения потерь на нагревание вихревыми токами.

Принцип действия основан на явлении электромагнитной индукции. При подключении первичной обмотки к полюсам источника напряжения в ней возникает переменный ток. Напряжение изменяется с течением времени по гармоническому закону. С такой же частотой будут изменяться сила тока в катушке и магнитный поток, создаваемый этим током.

При изменении магнитного потока в каждом витке провода первичной обмотки возникает переменная ЭДС самоиндукции. Этот магнитный поток будет пронизывать и вторую катушку. В каждом ее витке возникает ЭДС индукции, изменяющаяся по гармоническому закону с той же частотой. Число витков в обмотках различно. Отношение ЭДС самоиндукции ( varepsilon_1 ) в первичной обмотке к ЭДС индукции во вторичной обмотке ( varepsilon_2 ) равно отношению числа витков в первичной обмотке ( N_1 ) к числу витков во вторичной обмотке ( N_2 ):

Режим работы

Режим холостого хода – разомкнута цепь вторичной обмотки. Напряжение ( U_2 ) на ее концах в любой момент времени равно ЭДС индукции ( varepsilon_2 ), взятой с противоположным знаком. Поэтому можно записать:

где ( k ) – коэффициент трансформации.

Если ( k>1 ), то трансформатор понижающий, если ( k<1 ), то повышающий.

Режим нагрузки. При подключении нагрузки к концам вторичной обмотки в ней возникает переменный ток. Напряжение ( U_2 ) на ее концах в любой момент времени отличается от ЭДС индукции ( varepsilon_2 ) на величину падения напряжения на внутреннем сопротивлении вторичной обмотки ( r ): ( U_2=varepsilon_2-I_2r ) или ( U_2=I_2R ).

Мощность тока в обмотках одинакова. Поэтому увеличение напряжения на входе повышающего трансформатора в ( k ) раз сопровождается уменьшением силы тока во вторичной катушке во столько же раз.

В трансформаторе нет потерь на трение, так как нет вращающихся частей. Потери в сердечнике состоят из потерь на нагревание и на перемагничивание.

Отношение мощности ( P_2 ), потребляемой нагрузкой, к мощности ( P_1 ), потребляемой первичной обмоткой трансформатора, называется коэффициентом полезного действия трансформатора:

КПД трансформатора – 98%.

Потребление электрической энергии: промышленность – около 70%; сельское хозяйство; транспорт; строительство; средства связи; в быту.

Электромагнитное поле

Электромагнитное поле – это особый вид материи, с помощью которого осуществляется электромагнитное взаимодействие заряженных тел или частиц.

Это понятие было введено Д. Максвеллом, развившим идеи Фарадея о том, что переменное магнитное поле порождает вихревое электрическое поле.

Всякое изменение магнитного поля порождает в окружающем пространстве вихревое электрическое поле, силовые линии которого замкнуты. Вихревое электрическое поле порождает появление вихревого магнитного поля и так далее. Эти переменные электрическое и магнитное поля, существующие одновременно, и образуют единое электромагнитное поле.

Характеристиками этого поля являются вектор напряженности и вектор магнитной индукции.

Если электрический заряд покоится, то вокруг него существует только электрическое поле.

Если напряженность электрического поля равна нулю, а магнитная индукция отлична от нуля, то обнаруживается только магнитное поле.

Если электрический заряд двигается с постоянной скоростью, то вокруг него существует электромагнитное поле.

Максвелл предположил, что при ускоренном движении зарядов в пространстве будет возникать возмущение, которое будет распространяться в вакууме с конечной скоростью. Когда это возмущение достигнет второго заряда, то изменится сила, с которой электромагнитное поле действует на этот заряд.

При ускоренном движении заряда происходит излучение электромагнитной волны. Электромагнитное поле материально. Оно распространяется в пространстве в виде электромагнитной волны.

Свойства электромагнитных волн

Электромагнитная волна – это изменяющееся во времени и распространяющееся в пространстве электромагнитное поле.

Существование электромагнитных волн было теоретически предсказано английским физиком Дж. Максвеллом в 1864 году. Электромагнитные волны были открыты Г. Герцем.

Источник электромагнитной волны – ускоренно движущаяся заряженная частица – колеблющийся заряд.

Важно!
Наличие ускорения – главное условие излучения электромагнитной волны. Интенсивность излученной волны тем больше, чем больше ускорение, с которым движется заряд.

Источниками электромагнитных волн служат антенны различных конструкций, в которых возбуждаются высокочастотные колебания.

Электромагнитная волна называется монохроматической, если векторы ( vec{E} ) и ( vec{B} ) совершают гармонические колебания с одинаковой частотой (частотой волны).

Длина электромагнитной волны: ( lambda=cT=frac{c}{nu}, )

где ( c ) – скорость электромагнитной волны, ( T ) – период, ( nu ) – частота электромагнитной волны.

Свойства электромагнитных волн

В вакууме электромагнитная волна распространяется с конечной скоростью, равной скорости света 3·10⁸ м/с.
Электромагнитная волна поперечная. Колебания векторов напряженности переменного электрического поля и магнитной индукции переменного магнитного поля взаимно перпендикулярны и лежат в плоскости, перпендикулярной к вектору скорости волны.
Электромагнитная волна переносит энергию в направлении распространения волны.

Важно!
Электромагнитная волна в отличие от механической волны может распространяться в вакууме.

Плотность потока или интенсивность – это электромагнитная энергия, переносимая через поверхность единичной площади за единицу времени.

Обозначение – ( I ), единица измерения в СИ – ватт на квадратный метр (Вт/м²).

Важно!
Плотность потока излучения электромагнитной волны от точечного источника убывает обратно пропорционально квадрату расстояния от источника и пропорциональна четвертой степени частоты.

Электромагнитная волна обладает общими для любых волн свойствами, это:

отражение,
преломление,
интерференция,
дифракция,
поляризация.

Электромагнитная волна производит давление на вещество. Это означает, что у электромагнитной волны есть импульс.

Различные виды электромагнитных излучений и их применение

Электромагнитные излучения имеют длины волн от 10^-12 до 10⁴ м или частоты от 3·10⁴ до 3·10²⁰.

Различают следующие виды электромагнитных излучений:

радиоволны;
инфракрасное излучение;
видимое излучение (свет);
ультрафиолетовое излучение;
рентгеновское излучение;
гамма-излучение.

Границы между диапазонами условны, но излучения имеют качественные различия в свойствах. При переходе от излучений с малой частотой к излучениям с большей частотой волновые свойства проявляются слабее, а корпускулярные (квантовые) – сильнее.

Радиоволны

( lambda ) = 10³–10^-3 м, ( nu ) = 10⁵–10¹¹ Гц. Источники радиоволн – колебательный контур, вибратор.

Радиоволны делятся на:

длинные (длина больше 1 км);
средние (от 100 м до 1 км);
короткие (от 10 до 100 м);
ультракороткие (меньше 10 м).

Свойства: отражение, поглощение, интерференция, дифракция. Применение: радиосвязь, телевидение, радиолокация.

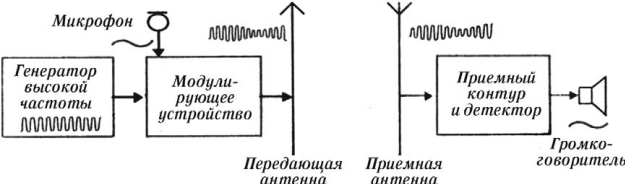
Радиосвязью называется передача информации с помощью радиоволн. Радиосвязь осуществляется с помощью модулированных радиоволн. Модуляцией радиоволны называется изменение ее параметров (амплитуды, частоты, начальной фазы) с частотой, меньшей частоты передаваемой волны.

Схема радиосвязи показана на рисунке:

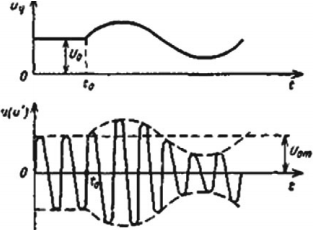
Передача радиоволн. Генератор высокой частоты вырабатывает высокочастотные колебания несущей частоты. Звуковые колебания поступают в микрофон, где преобразуются в электромагнитные колебания. В модуляторе эти колебания преобразуются в модулированные колебания. После усиления модулированные колебания поступают в передающую антенну, которая излучает электромагнитные волны. На рисунке показан звуковой сигнал низкой частоты и модулированный высокочастотный сигнал.

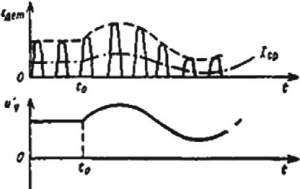
Прием радиоволн. Электромагнитные колебания поступают в приемную антенну и вызывают электромагнитные колебания в приемном контуре. Эти колебания поступают в усилитель, а затем в детектор. В качестве детектора используют устройство с односторонней проводимостью. Это может быть полупроводниковый диод. В детекторе сигнал демодулируют (детектируют). Процесс детектирования заключается в выделении из высокочастотных модулированных колебаний колебаний низкой (звуковой) частоты. После сглаживания и усиления сигнал поступает в динамик. На рисунке показаны процессы детектирования (демодуляции) и сглаживания.

Радиолокацией называют обнаружение и определение местоположения объектов с помощью радиоволн. Излучение осуществляется короткими импульсами. В интервале времени между излучением двух последовательных импульсов осуществляется прием отраженного от объекта сигнала. Для радиолокации используют ультракороткие радиоволны.

Инфракрасное (тепловое) излучение

( lambda ) = 10^-3 – 10^-7 м, ( nu ) = 10¹¹ – 10¹⁴ Гц. Источники – атомы и молекулы вещества.

Это излучение испускают все тела при температуре, отличной от 0 К. Свойства: нагревает вещество при поглощении; интерференция; дифракция; проходит через дождь, снег, дымку; невидимо; преломление, отражение. Применение: в приборах ночного видения, в физиотерапии, промышленности (для сушки). Регистрируют с помощью термопары, болометра, фотографическим методом.

Видимое излучение

( lambda ) = 8·10^-7 – 4·10^-7 м, ( nu ) = 4·10¹¹ – 8·10¹⁴ Гц.

Это излучение воспринимается глазом. Свойства: отражение, преломление, поглощение, интерференция, дифракция.

Ультрафиолетовое излучение

( lambda ) = 10^-8 – 4·10^-7 м, ( nu ) = 8·10¹⁴ – 3·10¹⁵ Гц. Источники – кварцевые лампы.

Ультрафиолетовое излучение дают светящиеся пары ртути и твердые тела, у которых температура выше 1000°С. Свойства: химическое действие; большая проникающая способность; биологическое действие; невидимо. Применение: в медицине, промышленности. Регистрируют фотографическими методами.

Рентгеновское излучение

( lambda ) = 10^-8 – 10^-11 м, ( nu ) = 3·10¹⁶ – 3·10¹⁹ Гц. Источник – рентгеновские трубки.

Возникает при торможении быстрых электронов. Свойства: высокая химическая активность; биологическое действие; интерференция; дифракция на кристаллической решетке; высокая проникающая способность. Применение: в медицине, промышленности, науке.

Гамма-излучение

Длина волны меньше 10^-11 м, частота от 10²⁰ Гц и выше. Источник – ядерные реакции.

Свойства: высокая проникающая способность, сильное биологическое действие. Применение: в медицине, промышленности (дефектоскопия), науке.

Шкала электромагнитных излучений позволяет сделать вывод: все электромагнитные излучения обладают одновременно волновыми и квантовыми свойствами, которые дополняют друг друга.

Важно!
Волновые свойства сильнее выражены при малых частотах и больших длинах волн, а квантовые – при больших частотах и малых длинах волн.

Решение задач по теме «Электромагнитные колебания и волны»

По этой теме можно выделить четыре группы задач:

на определение параметров колебательного контура;
на уравнения гармонических электромагнитных колебаний;
на применение закона Ома;
на расчет мощности и КПД трансформатора.

Решение первой группы задач на определение параметров колебательного контура основано на использовании формулы Томсона (формулы периода свободных электромагнитных колебаний) и закона сохранения и превращения энергии в колебательном контуре. Поэтому необходимо записать уравнения для мгновенных значений заряда и напряжения на конденсаторе и силы тока в катушке; записать уравнение для полной энергии колебательного контура в произвольный момент времени. В качестве дополнительных формул могут понадобиться формулы электроемкости плоского конденсатора, индуктивности катушки и длины электромагнитной волны. Помните, что скорость распространения электромагнитной волны в вакууме равна скорости света – 3·10⁸ м/с. В среде с показателем преломления ( n ) скорость света можно рассчитать по формуле: ( v=frac{c}{n}. )

Важно!
Амплитудное значение напряжения – ( U_m=frac{q_m}{C} ), амплитудное значение силы тока – ( I_m=q_momega ).

При решении второй группы задач на уравнения гармонических электромагнитных колебаний рекомендуется записать заданное в задаче уравнение и уравнение гармонических колебаний в общем виде. Сравнить эти уравнения и определить основные характеристики: амплитуду, частоту, фазу.

При решении задач на закон Ома нужно помнить, что электроизмерительные приборы показывают действующие значения напряжения и силы тока. Действующие значения величин пропорциональны амплитудным значениям. Важно помнить, что резонанс возникает при равенстве индуктивного и емкостного сопротивлений.

Решение четвертой группы задач на расчет мощности и КПД трансформатора опирается на знание формул КПД и мощности в цепи.

Основные формулы раздела «Электромагнитные колебания и волны»

Электромагнитные колебания и волны

3.3 (65.11%) 47 votes

Источник

Колебательный контур

Колебательный контур ― это электрическая цепь, содержащая катушку индуктивности и конденсатор. В такой электрической цепи происходят колебания электрического тока и напряжения, и взаимная трансформация энергии электрического поля и энергии магнитного поля.

Процессы в колебательном контуре У заряженного конденсатора на одной пластине находится определенное количество отрицательного заряда, а на другой ― положительного. Поскольку между пластинами конденсатора расположен диэлектрик (или воздух, и пластины не соприкасаются) ― заряд не может прямо перейти из одной пластины на другую. Но как только такой конденсатор оказывается подключенным к проводящей цепи, один конец которой связан с одной пластиной ― а другой с другой, заряды начинают переходить от пластины к пластине по «длинному пути» ― через всю цепь. Постепенно конденсатор разряжается ― теряет заряд, а в цепи наблюдается ток, ведь ток ― это направленные движения зарядов.

Если в цепи, кроме проводов и резисторов, находится катушка индуктивности, в равномерный и быстрый процесс перераспределения заряда вмешивается ЭДС самоиндукции катушки. Согласно правилу Ленца, втекающий в катушку ток вызывает ЭДС самоиндукции ― а ЭДС самоиндукции создает индуцированный ток, направленный так, чтобы препятствовать изменению тока в цепи. Если ток в цепи вдруг резко увеличивается ― индукционный ток стремиться его уменьшить, если ток в сети вдруг уменьшается ― индукционный ток стремиться его увеличивать.

Поэтому из―за катушки индуктивности заряд не переходит сразу через всю цепь, от одной обкладки конденсатора к другой. Сила тока в цепи медленно увеличивается ― потому что ее быстрому росту препятствует ЭДС самоиндукции катушки. Максимальной сила тока становится в тот момент, когда конденсатор разряжен (обе его обкладки обладают нулевым зарядом). В этот момент сила тока максимальна благодаря тому, что как только ее перестает наращивать конденсатор за счет потерянных зарядов ― ЭДС самоиндукции прекращает ей препятствовать.

Но разряженный конденсатор больше не может поддерживать силу току ― ведь заряда на его обкладках нет, и не будь в цепи катушки индукции, ток бы прекратился. Однако здесь вновь срабатывает правило Ленца: после того как сила тока достигла максимума и начала уменьшаться ― в катушке возникает ЭДС и индукционные токи, которые стремятся вернуть силу тока такой, как она была ― максимальной. Поэтому, даже после того, как конденсатор разряжен, в цепи продолжает течь ток. Заряды попадают на обкладку конденсатора и постепенно заряжают ее. На этот раз, та обкладка конденсатора, которая была заряжена положительно и принимала заряд, начинает накапливать отрицательный заряд, а так обкладка, которая была заряжена отрицательно, становится заряженной положительно.

После того как конденсатор зарядиться ― он вновь начинает разряжаться. Таким образом, в контуре происходят колебания заряда, силы тока, напряжения и энергий магнитного и электрического поля в катушке индуктивности и конденсаторе.

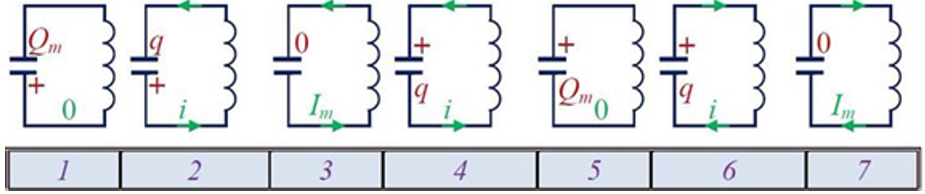
Цикл процессов, происходящих в колебательном контуре:

1: Начальное состояние ― конденсатор заряжен до максимального заряда Q_m, но силы тока в цепи пока нет.

2. Конденсатор разряжается ― заряд переходит от одной обкладки на другую через всю цепь, сила тока в цепи постепенно увеличивается.

3. Конденсатор разряжен ― весь заряд с обкладок уже ушел, сила тока в цепи максимальна и равна I_m.

4. Конденсатор заряжается ― сила тока в цепи уменьшается, а конденсатор получает заряд.

5. Конденсатор перезаряжен ― но теперь та обкладка, которая была положительно заряженной, стала отрицательно заряженной, и наоборот. Тока в цепи нет.

6. Конденсатор вновь разряжается, но в обратную сторону ― и ток течет в сторону, обратную тому, что был на этапе 2.

7. Конденсатор разряжен ― ток достиг максимума, а заряда на конденсаторе нет.

На графике показаны колебания изменения напряжения на конденсаторе (U), колебания изменения заряда на конденсаторе (Q), и колебания силы тока в катушке индуктивности (I). Период колебаний параметров колебательного контура равен T.

Для постоянного тока сила тока определялась как количество заряда, прошедшее через сечение проводника за некоторый промежуток времени: (I = frac{mathrm{Delta}q}{mathrm{Delta}t}), где

I ― сила тока, [А];

∆q ― количество заряда, [Кл];

∆t ― время, [c].

Но переменный ток изменяет в цепи свою величину и свое направление, поэтому силу переменного тока определяют как производную количества заряда по времени:

(I = frac{mathrm{Delta}q}{mathrm{Delta}t} = q^{‘}left( t right), )где

I ― сила тока, [А];

q ― количество заряда, [Кл];

t ― время, [c].

Заряд в колебательном контуре изменяется по гармоническому закону q(t) = Q_maxsin(ωt + φ₀), где

q ― количество заряда, [Кл];

Q_max ― максимальный заряд (амплитуда колебаний заряда), [Кл];

ω ― циклическая частота колебаний [рад/с];

φ₀ ― начальная фаза колебаний, [рад];

t ― время, [c].

Следовательно, сила тока в контуре изменяется по закону I = q_t^‘ = (Q_maxsin(ωt + φ₀))_t^‘ = Q_maxωcos(ωt + φ₀). При этом Q_maxω ― максимальная сила тока в цепи: I_max = Q_maxω.

Сила тока в цепи переменного тока равна I = I_maxcos(ωt + φ₀), где

I_max ― максимальная сила тока в цепи, [A];

ω ― циклическая частота колебаний [рад/с];

φ₀ ― начальная фаза колебаний, [рад];

t ― время, [c].

В колебательном контуре происходит трансформация энергии электрического поля в энергию магнитного поля.

(W_{e} = frac{text{qU}}{2} = frac{CU^{2}}{2} = frac{q^{2}}{2C})

где

W_e ― энергия электрического поля конденсатора, [Дж];

C ― электроемкость конденсатора, [Ф];

U ― напряжение на обкладках конденсатора, [В];

q ― заряд на обкладках конденсатора, [Кл].

Так как напряжение на обкладках конденсатора в цепи переменного тока величина переменная, то и энергия электрического поля конденсатора ― переменна.

Энергия электрического поля конденсатора всегда положительна.

Энергия магнитного поля индукционной катушки равна (W_{m} = frac{LI^{2}}{2}), где

W_m ― энергия магнитного поля индукционной катушки, [Дж];

L ― индуктивность катушки, [Гн];

I ― сила тока, [А].

Как видно из формулы, энергия магнитного поля катушка также всегда положительна ― вне зависимости от того, какое из направлений силы тока принято в качестве положительного, а какое ― в качестве отрицательно, сила тока, возведенная в квадрат, всегда будет положительной величиной.

График изменения энергии электрического поля конденсатора W_e и магнитного поля катушки W_m за один цикл работы колебательного контура показан на рисунке выше.

В начальный момент времени конденсатор полностью заряжен, и энергия его электрического поля максимальна и равна W_{e max}, а энергия магнитного поля катушки равна нулю, так как ток в цепи отсутствует. По мере разрядки конденсатора, энергия его электрического поля уменьшается ― из-за того, что уменьшается заряд обкладок, а энергия магнитного поля катушки увеличивается ― поскольку заряд, ушедший из конденсатора, создает ток в цепи, сила которого увеличивается. В момент, когда конденсатор разряжается полностью, энергия его электрического поля равна нулю ― а энергия магнитного поля катушки максимальна W_{m max}. Затем, по мере перезарядки конденсатора, энергия его электрического поля восстанавливается до максимума, а энергия магнитного поля катушки уменьшается до нуля.

Согласно закону сохранения энергии, полная энергия колебательного контура постоянна в любой момент времени: W = W_{m max} = W_{e max} = W_e + W_m, где

W ― полная энергия свободных электромагнитных колебаний, W = const, [Дж];

W_{m max} ― максимальная энергия магнитного поля катушки индуктивности, [Дж];

W_{e max} ― максимальная энергия электрического поля конденсатора, [Дж];

W_m ― энергия магнитного поля катушки индуктивности, [Дж];

W_e ― энергия электрического поля конденсатора, [Дж];

или (W = frac{CU^{2}}{2} + frac{LI^{2}}{2} = frac{CU_{max}^{2}}{2} = frac{LI_{max}^{2}}{2}), где

W ― полная энергия свободных электромагнитных колебаний, W = const, [Дж];

C ― электроемкость конденсатора, [Ф];

U ― напряжение на обкладках конденсатора, [В];

U_max ― максимальное напряжение на обкладках конденсатора, [В];

L ― индуктивность катушки, [Гн];

I ― сила тока в катушке индуктивности, [А];

I_max ― максимальная сила тока в катушке индуктивности, [A].

Частота колебаний силы тока и напряжения в колебательном контуре определяется формулой Томпсона и зависят только от индуктивности катушки и электроемкости конденсатора. Частота и период гармонических колебаний в колебательном контуре равны (nu = frac{1}{2pisqrt{text{LC}}}) и (T = 2pisqrt{text{LC}})где

v ― частота колебаний [Гц];

Т ― период колебаний [c];

L ― индуктивность катушки [Гн];

С ― электроёмкость конденсатора [Ф].

Источник

Электромагнитные колебания

Колебательный контур

Энергетические превращения в колебательном контуре

Электромеханические аналогии

Гармонический закон колебаний в контуре

Вынужденные электромагнитные колебания

Колебательный контур

Задачи для практики

Задача 1

Решение

Задача 2

Решение

Задача 3

Решение

Задача 4

Решение

Задача 5

Решение

Задача 6

Решение

Задача 7

Решение

Задача 8

Решение

Задача 9

Решение

Задача 10

Решение

Задача 11

Решение

Задача 12

Решение

Задача 13

Решение

Задача 14

Решение

Задача 15

Решение

Задача 16

Решение

Задача 17

Решение

Задача 18

Решение

Задача 19

Решение

Задача 20

Решение

Рекомендуемые курсы подготовки

Электромагнитные колебания и волны

Свободные электромагнитные колебания. Колебательный контур

Вынужденные электромагнитные колебания. Резонанс

Гармонические электромагнитные колебания

Переменный ток. Производство, передача и потребление электрической энергии

Емкостное сопротивление

Электромагнитное поле

Свойства электромагнитных волн

Различные виды электромагнитных излучений и их применение

Основные формулы раздела «Электромагнитные колебания и волны»

Колебательный контур