Комбинация тел формулы егэ

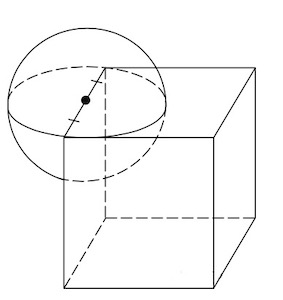
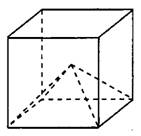
Задача 1. Объем прямоугольного параллелепипеда, описанного около сферы, равен 10648. Найдите радиус сферы.

Решение: + показать

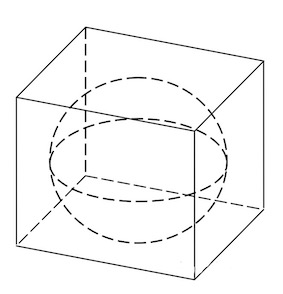
Задача 2. В куб вписан шар радиуса 7. Найдите объем куба.

Решение: + показать

Задача 3. Шар, объём которого равен 44pi, вписан в куб. Найдите объём куба.

Решение: + показать

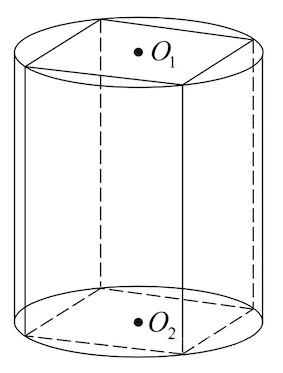
Задача 4. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 1. Объем параллелепипеда равен 5. Найдите высоту цилиндра.

353b267c2013feb3c313028d5a955343.jpg

Решение:  + показать

Задача 5. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 18. Найдите объем параллелепипеда.

Решение:  + показать

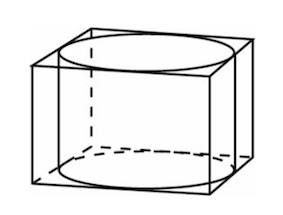
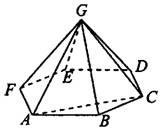
Задача 6. Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.

353b267c2013feb3c313028d5a955343.jpg

Решение: + показать

Задача 7. В основании прямой призмы лежит квадрат со стороной 8. Боковые ребра равны frac{5}{pi}. Найдите объем цилиндра, описанного около этой призмы.

Решение: + показать

Задача 8. Около шара описан цилиндр, площадь поверхности которого равна 81. Найдите площадь поверхности шара.

Решение: + показать

Задача 9.  Цилиндр описан около шара. Объем цилиндра равен 6. Найдите объем шара.

Решение: + показать

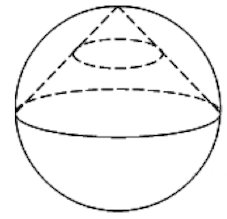
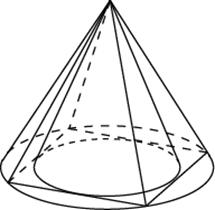
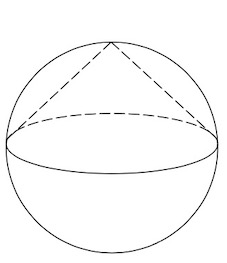
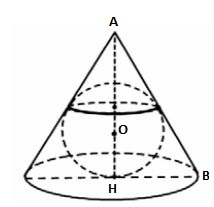
Задача 10. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 156. Найдите объем конуса.

Решение: + показать

Задача 11. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 27. Найдите объем шара.

Решение: + показать

Задача 12. Середина ребра куба со стороной 0,8 является центром шара радиуса 0,4. Найдите площадь S части поверхности шара, лежащей внутри куба. В ответе запишите frac{S}{pi}.

Решение: + показать

Задача 13. Вершина A куба ABCDA_1B_1C_1D_1  со стороной 0,7 является центром сферы, проходящей через точку A_1. Найдите площадь S части сферы, содержащейся внутри куба. В ответе запишите величину frac{S}{pi}.

Решение: + показать

Задача 14. Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 45.

Решение:  + показать

Задача 15. Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна 44sqrt2. Найдите площадь боковой поверхности конуса.

Решение:  + показать

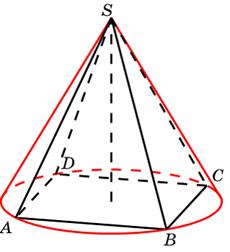
Задача 16. Конус описан около правильной четырехугольной пирамиды со стороной основания 3 и высотой 5. Найдите его объем, деленный на pi.

Решение:  + показать

Задача 17. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?

Решение:  + показать

Задача 18. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 156. Найдите объем конуса.

Решение:  + показать

Задача 19. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Радиус сферы равен 5sqrt2.  Найдите образующую конуса.

Решение:  + показать

Задача 20. В основании прямой призмы лежит прямоугольный треугольник с катетами 1 и 10. Боковые ребра равны frac{6}{pi}. Найдите объем цилиндра, описанного около этой призмы.

Решение:  + показать

Задача 21. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен sqrt3, а высота равна 1.

Решение:  + показать

Задача 22.  Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен 2sqrt3, а высота равна 4.

Решение:  + показать

Задача 23. Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 27.

Решение:  + показать

Задача 24. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен  sqrt3, а высота равна 1.

7cf26e083d9bb851575e3de37aa10183.jpg

Решение: + показать

Задача 25. Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен sqrt{0,03} , а высота равна 1.

104d513cea7de3f3a8f8400a1fd77d8c.jpg

Решение: + показать

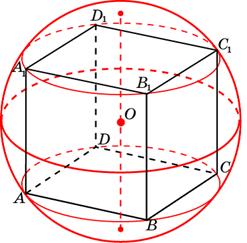
Задача 26. Около куба с ребром sqrt{243}  описан шар. Найдите объем этого шара, деленный на pi.

Решение: + показать

Задача 27. Куб вписан в шар радиуса 6,5sqrt3. Найдите объем куба.

Решение: + показать

тестВы можете пройти тест “Комбинация тел”

Источник


Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

1

Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шара.

2

Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.

3

Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.

4

В куб вписан шар радиуса 1. Найдите объем куба.

5

В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны дробь: числитель: 5, знаменатель: Пи конец дроби . Найдите объем цилиндра, описанного около этой призмы.

Пройти тестирование по этим заданиям

Источник
Skip to content

ЕГЭ Профиль №8. Комбинация тел

ЕГЭ Профиль №8. Комбинация телadmin2018-08-14T13:32:53+03:00

Используйте LaTeX для набора формулы
Источник

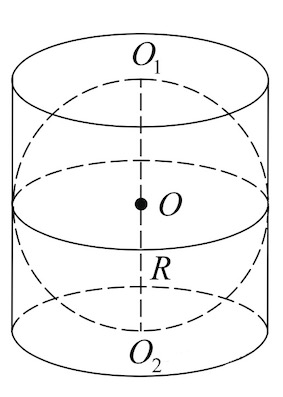
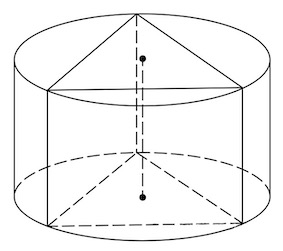
По условию цилиндр описан около шара.

Объем цилиндра известен. Требуется найти объем шара.

Введем обозначения:

  • (displaystyle r) – радиус основания цилиндра,
  • (displaystyle h) – высота цилиндра.


Радиусы шара и основания цилиндра совпадают, а высота цилиндра равна удвоенному радиусу:

 (displaystyle h=2r)

Определение

Цилиндр описан вокруг шара, если шар касается касается оснований цилиндра и всех его образующих.

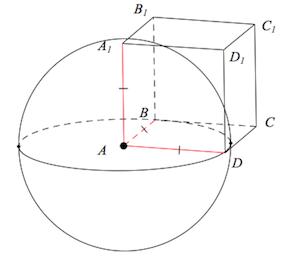
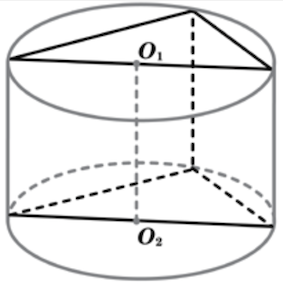
Рассмотрим осевое сечение (displaystyle AA_1B_1B small .)

Это прямоугольник, в который вписана окружность радиуса (displaystyle r small .)

Стороны прямоугольника равны между собой:

(displaystyle AB=AA_1=A_1B_1=BB_1=2r {small .})

Значит, (displaystyle AA_1B_1B ) – квадрат со стороной (displaystyle 2rsmall ,) где (displaystyle r) – радиус шара и оснований цилиндра. 

Поэтому высота цилиндра (displaystyle h=O_1O_2=2rsmall .)

Для нахождения объема шара воспользуемся формулой: 

(displaystyle V_ш=frac {4}{3} pi cdot r^3 { small ,})

где (displaystyle r) –  радиус шара.

Значит, для вычисления объема шара необходимо знать (displaystyle r^3small .)

По условию задачи известен объем цилиндра.

Объём цилиндра вычисляется по формуле:

(displaystyle V_ц=pi r^2 cdot h { small .})

Так как (displaystyle h=2r{ small ,}) формула для вычисления объема цилиндра примет вид:

(displaystyle V_ц=pi r^2 cdot 2r { small ,})

(displaystyle V_ц=2pi cdot r^3 small .)

Найдем (displaystyle r^3 {small,}) используя известный объем цилиндра (displaystyle V_ц=33 {small:})


 (displaystyle r^3 = frac{33}{2 pi} )

Подставляя (displaystyle V_ц=33) в формулу объема цилиндра, получаем:

(displaystyle V_ц=2pi cdot r^3 small ,)

(displaystyle 33=2pi cdot r^3 { small ,})

откуда

(displaystyle r^3 = frac{33}{2 pi} small .)

Подставим найденное значение (displaystyle r^3) в формулу для вычисления объема шара:

(displaystyle V_ш=frac {4}{3} pi cdot r^3 { small ,})

(displaystyle V_ш=frac {4}{3} pi cdot frac{33}{2 pi}= frac{4 pi cdot 33}{3 cdot 2 pi}=22{ small .})

Значит, объем шара равен (displaystyle 22 small .)

Ответ: (displaystyle 22{small .} )

Источник
Задачи на комбинации тел. Готовимся к ЕГЭ по математике. Геометрия. Урок 32

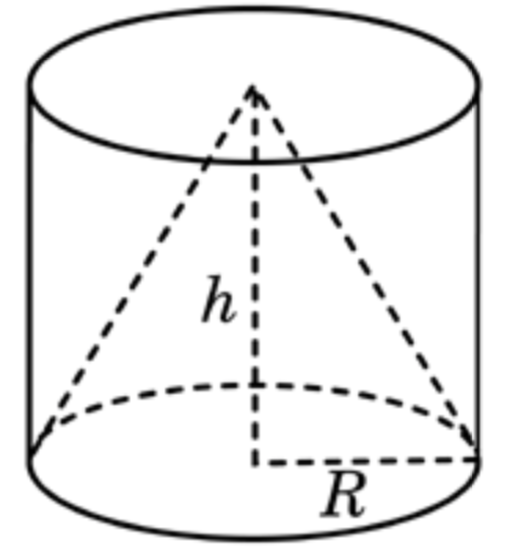
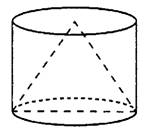
Задача 1. Цилиндр и конус имеют общее основание и общую высоту (см. рис. 1). Вычислите объём цилиндра, если объём конуса равен 16.
cilinder_016

Рис. 1.

Решение.
Объём конуса равен displaystyle frac{1}{3}Sh, а объём цилиндра — displaystyle Sh, где S — площадь их общего основания, h — общая высота. Видно, что объём цилиндра в 3 раза больше объёма конуса и равен displaystyle 16cdot 3=48.
Ответ: 48.
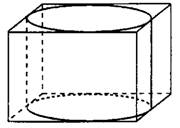
Задача 2. Прямоугольный параллелепипед описан около цилиндра (см. рис. 2), радиус основания которого равен 5. Объём параллелепипеда равен 600. Найдите высоту цилиндра.
Решение.
Каждая сторона прямоугольника в основании параллелепипеда равна диаметру цилиндра, то есть displaystyle 2cdot 5=10. Площадь основания параллелепипеда равна displaystyle 10cdot 10=100.
cilinder_018

Рис. 2.

Высоту h параллелепипеда находим из формулы объёма параллелепипеда: displaystyle 100h=600;; h=6. Найденная высота параллелепипеда одновременно является и высотой цилиндра.
Ответ: 6.
Задача 3. Объём куба равен 30 (см. рис. 3). Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
cilinder_020

Рис. 3.

Решение.
Рассмотрим куб как четырёхугольную призму. Его объём равен displaystyle V=S_{OCH}h. Основание пирамиды совпадает с основанием призмы, а высота вдвое меньше высоты призмы. Поэтому
displaystyle V_{Pi }=frac{1}{3}S_{OCH}h_{Pi }=frac{1}{3}S_{OCH}cdot frac{1}{2}h_{K}=frac{1}{6}cdot V_{K}=frac{1}{6}cdot 30=5.
Ответ: 5.
Задача 4. Объём правильной шестиугольной пирамиды GABCDEF равен 60 (см. рис. 4). Найдите объём треугольной пирамиды GABC.
cilinder_022

Рис. 4.

Решение.
Обозначим сторону шестиугольника в основании пирамиды через r. Правильный шестиугольник можно разбить на 6 правильных треугольников, поэтому площадь шестиугольника равна displaystyle 6cdot frac{r^{2}sqrt{3}}{4}=frac{3sqrt{3}}{2}r^{2}. Найдём площадь треугольника ABC.
displaystyle S_{ABC}=frac{1}{2}cdot ABcdot BCcdot sinangle ABC=frac{1}{2}cdot r^{2}cdot frac{sqrt{3}}{2}=frac{sqrt{3}}{4}r^{2}=frac{1}{6}S_{ABCDEF}.
Таким образом, площадь основания пирамиды GABC в 6 раз меньше площади основания шестиугольной пирамиды, а их высоты совпадают. Поэтому объёмы этих пирамид находятся в том же соотношении, что и площади их оснований.
displaystyle V_{GABC}=frac{1}{6}V_{GABCDEF}=frac{1}{6}cdot 60=10.
Ответ: 10.

Источник

Инфоурок

›

Геометрия

›Презентации›Презентация. Задачи ЕГЭ №5. Стереометрия. «Комбинации тел»



Скачать материал

Задачи ЕГЭ№5 Стереометрия«Комбинации тел»17 января 2022гСоставила: Пименова...



Скачать материал

  • Сейчас обучается 20 человек из 12 регионов

  • Сейчас обучается 32 человека из 22 регионов

  • Сейчас обучается 1081 человек из 83 регионов

Описание презентации по отдельным слайдам:

  • Задачи ЕГЭ№5 Стереометрия«Комбинации тел»17 января 2022гСоставила: Пименова...

    1 слайд

    Задачи ЕГЭ
    №5 Стереометрия
    «Комбинации тел»
    17 января 2022г
    Составила:
    Пименова Мария Юрьевна,
    Учитель математики первой категории
    МБОУ «Шалинской СОШ №45»
    Задания взяты из «Решу ЕГЭ»

  • Задача №1Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18....

    2 слайд

    Задача №1
    Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шара.
    Задания взяты из «Решу ЕГЭ»

  • Задача №1. РешениеШар вписан в цилиндр. Площадь полной поверхности цилиндра р...

    3 слайд

    Задача №1. Решение
    Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шара.
    Радиусы шара и основания цилиндра равны. Площадь поверхности цилиндра, с радиусом основания r и высотой 2r равна

    Задания взяты из «Решу ЕГЭ»

  • Задача №2Прямоугольный параллелепипед описан около цилиндра, радиус основания...

    4 слайд

    Задача №2
    Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.
    Задания взяты из «Решу ЕГЭ»

  • Задача №2. РешениеПрямоугольный параллелепипед описан около цилиндра, радиус...

    5 слайд

    Задача №2. Решение
    Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.
    Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому площадь основания равна 4, а объем параллелепипеда равен

    Задания взяты из «Решу ЕГЭ»

  • Задача №3Прямоугольный параллелепипед описан около цилиндра, радиус основания...

    6 слайд

    Задача №3
    Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.
    Задания взяты из «Решу ЕГЭ»

  • Задача №3. РешениеПрямоугольный параллелепипед описан около цилиндра, радиус...

    7 слайд

    Задача №3. Решение
    Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.
    Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому сторона основания равна 8, а площадь основания равна 64. Тогда высота цилиндра равна

    Задания взяты из «Решу ЕГЭ»

  • Задача №4В куб вписан шар радиуса 1. Найдите объем куба.Задания взяты из "Реш...

    8 слайд

    Задача №4
    В куб вписан шар радиуса 1. Найдите объем куба.
    Задания взяты из «Решу ЕГЭ»

  • Задача №4. РешениеВ куб вписан шар радиуса 1. Найдите объем куба. Ребро куба...

    9 слайд

    Задача №4. Решение
    В куб вписан шар радиуса 1. Найдите объем куба.
    Ребро куба равно диаметру вписанного в него шара, а объем куба равен кубу его ребра. Отсюда имеем:

    Задания взяты из «Решу ЕГЭ»

  • Задача №5Задания взяты из "Решу ЕГЭ"

    10 слайд

    Задача №5
    Задания взяты из «Решу ЕГЭ»

  • Задача №5. РешениеПо теореме Пифагора длина гипотенузы треугольника в основан...

    11 слайд

    Задача №5. Решение
    По теореме Пифагора длина гипотенузы треугольника в основании
    Поскольку гипотенуза является диаметром основания описанного цилиндра, его объем
    Задания взяты из «Решу ЕГЭ»

  • Задача №6Объём куба, описанного около сферы, равен 216. Найдите радиус сферы....

    12 слайд

    Задача №6
    Объём куба, описанного около сферы, равен 216. Найдите радиус сферы.
    Задания взяты из «Решу ЕГЭ»

  • Задача №6. РешениеОбъём куба, описанного около сферы, равен 216. Найдите ради...

    13 слайд

    Задача №6. Решение
    Объём куба, описанного около сферы, равен 216. Найдите радиус сферы.
    Прямоугольный параллелепипед, описанный вокруг сферы, является кубом. Тогда длина его ребра

    Радиус сферы равен половине длины ребра r=3
    Задания взяты из «Решу ЕГЭ»

  • Задача №7Цилиндр описан около шара. Объем цилиндра равен 33. Найдите объем ша...

    14 слайд

    Задача №7
    Цилиндр описан около шара. Объем цилиндра равен 33. Найдите объем шара.
    Задания взяты из «Решу ЕГЭ»

  • Задача №7. РешениеЗадания взяты из "Решу ЕГЭ"

    15 слайд

    Задача №7. Решение
    Задания взяты из «Решу ЕГЭ»

  • Задача №8Цилиндр описан около шара. Объем шара равен 24. Найдите объем цилинд...

    16 слайд

    Задача №8
    Цилиндр описан около шара. Объем шара равен 24. Найдите объем цилиндра.
    Задания взяты из «Решу ЕГЭ»

  • Задача №8. РешениеЦилиндр описан около шара. Объем шара равен 24. Найдите объ...

    17 слайд

    Задача №8. Решение
    Цилиндр описан около шара. Объем шара равен 24. Найдите объем цилиндра.
    Объем цилиндра равен произведению площади основания на высоту. Площадь основания цилиндра равна площади большого круга вписанного шара, а высота цилиндра равна диаметру вписанного шара. Поэтому
    Задания взяты из «Решу ЕГЭ»

  • Задача №9Конус и цилиндр имеют общее основание и общую высоту (конус вписан в...

    18 слайд

    Задача №9
    Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса равен 5.
    Задания взяты из «Решу ЕГЭ»

  • Задача №9. РешениеКонус и цилиндр имеют общее основание и общую высоту (конус...

    19 слайд

    Задача №9. Решение
    Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса равен 5.

    конус и цилиндр имеют общую высоту и основание
    Задания взяты из «Решу ЕГЭ»

  • Задача №10Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объ...

    20 слайд

    Задача №10
    Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 28. Найдите объем конуса.
    Задания взяты из «Решу ЕГЭ»

  • Задача №10. РешениеКонус вписан в шар. Радиус основания конуса равен радиусу...

    21 слайд

    Задача №10. Решение
    Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 28. Найдите объем конуса.

    Объём конуса в 4 раза меньше:
    Задания взяты из «Решу ЕГЭ»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 153 913 материалов в базе

  • Выберите категорию:

  • Выберите учебник и тему

  • Выберите класс:

  • Тип материала:

    • Все материалы

    • Статьи

    • Научные работы

    • Видеоуроки

    • Презентации

    • Конспекты

    • Тесты

    • Рабочие программы

    • Другие методич. материалы

Найти материалы

Материал подходит для УМК

  • «Геометрия. Учебник 10-11 класс », Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б.

Другие материалы

«Геометрия. Учебник 10-11 класс », Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б.

«Геометрия. Учебник 10-11 класс », Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б.

  • 21.01.2022
  • 112
  • 2

«Геометрия. Учебник 10-11 класс », Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б.

«Геометрия. Учебник 10-11 класс », Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б.

«Математика (базовый уровень)», Мордкович А.Г., Смирнова И.М.

«Геометрия», Мерзляк А.Г., Полонский В.Б., Якир М.С./ Под ред. Подольского В.Е.

«Геометрия. Учебник 10-11 класс », Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б.

Вам будут интересны эти курсы:

  • Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»

  • Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»

  • Курс повышения квалификации «Применение MS Word, Excel в финансовых расчетах»

  • Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»

  • Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»

  • Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»

  • Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»

  • Курс повышения квалификации «Учебная деятельность по предметной области «Черчение»: основы предмета и реализация обучения в условиях ФГОС»

  • Курс профессиональной переподготовки «Деятельность по хранению музейных предметов и музейных коллекций в музеях всех видов»

  • Курс профессиональной переподготовки «Организация процесса страхования (перестрахования)»

  • Курс профессиональной переподготовки «Осуществление и координация продаж»

  • Курс профессиональной переподготовки «Информационная поддержка бизнес-процессов в организации»

  • Настоящий материал опубликован пользователем Пименова Мария Юрьевна. Инфоурок является
    информационным посредником и предоставляет пользователям возможность размещать на сайте
    методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
    сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

    Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
    сайта, Вы можете оставить жалобу на материал.

    Удалить материал

  • Пименова Мария Юрьевна

    • На сайте: 5 лет и 6 месяцев
    • Подписчики: 1
    • Всего просмотров: 24144
    • Всего материалов:

      53

Источник

Задание 1176

В равносторонний конус (диаметр основания конуса равен длине его образующей) вписан шар. Найдите отношение объема конуса к объему шара.

 

Ответ: 2.25

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

Объем конуса вычисляется по формуле:

$$V_{1}=frac{1}{3}S*h=frac{1}{3}pi HB^{2}*AH$$

Объем шара вычисляется по формуле:

$$V_{2}=frac{4}{3}pi R^{3}=frac{4}{3}pi OH^{3}$$

Дан равносторонний конус, то есть в осевом сечении будет равносторонний треугольник. Пусть AB = x, тогда HB = 0,5x и по теореме Пифагора из треугольника AHB: $$AH = frac{sqrt{3}}{2}x$$. OH — радиус вписанной в правильный треугольник окружности, и он равен 1/3 от высоты: $$OH = frac{1}{3}AH = frac{sqrt{3}}{6}x$$

Значит объем конуса равен:

$$V_{1}=frac{1}{3}S*h=frac{1}{3}pi (0.5x)^{2}* frac{sqrt{3}}{2}x$$

Объем шара равен:

$$V_{2}=frac{4}{3}pi R^{3}=frac{4}{3}pi (frac{sqrt{3}}{6}x)^{3}$$

Тогда:

$$frac{V_{1}}{V_{2}}=frac{frac{1}{3}pi (0.5x)^{2}* frac{sqrt{3}}{2}x}{frac{4}{3}pi (frac{sqrt{3}}{6}x)^{3}}$$

$$frac{V_{1}}{V_{2}}=frac{0.25x^{3}* frac{sqrt{3}}{2}}{ 4(frac{sqrt{3}}{6}x)^{3}}=2.25$$

Задание 3867

Пря­мо­уголь­ный па­рал­ле­ле­пи­пед опи­сан около ци­лин­дра, ра­ди­ус ос­но­ва­ния и вы­со­та ко­то­ро­го равны 1. Най­ди­те объем па­рал­ле­ле­пи­пе­да.

Ответ: 4

Задание 3868

Пря­мо­уголь­ный па­рал­ле­ле­пи­пед опи­сан около ци­лин­дра, ра­ди­ус ос­но­ва­ния ко­то­ро­го равен 4. Объем па­рал­ле­ле­пи­пе­да равен 16. Най­ди­те вы­со­ту ци­лин­дра.

Ответ: 0,25

Задание 3869

В куб впи­сан шар ра­ди­у­са 1. Най­ди­те объем куба.

Ответ: 8

Задание 3870

В ос­но­ва­нии пря­мой приз­мы лежит пря­мо­уголь­ный тре­уголь­ник с ка­те­та­ми 6 и 8. Бо­ко­вые ребра равны $$frac{5}{pi}$$. Най­ди­те объем ци­лин­дра, опи­сан­но­го около этой приз­мы.

Ответ: 125

Задание 3871

В ос­но­ва­нии пря­мой приз­мы лежит квад­рат со сто­ро­ной 2. Бо­ко­вые ребра равны $$frac{2}{pi}$$. Най­ди­те объем ци­лин­дра, опи­сан­но­го около этой приз­мы.

Ответ: 4

Задание 3872

Шар впи­сан в ци­линдр. Пло­щадь пол­ной по­верх­но­сти ци­лин­дра равна 18. Най­ди­те пло­щадь по­верх­но­сти шара.

Ответ: 12

Задание 3873

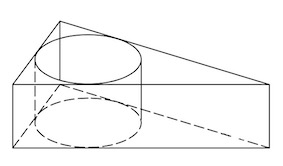
Из еди­нич­но­го куба вы­ре­за­на пра­виль­ная че­ты­рех­уголь­ная приз­ма со сто­ро­ной ос­но­ва­ния 0,5 и бо­ко­вым реб­ром 1. Най­ди­те пло­щадь по­верх­но­сти остав­шей­ся части куба.

Ответ: 7,5

Задание 3874

Ци­линдр и конус имеют общие ос­но­ва­ние и вы­со­ту. Объём ко­ну­са равен 25. Най­ди­те объём ци­лин­дра.

Ответ: 75

Задание 3875

Ци­линдр и конус имеют общие ос­но­ва­ние и вы­со­ту. Най­ди­те объем ко­ну­са, если объем ци­лин­дра равен 150.

Ответ: 50

Задание 3876

Объём куба, опи­сан­но­го около сферы, равен 216. Най­ди­те ра­ди­ус сферы.

Ответ: 3

Задание 3877

Конус опи­сан около пра­виль­ной че­ты­рех­уголь­ной пи­ра­ми­ды со сто­ро­ной ос­но­ва­ния 4 и вы­со­той 6. Най­ди­те его объем, де­лен­ный на $$pi$$.

Ответ: 16

Задание 3878

Во сколь­ко раз объем ко­ну­са, опи­сан­но­го около пра­виль­ной че­ты­рех­уголь­ной пи­ра­ми­ды, боль­ше объ­е­ма ко­ну­са, впи­сан­но­го в эту пи­ра­ми­ду?

Ответ: 2

Задание 3879

В куб с реб­ром 3 впи­сан шар. Най­ди­те объем этого шара, де­лен­ный на $$pi$$.

Ответ: 4,5

Задание 3880

Около куба с реб­ром $$sqrt{3}$$ опи­сан шар. Най­ди­те объем этого шара, де­лен­ный на $$pi$$.

Ответ: 4,5

Источник

Понравилась статья? Поделить с друзьями:
  • Комбинация предметов егэ для поступления в вуз
  • Комбинации егэ с информатикой
  • Комбинации егэ с английским языком
  • Комбинации егэ на психолога
  • Комбинации егэ мгу