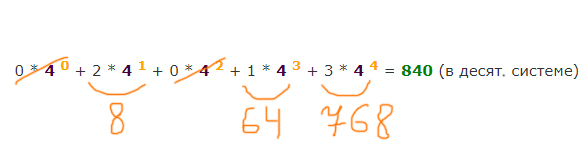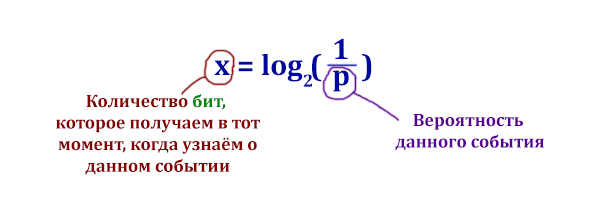Комбинаторика егэ информатика на питоне

Сегодня будем решать 8 задание из ЕГЭ по информатике 2022 с помощью программирования.

Восьмое задание легко решается с помощью Python.

Приступим к практике решения задач.

Задача (Классическая)

Женя составляет 5-буквенные слова, в которых встречаются только буквы А, Б, В, Г, причём буква А появляется ровно 1 раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, не обязательно осмысленная. Сколько существует таких слов, которые может написать Женя?

Решение:

Напишем программу на языке Python.

k=0
for x1 in 'АБВГ':
    for x2 in 'АБВГ':
        for x3 in 'АБВГ':
            for x4 in 'АБВГ':
                for x5 in 'АБВГ':
                    s=x1+x2+x3+x4+x5
                    if s.count('А')==1:
                        k=k+1
print(k)

Т.к. слова состоят из 5-ти символов, то мы формируем пять вложенных циклов! В каждом цикле перебираем все буквы, которые нам дали.

Внутри циклов мы составляем само слово в переменной s. Таким образом, в переменной s «прокрутятся» все возможные комбинации.

Но мы подсчитываем не все комбинации, а только те, где всего одна буква А.

Важно не перепутать русские и английские буквы.

Ответ: 405

Продолжим развивать навыки решения 8 задания из ЕГЭ по информатике 2022.

Задача (Каждую букву можно использовать один раз)

Артур составляет 5-буквенные коды из букв Е, С, А, У, Л. Каждую букву нужно использовать ровно один раз, при этом нельзя ставить рядом две гласные. Сколько различных кодов может составить Артур?

Источник задачи: https://kpolyakov.spb.ru/

Решение:

Запрограммируем решение этой задачи на Питоне.

k=0
for x1 in 'ЕСАУЛ':
    for x2 in 'ЕСАУЛ':
        for x3 in 'ЕСАУЛ':
            for x4 in 'ЕСАУЛ':
                for x5 in 'ЕСАУЛ':
                    s=x1+x2+x3+x4+x5
                    if s.count(x1)==1 and s.count(x2)==1 and s.count(x3)==1 and s.count(x4)==1 and s.count(x5)==1:
                        if s.count('ЕА')==0 and s.count('АЕ')==0 and s.count('ЕУ')==0 and s.count('УЕ')==0 and s.count('АУ')==0 and s.count('УА')==0:
                            k=k+1   
print(k)

В первом условии учли, что каждая буква встречается в слове только один раз. Второе условие говорит о том, что две гласные не стоят рядом (перебрали все возможные сочетания гласных).

Ответ: 12

Задача(Буквы составляют перестановкой)

Петя составляет шестибуквенные слова перестановкой букв слова КАБАЛА. При этом он избегает слов с двумя подряд одинаковыми буквами. Сколько всего различных слов может составить Петя?

Решение:

k=0
for x1 in 'КБЛА':
    for x2 in 'КБЛА':
        for x3 in 'КБЛА':
            for x4 in 'КБЛА':
                for x5 in 'КБЛА':
                    for x6 in 'КБЛА':
                        s=x1+x2+x3+x4+x5+x6
                        if s.count('К')==1 and s.count('А')==3 and s.count('Б')==1 and s.count('Л')==1:
                            if s.count('АА')==0:
                                k=k+1
print(k)

Повторяющиеся буквы в строке, из который берём символы в циклах, всегда убираем.

Слова составляются перестановкой, значит, можно представить, что просто собирают из кубиков КАБАЛА различные слова. Следовательно, в наших словах будет ровно одна буква «К», три буквы «А», одна буква «Б» и одна буква «Л». Это программируем с помощью условия и функции .count().

Т.к. повторятся может только буква «A», то мы прописываем условие, что две буквы «А» подряд не могут находится в наших комбинациях.

Если все условия будут пройдены, то мы подсчитываем такие комбинации.

Ответ: 24

В задании 8 из ЕГЭ по информатике часто нужно проанализировать первую или последнюю букву в слове. Узнаем, как это можно сделать с помощью питона.

Задача (Проверяем первую букву слова)

Сколько слов длины 5, начинающихся с гласной буквы, можно составить из букв Е, Г, Э? Каждая буква может входить в слово несколько раз. Слова не обязательно должны быть осмысленными словами русского языка.

Источник задачи: https://kpolyakov.spb.ru/

Решение:

В этой тренировочной задаче из 8 задания ЕГЭ по информатике 2022 нужно держать на контроле первую букву в слове.

k=0
for x1 in 'ЕГЭ':
    for x2 in 'ЕГЭ':
        for x3 in 'ЕГЭ':
            for x4 in 'ЕГЭ':
                for x5 in 'ЕГЭ':
                    s=x1+x2+x3+x4+x5
                    if x1=='Е' or x1=='Э':
                        k=k+1   
print(k)

Подсчитываем только те комбинации, которые начинаются с гласных букв.

Ответ: 162

Интересный пример, где можно ошибиться в 8 задании из ЕГЭ по информатике.

Задача (Важный пример)

Сергей составляет 6-буквенные коды из букв С, О, Л, О, В, Е, Й. Буква Й может использоваться в коде не более одного раза, при этом она не может стоять на первом месте, на последнем месте и рядом с буквой Е. Все остальные буквы могут встречаться произвольное количество раз или не встречаться совсем. Сколько различных кодов может составить Сергей?

Источник задачи: https://kpolyakov.spb.ru/

Решение:

Эта задача примечательная тем, что буква «О» в слове «СОЛОВЕЙ» повторяется. В этом случае мы должны убрать повторение буквы из перебора.

k=0
for x1 in 'СОЛВЕЙ':
    for x2 in 'СОЛВЕЙ':
        for x3 in 'СОЛВЕЙ':
            for x4 in 'СОЛВЕЙ':
                for x5 in 'СОЛВЕЙ':
                    for x6 in 'СОЛВЕЙ':
                        s=x1+x2+x3+x4+x5+x6
                        if s.count('Й')<=1 and x1!='Й' and x6!='Й' and s.count('ЕЙ')==0 and s.count('ЙЕ')==0:
                            k=k+1   
print(k)

Здесь также учитываем остальные условия.

Ответ: 23625

Задача (Количество гласных)

Василий составляет 4-буквенные коды из букв Г, А, Ф, Н, И, Й. Каждую букву можно использовать любое количество раз, при этом код не может начинаться с буквы Й и должен содержать хотя бы одну гласную. Сколько различных кодов может составить Василий?

Источник задачи: https://kpolyakov.spb.ru/

Решение:

Напишем программу.

k=0
for x1 in 'ГАФНИЙ':
    for x2 in 'ГАФНИЙ':
        for x3 in 'ГАФНИЙ':
            for x4 in 'ГАФНИЙ':
                s=x1+x2+x3+x4
                if x1!='Й' and s.count('А') + s.count('И') >= 1:
                    k=k+1
            
print(k)

Ответ: 888

Порешаем задачи из восьмого задания ЕГЭ по информатике на перебор чисел.

Задача (Перебор чисел)

Сколько существует чисел, восьмеричная запись которых содержит 7 цифр, причём все цифры различны и никакие две чётные и две нечётные цифры не стоят рядом.

Источник задачи: https://kpolyakov.spb.ru/

Решение:

k1=0
k2=0
for x1 in '1234567':
    for x2 in '01234567':
        for x3 in '01234567':
            for x4 in '01234567':
                for x5 in '01234567':
                    for x6 in '01234567':
                        for x7 in '01234567':
                            s=x1+x2+x3+x4+x5+x6+x7
                            if s.count(x1)==1 and s.count(x2)==1 and s.count(x3)==1 and s.count(x4)==1 and s.count(x5)==1 and s.count(x6)==1 and s.count(x7)==1:
                                if int(x1)%2==0 and int(x2)%2==1 and int(x3)%2==0 and int(x4)%2==1 and int(x5)%2==0 and int(x6)%2==1 and int(x7)%2==0:
                                    k1=k1+1
                                if int(x1)%2==1 and int(x2)%2==0 and int(x3)%2==1 and int(x4)%2==0 and int(x5)%2==1 and int(x6)%2==0 and int(x7)%2==1:
                                    k2=k2+1

print(k1+k2)

Число не может начинаться с нуля. Поэтому ноль был исключён из первого цикла.

Первое условие следит за тем, чтобы каждая цифра встречалась один раз в числе. Второе условие подсчитывает количество вариантов, когда первая цифра чётная. Второе условие следит за тем, чтобы чётность и нечётность цифр чередовалась. Третье условие, наоборот, подсчитывает варианты, когда первая цифра нечётная.

Операция % — остаток от деления. Если остаток от деления на 2 равен нулю, то число чётное. Если остаток от деления на 2 равен 1, то число нечётное.

Функция int() преобразует символ в число. Ведь мы работаем именно с символами, а не с реальными числами.

Ответ: 1008

Задача (Числа, Закрепление)

Сколько существует четырёхзначных чисел, записанных в восьмеричной системе счисления, в записи которых ровно две одинаковые цифры, причём стоящие рядом ?

Решение:

k=0
for x1 in '1234567':
    for x2 in '01234567':
        for x3 in '01234567':
            for x4 in '01234567':
                if (x1==x2 and x2!=x3 and x2!=x4 and x3!=x4) or (x2==x3 and x3!=x1 and x3!=x4 and x1!=x4) or (x3==x4 and x3!=x2 and x3!=x1 and x1!=x2):
                    k=k+1
print(k)

Здесь следующий принцип составления условия. Два соседа должны быть равны. Берём одного соседа из пары, где цифры должны быть равны, и комбинируем его с другими цифрами. Пишем уже, чтобы цифры были не равны. Так же прописываем, чтобы две оставшиеся цифры также не были равны. Таким образом, перебираем все варианты.

Ответ: 882

Задача (Числа, важный приём)

Сколько существует различных трёхзначных чисел в шестнадцатиричной системе счисления, в записи которых цифры следуют слева направо в невозрастающем порядке?

Решение:

k=0
for x1 in '123456789ABCDEF':
    for x2 in '0123456789ABCDEF':
        for x3 in '0123456789ABCDEF':
            if x1 >= x2 >= x3:
                k=k+1    

print(k)

Символы можно сравнивает знаками больше или меньше. Символы-цифры сравниваются, как обычные числа. Буквы сравниваются в алфавитном порядке.

Применяем этот приём и получаем ответ.

Ответ: 815

Задача(Две чётные и две нечётные цифры не стоят рядом)

Сколько существует чисел, делящихся на 5, десятичная запись которых содержит 7 цифр, причём все цифры различны и никакие две чётные и две нечётные цифры не стоят рядом.

Решение:

k=0
for x1 in '123456789':
    for x2 in '0123456789':
        for x3 in '0123456789':
            for x4 in '0123456789':
                for x5 in '0123456789':
                    for x6 in '0123456789':
                        for x7 in '05':

                            s=x1+x2+x3+x4+x5+x6+x7

                            if s.count(x1)==1 and s.count(x2)==1 and s.count(x3)==1 and s.count(x4)==1 and s.count(x5)==1 and s.count(x6)==1 and s.count(x7)==1:
                                
                                if x1 in '02468' and x2 in '13579' and x3 in '02468' and x4 in '13579' and x5 in '02468' and x6 in '13579' and x7 in '02468':
                                    k=k+1
                                if x1 in '13579' and x2 in '02468' and x3 in '13579' and x4 in '02468' and x5 in '13579' and x6 in '02468' and x7 in '13579':
                                    k=k+1

print(k)

Перебираем 7 разрядов десятичного числа. С нуля число не может начинаться, поэтому из первого цикла удаляем ноль.

Число должно делиться на 5, значит, в последнем цикле оставляем только 0 и 5.

Все цифры различны, поэтому применяем условие, что символ x1 встречается 1 раз, символ x2 встречается 1 раз и т.д.

Фраза «две чётные и две нечётные цифры не стоят рядом» обозначает, что цифры должны чередоваться. Например, чётная, нечётная, чётная, нечётная и т.д. (или наоборот).

Направление задаёт именно первая цифра, остальные цифры выстраиваются по ней.

Проверить чётность/нечётность цифр просто, мы проверям существует ли конкретный символ с троке из чётных или нечётных цифр.

У нас два равноправных случая: когда первая цифра чётная, и когда первая цифра нечётная.

Ответ: 2880

Следующий тип задач из задания 8 ЕГЭ по информатике лучше решать без программирования.

Задача (Со списками, классическая)

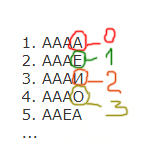
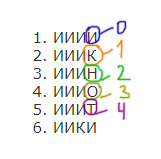
Все 4-буквенные слова, составленные из букв А, Е, И, О записаны в алфавитном порядке и пронумерованы. Вот начало списка:

1. АААА
2. АААЕ
3. АААИ
4. АААО
5. ААЕА
…

Запишите слово, стоящее на 248-м месте от начала списка.

Источник задачи: https://inf-ege.sdamgia.ru/

Решение:

Обозначим условно А — 0, Е — 1, И — 2, О — 3.

Важно: Нужно буквам присваивать цифры именно в том порядке, в котором они идут в самом правом столбце, потому что буквы могут дать в «перепутанном порядке» (например Е, А, И, О), и тогда ничего не получится.

Теперь запишем список с помощью цифр.

1. 0000
2. 0001
3. 0002
4. 0003
5. 0010
…

Получился обычный счёт в четверичной системе!! (всего используются 4 цифры: 0, 1, 2, 3). А слева нумерация показывает соответствие нашей десятичной системе. Но все числа десятичной системы в этой таблице соответствия сдвинуты на 1, ведь мы должны были начать с нуля.

Нас просят записать слово стоящее на 248, т.е. если была обычная таблица соответствия чисел десятичной системы и четверичной системы, слово стоящее на 248 месте, находилось бы на 247 (248 — 1) месте. Значит, наше искомое четверичное число соответствует 247 в десятичной системе.

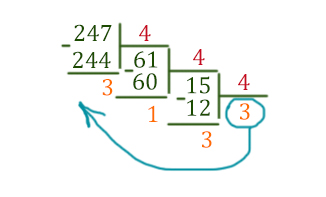
Переведём число 247 в четверичную систему!

Получилось число 3313₄ в четверичной системе. Сделаем обратное декодирование в буквы. Таким образом, ответ будет ООЕО.

Ответ: ООЕО

Ещё одна похожая задача 8 задания из примерных вариантов ЕГЭ по информатике 2022, но другой вариации.

Задача (Классика, Другая вариация)

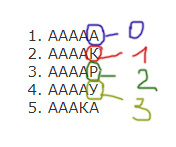
Все 5-буквенные слова, составленные из букв А, Р, У, К записаны в алфавитном порядке. Вот начало списка:

1. ААААА
2. ААААК
3. ААААР
4. ААААУ
5. АААКА
……
Укажите номер слова УКАРА

Источник задачи: https://inf-ege.sdamgia.ru/

Решение:

Закодируем буквы цифрами: А — 0, К — 1, Р — 2, У — 3. Здесь как раз буквы даны не в том порядке, как они идут в самом правом столбце. Но мы должны кодировать именно в том порядке, как буквы идут в самом правом столбце.

У нас получилось четыре цифры! Значит снова можно слова превратить в таблицу соответствия между десятичной системой и четверичной системой. Но десятичная система смещена на 1 позицию.

1. 00000
2. 00001
3. 00002
4. 00003
5. 00010
……

Выписываем данное нам слово и посмотрим, какое число в четверичной системе было бы, если бы у нас были в место слов числа в четверичной системе!

Получили число в четверичной системе 31020₄. Узнаем, какое число в десятичной системе соответствовало этому числу, если бы была обычная таблица соответствия. Для этого переведём число 31020₄ из четверичной системы в десятичную. Перевод делаем по аналогии перевода из двоичной системы в десятичную.

Но помним, что у нас нумерация идёт на 1 быстрее, нежели мы бы поставили десятичные числа, как в таблице соответствия, потому что нумерация начинается не с нуля, а с 1. Поэтому к числу 840 нужно прибавить 1, и в ответе будет 841

Ответ: 841

Задача (Демонстрационный вариант ЕГЭ по информатике, 2020)

Все 4-буквенные слова, в составе которых могут быть буквы Н, О, Т, К, И,
записаны в алфавитном порядке и пронумерованы, начиная с 1.
Ниже приведено начало списка.

1. ИИИИ
2. ИИИК
3. ИИИН
4. ИИИО
5. ИИИТ
6. ИИКИ
…

Под каким номером в списке идёт первое слово, которое начинается
с буквы О?

Решение:

Закодируем буквы цифрами.

Получилось 5 цифр ( 0, 1, 2, 3, 4 ), значит, будем работать в пятеричной системе.

Нужно найти номер первого слова, которое начинается с буквы О. Если говорить на языке пятеричных чисел, то нужно найти номер числа 3000₅. Мы «забиваем нулями», чтобы число было четырёхразрядное, т.к. слова 4-х буквенные. Именно нулями, потому что нужно именно первое слово найти.

Теперь, как в предыдущей задаче, переведём число 3000₅ из пятеричной системы в десятичную.

0 * 5 ⁰ + 0 * 5 ¹ + 0 * 5 ² +
3 * 5 ³ = 375 (в десят. системе)

Но опять же должны прибавить 1 к числу 375, т.к. нумерация отличается от десятичных чисел на 1 в большую сторону.

Ответ: 376

Задача (Формула Шеннона)

В корзине лежат 8 черных шаров и 24 белых. Сколько бит информации несет сообщение о том, что достали черный шар?

Источник задачи: https://inf-ege.sdamgia.ru/

Решение:

Найдём вероятность p того, что вытащили чёрный шарик.

p = (количество чёрных шаров) / (количество всех шаров) = 8 / (24 + = 8 / 32 = 1 /4

p = 1 / 4

Применим формулу Шеннона.

x = log₂(4)
2^x = 4

x = 2 бита

Ответ: 2

Счастливых экзаменов!

Задание номер 8 — задание базового уровня сложности, выполнение которого предполагает знание о методах измерения количества информации и не требует использования специального ПО.

Зачастую в номере 8 мы можем встретить задания связанные с комбинаторикой — перестановками, количеством вариантов выборки и т.д. Для решения заданий такого типа можно приспособить модуль itertools языка python.

Сразу оговорюсь, что я не рекомендую решать задание именно таким способом. Я советую проверять свой ответ, полученный ручным решением. Написанная программа не должна быть единственным вариантом решения.

Модуль itertools доступен в питоне «из коробки», т.е. его нет необходимости устанавливать дополнительно. А значит, он будет доступен на экзамене.

Ссылка на документацию по модулю https://docs.python.org/3/library/itertools.html

Использованные в данной статье методы и функции доступны как минимум с версии питона 3.6

Для импорта необходимых функции необходимо их импортировать из модуля

from itertools import product, permutations

1. product

Позволяет получить прямое, или декартово произведеение двух множеств — множество, элементами которого являются все возможные упорядоченные пары элементов исходных множеств.

a = ‘AB’

b = ‘CD’

print(*product(a, b))

(‘A’, ‘C’) (‘A’, ‘D’) (‘B’, ‘C’) (‘B’, ‘D’)

Получение произведения двух множеств не очень актуально в 8 задании, но мы можем использовать другую возможность функции product: получение всевозможных комбинаций определенной длины для одного множества.

a = ‘AB’

print(*product(a, repeat=3))

(‘A’, ‘A’, ‘A’) (‘A’, ‘A’, ‘B’) (‘A’, ‘B’, ‘A’) (‘A’, ‘B’, ‘B’) (‘B’, ‘A’, ‘A’) (‘B’, ‘A’, ‘B’) (‘B’, ‘B’, ‘A’) (‘B’, ‘B’, ‘B’)

Мы получили всевозможные комбинации длины 3 для набора из двух букв АВ. Причем результат работы функции — набор кортежей.

Параметр repeat отвечает за длину слова.

Из полученных наборов мы можем выбрать подходящие для нас. Например, так можно решить задание из демоверсии 2021.

Длина слова здесь 3, а набор букв — ШКОЛА. Получим всевозможные комбинации:

a = ‘ШКОЛА’

comb = product(a, repeat=3))

Осталось выбрать те, где буква К встречается ровно 1 раз.

Поскольку подсчет количества вхождений в кортеж организовать сложнее, чем в строке, здесь элементы кортежа «склеиваются» по пустой строке, образуя тем самым не кортеж, а строку. Метод count подсчитывает количество вхождений подстроки ‘K’.

Этот же код можно оформить в одну строку через списочное выражение

print(len([item for item in product(‘ШКОЛА’, repeat=3) if ”.join(item).count(‘К’) == 1]))

2. permutations

Позволяет получить всевозможные перестановки.

print(*permutations(‘ABC’))

(‘A’, ‘B’, ‘C’) (‘A’, ‘C’, ‘B’) (‘B’, ‘A’, ‘C’) (‘B’, ‘C’, ‘A’) (‘C’, ‘A’, ‘B’) (‘C’, ‘B’, ‘A’)

Это опять набор кортежей.

Рассмотрим такое задание с сайта kpolyakov.spb.ru

Получаем перестановки

a = ‘КАПКАН’

comb = permutations(a)

И отбираем нужные варианты

Поскольку в слове КАПКАН есть повторяющиеся буквы А и К, мы должны поделить итоговое количество на 4 (дважды поделить на 2), поскольку с нашей точки зрения эти комбинации неотличимы друг от друга.

Другой способ убрать повторяющиеся комбинации — превратить набор перестановок в множество, которое в питоне исключает повторы

Так-же можно написать решение в одну строку

print(len([i for i in set(permutations(‘КАПКАН’)) if all(i[j] != i[j + 1] for j in range(5))]))

Подведем итог. Задачи на составление слов путем выбора букв из набора или путем перестановки букв в слове можно решить с использованием модуля itertools. Написание кода не займет много времени, зато будет уверенность в ручном решении.

🧑‍💼 Сергей составляет 6-буквенные коды из букв Е, Л, Е, Й. Буква Й может использоваться в коде не более одного раза, при этом она не может стоять на первом месте, на последнем месте и рядом с буквой Е. Все остальные буквы могут встречаться произвольное количество раз или не встречаться совсем. Сколько различных кодов может составить Сергей?

Для задач комбинаторики можно использовать библиотеку itertools, которая позволяет делать переборы по различным комбинациям.

Основные необходимые методы библиотеки:
▪️product() — декартовое произведение всех вариантов

Например: (1 2 3) * (1 2 3) = (1 1 ), (2 2), (3 3), (1 2) и тд..

▪️permutations() — перестановки

Например: (1 2 3) = (1 2 3 ), (2 1 3), (3 2 1) и тд..

В данной задаче используем декартовое произведение всех вариантов, в котором количество символ будет = 6, задается параметром repeat.

✌️ полный гайд по itertools:
youtube.com/watch?v=xIEVAm7BakE

Учитель информатики высшей
категории Жевтило Ирина Аскольдовна

МБОУ «Лицей «Дубна»

Использование
библиотеки itertools при решении задач ЕГЭ по информатике

В встроенном в Python модуле itertools существует
ряд комбинаторных функций. Рассмотрим некоторые из них:

· product() –
прямое произведение одного или нескольких итераторов.

· permutations() –
перестановки и размещения элементов множества.

Данная библиотека позволяет
решать задачи с комбинаторикой, упрощая программу решения.

Вызов модуля itertools:

from itertools import *

Данный модуль можно
использовать для решения задач №8 ЕГЭ по информатике.

Примеры заданий и способы
использования данного модуля.

Пример 1. МАРИНА из букв своего имени составляет слова перестановкой
исходных букв. Сколько различных слов может составить МАРИНА, если первая буква
не может быть гласной?

Аналитический способ решения

Общее количество слов с
учетом, что в слове две буквы «А» (перестановка этих букв не дает нового слова)

Вычтем количество слов,
начинающихся с гласной с учетом 2 букв «А»:

Получаем =180 слов

Итого: 360 – 180 = 180

Программа для решения данной
задачи:

from itertools import *

a=’МАРИНА‘

k=0

for i in set(permutations(a)):

    s=».join(i)

    if s[0] not in ‘АИ‘:

        k+=1

print(k)

В программе
используем

1)    функцию: 
permutations(a), т.к. слова составляются
перестановкой букв;

2)   
используем множества (set), чтобы слова не повторялись;

3)    в условии проверяем отсутствие гласных  в начале слова.

Пример 2. Используем функцию product

Миша составляет
5-буквенные коды из букв К, А, Л, Ь, К, А. Каждая допустимая гласная буква
может входить в код не более одного раза. Сколько кодов может составить Миша?

Аналитический способ решения

Количество слов без «А»

3*3*3*3*3= 3⁵ =243

Количество слов с одной  «А»

5 вариантов *3*3*3*3 = 405

Итого: 243 + 405 = 648

Программа для решения данной
задачи:

from itertools import*

a=’КАЛЬ’

k=0

for i in product(a, repeat=5):

    s=».join(i)

    if s.count(‘А’)<=1 :

        k+=1                               

print (k)

В программе
используем

1)    функцию
product (a, repeat=5):
, т.к. буквы в слове могут повторяться;

2)    в условии проверяем количество гласных  не более 1.

https://doi.org/10.32517/2221-1993-2021-20-10-54-60

• Аннотация
• Об авторе
• Список литературы

Просмотров: 200

Время на прочтение
4 мин

Количество просмотров 84K

Стандартная библиотека python, начиная с версии 2.2, предоставляет множество средств для генерирования комбинаторных объектов, но в интернете мне не удалось найти ни одной статьи, которая подробно рассказывала бы о работе с ними. Поэтому я решил исправить это упущение.

Начну с того, что расскажу о комбинаторике и ее основных формулах. Если же вы уже знакомы с этим разделом математики — можете пропустить эти абзацы.

Допустим, у нас есть строка, состоящая из n разных букв и мы хотим вычислить все способы переставить эти буквы местами так, чтобы получить новую строку. На первую позицию в строке мы можем выбрать одну из n букв, имеющихся у нас, на вторую позицию одну из n-1-ой буквы и так далее. В итоге получаем произведение n (n-1)… *1 = n! количество перестановок из n элементов без повторений.

Теперь представим, что количество букв в строке ограничено. У нас есть n доступных букв и мы хотим вычислить количество способов составить из них строку длины k, где k < n, каждую букву мы можем использовать лишь единожды. Тогда на первую позицию в строке мы можем поставить одну из n букв, на вторую позицию одну из n-1 буквы и на k-ую позицию одну из n-k+1 буквы. Общее количество строк будет равно n (n — 1) (n — 2) … (n — k + 2) (n — k + 1) = n!/(n-k)! количество размещений из n по k. Если же уникальность букв не требуется, то мы получим формулу n…nn = n^k количество размещений из n по k с повторениями.

До этого мы перебирали последовательности с учетом порядка элементов, а что если порядок для нас не имеет значения. Например, у нас есть есть n разных конфет и мы хотим выбрать k из них, чтобы подарить другу, при чем k < n. Сколько существует способов выбрать k конфет из n без учета порядка? Ответ прост, в начале найдем размещение из n по k без повторений, но тогда одинаковые наборы конфет, имеющие разный порядок их следования будут повторяться. Сколько существует способов переставить k конфет? Правильно, перестановка из k элементов без повторений. Итоговый ответ: размещения из n по k делим на перестановки из k без повторений. Формула: количество сочетаний из n по k.

Рассмотрим случай посложнее, у нас есть n коробок каждая из которых содержит множество конфет одного вкуса, но в разных коробках вкусы разные. Сколько существует способов составить подарок другу из k конфет, при чем один и тот же вкус может встречаться любое количество раз? Так как порядок для нас значения не имеет, давайте разложим подарочные сладости следующим образом: в начале будут лежать последовательно конфеты первого вкуса, затем второго и так далее, а между конфетами разных вкусов положим спички, если конфеты какого-то вкуса отсутствуют в нашем подарке — спички, которые должны были окаймлять этот вкус слева и справа будут стоять рядом. Того у нас получится последовательность, состоящая из k конфет и n-1 спички, ибо вкусов всего n, а спички разделяют их. Теперь заметим, что по расположению спичек, мы можем восстановить исходное множество. Тогда ответом будет количество способов разместить n-1 спичку в n+k-1 ячейку без учета порядка, что равно количеству сочетаний из n+k-1 по n-1, формула: количество сочетаний из n по k с повторениями.

Теперь рассмотрим несколько задач на комбинаторику, чтобы закрепить материал.

Задача 1

Есть 20 человек, сколько существует способов разбить их на пары
Решение: возьмем первого человека, сколько существует способов выбрать ему пару: , возьмем второго человека, сколько существует способов выбрать ему пару: . Ответ: 19!!! = 654729075

Задача 2

Есть 10 мужчин и 10 девушек, сколько существует способов разбить их на компании, состоящие из одинакового количества и мужчин и девушек, пустая компания не считается
Решение:
Cпособ 1: количество способов собрать компанию из одного мужчины и одной девушки равно произведению количества способов выбрать одну девушку и количества способов выбрать одного мужчину. Количество способов выбрать одну девушку из 10 равно сочетанию из 10 по 1 без повторений, с мужчинами аналогично, поэтому возведем в квадрат. Далее аналогично вычислим сочетания из 10 по 2, из 10 по 3 и так далее до сочетания из 10 по 10. Итоговая формула: .
Способ 2: рассмотрим множество мужчин, входящих в компанию и множество девушек, не входящих в нее. По этому множеству можно однозначно восстановить компанию, а количество людей в нем всегда равно 10, так как , k — количество мужчин в компании, — количество девушек, не вошедших в нее. Количество таких множеств равно количеству сочетаний из 20 по 10, в конечном ответе мы также вычтем единицу, чтобы не учитывать пустую компанию, когда в нашем множестве 10 девушек. Итоговая формула: .

Итак, мы разобрались с теорией, теперь научимся генерировать комбинаторные объекты с помощью стандартной библиотеки python.
Работать мы будем с библиотекой itertools

from itertools import *

С помощью функции permutations можно сгенерировать все перестановки для итерируемого объекта.

Пример 1

for i in permutations('abc'):
    print(i, end=' ') # abc acb bac bca cab cba
print()
for i in permutations('abb'):
    print(i, end=' ') # abb abb bab bba bab bba 

Исходя из второго вызова заметим, что одинаковые элементы, стоящие на разных позициях, считаются разными.

Пример 2

for i in permutations('abc', 2):
    print(i, end=' ') # ab ac ba bc ca cb 

Размещение отличается от перестановки ограничением на количество доступных ячеек

Пример 3

for i in product('abc', repeat=2):
    print(i, end=' ') # aa ab ac ba bb bc ca cb cc

C помощью размещений с повторениями можно легко перебрать все строки фиксированной длины, состоящие из заданных символов

Пример 4

for i in combinations('abcd', 2):
    print(i, end=' ') # ab ac ad bc bd cd 

С помощью сочетаний без повторений можно перебрать все наборы не повторяющихся букв из заданной строки, массива или другого итерируемого объекта без учета порядка

Пример 5

for i in combinations_with_replacement('abcd', 2):
    print(i, end=' ') # aa ab ac ad bb bc bd cc cd dd  

Результат аналогичен вызову combinations, но в результат также добавлены множества с одинаковыми элементами.

Материалы:
Н.В. Горбачев «Сборник олимпиадных задач по математике»
Документация по python на русском