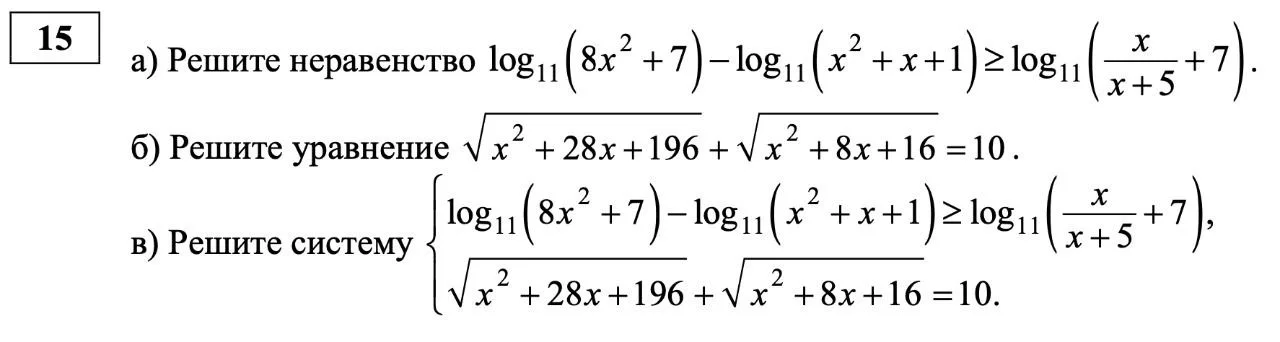Пройти тестирование по 10 заданиям
Пройти тестирование по всем заданиям
Вернуться к каталогу заданий
Без метода (8 шт.)
Категория:
Версия для печати и копирования в MS Word
1
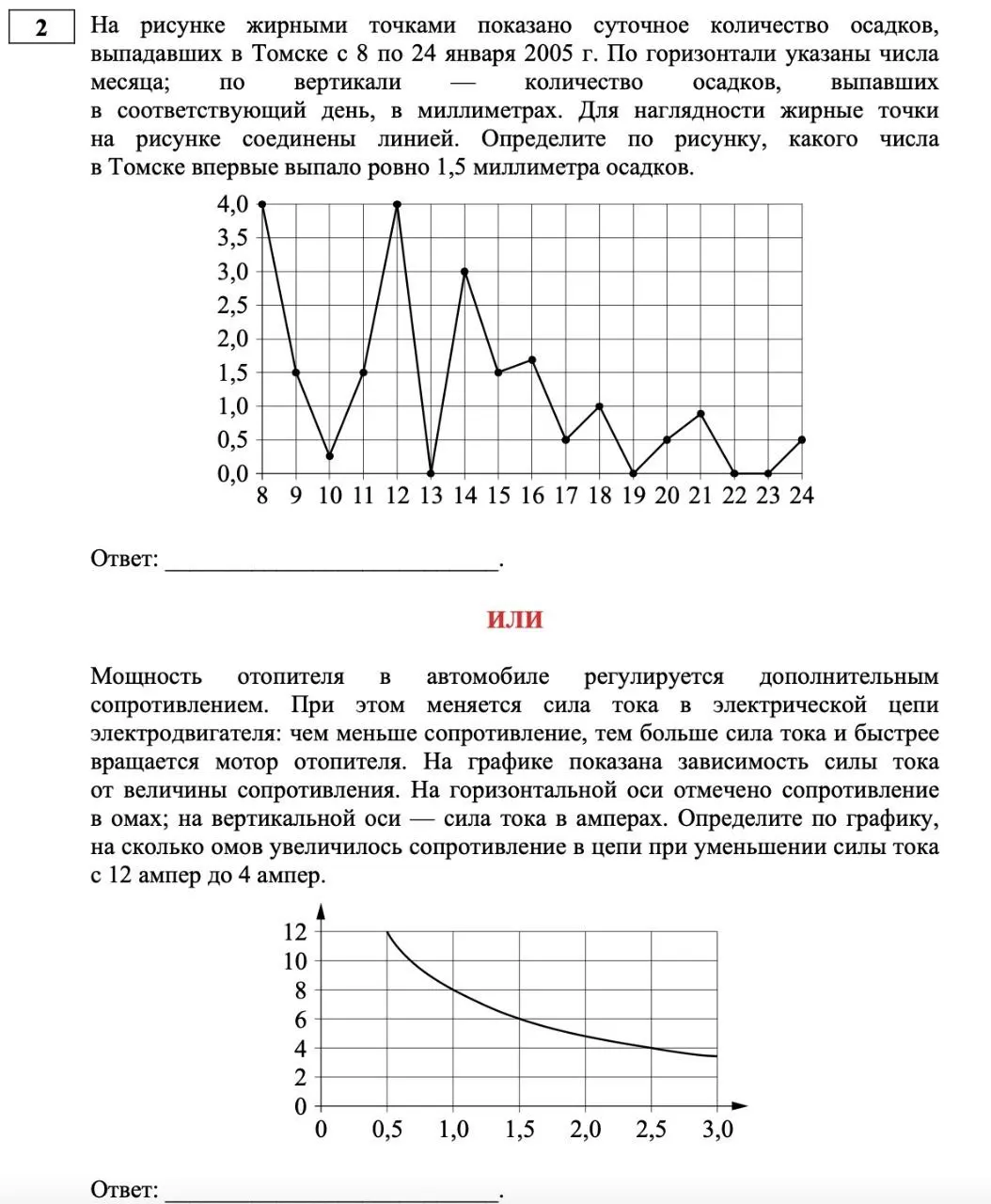
На рок-фестивале выступают группы — по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из Дании будет выступать после группы из Швеции и после группы из Норвегии? Результат округлите до сотых.
2
За круглый стол на 9 стульев в случайном порядке рассаживаются 7 мальчиков и 2 девочки. Найдите вероятность того, что обе девочки будут сидеть рядом.
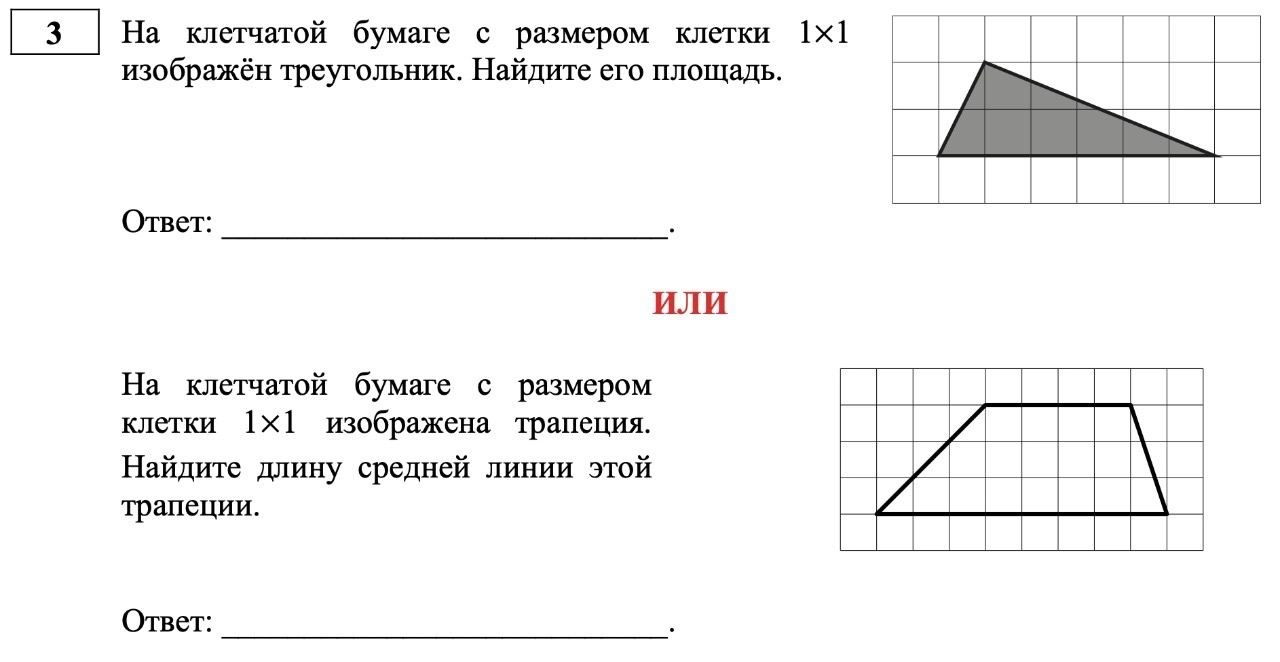
3
За круглый стол на 5 стульев в случайном порядке рассаживаются 3 мальчика и 2 девочки. Найдите вероятность того, что девочки будут сидеть рядом.
4
За круглый стол на 5 стульев в случайном порядке рассаживаются 3 мальчика и 2 девочки. Найдите вероятность того, что девочки не будут сидеть рядом.
5
За круглый стол на 201 стул в случайном порядке рассаживаются 199 мальчиков и 2 девочки. Найдите вероятность того, что между девочками будет сидеть один мальчик.
Пройти тестирование по этим заданиям
Тема 4.
Задачи на теорию вероятностей
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
задачи на теорию вероятностей
4.01Умножение вероятностей вдоль цепочки событий
4.02Условная вероятность
4.03Комбинаторика
4.04Задачи повышенного уровня сложности
Решаем задачи
На экзамене по геометрии всего 20 билетов. Из них 10 билетов про трапецию, 7 билетов про окружность и 3 билета
про треугольники. Известно, что не существует билетов по двум темам сразу. Сдающий вытягивает два билета.
Найдите вероятность того, что среди вытянутых билетов не будет билетов про треугольники. Ответ округлите до
сотых.
Показать ответ и решение
Найдём количество всевозможных пар вытянутых билетов. Так как на экзамене всего 20 билетов, то таких пар
ровно
Найдём количество пар билетов, в которых оба билета не про треугольники. Всего на экзамене билетов не про
треугольники, поэтому таких пар ровно
Вероятность того, что среди вытянутых билетов не будет билетов про треугольники, равна отношению количества пар
билетов, в которых оба билета не про треугольники, к количеству всевозможных пар вытянутых билетов, то есть После
деления в столбик и округления результата до сотых получим 0,72.
На ЕГЭ 2023 в каждом из 7 номеров второй части есть 2 прототипа, один из которых простой, а второй сложный. Генератор
случайным образом составляет вариант второй части. Какова вероятность того, что ученику попадется вторая часть только со
сложными задачами? Ответ округлите до тысячных.
Показать ответ и решение
Посчитаем вероятность как отношение числа благоприятных исходов к числу всех исходов. Благоприятный исход ровно один:
когда в каждом номере второй части выбрали сложный прототип. Всего исходов так как у нас есть 7 номеров и для каждого
из них можно двумя способами выбрать задачу. Тогда искомая вероятность равна
Округлив до тысячных, получим 0,008.
Дана колода из 20 карт, по 5 карт каждой из четырех мастей. Из колоды случайным образом тянут 3 карты. Найдите
вероятность того, что не все 3 карты окажутся одной масти. Ответ округлите до сотых.
Показать ответ и решение
Заметим, что три вытянутые карты либо все одной масти, либо не все одной масти, значит, это два противоположных
события. То есть вероятность того, что не все вытянутые карты окажутся одной масти, равна разности единицы и
вероятности того, что все три карты имеют одинаковую масть. Всего количество способов вытянуть 3 карты из 20
равно
Найдём количество способов вытянуть три карты одной масти. Количество способов вытянуть три карты из карт
одной конкретной масти равно
Всего 4 масти, поэтому количество способов вытянуть три карты одной масти равно . Тогда вероятность
того, что не все 3 карты окажутся одной масти, равна
Чтобы округлить, поделим в столбик, получим
Нас просят округлить с точностью до сотых, следовательно, ответ .
Плейлист айпода содержит 25 треков, из которых 9 исполняет группа Битлз. Функция «shuffle» воспроизводит все треки в
случайном порядке, каждый по одному разу. Какова вероятность того, что трек Битлз будет играть вторым, причем первым
будет воспроизведен трек другого исполнителя?
Показать ответ и решение
Посчитаем количество исходов, в которых вторую позицию занимает трек Битлз, причем первый трек другого
исполнителя.
Количество способов выбрать первый трек не Битлз равно . Количество способов выбрать второй трек Битлз
равно 9. Количество способов расставить оставшиеся 23 трека на 23 позициях равно . Получаем
исходов.
Общее количество исходов равно , поскольку это количество перестановок из 25 попарно различных элементов.
Тогда искомая вероятность равна
В группе туристов 12 человек. С помощью жребия они выбирают трех человек, которые должны идти в село в магазин за
продуктами. Какова вероятность того, что турист Д., входящий в состав группы, пойдет в магазин?
Показать ответ и решение
Посчитаем число исходов, в которых Д. отправляется в магазин. Оно равно числу способов выбрать ему двух компаньонов из
оставшихся 11 человек:
Общее число способов выбрать троих человек из 12:
Искомая вероятность равна
В группе туристов восемь человек. С помощью жребия они выбирают шестерых человек, которые должны идти
в село в магазин за продуктами. Какова вероятность того, что входящий в состав группы турист Г. пойдёт в
магазин?
Показать ответ и решение
Найдем количество различных способов выбрать шесть человек из восьми. Это количество равно количеству способов не выбрать
двух человек из восьми. То есть всего есть
способов выбрать шесть человек из восьми.
Теперь найдем количество способов выбрать группу из шести человек, в которой обязательно есть турист Г. То есть надо
найти количество способов добрать пять человек из семи оставшихся. Это количество равно количеству способов не выбрать
двух человек из семи. То есть всего есть
способ выбрать шесть человек из восьми, если среди выбранных людей должен быть турист Г. Заметим, что с
помощью жребия каждую группу мы могли выбрать с одинаковой вероятностью. Значит, вероятность того, что
турист Г. должен будет пойти в магазин, равна отношению количества способов выбрать шесть человек с его
участием из восьми к количеству способов выбрать шесть любых человек из восьми. То есть искомая вероятность
равна
Монету бросают 8 раз. Во сколько раз событие «орел выпадает ровно шесть раз» более вероятно, чем событие «орел
выпадает ровно один раз»?
Показать ответ и решение
Количество возможных исходов равно , все они равновероятны и реализуются с вероятностью
.
Очевидно, что ровно в восьми исходах орел выпадет ровно 1 раз (первый бросок орел, остальные решки, второй
бросок орел, остальные решки и т.д.), значит вероятность такого события .
Выпадение орла ровно шесть раз эквивалентно выпадению ровно двух решек. Количество исходов с ровно
двумя решками равно количеству способов выбрать из восьми бросков два, на которые выпадут решки.
Таких способов , тогда вероятность выпадения ровно шести орлов равна
. Ответом будет
отношение.
Клиент получает в банке кредитную карту. Четыре последние цифры номера карты случайные. Какова
вероятность того, что эти последние четыре цифры идут подряд в порядке убывания, например 3210 или
6543?
За круглый стол на 21 стул в случайном порядке рассаживаются 19 мальчиков и 2 девочки. Найдите вероятность того,
что девочки не окажутся на соседних местах.
Показать ответ и решение
Пусть — число способов рассадить 19 человек на 19 мест.
Посчитаем количество исходов, в которых девочки сидят рядом. Количество пар соседних мест за столом равно 21
(если пронумеровать места от 1 до 21, то это пары мест ). На каждую такую пару мест мы
можем посадить девочек двумя способами, остальные 19 мест могут быть распределены между мальчиками
способами. Получаем .
Общее число способов рассадить людей равно , а вероятность того, что девочки сидят рядом
p = = 0,1
Тогда искомая вероятность того, что девочки не окажутся на соседних местах равна .
Какова вероятность того, что последние три цифры телефонного номера случайного абонента совпадают?
Показать ответ и решение
Заметим, что каждой комбинации трех последних цифр соответствует равное число способов дополнить ее до
полноценного номера (каким бы ни был стандарт на его длину). Всего цифр 10, значит, количество интересных нам
исходов равно 10. Общее число исходов равно , т.к. каждую из трех цифр можно выбрать 10 способами. Тогда
искомая вероятность .
На уроке физкультуры 26 школьников, из них 12 девочек, остальные — мальчики. По сигналу учителя физкультуры
все быстро выстраиваются в одну шеренгу в случайном порядке. Найдите вероятность того, что справа в шеренге
первые двое окажутся мальчиками.
Показать ответ и решение
Посчитаем количество исходов, в которых первые два места занимают мальчики. На первую позицию человек может
быть выбран 14 способами (любой из мальчиков), на вторую — 13 (любой из оставшихся мальчиков, кроме выбранного
на первую позицию). Число способов расставить остальных 24 людей в некотором порядке равно . Итого имеем
.
Общее число возможных расстановок равно , тогда имеем
Из ящика, в котором лежат фломастеры, не глядя достали два фломастера. Найдите вероятность того, что эти
фломастеры оказались одного цвета, если известно, что в ящике 12 синих и 13 красных фломастеров.
Показать ответ и решение
Посчитаем число исходов, в которых оба фломастера синие. Оно равно числу способов выбрать 2 фломастера из 12
синих: .
Посчитаем число исходов, в которых оба фломастера красные. Оно равно числу способов выбрать 2 фломастера из
13 красных: .
Общее число исходов равно количеству способов выбрать 2 фломастера из 25: . Тогда искомая вероятность
.
Симметричную монету бросают 11 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше
вероятности события «выпадет ровно 4 орла»?
Показать ответ и решение
Посчитаем количество исходов, в которых выпало ровно 5 орлов. Оно равно количеству способов выбрать из 11
произведенных бросков 5, в которых выпали орлы
k5 =
Посчитаем количество исходов, в которых выпало ровно 4 орла. Оно равно количеству способов выбрать из 11
произведенных бросков 4, в которых выпали орлы
k4 =
Общее количество исходов равно (орел либо решка на каждом из 11 бросков), тогда искомое отношение
вероятностей
В коробке 6 синих, 9 красных и 10 черных носков. Случайным образом выбирают два носка. Найдите вероятность того, что
выбранные носки окажутся разноцветными.
Показать ответ и решение
Рассмотрим два варианта: носки могли оказаться одноцветными и разноцветными. Это события несовместны и покрывают все
пространство элементарных исходов. Поэтому сумма вероятностей этих событий равна 1.
Найдем вероятность того, что носки окажутся одноцветными. Для этого найдем вероятность того, что оба носка оказались
синими, красными и чёрными по отдельности. Количество способов выбрать два синих носка из 6 равно Количество
способов выбрать два носка из всех равно так как всего носков
Тогда вероятность того, что оба носка оказались синими, равна
Вероятность того, что оба носка оказались красными, равна
Вероятность того, что оба носка оказались черными, равна
Значит, вероятность того, что носки окажутся одноцветными, равна
Тогда вероятность того, что носки окажутся разноцветными, равна
Замечание.
Можно считать, что носки выбирают по очереди, и решать задачу через цепочки событий.
Вероятность первого и второго носков синего цвета равна
Вероятность первого и второго носков красного цвета равна
Вероятность первого и второго носков черного цвета равна
Тогда вероятность двух разноцветных носков равна
На полке помещается 11 книг. Настя расставляет книги на полке случайным образом. Какова
вероятность того, что два тома стихов Пушкина окажутся рядом? Ответ округлите до сотых.
Показать ответ и решение
Так как вероятности постановки на каждое место любой книги одинаковы, то искомая вероятность есть
просто отношение суммарного количества способов расстановки, в которых тома Пушкина стоят рядом,
к количеству всевозможных способов расстановки книг на полке.
Найдем число способов, которыми можно поставить книги так, чтобы тома Пушкина стояли рядом:
для этого мысленно объединим два тома в одну книгу, занимающую 2 места, тогда ее можно поставить
на любое из 10 мест на полке.
На первое место можно поставить одну из 10 книг, на второе одну из 9, …, на последнее место можно
поставить последнюю книгу. Итого: способов. При этом каждому такому способу в
исходной задаче будут соответствовать 2 разных способа (объединить тома в одну книгу можно
было двумя способами, в зависимости от того, какой том слева, а какой справа). В итоге
количество подходящих способов равно . При этом поставить 11 книг на полку можно
способами.
Вероятность того, что два тома стихов Пушкина окажутся рядом, равна
После округления имеем окончательно .
Монетку подбросили 10 раз. Какова вероятность того, что выпало не менее 9 орлов? Ответ округлите до
тысячных.
Показать ответ и решение
Условие того, что выпало не менее 9 орлов эквивалентно тому, что выпало не более 1 решки, то есть
либо ровно 1 решка, либо 0 решек.
Количество всевозможных различных исходов в серии из 10 испытаний равно .
Среди них есть 11 исходов, подходящих под условие: (Орёл; Орёл; …; Орёл), (Орёл; Орёл; …; Орёл;
Решка), (Орёл; Орёл; …; Решка; Орёл), …, (Решка; Орёл; …; Орёл), следовательно, искомая вероятность
равна
После округления получим .
Навигатор самостоятельной подготовки к ЕГЭ 2022, Математика, Профильный уровень, Элементы комбинаторики, статистики и теории вероятностей, 2022.
«Навигатор ЕГЭ» позволяет найти необходимую информацию на сайте ФИПИ. Там содержатся материалы для выпускников девятых и одиннадцатых классов, а также информация для учителей и репетиторов: самые распространенные ошибки, методические рекомендации по подготовке, журнал «Педагогические измерения».
УМЕТЬ.
вычислять вероятность случайного события;
вычислять вероятность случайного события с использованием графических представлений;
применять формулу сложения вероятностей;
применять формулу умножения вероятностей;
применять формулу Бернулли.
Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:
Скачать книгу Навигатор самостоятельной подготовки к ЕГЭ 2022, Математика, Профильный уровень, Элементы комбинаторики, статистики и теории вероятностей, 2022 — fileskachat.com, быстрое и бесплатное скачивание.
Скачать pdf
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России.Купить эту книгу
Скачать
— pdf — Яндекс.Диск.
Дата публикации: 29.03.2022 06:10 UTC
Теги:
ЕГЭ по математике :: 11 класс :: математика :: КИМ :: описание ЕГЭ :: навигатор по ЕГЭ :: подготовка к ЕГЭ :: ЕГЭ 2022 :: структура ЕГЭ :: задания ЕГЭ
Следующие учебники и книги:
- ЕГЭ 2022, Математика, 11 класс, Профильный уровень, Досрочник
- ЕГЭ 2022, Математика, 11 класс, Досрочная волна
- ЕГЭ 2022, Математика, 11 класс, Досрочный образец варианта, Профильный уровень
- ЕГЭ 2022, Математика, 11 класс, Методические рекомендации, Профильный уровень, Ященко И.В., Семенов А.В., Высоцкий И.Р., Черняева М.А.
Предыдущие статьи:
- Навигатор самостоятельной подготовки к ЕГЭ 2022, Математика, Профильный уровень, Рациональные, иррациональные, показательные, логарифмические и тригонометрические выражения, 2022
- Навигатор самостоятельной подготовки к ЕГЭ 2022, Математика, Профильный уровень, Неравенства, 2022
- Навигатор самостоятельной подготовки к ЕГЭ 2022, Математика, Базовый уровень, Практико-ориентированные задачи, 2022
- Навигатор самостоятельной подготовки к ЕГЭ 2022, Математика, Базовый уровень, Числа, уравнения, неравенства, функции, 2022
Перспективные модели ЕГЭ уже опубликованы на сайте ФИПИ. Разбираем возможные изменения в ЕГЭ 2022 по математике и рассказываем, чего ожидать от реального экзамена.
ЕГЭ по математике не менялся с 2015 года! На фоне масштабных изменений в других предметах это было необычно. Но с учётом сложности этого предмета и сравнительно невысоких средних баллов из года в год, никого это не удивляло. Преподаватели вздыхали с облегчением, что программу подготовки можно не менять. А ученики радовались, что можно посоветоваться с бывшими 11-классниками, потому что они сдавали то же самое.
Но вот появилась перспективная модель ЕГЭ по математике, а значит ФИПИ начал планировать изменения в экзамене. В этой статье мы обсудим их все.
Сразу хочу отметить, что пока перспективная модель только вынесена на обсуждение. А вот демоверсия экзамена по математике 2022 (то есть более точный вариант) уже вышла, и я сделала ее подробный разбор в этой статье. Спойлер: демоверсия отличается от перспективной модели.
При подготовке к ЕГЭ очень важно учитывать все актуальные изменения экзамена. Ровно за это отвечают в образовательном центре MAXIMUM. Наши преподаватели используют лучшие учебные пособия, в которых отражены последние нововведения ЕГЭ. Мы даем нашим ученикам только полезные знания и лайфхаки, которые гарантированно помогут им сдать экзамен на высокий балл. Записывайтесь к нам на бесплатный открытый урок и узнайте все об успешной подготовке к ЕГЭ.
Количество заданий в перспективной модели ЕГЭ по математике
Первая новость хорошая – количество заданий в ЕГЭ по математике НЕ ИЗМЕНИТСЯ! А хорошая она потому, что на существующие 19 заданий не у всех учеников хватало времени. Поверьте преподавателю, который «вытирал слёзы» ученикам, не успевшим написать 19в или 16б.
Изменения в количестве баллов за ЕГЭ по математике
Здесь тоже сильных изменений не будет. Добавится 1 первичный балл за счёт изменений в № 15, но об этом поговорим подробнее чуть позже.
В итоге общий балл будет поднят с 32 до 33.
Общие изменения в перспективной модели ЕГЭ по математике
Самые значительные изменения коснулись части с кратким ответом. В ней мы увидим и исключение заданий, и совершенно новые форматы, а также очень много перестановок. Однако она, как и прежде, будет приносить ученикам 12 первичных баллов.
Что касается части с развёрнутым ответом, то изменения там будут самые незначительные. Содержательно могут изменить только 2 задания, и как раз одно из них и принесёт дополнительный балл. Остальные задания не изменят.
Что убрали из краткой части в перспективной модели ЕГЭ по математике
Как я уже сказала, больше всего изменений планируется в части с кратким ответом. Во-первых, теперь все первые 12 заданий будут называться «Часть 1».
Раньше «Часть 1» включала в себя только первые 8 заданий. Номера 9-12 относились к «Части 2», но записывались в бланк с кратким ответом.
Во-вторых, именно в этой части экзамена мы можем потерять задания. В перспективной модели ЕГЭ по математике нет:
№ 1 – простейшей текстовой задачи
Тип заданий, исключенный из перспективной модели ЕГЭ по математике 2022
№ 2 – задачи на анализ графиков и диаграмм
Тип задач, которых нет в перспективной модели ЕГЭ по математике 2022
№ 3 – простейшей планиметрии на клеточках или координатной плоскости
Тип заданий, больше не встречающийся в перспективной модели ЕГЭ по математике 2022
Данные задания могут исключить из-за стабильно высокого процента решаемости, что противоречит изначальному принципу ЕГЭ – ранжировать абитуриентов.
Как теперь выглядит краткая часть
А что же тогда будет в новом экзамене?
Задание № 1
В перспективной модели на позиции №1 мы видим бывшее заданий № 5 – простейшее уравнение:
Простейшие уравнения в перспективной модели ЕГЭ по математике 2022
Задание № 2
На позиции № 2 – бывший № 4, задача по теории вероятности:
Задачи по теории вероятности, перспективная модель ЕГЭ по математике 2022
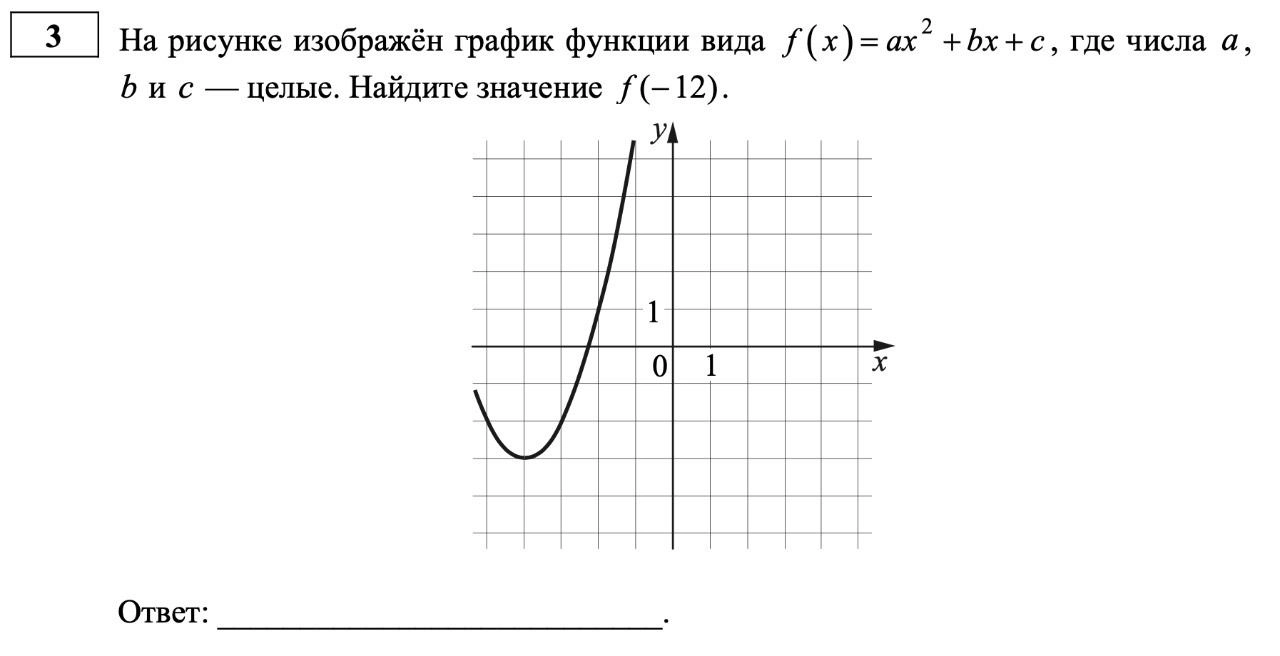
Задание № 3
Вместо № 3 – новое задание на анализ функций. Это совершенно новый формат задания, хотя тема пересекается с ОГЭ, где обычно нужно сопоставить графики и формулы. Здесь же представлено более сложное задание на анализ.
Задание на графики, перспективная модель ЕГЭ по математике 2022
Задание № 4
Вместо бывшей задачи на вероятность в № 4 переместилась планиметрическая задача (раньше она была под № 6):
Планиметрические задачи, перспективная модель ЕГЭ по математике 2022
Задание № 5
В № 5 мы видим задание на выражение, которое раньше находилось под № 9. Раньше оно относилось к заданиям повышенной сложности. Сейчас же выражение относится к базовому уровню сложности, хотя содержательно ничего не изменилось.
Задание на выражение, перспективная модель ЕГЭ по математике 2022
Задание № 6
№ 6 стал стереометрической задачей, которая ранее была № 8:
Стереометрические задачи, перспективная модель ЕГЭ по математике 2022
Задание № 7
№ 7 – это один из двух номеров, которых не коснулись изменения. Как был номером на анализ функций, так им и остался (все прототипы сохранены).
Задание № 8
В № 8 переместилась прикладная задача (ранее № 10):
Прикладная задача, перспективная модель ЕГЭ по математике 2022
Задание № 9
№ 9 теперь будет текстовой задачей на движение, проценты или сплавы и смеси:
Задача на движение, перспективная модель ЕГЭ по математике 2022
Задание № 10
А № 10 – это новое задание из блока «Элементы комбинаторики, статистики и теории вероятностей» повышенного уровня сложности. Кстати, в 2021 в перспективной модели ОГЭ тоже были 2 задания из этого блока – в первой и второй частях. Однако такое изменение в итоге не было реализовано.
Задания из блока «Элементы комбинаторики, статистики и теории вероятностей»,
перспективная модель ЕГЭ по математике 2022
Задание № 11
В № 11 также планируется ввести совершенно новое задание на комплексные числа. Это новая тема, которая не освещалась ранее в ЕГЭ. По спецификации формат данного задания – «Вычисления и преобразования» повышенного уровня сложности:
Задание на комплексные числа, перспективная модель ЕГЭ по математике 2022
Задание № 12
И № 12 – второе задание, которое осталось неизменным. Это задание на экстремумы – поиск точек максимума/минимума и наибольшего/наименьшего значений функции.
Задания на экстремумы, перспективная модель ЕГЭ по математике 2022
Изменения в части с развёрнутым ответом
Что касается части с развёрнутым ответом, то здесь всего 3 ощутимых изменения.
1. Из № 13 убрали пункт б), посвящённый отбору корней на заданном промежутке
Скорее всего, это было сделано для того, чтобы было проще набрать частичные баллы.
Ранее ученики получали по одному баллу за каждый пункт и в случае неверного решения они теряли оба балла. Сейчас 1 балл можно получить при условии совершённой вычислительной ошибки, но верной последовательности всех действий. 2 балла – за полностью верное решение.
Задание № 13, перспективная модель ЕГЭ по математике 2022
2. № 15 – самые большие изменения
Когда-то в этом номере была система из уравнения и неравенства. Стоило такое задание 3 балла. Потом задание упростили до решения неравенства и понизили стоимость до 2 баллов. А сейчас мы видим, что эксперты хотят вернуться к прошлому опыту, добавить уравнение и детализировать критерии:
- неравенство, пункт а), решено – 1 балл;
- уравнение, пункт б), решено – 1 балл;
- система из неравенства и уравнения решена – 1 балл.
Задание № 15, перспективная модель ЕГЭ по математике 2022
Несмотря на детализацию, № 15 стал сложнее. Поэтому выросла его цена – задание снова будет стоить 3 балла. Вот мы и нашли новый, 33-й балл!
3. Меняют местами номера 16 и 17
Теперь экономическая задача будет под № 16, а планиметрия второй части под № 17.
Задание № 16, экономическая задача, перспективная модель ЕГЭ по математике 2022
Задание № 17, планиметрия, перспективная модель ЕГЭ по математике 2022
Оба задания, как и раньше будут стоить 3 балла. Меняют их местами, скорее всего, из-за того, что процент решаемости экономической задачи намного выше, чем у задачи на планиметрию.
Вектор изменений в ЕГЭ по математике
О чем же говорят предлагаемые изменения? Несмотря на стабильно невысокие результаты экзамена из года в год, ЕГЭ по математике скорее всего будет усложняться с 2022 года. Темы младшей и средней школы будут убирать, а на их место ставить темы старших классов. Сами задания также будут становиться сложнее.
Можно наблюдать огромную волну возмущений по поводу ЕГЭ, которая растёт из года в год, организации петиций и попытки собрать подписи по поводу отмены ЕГЭ. На самом деле, ЕГЭ нужно не отменять, а совершенствовать. Если экзамен будет не для набора баллов и поступления, а для подготовки к высшему образованию, то возмущений будет меньше. Ровно это и делают эксперты ФИПИ! Они стремятся повлиять на изучение тем в школах, чтобы важные для высшего образования вопросы не опускались в старших классах, а изучались глубоко и в полном объёме.
Но не спешите расстраиваться и пугаться. При качественной подготовке и вложенных усилиях возможно подготовиться к экзамену и получить высокий балл, так что всё в ваших руках! Не ждите озарения, начинайте готовиться уже сейчас!
Подготовиться к ЕГЭ на высокий балл вы можете вместе с нашими преподавателями. Они поделятся с вами всеми секретами сдачи экзамена и научат быстро и правильно решать самые сложные задания. Приходите к нам на бесплатный пробный урок и начните готовиться к ЕГЭ прямо сейчас!
Что такое комбинаторика и зачем оно нам надо на ЕГЭ по информатике?
Комбинаторика — область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из элементов заданного множества.
Рассмотрим элементы комбинаторики: бывают перестановки, размещения и сочетания.
◾ПЕРЕСТАНОВКИ
Перестановками называются такие выборки элементов, которые отличаются только порядком расположения элементов.
Представь, что у тебя есть 10 книжек и тебе необходимо их расставить на полке в каком-то порядке, так сколько способов это сделать у тебя есть?
Формула подсчета перестановок:
📍Pn = n·(n−1)·(n−2)…3·2·1 = n!, где n- количество элементов данного множества.
! — это факториал числа — произведение натуральных чисел от 1 до самого числа (включая данное число.
То есть, решением поставленной задачей будет: P(10) = 10·(10−1)·(10−2)…3·2··1 = 3628800
◾РАЗМЕЩЕНИЯ
Размещениями из n элементов по m (мест) называются такие выборки, которые имея по m элементов, выбранных из числа данных n элементов, отличаются одна от другой либо составом элементов, либо порядком их расположения.
Например, тебе уже надо не все 10 книжек расставить по порядку, а только 5 из них,так вот сколько будет способов это сделать?
Число размещений из n по m обозначается A(n;m) и определяется по формуле
📍A(n;m) = n·(n − 1)·(n − 2)·…·(n − m + 1) = n!/(n − m)!
Так вот количество способов подсчитать такое расположение пяти книжек из 10 на полке и будет число размещений из 10 по 5. То есть: A(10;5) = 10!/(10 − 5)! =10!/5!=30240
◾СОЧЕТАНИЯ
Неупорядоченные выборки называются сочетаниями из n элементов по m и обозначаются С(n;m)
Ключевое слово здесь неупорядоченные, то есть нам не важно, какая книжка будет стоять на первом месте, а какая на втором, мы хотим посчитать любые варианты расстановки. Можно интерпретировать как: у нас все также есть 10 книжек, пять из которых нужно расставить в любом порядке, сколько существует возможных вариантов?
📍Число сочетаний определяется по формуле С(n;m) = n!/((n − m)!*m!)
То есть в нашей задаче получится: С(10;5) = 10!/((10 − 5)!*5!)= 252
ВАЖНО: далеко не всегда в ЕГЭ применяются формулы комбинаторики (иногда задачу проще решить перебором), но в любом случае знать основы необходимо.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!
19. Задачи на теорию чисел
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи по комбинаторике
Задание
1
#2209
Уровень задания: Легче ЕГЭ
Боря выписал все различные делители числа (12). Сколько чисел выписал Боря?
Различные делители числа (12) – это (1), (2), (3), (4), (6), (12), то есть 6 чисел.
Ответ:
(6)
Задание
2
#2210
Уровень задания: Легче ЕГЭ
Шесть пчёлок прилетели опылять два разных цветочка. Они договорились, что один цветочек будет опылять ровно одна пчёлка. Им предстоит решить, кому достанутся эти два цветочка на опыление. Сколькими способами они могут распределить двух пчёлок по двум разным цветочкам?
На первый цветочек может претендовать любая из 6 пчёлок. Как только выбрана пчёлка, которая будет опылять первый цветочек, на второй цветочек может претендовать любая из 5 оставшихся пчёлок.
Какую бы пчёлку не назначили на первый цветочек, после этого назначения остаётся 5 различных возможных вариантов назначить пчёлку на второй цветочек. То есть каждый из 6 вариантов для первого цветочка даёт 5 различных вариантов для второго цветочка.
Получаем, что всего вариантов – “шесть раз по пять”( ), то есть (6cdot 5 = 30).
Ответ:
(30)
Задание
3
#2211
Уровень задания: Легче ЕГЭ
Боря выписал все различные делители числа (120). Сколько чисел выписал Боря?
Разложим (120) на простые множители: (120 = 2^3cdot 3cdot 5). Все делители числа (120) равны (2^acdot 3^bcdot 5^c), где
(a) может принимать значения (0, 1, 2) или (3),
(b) может принимать значения (0) или (1),
(c) может принимать значения (0) или (1).
При этом если тройки ((a_1, b_1, c_1)) и ((a_2, b_2, c_2)) не совпадают, то числа (2^{a_1}cdot 3^{b_1}cdot 5^{c_1}) и (2^{a_2}cdot 3^{b_2}cdot 5^{c_2}) – различны.
Таким образом, у числа (120) столько же различных делителей, сколько существует различных троек вида ((a, b, c)), где (a) принимает одно из четырёх значений, (b) принимает одно из двух значений, (c) принимает одно из двух значений, то есть количество подходящих троек равно (4cdot 2cdot 2 = 16).
Ответ:
(16)
Задание
4
#2212
Уровень задания: Легче ЕГЭ
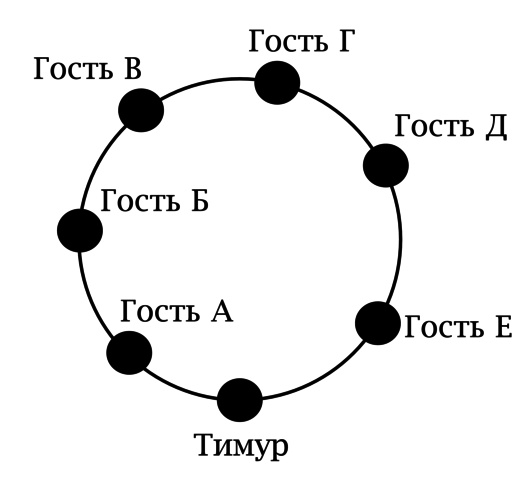
В честь своего дня рождения Тимур накрыл праздничный стол на себя и шестерых гостей. Тимур хочет сесть во главе стола (его место фиксировано). Он думает, как ему рассадить гостей, ведь у него имеется шесть разных гостевых стульев (которые уже стоят у стола и двигать их он не намерен). Сколькими способами он может это сделать?
Так как место Тимура за столом фиксировано, то можно считать, что его за столом не будет (ответ от этого не изменится).
Пусть Тимур как-то занумеровал стулья. Тогда на первый стул может претендовать любой из 6 гостей.
Какой бы из 6 гостей не занял первый стул, на второй стул может претендовать любой из оставшихся на этот момент 5 гостей. [dots]
На последний шестой стул будет претендовать один единственный гость.
В итоге: каждый из 6 вариантов для первого стула даёт пять различных вариантов для второго стула и т.д., то есть всего есть (6! = 1cdot 2cdot 3cdot 4cdot 5cdot 6 = 720) различных способов рассадить гостей.
Ответ:
(720)
Задание
5
#2213
Уровень задания: Легче ЕГЭ
Боря выписал все различные делители числа (2016). Сколько чисел выписал Боря?
Разложим (2016) на простые множители: (2016 = 2^5cdot 3^2cdot 7). Все делители числа (2016) равны (2^acdot 3^bcdot 7^c), где
(a) может принимать значения (0, 1, 2), (3), (4) или (5),
(b) может принимать значения (0), (1) или (2),
(c) может принимать значения (0) или (1).
При этом если тройки ((a_1, b_1, c_1)) и ((a_2, b_2, c_2)) не совпадают, то числа (2^{a_1}cdot 3^{b_1}cdot 7^{c_1}) и (2^{a_2}cdot 3^{b_2}cdot 7^{c_2}) – различны.
Таким образом, у числа (2016) столько же различных делителей, сколько существует различных троек вида ((a, b, c)), где (a) принимает одно из шести значений, (b) принимает одно из трёх значений, (c) принимает одно из двух значений, то есть количество подходящих троек равно (6cdot 3cdot 2 = 36).
Ответ:
(36)
Задание
6
#2214
Уровень задания: Легче ЕГЭ
В честь своего следующего дня рождения Тимур планирует накрыть праздничный стол на себя и шестерых гостей. Тимур хочет сесть во главе стола (его место фиксировано). Он думает, как ему рассадить гостей на шесть одинаковых гостевых стульев (ему не важно, на какой гостевой стул кто сядет, важно лишь кто будет соседями каждого гостя). Сколькими способами он может это сделать?
Справа от Тимура может сесть любой из 6 гостей. После того, как Тимур определится со своим правым соседом, на место справа от правого соседа Тимура может сесть любой из 5 гостей и т.д.
В итоге сосед, сидящий слева от Тимура будет, определён однозначно, то есть имеется (6! = 720) вариантов, но не все они различны.
Пусть Тимур зафиксировал гостя, который будет его соседом справа, зафиксировал и его соседа справа и т.д. Он получил некоторую последовательность, в которой он будет сажать гостей, двигаясь в одну сторону вдоль граничной окружности стола.
Но если он будет сажать гостей в той же последовательности, двигаясь в другую сторону вдоль окружности, то при этом для каждого гостя состав его соседей не изменится.
Таким образом, когда мы получили (6!) вариантов, каждый вариант рассадки мы учли ровно по два раза, следовательно, у Тимура есть (dfrac{6!}{2} = 360) способов рассадить гостей.
Ответ:
(360)
Задание
7
#2215
Уровень задания: Легче ЕГЭ
Белоснежка и семь гномов садятся за круглый стол. Известно, что Ворчун не хочет сидеть рядом с Весельчаком и Соней. Сколькими способами их можно рассадить за стол так, чтобы Ворчуна всё устраивало, если считать, что не важно, кто на какое место сядет, важно только, кто будет соседями каждого гнома и Белоснежки?
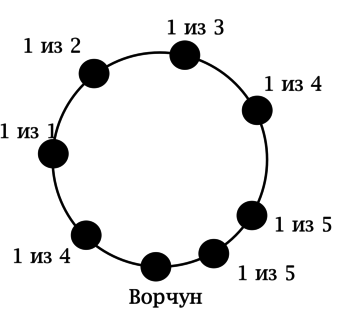
Ответ не зависит от того, в каком порядке мы будем сажать Белоснежку и гномов за стол. Пусть первым за стол садится всегда Ворчун. Тогда его правым соседом может быть один из 5 кандидатов. После того, как его правый сосед выбран, на роль левого соседа Ворчуна могут претендовать 4 кандидата.
Далее имеем ситуацию как на рисунке:
Таким образом, есть (1cdot 2cdot 3cdot 4cdot 4cdot 5cdot 5 = 2400) способов, но не все они различны. На самом деле каждый способ мы учли по два раза (если рассаживать кандидатов по часовой стрелке в определённой последовательности и если рассаживать их против часовой стрелки в той же последовательности, то рассадки будут одинаковыми).
В итоге есть (2400 : 2 = 1200) способов, которыми можно рассадить за стол гномов и Белоснежку так, чтобы Ворчуна всё устроило.
Ответ:
(1200)
При подготовке к сдаче Единого государственного экзамена по математике у большинства школьников возникают сложности с решением задач из раздела «Комбинаторика». Ученикам нелегко даются способы вычисления распределения элементов, поэтому стоит обратить на данную тему особое внимание.
Выбирайте образовательный портал «Школково» для качественной подготовки к аттестационному тестированию по математике!
Чтобы знать все необходимые формулы раздела «Комбинаторика» и быстро распределять элементы, воспользуйтесь нашим удобным онлайн-сервисом. На сайте вы найдете все необходимое для грамотной подготовки к ЕГЭ: правила, примеры с решениями и индивидуальные задания, которые постоянно обновляются и дополняются. Вся информация собрана преподавателями «Школково». Они систематизировали и изложили ее в максимально понятной форме, поэтому проблем даже с упражнениями сложного уровня у учеников не возникнет.
Мы предлагаем наиболее удобный метод повторения и усвоения информации по трудным тематикам. Для того, чтобы эффективно подготовиться к сдаче заключительного экзаменационного тестирования, рекомендуем начать с основ — легких задач по распределению элементов, постепенно переходя к сложным. Благодаря такому подходу каждый ученик сможет выявить для себя наиболее сложные типы упражнений и при подготовке уделить им больше времени.
Перед тем, как приступать к выполнению заданий, ознакомьтесь с формулами в разделе «Теоретическая справка». Потренируйтесь, решая типовые примеры, и переходите в раздел «Каталоги». В нем вы найдете большое количество упражнений различного уровня сложности и сможете выбрать подходящие для вас варианты.
При возникновении трудностей выпускник может отложить решение задачи по комбинаторике, добавив ее в «Избранное». Позже к ней можно вернуться для повторного изучения самостоятельно или уже с помощью преподавателя.
Если вы понимаете, что задания легкого и среднего уровня даются вам без проблем, смело пропускайте их и переходите к сложным упражнениям.
Начните готовиться к Единому государственному экзамену уже сейчас на портале «Школково»! Уделяйте достаточное количество времени выполнению заданий на нашем сайте, и результат не заставит себя ждать. С нашей помощью в скором времени вы сможете выполнять упражнения на сочетание чисел, с которыми ранее не справлялись.
Занятия на портале «Школково» совершенно бесплатны. Онлайн-сервисом могут пользоваться не только школьники из Москвы, но и других городов России. Просто зарегистрируйтесь на сайте для сохранения личных достижений и начинайте занятия! Желаем успехов в подготовке к ЕГЭ!

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Автор материала — Анна Малкова
На этой странице – решения новых задач из Открытого Банка заданий, из которого формируется Банк заданий ФИПИ. Вы знаете, что в Проекте ЕГЭ-2022 в варианте Профильного ЕГЭ по математике не одна задача на теорию вероятностей, а две, причем вторая – повышенной сложности. Покажем, какие задачи могут вам встретиться на ЕГЭ-2022. Проект пока не утвержден, возможны изменения, но ясно одно – теория вероятностей на ЕГЭ будет на более серьезном уровне, чем раньше. Раздел будет дополняться, так что заходите на наш сайт почаще!
1. Игральный кубик бросают дважды. Известно, что в сумме выпало 8 очков. Найдите вероятность того, что во второй раз выпало 3 очка.
Решение:
Выпишем возможные варианты получения 8 очков в сумме:
Подходит только вариант 5; 3. Вероятность этого события равна 1 : 5 = 0,2 (один случай из 5 возможных).
Ответ: 0,2.
2. В ящике 4 красных и 2 синих фломастера. Фломастеры вытаскивают по очереди в случайном порядке. Какова вероятность того, что первый раз синий фломастер появится третьим по счету?
Решение:
Благоприятными будут следующие исходы:
Первый раз – вытащили красный фломастер,
И второй раз – красный,
А третий раз – синий.
Вероятность вытащить красный фломастер (которых в ящике 4) равна
После этого в ящике остается 5 фломастеров, из них 3 красных, вероятность вытащить красный равна
Наконец, когда осталось 4 фломастера и из них 2 синих, вероятность вытащить синий равна
Вероятность события {красный – красный – синий } равна произведению этих вероятностей, то есть
Ответ: 0,2.
3. В коробке 10 синих, 9 красных и 6 зеленых фломастеров. Случайным образом выбирают 2 фломастера. Какова вероятность того, что окажутся выбраны один синий и один красный фломастер?
Решение:
Всего в коробке 25 фломастеров.
В условии не сказано, какой из фломастеров вытащили первым – красный или синий.
Предположим, что первым вытащили красный фломастер. Вероятность этого в коробке остается 24 фломастера, и вероятность вытащить вторым синий равна
Вероятность того, что первым вытащили красный, а вторым синий, равна
А если первым вытащили синий фломастер? Вероятность этого события равна Вероятность после этого вытащить красный равна
вероятность того, что синий и красный вытащили один за другим, равна
Значит, вероятность вытащить первым красный, вторым синий или первым синий, вторым красный равна
А если их доставали из коробки не один за другим, а одновременно? Вероятность остается такой же: 0,3. Потому что она не зависит от того, вытащили мы фломастеры один за другим, или с интервалом в 2 секунды, или с интервалом в 0,5 секунды… или одновременно!
Ответ: 0,3.
4. При подозрение на наличие некоторого заболевания пациента отправляют на ПЦР-тест. Если заболевание действительно есть, то тест подтверждает его в 86 % случаев. Если заболевания нет, то тест выявляет отсутствие заболевания в среднем в 94% случаев.
Известно, что в среднем тест оказывается положительным у 10% пациентов, направленных на тестирование. При обследовании некоторого пациента врач направил его на ПЦР-тест, который оказался положительным. Какова вероятность того, что пациент действительно имеет это заболевание?
Решение:
Задача похожа на уже знакомую тем, кто готовится к ЕГЭ (про гепатит), однако вопрос здесь другой.
Уточним условие: «Какова вероятность того, что пациент, ПЦР-тест которого положителен, действительно имеет это заболевание?». В такой формулировке множество возможных исходов — это число пациентов с положительным результатом ПЦР-теста, причем только часть из них действительно заболевшие.
Пациент приходит к врачу и делает ПЦР-тест. Он может быть болен этим заболеванием – с вероятностью х. Тогда с вероятностью 1 – х он этим заболеванием не болен.
Анализ пациента может быть положительным по двум причинам:
а) пациент болеет заболеванием, которое нельзя называть, его анализ верен; событие А,
б) пациент не болен этим заболеванием, его анализ ложно-положительный, событие В.
Это несовместные события, и вероятность их суммы равна сумме вероятностей этих событий.
Имеем:
Мы составили уравнение, решив которое, найдем вероятность
Что такое вероятность х? Это вероятность того, что пациент, пришедший к доктору, действительно болен. Здесь множество возможных исходов — это количество всех пациентов, пришедших к доктору.
Нам же нужно найти вероятность z того, что пациент, ПЦР-тест которого положителен, действительно имеет это заболевание. Вероятность этого события равна (пациент болен и ПЦР-тест выявил заболевание, произведение событий). С другой стороны, эта вероятность равна
(у пациента положительный результат ПЦР-теста, и при выполнении этого условия он действительно болен).
Получим: отсюда z = 0,43.
Ответ: 0,43.
Вероятность того, что пациент с положительным результатом ПЦР-теста действительно болен, меньше половины!
Кстати, это реальная проблема для диагностики в медицине, то есть в задаче отражена вполне жизненная ситуация.
5. Телефон передает sms-сообщение. В случае неудачи телефон делает следующую попытку. Вероятность того, что сообщение удастся передать без ошибок в каждой следующей попытке, равна 0,4. Найдите вероятность того, что для передачи сообщения потребуется не больше 2 попыток.
Решение:
Здесь все просто. Либо сообщение удалось передать с первой попытки, либо со второй.
Вероятность того, что сообщение удалось передать с первой попытки, равна 0,4.
С вероятностью 0,6 с первой попытки передать не получилось. Если при этом получилось со второй, то вероятность этого события равна
Значит, вероятность того, что для передачи сообщения потребовалось не более 2 попыток, равна
Ответ: 0,64.
6. Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4 орла»?
Решение:
А это более сложная задача. Можно, как и в предыдущих, пользоваться определением вероятности и понятиями суммы и произведения событий. А можно применить формулу Бернулли.
Формула Бернулли:
– Вероятность того, что в
независимых испытаниях некоторое случайное событие
наступит ровно
раз, равна:
где:
– вероятность появления события
в каждом испытании;
– вероятность непоявления события
в каждом испытании.
Коэффициент часто называют биномиальным коэффициентом.
О том, что это такое, расскажем с следующих статьях на нашем сайте. Чтобы не пропустить – подписывайтесь на нашу рассылку.
А пока скажем просто, как их вычислять.
Нет, это не заклинание. Не нужно громко кричать: Эн!!!! Поделить на эм! И на эн минус эм! 🙂 То, что вы видите в формуле, – это не восклицательные знаки. Это факториалы.
На самом деле все просто: n! (читается: эн факториал) – это произведение натуральных чисел от 1 до n. Например,
Пусть вероятность выпадения орла при одном броске монеты равна вероятность решки тоже
Давайте посчитаем вероятность того, что из 10 бросков монеты выпадет ровно 5 орлов.
Вероятность выпадения ровно 4 орлов равна
Найдем, во сколько раз больше, чем
Ответ: 1,2.
7. Стрелок стреляет по пяти одинаковым мишеням. На каждую мишень дается не более двух выстрелов, и известно, что вероятность поразить мишень каждым отдельным выстрелом равна 0,6. Во сколько раз вероятность события «стрелок поразит ровно 5 мишеней» больше вероятности события «стрелок поразит ровно 4 мишени»?
Решение:
Стрелок поражает мишень с первого или со второго выстрела.
Вероятность поразить мишень равна
Вероятность поразить 5 мишеней из 5 равна
Вероятность поразить 4 мишени из 5 находим по формуле Бернулли:
8. В одном ресторане в г. Тамбове администратор предлагает гостям сыграть в «Шеш-беш»: гость бросает одновременно 2 игральные кости. Если он выбросит комбинацию 5 и 6 очков хотя бы один раз из двух попыток, то получит комплимент от ресторана: чашку кофе или десерт бесплатно. Какова вероятность получить комплимент? Результат округлите до сотых.
Решение:
Ресторан «Шеш-Беш» должен сказать составителям задачи спасибо: теперь популярность вырастет во много раз 
Заметим, что условие не вполне корректно. Например, я бросаю кости и при первом броске получаю 5 и 6 очков. Надо ли мне бросать второй раз? Могу ли я получить 2 десерта, если дважды выброшу комбинацию из 5 и 6 очков?
Поэтому уточним условие. Если при первом броске получилась комбинация из 5 и 6 очков, то больше кости я не бросаю и забираю свой десерт (или кофе).
Если первый раз не получилось – у меня есть вторая попытка.
Решим задачу с учетом этих условий.
При броске одной игральной кости возможны 6 исходов, при броске 2 костей – 36 исходов. Только два из них благоприятны: это 5; 6 и 6; 5, вероятность каждого из них равна Вероятность выбросить 5 и 6 при первом броске равна
Вероятность того, что с первой попытки не получилось, равна
Если в первый раз не получилось выбросить 5 и 6, а во второй раз получилось – вероятность этого события равна
Вероятность выбросить 5 и 6 с первой или со второй попытки равна
9. Игральную кость бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна 4. Какова вероятность того, что был сделан один бросок? Ответ округлите до сотых.
Решение:
Рассмотрим возможные варианты. Игральную кость могли бросить:
1 раз, выпало 4 очка. Вероятность этого события равна (1 благоприятный исход из 6 возможных). При этом, если получили 4 очка, кость больше не бросаем.
2 раза, выпало 3 и 1 или 1 и 3 или 2 и 2. При этом, если получили 4 очка, больше не бросаем кость. Для 2 бросков: всего 36 возможны исходов, из них 3 благоприятных, вероятность получить 4 очка равна
3 раза, выпало 1, 1, 2 или 1, 2, 1 или 2, 1, 1. Если получили 4 очка – больше не бросаем кость. Для 3 бросков: всего возможны исходов, из них 3 благоприятных, вероятность получить 4 очка равна
4 раза, каждый раз по 1 очку. Вероятность этого события равна
Вероятность получить 4 очка равна
Воспользуемся формулой условной вероятности.
Пусть — вероятность получить 4 очка, сделав 1 бросок;
(для одного броска: 6 возможных исходов, 1 благоприятный);
— вероятность получить 4 очка с одной или нескольких попыток,
— вероятность, что при этом был сделан только один бросок;
Ответ: 0,63.
10. В викторине участвуют 6 команд. Все команды разной силы, и в каждой встрече выигрывает та команда, которая сильнее. В первом раунде встречаются две случайно выбранные команды.
Ничья невозможна. Проигравшая команда выбывает из викторины, а победившая команда играет со следующим случайно выбранным соперником. Известно, что в первых трех играх победила команда А. Какова вероятность того, что эта команда выиграет следующий раунд?
Решение:
Пусть силы команд равны 1, 2, 3, 4, 5 и 6.
В трех раундах участвуют 4 команды, то есть выбирается 4 числа из 6 и среди этих четырех находится наибольшее.
Выпишем в порядке возрастания, какие 4 команды могли участвовать в первых трех раундах:
1234, 1235, 1236, 1245, 1246, 1256, 1345, 1346, 1356, 1456, 2345, 2346, 2356, 2456, 3456 — всего 15 вариантов.
Среди этих 15 групп есть только одна, в которой 4 — наибольшее число. Это группа 1234. Однако, если команда 4 победила команды 1, 2 и 3, то у нее нет шансов выиграть в следующем раунде у команды 5 или 6.
Есть также 4 группы, в которых 5 — наибольшее число. Вероятность того, что команда 5 победила в трех первых раундах, равна В следующем туре команда 5 встретится либо с командой 6 (и проиграет), либо с командой 1, 2, 3 или 4 и выиграет, то есть в четвертом раунде команда 5 побеждает с вероятностью
Есть также 10 групп, где 6 — наибольшее число. Вероятность того, что команда 6 победила в трех первых раундах, равна В четвертом туре команда 6 побеждает с вероятностью 1 (она самая сильная). Соответственно, в следующем туре команда 6 побеждает с вероятностью 1.
Получается — вероятность команды, победившей в 3 первых турах, победить в четвертном.
Ответ:
И наконец, хитроумная задача, совсем не похожая на школьную теорию вероятностей. В математике ее называют «задачей о разорении игрока». Это уже крутейший теорвер! Будем надеяться, что в варианты ЕГЭ ее все-таки включать не будут.
11. Первый член последовательности целых чисел равен 0. Каждый следующий член последовательности с вероятностью р = 0,8 на единицу больше предыдущего и с вероятностью 1 – р меньше предыдущего. Какова вероятность того, что какой-то член этой последовательности окажется равен – 1?
Решение:
Кошмар, что и говорить, и точно не задача из Части 1 ЕГЭ. Будем разбираться.
Вначале мы находимся в точке 0, из нее можем попасть в точку с координатой 1 или в точку с координатой -1. Дальше возможно увеличение или уменьшение координаты на каждом шаге, а найти надо вероятность того, что когда-либо попадем в точку -1.
Обозначим – вероятность когда-либо попасть в точку -1, если сейчас мы находимся в точке 0,
– вероятность когда-либо попасть в точку -1, если сейчас мы находимся в точке i.
Из точки 0 можно пойти вверх или вниз. Если мы идем вниз (с вероятностью q=1 – р) – мы сразу попадаем в точку -1.
Поскольку из точки 0 можно пойти вверх или вниз, и эти события несовместны, получим:
где
– вероятность попасть когда-нибудь в точку -1, находясь в данный момент в точке 1.
А из точки 1 в точку – 1 можно попасть следующим образом: сначала в точку 0, потом в точку – 1; вероятность каждого из этих событий равна
Да, это сложно воспринять! Но давайте вернемся к обозначениям: Р1 – вероятность когда-либо попасть в точку -1, если сейчас мы находимся в точке 0. И она точно такая же, как вероятность когда-либо попасть в точку 0, если сейчас мы находимся в точке 1.
Значит, вероятность попадания из точки 1 в точку – 1 равна Мы получаем квадратное уравнение:
По условию, Тогда
Корни этого уравнения:
или
Какой из этих корней выбрать? Оказывается, если по условию то в ответе получится 1 (всегда попадем в точку -1).
А если, как в нашем случае, то ответ
то есть 0,25.
Ответ: 0,25.
А теперь представим себе, что будет, если эту задачи все-таки включат в курс подготовки к ЕГЭ. Учителя будут говорить ученикам: если тебе надо попасть из 0 в точку – 1, вероятность перехода вверх равна р, вероятность перехода вниз равна q, и если то в ответе будет
а если
то в ответе будет 1. Бессмысленная зубрежка, короче говоря.
Задачи, разобранные в этой статье, взяты из Открытого Банка заданий ЕГЭ по математике: mathege.ru
Будут ли эти задачи — и особенно последние — на ЕГЭ-2022? Вот официальный ответ ФИПИ:
«Открытость и прозрачность ЕГЭ, наличие открытых банков, дает возможность развивать различные ресурсы, способствующие повышению качества образования.
При этом вся официальная информация, спецификации, демонстрационные варианты, открытые банки, содержатся только на сайте ФИПИ. Типы заданий, которые будут включены в ЕГЭ по математике в 2022 году прошли широкое обсуждение и апробацию в регионах, соответствуют ФГОС.
ФИПИ не комментирует содержание других ресурсов».
Ждем, когда на сайте ФИПИ появятся подборки задач №10 ЕГЭ-2022.
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Новые задачи по теории вероятностей из Открытого Банка заданий ЕГЭ, 2021-2022 год» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
09.03.2023