Комбинированные неравенства егэ - Помощь в подготовке к экзаменам и поступлению

Лучшие репетиторы для сдачи ЕГЭ

Задания по теме «Комбинированные неравенства»

Открытый банк заданий по теме комбинированные неравенства. Задания C3 из ЕГЭ по математике (профильный уровень)

Стереометрия. Расстояния и углы в пространстве

Задание №1194

Тип задания: 15
Тема:
Комбинированные неравенства

Условие

Решите неравенство frac{3^x-5^{x+1}}{4^x-2^{x+log_25}+4}leqslant 0.

Показать решение

Решение

План решения.

1. Отдельно преобразуем числитель и знаменатель.

1.1. В числителе вынесем за скобки 5^x, чтобы в скобке осталась разность некоторого числа в степени x и константы (вместо этого можно вынести за скобки 3^x, а потом дополнительно преобразовать, или сразу вынести за скобки 3^{x+1}).

1.2. В знаменателе «избавимся» от log_2 5 в показателе степени (преобразуем его в множитель). После этого получим квадратичное выражение от 2^x (если сделать замену t=2^x, то получим квадратичное выражение от t). Квадратичное выражение разложим на множители.

2. Все множители в числителе и знаменателе заменим более простыми, совпадающими по знаку (в том числе равными нулю одновременно с исходными — таким образом, не надо будет дополнительно думать об ОДЗ).

3. Решим неравенство, полученное на предыдущем шаге, методом интервалов.

Решение.

1. frac{3^x-5^{x+1}}{4^x-2^{x+log_25}+4}leqslant 0,

frac{left( left( dfrac35right) ^x-5right)cdot 5^x}{2^{2x}-5cdot 2^x+4}leqslant 0,

frac{left( dfrac35right) ^x-5}{(2^x-4)(2^x-1)}leqslant 0.

2. frac{left( dfrac35right) ^x-left( dfrac35right) ^{log_tfrac355}}{(2^x-2^2)(2^x-2^0)}leqslant 0.

Выражения left( frac35right) ^x-5, 2^x-2^2, 2^x-2^0 совпадают по знаку с выражениями left( frac35-1right)cdot {x-log_{tfrac35}5}, (2-1)cdot (x-2) и (2-1)cdot (x-0) соответственно.

frac{left( dfrac35-1right)cdot (x-log_{tfrac35}5)}{(2-1)cdot (x-2)cdot (2-1)cdot (x-0)}leqslant 0.

3. frac{x-log_{tfrac35}5}{(x-2)cdot x}geqslant 0.

xin[log_{tfrac35}5; 0)cup (2; +infty ).

Ответ

[log_{tfrac35}5; 0)cup(2; +infty ).

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1190

Тип задания: 15
Тема:
Комбинированные неравенства

Условие

Решите неравенство frac{4log_2(x+0,5)}{5^{1-sqrt x}-1}leqslant 5^{sqrt x}log_2(x+0,5).

Показать решение

Решение

ОДЗ: begin{cases} x+0,5>0,\5^{1-sqrt x}-1neq 0,\xgeqslant 0; end{cases} begin{cases} xgeqslant 0,\xneq 1. end{cases}

xin[0; 1) cup (1; +infty).

frac{4 log_2(x+0,5)-5^{sqrt x} log_2(x+0,5)cdot (5^{1-sqrt x}-1)}{5^{1-sqrt x}-1}leqslant 0,

frac{log_2(x+0,5)(4-5^{sqrt {x}+1-sqrt x}+5^{sqrt x})}{5^{1-sqrt x}-1}leqslant 0.

frac{log_2(x+0,5)(5^{sqrt x}-5^0)}{5^{1-sqrt x}-5^0}leqslant 0.

Применим метод замены множителя, учитывая, что:

а) log_{h(x)}f(x)rightarrow (h(x)-1)(f(x)-1), тогда log_2(x+0,5)rightarrow (2-1)(x+0,5-1)=x-0,5.

б) h(x)^{p(x)}-h(x)^{q(x)}rightarrow (h(x)-1)(p(x)-q(x)),

тогда 5^{sqrt x}-5^0=(5-1)(sqrt x-0)=4sqrt x,

5^{1-sqrt x}-5^0= (5-1)(1-sqrt x-0)= 4(1-sqrt x).

Неравенство примет вид frac{(x-0,5)cdot sqrt x}{1-sqrt x}leqslant 0.

На ОДЗ имеем 0 leqslant x leqslant 0,5; x>1.

Ответ

[0; 0,5] cup (1; +infty ).

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №992

Тип задания: 15
Тема:
Комбинированные неравенства

Условие

Решите неравенство frac{(|2x+1|-x-2) cdot left ( log_{tfrac{1}{3}}(x+4)+1 right )}{5^{x^{2}+1}-5^{x}} geq 0.

Показать решение

Решение

Найдём область определения неравенства.

begin{cases}x+4 >0, \5^{x^{2}+1}-5^{x} neq0; end{cases}

begin{cases} x > -4, \ x^{2}+1 neq x;end{cases}

begin{cases} x > -4, \ x^{2}-x+1 neq 0;end{cases}

x > -4.

Для решения данного неравенства применяем метод интервалов.

а) Пусть f(x)= frac{(|2x+1|-x-2) cdot left ( log_{tfrac{1}{3}}(x+4)+1 right )}{5^{x^{2}+1}-5^{x}}.

б) Область определения функции f(x): D(f)=(-4;+infty ).

в) Нули функции f(x): f(x)=0.

frac{(|2x+1|-x-2) cdot left ( log_{tfrac{1}{3}}(x+4)+1 right )}{5^{x^{2}+1}-5^{x}}=0Leftrightarrow

Leftrightarrow begin{cases} (|2x+1|-x-2) cdot left ( log_{tfrac{1}{3}}(x+4)+1 right )=0, \ x >-4; end{cases}

begin{cases} left[!!begin{array}{l} |2x+1|-x-2=0, \ log_{tfrac{1}{3}}(x+4)+1=0 end{array}right. \x > -4. end{cases}

Уравнение |2x+1|-x-2=0 или |2x+1|=x+2 равносильно системе

begin{cases} (2x+1)^2=(x+2)^2,\x+2 geq 0; end{cases} Leftrightarrow begin{cases}left[!!begin{array}{l}x=-1,\x=1,end{array}right.\ x+2 geq 0;end{cases} Leftrightarrow x=pm 1.

Уравнение log_{tfrac{1}{3}}(x+4)+1=0 имеет корень x=-1.

г) Промежутки знакопостоянства функции f(x). На каждом из промежутков (-4;-1), (-1;1), (1; +infty ) функция f(x) непрерывна и сохраняет постоянный знак. Так как f(-2) > 0, f(0) > 0, f(2) < 0, то f(x) geq 0 при всех значениях x in (-4;1].

Ответ

(-4;1].

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №991

Тип задания: 15
Тема:
Комбинированные неравенства

Условие

Решите неравенство 3^{x}sqrt{5x-x^{2}+14} leq 27sqrt{5x-x^{2}+14}.

Показать решение

Решение

Данное неравенство равносильно неравенству (3^{x}-27)sqrt{5x-x^{2}+14} leq 0. Будем использовать метод интервалов, предварительно найдя ОДЗ и нули левой части неравенства.

Найдём ОДЗ неравенства:

-x^{2}+5x+14 geq 0, x^{2}-5x-14 leq 0, (x-7)(x+2) leq 0, x in [-2;7].

Найдём нули левой части неравенства: (3^{x}-27)sqrt{5x-x^{2}+14}=0,

3^{x}-27=0, 3^{x}=3^{3}, x=3.

sqrt{5x-x^{2}+14}=0, -x^{2}+5x+14=0, x_{1}=-2, x_{2}=7.

Найдем знаки выражения (3^{x}-27)sqrt{5x-x^{2}+14}

x in [-2;3] cup {7}.

Ответ

[-2;3]cup{7}

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №960

Тип задания: 15
Тема:
Комбинированные неравенства

Условие

Решите неравенство: frac{log_2(x+5)}{2^{x+2}-4^x-3}leqlog_2(x+5).

Показать решение

Решение

ОДЗ: begin{cases} x+5 > 0,\2^{x+2}-4^x-3 neq 0;end{cases}enspace begin{cases} x> -5, \ 2^{2x} -4 cdot 2^x+3 neq0;end{cases}enspace begin{cases} x > -5, \ xneq 0, \ x neq log_2 3end{cases}.

x in(-5;0)cup(0;log_2 3)cup (log_2 3; +infty ).

frac{(1-4cdot2^x+4^x+3)log_2 (x+5)}{(2^x -1)(2^x -3)} geq0,

frac{(2^x -2)^2 log_2 (x+5)}{(2^x — 2^0)(2^x -2^{log_2 3})} geq0.

Применим метод замены множителя, учитывая, что

а) log_{h(x)} f(x)rightarrow (h(x)-1)(f(x)-1), тогда

log_2 (x+5) rightarrow (2-1)(x+5-1)= x+4.

б) h(x)^{p(x)}-h(x)^{q(x)} rightarrow (h(x)-1) (p(x)-q(x)), тогда

2^x -2rightarrow (2-1)(x-1)=x-1,

2^x -2^0 =(2-1)(x-0)=x ,

2^x -2^{log_2 3}= (2-1)(x-log_2 3)= x-log_2 3.

Неравенство примет вид frac{(x+4)(x-1)^2}{x(x-log_2 3)} geq 0. Решим его методом интервалов.

Учитывая ОДЗ x> -5, x neq 0 и xneq log_2 3, получим -4 leq x < 0; x > log_2 3. x=1.

Ответ

[-4;0)cupleft{1right}cup(log_2 3;+infty)

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №235

Тип задания: 15
Тема:
Комбинированные неравенства

Условие

Решите неравенство frac{4^{x}+log_{2}x-12}{log_{2}x-2^{x}} geq 1.

Показать решение

Решение

Очевидно, что x > 0. Заметим, что log_{2}x < 2^{x} при x > 0, график функции y=log_{2}x лежит ниже прямой y=x, а график функции y=2^{x} лежит выше этой прямой, поэтому знаменатель дроби принимает только отрицательные значения. Докажем, что это верно.

Докажем, что 2^{x} > x. Рассмотрим f(x)=2^{x}-x.

f'(x)=2^{x} ln2-1.

f'(x)=0 при 2^{x} ln2-1=0,

2^{x}=frac{1}{ln2},

x_{1}=log_{2} frac{1}{ln2} — точка минимума, f(x_{1}) — наименьшее значение f(x).

Докажем, что f(x_{1}) > 0.

frac{1}{ln2}-log_{2}frac{1}{ln2} > 0;

log_{2}e-log_{2}log_{2}e > 0;

log_{2}e > log_{2}log_{2}e;

e > log_{2}e;

2^{e} > e.

Это верно, так как 2^{e} > 2^{2} > e.

Мы доказали, что 2^{x} > x. Но тогда log_{2}2^{x} > log_{2}x и x > log_{2}x.

2^{x} > x > log_{2}x, значит, 2^{x}-log_{2}x > 0.

Умножив обе части неравенства на log_{2}x-2^{x}, получим неравенство 4^{x}+log_{2}x-12 leq log_{2}x-2^{x}, которое легко сводится к неравенству 4^{x}+2^{x}-12 leq 0. Решив его методом подстановки, найдем все его решения x leq log_{2}3. Учитывая, что x > 0, получим все решения данного неравенства: x in (0; log_{2}3]

Ответ

(0; log_{2}3]

Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №206

Тип задания: 15
Тема:
Комбинированные неравенства

Условие

Решите неравенство frac{(3^x-27)(log_{x-1}x-log_{x-1}3)}{(sqrt{x^2+x}-sqrt{x^2+5)(|x+2|-|x|)}}geqslant 0.

Показать решение

Решение

ОДЗ:

begin{cases}x>0, \ x-1>0, \ x-1neq1, \ x^2+xgeqslant0, \ x^2+x neq x^2+5, \ |x+2|neq |x|; end{cases} begin{cases}x>0, \ x>1, \ xneq2, \left[!!begin{array}{l} xgeqslant 0, \ xleqslant -1, end{array}right. \ x neq 5, \ x^2+4x+4neq x^2; end{cases} begin{cases} x>1, \ xneq2, \ xneq 5.end{cases}

xin (1;2)cup (2;5)cup (5;+infty ).

На ОДЗ данное неравенство равносильно неравенству

frac{(x-3)(x-1-1)(x-3)}{(x^2+x-x^2-5)((x+2)^2-x^2)}geqslant0,

frac{(x-3)^2(x-2)}{(x-5)(4x+4)}geqslant0,

frac{(x-3)^2(x-2)}{(x-5)(x+1)}geqslant0,

xin (1;2]cup left { 3 right }cup (5;+infty ).

Учитывая ОДЗ, получим xin (1;2)cup left { 3 right }cup (5;+infty ).

Ответ

(1;2)cup left { 3 right }cup (5;+infty ).

Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №200

Тип задания: 15
Тема:
Комбинированные неравенства

Условие

Решите неравенство frac{dfrac{3}{2x+1}+log_2dfrac{x+2}{4}}{sqrt{-x}}>0.

Показать решение

Решение

ОДЗ:enspacebegin{cases}2x+1neq0,\-x>0,\ x+2>0; end{cases}enspacebegin{cases} xneqfrac{1}{2},\ x<0; \ x>-2.end{cases}

-2<x<-frac{1}{2}, -frac{1}{2}<x<0. Данное неравенство для всех x из ОДЗ равносильно неравенству log_2frac{x+2}{4}>-frac{3}{2x+1}.

Решим последнее неравенство на каждом из промежутков ОДЗ.

1) -2<x<-frac{1}{2}. Оценим левую и правую части неравенства:

log_2frac{x+2}{4}<log_2frac{3}{8}<0, -frac{3}{2x+1}>0.

Так как для всех x из промежутка left(-2;-frac{1}{2}right) выполняется неравенство log_2frac{x+2}{4}<0<-frac{3}{2x+1}, то неравенство log_2frac{x+2}{4}>-frac{3}{2x+1}, а следовательно, и исходное неравенство на промежутке left(-2;-frac{1}{2}right) не имеет решений.

2) Если -frac{1}{2}<x<0, то выполняется неравенства

log_2frac{x+2}{4}>log_2frac{3}{8}>log_2frac{1}{4}>-2.

-frac{3}{2x+1}<-3, так как 0<2x+1<1. Значит, любое значение из промежутка left(-frac{1}{2};0right) является решением неравенства log_2frac{x+2}{4}>-frac{3}{2x+1}, а следовательно, и исходного неравенства.

Итак, множеством решений исходного неравенства является промежуток left(-frac{1}{2};0right).

Ответ

left(-frac{1}{2};0right)

Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №160

Тип задания: 15
Тема:
Комбинированные неравенства

Условие

Решите неравенство 7^{ln left ( x^{2}-2x right )}leq left ( 2-x right )^{ln 7}.

Показать решение

Решение

Преобразуем неравенство:

ln left ( 7^{ln left ( x^{2}-2x right )} right )leq ln left ( left ( 2-x right )^{ln 7} right )

ln 7cdot ln left ( x^{2}-2x right )leq ln7cdot lnleft ( 2-x right )

lnleft ( x^{2}-2x right )leq lnleft ( 2-x right )

0< x^{2}-2xleq 2-x

begin{cases} x^{2}-2x> 0 \ left ( x-2 right )left ( x+1 right )leq 0 end{cases}

Получим -1leq x< 0.

Ответ

[-1; 0).

Источник: «Математика ЕГЭ 2016. Типовые тестовые задания». Под ред. И. В. Ященко.

Лучшие репетиторы для сдачи ЕГЭ

Сложно со сдачей ЕГЭ?

Звоните, и подберем для вас репетитора: 78007750928

Источник

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Смешанные неравенства

Задание
1

#1607

Уровень задания: Легче ЕГЭ

Решите неравенство

[begin{aligned}
ln(-5e^x)geqslant -1
end{aligned}]

Так как (e^x > 0) – при любом (x), то (-5e^x < 0), следовательно, (ln(-5e^x)) не определён ни при каких (xinmathbb{R}).

Ответ:

(varnothing)

Задание
2

#1608

Уровень задания: Легче ЕГЭ

Решите неравенство

[begin{aligned}
ln(5e^x)geqslant 1
end{aligned}]

Так как (e^x > 0) – при любом (x), то

[begin{aligned}
&ln(5e^x)geqslant 1qquadLeftrightarrowqquadln(5e^x)geqslant ln eqquadLeftrightarrowqquad 5e^xgeqslant eqquadLeftrightarrowqquad e^{ln 5}e^xgeqslant eqquadLeftrightarrow\
&Leftrightarrowqquad e^xgeqslant dfrac{e}{e^{ln 5}}qquadLeftrightarrowqquad e^xgeqslant e^{1 — ln 5}qquadLeftrightarrowqquad xgeqslant 1 — ln 5,.
end{aligned}]

Ответ:

([1-ln 5; +infty))

Задание
3

#1612

Уровень задания: Легче ЕГЭ

Решите неравенство

[begin{aligned}
xlog_{x + frac{pi}{2}} (x + 3) leqslant 0
end{aligned}]

ОДЗ:

[begin{aligned}
begin{cases}
x + dfrac{pi}{2} > 0\
x + dfrac{pi}{2}neq 1\
x + 3 > 0
end{cases}
qquadLeftrightarrowqquad
begin{cases}
x > -dfrac{pi}{2}\
x neq -dfrac{pi}{2} + 1
end{cases}
end{aligned}]

Заметим, что [x + 3 > x + dfrac{pi}{2} + 1]

Рассмотрим два случая:
1) (x > -dfrac{pi}{2} + 1), тогда [log_{x + frac{pi}{2}} (x + 3) > 0] и исходное неравенство равносильно [x leqslant 0,] то есть в этом случае подходят [xin left(-dfrac{pi}{2} + 1; 0right]] 2) (-dfrac{pi}{2} < x < -dfrac{pi}{2} + 1), тогда [log_{x + frac{pi}{2}} (x + 3) < 0] и исходное неравенство равносильно [x geqslant 0,] то есть в этом случае подходящих (x) нет.
В итоге ответ с учётом ОДЗ: [xin left(-dfrac{pi}{2} + 1; 0right],.]

Ответ:

(left(-dfrac{pi}{2} + 1; 0right])

Задание
4

#1609

Уровень задания: Равен ЕГЭ

Решите неравенство

[begin{aligned}
(2x + 15)log_{x + 2} (x^2 + 7x) leqslant 0
end{aligned}]

ОДЗ:

[begin{aligned}
begin{cases}
x + 2 > 0\
x + 2neq 1\
x^2 + 7x > 0
end{cases}
qquadLeftrightarrowqquad
x > 0
end{aligned}]

На ОДЗ (2x + 15 > 0), (x + 2 > 1), следовательно, исходное неравенство на ОДЗ равносильно

[begin{aligned}
log_{x + 2} (x^2 + 7x) leqslant log_{x + 2} 1qquadLeftrightarrowqquad x^2 + 7x — 1leqslant 0
end{aligned}]

По методу интервалов:

откуда (xinleft[dfrac{-7 — sqrt{53}}{2}; dfrac{-7 + sqrt{53}}{2}right]).
Пересечём ответ с ОДЗ: [xinleft(0; dfrac{-7 + sqrt{53}}{2}right]]

Ответ:

((0; -3,5 + 0,5sqrt{53}])

Задание
5

#1611

Уровень задания: Равен ЕГЭ

Решите неравенство

[begin{aligned}
dfrac{log_{x}(x — 3)}{(e^x + 2)cdotlog_{2}(x + 11)}leqslant 0
end{aligned}]

ОДЗ:

[begin{aligned}
begin{cases}
x > 0\
xneq 1\
x — 3 > 0\
e^x + 2neq 0\
log_{2}(x + 11)neq 0\
x + 11 > 0
end{cases}
qquadLeftrightarrowqquad
x > 3,.
end{aligned}]

По методу рационализации: на ОДЗ

[begin{aligned}
dfrac{log_{x}(x — 3)}{(e^x + 2)cdotlog_{2}(x + 11)}leqslant 0qquad&Rightarrowqquad dfrac{(x — 1)(x — 3 — 1)}{(e^x + 2)cdot(2 — 1)(x + 11 — 1)}leqslant 0,.
end{aligned}]

С учётом ОДЗ последнее неравенство равносильно

[begin{aligned}
x — 4leqslant 0
end{aligned}]

Таким образом, с учётом ОДЗ: [xin (3; 4].]

Ответ:

((3; 4])

Задание
6

#3901

Уровень задания: Равен ЕГЭ

Решите неравенство [4^{frac{9x^2}4}-
left(left(frac32x+1right)^{log_{frac32x+1}2}right)^
{frac{9x^2-4}4}leqslant 3]

ОДЗ неравенства: [begin{cases} dfrac32x+1>0\[2ex]
dfrac32x+1ne 1end{cases}quad Leftrightarrowquad xin
left(-dfrac23;0right)cup(0;+infty)] Решим неравенство на ОДЗ. Так как (a^{log_ab}=b), то [4^{frac{9x^2}4}-2^{frac{9x^2}4-1}leqslant 3] Сделаем замену (t=2^{frac{9x^2}4}), (t>0), тогда [t^2-0,5t-3leqslant 0quadLeftrightarrowquad
left(t+frac32right)(t-2)leqslant 0quadLeftrightarrowquad tin
left[-dfrac32;2right]] Так как (t>0), то получаем (tleqslant
2). Сделаем обратную замену: [begin{aligned}
&2^{frac{9x^2}4}leqslant 2quadLeftrightarrowquad
dfrac{9x^2}4leqslant 1quadLeftrightarrowquad
left(x-dfrac23right)left(x+dfrac23right)leqslant
0quadLeftrightarrow\[2ex]
&xin left[-dfrac23;dfrac23right]end{aligned}] Пересечем ответ с ОДЗ и получим [xin left(-dfrac23; 0right)cupleft(0;dfrac23right]]

Ответ:

(xin left(-frac23; 0right)cupleft(0;frac23right])

Задание
7

#1614

Уровень задания: Равен ЕГЭ

Решите неравенство

[begin{aligned}
log_{5^x} 25^{x + 1} + log_{25^{x + 1}} 5^x — 2 > 0
end{aligned}]

ОДЗ:

[begin{aligned}
begin{cases}
5^x > 0\
5^x neq 1\
25^{x + 1} > 0\
25^{x + 1}neq 1
end{cases}
qquadLeftrightarrowqquad
x in(-infty; -1)cup(-1; 0)cup(0; +infty)
end{aligned}]

Сделаем замену (log_{5^x} 25^{x + 1} = y):

[begin{aligned}
y + dfrac{1}{y} — 2 > 0quadLeftrightarrowquad dfrac{y^2 — 2y + 1}{y} > 0quadLeftrightarrowquad dfrac{(y — 1)^2}{y} > 0quadLeftrightarrowquad
begin{cases}
y > 0\
yneq 1,
end{cases}
end{aligned}]

откуда

[begin{aligned}
begin{cases}
log_{5^x} 25^{x + 1} > 0\
log_{5^x} 25^{x + 1}neq 1
end{cases}
qquadLeftrightarrowqquad
begin{cases}
dfrac{2x + 2}{x} > 0\
dfrac{2x + 2}{x} neq 1
end{cases}
end{aligned}]

Решая первое неравенство последней системы, получаем: [xin (-infty; -1)cup(0; +infty)] Решая второе неравенство последней системы, получаем: [xin (-infty; -2)cup(-2; 0)cup(0; +infty)] В итоге: [xin (-infty; -2)cup(-2; -1)cup(0; +infty)] – подходит по ОДЗ.

Ответ:

((-infty; -2)cup(-2; -1)cup(0; +infty))

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Задания по теме «Комбинированные неравенства»

Задание №1194

Условие

Решение

1. Отдельно преобразуем числитель и знаменатель.

1.2. В знаменателе «избавимся» от log_2 5 в показателе степени (преобразуем его в множитель). После этого получим квадратичное выражение от 2^x (если сделать замену t=2^x, то получим квадратичное выражение от t ). Квадратичное выражение разложим на множители.

3. Решим неравенство, полученное на предыдущем шаге, методом интервалов.

Выражения left( frac35right) ^x-5, 2^x-2^2, 2^x-2^0 совпадают по знаку с выражениями left( frac35-1right)cdot 5>, (2-1)cdot (x-2) и (2-1)cdot (x-0) соответственно.

Репетитор по математике

Меня зовут Виктор Андреевич, — я репетитор по математике . Последние десять лет я занимаюсь только преподаванием. Я не «натаскиваю» своих учеников. Моя цель — помочь ребенку понять предмет, научить его мыслить, а не применять шаблоны, передать свои знания, а не просто «добиться результата».

Предусмотрен дистанционный формат занятий (через Skype или Zoom). На первом же уроке оцениваем уровень подготовки ребенка. Если ребенка устраивает моя подача материала, то принимаем решение о дальнейшем сотрудничестве — составляем расписание и индивидуальный план работы. После каждого занятия дается домашнее задание — оно всегда обязательно для выполнения. [в личном кабинете родители могут контролировать успеваемость ребенка]

Стоимость занятий

Набор на 2020/2021 учебный год открыт. Предусмотрен дистанционный формат.

Видеокурсы подготовки к ЕГЭ-2021

Решения авторские, то есть мои (автор ютуб-канала mrMathlesson — Виктор Осипов). На видео подробно разобраны все задания.

Теория представлена в виде лекционного курса, для понимания методик, которые используются при решении заданий.

Группа Вконтакте

В группу выкладываются самые свежие решения и разборы задач. Подпишитесь, чтобы быть в курсе и получать помощь от других участников.

Преимущества

Педагогический стаж

Сейчас существует много сайтов, где вам подберут репетитора по цене/опыту/возрасту, в зависимости от желаний. Но большинство анкет там принадлежат либо студентам, либо школьным учителям. Для них репетиторство — дополнительный временный заработок, из этого формируется отношение к деятельности. У студентов нет опыта и желания совершенствоваться, у школьных учителей — нет времени и сил после основной деятельности. Я занимаюсь только репетиторством с 2010 года. Все свои силы и знания трачу на совершенствование только в этой области.

Собственная методика

За время работы я накопил огромное количество материала для подготовки к итоговым экзаменам. Ребенку не будет даваться неадаптированная школьная программа. С каждым я разберу поэтапно специфичные примеры, темы, способы решений, необходимые для успешной сдачи ЕГЭ и ОГЭ. При этом это не будет «натаскиванием» на решение конкретных задач, но полноценная структурированная подготовка. Естественно, если таковые найдутся, устраню «пробелы» и в школьной программе.

Гарантированный результат

За время моей работы не было ни одного случая, где не прослеживалась бы четкая тенденция к улучшению знаний у ученика. Ни один откровенно не «завалил» экзамен. Каждый вырос в «понимании» математики в сравнении со своим первоначальным уровнем. Естественно, я не могу гарантировать, что двоечник за полгода подготовится на твердую «пять». Но могу с уверенностью сказать, что я подготовлю ребенка на его максимально возможный уровень за то время, что осталось до экзамена.

Индивидуальная работа

Все дети разные, поэтому способ и форма объяснения корректируются в зависимости от уровня понимания ребенком предмета. Индивидуальная работа с каждым учеником — каждому даются отдельные задания, теоретический материал.

Задание 14. Неравенства — профильный ЕГЭ по математике

Задание 14 Профильного ЕГЭ по математике можно считать границей между «неплохо сдал ЕГЭ» и «поступил в вуз с профильной математикой». Здесь не обойтись без отличного знания алгебры. Потому что встретиться вам может любое неравенство: показательное, логарифмическое, комбинированное (например, логарифмы и тригонометрия). И еще бывают неравенства с модулем и иррациональные неравенства. Некоторые из них мы разберем в этой статье.

Хотите получить на Профильном ЕГЭ не менее 70 баллов? Учитесь решать неравенства!

Темы для повторения:

Разберем неравенства разных типов из вариантов ЕГЭ по математике.

Дробно-рациональные неравенства

1. Решите неравенство:

Решим неравенство относительно t методом интервалов:

Вернемся к переменной x:

Показательные неравенства

2. Решите неравенство

Сделаем замену Получим:

Умножим неравенство на

Дискриминант квадратного уравнения

Значит, корни этого уравнения:

Разложим квадратный трехчлен на множители.

. Вернемся к переменной x.

Внимание. Сначала решаем неравенство относительно переменной t. Только после этого возвращаемся к переменной x. Запомнили?

Следующая задача — с секретом. Да, такие тоже встречаются в вариантах ЕГЭ,

3. Решите неравенство

Сделаем замену Получим:

Вернемся к переменной

Первое неравенство решим легко: С неравенством тоже все просто. Но что делать с неравенством ? Ведь Представляете, как трудно будет выразить х?

Оценим Для этого рассмотрим функцию

Сначала оценим показатель степени. Пусть Это парабола с ветвями вниз, и наибольшее значение этой функции достигается в вершине параболы, при х = 1. При этом

Мы получили, что

Тогда , и это значит, что Значение не достигается ни при каких х.

Логарифмические неравенства

4. Решите неравенство

Запишем решение как цепочку равносильных переходов. Лучше всего оформлять решение неравенства именно так.

Следующее неравенство — комбинированное. И логарифмы, и тригонометрия!

5. Решите неравенство

А вот и метод замены множителя (рационализации). Смотрите, как он применяется. А на ЕГЭ не забудьте доказать формулы, по которым мы заменяем логарифмический множитель на алгебраический.

6. Решите неравенство:

Мы объединили в систему и область допустимых значений, и само неравенство. Применим формулу логарифма частного, учитывая, что . Используем также условия

Обратите внимание, как мы применили формулу для логарифма степени. Строго говоря,

Согласно методу замены множителя, выражение заменим на

Решить ее легко.

Разберем какое-нибудь нестандартное неравенство. Такое, что не решается обычными способами.

7. Решите неравенство:

Привести обе части к одному основанию не получается. Ищем другой способ.

Заметим, что при x = 9 оба слагаемых равны 2 и их сумма равна 4.

Функции и — монотонно возрастающие, следовательно, их сумма также является монотонно возрастающей функцией и каждое свое значение принимает только один раз.

Поскольку при x=9 значение монотонно возрастающей функции равно 4, при значения этой функции меньше 4. Конечно, при этом , то есть x принадлежит ОДЗ.

источники:

http://mathlesson.ru/node/8046

http://ege-study.ru/ru/ege/materialy/matematika/zadanie-15-profilnogo-ege-po-matematike-neravenstva/

Источник

Хотите получить на Профильном ЕГЭ не менее 70 баллов? Учитесь решать неравенства!

Темы для повторения:

^New

Решаем задачи из сборника И. В. Ященко, 2021

Квадратичные неравенства

Метод интервалов

Уравнения и неравенства с модулем

Иррациональные неравенства

Показательные неравенства

Логарифмические неравенства

Метод замены множителя (рационализации)

Решение неравенств: основные ошибки и полезные лайфхаки

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 8, задача 15

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 32, задача 15

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 36, задача 15

Логарифмические неравенства повышенной сложности

Разберем неравенства разных типов из вариантов ЕГЭ по математике.

Дробно-рациональные неравенства

1. Решите неравенство:

$frac{{ 2}}{{ 0,5x}sqrt{{ 5}}{ -}{ 1}}{ +}frac{{ 0,5x}sqrt{{ 5}}{ -}{ 2}}{{ 0,5x}sqrt{{ 5}}{ -}{ 3}} geq { 2.}$

Сделаем замену

Тогда , а

Получим:

$frac{{ 2}}{{ t+1}}{ +}frac{{ t}}{{ t-1}} geq { 2};$

$frac{{ 2}{ t}{ -}{ 2+}{{ t}}^{{ 2}}{ +}{ t}}{{{ t}}^{{ 2}}{ -}{ 1}}{ -}{ 2} geq{ 0};$

$frac{{{ t}}^{{ 2}}{ +3}{ t}{ -}{ 2-2}{{ t}}^{{ 2}}{ +2}}{{{ t}}^{{ 2}}{ -}{ 1}} geq { 0};$

$frac{{ 3}{ t}{ -}{{ t}}^{{ 2}}}{{{ t}}^{{ 2}}{ -}{ 1}} geq { 0};$

$frac{{ t}left({ t}{ -}{ 3}right)}{left({ t}{ -}{ 1}right)left({ t}{ +1}right)}le { 0}.$

Решим неравенство относительно t методом интервалов:

Получим:

$left[ begin{array}{c}{ -}{ 1 textless t}le { 0} \{ 1 textless t}le { 3} end{array}right..$

Вернемся к переменной x: $left[ begin{array}{c} -1 textless 0,5xsqrt{5}-2leq0 \ 1 textless 0,5xsqrt{5}-2leq 3 end{array} right. .$

$left[ begin{array}{c} {{2}over{sqrt{5}}} textless xleq {{4}over{sqrt{5}}}\ {{6}over{sqrt{5}}} textless xleq {{10}over{sqrt{5}}} end{array} right. .$

Ответ: $xin left(frac{{ 2}}{sqrt{{ 5}}};frac{{ 4}}{sqrt{{ 5}}}right]cup left(frac{{ 6}}{sqrt{{ 5}}};{ 2}sqrt{{ 5}}right].$

Показательные неравенства

2. Решите неравенство $2^x+17cdot 2^{3-x}le 25.$

$2^x+17cdot frac{8}{2^x}le 25.$

Сделаем замену Получим:

$t+17cdot frac{8}{t}-25le 0.$ Умножим неравенство на

Дискриминант квадратного уравнения

$D={left(-25right)}^2-4cdot 136=625-544=81.$ Значит, корни этого уравнения: $left[ begin{array}{c}t_1=17 \t_2=8 end{array}.right.$

Разложим квадратный трехчлен на множители.

. Вернемся к переменной x.

$2^3le 2^xle 2^{{{log }_2 17}};$

$3le xle {{log }_2 17};$

Ответ: $xin left[3;{{log }_2 17}right].$

Следующая задача — с секретом. Да, такие тоже встречаются в вариантах ЕГЭ.

3. Решите неравенство $2^{2x-x^2-1}+frac{1}{2^{2x-x^2}-1}le 2.$

Сделаем замену $2^{2x-x^2}=t,t textgreater 0.$ Получим:

$frac{t}{2}+frac{1}{t-1}-2le 0;$

$frac{t^2-t+2-4t+4}{2left(t-1right)}le 0;$

$frac{t^2-5t+6}{t-1}le 0;$

$frac{left(t-2right)left(t-3right)}{t-1}le 0.$

$left[ begin{array}{c}t textless 1 \2le tle 3 end{array} .right.$

Вернемся к переменной $x:left[ begin{array}{c}2^{2x-x^2} textless 1 \{2le 2}^{2x-x^2}le 3 end{array}.right.$

Первое неравенство решим легко: С неравенством ${2le 2}^{2x-x^2}$ тоже все просто. Но что делать с неравенством $2^{2x-x^2}le 3$ ? Ведь $3 = 2^{{{log }_2 3}}.$ Представляете, как трудно будет выразить х?

Оценим $t=2^{2x-x^2}.$ Для этого рассмотрим функцию $tleft(xright)=2^{2x-x^2}.$

Мы получили, что

Тогда $2^{zleft(xright)}le 2$ , и это значит, что Значение не достигается ни при каких х.

Но если ${2le 2}^{2x-x^2}$ и $2^{2x-x^2}le 2$ , то $2^{2x-x^2}=2.$

Мы получили:

$left[ begin{array}{c} 2x-x^2 textless 0\ 2x-x^2=1end{array} right. Leftrightarrow left[ begin{array}{c} x(x-2) textgreater 0\ x^2-2x+1=0end{array} right. Leftrightarrow left[ begin{array}{c} x textless 0\ x textgreater 2\(x-1)^2=0end{array} right. Leftrightarrow$

$Leftrightarrow left[ begin{array}{c} x textless 0\ x textgreater 2\ x=1end{array}. right.$

Ответ:

Логарифмические неравенства

4. Решите неравенство $2{{log}_{frac{1}{2}} left(1-xright) textless {{log}_{frac{1}{2}} left(3x+1right)}}.$

Запишем решение как цепочку равносильных переходов. Лучше всего оформлять решение неравенства именно так.

$2log_{{1}over{2}}(1-x) textless log_{{1}over{2}}(3x+1)Leftrightarrow left{begin{matrix} 1-x textgreater 0\3x+1 textgreater 0 \(1-x)^2 textgreater 3x+1 end{matrix}right.Leftrightarrow left{begin{matrix} x textless 1\x textgreater -{{1}over{3}} \ 1+x^2-2x textgreater 3x+1 end{matrix}right.Leftrightarrow$

$Leftrightarrow left{begin{matrix} x textless 1\x textgreater {-{{1}over{3}}} \ x^2-5x textgreater 0 end{matrix}right.Leftrightarrow left{begin{matrix} x textless 1\ x textgreater {-{{1}over{3}}} \ x(x-5) textgreater 0 end{matrix} .right.$

Ответ: $xin left(-frac{1}{3};0right).$

Следующее неравенство — комбинированное. И логарифмы, и тригонометрия!

5. Решите неравенство $2{{{log}_2}^2 {{cos}^2 x+7{{log}_2 {cos x} geq 1}}}.$

$2{{{log }_2}^2 {{cos }^{{ 2}} x+7{{log }_2 {cos x} geq 1}}}.$

ОДЗ:

Замена ${{log }_2 {cos x}=t} Rightarrow {{log }_2 {{cos }^{{ 2}} x}}=2{{log }_2 {cos x=2t}}.$

$2cdot {left(2tright)}^2+7t-1 geq 0;$

$t_1=frac{-7-9}{16}=-1;$

$t_2=frac{-7+9}{16}=frac{1}{8}.$

$(t+1)(t-{{1}over{8}})geq 0Leftrightarrow left[ begin{array}{c} t leq -1 \ t geq {{1}over{8}} end{array} right. Leftrightarrow left[ begin{array}{c} log_2,cosx leq-1 \ log_2,cosx geq {{1}over{8}} end{array} right.$
$Leftrightarrow left{begin{matrix} left[ begin{array}{c} cosxleq{{1}over{2}} \ cosxgeqsqrt[8]{2} end{array} right. \ cosx textgreater 0 end{matrix}right.Leftrightarrow 0 textless cosxleq{{1}over{2}}.$

Ответ: $xin left(-frac{pi }{2}+2pi k;left.-frac{pi }{3}+2pi kright]right.cup left[frac{pi }{3}+2pi k;left.frac{pi }{2}+2pi kright), kright.in Z.$

6. Решите неравенство: ${{log }_{{ 3-x}} frac{{ x+4}}{{left({ x-3}right)}^{{ 2}}}} geq { -2}.$

$log_{3-x}frac{x+4}{(x-3)^2}geq-2Leftrightarrow left{begin{matrix} 3-x textgreater 0\3-xneq1 \ {x+4over (x-3)^2} textgreater 0 \ log_{3-x} {{x+4}over(x-3)^2}+2geq 0 end{matrix} .right.$

Мы объединили в систему и область допустимых значений, и само неравенство. Применим формулу логарифма частного, учитывая, что ${left({ a-b}right)}^{{ 2}}{ =}{left({ b-a}right)}^{{ 2}}{ }$ . Используем также условия

$left{begin{matrix} x textless 3\xneq2 \ x+4 textgreater 0 \ log_{3-x}(x+4)-log_{3-x}(3-x)^2+2geq0 end{matrix}right. Leftrightarrow$

$Leftrightarrow left{begin{matrix} x textless 3\xneq2 \ x textgreater -4 \ log_{3-x}(x+4)geq0 end{matrix}.right.$

Обратите внимание, как мы применили формулу для логарифма степени. Строго говоря, ${{log }_{{ a}} {left({ b}left({ x}right)right)}^{{ 2}}{ =2}{{log }_{{ a}} left|{ b}left({ x}right)right|}}.$

Поскольку ${ 3-}{ x}{ textgreater 0,}{{ log}}_{{ 3-x}}{left({ 3-x}right)}^{{ 2}}{ =2}{{log }_{{ 3-x}} left|{ 3-x}right|{ =}}{ 2}{{log }_{{ 3-x}} left({ 3-x}right){ =2.}}$

Согласно методу замены множителя, выражение ${{ log}}_{{ 3-x}}left({ x+4}right)$ заменим на

Получим систему:

$left{ begin{array}{c}{ x}ne { 2} \{ -}{ 4}{ textless x textless 3} \left({ 2-x}right)left({ x+3}right) geq { 0} end{array}.right.$

Решить ее легко.

Ответ: .

Разберем какое-нибудь нестандартное неравенство. Такое, что не решается обычными способами.

7. Решите неравенство:

${{log }_2 left(x-5right)+{{log }_3 xleq 4}}.$

ОДЗ: $left{ begin{array}{c}x-5 textgreater 0 \x textgreater 0 end{array}Longleftrightarrow x textgreater 5.right.$

Привести обе части к одному основанию не получается. Ищем другой способ.

Заметим, что при x = 9 оба слагаемых равны 2 и их сумма равна 4.

${{log }_2 left(9-5right)={{log }_2 4=2}};$

${{log }_3 9=2};$

${{log }_2 left(9-5right)+{{log }_3 9=4}}.$

Поскольку при x=9 значение монотонно возрастающей функции ${{{ y=}log }_2 left(x-5right)+{{log }_3 x}}$ равно 4, при значения этой функции меньше 4. Конечно, при этом , то есть x принадлежит ОДЗ.

Ответ: (5; 9].

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 14. Неравенства u0026#8212; профильный ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

Тема 14.

Решение неравенств

Смешанные неравенства

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

решение неравенств

14.01Задачи из ЕГЭ прошлых лет

14.02Задачи из сборника И.В. Ященко ЕГЭ 2023

14.03Рациональные неравенства и метод интервалов

14.04Показательные неравенства

14.05Логарифмические неравенства с числовым основанием

14.06Логарифмические неравенства с переменным основанием

14.07Метод рационализации

14.08Смешанные неравенства

14.09Системы неравенств

Решаем задачи

Решите неравенство

Показать ответ и решение

Ответ:

Решите неравенство

x 1-
ln(7e ) ≥ x

Показать ответ и решение

ОДЗ:

{
7ex > 0
⇔ x ⁄= 0.
x ⁄= 0

На ОДЗ:

x 1- x 1x x 1x ln7 x 1x
ln (7e ) ≥ x ⇔ ln(7e ) ≥ lne ⇔ 7e ≥ e ⇔ e e ≥ e ⇔
1x 2
⇔ ex ≥ -e-- ⇔ ex ≥ e 1x−ln7 ⇔ x ≥ 1-− ln7 ⇔ x--+-xln-7 −-1 ≥ 0.
eln7 x x

По методу интервалов

Таким образом, с учётом ОДЗ

Ответ:

Решите неравенство

Показать ответ и решение

Ответ:

Решите неравенство:

-1 9log16(7−x) log216(x− 7)2
32 ⋅2 ≥ 2 .

Показать ответ и решение

-1 9log16(7−x) log216(x−7)2
32 ⋅2 ≥ 2

Найдем ОДЗ данного неравенства:

(
{7 − x > 0 ⇔ 7 − x > 0 ⇔ x < 7
((x− 7)2 > 0

Преобразуем левую часть неравенства:

Преобразуем показатель степени в правой части неравенства:

На ОДЗ и исходное неравенство примет вид:

Обозначим , тогда

Перепишем неравенство в виде

pict

Решим неравенство методом интервалов:

Произведем обратную замену:

Учтем ОДЗ:

(
{ x < 7
( ⇔ − 25 ≤ x ≤ − 9 ⇔ x ∈ [− 25;− 9]
− 25 ≤ x ≤ − 9

Ответ:

Решите неравенство

( 35 x−1 x− 1)
2x≥ log2 3-⋅6 − 2⋅9 2

Показать ответ и решение

Преобразуем неравенство

({ 2x 35 x 2 x ({ x x x
2 ≥ 18 ⋅6 − 3 ⋅9 ⇔ 18⋅4( − 35⋅6 + 1)2⋅9 ≥ 0
( 3518-⋅6x − 23 ⋅9x > 0 ( 3x3- 356-⋅2x − 2 ⋅3x > 0

Из второго неравенства получаем

( )x
35⋅2x− 2⋅3x > 0 ⇔ 2 > 12 ⇔ x <log212
6 3 35 335

Из первого неравенства получаем

(2)2x ( 2)x
18⋅ 3 − 35 ⋅ 3 +12 ≥0

Замена ( )x
t= 2
3 дает:

( ] [ )
18 ⋅t2− 35t+ 12≥ 0 ⇔ t∈ −∞; 4 ∪ 3;+ ∞
9 2

Сделаем обратную замену:

⌊(2)x ≤ 4
⌈(3)x 9 ⇔ x∈ (− ∞;− 1]∪ [2;+ ∞)
23 ≥ 32

log23 12 > 2
35 , т.к. ( )2
2 = 4= 4-⋅35 = 140> 108 = 9⋅12= 12-
3 9 9 ⋅35 315 315 9⋅35 35 , и основание логарифма меньше 1.

Поскольку x < log2 12-
3 35 , получаем [ )
x∈ (−∞; −1]∪ 2;log2 12
3 35 .

Ответ:

[ 12)
(−∞; −1]∪ 2;log2335

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	2

Обоснованно получен ответ, отличающийся от верного исключением/включением граничных точек,	1
ИЛИ
получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	2

При этом в первом случае выставления 1 балла допускаются только ошибки
в строгости неравенства: «» вместо «» или наоборот. Если в
ответ включено значение переменной, при котором одна из
частей неравенства не имеет смысла, то выставляется оценка «0
баллов».

Решите неравенство

log1log3(−2x) log1log5(−2x)
5 5 < 3 3

Показать ответ и решение

По свойствам логарифма исходное неравенство равносильно:

pict

Последний переход корректен, так как первое неравенство системы выполняется при всех из ОДЗ: ведь
основание логарифма левой части больше основания логарифма правой части, а аргументы равны.

Ответ:

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	2

Обоснованно получен ответ, отличающийся от верного исключением/включением граничных точек,	1
ИЛИ
получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	2

Решите неравенство

Показать ответ и решение

ОДЗ: x > 0.

Решим неравенство на ОДЗ.

Сделаем замену .

Тогда

16 t2-−-17t+-16
t+ t < 17 ⇔ t < 0

Решая неравенство методом интервалов, получим:

[
t < 0
1 < t < 16

Так как из-за замены t > 0 , то неравенство t < 0 не имеет решений.

Делаем обратную замену:

lnx⋅logx 0 lnx⋅log x ln 16
1 < e 2 < 16 ⇔ e < e 2 < e ⇔ 0 < lnx ⋅log2x < ln16

Решим данное двойное неравенство как два неравенства по отдельности и затем пересечем решения.

1) Решим с помощью метода рационализации:

2
(e− 1)(x − 1)(2 − 1)(x− 1) > 0 ⇔ (x − 1) > 0 ⇔ x ⁄= 1

2) . Разделим обе части неравенства на положительное число ln16 :

Пересекая решения этих двух неравенств между собой и с ОДЗ, получаем окончательный ответ.

Ответ:

Решите неравенство

∘ -----
x+ 1⋅log0,5(log2|1− x|)≥ 0
2

Показать ответ и решение

При левая часть неравенства имеет смысл и равна нулю. Тогда
пойдет в ответ.

При условии получаем неравенство

log (log |1 − x|)≥ 0
0,5 2

Отсюда имеем:

Следовательно, или

Учитывая условие находим:

1
− 2< x< 0 или 2< x ≤3

Объединяя полученные множества c получаем

[ )
x ∈ − 1;0 ∪(2;3]
2

Ответ:

[ )
− 1;0 ∪(2;3]
2

Найдите все такие , которые являются решениями неравенства

N ⋅ log 3 ⋅ log (1 + x) ≥ 1
(1+Nx) 3

при любых

Показать ответ и решение

ОДЗ:

(
|{ 1 + N x > 0

|( 1 + N x ⁄= 1 — при лю бы х N ∈ ℕ
1 + x > 0

Покажем, что x < 0 не подходят по ОДЗ:
зафиксируем произвольное x < 0 , тогда . Существует , такое что

1
n > ----.
− x

Положим N = n , тогда

что
не подходит по ОДЗ. Таким образом, x ≥ 0 .

Также по ОДЗ не подходит x = 0 , а x > 0 подходят по ОДЗ, следовательно,
ОДЗ:

x > 0.

На
ОДЗ:
исходное неравенство равносильно неравенству

Так как на ОДЗ

то
, следовательно,

------1------ N N
log (1 + N x) ⋅ log3(1 + x) ≥ 1 ⇔ log3(1 + x) ≥ log3(1 + N x) ⇔
3 N
⇔ (1 + x ) ≥ (1 + N x).

Зафиксируем произвольный x > 0 .
Докажем по индукции, что данное неравенство выполнено для всех :

1) N = 1 :

–
верно.

2) Рассмотрим произвольное , такое что , тогда

m+1 m 2
(1 + x) = (1 + x) ⋅ (1 + x) ≥ (1 + x) ⋅ (1 + mx ) = 1 + mx + x + mx ≥ 1 + x(m + 1),

таким образом, мы доказали, что рассматриваемый подходит. Так как мы фиксировали
произвольный x > 0 , то все x > 0 являются решениями исходной задачи.

Ответ:

Решите неравенство

( )log (2x+3)
3log2(x2)+ 2⋅|x|log29 ≤ 3⋅ 1 0,5
3

Показать ответ и решение

Запишем ОДЗ:

{
x2 >0 ⇒ x∈ (−1,5;0)∪ (0;+∞ )
2x +3 > 0

Тогда на ОДЗ второе слагаемое левой части можно преобразовать так:

( ) ( )
2⋅|x|log29 = 2 ⋅|x|log23 2 = 2 ⋅3log2|x| 2 = 2⋅3log2x2

Правую часть можно преобразовать так:

Тогда все неравенство перепишется в виде

Получили квадратичное неравенство

Пересекая полученное множество с ОДЗ, получим

Ответ:

Решите неравенство

Показать ответ и решение

ОДЗ:

На ОДЗ:
исходное неравенство равносильно неравенству

x log (--1- ) x 1 x
2 ⋅ 2 21+xln2 ≥ 1 ⇔ 2 ⋅--------- ≥ 1 ⇔ 2 ≥ 1 + xln 2 ⇔
x 1 + x ln 2
⇔ 2 − 1 − xln 2 ≥ 0.

Рассмотрим функцию

Найдём её промежутки возрастания/убывания:

Легко проверить, что x = 0 – единственная точка локального минимума функции , тогда она
является точкой минимума и наименьшее значение равно

0
f(0) = 2 − 1 − 0 ⋅ ln 2 = 0.

Таким образом, x
2 − 1 − xln2 ≥ 0 – верно при всех , тогда ответ совпадает с
ОДЗ:

x > − -1--.
ln2

Ответ:

( )
− -1--;+ ∞
ln 2

Решите неравенство

Показать ответ и решение

Найдем ОДЗ неравенства:

(
| 5x > 0
||{ x
5 ⁄= 1 ⇔ x ∈ (− ∞; − 1) ∪ (− 1; 0) ∪ (0;+ ∞ )
|| 25x+1 > 0
|( x+1
25 ⁄= 1

Сделаем замену :

{
1 y2 − 2y + 1 (y − 1 )2 y > 0
y + --− 2 > 0 ⇔ ------------> 0 ⇔ --------> 0 ⇔
y y y y ⁄= 1,

откуда

(
{ | 2x + 2
log5x 25x+1 > 0 { ---x---> 0
x+1 ⇔ | 2x + 2
log5x 25 ⁄= 1 ( -------⁄= 1
x

Решая первое неравенство последней системы, получаем

Решая второе неравенство последней системы, получаем

В
итоге

–
входит в ОДЗ

Ответ:

Решите неравенство

x log π (x + 3 ) ≤ 0
x+2

Показать ответ и решение

ОДЗ:

(
| x + π-> 0 ( π
|{ 2π { x > − --
x + --⁄= 1 ⇔ 2π
||( 2 ( x ⁄= − --+ 1
x + 3 > 0 2

Заметим, что

x + 3 > x + π- + 1
2

Рассмотрим два случая:
1) x > − π-+ 1
2 , тогда

π
logx+ 2(x + 3) > 0

и
исходное неравенство равносильно

то
есть в этом случае подходят

( ]
x ∈ − π-+ 1;0
2

2)
π π
− --< x < − --+ 1
2 2 , тогда

и
исходное неравенство равносильно

то
есть в этом случае подходящих нет.
В итоге ответ с учётом ОДЗ:

( π ]
x ∈ − --+ 1;0 .
2

Ответ:

( π ]
− --+ 1;0
2

Решите неравенство

(2x + 15)log (x2 + 7x) ≤ 0
x+2

Показать ответ и решение

ОДЗ:

(
| x + 2 > 0
{
| x + 2 ⁄= 1 ⇔ x > 0
( x2 + 7x > 0

На ОДЗ , , следовательно, исходное неравенство на ОДЗ равносильно

2 2
logx+2(x + 7x) ≤ logx+2 1 ⇔ x + 7x − 1 ≤ 0

По методу интервалов:

откуда [ √ --- √---]
− 7-−--53- −-7 +--53-
x ∈ 2 ; 2 .
Пересечём ответ с ОДЗ:

( √ --]
x ∈ 0; −-7-+--53
2

Ответ:

√ ---
(0;− 3,5 + 0,5 53]

Решите неравенство

2
2 (( )log3x+12) 9x4−4-
49x4-− 3-x + 1 2 ≤ 3
2

Показать ответ и решение

Найдем ОДЗ неравенства:

(
|| 3x + 1 > 0 ( )
{ 2 2-
| 3 ⇔ x ∈ − 3;0 ∪ (0;+ ∞ )
|( -x + 1 ⁄= 1
2

Решим неравенство на ОДЗ. Так как по основному логарифмическому свойству ,
то

9x24- 9x42−1
4 − 2 ≤ 3

Сделаем замену 9x42-
t = 2 , t > 0 , тогда

( 3 ) [ 3 ]
t2 − 0,5t − 3 ≤ 0 ⇔ t +-- (t − 2) ≤ 0 ⇔ t ∈ − --;2
2 2

Так
как согласно замене t > 0 , то получаем . Сделаем обратную замену:

2 2 ( ) ( )
0 < 2 9x4--≤ 2 ⇔ 9x--≤ 1 ⇔ x − 2- x + 2- ≤ 0 ⇔
4 3 3
[ ]
2 2
x ∈ − --;--
3 3

Пересечем ответ с ОДЗ и получим

( ) ( ]
x ∈ − 2;0 ∪ 0; 2
3 3

Ответ:

( ) ( ]
x ∈ − 23;0 ∪ 0; 23

Решите неравенство

Показать ответ и решение

Выпишем ОДЗ:

(
|| sinx + cos x + 4 > 0
||||
{ sinx + cos x + 4 ⁄= 1
x2 + 1 > 0
|||| 2 sin x cosx + 4,5 > 0
||(
2 sin x cosx + 4,5 ⁄= 1

Так
как по формуле вспомогательного аргумента

√--( √ -- √ -- ) √ -- ( )
sin x + cosx = 2 --2-sin x + --2-cosx = 2 sin x + π- ,
2 2 4

а по
формуле двойного угла , то

( ( π) √ --
||| sin x + -- > − 2 2
||| ( 4)
|{ π- 3√ --
sin x + 4 ⁄= − 2 2 ⇔ x ∈ ℝ.
|||
|||| sin2x > − 4,5
( sin2x ⁄= − 3,5

Заметим, что при одинаковых аргументах один логарифм будет другого логарифма в одном из
двух случаев:

1) Аргументы этих логарифмов равны . Тогда .
Тогда неравенство принимает вид: что на ОДЗ равносильно

что
является верным неравенством. Следовательно, x = 0 является решением неравенства.

2) При .
Заметим, что функция f (x) = log a
x является убывающей (докажите это самостоятельно) при a > 1 и
возрастающей при a < 1 . В нашем случае 2
x + 1 > 1 , следовательно, функция убывает. Значит, чем
больше значение функции, тем меньше значение . Следовательно, при неравенство
равносильно

Данное неравенство равносильно совокупности систем:

⌊ (
||{ sin x ≥ 1-
|| 2
| || 1
|| ( cosx ≥ --
|| ( 2
| ||{ sin x ≤ 1-
|| 2
⌈ | 1
|( cosx ≤ --
2

Решим каждую систему по окружности:
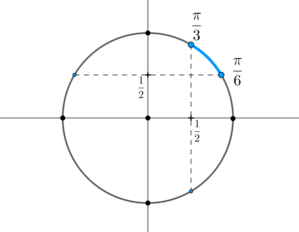
первая система:

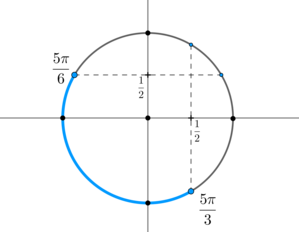
вторая система:

Тогда ответом будут [ ]
[π- π- ] 5-π 5π-
x ∈ 6 + 2πn; 3 + 2πn ∪ 6 + 2πn; 3 + 2 πn , .

Тогда окончательный ответ – это объединение решений x = 0 и [ ]
[π- π- ] 5-π 5π-
x ∈ 6 + 2πn; 3 + 2πn ∪ 6 + 2πn; 3 + 2πn ,
, то есть

[π π ] [ 5π 5π ]
x ∈ --+ 2πn; --+ 2πn ∪ ---+ 2πn; ---+ 2πn ∪ {0 }, n ∈ ℤ.
6 3 6 3

Ответ:

[ ] [ ]
x ∈ π6 + 2 πn; π3 + 2 πn ∪ 56π+ 2πn; 53π+ 2πn ∪ {0}, n ∈ ℤ

Решите неравенство

−|x− 2| 2
2 ⋅log2(4x− x − 2)≥ 1

Показать ответ и решение

Рассмотрим первый множитель левой части Так как модуль при всех значениях неотрицателен, то

Следовательно,

Рассмотрим второй множитель log(4x− x2− 2).
2 Выделим полный квадрат:

Так как квадрат любого выражения — число неотрицательное, то

Следовательно,

Получили, что оба множителя в левой части ≤ 1, а значит и их произведение ≤ 1.

Значит, неравенство будет иметь решения тогда и только тогда, когда оба они равны по 1.

Таким образом, получаем, что x = 2 — единственное решение неравенства.

Ответ:

{2}

Решите неравенство

при каждом .

Показать ответ и решение

ОДЗ:

(
| x > 0
||||
||| x ⁄= 1
||| x + 1 > 0
||||
||| x + 2 > 0 {
{ x + 2 ⁄= 1 x > 0
| ⇔
||| x + 3 > 0 x ⁄= 1
||| ...
|||| x + 2n > 0
|||
||| x + 2n ⁄= 1
|( x + 2n + 1 > 0

По методу рационализации: на ОДЗ

С учётом ОДЗ последнее неравенство равносильно

Таким образом, с учётом ОДЗ:

Ответ:

(0;1)

Решите неравенство

Показать ответ и решение

ОДЗ:

(
|| x2 > 0
|||
||| 2x + 7 > 0
|||{ 2x + 7 ⁄= 1 {
x > 0
| x + 7 > 0 ⇔ x ⁄= 0,5
|||| 5x − 1 ⁄= 0
|||
||| x > 0
( lg 2x ⁄= 0

На ОДЗ , тогда исходное неравенство на ОДЗ равносильно

На ОДЗ , следовательно, , тогда на ОДЗ

и
исходное неравенство на ОДЗ равносильно

lg2x2-
lg 2x ≤ 0

Найдём нули числителя:

2 2 2
lg x = 0 ⇔ lg x = lg1 ⇔ x = ±1

Найдём нули знаменателя:

По методу интервалов на ОДЗ:

откуда

Ответ:

Решите неравенство

Показать ответ и решение

ОДЗ:

(
|| x2 + 1 > 0
||| (
|{ 4x > 0 |{ x ⁄= log3 2
3x − 2 ⁄= 0 ⇔ x > 0
||| |(
||| x > 0 x ⁄= 1
( x ⁄= 1

На ОДЗ , следовательно, , тогда исходное неравенство на ОДЗ
равносильно

2
log24x-+-log24x-−--log2-4 ≤ 0
(3x − 2)lnx

Найдём нули числителя:

2
log24x + log24x − log2 4 = 0

Сделаем замену :

t2 + t − 2 = 0 ⇔ t = −-1-±-3
2

1
log2 4x = − 2 ⇔ log2 4x = log20,25 ⇔ 4x = 0,25 ⇔ x = ---
16

Найдём нули знаменателя:
1)

По методу интервалов:

откуда [ ]
1 1
x ∈ 16;2- ∪ (log32;1 )
пересечём ответ с ОДЗ:

[ ]
-1- 1-
x ∈ 16 ;2 ∪ (log32;1 ).

Ответ:

Источник

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

ОДЗ: $$left{begin{matrix}x>0\1+2x>0\xneq1\1+2xneq1end{matrix}right.$$ $$Leftrightarrow$$ $$left{begin{matrix}x>0\x>-0,5\xneq1\xneq0end{matrix}right.$$ $$Leftrightarrow$$ $$xin(0;1)cup(1;+infty)$$; $$frac{frac{1}{3}log_{2}x}{log_{2}(1+2x)}leqfrac{frac{1}{3}log_{2}(1+2x)}{log_{2}x}$$; $$log_{1+2x}xleqlog_{x}(1+2x)$$;

Пусть $$log_{1+2x}x=y$$; $$yleqfrac{1}{y}$$; $$frac{y^{2}-1}{y}leq0$$ $$Leftrightarrow$$ $$frac{(y-1)(y+1)}{y}leq0$$

$$left{begin{matrix}yleq-1\left{begin{matrix}y>0\yleq1end{matrix}right.end{matrix}right.$$ $$Leftrightarrow$$ $$left{begin{matrix}log_{1+2x}xleq-1(1)\left{begin{matrix}log_{1+2x}x>0(2)\log_{1+2x}xleq1(3)end{matrix}right.end{matrix}right.$$

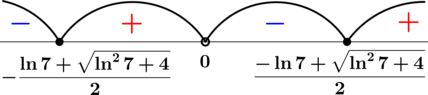
1) $$log_{1+2x}xleqlog_{1+2x}frac{1}{1+2x}$$; $$(x-frac{1}{1+2x})(1+2x-1)leq0$$; $$frac{x+2x^{2}-1}{1+2x}cdot2xleq0$$; $$frac{2x(x-0,5)(x+1)}{1+2x}leq0$$

$$xin[-1;-0,5)cup[0;0,5]$$

2) $$log_{1+2x}x>0$$; $$(x-1)(1+2x-1)>0$$; $$(x-1)cdot2x>0$$

$$xin(-infty;0)cup(1;+infty)$$

3) $$log_{1+2x}xleq1$$; $$log_{1+2x}xleqlog_{1+2x}(1+2x)$$; $$(x-1-2x)(1+2x)leq0$$; $$(-x-1)(2x+1)leq0$$

$$xin(-infty;-1]cup[-0,5;+infty)$$

Найдем пересечение 2 и 3 и объединим результаты с 1: $$xin(-infty;0,5]cup(1;+infty;)$$

Ответ с учетом ОДЗ: $$xin(0;0,5]cup(1;+infty;)$$

Источник

Конспект
урока математики в 11 классе по теме

«Решение заданий ЕГЭ по теме «Комбинированные
уравнения и неравенства»»

МБОУ
«ЛСОШ № 2 им. Героя

Советского
союза Б.К. Кузнецова»

учитель математики и информатики

высшей
квалификационной категории

Кузнецова
Ирина Анатольевна.

Цель
урока:

закрепить
навыки решения сложных уравнений различными методами.

Ход
урока:

I
Организационный момент:

а)
готовность класса к уроку;

б)
сообщение цели и задач урока.

ІI
Актуализация опорных знаний

Вариант 1

1) Решите уравнение:

2) Решите неравенство:

3) Решите уравнение:

4) Решите неравенство:

Вариант 2

1) Решите уравнение:

2) Решите неравенство:

3) Решите уравнение:

4) Решите неравенство:

1.-Дать
определение равносильности преобразования уравнения и перечислить основные
равносильные преобразования.

Ответ:

Замену
одного уравнения другим, равносильным ему уравнением называют равносильным
преобразованием уравнения

-какие
преобразования равносильными?

Равносильными
преобразованиями уравнения являются:

·
перенос члена уравнения с противоположным знаком из одной части
уравнения в другую;

·
умножение (деление) обеих частей уравнения на отличную от нуля
число;

·
возведение уравнения в нечетную степень;

·
извлечение корня нечетной степени с обеих частей уравнения:

·
логарифмирование показательного уравнения;

·
применение тождеств, т. е равенств, справедливых для любого числа.

2.Рассказать,
какие равносильные преобразования нужно выполнить, чтобы решить следующие
уравнения:

;

4.
Дайте определение уравнения – следствия и
перечислите преобразования, приводящие к уравнению следствия.

Ответ:

Пусть даны два уравнения. Если любой корень первого
уравнения является корнем второго уравнения, то второе уравнение называют
уравнением- следствием первого.

Замену уравнения другим уравнением, которое является его
следствием, называют переходом к уравнению- следствию.

При
переходе к уравнению- следствия возможно появление лишних корней, посторонних
для исходного уравнения, поэтому проверка полученных корней является
обязательной частью решения уравнения.

Преобразованиями,
приводящими к уравнению- следствия является:

·
возведение уравнения в четную степень;

·
потенцирование логарифмического уравнения;

·
освобождение уравнения от знаменателя;

·
приведение подобных членов;

·
применение формул (тригонометрических, логарифмических и других).

;

С.р.
для сдающих базу (в-7392675, 7392637)

Решение комбинированных уравнений и неравенств

Каждое задание решает группа учащихся. Затем один из
группы записывает решение на доске и поясняет его.

1).

Решение:

Преобразуем показатели степеней:

геометрическая
прогрессия, ,

Получим:

, ,

Ответ:

2).

Решение:

Перейдем к одному основанию и воспользуемся
свойствами степеней:

Из монотонности показательной
функции следует:

,
Решением системы является: х = 9

Ответ: 9

3).

Решение:

Пусть

Тогда

Ответ:

4).

Решение:

Перейдем к одному основанию и воспользуемся
формулами тригонометрии:

Пусть , тогда
уравнение примет вид

Ответ:

С.р. для сдающих профиль

Вариант № 23819621

1. Задание 13 № 484541

Решите уравнение

Решение.

Найдем
ОДЗ:

Найдем корни числителя:

Отметим корни на тригонометрической окружности:

С учетом ОДЗ (см. рис.) получаем:

Ответ:

2. Задание 13 № 513091

а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие
промежутку

Решение.

а) Имеем:

б) С помощью числовой окружности (см. рис.) отберём корни, принадлежащие
отрезку Получим
точку

Ответ: а) б)

3. Задание 15 № 517264

Решите неравенство:

Решение.

Неравенство является квадратным относительно выражения в скобках:

Ответ:

4. Задание 15 № 508488

Решите неравенство:

Решение.

Первый способ:

Рассмотрим два случая. Первый случай:

Учитывая условие ,
получаем:

Второй случай:

Учитывая условие получаем или

Множество решений неравенства системы:

Ответ:

Второй способ:

Приведём другое решение.

Перепишем правую часть неравенства:

Воспользуемся методом рационализации:

Вариант № 23819712

1. Задание 13

а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие отрезку

Решение.

а) Заметим, что уравнение определено при любом Запишем
исходное уравнение в виде:

Значит, либо откуда или либо ,
откуда или

б) Поскольку отрезку принадлежат
корни и

Ответ: а) б)

2. Задание 13

Решите уравнение:

Решение.

Левая часть уравнения имеет смысл при Преобразуем
уравнение:

Поскольку получаем:

Учитывая, что получаем,

Ответ:

3. Задание 15

Решите неравенство:

Решение.

Пусть получаем:

Возвращаясь к исходной переменной, получаем: или

Ответ:

4. Задание 15

Решите неравенство:

Решение.

Перенесём все члены в правую часть и умножим на 2:

Заметим, что поэтому Получаем

Решение неравенства: или

Ответ:

Д.З. решают не свои варианты.

Источник

Лучшие репетиторы для сдачи ЕГЭ

Задания по теме «Комбинированные неравенства»

Условие

Решение

Ответ

Условие

Решение

Ответ

Условие

Решение

Ответ

Условие

Решение

Ответ

Условие

Решение

Ответ

Условие

Решение

Ответ

Условие

Решение

Ответ

Условие

Решение

Ответ

Условие

Решение

Ответ

Лучшие репетиторы для сдачи ЕГЭ

Сложно со сдачей ЕГЭ?

Смешанные неравенства

Задания по теме «Комбинированные неравенства»

Задание №1194

Условие

Решение

Репетитор по математике

Стоимость занятий

Видеокурсы подготовки к ЕГЭ-2021

Группа Вконтакте

Преимущества

Педагогический стаж

Собственная методика

Гарантированный результат

Индивидуальная работа

Задание 14. Неравенства — профильный ЕГЭ по математике

Вариант 1

Вариант 2

Решение комбинированных уравнений и неравенств

Каждое задание решает группа учащихся. Затем один из группы записывает решение на доске и поясняет его.

Каждое задание решает группа учащихся. Затем один из
группы записывает решение на доске и поясняет его.