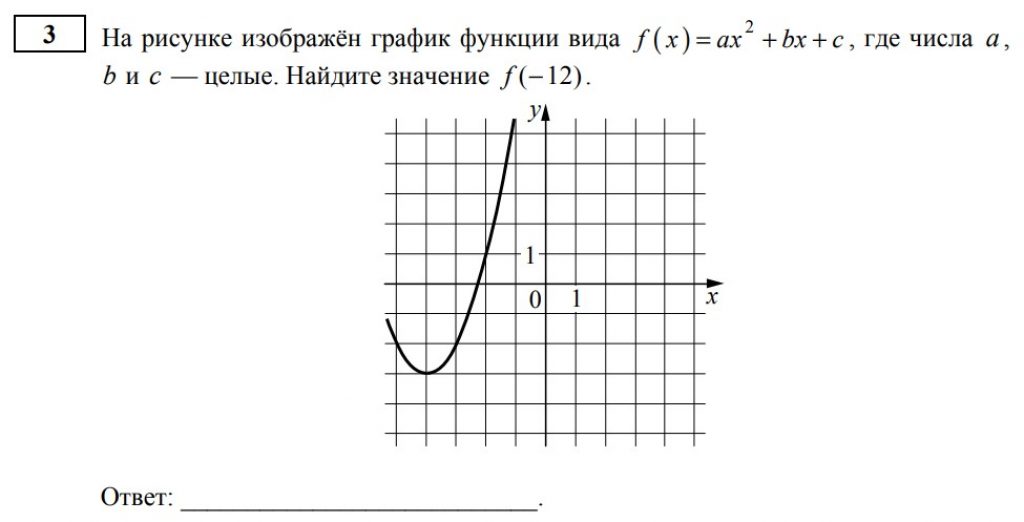
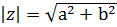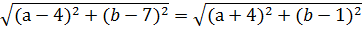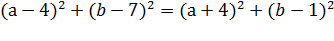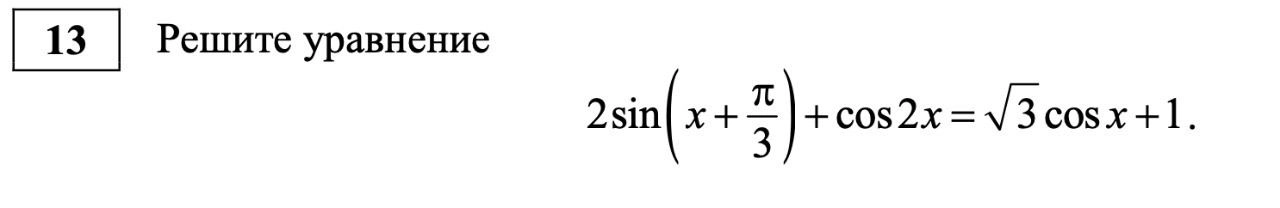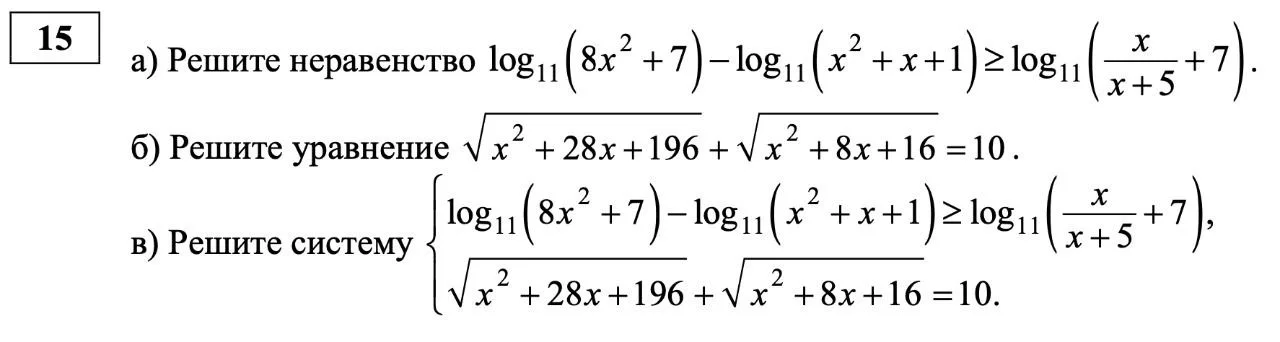Автор материала — Анна Малкова
Что такое комплексные числа
Все знают, что ЕГЭ по математике Профильного уровня в ближайшие годы будет меняться. Например, предлагается добавить в школьную программу по математике тему «Комплексные числа». Но что же это такое?
Начнем с хорошо известных вам фактов.
Вспомним, что возвести число в квадрат — значит умножить его само на себя.
Если положительное число возвести в квадрат — результат будет положительный.
Если отрицательное число возвести в квадрат — результат тоже положительный. «Минус на минус дает плюс», — это мы не раз слышали на уроках математики.
Например, уравнение имеет 2 решения: х = 2 и х = -2.
Число 2 называют арифметическим квадратным корнем из 4, то есть
А можно ли какое-нибудь число возвести в квадрат, чтобы результат получился отрицательный? И если нет, то почему?
Ведь отрицательные числа ничем не хуже положительных. Баланс мобильного телефона может быть положительным или отрицательным. Температура может быть равна +5 градусов Цельсия, а может быть и минус 5 градусов. На числовой оси положительные и отрицательные числа расположены симметрично. Почему же из положительных чисел квадратный корень извлекать можно, из нуля тоже можно (он равен нулю), а из отрицательных нельзя?
А что, если — сказали однажды математики, — существует такое число, квадрат которого равен минус единице?
И называется это число мнимой единицей, а обозначается буквой
Вот какая необычная формула получилась:
Получается, что уравнение имеет 2 решения: i и минус i.
А уравнение имеет решения — 2i и 2i.
Теперь нам не страшны квадратные уравнения, в которых дискриминант отрицателен.
Например, уравнение
Его дискриминант равен 1 — 4 = — 3.
Его корни:
Числа вида называются комплексными. При этом х называется действительной частью комплексного числа z, а у — его мнимой частью.
Записывается это так:
Сокращения понятны тем, кто изучает английский: Re — Real, Im — Imaginary.
Помните, мы говорили о том, какие бывают числа?
Натуральные числа применяются для счета предметов. Множество натуральных чисел обозначается N.
Целые числа — это положительные, отрицательные и ноль. Например, 4, 78, -121, 0 — целые числа. Множество целых чисел Z содержит в себе множество натуральных.
Рациональные числа — те, которые можно записать в виде обыкновенной дроби вида р/q, где р — целое, q — натуральное. Например, — числа рациональные. Мы проходили их в начальной и средней школе. Если рациональное число записать в виде десятичной дроби, она будет периодической, например,
Множество рациональных чисел обозначается Q и содержит в себе множество целых чисел.
В старших классах мы узнали об иррациональных числах — таких, как или
Их невозможно записать в виде обыкновенной дроби, а если выразить в виде десятичной — она будет бесконечной непериодической. И казалось, что мы знаем о числах всё. Все числа, какие только нам встречались, входили в множество действительных чисел R.
Когда мы пишем: — это значит, что число х действительное. Мы помним, что действительные числа можно изображать точками на числовой прямой, которую еще называют действительной осью.
А теперь оказывается, что R — это подмножество множества комплексных чисел С.
Действительные числа еще называют «вещественными». Они описывают наш вещественный мир. В самом деле, натуральные числа применяем для счета предметов. С дробями тоже понятно: половинка яблока или пиццы. С отрицательными числами все знакомы: достаточно зимой посмотреть на градусник за окном. И даже иррациональные числа можно «увидеть»: например, длина окружности радиуса 1 или диагональ квадрата со стороной 1 являются иррациональными числами.
Но где же в мире — мнимые и комплексные числа? Неужели они нужны для описания того, что мы не можем потрогать или посчитать по пальцам?
Да, так и есть. Комплексные числа — удобный инструмент для построения математических моделей волн и колебаний. Электро- и радиотехника, теоретическая и квантовая физика — все они пользуются комплексными числами. Мир элементарных частиц живет по законам, описываемым функциями комплексных переменных. Так что продолжим их изучение.
Комплексная плоскость
Где же находятся мнимые числа, если на числовой прямой для них места нет?
Очень просто. Мнимые числа — на мнимой оси. А комплексные числа вида — на комплексной плоскости.
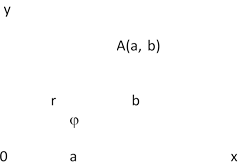
Каждому комплексному число соответствует точка на комплексной плоскости.
Расстояние от нуля до этой точки называется модулем комплексного числа:
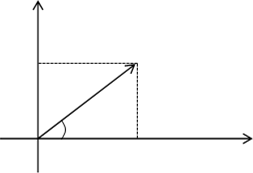
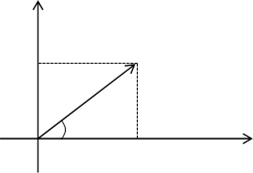
Угол между направлением на эту точку и положительным направлением действительной оси называется аргументом комплексного числа:
Аргумент комплексного числа определен с точностью до
Аналогично в тригонометрии: каждая точка на единичной окружности соответствует бесконечному множеству углов, отличающихся на где k — целое.
Здесь
— главное значение аргумента
Иногда главное значение аргумента комплексного числа определяют на отрезке
Если
не определен.
Комплексное число можно записать как в алгебраической форме так и в тригонометрической.
Поскольку
получим:
Это тригонометрическая форма записи комплексного числа.
Здесь
При переходе от алгебраической формы записи к тригонометрической считаем, что принимает значения
Обратите внимание, что в записи число х — действительное.
Число — мнимое.
Задача 1. Запишите число
в тригонометрической форме.
Решение:
Так как
Как видим, для освоения темы «Комплексные числа» надо отлично знать тригонометрию.
Действия над комплексными числами
Два комплексных числа равны друг другу, если равны соответственно их действительные и мнимые части.
Сравнивать комплексные числа нельзя. Операции «больше» и «меньше» для комплексных чисел не определены.
Два комплексных числа, отличающиеся только знаком мнимой части, называются комплексно-сопряженными. Вот такие:
Возьмем два комплексных числа:
и
.
Определим для них операции сложения и вычитания.
Сложение:
Похоже на правило сложение векторов, не правда ли?
Так же, как и для действительных чисел, то есть от перемены мест слагаемых сумма не меняется (коммутативность сложения). Также выполняется ассоциативность сложения, то есть
Еще одно важное свойство:
Это знакомое нам неравенство треугольника.
Вычитание:
— расстояние между точками
и
Задача 2. Определите, какая фигура на комплексной плоскости является решением уравнения
Решение:
Прочитаем это уравнение так же, как мы делали с обычными уравнениями с модулем. Расстояние от точки z до точки 2i равно 1. Это значит, что точки, соответствующие решениям данного уравнения, лежат на окружности с центром в точке радиусом 1.
Если сложение и вычитание комплексных чисел вопросов не вызывают, то для умножения правила не такие очевидные. Вот какой будет формула произведения комплексных чисел:
Например, подставив в эту формулу получим уже знакомое равенство:
Умножение комплексных чисел обладает теми же свойствами, что и умножение действительных:
Но если умножение комплексных чисел настолько сложно — что же делать с возведением в степень? Оказывается, что и умножение, и возведение комплексных чисел в степень удобнее выполнять, записывая числа в тригонометрической форме.
Возведение в степень:
Последнее равенство называется формула Муавра.
Задача 3.
Вычислите:
Решение:
Для числа
Деление комплексных чисел определяем как действие, обратное умножению.
если
Пусть
отсюда
Сложные формулы, не правда ли? Попробуем применить.
Задача 4.
.
Намного удобнее выполнять деление комплексных чисел, записав их в тригонометрической форме:
.
Извлечение корней из комплексных чисел — еще интереснее. Во-первых, для извлечения корня n-ной степени из комплексного числа лучше всего записать его в тригонометрической форме.
Во-вторых, для любого выражение
принимает ровно
различных значений.
Пусть — корень
-ной степени из комплексного числа
;
Тогда Записав число z в тригонометрической форме, получим:
Обратите внимание — для корня n-ной степени получим различных значений корня.
Задача 5.
Найдем
При
При
При
Задача ЕГЭ-2022, Комплексные числа
Решим задачу из варианта ЕГЭ — 2022 по теме «Комплексные числа».
Задача 6.
Про комплексное число известно, что
Найдите наименьшее значение
Решение:
Обозначим
Пусть
Известно, что
Получим:
1 способ.
Расстояния от точки, соответствующей числу z, до точек и
должны быть равны. Отметим точки
и
на комплексной плоскости. Равноудаленными от точек
и
будут все точки, лежащие на серединном перпендикуляре к отрезку, соединяющему
и
По условию задачи, из этих точек надо выбрать такую, для которой
принимает наименьшее значение, то есть наименее удаленную от начала координат. Другими словами — найдем расстояние от начала координат до данной прямой.
Это показано на рисунке. Точка Н соответствует комплексному числу z, лежащему на прямой, все точки которой равноудалены от и
при этом расстояние от 0 до z — наименьшее. Найдем это расстояние (равное ОН) из прямоугольного треугольника АОВ. Его катеты равны 3 и 4, гипотенуза равна 5. Записав площадь треугольника АОВ двумя способами, получим:
2 способ.
Вернемся к выражению
Запишем его в виде:
Мы получили, что модули двух комплексных чисел равны. Модуль комплексного числа равен Возведя это выражение в квадрат, получим, что
Значит, если равны модули двух комплексных чисел
и
то
В нашем случае:
Выразим отсюда х;
и найдем наименьшее значение выражения
Мы получили функцию . Обычную функцию от действительной переменной. Найдем наименьшее значение функции
Это квадратичная функция, ее график — парабола с ветвями вверх, и наименьшее значение достигается в вершине параболы.
Еще несколько задач по теме «Комплексные числа»:
Задача 7.
Представьте в тригонометрической форме числа:
а)
б) 1 — i.
Решение:
а) .
б) i.
Задача 8.
Вычислить
Задача 9.
Считая х и у действительными числами, решите уравнение:
Решение:
Пользуясь определением равенства комплексных чисел, получим:
Умножим первое уравнение на 2, а второе на 5, и вычтем из второго уравнения первое.
Получим, что
тогда
Задача 10.
Известно, что число является корнем уравнения
где
Найти а и решить уравнение при этом значении а.
Решение:
По условию, — корень уравнения
Подставив
получим
Уравнение примет вид:
Так как — корень уравнения, разделим левую часть на х + 9. Получим:
Найдем корни квадратного уравнения
Экспоненциальная форма записи комплексного числа
Хорошо, что в ЕГЭ по математике появились комплексные числа. Чтобы их освоить, надо отлично знать алгебру, геометрию и тригонометрию, потому что эта тема связана со многими областями математики.
Помните, например, тему «Элементарные функции и их графики»? Там мы говорили о 5 типах элементарных функций: степенных, показательных, логарифмических, тригонометрических и обратных тригонометрических. И казалось, что у показательных и тригонометрических функций общего мало.
А теперь посмотрите, как выглядит экспоненциальная форма записи комплексного числа:
Формула носит имя Леонарда Эйлера — одного из величайших математиков в истории.
Здесь — периодическая функция, период
С помощью формулы Эйлера знакомые нам косинус и синус можно выразить через комплексные экспоненты:
Если мы получим самую красивую и удивительную формулу математики:
Она связывает две мировые константы, то есть числа и
знакомую нам обычную единицу и ту самую мнимую единицу i, с которой мы начали это первое знакомство с комплексными числами.
Задачи взяты из книги Д. Письменного «Конспект лекций по высшей математике» и Проекта ЕГЭ-2022 по математике Профильного уровня.
На ЕГЭ-2022 по математике комплексных чисел не будет. Но рано или поздно эта тема будет добавлена в школьную программу.
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Комплексные числа на ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.03.2023
Недавно ФИПИ опубликовал новые проекты КИМов ЕГЭ почти по всем предметам. После общественного обсуждения по этим вариантам, возможно, будут сдавать экзамен нынешние 10-классники.
Следует отметить, что, возможно, эта “перспективная модель” ещё очень сильно поменяется, прежде чем стать официальной демоверсией [так и случилось, см. ниже]. Так было, например, при внесении существенных изменений в формат ОГЭ: проект был очень страшным, но в итоговую демоверсию внесли не такие “жесткие” изменения.
Кстати, что изменения ОГЭ, что изменения ЕГЭ свалились на головы именно школьникам 2011 года поступления. Это связано, как я думаю, с введением новых федеральных стандартов – ФГОС. Так что изменения в ЕГЭ – 2022 были для меня вполне ожидаемы.
📌Изменения в ЕГЭ по математике. Новая задача: найдите наименьшее значение модуля комплексного числа.
Основные изменения
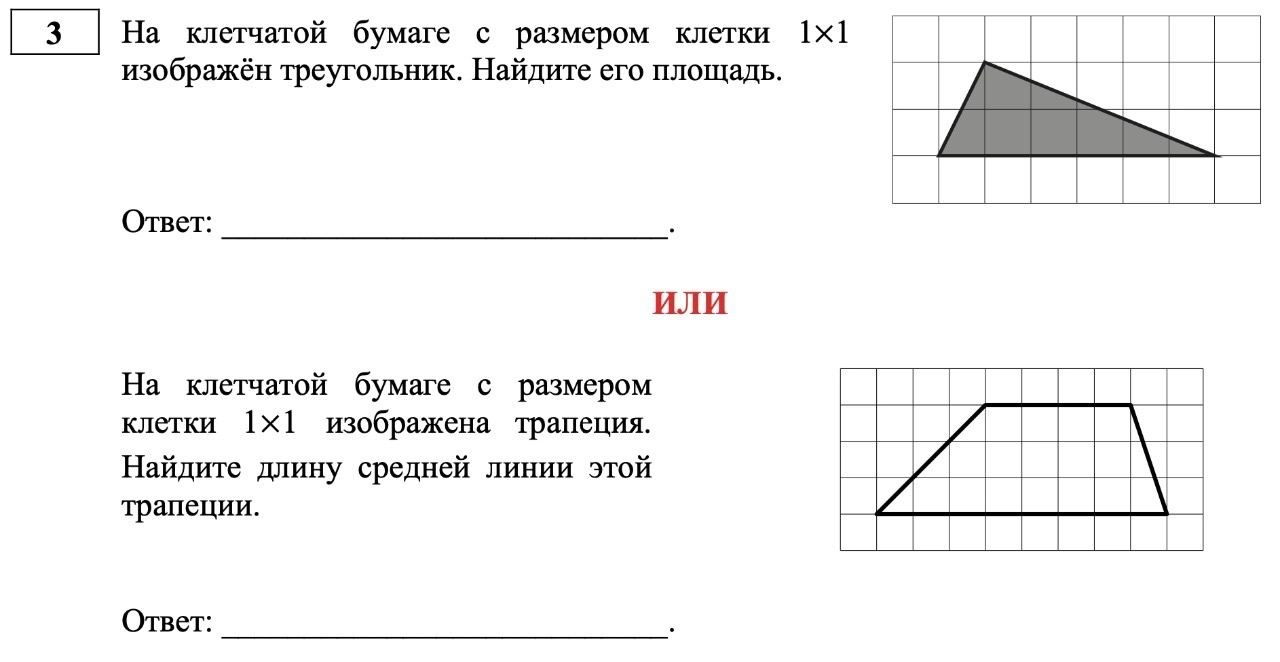
В тестовой части ЕГЭ ликвидировали самые простые номера 1-3. Это простейшая текстовая задача, умение находить наименьшую/наибольшую точку на графике и простейшая геометрия как правило на знание формул площадей треугольника, прямоугольника и трапеции. А ещё почти все “старые” номера поменяли местами. Теперь вариант выглядит так:
Часть с кратким ответом:
Новый №1 — это №5 из нынешнего ЕГЭ, простое уравнение: показательное, логарифмическое или иррациональное.
Новый №2 — это “старый” №4, теория вероятностей.
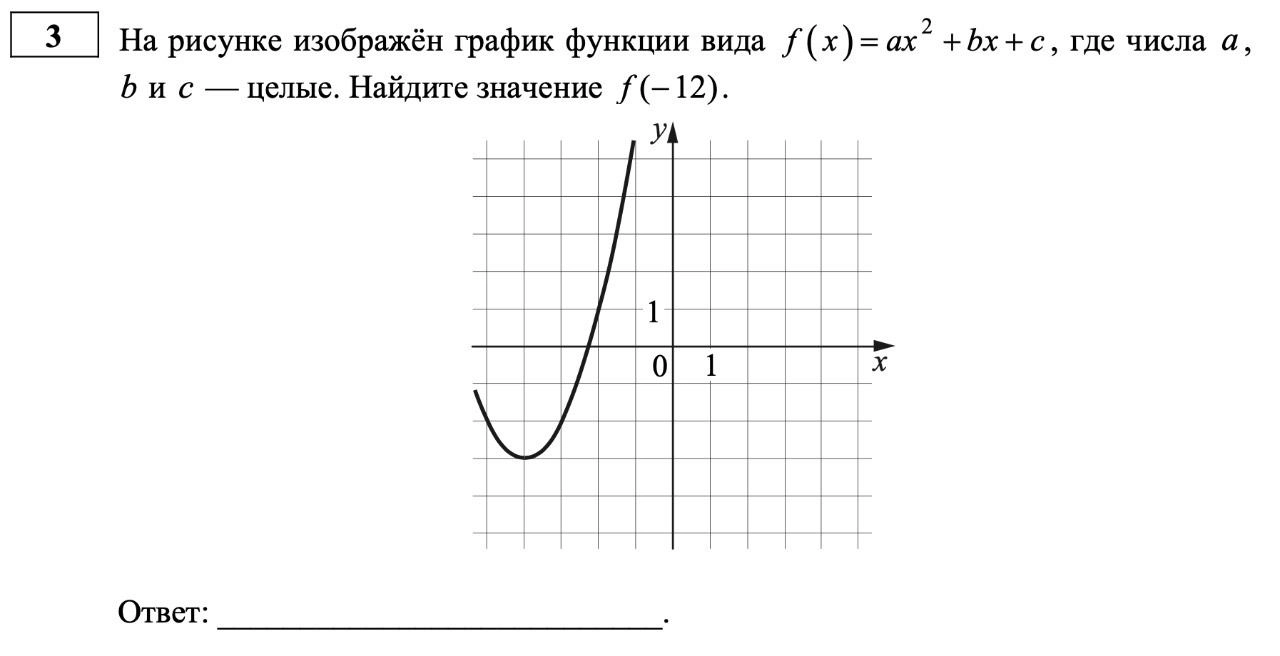
Новый №3 — новое задание, на умение работать с графиком функции
Новый №4 — это “старый” №6, простая задачка по планиметрии.
Новый №5 — это “старый” №9, пример для вычисления с тригонометрией, степенями или логарифмами.
Новый №6 — это “старый” №8, стереометрия.
Новый №7 — без изменений, на производную функции.
Новый №8 — это “старый” №10: вычисления по заранее известной формуле.
Новый №9 — это “старый” №11: сложная текстовая задача.
Новый №10 — опять теория вероятностей, но немного труднее чем №2.
Новый №11 — новое задание, на комплексные числа. Её условие приведём ниже.
Новый №12 — без изменений, нахождение экстремумов функции через производную.
Часть с развернутым ответом:
В 13-ой задаче убрали пункт б) – отбор корней уравнения, принадлежащих промежутку. Оценивается задача по-прежнему в 2 балла.
Задача №15 теперь состоит из трёх пунктов: нужно решить неравенство, уравнение и ещё их систему. Оценивается она теперь в 3 балла, раньше было 2 балла.
В остальном изменений почти нет. Разве что поменяли местами 16 и 17 задачи.
Комплексные числа
Одно из новшеств в “новом” ЕГЭ по математике – задача на комплексные числа. Вот так она выглядит:
Про комплексное число z известно, что |z-4-7ⅈ|=|z+4-ⅈ|. Найдите наименьшее значение |z|.
Решение задачи строится на использовании формулы для модуля комплексного числа :
. Следует представить z в виде
, воспользоваться формулой для модуля, упростить выражение, а затем изобразить решение уравнения на плоскости (a;b) – это будет прямая. Модуль числа z при этом будет иметь смысл рассояния до точки на прямой до начала координат. Наименьшим это расстояние будет в случае перпендикулярности отрезка от точки на прямой до начала координат к этой самой прямой.
Полное решение посмотреть можно тут:
📌Изменения в ЕГЭ по математике. Новая задача: найдите наименьшее значение модуля комплексного числа.
Не стоит бояться необычных формулировок, требующих геометрических построений: рецепт здесь один — тренировки. Чем больше задач вы решите — тем легче вы сможете применять геометрические трюки в необычных ситуациях.
ВНИМАНИЕ! Выше рассмотрена ПЕРСПЕКТИВНАЯ МОДЕЛЬ, от которой все же решили отказаться. Опубликована официальная демоверсия, и она имеет мало общего с перспективной моделью, о которой мы говорили выше.
- Авторы
- Файлы
- Ключевые слова
- Литература
Грудинина О.С.
1
1 МБОУ ШР «СОШ №2»
перспективная модель
контрольно-измерительные материалы
единый государственный экзамен
профильный уровень
комплексные числа
1. «Министерство сельского хозяйства Российской Федерации Департамент научно-технологической политики и образования Федеральное государственное бюджетное образовательное учреждение высшего образования «Волгоградский государственный аграрный университет» Комплексные числа 2020.
2. ФГБНУ « Федеральный институт педагогических измерений» [Электронный ресурс]. – Режим доступа: https://fipi.ru/ (дата обращения 22.03.2021).
Введение
В декабре 2020 года Федеральный институт педагогических измерений [2] опубликовал для общественного обсуждения перспективные модели измерительных материалов ЕГЭ на 2022 год, в том числе, по математике профильного уровня. Напомню, что в 2021 году ЕГЭ базового уровня отменен.
Особое волнение среди педагогов и старшеклассников вызывает тот факт, что в предложенной демоверсии три первых базовых задания, позволяющие выпускнику преодолеть минимальный порог на экзамене, заменили более сложными заданиями, в том числе, появилось задание по теме «Комплексные числа».
Мне стало интересно, и я решила сравнить демоверсии измерительных материалов 2021 года и перспективной, которая возможно будет внедрена в 2022 году, когда я буду выпускницей.
Мой вклад в решение проблемы: сравнение демоверсий измерительных материалов, разбор задания по теме «Комплексные числа».
Обзор литературы
Методическое пособие «Министерство сельского хозяйства Российской Федерации Департамент научно- технологической политики и образования Федеральное государственное бюджетное образовательное учреждение высшего образования «Волгоградский государственный аграрный университет». Комплексные числа. Практикум. 2020 год [1].
Цель
Сравнение демоверсий измерительных материалов 2021 года и перспективной модели на 2022 год по математике профильного уровня [2]. Разбор задания по теме «Комплексные числа» из демоверсии перспективной модели измерительных материалов ЕГЭ профильного уровня.
Методы исследования
1.Поисковый.
2. Анализ, синтез (отбор необходимой информации, обобщение)
3.Практический
Результаты исследования
Сейчас измерительные материалы ЕГЭ профильного уровня включают 19 заданий:
-часть 1 содержит 8 заданий базового уровня (задания 1–8);
-часть 2 содержит 9 заданий повышенного уровня (задания 9–17) и 2 задания высокого уровня сложности (задания 18, 19).
Что предлагается изменить?!
Убрать три базовых задания:
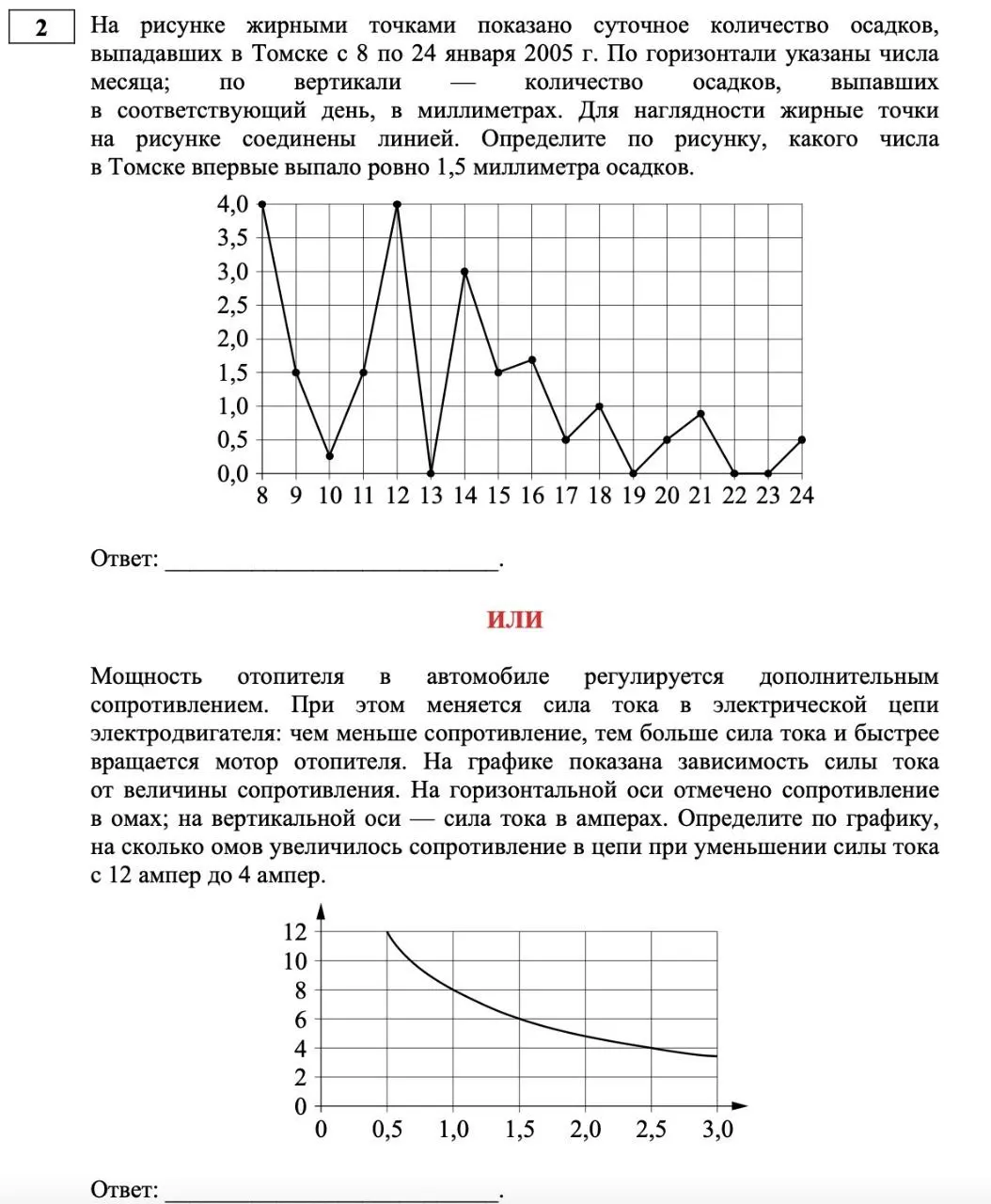
1 задание. – Простейшие текстовые задачи;
2 задание. – Чтение графиков и диаграмм;
3 задание. –Квадратная решетка.
Наряду с выше обозначенными изменениями происходит замена нумерации заданий:
№1. Простейшие уравнения;
№2. Начало теории вероятности;
№ 3. Функции, графики функций (новое);
Приведу пример задания №3 из демоверсии измерительных материалов перспективной модели ЕГЭ профильного уровня:
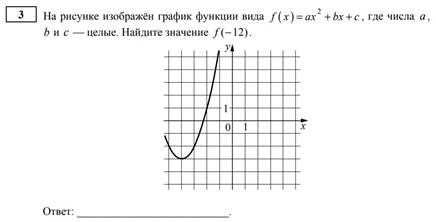
№4. Планиметрия;
№5. Вычисления и преобразования;
№6. Стереометрия;
№7. Производная и первообразная;
№8. Задачи с прикладным содержанием;
№9. Текстовые задачи;
№10. Вероятности повышенного уровня (новое);
№11. Комплексные числа (новое);
№12. Наибольшее и наименьшее значение функций;
№13. Уравнения;
№14. Стереометрическая задача;
№15. Неравенства;
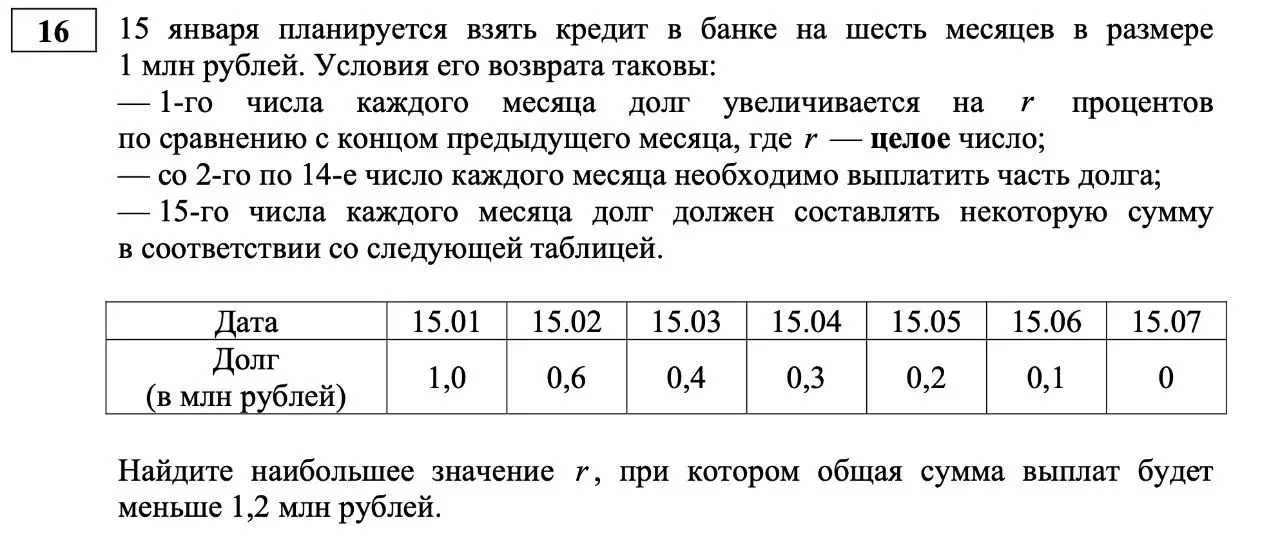
№16. Финансовая математика;
№17. Планиметрия;
№18. Задача с параметром;
№19. Числа и их свойства;
Рассмотрим задание №11 по теме «Комплексные числа».
Для начала приведу основные теоретические сведения по теме «Комплексные числа».
Определение. Комплексным числом z называется упорядоченная пара чисел (а,b), над множеством которых по определенным правилам можно производить следующие операции: сложение , умножение, деление, возведение в степень результаты которых также являются комплексными числами [1, с.2].
Определение. Комплексное число — это упорядоченная пара вещественных, или символ z = а + ib, где i — мнимая единица: i2 = −1; а называется действительной, а b — мнимой частью z [1, с.2].
Понятие комплексного числа имеет геометрическое истолкование. Множество комплексных чисел является расширением множества действительных чисел за счет включения множества мнимых чисел. Комплексные числа включают в себя все множества чисел, которые изучались ранее. Так натуральные, целые, рациональные, иррациональные, действительные числа являются, вообще говоря, частными случаями комплексных чисел.
Если любое действительное число может быть геометрически представлено в виде точки на числовой прямой, то комплексное число представляется точкой на плоскости, (комплексной плоскости z) координатами которой будут соответственно действительная и мнимая части комплексного числа. При этом горизонтальная ось будет являться действительной числовой осью, а вертикальная — мнимой осью.
Таким образом, на оси ОХ располагаются действительные числа a, а на оси ОY – чисто мнимые-b [1, с.2].
Модулемкомплексного числа называется длина вектора, соответствующего этому числу:
Задание №11:
Про комплексное число z известно, что |z-4-7i|=|z+4-i|. Найдите наименьшее значение |z| [2].
z = а + ib, в свою очередь 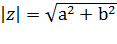
| а + ib-4-7i|=| а + ib+4-i|
Сгруппируем:
|(a-4) +i(b-7) |=|(a+4) +i(b-1) |
Видим, что внутри модуля комплексное число вида z = а + ib. Применим свойство 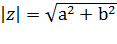
Применим формулы квадратов суммы и разности, упростим:
-16а-12b=-48
4а+3b=12
Выразим b: b=4-
Модулем является расстояниеот начала отсчёта до точки координатной прямой, соответствующейэтомучислу. Кратчайшее (наименьшее) расстояние – перпендикуляр.

Если b=0, то а = 3
Если а=0, то b=4
Рассмотрим прямоугольный треугольник с катетами 3 и 4, гипотенузой 5.
С одной стороны, площадь треугольника равна: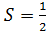
С другой стороны: 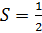
Отсюда следует: 6=0,5·h·5, h=2,4. Высота – перпендикуляр, наименьшее расстояние, которое соответствует |z|.
Ответ: 2,4
Заключение
Я сравнила демоверсии измерительных материалов 2021 года и перспективной модели на 2022 год по математике профильного уровня [2]. Разобрала задание по теме «Комплексные числа» из демоверсии перспективной модели измерительных материалов ЕГЭ профильного уровня. На мой взгляд, уже в следующем учебном году задания по теме «Комплексные числа» необходимо включать в рабочие программы уроков, курсов внеурочной деятельности. И тогда у выпускников не возникнет сложностей с решением этого задания на экзамене.
Библиографическая ссылка
Грудинина О.С. ПЕРСПЕКТИВНАЯ МОДЕЛЬ ЕГЭ ПО МАТЕМАТИКЕ. КОМПЛЕКСНЫЕ ЧИСЛА // Старт в науке. – 2021. – № 2.
;
URL: https://science-start.ru/ru/article/view?id=2027 (дата обращения: 11.03.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
В опубликованных перспективных моделях ЕГЭ по профильной математике на 2022 год появились задания с комплексными числами. Что делать, если в некоторых школах ученики их не проходят, рассказала заместитель директора ФИПИ Ольга Котова в интервью “Российской газете”.
В России каждая школа формирует свой учебный план, отметила Ольга Котова. Поэтому в некоторых образовательных учреждениях тема комплексных чисел оказалась не включена в программу. Однако по действующим ФГОС для старшеклассников предусмотрен выбор профиля обучения: медико-биологический, физико-математический, гуманитарный и другие классы. Если школьнику для поступления в вуз нужна профильная математика, ему стоит выбрать такой профиль, на уроках которого будут изучать комплексные числа.
Также Ольга Котова напомнила, что новые задания только проходят апробацию. Если какие-то из них будут большинству школьников не по силам, их не включат в окончательный список заданий ЕГЭ-2022 или введут через несколько лет.
Ранее сайт “Учительской газеты” сообщал, что на ЕГЭ по физике и химии пока не планируют вводить задания с реальными экспериментами.
Фото: pixabay.com
Перспективные модели ЕГЭ уже опубликованы на сайте ФИПИ. Разбираем возможные изменения в ЕГЭ 2022 по математике и рассказываем, чего ожидать от реального экзамена.
ЕГЭ по математике не менялся с 2015 года! На фоне масштабных изменений в других предметах это было необычно. Но с учётом сложности этого предмета и сравнительно невысоких средних баллов из года в год, никого это не удивляло. Преподаватели вздыхали с облегчением, что программу подготовки можно не менять. А ученики радовались, что можно посоветоваться с бывшими 11-классниками, потому что они сдавали то же самое.
Но вот появилась перспективная модель ЕГЭ по математике, а значит ФИПИ начал планировать изменения в экзамене. В этой статье мы обсудим их все.
Сразу хочу отметить, что пока перспективная модель только вынесена на обсуждение. А вот демоверсия экзамена по математике 2022 (то есть более точный вариант) уже вышла, и я сделала ее подробный разбор в этой статье. Спойлер: демоверсия отличается от перспективной модели.
При подготовке к ЕГЭ очень важно учитывать все актуальные изменения экзамена. Ровно за это отвечают в образовательном центре MAXIMUM. Наши преподаватели используют лучшие учебные пособия, в которых отражены последние нововведения ЕГЭ. Мы даем нашим ученикам только полезные знания и лайфхаки, которые гарантированно помогут им сдать экзамен на высокий балл. Записывайтесь к нам на бесплатный открытый урок и узнайте все об успешной подготовке к ЕГЭ.
Количество заданий в перспективной модели ЕГЭ по математике
Первая новость хорошая – количество заданий в ЕГЭ по математике НЕ ИЗМЕНИТСЯ! А хорошая она потому, что на существующие 19 заданий не у всех учеников хватало времени. Поверьте преподавателю, который «вытирал слёзы» ученикам, не успевшим написать 19в или 16б.
Изменения в количестве баллов за ЕГЭ по математике
Здесь тоже сильных изменений не будет. Добавится 1 первичный балл за счёт изменений в № 15, но об этом поговорим подробнее чуть позже.
В итоге общий балл будет поднят с 32 до 33.
Общие изменения в перспективной модели ЕГЭ по математике
Самые значительные изменения коснулись части с кратким ответом. В ней мы увидим и исключение заданий, и совершенно новые форматы, а также очень много перестановок. Однако она, как и прежде, будет приносить ученикам 12 первичных баллов.
Что касается части с развёрнутым ответом, то изменения там будут самые незначительные. Содержательно могут изменить только 2 задания, и как раз одно из них и принесёт дополнительный балл. Остальные задания не изменят.
Что убрали из краткой части в перспективной модели ЕГЭ по математике
Как я уже сказала, больше всего изменений планируется в части с кратким ответом. Во-первых, теперь все первые 12 заданий будут называться «Часть 1».
Раньше «Часть 1» включала в себя только первые 8 заданий. Номера 9-12 относились к «Части 2», но записывались в бланк с кратким ответом.
Во-вторых, именно в этой части экзамена мы можем потерять задания. В перспективной модели ЕГЭ по математике нет:
№ 1 – простейшей текстовой задачи
Тип заданий, исключенный из перспективной модели ЕГЭ по математике 2022
№ 2 – задачи на анализ графиков и диаграмм
Тип задач, которых нет в перспективной модели ЕГЭ по математике 2022
№ 3 – простейшей планиметрии на клеточках или координатной плоскости
Тип заданий, больше не встречающийся в перспективной модели ЕГЭ по математике 2022
Данные задания могут исключить из-за стабильно высокого процента решаемости, что противоречит изначальному принципу ЕГЭ – ранжировать абитуриентов.
Как теперь выглядит краткая часть
А что же тогда будет в новом экзамене?
Задание № 1
В перспективной модели на позиции №1 мы видим бывшее заданий № 5 – простейшее уравнение:
Простейшие уравнения в перспективной модели ЕГЭ по математике 2022
Задание № 2
На позиции № 2 – бывший № 4, задача по теории вероятности:
Задачи по теории вероятности, перспективная модель ЕГЭ по математике 2022
Задание № 3
Вместо № 3 – новое задание на анализ функций. Это совершенно новый формат задания, хотя тема пересекается с ОГЭ, где обычно нужно сопоставить графики и формулы. Здесь же представлено более сложное задание на анализ.
Задание на графики, перспективная модель ЕГЭ по математике 2022
Задание № 4
Вместо бывшей задачи на вероятность в № 4 переместилась планиметрическая задача (раньше она была под № 6):
Планиметрические задачи, перспективная модель ЕГЭ по математике 2022
Задание № 5
В № 5 мы видим задание на выражение, которое раньше находилось под № 9. Раньше оно относилось к заданиям повышенной сложности. Сейчас же выражение относится к базовому уровню сложности, хотя содержательно ничего не изменилось.
Задание на выражение, перспективная модель ЕГЭ по математике 2022
Задание № 6
№ 6 стал стереометрической задачей, которая ранее была № 8:
Стереометрические задачи, перспективная модель ЕГЭ по математике 2022
Задание № 7
№ 7 – это один из двух номеров, которых не коснулись изменения. Как был номером на анализ функций, так им и остался (все прототипы сохранены).
Задание № 8
В № 8 переместилась прикладная задача (ранее № 10):
Прикладная задача, перспективная модель ЕГЭ по математике 2022
Задание № 9
№ 9 теперь будет текстовой задачей на движение, проценты или сплавы и смеси:
Задача на движение, перспективная модель ЕГЭ по математике 2022
Задание № 10
А № 10 – это новое задание из блока «Элементы комбинаторики, статистики и теории вероятностей» повышенного уровня сложности. Кстати, в 2021 в перспективной модели ОГЭ тоже были 2 задания из этого блока – в первой и второй частях. Однако такое изменение в итоге не было реализовано.
Задания из блока «Элементы комбинаторики, статистики и теории вероятностей»,
перспективная модель ЕГЭ по математике 2022
Задание № 11
В № 11 также планируется ввести совершенно новое задание на комплексные числа. Это новая тема, которая не освещалась ранее в ЕГЭ. По спецификации формат данного задания – «Вычисления и преобразования» повышенного уровня сложности:
Задание на комплексные числа, перспективная модель ЕГЭ по математике 2022
Задание № 12
И № 12 – второе задание, которое осталось неизменным. Это задание на экстремумы – поиск точек максимума/минимума и наибольшего/наименьшего значений функции.
Задания на экстремумы, перспективная модель ЕГЭ по математике 2022
Изменения в части с развёрнутым ответом
Что касается части с развёрнутым ответом, то здесь всего 3 ощутимых изменения.
1. Из № 13 убрали пункт б), посвящённый отбору корней на заданном промежутке
Скорее всего, это было сделано для того, чтобы было проще набрать частичные баллы.
Ранее ученики получали по одному баллу за каждый пункт и в случае неверного решения они теряли оба балла. Сейчас 1 балл можно получить при условии совершённой вычислительной ошибки, но верной последовательности всех действий. 2 балла – за полностью верное решение.
Задание № 13, перспективная модель ЕГЭ по математике 2022
2. № 15 – самые большие изменения
Когда-то в этом номере была система из уравнения и неравенства. Стоило такое задание 3 балла. Потом задание упростили до решения неравенства и понизили стоимость до 2 баллов. А сейчас мы видим, что эксперты хотят вернуться к прошлому опыту, добавить уравнение и детализировать критерии:
- неравенство, пункт а), решено – 1 балл;
- уравнение, пункт б), решено – 1 балл;
- система из неравенства и уравнения решена – 1 балл.
Задание № 15, перспективная модель ЕГЭ по математике 2022
Несмотря на детализацию, № 15 стал сложнее. Поэтому выросла его цена – задание снова будет стоить 3 балла. Вот мы и нашли новый, 33-й балл!
3. Меняют местами номера 16 и 17
Теперь экономическая задача будет под № 16, а планиметрия второй части под № 17.
Задание № 16, экономическая задача, перспективная модель ЕГЭ по математике 2022
Задание № 17, планиметрия, перспективная модель ЕГЭ по математике 2022
Оба задания, как и раньше будут стоить 3 балла. Меняют их местами, скорее всего, из-за того, что процент решаемости экономической задачи намного выше, чем у задачи на планиметрию.
Вектор изменений в ЕГЭ по математике
О чем же говорят предлагаемые изменения? Несмотря на стабильно невысокие результаты экзамена из года в год, ЕГЭ по математике скорее всего будет усложняться с 2022 года. Темы младшей и средней школы будут убирать, а на их место ставить темы старших классов. Сами задания также будут становиться сложнее.
Можно наблюдать огромную волну возмущений по поводу ЕГЭ, которая растёт из года в год, организации петиций и попытки собрать подписи по поводу отмены ЕГЭ. На самом деле, ЕГЭ нужно не отменять, а совершенствовать. Если экзамен будет не для набора баллов и поступления, а для подготовки к высшему образованию, то возмущений будет меньше. Ровно это и делают эксперты ФИПИ! Они стремятся повлиять на изучение тем в школах, чтобы важные для высшего образования вопросы не опускались в старших классах, а изучались глубоко и в полном объёме.
Но не спешите расстраиваться и пугаться. При качественной подготовке и вложенных усилиях возможно подготовиться к экзамену и получить высокий балл, так что всё в ваших руках! Не ждите озарения, начинайте готовиться уже сейчас!
Подготовиться к ЕГЭ на высокий балл вы можете вместе с нашими преподавателями. Они поделятся с вами всеми секретами сдачи экзамена и научат быстро и правильно решать самые сложные задания. Приходите к нам на бесплатный пробный урок и начните готовиться к ЕГЭ прямо сейчас!
Версия для печати и копирования в MS Word
1
Изобразите на чертеже множество точек комплексной плоскости, для которых выполняется условие Среди чисел, удовлетворяющих этому равенству, найдите число с наименьшим модулем. Запишите найденное число в тригонометрической форме.
Загрузка решений доступна для зарегистрировавшихся пользователей
2
Среди комплексных чисел z, удовлетворяющих условию найдите число с наименьшим модулем.
Загрузка решений доступна для зарегистрировавшихся пользователей
3
Среди чисел z, таких, что найдите числа с наименьшим и наибольшим модулем.
Загрузка решений доступна для зарегистрировавшихся пользователей
4
Найдите наибольший модуль комплексного числа z, удовлетворяющего условию
Загрузка решений доступна для зарегистрировавшихся пользователей
5
Загрузка решений доступна для зарегистрировавшихся пользователей
6
Известно, что комплексные числа z и имеют одинаковый модуль. В каких пределах может изменяться значение этого модуля?
Загрузка решений доступна для зарегистрировавшихся пользователей
7
Загрузка решений доступна для зарегистрировавшихся пользователей
8
Множество точек комплексной плоскости определяется условием В каких пределах изменяется
Загрузка решений доступна для зарегистрировавшихся пользователей
9
Загрузка решений доступна для зарегистрировавшихся пользователей
10
Найдите такое мнимое число z, что сумма минимальна.
Загрузка решений доступна для зарегистрировавшихся пользователей
11
Из всех чисел z, удовлетворяющих условию найдите такие, что
принимает наименьшее значение.
Загрузка решений доступна для зарегистрировавшихся пользователей
12
Загрузка решений доступна для зарегистрировавшихся пользователей
Завершить тестирование, свериться с ответами, увидеть решения.
ЕГЭ-2022 по математике. Профильный уровень. Вероятность и комплексные числа
ФИПИ опубликовал документ с длинным названием Перспективная модель измерительных материалов для государственной итоговой аттестации по программам среднего общего образования по МАТЕМАТИКЕ. Демонстрационный вариант
Matematika_ma-11-ege-pm2022-demo.pdf (userapi.com)
По знакомому оформлению и «ege-pm2022» в адресе сайта узнаётся перспективная демоверсия ЕГЭ для 2022 года. Давайте посмотрим, что ждёт выпускников в перспективе. Сегодня остановлюсь на задачах по вероятности.
Первая задача до боли знакома. не обсуждаем. Вторая задача может поставить в тупик. Здесь надо разобраться, что означает событие А — «мотор проработал более года». Это значит, что произошло одно из двух событий:
B — «мотор проработал более года, но не более двух лет» и
С — «мотор проработал более двух лет».
По условию задачи P (А) = 0,8, P (C) = 0,6.
Событие А произойдёт, если наступит или событие В, или событие С, то есть
A = B + C, P (A) = P (B + C).
А так как события В и С несовместные (не могут произойти одновременно), то
P (B + C) = P (B) + P (C). Окончательно имеем:
0,8 = P (B) + 0,6,
P (B) = 0,2.
Ответ. 0,2.

Обратим внимание на появление в варианте ещё одной задачи на вероятность, её номер 10. Вот два примера.
Разбираем решение первой задачи. После трёх бросков сумма 6 очков могла получиться лишь при таких наборах очков 1 + 1 + 4; 1 + 2 + 3; 2 + 2 + 2 (без учета порядка следования очков в сумме). За счёт перестановок слагаемых получаем:
114, 141, 411 — 3 исхода;
123, 132, 213, 231, 312, 321 — 6 исходов;
222 — 1 исход.
Всех равновозможных исходов для получения в сумме 6 оков — 10, только 6 из них благоприятствуют событию «хотя бы раз выпало 3 очка». Вероятность этого события
6 : 10 = 0,6.
Ответ. 0,6. (В таблице ответ 0,5 — опечатка).
Вторая задача, как мне показалось, к теме «вероятность» притянута за уши, так как ответ к ней получается при решении задачи на проценты. Сформулируем её, заменив «выбрали взрослого мужчину» на «выбрали мужчину», так как взрослые делятся на мужчин и женщин, невзрослых мужчин по смыслу задачи нет. Слово «взрослого» лишнее.
В городе 48 % взрослого населения мужчины. Пенсионеры составляют 12,6 % взрослого населения, причём доля пенсионеров среди женщин составляет 15 %. Какова доля пенсионеров среди мужчин?
Если доля пенсионеров окажется равной m/n, то вероятность случайного выбора пенсионера из мужчин составляет m/n.
Пусть в городе было x взрослых — мужчин и женщин. Тогда в нём 0,48x мужчин, 0,52x женщин, 0,126x пенсионеров,
0,15 * 0,52x = 0,078x женщин-пенсионеров и
0,126x – 0,078x = 0,048x — мужчин-пенсионеров.
Доля мужчин-пенсионеров среди мужчин составляет
0,048x : 0,48x = 0,1.
Ответ. 0,1.
Рассмотрим теперь задачу по комплексным числам, которых до сих пор никогда не было в ЕГЭ, но они всегда присутствовали в выпускном экзамене по программе углубленного изучения математики. На мой взгляд, это ошибка составителей варианта. Нельзя устраивать дискриминацию учащихся, не изучавших математику углублённо. Рассмотрим задачу.
Ученику обычного класса придётся прочитать про комплексные числа, про мнимую единицу i, квадрат которой равен –1. Про то, что комплексным числом называют выражение z, записанное в виде z = a + bi, где a и b — действительные числа, а i — мнимая единица. Комплексное число задаётся парой действительных чисел (a; b), его удобно изображать в системе координат точкой (a; b). Модулем комплексного числа называют расстояние от начала отсчёта системы координат до точки, изображающей число z. Модуль комплексного числа z = a + bi вычисляют по формуле: |z| = 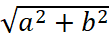
Решаем задачу 11.
Пусть число z = a + bi, тогда число 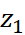
| 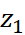
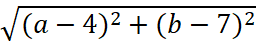
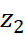
| 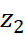
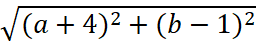
Равенство | 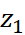
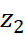

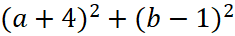
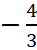
Найдём значение a, при котором величина |z| = 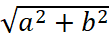
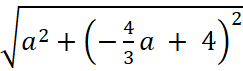
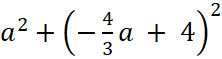
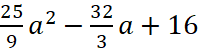
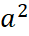
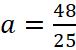
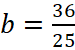
|z| = 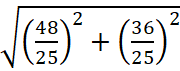
Ответ. 2,4.
Решим задачу, изображая комплексное число точкой координатной плоскости. Этот способ вполне годится для решения задачи на ЕГЭ, так как там подробное решение не требуется, достаточно привести правильный ответ. Изобразим на клетчатой бумаге точками числа z = a + bi, 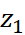
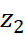
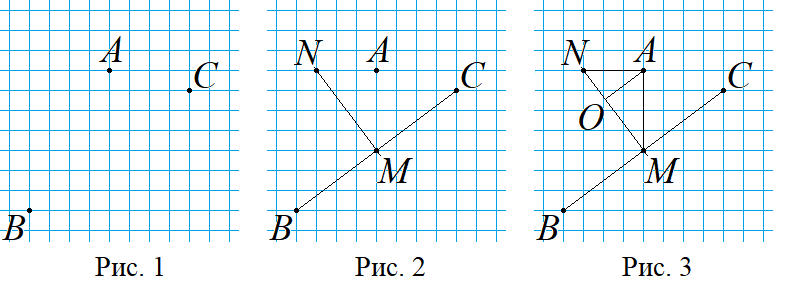
Знать, где находятся оси координат не нужно, главное взаимное расположение точек A (a; b), B (a – 4; b – 7) и С (a + 4; b – 1), соответствующих числам z, 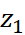
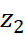
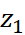
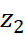
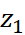
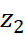
Точка O лежит на прямой MN, а нам нужно, чтобы расстояние AO было наименьшим, это возможно лишь тогда, когда является перпендикуляром к AO. Строим AO и находим его длину как высоту прямоугольного треугольника AMN с гипотенузой MN (рис 3).
Вычислив площадь треугольника AMN двумя способами, выразим длину высоты, проведённой к гипотенузе MN. Получим 2,4.
Шевкин А.В., avshevkin@mail.ru