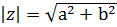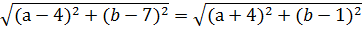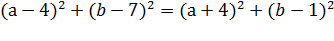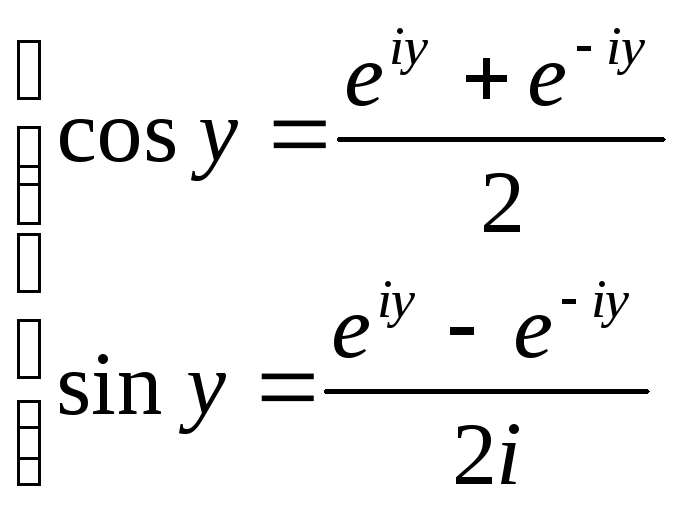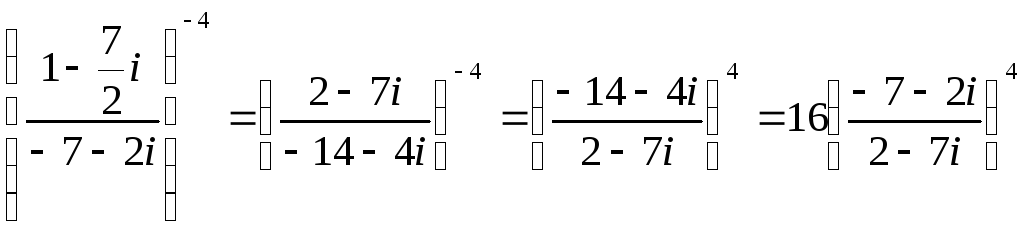Комплексные числа
В математике кроме натуральных, рациональных и вещественных чисел имеется ещё один вид, называемый комплексными числами. Такое множество принято обозначать символом $ mathbb{C} $.
Рассмотрим, что из себя представляет комплексное число. Запишем его таким образом: $ z = a + ib $, в котором мнимая единица $ i = sqrt{-1} $, числа $ a,b in mathbb{R} $ вещественные.
Если положить $ b = 0 $, то комплексное число превращается в вещественное. Таким образом, можно сделать вывод, что действительные числа это частный случай комплексных и записать это в виде подмножества $ mathbb{R} subset mathbb{C} $. К слову говоря также возможно, что $ a = 0 $.
Принято записывать мнимую часть комплексного числа как $ Im(z) = b $, а действительную $ Re(z) = a $.
Введем понятие комплексно-сопряженных чисел. К каждому комплексному числу $ z = a+ib $ существует такое, что $ overline{z} = a-ib $, которое и называется сопряженным. Такие числа отличаются друг от друга только знаками между действительной и мнимой частью.
Формы
Так сложилось в математике, что у данных чисел несколько форм. Число одно и тоже, но записать его можно по-разному:
- Алгебраическая $ z = a+ib $
- Показательная $ z = |z|e^{ivarphi} $
- Тригонометрическая $ z = |z|cdot(cos(varphi)+isin(varphi)) $
Далее с примерами решений вы узнаете как переводить комплексные числа из одной формы в другую путем несложных действий в обе стороны.
Изображение
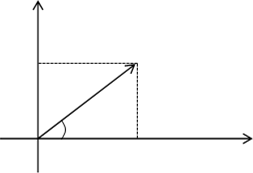
Изучение выше мы начали с алгебраической формы. Так как она является основополагающей. Чтобы было понятно в этой же форме изобразим комплексное число на плоскости:
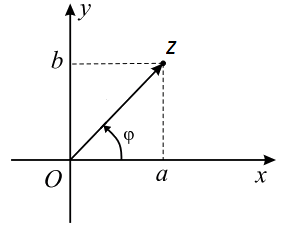
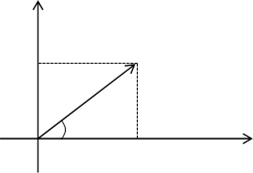
Комплексное число $ z = a+ib $ представляется в виде вектора $ overline{z} $.
Аргумент обозначается $ varphi $.
Модуль $ |z| $ равняется длине вектора $ overline{z} $ и находится по формуле $ |z| = sqrt{a^2+b^2} $
Аргумент комплексного числа $ varphi $ нужно находить по различным формулам в зависимости от полуплоскости, в которой лежит само число.
Если:
- $ a>0 $, то $ varphi = arctgfrac{b}{a} $
- $ a<0, b>0 $, то $ varphi = pi + arctgfrac{b}{a} $
- $ a<0, b<0 $, то $ varphi = -pi + arctgfrac{b}{a} $
Операции
Над комплексными числами можно проводить различные операции, а именно:
- Складывать и вычитать
- Умножать и делить
- Извлекать корни и возводить в степень
- Переводить из одной формы в другую
Для нахождения суммы и разности складывается и вычитаются только соответствующие друг другу члены. Мнимая часть только с мнимой, а действительная только с действительной:
$$ z_1 + z_2 = (a_1+ib_1) + (a_2+ib_2) = (a_1 + a_2)+i(b_1 + b_2) $$
$$ z_1 — z_2 = (a_1+ib_1) — (a_2+ib_2) = (a_1 — a_2)+i(b_1 — b_2) $$
Умножение в алгебраической форме:
$$ z_1 cdot z_2 = (a_1+ib_1) cdot (a_2+ib_2) = (a_1 a_2 — b_1 b_2)+i(a_1 b_2 + a_2 b_1) $$
Умножение в показательной форме:
$$ z_1 cdot z_2 = |z_1|e^{ivarphi_1} cdot |z_2|e^{ivarphi_2} = |z_1|cdot|z_2|cdot e^{i(varphi_1 + varphi_2)} $$
Деление в алгебраической форме:
$$ frac{z_1}{z_2} = frac{a_1+ib_1}{a_2+ib_2} = frac{a_1 a_2 + b_1 b_2 }{a_2 ^2 + b_2 ^2} + i frac{a_2 b_1 — a_1 b_2}{a_2 ^2 + b_2 ^2} $$
Деление в показательной форме:
$$ frac{z_1}{z_2} = frac{|z_1|e^{ivarphi_1}}{|z_2|e^{ivarphi_2}} = frac{|z_1|}{|z_2|}e^{i(varphi_1 — varphi_2)} $$
Для возведения в степень необходимо умножить комплексное число само на себя необходимое количество раз, либо воспользоваться формулой Муавра:
$$ z^n = |z|^n(cos nvarphi+isin nvarphi) $$
Для извлечения корней необходимо также воспользоваться формулой Муавра:
$$ z^frac{1}{n} = |z|^frac{1}{n}bigg(cos frac{varphi + 2pi k}{n}+isin frac{varphi + 2pi k}{n}bigg), k=0,1,…,n-1 $$
Так же теория комплексных чисел помогает находить корни многочленов. Например, в квадратном уравнении, если $ D<0 $, то вещественных корней нет, но есть комплексные. В последнем примере рассмотрен данный случай.
Рассмотрим на практике комплексные числа: примеры с решением.
Примеры с решением
| Пример 1 |
| Перевести из алгебраической в тригонометрическую и показательную форму:$$ z = 4-4i $$ |
| Решение |
|
Для начала приступим к нахождению модуля комплексного числа: $$ |z| = sqrt{4^2 + (-4)^2} = sqrt{16 + 16} = sqrt{32} = 4sqrt{2} $$ Осталось найти аргумент: $$ varphi = arctg frac{b}{a} = arctg frac{-4}{4} = arctg (-1) = -frac{pi}{4} $$ Теперь составляем тригонометрическую запись комплексного числа, указанного в условии примера: $$ z = 4sqrt{2}bigg(sin(-frac{pi}{4}) + isin(-frac{pi}{4}) bigg) $$ Тут же можно записать показательную форму: $$ z = 4sqrt{2} e^{-frac{pi}{4}i} $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
|
$$ z = 4sqrt{2}bigg(sin(-frac{pi}{4}) + isin(-frac{pi}{4}) bigg) $$ $$ z = 4sqrt{2} e^{-frac{pi}{4}i} $$ |
| Пример 2 |
|
Вычислить сумму и разность заданных комплексных чисел: $$ z_1 = 3+i, z_2 = 5-2i $$ |
| Решение |
|
Сначала выполним сложение. Для этого просуммируем соответствующие мнимые и вещественные части комплексных чисел: $$ z_1 + z_2 = (3+i) + (5-2i) = (3+5)+(i-2i) = 8 — i $$ Аналогично выполним вычитание чисел: $$ z_1 — z_2 = (3+i) — (5-2i) = (3-5)+(i+2i) = -2 + 3i $$ |
| Ответ |
| $$ z_1 + z_2 = 8 — i; z_1 — z_2 = -2 + 3i $$ |
| Пример 3 |
|
Выполнить умножение и деление комплексных чисел: $$ z_1 = 3+i, z_2 = 5-2i $$ |
| Решение |
|
$$ z_1 cdot z_2 = (3+i) cdot (5-2i) = $$ Просто на просто раскроем скобки и произведем приведение подобных слагаемых, так же учтем, что $ i^2 = -1 $: $$ = 15 — 6i + 5i -2i^2 = 15 — i — 2cdot(-1) = $$ $$ = 15 — i + 2 = 17 — i $$ Так, теперь разделим первое число на второе: $$ frac{z_1}{z_2} = frac{3+i}{5-2i} = $$ Суть деления в том, чтобы избавиться от комплексного числа в знаменателе. Для этого нужно домножить числитель и знаменатель дроби на комплексно-сопряженное число к знаменателю и затем раскрываем все скобки: $$ = frac{(3+i)(5+2i)}{(5-2i)(5+2i)} = frac{15 + 6i + 5i + 2i^2}{25 + 10i — 10i -4i^2} = $$ $$ = frac{15 + 11i -2}{25 + 4} = frac{13 + 11i}{29} $$ Разделим числитель на 29, чтобы записать дробь в виде алгебраической формы: $$ frac{z_1}{z_2} = frac{13}{29} + frac{11}{29}i $$ |
| Ответ |
| $$ z_1 cdot z_2 = 17 — i; frac{z_1}{z_2} = frac{13}{29} + frac{11}{29}i $$ |
| Пример 4 |
| Возвести комплексное число $ z = 3+3i $ в степень: a) $ n=2 $ б) $ n=7 $ |
| Решение |
|
1) $ n = 2 $ Для возведения в квадрат достаточно умножить число само на себя: $$ z^2 = (3+3i)^2 = (3+3i)cdot (3+3i) = $$ Пользуемся формулой для умножения, раскрываем скобки и приводим подобные: $$ =9 + 9i + 3icdot 3 + 9i^2 = 9 + 18i — 9 = 18i $$ Получили ответ, что $$ z^2 = (3+i)^2 = 18i $$ 2) $ n = 7 $ В этом случае не всё так просто как в предыдущем случае, когда было возведение в квадрат. Конечно, можно прибегнуть к способу озвученному ранее и умножить число само на себя 7 раз, но это будет очень долгое и длинное решение. Гораздо проще будет воспользоваться формулой Муавра. Но она работает с числами в тригонометрической форме, а число задано в алгебраической. Значит, прежде переведем из одной формы в другую. Вычисляем значение модуля: $$ |z| = sqrt{3^2 + 3^2} = sqrt{9 + 9} = sqrt{18} = 3sqrt{2} $$ Найдем чем равен аргумент: $$ varphi = arctg frac{3}{3} = arctg(1) = frac{pi}{4} $$ Записываем в тригонометрическом виде: $$ z = 3sqrt{2}(cos frac{pi}{4} + isin frac{pi}{4}) $$ Возводим в степень $ n = 7 $: $$ z^7 = (3sqrt{2})^7 (cos frac{7pi}{4} + isin frac{7pi}{4}) = $$ Преобразуем в алгебраическую форму для наглядности: $$ =(3sqrt{2})^7 (frac{1}{sqrt{2}}-ifrac{1}{sqrt{2}}) = $$ $$ = 3^7 sqrt{2}^7 (frac{1}{sqrt{2}}-ifrac{1}{sqrt{2}}) = $$ $$ = 3^7 sqrt{2}^6 (1-i) = 3^7 cdot 8(1-i) = $$ $$ = 2187 cdot 8 (1-i) = 17496(1-i) $$ |
| Ответ |
|
$$ z^2 = (3+i)^2 = 18i $$ $$ z^7 = 17496(1-i) $$ |
| Пример 5 |
| Извлечь корень $ sqrt[3]{-1} $ над множеством $ mathbb{C} $ |
| Решение |
|
Представим число в тригонометрической форме. Найдем модуль и аргумент: $$ |z| = sqrt{(-1)^2 + 0^2} = sqrt{1+0} = sqrt{1}=1 $$ $$ varphi = arctg frac{0}{-1} +pi = arctg 0 + pi = pi $$ Получаем: $$ z = (cos pi + isin pi) $$ Используем знакомую формулу Муавра для вычисления корней любой степени: $$ z^frac{1}{n} = r^frac{1}{n}bigg(cos frac{varphi + 2pi k}{n}+isin frac{varphi + 2pi k}{n}bigg), k=0,1,…,n-1 $$ Так как степень $ n = 3 $, то по формуле $ k = 0,1,2 $: $$ z_0 = sqrt[3]{1} (cos frac{pi}{3}+isin frac{pi}{3}) = frac{1}{2}+ifrac{sqrt{3}}{2} $$ $$ z_1 = sqrt[3]{1} (cos frac{3pi}{3}+isin frac{3pi}{3}) = -1 $$ $$ z_2 = sqrt[3]{1} (cos frac{5pi}{3}+isin frac{5pi}{3}) = frac{1}{2} — ifrac{sqrt{3}}{2} $$ |
| Ответ |
|
$$ z_0 = frac{1}{2}+ifrac{sqrt{3}}{2} $$ $$ z_1 = -1 $$ $$ z_2 = frac{1}{2} — ifrac{sqrt{3}}{2} $$ |
| Пример 6 |
| Решить квадратное уравнение $ x^2 + 2x + 2 = 0 $ над $ mathbb{C} $ |
| Решение |
|
Решать будем по общей формуле, которую все выучили в 8 классе. Находим дискриминант $$ D = b^2 — 4ac = 2^2 — 4cdot 1 cdot 2 = 4-8 = -4 $$ Получили, что $ D=-4<0 $ и казалось бы, что решение можно заканчивать. Но нет! В нашем задании требуется решить уравнение над комплексным множеством, а то что дискриминант отрицательный означает только лишь отсутствие вещественных корней. А комплексные корни есть! Найдем их продолжив решение: $$ x_{1,2} = frac{-bpm sqrt{D}}{2a} = frac{-2pm sqrt{-4}}{2} = $$ Заметим, что $ sqrt{-4} = 2sqrt{-1} = 2i $ и продолжим вычисление: $$ = frac{-2 pm 2i}{2} = -1 pm i $$ Получили комплексно-сопряженные корни: $$ x_1 = -1 — i; x_2 = -1 — i $$ Как видите любой многочлен можно решить благодаря комплексным числам. |
| Ответ |
| $$ x_1 = -1 — i; x_2 = -1 — i $$ |
В статье «Комплексные числа: примеры с решением» было дано определение, основные понятия, формы записи, алгебраические операции и решение практических примеров.
Автор материала — Анна Малкова
Что такое комплексные числа
Все знают, что ЕГЭ по математике Профильного уровня в ближайшие годы будет меняться. Например, предлагается добавить в школьную программу по математике тему «Комплексные числа». Но что же это такое?
Начнем с хорошо известных вам фактов.
Вспомним, что возвести число в квадрат — значит умножить его само на себя.
Если положительное число возвести в квадрат — результат будет положительный.
Если отрицательное число возвести в квадрат — результат тоже положительный. «Минус на минус дает плюс», — это мы не раз слышали на уроках математики.
Например, уравнение имеет 2 решения: х = 2 и х = -2.
Число 2 называют арифметическим квадратным корнем из 4, то есть
А можно ли какое-нибудь число возвести в квадрат, чтобы результат получился отрицательный? И если нет, то почему?
Ведь отрицательные числа ничем не хуже положительных. Баланс мобильного телефона может быть положительным или отрицательным. Температура может быть равна +5 градусов Цельсия, а может быть и минус 5 градусов. На числовой оси положительные и отрицательные числа расположены симметрично. Почему же из положительных чисел квадратный корень извлекать можно, из нуля тоже можно (он равен нулю), а из отрицательных нельзя?
А что, если — сказали однажды математики, — существует такое число, квадрат которого равен минус единице?
И называется это число мнимой единицей, а обозначается буквой
Вот какая необычная формула получилась:
Получается, что уравнение имеет 2 решения: i и минус i.
А уравнение имеет решения — 2i и 2i.
Теперь нам не страшны квадратные уравнения, в которых дискриминант отрицателен.
Например, уравнение
Его дискриминант равен 1 — 4 = — 3.
Его корни:
Числа вида называются комплексными. При этом х называется действительной частью комплексного числа z, а у — его мнимой частью.
Записывается это так:
Сокращения понятны тем, кто изучает английский: Re — Real, Im — Imaginary.
Помните, мы говорили о том, какие бывают числа?
Натуральные числа применяются для счета предметов. Множество натуральных чисел обозначается N.
Целые числа — это положительные, отрицательные и ноль. Например, 4, 78, -121, 0 — целые числа. Множество целых чисел Z содержит в себе множество натуральных.
Рациональные числа — те, которые можно записать в виде обыкновенной дроби вида р/q, где р — целое, q — натуральное. Например, — числа рациональные. Мы проходили их в начальной и средней школе. Если рациональное число записать в виде десятичной дроби, она будет периодической, например,
Множество рациональных чисел обозначается Q и содержит в себе множество целых чисел.
В старших классах мы узнали об иррациональных числах — таких, как или
Их невозможно записать в виде обыкновенной дроби, а если выразить в виде десятичной — она будет бесконечной непериодической. И казалось, что мы знаем о числах всё. Все числа, какие только нам встречались, входили в множество действительных чисел R.
Когда мы пишем: — это значит, что число х действительное. Мы помним, что действительные числа можно изображать точками на числовой прямой, которую еще называют действительной осью.
А теперь оказывается, что R — это подмножество множества комплексных чисел С.
Действительные числа еще называют «вещественными». Они описывают наш вещественный мир. В самом деле, натуральные числа применяем для счета предметов. С дробями тоже понятно: половинка яблока или пиццы. С отрицательными числами все знакомы: достаточно зимой посмотреть на градусник за окном. И даже иррациональные числа можно «увидеть»: например, длина окружности радиуса 1 или диагональ квадрата со стороной 1 являются иррациональными числами.
Но где же в мире — мнимые и комплексные числа? Неужели они нужны для описания того, что мы не можем потрогать или посчитать по пальцам?
Да, так и есть. Комплексные числа — удобный инструмент для построения математических моделей волн и колебаний. Электро- и радиотехника, теоретическая и квантовая физика — все они пользуются комплексными числами. Мир элементарных частиц живет по законам, описываемым функциями комплексных переменных. Так что продолжим их изучение.
Комплексная плоскость
Где же находятся мнимые числа, если на числовой прямой для них места нет?
Очень просто. Мнимые числа — на мнимой оси. А комплексные числа вида — на комплексной плоскости.
Каждому комплексному число соответствует точка на комплексной плоскости.
Расстояние от нуля до этой точки называется модулем комплексного числа:
Угол между направлением на эту точку и положительным направлением действительной оси называется аргументом комплексного числа:
Аргумент комплексного числа определен с точностью до
Аналогично в тригонометрии: каждая точка на единичной окружности соответствует бесконечному множеству углов, отличающихся на где k — целое.
Здесь
— главное значение аргумента
Иногда главное значение аргумента комплексного числа определяют на отрезке
Если
не определен.
Комплексное число можно записать как в алгебраической форме так и в тригонометрической.
Поскольку
получим:
Это тригонометрическая форма записи комплексного числа.
Здесь
При переходе от алгебраической формы записи к тригонометрической считаем, что принимает значения
Обратите внимание, что в записи число х — действительное.
Число — мнимое.
Задача 1. Запишите число
в тригонометрической форме.
Решение:
Так как
Как видим, для освоения темы «Комплексные числа» надо отлично знать тригонометрию.
Действия над комплексными числами
Два комплексных числа равны друг другу, если равны соответственно их действительные и мнимые части.
Сравнивать комплексные числа нельзя. Операции «больше» и «меньше» для комплексных чисел не определены.
Два комплексных числа, отличающиеся только знаком мнимой части, называются комплексно-сопряженными. Вот такие:
Возьмем два комплексных числа:
и
.
Определим для них операции сложения и вычитания.
Сложение:
Похоже на правило сложение векторов, не правда ли?
Так же, как и для действительных чисел, то есть от перемены мест слагаемых сумма не меняется (коммутативность сложения). Также выполняется ассоциативность сложения, то есть
Еще одно важное свойство:
Это знакомое нам неравенство треугольника.
Вычитание:
— расстояние между точками
и
Задача 2. Определите, какая фигура на комплексной плоскости является решением уравнения
Решение:
Прочитаем это уравнение так же, как мы делали с обычными уравнениями с модулем. Расстояние от точки z до точки 2i равно 1. Это значит, что точки, соответствующие решениям данного уравнения, лежат на окружности с центром в точке радиусом 1.
Если сложение и вычитание комплексных чисел вопросов не вызывают, то для умножения правила не такие очевидные. Вот какой будет формула произведения комплексных чисел:
Например, подставив в эту формулу получим уже знакомое равенство:
Умножение комплексных чисел обладает теми же свойствами, что и умножение действительных:
Но если умножение комплексных чисел настолько сложно — что же делать с возведением в степень? Оказывается, что и умножение, и возведение комплексных чисел в степень удобнее выполнять, записывая числа в тригонометрической форме.
Возведение в степень:
Последнее равенство называется формула Муавра.
Задача 3.
Вычислите:
Решение:
Для числа
Деление комплексных чисел определяем как действие, обратное умножению.
если
Пусть
отсюда
Сложные формулы, не правда ли? Попробуем применить.
Задача 4.
.
Намного удобнее выполнять деление комплексных чисел, записав их в тригонометрической форме:
.
Извлечение корней из комплексных чисел — еще интереснее. Во-первых, для извлечения корня n-ной степени из комплексного числа лучше всего записать его в тригонометрической форме.
Во-вторых, для любого выражение
принимает ровно
различных значений.
Пусть — корень
-ной степени из комплексного числа
;
Тогда Записав число z в тригонометрической форме, получим:
Обратите внимание — для корня n-ной степени получим различных значений корня.
Задача 5.
Найдем
При
При
При
Задача ЕГЭ-2022, Комплексные числа
Решим задачу из варианта ЕГЭ — 2022 по теме «Комплексные числа».
Задача 6.
Про комплексное число известно, что
Найдите наименьшее значение
Решение:
Обозначим
Пусть
Известно, что
Получим:
1 способ.
Расстояния от точки, соответствующей числу z, до точек и
должны быть равны. Отметим точки
и
на комплексной плоскости. Равноудаленными от точек
и
будут все точки, лежащие на серединном перпендикуляре к отрезку, соединяющему
и
По условию задачи, из этих точек надо выбрать такую, для которой
принимает наименьшее значение, то есть наименее удаленную от начала координат. Другими словами — найдем расстояние от начала координат до данной прямой.
Это показано на рисунке. Точка Н соответствует комплексному числу z, лежащему на прямой, все точки которой равноудалены от и
при этом расстояние от 0 до z — наименьшее. Найдем это расстояние (равное ОН) из прямоугольного треугольника АОВ. Его катеты равны 3 и 4, гипотенуза равна 5. Записав площадь треугольника АОВ двумя способами, получим:
2 способ.
Вернемся к выражению
Запишем его в виде:
Мы получили, что модули двух комплексных чисел равны. Модуль комплексного числа равен Возведя это выражение в квадрат, получим, что
Значит, если равны модули двух комплексных чисел
и
то
В нашем случае:
Выразим отсюда х;
и найдем наименьшее значение выражения
Мы получили функцию . Обычную функцию от действительной переменной. Найдем наименьшее значение функции
Это квадратичная функция, ее график — парабола с ветвями вверх, и наименьшее значение достигается в вершине параболы.
Еще несколько задач по теме «Комплексные числа»:
Задача 7.
Представьте в тригонометрической форме числа:
а)
б) 1 — i.
Решение:
а) .
б) i.
Задача 8.
Вычислить
Задача 9.
Считая х и у действительными числами, решите уравнение:
Решение:
Пользуясь определением равенства комплексных чисел, получим:
Умножим первое уравнение на 2, а второе на 5, и вычтем из второго уравнения первое.
Получим, что
тогда
Задача 10.
Известно, что число является корнем уравнения
где
Найти а и решить уравнение при этом значении а.
Решение:
По условию, — корень уравнения
Подставив
получим
Уравнение примет вид:
Так как — корень уравнения, разделим левую часть на х + 9. Получим:
Найдем корни квадратного уравнения
Экспоненциальная форма записи комплексного числа
Хорошо, что в ЕГЭ по математике появились комплексные числа. Чтобы их освоить, надо отлично знать алгебру, геометрию и тригонометрию, потому что эта тема связана со многими областями математики.
Помните, например, тему «Элементарные функции и их графики»? Там мы говорили о 5 типах элементарных функций: степенных, показательных, логарифмических, тригонометрических и обратных тригонометрических. И казалось, что у показательных и тригонометрических функций общего мало.
А теперь посмотрите, как выглядит экспоненциальная форма записи комплексного числа:
Формула носит имя Леонарда Эйлера — одного из величайших математиков в истории.
Здесь — периодическая функция, период
С помощью формулы Эйлера знакомые нам косинус и синус можно выразить через комплексные экспоненты:
Если мы получим самую красивую и удивительную формулу математики:
Она связывает две мировые константы, то есть числа и
знакомую нам обычную единицу и ту самую мнимую единицу i, с которой мы начали это первое знакомство с комплексными числами.
Задачи взяты из книги Д. Письменного «Конспект лекций по высшей математике» и Проекта ЕГЭ-2022 по математике Профильного уровня.
На ЕГЭ-2022 по математике комплексных чисел не будет. Но рано или поздно эта тема будет добавлена в школьную программу.
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Комплексные числа на ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.03.2023
- Авторы
- Файлы
- Ключевые слова
- Литература
Грудинина О.С.
1
1 МБОУ ШР «СОШ №2»
перспективная модель
контрольно-измерительные материалы
единый государственный экзамен
профильный уровень
комплексные числа
1. «Министерство сельского хозяйства Российской Федерации Департамент научно-технологической политики и образования Федеральное государственное бюджетное образовательное учреждение высшего образования «Волгоградский государственный аграрный университет» Комплексные числа 2020.
2. ФГБНУ « Федеральный институт педагогических измерений» [Электронный ресурс]. – Режим доступа: https://fipi.ru/ (дата обращения 22.03.2021).
Введение
В декабре 2020 года Федеральный институт педагогических измерений [2] опубликовал для общественного обсуждения перспективные модели измерительных материалов ЕГЭ на 2022 год, в том числе, по математике профильного уровня. Напомню, что в 2021 году ЕГЭ базового уровня отменен.
Особое волнение среди педагогов и старшеклассников вызывает тот факт, что в предложенной демоверсии три первых базовых задания, позволяющие выпускнику преодолеть минимальный порог на экзамене, заменили более сложными заданиями, в том числе, появилось задание по теме «Комплексные числа».
Мне стало интересно, и я решила сравнить демоверсии измерительных материалов 2021 года и перспективной, которая возможно будет внедрена в 2022 году, когда я буду выпускницей.
Мой вклад в решение проблемы: сравнение демоверсий измерительных материалов, разбор задания по теме «Комплексные числа».
Обзор литературы
Методическое пособие «Министерство сельского хозяйства Российской Федерации Департамент научно- технологической политики и образования Федеральное государственное бюджетное образовательное учреждение высшего образования «Волгоградский государственный аграрный университет». Комплексные числа. Практикум. 2020 год [1].
Цель
Сравнение демоверсий измерительных материалов 2021 года и перспективной модели на 2022 год по математике профильного уровня [2]. Разбор задания по теме «Комплексные числа» из демоверсии перспективной модели измерительных материалов ЕГЭ профильного уровня.
Методы исследования
1.Поисковый.
2. Анализ, синтез (отбор необходимой информации, обобщение)
3.Практический
Результаты исследования
Сейчас измерительные материалы ЕГЭ профильного уровня включают 19 заданий:
-часть 1 содержит 8 заданий базового уровня (задания 1–8);
-часть 2 содержит 9 заданий повышенного уровня (задания 9–17) и 2 задания высокого уровня сложности (задания 18, 19).
Что предлагается изменить?!
Убрать три базовых задания:
1 задание. – Простейшие текстовые задачи;
2 задание. – Чтение графиков и диаграмм;
3 задание. –Квадратная решетка.
Наряду с выше обозначенными изменениями происходит замена нумерации заданий:
№1. Простейшие уравнения;
№2. Начало теории вероятности;
№ 3. Функции, графики функций (новое);
Приведу пример задания №3 из демоверсии измерительных материалов перспективной модели ЕГЭ профильного уровня:
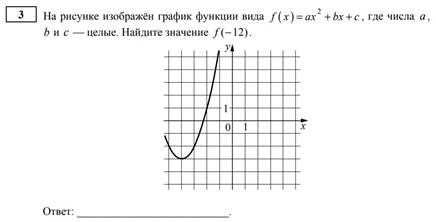
№4. Планиметрия;
№5. Вычисления и преобразования;
№6. Стереометрия;
№7. Производная и первообразная;
№8. Задачи с прикладным содержанием;
№9. Текстовые задачи;
№10. Вероятности повышенного уровня (новое);
№11. Комплексные числа (новое);
№12. Наибольшее и наименьшее значение функций;
№13. Уравнения;
№14. Стереометрическая задача;
№15. Неравенства;
№16. Финансовая математика;
№17. Планиметрия;
№18. Задача с параметром;
№19. Числа и их свойства;
Рассмотрим задание №11 по теме «Комплексные числа».
Для начала приведу основные теоретические сведения по теме «Комплексные числа».
Определение. Комплексным числом z называется упорядоченная пара чисел (а,b), над множеством которых по определенным правилам можно производить следующие операции: сложение , умножение, деление, возведение в степень результаты которых также являются комплексными числами [1, с.2].
Определение. Комплексное число — это упорядоченная пара вещественных, или символ z = а + ib, где i — мнимая единица: i2 = −1; а называется действительной, а b — мнимой частью z [1, с.2].
Понятие комплексного числа имеет геометрическое истолкование. Множество комплексных чисел является расширением множества действительных чисел за счет включения множества мнимых чисел. Комплексные числа включают в себя все множества чисел, которые изучались ранее. Так натуральные, целые, рациональные, иррациональные, действительные числа являются, вообще говоря, частными случаями комплексных чисел.
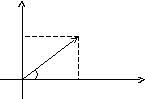
Если любое действительное число может быть геометрически представлено в виде точки на числовой прямой, то комплексное число представляется точкой на плоскости, (комплексной плоскости z) координатами которой будут соответственно действительная и мнимая части комплексного числа. При этом горизонтальная ось будет являться действительной числовой осью, а вертикальная — мнимой осью.
Таким образом, на оси ОХ располагаются действительные числа a, а на оси ОY – чисто мнимые-b [1, с.2].
Модулемкомплексного числа называется длина вектора, соответствующего этому числу:
Задание №11:
Про комплексное число z известно, что |z-4-7i|=|z+4-i|. Найдите наименьшее значение |z| [2].
z = а + ib, в свою очередь 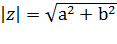
| а + ib-4-7i|=| а + ib+4-i|
Сгруппируем:
|(a-4) +i(b-7) |=|(a+4) +i(b-1) |
Видим, что внутри модуля комплексное число вида z = а + ib. Применим свойство 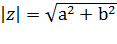
Применим формулы квадратов суммы и разности, упростим:
-16а-12b=-48
4а+3b=12
Выразим b: b=4-
Модулем является расстояниеот начала отсчёта до точки координатной прямой, соответствующейэтомучислу. Кратчайшее (наименьшее) расстояние – перпендикуляр.

Если b=0, то а = 3
Если а=0, то b=4
Рассмотрим прямоугольный треугольник с катетами 3 и 4, гипотенузой 5.
С одной стороны, площадь треугольника равна: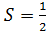
С другой стороны: 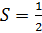
Отсюда следует: 6=0,5·h·5, h=2,4. Высота – перпендикуляр, наименьшее расстояние, которое соответствует |z|.
Ответ: 2,4
Заключение
Я сравнила демоверсии измерительных материалов 2021 года и перспективной модели на 2022 год по математике профильного уровня [2]. Разобрала задание по теме «Комплексные числа» из демоверсии перспективной модели измерительных материалов ЕГЭ профильного уровня. На мой взгляд, уже в следующем учебном году задания по теме «Комплексные числа» необходимо включать в рабочие программы уроков, курсов внеурочной деятельности. И тогда у выпускников не возникнет сложностей с решением этого задания на экзамене.
Библиографическая ссылка
Грудинина О.С. ПЕРСПЕКТИВНАЯ МОДЕЛЬ ЕГЭ ПО МАТЕМАТИКЕ. КОМПЛЕКСНЫЕ ЧИСЛА // Старт в науке. – 2021. – № 2.
;
URL: https://science-start.ru/ru/article/view?id=2027 (дата обращения: 11.03.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Версия для печати и копирования в MS Word
1
Изобразите на чертеже множество точек комплексной плоскости, для которых выполняется условие Среди чисел, удовлетворяющих этому равенству, найдите число с наименьшим модулем. Запишите найденное число в тригонометрической форме.
Загрузка решений доступна для зарегистрировавшихся пользователей
2
Среди комплексных чисел z, удовлетворяющих условию найдите число с наименьшим модулем.
Загрузка решений доступна для зарегистрировавшихся пользователей
3
Среди чисел z, таких, что найдите числа с наименьшим и наибольшим модулем.
Загрузка решений доступна для зарегистрировавшихся пользователей
4
Найдите наибольший модуль комплексного числа z, удовлетворяющего условию
Загрузка решений доступна для зарегистрировавшихся пользователей
5
Загрузка решений доступна для зарегистрировавшихся пользователей
6
Известно, что комплексные числа z и имеют одинаковый модуль. В каких пределах может изменяться значение этого модуля?
Загрузка решений доступна для зарегистрировавшихся пользователей
7
Загрузка решений доступна для зарегистрировавшихся пользователей
8
Множество точек комплексной плоскости определяется условием В каких пределах изменяется
Загрузка решений доступна для зарегистрировавшихся пользователей
9
Загрузка решений доступна для зарегистрировавшихся пользователей
10
Найдите такое мнимое число z, что сумма минимальна.
Загрузка решений доступна для зарегистрировавшихся пользователей
11
Из всех чисел z, удовлетворяющих условию найдите такие, что
принимает наименьшее значение.
Загрузка решений доступна для зарегистрировавшихся пользователей
12
Загрузка решений доступна для зарегистрировавшихся пользователей
Завершить тестирование, свериться с ответами, увидеть решения.
7
Лекция
Комплексные
числа.
Определение.
Комплексным
числом z
называется
выражение
,
где a
и b
– действительные числа, i
– мнимая единица, которая определяется
соотношением:
При
этом число a
называется действительной
частью числа
z
(a
= Re
z),
а b—
мнимой частью
(b
= Im
z).
Если
a
=Re
z
=0, то число
z
будет чисто
мнимым, если
b
= Im
z
= 0, то число
z
будет действительным.
Определение.
Числа
и
называются
комплексно
– сопряженными.
Определение.
Два комплексных числа
и
называются равными, если соответственно
равны их действительные и мнимые части:
Определение.
Комплексное число равно нулю, если
соответственно равны нулю действительная
и мнимая части.
Понятие
комплексного числа имеет геометрическое
истолкование. Множество комплексных
чисел является расширением множества
действительных чисел за счет включения
множества мнимых чисел. Комплексные
числа включают в себя все множества
чисел, которые изучались ранее. Так
натуральные, целые, рациональные,
иррациональные, действительные числа
являются, вообще говоря, частными
случаями комплексных чисел.
Если
любое действительное число может быть
геометрически представлено в виде точки
на числовой прямой, то комплексное число
представляется точкой на плоскости,
координатами которой будут соответственно
действительная и мнимая части комплексного
числа. При этом горизонтальная ось будет
являться действительной числовой осью,
а вертикальная — мнимой осью.
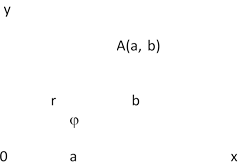
у
A(a,
b)
r b
0 a
x
Таким
образом, на оси Оx
располагаются действительные числа, а
на оси Оy
– чисто мнимые.
С
помощью подобного геометрического
представления можно представлять числа
в так называемой тригонометрической
форме.
Тригонометрическая
форма комплексного числа.
Из
геометрических соображений видно, что
.
Тогда комплексное число можно представить
в виде:
Такая
форма записи называется тригонометрической
формой записи комплексного числа.
При
этом величина r
называется модулем
комплексного
числа, а угол
— аргументом
комплексного
числа.
.
Из
геометрических соображений видно:
Очевидно,
что комплексно – сопряженные числа
имеют одинаковые модули и противоположные
аргументы.
Действия с
комплексными числами.
Основные
действия с комплексными числами вытекают
из действий с многочленами.
1)
Сложение и
вычитание.
2)
Умножение.
В
тригонометрической форме:
,
С
случае комплексно – сопряженных чисел:
3)
Деление.
В
тригонометрической форме:
4)
Возведение
в степень.
Из
операции умножения комплексных чисел
следует, что
В
общем случае получим:
,
где
n
– целое
положительное число.
Это
выражение называется формулой
Муавра. (Абрахам
де Муавр (1667 – 1754) – английский математик)
Формулу
Муавра можно использовать для нахождения
тригонометрических функций двойного,
тройного и т.д. углов.
Пример.
Найти формулы sin2
и cos2.
Рассмотрим
некоторое комплексное число
Тогда
с одной стороны
.
По
формуле Муавра:
Приравнивая,
получим
Т.к.
два комплексных числа равны, если равны
их действительные и мнимые части, то
Получили
известные формулы двойного угла.
5)
Извлечение
корня из комплексного числа.
Возводя
в степень, получим:
Отсюда:
Таким
образом, корень n
– ой степени из комплексного числа
имеет n
различных значений для k=0,1,…,n-1.
Показательная
форма комплексного числа.
Рассмотрим
показательную функцию
Можно
показать, что функция w
может быть записана в виде:
Данное
равенство называется уравнением
Эйлера. Вывод
этого уравнения будет рассмотрен
позднее.
Для
комплексных чисел будут справедливы
следующие свойства:
1)
2)
3)
где m
– целое число.
Если
в уравнении Эйлера показатель степени
принять за чисто мнимое число (х=0),
то получаем:
Для
комплексно – сопряженного числа
получаем:
Из
этих двух уравнений получаем:
Этими
формулами пользуются для нахождения
значений степеней тригонометрических
функций через функции кратных углов.
Если
представить комплексное число в
тригонометрической форме:
и
воспользуемся формулой Эйлера:
Полученное
равенство и есть показательная
форма комплексного числа.
Разложение
многочлена на множители.
Определение.
Функция вида f(x)
называется целой
рациональной
функцией от х.
Теорема
Безу.
(Этьенн Безу (1730 – 1783) – французский
математик)
При
делении многочлена f(x)
на разность x
– a
получается остаток, равный f(a).
Доказательство.
При делении многочлена f(x)
на разность x
– a
частным
будет многочлен f1(x)
степени на
единицу меньшей, чем f(x),
а остатком
– постоянное число R.
Переходя
к пределу при х
a,
получаем
f(a)
= R.
Следствие.
Если, а – корень многочлена, т.е. f(a)
= 0, то многочлен f(x)
делится на (х – а) без остатка.
Определение.
Если уравнение имеет вид Р(х)
= 0, где Р(х)
– многочлен степени n,
то это уравнение называется алгебраическим
уравнением степени n.
Теорема.
(Основная теорема алгебры) Всякая целая
рациональная функция f(x)
имеет, по крайней мере, один корень,
действительный или комплексный.
Теорема.
Всякий многочлен n
– ой степени разлагается на n
линейных множителей вида (x
– a)
и множитель, равный коэффициенту при
xn.
Теорема.
Если два многочлена тождественно равны
друг другу, то коэффициенты одного
многочлена равны соответствующим
коэффициентам другого.
Если среди корней
многочлена встречаются кратные корни,
то разложение на множители имеет вид:
ki
— кратность соответствующего корня.
Отсюда
следует, что любой
многочлен n
– ой степени имеет ровно n
корней (действительных или комплексных).
Это
свойство имеет большое значение для
решения алгебраических уравнений,
дифференциальных уравнений и играет
важную роль в анализе функций.
Рассмотрим
несколько примеров действий с комплексными
числами.
Пример.
Даны два комплексных числа
.
Требуется а) найти значение выражения
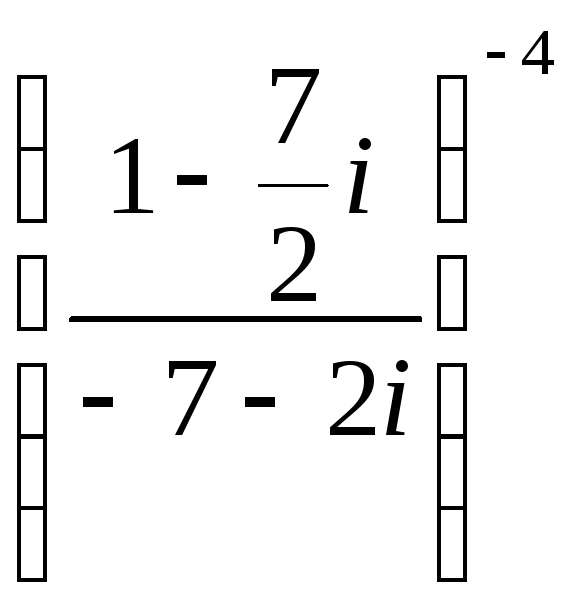
алгебраической форме, б) для числа
найти тригонометрическую форму, найти
z20,
найти корни уравнения
-
Очевидно,
справедливо следующее преобразование:
Далее
производим деление двух комплексных
чисел:
Получаем
значение заданного выражения: 16(-i)4
= 16i4
=16.
б)
Число
представим в виде
,
где
Тогда
.
Для
нахождения
воспльзуемся формулой Муавра.
Если
,
то
Подставляя
последовательно k=0,
k=1
и k=2
и производя вычисления получим 3 значения
корня кубического.