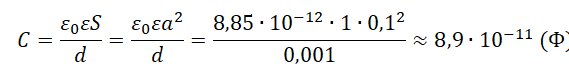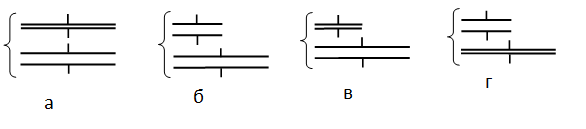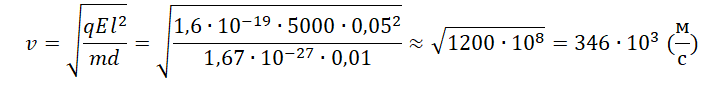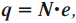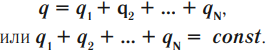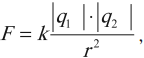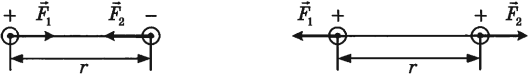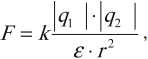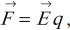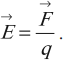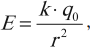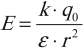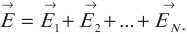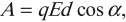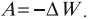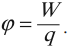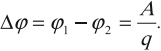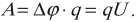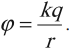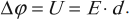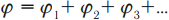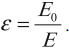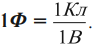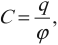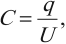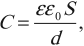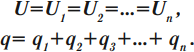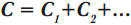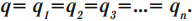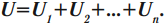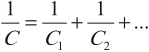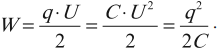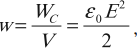Конденсаторы егэ теория - Помощь в подготовке к экзаменам и поступлению

Конденсатор. Энергия электрического поля

Темы кодификатора ЕГЭ: электрическая ёмкость, конденсатор, энергия электрического поля конденсатора.
Ёмкость уединённого проводника
Ёмкость плоского конденсатора
Энергия заряженного конденсатора
Энергия электрического поля

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: электрическая ёмкость, конденсатор, энергия электрического поля конденсатора.

Предыдущие две статьи были посвящены отдельному рассмотрению того, каким образом ведут себя в электрическом поле проводники и каким образом — диэлектрики. Сейчас нам понадобится объединить эти знания. Дело в том, что большое практическое значение имеет совместное использование проводников и диэлектриков в специальных устройствах — конденсаторах.

Но прежде введём понятие электрической ёмкости.

к оглавлению ▴

Ёмкость уединённого проводника

Предположим, что заряженный проводник расположен настолько далеко от всех остальных тел, что взаимодействие зарядов проводника с окружающими телами можно не принимать во внимание. В таком случае проводник называется уединённым.

Потенциал всех точек нашего проводника, как мы знаем, имеет одно и то же значение varphi , которое называется потенциалом проводника. Оказывается, что потенциал уединённого проводника прямо пропорционален его заряду. Коэффициент пропорциональности принято обозначать 1/C , так что

$varphi = frac{displaystyle q}{displaystyle C vphantom{1^a}}.$

Величина называется электрической ёмкостью проводника и равна отношению заряда проводника к его потенциалу:

$C = frac{displaystyle q}{displaystyle varphi }.$ (1)

Например, потенциал уединённого шара в вакууме равен:

$varphi = frac{displaystyle kq}{displaystyle R vphantom{1^a}}=frac{displaystyle q}{displaystyle 4 pi varepsilon_0R vphantom{1^a}},$

где — заряд шара, — его радиус. Отсюда ёмкость шара:

(2)

Если шар окружён средой-диэлектриком с диэлектрической проницаемостью , то его потенциал уменьшается в раз:

$varphi = frac{displaystyle q}{displaystyle 4 pi varepsilon_0 varepsilon R vphantom{1^a}}.$

Соответственно, ёмкость шара в раз увеличивается:

(3)

Увеличение ёмкости при наличии диэлектрика — важнейший факт. Мы ещё встретимся с ним при рассмотрении конденсаторов.

Из формул (2) и (3) мы видим, что ёмкость шара зависит только от его радиуса и диэлектрической проницаемости окружающей среды. То же самое будет и в общем случае: ёмкость уединённого проводника не зависит от его заряда; она определяется лишь размерами и формой проводника, а также диэлектрической проницаемостью среды, окружающей проводник. От вещества проводника ёмкость также не зависит.

В чём смысл понятия ёмкости? Ёмкость показывает, какой заряд нужно сообщить проводнику, чтобы увеличить его потенциал на В. Чем больше ёмкость — тем, соответственно, больший заряд требуется поместить для этого на проводник.

Единицей измерения ёмкости служит фарад (Ф). Из определения ёмкости (1) видно, что Ф = Кл/В.

Давайте ради интереса вычислим ёмкость земного шара (он является проводником!). Радиус считаем приближённо равным 6400 км.

$C = 4 pi varepsilon_0 R approx 4 cdot 3,14 cdot 8,85 cdot 10^{-12} cdot 6400 cdot 10^3 approx 712$ мкФ.

Как видите, Ф — это очень большая ёмкость.

Единица измерения ёмкости полезна ещё и тем, что позволяет сильно сэкономить на обозначении размерности диэлектрической постоянной . В самом деле, выразим из формулы (2):

$varepsilon_0 = frac{displaystyle C} {displaystyle 4 pi R vphantom{1^a}}.$

Следовательно, диэлектрическая постоянная может измеряться в Ф/м:

$varepsilon_0 = 8,85 cdot 10^{-12}$ Ф.

Так легче запомнить, не правда ли?

к оглавлению ▴

Ёмкость плоского конденсатора

Ёмкость уединённого проводника на практике используется редко. В обычных ситуациях проводники не являются уединёнными. Заряженный проводник взаимодействует с окружающими телами и наводит на них заряды, а потенциал поля этих индуцированных зарядов (по принципу суперпозиции!) изменяет потенциал самого проводника. В таком случае уже нельзя утверждать, что потенциал проводника будет прямо пропорционален его заряду, и понятие ёмкости проводника самого по себе фактически утрачивает смысл.

Можно, однако, создать систему заряженных проводников, которая даже при накоплении на них значительного заряда почти не взаимодействует с окружающими телами. Тогда мы сможем снова говорить о ёмкости — но на сей раз о ёмкости этой системы проводников.

Наиболее простым и важным примером такой системы является плоский конденсатор. Он состоит из двух параллельных металлических пластин (называемых обкладками), разделённых слоем диэлектрика. При этом расстояние между пластинами много меньше их собственных размеров.

Для начала рассмотрим воздушный конденсатор, у которого между обкладками находится воздух

Пусть заряды обкладок равны и . Именно так и бывает в реальных электрических схемах: заряды обкладок равны по модулю и противоположны по знаку. Величина — заряд положительной обкладки — называется зарядом конденсатора.

Пусть — площадь каждой обкладки. Найдём поле, создаваемое обкладками в окружающем пространстве.

Поскольку размеры обкладок велики по сравнению с расстоянием между ними, поле каждой обкладки вдали от её краёв можно считать однородным полем бесконечной заряженной плоскости:

$E_+ = E_-=frac{displaystyle sigma }{displaystyle 2 varepsilon_0 vphantom{1^a}}.$

Здесь E_+ — напряжённость поля положительной обкладки, E_- — напряженность поля отрицательной обкладки, sigma — поверхностная плотность зарядов на обкладке:

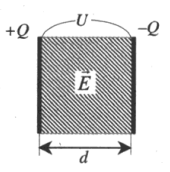
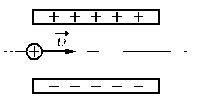
$sigma =frac{displaystyle q}{displaystyle S vphantom{1^a}}.$

На рис. 1 (слева) изображены векторы напряжённости поля каждой обкладки в трёх областях: слева от конденсатора, внутри конденсатора и справа от конденсатора.

Рис. 1. Электрическое поле плоского конденсатора

Согласно принципу суперпозиции, для результирующего поля vec{E} имеем:

$vec{E} = vec{E}_+ + vec{E}_-$

Нетрудно видеть, что слева и справа от конденсатора поле обращается в нуль (поля обкладок погашают друг друга):

Внутри конденсатора поле удваивается:

$E = E_+ + E_-= frac{displaystyle sigma }{displaystyle varepsilon_0},$

или

$E = frac{displaystyle q}{displaystyle varepsilon_0 S vphantom{1^a}}.$ (4)

Результирующее поле обкладок плоского конденсатора изображено на рис. 1 справа. Итак:

Внутри плоского конденсатора создаётся однородное электрическое поле, напряжённость которого находится по формуле (4). Снаружи конденсатора поле равно нулю, так что конденсатор не взаимодействует с окружающими телами.

Не будем забывать, однако, что данное утверждение выведено из предположения, будто обкладки являются бесконечными плоскостями. На самом деле их размеры конечны, и вблизи краёв обкладок возникают так называемые краевые эффекты: поле отличается от однородного и проникает в наружное пространство конденсатора. Но в большинстве ситуаций (и уж тем более в задачах ЕГЭ по физике) краевыми эффектами можно пренебречь и действовать так, словно утверждение, выделенное курсивом, является верным без всяких оговорок.

Пусть расстояние между обкладками конденсатора равно . Поскольку поле внутри конденсатора является однородным, разность потенциалов между обкладками равна произведению на (вспомните связь напряжения и напряжённости в однородном поле!):

$U=Ed=frac{displaystyle qd}{displaystyle varepsilon_0 S vphantom{1^a}}.$ (5)

Разность потенциалов между обкладками конденсатора, как видим, прямо пропорциональна заряду конденсатора. Данное утверждение аналогично утверждению «потенциал уединённого проводника прямо пропорционален заряду проводника», с которого и начался весь разговор о ёмкости. Продолжая эту аналогию, определяем ёмкость конденсатора как отношение заряда конденсатора к разности потенциалов между его обкладками:

$C=frac{displaystyle q}{displaystyle U vphantom{1^a}}.$ (6)

Ёмкость конденсатора показывает, какой заряд ему нужно сообщить, чтобы разность потенциалов между его обкладками увеличилась на В. Формула (6), таким образом, является модификацией формулы (1) для случая системы двух проводников — конденсатора.

Из формул (6) и (5) легко находим ёмкость плоского воздушного конденсатора:

$C=frac{displaystyle varepsilon_0 S}{displaystyle d vphantom{1^a}}.$ (7)

Она зависит только от геометрических характеристик конденсатора: площади обкладок и расстояния между ними.
Предположим теперь, что пространство между обкладками заполнено диэлектриком с диэлектрической проницаемостью . Как изменится ёмкость конденсатора?

Напряжённость поля внутри конденсатора уменьшится в раз, так что вместо формулы (4) теперь имеем:

$E=frac{displaystyle q}{displaystyle varepsilon_0 varepsilon S vphantom{1^a}}.$ (8)

Соответственно, напряжение на конденсаторе:

$U=Ed=frac{displaystyle qd}{displaystyle varepsilon_0 varepsilon S vphantom{1^a}}.$ (9)

Отсюда ёмкость плоского конденсатора с диэлектриком:

$C=frac{displaystyle varepsilon_0 varepsilon S}{displaystyle d vphantom{1^a}}.$ (10)

Она зависит от геометрических характеристик конденсатора (площади обкладок и расстояния между ними) и от диэлектрической проницаемости диэлектрика, заполняющего конденсатор.

Важное следствие формулы (10): заполнение конденсатора диэлектриком увеличивает его ёмкость.

к оглавлению ▴

Энергия заряженного конденсатора

Заряженный конденсатор обладает энергией. В этом можно убедиться на опыте. Если зарядить конденсатор и замкнуть его на лампочку, то (при условии, что ёмкость конденсатора достаточно велика) лампочка ненадолго загорится.

Следовательно, в заряженном конденсаторе запасена энергия, которая и выделяется при его разрядке. Нетрудно понять, что этой энергией является потенциальная энергия взаимодействия обкладок конденсатора — ведь обкладки, будучи заряжены разноимённо, притягиваются друг к другу.

Мы сейчас вычислим эту энергию, а затем увидим, что существует и более глубокое понимание происхождения энергии заряженного конденсатора.

Начнём с плоского воздушного конденсатора. Ответим на такой вопрос: какова сила притяжения его обкладок друг к другу? Величины используем те же: заряд конденсатора , площадь обкладок .

Возьмём на второй обкладке настолько маленькую площадку, что заряд q_0 этой площадки можно считать точечным. Данный заряд притягивается к первой обкладке с силой

где E_1 — напряжённость поля первой обкладки:

$E_1=frac{displaystyle sigma }{displaystyle 2 varepsilon _0 vphantom{1^a}}=frac{displaystyle q}{displaystyle 2varepsilon_0 S vphantom{1^a}}.$

Следовательно,

$F_0=frac{displaystyle q_0q}{displaystyle 2 varepsilon_0 S vphantom{1^a}}.$

Направлена эта сила параллельно линиям поля (т. е. перпендикулярно пластинам).

Результирующая сила притяжения второй обкладки к первой складывается из всех этих сил F_0 , с которыми притягиваются к первой обкладке всевозможные маленькие заряды q_0 второй обкладки. При этом суммировании постоянный множитель вынесется за скобку, а в скобке просуммируются все q_0 и дадут . В результате получим:

$F=frac{displaystyle q^2}{displaystyle 2 varepsilon_0 S vphantom{1^a}}.$ (11)

Предположим теперь, что расстояние между обкладками изменилось от начальной величины d_1 до конечной величины d_2 . Сила притяжения пластин совершает при этом работу:

Знак правильный: если пластины сближаются , то сила совершает положительную работу, так как пластины притягиваются друг к другу. Наоборот, если удалять пластины , то работа силы притяжения получается отрицательной, как и должно быть.

С учётом формул (11) и (7) имеем:

$A=frac{displaystyle q^2}{displaystyle 2 varepsilon_0 S vphantom{1^a}}left ( d_1-d_2 right )=frac{displaystyle q^2d_1}{displaystyle 2varepsilon_0 S vphantom{1^a}}-frac{displaystyle q^2d_2}{displaystyle 2varepsilon_0 S vphantom{1^a}}=frac{displaystyle q^2}{displaystyle 2C_1 vphantom{1^a}}-frac{displaystyle q^2}{displaystyle 2C_2 vphantom{1^a}}=W_1-W_2,$

где
$W_1=frac{displaystyle q^2}{displaystyle 2C_1 vphantom{1^a}},$
$W_2=frac{displaystyle q^2}{displaystyle 2C_2 vphantom{1^a}}$

Это можно переписать следующим образом:

где

$W=frac{displaystyle q^2}{displaystyle 2C vphantom{1^a}}.$ (12)

Работа потенциальной силы притяжения обкладок оказалась равна изменению со знаком минус величины . Это как раз и означает, что — потенциальная энергия взаимодействия обкладок, или энергия заряженного конденсатора.

Используя соотношение q = CU , из формулы (12) можно получить ещё две формулы для энергии конденсатора (убедитесь в этом самостоятельно!):

$W=frac{displaystyle qU}{displaystyle 2 vphantom{1^a}},$ (13)

$W=frac{displaystyle CU^2}{displaystyle 2 vphantom{1^a}}.$ (14)

Особенно полезными являются формулы (12) и (14).

Допустим теперь, что конденсатор заполнен диэлектриком с диэлектрической проницаемостью . Сила притяжения обкладок уменьшится в раз, и вместо (11) получим:

$F=frac{displaystyle q^2}{displaystyle 2 varepsilon_0 varepsilon S vphantom{1^a}}.$

При вычислении работы силы , как нетрудно видеть, величина войдёт в ёмкость , и формулы (12) — (14) останутся неизменными. Ёмкость конденсатора в них теперь будет выражаться по формуле (10).

Итак, формулы (12) — (14) универсальны: они справедливы как для воздушного конденсатора, так и для конденсатора с диэлектриком.

к оглавлению ▴

Энергия электрического поля

Мы обещали, что после вычисления энергии конденсатора дадим более глубокое истолкование происхождения этой энергии. Что ж, приступим.

Рассмотрим воздушный конденсатор и преобразуем формулу (14) для его энергии:

$W=frac{displaystyle CU^2}{displaystyle 2 vphantom{1^a}}=frac{displaystyle varepsilon_0 S}{displaystyle d vphantom{1^a}} cdot frac{displaystyle (Ed)^2}{displaystyle 2 vphantom{1^a}}=frac{displaystyle varepsilon_0 E^2}{displaystyle 2 vphantom{1^a}}Sd.$

Но Sd = V — объём конденсатора. Получаем:

$W=frac{displaystyle varepsilon_0 E^2}{displaystyle 2 vphantom{1^a}}V.$ (15)

Посмотрите внимательно на эту формулу. Она уже не содержит ничего, что являлось бы специфическим для конденсатора! Мы видим энергию электрического поля , сосредоточенного в некотором объёме .

Энергия конденсатора есть не что иное, как энергия заключённого внутри него электрического поля.

Итак, электрическое поле само по себе обладает энергией. Ничего удивительного для нас тут нет. Радиоволны, солнечный свет — это примеры распространения энергии, переносимой в пространстве электромагнитными волнами.

Величина — энергия единицы объёма поля — называется объёмной плотностью энергии. Из формулы (15) получим:

$omega =frac{displaystyle varepsilon_0 E^2}{displaystyle 2 vphantom{1^a}}.$ (16)

В этой формуле не осталось вообще никаких геометрических величин. Она даёт максимально чистую связь энергии электрического поля и его напряжённости.

Если конденсатор заполнен диэлектриком, то его ёмкость увеличивается в раз, и вместо формул (15) и (16) будем иметь:

$W =frac{displaystyle varepsilon_0 varepsilon E^2}{displaystyle 2 vphantom{1^a}}V.$ (17)

$omega =frac{displaystyle varepsilon_0 varepsilon E^2}{displaystyle 2 vphantom{1^a}}.$ (18)

Как видим, энергия электрического поля зависит ещё и от диэлектрической проницаемости среды, в которой поле находится.
Замечательно, что полученные формулы для энергии и плотности энергии выходят далеко за пределы электростатики: они справедливы не только для электростатического поля, но и для электрических полей, меняющихся во времени.

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Конденсатор. Энергия электрического поля» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

Проводники и диэлектрики в электростатическом поле. Диэлектрическая проницаемость вещества. Электроемкость. Конденсаторы. Поле плоского конденсатора. Электроемкость плоского конденсатора. Последовательное и параллельное соединение конденсаторов. Энергия заряженного конденсатора.

Проводники и диэлектрики в электростатическом поле

Вещества в природе можно разделить на проводники и диэлектрики.

Основная особенность — наличие свободных зарядов (электронов), которые участвуют в тепловом движении и могут перемещаться по всему объему проводника.

Типичные проводники — металлы.

Диэлектрическая проницаемость вещества

В отсутствие внешнего поля в любом элементе объема проводника отрицательный свободный заряд компенсируется положительным зарядом ионной решетки. В проводнике, внесенном в электрическое поле, происходит перераспределение свободных зарядов, в результате чего на поверхности проводника возникают нескомпенсированные положительные и отрицательные заряды. Этот процесс называют электростатической индукцией, а появившиеся на поверхности проводника заряды — индукционными зарядами.

В отличие от проводников, в диэлектриках (изоляторах) нет свободных электрических зарядов. Они состоят из нейтральных атомов или молекул. Заряженные частицы в нейтральном атоме связаны друг с другом и не могут перемещаться под действием электрического поля по всему объему диэлектрика.

Физическая величина, равная отношению модуля напряженности (vec{E}_0) внешнего электрического поля в вакууме к модулю напряженности (vec{E}) полного поля в однородном диэлектрике, называется диэлектрической проницаемостью вещества (varepsilon).

[varepsilon=dfrac{vec{E}_0}{vec{E}}]

Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда (q) одного из проводников к разности потенциалов (Delta varphi) между ними:

[fbox{$C=dfrac{q}{Delta varphi}$}]

Единицы измерения: (displaystyle [text{Ф}]) (фарад).

Величина электроемкости зависит от формы и размеров проводников и от свойств диэлектрика, разделяющего проводники.

Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами, а проводники, составляющие конденсатор, — обкладками.

Плоский конденсатор — система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика.

Электроемкость плоского конденсатора

Разность потенциалов (Delta varphi) между пластинами в однородном электрическом поле равна (Ed), где (d) — расстояние между пластинами. Из этих соотношений можно получить формулу для электроемкости плоского конденсатора:

[C=dfrac{q}{Delta varphi}=dfrac{sigma S}{Ed}=dfrac{varepsilon_0S}{d}]

Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в (varepsilon) раз:

[fbox{$C=dfrac{varepsilon_0varepsilon S}{d}$}]

Электрическое поле плоского конденсатора в основном локализовано между пластинами; однако, вблизи краев пластин и в окружающем пространстве также возникает сравнительно слабое электрическое поле, которое называют полем рассеяния. В целом ряде задач приближенно можно пренебрегать полем рассеяния и полагать, что электрическое поле плоского конденсатора целиком сосредоточено между его обкладками.

Последовательное и параллельное соединение конденсаторов

Для достижения нужной емкости или при напряжении, превышающем номинальное напряжение, конденсаторы, могут соединяться последовательно или параллельно. Любое же сложное соединение состоит из нескольких комбинаций последовательного и параллельного соединений.

Последовательное соединение конденсаторов

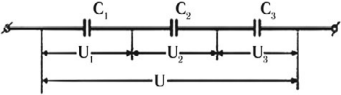
При последовательном соединении, конденсаторы подключены таким образом, что только первый и последний конденсатор подключены к источнику тока одной из своих пластин. Заряд одинаков на всех пластинах, но внешние заряжаются от источника, а внутренние образуются только за счет разделения зарядов ранее нейтрализовавших друг друга. При этом заряд конденсаторов в батарее меньше, чем, если бы каждый конденсатор подключался бы отдельно. Следовательно, и общая емкость батареи конденсаторов меньше.

Напряжение на данном участке цепи соотносятся следующим образом:

[fbox{$U=U_1+U_2$}]

Зная, что напряжение конденсатора можно представить через заряд и емкость, запишем:

[dfrac{q}{C}=dfrac{q}{C_1}+dfrac{q}{C_2}]

Сократив выражение на (Q), получим формулу:

[fbox{$dfrac{1}{C}=dfrac{1}{C_1}+dfrac{1}{C_2}$}]

Откуда эквивалентная емкость батареи конденсаторов соединенных последовательно:

[fbox{$C=dfrac{C_1C_2}{C_1+C_2}$}]
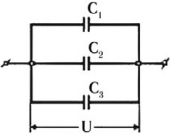
Параллельное соединение конденсаторов

При параллельном соединении конденсаторов напряжение на обкладках одинаковое, а заряды разные.

Величина общего заряда полученного конденсаторами, равна сумме зарядов всех параллельно подключенных конденсаторов. В случае батареи из двух конденсаторов:

[fbox{$q=q_1+q_2$}]

Так как заряд конденсатора

[q=CU]

А напряжения на каждом из конденсаторов равны, получаем следующее выражение для эквивалентной емкости двух параллельно соединенных конденсаторов

[CU=C_1U+C_2U]

[fbox{$C=C_1+C_2$}]
По сути, расчет общей емкости конденсаторов схож с расчетом общего сопротивления цепи в случае с последовательным или параллельным соединением, но при этом, зеркально противоположен.

Энергия заряженного конденсатора

Заряженный конденсатор обладает энергией. В этом можно убедиться на опыте. Если зарядить конденсатор и замкнуть его на лампочку, то (при условии того, что ёмкость конденсатора достаточно велика) лампочка ненадолго загорится. Следовательно, в заряженном конденсаторе запасена энергия, которая и выделяется при его разрядке.

Вычислим эту энергию: начнём с плоского воздушного конденсатора.

Ответим на такой вопрос: какова силу притяжения его обкладок друг к другу. Величины используем следующие: заряд конденсатора (q), площадь обкладок (S). Возьмём на второй обкладке настолько маленькую площадку, что заряд (q_0) этой площадки можно считать точечным. Данный заряд притягивается к первой обкладке с силой

[F_0 = q_0E_1,]

где (E_1) — напряжённость поля первой обкладки:

[E_1=dfrac{sigma}{2varepsilon_0}=dfrac{q}{2varepsilon_0S}]

Значит

[F_0=dfrac{qq_0}{2varepsilon_0S}]

Направлена эта сила параллельно линиям поля (т.е. перпендикулярно пластинам). Результирующая сила (F) притяжения второй обкладки к первой складывается из всех этих сил (F_0), с которыми притягиваются к первой обкладке всевозможные маленькие заряды (q_0) второй обкладки. При этом суммировании постоянный множитель (displaystyledfrac{q}{2varepsilon_0S}) вынесется за скобку, а в скобке просуммируются все (q_0) и дадут (q). В результате получим

[F=dfrac{q^2}{2varepsilon_0S}]

Предположим теперь, что расстояние между обкладками изменилось от начальной величины (d_1) до конечной величины (d_2). Сила притяжения пластин совершает при этом работу [A = F(d_1 -d_2)]

Знак правильный: если пластины сближаются ((d_2 < d_1)), то сила совершает положительную работу, так как пластины притягиваются друг к другу. Наоборот, если удалять пластины ((d_2 > d_1)), то работа силы притяжения получается отрицательной, как и должно быть.

Получаем

[A=dfrac{q^2}{2varepsilon_0S}(d_1-d_2)=dfrac{q^2d_1}{2varepsilon_0S}-dfrac{q^2d_2}{2varepsilon_0S}=dfrac{q^2}{2C_1}-dfrac{q^2}{2C_2}=W_1-W_2]

Это можно переписать следующим образом: [A =-(W_2-W_1) =-Delta W,]

где [fbox{$W=dfrac{q^2}{2C}$}, (1)]

Работа потенциальной силы (F) притяжения обкладок оказалась равна изменению со знаком минус величины (W). Это как раз и означает, что (W) — потенциальная энергия взаимодействия обкладок, или энергия заряженного конденсатора. Используя соотношение (q = CU), можно получить ещё две формулы для энергии конденсатора (проделать это самостоятельно).

[fbox{$W=dfrac{qU}{2}$}, (2)]

[fbox{$W=dfrac{CU^2}{2}$}, (3)]

Формулы (1)—(3) универсальны: они справедливы как для воздушного конденсатора, так и для конденсатора с диэлектриком.

Источник

ЕГЭ по физике 2023
/
Теория по физике
/
Теория по теме «Конденсатор. Соединение конденсаторов»
/

Источник

Определение

Конденсатор служит для накопления электрического заряда. Он представляет собой два проводника, разделенных слоем диэлектрика.

Плоский конденсатор — система двух разноименно заряженных пластин.

Разность потенциалов U (В) между обкладками конденсатора (напряжение между пластинами), определяется произведением напряженности создаваемого ими электрического поля на расстояние между ними:

U=Ed

Электроемкость конденсатора

Определение

Электрическая емкость — характеристика проводника, мера его способности накапливать электрический заряд.

Электроемкость обозначается как C. Единица измерения электрической емкости — Фарад (Ф).

Электроемкость конденсатора определяется формулой:

C=ε0εSd

ε0 — диэлектрическая постоянная, равная 8,85∙10^–12 Кл²/(Н∙м²);
ε — диэлектрическая проницаемость среды;
S (м²) — площадь каждой пластины.

Внимание! У воздушного конденсатора диэлектрическая проницаемость среды равна 1.

Связь между электроемкостью конденсатора, зарядом и напряжением определяется формулами:

C=QU=qU

Важно! Электроемкость конденсатора зависит только от площади его пластин, расстояния между ними и диэлектрической проницаемости среды. От заряда и напряжения эта величина не зависит.

Энергия конденсатора

Формула энергии конденсатора

Энергия конденсатора связана с его электроемкостью и вычисляется по следующим формулам:

Wэ=q22C=CU22

Подсказки к задачам

Конденсатор отключен от источника	q = q′
Конденсатор подключен к источнику	U = U′
Количество теплоты и энергия конденсатора	Q = ∆W_э

Пример №1. Вычислить электроемкость плоского воздушного конденсатора с квадратными пластинами со стороной 10 см, расположенными на расстоянии 1 мм друг от друга. Ответ округлить до десятых.

10 см = 0,1 м

1 мм = 0,001 м

Так как между обкладками конденсатора находится воздух, примем диэлектрическую проницаемость среды за единицу.

Площадь квадратной пластины равна квадрату ее стороны:

S = a²

Соединения конденсаторов

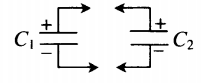
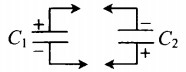
	Последовательное соединение	Параллельное соединение
Схема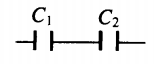
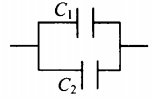Напряжение	U=U1+U2	U=U1=U2
Заряд	q=q1=q2	q=q1+q2
Электроемкость	1C=1C1+1C2	C=C1+C2

Подсказки к задачам

Два конденсатора, электроемкости которых C₁и C₂, заряжены до напряжения U₁и U₂. Найдите разность потенциалов после соединения конденсаторов одноименными полюсами.

Схема соединения конденсаторов одноименными полюсами:

Заряд системы после соединения:

q′
=C1U1+C2U2

Электрическая емкость системы:

C′
=C1+C2

Напряжение:

U′
=q′C′=C1U1+C2U2C1+C2

Два конденсатора, электроемкости которых C₁и C₂, заряжены до напряжения U₁и U₂. Найдите разность потенциалов после соединения конденсаторов разноименными полюсами.

Схема соединения конденсаторов разноименными полюсами:

Заряд системы после соединения:

q′
=C1U1−C2U2

Электрическая емкость системы:

C′
=C1+C2

Напряжение:

U′
=q′C′=C1U1−C2U2C1+C2

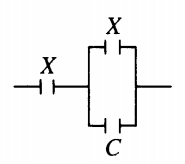
Пример №2. К конденсатору, электрическая емкость которого C = 16 пФ, подключают два одинаковых конденсатора емкостью X: один параллельно, а второй — последовательно (см. рисунок). Емкость образовавшейся батареи конденсаторов равна емкости C. Какова емкость X? Ответ округлите до десятых.

Электрическая емкость параллельного соединения равна:

Cпарал=X+C

Электроемкость последовательного соединения:

1Cпослед=1Cпарал+1X=1X+C+1X

Учтем, что суммарная электроемкость равна C:

1C=1X+C+1X

Преобразуем, умножим выражение на CX(X+C):

X(X+C)=CX+C(X+C)

Раскроем скобки:

X2+XC=CX+CX+C2

X2−CX−C2=0

Решив уравнение, получим: X = 25,9 пФ.

Разбор задач на тему «Заряженная частица в поле конденсатора»

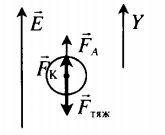
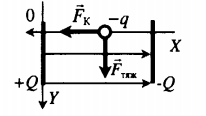
Шарик, находящийся в масле плотностью ρ, «висит» в поле плоского конденсатора. Плотность вещества шарика ρ_ш > ρ, его радиус r, расстояние между обкладками конденсатора d. Каков заряд шарика, если электрическое поле направлено вверх, а разность потенциалов между обкладками U?	Условие равновесия исходит из второго закона Ньютона: −Fтяж+−FK+−FA=0 ρ_ш > ρ, поэтому −Fтяж> −FA. В этом случае сила Кулона направлена вверх, а заряд шарика положительный. Схематически это можно отобразить так: Проекция второго закона Ньютона на ось ОУ: FK+FA=Fтяж Сила тяжести равна произведению объема на плотность шарика и на ускорение свободного падения: Fтяж=ρш43πr3g Архимедова сила равна произведению объема шарика на плотность масла и на ускорение свободного падения: FА=ρ43πr3g Сила Кулона: FK=qUd qUd+ρ43πr3g=ρш43πr3g q=(ρш43πr3g−ρ43πr3g)dU=4πr3gd(ρш−ρ)3U
Маленький шарик с зарядом q и массой m, подвешенный на невесомой нити с коэффициентом упругости k, находится между вертикальными пластинами воздушного конденсатора. Расстояние между обкладками конденсатора d. Какова разность потенциалов между обкладками конденсатора U, если удлинение нити ∆l?	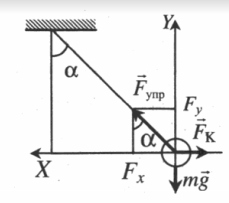Условие равновесия исходит из второго закона Ньютона: −Fтяж+−FK+−Fупр=0 Проекции на оси ОХ и ОУ соответственно: Fупрsinα−FK=0 Fупрcosα−mg=0 Отсюда: kΔlsinα=qUd kΔlcosα=mg Чтобы избавиться от угла α, возведем уравнения в квадрат и сложим их: (kΔl)2sin2α+(kΔl)2cos2α=(qUd)2+(mg)2 (kΔl)2(sin2α+cos2α)=(qUd)2+(mg)2 sin2α+cos2α=1 (kΔl)2=(qUd)2+(mg)2 U=dq√(kΔl)2−(mg)2
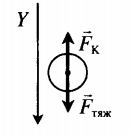
Пластины плоского конденсатора расположены горизонтально на расстоянии d друг от друга. Напряжение на пластинах конденсатора U. В пространстве между пластинами падает капля жидкости. Масса капли m, ее заряд q. Определите расстояние между пластинами. Влиянием воздуха на движение капли пренебречь.	Второй закон Ньютона в векторной форме: −Fтяж+−FK=0 Проекция на вертикальную ось: Fтяж−FK=0 Fтяж=mg FK=qUd mg=qUd d=qUmg
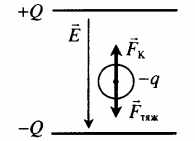
Между двумя параллельными горизонтально расположенными диэлектрическими пластинами создано однородное электрическое поле с напряженностью −E, направленное вертикально вниз. Между пластинами помещен шарик на расстоянии d от верхней пластины и b от нижней. Заряд шарика –q, масса m. Шарик освобождают, и он начинает двигаться. Через какой промежуток времени t шарик ударится об одну из пластин, если система находится в поле силы тяжести Земли?	Второй закон Ньютона в векторной форме: −Fтяж+−FK=m−a Согласно условию данной задачи, сила тяжести противоположно направлена силе Кулона. Построим рисунок: Если F_тяж> F_K, то шарик движется с ускорением вниз. Ускорение и перемещение в этом случае равны: a=mg−qEm s=b Если F_тяж< F_K, то шарик движется с ускорением верх. Ускорение и перемещение в этом случае равны: a=qE−mgm s=d Начальная скорость шарика равна нулю. Поэтому перемещение также равно: s=at22 Сделаем вычисления для случая F_тяж> F_K: at22=b mg−qEmt22=b t=√2bmmg−qE Выполняя вычисления для случая Сделаем вычисления для случая F_тяж< F_K, получим: t=√2bmqE−mg
Между двумя параллельными, вертикально расположенными диэлектрическими пластинами создано однородное электрическое поле, напряженность которого −E и направлена слева направо. Между пластинами помещен шарик на расстоянии b от левой пластины и d от правой. Заряд шарика –q, масса m. Шарик освобождают, и он начинает двигаться. Найдите смещение шарика по вертикали ∆h до удара об одну из пластин. Пластины имеют достаточно большой размер.	Второй закон Ньютона в векторной форме: −Fтяж+−FK=m−a Если сила Кулона направлена вправо, то s_x = d. Если сила Кулона направлена вправо, то s_x = b. Учитывая, что заряд меньше нуля, а вектор напряженности направлен вправо, делаем вывод, что кулоновская сила направлена влево. Из проекций второго закона Ньютона выразим проекции ускорения на оси ОХ и ОУ соответственно: ax=qEm ay=g Проекции перемещений на эти же оси: sx=axt22 sx=Δh=gt22 axt22=b Или: qEmt22=b Так как время движения шарика по вертикали и горизонтали одинаково: t2=2Δhg=2mbqE Δh=mbgqE

Задание EF17979

Введите ответ в поле ввода
Плоский конденсатор подключён к гальваническому элементу. Как изменятся при уменьшении зазора между обкладками конденсатора три величины: ёмкость конденсатора, величина заряда на его обкладках, разность потенциалов между ними?

Для каждой величины определите соответствующий характер изменения:

увеличится
уменьшится
не изменится

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения

1.Определить, от чего зависит емкость конденсатора, и как она изменится при уменьшении зазора между его обкладками.

2.Определить, от чего зависит величина заряда конденсатора, и как она изменится после уменьшения зазора между его обкладками.

3.Определить, от чего зависит разность потенциалов между обкладками конденсатора, и как она изменится при уменьшении зазора.

Решение

Емкость конденсатора определяется формулой:

C=ε0εSd

Следовательно, емкость имеет обратно пропорциональную зависимость от расстояния между обкладками. Если расстояние уменьшить, то емкость увеличится.

Вот как взаимосвязана электроемкость и заряд конденсатора:

C=qU

Мы выяснили, что электроемкость увеличивается. Следовательно, увеличится и заряд, так как они имеют прямо пропорциональную зависимость.

С учетом того, что плоский конденсатор подключен к гальваническому элементу, разность потенциалов никак не зависит от расстояния между обкладками. Поэтому величина U остается неизменной.

Ответ: 113

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18574

Воспользовавшись оборудованием, представленным на рис. 1, учитель собрал модель плоского конденсатора (рис. 2), зарядил нижнюю пластину положительным зарядом, а корпус электрометра заземлил. Соединённая с корпусом электрометра верхняя пластина конденсатора приобрела отрицательный заряд, равный по модулю заряду нижней пластины. После этого учитель сместил одну пластину относительно другой не изменяя расстояния между ними (рис. 3). Как изменились при этом показания электрометра (увеличились, уменьшились, остались прежними)? Ответ поясните, указав, какие явления и закономерности Вы использовали для объяснения. Показания электрометра в данном опыте прямо пропорциональны разности потенциалов между пластинами конденсатора.

Алгоритм решения

1.Проанализировать каждый этап эксперимента.

2.Установить, от чего зависит угол отклонения стрелки электрометра.

3.Выяснить, что поменяется при смещении одной пластины конденсатора относительно другой, и что при этом произойдет со стрелкой электрометра.

Решение

На первом рисунке стрелка и стержень электрометра, соединённые с нижней пластиной, но изолированные от корпуса, заряжаются положительно. Поэтому стрелка отклоняется на некоторый угол. В верхней пластине и металлическом корпусе электрометра происходит перераспределение свободных электронов таким образом, что верхняя пластина заряжается отрицательно.

На втором рисунке заряды пластин одинаковы по модулю и противоположны по знаку, пластины образуют конденсатор с ёмкостью:

C=ε0εSd

S — площадь перекрытия пластин, d — расстояние между ними, ε — диэлектрическая проницаемость диэлектрика между пластинами.

Характер изменения угла отклонения стрелки совпадает с изменением разности потенциалов между пластинами: при увеличении разности потенциалов увеличивается угол отклонения, при уменьшении разности потенциалов угол уменьшается.

На рисунке 3 площадь перекрытия пластин уменьшилась. Следовательно, уменьшилась электроемкость, которая имеет обратно пропорциональную зависимость от разности потенциалов:

C=qU

Заряд остается постоянным, поскольку система изолированная — заряду просто некуда деться. Поэтому с уменьшением электроемкость растет разность потенциалов. Поэтому показания электрометра увеличатся.

Ответ: Увеличатся

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18695

Ученик изучает свойства плоского конденсатора. Какую пару конденсаторов (см. рисунок) он должен выбрать, чтобы на опыте обнаружить зависимость ёмкости конденсатора от расстояния между его обкладками?

Алгоритм решения

Установить, какие величины в данном эксперименте должны быть переменными, а какие — постоянными.
Найти рисунок с парой конденсаторов, удовлетворяющий требованиям, выявленным в шаге 1.

Решение

Чтобы на опыте обнаружить зависимость ёмкости конденсатора от расстояния между его обкладками, нужно сохранить все величины постоянными, кроме самого расстояния. Поэтому площади обкладок должны быть одинаковыми, но расстояние между ними разными, как на рисунке 1.

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18703

Протон влетает в электрическое поле конденсатора параллельно его пластинам в точке, находящейся посередине между пластинами (см. рисунок). Найдите минимальную скорость υ, с которой протон должен влететь в конденсатор, чтобы затем вылететь из него. Длина пластин конденсатора 5 см, расстояние между пластинами 1 см, напряжённость электрического поля конденсатора 5000 В/м. Поле внутри конденсатора считать однородным, силой тяжести пренебречь.

Ответ записать в км/с, округлив до десятков.

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения величин в СИ.

2.Выполнить рисунок. Указать направление движения протона и силы, действующие на него.

3.Выяснить, при каком условии протон успеет вылететь из конденсатора.

4.Выполнить решение в общем виде.

5.Подставить известные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• Масса протона: m = 1,67∙10^–27 кг.

• Заряд протона: q = 1,6∙10^–19 Кл.

• Расстояние между обкладками конденсатора: d = 1 см.

• Длина пластин конденсатора: l = 5 см.

• Напряженность однородного поля внутри конденсатора: E = 5000 В/м.

1 см = 0,01 м

5 см = 0,05 м

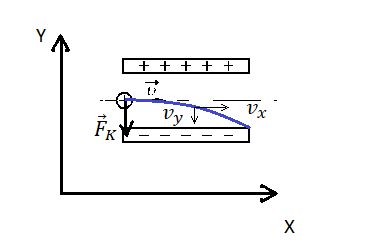
Сделаем рисунок:

Изначально протон обладает только горизонтальной скоростью v, равной v_x. Влетев в однородное электростатическое поле внутри конденсатора, протон обретает вертикальную компоненту скорости, которая растет за счет ускорения, придаваемого кулоновскими силами. Положительно заряженный протон притягивается нижней отрицательно зараженной пластиной конденсатора.

Чтобы протон вылетел из конденсатора, его горизонтальная компонента скорости должна быть достаточной для того, чтобы частица не притянулась к нижней пластине раньше. Время, которое понадобится протону для преодоления длины пластин конденсатора со скоростью v_x:

t=lvx=lv

Протон влетел в пространство между обкладками конденсатора на одинаковом расстоянии от них. Следовательно, прежде чем он упадет на нижнюю пластину, по оси OY он переместится на расстояние, равное 0,5d. Так как начальная компонента скорости равна нулю (мы пренебрегаем силой тяжести):

0,5d=at22

Протон вылетит из конденсатора, а не упадет на его пластину, если время горизонтального перемещения до конца пластин будет как минимум равно времени падения. Выразим время падения:

t=√da

Приравняем правые части уравнений времени и получим:

lv=√da

Отсюда скорость равна:

v=√al2d

Ускорение выразим из второго закона Ньютона:

FK=ma=qUd

a=qUmd

Но известно, что:

U=Ed

Поэтому:

a=qEdmd=qEm

Отсюда:

Минимальная скорость, с которой протон должен влететь в конденсатор, составляет 346∙10³ м/с. Округлим до десятков и переведем в км/с. Получим 350 км/с.

Ответ: 350

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алиса Никитина | Просмотров: 5.5k

Источник

Электрическое поле

Электродинамика – раздел физики, изучающий свойства и взаимодействия электрических зарядов, осуществляемые посредством электромагнитного поля.

Электростатикой называется раздел электродинамики, в котором рассматриваются свойства и взаимодействия неподвижных электрически заряженных тел или частиц.

Электромагнитное взаимодействие – это взаимодействие между электрически заряженными частицами или макротелами.

Точечный заряд – заряженное тело, размер которого мал по сравнению с расстоянием, на котором оценивается его действие.

Содержание

Электризация тел
Взаимодействие зарядов. Два вида зарядов
Закон сохранения электрического заряда
Закон Кулона
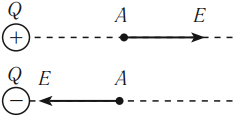
Действие электрического поля на электрические заряды
Напряженность электрического поля
Принцип суперпозиции электрических полей
Потенциальность электростатического поля
Потенциал электрического поля. Разность потенциалов
Проводники в электрическом поле
Диэлектрики в электрическом поле
Электрическая емкость. Конденсатор
Энергия электрического поля конденсатора
Основные формулы раздела «Электрическое поле»

Электризация тел

Электризация – процесс сообщения телу электрического заряда, т. е. нарушение его электрической нейтральности. Процесс электризации представляет собой перенесение с одного тела на другое электронов или ионов. В результате электризации тело получает возможность участвовать в электромагнитном взаимодействии.

Способы электризации:

трением, – например, электризация эбонитовой палочки при трении о мех. При тесном соприкосновении двух тел часть электронов переходит с одного тела на другое; в результате этого на поверхности у одного из тел создается недостаток электронов и тело получает положительный заряд, а у другого – избыток, и тело заряжается отрицательно. Величины зарядов тел одинаковы;
через влияние (электростатическая индукция) – тело остается электрически нейтральным, электрические заряды внутри него перераспределяются так, что разные части тела приобретают разные по знаку заряды;
при соприкосновении заряженного и незаряженного тела – заряд при этом распределяется между этими телами пропорционально их размерам. Если размеры тел одинаковы, то заряд распределяется между ними поровну;
при ударе;
под действием излучения – под действием света с поверхности проводника могут вырываться электроны, при этом проводник приобретает положительный заряд.

Взаимодействие зарядов. Два вида зарядов

Электрический заряд – скалярная физическая величина, характеризующая способность тела участвовать в электромагнитных взаимодействиях.

Обозначение – ( q ), единица измерения в СИ – кулон (Кл).

Существуют два вида электрических зарядов: положительный и отрицательный. Наименьший отрицательный заряд имеет электрон (–1,6·10^-19 Кл), наименьший положительный заряд (1,6·10^-19 Кл) – протон. Минимальный заряд, который может быть сообщен телу, равен заряду электрона (элементарный заряд). Если тело имеет избыточные (лишние) электроны, то тело заряжено отрицательно, если у тела недостаток электронов, то тело заряжено положительно.

Величина заряда тела будет равна

где ( N ) — число избыточных или недостающих электронов;
( e ) — элементарный заряд, равный 1,6·10^-19 Кл.

Важно!
Частица может не иметь заряда, но заряд без частицы не существует.

Электрические заряды взаимодействуют:

заряды одного знака отталкиваются:

заряды противоположных знаков притягиваются:

Прибор для обнаружения электрического заряда называется электроскоп. Основная часть прибора – металлический стержень, на котором закреплены два листочка металлической фольги, помещенные в стеклянный сосуд. При соприкосновении заряженного тела со стержнем электроскопа заряды распределяются между листочками фольги. Так как заряд листочков одинаков по знаку, они отталкиваются.

Для измерения зарядов можно использовать и электрометр. Основные части его – металлический стержень и стрелка, которая может вращаться вокруг горизонтальной оси. Стержень со стрелкой закреплен в пластмассовой втулке и помещен в металлический корпус, закрытый стеклянными крышками. При соприкосновении заряженного тела со стержнем стержень и стрелка получают электрические заряды одного знака. Стрелка поворачивается на некоторый угол.

Закон сохранения электрического заряда

Систему называют замкнутой (электрически изолированной), если в ней не происходит обмена зарядами с окружающей средой.

В любой замкнутой (электрически изолированной) системе сумма электрических зарядов остается постоянной при любых взаимодействиях внутри нее.

Полный электрический заряд ( (q) ) системы равен алгебраической сумме ее положительных и отрицательных зарядов ( (q_1, q_2 … q_N) ):

Важно!
В природе не возникают и не исчезают заряды одного знака: положительный и отрицательный заряды могут взаимно нейтрализовать друг друга, если они равны по модулю.

Закон Кулона

Закон Кулона был открыт экспериментально: в опытах с использованием крутильных весов измерялись силы взаимодействия заряженных шаров.

Закон Кулона формулируется так:
сила взаимодействия ( F ) двух точечных неподвижных электрических зарядов в вакууме прямо пропорциональна их модулям ( q_1 ) и ( q_2 ) и обратно пропорциональна квадрату расстояния между ними ( r ):

где ( k=frac{1}{4pivarepsilon_0}=9cdot10^9 ) (Н·м²)/Кл² – коэффициент пропорциональности,
( varepsilon_0=8.85cdot10^{-12} ) Кл²/(Н·м²) – электрическая постоянная.

Коэффициент ( k ) численно равен силе, с которой два точечных заряда величиной 1 Кл каждый взаимодействуют в вакууме на расстоянии 1 м.

Сила Кулона направлена вдоль прямой, соединяющей взаимодействующие заряды. Заряды взаимодействуют друг с другом с силами, равными по величине и противоположными по направлению.

Значение силы Кулона зависит от среды, в которой они находятся. В этом случае формула закона:

где ( varepsilon ) – диэлектрическая проницаемость среды.

Закон Кулона применим к взаимодействию

неподвижных точечных зарядов;
равномерно заряженных тел сферической формы.

В этом случае ( r ) – расстояние между центрами сферических поверхностей.

Важно!
Если заряженное тело протяженное, то его необходимо разбить на точечные заряды, рассчитать силы их попарного взаимодействия и найти равнодействующую этих сил (принцип суперпозиции).

Действие электрического поля на электрические заряды

Электрическое поле – это особая форма материи, существующая вокруг электрически заряженных тел.

Впервые понятие электрического поля было введено Фарадеем. Он объяснял взаимодействие зарядов следующим образом: каждый заряд создает вокруг себя электрическое поле, которое с некоторой силой действует на другой заряд.

Свойства электрического поля заключаются в том, что оно:

материально;
создается зарядом;
обнаруживается по действию на заряд;
непрерывно распределено в пространстве;
ослабевает с увеличением расстояния от заряда.

Действие заряженного тела на окружающие тела проявляется в виде сил притяжения и отталкивания, стремящихся поворачивать и перемещать эти тела по отношению к заряженному телу.

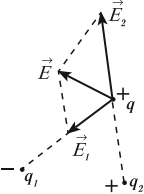
Силу, с которой электрическое поле действует на заряд, можно рассчитать по формуле:

где ( vec{E} ) – напряженность электрического поля, ( q ) – заряд.

Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов механики с учетом закона Кулона и вытекающих из него следствий.

Алгоритм решения задач о точечных зарядах и системах, сводящихся к ним:

сделать рисунок; указать силы, действующие на точечный заряд, помещенный в электрическое поле;
записать для заряда условие равновесия или основное уравнение динамики материальной точки;
выразить силы электрического взаимодействия через заряды и поля и подставить эти выражения в исходное уравнение;
если при взаимодействии заряженных тел между ними происходит перераспределение зарядов, к составленному уравнению добавить уравнение закона сохранения зарядов;
записать математически все вспомогательные условия;
решить полученную систему уравнений относительно неизвестной величины;
проверить решение

Напряженность электрического поля

Напряженность электрического поля ( vec{E} ) – векторная физическая величина, равная отношению силы ( F ), действующей на пробный точечный заряд, к величине этого заряда ( q ):

Обозначение – ( vec{E} ), единица измерения в СИ – Н/Кл или В/м.

Напряженность поля точечного заряда в вакууме вычисляется по формуле:

где ( k=frac{1}{4pivarepsilon_0}=9cdot10^9 ) (Н·м²)/Кл²,
( q_0 ) – заряд, создающий поле,
( r ) – расстояние от заряда, создающего поле, до данной точки.

Напряженность поля точечного заряда в среде вычисляется по формуле:

где ( varepsilon ) – диэлектрическая проницаемость среды.

Важно!
Напряженность электрического поля не зависит от величины пробного заряда, она определяется величиной заряда, создающего поле.

Направление вектора напряженности в данной точке совпадает с направлением силы, с которой поле действует на положительный пробный заряд, помещенный в эту точку.

Линией напряженности электрического поля называется линия, касательная к которой в каждой точке направлена вдоль вектора напряженности ( vec{E} ).

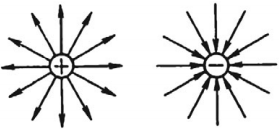
Линии напряженности электростатического поля начинаются на положительных электрических зарядах и заканчиваются на отрицательных электрических зарядах или уходят в бесконечность от положительного заряда и приходят из бесконечности к отрицательному заряду.

Распределение линий напряженности вокруг положительного и отрицательного точечных зарядов показано на рисунке.

Определяя направление вектора ( vec{E} ) в различных точках пространства, можно представить картину распределения линий напряженности электрического поля.

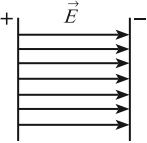
Поле, в котором напряженность одинакова по модулю и направлению в любой точке, называется однородным электрическим полем. Однородным можно считать электрическое поле между двумя разноименно заряженными металлическими пластинами. Линии напряженности в однородном электрическом поле параллельны друг другу.

Принцип суперпозиции электрических полей

Каждый электрический заряд создает в пространстве электрическое поле независимо от наличия других электрических зарядов.

Принцип суперпозиции электрических полей: напряженность электрического поля системы ( N ) зарядов равна векторной сумме напряженностей полей, создаваемых каждым из них в отдельности:

Электрические поля от разных источников существуют в одной точке пространства и действуют на заряд независимо друг от друга.

Потенциальность электростатического поля

Электрическое поле с напряженностью ( vec{E} ) при перемещении заряда ( q ) совершает работу. Работа ( A ) электростатического поля вычисляется по формуле:

где ( d ) – расстояние, на которое перемещается заряд,
( alpha ) – угол между векторами напряженности электрического поля и перемещения заряда.

Важно!
Эта формула применима для нахождения работы только в однородном электростатическом поле.

Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только начальным и конечным положением заряда.

Потенциальным называется поле, работа сил которого по перемещению заряда по замкнутой траектории равна нулю.

Важно!
Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю. Электростатическое поле является потенциальным.

Работа электростатического поля по перемещению заряда равна изменению потенциальной энергии, взятому с противоположным знаком. В электродинамике энергию принято обозначать буквой ( W ), так как буквой ( E ) обозначают напряженность поля:

Потенциальная энергия заряда ( q ), помещенного в электростатическое поле, пропорциональна величине этого заряда. Потенциальная энергия взаимодействия зарядов вычисляется относительно нулевого уровня (аналогично потенциальной энергии поля силы тяжести). Выбор нулевого уровня потенциальной энергии определяется исходя из соображений удобства при решении задачи.

Потенциал электрического поля. Разность потенциалов

Потенциал – скалярная физическая величина, равная отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда.

Обозначение – ( varphi ), единица измерения в СИ – вольт (В).

Потенциал ( varphi ) является энергетической характеристикой электростатического поля.

Разность потенциалов численно равна работе, которую совершает электрическая сила при перемещении единичного положительного заряда между двумя точками поля:

Обозначение – ( Deltavarphi ), единица измерения в СИ – вольт (В).

Иногда разность потенциалов обозначают буквой ( U ) и называют напряжением.

Важно!
Разность потенциалов ( Deltavarphi=varphi_1-varphi_2 ), а не изменение потенциала ( Deltavarphi=varphi_2-varphi_1 ). Тогда работа электростатического поля равна:

Важно!
Эта формула позволяет вычислить работу электростатических сил в любом поле.

В электростатике часто вычисляют потенциал относительно бесконечно удаленной точки. В этом случае потенциал поля в данной точке равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.

Потенциал поля точечного заряда ( q ) в точке, удаленной от него на расстояние ( r ), вычисляется по формуле:

Для наглядного представления электрического поля используют эквипотенциальные поверхности.

Важно!
Внутри проводящего шара потенциал всех точек внутри шара равен потенциалу поверхности шара и вычисляется по формуле потенциала точечного заряда (( r =R ), где ( R ) – радиус шара). Напряженность поля внутри шара равна нулю.

Эквипотенциальной поверхностью, или поверхностью равного потенциала, называется поверхность, во всех точках которой потенциал имеет одинаковое значение.

Свойства эквипотенциальных поверхностей

Вектор напряженности перпендикулярен эквипотенциальным поверхностям и направлен в сторону убывания потенциала.
Работа по перемещению заряда по эквипотенциальной поверхности равна нулю.

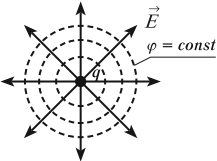
В случае однородного поля эквипотенциальные поверхности представляют собой систему параллельных плоскостей. Для точечного заряда эквипотенциальные поверхности представляют собой концентрические окружности.

Разность потенциалов и напряженность связаны формулой:

Из принципа суперпозиции полей следует принцип суперпозиции потенциалов:

Потенциал результирующего поля равен сумме потенциалов полей отдельных зарядов.

Важно!
Потенциалы складываются алгебраически, а напряженности – по правилу сложения векторов.

Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов сохранения, теоремы об изменении кинетической энергии заряда с учетом работы электростатических сил.

Алгоритм решения таких задач:

установить характер и особенности электростатических взаимодействий объектов системы;
ввести характеристики (силовые и энергетические) этих взаимодействий, сделать рисунок;
записать законы сохранения и движения для объектов;
выразить энергию электростатического взаимодействия через заряды, потенциалы, напряженности;
составить систему уравнений и решить ее относительно искомой величины;
проверить решение.

Проводники в электрическом поле

Проводниками называют вещества, в которых может происходить упорядоченное перемещение электрических зарядов, т. е. протекать электрический ток.

Проводниками являются металлы, водные растворы солей, кислот, ионизованные газы. В проводниках есть свободные электрические заряды. В металлах валентные электроны взаимодействующих друг с другом атомов становятся свободными.

Если металлический проводник поместить в электрическое поле, то под его действием свободные электроны проводника начнут перемещаться в направлении, противоположном направлению напряженности поля. В результате на одной поверхности проводника появится избыточный отрицательный заряд, а на противоположной – избыточный положительный заряд.

Эти заряды создают внутри проводника внутреннее электрическое поле, вектор напряженности которого направлен противоположно вектору напряженности внешнего поля. Под действием внешнего электростатического поля электроны проводимости в металлическом проводнике перераспределяются так, что напряженность результирующего поля в любой точке внутри проводника равна нулю. Электрические заряды расположены на поверхности проводника.

Важно!
Если внутри проводника есть полость, то напряженность в ней будет равна нулю независимо от того, какое поле имеется вне проводника и как заряжен проводник. Внутренняя полость в проводнике экранирована (защищена) от внешних электростатических полей. На этом основана электростатическая защита.

Явление перераспределения зарядов во внешнем электростатическом поле называется электростатической индукцией.

Заряды, разделенные электростатическим полем, взаимно компенсируют друг друга, если проводник удалить из поля. Если такой проводник разрезать, не вынося из поля, то его части будут иметь заряды разных знаков.

Важно!
Во всех точках поверхности проводника вектор напряженности направлен перпендикулярно к его поверхности. Поверхность проводника является эквипотенциальной (потенциалы всех точек поверхности проводника равны).

Диэлектрики в электрическом поле

Диэлектриками называют вещества, не проводящие электрический ток. Диэлектриками являются стекло, фарфор, резина, дистиллированная вода, газы.

В диэлектриках нет свободных зарядов, все заряды связаны. В молекуле диэлектрика суммарный отрицательный заряд электронов равен положительному заряду ядра. Различают полярные и неполярные диэлектрики.

В молекулах полярных диэлектриков ядра и электроны расположены так, что центры масс положительных и отрицательных зарядов не совпадают и находятся на некотором расстоянии друг от друга. То есть молекулы представляют собой диполи независимо от наличия внешнего электрического поля. В отсутствие внешнего электрического поля из-за теплового движения молекул диполи расположены хаотично, поэтому суммарная напряженность поля всех диполей диэлектрика равна нулю.

Если в отсутствие внешнего электрического поля центры масс положительных и отрицательных зарядов в молекуле диэлектрика совпадают, то он называется неполярным. Пример такого диэлектрика – молекула водорода. Если такой диэлектрик поместить во внешнее электрическое поле, то направления векторов сил, действующих на положительные и отрицательные заряды, будут противоположными. В результате молекула деформируется и превращается в диполь. При внесении диэлектрика в электрическое поле происходит его поляризация.

Поляризация диэлектрика – процесс смещения в противоположные стороны разноименных связанных зарядов, входящих в состав атомов и молекул вещества в электрическом поле.

Если диэлектрик неполярный, то в его молекулах происходит смещение положительных и отрицательных зарядов. На поверхности диэлектрика появятся поверхностные связанные заряды. Связанными эти заряды называют потому, что они не могут свободно перемещаться отдельно друг от друга.

Внутри диэлектрика суммарный заряд равен нулю, а на поверхностях заряды не скомпенсированы и создают внутри диэлектрика поле, вектор напряженности которого направлен противоположно вектору напряженности внешнего поля. Это значит, что внутри диэлектрика поле имеет меньшую напряженность, чем в вакууме.

Физическая величина, равная отношению модуля напряженности электрического поля в вакууме к модулю напряженности электрического поля в однородном диэлектрике, называется диэлектрической проницаемостью вещества:

В полярном диэлектрике во внешнем электрическом поле происходит поворот диполей, и они выстраиваются вдоль линий напряженности.

Если внесенный в электрическое поле диэлектрик разрезать, то его части будут электрически нейтральны.

Электрическая емкость. Конденсатор

Электрическая емкость (электроемкость) – скалярная физическая величина, характеризующая способность уединенного проводника удерживать электрический заряд.

Обозначение – ( C ), единица измерения в СИ – фарад (Ф).

Уединенный проводник – это проводник, удаленный от других проводников и заряженных тел.

Фарад – электроемкость такого уединенного проводника, потенциал которого изменяется на 1 В при сообщении ему заряда 1 Кл:

Формула для вычисления электроемкости:

где ( q ) – заряд проводника, ( varphi ) – его потенциал.

Электроемкость зависит от его линейных размеров и геометрической формы. Электроемкость не зависит от материала проводника и его агрегатного состояния. Электроемкость проводника прямо пропорциональна диэлектрической проницаемости среды, в которой он находится.

Конденсатор – это система из двух проводников, разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников.

Проводники называют обкладками конденсатора. Заряды обкладок конденсатора равны по величине и противоположны по знаку заряда. Электрическое поле сосредоточено между обкладками конденсатора. Конденсаторы используют для накопления электрических зарядов.

Электроемкость конденсатора рассчитывается по формуле:

где ( q ) – модуль заряда одной из обкладок,
( U ) – разность потенциалов между обкладками.

Электроемкость конденсатора зависит от линейных размеров и геометрической формы и расстояния между проводниками. Электроемкость конденсатора прямо пропорциональна диэлектрической проницаемости вещества между проводниками.

Плоский конденсатор представляет две параллельные пластины площадью ( S ), находящиеся на расстоянии ( d ) друг от друга.

Электроемкость плоского конденсатора:

где ( varepsilon ) – диэлектрическая проницаемость вещества между обкладками,
( varepsilon_0 ) – электрическая постоянная.

На электрической схеме конденсатор обозначается:

Виды конденсаторов:

по типу диэлектрика – воздушный, бумажный и т. д.;
по форме – плоский, цилиндрический, сферический;
по электроемкости – постоянной и переменной емкости.

Конденсаторы можно соединять между собой.

Параллельное соединение конденсаторов

При параллельном соединении конденсаторы соединяются одноименно заряженными обкладками. Напряжения конденсаторов равны:

Общая емкость:

Последовательное соединение конденсаторов

При последовательном соединении конденсаторов соединяют их разноименно заряженные обкладки.

Заряды конденсаторов при таком соединении равны:

Общее напряжение:

Величина, обратная общей емкости:

При таком соединении общая емкость всегда меньше емкостей отдельных конденсаторов.

Важно!
Если конденсатор подключен к источнику тока, то разность потенциалов между его обкладками не изменяется при изменении электроемкости и равна напряжению источника. Если конденсатор заряжен до некоторой разности потенциалов и отключен от источника тока, то его заряд не изменяется при изменении электроемкости.

Применение конденсаторов
Конденсаторы используются в радиоэлектронных приборах как накопители заряда, для сглаживания пульсаций в выпрямителях переменного тока.

Энергия электрического поля конденсатора

Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.

Электрическая энергия конденсатора сосредоточена в пространстве между обкладками конденсатора, то есть в электрическом поле, поэтому ее называют энергией электрического поля. Формулы для вычисления энергии электрического поля:

Так как напряженность электрического поля прямо пропорциональна напряжению, то энергия электрического поля конденсатора пропорциональна квадрату напряженности.

Плотность энергии электрического поля:

где ( V ) – объем пространства между обкладками конденсатора.

Плотность энергии не зависит от параметров конденсатора, а определяется только напряженностью электрического поля.

Основные формулы раздела «Электрическое поле»

Электрическое поле

2.9 (58.51%) 121 votes

Источник

Скачать материал

Сейчас обучается 460 человек из 72 регионов

Сейчас обучается 97 человек из 42 регионов

Сейчас обучается 35 человек из 20 регионов

Описание презентации по отдельным слайдам:

1 слайд

Подготовка учащихся к ЕГЭ . Задание №17. (ФИПИ). ФИЗИКА.
Материал подготовлен (для дистанционного обучения на платформе Zoom)
учителем физики
Масалида Г.А.
Задание 17 (Конденсатор)
4 слайд

1. Обкладки плоского воздушного конденсатора подсоединили к полюсам источника тока, а затем отсоединили от него. Что произойдет с зарядом на обкладках конденсатора, электроемкостью конденсатора и разностью потенциалов между его обкладками, если между обкладками вставить пластину из органического стекла? Краевыми эффектами пренебречь, считая обкладки бесконечно длинными. Диэлектрическая проницаемость воздуха равна 1, диэлектрическая проницаемость органического стекла равна 5.

А) Заряд конденсатора
Б) Электроемкость конденсатора
В) Разность потенциалов между обкладками
5 слайд

2. Между пластинами заряженного плоского конденсатора поместили диэлектрик с диэлектрической проницаемостью так, что он полностью заполнил объем между пластинами. Как изменились емкость конденсатора, заряд на пластинах и напряжение между ними, если конденсатор отключен от источника?

А) Заряд на пластинах
Б) Напряжение между пластинами
В) Емкость конденсатора

1) Уменьшится в раз
2) Останется неизменной
3) Увеличится в раз
6 слайд

3. Между пластинами заряженного плоского конденсатора поместили диэлектрик с диэлектрической проницаемостью так, что он полностью заполнил объем между пластинами. Как изменились емкость конденсатора, заряд на пластинах и напряжение между ними, если конденсатор подключен к источнику?

А) Заряд на пластинах
Б) Напряжение между пластинами
В) Емкость конденсатора

1) Уменьшится в раз
2) Останется неизменной
3) Увеличится в раз
7 слайд

4.В колебательном контуре, состоящем из конденсатора и катушки индуктивности, происходят свободные электромагнитные колебания. В момент, когда конденсатор разряжен, параллельно к нему подключают второй такой же конденсатор. Как после этого изменятся следующие физические величины: запасенная в контуре энергия, частота свободных электромагнитных колебаний, амплитуда напряжения между пластинами первого конденсатора?
А) Запасенная в контуре энергия
Б) Частота свободных электромагнитных колебаний
В) Амплитуда напряжения между пластинами первого конденсатора
8 слайд

A) Электрическая ёмкость конденсатора
Б) Модуль напряжённости электрического поля между пластинами конденсатора
B) Заряд конденсатора
5. Пластины плоского конденсатора, подключённого к батарее, сделаны из металлических листов в виде квадрата со стороной а. Квадратные пластины заменили на круглые диаметром а. При этом расстояние между пластинами увеличили, а батарею оставили прежней. Как в результате изменятся следующие физические величины: электрическая ёмкость конденсатора, модуль напряжённости электрического поля между пластинами конденсатора, заряд конденсатора?
9 слайд

A) Электрическая ёмкость конденсатора
Б) Модуль напряжённости электрического поля между пластинами конденсатора
В) Заряд конденсатора
6. Пластины плоского конденсатора, подключённого к батарее, сделаны из металлических листов в виде круга диаметром а. Круглые пластины заменили на квадратные со стороной а. При этом расстояние между пластинами уменьшили, а батарею оставили прежней. Как в результате изменятся следующие физические величины: электрическая ёмкость конденсатора, модуль напряжённости электрического поля между пластинами конденсатора, заряд конденсатора?
10 слайд

7.Плоский воздушный конденсатор ёмкостью 5,9 пФ имеет две металлические пластины. Пластины несут заряды 0,25 нКл и –0,25 нКл, между ними существует электрическое поле напряженностью 2,8 кВ/м.

А) модуль разности потенциалов между
пластинами конденсатора

Б) расстояние между пластинами конденсатора

1) 3,5 · 10-13
2) 7,1
3) 42
4) 1,5 · 10-2
11 слайд

.8. Плоский воздушный конденсатор подключён к аккумулятору. Не отключая конденсатор от аккумулятора, уменьшили расстояние между пластинами конденсатора. Как изменятся при этом ёмкость конденсатора и величина заряда на его обкладках?

Ёмкость
конденсатора
Величина заряда
конденсатора
12 слайд

9. Плоский конденсатор с воздушным зазором между обкладками подключён к источнику постоянного напряжения. Как изменятся величина заряда конденсатора и разность потенциалов между его обкладками при увеличении зазора между ними?

Величина заряда конденсатора
Разность потенциалов
между обкладками
конденсатора
13 слайд

10. На пластинах плоского воздушного конденсатора находятся электрические заряды +q и −q. Площадь каждой пластины S, расстояние между ними d. Конденсатор отключён от источника. Как изменятся следующие физические величины: модуль напряжённости поля в конденсаторе, ёмкость конденсатора, если увеличить расстояние между пластинами?
14 слайд

11. Плоский воздушный конденсатор с диэлектриком между пластинами подключён к аккумулятору. Не отключая конденсатор от аккумулятора, диэлектрик удаляют из конденсатора. Как изменятся при этом ёмкость конденсатора и разность потенциалов между его обкладками?

Ёмкость конденсатора
Разность потенциалов между
обкладками конденсатора
15 слайд

12. С помощью тонкой собирающей линзы с фокусным расстоянием 20 см получают изображение предмета, находящегося на расстоянии 30 см от линзы и расположенного перпендикулярно главной оптической оси. Как изменятся расстояние от линзы до изображения и размер изображения, если, не изменяя расположение предмета, заменить линзу на другую тонкую собирающую линзу с фокусным расстоянием 10 см?

Расстояние от линзы до
изображения
Размер изображения
17 слайд

13. С помощью тонкой собирающей линзы с фокусным расстоянием 20 см, получают изображение предмета, находящегося на расстоянии 30 см от линзы и расположенного перпендикулярно главной оптической оси. Как изменятся расстояние от линзы до изображения и размер изображения, если, не изменяя расположение предмета, заменить линзу на другую тонкую собирающую линзу с фокусным расстоянием 25 см?

Расстояние от линзы до
изображения
Размер изображения
19 слайд

15. Оптическая система состоит из тонкой собирающей линзы, имеющей фокусное расстояние F. На расстоянии a от линзы находится точечный источник света S, удалённый от главной оптической оси OO’ линзы на расстояние b. Вплотную к этой линзе ставят точно такую же вторую линзу так, что главные оптические оси линз совпадают. Определите, как в результате этого изменятся следующие физические величины: фокусное расстояние оптической системы и расстояние от изображения источника до главной оптической оси.
21 слайд

16. Оптическая система состоит из тонкой собирающей линзы, имеющей фокусное расстояние F. На расстоянии a от линзы находится точечный источник света S, удалённый от главной оптической оси OO’ линзы на расстояние b. Вплотную к этой линзе ставят точно такую же вторую линзу так, что главные оптические оси линз совпадают. Определите, как в результате этого изменятся следующие физические величины: расстояние от линзы до изображения источника и оптическая сила системы.

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 153 941 материал в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Материал подходит для УМК

«Физика (базовый уровень)», Мякишев Г.Я., Буховцев Б.Б., Чаругин В.М. / Под ред. Парфентьевой Н.А.

Тема

§ 33. Конденсатор в цепи переменного тока

Больше материалов по этой теме

Другие материалы

26.05.2021
419
32

26.05.2021
141
3

Презентация Подготовка к ЕГЭ

Учебник: «Физика (базовый уровень)», Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. / Под ред. Парфентьевой Н.А.
Тема: § 14. Движение с постоянным ускорением

26.05.2021
467
2

26.05.2021
4379
145

26.05.2021
468
57

26.05.2021
175
1

Вам будут интересны эти курсы:

Курс повышения квалификации «Информационные технологии в деятельности учителя физики»
Курс профессиональной переподготовки «Клиническая психология: организация реабилитационной работы в социальной сфере»
Курс повышения квалификации «Этика делового общения»
Курс повышения квалификации «Маркетинг в организации как средство привлечения новых клиентов»
Курс повышения квалификации «Использование активных методов обучения в вузе в условиях реализации ФГОС»
Курс повышения квалификации «Организация маркетинга в туризме»
Курс повышения квалификации «ЕГЭ по физике: методика решения задач»
Курс повышения квалификации «Мировая экономика и международные экономические отношения»
Курс профессиональной переподготовки «Риск-менеджмент организации: организация эффективной работы системы управления рисками»
Курс профессиональной переподготовки «Организация деятельности специалиста оценщика-эксперта по оценке имущества»
Курс профессиональной переподготовки «Теория и методика музейного дела и охраны исторических памятников»
Курс профессиональной переподготовки «Стратегическое управление деятельностью по дистанционному информационно-справочному обслуживанию»

Источник

Конденсаторы: сила притяжения пластин, напряжения, эквивалентные емкости.

В этой статье рассматриваются задачи на определение напряжения на конденсаторе и в схеме с конденсаторами, между точками этих схем. Также мы рассмотрим задачи, связанные с силой притяжения пластин. В конце будет рассмотрен сложный (для запоминания) перерасчет звезды из конденсаторов в треугольник.

Задача 1. В плоский конденсатор, подключенный к источнику с постоянной ЭДС, помещена плоская пластина, имеющая заряд . Расстояние от пластины до обкладок и . Площадь пластины . Определите силу, действующую на пластину со стороны электрического поля.

К задаче 1

Запишем силу как произведение заряда пластины на напряженность поля:

Обозначим потенциал пластины , примем потенциал левой пластины конденсатора равным нулю, а правой — .

Составим систему уравнений. Запишем разности потенциалов между левой обкладкой и пластиной и между правой и пластиной, учтем наложение поля конденсатора на поле, создаваемое пластиной:

Сложим уравнения:

Откуда

Тогда сила равна

Задача 2.

Когда к батарее, изображенной на рисунке, подвели напряжение , заряд среднего конденсатора оказался равным нулю. Какова емкость Сх?

К задаче 2

Так как заряд равен нулю, то . Следовательно, потенциалы точек и — равны. А это означает, что разности потенциалов и . Также известно, что при последовательном соединении заряд на всех конденсаторах одинаков, поэтому

Тогда отношение напряжений равно отношению емкостей:

И во второй ветви будет соблюдаться то же отношение:

Откуда .

Задача 3.

В цепи известны емкости и ЭДС . Кроме того, известно, что заряд первого конденсатора равен . Найдите ЭДС второго элемента.

К задаче 3

Зная заряд первого конденсатора и его емкость, найдем напряжение между точками и :

Напряжение это мы еще можем записать для каждой ветви так:

Или:

Так как обкладки конденсаторов соединены в точке , то алгебраическая сумма зарядов на этих обкладках равна нулю:

Домножим на емкость и разделим на :

Тогда

Определяем ЭДС:

Ответ:

Задача 4.

Найдите разность потенциалов между точками и .

К задаче 4

Запишем напряжение между точками и с двух сторон, и в прямом, и в переносном смысле:

Напряжение на параллельно включенных конденсаторах и равно:

Так как конденсаторы соединены в одной точке – точке , то алгебраическая сумма зарядов на этих обкладках равна 0:

Напряжение на тогда

Напряжение на :

Тогда заряд равен:

Тогда

Подставим найденный заряд:

Ответ:

Задача 5.

Найдите разность потенциалов между точками и в этой цепи.

К задаче 5

Запишем напряжение между точками и :

Для точки :

Где — напряжение на .

Отсюда получим, что

Для точки :

Где — напряжение на .

Отсюда получим, что

Тогда для получим:

Ответ:

Задача 6.

Найдите разность потенциалов между точками и в этой цепи.

К задаче 6

Запишем уравнение Кирхгофа (по 2-му закону) для обоих контуров (справа и слева):

Вычтем из первого второе:

Так как конденсаторы соединены последовательно, то заряды на них равны:

Тогда :

Или:

Подставим (2) в (1):

Подставим (3) в (1):

Наконец,

Можно было также воспользоваться (4) и найти .

Ответ:

Задача 7.

Найдите силу притяжения между пластинами плоского конденсатора в схеме, изображенной на рисунке, если , , , , а расстояние между пластинами конденсатора равно .

К задаче 7

Конденсаторы в схеме, по сути, соединены последовательно, поэтому их заряды одинаковы. Напряжение на первом тогда

А на втором

Сумма напряжений в контуре по второму закону равна сумме ЭДС:

Сила притяжения пластин будет равна:

Ответ:

Задача 8.

В схеме, изображенной на рисунке, сила притяжения между пластинами плоского конденсатора равна . Найдите расстояние между пластинами этого конденсатора, если ,, , .

К задаче 8

Напряжение на первом конденсаторе тогда

А на втором

Сумма напряжений в контуре по второму закону равна сумме ЭДС:

Сила притяжения пластин будет равна:

Откуда

Ответ:

Задача 9.

Найдите емкость батареи. Емкость каждого конденсатора равна .

К задаче 9

Чтобы было проще решить эту задачу, применим перерасчет (переход) от треугольника емкостей к звезде и обратно. Нам понадобится как раз обратный: от звезды к треугольнику. Выполняются оба перехода так: