Вероятностью события $А$ называется отношение числа благоприятных для $А$ исходов к числу всех
равновозможных исходов
$P(A)={m}/{n}$, где $n$ – общее количество возможных исходов, а $m$ – количество исходов, благоприятствующих событию
$А$.
Вероятность события — это число из отрезка $[0; 1]$
В фирме такси в наличии $50$ легковых автомобилей. $35$ из них чёрные, остальные — жёлтые.
Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета.
Решение:
Найдем количество желтых автомобилей:
$50-35=15$
Всего имеется $50$ автомобилей, то есть на вызов приедет одна из пятидесяти. Желтых автомобилей $15$,
следовательно, вероятность приезда именно желтого автомобиля равна ${15}/{50}={3}/{10}=0,3$
Ответ:$0,3$
Противоположные события
Два события называются противоположными, если в данном испытании они несовместимы и одно из них обязательно
происходит. Вероятности противоположных событий в сумме дают 1.Событие, противоположное событию $А$, записывают
${(А)}↖{-}$.
$Р(А)+Р{(А)}↖{-}=1$
Независимые события
Два события $А$ и $В$ называются независимыми, если вероятность появления каждого из них не зависит от того,
появилось другое событие или нет. В противном случае события называются зависимыми.
Вероятность произведения двух независимых событий $A$ и $B$ равна произведению этих
вероятностей:
$Р(А·В)=Р(А)·Р(В)$
Иван Иванович купил два различных лотерейных билета. Вероятность того, что выиграет первый
лотерейный билет, равна $0,15$. Вероятность того, что выиграет второй лотерейный билет, равна $0,12$. Иван Иванович
участвует в обоих розыгрышах. Считая, что розыгрыши проводятся независимо друг от друга, найдите вероятность того,
что Иван Иванович выиграет в обоих розыгрышах.
Решения:
Вероятность $Р(А)$ — выиграет первый билет.
Вероятность $Р(В)$ — выиграет второй билет.
События $А$ и $В$ – это независимые события. То есть, чтобы найти вероятность того, что они произойдут оба
события, нужно найти произведение вероятностей
$Р(А·В)=Р(А)·Р(В)$
$Р=0,15·0,12=0,018$
Ответ: $0,018$
Несовместные события
Два события $А$ и $В$ называют несовместными, если отсутствуют исходы, благоприятствующие одновременно как событию
$А$, так и событию $В$. (События, которые не могут произойти одновременно)
Вероятность суммы двух несовместных событий $A$ и $B$ равна сумме вероятностей этих
событий:
$Р(А+В)=Р(А)+Р(В)$
На экзамене по алгебре школьнику достается один вопрос их всех экзаменационных. Вероятность
того, что это вопрос на тему «Квадратные уравнения», равна $0,3$. Вероятность того, что это вопрос на тему
«Иррациональные уравнения», равна $0,18$. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите
вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Решение:
Данные события называются несовместные, так как школьнику достанется вопрос ЛИБО по теме «Квадратные уравнения»,
ЛИБО по теме «Иррациональные уравнения». Одновременно темы не могут попасться. Вероятность суммы двух
несовместных событий $A$ и $B$ равна сумме вероятностей этих событий:
$Р(А+В)=Р(А)+Р(В)$
$Р = 0,3+0,18=0,48$
Ответ: $0,48$
Совместные события
Два события называются совместными, если появление одного из них не исключает появление другого в одном и том же
испытании. В противном случае события называются несовместными.
Вероятность суммы двух совместных событий $A$ и $B$ равна сумме вероятностей этих событий минус
вероятность их произведения:
$Р(А+В)=Р(А)+Р(В)-Р(А·В)$
В холле кинотеатра два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится
кофе, равна $0,6$. Вероятность того, что кофе закончится в обоих автоматах, равна $0,32$. Найдите вероятность того,
что к концу дня кофе закончится хотя бы в одном из автоматов.
Решение:
Обозначим события, пусть:
$А$ = кофе закончится в первом автомате,
$В$ = кофе закончится во втором автомате.
Тогда,
$A·B =$ кофе закончится в обоих автоматах,
$A + B =$ кофе закончится хотя бы в одном автомате.
По условию, $P(A) = P(B) = 0,6; P(A·B) = 0,32$.
События $A$ и $B$ совместные, вероятность суммы двух совместных событий равна сумме вероятностей этих событий,
уменьшенной на вероятность их произведения:
$P(A + B) = P(A) + P(B) − P(A·B) = 0,6 + 0,6 − 0,32 = 0,88$
Ответ: $0,88$
Пример:
В одном
ящике 8 красных и 2 белых шара, в другом- 4 красных и 5 белых шаров. Из
каждого ящика наугад достают по одному шару. Найти вероятность, что оба шара
будут белыми.
Решение:
А-событие
того, что из первого ящика достали белый шар.
В-
событие того, что из второго ящика достали белый шар.
Аи В-
независимые события. Значит Р(А) =, Р(В) =
Р(А·В)=Р(А) · Р(В)=
·
Пример:
В ящике
перемешаны 8 красных и 4 белых шара. Из ящика наугад достают 2 шара. Найти
вероятность, что оба шара будут белыми.
Решение:
А-событие
того, что первый шар достали белый .
В-
событие того, что второй шар достали белый .
Аи В-
зависимые события. Значит Р(А) =, Р(В/А) =
Р(А·В)=Р(А)
· Р(В/А)= ·
Пример:
Бросают
игральный кубик. Найти вероятность того, что выпадет четное число очков или
число очков, кратное четырем.
Решение:
А-событие
, что выпадает четное число очков.
В-
событие того, что выпадает число очков, кратное четырем.
События
совместные, т.к. при выпадении «4» реализуются оба события. Значит
Р(А) =, Р(В) =
Р(А+В)
=Р(А)+Р(В)- Р(А·В) = +
—
·
Пример:
Найти
вероятность того, что при одном бросании игрального кубика выпадет 2 очка
или 3 очка.
Решение:
А-событие,
что выпадает 2 очка.
В-
событие, что выпадет 3 очка.
События
несовместные, т.к. выпадение 2 очков исключает выпадение или 3 очков.
Значит
Р(А) =, Р(В) =
Р(А+В)
=Р(А)+Р(В) = +
Задание 3. Теория вероятностей на ЕГЭ по математике.
Мы начнем с простых задач и основных понятий теории вероятностей.
Случайным называется событие, которое нельзя точно предсказать заранее. Оно может либо произойти, либо нет.
Вы выиграли в лотерею — случайное событие. Пригласили друзей отпраздновать выигрыш, а они по дороге к вам застряли в лифте — тоже случайное событие. Правда, мастер оказался поблизости и освободил всю компанию через десять минут — и это тоже можно считать счастливой случайностью…
Наша жизнь полна случайных событий. О каждом из них можно сказать, что оно произойдет с некоторой вероятностью. Скорее всего, вы интуитивно знакомы с этим понятием. Теперь мы дадим математическое определение вероятности.
Начнем с самого простого примера. Вы бросаете монетку. Орел или решка?
Такое действие, которое может привести к одному из нескольких результатов, в теории вероятностей называют испытанием.
Орел и решка — два возможных исхода испытания.
Орел выпадет в одном случае из двух возможных. Говорят, что вероятность того, что монетка упадет орлом, равна .
Бросим игральную кость. У кубика шесть граней, поэтому возможных исходов тоже шесть.
Например, вы загадали, что выпадет три очка. Это один исход из шести возможных. В теории вероятностей он будет называться благоприятным исходом.
Вероятность выпадения тройки равна (один благоприятный исход из шести возможных).
Вероятность четверки — тоже .
А вот вероятность появления семерки равна нулю. Ведь грани с семью точками на кубике нет.
Вероятность события равна отношению числа благоприятных исходов к общему числу исходов.
Очевидно, что вероятность не может быть больше единицы.
Вот другой пример. В пакете яблок, из них
— красные, остальные — зеленые. Ни формой, ни размером яблоки не отличаются. Вы запускаете в пакет руку и наугад вынимаете яблоко. Вероятность вытащить красное яблоко равна
, а зеленое —
.
Вероятность достать красное или зеленое яблоко равна .
БЕСПЛАТНЫЙ МИНИ-КУРС ПО ТЕОРВЕРУ
Определение вероятности. Простые задачи из вариантов ЕГЭ.
Разберем задачи по теории вероятностей, входящие в сборники для подготовки к ЕГЭ.
В фирме такси в данный момент свободно
машин:
красных,
желтых и
зеленых. По вызову выехала одна из машин, случайно оказавшихся ближе всего к заказчице. Найдите вероятность того, что к ней приедет желтое такси.
Всего имеется машин, то есть к заказчице приедет одна из пятнадцати. Желтых — девять, и значит, вероятность приезда именно желтой машины равна
, то есть
.
В сборнике билетов по биологии всего
билетов, в двух из них встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет. Найдите вероятность того, что в этом билете не будет вопроса о грибах.
Очевидно, вероятность вытащить билет без вопроса о грибах равна , то есть
.
Родительский комитет закупил
пазлов для подарков детям на окончание учебного года, из них
с картинами известных художников и
с изображениями животных. Подарки распределяются случайным образом. Найдите вероятность того, что Вовочке достанется пазл с животным.
Задача решается аналогично.
Ответ: .
В чемпионате по гимнастике участвуют
спортсменок:
— из России,
— из США, остальные — из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая последней, окажется из Китая.
Давайте представим, что все спортсменки одновременно подошли к шляпе и вытянули из нее бумажки с номерами. Кому-то из них достанется двадцатый номер. Вероятность того, что его вытянет китайская спортсменка, равен (поскольку из Китая —
спортсменок). Ответ:
.
Ученика попросили назвать число от
до
. Какова вероятность того, что он назовет число кратное пяти?
Каждое пятое число из данного множества делится на . Значит, вероятность равна
.
Брошена игральная кость. Найдите вероятность того, что выпадет нечетное число очков.
— нечетные числа;
— четные. Вероятность нечетного числа очков равна
.
Ответ: .
Монета брошена три раза. Какова вероятность двух «орлов» и одной «решки»?
Заметим, что задачу можно сформулировать по-другому: бросили три монеты одновременно. На решение это не повлияет.
Как вы думаете, сколько здесь возможных исходов?
Бросаем монету. У этого действия два возможных исхода: орел и решка.
Две монеты — уже четыре исхода:
| орел | орел |
| орел | решка |
| решка | орел |
| решка | решка |
Три монеты? Правильно, исходов, так как
.
Вот они:
| орел | орел | орел |
| орел | орел | решка |
| орел | решка | орел |
| решка | орел | орел |
| орел | решка | решка |
| решка | орел | решка |
| решка | решка | орел |
| решка | решка | решка |
Два орла и одна решка выпадают в трех случаях из восьми.
Ответ: .
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет
очков. Результат округлите до сотых.
Бросаем первую кость — шесть исходов. И для каждого из них возможны еще шесть — когда мы бросаем вторую кость.
Получаем, что у данного действия — бросания двух игральных костей — всего возможных исходов, так как
.
А теперь — благоприятные исходы:
Вероятность выпадения восьми очков равна .
Стрелок попадает в цель с вероятностью
. Найдите вероятность того, что он попадёт в цель четыре выстрела подряд.
Если вероятность попадания равна — следовательно, вероятность промаха
. Рассуждаем так же, как и в предыдущей задаче. Вероятность двух попадания подряд равна
. А вероятность четырех попаданий подряд равна
.
Лень разбираться самому?
Присоединяйся к мини-курсу по теории вероятностей
ПОДРОБНЕЕ
Вероятность: логика перебора.
В кармане у Пети было
монеты по
рублей и
монеты по
рублей. Петя не глядя переложил какие-то
монеты в другой карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных карманах.
Мы знаем, что вероятность события равна отношению числа благоприятных исходов к общему числу исходов. Но как посчитать все эти исходы?
Можно, конечно, обозначить пятирублевые монеты цифрами , а десятирублевые цифрами
— а затем посчитать, сколькими способами можно выбрать три элемента из набора
.
Однако есть более простое решение:
Кодируем монеты числами: ,
(это пятирублёвые),
(это десятирублёвые). Условие задачи можно теперь сформулировать так:
Есть шесть фишек с номерами от до
. Сколькими способами можно разложить их по двум карманам поровну, так чтобы фишки с номерами
и
не оказались вместе?
Давайте запишем, что у нас в первом кармане.
Для этого составим все возможные комбинации из набора . Набор из трёх фишек будет трёхзначным числом. Очевидно, что в наших условиях
и
— это один и тот же набор фишек. Чтобы ничего не пропустить и не повториться, располагаем соответствующие трехзначные числа по возрастанию:
…
А дальше? Мы же говорили, что располагаем числа по возрастанию. Значит, следующее — , а затем:
.
Все! Мы перебрали все возможные комбинации, начинающиеся на . Продолжаем:
.
Всего возможных исходов.
У нас есть условие — фишки с номерами и
не должны оказаться вместе. Это значит, например, что комбинация
нам не подходит — она означает, что фишки
и
обе оказались не в первом, а во втором кармане. Благоприятные для нас исходы — такие, где есть либо только
, либо только
. Вот они:
134, 135, 136, 145, 146, 156, 234, 235, 236, 245, 246, 256 – всего благоприятных исходов.
Тогда искомая вероятность равна .
Ответ: .
Сумма событий, произведение событий и их комбинации
Вероятность того, что новый электрический чайник прослужит больше года, равна 0,93. Вероятность того, что он прослужит больше двух лет, равна 0,87. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
Проработав год, чайник может либо сломаться на второй год, либо благополучно служить и после 2 лет работы.
Пусть – вероятность того, что чайник прослужил больше года.
– вероятность того, что он сломается на второй год,
– вероятность того, что он прослужит больше двух лет.
Очевидно,
Тогда
Ответ: 0,06.
События, взаимоисключающие друг друга в рамках данной задачи, называются несовместными. Появление одного из несовместных событий исключает появление других.
Сумма двух событий – термин, означающий, что произошло или первое событие, или второе, или оба сразу.
Вероятность суммы несовместных событий равна сумме их вероятностей.
В нашей задаче события «чайник сломался на второй год работы» и «чайник работает больше двух лет» — несовместные. Чайник или сломался, или остается в рабочем состоянии.
На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук выйдет через выход А.
Пронумеруем развилки, на которых паук может случайным образом свернуть в ту или другую сторону.
Он может либо выйти в выход D, и вероятность этого события равна Либо уйти дальше в лабиринт. На второй развилке он может либо свернуть в тупик, либо выйти в выход В (с вероятностью
На каждой развилке вероятность свернуть в ту или другую сторону равна
а поскольку развилок пять, вероятность выбраться через выход А равна
то есть 0,03125.
События А и В называют независимыми, если вероятность появления события А не меняет вероятности появления события В.
В нашей задаче так и есть: неразумный паук сворачивает налево или направо случайным образом, независимо от того, что он делал до этого.
Для нескольких независимых событий вероятность того, что все они произойдут, равна произведению вероятностей.
(А) Два грузовика, работая совместно, вывозят снег с улицы Нижняя Подгорная, причем первый грузовик должен сделать три рейса с грузом снега, а второй — два. Вероятность застрять с грузом снега при подъеме в горку равна 0,2 для первого грузовика и 0,25 — для второго. С какой вероятностью грузовики вывезут снег с улицы Нижняя Подгорная, ни разу не застряв на горке?
Вероятность для первого грузовика благополучно одолеть горку Для второго
Поскольку первый грузовик должен сделать 3 рейса, а второй – два, грузовики ни разу не застрянут на горке с вероятностью
Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 20% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
Нарисуем все возможные исходы ситуации. Покупатель пришел в магазин, который принадлежит агрофирме, и купил яйцо. Надо найти вероятность того, что это яйцо из первого хозяйства.
Яйца могут быть только или из первого домашнего хозяйства, или из второго, причем эти два события несовместны. Других яиц в этот магазин не поступает.
Пусть вероятность того, что купленное яйцо из первого хозяйства, равна . Тогда вероятность того, что яйцо из второго хозяйства (противоположного события), равна
.
Яйца могут быть высшей категории и не высшей.
В первом хозяйстве 40% яиц имеют высшую категорию, а 60% — не высшую. Это значит, что случайно выбранное яйцо из первого хозяйства с вероятностью 40% будет высшей категории.
Во втором хозяйстве 20% яиц высшей категории, а 80% — не высшей.
Пусть случайно выбранное в магазине яйцо — из первого хозяйства и высшей категории. Вероятность этого события равна произведению вероятностей:
Вероятность того, что яйцо из второго хозяйства и высшей категории, равна
Если мы сложим эти две вероятности, мы получим вероятность того, что яйцо имеет высшую категорию. По условию, высшую категорию имеют 35% яиц, значит, эта вероятность равна 0,35.
Мы получили уравнение:
Решаем это уравнение и находим, что – вероятность того, что яйцо, купленное у этой агрофирмы, оказалось из первого хозяйства.
Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
С чем пришел пациент в клинику? – С подозрением на гепатит. Возможно, он действительно болен гепатитом, а возможно, у его плохого самочувствия другая причина. Может быть, он просто съел что-нибудь. Вероятность того, что он болен гепатитом, равна 0,05 (то есть 5%). Вероятность того, что он здоров, равна 0,95 (то есть 95%).
Пациенту делают анализ. Покажем на схеме все возможные исходы:
Если он болен гепатитом, анализ дает положительный результат с вероятностью 0,9. То есть анализ покажет: «есть гепатит».
Заметим, что анализ не во всех случаях выявляет гепатит у того, кто действительно им болен. С вероятностью 0,1 анализ не распознает гепатит у больного.
Более того. Анализ может ошибочно дать положительный результат у того, кто не болеет гепатитом. Вероятность такого ложного положительного результата 0,01. Тогда с вероятностью 0,99 анализ даст отрицательный результат, если человек здоров.
Найдем вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
Благоприятные для этой ситуации исходы: человек болен, и анализ положительный (вероятность одновременного наступления этих двух событий равна ), или человек здоров, и анализ ложный положительный (вероятность одновременного наступления этих двух событий равна
). Так как события «человек болен» и «человек не болен» несовместны, то вероятность того, что результат анализа будет положительным, равна
Ответ: 0,0545.
Чтобы поступить в институт на специальность «Лингвистика», абитуриент З. должен набрать на ЕГЭ не менее 70 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция», нужно набрать не менее 70 баллов по каждому из трёх предметов — математика, русский язык и обществознание.
Вероятность того, что абитуриент З. получит не менее 70 баллов по математике, равна 0,6, по русскому языку — 0,8, по иностранному языку — 0,7 и по обществознанию — 0,5.
Найдите вероятность того, что З. сможет поступить хотя бы на одну из двух упомянутых специальностей.
Заметим, что в задаче не спрашивается, будет ли абитуриент по фамилии З. учиться и лингвистике, и коммерции сразу и получать два диплома. Здесь надо найти вероятность того, что З. сможет поступить хотя бы на одну из двух данных специальностей – то есть наберет необходимое количество баллов.
Для того чтобы поступить хотя бы на одну из двух специальностей, З. должен набрать не менее 70 баллов по математике. И по русскому. И еще – обществознание или иностранный.
Вероятность набрать 70 баллов по математике для него равна 0,6.
Вероятность набрать баллы по математике и русскому равна
Разберемся с иностранным и обществознанием. Нам подходят варианты, когда абитуриент набрал баллы по обществознанию, по иностранному или по обоим. Не подходит вариант, когда ни по языку, ни по «обществу» он не набрал баллов. Значит, вероятность сдать обществознание или иностранный не ниже чем на 70 баллов равна
В результате вероятность сдать математику, русский и обществознание или иностранный равна Это ответ.
Чтобы полностью освоить тему, смотрите видеокурс по теории вероятностей. Это бесплатно.
Еще задачи ЕГЭ по теме «Теория вероятностей».
Смотрите также: парадокс Монти Холла.
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 3. Теория вероятностей на ЕГЭ по математике.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
09.03.2023
Обновлено: 10.03.2023
1. Начнём с теоретической части. В задании №2 используется основная формула вероятности случайного события. Но она может пригодиться и в задании №10. Вот как она выглядит:
Проще говоря, если все исходы какого-либо эксперимента равновозможны, то вероятность события в этом эксперименте равна отношению числа благоприятных для него исходов к числу всех равновозможных., то есть m — число благоприятных исходов, n — число всех равновозможных исходов. P(a)
Благоприятные исходы — исходы, при которых происходит некоторое событие.
Какие события называются независимыми?
Рассмотрим пример:
Пусть в одной коробке находится 10 деталей, из которых 3 бракованные, а в другой — 16 деталей, из которых 4 бракованные. Из каждой коробки вынимают по одной детали. Какова вероятность того, что обе детали окажутся бракованными?
Пусть событие А — из первой коробки вынимают бракованную деталь;
Событие В — из второй коробки вынимают бракованную деталь.
Очевидно,что события А и В являются независимыми.
Вероятность того, что достанут бракованную деталь из первой коробки равна: P(A)=3/10, а из второй — P(B)=4/16.
По условию задачи нам нужно найти вероятность совместного наступления событий A и B, применяя теорему P(AB)=P(A)*P(B), получим
Ответ: вероятность того, что обе детали окажутся бракованными равна 0,075.
3. Как различить совместные события от несовместных?
Совместные события – это те, которые могут происходить одновременно . Например,
События А и В совместны, А и С совместны (попарно совместны) и также все три события могут наступить одновременно.
Данные события совместны, т.к. можно извлечь карту – червовый король.
Мы можем сказать, что извлечена карта король и карта червовой масти.
Несовместные события – это те, которые не могут происходить одновременно . Например,
- Для учеников 1-11 классов и дошкольников
- Бесплатные сертификаты учителям и участникам
Опорный конспект по теории вероятности при подготовке к ЕГЭ
Определение
Никогда не произойдет при данном испытании =0
Какова вероятность того, что при бросании игральной кости выпадет 7 очков?
Пусть А- событие выпадения 7 очков, =0
Обязательно произойдет при данном испытании =1
Какова вероятность того, что при бросании игральной кости она не останется в воздухе, а упадёт?
Пусть А- событие того, что при бросании кость упадет, = 1
При заданных условиях может произойти или не произойти ‹ 1 = , n — число всех исходов, m -число исходов, благоприятствующих событию A .
Из 20 билетов по биологии 3 содержат вопросы о грибах. Какова вероятность, что в случайно выбранном билете достанется вопрос о грибах?
Пусть А- событие выбора вопроса о грибах, тогда =
Ни одно из событий не является более возможным, чем другое
А и В –равновозможные события, =
А- событие появление герба при бросании монеты,
В- событие появления решки при бросании монеты = =
Появление одного из событий исключает появление другого
При бросании одной игральной кости выпадет одновременно и «5» и «6»
Появление одного из событий не исключает появление другого
А- выпадение нечетного числа очков при бросании игральной кости,
В- выпадение числа очков, кратных трем.
Когда выпадает три, реализуются оба события.
Наступление одного из событий изменяет вероятность наступления другого
При вытягивании экзаменационных билетов вероятность вытащить самый простой билет (№1) вторым студентом зависит от результата предыдущего студента.
Наступление одного из событий не изменяет вероятность наступления другого
При одновременном броске двух кубиков выпадение на одном из них 1 очка, а на втором 5очков – независимые события.
В условиях, являясь единственными его исходами, являются несовместными
Ᾱ- событие, противоположное событию А, + = 1.
· D — из колоды карт будет извлечена дама, D̅ — из колоды карт будет извлечена не дама.
Теоремы о вероятностях событий
независимые
совместные
несовместные
Р(В/А)-вероятность события А, если событие В произошло
В одном ящике 8 красных и 2 белых шара, в другом- 4 красных и 5 белых шаров. Из каждого ящика наугад достают по одному шару. Найти вероятность, что оба шара будут белыми.
А-событие того, что из первого ящика достали белый шар.
В- событие того, что из второго ящика достали белый шар.
Аи В- независимые события. Значит Р(А) = , Р(В) = Р(А·В)=Р(А) · Р(В)= ·
В ящике перемешаны 8 красных и 4 белых шара. Из ящика наугад достают 2 шара. Найти вероятность, что оба шара будут белыми.
А-событие того, что первый шар достали белый .
В- событие того, что второй шар достали белый .
Аи В- зависимые события. Значит Р(А) = , Р(В/А) =
Бросают игральный кубик. Найти вероятность того, что выпадет четное число очков или число очков, кратное четырем.
А-событие , что выпадает четное число очков.
В- событие того, что выпадает число очков, кратное четырем.
Найти вероятность того, что при одном бросании игрального кубика выпадет 2 очка или 3 очка.
А-событие, что выпадает 2 очка.
В- событие, что выпадет 3 очка.
События несовместные, т.к. выпадение 2 очков исключает выпадение или 3 очков. Значит
Краткое описание документа:
Опорный конспект позволяет систематизировать материал всего раздела по теории вероятности основной и старшей школы. В одной странице конспекта уместились все виды событий, основные теоремы, используемые при решении задач открытого банка заданий ФИПИ. Ко всем понятиям и теоремам приведены примеры.
- подготовка к ЕГЭ/ОГЭ и ВПР
- по всем предметам 1-11 классов
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 933 человека из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 683 человека из 75 регионов
Курс повышения квалификации
Инструменты онлайн-обучения на примере программ Zoom, Skype, Microsoft Teams, Bandicam
- Курс добавлен 31.01.2022
- Сейчас обучается 24 человека из 17 регионов
- ЗП до 91 000 руб.
- Гибкий график
- Удаленная работа
Дистанционные курсы для педагогов
Свидетельство и скидка на обучение каждому участнику
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 608 486 материалов в базе
Материал подходит для УМК
Глава XII. Элементы теории вероятностей
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
Свидетельство и скидка на обучение каждому участнику
Другие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
- 12.09.2021 710
- DOCX 35.8 кбайт
- 40 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Вагнер Оксана Анатольевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
40%
- Подготовка к ЕГЭ/ОГЭ и ВПР
- Для учеников 1-11 классов
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Новые курсы: функциональная грамотность, ФГОС НОО, инклюзивное обучение и другие
Время чтения: 15 минут
В Россию приехали 10 тысяч детей из Луганской и Донецкой Народных республик
Время чтения: 2 минуты
Время чтения: 2 минуты
Каждый второй ребенок в школе подвергался психической агрессии
Время чтения: 3 минуты
Отчисленные за рубежом студенты смогут бесплатно учиться в России
Время чтения: 1 минута
Минтруд предложил упростить направление маткапитала на образование
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Мы начнем с простых задач и основных понятий теории вероятностей.
Случайным называется событие, которое нельзя точно предсказать заранее. Оно может либо произойти, либо нет.
Вы выиграли в лотерею — случайное событие. Пригласили друзей отпраздновать выигрыш, а они по дороге к вам застряли в лифте — тоже случайное событие. Правда, мастер оказался поблизости и освободил всю компанию через десять минут — и это тоже можно считать счастливой случайностью…
Наша жизнь полна случайных событий. О каждом из них можно сказать, что оно произойдет с некоторой вероятностью. Скорее всего, вы интуитивно знакомы с этим понятием. Теперь мы дадим математическое определение вероятности.
Начнем с самого простого примера. Вы бросаете монетку. Орел или решка?
Такое действие, которое может привести к одному из нескольких результатов, в теории вероятностей называют испытанием.
Орел и решка — два возможных исхода испытания.
Орел выпадет в одном случае из двух возможных. Говорят, что вероятность того, что монетка упадет орлом, равна .
Бросим игральную кость. У кубика шесть граней, поэтому возможных исходов тоже шесть.
Например, вы загадали, что выпадет три очка. Это один исход из шести возможных. В теории вероятностей он будет называться благоприятным исходом.
Вероятность выпадения тройки равна (один благоприятный исход из шести возможных).
Вероятность четверки — тоже
А вот вероятность появления семерки равна нулю. Ведь грани с семью точками на кубике нет.
Вероятность события равна отношению числа благоприятных исходов к общему числу исходов.
Очевидно, что вероятность не может быть больше единицы.
Вот другой пример. В пакете яблок, из них — красные, остальные — зеленые. Ни формой, ни размером яблоки не отличаются. Вы запускаете в пакет руку и наугад вынимаете яблоко. Вероятность вытащить красное яблоко равна , а зеленое — .
Вероятность достать красное или зеленое яблоко равна .
Определение вероятности. Простые задачи из вариантов ЕГЭ.
Разберем задачи по теории вероятностей, входящие в сборники для подготовки к ЕГЭ.
В фирме такси в данный момент свободно машин: красных, желтых и зеленых. По вызову выехала одна из машин, случайно оказавшихся ближе всего к заказчице. Найдите вероятность того, что к ней приедет желтое такси.
Всего имеется машин, то есть к заказчице приедет одна из пятнадцати. Желтых — девять, и значит, вероятность приезда именно желтой машины равна , то есть .
В сборнике билетов по биологии всего билетов, в двух из них встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет. Найдите вероятность того, что в этом билете не будет вопроса о грибах.
Очевидно, вероятность вытащить билет без вопроса о грибах равна , то есть .
Родительский комитет закупил пазлов для подарков детям на окончание учебного года, из них с картинами известных художников и с изображениями животных. Подарки распределяются случайным образом. Найдите вероятность того, что Вовочке достанется пазл с животным.
Задача решается аналогично.
В чемпионате по гимнастике участвуют спортсменок: из России, из США, остальные — из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая последней, окажется из Китая.
Давайте представим, что все спортсменки одновременно подошли к шляпе и вытянули из нее бумажки с номерами. Кому-то из них достанется двадцатый номер. Вероятность того, что его вытянет китайская спортсменка, равен (поскольку из Китая — спортсменок). Ответ: .
Ученика попросили назвать число от до . Какова вероятность того, что он назовет число кратное пяти?
Каждое пятое число из данного множества делится на . Значит, вероятность равна .
Брошена игральная кость. Найдите вероятность того, что выпадет нечетное число очков.
— нечетные числа; — четные. Вероятность нечетного числа очков равна .
Заметим, что задачу можно сформулировать по-другому: бросили три монеты одновременно. На решение это не повлияет.
Как вы думаете, сколько здесь возможных исходов?
Бросаем монету. У этого действия два возможных исхода: орел и решка
Две монеты — уже четыре исхода:
| орел | орел |
| орел | решка |
| решка | орел |
| решка | решка |
Три монеты? Правильно, исходов, так как .
| орел | орел | орел |
| орел | орел | решка |
| орел | решка | орел |
| решка | орел | орел |
| орел | решка | решка |
| решка | орел | решка |
| решка | решка | орел |
| решка | решка | решка |
Два орла и одна решка выпадают в трех случаях из восьми.
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет очков. Результат округлите до сотых.
Бросаем первую кость — шесть исходов. И для каждого из них возможны еще шесть — когда мы бросаем вторую кость.
Получаем, что у данного действия — бросания двух игральных костей — всего возможных исходов, так как .
А теперь — благоприятные исходы:
Вероятность выпадения восьми очков равна .
Стрелок попадает в цель с вероятностью . Найдите вероятность того, что он попадёт в цель четыре раза выстрела подряд.
Если вероятность попадания равна — следовательно, вероятность промаха . Рассуждаем так же, как и в предыдущей задаче. Вероятность двух попадания подряд равна . А вероятность четырех попаданий подряд равна .
Вероятность: логика перебора.
В кармане у Пети было монеты по рублей и монеты по рублей. Петя, не глядя, переложил какие-то монеты в другой карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных карманах.
Мы знаем, что вероятность события равна отношению числа благоприятных исходов к общему числу исходов. Но как посчитать все эти исходы?
Можно, конечно, обозначить пятирублевые монеты цифрами , а десятирублевые цифрами — а затем посчитать, сколькими способами можно выбрать три элемента из набора .
Однако есть более простое решение:
Кодируем монеты числами: , (это пятирублёвые), (это десятирублёвые). Условие задачи можно теперь сформулировать так:
Есть шесть фишек с номерами от до . Сколькими способами можно разложить их по двум карманам поровну, так чтобы фишки с номерами и не оказались вместе?
Давайте запишем, что у нас в первом кармане.
Для этого составим все возможные комбинации из набора . Набор из трёх фишек будет трёхзначным числом. Очевидно, что в наших условиях и — это один и тот же набор фишек. Чтобы ничего не пропустить и не повториться, располагаем соответствующие трехзначные числа по возрастанию:
А дальше? Мы же говорили, что располагаем числа по возрастанию. Значит, следующее — , а затем:
Все! Мы перебрали все возможные комбинации, начинающиеся на . Продолжаем:
Всего возможных исходов.
У нас есть условие — фишки с номерами и не должны оказаться вместе. Это значит, например, что комбинация нам не подходит — она означает, что фишки и обе оказались в не в первом, а во втором кармане. Благоприятные для нас исходы — такие, где есть либо только , либо только . Вот они:
134, 135, 136, 145, 146, 156, 234, 235, 236, 245, 246, 256 – всего благоприятных исходов.
Тогда искомая вероятность равна .
Сумма событий, произведение событий и их комбинации
Вероятность того, что новый электрический чайник прослужит больше года, равна 0,93. Вероятность того, что он прослужит больше двух лет, равна 0,87. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
Проработав год, чайник может либо сломаться на второй год, либо благополучно служить и после 2 лет работы.
Пусть – вероятность того, что чайник прослужил больше года.
– вероятность того, что он сломается на второй год, – вероятность того, что он прослужит больше двух лет. Очевидно,
События, взаимоисключающие друг друга в рамках данной задачи, называются несовместными. Появление одного из несовместных событий исключает появление других.
Сумма двух событий – термин, означающий, что произошло или первое событие, или второе, или оба сразу.
Пронумеруем развилки, на которых паук может случайным образом свернуть в ту или другую сторону.
Он может либо выйти в выход D, и вероятность этого события равна Либо уйти дальше в лабиринт. На второй развилке он может либо свернуть в тупик, либо выйти в выход В (с вероятностью На каждой развилке вероятность свернуть в ту или другую сторону равна а поскольку развилок пять, вероятность выбраться через выход А равна то есть 0,03125.
События А и В называют независимыми, если вероятность появления события А не меняет вероятности появления события В.
В нашей задаче так и есть: неразумный паук сворачивает налево или направо случайным образом, независимо от того, что он делал до этого.
Для нескольких независимых событий вероятность того, что все они произойдут, равна произведению вероятностей.
(А) Два грузовика, работая совместно, вывозят снег с улицы Нижняя Подгорная, причем первый грузовик должен сделать три рейса с грузом снега, а второй — два. Вероятность застрять с грузом снега при подъеме в горку равна 0,2 для первого грузовика и 0,25 — для второго. С какой вероятностью грузовики вывезут снег с улицы Нижняя Подгорная, ни разу не застряв на горке?
Вероятность для первого грузовика благополучно одолеть горку Для второго Поскольку первый грузовик должен сделать 3 рейса, а второй – два, грузовики ни разу не застрянут на горке с вероятностью
Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 20% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
Нарисуем все возможные исходы ситуации. Покупатель пришел в магазин, который принадлежит агрофирме, и купил яйцо. Надо найти вероятность того, что это яйцо из первого хозяйства.
Яйца могут быть только или из первого домашнего хозяйства, или из второго, причем эти два события несовместны. Других яиц в этот магазин не поступает.
Пусть вероятность того, что купленное яйцо из первого хозяйства, равна . Тогда вероятность того, что яйцо из второго хозяйства (противоположного события), равна .
Яйца могут быть высшей категории и не высшей.
В первом хозяйстве 40% яиц имеют высшую категорию, а 60% — не высшую. Это значит, что случайно выбранное яйцо из первого хозяйства с вероятностью 40% будет высшей категории.
Во втором хозяйстве 20% яиц высшей категории, а 80% — не высшей.
Пусть случайно выбранное в магазине яйцо — из первого хозяйства и высшей категории. Вероятность этого события равна произведению вероятностей:
Вероятность того, что яйцо из второго хозяйства и высшей категории, равна
Если мы сложим эти две вероятности, мы получим вероятность того, что яйцо имеет высшую категорию. По условию, высшую категорию имеют 35% яиц, значит, эта вероятность равна 0,35.
Мы получили уравнение:
Решаем это уравнение и находим, что – вероятность того, что яйцо, купленное у этой агрофирмы, оказалось из первого хозяйства.
Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
С чем пришел пациент в клинику? – С подозрением на гепатит. Возможно, он действительно болен гепатитом, а возможно, у его плохого самочувствия другая причина. Может быть, он просто съел что-нибудь. Вероятность того, что он болен гепатитом, равна 0,05 (то есть 5%). Вероятность того, что он здоров, равна 0,95 (то есть 95%).
Пациенту делают анализ. Покажем на схеме все возможные исходы:
Более того. Анализ может ошибочно дать положительный результат у того, кто не болеет гепатитом. Вероятность такого ложного положительного результата 0,01. Тогда с вероятностью 0,99 анализ даст отрицательный результат, если человек здоров.
Найдем вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
Заметим, что в задаче не спрашивается, будет ли абитуриент по фамилии З. учиться и лингвистике, и коммерции сразу и получать два диплома. Здесь надо найти вероятность того, что З. сможет поступить хотя бы на одну из двух данных специальностей – то есть наберет необходимое количество баллов.
Для того чтобы поступить хотя бы на одну из двух специальностей, З. должен набрать не менее 70 баллов по математике. И по русскому. И еще – обществознания или иностранный.
Вероятность набрать 70 баллов по математике для него равна 0,6.
Вероятность набрать баллы по математике и русскому равна
В результате вероятность сдать математику, русский и обществознание или иностранный равна Это ответ.
Чтобы полностью освоить тему, смотрите видеокурс по теории вероятностей. Это бесплатно.

Развивающая – способствовать развитию логического мышления, внимания, умения анализировать, обобщать изучаемые факты, выделять и сравнивать существенные признаки, выбирать наиболее эффективные способы решения задач
Воспитательная – воспитывать сознательное отношение к подготовке к ЕГЭ, повышение интереса к математике, умения работать в группе, навыки самооценки и умения оценивать деятельность других
Тип урока: урок обобщения и систематизации знаний
Методы: обучения – диалогический (беседа, фронтальная работа, самостоятельная работа)
Учения – репродуктивный, частично-поисковый
Технологии: обучение в сотрудничестве (групповая), информационные, игровые, деятельностного подхода, технологии исследовательской деятельности.
Формы работы на уроке: групповая, коллективная; устная, письменная.
Оборудование: карточки, задания на листочках, компьютер, проектор
2. Актуализация знаний учащихся-8 мин.
3. Закрепление изученного материала-15 мин
4. Физкультминутка — 2 мин
5. Самостоятельная работа в группах – 15 мин
6. Подведение итогов урока- 2 мин.
7. Домашнее задание-1 мин.
Организационный момент.
Психологический настрой “Все в твоих руках”.
“Жил мудрец, который знал все. Один человек захотел доказать, что мудрец знает не все. Зажав в ладонях бабочку, он спросил: “Скажи, мудрец, какая бабочка у меня в руках: мертвая или живая?” А сам думает: “Скажет живая – я ее мертвлю, скажет мертвая – выпущу”. Мудрец, подумав, ответил: “Все в твоих руках”.
От того на сколько плодотворно и успешно пройдет наш урок все в ваших руках. Запишите классная работа. (Слайд 1)
Перед вами слова из которых попробуйте сформулировать тему урока: ВЕРОЯТНОСТЬ, ЗАДЧИ, ТЕОРИЯ, ЕГЭ (Слайд 2)
— систематизировать знания и умения по теории вероятностей
— отработать навыки решения основных типов задач на ЕГЭ
Сегодняшний урок мы проведем в форме работы группами. До начала работы я вас просила определиться с лидером группы, который будет назначать отвечающего на поставленный вопрос или задачу. За каждое правильно выполненное группой задание вы получаете 1 ум. Отвечает первой та группа, которая вперед выполнила задание. Если отвечают неправильно, то у соперников есть шанс ответить.
Актуализация опорных знаний
Начнем с повторения теории. Каждой группе необходимо
объяснить смысл терминов
1 группа: достоверное, невозможное, случайное события
2 группа: противоположные, независимые события
3 группа: несовместные, совместные события
Составление схемы на доске
Повторим как вычислить вероятность.
Вопросы группам: 1) дайте определение вероятности (Слайд 4)
2) чему равна вероятность невозможного события
3) достоверного события
4) как найти вероятность противоположного события
5) что называется суммой событий (Слайд 5)
6) что называется произведением событий (Слайд 5)
7) как будем находить вероятность несовместных, совместных и независимых событий
— Два события называются несовместными, если они не могут происходить одновременно в одном и том же испытании.
Например, выигрыш, ничейный исход, и проигрыш одного игрока в одной партии в шахматы – три несовместных события. Вероятность суммы двух несовместных событий (появления хотя бы одного) равна сумме вероятностей.
— События называются совместными, если они могут происходить одновременно.
Например, при бросании двух монет выпадение решки на одной не исключает возможность появления решки на другой. Вероятность суммы двух совместных событий (появления хотя бы одного) равна сумме их вероятностей без вероятности их совместного появления.
— Два случайных события называются независимыми, если наступление одного из них не изменяет вероятность наступления другого.
Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.
— Два события являются зависимыми, если появление одного из них изменяет вероятность появления другого.
Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие произошло.
Закрепление изученного материала
Задания на карточках: определите о каких событиях идет речь в задачах и вычислите вероятность.
1.Фабрика выпускает сумки. В среднем на 80 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной.
Решение: N(A) = 80, N= 80+8=88, P(A) = 80/88 = 0,91 (Слайд 6)
3.Стрелок попадает в цель с вероятностью 0,9. Найдите вероятность того, что он попадет в цель четыре выстрела подряд.
Попадание в цель при каждом последующем выстреле – независимое от предыдущего исхода событие.
Вероятность р = 0,9*0,9*0,9*0,9 = 0,6561 (Слайд 
4.В торговом центре два одинаковых кофейных автомата. Вероятность того, что к концу дня в автомате закончится кофе равна 0,3. Вероятность того, что кофе закончится в обоих автоматах – 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Задачи для коллективного решения:
5. С первого станка поступает 40%, со второго – 30% и с третьего – 30% всех деталей. Вероятность изготовления бракованной детали равны для каждого станка соответственно 0,01, 0,03, 0,05. Найдите вероятность того, что наудачу взятая деталь будет бракованной. (Слайд 10)
Решение: Р = 0,4*0,01+0,3*0,03+0,3*0,05 = 0,028
6. Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства – яйца высшей категории, а из второго хозяйства – 20% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства. (Слайд 11)
Решение: 0,4х + 0,2(1 – х) = 0,35 х = 0,75
7. Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным
Решение: 0,05∙ 0,9 + 0,95 ∙ 0,01 = 0.0545 (Слайд 12)
Физкультминутка
Предложить уч-ся пересесть на другие места. Сколько всего существует способов рассаживания без повторения.
Сколько всего существует способов рассаживания без повторения, если капитан остается на своем месте.
8. Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 20 пассажиров, равна 0,94. Вероятность того, что окажется меньше 15 пассажиров, равна 0,56. Найдите вероятность того, что число пассажиров будет от 15 до 19.
Решение: р = 0,94 — 0, 56 = 0,38 (Слайд 13)
9. В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,7 погода завтра будет такой же, как и сегодня. Сегодня 16 июня, погода в Волшебной стране хорошая. Найдите вероятность того, что 19 июня в Волшебной стране будет отличная погода (Слайд 14)
Решение: р = 0,7∙0,7∙0,3 + 0,7∙0,3∙0,7 + 0,3∙0,3∙0,3 + 0,3∙0,7∙0,7 = 0,468
Самостоятельная работа в группах
1. Вероятность того, что новая кофемолка прослужит больше года, равна 0,93. Вероятность того, что она прослужит больше двух лет, равна 0,81. Найдите вероятность того, что кофемолка прослужит меньше двух лет, но больше года. (0,12)
2. Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,6. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,4. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
Решение. Рассмотрим два события:
– гроссмейстер А. играет белыми и выигрывает у гроссмейстера Б.;
– гроссмейстер А. играет черными и выигрывает у гроссмейстера Б.
Так как гроссмейстеры играют две партии, причем во второй партии меняют цвет фигур, то будет происходить и событие и событие , которые независимы друг от друга. Таким образом, искомая вероятность того, что А. выиграет оба раза, равна произведению вероятностей событий и :
.
3. Научная конференция проводится в 5 дней. Всего запланировано 50 докладов— первые три дня по 12докладов, остальные распределены поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора Н. окажется запланированным на последний день конференции? (0,14)
4. Два студента читают книгу. Первый студент дочитает книгу с вероятностью – 0,6; второй – 0,8. Найти вероятность того, что книга будет прочитана хотя бы одним из студентов.
Решение. Вероятность того, что книга будет прочитана каждым из студентов не зависит от результата отдельно взятого студента, поэтому события А (первый студент дочитал книгу) и B (второй студент дочитал книгу) независимы и совместны. Искомую вероятность находим по формуле Вероятность события АB (оба студента дочитали книгу):
P (AB) = P (A) * P (B) = 0,6 * 0,8 = 0,48.
Тогда P (A + B) = 0,6 + 0,8 — 0,48 = 0,92.
Подведение итогов урока (Слайд 16)
Выставление оценок за урок.
Подведите итог урока, составив синквейн
Синквейн – это не простое стихотворение, а стихотворение, написанное по следующим правилам:
1 строка – одно существительное, выражающее главную тему синквейн.
2 строка – два прилагательных, выражающих главную мысль.
3 строка – три глагола, описывающие действия в рамках темы.
4 строка – фраза, несущая определенный смысл.
5 строка – заключение в форме существительного (ассоциация с первым словом).
Задание на дом (Слайд 17)
Выполнить задания на карточках
1.В чемпионате мира участвуют 24 команды. С помощью жребия их нужно разделить на четыре группы по шесть команд в каждой. В ящике вперемешку лежат карточки с номерами групп: 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4. Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется в третьей группе?
Вероятность того, что команда России окажется во второй группе, равна отношению количества карточек с номером 2, к общему числу карточек.
Р(А) = = = 0,25
2.Вероятность того, что новый чайник прослужит больше года, равна 0,97. Вероятность того, что он прослужит более двух лет, равна 0,89. Найдите вероятность того, что чайник прослужит меньше двух лет, но больше года
3.Вероятность того, что батарейка бракованная, равна 0,02. Покупатель выбирает в магазине случайную упаковку, в которой две такие батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.
4.Помещение освещается фонарем с двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,17. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Читайте также:
- Конспект занятия по рисованию на тему лес
- Контраст и нюанс в скульптуре урок изо 3 класс конспект
- Односоставные предложения в текстах разных функциональных разновидностей языка конспект
- Окончание и основа слова 5 класс конспект урока
- Конспект правила поведения в лесу в подготовительной группе
Слайд 1
Вероятность. Задачи профильного ЕГЭ по математике.
Слайд 2
Определение вероятности Вероятностью события A называют отношение числа m благоприятствующих этому событию исходов к общему числу n всех равновозможных несовместимых событий, которые могут произойти в результате одного испытания или наблюдения: Р = n m Пусть k – количество бросков монеты, тогда количество всевозможных исходов: n = 2 k . Пусть k – количество бросков кубика, тогда количество всевозможных исходов: n = 6 k .
Слайд 3
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз. Решение. Всего 4 варианта: о; о о ; р р ; р р ; о . Благоприятных 2: о; р и р ; о . Вероятность равна 2/4 = 1/2 = 0,5 . Ответ: 0,5.
Слайд 4
Решение. Игральные кости – это кубики с 6 гранями. На первом кубике может выпасть 1, 2, 3, 4, 5 или 6 очков. Каждому варианту выпадения очков соответствует 6 вариантов выпадения очков на втором кубике. Т.е. всего различных вариантов 6×6 = 36. Варианты (исходы эксперимента) будут такие: 1; 1 1; 2 1; 3 1; 4 1; 5 1; 6 2; 1 2; 2 2; 3 2; 4 2; 5 2; 6 и т.д. ………………………… 6; 1 6; 2 6; 3 6; 4 6; 5 6; 6 Подсчитаем количество исходов (вариантов), в которых сумма очков двух кубиков равна 8. 2; 6 3; 5; 4; 4 5; 3 6; 2. Всего 5 вариантов. Найдем вероятность: 5/36 = 0,138 ≈ 0,14. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых. Ответ: 0,14.
Слайд 5
В сборнике билетов по биологии всего 55 билетов, в 11 из них встречается вопрос по ботанике. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по ботанике. Ответ: 0,2. Решение: Вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по ботанике, равна 11/55 =1/5 = 0,2.
Слайд 6
В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России, 7 из США, остальные − из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая. Решение. Всего участвует 20 спортсменок, из которых 20 – 8 – 7 = 5 спортсменок из Китая. Вероятность того, что спортсменка, выступающая первой, окажется из Китая, равна 5/20 = 1/4 = 0,25. Ответ: 0,25.
Слайд 7
Научная конференция проводится в 5 дней. Всего запланировано 75 докладов − первые три дня по 17 докладов, остальные распределены поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции? Ответ: 0,16. Решение: В последний день конференции запланировано (75 – 17 × 3) : 2 = 12 докладов. Вероятность того, что доклад профессора М. окажется запланированным на последний день конференции, равна 12/75 = 4/25 = 0,16.
Слайд 8
Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России? Ответ: 0,36. Решение: Нужно учесть, что Руслан Орлов должен играть с каким-либо бадминтонистом из России. И сам Руслан Орлов тоже из России. Вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России, равна 9/25 = 36/100 = 0,36.
Слайд 9
Решение. В сумме на двух кубиках должно выпасть 8 очков. Это возможно, если будут следующие комбинации: 2 и 6 6 и 2 3 и 5 5 и 3 4 и 4 Всего 5 вариантов. Подсчитаем количество исходов (вариантов), в которых при первом броске выпало 2 очка. Такой вариант 1. Найдем вероятность: 1/5 = 0,2. Даша дважды бросает игральный кубик. В сумме у нее выпало 8 очков. Найдите вероятность того, что при первом броске выпало 2 очка. Ответ: 0,2.
Слайд 10
Решение: Всего команд 20, групп – 5. В каждой группе – 4 команды. Итак, всего исходов получилось 20, нужных нам – 4, значит, вероятность выпадения нужного исхода 4/20 = 0,2. В чемпионате мира участвует 20 команд. С помощью жребия их нужно разделить на пять групп по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп: 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5. Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется в третьей группе. Ответ: 0,2.
Слайд 11
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая – 55%. Первая фабрика выпускает 3% бракованных стекол, а вторая – 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным. Ответ: 0,019. Решение: Вероятность того, что стекло куплено на первой фабрике и оно бракованное: р 1 = 0,45 · 0,03 = 0,0135. Вероятность того, что стекло куплено на второй фабрике и оно бракованное: р 2 = 0,55 · 0,01 = 0,0055. Поэтому по формуле полной вероятности вероятность того, что случайно купленное в магазине стекло окажется бракованным равна р = р 1 + р 2 = 0,0135 + 0,0055 = 0,019.
Слайд 12
Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,52. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза. Ответ: 0,156. Решение: Возможность выиграть первую и вторую партию не зависят друг от друга. Вероятность произведения независимых событий равна произведению их вероятностей: р = 0,52 · 0,3 = 0,156.
Слайд 13
Решение: Результат каждого следующего выстрела не зависит от предыдущих. Поэтому события «попал при первом выстреле», «попал при втором выстреле» и т.д. независимы. Вероятность каждого попадания равна 0,8. Значит, вероятность промаха равна 1 – 0,8 = 0,2. 1 выстрел: 0,8 2 выстрел: 0,8 3 выстрел: 0,8 4 выстрел: 0,2 5 выстрел: 0,2 По формуле умножения вероятностей независимых событий, получаем, что искомая вероятность равна: 0,8 ∙ 0,8 ∙ 0,8 ∙ 0,2 ∙ 0,2 = 0,02048 ≈ 0,02. Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два раза промахнулся. Результат округлите до сотых. Ответ : 0,02 .
Слайд 14
Решение: Найдем вероятность того, что неисправны оба автомата. Эти события независимые, вероятность их произведения равна произведению вероятностей этих событий: 0,05 · 0,05 = 0,0025. Событие, состоящее в том, что исправен хотя бы один автомат, противоположное. Следовательно, его вероятность равна 1 − 0,0025 = 0,9975. Ответ: 0,9975. В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Слайд 15
Решение: Вероятность того, что Джон промахнется, если схватит пристрелянный револьвер равна: 0,4 · (1 − 0,9) = 0,04 Вероятность того, что Джон промахнется, если схватит непристрелянный револьвер равна: 0,6 · (1 − 0,2) = 0,48 Эти события несовместны, вероятность их суммы равна сумме вероятностей этих событий: 0,04 + 0,48 = 0,52. Ответ: 0,52. Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
Слайд 16
Решение: Можно решать задачу «по действиям», вычисляя вероятность уцелеть после ряда последовательных промахов: Р(1) = 0,6; Р(2) = Р(1) · 0,4 = 0,24; Р(3) = Р(2) · 0,4 = 0,096; Р(4) = Р(3) · 0,4 = 0,0384; Р(5) = Р(4) · 0,4 = 0,01536. Последняя вероятность меньше 0,02, поэтому достаточно пяти выстрелов по мишени. При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем – 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98? Ответ: 5.
Слайд 17
Решение: Пусть один из близнецов находится в некоторой группе. Вместе с ним в группе окажутся 12 человек из 25 оставшихся одноклассников. Вероятность того, что второй близнец окажется среди этих 12 человек, равна P = 12 : 25 = 0,48. В классе 26 человек, среди них два близнеца – Андрей и Сергей. Класс случайным образом делят на две группы по 13 человек в каждой. Найдите вероятность того, что Андрей и Сергей окажутся в одной группе. Ответ: 0,48 .
Слайд 18
Решение: На каждой из четырех отмеченных развилок паук с вероятностью 0,5 может выбрать или путь, ведущий к выходу D, или другой путь. Это независимые события, вероятность их произведения (паук дойдет до выхода D) равна произведению вероятностей этих событий. Поэтому вероятность прийти к выходу D равна (0,5) 4 = 0,0625. На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может, поэтому на каждом разветвлении паук выбирает один из путей, по которому ещё не полз. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью паук придёт к выходу D . Ответ: 0, 0625.
Урок алгебры в 10 классе по теме «Теория вероятностей»
Тема урока: “Теория вероятностей в задачах ЕГЭ ”
Цели урока:
Образовательная – систематизировать знания и умения по теории вероятностей и комбинаторике, отработать навыки необходимые для нахождения вероятности событий при решении задач на ЕГЭ
Развивающая – способствовать развитию логического мышления, внимания, умения анализировать, обобщать изучаемые факты, выделять и сравнивать существенные признаки, выбирать наиболее эффективные способы решения задач
Воспитательная – воспитывать сознательное отношение к подготовке к ЕГЭ, повышение интереса к математике, умения работать в группе, навыки самооценки и умения оценивать деятельность других
Тип урока: урок обобщения и систематизации знаний
Методы: обучения – диалогический (беседа, фронтальная работа, самостоятельная работа)
Преподавания – повторительно-стимулирующие
Учения – репродуктивный, частично-поисковый
Технологии: обучение в сотрудничестве (групповая), информационные, игровые, деятельностного подхода, технологии исследовательской деятельности.
Формы работы на уроке: групповая, коллективная; устная, письменная.
Оборудование: карточки, задания на листочках, компьютер, проектор
План урока.
1. Сообщение темы и постановка целей урока-2 мин.
2. Актуализация знаний учащихся-8 мин.
3. Закрепление изученного материала-15 мин
4. Физкультминутка — 2 мин
5. Самостоятельная работа в группах – 15 мин
6. Подведение итогов урока- 2 мин.
7. Домашнее задание-1 мин.
Ход урока
-
Организационный момент.
Психологический настрой “Все в твоих руках”.
“Жил мудрец, который знал все. Один человек захотел доказать, что мудрец знает не все. Зажав в ладонях бабочку, он спросил: “Скажи, мудрец, какая бабочка у меня в руках: мертвая или живая?” А сам думает: “Скажет живая – я ее мертвлю, скажет мертвая – выпущу”. Мудрец, подумав, ответил: “Все в твоих руках”.
От того на сколько плодотворно и успешно пройдет наш урок все в ваших руках. Запишите классная работа. (Слайд 1)
Перед вами слова из которых попробуйте сформулировать тему урока: ВЕРОЯТНОСТЬ, ЗАДЧИ, ТЕОРИЯ, ЕГЭ (Слайд 2)
Сообщение учащимся темы урока, формулировка целей
Тема урока: «Теория вероятностей в задачах ЕГЭ» (Слайд 3)
Цели урока:
— систематизировать знания и умения по теории вероятностей
— отработать навыки решения основных типов задач на ЕГЭ
Сегодняшний урок мы проведем в форме работы группами. До начала работы я вас просила определиться с лидером группы, который будет назначать отвечающего на поставленный вопрос или задачу. За каждое правильно выполненное группой задание вы получаете 1 ум. Отвечает первой та группа, которая вперед выполнила задание. Если отвечают неправильно, то у соперников есть шанс ответить.
-
Актуализация опорных знаний
Начнем с повторения теории. Каждой группе необходимо
объяснить смысл терминов
1 группа: достоверное, невозможное, случайное события
2 группа: противоположные, независимые события
3 группа: несовместные, совместные события
Составление схемы на доске
Повторим как вычислить вероятность.
Вопросы группам: 1) дайте определение вероятности (Слайд 4)
2) чему равна вероятность невозможного события
3) достоверного события
4) как найти вероятность противоположного события
5) что называется суммой событий (Слайд 5)
6) что называется произведением событий (Слайд 5)
7) как будем находить вероятность несовместных, совместных и независимых событий
— Два события называются несовместными, если они не могут происходить одновременно в одном и том же испытании.
Например, выигрыш, ничейный исход, и проигрыш одного игрока в одной партии в шахматы – три несовместных события. Вероятность суммы двух несовместных событий (появления хотя бы одного) равна сумме вероятностей.
— События называются совместными, если они могут происходить одновременно.
Например, при бросании двух монет выпадение решки на одной не исключает возможность появления решки на другой. Вероятность суммы двух совместных событий (появления хотя бы одного) равна сумме их вероятностей без вероятности их совместного появления.
— Два случайных события называются независимыми, если наступление одного из них не изменяет вероятность наступления другого.
Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.
— Два события являются зависимыми, если появление одного из них изменяет вероятность появления другого.
Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие произошло.
-
Закрепление изученного материала
Задания на карточках: определите о каких событиях идет речь в задачах и вычислите вероятность.
1.Фабрика выпускает сумки. В среднем на 80 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной.
Решение: N(A) = 80, N= 80+8=88, P(A) = 80/88 = 0,91 (Слайд 6)
2.На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос на тему «Параллелограмм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Решение:
События «вопрос о вписанной окружности» и «вопрос о параллелограмме» — несовместные, поэтому вероятность выбрать один из них равна сумме вероятностей: р = 0,2+0,15=0,35 (Слайд 7)
3.Стрелок попадает в цель с вероятностью 0,9. Найдите вероятность того, что он попадет в цель четыре выстрела подряд.
Решение:
Попадание в цель при каждом последующем выстреле – независимое от предыдущего исхода событие.
Вероятность р = 0,9*0,9*0,9*0,9 = 0,6561 (Слайд 
4.В торговом центре два одинаковых кофейных автомата. Вероятность того, что к концу дня в автомате закончится кофе равна 0,3. Вероятность того, что кофе закончится в обоих автоматах – 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Решение:
События «кофе останется в обоих автоматах» и «кофе закончится хотя бы в одном» — противоположные. Сумма их вероятностей 1. Найдем вероятность события «кофе закончится хотя бы в одном автомате» р=0,3+0,3-0,12 = 0,48. Тогда вероятность события «кофе останется в обоих автоматах» р = 1 – 0,48 = 0,52 (Слайд 9)
Задачи для коллективного решения:
Решение задач на нахождение «полной вероятности», т.е. задачи в которой используются обе теоремы: сложения и умножения вероятностей: для перебора всех возможных вариантов строится граф, при вычислении применяются оба правила.
5. С первого станка поступает 40%, со второго – 30% и с третьего – 30% всех деталей. Вероятность изготовления бракованной детали равны для каждого станка соответственно 0,01, 0,03, 0,05. Найдите вероятность того, что наудачу взятая деталь будет бракованной. (Слайд 10)
Решение: Р = 0,4*0,01+0,3*0,03+0,3*0,05 = 0,028
6. Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства – яйца высшей категории, а из второго хозяйства – 20% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства. (Слайд 11)
Решение: 0,4х + 0,2(1 – х) = 0,35 х = 0,75
7. Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным
Решение: 0,05∙ 0,9 + 0,95 ∙ 0,01 = 0.0545 (Слайд 12)
-
Физкультминутка
-
Предложить уч-ся пересесть на другие места. Сколько всего существует способов рассаживания без повторения.
-
Сколько всего существует способов рассаживания без повторения, если капитан остается на своем месте.
8. Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 20 пассажиров, равна 0,94. Вероятность того, что окажется меньше 15 пассажиров, равна 0,56. Найдите вероятность того, что число пассажиров будет от 15 до 19.
Решение: р = 0,94 — 0, 56 = 0,38 (Слайд 13)
9. В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,7 погода завтра будет такой же, как и сегодня. Сегодня 16 июня, погода в Волшебной стране хорошая. Найдите вероятность того, что 19 июня в Волшебной стране будет отличная погода (Слайд 14)
Решение: р = 0,7∙0,7∙0,3 + 0,7∙0,3∙0,7 + 0,3∙0,3∙0,3 + 0,3∙0,7∙0,7 = 0,468
10. Чтобы поступить в институт на специальность «Лингвистика», абитуриент должен набрать на ЕГЭ не менее 70 баллов по каждому из трёх предметов – математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция», нужно набрать не менее 70 баллов по каждому из трёх предметов – математика, русский язык и обществознание. Вероятность того, что абитуриент З. получит не менее 70 баллов по математике, равна 0,6, по русскому языку – 0,8, по иностранному языку – 0,7 и по обществознанию – 0,5. Найдите вероятность того, что З. сможет поступить хотя бы на одну из двух упомянутых специальностей (Слайд 15) (домашнее задание)
-
Самостоятельная работа в группах
1. Вероятность того, что новая кофемолка прослужит больше года, равна 0,93. Вероятность того, что она прослужит больше двух лет, равна 0,81. Найдите вероятность того, что кофемолка прослужит меньше двух лет, но больше года. (0,12)
2. Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,6. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,4. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
Решение. Рассмотрим два события:
– гроссмейстер А. играет белыми и выигрывает у гроссмейстера Б.;
– гроссмейстер А. играет черными и выигрывает у гроссмейстера Б.
Так как гроссмейстеры играют две партии, причем во второй партии меняют цвет фигур, то будет происходить и событие и событие
, которые независимы друг от друга. Таким образом, искомая вероятность того, что А. выиграет оба раза, равна произведению вероятностей событий
и
:
.
3. Научная конференция проводится в 5 дней. Всего запланировано 50 докладов— первые три дня по 12докладов, остальные распределены поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора Н. окажется запланированным на последний день конференции? (0,14)
4. Два студента читают книгу. Первый студент дочитает книгу с вероятностью – 0,6; второй – 0,8. Найти вероятность того, что книга будет прочитана хотя бы одним из студентов.
Решение. Вероятность того, что книга будет прочитана каждым из студентов не зависит от результата отдельно взятого студента, поэтому события А (первый студент дочитал книгу) и B (второй студент дочитал книгу) независимы и совместны. Искомую вероятность находим по формуле Вероятность события АB (оба студента дочитали книгу):
P (AB) = P (A) * P (B) = 0,6 * 0,8 = 0,48.
Тогда P (A + B) = 0,6 + 0,8 — 0,48 = 0,92.
-
Подведение итогов урока (Слайд 16)
Выставление оценок за урок.
Подведите итог урока, составив синквейн
Синквейн – это не простое стихотворение, а стихотворение, написанное по следующим правилам:
1 строка – одно существительное, выражающее главную тему синквейн.
2 строка – два прилагательных, выражающих главную мысль.
3 строка – три глагола, описывающие действия в рамках темы.
4 строка – фраза, несущая определенный смысл.
5 строка – заключение в форме существительного (ассоциация с первым словом).
-
Задание на дом (Слайд 17)
Выполнить задания на карточках
1.В чемпионате мира участвуют 24 команды. С помощью жребия их нужно разделить на четыре группы по шесть команд в каждой. В ящике вперемешку лежат карточки с номерами групп: 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4. Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется в третьей группе?
Решение:
Вероятность того, что команда России окажется во второй группе, равна отношению количества карточек с номером 2, к общему числу карточек.
Р(А) = 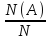
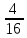
2.Вероятность того, что новый чайник прослужит больше года, равна 0,97. Вероятность того, что он прослужит более двух лет, равна 0,89. Найдите вероятность того, что чайник прослужит меньше двух лет, но больше года
Решение:
События «чайник прослужит больше двух лет» и «чайник прослужит больше года, но менее двух лет» — несовместные. Сумма этих событий равна событию «чайник прослужит более года». Поэтому искомая вероятность р = 0,97 — 0,89 = 0,08
3.Вероятность того, что батарейка бракованная, равна 0,02. Покупатель выбирает в магазине случайную упаковку, в которой две такие батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.
Решение:
События «батарейка бракованная» и «батарейка исправная» противоположные, поэтому вероятность события «батарейка исправная» р = 1-0,02 = 0,98.
События «1 батарейка исправная» и «2 батарейка исправная» — независимые, поэтому вероятность того, что обе батарейки исправны р = 0,98*0,98= 0,9604
4.Помещение освещается фонарем с двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,17. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Решение:
Событие « хотя бы одна лампа не перегорит» противоположно событию « обе лампы перегорят» . Вероятность события «обе лампы перегорят» равна произведению вероятностей (т.к. события независимые) р=0,17*0,17=0,0289
Тогда вероятность события « хотя бы одна лампа не перегорит» равна: 1 – 0,0289 = 0,9711













