МАОУ «Свердловская СОШ №2»
План- конспект открытого урока
по математике в 11 Б классе
«Подготовка к ЕГЭ. Решение сложных комбинированных уравнений»
Урок разработала и провела:
Сушкова Э.А.,
учитель математики
МАОУ «Свердловская СОШ №2»
Апрель 2021 г
https://yandex.ru/efir?stream_id=vIL5MDlVhUGQ&from_block=player_context_menu_yavideo
Тип урока: семинарское занятие.
Цели урока:
Познавательные: повторить и обобщить изученный за курс средней школы материал по математике, закрепить навыки решения сложных уравнений различными методами.
Развивающие: развивать ключевые коммуникативные компетенции, речь, внимание, память, логическое мышление, умение обобщать, делать выводы, развивать навыки самоконтроля и творческие способности учащихся.
Воспитательные: совершенствовать навыки этичного межличностного общения, сознательное отношение к математике; активизировать познавательную деятельность в коллективе, формировать навыки сотрудничества в решении поисковых задач, воспитывать у учащихся морально-ценностные чувства.
Задачи урока:
- Систематизировать теоретические знание по теме.
- Развивать умение работать с заданиями ЕГЭ.
Совершенствовать навыки решения сложных уравнений различными методами.
Ход урока:
I Организационный момент:
а) готовность класса к уроку;
б Слово учителя: Ребята, сегодня у нас необычный урок. Мы проверим наши знания, уровень нашей подготовки к сдаче ЕГЭ. И я хочу начать сегодняшний урок с притчи.
— Учитель, я уже целый год живу у тебя, но до сих пор выполняю только работы по хозяйству. Когда ты будешь меня учить? Разве я для этого пришёл к тебе в ученики, скажи?
— Имей терпение, — ответил учитель, — ещё не пришло время. Иди в нижнюю долину и посади дерево, вырасти его, а я подумаю.
Долгий и тяжёлый путь проделал ученик, пока спустился в долину. По дороге он выкопал маленький саженец и посадил его. С той поры, дважды в день он проходил опасный путь, между хижиной и долиной, чтобы полить деревце. Изо дня в день, он присматривал за деревом. Так прошёл год. Усилия его не пропали даром. Дерево выросло высоким и крепким. Однажды на рассвете, он вышел из хижины и увидел своего учителя, сидящего у ручья под деревом.
— Учитель! – обрадовался юноша. – Как я счастлив вновь увидеть тебя! Я должен извиниться перед тобой, что не смог стать твоим учеником, обманув твоё доверие! Ты подумал, что я слаб, когда я остался жить в долине. Но я должен был заботиться о своём деревеИ теперь, ты вряд ли возьмёшь меня обратно…
Выслушав пылкую речь юноши, старик сказал ему: — Именно в этот год, ты вместе с деревом взращивал такие качества своего характера, которые тебе помогут постигать знания.
Твоё дерево говорит о твоей готовности. Посмотри!
Ответственность ты имел, но только по необходимости, Был нетерпелив и эмоционален, как переплетенные побеги саженца. Чтобы обрести знания, нужна, прежде всего, дисциплина.
Ибо корни дерева – твоя ответственность,
ствол дерева – твоё терпение,
ветви дерева – спокойствие,
а листья – знания!
И вам я желаю такого же упорства и терпения, чтобы хорошо подготовиться к ЕГЭ и успешно его сдать.
А теперь приступим к выполнению заданий.
Проверка дз.
Дать определение уравнения и его корня, равносильности двух уравнений.
Ответ:
Арифметическое выражение, содержащее неизвестную переменную и знаки равенства называют уравнением. Значение переменной, превращающее уравнение в верное равенство, называют корнем уравнения. Два уравнения называют равносильными, если любой корень первого уравнения является корнем второго уравнения и любой корень второго уравнения является корнем первого уравнения.
Дать определение равносильности преобразования уравнения и перечислить основные равносильные преобразования.
Ответ:
Замену одного уравнения другим, равносильным ему уравнением называют равносильным преобразованием уравнения.
Равносильными преобразованиями уравнения являются:
- перенос члена уравнения с противоположным знаком из одной части уравнения в другую;
- умножение (деление) обеих частей уравнения на отличную от нуля число;
- возведение уравнения в нечетную степень;
- извлечение корня нечетной степени с обеих частей уравнения:
- логарифмирование показательного уравнения;
- применение тождеств, т. е равенств, справедливых для любого числа.
Рассказать, какие равносильные преобразования нужно выполнить, чтобы решить следующие уравнения

Дайте определение уравнения – следствия и перечислите преобразования, приводящие к уравнению следствия.
Ответ:
Пусть даны два уравнения. Если любой корень первого уравнения является корнем второго уравнения, то второе уравнение называют уравнением- следствием первого.
Замену уравнения другим уравнением, которое является его следствием, называют переходом к уравнению- следствию.
При переходе к уравнению- следствия возможно появление лишних корней, посторонних для исходного уравнения, поэтому проверка полученных корней является обязательной частью решения уравнения.
Преобразованиями, приводящими к уравнению- следствия является:
- возведение уравнения в четную степень;
- потенцирование логарифмического уравнения;
- освобождение уравнения от знаменателя;
- приведение подобных членов;
- применение формул (тригонометрических, логарифмических и других).
- Расскажите, каким способом приводится следующие уравнения к уравнению – следствия.



Карточки имеются у каждого ученика на парте.
Сложные уравнения можно решить, приводя их к системам. Правила перехода от уравнений к равносильным системам:
1.
2.
3.
4.
5.
6.
7.
М-область существования
8.
9.
10.
11.
Работа в группах.
Запишите системы, равносильные уравнениям. (Работы выполняют на листочках)..
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
Очень часто можно встретить уравнение, которое имеет дополнительное условие, например:
Как можно упростить решение такого типа уравнения?
Разбор решения на доске.
Ответ:
Учитывая, что левая часть уравнения неотрицательное число получаем 




Самыми сложными считаются уравнения с параметром. Дайте определение уравнения с параметром. Давайте рассмотрим несколько таких уравнений с использованием свойств функций:
а)

Ответ:
Для каждого значения a рассмотрим функцию
Она определена на множестве R, четная, поэтому, если 

Уравнение (1) имеет три корня тогда и только тогда, когда оно имеет 

При 

При 


Видеоурок.
Максимум за выполнение данного задания(18 задание) можно получить 4 балла.
В задачах с параметром допускают весьма разнообразные способы решений. Наиболее распространенными из них являются;
Чисто алгебраический способ решения;
-способ решения,основанный на построении и исследовании геометрической модели данной задачи;
-функциональный способ, в котором могут быть и алгебраические, и геометрические моменты, но базовым является исследование некоторой функции.
Критерии оценивания:
|
Обоснованно получен верный ответ |
4 балла |
|
|
С помощью верного рассуждения получены оба верных значения параметра, но -или в ответ включены и одно-два неверных значения; -или решение недостаточно обосновано. |
3 балла |
|
|
С помощью верного рассуждения получено хотя бы одно верное значение параметра |
2 балла |
|
|
Задача сведена к исследованию: -или взаимного расположения трех окружносей; -или двух квадратных уравнений с параметром. |
1 балл |
|
|
Решение не соответствует ни одному из критериев, перечисленных выше |
О баллов |
Выполнения тренировочных упражнений на закрепление навыков и умений решать уравнения.
;
VI Домашнее задание:
Разбор заданий типа С с индивидуальных карточек с сайта www.ege.edu.ru Банк заданий на доске.
Карточка №1
С1.(В13)
Карточка №2
C1.(B1)
Карточка №3
C1.(B12)
Карточка №4
C1.(B19)
Карточка №5
С5. Найти все значения a, такие, что уравнение имеет единственное решение:
Карточка №6
С5. Найти все значения a, такие, что уравнение имеет единственное решение:
Карточка № 7
Найти наибольший корень уравнения:

Карточка № 8
Найти значение р, при которых уравнение

Карточка №9
Решить уравнение
- Повторить теорию по темам:
- Уравнения-следствия.
- Равносильность уравнений системам.
- Равносильность уравнений на множествах.
VII Подведение итогов урока.
Оцените вашу работу на уроке.
Сколько баллов вы набрали?
К какому выводу пришли?
Лист самооценки работы учащегося
———————————————————————————(Ф.И. учащегося)
———————————————————————————(тема урока)
|
Мой вклад… |
Баллы |
|||
|
1(плохо) |
2(слабо) |
3(хорошо) |
4(отлично) |
|
|
В поисках материала по теме |
||||
|
В теоретическом изучении материала |
||||
|
В решении примеров |
||||
|
В групповой работе |
||||
|
В защите работ, анализе решений |
Перевод баллов:
0-9 баллов-2
10-13 баллов-3
14-16 баллов-4
15-20 баллов-5
Лист самооценки работы учащегося
———————————————————————————(Ф.И. учащегося)
———————————————————————————(тема урока)
|
Мой вклад… |
Баллы |
|||
|
1(плохо) |
2(слабо) |
3(хорошо) |
4(отлично) |
|
|
В поисках материала по теме |
||||
|
В теоретическом изучении материала |
||||
|
В решении примеров |
||||
|
В групповой работе |
||||
|
В защите работ, анализе решений |
Перевод баллов:
0-9 баллов-2
10-13 баллов-3
14-16 баллов-4
15-20 баллов-5
План урока по математике в 11 классе «Решение текстовых задач» при подготовке к
ЕГЭ
Тема урока: Решение текстовых задач
Тип урока: совершенствование ЗУН
Цели урока:
дидактическая: научить применять ранее полученные знания
при решении текстовых задач в выполнении заданий ЕГЭ разного уровня сложности,
стимулировать обучающихся к овладению рациональными приёмами и методами решения
текстовых задач;
развивающая: развивать логическое мышление, память, познавательный интерес,
продолжать формирование математической речи и графической культуры,
вырабатывать умение анализировать и сравнивать;
воспитательная: приучать к эстетическому оформлению записи в
тетради, умению выслушать других и умению общаться, прививать аккуратность и
трудолюбие.
Ход урока:
|
Этапы урока, их содержание |
|
|
|
учителя |
учащихся |
|
|
Постановка цели Сегодня мы |
Сообщает тему |
Записывают в |
|
Проверка домашнего На дом было задано |
На экране показано |
Сверяют своё |
|
Актуализация темы |
Проводит |
|
|
Фронтальная работа, |
Направляет на |
Комментируют |
|
Индивидуальная |
Раздаёт карточки с |
Самостоятельно |
|
Подведение итогов |
Комментирует работу |
|
|
Домашнее задание |
Поясняет домашнее |
Приложение 1 (домашняя работа)
Задача № 1. Два велосипедиста отправляются навстречу друг другу одновременно из
двух пунктов, расстояние между которыми равно 54
км, и встречаются через 2 ч. Определите скорость каждого велосипедиста, если
скорость у одного из них она на 3 км/ч больше, чем у другого.
Задача № 2. Сберегательный банк в конце года начисляет 3% к сумме, находившейся
на счету. На сколько рублей увеличится первоначальный вклад в 1000 рублей через
2 года?
Задача № 3. Под
строительную площадку отвели участок прямоугольной формы, длина которого на 30
метров больше его ширины. При утверждении плана застройки выяснилось, что
граница участка проходит по территории водоохраной зоны, поэтому его ширину
уменьшили на 20 метров. Найдите длину участка, если после утверждения плана
застройки площадь участка составила 2400
м2.
решение задачи № 1.
Устные рассуждения:
Одним из основных условий задачи является
одновременное отправление велосипедистов из пунктов, значит, каждый из них
находился в пути одно и то же время, т.е. 2 часа. Далее, даётся некая
зависимость между скоростями велосипедистов, поэтому меньшую скорость, пусть
это будет скорость первого велосипедиста, обозначим км/ч,
тогда скорость второго будет км/ч. По условию
задачи велосипедисты встретились через 2 часа после отправления. Зная время
движения и скорости велосипедистов, можно найти путь каждого из них. Таким
образом, первый велосипедист за 2 часа проехал путь км, а
второй за те же 2 часа – км. По условию задачи
через 2 часа велосипедисты встретились, т.е. проехали весь путь 54
км.
Запись в тетради:
Обозначим скорость первого велосипедиста км/ч, тогда скорость второго будет
км/ч.
По условию задачи каждый велосипедист
находился в пути 2 часа, значит, первый велосипедист проехал путь км, а второй –
км.
По условию задачи через 2 часа велосипедисты встретились, т.е. проехали весь
путь 54 км. Следовательно, уравнение составляем по проделанному пути обоими
велосипедистами: .
Решение:
,
,
,
. Получили:
скорость первого велосипедиста 13 км/ч, а второго – 16
км/ч.
Ответ: 13
км/ч; 16 км/ч.
Оставшиеся две
задачи разбирают устно.
Приложение 2
Ребята, давайте вспомним, какие типы текстовых
задач мы рассматривали и какие основные величины характеризуют тот или иной тип
задачи. И так:
- Задачи на движение:
а) движение
навстречу друг другу, движение в одном направлении, движение в противоположных
направлениях;
б) движение по
воде: по течению реки, против течения реки, в озере,
основные величины,
характеризующие движение – скорость, время, расстояние.
- Задачи на совершение работы, основные
величины – время, объём совершённой работы, производительность труда, где
объём совершённой работы принимается за 100% или 1. - Задачи на проценты:
а) товар и его
стоимость, где первоначальная стоимость принимается за 100% или 1, повышение
или понижение стоимости рассматривается как нахождение части от числа в сторону
увеличения или уменьшения числа;
б) суммы вкладов
в банки и банковские процентные ставки, где первоначальный вклад принимается за
100% или 1, увеличение вклада рассматривается как нахождение части от числа
дополнительно к основной сумме;
в) процентное
содержание кислоты в растворе и др.
Приложение 3
Задача № 1. Цена первого товара повысилась на 30%, а потом еще на 5%. Цена второго
товара повысилась на 25%. После повышения цены товаров сравнялись. Найдите, на
сколько процентов первоначальная цена одного товара больше первоначальной цены
другого товара.
Устные рассуждения:
Всякую математическую модель можно
рассматривать с трёх позиций, в данном случае – товар: в рублях, в процентах, в
частях. Пусть первоначальная цена первого товара будет х руб, т.е. 100% или 1.
Тогда первое повышение цены на 30% в денежном выражении составляет 0,3 х руб., а
новая цена будет составлять 130% или 1,3х руб. Второе повышение на 5% в
денежном выражении составляет 1,3х 0,05 = 0,065х руб., значит последняя цена
будет состоять из суммы предыдущей плюс 5%, т.е. 1,3х + 0,065х = 1,365х руб.
Аналогично, пусть первоначальная цена второго
товара будет у руб, т.е. 100% или 1. Тогда первое повышение цены на 25% в
денежном выражении составляет 0,25у руб., а новая цена будет составлять 125%
или 1,25у руб. По условию после повышения цены товаров сравнялись, т.е.1,365х =
1,25у, откуда у = 1,092х. Найдём разницу цен в частях: у – х = 1,092 – 1 =
0,092.
Запись в тетрадях:
Пусть первоначальная цена первого товара будет
х руб, т.е. 100% или 1. Тогда первое повышение цены на 30% в денежном выражении
составляет 0,3 х руб., а новая цена будет составлять 130% или 1,3х руб. Второе
повышение на 5% в денежном выражении составляет
1,3х0,05 = 0,065х руб., значит последняя цена
будет состоять из суммы предыдущей плюс 5%, т.е. 1,3х + 0,065х = 1,365х руб.
Аналогично, пусть первоначальная цена второго
товара будет у руб, т.е. 100% или 1. Тогда первое повышение цены на 25% в
денежном выражении равно 0,25у руб., а новая цена будет составлять 125% или
1,25у рублей. По условию после повышения цены товаров сравнялись, т.е.1,365х =
1,25у, откуда у = 1,092х. Найдём разницу цен в частях: у – х = 1,092 – 1 =
0,092.
Переведём полученную дробь в проценты: %.
Ответ :разница первоначальных цен товаров
составляет 9,2%.
Задача № 2. Найдите первоначальную сумму вклада (в рублях), если после истечения
двух лет она выросла на 304,5 рубля при 3% годовых.
Устные рассуждения:
Пусть первоначальная сумма взноса будет х
руб., т.е. 100% или1. По условию задачи через год сумма вклада увеличилась на
3%, что в денежном выражении составляет 0,03х руб. Значит, через год сумма
вклада будет равна 1,03х руб. Ещё через год сумма вклада снова увеличилась на
3% годовых, в денежном выражении это увеличение составляет 1,03х0,03 = 0,0309х
(руб.). А общая сумма вклада за два года будет состоять из предыдущей суммы
вклада плюс 3% годовых, т.е.1,03х + 0,0309х = 1,0609х (руб.). По условию задачи
за два года сумма вклада увеличилась на 304,5 руб. Уравнение данной задачи
представляет собой разницу вкладов.
Запись в тетрадях:
Пусть первоначальная сумма взноса будет х
руб., т.е. 100% или1. Через год сумма вклада увеличилась на 3% годовых,
значит, через год сумма вклада будет составлять 1,03х руб. Ещё через год сумма
вклада снова увеличилась на 3% годовых, в денежном выражении это увеличение
составляет 1,03х0,03 = 0,0309х (руб.). Значит, за два года сумма вклада будет
составлять 1,03х + 0,0309х = 1,0609х (руб.). По условию задачи за два года
сумма вклада увеличилась на 304,5 руб., т.е.:
1,0609х – х = 304,5 ,
0,0609х = 304,5 ,
х = 304,5:0,0609 ,
х = 5000. Получили первоначальную
сумму вклада 5000 руб.
Ответ: 5000 рублей.
Задача № 3.
Смешав 70%-й и 60%-й растворы кислоты и добавив 2
кг чистой воды, получили 50%-й раствор кислоты. Если бы вместо 2
кг воды добавили 2 кг 90%-го раствора той же кислоты, то получили бы 70%-й
раствор кислоты. Сколько килограммов 70%-го раствора использовали для получения
смеси?
Устные рассуждения:
Поскольку речь идёт о двух растворах разной
концентрации, значит надо вводить две переменные. Семидесяти процентный
раствор состоит из 70% кислоты и 30% воды, а шестидесяти процентный раствор
состоит из 60% кислоты и 40% воды. Если первоначальную массу 70%-го раствора
обозначить за х кг, значит в нём кислоты будет 0,7х кг, а воды будет 0,3х кг.
Аналогично, если первоначальную массу 60%-го раствора обозначить за у кг,
значит, в нём кислоты будет 0,6у кг, а воды будет 0,4у кг. После добавления 2
кг чистой воды, концентрация раствора стала равной 50%. Это означает, что в
новом растворе масса воды будет 0,5(х + у +2) кг. Поскольку дополнительным
условием задачи является добавление чистой воды, значит, уравнение составляем
по массе воды. И так, первоначальная масса воды растворов была 0,3х кг и 0,4у
кг, затем ещё добавили 2 кг воды, в итоге получили 0,5(х + у + 2) кг воды.
Аналогично разбирается второй случай, когда к имеющимся растворам кислоты
добавляют 2 кг 90%-го раствора той же кислоты и получается 70%-й раствор
кислоты. Поскольку здесь дополнительным условием является добавление 90%-й
кислоты, то второе уравнение составим по массе кислоты. И так, к имевшимся
массам кислот 0,7х кг и 0,6у кг добавили кислоту массой кг,
т.е. 1,8 кг и получили массу кислоты 0,7(х + у + 2) кг.
Запишем и решим систему двух уравнений с двумя
переменными.
Запись в тетрадях:
Пусть первоначальная масса 70%-го раствора
кислоты будет х кг, значит в нём кислоты будет 0,7х кг, а воды будет 0,3х кг.
Аналогично, пусть первоначальная масса 60%-й растворы кислоты будет у кг,
значит, в нём кислоты будет 0,6у кг, а воды будет 0,4у кг. По условию первый
раз добавили 2 кг чистой воды, после чего концентрация раствора стала равной
50%, т.е. в полученном растворе воды будет 0,5(х + у +2) кг. Следовательно,
первое уравнение имеет вид:
0,3х + 0,4у + 2 = 0,5(х + у +2). По условию
второй раз добавили 2 кг 90%-й кислоты, значит, т.е. по массе кг или 1,8
кг и получили 70%-й раствор кислоты, масса кислоты в котором будет 0,7(х + у +
2) кг. Соответственно второе уравнение составим по массе кислоты в растворах:
0,7х + 0,6у + 1,8 = 0,7(х + у + 2). Решим
систему двух уравнений с двумя переменными:
Получили 3
кг 70%-й кислоты.
Ответ: 3
кг.
1.
Имелось два
сплава серебра. Процент содержания серебра в первом сплаве был на 25% выше, чем
во втором. Когда сплавили их вместе, то получили сплав, содержащий 30% серебра.
Определить массы сплавов, если известно, что серебра в первом сплаве было 4кг,
а во втором 8
кг.
Ответ: 8 кг; 32 кг
2.
В первом сосуде растворили 0,36 л,
а во втором 0,42 л чистого спирта. Процентное
содержание спирта в первом сосуде оказалось на 6% больше, чем во втором. Каково
процентное содержание спирта во втором и первом сосудах, если известно, что растворы
в первом сосуде на 4 л
меньше?
Ответ: 12%
и 6%
3.
В 4 кг сплава
меди и олова содержится 40% олова. Сколько килограммов олова добавить к этому
сплаву, чтобы его процентное содержание в новом сплаве стало бы равным
70%? Ответ:
4кг
4.
К 40%
раствору серной кислоты добавили 50 г чистой серной кислоты, после чего
концентрация раствора стала равной 60%. Найти первоначальную массу раствора.
Ответ: 100 г
5.
К раствору,
содержащему 30 г соли, добавили 400 г, после чего концентрация соли
уменьшилась на 10%. Найти первоначальную концентрацию соли в растворе.
Ответ: 15%
6.
В 5 кг сплава
олова и цинка содержится 80% цинка. Сколько килограммов олова надо добавить к
сплаву, чтобы процентное содержание цинка стало вдвое
меньше? Ответ: 5 кг
Задача Первая
труба наполняет бак объёмом 570 литров, а вторая труба – бак объёмом 530
литров. Известно, что одна из труб пропускает в минуту на 4 литра воды больше,
чем другая. Сколько литров воды в минуту пропускает вторая труба, если баки
были наполнены за одно и то же время?
Устные рассуждения:
Поскольку первая труба наполняет больший бак,
значит у неё пропускная способность больше, чем у второй трубы. Если пропускную
способность первой трубы обозначить через (х + 4) л за минуту, тогда пропускная
способность второй трубы будет х л за минуту. Значит, время наполнения бака
объёмом 570 л первой трубой будет минут, а время
наполнения бака объёмом 530 л второй трубой будет минут.
По условию баки были наполнены за одно и то же время.
Запись в тетрадях:
Пусть пропускная способность первой трубы
будет (х + 4) л за минуту, тогда пропускная способность второй трубы будет х л
за минуту. Значит, время наполнения бака объёмом 570
л первой трубой будет минут, а время
наполнения бака объёмом 530 л второй трубой будет минут.
По условию баки были наполнены за одно и то же время, т.е.:
=
, 570
=
, 570
= 530
+ 2120 , 40
=
2120 , = 53.
Получили, что вторая труба за минуту
пропускает 53 л.
Ответ: 53
л.
Задача № 5
Теплоход, скорость которого в неподвижной воде равна 20
км/ч, проходит по течению реки до пункта назначения и после стоянки
возвращается в исходный пункт. Найдите расстояние, пройденное теплоходом за
весь рейс, если скорость течения равна 4
км/ч, стоянка длится 3 часа, а в исходный пункт теплоход возвращается через 13
часов после отплытия из него. Ответ дайте в километрах.
Устные рассуждения:
По условию задачи скорость теплохода в
неподвижной воде равна 20 км/ч, скорость течения равна 4
км/ч. Значит, скорость теплохода по течению реки будет 24
км/ч, а против течения –
16 км/ч. Обозначим
расстояние от исходного пункта до пункта назначения за км.
Тогда, время, затраченное от исходного пункта до пункта назначения будет ч, а время, затраченное на обратный путь
будет ч. А всё время в пути, исключая стоянку 3
часа, составляет 10 часов.
Запись в тетрадях:
По условию задачи скорость теплохода в
неподвижной воде равна 20 км/ч, скорость течения равна 4
км/ч. Значит, скорость теплохода по течению реки будет 24
км/ч, а против течения –
16 км/ч. Пусть расстояние
от исходного пункта до пункта назначения за км.
Тогда время, затраченное от исходного пункта до пункта назначения будет ч, а время, затраченное на обратный путь
будет ч. Всё время в пути, исключая стоянку 3
часа, составляет 10 часов, т.е.:
Получили
расстояние от исходного пункта до пункта назначения 96
км, значит
расстояние за весь рейс
составляет 192 км.
Ответ: 192
км.
Приложение 4
Вариант – 1.
Задача № 1. Катер прошел 15 км по течению реки и 4
км по озеру, затратив на весь путь 1 ч. Найдите собственную скорость лодки,
если скорость течения реки равна 4 км/ч.
Задача № 2. Цену товара повысили на 25%, затем новую цену повысили еще на 10% и
наконец, после перерасчета произвели повышение цены еще на 12%. На сколько
процентов повысили первоначальную цену товара?
Задача № 3. Сберегательный банк в конце года начисляет 2% к сумме, находящейся на
счету. На сколько рублей увеличится первоначальный вклад в 5000 рублей через 3
года?
Вариант – 2.
Задача № 1. Моторная лодка прошла 10 км по озеру и 4
км против течения реки, затратив на весь путь 1 ч. Найдите собственную
скорость лодки, если скорость течения реки равна 3
км/ч.
Задача № 2. Найдите первоначальную сумму вклада (в рублях), если после истечения
трех лет она выросла на 765,1 рубля при 2% годовых.
Задача № 3. Цену на некоторый товар сначала снизили на 30%, а затем повысили на
20%. На сколько процентов изменилась первоначальная цена товара?
Вариант – 3.
Задача № 1. Какое количество воды нужно добавить в 1
литр 9%-ного раствора уксуса, чтобы получить 3%-ный раствор?
Задача № 2. Найдите двузначное число, если произведение его цифр в 6 раз меньше
самого числа, а если к исходному числу прибавить 9, то получится число,
написанное теми цифрами, но в обратном порядке.
Задача № 3. Сумма двух чисел равна 1100. Найдите наибольшее из них, если 6% одного
из них равны 5% другого.
Приложение 5
Вариант – 1.
Задача № 1. Сберегательный банк в конце года начисляет 5% к сумме, находившейся на
счету. На сколько процентов увеличится первоначальный вклад в 2000 рублей через
2 года?
Задача № 2. Два пешехода отправляются навстречу друг другу одновременно из двух
пунктов, расстояние между которыми равно 50
км, и встречаются через 5 ч. Определите скорость первого пешехода, если его
скорость на 2 км/ч больше, чем у другого.
Задача № 3. Численность волков в двух заповедниках в 2009 году составляла 220
особей. Через год обнаружили, что в первом заповеднике численность волков
возросла на 10%, а во втором – на 20%. В результате общая численность волков в
двух заповедниках составила 250 особей. Сколько волков было в первом заповеднике
в 2009 году?
Вариант – 2.
Задача № 1. Сберегательный банк в конце года начисляет 3% к сумме, находившейся на
счету. На сколько рублей увеличится первоначальный вклад в 1000 рублей через 2
года?
Задача № 2. К 40% раствору соляной кислоты добавили 50
г чистой кислоты, после чего концентрация раствора стала равной 60%. Найдите
первоначальный вес раствора.
Задача № 3 Города А, В и С соединены прямолинейным шоссе, причём город В
расположен между городами А и С. Из города А в сторону города С выехал легковой
автомобиль, и одновременно с ним из города В в сторону города С выехал
грузовик. Через сколько часов после выезда легковой автомобиль догонит
грузовик, если скорость легкового автомобиля на 28
км/ч больше скорости грузовика, а расстояние между городами А и В равно 112
км ?
План урока по математике в 11 классе «Решение текстовых задач» при подготовке к ЕГЭ
Тема урока: Решение текстовых задач
Тип урока: совершенствование ЗУН
Цели урока:
дидактическая: научить применять ранее полученные знания при решении текстовых задач в выполнении заданий ЕГЭ разного уровня сложности, стимулировать обучающихся к овладению рациональными приёмами и методами решения текстовых задач;
развивающая: развивать логическое мышление, память, познавательный интерес, продолжать формирование математической речи и графической культуры, вырабатывать умение анализировать и сравнивать;
воспитательная: приучать к эстетическому оформлению записи в тетради, умению выслушать других и умению общаться, прививать аккуратность и трудолюбие.
Ход урока:
|
Этапы урока, их содержание |
Деятельность |
|
|
учителя |
учащихся |
|
|
Постановка цели Сегодня мы продолжим отрабатывать навыки решения текстовых задач, но уже по вариантам ЕГЭ, рассмотрим различные задачи |
Сообщает тему урока, цель урока, на доске записывает число и тему урока |
Записывают в тетрадях |
|
Проверка домашнего задания (приложение 1) На дом было задано три задачи. Какие вопросы и затруднения по задачам. Если вопросов нет, то проверим одну из них. |
На экране показано правильное оформление задачи. Комментирует решение, привлекая к работе учащихся |
Сверяют своё решение с записями на экране, задают вопросы учителю, отвечают на вопросы учителя |
|
Актуализация темы (приложение 2) |
Проводит фронтальную беседу по типам задач и приёмам их решения |
|
|
Фронтальная работа, решение задач (приложение 3) |
Направляет на правильный выбор решения, следит за верностью рассуждений и речью учащихся, активизирует их работу сопутствующими вопросами |
Комментируют условие задачи, предлагают свои подходы к решению: введение переменных, обозначение величин, составление уравнений. |
|
Индивидуальная работа самостоятельная работа, (приложение 4) |
Раздаёт карточки с заданиями в трёх вариантах с тремя задачами различной степени сложности |
Самостоятельно выполняют задания в тетрадях |
|
Подведение итогов |
Комментирует работу класса, отличившимся учащимся выставляет отметки, всем учащиеся за самостоятельную работу отметки будут также выставлены в классный журнал |
|
|
Домашнее задание (приложение 5) |
Поясняет домашнее задание, обращая внимание на то, что аналогичные задачи были разобраны на уроке |
Приложение 1 (домашняя работа)
Задача № 1. Два велосипедиста отправляются навстречу друг другу одновременно из двух пунктов, расстояние между которыми равно 54 км, и встречаются через 2 ч. Определите скорость каждого велосипедиста, если скорость у одного из них она на 3 км/ч больше, чем у другого.
Задача № 2. Сберегательный банк в конце года начисляет 3% к сумме, находившейся на счету. На сколько рублей увеличится первоначальный вклад в 1000 рублей через 2 года?
Задача № 3. Под строительную площадку отвели участок прямоугольной формы, длина которого на 30 метров больше его ширины. При утверждении плана застройки выяснилось, что граница участка проходит по территории водоохраной зоны, поэтому его ширину уменьшили на 20 метров. Найдите длину участка, если после утверждения плана застройки площадь участка составила 2400 м2.
решение задачи № 1.
Устные рассуждения:
Одним из основных условий задачи является одновременное отправление велосипедистов из пунктов, значит, каждый из них находился в пути одно и то же время, т.е. 2 часа. Далее, даётся некая зависимость между скоростями велосипедистов, поэтому меньшую скорость, пусть это будет скорость первого велосипедиста, обозначим км/ч, тогда скорость второго будет
км/ч. По условию задачи велосипедисты встретились через 2 часа после отправления. Зная время движения и скорости велосипедистов, можно найти путь каждого из них. Таким образом, первый велосипедист за 2 часа проехал путь
км, а второй за те же 2 часа –
км. По условию задачи через 2 часа велосипедисты встретились, т.е. проехали весь путь 54 км.
Запись в тетради:
Обозначим скорость первого велосипедиста км/ч, тогда скорость второго будет
км/ч.
По условию задачи каждый велосипедист находился в пути 2 часа, значит, первый велосипедист проехал путь км, а второй –
км. По условию задачи через 2 часа велосипедисты встретились, т.е. проехали весь путь 54 км. Следовательно, уравнение составляем по проделанному пути обоими велосипедистами:
.
Решение:
,
,
,
. Получили: скорость первого велосипедиста 13 км/ч, а второго – 16 км/ч.
Ответ: 13 км/ч; 16 км/ч.
Оставшиеся две задачи разбирают устно.
Приложение 2
Ребята, давайте вспомним, какие типы текстовых задач мы рассматривали и какие основные величины характеризуют тот или иной тип задачи. И так:
-
Задачи на движение:
а) движение навстречу друг другу, движение в одном направлении, движение в противоположных направлениях;
б) движение по воде: по течению реки, против течения реки, в озере,
основные величины, характеризующие движение – скорость, время, расстояние.
-
Задачи на совершение работы, основные величины – время, объём совершённой работы, производительность труда, где объём совершённой работы принимается за 100% или 1.
-
Задачи на проценты:
а) товар и его стоимость, где первоначальная стоимость принимается за 100% или 1, повышение или понижение стоимости рассматривается как нахождение части от числа в сторону увеличения или уменьшения числа;
б) суммы вкладов в банки и банковские процентные ставки, где первоначальный вклад принимается за 100% или 1, увеличение вклада рассматривается как нахождение части от числа дополнительно к основной сумме;
в) процентное содержание кислоты в растворе и др.
Приложение 3
Задача № 1. Цена первого товара повысилась на 30%, а потом еще на 5%. Цена второго товара повысилась на 25%. После повышения цены товаров сравнялись. Найдите, на сколько процентов первоначальная цена одного товара больше первоначальной цены другого товара.
Устные рассуждения:
Всякую математическую модель можно рассматривать с трёх позиций, в данном случае – товар: в рублях, в процентах, в частях. Пусть первоначальная цена первого товара будет х руб, т.е. 100% или 1. Тогда первое повышение цены на 30% в денежном выражении составляет 0,3 х руб., а новая цена будет составлять 130% или 1,3х руб. Второе повышение на 5% в денежном выражении составляет 1,3х 0,05 = 0,065х руб., значит последняя цена будет состоять из суммы предыдущей плюс 5%, т.е. 1,3х + 0,065х = 1,365х руб.
Аналогично, пусть первоначальная цена второго товара будет у руб, т.е. 100% или 1. Тогда первое повышение цены на 25% в денежном выражении составляет 0,25у руб., а новая цена будет составлять 125% или 1,25у руб. По условию после повышения цены товаров сравнялись, т.е.1,365х = 1,25у, откуда у = 1,092х. Найдём разницу цен в частях: у – х = 1,092 – 1 = 0,092.
Запись в тетрадях:
Пусть первоначальная цена первого товара будет х руб, т.е. 100% или 1. Тогда первое повышение цены на 30% в денежном выражении составляет 0,3 х руб., а новая цена будет составлять 130% или 1,3х руб. Второе повышение на 5% в денежном выражении составляет
1,3х0,05 = 0,065х руб., значит последняя цена будет состоять из суммы предыдущей плюс 5%, т.е. 1,3х + 0,065х = 1,365х руб.
Аналогично, пусть первоначальная цена второго товара будет у руб, т.е. 100% или 1. Тогда первое повышение цены на 25% в денежном выражении равно 0,25у руб., а новая цена будет составлять 125% или 1,25у рублей. По условию после повышения цены товаров сравнялись, т.е.1,365х = 1,25у, откуда у = 1,092х. Найдём разницу цен в частях: у – х = 1,092 – 1 = 0,092.
Переведём полученную дробь в проценты: %.
Ответ :разница первоначальных цен товаров составляет 9,2%.
Задача № 2. Найдите первоначальную сумму вклада (в рублях), если после истечения двух лет она выросла на 304,5 рубля при 3% годовых.
Устные рассуждения:
Пусть первоначальная сумма взноса будет х руб., т.е. 100% или1. По условию задачи через год сумма вклада увеличилась на 3%, что в денежном выражении составляет 0,03х руб. Значит, через год сумма вклада будет равна 1,03х руб. Ещё через год сумма вклада снова увеличилась на 3% годовых, в денежном выражении это увеличение составляет 1,03х0,03 = 0,0309х (руб.). А общая сумма вклада за два года будет состоять из предыдущей суммы вклада плюс 3% годовых, т.е.1,03х + 0,0309х = 1,0609х (руб.). По условию задачи за два года сумма вклада увеличилась на 304,5 руб. Уравнение данной задачи представляет собой разницу вкладов.
Запись в тетрадях:
Пусть первоначальная сумма взноса будет х руб., т.е. 100% или1. Через год сумма вклада увеличилась на 3% годовых, значит, через год сумма вклада будет составлять 1,03х руб. Ещё через год сумма вклада снова увеличилась на 3% годовых, в денежном выражении это увеличение составляет 1,03х0,03 = 0,0309х (руб.). Значит, за два года сумма вклада будет составлять 1,03х + 0,0309х = 1,0609х (руб.). По условию задачи за два года сумма вклада увеличилась на 304,5 руб., т.е.:
1,0609х – х = 304,5 ,
0,0609х = 304,5 ,
х = 304,5:0,0609 ,
х = 5000. Получили первоначальную сумму вклада 5000 руб.
Ответ: 5000 рублей.
Задача № 3. Смешав 70%-й и 60%-й растворы кислоты и добавив 2 кг чистой воды, получили 50%-й раствор кислоты. Если бы вместо 2 кг воды добавили 2 кг 90%-го раствора той же кислоты, то получили бы 70%-й раствор кислоты. Сколько килограммов 70%-го раствора использовали для получения смеси?
Устные рассуждения:
Поскольку речь идёт о двух растворах разной концентрации, значит надо вводить две переменные. Семидесяти процентный раствор состоит из 70% кислоты и 30% воды, а шестидесяти процентный раствор состоит из 60% кислоты и 40% воды. Если первоначальную массу 70%-го раствора обозначить за х кг, значит в нём кислоты будет 0,7х кг, а воды будет 0,3х кг. Аналогично, если первоначальную массу 60%-го раствора обозначить за у кг, значит, в нём кислоты будет 0,6у кг, а воды будет 0,4у кг. После добавления 2 кг чистой воды, концентрация раствора стала равной 50%. Это означает, что в новом растворе масса воды будет 0,5(х + у +2) кг. Поскольку дополнительным условием задачи является добавление чистой воды, значит, уравнение составляем по массе воды. И так, первоначальная масса воды растворов была 0,3х кг и 0,4у кг, затем ещё добавили 2 кг воды, в итоге получили 0,5(х + у + 2) кг воды. Аналогично разбирается второй случай, когда к имеющимся растворам кислоты добавляют 2 кг 90%-го раствора той же кислоты и получается 70%-й раствор кислоты. Поскольку здесь дополнительным условием является добавление 90%-й кислоты, то второе уравнение составим по массе кислоты. И так, к имевшимся массам кислот 0,7х кг и 0,6у кг добавили кислоту массой кг, т.е. 1,8 кг и получили массу кислоты 0,7(х + у + 2) кг.
Запишем и решим систему двух уравнений с двумя переменными.
Запись в тетрадях:
Пусть первоначальная масса 70%-го раствора кислоты будет х кг, значит в нём кислоты будет 0,7х кг, а воды будет 0,3х кг. Аналогично, пусть первоначальная масса 60%-й растворы кислоты будет у кг, значит, в нём кислоты будет 0,6у кг, а воды будет 0,4у кг. По условию первый раз добавили 2 кг чистой воды, после чего концентрация раствора стала равной 50%, т.е. в полученном растворе воды будет 0,5(х + у +2) кг. Следовательно, первое уравнение имеет вид:
0,3х + 0,4у + 2 = 0,5(х + у +2). По условию второй раз добавили 2 кг 90%-й кислоты, значит, т.е. по массе кг или 1,8 кг и получили 70%-й раствор кислоты, масса кислоты в котором будет 0,7(х + у + 2) кг. Соответственно второе уравнение составим по массе кислоты в растворах:
0,7х + 0,6у + 1,8 = 0,7(х + у + 2). Решим систему двух уравнений с двумя переменными:
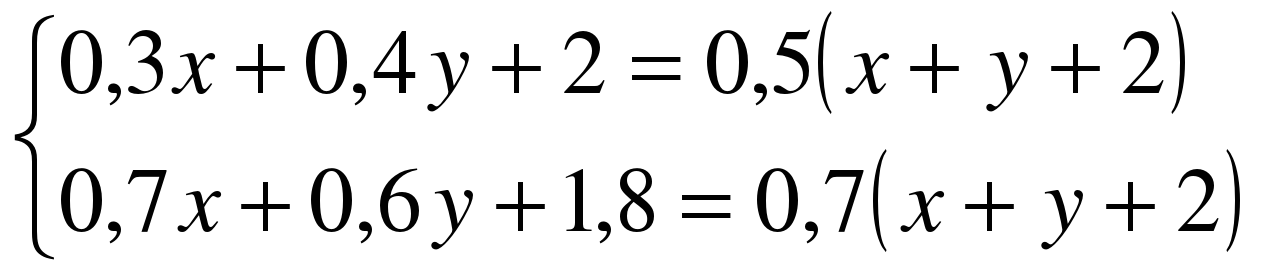
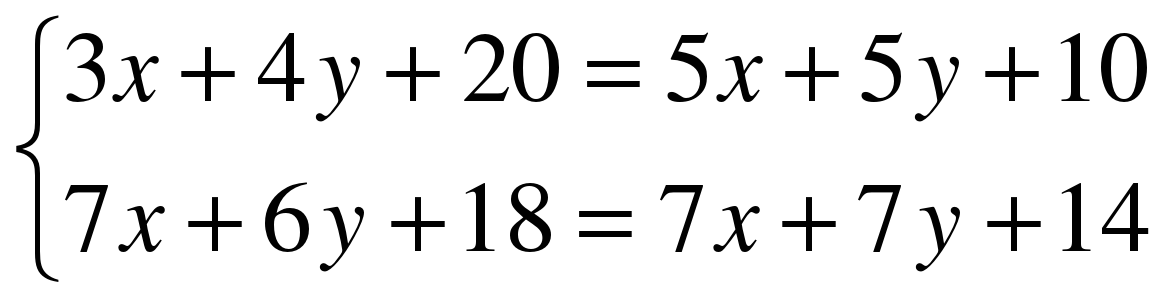
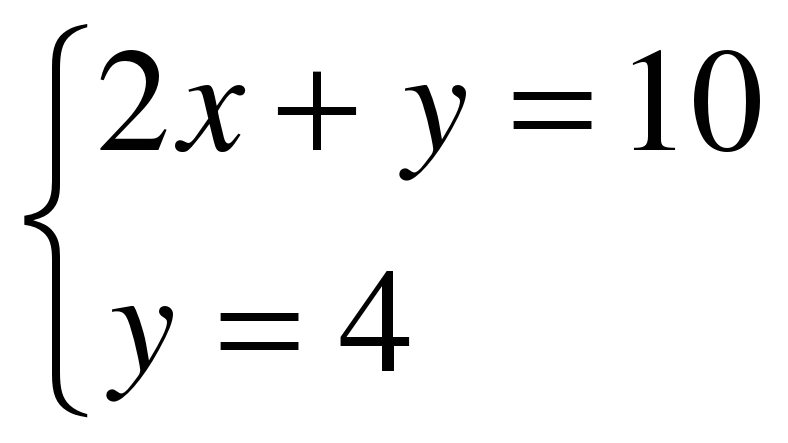
Получили 3 кг 70%-й кислоты.
Ответ: 3 кг.
-
Имелось два сплава серебра. Процент содержания серебра в первом сплаве был на 25% выше, чем во втором. Когда сплавили их вместе, то получили сплав, содержащий 30% серебра. Определить массы сплавов, если известно, что серебра в первом сплаве было 4кг, а во втором 8 кг. Ответ: 8 кг; 32 кг
-
В первом сосуде растворили 0,36 л, а во втором 0,42 л чистого спирта. Процентное
содержание спирта в первом сосуде оказалось на 6% больше, чем во втором. Каково процентное содержание спирта во втором и первом сосудах, если известно, что растворы в первом сосуде на 4 л меньше? Ответ: 12% и 6% -
В 4 кг сплава меди и олова содержится 40% олова. Сколько килограммов олова добавить к этому сплаву, чтобы его процентное содержание в новом сплаве стало бы равным 70%? Ответ: 4кг
-
К 40% раствору серной кислоты добавили 50 г чистой серной кислоты, после чего концентрация раствора стала равной 60%. Найти первоначальную массу раствора.
Ответ: 100 г -
К раствору, содержащему 30 г соли, добавили 400 г, после чего концентрация соли
уменьшилась на 10%. Найти первоначальную концентрацию соли в растворе.
Ответ: 15% -
В 5 кг сплава олова и цинка содержится 80% цинка. Сколько килограммов олова надо добавить к сплаву, чтобы процентное содержание цинка стало вдвое меньше? Ответ: 5 кг
Задача Первая труба наполняет бак объёмом 570 литров, а вторая труба – бак объёмом 530 литров. Известно, что одна из труб пропускает в минуту на 4 литра воды больше, чем другая. Сколько литров воды в минуту пропускает вторая труба, если баки были наполнены за одно и то же время?
Устные рассуждения:
Поскольку первая труба наполняет больший бак, значит у неё пропускная способность больше, чем у второй трубы. Если пропускную способность первой трубы обозначить через (х + 4) л за минуту, тогда пропускная способность второй трубы будет х л за минуту. Значит, время наполнения бака объёмом 570 л первой трубой будет минут, а время наполнения бака объёмом 530 л второй трубой будет
минут. По условию баки были наполнены за одно и то же время.
Запись в тетрадях:
Пусть пропускная способность первой трубы будет (х + 4) л за минуту, тогда пропускная способность второй трубы будет х л за минуту. Значит, время наполнения бака объёмом 570 л первой трубой будет минут, а время наполнения бака объёмом 530 л второй трубой будет
минут. По условию баки были наполнены за одно и то же время, т.е.:
=
, 570
= , 570
= 530
+ 2120 , 40
= 2120 ,
= 53.
Получили, что вторая труба за минуту пропускает 53 л.
Ответ: 53 л.
Задача № 5 Теплоход, скорость которого в неподвижной воде равна 20 км/ч, проходит по течению реки до пункта назначения и после стоянки возвращается в исходный пункт. Найдите расстояние, пройденное теплоходом за весь рейс, если скорость течения равна 4 км/ч, стоянка длится 3 часа, а в исходный пункт теплоход возвращается через 13 часов после отплытия из него. Ответ дайте в километрах.
Устные рассуждения:
По условию задачи скорость теплохода в неподвижной воде равна 20 км/ч, скорость течения равна 4 км/ч. Значит, скорость теплохода по течению реки будет 24 км/ч, а против течения –
16 км/ч. Обозначим расстояние от исходного пункта до пункта назначения за км. Тогда, время, затраченное от исходного пункта до пункта назначения будет ч, а время, затраченное на обратный путь будет ч. А всё время в пути, исключая стоянку 3 часа, составляет 10 часов.
Запись в тетрадях:
По условию задачи скорость теплохода в неподвижной воде равна 20 км/ч, скорость течения равна 4 км/ч. Значит, скорость теплохода по течению реки будет 24 км/ч, а против течения –
16 км/ч. Пусть расстояние от исходного пункта до пункта назначения за км. Тогда время, затраченное от исходного пункта до пункта назначения будет ч, а время, затраченное на обратный путь будет ч. Всё время в пути, исключая стоянку 3 часа, составляет 10 часов, т.е.:
Получили расстояние от исходного пункта до пункта назначения 96 км, значит
расстояние за весь рейс составляет 192 км.
Ответ: 192 км.
Приложение 4
Вариант – 1.
Задача № 1. Катер прошел 15 км по течению реки и 4 км по озеру, затратив на весь путь 1 ч. Найдите собственную скорость лодки, если скорость течения реки равна 4 км/ч.
Задача № 2. Цену товара повысили на 25%, затем новую цену повысили еще на 10% и наконец, после перерасчета произвели повышение цены еще на 12%. На сколько процентов повысили первоначальную цену товара?
Задача № 3. Сберегательный банк в конце года начисляет 2% к сумме, находящейся на счету. На сколько рублей увеличится первоначальный вклад в 5000 рублей через 3 года?
Вариант – 2.
Задача № 1. Моторная лодка прошла 10 км по озеру и 4 км против течения реки, затратив на весь путь 1 ч. Найдите собственную скорость лодки, если скорость течения реки равна 3 км/ч.
Задача № 2. Найдите первоначальную сумму вклада (в рублях), если после истечения трех лет она выросла на 765,1 рубля при 2% годовых.
Задача № 3. Цену на некоторый товар сначала снизили на 30%, а затем повысили на 20%. На сколько процентов изменилась первоначальная цена товара?
Вариант – 3.
Задача № 1. Какое количество воды нужно добавить в 1 литр 9%-ного раствора уксуса, чтобы получить 3%-ный раствор?
Задача № 2. Найдите двузначное число, если произведение его цифр в 6 раз меньше самого числа, а если к исходному числу прибавить 9, то получится число, написанное теми цифрами, но в обратном порядке.
Задача № 3. Сумма двух чисел равна 1100. Найдите наибольшее из них, если 6% одного из них равны 5% другого.
Приложение 5
Вариант – 1.
Задача № 1. Сберегательный банк в конце года начисляет 5% к сумме, находившейся на счету. На сколько процентов увеличится первоначальный вклад в 2000 рублей через 2 года?
Задача № 2. Два пешехода отправляются навстречу друг другу одновременно из двух пунктов, расстояние между которыми равно 50 км, и встречаются через 5 ч. Определите скорость первого пешехода, если его скорость на 2 км/ч больше, чем у другого.
Задача № 3. Численность волков в двух заповедниках в 2009 году составляла 220 особей. Через год обнаружили, что в первом заповеднике численность волков возросла на 10%, а во втором – на 20%. В результате общая численность волков в двух заповедниках составила 250 особей. Сколько волков было в первом заповеднике в 2009 году?
Вариант – 2.
Задача № 1. Сберегательный банк в конце года начисляет 3% к сумме, находившейся на счету. На сколько рублей увеличится первоначальный вклад в 1000 рублей через 2 года?
Задача № 2. К 40% раствору соляной кислоты добавили 50 г чистой кислоты, после чего концентрация раствора стала равной 60%. Найдите первоначальный вес раствора.
Задача № 3 Города А, В и С соединены прямолинейным шоссе, причём город В расположен между городами А и С. Из города А в сторону города С выехал легковой автомобиль, и одновременно с ним из города В в сторону города С выехал грузовик. Через сколько часов после выезда легковой автомобиль догонит грузовик, если скорость легкового автомобиля на 28 км/ч больше скорости грузовика, а расстояние между городами А и В равно 112 км ?
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа
пос. Мизур Алагирского района РСО-Алания
Открытый урок по теме
«Решение заданий ЕГЭ»
Учитель математики Агузарова Л.Д.
п. Мизур
2021г
Тема: Решение заданий ЕГЭ
(задачи с практическим содержанием, рациональные, показательные, логарифмические, иррациональные уравнения, логарифмические неравенства )
Цели занятия:
Образовательные:
-
Повторить материал по данной теме;
Развивающие:
-
Развитие познавательного интереса учащихся к уроку математики;
-
Развитие логического мышления;
-
Развитие скорости и аккуратности;
-
Развитие навыков коллективной работы в сочетании с индивидуальной.
Воспитательные:
-
Воспитание трудолюбия ;
-
Воспитание уважения к окружающим;
Тип урока: урок актуализации знаний и умений (урок повторения).
Ход урока
I. Организационный этап.
Приветствие. Открыли тетради, записали на полях число, классная работа.
I I. Проверка домашней работы
Как у вас обстоят дела с домашней работой? Для того чтобы урок прошел успешно, я должна знать какие затруднения у вас были в домашней работе. Поднимите руки у кого они были.
I I I. Постановка цели и задач урока.
У вас на столах лежат листы, посмотрите на заголовок и попробуйте сформулировать тему нашего урока. «Решение заданий ЕГЭ». Посмотрите на содержание и попробуйте сформулировать цели урока. Сегодня у нас необычный урок, на котором мы будем повторять почти все виды уравнений. Перед вами стоит задача – показать свои знания и умения по решению задач с практическим содержанием, рациональные, показательные, логарифмические, иррациональные уравнения. А так же задание 15 из второй части профильного уровня.
Древнегреческий поэт Нивей утверждал, что математику нельзя изучать, наблюдая, как это делает сосед. Поэтому будем сегодня работать самостоятельно.
IV. Актуализация знаний
-
Что такое процент? Какие три типа задач на % существуют? (% от числа, целого по части процента, сколько % составляет одна величина от другой)
-
Что такое корень уравнения? Что значить решить уравнение?
V. Повторение
Прототип задания 1 Задания с практическим содержанием
-
Шариковая ручка стоит 30 рублей. Какое наибольшее количество таких ручек можно будет купить на 300 рублей после повышения цены на 25%?
-
Цена на электрический чайник была повышена на 14% и составила 1596 рублей. Сколько рублей стоил чайник до повышения цены?
-
Для приготовления маринада для огурцов на 1 литр воды требуется 10 г лимонной кислоты. Лимонная кислота продается в пакетиках по 15 г. Какое наименьшее число пачек нужно купить хозяйке для приготовления 8 литров маринада?
-
В летнем лагере 152 ребенка и 21 воспитатель. Автобус рассчитан не более чем на 30 пассажиров. Какое наименьшее количество автобусов понадобится, чтобы за один раз перевезти всех из лагеря в город?
Прототип задания 5
Рациональные уравнения
-
=
Показательные уравнения
-
(
)х+4=49
-
2х-3=
-
(0,2)5+4х=125
Алгоритм решения задания:
-
Определяем вид уравнения.
-
Представляем правую часть в виде степени с одним и тем же основанием
-
Переходим к линейному уравнению и решаем уравнение.
-
Записываем ответ.
Логарифмические уравнения
-
log3(x+6)=log3(10-x)-1
-
log2(8-x)=2 log2(4+x)
Алгоритм решения задания:
-
Определяем вид уравнения.
-
Представляем правую часть в виде логарифма с одним и тем же основанием.
-
Потенцируем и решаем уравнение.
-
Проверяем корни.
-
Записываем ответ.
Иррациональные уравнения
-
√2х-3=х-3
VI. Применение знаний и умений в новой ситуации
Решить рациональное уравнение
(2х-11)2=(2х-1)2
(х-11)4=(х+3)4
Решить логарифмическое неравенство
х2log243(4-x)≤ log3(x2-8x+16)
VII.. Контроль усвоения, обсуждение допущенных ошибок
Самостоятельная работа в парах
Решите уравнения
Вариант 1
Решите уравнение
-
25-х=64
-
42х-17=
-
√4х+16=10
-
log8(x+4)=log8(5x-16)
-
=
Вариант 2
Решите уравнение
-
21-х=32
-
35х-12=
-
√14-5х=3
-
log2(x+3)=log2(3x-15)
-
=
VIII .Домашнее задание варианты 11-14 задания 7
IX. Рефлексия
Продолжи предложение
Сегодня на уроке я научился…
Сегодня на уроке мне понравилось…
Сегодня на уроке я повторил…
Сегодня на уроке я закрепил…
Цели урока:
- обобщить знания по теме: «Применение
производной к исследованию функций, к
нахождению наибольшего и наименьшего значения
функции на отрезке»; - формирование умения применять теоретические
знания к работе с графиком функции,
производной и касательной; - развитие интереса и внимания при решении задач
по готовым чертежам.
Задачи: отработка навыка работы с
производной при подготовке к ЕГЭ.
План урока:
- Организационный момент. Постановка цели урока.
Мотивация учебно-познавательной цели - Устная работа на вычисление производных
- Исследование функции и её производной.
Сопоставление полученных графиков. - Нахождение наименьшего и наибольшего значения
функции на отрезке с использованием графика
функции. - Динамическая пауза
- Вычисление значения производной в точке по
графику функции и касательной - Тест типовых вариантов реальных заданий ЕГЭ (В8,
В11) - Подведение итогов урока
- Рефлексия
- Домашнее задание
Оборудование: Мультимедиа
установка.
ХОД УРОКА
Задания для устной работы отображаются на
слайде 2 Приложения 1.
1. Найдите производную
2. Исследуйте функцию и постройте её график.
Исследование выполняется учеником на доске и
обсуждается с классом, график функции
отображается на слайде 3 Приложения
1. После этого учитель предлагает
исследовать и построить график самой
производной, на том же слайде 3 Приложения
1. отображается соответствующий график.
Теперь учитель предлагает сопоставить оба
графика и проследить за тем, как ведёт себя
функция по мере изменения производной. На слайде
можно проследить данный процесс за счёт
анимации. Учащиеся формулируют соответствующие
выводы.
Решение задач по готовым чертежам.
Укажите по графику производной функции
промежутки возрастания, убывания, экстремумы
самой функции (Приложение 1,
слайды 4, 5)
3. Нахождение наименьшего и наибольшего
значения функции на отрезке с использованием
графика функции и аналитически
Учащимся предлагается сначала по графику одной
функции слайд 6 Приложения 1.
найти наименьшее и наибольшее значения функции
на различных отрезках, после обсуждения
возможных ситуаций сформулировать алгоритм
решения таких задач без построения графика (Приложение 1, слайд 7).
Решение типовой задачи ЕГЭ на нахождение
наименьшего и наибольшего значения функции на
отрезке по алгоритму у доски: y = 14tgx – 14x+
5 – 5
(Приложение
1, слайд 
4. Вычисление значения производной в точке
по графику функции и касательной
Обратимся к следующему слайду 9 Приложения 1. Чтобы иметь
возможность проверить наши рассуждения,
рассмотрим не только график неизвестной функции
и касательной проведённой в некоторой точке (а
именно такой случай нас будет интересовать
позже), а и формулу, задающую эту функцию.
Зная и х0
= 2, учащиеся вычисляют значение производной в
данной точке и записывают ответ.
Учащиеся формулируют, в чём заключается
геометрический смысл производной и по чертежу
вычисляют tgA из прямоугольного
треугольника АВС. Полученные результаты
сравниваются.
Переход к следующему слайду 10 Приложения
1.
Учащиеся рассматривают случай, когда
касательная с положительным направлением оси ОХ
образует тупой угол. В ходе решения
рассматриваем смежные углы и формулу приведения.
Замечаем, что не всегда удобно вычислять тангенс
угла, и обращаемся в решении к уравнению прямой и
угловому коэффициенту.
Учащиеся формулируют способы нахождения
производной в точке касания по графику,
используя геометрический смысл производной.
Решение типовой задачи ЕГЭ на вычисление
значения производной в точке по графику функции
и касательной. Приложение 1.
Слайд 11.
5. Проверочный минитест по вариантам
Приложение 1. Слайды
12, 13, 14
6. Подведение итогов урока
7. Рефлексия
8. Домашнее задание
19.12.2022
Тип урока: семинарское занятие.
Цели урока:
Познавательные: повторить и обобщить изученный за курс средней школы материал по математике, закрепить навыки решения сложных уравнений различными методами.
Развивающие: развивать ключевые коммуникативные компетенции, речь, внимание, память, логическое мышление, умение обобщать, делать выводы, развивать навыки самоконтроля и творческие способности учащихся.
Воспитательные: совершенствовать навыки этичного межличностного общения, сознательное отношение к математике; активизировать познавательную деятельность в коллективе, формировать навыки сотрудничества в решении поисковых задач, воспитывать у учащихся морально-ценностные чувства.
Задачи урока:
1. Систематизировать теоретические знание по теме.
2. Развивать умение работать с заданиями ЕГЭ.
Совершенствовать навыки решения сложных уравнений различными методами.
Ход урока:
I Организационный момент:
а) готовность класса к уроку;
б Слово учителя: Ребята, сегодня у нас необычный урок. Мы проверим наши знания, уровень нашей подготовки к сдаче ЕГЭ. И я хочу начать сегодняшний урок с притчи.
— Учитель, я уже целый год живу у тебя, но до сих пор выполняю только работы по хозяйству. Когда ты будешь меня учить? Разве я для этого пришёл к тебе в ученики, скажи?
— Имей терпение, — ответил учитель, — ещё не пришло время. Иди в нижнюю долину и посади дерево, вырасти его, а я подумаю.
Долгий и тяжёлый путь проделал ученик, пока спустился в долину. По дороге он выкопал маленький саженец и посадил его. С той поры, дважды в день он проходил опасный путь, между хижиной и долиной, чтобы полить деревце. Изо дня в день, он присматривал за деревом. Так прошёл год. Усилия его не пропали даром. Дерево выросло высоким и крепким. Однажды на рассвете, он вышел из хижины и увидел своего учителя, сидящего у ручья под деревом.
— Учитель! – обрадовался юноша. – Как я счастлив вновь увидеть тебя! Я должен извиниться перед тобой, что не смог стать твоим учеником, обманув твоё доверие! Ты подумал, что я слаб, когда я остался жить в долине. Но я должен был заботиться о своём деревеИ теперь, ты вряд ли возьмёшь меня обратно…
Выслушав пылкую речь юноши, старик сказал ему: — Именно в этот год, ты вместе с деревом взращивал такие качества своего характера, которые тебе помогут постигать знания.
Твоё дерево говорит о твоей готовности. Посмотри!
Ответственность ты имел, но только по необходимости, Был нетерпелив и эмоционален, как переплетенные побеги саженца. Чтобы обрести знания, нужна, прежде всего, дисциплина.
Ибо корни дерева – твоя ответственность,
ствол дерева – твоё терпение,
ветви дерева – спокойствие,
а листья – знания!
И вам я желаю такого же упорства и терпения, чтобы хорошо подготовиться к ЕГЭ и успешно его сдать.
А теперь приступим к выполнению заданий.
Проверка дз.
Дать определение уравнения и его корня, равносильности двух уравнений.
Ответ:
Арифметическое выражение, содержащее неизвестную переменную и знак
Оценить
122
Содержимое разработки
МБОУ СОШ №1 с. Кизляр
План- конспект открытого урока
по математике в 11 классе
«Подготовка к ЕГЭ. Решение сложных комбинированных уравнений»
Урок разработала и провела:
Магометова Х. Н.,
учитель математики
МБОУ СОШ №1 с. Кизляр
Апрель 2021 г
Тип урока: семинарское занятие.
Цели урока:
Познавательные: повторить и обобщить изученный за курс средней школы материал по математике, закрепить навыки решения сложных уравнений различными методами.
Развивающие: развивать ключевые коммуникативные компетенции, речь, внимание, память, логическое мышление, умение обобщать, делать выводы, развивать навыки самоконтроля и творческие способности учащихся.
Воспитательные: совершенствовать навыки этичного межличностного общения, сознательное отношение к математике; активизировать познавательную деятельность в коллективе, формировать навыки сотрудничества в решении поисковых задач, воспитывать у учащихся морально-ценностные чувства.
Задачи урока:
-
Систематизировать теоретические знание по теме.
-
Развивать умение работать с заданиями ЕГЭ.
Совершенствовать навыки решения сложных уравнений различными методами.
Ход урока:
I Организационный момент:
а) готовность класса к уроку;
б Слово учителя: Ребята, сегодня у нас необычный урок. Мы проверим наши знания, уровень нашей подготовки к сдаче ЕГЭ. И я хочу начать сегодняшний урок с притчи.
— Учитель, я уже целый год живу у тебя, но до сих пор выполняю только работы по хозяйству. Когда ты будешь меня учить? Разве я для этого пришёл к тебе в ученики, скажи?
— Имей терпение, — ответил учитель, — ещё не пришло время. Иди в нижнюю долину и посади дерево, вырасти его, а я подумаю.
Долгий и тяжёлый путь проделал ученик, пока спустился в долину. По дороге он выкопал маленький саженец и посадил его. С той поры, дважды в день он проходил опасный путь, между хижиной и долиной, чтобы полить деревце. Изо дня в день, он присматривал за деревом. Так прошёл год. Усилия его не пропали даром. Дерево выросло высоким и крепким. Однажды на рассвете, он вышел из хижины и увидел своего учителя, сидящего у ручья под деревом.
— Учитель! – обрадовался юноша. – Как я счастлив вновь увидеть тебя! Я должен извиниться перед тобой, что не смог стать твоим учеником, обманув твоё доверие! Ты подумал, что я слаб, когда я остался жить в долине. Но я должен был заботиться о своём деревеИ теперь, ты вряд ли возьмёшь меня обратно…
Выслушав пылкую речь юноши, старик сказал ему: — Именно в этот год, ты вместе с деревом взращивал такие качества своего характера, которые тебе помогут постигать знания.
Твоё дерево говорит о твоей готовности. Посмотри!
Ответственность ты имел, но только по необходимости, Был нетерпелив и эмоционален, как переплетенные побеги саженца. Чтобы обрести знания, нужна, прежде всего, дисциплина.
Ибо корни дерева – твоя ответственность,
ствол дерева – твоё терпение,
ветви дерева – спокойствие,
а листья – знания!
И вам я желаю такого же упорства и терпения, чтобы хорошо подготовиться к ЕГЭ и успешно его сдать.
А теперьприступим к выполнению заданий.
Проверка дз.
Дать определение уравнения и его корня, равносильности двух уравнений.
Ответ:
Арифметическое выражение, содержащее неизвестную переменную и знаки равенства называют уравнением. Значение переменной, превращающее уравнение в верное равенство, называют корнем уравнения. Два уравнения называют равносильными, если любой корень первого уравнения является корнем второго уравнения и любой корень второго уравнения является корнем первого уравнения.
Дать определение равносильности преобразования уравнения и перечислить основные равносильные преобразования.
Ответ:
Замену одного уравнения другим, равносильным ему уравнением называют равносильным преобразованием уравнения.
Равносильными преобразованиями уравнения являются:
-
перенос члена уравнения с противоположным знаком из одной части уравнения в другую;
-
умножение (деление) обеих частей уравнения на отличную от нуля число;
-
возведение уравнения в нечетную степень;
-
извлечение корня нечетной степени с обеих частей уравнения:
-
логарифмирование показательного уравнения;
-
применение тождеств, т. е равенств, справедливых для любого числа.
Рассказать, какие равносильные преобразования нужно выполнить, чтобы решить следующие уравнения

Дайте определение уравнения – следствия и перечислите преобразования, приводящие к уравнению следствия.
Ответ:
Пусть даны два уравнения. Если любой корень первого уравнения является корнем второго уравнения, то второе уравнение называют уравнением- следствием первого.
Замену уравнения другим уравнением, которое является его следствием, называют переходом к уравнению- следствию.
При переходе к уравнению- следствия возможно появление лишних корней, посторонних для исходного уравнения, поэтому проверка полученных корней является обязательной частью решения уравнения.
Преобразованиями, приводящими к уравнению- следствия является:
-
возведение уравнения в четную степень;
-
потенцирование логарифмического уравнения;
-
освобождение уравнения от знаменателя;
-
приведение подобных членов;
-
применение формул (тригонометрических, логарифмических и других).
-
Расскажите, каким способом приводится следующие уравнения к уравнению – следствия.



Карточки имеются у каждого ученика на парте.
Сложные уравнения можно решить, приводя их к системам. Правила перехода от уравнений к равносильным системам:
1.
2.
3.
4.
5.
6.
7.
М-область существования
8.
9.
10.
11.
Работа в группах.
Запишите системы, равносильные уравнениям. (Работы выполняют на листочках)..
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
Очень часто можно встретить уравнение, которое имеет дополнительное условие, например:
Как можно упростить решение такого типа уравнения?
Разбор решения на доске.
Ответ:
Учитывая, что левая часть уравнения неотрицательное число получаем 




Самыми сложными считаются уравнения с параметром. Дайте определение уравнения с параметром. Давайте рассмотрим несколько таких уравнений с использованием свойств функций:
а)

Ответ:
Для каждого значения a рассмотрим функцию
Она определена на множестве R, четная, поэтому, если 

Уравнение (1) имеет три корня тогда и только тогда, когда оно имеет 

При 

При 


Видеоурок.
Максимум за выполнение данного задания(18 задание) можно получить 4 балла.
В задачах с параметром допускают весьма разнообразные способы решений. Наиболее распространенными из них являются;
Чисто алгебраический способ решения;
-способ решения,основанный на построении и исследовании геометрической модели данной задачи;
-функциональный способ, в котором могут быть и алгебраические, и геометрические моменты, но базовым является исследование некоторой функции.
Критерии оценивания:
|
Обоснованно получен верный ответ |
4 балла |
|
|
С помощью верного рассуждения получены оба верных значения параметра, но -или в ответ включены и одно-два неверных значения; -или решение недостаточно обосновано. |
3 балла |
|
|
С помощью верного рассуждения получено хотя бы одно верное значение параметра |
2 балла |
|
|
Задача сведена к исследованию: -или взаимного расположения трех окружносей; -или двух квадратных уравнений с параметром. |
1 балл |
|
|
Решение не соответствует ни одному из критериев, перечисленных выше |
О баллов |
Выполнения тренировочных упражнений на закрепление навыков и умений решать уравнения.
-
-
;
-
VI Домашнее задание:
Разбор заданий типа С с индивидуальных карточекс сайта www.ege.edu.ru Банк заданий на доске.
Карточка №1
С1.(В13)
Карточка №2
C1.(B1)
Карточка №3
C1.(B12)
Карточка №4
C1.(B19)
Карточка №5
С5. Найти все значения a, такие, что уравнение имеет единственное решение:
Карточка №6
С5. Найти все значения a, такие, что уравнение имеет единственное решение:
Карточка № 7
Найти наибольший корень уравнения:

Карточка № 8
Найти значение р, при которых уравнение

Карточка №9
Решить уравнение
-
Повторить теорию по темам:
-
Уравнения-следствия.
-
Равносильность уравнений системам.
-
Равносильность уравнений на множествах.
VII Подведение итогов урока.
-
Оцените вашу работу на уроке.
Сколько баллов вы набрали?
К какому выводу пришли?
Лист самооценки работы учащегося
———————————————————————————(Ф.И. учащегося)
———————————————————————————(тема урока)
|
Мой вклад… |
Баллы |
|||
|
1(плохо) |
2(слабо) |
3(хорошо) |
4(отлично) |
|
|
В поисках материала по теме |
||||
|
В теоретическом изучении материала |
||||
|
В решении примеров |
||||
|
В групповой работе |
||||
|
В защите работ, анализе решений |
Перевод баллов:
0-9 баллов-2
10-13 баллов-3
14-16 баллов-4
15-20 баллов-5
Лист самооценки работы учащегося
———————————————————————————(Ф.И. учащегося)
———————————————————————————(тема урока)
|
Мой вклад… |
Баллы |
|||
|
1(плохо) |
2(слабо) |
3(хорошо) |
4(отлично) |
|
|
В поисках материала по теме |
||||
|
В теоретическом изучении материала |
||||
|
В решении примеров |
||||
|
В групповой работе |
||||
|
В защите работ, анализе решений |
Перевод баллов:
0-9 баллов-2
10-13 баллов-3
14-16 баллов-4
15-20 баллов-5
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/518910-plankonspekt-otkrytogo-uroka-po-matematike-v

«Свидетельство участника экспертной комиссии»
Оставляйте комментарии к работам коллег и получите документ
БЕСПЛАТНО!
Конспект урока алгебры в 11 классе
Тема урока: Подготовка к ЕГЭ по математике. Задача В5. Уравнения.
Цели и задачи урока:
Подготовка к ЕГЭ по математике;
Создать условия для осознанного усвоения
видов уравнения и их решения;
Повторить основные алгоритмы решения
уравнений различных видов;
Развитие познавательных интересов на уровне
любопытства, любознательности, поиска
способов решения поставленной задачи;
Формирование самостоятельности мышления,
мыслительных операций: сравнения, анализа,
синтеза, обобщения, аналогии.
Оборудование урока:
1. Ноутбук, мультимедийный проектор, экран;
2. Карточки с заданиями.
ХОД УРОКА.
Урок обобщение по алгебре в 11 классе с компьютерной поддержкой, с использованием
электронных средств обучения. Весь ход урока сопровождается презентацией
Задание на дом(записано на доске):
Индивидуальные карточки задания для трёх учащихся класса (на повторение по теме
Логарифмы)
Два человека у доски (по два уравнения)
log
4
(x + 12) = log
2
x 25
3-х
= 0,2
Остальные работают устно по презентации.
Почтовая марка стоит 2 руб. 40 копеек.
Какое наибольшее число этих марок
можно купить на 80 рублей?
80 : 2, 4 = 800: 24 = 33, 333…. ≈ 33 марки
800 ,0 24
72 33,33
80
72
80…
В 1. Задания с практическим содержанием
В 2. Анализ и чтение графиков функции.
На диаграмме показана среднемесячная температура
воздуха (в градусах Цельсия) в Ярославле по
результатам многолетних наблюдений. Найдите по
диаграмме количество месяцев, когда средняя
температура в Ярославле была отрицательной.
На рисунке изображён график функции y=f(x)
и касательная к нему
в точке с абсциссой x0.
Найдите значение
производной функции
f(x) в точке x0.
(+)
На экзамен вынесено 60 вопросов, Андрей не
выучил 3 из них. Найдите вероятность
того, что ему попадется выученный
билет.
Андрей выучил 60 – 3 = 57 вопросов.
Поэтому вероятность того, что на
экзамене ему попадется выученный билет
равна
Ответ: 0,95
Задачи В5 ЕГЭ по математике это задачи на проверку
навыков умения решать уравнения.
Линейные и квадратные уравнения
Рациональные уравнения
Иррациональные уравнения
Показательные уравнения
Логарифмические уравнения
Тригонометрические уравнения
Будьте внимательны, записывая ответ.
В любом случае, ОБЯЗАТЕЛЬНО делайте проверку,
много времени это не займёт, а вас избавит от ошибок.
Помните, что ответ это целое число
или конечная десятичная дробь.
Итог урока:
Типичные ошибки ЕГЭ:
Невнимательно читаем вопрос, решая
уравнения, в которых получается больше
одного корня; в вопросе всегда указывается
какое значение требуется найти.
Знают как решать, начинают решать, но на
радостях могут не дорешать, например, в
уравнении log
2
(2x- 
даже не вспомнив, что искать надо х.
Забывают, что нуль не относится ни к
отрицательным, ни к положительным числам


















































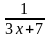 =
=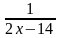
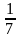 )х+4=49
)х+4=49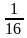
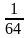
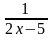 =
=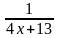
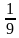
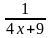 =
=








































 ;
;






