Конспект урока егэ производная

МБОУ СОШ №21

Конспект открытого урока по алгебре в 11 классе

на тему:

«Производная в заданиях  ЕГЭ»

учитель математики

                                                                                      Скороходова Н.Ф.

2019г.

                                                   План-конспект

открытого урока по алгебре в 11 классе по теме:

«Производная в заданиях ЕГЭ»

Дата проведения: 24.04.2019г.

Тип урока: Урок повторения, обобщения и систематизации знаний. Урок-практикум.

Цель урока:    В рамках повторения изученного необходимо закрепить теоретический материал при решении задач типа №14(база)  при подготовке к ЕГЭ.

Задачи:

Обучающие: 

• Повторить основные понятия раздела «Производная»
• Научить учащихся  решению задач на тему «Производная» из вариантов ЕГЭ

Развивающие:

• Развитие познавательного интереса, логического мышления, развитие памяти, внимательности.
• воспитывать интерес к структуре компьютерных сетей.

Воспитательные: 

• воспитывать добросовестное отношение к труду, инициативность;
• воспитание дисциплины и организованности

Структура урока: 

• организационный момент;
• актуализация опорных знаний
• решение задач
• домашнее задание

Оборудование:  презентация, компьютер, мультимедиа проектор.

План урока:

1. Вводное слово учителя. Постановка цели урока – 2 мин
2. Теоретический фундамент – повторение основных понятий, формул и правил по теме «Производная» — 10 мин.
3. Практикум: решение ключевых типов задач №14 из ЕГЭ по математике – 15 мин.
4. Самостоятельная работа учащихся — решение задач №14 из ЕГЭ»  – 8 мин. (см. Приложение)
5. Проверка результатов самостоятельной работы – 2 мин.
6. Домашнее задание – 1 мин.
7. Рефлексия. Подведение итогов урока. – 2 мин.

Ход урока:

Постановка цели урока:

Совсем скоро вам предстоит сдавать экзамены в форме ЕГЭ. Мы с вами уже несколько  раз писали ДКР и анализ диагностических работ показал, что некоторые ученики испытывают затруднения при выполнении заданий №14 из ЕГЭ(базового уровня). Поэтому нам надо восполнить этот пробел и  для успешного решения таких задач на экзамене нам предстоит серьезная работа. Сегодня на уроке мы вспомним и повторим материал по этой теме, решим ключевые типы задач №14, входящие в ЕГЭ.

У вас на партах лежат листочки с заданиями, которые вам надо  будет решить в конце урока.  Посмотрите внимательно на задания, на какую тему? Итак, тема нашего урока «Производная в заданиях ЕГЭ».

Цель урока: формирование практических навыков решения задач по теме «Производная»

В ходе беседы, учащиеся сами ставят задачи урока:

1. Повторить теоретические знания по теме «Производная функции  и ее геометрический смысл.
2. Научиться решать все виды задач типа №14 из открытого банка заданий для подготовки к ЕГЭ.

Поэтому я вас заранее попросила повторить теоретический материал по этой теме.

Если вы хотите быть уверенным в своем понимании, поделитесь своим знанием с кем-нибудь (идеально, если этот кто-то очень плохо разбирается в предмете).

 Лучший тест на знание предмета — способность передать его другому человеку.

Об этом как никто лучше других сказал римский философ Сенека

«Уча других, мы учимся сами»

Есть такая старая истина: «Хочешь научиться сам — начни учить других». Она в полной мере касается и нас. Т.к. обучая других, человек учится сам. При учении, наши знания обновляются и пополняются, даже тогда, когда мы с информацией уже знакомы. Не зря говорят, повторение – мать учения.

Т.е. сегодня некоторые из вас будут в роли учителей.

2. Актуализация опорных знаний. Один ученик у доски рассказывает теорию по данной теме, используя презентацию.

Учащиеся вспоминают:

• В чём заключается геометрический смысл производной?
• Что происходит с функцией, если её производная положительна, отрицательна, равна нулю?
• Как меняется знак производной в точке максимума и минимума функции?
•  Как находятся промежутки возрастания (убывания) функции?
• Какие точки называются точками экстремума?

3.Теперь решаем задачи

.Все задания взяты из открытого банка заданий для подготовки к ЕГЭ.

 Соответствие точкам графика функции значений производный.

      Видеоурок  (разбор примера). Габсаликова  В. У доски объясняет решение аналогичного примера.

• Третий тип задач

 Соответствие каждому интервалу характеристику функции или её производной.

• четвертый тип задач

  соответствие между графиками функций и графиками их производных.

Раздать листочки с готовым решением (время для изучения 2 мин.). Работа в парах с обсуждением. Затем разбор аналогичного задания у доски.

К сегодняшнему уроку, я вас просила разобрать по одному типу заданий, но вы наверно убедились сейчас , что разобравшись с одним заданием, можно легко справиться с остальными.

1. Самостоятельная работа   (5 мин) с проверкой в классе.

( См. Приложение 2)

Ответы:

1 вариант                                                2 вариант

№1  4132                                                №1    2431

№2   1324                                               №2    2314

№3      3                                                  №3       4

№4      0,5                                               №4       0,5

№5      5                                                  №5       5

5. Рефлексия.

После того, как все задания  выполнены, ученикам предлагается оценить свой вклад в достижение поставленных в начале урока целей, свою активность, эффективность работы класса, увлекательность и полезность выбранных форм работы.

У вас на партах лежат оценочные листы. Оцените себя и друг друга.

 Ребята по кругу высказываются одним предложением, выбирая начало фразы файла:

сегодня я узнал…

я понял, что…

теперь я могу…

я научился…

у меня не получилось …

я смогу…

я попробую…

Ответьте мне на 3 вопроса:

1. Кто считает, что получил пользу от урока?
2. Кто считает, что сам принес пользу уроку?
3. Кто планирует на ЕГЭ решать задание №14?

Рефлексивная контрольно-оценочная деятельность при организации коллективно-учебной деятельности в группе предполагает включение каждого учащегося в действие взаимоконтроля и   взаимооценки.

— Итак, вы повторили теоретические вопросы о производной функции, применили свои знания при решении практических задач.

-Мне приятно было с вами работать,  и надеюсь, что знания, полученные на уроках математики, вы сможете успешно применить не только при сдаче  ЕГЭ, но и в дальнейшей своей  учёбе.

Оцените себя (Приложение 1)

— Закончить урок мне хотелось бы словами итальянского философа Фомы Аквинского «Знание – столь  драгоценная вещь, что его не зазорно добывать из любого источника».

Спасибо за урок!

 Приложение 1

 Оценочный лист ученика 11 класса

_____________________________________________

	Вид  работы	отметка
1.	Устная работа
2.	Ответы на вопросы, дополнения
3.	Самостоятельная работа
4.	Ваш вклад в проведение урока
	Общая отметка за урок

Приложение 2         Самостоятельная работа

1 вариант

№1

На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами    и .

В правом столбце указаны значения производной функции в точках    и . Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.

                                                             №2

На рисунке изображён график функции y=f(x). На оси абсцисс отмечены шесть точек: x1, x2, x3, x4, x5, x6. В скольких из этих точек производная функции f(x) отрицательна?

                                                    №3

На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.

                                                   №4

На рисунке изображён график функции y=f(x), определенной на интервале (-8; 6).Определите количество точек, в которых производная функции равна нулю.

2 вариант

 №1

На рисунке изображен график функции, к которому проведены касательные в четырех точках. Ниже указаны значения производной в данных точках. Пользуясь графиком, поставьте в соответствие каждой точке значение производной в ней.

№2

На рисунке изображён график функции y=f(x). На оси абсцисс отмечены семь точек: x1, x2, x3, x4, x5, x6, х 7. . В скольких из этих точек производная функции f(x) положительна?

                                                                    №3

На рисунке изображён график функции f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.

№4

На рисунке изображён график функции y=f(x), определенной на интервале (-8; 3).Определите количество точек, в которых производная функции равна нулю.

План
– конспект урока по элективному курсу в 11 классе по теме «Производная на ЕГЭ
по математике»

                                            
                Семенова Секинат Магомедовна, учитель
математики

                                                                                  
МКОУ « СОШ № 2  г.Усть-Джегуты»

     
«…нет ни одной области в математике, которая когда-либо не окажется применимой
к

явлениям
действительного мира…»

Н.И.
Лобачевский.

Цели урока :

Образовательные :

-уметь применять знания по теме
«Производная» при решении заданий из материалов КИМ ов ФИПИ

Развивающие :

— продолжить формирование мыслительных
операций; развитие умения учащихся опираться на предыдущие знания, а именно-на
правила дифференцирования, формулы производных

Воспитательные :

-продолжить воспитание отношения к
математике как к жизненной науке; воспитывать познавательную активность
учащихся

Оборудование :
ПК, проектор, экран

Ресурсный материал  :

-ЕГЭ. Задания профильного  уровня  № 8,14

-ЕГЭ. Математика  . Модульный курс « Я
сдам ЕГЭ». Профильный уровень. Рабочая тетрадь.

Тип урока:
комбинированный

Методы обучения:  объяснительно-иллюстративный,
репродуктивный.

                                                        
Ход урока :

I.Оргмомент

II.Актуализация
знаний ( Слайды  1-2)

1.Повторяем правила дифференцирования

2. В чем состоит геометрический смысл
производной?

3.В чем состоит физический смысл
производной?

4.Написать  формулы дифференцирования.

5.Написать уравнения касательной.

6 .Какие точки называются критическими?

(
Внутренние точки области определения функции, в которых ее производная равна
нулю или не существует, называются критическими точками этой функции.)

7.В чем состоит необходимое условие
экстремума?

 (
Если точка  х₀ является
точкой экстремума функции f  и в этой точке существует

                        производная  f '(x), то
она равна нулю: f '(x)= 0)

8.В чем состоит достаточный признак
существования экстремума?

(
Признак  максимума. Если функция f непрерывна
в точке х₀,
a f '(x)
0
на интервале (а; х₀) и f '(x)= (x)0
на интервале (х_о; в), то точка х_о является
точкой максимума функции f.

Удобно пользоваться упрощенной
формулировкой этого признака: если в точке х₀
производная меняет знак с плюса на минус,
то хо —
есть точка максимума.

Признак минимума функции. Если
функция f непрерывна в точке х_о, а f '(x)<0 на интервале

(а; х_о) и f '(x)>0
на интервале (х₀; в),
то точка х₀ является
точкой минимума функции f. (Если в точке х₀
производная меняет знак с минуса на плюс,
то х₀ есть
точка минимума функции f).

9.Алгоритм отыскания
наибольшего и наименьшего значений функции у= f(x), непрерывной на отрезке [a;
b].

1.Найти f '(x)

2.Найти критические точки, т.е. где f '(x) =0 и
f '(x)
не существует, и отобрать из них те, что лежат внутри отрезка [a; b].

3.Вычислить значения функции y= f(x) в
критических точках и на концах отрезка, и выбрать из них наибольшее и
наименьшее; они и будут соответственно наибольшим и наименьшим значениями функции
y=f(x) на отрезке [a; b], которые обозначают так: max _{[a; b]} y(x)
и

min _[a;b]y(x).

III.Выполнение
упражнений ( Слайды 3-15)

1. На
рисунке изображён график функции y=f(x). На оси абсцисс отмечены шесть точек: x₁, x₂, x₃, x₄, x₅, x₆. В скольких из этих точек производная функции f(x) отрицательна?

2.На рисунке изображён график
функции y=f(x).
На оси абсцисс отмечены семь точек: x₁, x₂, x₃, x₄, x₅, x_6, х ₇. . В скольких из этих точек производная функции f(x) положительна?

3.На рисунке изображены график
функции y=f(x) и
касательная к нему в точке с абсциссой x₀. Найдите значение
производной функции f(x) в точке x₀.

4.Найдите наименьшее значение
функции y=x³−x²−8x+4 на отрезке [1; 7]

5.На
рисунке изображён график y=f′(x) — производной функции f(x), определённой на интервале (−9; 8). Найдите
точку экстремума функции f(x) на отрезке [−3; 3].

6.На рисунке изображён график функции y=f(x), определённой на интервале (− 9; 5). Найдите
количество точек, в которых производная функции f(x) равна 0.

7.На рисунке изображён
график y=f′(x) производной
функции f(x),
определённой на интервале (− 2; 9). В какой точке отрезка [2; 8] функция f(x) принимает
наименьшее значение?

8.На рисунке изображён
график y=f '(x) — производной
функции f(x),
определённой на интервале (− 11 ; 6). Найдите количество точек минимума функции f(x), принадлежащих
отрезку [− 6 ; 4].

9.На рисунке изображён график
функции y=f(x),
определённой на интервале (− 6 ; 6). Найдите количество решений уравнения f '(x)=0 на
отрезке [− 4,5 ; 2,5].

10.Материальная точка движется
прямолинейно по закону x(t)=16 t³−2 t²+6 t+250, где x —
расстояние от точки отсчёта в метрах, t — время в секундах, измеренное с
момента начала движения. В какой момент времени (в секундах) её скорость была
равна 96 м/с?

11. Найдите
силу F , действующую на материальную точку с массой m , движущуюся прямолинейно
по закону х ( t ) =5 t ³ — 4t ²  ,при t = 5.

12. При
извержении вулкана магма своим поведением напоминает
дрожжевое тесто: она увеличивается в объёме и занимает абсолютно всю свободную
территорию, до которой только может добраться, поднимаясь из недр нашей планеты
по всем доступным ей трещинам. Добравшись до наименее плотно закупоренных мест,
под влиянием содержащихся в ней газов, что пытаются любым способом её покинуть
(процесс этот называется дегазация магмы), она пробивает земную кору и, выбив
«пробку» вулкана, вырывается наружу. После
того как магма вышибает пробку вулкана, давление в магматическом очаге (его
верхней части) моментально понижается. Пусть движение этой « пробки»
описывается законом : р(t) = t²—
5 t+12,
где t—
время в секундах. В какой момент времени (в секундах) скорость движения
«пробки» вулкана  будет равна 15 м/с?

13. Популяцией в экологии называют группу
особей одного вида, находящихся во взаимодействии между собой и совместно
населяющих общую территорию. Слово «популяция» происходит от латинского
«популюс» – народ, население. Экологическую популяцию, таким образом, можно
определить как население одного вида на определенной территории. Скорость роста
популяции — изменение численности популяции за единицу времени.

Задача :

Зависимость численности популяции тигров
задана формулой N(t)=
5 t³-4
t²+1.
Найдите прирост популяции в момент времени t
= 3.

IV.Самостоятельная
работа

Теперь поработаем самостоятельно в рабочих
тетрадях модульного курса «Я сдам ЕГЭ»

С.163 ,№ 6,7,8,9

С.174, № 5,6

С.193 , №1,2

С.198, № 1,2

(1 вариант- четные номера, 2 вариант –
нечетные)

В работе 5 заданий, каждое задание в
отдельности составляет 20 %.

Критерий оценивания :

Количество, в %	Оценка
10-29	«1»
30-39	«2»
40-59	«3»
60-79	«4»
80 -100	«5»

V.
 Подведение  итогов. Рефлексия.

Урок хотелось бы закончить словами Крылова
Алексея Николаевича ,советского математика и кораблестроителя: «Теория без
практики мертва или бесполезна, практика без теории невозможна или пагубна».

VI.Домашнее
 задание :  Модульный курс .Я
сдам ЕГЭ.(профильный уровень) ,

   с.193-№ 3,4;

 с.198-№3-5;

с.202-№ 1,2.

Урок совершенствования умений по теме

«Производная в задачах ЕГЭ»

11 класс

Дидактическая цель: развивать у учащихся умения применения теоретических знаний по теме «Производная функции» для решения задач единого государственного экзамена.

Задачи:

Образовательные: обобщить и систематизировать знания учащихся по теме «Производная функции»,рассмотреть прототипы задач ЕГЭ по данной теме, предоставить обучающимся возможность проверить свои знания при самостоятельном решении задач.

Развивающие: способствовать развитию памяти, внимания, навыков самооценки и самоконтроля; формированию основных ключевых компетенций (сравнение, сопоставление, классификация объектов, определение адекватных способов решения учебной задачи на основе заданных алгоритмов, способность самостоятельно действовать в ситуации неопределённости, контролировать и оценивать свою деятельность, находить и устранять причины возникших трудностей).

Воспитательные: способствовать: формированию у учащихся ответственного отношения к учению; развитию устойчивого интереса к математике; созданию положительной внутренней мотивации к изучению математики.

Методы обучения: словесный, наглядный, практический, проблемный.

Формы работы: индивидуальная, фронтальная, работа в группе.

Продолжительность урока – 90 мин.

Ход урока

1. Организационный момент

Приветствие. Эмоциональный настрой на урок.

1. Мотивации учебной деятельности учащихся. Постановка цели урока

Учитель. Ребята, отгадайте ключевое слово урока:

1) с ее появлением математика перешагнула из алгебры в математический анализ;

2) Ньютон назвал ее «флюксией» и обозначал точкой;

3) бывает первой, второй, … ;

4) обозначается штрихом.

Ответ. Производная.

Вопрос. Ребята, а зачем нужна производная?

Вопрос. Где мы встречаемся с производной и используем её?

Вопрос. Можно ли без нее обойтись в математике и не только?(Слайд 2)

Вывод: Производная – одно из самых важных понятий математического анализа. Знание производной необходимо инженерам-технологам, конструкторам, экономистам, физикам, учёным. (Слайд 3)

Учитель. Ребята, всем известно такое высказывание «Мал золотник да дорог». Одним из таких «золотников» в математике является производная. Производная применяется при решении многих практических задач математики, физики, химии, экономики и других дисциплин. Она позволяет решать задачи просто, красиво, интересно. Поэтому тема «Производная» внесена в материалы ЕГЭ, которая представлена в заданиях №7 (1 часть) и №12 (2 часть). Некоторые задания №18 также можно решить с применением производной, но для решения этих задач требуется хорошая математическая подготовка и нестандартное мышление.

— Мы в школьном курсе анализа рассматриваем и решаем посильные задачи. О некоторых из них будет сегодня идти речь.

Учитель. Как вы думаете, ребята, какова цель нашего урока! (Дети формулируют цель).

Ответ. Повторить теоретический материал темы «Производная», рассмотреть прототипы задач ЕГЭ по данной теме, проверить свои знания при самостоятельном решении задач.

Учитель. Сегодня у нас есть возможность еще раз повторить, обобщить и систематизировать весь изученный материал по теме «Производная». Запишите тему урока: «Производная в задачах ЕГЭ». (Слайд 1)

Учитель. Я надеюсь, что вы все хорошо знаете теоретический материал, посвященный данной теме, понимаете геометрический, механический смысл производной, алгоритмы исследования свойств функции с помощью производной. А для тех, кто ещё не совсем понял материал этой темы, сегодня может ещё раз разобраться в её основных вопросах. Я уверена, что вы продемонстрируете умение применять полученные знания при решении задач разного уровня сложности.

III. Актуализация опорных знаний.

Учитель. Давайте проверим, как вы владеете теорией.

1. Фронтальный опрос (Слайд 4)

Вопрос. Что такое производная?

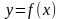
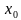
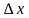
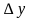
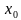
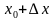
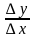
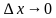
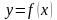
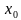
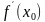
Ответ. Пусть функция определена в некотором интервале, содержащем внутри себя точку . Дадим аргументу приращение такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции (при переходе от точки к точке ) и составим отношение . Если существует предел этого отношения при , то указанный предел называют производной функции в точке и обозначают .

Вопрос. В чем заключается механический и геометрический смыслы производной?

Ответ. Физический (механический) смысл производной состоит в следующем. Если s = s(t) – закон прямолинейного движения тела, то производная выражает мгновенную скорость в момент времени t: v(t) = s΄(t).

Геометрический смысл производной состоит в следующем. Если к графику у = f (x) в точке с абсциссой х = а можно провести касательную, непараллельную оси у, то f΄ (a) выражает угловой коэффициент касательной: k = f΄(a).

Вопрос. Что такое точки экстремума функции?

Ответ. Точки минимума и максимума функции называются точками экстремума.

Вопрос. Сформулируйте необходимые условия существования экстремума?

Ответ. Если функция у = f (х)имеет экстремум в точке х = х₀, то в этой точке производная функции либо равна нулю, либо не существует.

Вопрос. Сформулируйте достаточные условия экстремума функции?

Ответ. Пусть функция у = f (х) непрерывна на промежутке Х и имеет внутри промежутка стационарную или критическую точку х = х₀. Тогда:

а) если у этой точки существует такая окрестность, в которой при х х₀ выполняется неравенство f΄ (x) х х₀ – неравенство f΄ (х) 0, то х = х₀ – точка минимума функции у = f (х);

б) если у этой точки существует такая окрестность, в которой при х х₀ выполняется неравенство f΄(х) 0, а при х х₀ – неравенство f΄ (х) х = х₀ – точка максимума функции у = f (х);

в) если у этой точки существует такая окрестность, что в ней и слева и справа от точки х₀ знаки производной одинаковы, то в точке х₀ экстремума нет.

Вопрос. Что такое стационарные точки?

Ответ. Внутренние точки области определения функции, в которых производная функции равна нулю называют стационарными.

Вопрос. Сформулируйте достаточные условия монотонности функции?

Вопрос. Как найти промежутки монотонности функции по графику производной?

Вопрос. Каковы этапы нахождения экстремумов функции?

Вопрос. Как найти наибольшее и наименьшее значение функции на отрезке?

Учитель. Хорошо, ребята! Вы владеете теоретическими знаниями по теме «Производная». Сегодня мы будем учиться применять знания о производной функции для решения задач ЕГЭ.

Учитель. Ведь недаром Аристотель говорил, что «Ум заключается не только в знании, но и умении применять знания на практике».

IV. Решение задач из банка ЕГЭ

1. Решение задач

Задание 1.На рисунке изображён график функции y = f (x). На оси абсцисс отмечены восемь точек: х₁, х₂, х₃, х₄, х₅, х₆, х₇, х₈. В скольких из этих точек производная функции f (x) отрицательна?(Слайд 5)

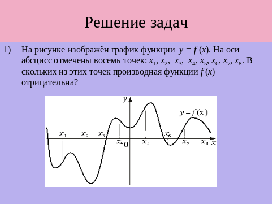
Вопрос. Что известно по условию задачи?

Ответ. График функции.

Вопрос. Что требуется найти?

Ответ. В скольких точках производная функции f (x) отрицательна.

Вопрос. Как определить в каких точках производная функции f (x) отрицательна.

Ответ. Производная функции f (x) отрицательна на промежутках убывания функции.

Вопрос. В каких точках производная функции f (x) отрицательна?

Ответ. Производная функции f (x) отрицательна в точках: х₂, х₄, х₆, х₈.

Вопрос. Сколько таких точек?

Ответ. 4 точки.

Вопрос. А как найти количество точек, в которых производная функции f (x) положительна?

Ответ. Производная функции f (x) положительна на промежутках возрастания функции.

Задание 2. На рисунке изображён график y = f ’(x) — производной функции f (x). На оси абсцисс отмечены шесть точек: х₁, х₂, х₃, х₄, х₅, х₆. Сколько из этих точек лежит на промежутках возрастания функции f (x)?(Слайд 6)

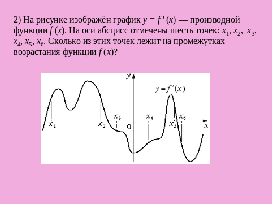
Вопрос. Что известно по условию задачи?

Ответ. График производной функции f (x).

Вопрос. Что требуется найти?

Ответ. Количество точек, которые лежат на промежутках возрастания функции f (x)?

Вопрос. Как определить точки, которые лежат на промежутках возрастания функции f (x)?

Ответ. Это точки, в которых производная положительна.

Вопрос. В каких точках производная функции f (x) положительна?

Ответ. Производная функции f (x) положительна в точках: х₁, х₂, х₅, значит эти точки лежат на промежутках возрастания функции f (x).

Вопрос. Сколько таких точек?

Ответ. 3 точки.

Задание 3.На рисунке изображены график функции y = f (x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f (x) в точке x₀. (Слайд 7)

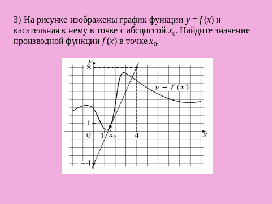
Вопрос. Что известно по условию задачи?

Ответ. График функции y = f (x) и касательная к нему в точке с абсциссой x₀.

Вопрос. Что требуется найти в задаче?

Ответ. Значение производной функции f (x) в точке x₀.

Вопрос. Чему равно значение производной функции f (x) в точке x₀?

Ответ. Тангенсу угла, образованного касательной с положительным направлением оси Ох.

Вопрос. Какая фигура помогает определить тангенс угла?

Ответ. Прямоугольный треугольник.

Вопрос. Что нужно знать, чтобы можно было найти тангенс острого угла прямоугольного треугольника?

Ответ. Отношение противолежащего катета к прилежащему катету.

Вопрос. Как выбирают прямоугольный треугольник, чтобы можно было найти тангенс острого угла?

Ответ. На графике касательной выбирают такую точку, чтобы её координаты были удобны для вычисления?

Вопрос. Чему равен тангенс угла наклона?

Ответ. Тангенс угла наклона равен отношению 12 к 4 и равен 3, значит значение производной функции f (x) в точке x₀ равно 3.

Вопрос. Можно ли решить эту задачу иначе?

Ответ. Можно, составив систему из двух линейных уравнений.

Задание 4.На рисунке изображены график функции y = f (x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f (x) в точке x₀. (Слайд

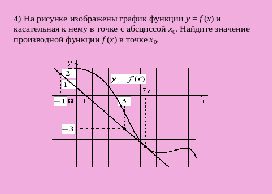
Вопрос. Что известно по условию задачи?

Ответ. График функции y = f (x) и касательная к нему в точке с абсциссой x₀.

Вопрос. Что требуется найти?

Ответ. Значение производной функции f (x) в точке x₀.

Вопрос. Чему равно значение производной функции f (x) в точке x₀?

Ответ. Тангенсу угла, образованного касательной с положительным направлением оси Ох.

Вопрос. Какой угол образовался между касательной и положительным направлением оси Ох?

Ответ. Тупой.

Вопрос. Как поступают, если угол наклона касательной к графику функции является тупым, т. е. не может быть углом прямоугольного треугольника?

Ответ. Находят тангенс угла, смежного с рассматриваемым углом; определяют тангенс искомого угла, пользуясь формулой приведения tg (180° – α) = – tg α.

Вопрос. Найдите значение производной функции f (x) в точке x₀.

Ответ. Значение производной функции f (x) в точке x₀ равно –1,25.

Вопрос. Можно ли решить задачи 3и 4 другим способом? Если можно, то как?

Ответ. Можно взять на касательной 2 точки и их значение подставить в уравнение касательной. Решить систему, состоящую из двух линейных уравнений.

Вопрос. Что мы тогда найдем?

Ответ. Угловой коэффициент касательной к графику функции f (x).

Вопрос. Как связаны между собой значение производной функции f (x) в точке x₀ и угловой коэффициент касательной?

Ответ. Значение производной функции f (x) в точке x₀ и угловой коэффициент касательной равны.

Вопрос. Решите задание 4 двумя способами и сравните полученные ответы.

Учащиеся. 1 способ. Тангенс угла наклона равен отношению 5 к 4 и ранен 1, 25, но так как угол образованный между касательной и положительным направлением оси Ох – тупой, значит значение производной в точке x₀ = –1,25.

2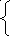 способ.

– 2 = – k + b,

–3 = 3k +b.

5 = – 4k.

k = 5 : (– 4).

k = –1, 25.

Учащиеся. Ответы равны.

Задание 5. На рисунке изображён график y = f′(x) − производной функции f (x), определённой на интервале (−9; 8). Найдите точку экстремума функции f (x) на отрезке [−3; 3]. (Слайд 9)

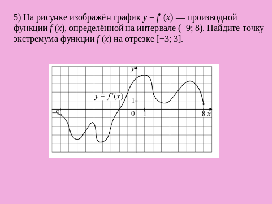
Вопрос. Что известно в задаче?

Ответ. График производной функции f (x), определённой на интервале (−9; 8).

Вопрос. Что требуется найти?

Ответ. Точку экстремума функции f (x) на отрезке [−3; 3].

Вопрос. Что такое точка экстремума?

Ответ. Точка экстремума – это точка максимума или минимума функции.

Вопрос. Как по графику производной функции f (x) отыскать точку экстремума функции f (x) на отрезке [−3; 3].

Ответ. Это точка, в которой производная меняет свой знак.

Вопрос. Чему равно значение точки экстремума?

Ответ. Из графику производной функции f (x) видно, что в точке – 2 производная меняет знак с минуса на плюс, значит точка – 2 и есть точка экстремума.

Задание 6. На рисунке изображён график функции y = f(x), определённой на интервале (− 9; 5). Найдите количество точек, в которых производная функции f (x) равна 0. (Слайд 10)

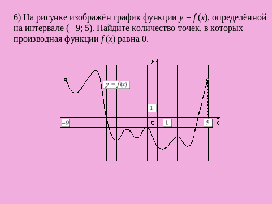
Вопрос. Что известно в задаче?

Ответ. График функции y = f (x), определённой на интервале (− 9; 5).

Вопрос. Что требуется найти?

Ответ. Количество точек, в которых производная функции f (x) равна 0.

Вопрос. Как определить в каких точках функции y = f (x) производная функции f (x) равна 0?

Ответ. Производная функции f (x) равна 0 в точках максимума и минимума функции.

Вопрос. Определите количество точек?

Ответ. 9 точек.

Задание 7. Материальная точка движется прямолинейно по закону x (t) =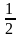 t² + 4t + 27, где x − расстояние от точки отсчёта в метрах, t − время в секундах, измеренное с момента начала движения. Найдите её скорость (в метрах в секунду) в момент времени t = 2 с. (Слайд 11)

Вопрос. Что известно по условию задачи?

Ответ. Закон движения материальной точки.

Вопрос. Каков способ задания функции?

Ответ. Зависимость координаты от времени задана формулой.

Вопрос. Что ещё известно?

Ответ. Момент времени t.

Вопрос. Что нужно найти?

Ответ. Скорость в момент времени t.

Вопрос. Как найти скорость в момент времени t?

Ответ. sˊ(t) = v(t).

Вопрос. Найдите значение скорости в момент времени t.

Ответ. Скорость равна 6 м/с.

2. Выполнение тренажера «Готовимся к ЕГЭ».

Индивидуальное выполнение работы.

3. Групповая работа.

Класс делится на 2 группы, каждая группа работает под руководством ученика, ответственного за данную группу. У каждого учащегося 1 и 2 группы своя зачётная карточка. Все решают. На возникшие вопросы, получают консультацию у ответственного за группу (при необходимости у учителя). После выполнения работы

учитель проверяет работы у ответственных, а ответственные у членов своей группы.

Перед учащимися поставлена проблема:

«Подумайте, можно ли решить некоторые задачи №12 другим способом, без применения производной?» (Слайд 12)

Задания для 1 группы

1) Найдите наибольшее значение функции y = x³−6x²+9x+5 на отрезке [0;3].

2) Найдите наибольшее значение функции y =

Задания для 2 группы

1) Найдите наименьшее значение функции y =e^2x−4e^x+4на отрезке [− 1; 2].

2) Найдите наименьшее значение функции y = .

Учитель. Попытайтесь решить вторую задачу двумя способами.

(Учащиеся защищают своё решение, записывая основные этапы решения задач на доске. Предоставляют два способа решения задачи №2.)

Вопрос. Проанализируйте, какая ошибка была допущена вами в задаче?

Вопрос. Какие теоретические вопросы вам необходимо повторить?

Разрешение проблемы. Вывод, который должны сделать учащиеся:

«Некоторые задачи В12 ЕГЭ на нахождение наименьшего и наибольшего значения функции можно решить без применения производной, опираясь на свойства функций».

4.Тестирование (Слайд 13)

Сайт для тестирования на уроке: http://www.ege-online-test.ru/

Вопрос. Кто не допустил ошибок?

Вопрос. Кто испытывал трудность при тестировании? Почему?

Вопрос. В каких заданиях допущены ошибки?

Вопрос. Сделайте вывод, какие теоретические вопросы вам необходимо знать?

VI. Подведение итогов. Рефлексия

Учитель. Подведем итог нашей работы. Какова была цель урока? Как вы считаете, достигнута ли она?

Учитель. Посмотрите на доску и одним предложением, выбирая начало фразы, продолжите предложение, которое вам больше всего подходит. (Слайд 14)

Я почувствовал…

Я научился…

У меня получилось …

Я смог…

Я попробую…

Меня удивило, что…

Мне захотелось…

Вопрос. Можете ли вы сказать, что в ходе урока произошло обогащение запаса ваших знаний?

Вопрос. Итак, вы повторили теоретические вопросы о производной функции, применили свои знания при решении прототипов заданий ЕГЭ (№7, №12).

Учитель. Мне приятно было с вами работать, и надеюсь, что знания, полученные на уроках математики, вы сможете успешно применить не только при сдаче ЕГЭ, но и в дальнейшей своей учёбе.

Учитель. Закончить урок мне хотелось бы словами итальянского философа Фомы Аквинского «Знание – столь драгоценная вещь, что его не зазорно добывать из любого источника».

Желаю успехов в подготовке к ЕГЭ!(Слайд 15)

VII. Домашнее задание. Выставление оценок

К следующему уроку вам нужно: 1) повторить теоретический материал по теме «Производная функции»; 2) на сайте «Открытый банк заданий по математике» (http://mathege.ru/) найти прототипы заданий №7 и №12 и решить не менее 10 задач. (Слайд 16)

МБОУ «Сергиевская СОШ»

Конспект урока

алгебры в 11 классе

по теме:

«Применение производной в заданиях ЕГЭ»

Подготовила

Ушакова М.А.

учитель математики

высшей категории

Декабрь 2016 г.

Цель: повторить основные направления применения производной для решения различных (избранных) задач дифференциального исчисления, а так же подготовиться к сдаче ЕГЭ, так как задания на применение производной включены в номера 7 и 12 профильного уровня.

Задачи:

1. Обучающая. Обобщить знания по теме: «Применение производной к исследованию функций, к нахождению наибольшего и наименьшего значения функции на отрезке»; формирование умения применять теоретические знания к  работе с графиком функции, производной и касательной; развитие интереса и внимания при решении задач по готовым чертежам.

2. Развивающая. Развитие умений применять знания в конкретной ситуации; развитие логического мышления, развитие монологической речи, развитие навыка работы в группе, умение работать в проблемной ситуации; развитие умения сравнивать, обобщать, правильно формулировать задачи и излагать мысли; развитие самостоятельной деятельности учащихся.

3. Воспитательная. Формирование у учащихся ответственного отношения к учению; умение работать в коллективе, взаимопомощи, культуры общения; воспитание таких качеств характера, как настойчивость в достижении цели; развитие устойчивого интереса к математике; создание положительной внутренней мотивации к изучению математики.

1.Организационный момент. Мотивация учебно-познавательной деятельности.

-Тема нашего занятия «Производная функции в заданиях ЕГЭ». Всем известно высказывание «Мал золотник да дорог». Одним из таких «золотников» в математике является производная. Производная применяется при решении многих практических задач математики, физики, химии, экономики и других дисциплин. Она позволяет решать задачи просто, красиво, интересно.

Тема «Производная» представлена в заданиях №7 и №12 профильного уровня единого государственного экзамена. Некоторые задания 2 части также можно решить с применением производной. Но для решения этих задач требуется хорошая математическая подготовка и нестандартное мышление.

Вы работали с документами, регламентирующими структуру и содержание контрольных измерительных материалов единого государственного экзамена по математике. Сделайте вывод о том, какие знания и умения вам нужны для успешного решения задач ЕГЭ по теме «Производная».

Необходимо

• ЗНАТЬ

правила вычисления производных;

производные основных элементарных функций;

геометрический и физический смысл производной;
уравнение касательной к графику функции;
исследование функции с помощью производной.

• УМЕТЬ

выполнять действия с функциями (описывать по графику поведение и свойства функции, находить её наибольшее и наименьшее значения).

• ИСПОЛЬЗОВАТЬ

приобретенные знания и умения в практической деятельности и повседневной жизни.

— Вы владеете теоретическими знаниями по теме «Производная». Сегодня мы будем УЧИТЬСЯ ПРИМЕНЯТЬ ЗНАНИЯ О ПРОИЗВОДНОЙ ФУНКЦИИ ДЛЯ РЕШЕНИЯ ЗАДАЧ ЕГЭ.

Ведь недаром Аристотель говорил, что “УМ ЗАКЛЮЧАЕТСЯ НЕ ТОЛЬКО В ЗНАНИИ, НО И В УМЕНИИ ПРИМЕНЯТЬ ЗНАНИЯ НА ПРАКТИКЕ”

2. Устная работа

А) Фронтальный опрос

1. Какая функция называется убывающей (возрастающей) на множестве Х?

2. Что такое экстремумы функции? Чему равна производная в экстемумах ? Напомню

— Стационарные точки – это внутренние точки области определения в которых производная функции равна нулю, а критические точки – это внутренние точки области определения , в которых функция непрерывна, но производная в них не существует.

3. В чем состоит физический и геометрический смысл производной?

4. Если функция возрастает (убывает), то какой знак имеет производная?

5. Как называется процесс , когда находят производную по заданной функции?

Давайте теперь повторим основные формулы нахождения производных . Для этого найдите производную данных функций.

Ответы: f(x)=3x³+6x-1. f(x)=—

f(x)=+5 f(x)=6cos3x

1. Упражнения по отработке навыков

При ответах на вопросы задания 7 вы должны уметь описывать по графику производной поведение и свойства функции, а по графику функции – поведение и свойства производной функции. А для этого нужны хорошие теоретические знания по следующим темам: «Геометрический и механический смысл производной. Касательная к графику функции. Применение производной к исследованию функций».

Повторим связь между возрастанием и убыванием функции и знаком производной.

Выполним задания на экране

Слайд

Ответ 3

Слайд

Ответ 3

Слайд

Ответ 3

Слайд

Ответ 1

Слайд

Слайд

Найдите f(3)

-Вспомните алгоритм решения задач №12 на нахождение наибольшего и наименьшего значений функции на промежутке с помощью производной.

Найдите наибольшее значение функции у=х³-3х²-45х+1 на отрезке [-4;6]

Ответ 82

1. Самостоятельная работа

Вариант 9 №7, 12 ,

Вариант 10 № 7,12

Вариант 14 №7, 12

Вариант 15 № 7, 12

Задания из сборника Подготовка к ЕГЭ-2017 по математике под редакцией Лысенко.

1. Домашнее задание

Найти на сайте Решу ЕГЭ 3 задания № 12 и решить его в тетради.

6. Итог урока

-Итак, вы повторили теоретические вопросы о производной функции, применили свои знания при решении прототипов заданий ЕГЭ.

-Мне приятно было с вами работать, и надеюсь, что полученные знания, вы сможете успешно применить не только при сдаче ЕГЭ, но и в дальнейшей своей учёбе.

— Закончить выступление мне хотелось бы словами Пьера Лапласа: «То, что мы знаем, — ограниченно, а то чего мы не знаем, — бесконечно». Поэтому обогащайтесь знаниями, чаще находитесь в этой бесконечности.

Желаю успехов в подготовке к ЕГЭ!

Пояснительная записка

Данная методическая разработка факультативного занятия поможет в проектировании урока с позиции формирования УУД.

Методическую разработку могут применять в своей работе как молодые специалисты, так и учителям со стажем, работающим по ФГОС.

Практическая значимость методической разработки состоит в том, что в ней определены организационные условия проведения занятия с обучающимися, содержание учебного материала, подобраны оптимальные формы, методы и средства обучения, использованы современные педагогические технологии.

Актуальность

Факультативное занятие на тему «Производная функции в заданиях ЕГЭ» — занятие подготовки к успешной сдаче Государственной итоговой аттестации. Строится с применением технологии обучения в сотрудничестве: через создание проблемной ситуации и ведение проблемного диалога учащиеся открывают новые знания, самостоятельно формулируют тему и цель урока, даёт возможность учителю по-новому открывать знания с учениками.

Содержание

Цель разработки: освоение технологии проектирования урока в соответствии с современными требованиями.

Особенности занятия: При проектировании урока учтены основные принципы личностно-ориентированного, индивидуального, дифференцированного и системно-деятельностного подходов.

Класс: 11.

Предмет: математика.

Цель факультативного занятия — развивать у учащихся навыки применения теоретических знаний по теме «Производная функции» для решения заданий единого государственного экзамена.

Планируемые результаты:

а) предметные: обобщить и систематизировать знания учащихся по теме «Производная функции», рассмотреть прототипы задач ЕГЭ по данной теме, предоставить обучающимся возможность проверить свои знания при самостоятельном решении заданий.

б) метапредметные:

регулятивные:

• умение ставить перед собой цель, управлять своей деятельностью, видеть ожидаемый результат работы;
• умение рационально распределять рабочее время, проявлять инициативность и самостоятельность
• умение объективно оценивать свои возможности, анализировать свои результаты, корректировать свои действия и знания;

познавательные:

• самостоятельное выделение, формулирование познавательной цели;
• поиск и отбор необходимой информации, умение работать с информацией, применение методов информационного поиска;
• выполнять логические операции, самостоятельно выделять и формулировать познавательную цель задания;
• способствовать развитию памяти, внимания, навыков самооценки и самоконтроля; формированию основных ключевых компетенций (сравнение, сопоставление, контроль и оценивание своей деятельности, корректировка возникших трудностей).
• осознанное и произвольное построение речевого высказывания в устной и письменной форме;

коммуникативные:

• планирование учебного сотрудничества с преподавателем и сверстниками;
• определение цели, функций участников, способов взаимодействия;
• формирование речевой деятельности, навыков сотрудничества, умение находить общее решение, умение аргументировать своё предложение, взаимоконтроль и взаимопомощь по ходу выполнения задания.

в) личностные:

• осознание социальной, практической и личностной значимости учебного материала;
• формирование способности к самоопределению и саморегуляции.

Педагогические технологии: технология обучения в сотрудничестве.

Методы обучения: проблемно-поисковый, диалогические, творческие.

Формы работы: индивидуальная, в парах, в группе.

Оборудование и материалы для урока: проектор, экран, презентация, индивидуально-дифференцированные карточки для самостоятельной работы, сайты сети Интернет.

Структура урока: актуализация субъектного опыта (→ мотивация личностные смыслы, опорные знания и умения, ценностные отношения) рефлексия. → анализ закрепления умений → организация закрепления учебного материала → проверка правильности понимания учебного материала → организация восприятия, осмысления и запоминания учебного материала как единого процесса.

Ход урока

1. Организационный момент

слайд 1

Всем известно высказывание «Мал золотник да дорог». Одним из таких «золотников» в математике является производная. Производная применяется при решении многих практических задач математики, физики, химии, экономики и других дисциплин. Она позволяет решать задачи просто, красиво, интересно.

Тема нашего занятия «Производная функции в заданиях ЕГЭ». Тема «Производная» представлена в заданиях номер 7, 11 единого государственного экзамена. Некоторые задания С5 также можно решить с применением производной. Но для решения этих задач требуется хорошая математическая подготовка и нестандартное мышление. Цель урока ребята поставьте сами.

2. Мотивация к учебной деятельности

Цель: мотивировать учащихся к учебной деятельности.

Учитель: Ребята, я не сомневаюсь в том, что вы знаете, какой непростой этап переживает экономика России и всего мира. Связано это в первую очередь с тем, что экономисты ведущих мировых стран неверно рассчитали риски реализуемых проектов. Многие предприятия из-за кризиса оказались под угрозой закрытия, а значит, работники этих предприятий окажутся уволенными. Чтобы нормализовать деятельность предприятия, терпящего кризис, и избежать освобождения людей, на предприятие его владельцем приглашается антикризисный менеджер или даже целая команда антикризисных менеджеров. Задача этой команды найти пути решения проблемы — выведения предприятия из кризиса. Работа антикризисных менеджеров считается хорошо выполненной, если найден путь решения поставленной задачи. Антикризисный менеджер должен в первую очередь уметь решать стоящие перед ним задачи, верно просчитывая каждый свой шаг. Мы тоже сегодня с вами, решать задания В9. Но сегодня мы соотнесем наши знания с дипломами различных уровней антикризисного менеджера.

Итак, сегодня вы можете получить дипломы 4 цветов.

Сегодня в течение урока мы будем начислять вам бонусы, которые и определят цвет вашего диплома, чтобы получить

• диплом красного цвета «успешный антикризисный менеджер» нужно набрать 17 и более бонусов за урок
• диплом оранжевого цвета «старательный антикризисный менеджер » нужно набрать от 12 до 16 бонусов за урок
• диплом синего цвета «антикризисный менеджер не всегда находящий верный путь выхода из кризиса» нужно набрать от 6 до 11 бонусов за урок
• диплом зеленого цвета «антикризисный менеджер не способный найти выхода из кризиса» (меньше 6 бонусов за урок)

Маршрутный лист по теме «Производная функции в заданиях ЕГЭ» ФИ________________
Уровень	Этап занятия	Количество бонусов
1	«Вспомним, как это было»
2	«Да или нет вот в чем вопрос»
3	«Подумай и сделай открытие»
4	«Минута отдыха ли!»
5	«Вспомним про открытое»
6	«Попробуй сам»
7	Итого

Итак, вперед зарабатывать бонусы.

3. Актуализация и пробное учебное действие

Цель этапа: Поиск решения учебной задачи.

Уровень 1. «Вспомним, как это было»

Учитель предлагает ученикам перечислить правила, которые вы применяли при выполнении заданий 11. (за каждое правило дополнительный бонус)

Вы работали с документами, регламентирующими структуру и содержание контрольных измерительных материалов единого государственного экзамена по математике 2021. Сделайте вывод о том, какие знания и умения вам нужны для успешного решения задач ЕГЭ по теме «Производная».

Составить кластер «Какие знания и умения вам нужны для успешного решения задач ЕГЭ по теме «Производная»».

Уровень 2. «Да или нет вот в чем вопрос» работа в парах

Проводится в форме математического диктанта. Ученикам необходимо определить верно, утверждение или нет.

Верно ли утверждение, определение?

Верно ли утверждение, определение?

1. Определение производной с помощью математических символов

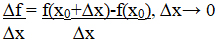
2. Верно ли, что значение производной функции в точке равно угловому коэффициенту касательной к графику функции в этой точке?

3. Функция дифференцируема в точке х₀, если функция не имеет производную в точке x₀.

4. Верно ли, что если производная функции в некоторой точке равна нулю, то в этой точке имеется экстремум?

5. Верно ли, что наибольшее или наименьшее значение функции на некотором отрезке наблюдается или в критических точках, или на концах отрезка?

6. Верно ли, что в точке возрастания функции её производная больше нуля?

7. Площадь криволинейной трапеции вычисляется по формуле S=F(b) + F(a).

8. По определению первообразной справедливо равенство f(x) = F'(x)

Ученики осуществляют самопроверку по выведенным ответам, проверяем за верный ответ 1 бонус

1	2	3	4	5	6	7	8
да	да	нет	нет	да	да	нет	да

4. Этап выявления места и причин затруднения (определение границ знания и незнания)

Цель: фиксация в модели существенных отношений изучаемого объекта.

Уровень 3. «Подумай и сделай открытие»

Работа в группах

Учитель: Еще древние мудрецы считали, что «Величие человека в его способности мыслить». Нам сегодня предстоит на основании имеющихся у вас знаний применить их при решении задания В9.

Учитель: Запишем тему урока «Производная функции в заданиях ЕГЭ»

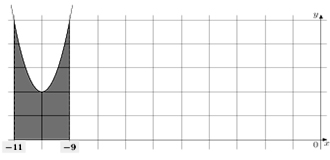
На рисунке изображён график некоторой функции y = f(x). Функция — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.

Решение:

1 способ. S = F(a) — F(b), a>b Площадь закрашенной фигуры равна F(-9) — F(-11).

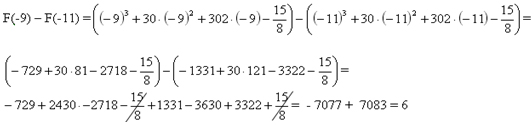
2 способ.

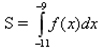
Найдем подинтегральную функцию f(x), если F(x) = x³ + 30x² + 302x — . По определению первообразной справедливо равенство f(x)=F'(x). Тогда, f(x)= 3х² + 60х + 302. Если мы сразу подставим эту функцию и будем вычислять интеграл, то получим такие же громоздкие вычисления, как и в 1 способе:

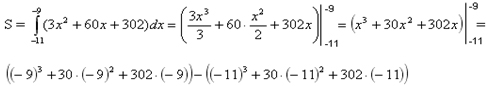
На рисунке изображён график функции y=F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (-3; 5). Пользуясь рисунком, определите количество решений уравнения f(x) = 0 на отрезке [-2; 4]

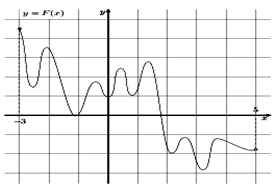
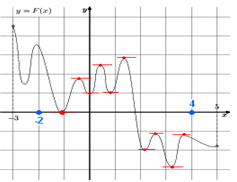
Решение: По определению первообразной справедливо равенство f(x)=F'(x). Т.е. перед нами график функции, а производная ее равна 0 в точках экстремума. Следовательно, решениями уравнения f(x) = 0 являются точки экстремумов изображенной на рисунке функции F(x). Из них на отрезке [−2;4] лежат 10 точек. Таким образом, на отрезке [−2;4] уравнение f(x) = 0 имеет 10 решений.

2 бонуса

Динамическая пауза

Уровень, 4

Впрочем, сделаем небольшую остановку, дадим себе немного отдохнуть, сейчас я буду говорить вам задания, а вы будете выполнять — «Птица, расправляющая крылья».

Представьте, что вы — птица, крылья которой крепко сжаты. Соедините лопатки, напрягите спину так сильно, как только можете. Вы ощущаете напряжение. А теперь медленно, не торопясь, освобождайте свои мышцы. Ваши крылья расправляются. Становятся сильными и легкими, невесомыми. Вы ощущаете расслабление. Повторить упражнение 3-5 раз.

5. Этап. Применение общего способа действия для решения частных задач

Задача этапа: Установление правильности и осознанности усвоения нового учебного материала; выявление пробелов и неверных представлений и их коррекция. Усвоение сущности усваиваемых знаний и способов действий на репродуктивном уровне. Ликвидация типичных ошибок и неверных представлений у учащихся.

Уровень 5. «Вспомним про открытое»

Молодцы, мы справились, но усложним задачу.

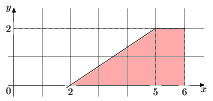
На рисунке изображён график функции y=f(x). Пользуясь рисунком, вычислите F(6) — F(2), где F(x) — одна из первообразных функции f(x).

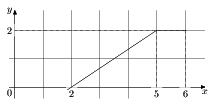
Решение:

S = F(a) — F(b), a>b. Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции ABCD. Поэтому S = F(6) — F(2) = ½(1+4) * 2 = 5

6. Самостоятельная работа с самопроверкой по эталону

Уровень 5. «Попробуй сам»

Задача этапа: обеспечение самостоятельного выполнения заданий, требующих применения знаний в знакомой ситуации, для учащихся работающих на репродуктивном уровне и измененной ситуации, для учащихся работающих на конструктивном и творческом уровнях).

Самостоятельная работа. 1 вариант

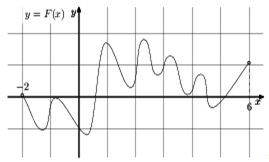
№1. На рисунке изображён график функции y=F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (-2; 6). Пользуясь рисунком, определите количество решений уравнения f(x) = 0 на отрезке [-1; 5].

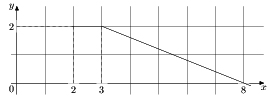
№2. На рисунке изображён график функции y=f(x). Пользуясь рисунком, вычислите F(8) — F(2), где F(x) — одна из первообразных функции f(x).

На рисунке изображён график некоторой функции у = f(х). Функция — одна из первообразных функции f(х). Найдите площадь закрашенной фигуры.

Самостоятельная работа. 2 вариант

Ответы:

1 вариант № 1. 10	2 вариант №1. 6
№ 2. 7	№2. 3
№ 3. 6	№3. 4

Проверка самостоятельной работы 2 бонуса.

7. Этап подведения итогов занятия

Задача этапа: дать анализ и оценку успешности достижения цели и наметить перспективу последующей работы. Адекватность самооценки учащегося оценке учителя. Получение учащимися информации о реальных результатах учения.

Уровень 6. «Момент истины»

Посчитайте бонусы

И определим, кто из вас вышел на уроке антикризисный менеджер

• диплом красного цвета «успешный антикризисный менеджер» нужно набрать 17 и более бонусов за урок
• диплом оранжевого цвета «старательный антикризисный менеджер » нужно набрать от 12 до 16 бонусов за урок
• диплом синего цвета «антикризисный менеджер не всегда находящий верный путь выхода из кризиса» нужно набрать от 6 до 11 бонусов за урок
• диплом зеленого цвета «антикризисный менеджер не способный найти выхода из кризиса» (меньше 6 бонусов за урок)

Рекомендации для самоподготовки. (задача этапа: обеспечение понимания цели, содержания и способов выполнения домашнего задания. Проверка соответствующих записей. Реализация необходимых и достаточных условий для успешного выполнения домашнего задания всеми учащимися в соответствии с актуальным уровнем их развития.

Уровень 8. «Еще не поздно все исправить, если дома потрудиться»

Повторить теоретический материал по теме «Производная функции»;

— на сайте «Открытый банк заданий по математике» найти задания 7, 11 и решить.

8. Рефлексия учебной деятельности

Задача этапа: мобилизация учащихся на рефлексию учебной деятельности.

Уровень 9 и последний «Что я думаю обо всем этом»

Заполнить блокнот. Предприятие имеет книгу отзывов и предложений. Учащиеся записывают свои отзывы о проведенном занятии.

— Мне приятно было с вами работать, и надеюсь, что полученные знания, вы сможете успешно применить не только при сдаче ЕГЭ, но и в дальнейшей своей учёбе.

— Закончить занятие мне хотелось бы словами Пьера Лапласа: «То, что мы знаем, — ограниченно, а то чего мы не знаем, — бесконечно». Поэтому обогащайтесь знаниями, чаще находитесь в этой бесконечности.

Желаю успехов в подготовке к ЕГЭ!

Список использованных источников

1. УМК: Алимов А.Ш, Колягин Ю.М. и др. Алгебра и начала математического анализа. 10-11 классы. Учебник. (базовый уровень). М.: Просвещение, 2018.
2. www.fipi.ru
3. mathgia.ru
4. Математика. ГИА. Комплексная подготовка/ В.И.Глизбург. — М.: Айрис-пресс, 2012. — 176 с.
5. И.В.Ященко, И.Р.Высоцкий, А.В.Семенов, МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ для учителей, подготовленные на основе анализа типичных ошибок участников ЕГЭ-2021 года по МАТЕМАТИКЕ.
6. ЕГЭ. Математика. Профильный уровень: типовые Е31 экзаменационные варианты: 36 вариантов / под ред. И.В.Ященко. — Москва: Издательство «Национальное образование», 2022 — 224 с. — (ЕГЭ. ФИПИ — школе).

ПОНЯТИЕ ПРОИЗВОДНОЙ.

МЕХАНИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ

Цель: ввести понятие производной, рассмотреть задачи, приводящие к понятию производной.

Ход урока

І. Анализ контрольной работы.

1. Итоги работы.

2. Характерные ошибки, допущенные при выполнении работы.

3. Решение упр. из КР.

ІІ. Изучение нового материала

Обратите внимание, что наш учебник называется «Алгебра и начала математического анализа». Мы начинаем изучать новый раздел математики «Математический анализ». В нашей учебной программе мы будем изучать только основы – «начала» анализа. Одна из тем этого раздела – «Понятие производной». Математика в школе – это достаточно сложный предмет и самое главное для учащихся – понять, зачем она нужна. Мы изучаем производную. А так ли это важно в жизни? Давайте попробуем вместе в этом разобраться.

Историческая справка.

Понятие «производная» возникло в XVII веке в связи с необходимостью решения ряда задач из физики, механики и математики.

Великий французский математик Пьер Ферма в 1629 г. Научился находить касательные к алгебраическим прямым.

В 1638г Ферма поделился этим открытием со своим земляком Рене Декартом, который тоже занимался этой проблемой и нашел свой метод построения касательных к алгебраическим кривым.

Ферма далеко продвинулся в применении дифференциальных методов. Он использовал их не только для проведения касательных, но, к примеру, для нахождения максимумов, вычисления площадей.

Однако ни Ферма, ни Декарт не сумели свести полученные научные выводы и результаты в единую систему. Тем не менее, выдвинутые идеи не пропали впустую. Многие из них легли в основу нового метода математического анализа – дифференциального исчисления.

«Дифференциальное исчисление – это описание окружающего нас мира, выполненное на математическом языке. Производная помогает нам успешно решать не только математические задачи, но и задачи практического характера в разных областях науки и техники».

Основоположниками этого метода считаются Вильгельм Лейбниц (1646 – 1716) и Исаак Ньютон (1642 – 1727).

Независимо друг от друга И. Ньютон и Г. Лейбниц разработали аппарат, которым мы и пользуемся в настоящее время.

И. Ньютон в основном опирался на физическое представление о мгновенной скорости движения, а Г. Лейбниц использовал понятие бесконечно малой.

С помощью дифференциального исчисления был решен целый ряд задач теоретической механики, физики и астрономии. В частности, ученые предсказали возвращение кометы Галлея, что было большим триумфом науки XVII века.

Очень многие великие ученые внесли свой вклад в зарождение и развитие дифференциального исчисления. Среди них – Джеймс Грегори, Якоб Бернулли, Гийом Франсуа Лопиталь, Леонард Эйлер, Карл Фридрих Гаусс, Жозеф Луи Лагранж, который в 1797 г. ввел термин «производная» и современные обозначения y´, f´.

В настоящее время понятие производной находит большое применение в логистике и коммерческой деятельности. Умение применять производную к исследованию функции – важный элемент математической культуры.

Продолжить свой урок мне хочется словами Бориса Пастернака

И сейчас мы постараемся дойти до самой сути определения производной и покажем ее применение в различных областях знаний.

Сегодня у нас будет встречаться много новых терминов. «Производная» – это то, что «произведено» какой-то функцией. Простой пример: Яйцо – это производная курицы. Понятие производной довольно трудное, т.к. основано на абстрактном восприятии. Мы рассмотрим ситуацию, известную нам из повседневной жизни.

Мы едем из Амвросиевки до Ростова (240 км). Рассмотрим график этого движения. На оси абсцисс – время t, по оси ординат – пройденный путь s(t). На весь путь ушло 4 часа. Как узнать, с какой скоростью мы ехали. (Пройденный путь разделить на время 240 : 4 = 60 км/ч)

— Мы всё время ехали с такой скоростью? (Нет, в течение пути она менялась, могла быть и больше 60 и меньше).

— Так какую скорость мы получим? (Среднюю).

— Рассмотрим участок времени Δt (пусть с 10 до 11 часов). За это время мы проехали отрезок пути Δs (пусть 40 км). С какой скоростью мы проехали этот отрезок пути? (40 : 1 = 40 км/ч или Δs : Δt).

— Какая скорость получится? (Средняя) Vср. = Δs : Δt

— Если мы уменьшим отрезок времени до 0, что произойдет со скоростью? Представьте себе, на посту ГИБДД скорость отслеживается с помощью радара. В момент пересечения луча радара автомобилем на табло радара высвечивается цифры скорости. Будет ли она равна средней скорости (может да, а может, нет). Как можно назвать такую скорость (мгновенной), т.к. мы рассматриваем скорость в какое-то мгновение.

Если отрезок времени стремится к 0, скорость из средней превращается в мгновенную:

 Вот мы подошли к понятию производной пути.

Производная пути – это мгновенная скорость. Vмгнов. = S´(t)

— Где мы можем увидеть значение мгновенной скорости? (Радар, спидометр).
— Можем мы увидеть значение средней скорости? (Нет, её можно вычислить)

Перейдем от конкретной ситуации к любой математической функции f(x) по той же схеме.

f´(x) = lim , где Δx – приращение аргумента, Δf – приращение функции.

Определение производной.

Производной функции y = f(x) в данной точке x0 называется предел отношения приращения функции в этой точке к приращению аргумента, при условии, что приращение аргумента стремится к нулю.

Обозначение производной: .

— Где в жизни применяется понятие производной? В физике – это скорость, ускорение, работа; в математике – это исследование различных функций при практических расчетах в автомобилестроении, судостроении, электронике и т.д.

Операция вычисления производной называется дифференцированием.

III. Закрепление изученного материала.

№ 776 (2): S(t) = 1 + 3t, от t = 0,8 до t = 1.

h = 1 – 0,8 = 0,2; vср. = = = 3.

№ 780 (2, 4), № 781 (2, 4), № 778 (самостоятельно)

ІV. Итог урока.

1. Как называется раздел математики, который мы начали изучать?

2. Как найти скорость, зная расстояние и время?

3. Какую скорость мы получим?

4. Какую скорость мы видим на спидометре?

5. Где ещё можно увидеть значение мгновенной скорости?

6. Чем является мгновенная скорость для пути?

7. Как обозначается производная?

8. Что означает lim?

9. Что означает Δx; Δf?

10. Определение производной.

11. Как называется операция вычисления производной?

12. Где применяется понятие производной?

Чтобы проконтролировать себя, запишите в тетради все опорные слова, старые и новые, которые использовались нами в течение урока. (4 минуты).

Проверка в виде самоконтроля:

— Я диктую термин, а вы ставите +, если он у вас записан.

Количество «+» разделите на 2 и поставьте себе отметку.

VІ. Домашнее задание: §44, № 780 (1, 3), № 781 (1, 3), № 776(1).

ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ

Цель: формирование навыков решения задач на применение определения производной.

Ход урока

І. Актуализация знаний.

1. Как называется раздел математики, который мы начали изучать?

2. Как найти скорость, зная расстояние и время?

3. Какую скорость мы получим?

4. Какую скорость мы видим на спидометре?

5. Где ещё можно увидеть значение мгновенной скорости?

6. Чем является мгновенная скорость для пути?

7. Как обозначается производная?

8. Определение производной.

9. Где применяется понятие производной?

10. Как называется операция вычисления производной?

11. Задания по карточкам.

II. Решение упражнений.

1. По определению найти производную функции:

а) у = 3х2 – 4х + 5 в точке х0 = 2, в) у = х – 2х3,

б) у = х3 + 3х2, г) у = 4х3 + 5х2 – 7х – 4.

2. № 782 (2), № 783 (2), № 785.

3. Тело, масса которого m = 5 кг, движется прямолинейно по закону s = l – t + t2. Найти кинетическую энергию тела через 10 с после начала движения.

4. Самостоятельно.

ІII. Итог урока.

ІV. Домашнее задание: §44, № 782 (1), № 783 (1), № 784.