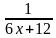МАОУ «Свердловская СОШ №2»
План- конспект открытого урока
по математике в 11 Б классе
«Подготовка к ЕГЭ. Решение сложных комбинированных уравнений»
Урок разработала и провела:
Сушкова Э.А.,
учитель математики
МАОУ «Свердловская СОШ №2»
Апрель 2021 г
https://yandex.ru/efir?stream_id=vIL5MDlVhUGQ&from_block=player_context_menu_yavideo
Тип урока: семинарское занятие.
Цели урока:
Познавательные: повторить и обобщить изученный за курс средней школы материал по математике, закрепить навыки решения сложных уравнений различными методами.
Развивающие: развивать ключевые коммуникативные компетенции, речь, внимание, память, логическое мышление, умение обобщать, делать выводы, развивать навыки самоконтроля и творческие способности учащихся.
Воспитательные: совершенствовать навыки этичного межличностного общения, сознательное отношение к математике; активизировать познавательную деятельность в коллективе, формировать навыки сотрудничества в решении поисковых задач, воспитывать у учащихся морально-ценностные чувства.
Задачи урока:
- Систематизировать теоретические знание по теме.
- Развивать умение работать с заданиями ЕГЭ.
Совершенствовать навыки решения сложных уравнений различными методами.
Ход урока:
I Организационный момент:
а) готовность класса к уроку;
б Слово учителя: Ребята, сегодня у нас необычный урок. Мы проверим наши знания, уровень нашей подготовки к сдаче ЕГЭ. И я хочу начать сегодняшний урок с притчи.
— Учитель, я уже целый год живу у тебя, но до сих пор выполняю только работы по хозяйству. Когда ты будешь меня учить? Разве я для этого пришёл к тебе в ученики, скажи?
— Имей терпение, — ответил учитель, — ещё не пришло время. Иди в нижнюю долину и посади дерево, вырасти его, а я подумаю.
Долгий и тяжёлый путь проделал ученик, пока спустился в долину. По дороге он выкопал маленький саженец и посадил его. С той поры, дважды в день он проходил опасный путь, между хижиной и долиной, чтобы полить деревце. Изо дня в день, он присматривал за деревом. Так прошёл год. Усилия его не пропали даром. Дерево выросло высоким и крепким. Однажды на рассвете, он вышел из хижины и увидел своего учителя, сидящего у ручья под деревом.
— Учитель! – обрадовался юноша. – Как я счастлив вновь увидеть тебя! Я должен извиниться перед тобой, что не смог стать твоим учеником, обманув твоё доверие! Ты подумал, что я слаб, когда я остался жить в долине. Но я должен был заботиться о своём деревеИ теперь, ты вряд ли возьмёшь меня обратно…
Выслушав пылкую речь юноши, старик сказал ему: — Именно в этот год, ты вместе с деревом взращивал такие качества своего характера, которые тебе помогут постигать знания.
Твоё дерево говорит о твоей готовности. Посмотри!
Ответственность ты имел, но только по необходимости, Был нетерпелив и эмоционален, как переплетенные побеги саженца. Чтобы обрести знания, нужна, прежде всего, дисциплина.
Ибо корни дерева – твоя ответственность,
ствол дерева – твоё терпение,
ветви дерева – спокойствие,
а листья – знания!
И вам я желаю такого же упорства и терпения, чтобы хорошо подготовиться к ЕГЭ и успешно его сдать.
А теперь приступим к выполнению заданий.
Проверка дз.
Дать определение уравнения и его корня, равносильности двух уравнений.
Ответ:
Арифметическое выражение, содержащее неизвестную переменную и знаки равенства называют уравнением. Значение переменной, превращающее уравнение в верное равенство, называют корнем уравнения. Два уравнения называют равносильными, если любой корень первого уравнения является корнем второго уравнения и любой корень второго уравнения является корнем первого уравнения.
Дать определение равносильности преобразования уравнения и перечислить основные равносильные преобразования.
Ответ:
Замену одного уравнения другим, равносильным ему уравнением называют равносильным преобразованием уравнения.
Равносильными преобразованиями уравнения являются:
- перенос члена уравнения с противоположным знаком из одной части уравнения в другую;
- умножение (деление) обеих частей уравнения на отличную от нуля число;
- возведение уравнения в нечетную степень;
- извлечение корня нечетной степени с обеих частей уравнения:
- логарифмирование показательного уравнения;
- применение тождеств, т. е равенств, справедливых для любого числа.
Рассказать, какие равносильные преобразования нужно выполнить, чтобы решить следующие уравнения

Дайте определение уравнения – следствия и перечислите преобразования, приводящие к уравнению следствия.
Ответ:
Пусть даны два уравнения. Если любой корень первого уравнения является корнем второго уравнения, то второе уравнение называют уравнением- следствием первого.
Замену уравнения другим уравнением, которое является его следствием, называют переходом к уравнению- следствию.
При переходе к уравнению- следствия возможно появление лишних корней, посторонних для исходного уравнения, поэтому проверка полученных корней является обязательной частью решения уравнения.
Преобразованиями, приводящими к уравнению- следствия является:
- возведение уравнения в четную степень;
- потенцирование логарифмического уравнения;
- освобождение уравнения от знаменателя;
- приведение подобных членов;
- применение формул (тригонометрических, логарифмических и других).
- Расскажите, каким способом приводится следующие уравнения к уравнению – следствия.



Карточки имеются у каждого ученика на парте.
Сложные уравнения можно решить, приводя их к системам. Правила перехода от уравнений к равносильным системам:
1.
2.
3.
4.
5.
6.
7.
М-область существования
8.
9.
10.
11.
Работа в группах.
Запишите системы, равносильные уравнениям. (Работы выполняют на листочках)..
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
Очень часто можно встретить уравнение, которое имеет дополнительное условие, например:
Как можно упростить решение такого типа уравнения?
Разбор решения на доске.
Ответ:
Учитывая, что левая часть уравнения неотрицательное число получаем 




Самыми сложными считаются уравнения с параметром. Дайте определение уравнения с параметром. Давайте рассмотрим несколько таких уравнений с использованием свойств функций:
а)

Ответ:
Для каждого значения a рассмотрим функцию
Она определена на множестве R, четная, поэтому, если 

Уравнение (1) имеет три корня тогда и только тогда, когда оно имеет 

При 

При 


Видеоурок.
Максимум за выполнение данного задания(18 задание) можно получить 4 балла.
В задачах с параметром допускают весьма разнообразные способы решений. Наиболее распространенными из них являются;
Чисто алгебраический способ решения;
-способ решения,основанный на построении и исследовании геометрической модели данной задачи;
-функциональный способ, в котором могут быть и алгебраические, и геометрические моменты, но базовым является исследование некоторой функции.
Критерии оценивания:
|
Обоснованно получен верный ответ |
4 балла |
|
|
С помощью верного рассуждения получены оба верных значения параметра, но -или в ответ включены и одно-два неверных значения; -или решение недостаточно обосновано. |
3 балла |
|
|
С помощью верного рассуждения получено хотя бы одно верное значение параметра |
2 балла |
|
|
Задача сведена к исследованию: -или взаимного расположения трех окружносей; -или двух квадратных уравнений с параметром. |
1 балл |
|
|
Решение не соответствует ни одному из критериев, перечисленных выше |
О баллов |
Выполнения тренировочных упражнений на закрепление навыков и умений решать уравнения.
;
VI Домашнее задание:
Разбор заданий типа С с индивидуальных карточек с сайта www.ege.edu.ru Банк заданий на доске.
Карточка №1
С1.(В13)
Карточка №2
C1.(B1)
Карточка №3
C1.(B12)
Карточка №4
C1.(B19)
Карточка №5
С5. Найти все значения a, такие, что уравнение имеет единственное решение:
Карточка №6
С5. Найти все значения a, такие, что уравнение имеет единственное решение:
Карточка № 7
Найти наибольший корень уравнения:

Карточка № 8
Найти значение р, при которых уравнение

Карточка №9
Решить уравнение
- Повторить теорию по темам:
- Уравнения-следствия.
- Равносильность уравнений системам.
- Равносильность уравнений на множествах.
VII Подведение итогов урока.
Оцените вашу работу на уроке.
Сколько баллов вы набрали?
К какому выводу пришли?
Лист самооценки работы учащегося
———————————————————————————(Ф.И. учащегося)
———————————————————————————(тема урока)
|
Мой вклад… |
Баллы |
|||
|
1(плохо) |
2(слабо) |
3(хорошо) |
4(отлично) |
|
|
В поисках материала по теме |
||||
|
В теоретическом изучении материала |
||||
|
В решении примеров |
||||
|
В групповой работе |
||||
|
В защите работ, анализе решений |
Перевод баллов:
0-9 баллов-2
10-13 баллов-3
14-16 баллов-4
15-20 баллов-5
Лист самооценки работы учащегося
———————————————————————————(Ф.И. учащегося)
———————————————————————————(тема урока)
|
Мой вклад… |
Баллы |
|||
|
1(плохо) |
2(слабо) |
3(хорошо) |
4(отлично) |
|
|
В поисках материала по теме |
||||
|
В теоретическом изучении материала |
||||
|
В решении примеров |
||||
|
В групповой работе |
||||
|
В защите работ, анализе решений |
Перевод баллов:
0-9 баллов-2
10-13 баллов-3
14-16 баллов-4
15-20 баллов-5
27.04.16г.
Открытый
урок .
Тема. Подготовка к ЕГЭ по математике
(базовый уровень).
Тип
урока. Комбинированный.
Цели
урока.
Показать в
доступной форме и объяснить способы и приемы решения типовых экзаменационных заданий. Вовлечение
учащихся в деятельность по подготовке к ЕГЭ по математике.
Развивать
познавательный интерес к экзаменационным заданиям и желание детей их решать.
Формировать логическое, абстрактное и системное мышление.
Воспитывать
самостоятельность, настойчивость для достижения конечных результатов.
Формы
организации учебной деятельности. Фронтальная, индивидуальная, групповая.
Оборудование.
Типовые
задания из открытого банка заданий ФИПИ, мультимедийный проектор, ноутбук,
экран.
Девиз урока. Никогда не надо стыдиться сказать:
«Я не знаю, объясните мне».
(Дж. Даррелл)
П л а н у р о к а.
( Класс делится на группы по два человека: сильный+слабый).
1.
Орг. момент. ( Приветствие. Объявление темы, цели и девиза урока).
2. Решение заданий демоварианта. Математика. 11 класс. ЕГЭ 2016. Базовый уровень.
(
В 2016 году
(базовый уровень) экзамен включает в себя 20 задач.)
№1:
Арифметические действия с целыми
числами или дробями
При
работе с обыкновенными дробями помните простые правила:
1) Дроби приводят к общему знаменателю при сложении и вычитании.
2) Для умножения 2-ух правильных обыкновенных дробей достаточно числитель
умножить на числитель, а знаменатель на знаменатель.
3) Разделить на дробь — то же самое, что умножить на перевернутое.
№2:
Арифметические
действия со степенями
Повторить формулы свойства степени.
№3:
Практические задачи с текстовым условием на проценты

Такие задачи можно решать по правилам нахождения части от
числа (умножением на дробь) или числа по его части (делением на дробь). Если вы
испытываете затруднения с этими правилами, то такие задачи можно решать
пропорцией.
№4:
Вычисления и преобразования по данным
формулам
Нужно аккуратно подставить заданные числа в формулу,
привести подобные члены, если они есть, затем решить простое уравнение, в
котором в качестве неизвестной величины будет искомая переменная.
№5:
Вычисления и преобразования алгебраических
выражений
( Формулы сокращенного умножения. Сокращение дробей.)
(Арифметические действия с корнями и иррациональными выражениями)
(Вычисление значений показательных выражений)
(Логарифмы. Вычисление значений логарифмических выражений)
(Основные формулы тригонометрии. Вычисление тригонометрических выражений)
Повторите простейшие формулы тригонометрии: sin2α
+ cos2α = 1; tgα·ctgα=1 , периодичность функций и т.п. А чтобы не запутаться со
знаками функций потренируйтесь определять их
значения по тригонометрическому кругу.
№6:
Практические арифметические задачи с
текстовым условием
Потренировать решение задач на наибольшее/наименьшее с
целыми (по смыслу) ответами, простейшие задачи на действия с рациональными
числами.
№7:
Уравнения
(линейные и квадратные
уравнения)
(дробно-рациональные
уравнения)
(простейшие
иррациональные уравнения)
(простейшие
показательные уравнения)
(простейшие
логарифмические уравнения)
(простейшие тригонометрические уравнения)
Прорешать простейшие типовые уравнения школьного курса
№8:
Практические и прикладные задачи
по планиметрии
Это наиболее простые задачи на свойства геометрических фигур. В
частности, нужно вспомнить понятия периметр и площадь
плоской фигуры, подобие фигур.
№9:
Соответствие между величинами и их возможными
значениями
( Перевод единиц измерений, сравнение величин, прикидка и
оценка, соответствия между величинами и их значениями )
Фактически, задача на разумность. И, конечно, на знание единиц
измерения. Лучше всего повторить их по учебнику физики.
№10:
Понятие вероятности. Практические задачи на вычисление вероятностей
Повторить формулы на классическое определение вероятности.
№11:
Чтение данных, представленных в виде графиков, диаграмм и
таблиц.
По табличной форме представления данных можно задать вопрос на поиск
нужной информации.
№12:
Практические арифметические задачи с текстовым условием. Оптимальный
выбор
Эти задачи на анализ данных в табличном и
графическом представлении.
№13:
Практические и прикладные задачи по
стереометрии
№14:
Функция. График функции.
(Возрастание, убывание, точки максимума, минимума, наибольшие, наименьшие
значения функции. Чтение графиков функций)
(Графики
тригонометрических функций)
(Графики
показательных функций)
(Графики
логарифмических функций)
(Прямая. Угловой коэффициент прямой. График линейной функции)
(Понятие касательной к графику функции. Связь между знаком углового
коэффициента касательной и монотонностью функции. Связь между угловым
коэффициентом касательной и точками экстремума)
(Понятие производной. Производная как угловой коэффициент
касательной)
(Чтение свойств производной функции по графику этой
функции. Чтение свойств графика функции по графику производной этой функции)
№15:
Планиметрия.
(Треугольник)
(Прямоугольник. Квадрат. Ромб)
(Параллелограмм)
(Трапеция)
(Окружность и круг)
(Вписанные и описанные
окружности)
(Геометрия на клетчатой
бумаге)
(Простейшие задачи в
координатах)
№16:
Стереометрия.
( Призма, её элементы. Прямая призма. Правильная призма. Правильная
треугольная призма )
( Параллелепипед, его элементы. Прямоугольный
параллелепипед )
(Площадь поверхности призмы. Объём призмы)
( Пирамида, её элементы. Правильная пирамида, её элементы. Правильная
треугольная пирамида )
( Правильная четырёхугольная пирамида. Правильная
шестиугольная пирамида )
(Пирамида. Вычисление
площадей и объёмов)
(Сфера и шар, их элементы. Площадь сферы
и объём шара)
(Цилиндр, её элементы. Площадь поверхности
цилиндра)
(Конус, его элементы. Площадь
поверхности конуса)
(Объём цилиндра и объём
конуса)
(Задачи по стереометрии на вычисления)
№17:
Неравенства.
(Общие сведения о неравенствах. Метод
интервалов)
(Линейные
неравенства)
(Квадратные
неравенства)
(Простейшие дробно-рациональные неравенства)
(Простейшие
показательные неравенства)
(Простейшие
логарифмические неравенства)
№18:
Задачи с логической составляющей. Следствия.
№19:
Задачи с логической составляющей. Делимость.
№20:
Текстовые арифметические задачи с логической составляющей
3.Подведение
итогов урока:
Выставление
оценок за работу на уроке.
Д/з:
Решение вариантов из демверсии. Проведение самоанализа подготовки к ЕГЭ.
Ваш высокий результат никому
кроме вас самих не нужен.
Какой уровень знания математики у вас сейчас? Как вы
его оцениваете? Обозначим моменты, которые не должны вызывать затруднений:
1.
Сложить в уме два трёхзначных числа, например 185 и 238.
2.
Сложить, найти разность, умножить и разделить столбиком любые целые числа.
3.
Произвести действия с дробями (сложение, вычитание, умножение, деление),
сократить дробь.
4.
Найти результат умножения (деления) положительных и отрицательных чисел
(не потерять знак).
5.
Выразить из равенства любую неизвестную величину.
6.
Найти результат умножения многочленов.
7.
Записать свойства корней и степеней по памяти.
8.
Решить квадратное уравнение, неравенство.
9.
Перечислить и построить графики основных функций.
10.
Воспроизвести основные теоремы (Пифагора, косинусов, синусов, сумма углов
треугольника и пр).
11.
Назвать признаки равенства треугольников, подобия треугольников.
12.
Озвучить определения синуса, косинуса, тангенса и котангенса в прямоугольном
треугольнике.
13.Воспроизвести
формулы площадей (треугольник, квадрат, прямоугольник, параллелограмм,
трапеция, круг, сектор круга).
14.Записать
все формулы, связанные с координатной плоскостью (длина отрезка, координаты
середины отрезка, координаты вектора, длина вектора, скалярное произведение).
15.
Записать основные формулы тригонометрии.
16.
Записать формулы сокращённого умножения.
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа
пос. Мизур Алагирского района РСО-Алания
Открытый урок по теме
«Решение заданий ЕГЭ»
Учитель математики Агузарова Л.Д.
п. Мизур
2021г
Тема: Решение заданий ЕГЭ
(задачи с практическим содержанием, рациональные, показательные, логарифмические, иррациональные уравнения, логарифмические неравенства )
Цели занятия:
Образовательные:
-
Повторить материал по данной теме;
Развивающие:
-
Развитие познавательного интереса учащихся к уроку математики;
-
Развитие логического мышления;
-
Развитие скорости и аккуратности;
-
Развитие навыков коллективной работы в сочетании с индивидуальной.
Воспитательные:
-
Воспитание трудолюбия ;
-
Воспитание уважения к окружающим;
Тип урока: урок актуализации знаний и умений (урок повторения).
Ход урока
I. Организационный этап.
Приветствие. Открыли тетради, записали на полях число, классная работа.
I I. Проверка домашней работы
Как у вас обстоят дела с домашней работой? Для того чтобы урок прошел успешно, я должна знать какие затруднения у вас были в домашней работе. Поднимите руки у кого они были.
I I I. Постановка цели и задач урока.
У вас на столах лежат листы, посмотрите на заголовок и попробуйте сформулировать тему нашего урока. «Решение заданий ЕГЭ». Посмотрите на содержание и попробуйте сформулировать цели урока. Сегодня у нас необычный урок, на котором мы будем повторять почти все виды уравнений. Перед вами стоит задача – показать свои знания и умения по решению задач с практическим содержанием, рациональные, показательные, логарифмические, иррациональные уравнения. А так же задание 15 из второй части профильного уровня.
Древнегреческий поэт Нивей утверждал, что математику нельзя изучать, наблюдая, как это делает сосед. Поэтому будем сегодня работать самостоятельно.
IV. Актуализация знаний
-
Что такое процент? Какие три типа задач на % существуют? (% от числа, целого по части процента, сколько % составляет одна величина от другой)
-
Что такое корень уравнения? Что значить решить уравнение?
V. Повторение
Прототип задания 1 Задания с практическим содержанием
-
Шариковая ручка стоит 30 рублей. Какое наибольшее количество таких ручек можно будет купить на 300 рублей после повышения цены на 25%?
-
Цена на электрический чайник была повышена на 14% и составила 1596 рублей. Сколько рублей стоил чайник до повышения цены?
-
Для приготовления маринада для огурцов на 1 литр воды требуется 10 г лимонной кислоты. Лимонная кислота продается в пакетиках по 15 г. Какое наименьшее число пачек нужно купить хозяйке для приготовления 8 литров маринада?
-
В летнем лагере 152 ребенка и 21 воспитатель. Автобус рассчитан не более чем на 30 пассажиров. Какое наименьшее количество автобусов понадобится, чтобы за один раз перевезти всех из лагеря в город?
Прототип задания 5
Рациональные уравнения
-
=
Показательные уравнения
-
(
)х+4=49
-
2х-3=
-
(0,2)5+4х=125
Алгоритм решения задания:
-
Определяем вид уравнения.
-
Представляем правую часть в виде степени с одним и тем же основанием
-
Переходим к линейному уравнению и решаем уравнение.
-
Записываем ответ.
Логарифмические уравнения
-
log3(x+6)=log3(10-x)-1
-
log2(8-x)=2 log2(4+x)
Алгоритм решения задания:
-
Определяем вид уравнения.
-
Представляем правую часть в виде логарифма с одним и тем же основанием.
-
Потенцируем и решаем уравнение.
-
Проверяем корни.
-
Записываем ответ.
Иррациональные уравнения
-
√2х-3=х-3
VI. Применение знаний и умений в новой ситуации
Решить рациональное уравнение
(2х-11)2=(2х-1)2
(х-11)4=(х+3)4
Решить логарифмическое неравенство
х2log243(4-x)≤ log3(x2-8x+16)
VII.. Контроль усвоения, обсуждение допущенных ошибок
Самостоятельная работа в парах
Решите уравнения
Вариант 1
Решите уравнение
-
25-х=64
-
42х-17=
-
√4х+16=10
-
log8(x+4)=log8(5x-16)
-
=
Вариант 2
Решите уравнение
-
21-х=32
-
35х-12=
-
√14-5х=3
-
log2(x+3)=log2(3x-15)
-
=
VIII .Домашнее задание варианты 11-14 задания 7
IX. Рефлексия
Продолжи предложение
Сегодня на уроке я научился…
Сегодня на уроке мне понравилось…
Сегодня на уроке я повторил…
Сегодня на уроке я закрепил…
План урока по математике в 11 классе «Решение текстовых задач» при подготовке к ЕГЭ
Тема урока: Решение текстовых задач
Тип урока: совершенствование ЗУН
Цели урока:
дидактическая: научить применять ранее полученные знания при решении текстовых задач в выполнении заданий ЕГЭ разного уровня сложности, стимулировать обучающихся к овладению рациональными приёмами и методами решения текстовых задач;
развивающая: развивать логическое мышление, память, познавательный интерес, продолжать формирование математической речи и графической культуры, вырабатывать умение анализировать и сравнивать;
воспитательная: приучать к эстетическому оформлению записи в тетради, умению выслушать других и умению общаться, прививать аккуратность и трудолюбие.
Ход урока:
|
Этапы урока, их содержание |
Деятельность |
|
|
учителя |
учащихся |
|
|
Постановка цели Сегодня мы продолжим отрабатывать навыки решения текстовых задач, но уже по вариантам ЕГЭ, рассмотрим различные задачи |
Сообщает тему урока, цель урока, на доске записывает число и тему урока |
Записывают в тетрадях |
|
Проверка домашнего задания (приложение 1) На дом было задано три задачи. Какие вопросы и затруднения по задачам. Если вопросов нет, то проверим одну из них. |
На экране показано правильное оформление задачи. Комментирует решение, привлекая к работе учащихся |
Сверяют своё решение с записями на экране, задают вопросы учителю, отвечают на вопросы учителя |
|
Актуализация темы (приложение 2) |
Проводит фронтальную беседу по типам задач и приёмам их решения |
|
|
Фронтальная работа, решение задач (приложение 3) |
Направляет на правильный выбор решения, следит за верностью рассуждений и речью учащихся, активизирует их работу сопутствующими вопросами |
Комментируют условие задачи, предлагают свои подходы к решению: введение переменных, обозначение величин, составление уравнений. |
|
Индивидуальная работа самостоятельная работа, (приложение 4) |
Раздаёт карточки с заданиями в трёх вариантах с тремя задачами различной степени сложности |
Самостоятельно выполняют задания в тетрадях |
|
Подведение итогов |
Комментирует работу класса, отличившимся учащимся выставляет отметки, всем учащиеся за самостоятельную работу отметки будут также выставлены в классный журнал |
|
|
Домашнее задание (приложение 5) |
Поясняет домашнее задание, обращая внимание на то, что аналогичные задачи были разобраны на уроке |
Приложение 1 (домашняя работа)
Задача № 1. Два велосипедиста отправляются навстречу друг другу одновременно из двух пунктов, расстояние между которыми равно 54 км, и встречаются через 2 ч. Определите скорость каждого велосипедиста, если скорость у одного из них она на 3 км/ч больше, чем у другого.
Задача № 2. Сберегательный банк в конце года начисляет 3% к сумме, находившейся на счету. На сколько рублей увеличится первоначальный вклад в 1000 рублей через 2 года?
Задача № 3. Под строительную площадку отвели участок прямоугольной формы, длина которого на 30 метров больше его ширины. При утверждении плана застройки выяснилось, что граница участка проходит по территории водоохраной зоны, поэтому его ширину уменьшили на 20 метров. Найдите длину участка, если после утверждения плана застройки площадь участка составила 2400 м2.
решение задачи № 1.
Устные рассуждения:
Одним из основных условий задачи является одновременное отправление велосипедистов из пунктов, значит, каждый из них находился в пути одно и то же время, т.е. 2 часа. Далее, даётся некая зависимость между скоростями велосипедистов, поэтому меньшую скорость, пусть это будет скорость первого велосипедиста, обозначим км/ч, тогда скорость второго будет
км/ч. По условию задачи велосипедисты встретились через 2 часа после отправления. Зная время движения и скорости велосипедистов, можно найти путь каждого из них. Таким образом, первый велосипедист за 2 часа проехал путь
км, а второй за те же 2 часа –
км. По условию задачи через 2 часа велосипедисты встретились, т.е. проехали весь путь 54 км.
Запись в тетради:
Обозначим скорость первого велосипедиста км/ч, тогда скорость второго будет
км/ч.
По условию задачи каждый велосипедист находился в пути 2 часа, значит, первый велосипедист проехал путь км, а второй –
км. По условию задачи через 2 часа велосипедисты встретились, т.е. проехали весь путь 54 км. Следовательно, уравнение составляем по проделанному пути обоими велосипедистами:
.
Решение:
,
,
,
. Получили: скорость первого велосипедиста 13 км/ч, а второго – 16 км/ч.
Ответ: 13 км/ч; 16 км/ч.
Оставшиеся две задачи разбирают устно.
Приложение 2
Ребята, давайте вспомним, какие типы текстовых задач мы рассматривали и какие основные величины характеризуют тот или иной тип задачи. И так:
-
Задачи на движение:
а) движение навстречу друг другу, движение в одном направлении, движение в противоположных направлениях;
б) движение по воде: по течению реки, против течения реки, в озере,
основные величины, характеризующие движение – скорость, время, расстояние.
-
Задачи на совершение работы, основные величины – время, объём совершённой работы, производительность труда, где объём совершённой работы принимается за 100% или 1.
-
Задачи на проценты:
а) товар и его стоимость, где первоначальная стоимость принимается за 100% или 1, повышение или понижение стоимости рассматривается как нахождение части от числа в сторону увеличения или уменьшения числа;
б) суммы вкладов в банки и банковские процентные ставки, где первоначальный вклад принимается за 100% или 1, увеличение вклада рассматривается как нахождение части от числа дополнительно к основной сумме;
в) процентное содержание кислоты в растворе и др.
Приложение 3
Задача № 1. Цена первого товара повысилась на 30%, а потом еще на 5%. Цена второго товара повысилась на 25%. После повышения цены товаров сравнялись. Найдите, на сколько процентов первоначальная цена одного товара больше первоначальной цены другого товара.
Устные рассуждения:
Всякую математическую модель можно рассматривать с трёх позиций, в данном случае – товар: в рублях, в процентах, в частях. Пусть первоначальная цена первого товара будет х руб, т.е. 100% или 1. Тогда первое повышение цены на 30% в денежном выражении составляет 0,3 х руб., а новая цена будет составлять 130% или 1,3х руб. Второе повышение на 5% в денежном выражении составляет 1,3х 0,05 = 0,065х руб., значит последняя цена будет состоять из суммы предыдущей плюс 5%, т.е. 1,3х + 0,065х = 1,365х руб.
Аналогично, пусть первоначальная цена второго товара будет у руб, т.е. 100% или 1. Тогда первое повышение цены на 25% в денежном выражении составляет 0,25у руб., а новая цена будет составлять 125% или 1,25у руб. По условию после повышения цены товаров сравнялись, т.е.1,365х = 1,25у, откуда у = 1,092х. Найдём разницу цен в частях: у – х = 1,092 – 1 = 0,092.
Запись в тетрадях:
Пусть первоначальная цена первого товара будет х руб, т.е. 100% или 1. Тогда первое повышение цены на 30% в денежном выражении составляет 0,3 х руб., а новая цена будет составлять 130% или 1,3х руб. Второе повышение на 5% в денежном выражении составляет
1,3х0,05 = 0,065х руб., значит последняя цена будет состоять из суммы предыдущей плюс 5%, т.е. 1,3х + 0,065х = 1,365х руб.
Аналогично, пусть первоначальная цена второго товара будет у руб, т.е. 100% или 1. Тогда первое повышение цены на 25% в денежном выражении равно 0,25у руб., а новая цена будет составлять 125% или 1,25у рублей. По условию после повышения цены товаров сравнялись, т.е.1,365х = 1,25у, откуда у = 1,092х. Найдём разницу цен в частях: у – х = 1,092 – 1 = 0,092.
Переведём полученную дробь в проценты: %.
Ответ :разница первоначальных цен товаров составляет 9,2%.
Задача № 2. Найдите первоначальную сумму вклада (в рублях), если после истечения двух лет она выросла на 304,5 рубля при 3% годовых.
Устные рассуждения:
Пусть первоначальная сумма взноса будет х руб., т.е. 100% или1. По условию задачи через год сумма вклада увеличилась на 3%, что в денежном выражении составляет 0,03х руб. Значит, через год сумма вклада будет равна 1,03х руб. Ещё через год сумма вклада снова увеличилась на 3% годовых, в денежном выражении это увеличение составляет 1,03х0,03 = 0,0309х (руб.). А общая сумма вклада за два года будет состоять из предыдущей суммы вклада плюс 3% годовых, т.е.1,03х + 0,0309х = 1,0609х (руб.). По условию задачи за два года сумма вклада увеличилась на 304,5 руб. Уравнение данной задачи представляет собой разницу вкладов.
Запись в тетрадях:
Пусть первоначальная сумма взноса будет х руб., т.е. 100% или1. Через год сумма вклада увеличилась на 3% годовых, значит, через год сумма вклада будет составлять 1,03х руб. Ещё через год сумма вклада снова увеличилась на 3% годовых, в денежном выражении это увеличение составляет 1,03х0,03 = 0,0309х (руб.). Значит, за два года сумма вклада будет составлять 1,03х + 0,0309х = 1,0609х (руб.). По условию задачи за два года сумма вклада увеличилась на 304,5 руб., т.е.:
1,0609х – х = 304,5 ,
0,0609х = 304,5 ,
х = 304,5:0,0609 ,
х = 5000. Получили первоначальную сумму вклада 5000 руб.
Ответ: 5000 рублей.
Задача № 3. Смешав 70%-й и 60%-й растворы кислоты и добавив 2 кг чистой воды, получили 50%-й раствор кислоты. Если бы вместо 2 кг воды добавили 2 кг 90%-го раствора той же кислоты, то получили бы 70%-й раствор кислоты. Сколько килограммов 70%-го раствора использовали для получения смеси?
Устные рассуждения:
Поскольку речь идёт о двух растворах разной концентрации, значит надо вводить две переменные. Семидесяти процентный раствор состоит из 70% кислоты и 30% воды, а шестидесяти процентный раствор состоит из 60% кислоты и 40% воды. Если первоначальную массу 70%-го раствора обозначить за х кг, значит в нём кислоты будет 0,7х кг, а воды будет 0,3х кг. Аналогично, если первоначальную массу 60%-го раствора обозначить за у кг, значит, в нём кислоты будет 0,6у кг, а воды будет 0,4у кг. После добавления 2 кг чистой воды, концентрация раствора стала равной 50%. Это означает, что в новом растворе масса воды будет 0,5(х + у +2) кг. Поскольку дополнительным условием задачи является добавление чистой воды, значит, уравнение составляем по массе воды. И так, первоначальная масса воды растворов была 0,3х кг и 0,4у кг, затем ещё добавили 2 кг воды, в итоге получили 0,5(х + у + 2) кг воды. Аналогично разбирается второй случай, когда к имеющимся растворам кислоты добавляют 2 кг 90%-го раствора той же кислоты и получается 70%-й раствор кислоты. Поскольку здесь дополнительным условием является добавление 90%-й кислоты, то второе уравнение составим по массе кислоты. И так, к имевшимся массам кислот 0,7х кг и 0,6у кг добавили кислоту массой кг, т.е. 1,8 кг и получили массу кислоты 0,7(х + у + 2) кг.
Запишем и решим систему двух уравнений с двумя переменными.
Запись в тетрадях:
Пусть первоначальная масса 70%-го раствора кислоты будет х кг, значит в нём кислоты будет 0,7х кг, а воды будет 0,3х кг. Аналогично, пусть первоначальная масса 60%-й растворы кислоты будет у кг, значит, в нём кислоты будет 0,6у кг, а воды будет 0,4у кг. По условию первый раз добавили 2 кг чистой воды, после чего концентрация раствора стала равной 50%, т.е. в полученном растворе воды будет 0,5(х + у +2) кг. Следовательно, первое уравнение имеет вид:
0,3х + 0,4у + 2 = 0,5(х + у +2). По условию второй раз добавили 2 кг 90%-й кислоты, значит, т.е. по массе кг или 1,8 кг и получили 70%-й раствор кислоты, масса кислоты в котором будет 0,7(х + у + 2) кг. Соответственно второе уравнение составим по массе кислоты в растворах:
0,7х + 0,6у + 1,8 = 0,7(х + у + 2). Решим систему двух уравнений с двумя переменными:
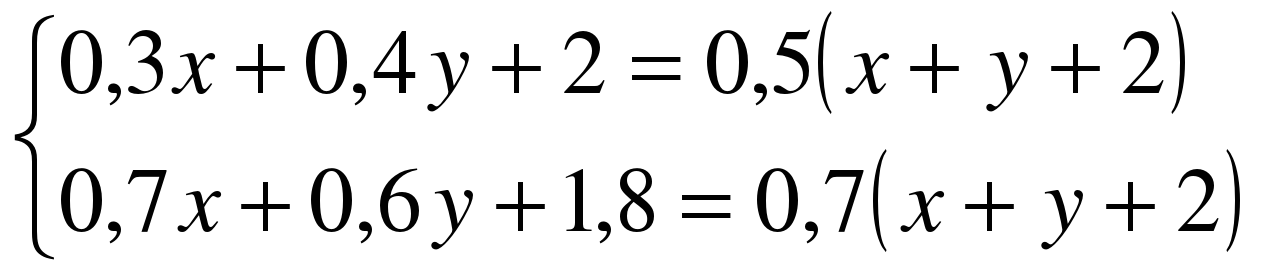
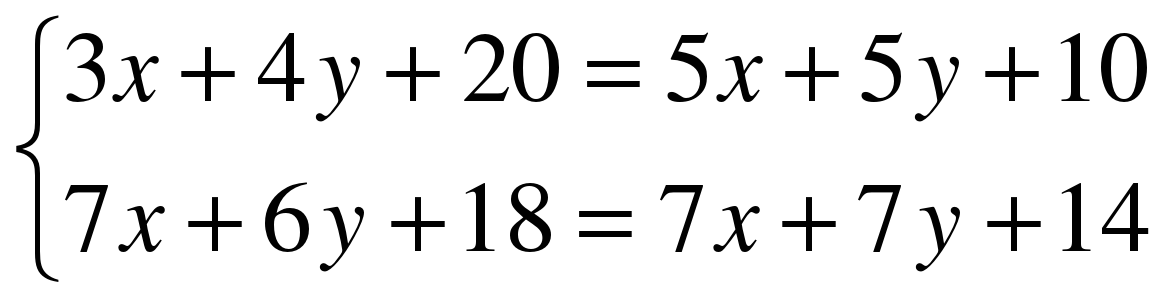
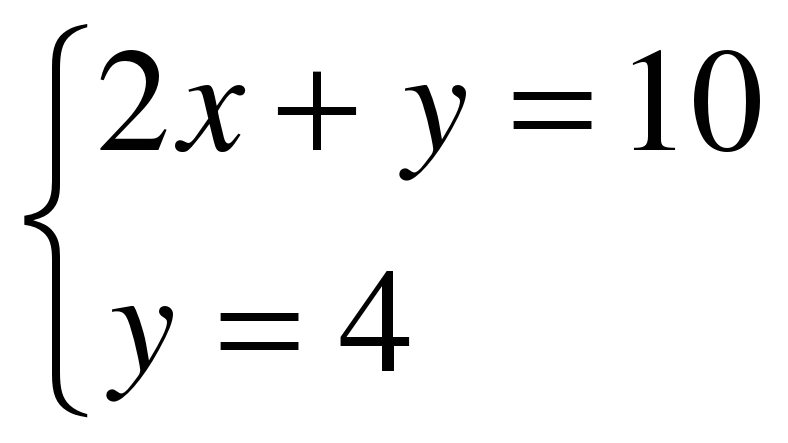
Получили 3 кг 70%-й кислоты.
Ответ: 3 кг.
-
Имелось два сплава серебра. Процент содержания серебра в первом сплаве был на 25% выше, чем во втором. Когда сплавили их вместе, то получили сплав, содержащий 30% серебра. Определить массы сплавов, если известно, что серебра в первом сплаве было 4кг, а во втором 8 кг. Ответ: 8 кг; 32 кг
-
В первом сосуде растворили 0,36 л, а во втором 0,42 л чистого спирта. Процентное
содержание спирта в первом сосуде оказалось на 6% больше, чем во втором. Каково процентное содержание спирта во втором и первом сосудах, если известно, что растворы в первом сосуде на 4 л меньше? Ответ: 12% и 6% -
В 4 кг сплава меди и олова содержится 40% олова. Сколько килограммов олова добавить к этому сплаву, чтобы его процентное содержание в новом сплаве стало бы равным 70%? Ответ: 4кг
-
К 40% раствору серной кислоты добавили 50 г чистой серной кислоты, после чего концентрация раствора стала равной 60%. Найти первоначальную массу раствора.
Ответ: 100 г -
К раствору, содержащему 30 г соли, добавили 400 г, после чего концентрация соли
уменьшилась на 10%. Найти первоначальную концентрацию соли в растворе.
Ответ: 15% -
В 5 кг сплава олова и цинка содержится 80% цинка. Сколько килограммов олова надо добавить к сплаву, чтобы процентное содержание цинка стало вдвое меньше? Ответ: 5 кг
Задача Первая труба наполняет бак объёмом 570 литров, а вторая труба – бак объёмом 530 литров. Известно, что одна из труб пропускает в минуту на 4 литра воды больше, чем другая. Сколько литров воды в минуту пропускает вторая труба, если баки были наполнены за одно и то же время?
Устные рассуждения:
Поскольку первая труба наполняет больший бак, значит у неё пропускная способность больше, чем у второй трубы. Если пропускную способность первой трубы обозначить через (х + 4) л за минуту, тогда пропускная способность второй трубы будет х л за минуту. Значит, время наполнения бака объёмом 570 л первой трубой будет минут, а время наполнения бака объёмом 530 л второй трубой будет
минут. По условию баки были наполнены за одно и то же время.
Запись в тетрадях:
Пусть пропускная способность первой трубы будет (х + 4) л за минуту, тогда пропускная способность второй трубы будет х л за минуту. Значит, время наполнения бака объёмом 570 л первой трубой будет минут, а время наполнения бака объёмом 530 л второй трубой будет
минут. По условию баки были наполнены за одно и то же время, т.е.:
=
, 570
= , 570
= 530
+ 2120 , 40
= 2120 ,
= 53.
Получили, что вторая труба за минуту пропускает 53 л.
Ответ: 53 л.
Задача № 5 Теплоход, скорость которого в неподвижной воде равна 20 км/ч, проходит по течению реки до пункта назначения и после стоянки возвращается в исходный пункт. Найдите расстояние, пройденное теплоходом за весь рейс, если скорость течения равна 4 км/ч, стоянка длится 3 часа, а в исходный пункт теплоход возвращается через 13 часов после отплытия из него. Ответ дайте в километрах.
Устные рассуждения:
По условию задачи скорость теплохода в неподвижной воде равна 20 км/ч, скорость течения равна 4 км/ч. Значит, скорость теплохода по течению реки будет 24 км/ч, а против течения –
16 км/ч. Обозначим расстояние от исходного пункта до пункта назначения за км. Тогда, время, затраченное от исходного пункта до пункта назначения будет ч, а время, затраченное на обратный путь будет ч. А всё время в пути, исключая стоянку 3 часа, составляет 10 часов.
Запись в тетрадях:
По условию задачи скорость теплохода в неподвижной воде равна 20 км/ч, скорость течения равна 4 км/ч. Значит, скорость теплохода по течению реки будет 24 км/ч, а против течения –
16 км/ч. Пусть расстояние от исходного пункта до пункта назначения за км. Тогда время, затраченное от исходного пункта до пункта назначения будет ч, а время, затраченное на обратный путь будет ч. Всё время в пути, исключая стоянку 3 часа, составляет 10 часов, т.е.:
Получили расстояние от исходного пункта до пункта назначения 96 км, значит
расстояние за весь рейс составляет 192 км.
Ответ: 192 км.
Приложение 4
Вариант – 1.
Задача № 1. Катер прошел 15 км по течению реки и 4 км по озеру, затратив на весь путь 1 ч. Найдите собственную скорость лодки, если скорость течения реки равна 4 км/ч.
Задача № 2. Цену товара повысили на 25%, затем новую цену повысили еще на 10% и наконец, после перерасчета произвели повышение цены еще на 12%. На сколько процентов повысили первоначальную цену товара?
Задача № 3. Сберегательный банк в конце года начисляет 2% к сумме, находящейся на счету. На сколько рублей увеличится первоначальный вклад в 5000 рублей через 3 года?
Вариант – 2.
Задача № 1. Моторная лодка прошла 10 км по озеру и 4 км против течения реки, затратив на весь путь 1 ч. Найдите собственную скорость лодки, если скорость течения реки равна 3 км/ч.
Задача № 2. Найдите первоначальную сумму вклада (в рублях), если после истечения трех лет она выросла на 765,1 рубля при 2% годовых.
Задача № 3. Цену на некоторый товар сначала снизили на 30%, а затем повысили на 20%. На сколько процентов изменилась первоначальная цена товара?
Вариант – 3.
Задача № 1. Какое количество воды нужно добавить в 1 литр 9%-ного раствора уксуса, чтобы получить 3%-ный раствор?
Задача № 2. Найдите двузначное число, если произведение его цифр в 6 раз меньше самого числа, а если к исходному числу прибавить 9, то получится число, написанное теми цифрами, но в обратном порядке.
Задача № 3. Сумма двух чисел равна 1100. Найдите наибольшее из них, если 6% одного из них равны 5% другого.
Приложение 5
Вариант – 1.
Задача № 1. Сберегательный банк в конце года начисляет 5% к сумме, находившейся на счету. На сколько процентов увеличится первоначальный вклад в 2000 рублей через 2 года?
Задача № 2. Два пешехода отправляются навстречу друг другу одновременно из двух пунктов, расстояние между которыми равно 50 км, и встречаются через 5 ч. Определите скорость первого пешехода, если его скорость на 2 км/ч больше, чем у другого.
Задача № 3. Численность волков в двух заповедниках в 2009 году составляла 220 особей. Через год обнаружили, что в первом заповеднике численность волков возросла на 10%, а во втором – на 20%. В результате общая численность волков в двух заповедниках составила 250 особей. Сколько волков было в первом заповеднике в 2009 году?
Вариант – 2.
Задача № 1. Сберегательный банк в конце года начисляет 3% к сумме, находившейся на счету. На сколько рублей увеличится первоначальный вклад в 1000 рублей через 2 года?
Задача № 2. К 40% раствору соляной кислоты добавили 50 г чистой кислоты, после чего концентрация раствора стала равной 60%. Найдите первоначальный вес раствора.
Задача № 3 Города А, В и С соединены прямолинейным шоссе, причём город В расположен между городами А и С. Из города А в сторону города С выехал легковой автомобиль, и одновременно с ним из города В в сторону города С выехал грузовик. Через сколько часов после выезда легковой автомобиль догонит грузовик, если скорость легкового автомобиля на 28 км/ч больше скорости грузовика, а расстояние между городами А и В равно 112 км ?
Сортировка:
новинки,
темы
Класс:
Вычисление производных элементарных функций
2022
Цели урока: выяснение степени усвоения понятия производной функции, правил вычисления производных, таблицы производных элементарных функций.
производная функции
Методическая разработка факультативного занятия в 11-м классе. Тема: «Производная функции в заданиях ЕГЭ»
2022
Автор:
Анциферова Ольга Владимировна
Факультативное занятие на тему «Производная функции в заданиях ЕГЭ» – занятие подготовки к успешной сдаче Государственной итоговой аттестации. Строится с применением технологии обучения в сотрудничестве: через создание проблемной ситуации и ведение проблемного диалога учащиеся открывают новые знания, самостоятельно формулируют тему и цель урока, даёт возможность учителю по-новому открывать знания с учениками.
производная функции,
подготовка к ЕГЭ по математике
Рабочая программа элективного курса для учащихся 11-х классов «Решение геометрических задач повышенной сложности»
2022
Автор:
Бикбердина Клара Мутигулловна
Предлагаемый элективный курс адресован учащимся 11-х классов. Главная его идея – это организация систематического и системного повторения, углубления и расширения школьного курса геометрии, что, несомненно, будет направлено на осмысленное изучение геометрии, а значит и качественную подготовку к государственной итоговой аттестации. Данный курс позволит удовлетворить образовательные потребности учащихся, осваивающих как базовый уровень математики, так и профильный уровень.
Конспект урока по математике «Общие методы решения уравнений». 11-й класс
2022
Автор:
Базарон Оюна Будажаповна
Цель урока: определение уровня овладения знаниями и способами действий при решении уравнений; развитие умений обобщать, правильно отбирать методы решения уравнений; развитие умения оценивать свои возможности и достижения; формирование умений осуществлять самоконтроль, взаимоконтроль; воспитание ответственного отношения к коллективной деятельности, познавательной активности и самостоятельности.
решение уравнений
Производная на клетчатой бумаге. 10–11-е классы
2022
Автор:
Ткачева Марина Николаевна
В данной статье рассматриваются задачи по теме «Производная» из задания 6 профильного ЕГЭ по математике. Данные задачи можно разделить на две группы по темам: 1) геометрический смысл производной; 2) исследование функции с помощью производной.
Презентация к уроку по теме «Задачи с экономическим содержанием» (№17 ЕГЭ по математике профильный уровень)
2022
Автор:
Сердогалиева Сауле Айсагалиевна
Рассматривается решение некоторых задач с экономическим содержанием. Материал может использоваться на консультациях, на уроках повторения и подготовки к ЕГЭ по математике на профильном уровне в 10–11-х классах.
экономические задачи
Подготовка к ЕГЭ по математике. Методы решения задач по вычислению углов и расстояний в пространстве. 11-й класс
2022
Автор:
Пирцхалава Светлана Алексеевна
Все задачи по определению углов в пространстве сводятся к задаче по определению углов на плоскости. Углы же на плоскости, как правило, определяются из треугольников. Для вычисления углов в треугольнике используют теорему косинусов (если известны все три стороны), теорему синусов (если известны угол и две стороны). В прямоугольном треугольнике углы определяются через отношения сторон.
подготовка к ЕГЭ по математике
Методическая разработка урока «Объём шара и его частей. Площадь сферы и её частей». 11-й класс
2022
Автор:
Зенцов Андрей Григорьевич
В методической разработке урока геометрии «Объём шара и его частей. Площадь сферы и её частей», 11-й класс, рассматривается вычисление объемов тел с помощью интегрирования, вычисление площадей поверхности тел с помощью дифференцирования, решаются задачи на нахождение объёма шара и шарового сектора, шарового сегмента, площади сферической и полной поверхности шарового сегмента.
Объём шара
КВН для учащихся 9–11-х классов «В мире математики, физики, химии»
2022
Автор:
Бондаренко Светлана Васильевна
КВН для учащихся 9–11-х классов провидится в рамках декады «Точных и естественных наук» посвященной Дню российской науки. Нацелен на развитие познавательного интереса, творческой активности учащихся; на умение применять полученные знания в жизненных ситуациях; формирование у учащихся стремления к активной коллективной интеллектуальной деятельности; на развитие творческого мышления, чувство юмора и смекалки.
КВН
Урок-хакатон.»Обобщающее повторение по теме «Графики функций» ЕГЭ-2022″
2022
Автор:
Петренко Наталья Викторовна
Цель урока: повторить свойства графиков линейной функции, параболы, гиперболы, логарифмической, показательной и тригонометрической функции; применять свойства функций при распознавании графиков, по графику функции составлять уравнение функции, находить значение функции в точке.
О решении задач повышенного уровня сложности по теории вероятностей ЕГЭ по математике профильного уровня (по материалам ФИПИ)
2022
Авторы:
Бабкина Майя Сергеевна, Белова Ольга Львовна, Коваленко Елена Борисовна
Заметим, что открытом банке заданий ЕГЭ по математике профильного уровня ФИПИ, по-прежнему работающем в тестовом режиме, появились некоторые задачи по теории вероятностей повышенного уровня сложности, как и обещали его разработчики. Рассмотрению этих задач и посвящена эта работа.
Сценарий урока по теме «Равносильность уравнений»
2022
Автор:
Мухоморкина Татьяна Петровна
Цель урока: формирование математической культуры учащихся через применение свойств равносильности уравнений при решении уравнений с одной переменной.
Новые задачи по Теории вероятности в ЕГЭ-2022
2022
Автор:
Сенатова Ирина Александрвна
Представлены новые задачи по Теории вероятности в ЕГЭ-2022.
теория вероятностей,
подготовка к ЕГЭ по математике
Формирование функциональной грамотности на уроках математики
2022
Автор:
Горина Ксения Александровна
На уроках математики возможна дифференциация заданий, то есть, все задания должны иметь разные уровни сложности. При решении и составлении задач учащимся могут предлагаться различные картинки, по которым им нужно составить и решить задачу. Оформлением дети занимаются самостоятельно, однако учителю необходимо тщательно следить за работой учеников. При затруднении выполнить данное действие предполагается, что учитель будет задавать наводящие вопросы.
дроби,
инклюзивное образование,
ЗПР,
инклюзивный подход
Теорема Менелая и Чевы
2022
Автор:
Ситдикова Гузелия Ханифовна
Среди теорем о треугольниках есть такие, изучение которых позволяет существенно расширить круг решения геометрических задач. Значение этих теорем состоит, прежде всего, в том, что из них или с их помощью можно вывести большинство теорем геометрии, они служат основой многих дальнейших выводов. Но в геометрии треугольника много и таких теорем, авторы которых вошли в историю только благодаря треугольникам. Это теоремы Чевы и Менелая.
Об опыте применения новых образовательных технологий
2022
Автор:
Рыжкова Елена Игорьевна
Закон РФ «Об образовании» предписывает в обучении ориентироваться на обеспечение самоопределения личности, создание условий для ее самореализации. Сегодня создан инструмент, позволяющий решить эту задачу — это новые образовательные технологии обучения. Таких технологий очень много: дистанционные, технология проблемного, проектного и смешанного обучения, игровые методы и т.д. Все эти технологии позволяют учителю решить те или иные задачи, поставленные цели урока. В своей работе автор начал применять приложение, которое позволяет проводить фронтальные опросы с помощью одного мобильного телефона. Это приложение Plickers.
Применение инструмента «Рабочий лист» на уроках математики
2021
Автор:
Калюк Галина Руслановна
Рабочий лист содержит инструкции и материалы, предназначенные для отдельных учащихся с учетом их индивидуальных возможностей и способностей. Использование индивидуальных рабочих листов позволяет каждому ученику определять цель своих действий в предложенных рамках работы, искать возможные решения, чувствовать свободу выбора знаний и практических возможностей, проявлять самостоятельность при решении возникших проблем, то есть ученик становится активным участником процесса обучения. Главная задача «Рабочего листа» – обучать ученика, учить его учиться, показывать, что процесс обучения может быть увлекательным, что если ученик приложит некоторые усилия, он испытает радость от процесса обучения, от процесса понимания и собственных успехов. Практика – единственный способ улучшить успеваемость детей по математике, и использование рабочих листов – это лучший способ закрепить знания на практике.
Элементы теории графов
2021
Автор:
Епихина Лена Вячеславовна
Теория графов широко применяется в решении экономических и управленческих задач, в программировании, химии, конструировании и изучении электрических цепей, коммуникации, психологии, социологии, лингвистике и в других областях. Для чего строят графы: чтобы отобразить отношения на множествах. По сути, графы помогают визуально представить всяческие сложные взаимодействия: аэропорты и рейсы между ними, разные отделы в компании, молекулы в веществе.
Методическая разработка практического занятия с применением дистанционных образовательных технологий по теме «Тела вращения»
2021
Автор:
Дурнина Светлана Владимировна
Задачи урока: систематизировать знания обучающихся, обобщить изученный материал по теме «Тела вращения», формировать умение решать задачи практического содержания и профессиональной направленности.
дистанционные технологии,
задачи с практическим содержанием,
тела вращения
Видеоурок «Процент. Основные действия и задачи с процентами»
2021
Автор:
Епифанцева Инна Владимировна
Целью курса является обобщить методы решения задач с экономическим содержанием повышенного уровня сложности, при помощи построения и исследования математических моделей, выработать умение использовать приобретенные знания в практической деятельности и повседневной жизни. Курс предназначен для учащихся, которые предполагают сдавать ЕГЭ по математике профильный уровень (учащиеся 9–11-х классов).
проценты
Решение задач с экономическим содержанием
2021
Автор:
Цховребова Ирина Валериевна
Экзаменационные задания по математике (профильный уровень) содержат задачу с экономическим содержанием под №17. Это задание повышенного уровня сложности, которое оценивается максимально в 3 балла. Для того, чтобы успешно решать подобные задачи, ученики должны не только владеть определенным математическим инструментарием, но и уметь строить простейшие математические модели по заданным условиям. При подготовке учащихся к решению данных задач возникает ряд вопросов, которые надо с ними предварительно обсудить.
Различные подходы к решению уравнений и систем уравнений
2021
Автор:
Хасиева Алета Хасанбековна
Для успешного исследования многих задач повышенной трудности важно уметь пользоваться не только традиционными способами решения, но и нетрадиционными. Нестандартные методы решения уравнений и систем уравнений – это такие методы, для которых в курсе математики не существует общего алгоритма решения. Нестандартные задачи способствуют повышению интереса изучению математики и выбор метода их решения вызывает не меньший интерес, повышают логику мышления. Умение применять нетрадиционные пути решений требует углубленного уровня подготовки для обучающихся. Использование нетрадиционных методов решения уравнений и систем уравнений являются наиболее эффективными и незаменимыми в решении заданий повышенной трудности. Уравнения, неравенства системы уравнений и неравенств имеют широкий спектр применения не только в математике, но и в физике и химии. Решение многих прикладных задач не обходятся без их использования. Уравнения, неравенства системы уравнений и неравенств играют большую роль в формировании научного мировоззрения учащихся, в реализации межпредметных связей, которые содействуют пониманию строения всей системы наук и роли научного метода в познании и практике.
одаренные дети
Развитие познавательной деятельности учащихся с ОВЗ на уроках математики
2021
Автор:
Калачева Татьяна Александровна
При активизации познавательной деятельности учащихся с ОВЗ учитывают дефекты их познавательной деятельности. Поиски эффективных методов обучения и методических приемов, активизирующих мысли учащихся, стимулирующих их к приобретению знаний, являются целью работы. Повышение активности учащихся достигается совокупностью методов организации и управления учебно-познавательной деятельностью, которые принято называть активными. Индуктивный путь ориентирован на особенности развития мышления детей с ОВЗ.
активизация познавательной деятельности,
дидактическая игра
Применение инновационных инструментов цифровых ресурсов
2021
Автор:
Злобова Людмила Викторовна
Представлена презентация о применение инновационных инструментов образовательных цифровых ресурсов (интернет-ресурсов).
Обобщение педагогического опыта по использованию блочно-модульной технологии на уроках математики
2021
Автор:
Колобова Светлана Айратовна
Предлагаемая методическая разработка представляет собой пример решения одной из наиболее актуальных проблем методики преподавания математики в школе – дифференцированного подхода в обучении посредством использования блочно-модульной технологии. Цель разработки: создание условий для дифференцированного подхода к обучению по теме «Первообразная».
блочно-модульная технология
Применение современных образовательных технологий в условиях реализации ФГОС основного общего образования
2021
Автор:
Шафикова Татьяна Сергеевна
Обучение с использованием дистанционных образовательных технологий позволяет индивидуализировать обучение: каждый обучаемый занимается по персональному расписанию, варьируя темп и время обучения. Применение элементов технологии дистанционного обучения возможно как в учебной, так и во внеурочной деятельности: при подготовке к экзаменам, при работе с детьми с ОВЗ, с одаренными детьми. Особенно актуальным становится разработка и применение методических разработок с использованием дистанционных технологий: интерактивные инструкции, журналы, тренажеры, виртуальные панорамы. Эффективность такого внедрения просматривается в повышении качественного уровня обученности, увеличении количества обучающихся, принимающих участие в предметных олимпиадах, повышении качества творческих работ учащихся по предмету.
ФГОС,
дистанционные технологии, применение гипертекстовых сред
Тренажер «Все действия с целыми числами»
2021
Автор:
Погонец Наталия Сергеевна
Данный тренажер может использоваться на устном счете с 6–11-е классы, также на отработку навыков при изучении темы в 6 классе «Целые числа». Можно использовать материал при подготовке к ВПР, ОГЭ и ЕГЭ.
целые числа
Подготовка к уроку: организация процессов изложения и контроля учебного материала.
2021
Автор:
Малеева Наталья Петровна
Необходимость развивать общую культуру учащихся продиктована самой жизнью, социальным заказом, которое предъявляет современное общество к общеобразовательной подготовке детей. Этот заказ – сформировать социально-активную инициативную творческую личность, развивая природные задатки, склонности и индивидуальность каждого ученика. Поэтому необходимы самые оптимальные формы обучения, методы и приемы, используемые на уроках для расширения кругозора школьников и их общей культуры на основе индивидуального и дифференцированного подхода к учащимся.
Система работы с одаренными студентами средних профессиональных образовательных учреждений
2021
Автор:
Конопкина Елена Борисовна
Цель методического пособия — теоретическое обоснование и разработка основных этапов подготовки учащихся к участию в математических олимпиадах. Актуальность методического пособия определяется потребностью совершенствования методики подготовки учащихся к участию в олимпиадах по математике в аспекте развития познавательного интереса и способностей учащихся к математике.
одаренные дети
Интеллектуальная игра: «Навстречу солнечному ветру»
2021
Авторы:
Спивак Антон Владимирович, Спивак Ирина Михайловна
Данная работа – командная игра, задания которой направлены на использование знаний по астрономии, истории космонавтики, математики, информатики. Целевая аудитория: ученики 4–11-х классов. Примерная длительность игры 40 минут. Публикация содержит: презентацию, сценарий, бланки ответов команды и оценочные материалы жюри.
интеллектуальная игра
Список опорных конспектов по математике для 7 — 11 классов
Решение уравнений и неравенств c модулем
Решение уравнений и неравенств, содержащих неизвестное под знаком модуля — Конспект
Решение иррациональных уравнений и неравенств
Решение уравнений и неравенств c корнями — Конспект
Комбинаторика и теория множеств в школе
Комбинаторика и теория множеств в школе 9-11 классы — Конспект
Скачать в PDF
Теория вероятностей в школе
Теория вероятностей в школе — Конспект
Скачать в PDF
Справочник по геометрии в школе (7 — 9 классы)
Скачать в PDF Справочник по геометрии для 7 — 9 классов
Скачать в PDF Справочник по алгебре 9 класс
































































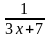 =
=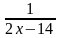
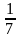 )х+4=49
)х+4=49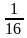
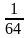
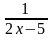 =
=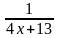
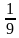
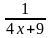 =
=