в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 278 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
Источник: А. Ларин: Тренировочный вариант № 56.
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Источник: Задания 13 (С1) ЕГЭ 2016, ЕГЭ по математике 06.06.2016. Основная волна. Юг (C часть).
а) Решите уравнение
б) Найдите все корни уравнения, принадлежащие отрезку
Источник: А. Ларин. Тренировочный вариант № 404.
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие промежутку
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие промежутку
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
Источник: Типовые тестовые задания по математике под редакцией И.В. Ященко, 2018.
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: А. Ларин. Тренировочный вариант № 386.
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: А. Ларин. Тренировочный вариант № 395.
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Решите уравнение:
Решите уравнение
а) Решите уравнение
б)Найдите все корни этого уравнения, принадлежащие промежутку
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Решите уравнение:
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Всего: 278 1–20 | 21–40 | 41–60 | 61–80 …
Основное тригонометрическое тождество
Классическое основное тригонометрическое тождество.
Перед тем, как переходить к различным тригонометрическим ужасам, в школе разбирают основное тригонометрическое тождество, благодаря которому, можно находить синус угла, зная его косинус, и наоборот.
Само тождество выглядит весьма мило:
Из этой формулы выразим синус и косинус:
Стоит обратить особое внимание на знаки «±». Почему их важно не забыть?
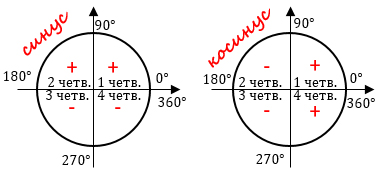
Посмотри на картинку ниже.
Если угол находится в первой четверти, то знаки его синуса и косинуса положительны.
Если угол находится во второй четверти, то знак его синуса положительный, а знак косинуса отрицательный.
Если угол находится в третьей четверти, то знаки его синуса и косинуса отрицательны.
Если угол находится в четвертой четверти, то знак его синуса отрицательный, а знак косинуса положительный.
Давай попробуем решить парочку примеров.
Задание 1.
Найдите sinx, если cosx = и 180° < x < 270°.
Угол х находится в третьей четверти, значит синус этого угла будет отрицательный и при выражении синуса из основного тригонометрического тождества мы должны перед корнем поставить знак минус.
Переводим дробь в десятичную.
Ответ: -0,2.
Задание 2.
Найдите cosx, если sinx = 0.6 и 90° < x < 180°.
Определяем знак косинуса. Угол х находится во второй четверти, значит значение косинуса будет отрицательным (см. окружности выше).
Тогда
Ответ: -0,8.
Другие полезные тождества.
Еще нельзя не упомянуть другие тригонометрические тождества, которые в своей сущности также являются основными.
1. Базовые формулы.
2. Связь между тангенсом и котангенсом.
3. Следствия из основного тригонометрического тождества.
Эти формулы получаются путем деления обеих частей равенства на косинус (первая формула) и на синус (вторая формула).
Рекомендую к изучению: статья о синусе, косинусе, тангенсе и котангенсе.
Успехов в учебе!
Лучшие репетиторы для сдачи ЕГЭ
Открытый банк заданий по теме тригонометрические функции. Задания B12 из ЕГЭ по математике (профильный уровень)
Тригонометрические уравнения
Задание №1135
Тип задания: 12
Тема:
Тригонометрические функции
Условие
Найдите наибольшее значение функции y=12x-12tg x-18 на отрезке left[0;,frac{pi}{4}right].
Показать решение
Решение
Найдём производную исходной функции:
y’= (12x)’-12(tg x)’-(18)’= 12-frac{12}{cos ^2x}= frac{12cos ^2x-12}{cos ^2x}leqslant0. Значит, исходная функция является невозрастающей на рассматриваемом промежутке и принимает наибольшее значение на левом конце отрезка, то есть при x=0. Наибольшее значение равно y(0)= 12cdot 0-12 tg (0)-18= -18.
Ответ
-18
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1128
Тип задания: 12
Тема:
Тригонометрические функции
Условие
Найдите наименьшее значение функции y=32tg x — 32x-8pi+103 на отрезке left[-frac{pi}{4}; frac{pi}{4}right].
Показать решение
Решение
Найдём производную исходной функции:
y’= 32(tg x)’-(32x)’-(8pi )’+(103)’= frac{32}{cos ^2x}-32= frac{32-32cos ^2x}{cos ^2x}geqslant0. Значит, исходная функция является неубывающей на рассматриваемом промежутке и принимает
наименьшее значение на левом конце отрезка, то есть при x=-frac{pi}{4}. Наименьшее значение равно yleft(-frac{pi}{4}right)= 32tgleft(-frac{pi}{4}right)-32cdotleft(-frac{pi}{4}right)-8pi+103= -32+103= 71.
Ответ
71
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1122
Тип задания: 12
Тема:
Тригонометрические функции
Условие
Найдите точку минимума функции y=(0,7-x)cos x+sin x+2, принадлежащую промежутку left(0; frac{pi}{2}right).
Показать решение
Решение
Найдём производную исходной функции: y’= (0,7-x)’ cos x,+ (0,7-x)(cos x)’+(sin x)’+(2)’ = -cos x+(0,7-x)cdot (- sin x)+ cos x= (x-0,7) sin x. Найдём нули производной на интервале left(0; frac{pi}{2}right), учитывая, что на этом множестве sin x>0.
Имеем (x-0,7) sin x=0;
x-0,7=0;
x=0,7.
Значение x=0,7 принадлежит интервалу left(0; frac{pi}{2}right). При x in (0; 0,7) выполняется неравенство y'(x)<0. При x in left(0,7; frac{pi}{2}right) выполняется неравенство y'(x)>0.
Отсюда x=0,7 является единственной точкой минимума на рассматриваемом интервале.
Ответ
0,7
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1118
Тип задания: 12
Тема:
Тригонометрические функции
Условие
Найдите наименьшее значение функции y=24+frac{9pi}{4}-9x-9sqrt2cos x на отрезке left[0; frac{pi}{2}right].
Показать решение
Решение
Найдём производную исходной функции: y’=-9+9sqrt 2 sin x. Вычислим нули производной: y’=0;
-9+9sqrt 2sin x=0;
sin x=frac{sqrt2}{2}.
На отрезке left[0; frac{pi}{2}right] этому уравнению удовлетворяет только x=frac{pi}{4}. Расставим знаки производной и определим промежутки монотонности исходной функции на рассматриваемом отрезке.
Из рисунка видно, что при x<frac{pi}{4} выполняется y'(x)<0 и исходная функция убывает. Аналогично, при x>frac{pi}{4} выполняется y'(x)>0 и исходная функция возрастает. Значит, наименьшее значение достигается при x=frac{pi}{4} и равно yleft(frac{pi}{4}right)= 24+frac{9pi}{4}-9cdotfrac{pi}{4}-9sqrt2cos frac{pi}{4}= 24-9=15.
Ответ
15
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №957
Тип задания: 12
Тема:
Тригонометрические функции
Условие
Найдите точку максимума функции y=(4x-5)cos x-4sin x+12, принадлежащую промежутку left ( 0; frac{pi}{2} right ).
Показать решение
Решение
Найдём производную исходной функции: y’= (4x-5)’cos x+(4x-5)(cos x)’-4(sin x)’+(12)’= 4cos x+(4x-5)cdot(-sin x)-4cos x= -(4x-5)sin x.
Найдём нули производной на интервале left ( 0; frac{pi}{2} right ), учитывая, что на этом множестве sin x>0.
Имеем -(4x-5)sin x=0,
4x-5=0,
x=frac54.
Значение x=frac54 принадлежит интервалу left ( 0; frac{pi}{2} right ). При xinleft ( 0; frac54 right ) выполняется неравенство y'(x)>0. При xinleft ( frac54; frac{pi}{2} right ) выполняется неравенство y'(x)<0. Отсюда x=frac54=1,25 является единственной точкой максимума на рассматриваемом интервале.
Ответ
1,25
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №955
Тип задания: 12
Тема:
Тригонометрические функции
Условие
Найдите наибольшее значение функции y=18cos x+9sqrt3 x-3sqrt3 pi+16 на отрезке left [ 0; frac{pi}{2} right ].
Показать решение
Решение
Найдём производную исходной функции: y’=-18sin x+9sqrt3. Вычислим нули производной: y’=0.
-18sin x+9sqrt3=0,
sin x=frac{sqrt3}{2}.
На отрезке left [ 0; frac{pi}{2} right ] этому уравнению удовлетворяет только x=frac{pi}{3}. Расставим знаки производной и определим промежутки монотонности исходной функции на рассматриваемом отрезке.
Из рисунка видно, что при x<frac{pi}{3} выполняется y'(x)>0 и исходная функция возрастает. Аналогично при x>frac{pi}{3} выполняется y'(x)<0 и исходная функция убывает. Значит, наибольшее значение достигается при x=frac{pi}{3} и равно yleft ( frac{pi}{3} right )= 18cosfrac{pi}{3}+9sqrt3cdotfrac{pi}{3}-3sqrt3 pi+16= 9+16=25.
Ответ
25
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №128
Тип задания: 12
Тема:
Тригонометрические функции
Условие
Найдите наибольшее значение функции y=13tgx-13x+5 на отрезке left [ -frac{pi}{4}; 0 right ].
Показать решение
Решение
Вычислим производную функции.
y’=frac{13}{cos^2x}-13=13(frac{1}{cos^2x}-1)=13tg^2x
Производная функции на всем промежутке возрастает, значит наибольшее значение функции она достигает на правом конце отрезка. Вычислим значение функции в этой точке.
y(0)=13tg0-13cdot0+5=5
Точка 5 – наибольшее значение функции.
Ответ
5
Задание №127
Тип задания: 12
Тема:
Тригонометрические функции
Условие
Найдите наименьшее значение функции y=8cos x-17x+6 на отрезке left [ -frac{3pi}{2}; 0 right ].
Показать решение
Решение
Вычислим производную функции.
y’=-8sin x-17
Так как выражение -8sin x при любых значениях x всегда не больше чем 8, то полученная разность меньше нуля, а это говорит о том, что функция убывает. Следовательно наименьшее значение функция достигает на правом конце отрезка. Вычислим это значение.
y(0)=8cos0-17cdot0+6 = 8+6=14
Точка 14 – наименьшее значение функции.
Ответ
14
Задание №126
Тип задания: 12
Тема:
Тригонометрические функции
Условие
Найдите точку максимума функции y=(2x-3)cos x-2sin x+2 на промежутке left ( 0; frac{pi}{2} right ).
Показать решение
Решение
Вычислим производную функции.
y’=2cos x-(2x-3)sin x-2cos x
y’=-(2x-3)sin x
y’=(3-2x)sin x
Найдем точки экстремума, в которых производная функции обращается в нуль.
(3-2x)sin x=0
left [begin{array}{l} 3-2x=0 sin x=0 end{array} right .
left [begin{array}{l} x=1,5 x=pi n, n in mathbb{Z} notin left ( 0; frac{pi}{2} right) end{array} right .
На числовой оси отложим граничные точки промежутка и точку экстремума и посмотрим как ведет себя функция.
При переходе через точку x = 1,5 производная меняет знак с плюса на минус. Значит x = 1,5 – точка максимума функции.
Ответ
1,5
Лучшие репетиторы для сдачи ЕГЭ
23 марта 2022
В закладки
Обсудить
Жалоба
Подборка заданий для тренировки профильного уровня.
Без ответов.
Задание 1. Простейшие уравнения
Задание 4. Вычисления и преобразования
Задание 7. Задачи с прикладным содержанием
Задание 11. Наибольшее и наименьшее значение функций
Задание 12
s-tr.pdf
Источник: vk.com/trigonometrics2122
Консультация по английскому языку
Английский | Сегодня, 10:14
Разработчики экзаменационных материалов, учителя и выпускники, расскажут, как подготовиться к экзамену, об особенностях заданий в ЕГЭ и ответят на вопросы старшеклассников.
Этапы закрепощения крестьян в России
Крепостное право на Руси появилось позже, чем во многих средневековых европейских королевствах. Это было связано с объективными причинами – низкая плотность населения, зависимость от ордынского ига.
Задания 12-18 досрочного ЕГЭ по математике
3 примера по каждому заданию. Досрочный ЕГЭ по математике прошёл 28 марта.
ЕГЭ Профиль №13. Тригонометрические уравненияadmin2018-09-28T21:10:10+03:00
Нашли ошибку в заданиях? Оставьте, пожалуйста, отзыв.
13 задания профильного ЕГЭ по математике представляет собой уравнение с отбором корней принадлежащих заданному промежутку. Одним из видов уравнений которое может оказаться в 13 задание является тригонометрическое уравнение. Как правило, это достаточно простое тригонометрическое уравнение для решения которого потребуется знания основных тригонометрических формул, и умение решать простейшие тригонометрические уравнения. Отбор корней тригонометрического уравнения принадлежащих заданному промежутку можно производить одним из четырех способов: методом перебора, с помощью тригонометрической окружности, с помощью двойного неравенства и графическим способом. В данном разделе представлены тригонометрические уравнения (всего 226) разбитые на три уровня сложности. Уровень А — это простейшие тригонометрические уравнения, которые являются подготовительными для решения реальных тригонометрических уравнений предлагаемых на экзамене. Уровень В — состоит из уравнений, которые предлагали на реальных ЕГЭ и диагностических работах прошлых лет. Уровень С — задачи повышенной сложности.
Тригонометрическими уравнениями называют уравнения, в которых переменная содержится под знаком тригонометрических функций. К их числу прежде всего относятся простейшие тригонометрические уравнения, т.е. уравнения вида $sin x=a, cos x=a, tg x=a$, где $а$ – действительное число.
Перед решением уравнений разберем некоторые тригонометрические выражения и формулы.
$1$ радиан $={180}/{π}≈57$ градусов
$1$ градус $={π}/{180}$ радиан
Значения тригонометрических функций некоторых углов
| $α$ | $ 0$ | ${π}/{6}$ | ${π}/{4}$ | ${π}/{3}$ | ${π}/{2}$ | $π$ | |
| $sinα$ | $ 0$ | $ {1}/{2}$ | $ {√2}/{2}$ | $ {√3}/{2}$ | $ 1$ | $ 0$ | |
| $cosα$ | $ 1$ | $ {√3}/{2}$ | $ {√2}/{2}$ | $ {1}/{2}$ | $ 0$ | $ -1$ | |
| $tgα$ | $ 0$ | $ {√3}/{3}$ | $ 1$ | $ √3$ | $ -$ | $ 0$ | |
| $ctgα$ | $ -$ | $ √3$ | $ 1$ | $ {√3}/{3}$ | $ 0$ | $ -$ |
Периоды повтора значений тригонометрических функций
Период повторения у синуса и косинуса $2π$, у тангенса и котангенса $π$
Знаки тригонометрических функций по четвертям
Эта информация нам пригодится для использования формул приведения. Формулы приведения необходимы для понижения углов до значения от $0$ до $90$ градусов.
Чтобы правильно раскрыть формулы приведения необходимо помнить, что:
- если в формуле содержатся углы $180°$ и $360°$ ($π$ и $2π$), то наименование функции не изменяется; (если же в формуле содержатся углы $90°$ и $270°$ (${π}/{2}$ и ${3π}/{2}$), то наименование функции меняется на противоположную (синус на косинус, тангенс на котангенс и т. д.);
- чтобы определить знак в правой части формулы ($+$ или $-$), достаточно, считая угол $α$ острым, определить знак преобразуемого выражения.
Преобразовать $сos(90° + α)$. Прежде всего, мы замечаем, что в формуле содержится угол $90$, поэтому $cos$ измениться на $sin$.
$сos(90° + α)=sinα$
Чтобы определить знак перед $sinα$, предположим, что угол $α$ острый, тогда угол $90° + α$ должен оканчиваться во 2-й четверти, а косинус угла, лежащего во 2-й четверти, отрицателен. Поэтому, перед $sinα$ нужен знак $-$.
$сos(90° + α)= — sinα$ — это конечный результат преобразования
Четность тригонометрических функций
Косинус четная функция: $cos(-t)=cos t$
Синус, тангенс и котангенс нечетные функции: $sin(-t)= — sin t; tg(-t)= — tg t; ctg(-t)= — ctg t$
Тригонометрические тождества
- $tgα={sinα}/{cosα}$
- $ctgα={cosα}/{sinα}$
- $sin^2α+cos^2α=1$ (Основное тригонометрическое тождество)
Из основного тригонометрического тождества можно выразить формулы для нахождения синуса и косинуса
$sinα=±√{1-cos^2α}$
$cosα=±√{1-sin^2α}$
- $tgα·ctgα=1$
- $1+tg^2α={1}/{cos^2α}$
- $1+ctg^2α={1}/{sin^2α}$
Вычислить $sin t$, если $cos t = {5}/{13} ; t ∈({3π}/{2};2π)$
Найдем $sin t$ через основное тригонометрическое тождество. И определим знак, так как $t ∈({3π}/{2};2π)$ -это четвертая четверть, то синус в ней имеет знак минус
$sint=-√{1-cos^2t}=-√{1-{25}/{169}}=-√{{144}/{169}}=-{12}/{13}$
Формулы двойного угла
- $sin2α=2sinα·cosα$
- $cos2α=cos^2α-sin^2α=2cos^2α-1=1-2sin^2α$
- $tg2α={2tgα}/{1-tg^2α}$
Формулы суммы и разности
$cosα+cosβ=2cos{α+β}/{2}·cos{α-β}/{2}$
$cosα-cosβ=2sin{α+β}/{2}·sin{β-α}/{2}$
$sinα+sinβ=2sin{α+β}/{2}·cos{α-β}/{2}$
$sinα-sinβ=2sin{α-β}/{2}·cos{α+β}/{2}$
Формулы произведения
$cosα·cosβ={cos(α-β)+cos(α+β)}/{2}$
$sinα·sinβ={cos(α-β)-cos(α+β)}/{2}$
$sinα·cosβ={sin(α+β)+sin(α-β)}/{2}$
Формулы сложения
$cos(α+β)=cosα·cosβ-sinα·sinβ$
$cos(α-β)=cosα·cosβ+sinα·sinβ$
$sin(α+β)=sinα·cosβ+cosα·sinβ$
$sin(α-β)=sinα·cosβ-cosα·sinβ$
Вычислить $sin12cos18+cos12sin18$
Данное выражение является синусом суммы
$sin12cos18+cos12sin18= sin(12+18)=sin30=0.5$
Задача (Вписать в ответ число)
Вычислить $sin{5π}/{12} cos {π}/{12}+cos {π}/{12} sin {5π}/{12}$
Решение:
Данное выражение является синусом суммы
$sin {5π}/{12} cos {π}/{12}+cos {π}/{12} sin {5π}/{12}=sin({π}/{12}+{5π}/{12})=sin {6π}/{12}=sin {π}/{2}=1$
Ответ: $1$
Обратные тригонометрические функции и простейшие тригонометрические уравнения
Арккосинус
Если, $|а|≤1$, то $arccos а$ – это такое число из отрезка $[0;π]$, косинус которого равен $а$.
Если, $|а|≤1$, то $arccos а = t ⇔ {table cos (t)=a; ≤t≤π;$
$arcos(-a) = π-arccosa$, где $0≤а≤1$
Уравнение вида $cos t=a$, eсли, $|а|≤1$, имеет решение
$t=±arccos a+2πk; k∈Z$
Частные случаи
$cos t =1, t = 2πk;k∈Z$
$cos t = 0, t = {π}/{2}+πk;k∈Z$
$cos t = -1, t=π+2πk;k∈Z$
Найдите наименьший положительный корень уравнения $сos{2πx}/{3}=-{√3}/{2}$
$сos{2πx}/{3}=-{√3}/{2}$
${2πx}/{3}=±arccos(-{√3}/{2})+2πk;kϵZ$
${2πx}/{3}=±(π-arccos{√3}/{2})+2πk;kϵZ$
${2πx}/{3}=±(π-{π}/{6})+2πk;kϵZ$
${2πx}/{3}=±{5π}/{6} +2πk;kϵZ$
Далее избавимся от всех величин, мешающих иксу. Для этого разделим обе части уравнения на ${2π}/{3}$
$x=±{5π·3}/{6·2π} +{2π·3}/{2π}k$
$x=±1,25+3k$
Чтобы найти наименьший положительный корень, подставим вместо $k$ целые значения
$k=0$
$x_1= -1,25$
$x_2=1,25$
$к=1$
$х_1=3-1,25=1,75$
$х_2=3+1,25=4,25$
Нам подходит $1,25$ – это и есть результат
Ответ: $1,25$
Арксинус
Если, $|а|≤1$, то $arcsin a$ – это такое число, из отрезка $[-{π}/{2};{π}/{2}]$, синус которого равен $а$.
Если, $|а|≤1$, то $arcsin a = t ⇔ {table sint=a; -{π}/{2}≤t≤{π}/{2};$
$arcsin(-a)= — arcsin a$, где $0≤а≤1$
Если, $|а|≤1$, то уравнение $sin t =a$ можно решить и записать двумя способами:
$1. t_1 = arcsin a+2πk;k∈Z$
$t_2 = (π- arcsin a)+ 2πk;k∈Z$
$2. t=(-1)^n arcsin a+πn; n∈Z$
$3.$ Частные случаи
$sin t = 0, t=πk;k∈Z$
$sin t = 1, t={π}/{2}+2πk;k∈Z$
$sin t = -1,t=-{π}/{2}+2πk;k∈Z$
Арктангенс
$arctg a$ — это такое число, из отрезка $[-{π}/{2};{π}/{2}]$, тангенс которого равен $а$.
$arctg a = t ⇔ {table tgt=a; -{π}/{2}≤t≤{π}/{2};$
$arctg(-a)= — arctg a$
Уравнение $tg t = a$ имеет решение $t= arctg a+πk;k∈Z$
Инфоурок
›
Геометрия
›Конспекты›Разбор задач на применение основного тригонометрического тождества
Разбор задач на применение основного тригонометрического тождества
Скачать материал
Скачать материал


- Сейчас обучается 630 человек из 77 регионов


- Сейчас обучается 140 человек из 49 регионов


- Сейчас обучается 96 человек из 32 регионов


Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 153 941 материал в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
-
«Геометрия. 7-9 класс», Волович М.Б., Атанасян Л.С.
Тема
§ 33. Синус, косинус, тангенс и котангенс угла. Основное тригонометрическое тождество
Больше материалов по этой теме
Другие материалы
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Специфика преподавания конституционного права с учетом реализации ФГОС»
-
Курс повышения квалификации «Организация практики студентов в соответствии с требованиями ФГОС юридических направлений подготовки»
-
Курс повышения квалификации «Этика делового общения»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Использование активных методов обучения в вузе в условиях реализации ФГОС»
-
Курс повышения квалификации «Организация маркетинга в туризме»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Управление сервисами информационных технологий»
-
Курс повышения квалификации «Учебная деятельность по предметной области «Черчение»: основы предмета и реализация обучения в условиях ФГОС»
-
Курс повышения квалификации «Финансовые инструменты»
-
Скачать материал
-
26.01.2019
2013
-
DOCX
22.2 кбайт -
103
скачивания -
Оцените материал:
-
-
Настоящий материал опубликован пользователем Михайлова Татьяна Валерьевна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 6 лет и 5 месяцев
- Подписчики: 5
- Всего просмотров: 61957
-
Всего материалов:
54

ПРИМЕРЫ НА ДОКАЗАТЕЛЬСТВО ТРИГОНОМЕТРИЧЕСКИХ ТОЖДЕСТВ
При доказательстве тождеств обычно используют следующие способы:
1) выражение, стоящее в одной части тождества, с помощью тождественных преобразований приводят к выражению, стоящему в другой части тождества;
2) выражения, стоящие в левой и правой частях тождества, приводят к одному и тому же виду;
3) доказывают, что разность между левой и правой частями тождества равна нулю.
Примеры 1—7. Доказать тождества:
1. ;
2. ;
3. ;
4. ;
5. ;
6. ;
7. .
Решение.
1.
2.
3.
4.
5.
6.
7. Это тождество можно рассматривать как пропорцию. Чтобы доказать справедливость пропорции , достаточно доказать, что
. Поэтому достаточно показать, что
. Это равенство очевидно, т. к.
.
Вывод: тождества доказаны.

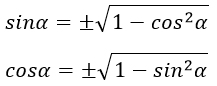
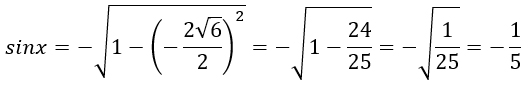
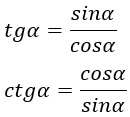
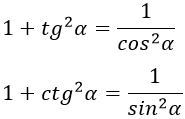

.png)
.png)
.png)


