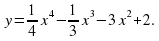Контрольная работа по теме: «Производная» в формате ЕГЭ.
№
I вариант
II вариант
1
Найдите значение производной функции в точке .
Найдите значение производной функции
в точке .
2
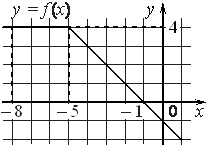
На рисунке изображён график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке .
На рисунке изображён график функции и касательная к нему в точке с абсциссой. Найдите значение производной функции в точке.
3
Найдите угловой коэффициент касательной к графику функции
в точке с абсциссой .
Найдите угловой коэффициент касательной к графику функции
в точке с абсциссой .
4
На рисунке изображен график функции , определенной на интервале (-3;9). Найдите количество точек, в которых касательная к графику функции параллельна прямой .
На рисунке изображен график функции, определенной на интервале (-3;11). Найдите количество точек, в которых касательная к графику функции параллельна прямой.
5
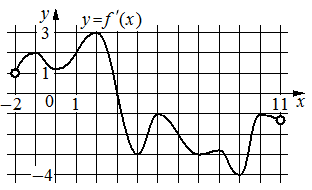
На рисунке изображен график производной функции, определенной на интервале(-12;4). Найдите промежутки возрастания функции,
в ответе укажите длину наибольшего из них.
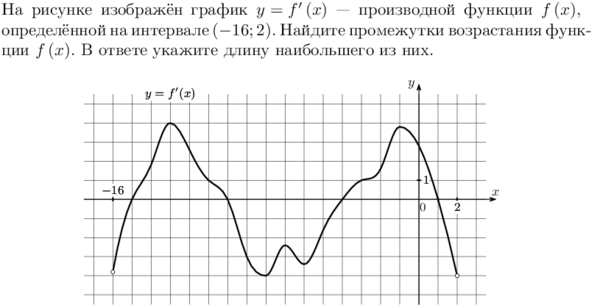
На рисунке изображен график производной функции, определенной на интервале(-1;17). Найдите промежутки убывания функции,
в ответе укажите длину наибольшего из них.
6
Укажите промежуток, на котором функция убывает.
Укажите промежуток, на котором функция возрастает.
7
На рисунке изображен график функции, определенной на интервале (-4;7).
Найдите сумму точек экстремума функции.
На рисунке изображен график функции, определенной на интервале (-7;5).
Найдите сумму точек экстремума функции.
8
Найдите точки экстремума функции .
Найдите точки экстремума функции .
9
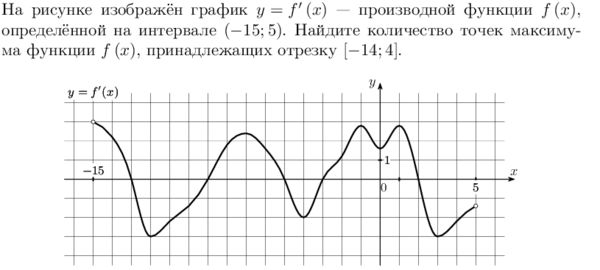
На рисунке изображен график производной функции, определенной на интервале (-4;16). Найдите количество точек максимума функции на отрезке .
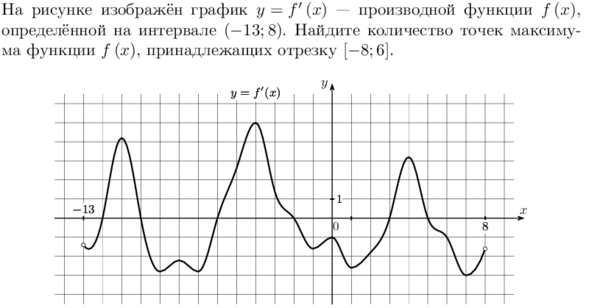
На рисунке изображен график производной функции, определенной на интервале(-17;2). Найдите количество точек минимума функции на отрезке.
10
На рисунке изображен график производной функции, определенной на интервале(-8; 4).
В какой точке отрезка функция принимает наименьшее значение.
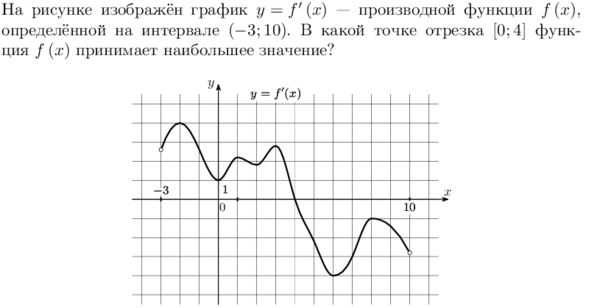
На рисунке изображен график производной функции, определенной на интервале(-8;3). В какой точке отрезка функция принимает наибольшее значение.
11
Прямая является касательной к графику функции . Найдите абсциссу точки касания.
Прямая является касательной к графику функции . Найдите абсциссу точки касания.
12
Найдите точку минимума функции .
Найдите точку максимума функции .
13
Найдите наибольшее значение функции на отрезке
.
Найдите наименьшее значение функции на отрезке
.
14
Точка движется прямолинейно по закону . Вычислите скорость и ускорение точки при t = 1.
Точка движется прямолинейно по закону . Вычислите скорость и ускорение точки при t = 1.
23 января 2020
В закладки
Обсудить
Жалоба
Производная и её применение
Итоговая контрольная работа по алгебре по теме «Производная и её применение».
2 варианта по 13 заданий. Ответы прилагаются.
itk-p.pdf
Аннотация:
Задания данного теста соответствуют теории по теме «Производная и ее применение». Тест предназначен для проверки знаний, умений и навыков учащихся 10 – 11 классов по теме «Применение производной». В тесте представлены два варианта, в каждом из которых десять заданий, прототипов задачи В8 ЕГЭ. К тесту прилагаются ответы и указания к решению заданий.
Целевая аудитория: для 11 класса
Автор: Макарова Татьяна Павловна
Место работы: ГБОУ СОШ №618
Добавил: МТП
Уважаемые коллеги! Автор ждёт Ваши отзывы! Оставьте своё мнение о разработке!
Всего комментариев: 1
Порядок вывода комментариев:

Физкультминутки
Физкультминутки обеспечивают кратковременный отдых детей на уроке, а также способствуют переключению внимания с одного вида деятельности на другой.

В помощь учителю
Уважаемые коллеги! Добавьте свою презентацию на Учительский портал и получите бесплатное свидетельство о публикации методического материала в международном СМИ.
Для добавления презентации на портал необходимо зарегистрироваться.
Конкурсы
Диплом и справка о публикации каждому участнику!
© 2007 — 2023 Сообщество учителей-предметников «Учительский портал»
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель / главный редактор: Никитенко Е.И.
Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание этих материалов и разрешение любых спорных вопросов с третьими лицами.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.
Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.
Фотографии предоставлены


СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой

Была в сети 17.12.2017 11:13

Тарасенко Татьяна Владимировна
учитель математики
65 лет
10 923
2 062
Самостоятельная работа по теме : » Применения производной», формат ЕГЭ
17.12.2017 11:18
данную самостоятельную работу можно использовать как на этапе изучения темы: » Применения производной», так и в период повторения
Просмотр содержимого документа
«Самостоятельная работа по теме : » Применения производной», формат ЕГЭ»
|
Применения производной 1 вариант 1. 2. 3. 4. 5. 6. |
|
2 вариант 1. 2. 3. 4. 5. 6. |
|
Применение производной 3 вариант 1. 2. 3. 4. 5. 6. |
|
4 вариант 1. 2. 3. 4. 5. 6. |
Рекомендуем курсы ПК и ППК для учителей
Куртакова Татьяна Владимировна.
ГБОУ Школа № 2126 «Перово»
Учитель математики высшей квалификационной категории.
Алгебра 11 класс.
Контрольная работа по теме: «Применение производной»
Контрольная работа представлена в двух моделях: 1 модель: для учащихся, сдающих экзамен на базовом уровне. (2 варианта)
2 модель: для учащихся, сдающих экзамен на профильном уровне. (4 варианта)
Цели:
Проверка знаний, умений и навыков по теме: «Применение производной к исследованию функций»
Знание геометрического смысла производной, умения находить координаты точек касания.
Умения находить значение производной в точке по графику функции и его касательной данной точке.
Умения находить промежутки возрастания и убывания функций с помощью производной и по графику производной данной функции.
Умения находить точки экстремума функции с помощью производной и определять их вид (точки максимума, минимума)
Умения определять точки максимума, минимума по графику производной функции.
Умения находить наибольшее и наименьшее значение функции, используя производную и ее график.
Умения проводить исследование свойств функции с помощью производной и выполнять построения ее графика.
|
Алгебра 11 Контрольная работа № 3 Вариант 1 «Применение производной» БАЗА |
Алгебра 11 Контрольная работа № 3 Вариант 2 «Применение производной» БАЗА |
|
1.Прямая у = 7х – 5 параллельна касательной к графику функции у = х2 +6х – 8. Найдите абсциссу точки касания. 2.Найдите промежутки возрастания и убывания функции у = х3 – 4х2 + 5х – 1 3.Найдите точки максимума и минимума: а)f(x) = х3 – 2х2 + х + 3; б)f(x) = . 4.Функция у = f(х) определена на промежутке ( -7; 7). На рисунке изображен график производной этой функции. Найдите точки минимума этой функции. 5.Найдите наибольшее и наименьшее значения функции: а) f(x) = 2х3 — 2,5х2 – х + 2 на отрезке . б) f(х) = 3х – 6 sinx на отрезке [ 0; ]. 6.Построить график функции у = х3 – 3х2 |
1.Прямая у = 6х + 6 параллельна касательной к графику функции у = х2 + 7х – 7. Найдите абсциссу точки касания. 2. Найдите промежутки возрастания и убывания функции у = 3 + 24х — 3х2 – х3 3.Найдите точки максимума и минимума: а)f(x) = х3— х2 — х +2; б)f(x) = . 4.Функция у = g(х) определена на промежутке ( -5; 7). На рисунке изображен график производной этой функции. Найдите точки максимума этой функции. 5.Найдите наибольшее и наименьшее значения функции а) f(x) = х3— х2 — х +2 на отрезке . б)f(х) = 8 cosx + 4х на отрезке [ 0; ]. 6.Построить график функции у = – х3 + 3х2 |
Алгебра – 11 Контрольная работа № 3 Вариант 1«Производная и ее применение» Профиль |
|||
ЧАСТЬ 1 |
5. На рисунке изображен график производной функции: y = f ‘(x), определенной на интервале (-7; 4). Найдите промежутки убывания функции. В ответе укажите сумму целых точек, входящих в эти промежутки. |
||
|
1. На рисунке изображён график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции в точке х0. |
|||
|
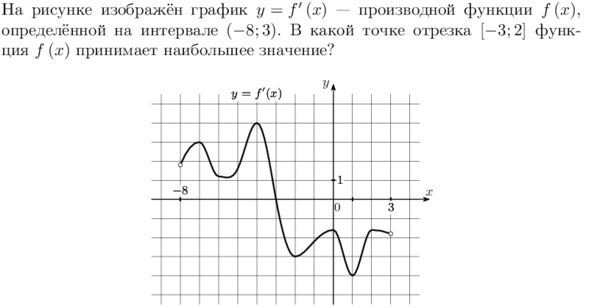
2. На рисунке изображен график производной функции: y = f ‘(x), определенной на интервале (-8; 3). В какой точке отрезка [-5; 0] функция f(x) принимает наибольшее значение. |
6. На рисунке изображен график производной функции: y = f ‘(x) , определенной на интервале (- 5; 5). Найдите количество точек, в которых касательная к графику функции параллельна прямой у = 3х – 7 или совпадает с ней. |
||
|
3. На рисунке изображен график функции y = f(x), определенной на интервале (-3; 8). Найдите количество точек, в которых касательная к графику функции параллельна прямой у = 15. |
ЧАСТЬ 2 |
||
|
7.Найдите наибольшее значение функции у = 12 cos x + 6 √ 3 х – 2 √ 3 π + 6 на отрезке [ 0; π/2] 8. Найдите точку максимума функции у = ln ( х + 5 ) – 2х + 9. |
|||
|
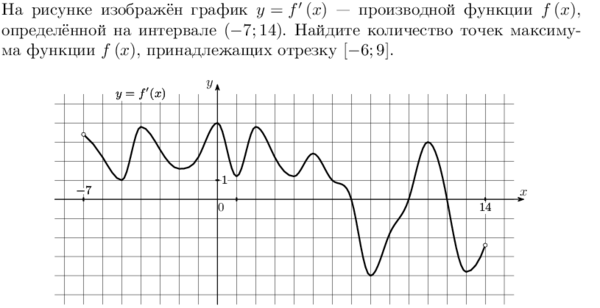
4. На рисунке изображен график производной функции:y = f ‘(x), определенной на интервале (-7; 14). Найдите количество точек максимума функции на отрезке [-6; 13]. |
ЧАСТЬ 3 |
||
|
9. Построить график функцииу = х3 + 3х2– 4 |
|||
Алгебра – 11 Контрольная работа № 3 Вариант 2«Производная и ее применение» Профиль |
|||
Ч АСТЬ 1 |
5. На рисунке изображен график производной функции: y = f ‘(x), определенной на интервале (-5; 7). Найдите промежутки убывания функции. В ответе укажите сумму целых точек, входящих в эти промежутки. |
||
|
1. На рисунке изображён график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции в точке х0. |
|||
|
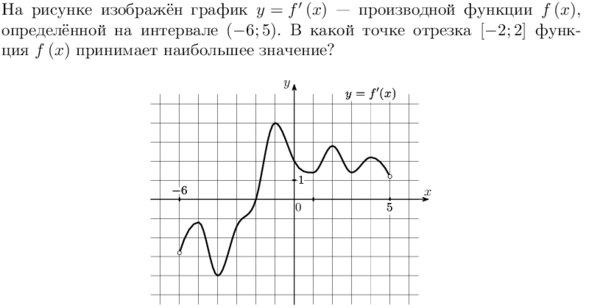
2. На рисунке изображен график производной функции: y = f ‘(x), определенной на интервале (-8; 4). В какой точке отрезка [-6; -2] функция f(x) принимает наибольшее значение. |
6. На рисунке изображен график производной функции: y = f ‘(x) , определенной на интервале (-9; 8). Найдите количество точек, в которых касательная к графику функции параллельна прямой у = 2х – 7 или совпадает с ней. |
||
|
3. На рисунке изображен график функции y = f(x), определенной на интервале (-11; 2). Найдите количество точек, в которых касательная к графику функции параллельна прямой у = -2. |
ЧАСТЬ 2 |
|
7.Найдите наименьшее значение функции у = 6 sin х – 9х + 5 на отрезке [ — 3π/2; 0] 8. Найдите точку минимума функции у = ( 3х2 – 36х + 36 ) e х – 36 |
|||
|
4. На рисунке изображен график производной функции:y = f ‘(x), определенной на интервале (-4; 16). Найдите количество точек максимума функции на отрезке [-3; 15]. |
ЧАСТЬ 3 |
||
|
9. Построить график функцииу = – х3 – 3х2 + 3 |
|||
Алгебра – 11 Контрольная работа № 3 Вариант 3«Производная и ее применение» Профиль |
|||
Ч АСТЬ 1 |
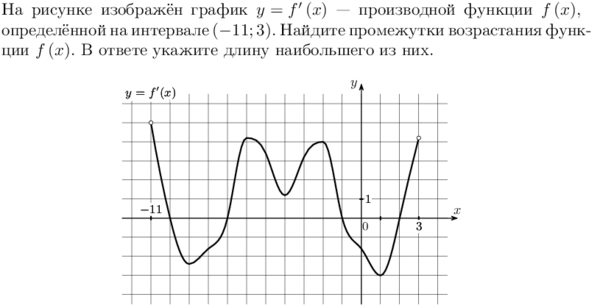
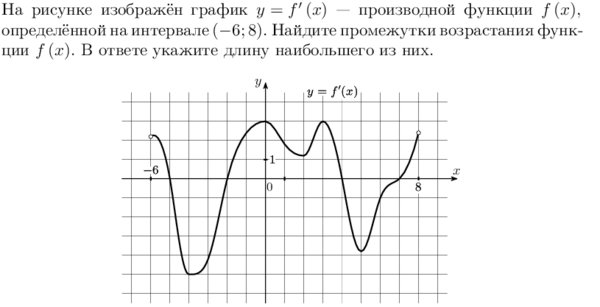
5. На рисунке изображен график производной функции: y = f ‘(x), определенной на интервале (-11; 3). Найдите промежутки возрастания функции. В ответе укажите длину наибольшего из них. |
||
|
1.На рисунке изображён график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции в точке х0. |
|||
|
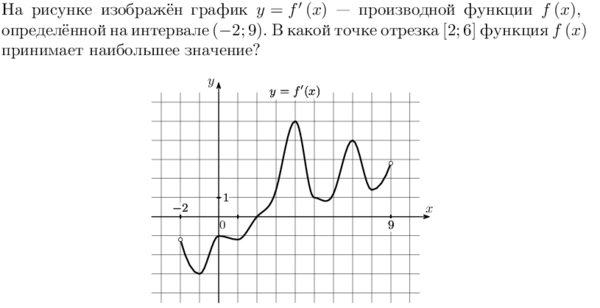
2. На рисунке изображен график производной функции: y = f ‘(x), определенной на интервале (-8; 3). В какой точке отрезка [-2; 1] функция f(x) принимает н аименьшее значение. |
6. На рисунке изображен график производной функции: y = f ‘(x) , определенной на интервале (- 5; 5). Найдите количество точек, в которых касательная к графику функции параллельна прямой у = — 2х – 7 или совпадает с ней. |
||
|
3. На рисунке изображен график функции y = f(x), определенной на интервале (-1;10). Найдите количество точек, в которых касательная к графику функции параллельна прямой у = -20. |
ЧАСТЬ 2 |
||
|
7.Найдите наибольшее значение функции у = 12 √ 2 cos x + 12х – 3π + 9 на отрезке [ 0; π/2] 8. Найдите точку минимума функции у = 2х – ln ( х + 3) + 7. |
|||
|
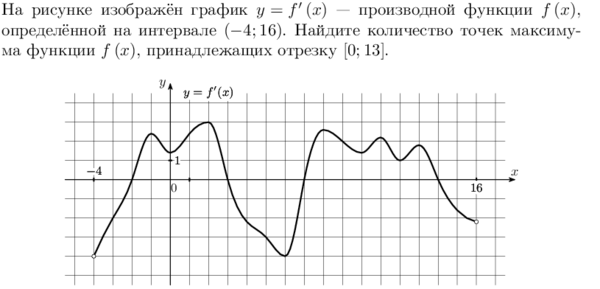
4. На рисунке изображен график производной функции:y = f ‘(x), определенной на интервале (-7; 14). Найдите количество точек минимума функции на отрезке [-6; 13]. |
ЧАСТЬ 3 |
||
|
9. Построить график функцииу = х3 + 3х2– 4 |
|||
Алгебра – 11 Контрольная работа № 3 Вариант 4« Производная и ее применение» Профиль |
|||
Ч АСТЬ 1 |
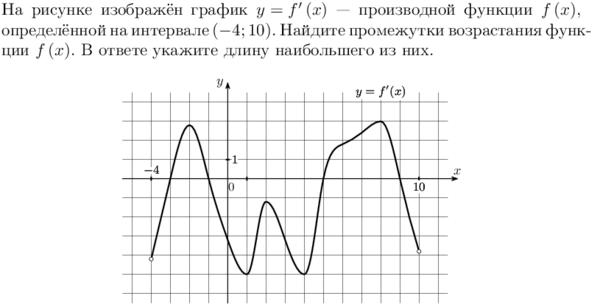
5. На рисунке изображен график производной функции: y = f ‘(x), определенной на интервале (-2; 12). Найдите промежутки убывания функции. В ответе укажите длину наибольшего из них. |
||
|
1.На рисунке изображён график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции в точке х0. |
|||
|
2. На рисунке изображен график производной функции: y = f ‘(x), определенной на интервале (-8; 4). В какой точке отрезка [0; 3] функция f(x) принимает н аименьшее значение. |
6. На рисунке изображен график производной функции: y = f ‘(x) , определенной на интервале (-9; 8). Найдите количеств о точек, в которых касательная к графику функции параллельна прямой у = — 2х – 7 или совпадает с ней. |
|
3. На рисунке изображен график функции y = f(x), определенной на интервале (-6; 8). Найдите количество точек, в которых касательная к графику функции параллельна прямой у = 4. |
ЧАСТЬ 2 |
|
|
7.Найдите наименьшее значение функции у = 2 sin х – 25х + 9 на отрезке [ — 3π/2; 0] 8.Найдите точку максимума функции у = ( х2 – 10х + 10 ) е 5 – х . |
||
|
4. На рисунке изображен график производной функции:y = f ‘(x), определенной на интервале (-4; 16). Найдите количество точек максимума функции на отрезке [-3; 15]. |
ЧАСТЬ 3 |
|
|
9. Построить график функцииу = – х3 – 3х2 + 3 |
Используемая литература и Интернет-ресурсы.
Алгебра и начала математического анализа. 10 класс. Контрольные работы в новом формате: учебное пособие/ Ю.П. Дудницын, А.В. Семенов; под общ. ред. А.В. Семенова; Московский центр непрерывного математического образования. – Москва: Интеллект-Центр, 2011.
Самостоятельные и контрольные работы по алгебре и началам анализа для 10-11 классов/ А.П. Ершова, В.В. Голобородько. – Москва: ИЛЕКСА, 2014.
Открытый банк заданий математике: http://mathege.ru/or/ege/
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/179015-algebra-11-kontrolnaja-rabota-po-temeprimenen
Методическое пособие для итогового повторения темы в 11 классе
«Производная функции и её применение».
Данный материал предназначается для подготовки учащихся к ЕГЭ по теме «Производная функции и её применение».
На итоговое повторение в 11 классе отводится определённое количество часов по всему курсу математики, поэтому очень важно отобрать для повторения каждой темы те ключевые моменты, которые нужны для решения тестовых задач.
На повторение данной темы отводится 3 часа, поэтому из них один час берём на контрольную работу, а 2 часа на решение задач, которые встречаются в базовом экзамене по математике и профильном.
«Применение производной» представлены двумя заданиями .
Задачи можно отнести к одной из следующих групп:
-
вычисление углового коэффициента касательной к графику функции в заданной точке или угла, образованного данной касательной с положительным направлением оси абсцисс;
-
нахождение промежутков возрастания или убывания функции;
-
нахождение точек максимума или минимума функции;
-
нахождение наибольшего или наименьшего значений функции.
Перед повторение темы учащимся предлагается дома составить опорный конспект.
На усмотрение учителя, можно выдать опорный конспект сразу и его использовать при подготовке на всех 3 уроках
Цели уроков:
-
Образовательные: повторить и обобщить знания учащихся по теме “Применение производной”, систематизировать способы деятельности учащихся по применению производной к исследованию функций, подготовка к ЕГЭ.
-
Развивающие: развивать способности применять теоретические знания на практике, развивать навыки работы с тестовыми заданиями, логическое мышление, память, внимание, развивать навыки самоконтроля.
-
Воспитательные: воспитывать ответственное отношение к изучению математики, трудолюбие, взаимопомощь, волю и настойчивость в достижении поставленной цели.
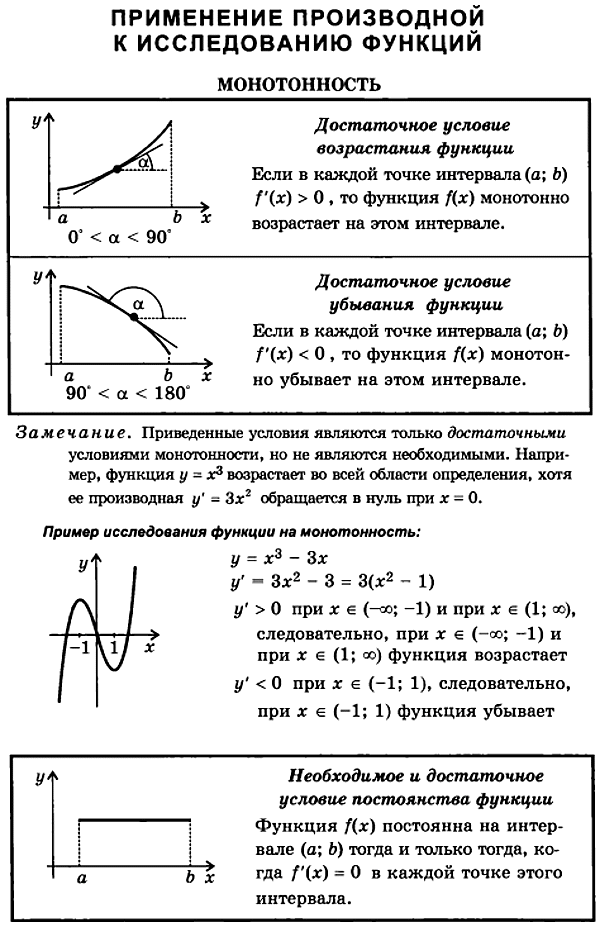
Опорный конспект по теме «Производная»
Таблица производных элементарных функций
|
Функция |
Производная |
|
Постоянная |
|
|
Степенная |
|
|
Показательная |
|
|
Экспоненциальная |
|
|
Синус |
|
|
Косинус |
|
|
Тангенс |
|
|
Котангенс |
|
|
Логарифмическая |
|
|
Натуральный логарифм |
|
Геометрический и механический смыслы производной.
Геометрический смысл производной состоит в существовании в точке 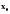

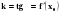
Механический смысл производной состоит в том, что 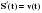
Основные правила вычисления производных
|
Название правила |
Математическое описание |
|
Производная суммы функций |
|
|
Производная разности функций |
|
|
Производная произведения функций |
|
|
Производная частного функций |
|
|
Производная сложной функции |
|
ПЕРВЫЙ УРОК.
-
Устная работа. Рассмотрим некоторые примеры:
Пример 1.На рисунке изображён график функции
и касательная к этому графику, проведённая в точке с абсциссой
. Найдите значение производной функции
в точке
.
Пример 2.
Функция определена на отрезке [-4;4]. На рисунке изображён её график. 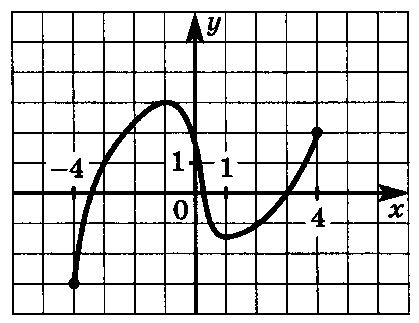
а). Найдите точку минимума этой функции на интервале
(-3;3).
б) В какой точке она принимает своё наименьшее значение?
Пример 3.
На рисунке изображён график производной функции. Найдите точку максимума функции на отрезке [-6;6].
Пример 4.
Функция определена на интервале (-8;8). На рисунке изображён график её производной. а) Найдите длину наибольшего промежутка возрастания функции
б). Найти количество точек экстремума на этом интервале.
в). Найдите сумму точек экстремума этой функции.
Пример 5.
Функция определена на интервале (-6;3). На рисунке изображён график её производной. В какой точке отрезка [-3;2] функция
принимает наибольшее значение?
Примечание: При решении задач подобного вида (примеры 2-5) следует внимательно прочитать условие и отметить, что на чертеже изображён либо график функции, либо график её производной.
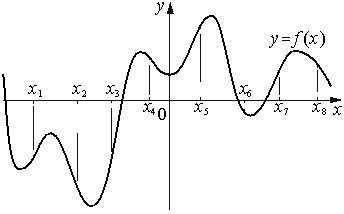
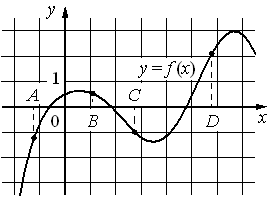
Пример 6. На рисунке изображён график функции y=f(x). На оси абсцисс отмечены восемь точек: x1, x2, x3, x4, x5, x6, x7, x8. а)В скольких из этих точек производная функции f(x) отрицательна? б)В скольких точках производная f(x) положительна?
Пример 7. На рисунке изображён график y=f '(x) — производной функции f(x).
На оси абсцисс отмечены шесть точек: x1, x2, x3, x4, x5, x6.
Сколько из этих точек лежит на промежутках возрастания функции f(x)?
Пример 8.
На рисунке изображён график функции y=f(x) и отмечены точки A, B, C и D на оси Ox. Пользуясь графиком, поставьте в соответствие каждой точке характеристики функции и её производной.
|
А |
B |
С |
D |
|
Характеристики функции и производной. |
||||||||
|
|
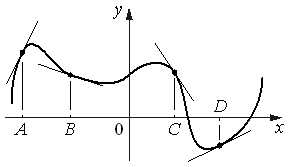
Пример 9. На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D. В Ниже указаны значения производной функции в точках A, B, C
|
|
Пример 10. На рисунке изображён график функции y=f(x). Точки a, b, c, d и e задают на оси Ox интервалы. Пользуясь графиком, поставьте в соответствие каждому интервалу характеристику функции или её производной. |
|
-
Работа в классе.
Алгоритмы к решению задач по теме: «Применение производной»
-
На рисунке изображён график y=F(x) одной из первообразных некоторой функции f(x), определённой на интервале (− 7; 5). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [− 5; 2].
-
На рисунке изображён график некоторой функции y=f(x) (два луча с общей начальной точкой).
-
Пользуясь рисунком, вычислите F(− 1)−F(− 8), где F(x) — одна из первообразных функции f(x).
-
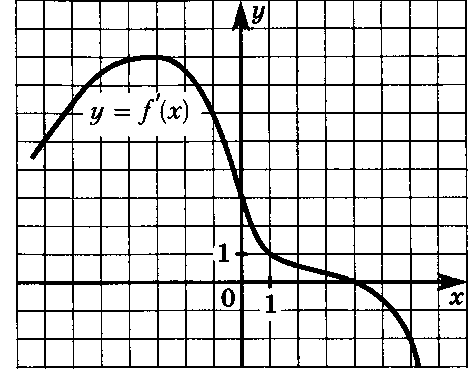
На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (− 2 ; 11). Найдите абсциссу точки, в которой касательная к графику функции y=f(x) параллельна оси абсцисс
или совпадает с ней. -
-
С помощью производной мы находим мгновенную скорость и ускорение точки; строим касательную к графику функции; находим критические точки; промежутки возрастания, убывания и постоянства функции; точки экстремума; экстремумы функции; используем производную для исследования функции и построения ее графика; для решения «экстремальных задач»; для нахождения наибольшего и наименьшего значения функции, непрерывной на отрезке. Почти все типы задач решаются с помощью алгоритмов.
-
Алгоритм нахождения критических точек функции.
-
Найти область определения функции.
-
Найти производную функции.
-
Решить уравнение f ‘(х) = 0.
-
Выяснить, являются ли корни уравнения f ‘(х) = 0 внутренними точками определения функции.
-
Сделать вывод.
-
Пример 14. Найти критические точки функций.
-
а)
б)
в)
.
-
Алгоритм нахождения промежутков возрастания и убывания функции.
-
Найти область определения функции и интервалы, на которых функция непрерывна.
-
Найти производную функции.
-
Найти критические точки: f ‘(х) = 0.
-
Отметим критические точки на области определения и определим знак производной на каждом из полученных интервалов. (Если на рассматриваемом интервале
f ‘(х) 0, то функция возрастает, а если f ‘(х)
-
Пример 15. Найти промежутки возрастания и убывания функции
-
-
Необходимое условие экстремума
-
В точках экстремума, производная функции равна нулю или не существует. Но не в каждой точке х0, где f ‘(х0) =0 или f ‘(х0) не существует, будет экстремум.
-
Достаточное условие экстремума
-
Если функция f (х) непрерывна в точке х0 и производная f ‘(х) меняет знак в точке х0, то х0 – точка экстремума функции f (х).
-
Если в точке х0 знак f ‘(х) меняется с «+» на «-», то х0 – точка максимума.
-
Если в точке х0 знак f ‘(х) меняется с «-» на «+», то х0 – точка минимума.
-
Точки максимума и минимума называются точками экстремума. А значения функции в точках экстремума называются экстремумами функции.
-
Алгоритм нахождения точек экстремума и экстремумов функций
-
Найти область определения.
-
Найти производную функции
-
Найти критические точки
-
Отметим критические точки на области определения и определим знак производной на каждом из полученных интервалов.
-
Относительно каждой критической точки определить, является ли она точкой максимума, минимума или не является точкой экстремума.
-
точки максимума
-
точки минимума =точки экстремума
-
Найти значения функции в точках экстремума – это экстремумы функции.
-
Записать требуемый результат исследования функции.
-
Пример 16. Найти точки экстремума функции f(x) = x2 · ex.
-
Если их несколько, найти их сумму.
-
Домашнее задание.
-
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
-
На рисунке изображён график функции y=f′(x) —производной функции f(x), определённой на интервале (1 ; 10). Найдите точку минимума
функции f(x).
-
На рисунке изображён график дифференцируемой функции y=f(x) и отмечены семь точек на оси абсцисс: x1, x2, x3, x4, x5, x6, x7. В скольких из этих точек производная функции f(x) отрицательна?
-
На рисунке изображён график дифференцируемой функции y=f(x), определённой на интервале (− 3 ; 8). Найдите точку из отрезка [− 2 ; 5],
в которой производная функции f(x) равна 0.
-
На рисунке изображён график функции y=f(x), определённой
на интервале (− 4 ; 13). Определите количество точек, в которых касательная к графику функции y=f(x) параллельна прямой y=14. -
22. Найти точки экстремума функции
.
-
23. Найти экстремумы функции
.
-
Банк задач.
-
На рисунке изображены график функции y=f(x) и касательная к этому графику, проведённая в точке с абсциссой x0.
-
Найдите значение производной функции f(x) в точке x0 .
-
На рисунке изображён график y=f′(x) — производной функции f(x), определённой на интервале (−9; 8). Найдите точку экстремума функции f(x) на отрезке [−3; 3].
-
На рисунке изображены график дифференцируемой функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
-
На рисунке изображён график функции y=f′(x) — производной функции f(x), определённой на интервале (− 3 ; 8). Найдите точку минимума функции f(x).
-
На рисунке изображён график функции y=f(x), определённой на интервале (− 9; 5). Найдите количество точек, в которых производная функции f(x) равна 0.
-
На рисунке изображён график y=f′(x) производной функции f(x), определённой на интервале (− 2; 9). В какой точке отрезка [2; 8] функция f(x) принимает наименьшее значение?
-
На рисунке изображён график функции y=f(x), определённой на интервале (− 7 ; 7). Определите количество целых точек, в которых производная функции положительна.
-
На рисунке изображён график функции y=f(x), определённой на интервале (− 6 ; 6). Найдите количество решений уравнения f '(x)=0 на отрезке [− 4,5 ; 2,5].
-
На рисунке изображён график y=f '(x) — производной функции f(x).
На оси абсцисс отмечены девять точек: x1, x2, x3, x4, x5, x6, x7, x8, x9. Сколько из этих точек лежит на промежутках убывания функции f(x)?
-
На рисунке изображён график y=F(x) одной из первообразных некоторой функции f(x), определённой на интервале (− 8; 7). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [− 5; 5].
-
На рисунке изображён график некоторой функции y=f(x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(− 1)−F(− 9), где F(x) — одна из первообразных функции f(x).
-
На рисунке изображён график y=F (x) одной из первообразных некоторой функции f (x), определённой на интервале (1;13). Пользуясь рисунком, определите количество решений уравнения f (x)=0 на отрезке [2;11].
-
На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (− 4 ; 13). Найдите количество точек, в которых касательная к графику функции y=f(x) параллельна прямой y=− 2x−10 или совпадает с ней.
-
Ответы.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-
ВТОРОЙ УРОК.
-
Устная работа.
-
Касательная к графику функции
параллельна прямой
. Найдите абсциссы точек касания.
-
Выберите правильный ответ.
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-
Примечание: Для устного счета можно взять задачи из банка задач предыдущего урока
-
Повторить и сформулировать:
-
Алгоритм нахождения наибольшего и наименьшего значения функции, непрерывной на отрезке
-
Найти область определения функции и проверить принадлежит ли отрезок области определения.
-
Найти производную f΄(x).
-
Найти критические точки.
-
Выбрать критические точки, принадлежащие заданному отрезку.
-
Вычислить значения функции в этих критических точках и на концах отрезка.
-
Сравнить полученные значения и выбрать из них наименьшее и наибольшее.
-
Работа в классе.
-
Пример 1. Найти наибольшее и наименьшее значение функции
;
-
на отрезке
-
Пример 2. Найдите наибольшее значение функции
-
на отрезке
-
Пример 3. Найдите точку минимума функции
-
Пример 4. Найдите наибольшее значение функции y =
-
на отрезке
-
Пример 5. Найдите наибольшее значение функции
-
на отрезке
-
Пример 6. Найдите точку минимума функции
.
-
Домашнее задание.
-
Пример 7. Найдите наибольшее значение функции на отрезке
-
Пример 8. Найдите точку максимума функции
-
Пример 9. Найдите наибольшее значение функции
на отрезке
.
-
Пример 10. Найдите точку минимума функции
-
Пример 11. Найдите точку минимума функции
.
-
Ответы.
-
Устно: 1. 2; 2. Вар.1 а). 4; б) – 80. Вар.2 а). 1; б) – 108.
-
Примеры:
-
1. Унаибольшее = — 4; Унаименьшее = — 8.
-
2. 3
-
3. 2
-
4. – 18
-
5. 5
-
6. 2
-
7. 1
-
8. 23
-
9. 10
-
10. 3
-
11. -2
-
Банк задач.
-
Задачи на нахождение наибольшего и наименьшего значения функции.
-
Задачи для самостоятельных работ дома и в классе.
-
-
1 вариант
-
2 вариант
-
1.Найдите наименьшее значение функции
на отрезке
.
-
1.Найдите точку минимума функции
.
-
2.Найдите наибольшее значение функции
на отрезке
.
-
2.Найдите точку минимума функции
.
-
3.Найдите наибольшее значение функции
на отрезке
-
3.Найдите наименьшее значение функции
на отрезке
.
-
4.Найдите точку максимума функции
.
-
4.Найдите наименьшее значение функции
на отрезке
.
-
5.Найдите точку минимума функции
.
-
5.Найдите наибольшее значение функции
на отрезке
.
-
6.Найдите наименьшее значение функции
на отрезке
.
-
6.Найдите точку максимума функции
.
-
7.Найдите точку минимума функции
.
-
7.Найдите наименьшее значение функции
на отрезке
.
-
8.Найдите наименьшее значение функции
на отрезке
.
-
8.Найдите точку максимума функции
.
-
9.Найдите наибольшее значение функции
на отрезке
.
-
9.Найдите точку минимума функции
.
-
10.Найдите точку минимума функции
.
-
10.Найдите наибольшее значение функции
.
-
-
ТРЕТИЙ УРОК.
-
Контрольная работа. «Производная и её применение».
-
Вариант №1.
-
ЧАСТЬ 1.
-
На рисунке изображён график
-
функции y = f(x) и касательная к
-
нему в точке с абсциссой x0.
-
Найдите значение производной
-
функции в точке х0.
-
На рисунке изображен график
-
производной функции: y = f ‘(x),
-
определенной на интервале (-8; 3).
-
В какой точке отрезка [-5; 0]
-
функция f(x) принимает
-
наибольшее значение
-
На рисунке изображен график функции
-
y = f(x), определенной на интервале (-6; 8).
-
Найдите количество точек, в которых
-
касательная к графику функции
-
параллельна прямой у = 4.
-
На рисунке изображен
-
график производной функции:
-
y = f ‘(x), определенной на интервале
-
(-4; 16). Найдите количество точек
-
максимума функции на отрезке [-3; 15].
-
На рисунке изображен график
-
производной функции: y = f ‘(x),
-
определенной на интервале (-2; 12).
-
Найдите промежутки убывания функции.
-
В ответе укажите длину наибольшего из них.
-
На рисунке изображен график
-
производной функции: y = f ‘(x) ,
-
определенной на интервале
-
(-9; 8). Найдите количеств о точек,
-
в которых касательная к графику
-
функции параллельна прямой
-
у = — 2х – 7 или совпадает с ней.
-
___________________________________________________________________________
-
ЧАСТЬ 2.
-
Прямая у = 7х – 5 параллельна касательной к графику функции
-
у = х2 +6х – 8. Найдите абсциссу точки касания.
-
8. Найдите точки максимума и минимума:
-
а) f(x) = х3 – 2х2 + х + 3;
-
б) f(x) =
.
-
___________________________________________________________________________
-
ЧАСТЬ 3.
-
9. Найдите наименьшее значение функции
-
у = 2 sin х + 25х + 9 на отрезке [ — 3π/2; 0]
-
10. Найдите точку максимума функции у = ln ( х + 5 ) – 2х + 9.
-
Контрольная работа. «Производная и её применение».
-
Вариант №2.
-
На рисунке изображён график функции y = f(x)
-
и касательная к нему в точке с абсциссой x0
-
.Найдите значение производной функции в точке х0
-
На рисунке изображен график производной
-
функции: y = f ‘(x),определенной
-
на интервале (-8; 4).
-
В какой точке отрезка [-6; -2]
-
функция f(x) принимает
-
наибольшее значение.
-
На рисунке изображен график функции
-
y = f(x), определенной на интервале
-
(-11; 2).Найдите количество точек, в
-
которых касательная к графику функции
-
параллельна прямой у = -2.
-
На рисунке изображен график производной
-
функции: y = f ‘(x), определенной на интервале
-
(-5; 7). Найдите промежутки убывания функции.
-
В ответе укажите количество целых точек,
-
входящих в эти промежутки.
-
На рисунке изображен график
-
производной функции: y = f ‘(x),
-
определенной на интервале (-4; 16).
-
Найдите количество точек
-
максимума функции на отрезке [-3; 15].
-
На рисунке изображен график
-
производной функции: y = f ‘(x) ,
-
определенной на интервале (-9; 8).
-
Найдите количество точек,
-
в которых касательная к графику
-
функции параллельна прямой
-
у = 2х – 7 или совпадает с ней.
-
____________________________________________________________________________
-
ЧАСТЬ 2.
-
7. Прямая у = 6х + 6 параллельна касательной к графику функции у = х2 + 7х – 7.
-
Найдите абсциссу точки касания.
-
8. Найдите точки максимума и минимума:
-
а) f(x) = х3— х2 — х +2;
-
б) f(x) =
.
-
_____________________________________________________________________________________
-
ЧАСТЬ 3.
-
9. Найдите наибольшее значение функции
-
у = 12 √ 2 cos x + 12х – 3π + 9 на отрезке [ 0; π/2]
-
10. Найдите точку минимума функции у = 2х – ln ( х + 3) + 7.
-
Ответы:
-
№
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
-
Вар.1
-
— 1
-
— 3
-
4
-
2
-
6
-
4
-
0,5
-
а). x max =
; x min = 1. б). x min = 2,5.
-
9
-
-4,5
-
Вар.2
-
2
-
— 1
-
7
-
9
-
2
-
4
-
-0,5
-
а).x max = —
; x min = 1.б).x min = 0,25
-
— 2,5
-
21
-
-
Литература:
-
ЕГЭ – 2017, Математика. Типовые варианты экзаменационных работ для подготовки к ЕГЭ. И. В. Ященко, И. Р. Высоцкий – Москва, АСТ, Астрель-2016.
-
Наглядный справочник по алгебре и началам анализа с примерами для 7 – 11 классов. Л. Е. Гендельштейн, А. П. Ершова.- ИЛЕКСА гимназия, Москва – Харьков – 1997.
-
Материалы с сайта ФИПИ, банк заданий и демонстрационные материалы по математике
-
Учебно – методическое пособие. Математика. Подготовка к ЕГЭ – 2016. Ф. Ф. Лысенко, С. Ю. Кулабухов – Ростов – на — Дону, Легион, 2015.
-
Методическое пособие для подготовки к ЕГЭ. Математика. Т. А. Корешкова. Ю. А. Глазков – Москва. «Экзамен» — 2016.
-
Сайт Гущина. Решу ЕГЭ.
Контрольная работа по теме: Производная в формате ЕГЭ.
Контрольная работа по теме: «Производная» в формате ЕГЭ.
Математика
| № | I вариант | II вариант |
Найдите значение производной функции 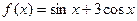 в точке в точке 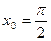 . . 
|
Найдите значение производной функции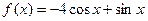 в точке в точке 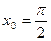 . .
|
|
На рисунке изображён график функции 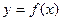 и касательная к нему в точке с абсциссой и касательная к нему в точке с абсциссой 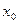 . Найдите значение производной функции . Найдите значение производной функции 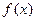 в точке в точке 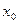 . .
|
На рисунке изображён график функции 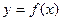 и касательная к нему в точке с абсциссой и касательная к нему в точке с абсциссой 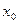 . Найдите значение производной функции . Найдите значение производной функции 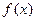 в точке в точке  . .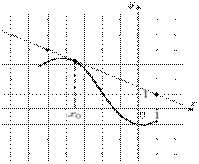
|
|
Найдите угловой коэффициент касательной к графику функции 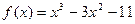 в точке с абсциссой 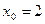 . .
|
Найдите угловой коэффициент касательной к графику функции 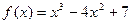 в точке с абсциссой 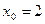 . .
|
|
На рисунке изображен график функции 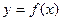 , определенной на интервале (-3;9). Найдите количество точек, в которых касательная к графику функции параллельна прямой , определенной на интервале (-3;9). Найдите количество точек, в которых касательная к графику функции параллельна прямой 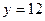 . .
|
На рисунке изображен график функции 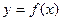 , определенной на интервале (-3;11). Найдите количество точек, в которых касательная к графику функции параллельна прямой , определенной на интервале (-3;11). Найдите количество точек, в которых касательная к графику функции параллельна прямой 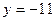 . .
|
|
На рисунке изображен график производной функции 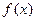 , определенной на интервале(-12;4). Найдите промежутки возрастания функции, , определенной на интервале(-12;4). Найдите промежутки возрастания функции,в ответе укажите длину наибольшего из них. 
|
На рисунке изображен график производной функции 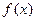 , определенной на интервале(-1;17). Найдите промежутки убывания функции, , определенной на интервале(-1;17). Найдите промежутки убывания функции,в ответе укажите длину наибольшего из них. 
|
|
Укажите промежуток, на котором функция 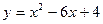 убывает. убывает.
|
Укажите промежуток, на котором функция 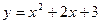 возрастает. возрастает.
|
|
На рисунке изображен график функции 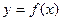 , определенной на интервале (-4;7). , определенной на интервале (-4;7).Найдите сумму точек экстремума функции 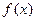 . .
|
На рисунке изображен график функции 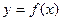 , определенной на интервале (-7;5). , определенной на интервале (-7;5).Найдите сумму точек экстремума функции 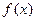 . .
|
|
Найдите точки экстремума функции 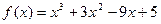 . .
|
Найдите точки экстремума функции 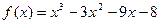 . .
|
|
На рисунке изображен график производной функции 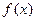 , определенной на интервале (-4;16). Найдите количество точек максимума функции на отрезке , определенной на интервале (-4;16). Найдите количество точек максимума функции на отрезке  . .
|
На рисунке изображен график производной функции 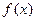 , определенной на интервале(-17;2). Найдите количество точек минимума функции на отрезке , определенной на интервале(-17;2). Найдите количество точек минимума функции на отрезке 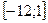 . .
|
|
На рисунке изображен график производной функции 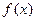 , определенной на интервале(-8; 4). , определенной на интервале(-8; 4).В какой точке отрезка 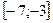 функция принимает наименьшее значение. функция принимает наименьшее значение.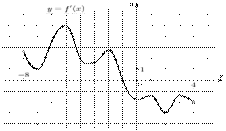
|
На рисунке изображен график производной функции 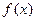 , определенной на интервале(-8;3). В какой точке отрезка , определенной на интервале(-8;3). В какой точке отрезка 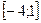 функция принимает наибольшее значение. функция принимает наибольшее значение.
|
|
Прямая 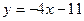 является касательной к графику функции является касательной к графику функции 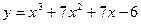 . Найдите абсциссу точки касания. . Найдите абсциссу точки касания.
|
Прямая 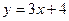 является касательной к графику функции является касательной к графику функции 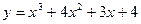 . Найдите абсциссу точки касания. . Найдите абсциссу точки касания.
|
|
Найдите точку минимума функции 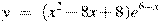 . .
|
Найдите точку максимума функции 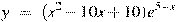 . .
|
|
Найдите наибольшее значение функции 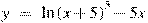 на отрезке на отрезке 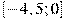 . .
|
Найдите наименьшее значение функции 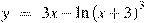 на отрезке на отрезке 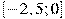 . .
|
|
Точка движется прямолинейно по закону 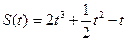 .Вычислите скорость и ускорение точки при t = 1. .Вычислите скорость и ускорение точки при t = 1. |
Точка движется прямолинейно по закону 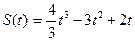 .Вычислите скорость и ускорение точки при t = 1. .Вычислите скорость и ускорение точки при t = 1. |













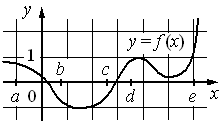
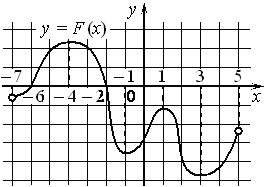
 б)
б) 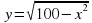 в)
в) 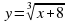 .
.