Конус егэ профиль теория

Цилиндр, конус, шар

Цилиндр – тело, ограниченное цилиндрической поверхностью и двумя кругами с границами $М$ и $М_1$. Цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги – основаниями цилиндра.

Образующие цилиндрической поверхности называются образующими цилиндра, на рисунке образующая $L$.

Цилиндр называется прямым, если его образующие перпендикулярны основаниям.
Осевое сечение цилиндра — это прямоугольник, у которого одна сторона равна диаметру основания, а вторая – высоте цилиндра.

Основные понятия и свойства цилиндра:

1. Основания цилиндра равны и лежат в параллельных плоскостях.
2. Все образующие цилиндра параллельны и равны.
3. Радиусом цилиндра называется радиус его основания ($R$).
4. Высотой цилиндра называется расстояние между плоскостями оснований (в прямом цилиндре высота равна образующей).
5. Осью цилиндра называется отрезок, соединяющий центры оснований ($ОО_1$).
6. Если радиус или диаметр цилиндра увеличить в n раз, то объем цилиндра увеличится в $n^2$ раз.
7. Если высоту цилиндра увеличить в m раз, то объем цилиндра увеличится в то же количество раз.
8. Если призму вписать в цилиндр, то ее основаниями будут являться равные многоугольники, вписанные в основание цилиндра, а боковые ребра — образующими цилиндра.
9. Если цилиндр вписан в призму, то ее основания — равные многоугольники, описанные около оснований цилиндра. Плоскости граней призмы касаются боковой поверхности цилиндра.
10. Если в цилиндр вписана сфера, то радиус сферы равен радиусу цилиндра и равен половине высоты цилиндра.

$R_{сферы}=R_{цилиндра}={h_{цилиндра}}/{2}$

Площадь поверхности и объем цилиндра.

Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту.

$S_{бок.пов.}=2πR·h$

Площадь поверхности цилиндра равна сумме двух площадей оснований и площади боковой поверхности.

$S_{полной.пов.}=2πR^2+2πR·h=2πR(R+h)$

Объем цилиндра равен произведению площади основания на высоту.

$V=πR^2·h$

Объем части цилиндра, в основании которого лежит сектор: $V={πR^2·n°·h}/{360}$, где $n°$ — это градусная мера центрального угла, отсекающего заданный сектор.

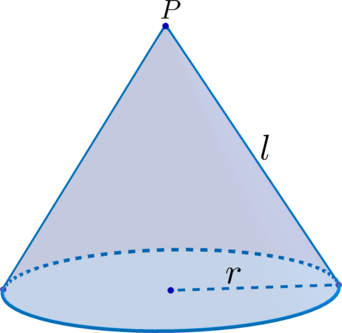
Конусом (круговым конусом) называется тело, которое состоит из круга, точки, не лежащей в плоскости этого круга, и всех отрезков, соединяющих заданную точку с точками круга.

Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими и обозначаются (l).

$l=SA$

Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. Ось прямого конуса и его высота равны.

$SО$ — высота и ось конуса.

Свойства конуса:

1. Все образующие конуса равны.
2. Осевым сечением конуса является равнобедренный треугольник, основание которого равно двум радиусам, а боковые стороны равны образующим конуса.
3. Если боковая поверхность конуса – полукруг, то осевым сечением является равносторонний треугольник, угол при вершине равен $60°$.
4. Если радиус или диаметр конуса увеличить в n раз, то его объем увеличится в $n^2$ раз.
5. Если высоту конуса увеличить в m раз, то объем конуса увеличится в то же количество раз.

Площадь поверхности и объем конуса.

Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.

$S_{бок.пов.}=πR·l$

Площадь поверхности конуса равна сумме площади основания и площади боковой поверхности.

$S_{полной.пов.}=πR^2+πR·l=πR(R+l)$

Объем конуса равен трети произведения площади основания на высоту.

$V={πR^2·h}/{3}$

Объем части конуса, в основании которого лежит сектор: $V={πR^2·n°·h}/{360·3}$, где $n°$ — это градусная мера центрального угла, отсекающего заданный сектор.

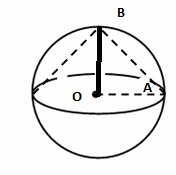
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии ($R$) от данной точки (центра сферы $О$).

Тело, ограниченное сферой, называется шаром.

Осевое сечение шара это круг, радиус которого равен радиусу шара. Осевым сечением является самый большой круг шара.

Площадь поверхности сферы: $S_{п.п}=4π·R^2=π·d^2$, где $R$ — радиус сферы, $d$ — диаметр сферы

Объем шара: $V={4π·R^3}/{3}={π·d^3}/{6}$, где $R$ — радиус шара, $d$ — диаметр шара.

Если радиус или диаметр шара увеличить в n раз, то площадь поверхности увеличится в $n^2$ раз, а объем в $n^3$ раз.

Теорема Пифагора

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

$АС^2+ВС^2=АВ^2$

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$:

Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.

1. Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.

Значения тригонометрических функций некоторых углов:

$α$	$30$	$45$	$60$
$sinα$	${1}/{2}$	${√2}/{2}$	${√3}/{2}$
$cosα$	${√3}/{2}$	${√2}/{2}$	${1}/{2}$
$tgα$	${√3}/{3}$	$1$	$√3$
$ctgα$	$√3$	$1$	${√3}/{3}$

Признаки подобия треугольников:

1. Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между ними равны, то такие треугольники подобны.
3. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны. Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.

Конус, подготовка к ЕГЭ по математике

22.12.2017

Таблицы с теорией на тему: «Конус» для подготовки к ЕГЭ по математике. В кратком содержании изложена вся необходимая теория для этой темы.

Смотреть в PDF:

Или прямо сейчас: cкачать в pdf файле.

Печать страницы

Формулы объема и площади поверхности. Цилиндр, конус и шар

Тела вращения, изучаемые в школе, — это цилиндр, конус и шар.

Если в задаче на ЕГЭ по математике вам надо посчитать объем конуса или площадь сферы — считайте, что повезло.

Применяйте формулы объема и площади поверхности цилиндра, конуса и шара. Все они есть в нашей таблице. Учите наизусть. Отсюда начинается знание стереометрии.

Смотрите также: Формулы объема и площади поверхности многогранников.
Кроме формул, в решении задач по стереометрии нужны также элементарная логика и пространственное воображение. Есть и свои небольшие секреты.

Например, такой важный факт:

Если все линейные размеры объемного тела увеличить в 2 раза, то площадь его поверхности увеличится в 4 раза, а объем — в 8 раз. 

(ведь , ).

Вот такая задача. Как и остальные на нашем сайте, она взята из банка заданий ФИПИ.

1. Объем конуса равен . Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

Очевидно, что объем меньшего конуса в раз меньше объема большого и равен двум.

Для решения некоторых задач полезны начальные знания стереометрии. Например — что такое правильная пирамида или прямая призма. Полезно помнить, что у цилиндра, конуса и шара есть еще общее название — тела вращения. Что сферой называется поверхность шара. А, например, фраза «образующая конуса наклонена к плоскости основания под углом 30 градусов предполагает, что вы знаете, что такое угол между прямой и плоскостью. Вам также может пригодиться теорема Пифагора и простые формулы площадей фигур.

Иногда неплохо нарисовать вид сверху. Или, как в этой задаче, — снизу.

2. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?

Всё просто — рисуем вид снизу. Видим, что радиус большего круга в раз больше, чем радиус меньшего. Высоты у обоих конусов одинаковы. Следовательно, объем большего конуса будет в раза больше.

Говорят, что хороший чертеж — это уже половина решения. Читайте о том, как строить чертежи в задачах по стереометрии.

Еще один важный момент. Помним, что в задачах части В вариантов ЕГЭ по математике ответ записывается в виде целого числа или конечной десятичной дроби. Поэтому никаких или у вас в ответе в части В быть не должно. Подставлять приближенное значение числа тоже не нужно! Оно обязательно должно сократиться! Именно для этого в некоторых задачах задание формулируется, например, так: «Найдите площадь боковой поверхности цилиндра, деленную на ».

А где же еще применяются формулы объема и площади поверхности тел вращения? Конечно же, в задаче 14 Профильного ЕГЭ по математике.
Мы тоже расскажем о ней.

---

Площадь поверхности – это суммарная площадь всех поверхностей, которые составляют объемную фигуру.

Призма

1. Призма — это многогранник, у которого две грани (основания) — равные (n)-угольники, лежащие в параллельных плоскостях, остальные (n) граней (боковые) — параллелограммы. Призмы подразделяются на треугольные, четырехугольные, пятиугольные и т. д. в зависимости от количества сторон основания.
Высотой призмы называется перпендикуляр, опущенный из точки верхнего основания на плоскость нижнего.

2. Призма, у которой боковое ребро перпендикулярно основанию, называется прямой. Ее боковые грани — прямоугольники, и высота равна боковому ребру.
Прямая призма, в основании которой лежит правильный многоугольник, называется правильной. Ее боковые грани, равные прямоугольники.

3. Площадь боковой поверхности призмы равна сумме площадей ее боковых граней: (S_{бок}= S_1+ S_2+…+ S_n).
Площадь поверхности призмы равна сумме площади боковой поверхности и двух площадей оснований: (S_{полн} = S_{бок}+ 2S_{осн}).

4. Объем произвольной призмы равен произведению площади основания на высоту: (V_{призмы}=S_{осн}cdot h).

Параллелепипед

5. Параллелепипедом называется призма, в основании которой лежит параллелограмм. Противоположные боковые грани параллелепипеда равны.
Прямой параллелепипед — это параллелепипед, у которого боковое ребро перпендикулярно основанию.
Прямоугольный параллелепипед — это прямой параллелепипед, у которого в основании лежит прямоугольник.
Диагональ прямоугольного параллелепипеда выражается через его измерения (ширину, длину и высоту) формулой (d^2=a^2+b^2+c^2).
Куб — параллелепипед, у которого все грани квадраты. Диагональ куба с ребром (a): (d=asqrt{3}).

Пирамида

6. Пирамидой называется многогранник, у которого одна грань (основание) — (n)—угольник, а остальные (n) граней (боковые) — треугольники с общей вершиной. Пирамиды подразделяются на треугольные, четырехугольные, пятиугольные и т. д. в зависимости от количества сторон основания.
Тетраэдер – другое название треугольной пирамиды.
Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на основание.

7. Пирамида называется правильной, если ее боковые ребра равны, а в основании лежит правильный многоугольник.
Основание высоты правильной пирамиды совпадает с центром ее основания, углы наклона боковых ребер к основанию равны, двугранные углы при основании равны, все боковые грани — равные равнобедренные треугольники.
Апофема – высота боковой грани правильной пирамиды, проведенная из её вершины к ребру основания.

8. Площадь боковой поверхности пирамиды равна сумме площадей ее боковых граней: (S_{бок}= S_1+ S_2+…+ S_n).
Площадь полной поверхности пирамиды равна сумме площади боковой поверхности и площади основания: (S_{полн} = S_{бок}+ S_{осн}).

9. Объем произвольной пирамиды равен произведению одной трети площади основания на высоту: (V=frac{1}{3} S_{осн}cdot h).

Сфера и шар

10. Сфера — это множество всех точек пространства, равноудаленных от данной точки, называемой центром сферы.
Радиусом сферы называется отрезок, соединяющий центр сферы с точкой на сфере, или длина этого отрезка.
Хордой сферы называется отрезок, соединяющий две точки на сфере.
Диаметр сферы — это хорда, которая проходит через центр сферы. Диаметр сферы равен двум радиусам сферы.

11. Площадь сферы находится по формуле: (S_{сф}=4πR^2).

12. Шаром называется часть пространства, ограниченная сферой, вместе с самой сферой и ее центром. Данная сфера называется поверхностью шара.
Сечение шара с радиусом (R) плоскостью, проходящей через центр шара, называется большим кругом шара. Радиус, хорда, диаметр шара те же, что и его сферы.

13. Объем шара находится по формуле (V_{шара}=frac{4}{3} πR^2).

Цилиндр

14. Цилиндром называется тело, полученное при вращении прямоугольника вокруг прямой, проходящей через одну из его сторон.
Прямая вращения называется осью цилиндра.
Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением.Осевое сечение цилиндра — прямоугольник со сторонами (2r) и (l), где (r) — радиус основания цилиндра, (l) — его образующая.
Образующая цилиндра — отрезок (обозначается (l) или (L)), перпендикулярный основаниям цилиндра и соединяющий точку окружности верхнего основания с точкой окружности нижнего основания.
Высотой цилиндра называется расстояние между плоскостями оснований (обозначается (h) или (H)).

15. Площадь боковой поверхности цилиндра: (S_{бок}=2πrh);      (S_{полн} = S_{бок}+ 2S_{осн}=2πrh+2πr^2).

16. Объем цилиндра (V_{цил}=S_{осн} h=πr^2 h).

Конус

17. Конусом называется тело, полученное при вращении прямоугольного треугольника вокруг прямой, проходящей через один из его катетов.
Прямая вращения называется осью конуса.
Сечение конуса, проходящее через ось, называется осевым сечением. Осевое сечение конуса — равнобедренный треугольник со стороной основания (2r) боковой стороной (l), где (r) — радиус основания конуса, (l) — его образующая.
Вершина осевого сечения является вершиной конуса.
Образующая конуса (обозначается (l) или (L)) — отрезок, соединяющий вершину конуса и точку окружности основания.
Высотой конуса называется расстояние от вершины конуса до плоскости основания (обозначается (h) или (H)). Высота конуса равна высоте осевого сечения, опущенной на основание.

18. Площадь боковой поверхности конуса: (S_{бок кон}=πrl),      (S_{кон}=S_{бок}+S_{осн}=πrl+2πr^2).

19. Объем конуса: (V_{кон}=frac{1}{3}S_{осн}h=frac{1}{3}πr^2 h).

Факт 1.
Конус
(bullet) Точка (P) – вершина конуса.
(bullet) Отрезок, соединяющий вершину конуса с границей основания, называется образующей (все образующие равны между собой).
(bullet) Отрезок, соединяющий вершину конуса с центром основания-круга, является высотой конуса.