Цилиндр, конус, шар
Цилиндр – тело, ограниченное цилиндрической поверхностью и двумя кругами с границами $М$ и $М_1$. Цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги – основаниями цилиндра.
Образующие цилиндрической поверхности называются образующими цилиндра, на рисунке образующая $L$.
Цилиндр называется прямым, если его образующие перпендикулярны основаниям.
Осевое сечение цилиндра — это прямоугольник, у которого одна сторона равна диаметру основания, а вторая – высоте цилиндра.
Основные понятия и свойства цилиндра:
- Основания цилиндра равны и лежат в параллельных плоскостях.
- Все образующие цилиндра параллельны и равны.
- Радиусом цилиндра называется радиус его основания ($R$).
- Высотой цилиндра называется расстояние между плоскостями оснований (в прямом цилиндре высота равна образующей).
- Осью цилиндра называется отрезок, соединяющий центры оснований ($ОО_1$).
- Если радиус или диаметр цилиндра увеличить в n раз, то объем цилиндра увеличится в $n^2$ раз.
- Если высоту цилиндра увеличить в m раз, то объем цилиндра увеличится в то же количество раз.
- Если призму вписать в цилиндр, то ее основаниями будут являться равные многоугольники, вписанные в основание цилиндра, а боковые ребра — образующими цилиндра.
- Если цилиндр вписан в призму, то ее основания — равные многоугольники, описанные около оснований цилиндра. Плоскости граней призмы касаются боковой поверхности цилиндра.
- Если в цилиндр вписана сфера, то радиус сферы равен радиусу цилиндра и равен половине высоты цилиндра.
$R_{сферы}=R_{цилиндра}={h_{цилиндра}}/{2}$
Площадь поверхности и объем цилиндра.
Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту.
$S_{бок.пов.}=2πR·h$
Площадь поверхности цилиндра равна сумме двух площадей оснований и площади боковой поверхности.
$S_{полной.пов.}=2πR^2+2πR·h=2πR(R+h)$
Объем цилиндра равен произведению площади основания на высоту.
$V=πR^2·h$
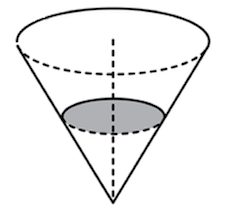
Объем части цилиндра, в основании которого лежит сектор: $V={πR^2·n°·h}/{360}$, где $n°$ — это градусная мера центрального угла, отсекающего заданный сектор.
Пример:
Цилиндр описан около шара. Объём цилиндра равен $30$. Найдите объём шара.
Решение:
Если в цилиндр вписан шар, то радиус цилиндра равен радиусу шара, а высота цилиндра в два раза больше радиуса шара.
$R_{цилиндр}=R_{шар}; h_{цилиндр}=2R_{шар}$
Распишем формулы объема цилиндра и шара.
$V_{цилиндра}=πR_{цилиндр}^2·h_{цилиндр}=πR_{шар}^2·2R_{шар}=2πR_{шар}^3$
$V_{шара}={4π·R_{шар}^3}/{3}$
Далее надо сравнить во сколько раз объем цилиндра больше объема шара, для этого разделим объемы друг на друга.
${V_{цилиндра}}/{V_{шара}}={2πR_{шар}^3·3}/{4π·R_{шар}^3}={3}/{2}=1.5$
Объем цилиндра больше объема шара в $1.5$ раза, следовательно, чтобы найти объем шара, надо объем цилиндра разделить на $1.5$.
$V_{шара}=30:1.5=20$
Ответ: $20$
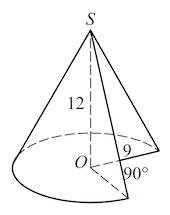
Конусом (круговым конусом) называется тело, которое состоит из круга, точки, не лежащей в плоскости этого круга, и всех отрезков, соединяющих заданную точку с точками круга.
Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими и обозначаются (l).
$l=SA$
Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. Ось прямого конуса и его высота равны.
$SО$ — высота и ось конуса.
Свойства конуса:
- Все образующие конуса равны.
- Осевым сечением конуса является равнобедренный треугольник, основание которого равно двум радиусам, а боковые стороны равны образующим конуса.
- Если боковая поверхность конуса – полукруг, то осевым сечением является равносторонний треугольник, угол при вершине равен $60°$.
- Если радиус или диаметр конуса увеличить в n раз, то его объем увеличится в $n^2$ раз.
- Если высоту конуса увеличить в m раз, то объем конуса увеличится в то же количество раз.
Площадь поверхности и объем конуса.
Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.
$S_{бок.пов.}=πR·l$
Площадь поверхности конуса равна сумме площади основания и площади боковой поверхности.
$S_{полной.пов.}=πR^2+πR·l=πR(R+l)$
Объем конуса равен трети произведения площади основания на высоту.
$V={πR^2·h}/{3}$
Объем части конуса, в основании которого лежит сектор: $V={πR^2·n°·h}/{360·3}$, где $n°$ — это градусная мера центрального угла, отсекающего заданный сектор.
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии ($R$) от данной точки (центра сферы $О$).
Тело, ограниченное сферой, называется шаром.
Осевое сечение шара это круг, радиус которого равен радиусу шара. Осевым сечением является самый большой круг шара.
Площадь поверхности сферы: $S_{п.п}=4π·R^2=π·d^2$, где $R$ — радиус сферы, $d$ — диаметр сферы
Объем шара: $V={4π·R^3}/{3}={π·d^3}/{6}$, где $R$ — радиус шара, $d$ — диаметр шара.
Если радиус или диаметр шара увеличить в n раз, то площадь поверхности увеличится в $n^2$ раз, а объем в $n^3$ раз.
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$АС^2+ВС^2=АВ^2$
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$:
Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.
- Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | ${1}/{2}$ | ${√2}/{2}$ | ${√3}/{2}$ |
| $cosα$ | ${√3}/{2}$ | ${√2}/{2}$ | ${1}/{2}$ |
| $tgα$ | ${√3}/{3}$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | ${√3}/{3}$ |
Признаки подобия треугольников:
- Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между ними равны, то такие треугольники подобны.
- Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны. Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
2
Найдите объем V конуса, образующая которого равна 2 и наклонена к плоскости основания под углом 30°. В ответе укажите
3
Во сколько раз уменьшится объем конуса, если его высота уменьшится в 3 раза, а радиус основания останется прежним?
4
Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 1,5 раза, а высота останется прежней?
5
Высота конуса равна 6, образующая равна 10. Найдите его объем, деленный на
Пройти тестирование по этим заданиям
09
Сен 2013
Категория: 02 Стереометрия
02. Конус
2013-09-09
2022-09-11
Задача 1. Высота конуса равна , образующая равна
Найдите его объем, деленный на
.
Решение: + показать
Задача 2. Конус получается при вращении равнобедренного прямоугольного треугольника вокруг катета, равного
Найдите его объем, деленный на
.
Решение: + показать
Задача 3. Высота конуса равна а диаметр основания –
Найдите образующую конуса.
Задача 4. Найдите объем конуса, образующая которого равна
и наклонена к плоскости основания под углом
В ответе укажите
Решение: + показать
Задача 5. Длина окружности основания конуса равна образующая равна
Найдите площадь боковой поверхности конуса.
Решение: + показать
Задача 6. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в раз?
Решение: + показать
Задача 7. Во сколько раз уменьшится объем конуса, если его высоту уменьшить в раз?
Решение: + показать
Задача 8. Во сколько раз увеличится объем конуса, если радиус его основания увеличится в раз, а высота останется прежней?
Решение: + показать
Задача 9. Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.
Решение: + показать
Задача 10. Объем конуса равен Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Решение: + показать
Задача 11. Площадь полной поверхности конуса равна Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Решение: + показать
Задача 12. Найдите объем конуса, образующая которого равна
и наклонена к плоскости основания под углом
В ответе укажите
.
Решение: + показать
Задача 13. Диаметр основания конуса равен а угол при вершине осевого сечения равен
°. Вычислите объем конуса, деленный на
.
Решение: + показать
Задача 14. Площадь основания конуса равна , высота —
Найдите площадь осевого сечения конуса.
Решение: + показать
Задача 15. Площадь основания конуса равна Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной
и
считая от вершины. Найдите площадь сечения конуса этой плоскостью.
Решение: + показать
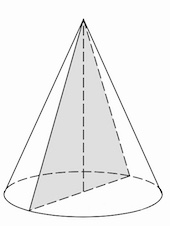
Задача 16. Найдите объем части конуса, изображенной на рисунке. В ответе укажите
.
Решение: + показать
Задача 17. Найдите объем части конуса, изображенной на рисунке. В ответе укажите
.
Решение: + показать
Задача 18. В сосуде, имеющем форму конуса, уровень жидкости достигает высоты. Объём жидкости равен
мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
Решение: + показать
Вы можете пройти тест
Автор: egeMax |
комментариев 10
Печать страницы
ЕГЭ Профиль №13. Фигуры вращения: цилиндр, конус, шар
Скачать файл в формате pdf.
ЕГЭ Профиль №13. Фигуры вращения: цилиндр, конус, шар
Цилиндр
Прямым круговым цилиндром называется фигура, полученная при вращении прямоугольника вокруг оси, содержащей его сторону. Радиусом цилиндра называется радиус его основания. Высотой цилиндра называется расстояние между плоскостями его оснований. Осью цилиндра называется прямая, проходящая через центры оснований.
Сечение цилиндра плоскостью, параллельной его оси, представляет собой прямоугольник. Две его стороны – образующие цилиндра, а две другие – параллельные хорды оснований. В частности, прямоугольником является осевое сечение. Это – сечение цилиндра плоскостью, проходящей через его ось.
Площадь боковой поверхности цилиндра находится по формуле: ({S_{{text{б}}{text{.п}}{text{.}}}} = 2,pi ,R,H); площадь полной поверхности цилиндра находится по формуле: (S = 2,pi ,R,H + 2pi ,{R^2}); объем цилиндра находится по формуле: (V = pi ,{R^2},H), где R – радиус основания; H – длина высоты цилиндра.
Конус
Прямым круговым конусом называется фигура, полученная при вращении прямоугольного треугольника вокруг оси, содержащей его катет. Другой катет треугольника, вращаясь вокруг этой же оси, дает круг, который называется основанием. При вращении вокруг этой оси гипотенузы получается фигура, называемая боковой поверхностью конуса. Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса. Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. Осью конуса называется прямая, содержащая его высоту.
Сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник, у которого боковые стороны являются образующими конуса. В частности, равнобедренным треугольником является осевое сечение конуса. Это сечение, которое проходит через ось конуса.
Площадь боковой поверхности конуса находится по формуле: ({S_{{text{б}}{text{.п}}{text{.}}}} = pi ,R,L,); площадь полной поверхности конуса находится по формуле: (S = pi ,R,L, + pi ,{R^2}); объем конуса находится по формуле: (V = frac{1}{3}pi ,{R^2},H), где R – радиус основания; L – длина образующей; H – длина высоты конуса.
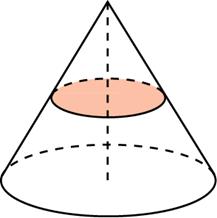
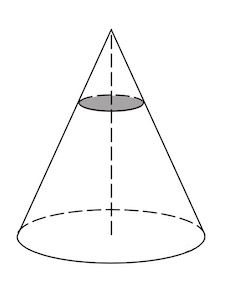
Плоскость, параллельная основанию конуса и пересекающая конус, отсекает от него меньший конус. Оставшаяся часть называется усеченным конусом.
Площадь боковой поверхности усеченного конуса находится по формуле:({S_{{text{б}}{text{.п}}}} = pi ,left( {,{R_1} + {R_2},} right),L); объем усеченного конуса находится по формуле:(V = frac{1}{3}pi ,H,left( {,R_1^2 + {R_1} cdot {R_2} + R_2^2,} right)), где ({R_1}) и ({R_2}) – радиусы оснований; L – длина образующей; H – длина высоты конуса.
Шар
Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии от данной точки, не большем данного положительного числа. Эта точка называется центром шара, а данное расстояние радиусом шара. Шаровой поверхностью или сферой шара называется множество всех точек пространства, находящихся на равном положительном расстоянии от некоторой точки. Эта точка называется центром сферы, а данное расстояние радиусом сферы. Таким образом, точками сферы являются все точки шара, которые удалены от центра на расстояние, равное радиусу. Любой отрезок, соединяющий центр шара с точкой шаровой поверхности, также называется радиусом. Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром.
Площадь поверхности шара находится по формуле: (S = 4,pi ,{R^2}); объем шара находится по формуле: (V = frac{4}{3}pi ,{R^3}), где R – радиус шара.
Шар, так же как цилиндр и конус, является телом вращения. Он получается при вращении полукруга вокруг его диаметра как оси. Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость. Плоскость, проходящая через центр шара, называется диаметральной плоскостью. Сечение шара диаметральной плоскостью называется большим кругом, а сечение сферы – большой окружностью. Шаровым сегментом называется часть шара, отсекаемая от него плоскостью. Шаровой сегмент можно получить, вращая круговой сегмент вокруг диаметра, перпендикулярного его хорде.
Площадь сегментной поверхности находится по формуле: (S = 2,pi ,R,H); объем шарового сегмента находится по формуле: (V = pi ,{H^2},left( {,R — frac{H}{3},} right)), где H – высота сегмента; R – радиус шара.
Шаровым сектором называется тело, которое получается из шарового сегмента и конуса следующим образом. Если шаровой сегмент меньше полушара, то он дополняется конусом, у которого вершина в центре шара, а основанием является основание сегмента. Если же сегмент больше полушара, то указанный конус из него удаляется.
Объем шарового сектора находится по формуле: (V = frac{2}{3}pi ,{R^2}H); площадь полной поверхности шарового сектора складывается из площади сегментной поверхности и площади боковой поверхности конуса и находится по формуле:({S_{{text{шар}}{text{.}};{text{сект}}}} = {S_{{text{шар}}{text{.}};{text{сегм}}}} + {S_{{text{б}}{text{.}};{text{п}}{text{.}};{text{кон}}}} = 2,pi ,R,H + pi ,R,sqrt {,2,R,H — {H^2}} ), где H – высота соответствующего шарового сегмента; R – радиус шара.
1В. В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки A, B и C, а на окружности другого основания — точка C1, причём CC1 — образующая цилиндра, а AC — диаметр основания. Известно, что (angle ,ACB = 30^circ ,;;AB = sqrt 2 ,) (C{C_1} = 2.)
а) Докажите, что угол между прямыми AC1 и BC равен (45^circ ).
б) Найдите объём цилиндра.
2В. В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А и В, а на окружности другого основания — точки В1 и С1, причем ВВ1 — образующая цилиндра, а отрезок АС1 пересекает ось цилиндра.
а) Докажите, что угол АВС1 прямой.
б) Найдите угол между прямыми ВВ1 и АС1, если АВ = 6, ВВ1 = 15, В1С1 = 8.
ОТВЕТ: ({rm{arctg}}frac{2}{3}).
3В. В конус, радиус основания которого равен 3, вписан шар радиуса 1,5.
а) Изобразите осевое сечение комбинации этих тел.
б) Найдите отношение площади полной поверхности конуса к площади поверхности шара.
4В. Диаметр окружности основания цилиндра равен 26, образующая цилиндра равна 21. Плоскость пересекает его основания по хордам длины 24 и 10. Расстояние между этими хордами равно (sqrt {730} ).
а) Докажите, что центры оснований цилиндра лежат по разные стороны от этой плоскости.
б) Найдите угол между этой плоскостью и плоскостью основания цилиндра.
ОТВЕТ: ({rm{arctg}}frac{{21}}{{17}}).
5В. Прямоугольник ABCD и цилиндр расположены таким образом, что AB — диаметр верхнего основания цилиндра, а CD лежит в плоскости нижнего основания и касается его окружности, при этом плоскость прямоугольника наклонена к плоскости основания цилиндра под углом 60°.
а) Докажите, что ABCD — квадрат.
б) Найдите длину той части отрезка BD, которая находится снаружи цилиндра, если радиус цилиндра равен (sqrt 2 ).
6В. В одном основании прямого кругового цилиндра с высотой 3 и радиусом основания 8 проведена хорда AB, равная радиусу основания, а в другом его основании проведён диаметр CD, перпендикулярный AB. Построено сечение ABNM, проходящее через прямую AB перпендикулярно прямой CD так, что точка C и центр основания цилиндра, в котором проведён диаметр CD, лежат с одной стороны от сечения.
а) Докажите, что диагонали этого сечения равны между собой.
б) Найдите объём пирамиды CABNM.
ОТВЕТ: (64 + 32sqrt 3 ).
7В. Отрезок AB — диаметр верхнего основания цилиндра, CD — диаметр нижнего, причём отрезки AB и CD не лежат на параллельных прямых.
а) Докажите, что у тетраэдра ABCD скрещивающиеся рёбра попарно равны.
б) Найдите объём этого тетраэдра, если AC = 6, AD = 8, а радиус цилиндра равен 3.
ОТВЕТ: (frac{{64}}{3}).
8В. Высота конуса равна 6, а радиус основания равен 8.
а) Докажите, что наибольшая площадь сечения конуса плоскостью, проходящей через его вершину, равна 50.
б) Найдите расстояние от центра основания конуса до этой плоскости.
ОТВЕТ: (frac{{6sqrt 7 }}{5}.)
9В. Проведены две параллельные плоскости по одну сторону от центра сферы на расстоянии 3 друг от друга. Эти плоскости дают в сечении две окружности, длины которых равны 18π и 24π.
а) Точка H — ортогональная проекция произвольной точки меньшей окружности на плоскость большей. Докажите, что точка H делит проходящий через неё диаметр большей окружности в отношении 1 : 7.
б) Найдите объём шара, ограниченного данной сферой.
ОТВЕТ: (4500{rm{pi }}).
10В. Плоскость α проходит через диаметр AB сферы. Через произвольную точку M, лежащую на сфере, но не лежащую в плоскости α, проведена плоскость β, перпендикулярная прямой AB. Отрезок CD — общая хорда окружностей сечений сферы плоскостями α и β.
а) Докажите, что (angle ,CMD = 90^circ ).
б) Вершина конуса совпадает с точкой A, а окружность основания — с окружностью сечения сферы плоскостью β. Найдите объём конуса, если диаметр сферы равен 15, а (MB = 3sqrt 5 ).
ОТВЕТ: (144{rm{pi }}).
11В. На окружности основания конуса с вершиной P выбраны точки A и B, делящие окружность на две дуги, длины которых относятся как 1 : 2.
а) Пусть MN — диаметр окружности основания, перпендикулярный хорде AB. Докажите, что объём одной из пирамид PABN и PABM втрое больше объёма другой.
б) Найдите площадь сечения конуса плоскостью ABP, если радиус основания конуса равен 6, а длина его образующей равна 7.
12В. Угол при вершине осевого сечения конуса равен (arccos frac{7}{8}).
а) Докажите, что площадь полной поверхности конуса в пять раз больше площади его основания.
б) Найдите угол в развёртке боковой поверхности.
13В. Радиус основания конуса с вершиной S и центром основания О равен 13, а его высота равна (3sqrt {41} ). Точки А и В – концы образующих, М – середина SA, N – точка в плоскости основания такая, что прямая MN параллельна прямой SB.
а) Докажите, что угол ANO – прямой.
б) Найдите угол между прямой ВМ и плоскостью основания конуса, если АВ = 10.
14В. Два конуса имеют общее основание, причем один из них находится внутри другого. Образующие этих конусов составляют с плоскостью основания углы ({60^ circ }) и ({30^ circ }).
а) Докажите, что вершина меньшего конуса делит высоту большего конуса в отношении (2:1), считая от вершины большего конуса.
б) Найдите объем тела, заключенного между боковыми поверхностями этих конусов, если известно, что сумма высот обоих конусов равна 4.
15В. В конус вписан шар.
а) Докажите, что отношение площади полной поверхности конуса к площади поверхности шара равно отношению их объемов.
б) Найдите угол между образующей конуса и плоскостью основания конуса, если отношение объема конуса к объему вписанного шара равно (frac{9}{4}), а отношение радиуса шара к радиусу основания конуса меньше (frac{3}{5}).
16В. Точки А, В и С лежат на окружности основания конуса с вершиной S, причем А и С диаметрально противоположны. Точка М – середина ВС.
а) Докажите, что прямая SM образует с плоскостью АВС такой же угол, как и прямая АВ с плоскостью SBC.
б) Найдите угол между прямой SA и плоскостью SBC, если АВ = 6, ВС = 8 и (SC = 5sqrt 2 .)
ОТВЕТ: (arcsin frac{{3sqrt {17} }}{{17}}.)
17В. В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А, В и С, а на окружности другого основания – точка С1, причем СС1 – образующая цилиндра, а АС – диаметр основания. Известно, что (angle ACB = {45^ circ },,,,AB = 3sqrt 2 ,,,,C{C_1} = 6.)
а) Докажите, что угол между прямыми АС1 и ВС равен (60^circ ).
б) Найдите расстояние от точки В до прямой АС1.
ОТВЕТ: (frac{{3sqrt 6 }}{2}.)
18В. Полушар и вписанный в него конус имеют общее основание и общую высоту.
а) Докажите, что объем части полушара, лежащей вне конуса равен объему конуса.
б) Через середину высоты конуса проведена плоскость, параллельная основанию. Найдите площадь сечения, заключенного между боковой поверхностью конуса и поверхностью полушара, если радиус полушара равен 4.
19В. На окружности основания конуса с вершиной S отмечены точки A, B и С так, что AB = BC. Медиана АМ треугольника ACS пересекает высоту конуса.
а) Точка N – середина отрезка АС. Докажите, что угол MNB прямой.
б) Найдите угол между прямыми АМ и SB, если (AS = 2,,,,AC = sqrt 6 .)
ОТВЕТ: (arccos frac{5}{{16}}.)
20В. Трапеция ABCD и цилиндр расположены таким образом, что AD — диаметр нижнего основания цилиндра, а точки C и B лежат на окружности верхнего основания и хорда CB равна радиусу основания. Прямая AB образует с плоскостью основания цилиндра угол равный (arccos frac{2}{3}.)
а) Докажите, что в трапецию ABCD можно вписать окружность.
б) Найдите угол между плоскостью основания цилиндра и плоскостью ABCD.
ОТВЕТ: (arccos frac{{sqrt 6 }}{4}.)
21В. Прямоугольник ABCD является осевым сечением цилиндра (AB и CD — образующие). Диаметры AD и KM пересекаются в точке О под прямым углом и (DO = CD.)
а) Докажите, что площадь поверхности цилиндра относится к площади описанной около этого цилиндра сферы как 4 : 5.
б) Найдите площадь сечения цилиндра, проходящего через точки K, M и B, если (AB = 
ОТВЕТ: (32sqrt 2 {rm{pi }}.)
Конус, подготовка к ЕГЭ по математике
- 22.12.2017
Таблицы с теорией на тему: «Конус» для подготовки к ЕГЭ по математике. В кратком содержании изложена вся необходимая теория для этой темы.
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.
Сохранить ссылку:
Комментарии (0)
Добавить комментарий
Добавить комментарий
Комментарии без регистрации. Несодержательные сообщения удаляются.
Имя (обязательное)
E-Mail
Подписаться на уведомления о новых комментариях
Отправить
Цилиндр — это геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны.
Основаниями цилиндра являются два равных круга, высота цилиндра — расстояние между плоскостями оснований.
Рис. (1). Цилиндр, его высота и радиус основания
Площадь боковой поверхности цилиндра находится по формуле
S=2πRh
, где (R) — радиус основания, (h) — высота цилиндра.
Объём цилиндра равен
V=πR2h
, где (R) — радиус основания, (h) — высота цилиндра.
Подробнее о цилиндре:
- элементы цилиндра;
- объём и площадь поверхности цилиндра.
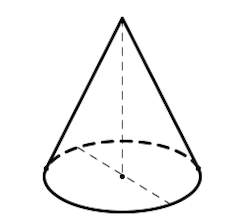
Конус — геометрическое тело, которое получается в результате вращения прямоугольного треугольника вокруг его катета.
Рис. (2). Конус, его высота, образующая и радиус основания
Площадь боковой поверхности конуса находится по формуле
S=πRl
, где (R) — радиус основания, (l) — образующая конуса.
Объём конуса равен
V=13πR2h
, где (R) — радиус основания, (h) — высота конуса.
Подробнее о конусе:
- элементы конуса;
- пощадь поверхности и объём конуса.
Шаром называется геометрическое тело, которое состоит из всех точек пространства, находящихся на расстоянии не больше данного от данной точки.
Поверхность шара называется сферой.
Рис. (3). Шар, его радиус
Площадь поверхности шара (сферы) находится по формуле
S=4πR2
, где (R) — радиус.
Объём шара (сферы) равен
V=43πR3
, где (R) — радиус.
Подробнее о шаре и сфере можно узнать здесь. Все формулы площадей поверхностей и объёмов нужно выучить наизусть.
В задании (8) может встретиться комбинация геометрических тел. Для успешного решения таких задач важно определить их общие точки и соотношение элементов этих тел.
Вписанные и описанные геометрические тела:
- комбинации цилиндра и призмы;
- конус с цилиндром и пирамидой;
- шар и куб, цилиндр, конус.
Источники:
Рис. 1. Цилиндр, его высота и радиус основания. © ЯКласс.
Рис. 2. Конус, его высота, образующая и радиус основания. © ЯКласс.
Рис. 3. Шар, его радиус. © ЯКласс.
Факт 1.
Конус
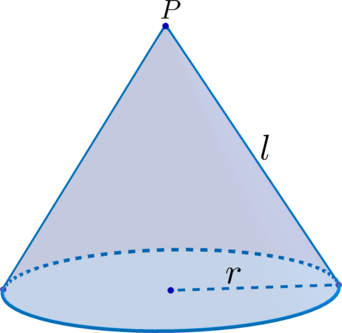
(bullet) Точка (P) – вершина конуса.
(bullet) Отрезок, соединяющий вершину конуса с границей основания, называется образующей (все образующие равны между собой).
(bullet) Отрезок, соединяющий вершину конуса с центром основания-круга, является высотой конуса.
Факт 2.
(bullet) Площадь боковой поверхности конуса [{large{S_{text{бок.пов.}}=pi rl}}] где (r) – радиус основания, (l) – образующая.
(bullet) Площадь полной поверхности конуса – эта сумма площади боковой поверхности и площади основания. [{large{S_{text{полн.пов.}}=pi rl+pi r^2=pi r(r+l)}}] (bullet) Объем конуса [{large{V=dfrac{1}{3}S_{text{осн.}}cdot
h=dfrac{1}{3}pi r^2h}}] где (h) – высота конуса.
(bullet) Заметим, что конус имеет некоторое сходство с пирамидой, только в основании пирамиды лежит многоугольник (граница которого – ломаная), а в основании конуса – круг (граница которого – гладкая).
Поэтому можно сказать, что поверхность пирамиды “ребристая” , а конуса – “гладкая”.