Конус усеченный конус в заданиях егэ по



СДАМ ГИА:

РЕШУ ЕГЭ

Образовательный портал для подготовки к экзаменам

Математика профильного уровня

Математика профильного уровня

≡ Математика

Базовый уровень

Профильный уровень

Информатика

Русский язык

Английский язык

Немецкий язык

Французский язык

Испанский язык

Физика

Химия

Биология

География

Обществознание

Литература

История

Сайты, меню, вход, новости

СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ

Об экзамене

Каталог заданий

Варианты

Ученику

Учителю

Школа

Эксперту

Справочник

Карточки

Теория

Сказать спасибо

Вопрос — ответ

Чужой компьютер

Зарегистрироваться

Восстановить пароль

Войти через ВКонтакте

Играть в ЕГЭ-игрушку

Новости

10 марта

Как подготовиться к ЕГЭ и ОГЭ за 45 дней

6 марта

Изменения ВПР 2023

3 марта

Разместили утвержденное расписание ЕГЭ

27 января

Вариант экзамена блокадного Ленинграда

23 января

ДДОС-атака на Решу ЕГЭ. Шантаж.

6 января

Открываем новый сервис: «папки в избранном»

22 декабря

От­кры­ли но­вый пор­тал Ре­шу Олимп. Для под­го­тов­ки к пе­реч­не­вым олим­пи­а­дам!

4 ноября

Материалы для подготовки к итоговому сочинению 2022–2023

31 октября

Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР

21 марта

Новый сервис: рисование

31 января

Внедрили тёмную тему!

НАШИ БОТЫ

Все новости

ЧУЖОЕ НЕ БРАТЬ!

Экзамер из Таганрога

10 апреля

Предприниматель Щеголихин скопировал сайт Решу ЕГЭ

Наша группа

Поиск

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 1    1–1

Добавить в вариант

Задания Д10 C2 № 505653

В усеченный конус, образующая которого наклонена под углом 45 градусов к нижнему основанию, вписан шар. Найти отношение величины боковой поверхности усеченного конуса к величине поверхности шара.

Источник: А. Ларин: Тренировочный вариант № 50.

Классификатор стереометрии: Комбинации круглых тел, Усеченный конус, Шар

Решение

·

·

Сообщить об ошибке · Помощь

Всего: 1    1–1

О проекте · Редакция · Правовая информация · О рекламе

© Гущин Д. Д., 2011—2023

Источник

09
Сен 2013

Категория: 02 Стереометрия

02. Конус

2013-09-09
2022-09-11

Задача 1. Высота конуса равна 12, образующая равна 14. Найдите его объем, деленный на pi.

u

Решение: + показать

Задача 2. Конус получается при вращении равнобедренного прямоугольного треугольника ABC вокруг катета, равного 6. Найдите его объем, деленный на pi.

задача на конус 2

Решение:  + показать

Задача 3. Высота конуса равна 15, а диаметр основания – 16. Найдите образующую конуса.

uРешение:  + показать

Задача 4. Найдите объем V конуса, образующая которого равна 3 и наклонена к плоскости основания под углом 30°. В ответе укажите frac{V}{pi}.

3

Решение:  + показать

Задача 5. Длина окружности основания конуса равна 5, образующая равна 8. Найдите площадь боковой поверхности конуса.

3

Решение:  + показать

Задача 6. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 9 раз?

4

Решение:  + показать

Задача 7. Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 6 раз?

8

Решение:  + показать

Задача 8. Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 17 раз, а высота останется прежней?

8

Решение:  + показать

Задача 9. Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.

5

Решение:  + показать

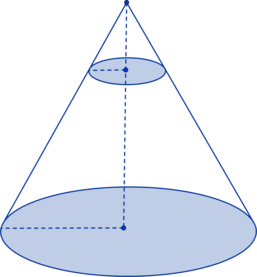
 Задача 10. Объем конуса равен 10. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

6

Решение:  + показать

 Задача 11. Площадь полной поверхности конуса равна 148. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.

6

Решение:  + показать

 Задача 12. Найдите объем V конуса, образующая которого равна 11 и наклонена к плоскости основания под углом 30^{circ}. В ответе укажите frac{V}{pi}.

7

Решение:  + показать

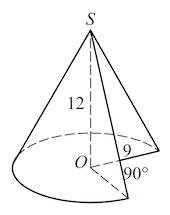
Задача 13. Диаметр основания конуса равен 66, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на pi.

11

Решение:  + показать

Задача 14. Площадь основания конуса равна 36pi, высота — 3. Найдите площадь осевого сечения конуса.

Решение:  + показать

Задача 15. Площадь основания конуса равна 48. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной 15 и 45, считая от вершины. Найдите площадь сечения конуса этой плоскостью.

Решение:  + показать

Задача 16. Найдите объем V части конуса, изображенной на рисунке. В ответе укажите frac{V}{pi}.

Решение:  + показать

Задача 17. Найдите объем V части конуса, изображенной на рисунке. В ответе укажите frac{V}{pi}.

Решение:  + показать

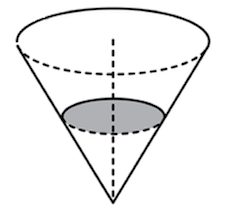
Задача 18. В сосуде, имеющем форму конуса, уровень жидкости достигает frac{1}{2} высоты. Объём жидкости равен 54 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?

v

Решение:  + показать

тест

Вы можете пройти тест

Автор: egeMax |

комментариев 10

Печать страницы

Источник

Слайд 1

Решение задач по теме «Конус» МБОУ «СОШ №1 г.Суздаля» Учитель : Плотникова Татьяна Владимировна

Слайд 2

Тела вращения

Слайд 3

Цилиндр

Слайд 4

Конус

Слайд 5

Усечённый конус

Слайд 6

Цилиндр Конус Усечённый конус Площадь боковой поверхности S бок =2πRh S бок = πRl S бок = πl ( R+R 1 ) Площадь полной поверхности S пол =2 πRh +2π R 2 S пол = πRl +π R 2 S пол = πl ( R+R 1 ) +π R 2 + πR l 2 Объём V= π R 2 h V= π R 2 h V= π h(R 2 + R 1 2 + RR 1 )

Слайд 7

Устные упражнения: Высота конуса равна 4 см, радиус основания – 3 см. Найти образующую конуса. 1 5

Слайд 8

Радиус конуса равен 5 см, образующая равна 8 см. Найдите площадь боковой поверхности конуса. 2 40 π

Слайд 9

Образующая конуса равна 13 см, радиус основания – 5 см. Найдите высоту конуса. 3 12

Слайд 10

Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 3 раза? 4 3

Слайд 11

Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 1,5 раза? 5 2,25

Слайд 12

Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 3 раза? 6 3

Слайд 13

Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшится в 1,5 раза, а образующая останется прежней? 7 1,5

Слайд 14

Высота конуса равна 6, образующая равна 10. Найдите его объем, деленный на π . 8 128

Слайд 15

Конус получается при вращении равнобедренного прямоугольного треугольника АВС вокруг катета, равного 6. Найдите его объем, деленный на π . 9 72

Слайд 16

Радиус основания конуса равен 3, высота равна 4. Найдите площадь полной поверхности конуса, деленную на π . . 10 24

Слайд 17

Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 27. 11 81

Слайд 18

12 Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса. 2

Слайд 19

1. Осевое сечение конуса равносторонний треугольник со стороной 10см. Найти площадь боковой поверхности конуса. 2. Высота конуса 12 см, образующая – 13 см. Найти площадь полной поверхности конуса. Работа в парах: 50 π 90 π 3. Высота конуса равна 2√3 см. Найдите площадь боковой поверхности и площадь осевого сечения конуса, если оно является правильным треугольником. 8π, 2√3

Слайд 20

Диаметр основания конуса равен 6, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на π . 9

Слайд 21

Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на π . . 16

Слайд 22

Длина окружности основания конуса равна 3, образующая равна 2. Найдите площадь боковой поверхности конуса. 6

Слайд 23

Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах. 60

Слайд 24

Площадь полной поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса. 3

Слайд 25

Найдите объем части конуса, изображенной на рисунке. В ответе укажите . 87,75

Слайд 26

. Найдите объем части конуса, изображенной на рисунке. В ответе укажите 243

Слайд 27

В сосуде, имеющем форму конуса, уровень жидкости достигает высоты. Объём жидкости равен 70 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд? 490

Слайд 28

Цилиндр и конус имеют общее основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна Найдите площадь боковой поверхности конуса. 3

Слайд 29

Конусообразная палатка высотой 3,5 м и диаметром основания 4 м покрыта парусиной. Сколько квадратных метров парусины пошло на палатку? Образующая конуса , что примерно составляет 8,06 м. Тогда площадь боковой поверхности конуса равна что примерно составляет 5,3 м 2 . На палатку пошло примерно 25,3 м 2 парусины. Ответ: 25,3 м 2 Решение. 25,3

Слайд 30

Домашнее задание: Подобрать по теме «Конус» 5 задач из банка данных по математике и решить их . Дополнительные задачи: Радиусы оснований усеченного конуса 10√3 и 6√3 , а образующая наклонена к плоскости основания под углом 60 о . Найти высоту усеченного конуса. Отношение площадей боковой и полной поверхности конуса равно Найти угол между образующей и плоскостью основания конуса .

Слайд 31

Источники: http://reshuege.ru/?theme=144&print=true — КАТАЛОГ ЗАДАНИЙ Геометрия, 10–11класс: Учебник для общеобразовательных учреждений: базовый и профильный уровни / Л.С. Атанасян , В.Ф. Бутузов, С.Б. Кадомцев и др. – М.: Просвещение, 2011.

Источник

Цели  урока:

  • Обучающие:
    • формировать умения применять понятия конуса, усечённого конуса и формулы для вычисления площади боковой поверхности, объёма при решении задач в контексте ЕГЭ;
    • рассмотреть задачи на комбинации тел и «найти подход» к решению таких задач.
  • Развивающие:
    • способствовать развитию умений учащихся обобщать полученные знания, проводить анализ синтез, сравнения, делать необходимые выводы при решении задач разного уровня сложности.
    • способствовать развитию умений творческого подхода к решению практической задачи.
  • Воспитательные:
    • обеспечить условия для воспитания положительного интереса к изучаемому предмету через решение практико-ориентированных задач.
    • обеспечить благоприятную психологическую  атмосферу для развития  творческих  способностей.
    • совершенствование математической речи, математического языка.

ХОД УРОКА

1. Организационный этап: Здравствуйте, ребята, садитесь! Начнем урок.

(Приложение 1, слайд №1)

2. Этап проверки домашнего задания и выравнивания знаний:

Предлагаю начать работу на уроке с устного опроса.

  1. Какие фигуры относятся к телам вращения? (слайд №2)
  2. Почему их так называют?
  3. Назвать основные элементы цилиндра, конуса. (слайд №3,4,5)
  4. Какие виды сечений может иметь цилиндр, конус?
  5. Что подразумевается под понятием «площади боковой и полной поверхности» тел вращения?
  6. Формулы для нахождения площади боковой поверхности, площади полной поверхности, объёма цилиндра, конуса, усечённого конуса.(слайд №6)
 

Цилиндр

Конус

Усечённый конус

Площадь боковой поверхности

Sбок = 2πRh

Sбок = πRl

Sбок = πl(R + R1)

Площадь полной поверхности

Sпол = 2πRh + 2πR2

Sпол = πRl + πR2

Sпол = πl(R + R1) + πR2 + πRl2

Объём

V= πR2h

V=  πR2h

V=  πh(R2+R12+RR1)

Откройте тетради с письменным домашним заданием. На прошлом уроке вам были заданы 2 задачи для самостоятельного решения. Сейчас проверим правильность выполнения домашнего задания, постараемся устранить в ходе проверки обнаруженные пробелы в знаниях (если такие имеют место!!!).

Задачи письменной  домашней работы

Домашняя работа проверяется фронтально. Обсуждаются вопросы и затруднения при выполнении этих задач.

Задача №1. Осевое сечение цилиндра – квадрат, площадь основания цилиндра равна 16π см2. Найти площадь поверхности цилиндра.
В результате проверки, выясняем, что радиус основания цилиндра равен 4 см, а высота цилиндра – 8 см. Тогда площадь поверхности цилиндра равна 96π см2.

Ответ.  96π см2

Задача №2: В цилиндрический сосуд налили 6 куб. см воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился в 1,5 раза. Найдите объём детали. Ответ выразите в куб. см.
В результате проверки, выясняем, что высота воды в цилиндре  равен 9 см, а произведение  R2= 1 см. Тогда объём детали будет равен 3 см3.

Ответ.  3 см3.

3. «Блиц-опрос»: Устные упражнения:

  1. Высота конуса 4 см, радиус основания – 3 см. Найти образующую конуса. (слайд №7)
  2. Радиус конуса 5 см, образующая – 8 см. Найти боковую поверхность конуса. (слайд №8)
  3. Образующая конуса равна 13 см, радиус основания – 5 см. Найдите высоту конуса. (слайд №9)
  4. Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 3 раза? (слайд №10)
  5. Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 1,5 раза? (слайд №11)
  6. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 3 раза? (слайд №12)
  7. Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшится в 1,5 раза, а образующая останется прежней? (слайд №13)
  8. Высота конуса равна 6, образующая равна 10. Найдите его объем, деленный на π. (слайд №14)
  9. Конус получается при вращении равнобедренного прямоугольного треугольника  АВС вокруг катета, равного 6. Найдите его объем, деленный на π . (слайд №15)
  10. Радиус основания конуса равен 3, высота равна 4. Найдите площадь полной поверхности конуса, деленную на  π. (слайд №16)
  11. Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 27. (слайд №17)
  12. Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса. (слайд №18)

4. «Тяжело в учении, легко на ЕГЭ». Работа в парах:

Задачи.

  1. Осевое сечение конуса равносторонний треугольник со стороной 10см. Найти площадь боковой поверхности конуса. (слайд №19)
  2. Высота конуса 12 см, образующая – 13 см. Найти площадь полной поверхности конуса.  ( Слайд №19)
  3. Высота конуса равна 2√3 см. Найдите площадь боковой поверхности и площадь осевого сечения конуса, если оно является правильным треугольником. (слайд №19)

5. Задачи по теме «Конус» в формате ЕГЭ (задачи решаем фронтально)

6. Итог урока

– Задачи,  с какими фигурами мы сегодня решали.

7. Домашнее задание: подобрать по теме «Конус» 5 задач из банка данных по математике и решить их.

Дополнительные задачи:

  1. Радиусы оснований усеченного конуса 10√3 и 6√3, а образующая наклонена к плоскости основания под углом 60о. Найти высоту усеченного конуса.
  2. Отношение площадей боковой и полной поверхности конуса равно   Найти угол между образующей и плоскостью основания конуса.

Ребята, спасибо за работу на уроке. Вам я желаю хорошо подготовиться и успешно сдать единый государственный экзамен. Урок окончен.

Источник

8. Геометрия в пространстве (стереометрия)


1. Вспоминай формулы по каждой теме


2. Решай новые задачи каждый день


3. Вдумчиво разбирай решения

Задачи по теме «Конус»

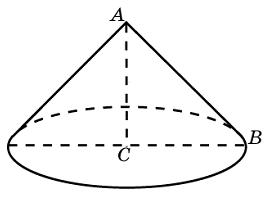
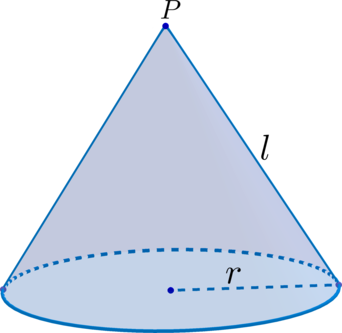
(blacktriangleright) Точка (P) – вершина конуса.

(blacktriangleright) Отрезок, соединяющий вершину конуса с границей основания, называется образующей (все образующие равны между собой).

(blacktriangleright) Отрезок, соединяющий вершину конуса с центром основания-круга, является высотой конуса.

(blacktriangleright) Площадь боковой поверхности конуса ({large{S_{text{бок.пов.}}=pi rl}}), где (r) – радиус основания, (l) – образующая.

(blacktriangleright) Площадь полной поверхности конуса – эта сумма площади боковой поверхности и площади основания. [{large{S_{text{полн.пов.}}=pi rl+pi r^2=pi r(r+l)}}]

(blacktriangleright) Объем конуса ({large{V=dfrac{1}{3}S_{text{осн.}}cdot h=dfrac{1}{3}pi
r^2h}}), где (h) – высота конуса.

Заметим, что конус имеет некоторое сходство с пирамидой, только в основании пирамиды лежит многоугольник (граница которого – ломаная), а в основании конуса – круг (граница которого – гладкая).
Поэтому можно сказать, что поверхность пирамиды “ребристая” , а конуса – “гладкая”.


Задание
1

#1886

Уровень задания: Равен ЕГЭ

Площадь боковой поверхности конуса равна (48pi), а площадь основания равна (36pi). Найдите длину образующей конуса.

Если радиус окружности, лежащей в основании конуса обозначить за (r), а длину образующей за (l), то площадь основания и площадь боковой поверхности конуса выразятся по формулам: (S_{text{осн.}} =
pi r^2), (S_{text{бок.пов.}} = pi r l). Из первой формулы следует: (pi r^2 = 36pi) (Rightarrow) (r^2 = 36) (Rightarrow) (r
= 6) (Rightarrow) (6pi l = 48pi) (Rightarrow) (6l = 48) (Rightarrow) (l = 8) .

Ответ: 8


Задание
2

#1887

Уровень задания: Равен ЕГЭ

Площадь боковой поверхности конуса равна (48pi), а площадь боковой поверхности усеченного конуса с такими же основанием и углом наклона образующей к плоскости основания равна (36pi). Найдите высоту усеченного конуса, если высота исходного конуса равна (10).

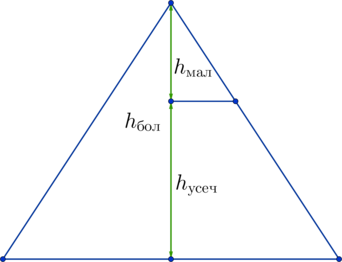
Площадь боковой поверхности меньшего конуса, который дополняет усеченный конус до полного, равна разности их площадей поверхностей: (S_{text{мал}} = 48pi — 36pi = 12pi). Отношение площадей боковых поверхностей большого и малого конусов равно квадрату коэффициента подобия между ними: [frac{S_{text{бол}}}{S_{text{мал}}} = k^2 =
frac{48pi}{12pi} = 4Rightarrow k = 2]

Тогда высоты конусов относятся друг к другу: (dfrac{h_{text{бол}}}{h_{text{мал}}} = dfrac{10}{h_{text{мал}}}
= k = 2). Тогда

[h_{text{мал}} = 5Rightarrow h_{text{усеч}} = h_{text{бол}}
— h_{text{мал}} = 10 — 5 = 5]

Ответ: 5


Задание
3

#962

Уровень задания: Сложнее ЕГЭ

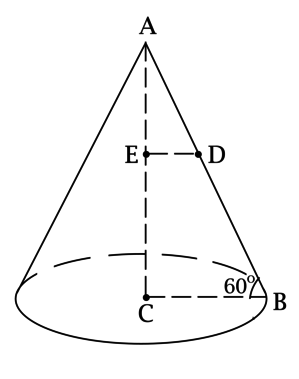
На высоте конуса с вершиной (A), центром основания (C) и радиусом основания (R = 4) отметили точку (E) такую, что расстояние от неё до основания равно (sqrt{3}(4-pi^{-0,5})). Известно, что угол между образующей конуса и плоскостью основания равен (60^circ). Найдите площадь сечения (T) конуса, проходящего через точку (E) и параллельного основанию конуса.

Рассмотрим треугольник (ABC), где (B) – некоторая точка на окружности основания. Так как (AC) – высота конуса, то (ACperp CB), тогда (angle CAB = 90^circ — angle ABC = 30^circ), следовательно, (AB = 2CB = 8) . По теореме Пифагора [AC = sqrt{AB^2 — CB^2} = 4sqrt{3}.]

Обозначим через (D) точку пересечения плоскости сечения (T) и (AB). Рассмотрим треугольник (AED): [AE = AC — CE = 4sqrt{3} — sqrt{3}(4 — pi^{-0,5}) = sqrt{dfrac{3}{pi}}.]

Так как сечение (T) параллельно плоскости основания, а (AC) – высота конуса, то (ACperp ED), тогда (triangle AED) – прямоугольный и (angle EAD = 30^circ), откуда [ED = AEcdot mathrm{tg}, angle EAD = sqrt{dfrac{3}{pi}}cdot dfrac{1}{sqrt{3}} = dfrac{1}{sqrt{pi}} = r] – радиус сечения (T).

Таким образом, площадь сечения (T) равна (pi r^2 = picdotdfrac{1}{pi} = 1).

Ответ: 1


Задание
4

#963

Уровень задания: Сложнее ЕГЭ

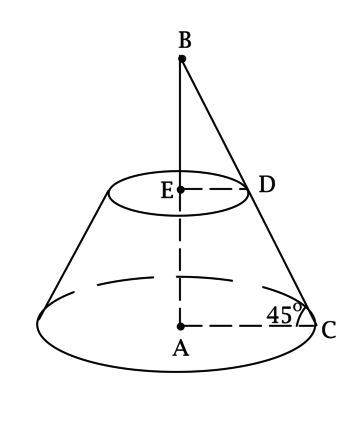
Радиусы оснований усечённого конуса равны [r = dfrac{2}{sqrt[4]{2}sqrt{pi}}qquad text{и}qquad R = dfrac{10}{sqrt[4]{2}sqrt{pi}},] а угол между его образующей и основанием равен (45^circ). Найдите площадь боковой поверхности этого усечённого конуса.

Обозначим центры оснований усечённого конуса через (A) и (E), так что (A) – центр большего основания. Отметим на большем основании точку (C), а точку меньшего основания, через которую проходит образующая, выходящая из (C), обозначим через (D).

Высота (AE) и образующая (CD) лежат в одной плоскости. Обозначим точку их пересечения через (B).

Так как (AE) – высота, то (AEperp CD) и (AEperp AC).

Рассмотрим прямоугольный треугольник (BAC):
в нём (angle BCA = 45^circ), тогда [AB = R = dfrac{10}{sqrt[4]{2}sqrt{pi}},qquadqquad BC = Rsqrt{2} = dfrac{10sqrt{2}}{sqrt[4]{2}sqrt{pi}}.]

Рассмотрим прямоугольный треугольник (BED):
так как (angle EBD = 45^circ), то [BE = r = dfrac{2}{sqrt[4]{2}sqrt{pi}},qquadqquad BD = rsqrt{2} = dfrac{2sqrt{2}}{sqrt[4]{2}sqrt{pi}},] тогда (EA = AB — BE = R — r), (DC = BC — BD = Rsqrt{2} — rsqrt{2} = sqrt{2}(R — r)). [S_{text{бок}} = pi(R + r)cdot I,] где (I) – образующая, тогда [S_{text{бок}} = pi(R + r)cdotsqrt{2}(R — r) = sqrt{2}pi(R^2 — r^2) = sqrt{2}pileft(dfrac{100}{sqrt{2}pi} — dfrac{4}{sqrt{2}pi}right) = 96.]

Ответ: 96

Старшеклассникам, которые готовятся к сдаче ЕГЭ по математике, непременно стоит научиться вычислять площадь и другие неизвестные параметры конуса. Как показывает практика предыдущих лет, подобные задания из раздела «Геометрия в пространстве» вызывают у выпускников определенные сложности.

При этом понимать, как найти площадь боковой поверхности или, к примеру, сечения конуса, параллельного основанию, должны все учащиеся, независимо от уровня их подготовки. Это позволит им успешно пройти аттестационное испытание по математике.

Базовая информация, которую стоит запомнить

  • Конус представляет собой геометрическое тело, которое образовано совокупностью круга, точки, находящейся вне его плоскости, и лучей, соединяющих заданную точку с точками круга. Его высотой называется перпендикуляр, который опущен из вершины на плоскость основания.
  • Все образующие конуса равны между собой.
  • Осевое сечение конуса представляет собой равнобедренный треугольник. Основание этой фигуры равняется двум радиусам. Боковые стороны треугольника равны образующим конуса.

Занимайтесь вместе с сайтом «Школково»!

Чтобы не допускать распространенных ошибок при решении задач по теме «Конус», выбирайте наш математический портал. Здесь есть весь необходимый материал для изучения разделов, требующих повторения.

Специалисты образовательного проекта «Школково» предлагают новый подход к подготовке к экзамену, предполагающий переход от простого к сложному. Вначале мы даем полную теорию, основные формулы и элементарные практические задачи с решением, в том числе и по теме «Конус», а затем постепенно переходим к заданиям экспертного уровня, которые также встречаются в ЕГЭ. Вся необходимая информация представлена в разделе «Теоретическая справка».

Вы также можете сразу приступить к решению онлайн-задач на вычисление высоты усеченного конуса, площади его боковой поверхности, объема, а также похожих задач на вычисление, например, нахождению объема или площади сечения куба. Большая база упражнений представлена в разделе «Каталог». Перечень заданий систематически обновляется.

Проверьте, насколько легко вы сможете определить площадь конуса в режиме онлайн. Если упражнение потребовало от вас минимальных усилий, рекомендуем вам не тратить время на простые задачи и переходить к более сложным. А если затруднения все же возникли, тогда вам непременно стоит находить время в своем ежедневном расписании на дистанционные занятия вместе со «Школково». С нами вы сможете быстро усвоить алгоритм решения задач на расчет объема конуса и других неизвестных параметров.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Решение
задач в контексте ЕГЭ по теме «Конус»

Цели  урока:

·          
Обучающие:

o    формировать
умения применять понятия конуса, усечённого конуса и формулы для вычисления
площади боковой поверхности, объёма при решении задач в контексте ЕГЭ;

o    рассмотреть
задачи на комбинации тел и «найти подход» к решению таких задач.

·          
Развивающие:

o    способствовать
развитию умений учащихся обобщать полученные знания, проводить анализ синтез,
сравнения, делать необходимые выводы при решении задач разного уровня
сложности.

o    способствовать
развитию умений творческого подхода к решению практической задачи.

·          
Воспитательные:

o    обеспечить
условия для воспитания положительного интереса к изучаемому предмету через
решение практико-ориентированных задач.

o    обеспечить
благоприятную психологическую  атмосферу для развития 
творческих  способностей.

o    совершенствование
математической речи, математического языка.

Форма
проведения урока: урок закрепления и совершенствования
знаний.

ХОД
УРОКА

1. Организационный
этап: Здравствуйте,
ребята, садитесь! Начнем урок.

2. Этап проверки
домашнего задания и выравнивания знаний:

Предлагаю начать
работу на уроке с устного опроса.

1)       
Какое геометрическое тело называется
конусом?

2)       
Назовите сечения конуса различными
плоскостями?

3)       
Что нужно знать, чтобы найти объем конуса?

4)       
Как вычислить объем конуса?

Заполнение
опорных листочков. (Заранее раздается каждому ученику листочек – заготовка.
По желанию, ученики могут сами себе изготовить опорные листочки).

Конус

Усеченный конус

http://открытыйурок.рф/%D1%81%D1%82%D0%B0%D1%82%D1%8C%D0%B8/568841/img5.gif

l –
h –
r –
S бок =
V =

http://открытыйурок.рф/%D1%81%D1%82%D0%B0%D1%82%D1%8C%D0%B8/568841/img6.gif

r –
r1 –
h –
l –
S бок =
V =

3. Задачи по теме «Конус» в формате ЕГЭ (задачи
решаем фронтально)

1.       
Высота
конуса 4 см, радиус основания – 3 см. Найти образующую конуса. (слайд №5)

2.       
Радиус
конуса 5 см, образующая – 8 см. Найти боковую поверхность конуса. (слайд №6)

3.       
Образующая
конуса равна 13 см, радиус основания – 5 см. Найдите высоту конуса. (слайд №7)

4.       
Во
сколько раз уменьшится объем конуса, если его высоту уменьшить в 3 раза? (слайд
№8)

5.       
Во
сколько раз увеличится объем конуса, если его радиус основания увеличить в 1,5
раза? (слайд №9)

6.       
Во
сколько раз увеличится площадь боковой поверхности конуса, если его образующую
увеличить в 3 раза? (слайд №10)

7.       
Во
сколько раз уменьшится площадь боковой поверхности конуса, если радиус его
основания уменьшится в 1,5 раза, а образующая останется прежней? (слайд №11)

8.       
Высота
конуса равна 6, образующая равна 10. Найдите его объем, деленный на π. (слайд
№12)

9.       
Конус
получается при вращении равнобедренного прямоугольного треугольника  АВС
вокруг катета, равного 6. Найдите его объем, деленный на π . (слайд №13)

10.    Радиус
основания конуса равен 3, высота равна 4. Найдите площадь полной поверхности
конуса, деленную на  π. (слайд №14)

11.    Объем
конуса равен 16. Через середину высоты параллельно основанию конуса проведено
сечение, которое является основанием меньшего конуса с той же вершиной. Найдите
объем меньшего конуса(слайд №15).

12.    В сосуде,
имеющем форму конуса, уровень жидкости достигает   высоты. Объём жидкости равен
70 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить
сосуд? (слайд №16)

13.    В сосуде,
имеющем форму конуса, уровень жидкости достигает   высоты. Объём жидкости равен
70 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью
наполнить сосуд? (слайд №17)

4. Решение  практических
задач по теме “Объем конуса”.

Задача 1. Куча
щебня имеет коническую форму, радиус основания которой 2 м и образующая 3,5 м.
Сколько надо возов, чтобы перевезти щебень, уложенный в кучу?

1 м3
щебня весит 3 т. На один воз грузят 0,5 т.

Решение.

Дано: конус,
(рисунок 5)

ОА = 2м,
АР = 3,5м,
1м3 = 3т,
1 воз = 0,5 т.

http://открытыйурок.рф/%D1%81%D1%82%D0%B0%D1%82%D1%8C%D0%B8/568841/img11.gif

Рисунок
1

Найти: количество
возов.

Решение: V =http://открытыйурок.рф/%D1%81%D1%82%D0%B0%D1%82%D1%8C%D0%B8/568841/Image4568.gif

Найдем высоту:

h =http://открытыйурок.рф/%D1%81%D1%82%D0%B0%D1%82%D1%8C%D0%B8/568841/Image4569.gifм
http://открытыйурок.рф/%D1%81%D1%82%D0%B0%D1%82%D1%8C%D0%B8/568841/Image4570.gifм,
тогда
V = http://открытыйурок.рф/%D1%81%D1%82%D0%B0%D1%82%D1%8C%D0%B8/568841/Image4571.gif=
12 м3,
12м3 • 3 т = 36 т в одной куче щебня,
36 : 0,5 = 72 воза потребуется.

Ответ: 72 воза.

Задача
2.  Авиационная бомба 
среднего калибра дает при взрыве воронку диаметром 6 м и глубиной
2 м.  Какое  количество земли (по массе) выбрасывает эта бомба, если
1 м3 земли имеет массу 1650 кг?  (Слайд 9)

Решение.

Так
как диаметр воронки 6 м и глубина 2 м, то радиус полученного конуса составляет
3 м, а высота – 2 м.

Составим
математическую модель задачи.

Найдем объем конуса:

Масса выброшенной земли
составляет

 кг31 т.

Ответ:
31 т

5.
Самостоятельная работа 30 мин

6.Домашнее задание

№1 Образующая
конуса L наклонена к плоскости основания под углом в 300. Найдите
высоту. Ответ: 2L.

№2: В
цилиндрический сосуд налили 6 куб. см воды. В воду полностью погрузили деталь.
При этом уровень жидкости в сосуде увеличился в 1,5 раза. Найдите объём детали.
Ответ выразите в куб. см.
В результате проверки, выясняем, что высота воды в цилиндре  равен 9 см, а
произведение http://открытыйурок.рф/%D1%81%D1%82%D0%B0%D1%82%D1%8C%D0%B8/659574/img3.gif R2=
1 см. Тогда объём детали будет равен 3 см3.

        Ответ.  3
см3.

№3 Осевое
сечение конуса равносторонний треугольник со стороной 10см. Найти площадь
боковой поверхности конуса.)

№4 Высота
конуса 12 см, образующая – 13 см. Найти площадь полной поверхности
конуса. )

№5 Высота
конуса равна 6, радиус основания равен 8. Найдите боковую поверхность. Ответ:
80.

Источник

Самостоятельная работа по теме «Конус»

I вариант

  1. Вы­со­та ко­ну­са равна 8, а диа­метр ос­но­ва­ния — 30. Най­ди­те об­ра­зу­ю­щую ко­ну­са.

  2. Вы­со­та ко­ну­са равна 21, а длина об­ра­зу­ю­щей — 75. Най­ди­те диа­метр ос­но­ва­ния ко­ну­са.

  3. Диа­метр ос­но­ва­ния ко­ну­са равен 144, а длина об­ра­зу­ю­щей — 75. Най­ди­те вы­со­ту ко­ну­са.

  4. Пло­щадь ос­но­ва­ния ко­ну­са равна 36π, вы­со­та — 3. Най­ди­те пло­щадь осе­во­го се­че­ния ко­ну­са.

  5. Пло­щадь ос­но­ва­ния ко­ну­са равна 9. Плос­кость, па­рал­лель­ная плос­ко­сти ос­но­ва­ния ко­ну­са, делит его вы­со­ту на от­рез­ки дли­ной 3 и 6, счи­тая от вер­ши­ны. Най­ди­те пло­щадь се­че­ния ко­ну­са этой плос­ко­стью.

  6. Вы­со­та ко­ну­са равна 28, а длина об­ра­зу­ю­щей — 35. Най­ди­те пло­щадь осе­во­го се­че­ния этого ко­ну­са.

  7. Диа­метр ос­но­ва­ния ко­ну­са равен 42, а длина об­ра­зу­ю­щей — 35. Най­ди­те пло­щадь осе­во­го се­че­ния этого ко­ну­са.

  8. Длина окруж­но­сти ос­но­ва­ния ко­ну­са равна 3, об­ра­зу­ю­щая равна 2. Най­ди­те пло­щадь бо­ко­вой по­верх­но­сти ко­ну­са.

  9. Вы­со­та ко­ну­са равна 20, об­ра­зу­ю­щая равна 25. Най­ди­те пло­щадь его пол­ной по­верх­но­сти, де­лен­ную на .

  10. Пло­щадь пол­ной по­верх­но­сти ко­ну­са равна 108. Па­рал­лель­но ос­но­ва­нию ко­ну­са про­ве­де­но се­че­ние, де­ля­щее вы­со­ту по­по­лам. Най­ди­те пло­щадь пол­ной по­верх­но­сти от­се­чен­но­го ко­ну­са.

  11. Пло­щадь бо­ко­вой по­верх­но­сти ко­ну­са в  раз боль­ше пло­ща­ди ос­но­ва­ния. Най­ди­те угол между об­ра­зу­ю­щей ко­ну­са и плос­ко­стью ос­но­ва­ния. Ответ дайте в гра­ду­сах.

  12. Ра­ди­ус ос­но­ва­ния ко­ну­са равен 12, вы­со­та равна 16. Най­ди­те пло­щадь пол­ной по­верх­но­сти ко­ну­са, де­лен­ную на .

  13. Объем ко­ну­са равен 16. Через се­ре­ди­ну вы­со­ты па­рал­лель­но ос­но­ва­нию ко­ну­са про­ве­де­но се­че­ние, ко­то­рое яв­ля­ет­ся ос­но­ва­ни­ем мень­ше­го ко­ну­са с той же вер­ши­ной. Най­ди­те объем мень­ше­го ко­ну­са.

  1. Най­ди­те объем V ко­ну­са, об­ра­зу­ю­щая ко­то­ро­го равна 3 и на­кло­не­на к плос­ко­сти ос­но­ва­ния под углом 30. В от­ве­те ука­жи­те .

  2. Диа­метр ос­но­ва­ния ко­ну­са равен 66, а угол при вер­ши­не осе­во­го се­че­ния равен 90°. Вы­чис­ли­те объем ко­ну­са, де­лен­ный на .

  3. Конус по­лу­ча­ет­ся при вра­ще­нии рав­но­бед­рен­но­го пря­мо­уголь­но­го тре­уголь­ни­ка ABC во­круг ка­те­та, рав­но­го 15. Най­ди­те его объем, де­лен­ный на .

  4. Вы­со­та ко­ну­са равна 3, об­ра­зу­ю­щая равна 6. Най­ди­те его объем, де­лен­ный на .

  5. В со­су­де, име­ю­щем форму ко­ну­са, уро­вень жид­ко­сти до­сти­га­ет  вы­со­ты. Объём жид­ко­сти равен 54 мл. Сколь­ко мил­ли­лит­ров жид­ко­сти нужно до­лить, чтобы пол­но­стью на­пол­нить сосуд?

  6. Най­ди­те объем V части ко­ну­са, изоб­ра­жен­ной на ри­сун­ке. В от­ве­те ука­жи­те .

  1. Во сколь­ко раз умень­шит­ся объем ко­ну­са, если его вы­со­ту умень­шить в 18,5 раза?

  2. Во сколь­ко раз уве­ли­чит­ся объем ко­ну­са, если его ра­ди­ус ос­но­ва­ния уве­ли­чить в 2,5 раза?

  3. Во сколь­ко раз умень­шит­ся пло­щадь бо­ко­вой по­верх­но­сти ко­ну­са, если ра­ди­ус его ос­но­ва­ния умень­шить в 8 раз?

  4. Во сколь­ко раз уве­ли­чит­ся пло­щадь бо­ко­вой по­верх­но­сти ко­ну­са, если его об­ра­зу­ю­щую уве­ли­чить в 36 раз?

Самостоятельная работа по теме «Конус»

II вариант

  1. Вы­со­та ко­ну­са равна 5, а диа­метр ос­но­ва­ния – 24. Най­ди­те об­ра­зу­ю­щую ко­ну­са.

  2. Вы­со­та ко­ну­са равна 72, а длина об­ра­зу­ю­щей — 90. Най­ди­те диа­метр ос­но­ва­ния ко­ну­са.

  3. Диа­метр ос­но­ва­ния ко­ну­са равен 108, а длина об­ра­зу­ю­щей — 90. Най­ди­те вы­со­ту ко­ну­са.

  4. Пло­щадь ос­но­ва­ния ко­ну­са равна 36π, вы­со­та — 10. Най­ди­те пло­щадь осе­во­го се­че­ния ко­ну­са.

  5. Пло­щадь ос­но­ва­ния ко­ну­са равна 32. Плос­кость, па­рал­лель­ная плос­ко­сти ос­но­ва­ния ко­ну­са, делит его вы­со­ту на от­рез­ки дли­ной 9 и 27, счи­тая от вер­ши­ны. Най­ди­те пло­щадь се­че­ния ко­ну­са этой плос­ко­стью.

  6. Вы­со­та ко­ну­са равна 8, а длина об­ра­зу­ю­щей — 10. Най­ди­те пло­щадь осе­во­го се­че­ния этого ко­ну­са.

  7. Диа­метр ос­но­ва­ния ко­ну­са равен 36, а длина об­ра­зу­ю­щей — 30. Най­ди­те пло­щадь осе­во­го се­че­ния этого ко­ну­са.

  8. Длина окруж­но­сти ос­но­ва­ния ко­ну­са равна 7, об­ра­зу­ю­щая равна 2. Най­ди­те пло­щадь бо­ко­вой по­верх­но­сти ко­ну­са.

  9. Вы­со­та ко­ну­са равна 36, об­ра­зу­ю­щая равна 45. Най­ди­те пло­щадь его пол­ной по­верх­но­сти, де­лен­ную на .

  10. Пло­щадь пол­ной по­верх­но­сти ко­ну­са равна 164. Па­рал­лель­но ос­но­ва­нию ко­ну­са про­ве­де­но се­че­ние, де­ля­щее вы­со­ту по­по­лам. Най­ди­те пло­щадь пол­ной по­верх­но­сти от­се­чен­но­го ко­ну­са.

  11. Пло­щадь бо­ко­вой по­верх­но­сти ко­ну­са в два раза боль­ше пло­ща­ди ос­но­ва­ния. Най­ди­те угол между об­ра­зу­ю­щей ко­ну­са и плос­ко­стью ос­но­ва­ния. Ответ дайте в гра­ду­сах.

  12. Ра­ди­ус ос­но­ва­ния ко­ну­са равен 28, вы­со­та равна 21. Най­ди­те пло­щадь пол­ной по­верх­но­сти ко­ну­са, де­лен­ную на .

  13. Объем ко­ну­са равен 10. Через се­ре­ди­ну вы­со­ты па­рал­лель­но ос­но­ва­нию ко­ну­са про­ве­де­но се­че­ние, ко­то­рое яв­ля­ет­ся ос­но­ва­ни­ем мень­ше­го ко­ну­са с той же вер­ши­ной. Най­ди­те объем мень­ше­го ко­ну­са.

  1. Най­ди­те объем V ко­ну­са, об­ра­зу­ю­щая ко­то­ро­го равна 44 и на­кло­не­на к плос­ко­сти ос­но­ва­ния под углом 300. В от­ве­те ука­жи­те .

  2. Диа­метр ос­но­ва­ния ко­ну­са равен 6, а угол при вер­ши­не осе­во­го се­че­ния равен 90°. Вы­чис­ли­те объем ко­ну­са, де­лен­ный на π.

  3. Конус по­лу­ча­ет­ся при вра­ще­нии рав­но­бед­рен­но­го пря­мо­уголь­но­го тре­уголь­ни­ка ABC во­круг ка­те­та, рав­но­го 6. Най­ди­те его объем, де­лен­ный на .

  4. Вы­со­та ко­ну­са равна 12, об­ра­зу­ю­щая равна 15. Най­ди­те его объем, де­лен­ный на .

  5. В со­су­де, име­ю­щем форму ко­ну­са, уро­вень жид­ко­сти до­сти­га­ет  вы­со­ты. Объём жид­ко­сти равен 14 мл. Сколь­ко мил­ли­лит­ров жид­ко­сти нужно до­лить, чтобы на­пол­нить сосуд до­вер­ху?

  6. Най­ди­те объем V части ко­ну­са, изоб­ра­жен­ной на ри­сун­ке. В от­ве­те ука­жи­те .

  1. Во сколь­ко раз умень­шит­ся объем ко­ну­са, если его вы­со­ту умень­шить в 20 раз?

  2. Во сколь­ко раз уве­ли­чит­ся объем ко­ну­са, если его ра­ди­ус ос­но­ва­ния уве­ли­чить в 3,5 раза?

  3. Во сколь­ко раз умень­шит­ся пло­щадь бо­ко­вой по­верх­но­сти ко­ну­са, если ра­ди­ус его ос­но­ва­ния умень­шить в 19 раз?

  4. Во сколь­ко раз уве­ли­чит­ся пло­щадь бо­ко­вой по­верх­но­сти ко­ну­са, если его об­ра­зу­ю­щую уве­ли­чить в 11 раз?

Самостоятельная работа по теме «Конус»

III вариант

  1. Вы­со­та ко­ну­са равна 15, а диа­метр ос­но­ва­ния – 16. Най­ди­те об­ра­зу­ю­щую ко­ну­са.

  2. Вы­со­та ко­ну­са равна 57, а длина об­ра­зу­ю­щей — 95. Най­ди­те диа­метр ос­но­ва­ния ко­ну­са.

  3. Диа­метр ос­но­ва­ния ко­ну­са равен 42, а длина об­ра­зу­ю­щей равна 75. Най­ди­те вы­со­ту ко­ну­са.

  4. Пло­щадь ос­но­ва­ния ко­ну­са равна , вы­со­та — 9. Най­ди­те пло­щадь осе­во­го се­че­ния ко­ну­са.

  5. Пло­щадь ос­но­ва­ния ко­ну­са равна 48. Плос­кость, па­рал­лель­ная плос­ко­сти ос­но­ва­ния ко­ну­са, делит его вы­со­ту на от­рез­ки дли­ной 15 и 45, счи­тая от вер­ши­ны. Най­ди­те пло­щадь се­че­ния ко­ну­са этой плос­ко­стью.

  6. Вы­со­та ко­ну­са равна 36, а длина об­ра­зу­ю­щей — 39. Най­ди­те пло­щадь осе­во­го се­че­ния этого ко­ну­са.

  7. Диа­метр ос­но­ва­ния ко­ну­са равен 30, а длина об­ра­зу­ю­щей — 25. Най­ди­те пло­щадь осе­во­го се­че­ния этого ко­ну­са.

  8. Длина окруж­но­сти ос­но­ва­ния ко­ну­са равна 6, об­ра­зу­ю­щая равна 2. Най­ди­те пло­щадь бо­ко­вой по­верх­но­сти ко­ну­са.

  9. Вы­со­та ко­ну­са равна 21, об­ра­зу­ю­щая равна 35. Най­ди­те пло­щадь его пол­ной по­верх­но­сти, де­лен­ную на .

  10. Пло­щадь пол­ной по­верх­но­сти ко­ну­са равна 84. Па­рал­лель­но ос­но­ва­нию ко­ну­са про­ве­де­но се­че­ние, де­ля­щее вы­со­ту по­по­лам. Най­ди­те пло­щадь пол­ной по­верх­но­сти от­се­чен­но­го ко­ну­са.

  11. Пло­щадь бо­ко­вой по­верх­но­сти ко­ну­са в  раз боль­ше пло­ща­ди ос­но­ва­ния. Най­ди­те угол между об­ра­зу­ю­щей ко­ну­са и плос­ко­стью ос­но­ва­ния. Ответ дайте в гра­ду­сах.

  12. Ра­ди­ус ос­но­ва­ния ко­ну­са равен 16, вы­со­та равна 12. Най­ди­те пло­щадь пол­ной по­верх­но­сти ко­ну­са, де­лен­ную на .

  13. Объем ко­ну­са равен 168. Через се­ре­ди­ну вы­со­ты па­рал­лель­но ос­но­ва­нию ко­ну­са про­ве­де­но се­че­ние, ко­то­рое яв­ля­ет­ся ос­но­ва­ни­ем мень­ше­го ко­ну­са с той же вер­ши­ной. Най­ди­те объем мень­ше­го ко­ну­са.

  1. Най­ди­те объем V ко­ну­са, об­ра­зу­ю­щая ко­то­ро­го равна 11 и на­кло­не­на к плос­ко­сти ос­но­ва­ния под углом 300. В от­ве­те ука­жи­те .

  2. Диа­метр ос­но­ва­ния ко­ну­са равен 30, а угол при вер­ши­не осе­во­го се­че­ния равен 90°. Вы­чис­ли­те объем ко­ну­са, де­лен­ный на π.

  3. Конус по­лу­ча­ет­ся при вра­ще­нии рав­но­бед­рен­но­го пря­мо­уголь­но­го тре­уголь­ни­ка ABC во­круг ка­те­та, рав­но­го 120. Най­ди­те его объем, де­лен­ный на .

  4. Вы­со­та ко­ну­са равна 12, об­ра­зу­ю­щая равна 14. Най­ди­те его объем, де­лен­ный на .

  5. В со­су­де, име­ю­щем форму ко­ну­са, уро­вень жид­ко­сти до­сти­га­ет  вы­со­ты. Объём жид­ко­сти равен 40 мл. Сколь­ко мил­ли­лит­ров жид­ко­сти нужно до­лить, чтобы на­пол­нить сосуд до­вер­ху?

  6. Най­ди­те объем V части ко­ну­са, изоб­ра­жен­ной на ри­сун­ке. В от­ве­те ука­жи­те .

  1. Во сколь­ко раз умень­шит­ся объем ко­ну­са, если его вы­со­ту умень­шить в 22 раза?

  2. Во сколь­ко раз уве­ли­чит­ся объем ко­ну­са, если его ра­ди­ус ос­но­ва­ния уве­ли­чить в 5,2 раз?

  3. Во сколь­ко раз умень­шит­ся пло­щадь бо­ко­вой по­верх­но­сти ко­ну­са, если ра­ди­ус его ос­но­ва­ния умень­шить в 15 раз?

  4. Во сколь­ко раз уве­ли­чит­ся пло­щадь бо­ко­вой по­верх­но­сти ко­ну­са, если его об­ра­зу­ю­щую уве­ли­чить в 9 раз?

Самостоятельная работа по теме «Конус»

IV вариант

  1. Вы­со­та ко­ну­са равна 6, а диа­метр ос­но­ва­ния – 16. Най­ди­те об­ра­зу­ю­щую ко­ну­са.

  2. Вы­со­та ко­ну­са равна 96, а длина об­ра­зу­ю­щей — 100. Най­ди­те диа­метр ос­но­ва­ния ко­ну­са.

  3. Диа­метр ос­но­ва­ния ко­ну­са равен 24, а длина об­ра­зу­ю­щей равна 13. Най­ди­те вы­со­ту ко­ну­са.

  4. Пло­щадь ос­но­ва­ния ко­ну­са равна , вы­со­та — 15. Най­ди­те пло­щадь осе­во­го се­че­ния ко­ну­са.

  5. Пло­щадь ос­но­ва­ния ко­ну­са равна 45. Плос­кость, па­рал­лель­ная плос­ко­сти ос­но­ва­ния ко­ну­са, делит его высоту на от­рез­ки дли­ной 4 и 8, счи­тая от вер­ши­ны. Най­ди­те пло­щадь се­че­ния ко­ну­са этой плос­ко­стью.

  6. Вы­со­та ко­ну­са равна 16, а длина об­ра­зу­ю­щей — 20. Най­ди­те пло­щадь осе­во­го се­че­ния этого ко­ну­са.

  7. Диа­метр ос­но­ва­ния ко­ну­са равен 10, а длина об­ра­зу­ю­щей — 13. Най­ди­те пло­щадь осе­во­го се­че­ния этого ко­ну­са.

  8. Длина окруж­но­сти ос­но­ва­ния ко­ну­са равна 5, об­ра­зу­ю­щая равна 8. Най­ди­те пло­щадь бо­ко­вой по­верх­но­сти ко­ну­са.

  9. Вы­со­та ко­ну­са равна 24, об­ра­зу­ю­щая равна 26. Най­ди­те пло­щадь его пол­ной по­верх­но­сти, де­лен­ную на .

  10. Пло­щадь пол­ной по­верх­но­сти ко­ну­са равна 148. Па­рал­лель­но ос­но­ва­нию ко­ну­са про­ве­де­но се­че­ние, де­ля­щее вы­со­ту по­по­лам. Най­ди­те пло­щадь пол­ной по­верх­но­сти от­се­чен­но­го ко­ну­са.

  11. Пло­щадь бо­ко­вой по­верх­но­сти ко­ну­са в два раза боль­ше пло­ща­ди ос­но­ва­ния. Най­ди­те угол между образующей ко­ну­са и плос­ко­стью ос­но­ва­ния. Ответ дайте в гра­ду­сах.

  12. Ра­ди­ус ос­но­ва­ния ко­ну­са равен 72, вы­со­та равна 21. Най­ди­те пло­щадь пол­ной по­верх­но­сти ко­ну­са, де­лен­ную на .

  13. Объем ко­ну­са равен 128. Через се­ре­ди­ну вы­со­ты па­рал­лель­но ос­но­ва­нию ко­ну­са про­ве­де­но се­че­ние, которое яв­ля­ет­ся ос­но­ва­ни­ем мень­ше­го ко­ну­са с той же вер­ши­ной. Най­ди­те объем мень­ше­го ко­ну­са.

  1. Най­ди­те объем V ко­ну­са, об­ра­зу­ю­щая ко­то­ро­го равна 27 и на­кло­не­на к плос­ко­сти ос­но­ва­ния под углом 300. В от­ве­те ука­жи­те .

  2. Диа­метр ос­но­ва­ния ко­ну­са равен 36, а угол при вер­ши­не осе­во­го се­че­ния равен . Вы­чис­ли­те объем конуса, де­лен­ный на .

  3. Конус по­лу­ча­ет­ся при вра­ще­нии рав­но­бед­рен­но­го пря­мо­уголь­но­го тре­уголь­ни­ка ABC во­круг ка­те­та, равно­го 3. Най­ди­те его объем, де­лен­ный на .

  4. Вы­со­та ко­ну­са равна 3, об­ра­зу­ю­щая равна 9. Най­ди­те его объем, де­лен­ный на .

  5. В со­су­де, име­ю­щем форму ко­ну­са, уро­вень жид­ко­сти до­сти­га­ет  вы­со­ты. Объём жид­ко­сти равен 21 мл. Сколь­ко мил­ли­лит­ров жид­ко­сти нужно до­лить, чтобы пол­но­стью на­пол­нить сосуд?

  6. Най­ди­те объем V части ко­ну­са, изоб­ра­жен­ной на ри­сун­ке. В от­ве­те ука­жи­те .

  1. Во сколь­ко раз умень­шит­ся объем ко­ну­са, если его вы­со­ту умень­шить в 16,5 раза?

  2. Во сколь­ко раз уве­ли­чит­ся объем ко­ну­са, если его ра­ди­ус ос­но­ва­ния уве­ли­чить в 12 раз?

  3. Во сколь­ко раз умень­шит­ся пло­щадь бо­ко­вой по­верх­но­сти ко­ну­са, если ра­ди­ус его ос­но­ва­ния умень­шить в 28 раз?

  4. Во сколь­ко раз уве­ли­чит­ся пло­щадь бо­ко­вой по­верх­но­сти ко­ну­са, если его об­ра­зу­ю­щую уве­ли­чить в 22 раза?

Самостоятельная работа по теме «Конус»

V вариант

  1. Вы­со­та ко­ну­са равна 12, а диа­метр ос­но­ва­ния – 10. Най­ди­те об­ра­зу­ю­щую ко­ну­са.

  2. Вы­со­та ко­ну­са равна 64, а длина об­ра­зу­ю­щей — 80. Най­ди­те диа­метр ос­но­ва­ния ко­ну­са.

  3. Диа­метр ос­но­ва­ния ко­ну­са равен 10, а длина об­ра­зу­ю­щей равна 13. Най­ди­те вы­со­ту ко­ну­са.

  4. Пло­щадь ос­но­ва­ния ко­ну­са равна , вы­со­та — 4. Най­ди­те пло­щадь осе­во­го се­че­ния ко­ну­са.

  5. Пло­щадь ос­но­ва­ния ко­ну­са равна 112. Плос­кость, па­рал­лель­ная плос­ко­сти ос­но­ва­ния ко­ну­са, делит его вы­со­ту на от­рез­ки дли­ной 10 и 30, счи­тая от вер­ши­ны. Най­ди­те пло­щадь се­че­ния ко­ну­са этой плос­ко­стью.

  6. Вы­со­та ко­ну­са равна 24, а длина об­ра­зу­ю­щей — 25. Най­ди­те пло­щадь осе­во­го се­че­ния этого ко­ну­са.

  7. Диа­метр ос­но­ва­ния ко­ну­са равен 24, а длина об­ра­зу­ю­щей — 37. Най­ди­те пло­щадь осе­во­го се­че­ния этого ко­ну­са.

  8. Длина окруж­но­сти ос­но­ва­ния ко­ну­са равна 7, об­ра­зу­ю­щая равна 8. Най­ди­те пло­щадь бо­ко­вой по­верх­но­сти ко­ну­са.

  9. Вы­со­та ко­ну­са равна 40, об­ра­зу­ю­щая равна 50. Най­ди­те пло­щадь его пол­ной по­верх­но­сти, де­лен­ную на .

  10. Пло­щадь пол­ной по­верх­но­сти ко­ну­са равна 36. Па­рал­лель­но ос­но­ва­нию ко­ну­са про­ве­де­но се­че­ние, де­ля­щее вы­со­ту по­по­лам. Най­ди­те пло­щадь пол­ной по­верх­но­сти от­се­чен­но­го ко­ну­са.

  11. Пло­щадь бо­ко­вой по­верх­но­сти ко­ну­са в  раз боль­ше пло­ща­ди ос­но­ва­ния. Най­ди­те угол между об­ра­зу­ю­щей ко­ну­са и плос­ко­стью ос­но­ва­ния. Ответ дайте в гра­ду­сах.

  12. Ра­ди­ус ос­но­ва­ния ко­ну­са равен 24, вы­со­та равна 18. Най­ди­те пло­щадь пол­ной по­верх­но­сти ко­ну­са, де­лен­ную на .

  13. Объем ко­ну­са равен 120. Через се­ре­ди­ну вы­со­ты па­рал­лель­но ос­но­ва­нию ко­ну­са про­ве­де­но се­че­ние, ко­то­рое яв­ля­ет­ся ос­но­ва­ни­ем мень­ше­го ко­ну­са с той же вер­ши­ной. Най­ди­те объем мень­ше­го ко­ну­са.

  1. Най­ди­те объем V ко­ну­са, об­ра­зу­ю­щая ко­то­ро­го равна 51 и на­кло­не­на к плос­ко­сти ос­но­ва­ния под углом 300. В от­ве­те ука­жи­те .

  2. Диа­метр ос­но­ва­ния ко­ну­са равен 12, а угол при вер­ши­не осе­во­го се­че­ния равен . Вы­чис­ли­те объем ко­ну­са, де­лен­ный на .

  3. Конус по­лу­ча­ет­ся при вра­ще­нии рав­но­бед­рен­но­го пря­мо­уголь­но­го тре­уголь­ни­ка ABC во­круг ка­те­та, рав­но­го 30. Най­ди­те его объем, де­лен­ный на .

  4. Вы­со­та ко­ну­са равна 4, об­ра­зу­ю­щая равна 10. Най­ди­те его объем, де­лен­ный на .

  5. В со­су­де, име­ю­щем форму ко­ну­са, уро­вень жид­ко­сти до­сти­га­ет  вы­со­ты. Объём жид­ко­сти равен 152 мл. Сколь­ко мил­ли­лит­ров жид­ко­сти нужно до­лить, чтобы пол­но­стью на­пол­нить сосуд?

  6. Най­ди­те объем V части ко­ну­са, изоб­ра­жен­ной на ри­сун­ке. В от­ве­те ука­жи­те .

  1. Во сколь­ко раз умень­шит­ся объем ко­ну­са, если его вы­со­ту умень­шить в 6 раз?

  2. Во сколь­ко раз уве­ли­чит­ся объем ко­ну­са, если его ра­ди­ус ос­но­ва­ния уве­ли­чить в 15 раз?

  3. Во сколь­ко раз умень­шит­ся пло­щадь бо­ко­вой по­верх­но­сти ко­ну­са, если ра­ди­ус его ос­но­ва­ния умень­шить в 40 раз?

  4. Во сколь­ко раз уве­ли­чит­ся пло­щадь бо­ко­вой по­верх­но­сти ко­ну­са, если его об­ра­зу­ю­щую уве­ли­чить в 35 раз?

Самостоятельная работа по теме «Конус»

VI вариант

  1. Вы­со­та ко­ну­са равна 21, а диа­метр ос­но­ва­ния — 144. Най­ди­те об­ра­зу­ю­щую ко­ну­са.

  2. Вы­со­та ко­ну­са равна 30, а длина об­ра­зу­ю­щей — 34. Най­ди­те диа­метр ос­но­ва­ния ко­ну­са.

  3. Диа­метр ос­но­ва­ния ко­ну­са равен 152, а длина об­ра­зу­ю­щей — 95. Най­ди­те вы­со­ту ко­ну­са.

  4. Пло­щадь ос­но­ва­ния ко­ну­са равна , вы­со­та — 10. Най­ди­те пло­щадь осе­во­го се­че­ния ко­ну­са.

  5. Пло­щадь ос­но­ва­ния ко­ну­са равна 128. Плос­кость, па­рал­лель­ная плос­ко­сти ос­но­ва­ния ко­ну­са, делит его вы­со­ту на от­рез­ки дли­ной 16 и 48, счи­тая от вер­ши­ны. Най­ди­те пло­щадь се­че­ния ко­ну­са этой плос­ко­стью.

  6. Вы­со­та ко­ну­са равна 24, а длина об­ра­зу­ю­щей — 30. Най­ди­те пло­щадь осе­во­го се­че­ния этого ко­ну­са.

  7. Диа­метр ос­но­ва­ния ко­ну­са равен 32, а длина об­ра­зу­ю­щей — 34. Най­ди­те пло­щадь осе­во­го се­че­ния этого ко­ну­са.

  8. Длина окруж­но­сти ос­но­ва­ния ко­ну­са равна 4, об­ра­зу­ю­щая равна 2. Най­ди­те пло­щадь бо­ко­вой по­верх­но­сти ко­ну­са.

  9. Вы­со­та ко­ну­са равна 28, об­ра­зу­ю­щая равна 35. Най­ди­те пло­щадь его пол­ной по­верх­но­сти, де­лен­ную на .

  10. Пло­щадь пол­ной по­верх­но­сти ко­ну­са равна 100. Па­рал­лель­но ос­но­ва­нию ко­ну­са про­ве­де­но се­че­ние, де­ля­щее вы­со­ту по­по­лам. Най­ди­те пло­щадь пол­ной по­верх­но­сти от­се­чен­но­го ко­ну­са.

  11. Пло­щадь бо­ко­вой по­верх­но­сти ко­ну­са в два раза боль­ше пло­ща­ди ос­но­ва­ния. Най­ди­те угол между об­ра­зу­ю­щей ко­ну­са и плос­ко­стью ос­но­ва­ния. Ответ дайте в гра­ду­сах.

  12. Ра­ди­ус ос­но­ва­ния ко­ну­са равен 24, вы­со­та равна 7. Най­ди­те пло­щадь пол­ной по­верх­но­сти ко­ну­са, де­лен­ную на .

  13. Объем ко­ну­са равен 112. Через се­ре­ди­ну вы­со­ты па­рал­лель­но ос­но­ва­нию ко­ну­са про­ве­де­но се­че­ние, ко­то­рое яв­ля­ет­ся ос­но­ва­ни­ем мень­ше­го ко­ну­са с той же вер­ши­ной. Най­ди­те объем мень­ше­го ко­ну­са.

  1. Най­ди­те объем V ко­ну­са, об­ра­зу­ю­щая ко­то­ро­го равна 7 и на­кло­не­на к плос­ко­сти ос­но­ва­ния под углом 30. В от­ве­те ука­жи­те .

  2. Диа­метр ос­но­ва­ния ко­ну­са равен 18, а угол при вер­ши­не осе­во­го се­че­ния равен . Вы­чис­ли­те объем ко­ну­са, де­лен­ный на .

  3. Конус по­лу­ча­ет­ся при вра­ще­нии рав­но­бед­рен­но­го пря­мо­уголь­но­го тре­уголь­ни­ка ABC во­круг ка­те­та, рав­но­го 21. Най­ди­те его объем, де­лен­ный на .

  4. Вы­со­та ко­ну­са равна 20, об­ра­зу­ю­щая равна 22. Най­ди­те его объем, де­лен­ный на .

  5. В со­су­де, име­ю­щем форму ко­ну­са, уро­вень жид­ко­сти до­сти­га­ет  вы­со­ты. Объём жид­ко­сти равен 49 мл. Сколь­ко мил­ли­лит­ров жид­ко­сти нужно до­лить, чтобы пол­но­стью на­пол­нить сосуд?

  6. Най­ди­те объем V части ко­ну­са, изоб­ра­жен­ной на ри­сун­ке. В от­ве­те ука­жи­те .

  1. Во сколь­ко раз умень­шит­ся объем ко­ну­са, если его вы­со­ту умень­шить в 6,5 раза?

  2. Во сколь­ко раз уве­ли­чит­ся объем ко­ну­са, если его ра­ди­ус ос­но­ва­ния уве­ли­чить в 17 раз?

  3. Во сколь­ко раз умень­шит­ся пло­щадь бо­ко­вой по­верх­но­сти ко­ну­са, если ра­ди­ус его ос­но­ва­ния умень­шить в 30 раз?

  4. Во сколь­ко раз уве­ли­чит­ся пло­щадь бо­ко­вой по­верх­но­сти ко­ну­са, если его об­ра­зу­ю­щую уве­ли­чить в 40 раз?

Самостоятельная работа по теме «Конус»

VII вариант

  1. Вы­со­та ко­ну­са равна 72, а диа­метр ос­но­ва­ния — 108. Най­ди­те об­ра­зу­ю­щую ко­ну­са.

  2. Вы­со­та ко­ну­са равна 25, а длина об­ра­зу­ю­щей — 65. Най­ди­те диа­метр ос­но­ва­ния ко­ну­са.

  3. Диа­метр ос­но­ва­ния ко­ну­са равен 56, а длина об­ра­зу­ю­щей — 100. Най­ди­те вы­со­ту ко­ну­са.

  4. Пло­щадь ос­но­ва­ния ко­ну­са равна , вы­со­та — 16. Най­ди­те пло­щадь осе­во­го се­че­ния ко­ну­са.

  5. Пло­щадь ос­но­ва­ния ко­ну­са равна 81. Плос­кость, па­рал­лель­ная плос­ко­сти ос­но­ва­ния ко­ну­са, делит его вы­со­ту на от­рез­ки дли­ной 2 и 4, счи­тая от вер­ши­ны. Най­ди­те пло­щадь се­че­ния ко­ну­са этой плос­ко­стью.

  6. Вы­со­та ко­ну­са равна 32, а длина об­ра­зу­ю­щей — 40. Най­ди­те пло­щадь осе­во­го се­че­ния этого ко­ну­са.

  7. Диа­метр ос­но­ва­ния ко­ну­са равен 60, а длина об­ра­зу­ю­щей — 50. Най­ди­те пло­щадь осе­во­го се­че­ния этого ко­ну­са.

  8. Длина окруж­но­сти ос­но­ва­ния ко­ну­са равна 4, об­ра­зу­ю­щая равна 5. Най­ди­те пло­щадь бо­ко­вой по­верх­но­сти ко­ну­са.

  9. Вы­со­та ко­ну­са равна 15, об­ра­зу­ю­щая равна 17. Най­ди­те пло­щадь его пол­ной по­верх­но­сти, де­лен­ную на .

  10. Пло­щадь пол­ной по­верх­но­сти ко­ну­са равна 144. Па­рал­лель­но ос­но­ва­нию ко­ну­са про­ве­де­но се­че­ние, де­ля­щее вы­со­ту по­по­лам. Най­ди­те пло­щадь пол­ной по­верх­но­сти от­се­чен­но­го ко­ну­са.

  11. Пло­щадь бо­ко­вой по­верх­но­сти ко­ну­са в  раз боль­ше пло­ща­ди ос­но­ва­ния. Най­ди­те угол между об­ра­зу­ю­щей ко­ну­са и плос­ко­стью ос­но­ва­ния. Ответ дайте в гра­ду­сах.

  12. Ра­ди­ус ос­но­ва­ния ко­ну­са равен 60, вы­со­та равна 32. Най­ди­те пло­щадь пол­ной по­верх­но­сти ко­ну­са, де­лен­ную на .

  13. Объем ко­ну­са равен 24. Через се­ре­ди­ну вы­со­ты па­рал­лель­но ос­но­ва­нию ко­ну­са про­ве­де­но се­че­ние, ко­то­рое яв­ля­ет­ся ос­но­ва­ни­ем мень­ше­го ко­ну­са с той же вер­ши­ной. Най­ди­те объем мень­ше­го ко­ну­са.

  1. Най­ди­те объем V ко­ну­са, об­ра­зу­ю­щая ко­то­ро­го равна 12 и на­кло­не­на к плос­ко­сти ос­но­ва­ния под углом 300. В от­ве­те ука­жи­те .

  2. Диа­метр ос­но­ва­ния ко­ну­са равен 42, а угол при вер­ши­не осе­во­го се­че­ния равен . Вы­чис­ли­те объем ко­ну­са, де­лен­ный на .

  3. Конус по­лу­ча­ет­ся при вра­ще­нии рав­но­бед­рен­но­го пря­мо­уголь­но­го тре­уголь­ни­ка ABC во­круг ка­те­та, рав­но­го 60. Най­ди­те его объем, де­лен­ный на .

  4. Вы­со­та ко­ну­са равна 7, об­ра­зу­ю­щая равна 8. Най­ди­те его объем, де­лен­ный на .

  5. В со­су­де, име­ю­щем форму ко­ну­са, уро­вень жид­ко­сти до­сти­га­ет  вы­со­ты. Объём жид­ко­сти равен 34 мл. Сколь­ко мил­ли­лит­ров жид­ко­сти нужно до­лить, чтобы пол­но­стью на­пол­нить сосуд?

  1. Най­ди­те объем V части ко­ну­са, изоб­ра­жен­ной на ри­сун­ке. В от­ве­те ука­жи­те .

  1. Во сколь­ко раз умень­шит­ся объем ко­ну­са, если его вы­со­ту умень­шить в 20,5 раза?

  2. Во сколь­ко раз уве­ли­чит­ся объем ко­ну­са, если его ра­ди­ус ос­но­ва­ния уве­ли­чить в 18 раз?

  3. Во сколь­ко раз умень­шит­ся пло­щадь бо­ко­вой по­верх­но­сти ко­ну­са, если ра­ди­ус его ос­но­ва­ния умень­шить в 2 раза?

  4. Во сколь­ко раз уве­ли­чит­ся пло­щадь бо­ко­вой по­верх­но­сти ко­ну­са, если его об­ра­зу­ю­щую уве­ли­чить в 20 раз?

Самостоятельная работа по теме «Конус»

VIII вариант

  1. Вы­со­та ко­ну­са равна 57, а диа­метр ос­но­ва­ния — 152. Най­ди­те об­ра­зу­ю­щую ко­ну­са.

  2. Вы­со­та ко­ну­са равна 48, а длина об­ра­зу­ю­щей — 52. Най­ди­те диа­метр ос­но­ва­ния ко­ну­са.

  3. Диа­метр ос­но­ва­ния ко­ну­са равен 96, а длина об­ра­зу­ю­щей — 80. Най­ди­те вы­со­ту ко­ну­са.

  4. Пло­щадь ос­но­ва­ния ко­ну­са равна , вы­со­та — 2. Най­ди­те пло­щадь осе­во­го се­че­ния ко­ну­са.

  5. Пло­щадь ос­но­ва­ния ко­ну­са равна 64. Плос­кость, па­рал­лель­ная плос­ко­сти ос­но­ва­ния ко­ну­са, делит его вы­со­ту на от­рез­ки дли­ной 8 и 24, счи­тая от вер­ши­ны. Най­ди­те пло­щадь се­че­ния ко­ну­са этой плос­ко­стью.

  6. Вы­со­та ко­ну­са равна 12, а длина об­ра­зу­ю­щей — 15. Най­ди­те пло­щадь осе­во­го се­че­ния этого ко­ну­са.

  7. Диа­метр ос­но­ва­ния ко­ну­са равен 54, а длина об­ра­зу­ю­щей — 45. Най­ди­те пло­щадь осе­во­го се­че­ния этого ко­ну­са.

  8. Длина окруж­но­сти ос­но­ва­ния ко­ну­са равна 3, об­ра­зу­ю­щая равна 8. Най­ди­те пло­щадь бо­ко­вой по­верх­но­сти ко­ну­са.

  9. Вы­со­та ко­ну­са равна 30, об­ра­зу­ю­щая равна 34. Най­ди­те пло­щадь его пол­ной по­верх­но­сти, де­лен­ную на .

  10. Пло­щадь пол­ной по­верх­но­сти ко­ну­са равна 192. Па­рал­лель­но ос­но­ва­нию ко­ну­са про­ве­де­но се­че­ние, де­ля­щее вы­со­ту по­по­лам. Най­ди­те пло­щадь пол­ной по­верх­но­сти от­се­чен­но­го ко­ну­са.

  11. Пло­щадь бо­ко­вой по­верх­но­сти ко­ну­са в два раза боль­ше пло­ща­ди ос­но­ва­ния. Най­ди­те угол между об­ра­зу­ю­щей ко­ну­са и плос­ко­стью ос­но­ва­ния. Ответ дайте в гра­ду­сах.

  12. Ра­ди­ус ос­но­ва­ния ко­ну­са равен 24, вы­со­та равна 45. Най­ди­те пло­щадь пол­ной по­верх­но­сти ко­ну­са, де­лен­ную на .

  13. Объем ко­ну­са равен 144. Через се­ре­ди­ну вы­со­ты па­рал­лель­но ос­но­ва­нию ко­ну­са про­ве­де­но се­че­ние, ко­то­рое яв­ля­ет­ся ос­но­ва­ни­ем мень­ше­го ко­ну­са с той же вер­ши­ной. Най­ди­те объем мень­ше­го ко­ну­са.

 

  1. Най­ди­те объем V ко­ну­са, об­ра­зу­ю­щая ко­то­ро­го равна 19 и на­кло­не­на к плос­ко­сти ос­но­ва­ния под углом 300. В от­ве­те ука­жи­те .

  2. Диа­метр ос­но­ва­ния ко­ну­са равен 30, а угол при вер­ши­не осе­во­го се­че­ния равен 90°. Вы­чис­ли­те объем ко­ну­са, де­лен­ный на π.

  3. Конус по­лу­ча­ет­ся при вра­ще­нии рав­но­бед­рен­но­го пря­мо­уголь­но­го тре­уголь­ни­ка ABC во­круг ка­те­та, рав­но­го 15. Най­ди­те его объем, де­лен­ный на .

  4. Вы­со­та ко­ну­са равна 20, об­ра­зу­ю­щая равна 25. Най­ди­те его объем, де­лен­ный на .

  5. В со­су­де, име­ю­щем форму ко­ну­са, уро­вень жид­ко­сти до­сти­га­ет  вы­со­ты. Объём жид­ко­сти равен 120 мл. Сколь­ко мил­ли­лит­ров жид­ко­сти нужно до­лить, чтобы пол­но­стью на­пол­нить сосуд?

  6. Най­ди­те объем V части ко­ну­са, изоб­ра­жен­ной на ри­сун­ке. В от­ве­те ука­жи­те .

  1. Во сколь­ко раз умень­шит­ся объем ко­ну­са, если его вы­со­ту умень­шить в 12,5 раза?

  2. Во сколь­ко раз уве­ли­чит­ся объем ко­ну­са, если его ра­ди­ус ос­но­ва­ния уве­ли­чить в 19 раз?

  3. Во сколь­ко раз умень­шит­ся пло­щадь бо­ко­вой по­верх­но­сти ко­ну­са, если ра­ди­ус его ос­но­ва­ния умень­шить в 37 раз?

  4. Во сколь­ко раз уве­ли­чит­ся пло­щадь бо­ко­вой по­верх­но­сти ко­ну­са, если его об­ра­зу­ю­щую уве­ли­чить в 2,5 раза?

Ответы

1 вариант

2 вариант

3 вариант

4 вариант

5 вариант

6 вариант

7 вариант

8 вариант

1

17

1

13

1

17

1

10

1

13

1

75

1

90

1

95

2

144

2

108

2

152

2

56

2

96

2

32

2

120

2

40

3

21

3

72

3

72

3

5

3

12

3

57

3

96

3

64

4

18

4

60

4

27

4

150

4

20

4

70

4

128

4

8

5

1

5

2

5

3

5

5

5

7

5

8

5

9

5

4

6

588

6

48

6

540

6

192

6

168

6

432

6

768

6

108

7

588

7

432

7

300

7

60

7

420

7

480

7

1200

7

972

8

3

8

7

8

6

8

20

8

28

8

4

8

10

8

12

9

600

9

1944

9

1764

9

360

9

2400

9

1176

9

200

9

800

10

27

10

41

10

21

10

37

10

9

10

25

10

36

10

48

11

45

11

60

11

45

11

60

11

45

11

60

11

45

11

60

12

384

12

1764

12

576

12

10584

12

1296

12

1176

12

7680

12

1800

13

2

13

1,25

13

21

13

16

13

15

13

14

13

3

13

18

14

3,375

14

10648

14

166,375

14

2460,375

14

16581,375

14

42,875

14

216

14

45,125

15

11979

15

9

15

1125

15

1944

15

72

15

243

15

3087

15

1125

16

1125

16

72

16

576000

16

9

16

9000

16

3087

16

72000

16

1125

17

27

17

324

17

208

17

72

17

112

17

560

17

35

17

1500

18

378

18

364

18

280

18

147

18

361

18

343

18

238

18

285

19

87,75

19

243

19

216

19

263,25

19

117

19

216

19

840

19

3510

20

18,5

20

20

20

22

20

16,5

20

6

20

6,5

20

20,5

20

12,5

21

6,25

21

12,25

21

27,04

21

144

21

225

21

289

21

324

21

361

22

8

22

19

22

15

22

28

22

40

22

30

22

2

22

37

23

36

23

11

23

9

23

22

23

35

23

40

23

20

23

2,5
Источник

Like this post? Please share to your friends:
  • Конус егэ профиль теория
  • Конус егэ профиль задания
  • Конус в заданиях егэ базовый
  • Контурные карты по истории россии для егэ
  • Контурные карты по истории россии 6 класс фгос издательство экзамен