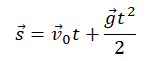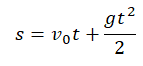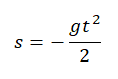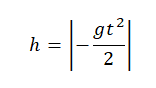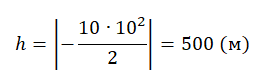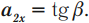Координаты анализ графиков физика егэ теория - Помощь в подготовке к экзаменам и поступлению

Архитектор, инженер, программист, технолог — это далеко не полный список специальностей, для которых нужно сдавать экзамен по физике. Задание 1 из ЕГЭ по этому предмету кажется школьникам простым, однако для его решения нужно выучить большой блок теории. Все задачи из первого номера относятся к теме «Движение». Выпускник должен разбираться в видах движения, уметь анализировать графики и знать принцип относительности. Если вы понимаете эту тему и хотите освежить знания перед ЕГЭ, наша статья напомнит вам основные формулы и правила. Также стоит обратить внимание на курсы подготовки к ЕГЭ: там преподаватель объяснит все подробно, с нуля. А чтобы быть уверенным в высоких баллах, можно выбрать комплексную программу, включающую также занятия по русскому языку и профильной математике.

Кинематика

Путь, траектория, перемещение — понятия, без знания которых не решить задание 1 на ЕГЭ по физике. Подготовка должна начинаться с теории. Когда вы будете хорошо ориентироваться в ней, можно переходить к практике. Наука кинематика, о которой идет речь в первом вопросе, изучает механическое движение тел без описания причин этого движения. А механическим движением называют изменение взаимного расположения тел или их частей в пространстве с течением времени. Для его изучения пользуются системами отсчета. В кинематике это система координат (X, Y, Z), тело отсчета (тело, относительно которого двигаются другие тела) и часы для измерения времени. Форма тел значения не имеет, поэтому в задачах их обозначают материальными точками — объектами, у которых есть масса, а размеры пренебрежимо малые. Не каждое тело может считаться материальной точкой, главное правило — расстояние, которое оно проходит, должно быть намного больше размера. Если мы исследуем скорость самолета на пути из одного города в другой, он является материальной точкой. Если мы определяем сопротивление воздуха в момент полета, нам важна форма, и представить самолет точкой уже нельзя.

Если материальная точка перемещается в пространстве, у нее есть траектория — это условная линия, описывающая движение. Форма траектории зависит от выбранной системы отсчета, в задачах ЕГЭ траектории обычно рассматривают относительно Земли. Если мы свяжем траекторию с часами, то получим путь — то, что прошло тело за определенный временной промежуток. Путь, как и траектория, может иметь любую форму, но у него есть начальная и конечная точка. Соединив их прямой линией, мы нарисуем вектор перемещения. Он не может быть больше пути, а иногда вовсе равняется нулю (в том случае, когда тело двигалось по замкнутой линии). Теория к заданию 1 из ЕГЭ по физике не будет полной без описания принципа относительности движения. Для этого представим, что мы сидим в поезде и видим еще один на соседнем пути. Сначала наш поезд стоит неподвижно, а потом трогается. Если посмотреть на ситуацию относительно Земли, мы двигаемся: были на станции, а теперь отъехали от нее. Относительно самого поезда мы стоим на месте — как сидели у окна, так и сидим. А если взглянуть на соседний состав? Он постепенно удаляется от нас. Несмотря на то, что он по-прежнему стоит на станции, нам кажется, что он перемещается. Вывод: движение зависит от того, в какой системе координат его изучают.

Виды движения

От теории мы переходим к решению задач. Чаще всего в них фигурируют два понятия: скорость и ускорение. Скорость — это быстрота и направление перемещения. Средняя скорость перемещения находится по формуле u = s / t, средняя путевая — u = l / t. Здесь u — скорость, l — путь, s — перемещение. Первая величина будет векторной, вторая — скалярной. Существует также мгновенная скорость, то есть скорость в определенной точке. Ее можно найти по графику или из уравнения u = u0 + at. a — ускорение, то есть изменение скорости за единицу времени. Это векторная величина, она рассчитывается следующим образом: a = u / t. При ускоренном движении она направлена так же, как и скорость, при замедленном — противоположно ей. В случае с движением по окружности эти величины перпендикулярны. Перечислим несколько формул для задания 1 ЕГЭ по физике, связанных с видами движения:

равномерное прямолинейное:

x = x0 + ut (x — координата точки в данный момент времени).
s = ut.
u = const.
a = 0.

прямолинейное равноускоренное:

x = x0 + u0t + аt2 / 2.
s = u0t + аt2 / 2.
u= uox+ at.
a = const.

движение по окружности (u = const):

T = t / N = 1 / v — период.
v = N / t = 1 / T — частота.
u = l / t = 2πR / T = 2πRv — линейная скорость.
ω = ϕ / t = 2π / T = 2πv — угловая скорость.
a = u2 / R = ω2R = ωu — ускорение.

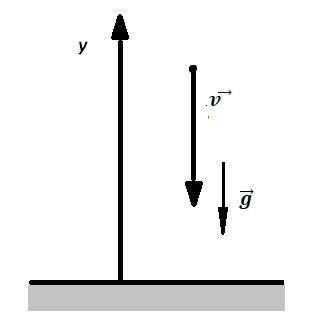
движение по параболе с ускорением свободного падения:

x = xo + uoxt + gt2 / 2.
y = yo + uoyt +gt2 / 2.
ux= uox+ gt.
uy= uoy+ gt.
uоx = u0 cosα.
uоy = u0 sinα.

Частные случаи равноускоренного движения под действием силы тяжести

В рамках теории к заданию 1 ЕГЭ по физике нужно знать два частных случая:

движение по вертикали:

при u0 = 0 высота h = gt2 / 2 и u = gt.
при u0↑ и движении вверх h = u0t — gt2 / 2 и u = u0 – gt.
при u0↑ и движении вниз h = -u0t + gt2 / 2 и u = -u0 + gt.
при υ0↓ h = u0t + gt2 / 2 и υ = υ0 + gt.

движение тела, брошенного горизонтально:

h = gt2 / 2 — высота полета.
s = uоt — дальность полета.
υy= gt — скорость относительно оси OY.

Дополнительная информация для частных случаев решения задач

Еще несколько формул для задания 1 ЕГЭ по физике:

модуль вектора: S=sx2+sy2.
средняя скорость: uср = (s1 + s2 + … + sn ) / (t1 + t2 + … + tn) = 2u1u2 / (u1 + u2).
площадь фигуры равна пройденному пути: S = S1 — S2.
физический смысл производной: ux = x΄ и uy = y΄, ах = u΄x = x΄΄ и аy = u΄y = y΄΄.
движение колеса без проскальзывания: uпост = uвращ и u = uпост + uвращ.

Пример решения задач

Задача 1: Велосипедисты движутся по уравнениям x1 = 3t и x2 = 12 — t. Найти координату их встречи.

Решение: В момент встречи велосипедистов их координаты совпадут: x1 = x2, следовательно, 3t = 12 — t. Решив уравнение, найдем, что t = 3 с. Чтобы найти координату, подставим значение в любое из уравнений (для самопроверки лучше подставить в оба): x1 = 3 • 3 = 9.

Ответ: 9.

Задача 2: Первую половину пути супермен пролетел со скоростью 30 км/ч, вторую — со скоростью 50 км/ч. Найти среднюю скорость супермена.

Решение: Нам известны две скорости: u1 и u2, поэтому мы можем воспользоваться формулой uср = 2u1u2 / u1 + u2 = 2 • 30 • 50 / (30 + 50) = 37,5 км/ч.

Ответ: 37,5.

Теперь вы знаете больше теории для ЕГЭ по физике в 2020 году. Задание 1 только кажется очень простым, в нем бывают нетипичные задачи, поэтому стоит уделить внимание его разбору. Грамотно подготовиться к ЕГЭ вам помогут курсы ЦМДО «Уникум» . На них вы разберете каждую тему из экзамена, переходя от простого к сложному. Много времени преподаватели уделяют решению задач, объяснению сложных моментов. Но независимо от того, какой способ подготовки вы выберете, мы желаем вам удачи, высоких баллов и поступления в вуз мечты.

Источник

Кинематика. Равномерное прямолинейное движение, равноускоренное прямолинейное движение, движение по окружности.

В. З. Шапиро

Первое задание ЕГЭ по физике проверяет ваши знания по разделу «Кинематика». Оно относится к базовому уровню, и в нем нет возможности выбора ответа. Для его решения необходимо проанализировать условие задачи, внимательно рассмотреть график зависимости кинематической величины от времени (при наличии такого графика), правильно подобрать формулу, провести расчет и записать ответ в предлагаемых единицах измерения.

Определение кинематических величин по графику

1. На рисунке приведён график зависимости проекции скорости тела от времени t.

Определите проекцию ускорения тела a_x в промежутке времени от 15 до 20 с.

Ответ: _________________________ м/с².Решение:

На графике представлена зависимость проекции скорости от времени. На участке от 15 до 20 с скорость тела изменяется от 10 м/с до -10 м/с. Это говорит о равноускоренном движении, причем проекция ускорения тела должна быть отрицательной. Для решения задачи необходимо воспользоваться формулой для определения проекции ускорения:

$a_x=frac{v_x-v_{0x}}{t}.$ Проведем расчет: $a_x=frac{-10-10}{5}=-4$ (м/с²).Полученный результат подтверждает, что движение равноускоренное, причем проекция ускорения отрицательная.

Ответ: -4 м/с².

Секрет решения: Долгое время в учебниках физики движение с переменной скоростью делилось на равноускоренное и равнозамедленное $(a_{x } , textless ,0).$ Но в последнее время в основном применяют термин «равноускоренное движение», подразумевая постоянство ускорения. Только знак проекции ускорения определяет возрастание или убывание скорости движения тела.

Необходимая теория: Равноускоренное движение

2. На рисунке приведён график зависимости координаты тела x от времени t при его прямолинейном движении по оси x.

Определите проекцию скорости тела в промежутке времени от 25 до 30 с.

Ответ: ___________________________ м/с.

Согласно представленному графику, зависимость координаты тела от времени является линейной. Это указывает на равномерный характер движения тела. Чтобы решить задачу, необходимо воспользоваться формулой для определения скорости при равномерном движении:

$v_x=frac{x-x_0}{t}.$ Проведем расчет: $v_x=frac{0-10}{5}=-2$ (м/с)

Ответ: -2 м/с.

Проекция скорости получилась отрицательной, и это означает, что в указанный временной интервал тело двигалось в направлении, противоположном выбранной оси Ох.

Необходимая теория: Вычисление перемещения по графику проекции скорости

3. Автомобиль движется по прямой улице вдоль оси Ox. На графике представлена зависимость проекции его скорости от времени.

Определите путь, пройденный автомобилем за 30 с от момента начала наблюдения.

Ответ: _________________________ м.

Так как по условию задачи нам дается график зависимости проекции скорости от времени, то пройденный путь будет определяться площадью геометрической фигуры под графиком. Для вычисления площади получившегося пятиугольника его можно разбить на несколько фигур, например, на две трапеции (см. рис.).

Используя известные формулы для нахождения площади трапеции, можно рассчитать путь за первые 10 с и последующие 20 с (от 10 с до 30 с).

$S_1= frac{10+20}{2} cdot 10=150$ (м); $S_2= frac{10+20}{2} cdot 20=300$ (м);

(м).

Ответ: 450 м.

Полученный пятиугольник можно разбить не только на две трапеции. Здесь можно выделить трапецию, прямоугольник и треугольник. Тогда необходимо рассчитывать площади трех фигур и так же их суммировать.

4. На рисунке приведен график зависимости проекции скорости тела, движущегося вдоль оси Ох, от времени.

Определите проекцию перемещения тела за 10 с от начала наблюдения.

Ответ: ________________________ м.

Так же, как в задаче №3, модуль перемещения будет определяться площадью геометрической фигуры под графиком. Но проекция перемещения за время от 0 до 6 с будет положительной, а от 6 до 10 с отрицательной. Общая проекция перемещения будет определяться их суммой.

$S_{1x}= frac{6+2}{2}cdot 10=40$ (м); $S_{2x}= frac{4cdot (-10)}{2}=-20$ (м); (м).

Ответ: 20 м.

При расчете $S_{2x}$ можно получить положительное число, но надо помнить, что в интервале от 6 до 10 с тело движется в направлении, противоположном оси Ох. Это означает, что проекция перемещения будет отрицательной. Пройденный путь за указанное время от 0 до 10 с определяется суммой модулей проекций перемещений и будет равным 60 м.

Относительность движения

5. Из двух городов навстречу друг другу с постоянной скоростью движутся два автомобиля. На графике показана зависимость расстояния между автомобилями от времени. Скорость второго автомобиля 25 м/с. С какой скоростью движется первый автомобиль?

Ответ: ________________________ м/с.

Формула для нахождения относительной скорости в векторной форме имеет вид:

Если два тела движутся навстречу друг другу, то в проекциях на ось оХ это уравнение выглядит следующим образом:

С учетом данных графика можно рассчитать относительную скорость этих автомобилей при движении навстречу друг другу. Это происходит на интервале от 0 до 60 мин.

, скорость первого автомобиля

Ответ: 15 м/с.

В курсе математики при изучении движения двух тел вводятся понятия «скорость сближения» и «скорость удаления». В первом случае скорости тел суммируются, во втором вычитаются. Эти действия основаны на знаках проекций скоростей движущихся тел. Действия с векторами и их проекциями на оси координат используются как в физике, так и в математике.

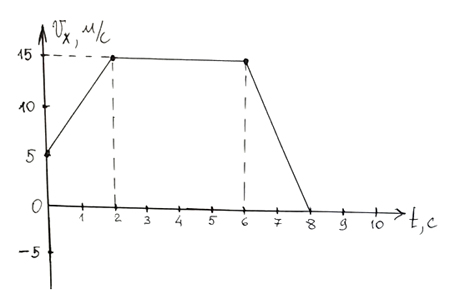
6. Два точечных тела начинают двигаться из одной точки вдоль оси OX в противоположных направлениях. На рисунке показаны графики зависимостей проекций их скоростей Vx на ось OX от времени t. Чему будет равно расстояние между этими телами через 8 секунд после начала движения?

Ответ: ___________________________ м.

Эта задача является комбинированной. Для её решения необходимо воспользоваться материалом двух тем: «Определение кинематических величин по графику» и «Относительность движения». Для определения проекций перемещений тел за 8 с необходимо рассчитать площади фигур под графиком.

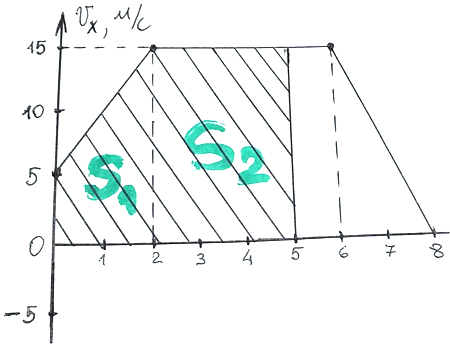
$S_{1x}=frac{8cdot 6}{2}=24$ (м); $S_{2x}=frac{8cdot (-4)}{2}=-16$ (м).

Знак «минус» для $S_{2x}$ показывает, что тела движутся в противоположных направлениях. Поэтому расстояние между ними через 8 с равно сумме модулей перемещений.

$S_{1x}+S_{2x}=24+16=40$ (м).

Ответ: 40 м.

Секрет решения:. Самое главное в этой задаче – выяснить, в каких направлениях двигаются тела. Для этого надо уметь извлекать информацию из графических зависимостей, другими словами, надо уметь «читать» графики. Это умения необходимы почти во всех разделах физики.

7. Катер плывёт по прямой реке, двигаясь относительно берега перпендикулярно береговой линии. Модуль скорости катера относительно берега равен 6 км/ч. Река течёт со скоростью 4,5 км/ч. Чему равен модуль скорости катера относительно воды?

Ответ: ___________________________ км/ч

Решение задачи удобно сопроводить чертежом или рисунком. Выберем направление скорости реки вправо. Тогда катеру необходимо держать курс немного левее, чтобы двигаться перпендикулярно береговой линии.

Векторы собственной скорости катера, скорости течения реки и скорости катера относительно береговой линии образуют прямоугольный треугольник. Запишем для него теорему Пифагора:

Ответ: 7,5 км/ч.

Равномерное движение тел по окружности

Необходимая теория: Равномерное движение по окружности

8. Установленная на станке фреза равномерно вращается с частотой 600 оборотов в минуту. Чему равен модуль ускорения точек, находящихся на расстоянии 3 см от оси фрезы? Ответ округлите до целого числа.

Ответ: ___________________________ м/с².

Так как тело движется равномерно по окружности, то найти требуется центростремительное ускорение. Его можно рассчитать по формуле: Линейная скорость v связана с угловой w соотношением Подставляя это выражение в первое уравнение и проводя сокращения, получим При частоте вращения 600 оборотов в минуту тело будет совершать 10 оборотов за секунду.

Проведем расчет:

Ответ: 118 м/с².

В теме «Равномерное движение тел по окружности» достаточно много формул, которые трудно запоминаются. Из них надо знать базовые, которые относятся к периоду, частоте, линейной скорости, угловой скорости и центростремительному ускорению. Все остальные можно получить через достаточно простые рассуждения и выводы.

9. Две шестерни, сцепленные друг с другом, вращаются вокруг неподвижных осей. Большая шестерня радиусом 20 см делает 20 оборотов за 10 секунд. Сколько оборотов в секунду делает меньшая шестерня радиусом 10 см?

Ответ: ___________________________ Гц.

Так как шестерни касаются друг друга, это условие говорит о равенстве линейных скоростей этих тел. Выразим скорости вращения через радиусы и периоды обращения.

$v_1=frac{2pi R_1}{T_1}; v_2=frac{2pi R_2}{T_2}.$

Приравняем скорости и проведем сокращения.

$frac{2pi R_1}{T_1}=frac{2pi R_2}{T_2} ; frac{R_1}{T_1}=frac{R_1}{T_1};$ с учетом того, что период и частота величины обратные, запишем следующее равенство:

$R_{1 }vartheta_1=R_2vartheta_2$

$vartheta_2=frac{R_{1 }vartheta_1}{R_2}.$

Проведем расчет: $vartheta_2=frac{0,2}{0,1}cdot 2=4$ (Гц).

Ответ: 4 Гц.

В задачах подобного типа всегда надо искать физическую величину, которая является общей для нескольких тел. В данной задаче – это скорость вращения обеих шестерней. Но надо иметь ввиду, что частоты их вращения и угловые скорости различны.

10. Волчок, вращаясь с частотой 20 с^-1, свободно падает с высоты 5 м. Сколько оборотов сделает волчок за время падения?

Ответ: ___________________________ оборотов.

Вначале определим время падения волчка с высоты 5 м. Так как он падает свободно, то начальную скорость будет равна 0. Тогда высота и время падения будут связаны формулой $h=frac{gt^2}{2};$ отсюда $t=sqrt{frac{2h}{g}}.$ Проведем расчет времени падения: $t=sqrt{frac{2cdot 5}{10}} =1$ (с). Так как волчок вращается с частотой 20 $c^{-1},$ то это означает, что за 1 секунду он делает 20 оборотов. Так как время падения составляет 1 с, то количество оборотов также равно 20.

Ответ: 20.

Секрет решения: Эта задача — комбинированная. В ней связаны два раздела кинематики: «Равноускоренное движение» и «Равномерное движение тел по окружности». Надо знать, что суть формул при движении тел с ускорением по горизонтали или по вертикали под действием силы тяжести не меняется. Главное — не ошибиться со знаками проекций для скорости и ускорения.

Если вы хотите разобрать большее количество заданий — записывайтесь на курсы подготовки к ЕГЭ по физике онлайн

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 1 ЕГЭ по физике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

По графику зависимости модуля скорости тела от времени, представленного на рисунке, определите путь, пройденный телом от момента времени 0 с до момента времени 2 с. (Ответ дайте в метрах.)

На рисунке представлен график зависимости модуля скорости автомобиля от времени. Определите по графику путь, пройденный автомобилем в интервале от момента времени 0 с до момента времени 5 с после начала отсчета времени. (Ответ дайте в метрах.)

На рисунке представлен график зависимости модуля скорости тела от времени. Какой путь пройден телом за вторую секунду? (Ответ дайте в метрах.)

На рисунке представлен график зависимости модуля скорости тела от времени.

Найдите путь, пройденный телом за время от момента времени 0 с до момента времени 5 с. (Ответ дайте в метрах.)

На рисунке представлен график зависимости пути от времени. Определите по графику скорость движения велосипедиста в интервале от момента времени 1 с до момента времени 3 с после начала движения. (Ответ дайте в метрах в секунду.)

Пройти тестирование по этим заданиям

Источник

За это задание ты можешь получить 1 балл. Уровень сложности: базовый.
Средний процент выполнения: 69.1%
Ответом к заданию 1 по физике может быть целое число или конечная десятичная дробь.

Алгоритм решения задания 1:

Первым делом определите, на какой вид движения задача (равномерное, равноускоренное и т.д).
Далее посмотрите, что вам необходимо найти. Обратите внимания на ключевые слова: МОДУЛЬ, ПРОЕКЦИЯ, ПУТЬ, ПЕРЕМЩЕНИЕ. Так как именно на этих словах вас хотят подловить.
Выбирайте наиболее подходящую для решения формулу.

Разбор сложных заданий в тг-канале

Задачи для практики

Задача 1

Уравнение движения тела имеет вид x = 2t + 0,5t². Найдите, с каким ускорением двигалось тело. Ответ выразите в (м/с²).

Решение

Дано:

$x=2t+0.5t^2$

$a-?$

Решение:

Запишем уравнение движения в общем виде и сравнив с имеющимся: $x=2t+0.5t^2; x=υ_0t+{at^2}/{2}$, тогда ${at^2}/{2}=0.5t^2; a=0.5·2$ или $a=1м/с^2$.

Ответ: 1

Задача 2

Первую четверть пути поезд прошёл со скоростью 60 км/ч. Средняя скорость на всём пути оказалась равной 40 км/ч. С какой скоростью поезд двигался на оставшейся части пути? Ответ выразите в (км/ч).

Решение

Дано:

$υ_1=60$км/ч

$S_1={1}/{4}S$

$S_2={3S}/{4}$

$υ_{ср}=40$км/ч

$υ_2-?$

Решение:

Средняя скорость определяется выражением: $υ_{ср}={S_{общ}}/{t_{общ}}$(1), где $S_{общ}=S_1+S_2={S}/{4}+{3S}/{4}={4S}/{4}=S$(2), $t_{общ}=t_1+t_2={S_1}/{υ_1}+{S_2}/{υ_2}={S}/{4υ_1}+{3S}/{4υ_2}={Sυ_2+3Sυ_1}/{4υ_1υ_2}$(3).

Подставим выражения (2) и (3) в (1), получим: $υ_{ср}={S}/{1}:{S(3υ_1+υ_2)}/{4υ_1υ_2}={S}/{1}·{4υ_1υ_2}/{S(3υ_1+υ_2)}={4υ_1υ_2}/{(3υ_1+υ_2)}$(4). Из (4) выразим скорость $υ_2$: $υ_{ср}(3υ_1+υ_2)=4υ_1υ_2⇒3υ_1υ_{ср}+υ_{ср}υ_2=4υ_1υ_2⇒4υ_1υ_2-υ_{ср}υ_2=3υ_1υ_{ср}⇒υ_2(4υ_1-υ_{ср})=3υ_1υ_{ср}⇒υ_2={3υ_1υ_{ср}}/{(4υ_1-υ_{ср})}$(5). Подставим числовые значения в (5): $υ_2={3·60·40}/{4·60-40}={7200}/{200}=36км/ч$.

Ответ: 36

Задача 3

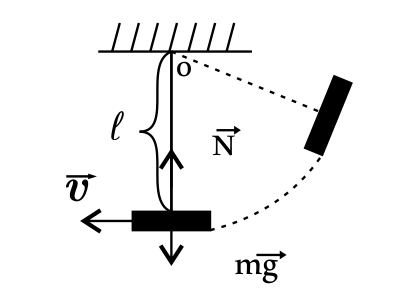
Цирковая гимнастка массой 50 кг качается на качелях с длиной верёвок 5 м. С какой силой она давит на сиденье при прохождении положения равновесия со скоростью 6 м/с? Ответ выразите в (Н). Ускорение свободного падения считать равным 10 м/с^2

Решение

Дано:

$m=50$кг

$g=10м/с^2$

$l=5$м

$υ=6$м/c

$N-?$

Решение:

При прохождении качелями среднего положения второй закон Ньютона в проекции на вертикальное направление иммет вид: $ma=N-mg$(1), здесь $a$ — ускорение гимнастики, совпадающее с центростремительным, $m$ — масса гимнастики, $N$ — сила реакции опоры (сиденья), равная по модулю, согласно третьему закону Ньютона, силе, с которой мальчик давит на сиденье. Так как центростремительное ускорение равно $a_{ц.с.}={υ^2}/{l}$(2), то сила, действующая на сиденье, равна: $N=ma+mg=m(a+g)=m({υ^2}/{l}+g)$(3). Подставим числовые значения в (3): $N=50·({36}/{5}+10)=50·17=860H$.

Ответ: 860

Задача 4

Из начала координат одновременно начинают движение две точки. Первая движется вдоль оси Ox со скоростью 3 м/с, а вторая — вдоль оси Oy со скоростью 4 м/с. (Оси перпендикулярны). С какой скоростью они будут удаляться друг от друга? Ответ выразите в (м/с).

Решение

Дано:

$υ_1=3$м/с

$υ_2=4$м/с

$υ_{отн}-?$

Решение:

Вектор относительной скорости $υ_{отн}$ есть разность векторов скоростей двух точек. По правилу вычитания векторов, вектор относительной скорости будет ижти от конца вектора скорости одной точки к концу векторая скорости другой точки. Так как скорости точек направлены перпендикулярно, длина вектора относительной скорости является гипотенузой прямоугольного треугольника и находится по теореме Пифагора: $υ_{отн}=√{υ_1^2+υ_2^2}=√{(3)^2+(4)^2}=√{9+16}=√{25}=5$м/с.

Ответ: 5

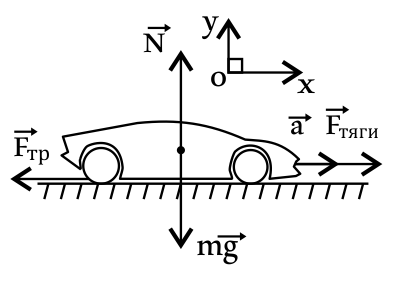
Задача 5

Автобус, масса которого 15 т, движется с ускорением 0,7 м/с². Чему равна сила тяги двигателя, если коэффициент сопротивления движению равен 0,03? Ответ выразите в (кН).

Решение

Дано:

$m=15·10^3$кг

$a=0.7м/с^2$

$μ=0.03$

$F_{тяги}-?$

Решение:

На автомобиль действуют силы: тяги, трения, тяжести и силы реакции опоры. Запишем второй закон Ньютона: $ma↖{→}={F_{тяги}}↖{→}+{F_{тр}}↖{→}+mg↖{→}+N↖{→}$(1).

В проекциях на оси координат имеем: $Ox:ma=F_{тяги}-F_{тр}$(2), откуда $F_{тяги}=ma+F_{тр}$(3). $Oy:O=N-mg$(4), откуда $N=mg$(5). Учитывая, что сила трения $F_{тр}=μN$, то с учетом (5) получим: $F_{тр}=μmg$(6). Подставим (6) в (3) и найдем $F_{тяги}:F_{тяги}=ma+μmg=m(a+μg)$(7), где $g≈10м/с^2$ — ускорение свободного падения.

Подставим числовые значения в (7), получим: $F_{тяги}=15·10^3·(0.7+0.03·10)=15·10^3·(0.7+0.3)=15·10^3·1=15·10^3=15$кН.

Ответ: 15

Задача 6

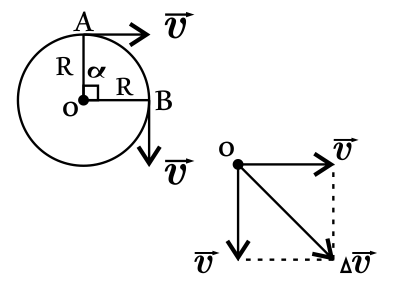
Тело движется по окружности равномерно. Радиус окружности 1 м. Найдите изменение вектора скорости при перемещении тела на угол 90◦. Период обращения 3,14 с. Ответ округлите до десятых. Ответ выразите в (м/с). Число ${π}$ принять равным 3,14

Решение

Дано:

$R=1$м

$α=90°$

$T=3.14$c

$∆υ-?$

Решение:

Изменение вектора скорости при перемещении тела на угол $90°$ равно по теореме Пифагора: $∆υ=√{υ^2+υ^2}=√{2υ^2}=√{2}υ$(1).

Найдем величину скорости $υ$: $υ={S}/{t}={2πR}/{T}={3.14·2·1}/{3.14}=2$м/с(2).

Подставим числовые значения в (1), получим: $∆υ=√2·υ=1.41·2=2.82=2.8$м/с.

Ответ: 2.8

Задача 7

Тело движется вдоль оси Ox. Чему равна проекция скорости тела v_x, координата x которого меняется с течением времени по закону x = 3 − 2t, где все величины выражены в системе СИ? Ответ выразите в (м/c).

Решение

Дано:

$x=3-2t$

$υ_х-?$

Решение:

Известно, что $υ_x=x'(t)$, тогда $x'(t)=-2·1=-2$.

Ответ: -2

Задача 8

Подъёмный кран поднимает груз вверх со скоростью 3 м/с. В некоторый момент времени трос обрывается и груз начинает падать вниз. Определите скорость груза в момент падения на землю, если время падения составляет 4 с. Ответ выразить в (м/с). Ускорение свободного падения принять равным $10м/с^2$

Решение

Дано:

$υ=3$м/с

$t=4$c

$υ_к-?$

Решение:

На тело действует сила тяжести и ускорение свободного падения $g=const=10м/с^2$

$g={υ_к-(-υ_0)}/{t}$, т.к. ускорение $g$ и $υ_0$ разнонаправлены. $υ_к=gt-υ_0=10·4-3=37$м/с.

Ответ: 37

Задача 9

Тело движется вдоль оси Ox. Чему равно перемещение тела за 10 с, координата x которого меняется с течением времени по закону x = 3 − 2t + t², где все величины выражены в системе СИ? Ответ выразить в (м).

Решение

Дано:

$t=10$c

$x=3-2t+t^2$

$x_0=3$

$r-?$

Решение:

$x=-20+100=80+3=83$

$r=x-x_0=83-3=80$м, т.к. изначально тело уже прошло 3м.

Ответ: 80

Задача 10

Планета имеет радиус в 2 раза меньший радиуса Земли. Найдите массу этой планеты, если известно, что ускорение свободного падения на поверхности этой планеты такое же, как и на Земле. Масса Земли 6 · 10²⁴ кг. Ответ выразить в (·10²⁴ кг).

Решение

Дано:

$R_n={R_3}/{2}$

$M_n-?$

$g_n=g_3$

$M_3=6·10^{24}$м

Решение:

${tableg_n=G{M_n}/{R_r^2}; g_3=G{M_3}/{R_3^2};$ ${M_n}/{R_n^2}={M_3}/{R_3^2}; M_n=M_3·{R_n^2}/{R_3^2}=6·10^{24}·{1}/{4}=1.5·10^{24}$кг

Ответ: 1.5

Задача 11

Материальная точка движется по окружности радиусом ${1.5}/{π}$ м. Найдите перемещение точки за 2 полных оборота. Ответ выразить в (м).

Решение

Дано:

$R={1.5}{π}$

Решение:

Точка делает 2 полных оборота и возвращается в начальную точку, ее перемещение равно 0.

Ответ: 0

Задача 12

Планета имеет массу в 4 раза меньшую массы Земли. Найдите радиус этой планеты, если известно, что ускорение свободного падения на поверхности этой планеты такое же, как на Земле, радиус Земли 6,4 · 10⁶ м. Ответ выразите в (км).

Решение

Дано:

$M_n={M_3}/{4}$

$R_n-?$

$g_n=g_3$

$R_3=6.4·10^6$м

Решение:

${tableg_n=G{M_n}/{R_n^2}; g_3=G{M_3}/{R_3^2};$ ${M_n}/{M_3}={R_n^2}/{R_3^2}; {1}/{2}={R_n}/{R_3}$

$R_n=3200$км

Ответ: 3200

Задача 13

Найдите, чему равно ускорение свободного падения на некоторой планете, если период колебаний секундного земного математического маятника на ней оказался равным 1,41 с. Ответ выразите в (м/с²).

Решение

Дано:

$g_n-?$

$T_n=1.41$с

$T_3=1c$

Решение:

${tableT_n=2π√{{l}/{g_n}}; T_3=2π√{{l}/{g_3}};$ ${T_n}/{T_3}=√{{g_3}/{g_n}}; {1.41^2}/{1}={10}/{g_n}$

$g_n=5м/с^2$

Ответ: 5

Задача 14

Мяч массой 800 г брошен под углом 90◦ к горизонту с начальной скоростью 5 м/с. Найдите модуль силы тяжести, действующей на мяч сразу после броска. Ответ выразите в (Н).

Решение

Дано:

$m=0.8$кг

$υ=5$м/с

$F_{тяж}-?$

Решение:

Модуль силы тяжести, равна: $m·g=0.8·10=8H$

Ответ: 8

Задача 15

Найдите значение ускорения свободного падения на некоторой планете, плотность которой в два раза меньше плотности Земли, если радиусы планет одинаковы. Ответ выразите в (м/с²). Ускорение свободного падения на Земле принять равным 10 м/с^2

Решение

Дано:

$R_n=R_3$

${ρ_3}/{2}=ρ_n$

$ρ_n-?$

Решение:

${tableg^3=G{M_3}/{r^2}; g_n=G{M_n}/{r_n^2};$

а $V={4}/{3}π·R^3$, то и $V_n=V_3$.

${g_3}/{g_n}={ρ_3·V_3·r_n^2}/{ρ_n·V_n·r_3^2}⇒g_3=2·g_n; g_n=5м/с^2$.

Ответ: 5

Задача 16

Висящий на пружинке груз массой 400 г растягивает её на 10 см. На сколько сантиметров растянется пружина, если груз заменить на другой, массой 300 г? Ускорение свободного падения принять равным $10 м/{с^2}$. Ответ выразите в (см).

Решение

Дано:

$m_1=0.4$кг

$m_2=0.3$кг

$x_1=10^{-1}$ м=10 см

$x_2-?$

Решение:

${tablem_1g=kx_1; m_2g=kx_2;$ $⇒x_2={m_2g}/{m_1g}·x_1={0.3}/{0.4}·10см=7.5$

Ответ: 7.5

Задача 17

Велосипедист за 30 мин проехал 4 км, затем полчаса отдыхал, а затем проехал ещё 4 км за 15 мин. Какой была его средняя скорость на всём пути? Ответ выразите в (км/ч).

Решение

Известно, $υ_{ср}={∆S}/{∆t}={4+0+4}/{30+30+15}={8}/{1.25}=6.4{км}/ч$.

Ответ: 6.4

Задача 18

Найдите жёсткость пружины, если под действием силы 2 Н она растянулась на 4 см. Ответ выразите в (Н/м).

Решение

Дано:

$А=2·H$

$∆x=4·10^{-2}$

$K-?$

Решение:

По закону Гука $K={F}/{∆x}={2}/{4·10^{-2}}=50Н/м$.

Ответ: 50

Задача 19

Материальная точка равномерно движется по окружности. Найдите отношение пути к модулю перемещения за половину периода. Ответ округлить до сотых.

Решение

Дано:

${L}/{|S↖{→}|}-?$

$t={T}/{2}$

Решение:

1) За полпериода тело проходит половину окружности, поэтому пройденный путь равен половине дуги окружности: $L=π·R$
2) Модуль перемещения равен длине прямой, соединяющей начальную и конечную точки: $|S↖{→}|=2·R$

3) ${L}/{|S↖{→}|}={π·R}/{2·R}=1.57$

Ответ: 1.57

Задача 20

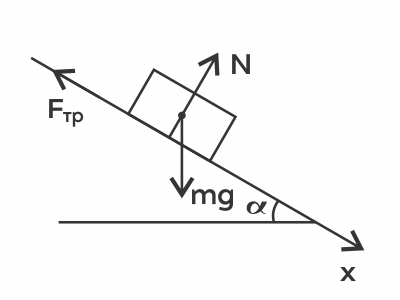
Брусок массой 2 кг покоится на наклонной плоскости с углом наклона 30◦ к горизонту. Определите силу трения, действующую на брусок, если коэффициент трения равен 0,7. Ответ выразите в (H). Ускорение свободного падения считать равным 10 $м/с^2$.

Решение

Дано:

$m=2$кг

$α=30°$

$μ=0.7$

Найти:$F_{тр}-?$

Решение:

Запишем 2-й закон Ньютона для тела: $ma↖{→}=mg↖{→}+N↖{→}+F_{тр}↖{→}=0$ (т.к. брусок покоится)

Направим ось х параллельно плоскости. 2-й закон Ньютона в проекции на ось х: $mg·sinα-F_{тр}=0⇒$

$F_{тр}=mgsinα=2·10·{1}/{2}=10Н$

Внимание! Многие при решении этой задачи используют неверную формулу $F_{тр}=μmgcosα$ — эта формула не может быть использована в этой задаче, потому что она описывает максимальную(!) силу трения покоя или силу трения скольжения. А в данной задаче тело покоится под действием силы трения, поэтому применять нужно формулы, указанные выше в решении.

Ответ: 10

Задание 1

Это задание проверяет знания учащихся в области кинематики, к основным понятиям которой относятся понятия ускорение, скорости и перемещения. Так как это векторные величины, то в подавляющем большинстве учебников приведены формулы в векторном виде и подавляющее большинство моих коллег, с которыми мне доводилось общаться, также заставляют своих учеников учить формулы в векторном виде, что совершенно избыточно, на мой взгляд, и чаще мешает решать задания ЕГЭ, чем помогает. Конечно, важно знать, что скорость, ускорение и перемещение — это векторные величины, как и импульс, и сила. Но гораздо важнее, чтобы они понимали, что вычисляем мы, в конечном итоге, не вектора, а их проекции и модули. И вот с этим-то учащиеся часто путаются. К примеру, необходимо по графику скорости определить модуль или проекцию ускорения. Сколько формул для этого нужно учить — три, две или одну? Конечно же одну, для проекции ускорения. А модуль ускорения а = |а_х|.

С перемещением ситуация ещё интереснее. Часто мне приходится сталкиваться с ситуацией, когда ученики из других школ, с которыми я занимаюсь подготовкой к экзамену по физике в центре подготовки к ЕГЭ в городе Ногинске, не понимают почему проекцию перемещения нужно находить по той или иной формуле. Они просто не могут понять откуда взялись те или иные формулы перемещения. Но зато они легко могут написать эти формулы в векторном виде, от которого, как правило, мало толку. Да, есть проблема — когда изучается кинематика, в 10 классе, дети ещё не знакомы с элементами математического анализа и не знают ни понятия производной, ни понятия интеграла. Но это и не обязательно. Достаточно показать на простом примере равномерного движения, что проекция перемещения может быть определена как площадь фигуры под графиком скорости и затем применить эту идею к равноускоренному движению. Это, в принципе, показано и в учебнике Пёрышкина для 9 класс, в разделе Кинематика, и в учебнике для 10 класса углублённого уровня Мякишева. Но тем не менее, почему-то многие ученики затрудняются с вычислением пройденного пути по графику скорости, который есть ни что иное как модуль перемещения при прямолинейном движении. Особенно, если график представляет собой ломаную линию.

Найти a_x в промежутке времени от 0 до 2 с.
Найти модуль ускорения в промежутке от 6 до 7 с.
Найти пройденный путь за первые 5 с движения

Вот несколько примеров.

2) На промежутке от 6 до 7 с ускорение такое же как и на промежутке от 6 до 8 с, а он удобнее, поэтому

a = │a_x│ = 7,5 м/с²

3) На графике площадь заштрихованной области и есть S_x, то есть:

ЕГЭ-2020. Физика. Решение задач

В книге содержатся материалы для успешной сдачи ЕГЭ: краткие теоретические сведения по всем темам, задания разных типов и уровней сложности, решение задач повышенного уровня сложности, ответы и критерии оценивания. Учащимся не придется искать дополнительную информацию в интернете и покупать другие пособия. В данной книге они найдут все необходимое для самостоятельной и эффективной подготовки к экзамену.

Купить

Источник

Кинематика

Механика — это раздел физики, изучающий механическое движение тел.

Кинематика — это раздел механики, в котором изучается механическое движение тел без учета причин, вызывающих это движение.

Материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь, если

расстояние, которое проходит тело, много больше его размера;
расстояние от данного тела до другого тела много больше его размера;
тело движется поступательно.

Система отсчета — это тело отсчета, связанная с ним система координат и прибор для измерения времени.
Траектория — это линия, которую описывает тело при своем движении.
Путь — это скалярная величина, равная длине траектории.
Перемещение — это вектор, соединяющий начальное положение тела с его конечным положением за данный промежуток времени.

Важно!
В процессе движения путь может только увеличиваться, а перемещение как увеличиваться, так и уменьшаться, например, когда тело поворачивает обратно.
При прямолинейном движении в одном направлении путь равен модулю перемещения, а при криволинейном — путь больше перемещения.
Перемещение на замкнутой траектории равно нулю.

Основная задача механики — определить положение тела в пространстве в любой момент времени.

Содержание

Механическое движение и его виды
Относительность механического движения
- Правило сложения перемещений
- Правило сложения скоростей
- Относительная скорость
Скорость
Ускорение
Равномерное движение
- График скорости (проекции скорости)
- График перемещения (проекции перемещения)
Прямолинейное равноускоренное движение
Свободное падение (ускорение свободного падения)
- Движение тела по вертикали
- Движение тела, брошенного горизонтально
- Движение тела, брошенного под углом к горизонту (баллистическое движение)
Движение по окружности с постоянной по модулю скоростью
Основные формулы по теме «Кинематика»

Механическое движение и его виды

Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.

Механическое движение может быть:
1. по характеру движения

поступательным — это движение, при котором все точки тела движутся одинаково и любая прямая, мысленно проведенная в теле, остается параллельна сама себе;
вращательным — это движение, при котором все точки твердого тела движутся по окружностям, расположенным в параллельных плоскостях;
колебательным — это движение, которое повторяется в двух взаимно противоположных направлениях;

2. по виду траектории

прямолинейным — это движение, траектория которого прямая линия;
криволинейным — это движение, траектория которого кривая линия;

3. по скорости

равномерным — движение, при котором скорость тела с течением времени не изменяется;
неравномерным — это движение, при котором скорость тела с течением времени изменяется;

4. по ускорению

равноускоренным — это движение, при котором скорость тела увеличивается с течением времени на одну и ту же величину;
равнозамедленным — это движение, при котором скорость тела уменьшается с течением времени на одну и ту же величину.

Относительность механического движения

Относительность движения — это зависимость характеристик механического движения от выбора системы отсчета.

Правило сложения перемещений

Перемещение тела относительно неподвижной системы отсчета равно векторной сумме перемещения тела относительно подвижной системы отсчета и перемещения подвижной системы отсчета относительно неподвижной системы отсчета:

где ( S ) — перемещение тела относительно неподвижной системы отсчета;
( S_1 ) — перемещение тела относительно подвижной системы отсчета;
( S_2 ) — перемещение подвижной системы отсчета относительно неподвижной системы отсчета.

Правило сложения скоростей

Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета:

где ( v ) — скорость тела относительно неподвижной системы отсчета;
( v_1 ) — скорость тела относительно подвижной системы отсчета;
( v_2 ) — скорость подвижной системы отсчета относительно неподвижной системы отсчета.

Относительная скорость

Важно! Чтобы определить скорость одного тела относительно другого, надо мысленно остановить то тело, которое мы принимаем за тело отсчета, а к скорости оставшегося тела прибавить скорость остановленного, изменив направление его скорости на противоположное.

Пусть ( v_1 ) — скорость первого тела, а ( v_2 ) — скорость второго тела.
Определим скорость первого тела относительно второго ( v_{12} ):

Определим скорость второго тела относительно первого ( v_{21} ):

Следует помнить, что траектория движения тела и пройденный путь тоже относительны.

Если скорости направлены перпендикулярно друг к другу, то относительная скорость рассчитывается по теореме Пифагора:

Если скорости направлены под углом ( alpha ) друг к другу, то относительная скорость рассчитывается по теореме косинусов:

Скорость

Скорость — это векторная величина, характеризующая изменение перемещения данного тела относительно тела отсчета с течением времени.

Обозначение — ( v ), единицы измерения — м/с (км/ч).

Средняя скорость — это векторная величина, равная отношению всего перемещения к промежутку времени, за которое это перемещение произошло:

Средняя путевая скорость — это скалярная величина, равная отношению всего пути, пройденного телом, к промежутку времени, за которое этот путь пройден:

Важно! Чтобы определить среднюю скорость на всем участке пути, надо время разделить на отдельные промежутки и все время представить в виде суммы этих промежутков.
Чтобы определить среднюю скорость за все время движения, надо путь разделить на отдельные участки и весь путь представить как сумму этих участков.

Мгновенная скорость — это скорость тела в данный момент времени или в данной точке траектории.
Мгновенная скорость направлена по касательной к траектории движения.

Ускорение

Ускорение – это векторная физическая величина, характеризующая быстроту изменения скорости.

Обозначение — ( a ), единица измерения — м/с².
В векторном виде:

где ( v ) – конечная скорость; ( v_0 ) – начальная скорость;
( t ) – промежуток времени, за который произошло изменение скорости.

В проекциях на ось ОХ:

где ( a_n ) – нормальное ускорение, ( a_{tau} ) – тангенциальное ускорение.

Тангенциальное ускорение сонаправлено с вектором линейной скорости, а значит, направлено вдоль касательной к кривой:

Нормальное ускорение перпендикулярно направлению вектора линейной скорости, а значит, и касательной к кривой:

Ускорение характеризует быстроту изменения скорости, а скорость – векторная величина, которая имеет модуль (числовое значение) и направление.

Важно!
Тангенциальное ускорение характеризует быстроту изменения модуля скорости. Нормальное ускорение характеризует быстроту изменения направления скорости.
Если ( a_{tau} ) ≠ 0, ( a_n ) = 0, то тело движется по прямой;
если ( a_{tau} ) = 0, ( a_n ) = 0, ( v ) ≠ 0, то тело движется равномерно по прямой;
если ( a_{tau} ) = 0, ( a_n ) ≠ 0, тело движется равномерно по кривой;
если ( a_{tau} ) = 0, ( a_n ) = const, то тело движется равномерно по окружности;
если ( a_{tau} ) ≠ 0, ( a_n ) ≠ 0, то тело движется неравномерно по окружности.

Равномерное движение

Равномерное движение – это движение, при котором тело за любые равные промежутки времени совершает равные перемещения.

Скорость при равномерном движении – величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло:

Проекция вектора скорости на ось ОХ:

Проекция вектора скорости на координатную ось равна быстроте изменения данной координаты:

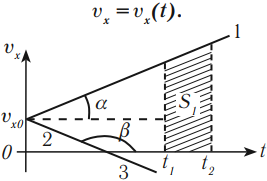
График скорости (проекции скорости)

График скорости (проекции скорости) представляет собой зависимость скорости от времени:

График скорости при равномерном движении – прямая, параллельная оси времени.
График 1 лежит над осью ( t ), тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ( t ), тело движется против оси ОХ.

Перемещение при равномерном движении – это величина, равная произведению скорости на время:

Проекция вектора перемещения на ось ОХ:

График перемещения (проекции перемещения)

График перемещения (проекции перемещения) представляет собой зависимость перемещения от времени:

График перемещения при равномерном движении – прямая, выходящая из начала координат.
График 1 лежит над осью ( t ), тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ( t ), тело движется против оси ОХ.

По графику зависимости скорости от времени можно определить перемещение, пройденное телом за время ( t ). Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).

Координата тела при равномерном движении рассчитывается по формуле:

График координаты представляет собой зависимость координаты от времени: ( x=x(t) ).

График координаты при равномерном движении – прямая.
График 1 направлен вверх, тело движется по направлению оси ОХ:

График 2 параллелен оси ОХ, тело покоится.
График 3 направлен вниз, тело движется против оси ОХ:

Прямолинейное равноускоренное движение

Прямолинейное равноускоренное движение – это движение по прямой, при котором тело движется с постоянным ускорением:

При движении с ускорением скорость может как увеличиваться, так и уменьшаться.

Скорость тела при равноускоренном движении рассчитывается по формуле:

При разгоне (в проекциях на ось ОХ):

При торможении (в проекциях на ось ОХ):

График ускорения (проекции ускорения) при равноускоренном движении представляет собой зависимость ускорения от времени:

График ускорения при равноускоренном движении – прямая, параллельная оси времени.
График 1 лежит над осью t, тело разгоняется, ( a_x ) > 0.
График 2 лежит под осью t, тело тормозит, ( a_x ) < 0.

График скорости (проекции скорости) представляет собой зависимость скорости от времени:

График скорости при равноускоренном движении – прямая.
График 1 направлен вверх, тело движется равноускоренно в положительном направлении оси ОХ, ( v_{0x} ) > 0, ( a_x ) > 0.

График 2 направлен вниз, тело движется равнозамедленно в положительном направлении оси ОХ, ( v_{0x} ) > 0, ( a_x ) < 0,

График 3 направлен вниз, тело движется равноускоренно против оси ОХ, ( v_{0x} ) < 0, ( a_x ) < 0. По графику зависимости скорости от времени можно определить перемещение, пройденное телом за промежуток времени ( t_2-t_1 ). Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).

Перемещение при равноускоренном движении рассчитывается по формулам:

Перемещение в ( n )-ую секунду при равноускоренном движении рассчитывается по формуле:

Координата тела при равноускоренном движении рассчитывается по формуле:

Свободное падение (ускорение свободного падения)

Свободное падение – это движение тела в безвоздушном пространстве под действием только силы тяжести.

Все тела при свободном падении независимо от массы падают с одинаковым ускорением, называемым ускорением свободного падения.
Ускорение свободного падения всегда направлено к центру Земли (вертикально вниз).

Обозначение – ( g ), единицы измерения – м/с².

Важно! ( g ) = 9,8 м/с², но при решении задач считается, что ( g ) = 10 м/с².

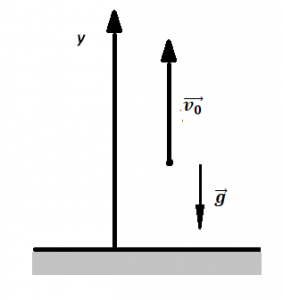
Движение тела по вертикали

Тело падает вниз, вектор скорости направлен в одну сторону с вектором ускорения свободного падения:

Если тело падает вниз без начальной скорости, то ( v_0 ) = 0.
Время падения рассчитывается по формуле:

Тело брошено вверх:

Если брошенное вверх тело достигло максимальной высоты, то ( v ) = 0.
Время подъема рассчитывается по формуле:

Движение тела, брошенного горизонтально

Движение тела, брошенного горизонтально, можно представить как суперпозицию двух движений:

равномерного движения по горизонтали со скоростью ( v_0=v_{0x} );
равноускоренного движения по вертикали с ускорением свободного падения ( g ) и без начальной скорости ( v_{0y}=0 ).

Уравнение скорости:

Уравнение координаты:

Скорость тела в любой момент времени:

Дальность полета:

Угол между вектором скорости и осью ОХ:

Движение тела, брошенного под углом к горизонту (баллистическое движение)

Движение тела, брошенного под углом к горизонту, можно представить как суперпозицию двух движений:

равномерного движения по горизонтали;
равноускоренного движения по вертикали с ускорением свободного падения.

Уравнение скорости:

Уравнение координаты:

Скорость тела в любой момент времени:

Угол между вектором скорости и осью ОХ:

Время подъема на максимальную высоту:

Максимальная высота подъема:

Время полета:

Максимальная дальность полета:

Важно!
При движении вверх вертикальная составляющая скорости будет уменьшаться, т. е. тело вдоль вертикальной оси движется равнозамедленно.
При движении вниз вертикальная составляющая скорости будет увеличиваться, т. е. тело вдоль вертикальной оси движется равноускоренно.
Скорость ( v_0 ), с которой тело брошено с Земли, будет равна скорости, с которой оно упадет на Землю. Угол ( alpha ), под которым тело брошено, будет равен углу, под которым оно упадет.

При решении задач на движение тела, брошенного под углом к горизонту, важно помнить, что в точке максимального подъема проекция скорости на ось ОУ равна нулю:

Это облегчает решение задач:

Движение по окружности с постоянной по модулю скоростью

Движение по окружности с постоянной по модулю скоростью – простейший вид криволинейного движения.

Траектория движения – окружность. Вектор скорости направлен по касательной к окружности.
Модуль скорости тела с течением времени не изменяется, а ее направление при движении по окружности в каждой точке изменяется, поэтому движение по окружности – это движение с ускорением.
Ускорение, которое изменяет направление скорости, называется центростремительным.
Центростремительное ускорение направлено по радиусу окружности к ее центру.

Центростремительное ускорение – это ускорение, характеризующее быстроту изменения направления вектора линейной скорости.
Обозначение – ( a_{цс} ), единицы измерения – м/с².

Движение тела по окружности с постоянной по модулю скоростью является периодическим движением, т. е. его координата повторяется через равные промежутки времени.
Период – это время, за которое тело совершает один полный оборот.
Обозначение – ( T ), единицы измерения – с.

где ( N ) – количество оборотов, ( t ) – время, за которое эти обороты совершены.
Частота вращения – это число оборотов за единицу времени.
Обозначение – ( nu ), единицы измерения – с^–1 (Гц).

Период и частота – взаимно обратные величины:

Линейная скорость – это скорость, с которой тело движется по окружности.
Обозначение – ( v ), единицы измерения – м/с.
Линейная скорость направлена по касательной к окружности:

Угловая скорость – это физическая величина, равная отношению угла поворота к времени, за которое поворот произошел.
Обозначение – ( omega ), единицы измерения – рад/с .

Направление угловой скорости можно определить по правилу правого винта (буравчика).
Если вращательное движение винта совпадает с направлением движения тела по окружности, то поступательное движение винта совпадает с направлением угловой скорости.
Связь различных величин, характеризующих движение по окружности с постоянной по модулю скоростью:

Важно!
При равномерном движении тела по окружности точки, лежащие на радиусе, движутся с одинаковой угловой скоростью, т. к. радиус за одинаковое время поворачивается на одинаковый угол. А вот линейная скорость разных точек радиуса различна в зависимости от того, насколько близко или далеко от центра они располагаются:

Если рассматривать равномерное движение двух сцепленных тел, то в этом случае одинаковыми будут линейные скорости, а угловые скорости тел будут различны в зависимости от радиуса тела:

Когда колесо катится равномерно по дороге, двигаясь относительно нее с линейной скоростью ( v_1 ), и все точки обода колеса движутся относительно его центра с такой же линейной скоростью ( v_1 ), то относительно дороги мгновенная скорость разных точек колеса различна.

Мгновенная скорость нижней точки ( (m) ) равна нулю, мгновенная скорость в верхней точке ( (n) ) равна удвоенной скорости ( v_1 ), мгновенная скорость точки ( (p) ), лежащей на горизонтальном радиусе, рассчитывается по теореме Пифагора, а мгновенная скорость в любой другой точке ( (c) ) – по теореме косинусов.

Основные формулы по теме «Кинематика»

Кинематика

3 (59.68%) 126 votes

Источник

Кинематика

Виды движения

Частные случаи равноускоренного движения под действием силы тяжести

Дополнительная информация для частных случаев решения задач

Пример решения задач

Кинематика. Равномерное прямолинейное движение, равноускоренное прямолинейное движение, движение по окружности.

Алгоритм решения задания 1:

Задачи для практики

Задача 1

Решение

Задача 2

Решение

Задача 3

Решение

Задача 4

Решение

Задача 5

Решение

Задача 6

Решение

Задача 7

Решение

Задача 8

Решение

Задача 9

Решение

Задача 10

Решение

Задача 11

Решение

Задача 12

Решение

Задача 13

Решение

Задача 14

Решение

Задача 15

Решение

Задача 16

Решение

Задача 17

Решение

Задача 18

Решение

Задача 19

Решение

Задача 20

Решение

Рекомендуемые курсы подготовки

Задание 1

Кинематика

Механическое движение и его виды

Относительность механического движения

Правило сложения перемещений

Правило сложения скоростей

Относительная скорость

Скорость

Ускорение

Равномерное движение

График скорости (проекции скорости)

График перемещения (проекции перемещения)

Прямолинейное равноускоренное движение

Свободное падение (ускорение свободного падения)

Движение тела по вертикали

Движение тела, брошенного горизонтально

Движение тела, брошенного под углом к горизонту (баллистическое движение)

Движение по окружности с постоянной по модулю скоростью

Основные формулы по теме «Кинематика»