Корень — вегетативный орган растения, обладающий положительным геотропизмом (растет по направлению силы притяжения), имеющий цилиндрическую форму и радиальную симметрию. До тех пор пока на кончике корня есть верхушечная (апикальная) меристема, корень способен к росту. Ключевое отличие корня от побега в том, что
верхушечная меристема защищена корневым чехликом, который покрывает ее. Запомните также, что на корне никогда нельзя найти листья. Основные функции корня:
- Опорная функция — закрепляет растение в почве (заякоривание)
- Всасывание воды и растворенных в ней минеральных веществ из почвенного раствора
- Синтез органических веществ — в клетках корня происходит образование важных для растения соединений (алкалоиды, гормоны, аминокислоты)
- Запасание питательных веществ — корень накапливает крахмал, масла
- Вегетативное размножение — может осуществляться частями корня
- Симбиоз с бактериями, грибами
Иногда на корнях закладываются придаточные почки — так называют почки, которые закладываются вне типичных мест развития почек (вне пазухи листа и верхушки побега). Из них прорастают побеги, часто называемые корневой порослью или корневыми отпрысками.
Клубеньковые (азотфиксирующие) бактерии объединяются на корнях в особые образования — клубеньки. Эти бактерии способны преобразовывать
атмосферный азот (молекулярное вещество) в азотсодержащие сложные вещества, которые усваиваются растениями. С мицелием грибов корень образует
симбиоз, который называется микориза (или грибокорень).
Корневая система и происхождение корней
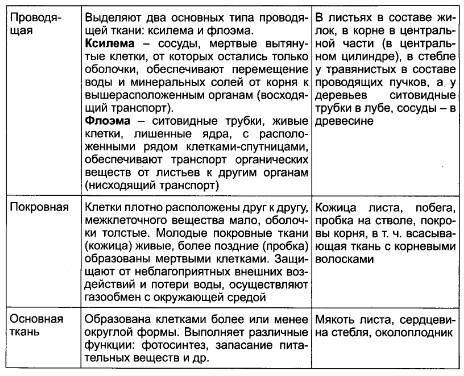
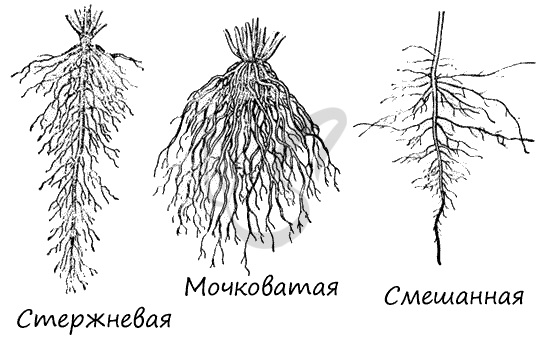
Корневую систему образуют в совокупности все корни растения. Она обеспечивает надежное заякоривание растения в почве. У растений встречается три основных типа:
- Стержневая корневая система
- Мочковатая корневая система
- Смешанная корневая система
Хорошо выражен, развит главный корень, выделяется на фоне остальных корней. Боковые и придаточные корни не выделяются, занимают по отношению
к главному подчиненное положение. Характерна для двудольных растений: клевера, одуванчика лекарственного, лопуха большого.
Главный корень не развит или быстро отмирает, преобладают придаточные корни, растущие от побега. Корни равнозначны между собой. Мочковатая система характерна для большинства однодольных растений: лук репчатый, злаки. Для некоторых двудольных: подорожник большой, лютик едкий.
Можно отличить главный корень, он выделяется по размеру. Однако, хорошо развиты множественные придаточные и боковые корни. Смешанная корневая
система характерна для клубники, земляники.
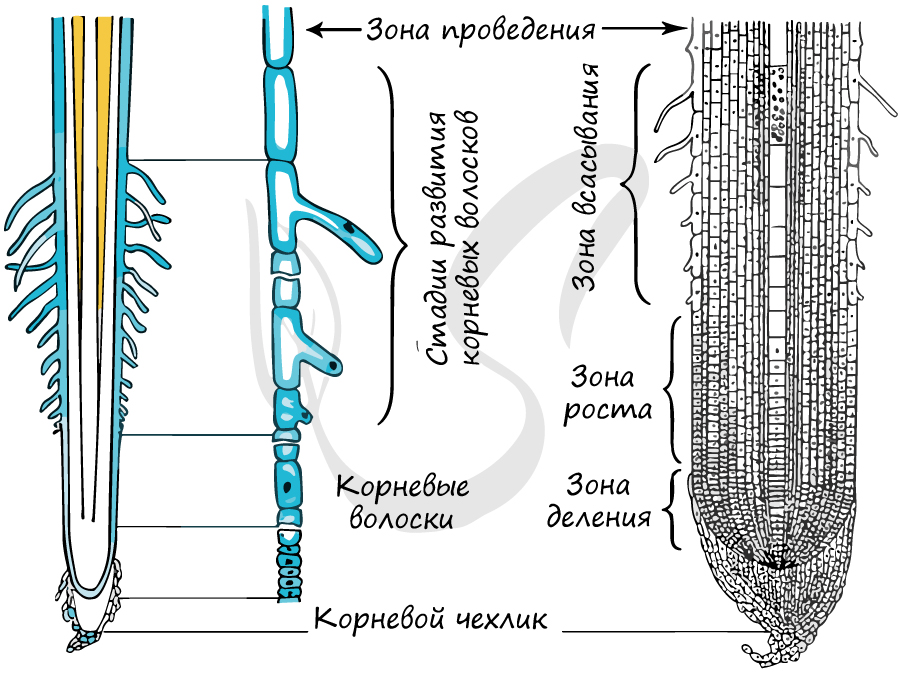
Зоны корня
Зоны корня являются отражением его роста и развития. Я всегда говорю учениками, что воображение — это самое важное. Представьте корень, растущий вглубь
почвы. Он сталкивается со множеством проблем и задач, которые зоны корня помогают решать. По мере роста вглубь, зоны корня сменяют друг друга в
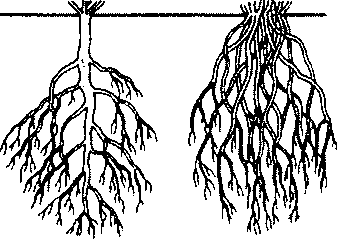
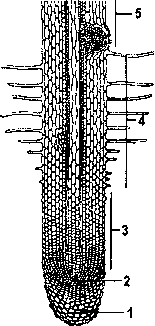
направлении роста. Итак, какие же зоны корны выделяют?
- Зона размножения (деления)
- Зона роста (растяжения)
- Зона всасывания
- Зона проведения
Это зона представлена мелкими, быстро делящимися клетками верхушечной (апикальной) меристемы, расположенной на верхушке конуса нарастания. Такие молодые
клетки особенно уязвимы, поэтому с целью защиты зону размножения покрывает корневой чехлик. Его клетки постоянно погибают от соприкосновения с почвой,
образуя слизистый чехол, способствующий росту корня вглубь почвы и снижающий трение о почву.
Корневой чехлик у злаковых растений образуется из меристематических клеток, совокупность которых называется калиптрогеном. У двудольных растений имеется
дерматокалиптроген, из которого помимо корневого чехлика развивается протодерма, из которой далее дифференцируется ризодерма (эпиблема).
В этой зоне поделившиеся «молодые клетки — взрослеют», набирают цитоплазматическую массу, увеличиваются в размерах. Именно за счет их роста зона деления
корня проталкивается вглубь почвы, что и обеспечивает рост корня.
Здесь происходит дифференцировка клеток, формируются основные типы тканей. Клетки ризодермы (эпиблемы) образуют корневые волоски — волосовидный вырост. Важно отметить, что
корневой волосок это вырост одной клетки. Однако клеток очень много, и в совокупности все их корневые волоски существенно увеличивают площадь всасывания корня.
Врастая в почву, корневые волоски выполняют одну из важнейших функций корня — всасывание воды и растворенных в ней минеральных солей из почвенного раствора. По длине зона
всасывания занимает 1-1,5 см.
По мере роста корня вглубь почвы корневые волоски отпадают, когда-то активная зона всасывания теперь становится другой крайне важной зоной — проведения. По протяженности
зона проведения корня превосходит все остальные: она тянется вплоть до корневой шейки — места перехода корня в стебель, достигает десятков сантиметров.
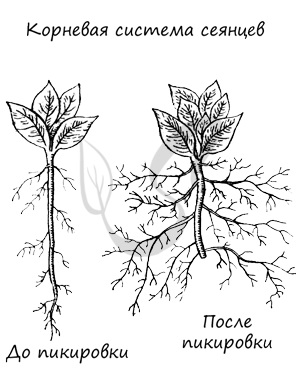
Пикирование (пикировка) корня
Это удаление верхушки главного корня вместе с зоной размножения. Таким образом садоводы останавливают рост главного корня и стимулируют развитие боковых и
придаточных корней, корневая система получается разветвленной, и растение дает хороший урожай.
Корневое дыхание
В корнях идет процесс дыхания, подобно тому, как и в других органах. Для нормального роста и развития к корню должен поступать свежий воздух, содержащий кислород.
При плохой структуре почвы ее насыщение водой приводит к настоящему кислородному голоданию корней — асфиксии, и далеко не все растения устойчивы к этому явлению.
Есть виды, которые совершенно не переносят затоплений и требуют хорошей аэрации почвы — дуб черешчатый, бук.
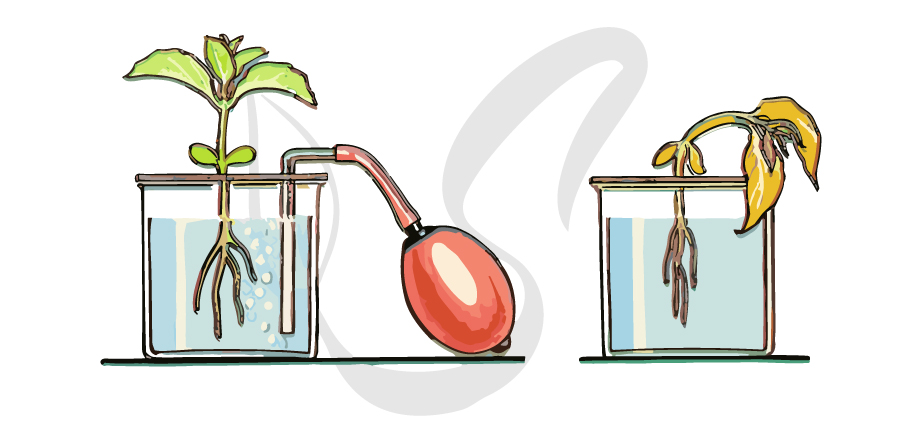
Отметьте для себя важность аэрации корней растения, посмотрев на следующий опыт. С помощью груши в левой части рисунка в воду накачивают воздух,
частично растворяющийся в воде — корни получают кислород, растение развивается. Справа корневое дыхание затруднено, развитие растения замедлено, и, если асфиксия
корней продолжится, растение погибнет.
Видоизменения корней
- Корнеплод
- Корневые клубни
- Питающие воздушные корни
- Корни прицепки (или корни-зацепки)
- Воздушные опорные корни (корни-подпорки)
- Дыхательные корни
- Ходульные корни
- Корни-присоски
- Клубеньки на корнях
Запасающий орган, в котором складируется крахмал, сахароза, белки, клетчатка, минеральные соли. Формируется корнеплод из главного корня и основания
стебля побега. Корнеплод характерен для двулетних растений: свеклы, петрушки, брюквы, моркови.
В первый год жизни у них формируется корнеплод с запасом питательных
веществ, к осени надземная часть отмирает. Следующей весной растение «оживает» именно благодаря запасу веществ в корнеплоде с прошлого года. На второй год
растения плодоносят и цветут, после чего отмирают полностью.
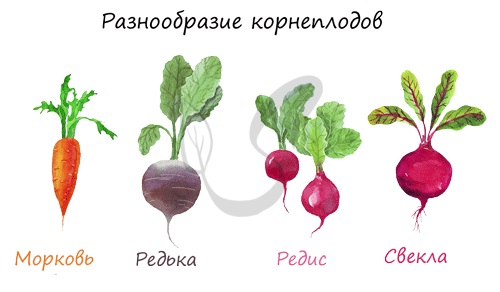
Представляют собой видоизменения боковых и придаточных корней. Выполняют запасающую функцию. Внешне утолщены и напоминают клубни. Имеются у чистяка,
ятрышника, георгина, батата (сладкий картофель).
Некоторые растения образуют корни в воздушной среде. Воздушные корни встречаются у лиан и эпифитов, растущих в условиях тропиков, где воздух настолько влажный, что из него в буквальном смысле можно всасывать воду, что и делают воздушные корни. Многослойная покровная ткань воздушных корней
подобно губке впитывает воду из влажного воздуха. Имеются у тропических папоротников, орхидеи, монстеры.
Слово эпифиты происходит от греч. ἐπι- — «на»
и φυτόν — «растение», так обозначают растения, прикрепленные или произрастающие на других растениях, при этом совершенно не получающие от них
питательных веществ, то есть явление паразитизма исключается.

Это видоизмененные придаточные корни, выполняющие опорную функцию. Они прикрепляют растения к объектам окружающей внешней среды: стволам деревьев, фасадам
зданий, корни прицепки помогают занять растению наиболее благоприятное с точки зрения освещенности место. Яркий примеры — плющ, ваниль.

Видоизмененные придаточные одревесневшие корни, растут на стволах и ветвях до почвы, у ее поверхности сильно разветвляются, тем самым «подпирая» растение. Придают опору
растению и его ветвям, закрепляют его в почве. Встречаются у тропических растений: баньян, фикус.

Формируются у растений, произрастающих в воде или на болоте, в качестве механизма адаптации к недостаточному снабжению корней воздухом. Они приподнимаются над
поверхностью воды и поглощают воздух. Такие корни имеет болотный кипарис (таксодиум).

Образуются на стволах деревьев для опоры. Могут поддерживать ствол дерева над уровнем воды при затоплениях, укрепляют растение в иле или
песчаном грунте приливной полосы морских побережий. Имеются у пандануса.

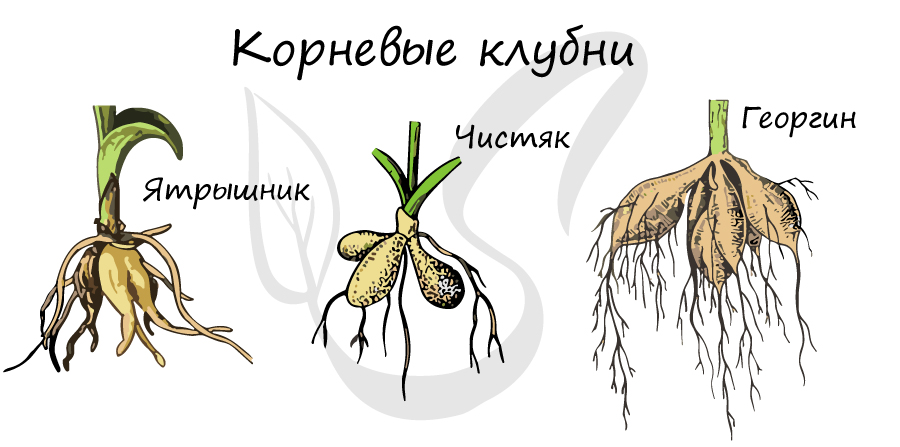
Видоизменения корней растений-паразитов, с помощью которых они высасывают питательные вещества из клеток растения-хозяина. Эти корни внедряются в стебли
других растений и поглощают их соки: воду, растворенные в ней минеральные вещества, органические вещества. Имеются у повилики и заразихи. У омелы, погремка
тоже имеются корни-присоски, но они всасывают только воду и растворенные в ней соли.
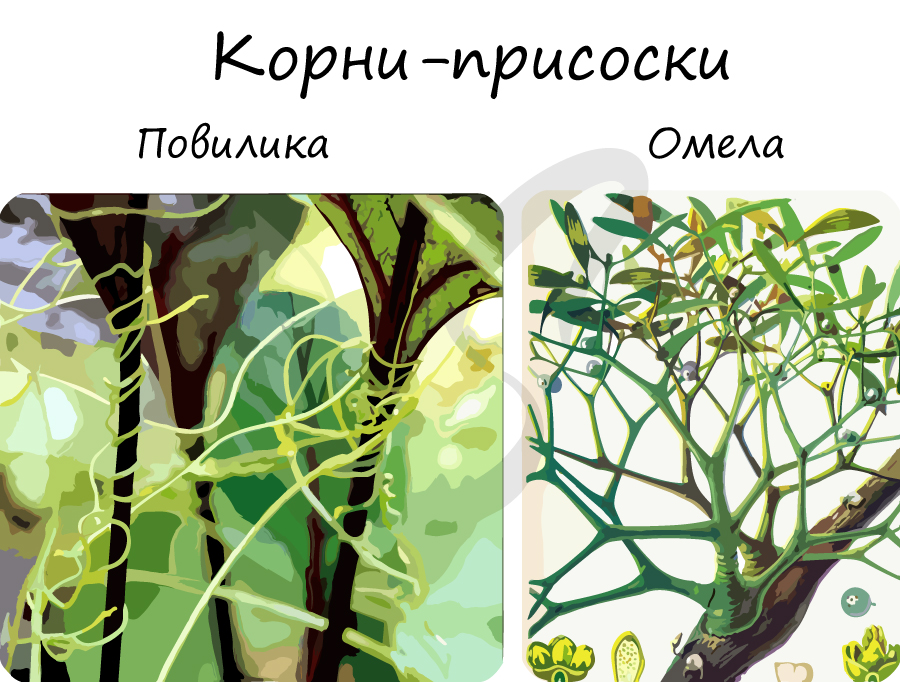
Бактериальные клубеньки представляют собой видоизмененные боковые корни, которые образуются в результате симбиоза растения и азотфиксирующих бактерий.

© Беллевич Юрий Сергеевич 2018-2023
Данная статья написана Беллевичем Юрием Сергеевичем и является его интеллектуальной собственностью. Копирование, распространение
(в том числе путем копирования на другие сайты и ресурсы в Интернете) или любое иное использование информации и объектов
без предварительного согласия правообладателя преследуется по закону. Для получения материалов статьи и разрешения их использования,
обратитесь, пожалуйста, к Беллевичу Юрию.
Скачать материал

Скачать материал




- Сейчас обучается 45 человек из 23 регионов


- Сейчас обучается 82 человека из 39 регионов


Описание презентации по отдельным слайдам:
-
-
2 слайд
Рассмотрите изображённые на рисунке объекты. Объясните причину группировки изображений (А,Б). Что представляют собой органы, обозначенные цифрой 3 на объекте д? Каковы их основные функции?
А – стержневая корневая система, Б – мочковатая корневая система;
видоизменённые придаточные корни (корнеклубни);
функции – запасают вещества и обеспечивают вегетативное размножение. -
3 слайд
Найдите ошибки в приведённом тексте, исправьте их, и укажите номера предложений, в которых они сделаны, запишите эти предложения без ошибок.
1. Придаточные корни развиваются на главном корне. 2. Боковые корни развиваются на главном и придаточных корнях. 3. Однодольные, как правило, имеют хорошо развитый главный корень и стержневую корневую систему. 4. Образование боковых корней происходит в зоне проведения. 5. По древесине корней вода движется в направлении от побега. 6. Зона деления корня расположена на границе с корневым чехликом.1 – придаточные корни развиваются только на листьях и стеблях;
3 – однодольные имеют придаточные корни, которые образуют мочковатую корневую систему;
5 – по древесине движется к побегу. -
4 слайд
Какие процессы обеспечивают передвижение воды и минеральных веществ по растению?
Из корня в листья вода и минеральные вещества передвигаются за счёт транспирации, в результате которой возникает сосущая сила, силы взаимного сцепления молекул воды между собой.
Восходящему току в растении способствует корневое давление, которое возникает в результате постоянного поступления воды в корень за счёт разницы концентраций веществ в клетках и окружающей среде. -
5 слайд
Какие функции выполняют различные зоны молодого корня растения? Укажите не менее четырёх функций.
В зоне деления увеличивается число молодых клеток, обеспечивая рост корня в длину.
В зоне роста клетки увеличиваются в размере, происходит их дифференцировка.
В зоне всасывания корневые волоски поглощают из почвы воду с растворёнными в ней минеральными веществами.
В зоне проведения осуществляется передвижение веществ. -
6 слайд
Рассмотрите на рисунке изображённый объект. Что представляют образования, обозначенные цифрой 1? Какое значение они имеют?
Клубеньки на корнях бобового растения.
Клубеньковые бактерии (азотофиксирующие)
способны фиксировать атмосферный азот, переводя его в связанное состояние.
3. Часть азотистых соединений усваивает растение, а бактерии используют вещества, находящиеся в корнях растения –хозяина. -
7 слайд
Объясните, почему при выращивании бобовых растений не требуется подкормка азотными удобрениями?
У бобовых на корнях поселяются клубеньковые бактерии.
Они усваивают азот воздуха и обеспечивают растения азотными удобрениями -
8 слайд
Рассмотрите на рисунке процесс роста корней, установите последовательность развития частей корневой системы. Как называется изображённая здесь корневая система? Для каких растений она характерна?
1- главный корень; 2 – боковые корни; 3 – придаточные корни.
Корневая система называется стержневой.
Характерна для двудольных растений. -
9 слайд
Рассмотрите на рисунке схему развития корневой системы у молодого проростка растения. Отметьте его составные части. Какова особенность клеток различных участков корня?
1- корневой чехлик; 2-3 – участок роста корня;
4-5 – всасывающий участок корня.Клетки корневого чехлика крупные, имеют
плотную оболочку, долго не живут.Клетки растущего участка корня имеют тонкую оболочку и крупные ядра. Делясь, они образуют новые клетки.
Корневые волоски представляют собой сильно удлинённый вырост наружной кожицы корня.
живут недолго, отмирая, заменяются новыми. -
10 слайд
Пользуясь изображением корневых систем различных растений, объясните, какие из этих корней характерны для растений пустынь (засушливых районов), болотистой местности, умеренно увлажнённых мест, влажных мест и водоёмов. Укажите причину, влияющую на развитие корневой системы.
1) 1 — Растения с воздушными корнями обитают во влажных тропических лесах; приспособлены к поглощению влаги, попадающих на них в виде дождя или росы.
2) 2 – Растения водоёмов имеют слаборазвитую корневую систему.
3) 3 — 4 — Растения засушливых мест (пустыни) имеют корни либо у поверхности почвы, либо глубоко проникающие ( до 15 м).
4) 5 – Корни растений умеренно увлажнённых мест.
5) 6 – Корни растений, произрастающих на болотистых почвах, располагаются у поверхности почвы, приспособлены к недостатку воздуха в болотистых почвах. -
11 слайд
Рассмотрите изображённые на рисунке объекты. Сравните их и объясните, какая существует связь между положением листьев и развитием корней у этих растений.
Листья «направляют» атмосферные осадки к всасывающей части корней.
У первого растения листовая пластинка приподнята вверх под углом, способствующему стеканию воды у основания листа, к боковым и придаточным корням, расположенным вдоль главного корня и уходящим глубоко в почву.
У второго и третьего растений листовые пластинки наклоняются вниз под углом, что способствует стеканию воды к корневой системе, которая разрастается в верхнем слое почвы.
Положение листьев способствует наиболее эффективному использованию атмосферных осадков корнями растений. -
12 слайд
Рассмотрите изображённые на рисунке растения одного вида и определите, почему у растений по — разному развиты корневая система и надземная часть. С чем это связано?
Первая сосна произрастает на песчаных почвах и имеет хорошо развитую
корневую систему.2. Вторая сосна растёт на болоте.
-
13 слайд
Объясните, почему у росянки корневая система «многоэтажная», к тому же корни нарастают не в глубину, кверху?
«Многоэтажность» корневой системы росянки вызвана ежегодным нарастанием мха, среди которого она растёт. -
14 слайд
Рассмотрите изображённые на рисунке объекты. Что представляют собой органы, обозначенные цифрами 1 – 4? Каковы их основные функции?
1 -2 -видоизменённые придаточные корни (корнеклубни).
3-4 -видоизменённые главные корни (корнеплоды)
Накапливают питательные вещества, которые расходуются растением на последующем году жизни и обеспечивают вегетативное размножение.1 2 3 4
-
15 слайд
Каким образом получают питательные вещества, необходимые для роста и развития , образования цветков и плодов растения, не имеющие корней? Как называются эти растения?
Растения –паразиты (повилика, заразиха).
Не имея корней они живут за счёт растений. На которых паразитируют. -
16 слайд
Рассмотрите изображённый на рисунке объект. Что представляет собой орган, обозначенный цифрой 2? Какую функцию он выполняет?
1. Видоизменённые придаточные корни (корни- подпорки, столбовидные
корни).
2. Достигнув почвы, они сильно разрастаются. Превращаясь в столбовидные образования, поддерживающие крону деревьев.
3. Такие корни-подпорки позволяют дереву разрастись в стороны, покрывая площадь до 2500 квад.см. -
17 слайд
В тропических странах встречаются деревья, корни которых растут вверх и выходят на поверхность земли, как забитые колья. С чем это связано? В каких условиях они обитают?
Мангровые растения растут на заиленных берегах тропических морей, где для корней мало кислорода в почве.
Поэтому надземные части корней предназначены для дыхания. -
18 слайд
Рассмотрите изображённый на рисунке объект. Что представляет собой орган, обозначенный цифрой 1? Какую функцию он выполняет?
1
Корни являются видоизменёнными
придаточными корнями (воздушные корни) эпифитов.Воздушные корни свободно висят в воздухе и приспособлены к поглощению влаги, попадающей на них в виде дождя или росы.
Эпифиты используют воздушные корни как субстрат, подпорку, для поднятия вверх, к свету.
-
19 слайд
Корневые системы разрастаются вглубь и вширь. Иногда они имеют причудливые формы и как «ходули» возвышаются над поверхностью почвы. Объясните, в чём причина появления таких видоизменённых корней и видоизменением каких видов корней они являются?
Корни являются видоизменёнными
придаточными корнями (ходульные корни).Ходульные корни образуются у деревьев, живущих в мангровых зарослях по берегам океанов.
Благодаря сильно разветвлённым корням деревья стоят словно на ходулях и сохраняют устойчивость на зыбком илистом грунте даже во время отлива, распределяя свою массу на большую площадь опоры («лыжный эффект»)
-
20 слайд
Во влажных тропических лесах произрастают очень высокие (более 80 м) деревья с огромными кронами: кампасия, птерокарпус и другие. У основания стволов этих деревьев часто отходят в стороны могучие досковидные боковые выросты, достигающие шести-девятиметровой высоты. Видоизменением каких видов корней они являются и какую функцию выполняют эти видоизменённые корни?
Корни являются видоизменениями
придаточных корней (досковидные корни).2. Досковидные корни придают огромному
дереву устойчивость и помогают переносить частые тропические бури
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 153 956 материалов в базе
-
Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
Другие материалы







Тест по ботанике «Корень»
- Учебник: «Биология. Бактерии, грибы, растения», Пасечник В.В.
- Тема: § 19. Виды корней и типы корневых систем
Рейтинг:
3 из 5
- 14.04.2018
- 4678
- 31

Вам будут интересны эти курсы:
-
Курс повышения квалификации «ФГОС общего образования: формирование универсальных учебных действий на уроке биологии»
-
Курс повышения квалификации «Методические аспекты реализации элективного курса «Антропология и этнопсихология» в условиях реализации ФГОС»
-
Курс повышения квалификации «Государственная итоговая аттестация как средство проверки и оценки компетенций учащихся по биологии»
-
Курс повышения квалификации «Нанотехнологии и наноматериалы в биологии. Нанобиотехнологическая продукция»
-
Курс повышения квалификации «Основы биоэтических знаний и их место в структуре компетенций ФГОС»
-
Курс профессиональной переподготовки «Анатомия и физиология: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Гендерные особенности воспитания мальчиков и девочек в рамках образовательных организаций и семейного воспитания»
-
Курс профессиональной переподготовки «Организация производственно-технологической деятельности в области декоративного садоводства»
-
Курс повышения квалификации «Составление и использование педагогических тестов при обучении биологии»
-
Курс повышения квалификации «Инновационные технологии обучения биологии как основа реализации ФГОС»
-
Курс профессиональной переподготовки «Организация и выполнение работ по производству продукции растениеводства»
Что такое арифметический квадратный корень
Квадратным корнем (арифметическим квадратным корнем) из неотрицательного числа (a) называется такое неотрицательное число, квадрат которого равен (a). ( (sqrt{a}=x, {{x}^{2}}=a; x, age 0)).
А почему же число ( a) (число под корнем) должно быть обязательно неотрицательным?
Например, чему равен ( sqrt{-9})?
Так-так, попробуем подобрать. Может, три?
Проверим: ( {{3}^{2}}=9), а не ( -9).
Может, ( left( -3 right))?
Опять же, проверяем: ( {{left( -3 right)}^{2}}=9).
Ну что же, не подбирается?
Это и следовало ожидать – потому что нет таких чисел, которые при возведении в квадрат дают отрицательное число! Это надо запомнить!
Число или выражение под знаком корня должно быть неотрицательным!
Однако ты наверняка уже заметил, что не только число под корнем должно быть неотрицательным, но и само значение тоже должно быть неотрицательным!
Ведь в определении сказано, что «квадратным корнем из числа( a)называется такое неотрицательное число, квадрат которого равен( a)».
Но подождите! В самом начале мы разбирали пример ( {{x}^{2}}=4) и один из ответов был отрицательным числом!
Мы подбирали числа, которые можно возвести в квадрат и получить при этом ( displaystyle 4). Ответом были ( displaystyle 2) и ( displaystyle -2)
А тут говорится, что квадратным корнем должно быть «неотрицательное число»! Почему?
Такой вопрос вполне уместен. Здесь необходимо просто разграничить понятия квадратного уравнения и арифметического квадратного корня.
К примеру, ( displaystyle {{x}^{2}}=4) (квадратное уравнение) не равносильно выражению ( x=sqrt{4}) (арифмитический квадратный корень).
Из ( {{x}^{2}}=4) следует, что
( left| x right|=sqrt{4}), то есть ( x=pm sqrt{4}=pm 2) или ( {{x}_{1}}=2); ( {{x}_{2}}=-2)
(не помнишь почему так? Почитай тему “Модуль числа”!)
А из ( x=sqrt{4}) следует, что ( x=2).
Конечно, это очень путает, но это необходимо запомнить, что знаки “плюс-минус” являются результатом решения квадратного уравнения, так как при решении уравнения мы должны записать все иксы, которые при подстановке в исходное уравнение дадут верный результат.
В наше квадратное уравнение подходит как ( 2), так и ( x=-2).
Однако, если просто извлекать квадратный корень из чего-либо, то всегда получаем один неотрицательный результат.
Запись иррациональных чисел с помощью квадратного корня
А теперь попробуй решить такое уравнение ( {{x}^{2}}=3).
Уже все не так просто и гладко, правда? Попробуй перебрать числа, может, что-то и выгорит?
Начнем с самого начала – с нуля: ( {{0}^{2}}=0) – не подходит.
Двигаемся дальше ( displaystyle x=1); ( displaystyle {{1}^{2}}=1) – меньше трех, тоже отметаем.
А что если ( displaystyle x=2)?
Проверим: ( displaystyle {{2}^{2}}=4) – тоже не подходит, т.к. это больше трех.
С отрицательными числами получится такая же история.
И что же теперь делать? Неужели перебор нам ничего не дал?
Совсем нет, теперь мы точно знаем, что ответом будет некоторое число между ( displaystyle 1) и ( displaystyle 2), а также между ( displaystyle -2) и ( displaystyle -1).
Кроме того, очевидно, что решения не будут целыми числами. Более того, они не являются рациональными.
И что дальше?
Давай построим график функции ( displaystyle y={{x}^{2}}) и отметим на нем решения.
Попробуем обмануть систему и получить ответ с помощью калькулятора (как мы это делали в начале)!
Извлечем корень из ( displaystyle 3), делов-то!
Ой-ой-ой, выходит, что ( sqrt{3}=1,732050807568ldots ) Такое число никогда не кончается.
Как же такое запомнить, ведь на экзамене калькулятора не будет!?
Все очень просто, это и не надо запоминать, необходимо помнить (или уметь быстро прикинуть) приблизительное значение. ( sqrt{3}) и ( -sqrt{3}) уже сами по себе ответы.
Такие числа называются иррациональными, именно для упрощения записи таких чисел и было введено понятие квадратного корня.
Деление корней
С умножением корней разобрались, теперь приступим к свойству деления.
Напомню, что формула в общем виде выглядит так:
( displaystyle sqrt[{}]{frac{a}{b}}=frac{sqrt[{}]{a}}{sqrt[{}]{b}}), если ( displaystyle age 0 , b>0).
А значит это, что корень из частного равен частному корней.
Ну что, давай разбираться на примерах:
( displaystyle frac{sqrt{12}}{sqrt{3}}=sqrt{frac{12}{3}}=sqrt{4}=2)
Вот и вся наука. А вот такой пример:
( displaystyle frac{sqrt{12}}{3}=frac{sqrt{12}}{sqrt{9}}=sqrt{frac{12}{9}}=sqrt{frac{4}{3}}=frac{2}{sqrt{3}})
Все не так гладко, как в первом примере, но, как видишь, ничего сложного нет.
А что, если попадется такое выражение:
( displaystyle sqrt{frac{144}{225}}=?)
Надо просто применить формулу в обратном направлении:
( displaystyle sqrt{frac{144}{225}}=frac{sqrt{144}}{sqrt{225}}=frac{12}{15}=frac{4}{5}=0,8)
А вот такой примерчик:
( displaystyle sqrt{0,16}=sqrt{frac{16}{100}}=frac{4}{10}=0,4)
Еще ты можешь встретить такое выражение:
( displaystyle sqrt{5frac{19}{25}}=?)
Все то же самое, только здесь надо вспомнить, как переводить дроби (если не помнишь, загляни в тему дроби и возвращайся!). Вспомнил? Теперь решаем!
( displaystyle sqrt{5frac{19}{25}}=sqrt{frac{144}{25}}=frac{12}{5}=2,4)
Уверена, что ты со всем, всем справился, теперь попробуем возводить корни в степени.
Возведение в степень
А что же будет, если квадратный корень возвести в квадрат? Все просто, вспомним смысл квадратного корня из числа ( displaystyle a) – это число, квадратный корень которого равен ( displaystyle a).
Так вот, если мы возводим число, квадратный корень которого равен ( displaystyle a), в квадрат, то что получаем?
Ну, конечно, ( displaystyle a)!
Рассмотрим на примерах:
( displaystyle {{left( sqrt{12} right)}^{2}}=12)
( displaystyle {{left( sqrt{17} right)}^{2}}=17)
Все просто, правда? А если корень будет в другой степени? Ничего страшного!
Придерживайся той же логики и помни свойства и возможные действия со степенями.
Забыл?
Почитай теорию по теме «Степень и ее свойства» и тебе все станет предельно ясно.
Вот, к примеру, такое выражение:
( displaystyle {{left( sqrt{5} right)}^{6}}={{left( {{left( sqrt{5} right)}^{2}} right)}^{3}}={{5}^{3}}=125)
В этом примере степень четная, а если она будет нечетная? Опять же, примени свойства степени и разложи все на множители:
( displaystyle {{left( sqrt{5} right)}^{7}}={{left( sqrt{5} right)}^{6}}cdot sqrt{5}=125sqrt{5})
С этим вроде все ясно, а как извлечь корень из числа в степени? Вот, к примеру, такое:
( displaystyle sqrt{{{3}^{2}}}=sqrt{9}=3)
Довольно просто, правда? А если степень больше двух? Следуем той же логике, используя свойства степеней:
( displaystyle sqrt{{{3}^{6}}}=sqrt{{{left( {{3}^{3}} right)}^{2}}}={{3}^{3}}=27)
( displaystyle sqrt{{{3}^{5}}}=sqrt{{{3}^{4}}cdot 3}=sqrt{{{left( {{3}^{2}} right)}^{2}}cdot 3}={{3}^{2}}cdot sqrt{3}=9sqrt{3})
Ну как, все понятно? Тогда реши самостоятельно примеры:
- ( displaystyle sqrt{{{left( -3 right)}^{2}}})
- ( displaystyle sqrt{{{6}^{6}}})
- ( displaystyle {{left( sqrt{8} right)}^{7}})
А вот и ответы:
Внесение под знак корня
Что мы только не научились делать с корнями! Осталось только потренироваться вносить число под знак корня!
Это совсем легко!
( displaystyle 4sqrt{6}-2sqrt{3}cdot sqrt{8}=sqrt{16cdot 6}-sqrt{4cdot 3cdot 8}=sqrt{96}-sqrt{96}=0)
Допустим, у нас записано число ( displaystyle 3sqrt{5})
Что мы можем с ним сделать? Ну конечно, спрятать тройку под корнем, помня при этом, что тройка – корень квадратный из ( displaystyle 9)!
( displaystyle 3sqrt{5}=sqrt{9}cdot sqrt{5}=sqrt{45})
Зачем нам это нужно? Да просто, чтобы расширить наши возможности при решении примеров:
( displaystyle 3sqrt{10}-sqrt{45}cdot sqrt{2}=sqrt{90}-sqrt{90}=0)
Как тебе такое свойство корней? Существенно упрощает жизнь? По мне, так точно! Только надо помнить, что вносить под знак квадратного корня мы можем только положительные числа.
Реши самостоятельно вот этот пример – ( displaystyle 4sqrt{6}-2sqrt{3}cdot sqrt{8})
Справился? Давай смотреть, что у тебя должно получиться:
( displaystyle 4sqrt{6}-2sqrt{3}cdot sqrt{8}=sqrt{16cdot 6}-sqrt{4cdot 3cdot 8}=sqrt{96}-sqrt{96}=0)
Молодец! У тебя получилось внести число под знак корня! Перейдем к не менее важному – рассмотрим, как сравнивать числа, содержащие квадратный корень!
Сравнение корней
Зачем нам учиться сравнивать числа, содержащие квадратный корень?
Очень просто. Часто, в больших и длиииинных выражениях, встречающихся на экзамене, мы получаем иррациональный ответ (помнишь, что это такое? Мы с тобой сегодня об этом уже говорили!)
Полученные ответы нам необходимо расположить на координатной прямой, например, чтобы определить, какой интервал подходит для решения уравнения. И вот здесь возникает загвоздка: калькулятора на экзамене нет, а без него как представить какое число больше, а какое меньше? То-то и оно!
Например, определи, что больше: ( displaystyle 3sqrt{7}) или ( displaystyle 2sqrt{17})?
Сходу и не скажешь. Ну что, воспользуемся разобранным свойством внесения числа под знак корня?
Тогда вперед:
( displaystyle 3sqrt{7}=sqrt{9cdot 7}=sqrt{63})
( displaystyle 2sqrt{17}=sqrt{4cdot 17}=sqrt{68})
Ну и, очевидно, что чем больше число под знаком корня, тем больше сам корень!
Т.е. если ( displaystyle 68>63), значит, ( displaystyle sqrt{68}>sqrt{63}).
Отсюда твердо делаем вывод, что ( displaystyle 3sqrt{7}<2sqrt{17}).
И никто не убедит нас в обратном!
Извлечение корней из больших чисел
До этого мы вносили множитель под знак корня, а как его вынести? Надо просто разложить его на множители и извлечь то, что извлекается!
( displaystyle sqrt{98}=sqrt{49cdot 2}=sqrt{49}cdot sqrt{2}=7sqrt{2})
Можно было пойти по иному пути и разложить на другие множители:
( displaystyle sqrt{98}=sqrt{7cdot 14})
Что дальше? А дальше раскладываем на множители до самого конца:
( displaystyle sqrt{98}=sqrt{7cdot 14}=sqrt{7cdot 7cdot 2}=sqrt{{{7}^{2}}cdot 2}=7sqrt{2})
Неплохо, да? Любой из этих подходов верен, решай как тебе удобно.
Разложение на множители очень пригодится при решении таких нестандартных заданий, как вот это:
( displaystyle sqrt{15}cdot sqrt{180}cdot sqrt{12})
Не пугаемся, а действуем! Разложим каждый множитель под корнем на отдельные множители:
А теперь попробуй самостоятельно (без калькулятора! его на экзамене не будет):
( displaystyle sqrt{15}cdot sqrt{180}cdot sqrt{12}=sqrt{5cdot 3}cdot sqrt{36cdot 5}cdot sqrt{2cdot 6})
Разве это конец? Не останавливаемся на полпути!
( displaystyle begin{array}{l}sqrt{5cdot 3}cdot sqrt{36cdot 5}cdot sqrt{2cdot 6}=sqrt{5cdot 3}cdot sqrt{3cdot 12cdot 5}cdot sqrt{2cdot 3cdot 2}=\=sqrt{5cdot 3}cdot sqrt{3cdot 2cdot 2cdot 3cdot 5}cdot sqrt{2cdot 3cdot 2}end{array})
На простые множители разложили. Что дальше? А дальше пользуемся свойством умножение корней и записываем все под одним знаком корня:
( displaystyle begin{array}{l}sqrt{5cdot 3cdot 3cdot 2cdot 2cdot 3cdot 5cdot 2cdot 3cdot 2}=sqrt{5cdot 5cdot 3cdot 3cdot 3cdot 3cdot 2cdot 2cdot 2cdot 2}=\=sqrt{25}cdot sqrt{81}cdot sqrt{16}=5cdot 9cdot 4=180end{array})
Вот и все, не так все и страшно, правда?
( displaystyle sqrt{15}cdot sqrt{54}cdot sqrt{10}=?)
Получилось ( displaystyle 90)? Молодец, все верно!
А теперь попробуй вот такой пример решить:
( displaystyle sqrt{4225}=?)
А пример-то – крепкий орешек, так сходу и не разберешься, как к нему подступиться. Но нам он, конечно, по зубам.
ЗАДАНИЕ
А11
РАСТЕНИЯ.
СТРОЕНИЕ, ЖИЗНЕДЕЯТЕЛЬНОСТЬ, РАЗМНОЖЕНИЕ
ЦВЕТКОВЫХ РАСТЕНИЙ
ЭЛЕМЕНТЫ
СОДЕРЖАНИЯ,
ПРОВЕРЯЕМЫЕ
НА ЕГЭ
-
Царство
растений. Строение (ткани, клетки,
органы), жизнедеятельность и
размножение растительного организма
(на примере покрытосеменных растений).
Распознавание (на рисунках) органов
растений.
ХАРАКТЕРНЫЕ
ОСОБЕННОСТИ РАСТЕНИЙ
-
Растения
— фотоавтотрофы, т. е. производят
органические вещества из неорганических,
используя энергию света в процессе
фотосинтеза. -
Для
растений характерен неограниченный
верхушечный рост. -
Большинство
растений (за исключением некоторых
одноклеточных водорослей, например
хламидомонады) не передвигаются. -
Клетки
растений имеют клеточную стенку из
целлюлозы, пластиды (в т. ч. зеленые
— хлоропласты, содержащие главный
пигмент фотосинтеза — хлорофилл), крупные
вакуоли (по мере взросления клетки
мелкие вакуоли сливаются в одну большую). -
В
качестве запасного углевода растения
откладывают крахмал.
ТКАНИ
И ОРГАНЫ
Растительные
ткани
ОРГАНЫ
ЦВЕТКОВОГО РАСТЕНИЯ
К
вегетативным
органам
относятся корень и побег (стебель с
листьями и почками), обеспечивающие
жизнедеятельность растения и участвующие
в бесполом размножении.
Генеративные
органы
(цветок, плод, семя) обеспечивают
половое размножение растений.
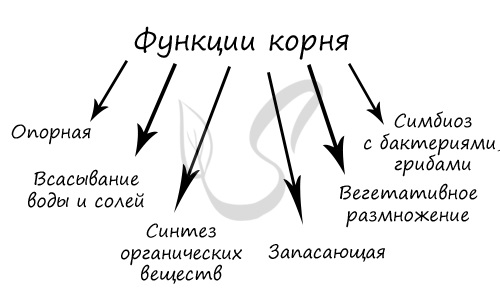
Функции
корня
(типичные):
-
закрепление
растения в почве; -
почвенное
питание (поглощение воды и минеральных
солей); -
запасание
питательных веществ; -
вегетативное
размножение.
КОРЕНЬ
Виды
корней: главный-1, придаточные —
2, боковые
—
3
Виды
корней
Главный
—
корень, развивающийся из зародышевого
корешка семени. Имеется только у
растений, выросших из семени.
Придаточные
—
корни, развивающиеся на побеге (на
стебле, листьях).
Боковые
—
корни, образующиеся на любых других
корнях.
Рис.
Корневые системы: стержневая
— А, мочковатая
— Б
Корневые
системы
Корневая
система —
совокупность всех корней. Различают
два типа корневых систем: стержневые,
в
которых главный корень хорошо развит
и заметен, и мочковатые,
в
которых главный корень либо рано
отмирает, либо развит слабо. В основном
мочковатые системы образованы
придаточными и боковыми корнями.
Стержневая
корневая система характерна для
двудольных растений, мочковатая —
для однодольных. Кроме того, мочковатую
систему имеют растения, полученные
путем вегетативного размножения.
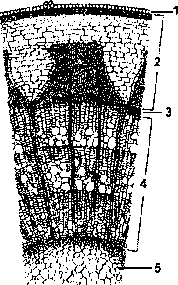
Зоны
корня
Зона
деления (2)
представлена образовательной тканью,
клетки которой делятся, образуя все
новые клетки корня. Обеспечивает рост
корня в длину. Снаружи зона деления
покрыта корневым
чехликом (1),
защищающим делящиеся клетки. Клетки
корневого чехлика выделяют слизь,
облегчающую продвижение корня в почве.
Зона
роста (3)
образована молодыми клетками. В зоне
роста клетки интенсивно растут,
растягиваются.
Зона
всасывания (4).
В этой зоне корня происходит всасывание
воды и минеральных солей. Клетки
покровной ткани образуют длинные
выросты – корневые волоски,
благодаря которым многократно
увеличивается площадь всасывающей
поверхности корня.
Зона
проведения (5)
служит для проведения поступивших в
корень воды и минеральных солей к
вышерасположенным органам растения.
Здесь же образуются боковые корни.
-
корнеплод
—
видоизмененный главный корень и нижняя
часть стебля (свекла, морковь), служит
для запасания питательных веществ; -
корнеклубни
—
утолщенные боковые корни (георгин,
батат), служат для запасания питательных
веществ; -
корни-прицепки
имеются
у лазающих растений (плющ); -
корни-присоски
характерны
для растений-паразитов (повилика,
петров крест); -
воздушные
корни имеются
у растений эпифитов (орхидеи); -
дыхательные
корни обеспечивают
газообмен у растений, обитающих на
заболоченных участках; -
корни-подпорки
(баньян),
ходульные
корни (кукуруза)
и досковидные
корни (некоторые
тропические виды) обеспечивают поддержку
надземных органов растения.
ПОБЕГ
Побег
—
стебель с расположенными на нем листьями
и почками.
ПОЧКА
Почка
—
зачаточный побег. По месту расположения
на побеге почки бывают:
Верхушечные
–
на вершине побега
Пазушные
(боковые)
–
в пазухах листа
Придаточные
–
располагаются на различных участках
вегетативных органов (кроме пазух
листа).
В
зависимости от внутреннего строения и
последующего развития почки делятся
на вегетативные,
из
которых развивается стебель с листьями,
и генеративные,
из
которых развивается цветоносный побег.
Существуют также смешанные почки.
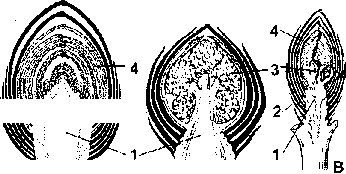
Рис.
11.5. Строение почки: А — вегетативная, Б
— генеративная, В – смешанная почка.
1- зачаточный стебель, 2-
почечные
чешуи 3- зачаточный цветок или соцветие,
4
—
зачаточные листья
ЛИСТ
Функиии
листа
(типичные):
-
фотосинтез;
-
газообмен;
-
испарение
воды (транспирация).
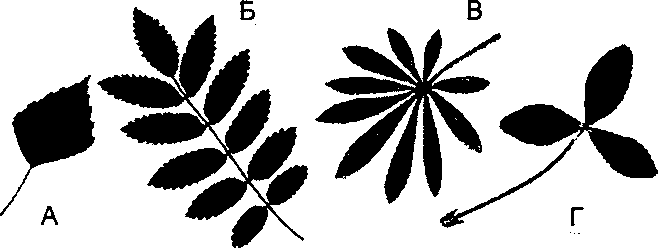
Внешнее
строение листа. Жилкование
1
– сетчатое
двудольные
растения
3
— дуговое
-
— Параллельное
Однодольные растения
Простые
и сложные листья
Основная
часть листа — листовая пластинка. Кроме
того, у листа могут быть или не быть
черешок и прилистники. Простые листья
имеют одну листовую пластинку, а сложные
— несколько.
1
— очередное (по одному в узле)
2
— супротивное (по два в узле)
3
— мутовчатое (по три и более в узле)
Рис.
11.6. Листья простые
(А) и
сложные
(Б, В, Г)
Расположение листьев (и почек)
Часто
у одного растения листовые пластинки
имеют неодинаковую величину, черешки
тоже неодинаковой длины и по-разному
изогнуты в пространстве. Например, у
плюща листовые пластинки всегда
повернуты к свету. Если вазон с плющом
повернуть, то через некоторое время
листья тоже повернутся к свету. В
результате листовые пластинки
располагаются так, что почти не затеняют
друг друга. Более мелкие листья заполняют
просветы между крупными. Такое
расположение листьев называют листовой
мозаикой.
Это способствует максимальному
использованию света. Светолюбивые
растения требуют больше света и в сильно
затененном месте растут плохо и погибают,
тенелюбивые растения – наоборот.
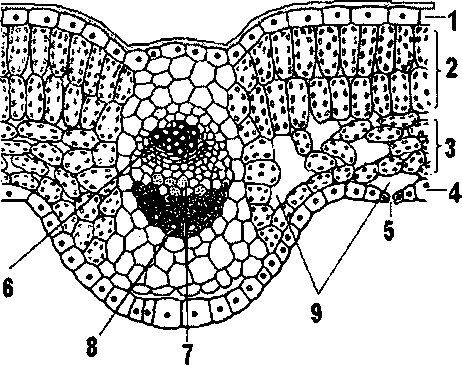
Листовая
мозаика
-
—
верхний эпидермис (кожица) — один
слой прозрачных клеток с толстой
оболочкой, не содержащих хлоропластов.
Поверх эпидермиса расположена
кутикула; -
—
столбчатая паренхима (столбчатый
мезофилл) основная фотосинтезирующая
ткань листа, образована вытянутыми
клетками с большим числом хлоропластов; -
—
губчатая паренхима (губчатый
мезофилл) также выполняет функцию
фотосинтеза. Крупные межклетники (9)
способствуют газообмену и
транспирации; -
—
нижний эпидермис, похож на верхний, но
содержит устьица 5, через которые и
происходит испарение воды и газообмен;
-
—
ксилема, т. е. сосуды, по которым движутся
вода и минеральные соли; -
—
флоэма, т. е. ситовидные трубки, по
которым движутся органические вещества; -
—
волокна механической ткани, обеспечивающие
механическую прочность листа;
Все
вместе они (6, 7 и образуют сосудисто-
волокнистый пучок, или жилку
Внутреннее
строение листа
Видоизменения
листьев
-
колючки
выполняют
защитную функцию, а также не испаряют
воду (кактус); -
усики
используются
для лазания (горох); -
ловчие
листья у
растений-хищников служат для ловли
добычи (росянка); -
сочные
листья у
растений-суккулентов содержат запас
воды (алоэ);
мясистые
чешуи луковичных
растений, содержащие запас воды и
питательных веществ, также представляют
собой видоизмененные листья.
Стебель
Функции
стебля (типичные)
-
опорная
—
выносят листья к свету; -
проводящая
—
проводят органические вещества от
листьев и воду с минеральными солями
от корней к другим органам; -
запасающая
—
стебли, не отмирающие на зиму, могут
содержать запас питательных веществ; -
фотосинтез
—
происходит обычно в молодых неодревесневших
стеблях.
Строение
древесного стебля
Корни и степени
-
Степень с натуральным показателем
-
Степень с целым показателем
-
Кубический корень
-
Корень -ной степени
-
Сравнение арифметических корней
-
Как избавиться от иррациональности в знаменателе
-
Как упрощать иррациональные выражения, пользуясь формулами сокращенного умножения
Степенью называется выражение вида .
Здесь — основание степени,
— показатель степени.
к оглавлению ▴
Степень с натуральным показателем
Проще всего определяется степень с натуральным (то есть целым положительным) показателем.
По определению, .
Выражения «возвести в квадрат» и «возвести в куб» нам давно знакомы.
Возвести число в квадрат — значит умножить его само на себя.
.
Возвести число в куб — значит умножить его само на себя три раза.
.
Возвести число в натуральную степень — значит умножить его само на себя
раз:
к оглавлению ▴
Степень с целым показателем
Показатель степени может быть не только натуральным (то есть целым положительным), но и равным нулю, а также целым отрицательным.
По определению,
.
Это верно для . Выражение 00 не определено.
Определим также, что такое степень с целым отрицательным показателем.
Конечно, все это верно для , поскольку на ноль делить нельзя.
Например,
Заметим, что при возведении в минус первую степень дробь переворачивается.
Показатель степени может быть не только целым, но и дробным, то есть рациональным числом. В статье «Числовые множества» мы говорили, что такое рациональные числа. Это числа, которые можно записать в виде дроби , где
— целое,
— натуральное.
Здесь нам понадобится новое понятие — корень -степени. Корни и степени — две взаимосвязанные темы. Начнем с уже знакомого вам арифметического квадратного корня.
Определение.
Арифметический квадратный корень из числа — это такое неотрицательное число, квадрат которого равен
.
Согласно определению,
В школьной математике мы извлекаем корень только из неотрицательных чисел. Выражение для нас сейчас имеет смысл только при
.
Выражение всегда неотрицательно, т.е.
. Например,
.
Свойства арифметического квадратного корня:
Запомним важное правило:
По определению, 
к оглавлению ▴
Кубический корень
Аналогично, кубический корень из — это такое число, которое при возведении в третью степень дает число
.
Например, , так как
;
, так как
;
, так как
.
Обратите внимание, что корень третьей степени можно извлекать как из положительных, так и из отрицательных чисел.
Теперь мы можем дать определение корня -ной степени для любого целого
.
к оглавлению ▴
Корень  -ной степени
-ной степени
Корень -ной степени из числа
— это такое число, при возведении которого в
-ную степень получается число
.
Например,
Заметим, что корень третьей, пятой, девятой — словом, любой нечетной степени, — можно извлекать как из положительных, так и из отрицательных чисел.
Квадратный корень, а также корень четвертой, десятой, в общем, любой четной степени можно извлекать только из неотрицательных чисел.
Итак, — такое число, что
. Оказывается, корни можно записывать в виде степеней с рациональным показателем. Это удобно.
По определению,
в общем случае .
Сразу договоримся, что основание степени больше 0.
Например,
Выражение по определению равно
.
При этом также выполняется условие, что больше 0.
Например,
Запомним правила действий со степенями:
— при перемножении степеней показатели складываются;
— при делении степени на степень показатели вычитаются;
— при возведении степени в степень показатели перемножаются;
Покажем, как применяются эти формулы в заданиях ЕГЭ по математике:
1.
Внесли все под общий корень, разложили на множители, сократили дробь и извлекли корень.
2.
3.
Здесь мы записали корни в виде степеней и использовали формулы действий со степенями.
4. Найдите значение выражения при
Решение:
При получим
Ответ: -0,5.
5. Найдите значение выражения при
Решение:
При a = 12 получим
Мы воспользовались свойствами степеней.
Ответ: 144.
6. Найдите значение выражения при b = — 5.
Решение:
При b = — 5 получим:
Ответ: -125.
7. Расположите в порядке возрастания:
Решение:
Запишем выражения как степени с положительным показателем и сравним.
Так как
то
Так как
то
Сравним и
для этого оценим их разность:
значит
Получим : поэтому
Ответ:
8. Представьте выражение в виде степени:
Решение:
Вынесем за скобку степень с меньшим показателем:
Ответ:
9. Упростите выражение:
Решение:
Приведем основания 6 и 12 к основаниям 2 и 3:
(выполним деление степеней с одинаковыми основаниями)
Ответ: 0,25.
10. Чему равно значение выражения при
?
Решение:
При получим
Ответ: 9.
к оглавлению ▴
Сравнение арифметических корней
11. Какое из чисел больше: или
?
Решение:
Возведем в квадрат оба числа (числа положительные):
Найдем разность полученных результатов:
так как
Значит, первое число больше второго.
Ответ:
к оглавлению ▴
Как избавиться от иррациональности в знаменателе
Если дана дробь вида то нужно умножить числитель и знаменатель дроби на
:
Тогда знаменатель станет рациональным.
Если дана дробь вида или
то нужно умножить числитель и знаменатель дроби на сопряженное выражение, чтобы получить в знаменателе разность квадратов.
Сопряженные выражения — это выражения, отличающиеся только знаками. Например,
и
и
— сопряженные выражения.
Пример:
12. Вот несколько примеров — как избавиться от иррациональности в знаменателе:
Пример 1.
Пример 2.
Пример 3.
Пример 4.
Совет. Если в знаменателе дана сумма двух корней, то в разности первым числом пишите то, которое больше, и тогда разность квадратов корней будет положительным числом.
Пример 5.
13. Сравните и
1)
2) Сравним и 14.
то и
а значит,
Ответ: меньше.
к оглавлению ▴
Как упрощать иррациональные выражения, пользуясь формулами сокращенного умножения
Покажем несколько примеров.
14. Упростите: выражения:
Пример 5.
т.к.
Пример 6.
Пример 7.
так как
Следующие несколько задач решаются с помощью формулы:
Решение:
Получим уравнение
Ответ:
19. Вычислите значение выражения:
Решение:
Ответ: 1.
20. Вычислите значение выражения:
Решение:
Ответ: 1.
21. Вычислите значение выражения: если
Решение.
Если то
следовательно
Ответ: — 1.
22. Вычислите:
Решение:
Ответ: 1.
Рассмотрим уравнение вида где
Это равенство выполняется, только если
Подробно об таких уравнениях — в статье «Показательные уравнения».
При решении уравнений такого вида мы пользуемся монотонностью показательной функции.
23. Решите уравнение:
а)
б)
в)
Решение.
23. Решите уравнение:
Решение:
тогда
Ответ: -1.
24. Решите уравнение:
Решение:
Ответ: 4.
25. Решите уравнение:
Решение:
Значит,
Ответ: -0,2.
Если вы хотите разобрать большее количество примеров — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Корни и степени» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
09.03.2023
Видоизменения корней и побегов на ЕГЭ
26.04.2021
5583
Одна из самых сложных тем в блоке «Ботаника» на ЕГЭ – видоизменения корня и побега. Что это такое и почему происходит? Все просто: органы растений приспосабливаются к условиям среды. А значит могут жить в самых разнообразных биотопах! Рассмотрим видоизменения корней и побегов и разберем их сходства и отличия друг от друга.
Видоизменения корней
Обычно корни растений выполняют две функции:
- осуществляют минеральное питание;
- закрепляют растение в почве.
С помощью корня растение поглощает из почвы воду и растворенные в ней минеральные вещества, а затем обеспечивает ими все остальные органы. Но существуют растения, которые используют корни необычно!
- Корнеплоды – видоизменение корня, которое служит для запаса питательных веществ. Корнеплоды развиваются главным образом у двулетних растений в первый год жизни. Кстати, человек использует корнеплоды моркови, свеклы, редиса и других растений в пищу потому, что там запасаются сахара и белки.
- Воздушные корни – встречаются у растений, живущих в тропическом климате. Когда среда слишком влажная, корни поглощают воду прямо из воздуха. Например, так себя ведут орхидеи: благодаря видоизменениям, они растут на других растениях, используя их исключительно для опоры. И в этом случае они не паразиты, а квартиранты.
- Дыхательные корни – в ходе эволюции появляются у растений, произрастающих в воде. Корню, как и любому другому органу, необходимо поступление кислорода для проведения метаболизма в клетках. Под водой кислорода мало, поэтому такие корни высовываются из воды и поглощают его.
- Корни-присоски – видоизменения у растений-паразитов. Эти корни проникают в растение-жертву, и через них идет поглощение органических и неорганических веществ.
- Бактериальные клубеньки – встречаются у растений семейства Бобовые. В них обитают симбиотические азотофиксирующие бактерии. Они забирают свободный азот из атмосферы и переводят его в тот формат, который могут усвоить растения и животные, питающиеся этими растениями.
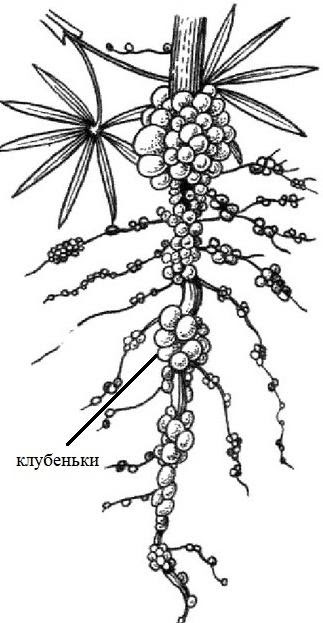
Вы когда-нибудь задумывались, зачем нам азот? Это макроэлемент, входящий в состав нуклеиновых кислот и белков – и вот такой важный компонент мы получаем благодаря клубеньковым бактериям.
До ЕГЭ по биологии осталось совсем немного, а ты переживаешь, что не успеваешь подготовиться ко всем заданиям? Записывайся на пробный бесплатный урок к нашим преподавателям! Они помогут тебе закрыть все пробелы, и на экзамен ты отправишься полный сил и уверенности в себе 😉
Видоизменения побегов
Что же такое видоизменение побегов? Проще всего начать с определения побега. Побег – это стебель с листьями и почками, который развивается из семени или из почки. Если от побега отходит корень, то это может быть только придаточный корень. Образуются видоизмененные побеги для выполнения важных функций, таких как:
- накопление органических веществ;
- вегетативное размножение.
Выделяют надземные и подземные видоизменения побегов, но мы поговорим только о подземных, так как их чаще всего путают с видоизменениями корней.
- Клубень – все побеги состоят из стебля с листьями и почками. Что будет, если оставить клубень картофеля в шкафу надолго? Он прорастет. А значит глазки, которые мы вырезаем при чистке – это почки. Сама мякоть – это стебель, на ростке развиваются чешуевидные листья. Соответственно, клубень – побег.
- Луковица – когда мы чистим лук, мы сначала отрезаем у него плоскую и жесткую структуру, находящуюся снизу. Так вот это – видоизмененный стебель и называется он донце, от него отходят придаточные корни. Чешуи лука, сочные и сухие – это видоизмененные листья: сочные служат для запаса питательных веществ, а сухие для защиты. Если поставить луковицу в воду, то скоро появятся молодые зеленые листья-«перья», которые образуются из почек, находящихся внутри.
- Корневище – побег, который путает своим названием. Это стебель, покрытый чешуевидными листьями, в пазухах которых располагаются почки. С помощью корневищ такие растения, как ландыш и пырей переживают неблагоприятные условия.
Как видите, корни и побеги имеют абсолютно разное строение и по-разному влияют на жизнедеятельность растений. Перед нами таблица, в которой зафиксированы основные различия между этими структурами:
| Видоизменения корней | Видоизменения побегов |
| развиваются из зародышевого корешка | развиваются из семени или почки |
| отсутствует способность к фотосинтезу | есть клетки, содержащие пластиды |
| нет листьев и почек | стебель с листьями и почками |
| частные приспособительные функции | вегетативное размножение, накопление органических веществ |
| корнеплоды, бактериальные клубеньки, дыхательные корни | корневище, клубень, луковица |
А еще можешь почитать по теме:
Разбор заданий ЕГЭ по биологии
Для закрепления материала давайте разберем несколько заданий. Кстати, эта тема встречается в заданиях на 1, 2 и на 3 балла, поэтому может очень пригодится вам при написании ЕГЭ.
Пример 1. Побегом являются:
- клубень картофеля
- клубенек фасоли
- усики гороха
- корневище ландыша
- луковица тюльпана
- ягода картофеля
После того, как мы разобрали теорию, задание уже не кажется таким сложным. Видоизмененные побеги – клубень картофеля, корневище ландыша и луковица тюльпана. Клубенек фасоли – это видоизмененный корень, усики гороха – видоизмененные листья, а ягода картофеля – плод.
Ответ: 145
Пример 2. Какой видоизмененный орган представлен на рисунке? Назовите элементы строения, обозначенные на рисунке цифрами 1, 2, 3, и функции, которые они выполняют.
Ответ:
- На рисунке изображена луковица – видоизмененный побег.
- 1 – Видоизмененные листья (чешуи) – в них запасаются органические и неорганические вещества.
2 – Почки, обеспечивают развитие и рост побега.
3 – Придаточные корни, отходят от донца, поглощают неорганические вещества из окружающей среды.
Ну что, готов к ЕГЭ по биологии на все 100%? Чтобы убедиться в этом, записывайся на пробный бесплатный урок к нашим преподавателям! Узнаешь, какие темы надо повторить и что нужно доучить перед самым важным днем 🤓💪
Лайфхаки экзамена
К рубрике
в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 78 1–20 | 21–40 | 41–60 | 61–78
Добавить в вариант
Почему при увеличении количества добавляемой перекиси свыше 2000 мкл не наблюдается увеличение скорости протекания реакции, катализируемой пероксидазой? Как изменятся результаты эксперимента, если перед его началом корень вымачивать в концентрированной уксусной кислоте в течение нескольких дней? Ответ поясните.
Показать
1
Какую нулевую гипотезу* смог сформулировать исследователь перед постановкой эксперимента? Объясните, какие будут результаты эксперимента, если добавить перекись к кусочку сырого мяса. Почему результаты эксперимента могут быть недостоверными, если проводить эксперимент при наличии прямых солнечных лучей?
*Нулевая гипотеза — принимаемое по умолчанию предположение, что не существует связи между двумя наблюдаемыми событиями, феноменами.
Отсутствие малых коренных зубов у человека наследуется как доминантный аутосомный признак. Один из супругов имеет малые коренные зубы, а у другого они отсутствуют и он гетерозиготен по этому признаку. Какова вероятность рождения детей без малых коренных зубов у этой супружеской пары?
Ответ запишите в виде числа, показывающего искомую вероятность в процентах. Знак % не используйте.
Источник: РЕШУ ЕГЭ
Корень большинства существующих растений не может выполнять функцию
3) запасания органических веществ
4) фотосинтеза
У моркови – корнеплод — это —
1) орган воздушного питания
4) подземный побег
Корень – это
3) подземный орган растения
4) часть побега
В процессе эволюции у голосеменных растений в отличие от споровых
Ласка и горностай относятся к отряду хищных млекопитающих, так как
1) это небольшие животные с длинным узким телом на коротких ногах
2) у них хорошо развиты клыки и коренные зубы
3) у них хорошо развит волосяной покров с подшерстком
4) они имеют покровительственную окраску тела
Если у растения сетчатое жилкование листьев, то у него, как правило,
1) мочковатая корневая система
2) одна семядоля в семени
4) цветок трёхчленного типа
Если у растения сетчатое жилкование листьев, то у него, как правило,
1) мочковатая корневая система
2) одна семядоля в семени
4) цветок трёхчленного типа
У лошади в связи с питанием грубой растительной пищей в процессе эволюции сформировались
2) хорошо развитые зрение и слух
3) конечности, снабжённые копытами
4) коренные зубы с большой жевательной поверхностью
Источник: ЕГЭ по биологии 05.05.2014. Досрочная волна. Вариант 1.
Установите соответствие между функцией и органом растения, для которого она характерна.
ФУНКЦИЯ
А) осуществление минерального питания
Б) поглощение воды
В) синтез органических веществ из неорганических
Г) транспирация
Д) сохранение питательных веществ во время зимовки растений
Е) поглощение углекислого газа и выделение кислорода
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| A | Б | В | Г | Д | Е |
Источник: Демонстрационная версия ЕГЭ—2016 по биологии, Демонстрационная версия ЕГЭ—2017 по биологии, Демонстрационная версия ЕГЭ—2018 по биологии
Установите соответствие между функциями и органами растения, которые выполняют эти функции: к каждой позиции, данной в первом столбце, подберите соответствующую позицию из второго столбца.
ФУНКЦИИ
А) осуществление минерального питания
Б) поглощение воды
В) синтез органических веществ из неорганических
Г) транспирация
Д) образование микоризы
Е) поглощение углекислого газа и выделение кислорода
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| А | Б | В | Г | Д | Е |
Источник: Демонстрационная версия ЕГЭ—2020 по биологии
Установите соответствие между функцией и органом растения, для которого она характерна.
ФУНКЦИЯ
А) обеспечение минеральными солями
Б) поглощение воды
В) синтез органических веществ из неорганических
Г) транспирация
Д) сохранение питательных веществ во время зимовки растений
Е) поглощение углекислого газа и выделение кислорода
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| A | Б | В | Г | Д | Е |
Источник: Демонстрационная версия ЕГЭ—2022 по биологии
Выберите три верно обозначенные подписи к рисунку, на котором изображено строение корня. Запишите в таблицу цифры, под которыми они указаны.
1) зона деления
2) зона всасывания воды
3) зона роста клеток
4) корневой чехлик
5) корневой волосок
6) боковой корень
Мочковатой называют такую корневую систему, у которой
1) главный корень не отличается от многочисленных придаточных
2) главный корень сильно развит и похож на стержень
3) от главного корня отходят боковые корни
4) главный корень развивается из корешка зародыша
У человека к рудиментарным относят зубы
Найдите три ошибки в приведённом тексте «Корни». Укажите номера предложений, в которых допущены ошибки, исправьте их.
(1)Выделяют три вида корней — главный, образующийся из зародышевого корешка, боковые, образующиеся на побегах, и придаточные — корни более низкого порядка, образующиеся в результате ветвления других корней. (2)Корневая система двудольных стержневая, в ней хорошо выражен главный корень, тогда как у однодольных главный корень рано отмирает, образуется мочковатая корневая система. (3)Увеличение корней в длину происходит на верхушке корня, там находится зона деления клеток. (4)Всасывание воды и растворённых в ней минеральных веществ происходит через всю поверхность корня с помощью корневых волосков. (5)Вода с минеральными веществами поднимается вверх по растению по специальной проводящей ткани — ксилеме. (6)Значительная часть воды испаряется с листьев через особые отверстия в эпидерме — поры.
Для изучения активности фермента пероксидазы, расщепляющей перекись водорода, ученый провёл эксперимент с корнем хрена. Для этого он нарезал корень на кусочки массой по 1 грамму. Затем на каждый кусочек он добавил 3% перекись водорода в различном объёме. Результаты эксперимента представлены на графике. Какой параметр был задан экспериментатором (независимая переменная), какой параметр менялся в зависимости от заданного (зависимая переменная)? Почему при увеличении количества добавляемой перекиси свыше 2000 мкл не наблюдается увеличение скорости протекания реакции, катализируемой пероксидазой? Как изменятся результаты эксперимента, если перед его началом корень вымачивать в концентрированной уксусной кислоте в течение нескольких дней? Ответ поясните.
Источник: ЕГЭ по биологии 14.06.2022. Основная волна. Разные задачи
Выберите три верно обозначенные подписи к рисунку, на котором изображено строение корня. Запишите в таблицу цифры, под которыми они указаны.
1) придаточный корень
2) зона, образованная постоянно делящимися клетками верхушечной образовательной ткани
3) зона растущих клеток с начальной дифференциацией
4) зона проведения
5) боковой корень
6) структура, обеспечивающая всасывание воды
Какой орган отсутствует у мха
Всего: 78 1–20 | 21–40 | 41–60 | 61–78