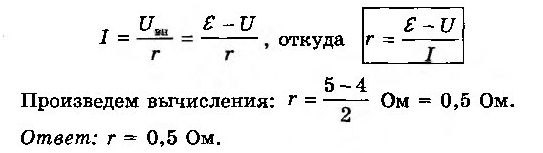Короткое замыкание физика егэ - Помощь в подготовке к экзаменам и поступлению

Каталог заданий

Версия для печати и копирования в MS Word

Тип 28 № 3007

При коротком замыкании клемм аккумулятора сила тока в цепи равна 20 А. При подключении к клеммам аккумулятора электрической лампы с электрическим сопротивлением нити 5,4 Ом сила тока в цепи равна 2 А. По этим результатам измерений определите ЭДС и внутреннее сопротивление аккумулятора.

Раздел кодификатора ФИПИ/Решу ЕГЭ: 3.2.6 Закон Ома для полной (замкнутой) электрической цепи

Решение

1 комментарий · Сообщить об ошибке · Помощь

Источник

Закон Ома для всей цепи.
ЗАДАЧИ на ЕГЭ

Формулы, используемые на уроках физики в 10-11 классах «Закон Ома для всей цепи. Расчет электрических цепей» для подготовки к ЕГЭ по физике.

Смотрите также другие конспекты по решению задач:

ЕГЭ: Закон Ома для участка цепи
ОГЭ: Закон Ома в 8 классе

Закон Ома для всей цепи.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1.
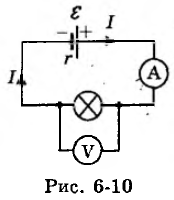
Вольтметр, подключенный к лампочке, показывает U = 4 В, а амперметр — I = 2 А (рис. 6-10). Чему равно внутреннее сопротивление r источника тока, к которому эта лампочка присоединена, если ЭДС источника ε = 5 В?
Примечание: если в условии задачи ничего не сказано о сопротивлении амперметра, то этим сопротивлением можно пренебречь, а если ничего не сказано о сопротивлении вольтметра, то его следует считать бесконечно большим, а силу тока, текущего через вольтметр, равной нулю.

РЕШЕНИЕ.

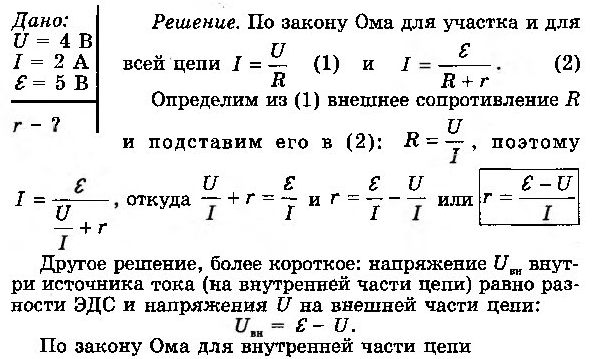
Задача № 2.
Дана схема (рис. 6-11, а). Во сколько раз изменится сила тока, текущего в неразветвленной части цепи, и напряжение на полюсах источника тока, если ключ К замкнуть? Сопротивление лампы Л₂ вдвое больше сопротивления лампы Л₁, а внутреннее сопротивление источника тока в 10 раз меньше сопротивления лампы Л₁.

Задача № 3.
В резисторе сопротивлением R = 5 Ом сила тока I = 0,2 А. Резистор присоединен к источнику тока с ЭДС ε = 2 В. Найти силу тока короткого замыкания I_к.з.

Смотреть решение и ответ

Задача № 4.
Вольтметр, подключенный к полюсам источника тока при разомкнутой внешней цепи, показал U₁ = 8 В. Когда же цепь замкнули на некоторый резистор (рис. 6-12, а), вольтметр показал U₂ = 5 В. Что покажет этот вольтметр, если последовательно к этому резистору подключить еще один такой же (рис. 6-12, б) ? Что покажет этот вольтметр, если второй резистор присоединить к первому параллельно (рис. 6-12, в)?

Задача № 5.
Цепь питается от источника тока с ЭДС ε = 4 В и внутреннем сопротивлением г = 0,2 Ом. Построить график зависимости силы тока I в цепи и напряжения U на полюсах источника тока от внешнего сопротивления R.

Задача № 6.
Амперметр, будучи накоротко присоединен к гальваническому элементу с ЭДС ε = 2 В и внутренним сопротивлением r = 0,2 Ом, показал ток силой I₁ = 3 А . Какую силу тока I₂ покажет этот амперметр, если его зашунтировать сопротивлением R_ш = 0,1 Ом?

Задача № 7.
Дана схема (рис. 6-16). Емкости конденсаторов С₁, С₂ и ЭДС источника тока ε известны. Известно также, что ток короткого замыкания I_к.з. этого источника в три раза превосходит ток I, текущий в этой цепи. Найти напряженности Е₁ и Е₂ полей в конденсаторах, если расстояния между их обкладками равны d.

Задача № 8.
Дана схема (рис. 6-17). Известны емкости С и 2С конденсаторов, сопротивления R и 2R проводников и ЭДС источника тока ε. Внутренним сопротивлением источника тока можно пренебречь (г = 0). Определить напряжения U₁ и U₂ на конденсаторах и заряды q₁ и q₂ этих конденсаторов.

Смотреть решение и ответ

Задача № 9.
Имеется N одинаковых источников тока, которые соединяют сначала последовательно, затем параллельно, подключая каждый раз к одному и тому же внешнему сопротивлению R. Внутреннее сопротивление каждого источника r. Во сколько раз при этом изменяется напряжение на внешней части цепи?

Задача № 10.
Электрическая цепь состоит из источника тока с ЭДС ε = 180 В и потенциометра сопротивлением R = 5 кОм. Ползунок потенциометра стоит посередине прибора (рис. 6-21, а). Найти показания вольтметров U₁ и U₂, подключенных к потенциометру, если их сопротивления R₁ = 6 кОм и R₂ = 4 кОм. Внутренним сопротивлением r источника тока пренебречь.

Задача № 11.
Дана схема, изображенная на рис. 6-22, а. Сопротивления R1, R2 и R известны. Известны также ЭДС источника тока ε и его внутреннее сопротивление r. Найти силу тока I₂ в сопротивлении R₂.

Задача № 12.
Проволока из нихрома образует кольцо диаметром D = 2 м (рис. 6-23, а). В центре кольца помещен источник тока с ε = 2В и внутренним сопротивлением r = 1,5 Ом, соединенный в точках а и b с кольцом такой же проволокой. Найти разность потенциалов φ_b – φ_а между точками b и а. Удельное сопротивление нихрома р = 1,1 мкОм•м, площадь поперечного сечения проволоки S = 1 мм².

Это конспект по теме «Закон Ома для всей цепи. ЗАДАЧИ на ЕГЭ». Выберите дальнейшие действия:

Вернуться к списку конспектов по Физике.
Проверить свои знания по Физике.

Источник

Каждый раз, когда вы вставляете вилку электроприбора в розетку, вы замыкаете электрическую цепь, и по ней начинает течь электрический ток.

Потребитель электрического тока преобразует электрическую энергию, которая к нему поступает, в другие виды энергии — механическую (например, в электродвигателях), тепловую (в утюгах, нагревательных приборах), световую (в осветительных приборах).

При создании электроприборов обязательно рассчитываются и указываются в маркировках и технических паспортах оптимальное и максимальное значение силы тока и напряжения. При превышении максимальных значений перегрев элементов прибора может нарушить их электрическую изоляцию, повлиять на работоспособность прибора.

Рассмотрим простейшую электрическую цепь, которая состоит из источника тока (1), выключателя (2) и потребителя электроэнергии (3), соединённых между собой проводами (рис. 1).

Рис. (1). Электрическая цепь

Сила тока в этой цепи определяется по закону Ома:

(U) — напряжение в сети;

(R) — сопротивление потребителя электроэнергии (электроприбора).

Сила тока прямо пропорциональна напряжению в сети и обратно пропорциональна сопротивлению, которое создаёт электроприбор.

Что произойдёт, если цепь замкнуть проводником так, как показано на рисунке 2, то есть между точками (A) и (B) напрямую?

Рис. (2). Электрическая цепь, возможность замыкания

В этом случае основная часть электрического тока потечёт по проводнику (AB), минуя потребитель тока, так как сопротивление участка (AB) намного меньше, чем сопротивление электроприбора.

При этом общее сопротивление цепи сильно уменьшится, а в результате, согласно закону Ома для участка цепи, сила тока в ней резко возрастёт. Возникнет короткое замыкание.

Короткое замыкание (КЗ) — явление резкого увеличения значения электрического тока в цепи вследствие уменьшения внешнего сопротивления до нуля.

Ток короткого замыкания прямо пропорционален ЭДС цепи и обратно пропорционален внутреннему сопротивлению ЭДС: (I_{кз}=frac{varepsilon}{r}).

Как известно из закона Джоуля-Ленца, количество теплоты (Q), выделяемое на участке цепи (R), пропорционально квадрату силы тока (I) на этом участке:

(t) — время протекания тока по цепи.

Согласно этому закону, если при коротком замыкании ток увеличится в (10) раз, то количество теплоты, выделяющейся при этом, возрастёт примерно в (100) раз (при прочих равных условиях)!

Вот почему короткое замыкание может вызвать расплавление проводов, воспламенение изоляции и в конечном итоге привести к возгоранию горючих предметов вокруг места короткого замыкания и к пожару.

Чаще всего причиной короткого замыкания является нарушение изоляции проводов (из-за их износа, неправильной эксплуатации и т.п.). Также причиной короткого замыкания могут быть механические повреждения в электрической цепи или в электроприборе, а также перегрузки сети.

Источники:

Рис. 1. Электрическая цепь. © ЯКласс.
Рис. 2. Электрическая цепь, возможность замыкания. © ЯКласс.

Источник

ЭДС. Закон Ома для полной цепи

Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.
Сторонняя сила
Закон Ома для полной цепи
КПД электрической цепи
Закон Ома для неоднородного участка

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.

До сих пор при изучении электрического тока мы рассматривали направленное движение свободных зарядов во внешней цепи, то есть в проводниках, подсоединённых к клеммам источника тока.

Как мы знаем, положительный заряд :

• уходит во внешнюю цепь с положительной клеммы источника;

• перемещается во внешней цепи под действием стационарного электрического поля, создаваемого другими движущимися зарядами;

• приходит на отрицательную клемму источника, завершая свой путь во внешней цепи.

Теперь нашему положительному заряду нужно замкнуть свою траекторию и вернуться на положительную клемму. Для этого ему требуется преодолеть заключительный отрезок пути — внутри источника тока от отрицательной клеммы к положительной. Но вдумайтесь: идти туда ему совсем не хочется! Отрицательная клемма притягивает его к себе, положительная клемма его от себя отталкивает, и в результате на наш заряд внутри источника действует электрическая сила $vec{F_E}$ , направленная против движения заряда (т.е. против направления тока).

к оглавлению ▴

Сторонняя сила

Тем не менее, ток по цепи идёт; стало быть, имеется сила, «протаскивающая» заряд сквозь источник вопреки противодействию электрического поля клемм (рис. 1).

Рис. 1. Сторонняя сила

Эта сила называется сторонней силой; именно благодаря ей и функционирует источник тока. Сторонняя сила $vec{F_{CT}}$ не имеет отношения к стационарному электрическому полю — у неё, как говорят, неэлектрическое происхождение; в батарейках, например, она возникает благодаря протеканию соответствующих химических реакций.

Обозначим через $A_{CT}$ работу сторонней силы по перемещению положительного заряда q внутри источника тока от отрицательной клеммы к положительной. Эта работа положительна, так как направление сторонней силы совпадает с направлением перемещения заряда. Работа сторонней силы $A_{CT}$ называется также работой источника тока.

Во внешней цепи сторонняя сила отсутствует, так что работа сторонней силы по перемещению заряда во внешней цепи равна нулю. Поэтому работа сторонней силы по перемещению заряда вокруг всей цепи сводится к работе по перемещению этого заряда только лишь внутри источника тока. Таким образом, $A_{CT}$ — это также работа сторонней силы по перемещению заряда по всей цепи.

Мы видим, что сторонняя сила является непотенциальной — её работа при перемещении заряда по замкнутому пути не равна нулю. Именно эта непотенциальность и обеспечивает циркулирование электрического тока; потенциальное электрическое поле, как мы уже говорили ранее, не может поддерживать постоянный ток.

Опыт показывает, что работа $A_{CT}$ прямо пропорциональна перемещаемому заряду . Поэтому отношение $A_{CT}/q$ уже не зависит от заряда и является количественной характеристикой источника тока. Это отношение обозначается :

$mathcal E = frac{displaystyle A_{CT}}{displaystyle q vphantom{1^a}}.$ (1)

Данная величина называется электродвижущей силой (ЭДС) источника тока. Как видим, ЭДС измеряется в вольтах (В), поэтому название «электродвижущая сила» является крайне неудачным. Но оно давно укоренилось, так что приходится смириться.

Когда вы видите надпись на батарейке: «1,5 В», то знайте, что это именно ЭДС. Равна ли эта величина напряжению, которое создаёт батарейка во внешней цепи? Оказывается, нет! Сейчас мы поймём, почему.

к оглавлению ▴

Закон Ома для полной цепи

Любой источник тока обладает своим сопротивлением , которое называется внутренним сопротивлением этого источника. Таким образом, источник тока имеет две важных характеристики: ЭДС и внутреннее сопротивление.

Пусть источник тока с ЭДС, равной , и внутренним сопротивлением подключён к резистору (который в данном случае называется внешним резистором, или внешней нагрузкой, или полезной нагрузкой). Всё это вместе называется полной цепью (рис. 2).

Рис. 2. Полная цепь

Наша задача — найти силу тока в цепи и напряжение на резисторе .

За время по цепи проходит заряд q = It . Согласно формуле (1) источник тока совершает при этом работу:

$A_{CT} = Eq = EIt.$ (2)

Так как сила тока постоянна, работа источника целиком превращается в теплоту, которая выделяется на сопротивлениях и . Данное количество теплоты определяется законом Джоуля–Ленца:

(3)

Итак, $A_{CT} = Q$ , и мы приравниваем правые части формул (2) и (3):

После сокращения на получаем:

Вот мы и нашли ток в цепи:

$I = frac{displaystyle mathcal E}{displaystyle R + r vphantom{1^a}}.$ (4)

Формула (4) называется законом Ома для полной цепи.

Если соединить клеммы источника проводом пренебрежимо малого сопротивления (R = 0) , то получится короткое замыкание. Через источник при этом потечёт максимальный ток — ток короткого замыкания:

$I_{K3} = frac{displaystyle mathcal E}{displaystyle r vphantom{1^a}}.$

Из-за малости внутреннего сопротивления ток короткого замыкания может быть весьма большим. Например, пальчиковая батарейка разогревается при этом так, что обжигает руки.

Зная силу тока (формула (4)), мы можем найти напряжение на резисторе с помощью закона Ома для участка цепи:

$U = IR = frac{displaystyle mathcal E R}{displaystyle R + r vphantom{1^a}}.$ (5)

Это напряжение является разностью потенциалов между точками и (рис. 2). Потенциал точки равен потенциалу положительной клеммы источника; потенциал точки равен потенциалу отрицательной клеммы. Поэтому напряжение (5) называется также напряжением на клеммах источника.

Мы видим из формулы (5), что в реальной цепи будет — ведь умножается на дробь, меньшую единицы. Но есть два случая, когда .

1. Идеальный источник тока. Так называется источник с нулевым внутренним сопротивлением. При r = 0 формула (5) даёт .

2. Разомкнутая цепь. Рассмотрим источник тока сам по себе, вне электрической цепи. В этом случае можно считать, что внешнее сопротивление бесконечно велико: . Тогда величина R + r неотличима от , и формула (5) снова даёт нам .

Смысл этого результата прост: если источник не подключён к цепи, то вольтметр, подсоединённый к полюсам источника, покажет его ЭДС.

к оглавлению ▴

КПД электрической цепи

Нетрудно понять, почему резистор называется полезной нагрузкой. Представьте себе, что это лампочка. Теплота, выделяющаяся на лампочке, является полезной, так как благодаря этой теплоте лампочка выполняет своё предназначение — даёт свет.

Количество теплоты, выделяющееся на полезной нагрузке за время , обозначим $Q_{polezn}$ .

Если сила тока в цепи равна , то

$Q_{polezn} = I^2Rt.$

Некоторое количество теплоты выделяется также на источнике тока:

$Q_{ist} = I^2rt.$

Полное количество теплоты, которое выделяется в цепи, равно:

$Q_{poln} = Q_{polezn} + Q_{ist} = I^2Rt + I^2rt = I^2(R + r)t.$

КПД электрической цепи — это отношение полезного тепла к полному:

$eta = frac{displaystyle Q_{polezn}}{displaystyle Q_{poln} vphantom{1^a}} = frac{displaystyle I^2Rt}{displaystyle I^2(R+r)t vphantom{1^a}} = frac{displaystyle R}{displaystyle R+r vphantom{1^a}}.$

КПД цепи равен единице лишь в том случае, если источник тока идеальный (r = 0) .

к оглавлению ▴

Закон Ома для неоднородного участка

Простой закон Ома U = IR справедлив для так называемого однородного участка цепи — то есть участка, на котором нет источников тока. Сейчас мы получим более общие соотношения, из которых следует как закон Ома для однородного участка, так и полученный выше закон Ома для полной цепи.

Участок цепи называется неоднородным, если на нём имеется источник тока. Иными словами, неоднородный участок — это участок с ЭДС.

На рис. 3 показан неоднородный участок, содержащий резистор и источник тока. ЭДС источника равна , его внутреннее сопротивление считаем равным нулю (если внутреннее сопротивление источника равно , можно просто заменить резистор на резистор R + r ).

Рис. 3. ЭДС «помогает» току:

Сила тока на участке равна , ток течёт от точки к точке . Этот ток не обязательно вызван одним лишь источником . Рассматриваемый участок, как правило, входит в состав некоторой цепи (не изображённой на рисунке), а в этой цепи могут присутствовать и другие источники тока. Поэтому ток является результатом совокупного действия всех источников, имеющихся в цепи.

Пусть потенциалы точек и равны соответственно и . Подчеркнём ещё раз, что речь идёт о потенциале стационарного электрического поля, порождённого действием всех источников цепи — не только источника, принадлежащего данному участку, но и, возможно, имеющихся вне этого участка.

Напряжение на нашем участке равно: . За время через участок проходит заряд q = It , при этом стационарное электрическое поле совершает работу:

$A_{POL} = Uq = UIt.$

Кроме того, положительную работу совершает источник тока (ведь заряд прошёл сквозь него!):

$A_{CT} = mathcal Eq = mathcal EIt.$

Сила тока постоянна, поэтому суммарная работа по продвижению заряда , совершаемая на участке стационарным электрическим полем и сторонними силами источника, целиком превращается в тепло: $A_{POL} + A_{CT} = Q$ .

Подставляем сюда выражения для $A_{POL}$ , $A_{CT}$ и закон Джоуля–Ленца:

Сокращая на , получаем закон Ома для неоднородного участка цепи:

(6)

или, что то же самое:

(7)

Обратите внимание: перед стоит знак «плюс». Причину этого мы уже указывали — источник тока в данном случае совершает положительную работу, «протаскивая» внутри себя заряд от отрицательной клеммы к положительной. Попросту говоря, источник «помогает» току протекать от точки к точке .

Отметим два следствия выведенных формул (6) и (7).

1. Если участок однородный, то . Тогда из формулы (6) получаем U = IR — закон Ома для однородного участка цепи.

2. Предположим, что источник тока обладает внутренним сопротивлением . Это, как мы уже упоминали, равносильно замене на R + r :

Теперь замкнём наш участок, соединив точки и . Получим рассмотренную выше полную цепь. При этом окажется, что и предыдущая формула превратится в закон Ома для полной цепи:

Таким образом, закон Ома для однородного участка и закон Ома для полной цепи оба вытекают из закона Ома для неоднородного участка.

Может быть и другой случай подключения, когда источник «мешает» току идти по участку. Такая ситуация изображена на рис. 4. Здесь ток, идущий от к , направлен против действия сторонних сил источника.

Рис. 4. ЭДС «мешает» току:

Как такое возможно? Очень просто: другие источники, имеющиеся в цепи вне рассматриваемого участка, «пересиливают» источник на участке и вынуждают ток течь против . Именно так происходит, когда вы ставите телефон на зарядку: подключённый к розетке адаптер вызывает движение зарядов против действия сторонних сил аккумулятора телефона, и аккумулятор тем самым заряжается!

Что изменится теперь в выводе наших формул? Только одно — работа сторонних сил станет отрицательной:

$A_{CT} = mathcal E q = mathcal EIt.$

Тогда закон Ома для неоднородного участка примет вид:

(8)

или:

где по-прежнему — напряжение на участке.

Давайте соберём вместе формулы (7) и (8) и запишем закон Ома для участка с ЭДС следующим образом:

Ток при этом течёт от точки к точке . Если направление тока совпадает с направлением сторонних сил, то перед ставится «плюс»; если же эти направления противоположны, то ставится «минус».

Повторим основные понятия и определения по теме «Закон Ома».

Напомним, что напряжение измеряется в вольтах.

Сила тока измеряется в амперах.

Сопротивление измеряется в омах. Эта единица измерения названа в честь Георга Симона Ома, открывшего взаимосвязь между напряжением, сопротивлением цепи и силой тока в этой цепи.

Основные определения, которые мы используем в решении задач:

Источник тока – это устройство, способное создавать необходимую для существования тока разность потенциалов.

Можно сказать, что источник тока действует, как насос. Он «качает» электроны по проводникам, как водяной насос воду по трубам. Эту аналогию можно продолжить. При этом источник тока совершает работу, за счёт химических реакций, происходящих внутри него.

Если эту работу разделить на переносимый источником заряд q (суммарный заряд всех проходящих через источник электронов), то мы получим величину, которую называют электродвижущей силой или сокращённо ЭДС.

Измеряется эта ЭДС, как и разность потенциалов, в вольтах и имеет примерно тот же смысл.

По определению, сила тока равна отношению суммарного заряда электронов, проходящих через сечение проводника, ко времени прохождения. Измеряется сила тока в амперах (А).

Свойство проводника препятствовать прохождению по нему тока характеризуется величиной, которую назвали электрическим сопротивлением – R. Проходя через проводник, электрический ток нагревает его.

Сопротивление измеряют в омах (Ом).

Сам источник тока тоже обладает сопротивлением. Такое сопротивление принято называть внутренним сопротивлением источника r (Ом).

Именно немецкому учёному Георгу Ому удалось установить, от чего может зависеть электрическое сопротивление проводника. Проведя многочисленные эксперименты, Ом сделал следующие выводы:

Сопротивление проводника тем больше, чем больше его длина.
Сопротивление проводника тем больше, чем меньше его толщина или площадь поперечного сечения.

Кроме того, Ом выяснил, что каждый материал обладает своим электрическим сопротивлением. Величина, которая показывает, каким сопротивлением будет обладать проводник единичной длины и единичной площади сечения из данного материала, называется удельным электрическим сопротивлением: (Ом*мм²/м). Эта величина справочная. Таким образом, получается, что электрическое сопротивление проводника равно:

Рассмотрим задачи ЕГЭ по теме «Закон Ома» для полной цепи.

Задача 1. На рисунке приведён график зависимости напряжения на концах железного провода площадью поперечного сечения 0,05 мм² от силы тока в нём. Чему равна длина провода? Ответ дайте в метрах. Удельное сопротивление железа 0,1 Ом*мм²/м.

Решение:

Из закона Ома для проводника или участка цепи без источника следует:

$displaystyle I=frac{U}{R};$

$displaystyle R=frac{U}{I}.$

По графику: при

Из формулы сопротивления выражаем и находим длину проводника:

Ответ: 10.

Задача 2. Через поперечное сечение проводников за 8 с прошло 10²⁰ электронов. Какова сила тока в проводнике? Ответ дайте в амперах.

Решение:

По определению силы тока:

$displaystyle I=frac{q}{t}.$

Заряд всех электронов: где е — модуль заряда электрона, $e=1,6cdot 10^{-19}$ Кл.

Тогда $displaystyle I=frac{Ncdot e}{t}=frac{10^{20}cdot 1,6cdot 10^{-19}}{8}=2 A.$

Ответ: 2.

Задача 3. Идеальный амперметр и три резистора общим сопротивлением 66 Ом включены последовательно в электрическую цепь, содержащую источник с ЭДС равной 5 В, и внутренним сопротивлением r=4 Ом. Каковы показания амперметра? (Ответ дайте в амперах, округлив до сотых.)

Решение:

По закону Ома для полной цепи:

Тогда $displaystyle I=frac{5}{66+4}=0,07 A.$

Ответ: 0,07.

Задача 4. ЭДС источника тока равна 1,5 В. Определите сопротивление внешней цепи, при котором сила тока будет равна 0,6 А, если сила тока при коротком замыкании равна 2,5 А. Ответ дайте в Ом, округлив до десятых.

Решение:

Сила тока короткого замыкания определяется следующим образом:

Отсюда выражаем и находим внутреннее сопротивление источника:

При внешнем сопротивлении, не равном нулю, сила тока в цепи определяется законом Ома для полной цепи:

Отсюда выражаем сопротивление резистора и находим его:

Ответ: 1,9.

Задача 5. На рисунке изображена схема электрической цепи, состоящей из источника постоянного напряжения с ЭДС 5 В и пренебрежимо малым внутренним сопротивлением, ключа, резистора с сопротивлением 2 Ом и соединительных проводов. Ключ замыкают. Какой заряд протечет через резистор за 10 минут? Ответ дайте в кулонах.

Решение:

Выражаем время в секундах: t = 10 минут = 600 с.

Определяем силу тока по закону Ома для полной цепи:

Внутреннее сопротивление пренебрежимо мало, поэтому r = 0.

По определению силы тока:

$displaystyle I=frac{q}{t}.$

Отсюда Кл.

Ответ: 1500.

Если вам нравятся наши материалы — записывайтесь на курсы подготовки к ЕГЭ по физике онлайн

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «ЭДС. Закон Ома для полной цепи» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

31. Электродинамика (расчетная задача)

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

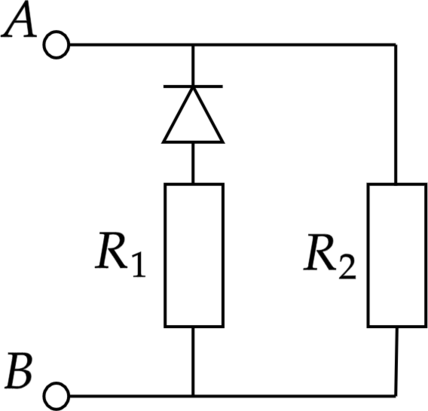
В цепь включен диод, сопротивление которого в прямом направлении пренебрежительно мало, а в обратном превышает многократно сопротивление резисторов, резисторы (R_1) и (R_2) и источник тока с ЭДС (см. рисунок). При подключении к точке А положительного полюса, а к точке Б отрицательного полюса источника тока потребляемая мощность равна 14,4 Вт. При изменении полярности потребляемая мощность возрастает до 21,6 Вт. Укажите, как течёт ток через диод и резисторы в обоих случаях, и определите сопротивления резисторов в этой цепи. Ответ выразите в Омах. ЭДС источника 12 В.
Сборник Демидова 2020

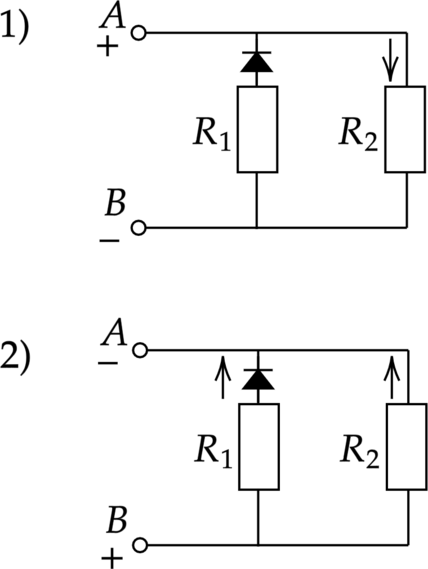
В первом случае ток течет только через резистор (R_2), а значит мощность, выделяемая в цепи равна [P_1=dfrac{xi^2}{R_2},] где (xi) – ЭДС источника.
Отсюда сопротивление второго резистора [R_2=dfrac{xi^2}{P_1}=dfrac{(12text{ В})^2}{14,4text{ Вт}}=10 text{ Ом}] Во втором случае ток будет течь через оба резистора, кроме того, так как резисторы подключены параллельно, то на каждом из них будет напряжение (xi), а мощность, выделяемая в цепи, равна [P_2=dfrac{xi^2}{R_1}+dfrac{xi^2}{R_2}=dfrac{xi^2}{R_1}+P_1] Откуда сопротивление второго резистора [R_2=dfrac{xi^2}{P_2-P_1}=dfrac{(12text{ В})^2}{21,6text{ Вт}-14,4text{ Вт}}=20text{ Ом}]

Ответ: 20

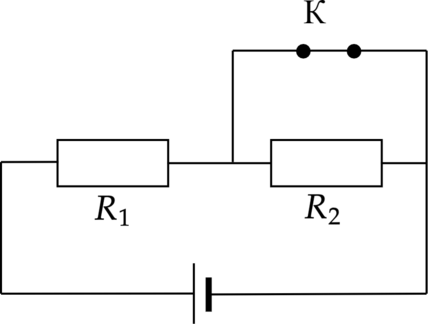
В цепи, изображенной на рисунке, подключены источника тока без внутреннего сопротивления, резисторы (R_1) и (R_2) и ключ. При замкнутом ключе на резисторе (R_1) выделяется мощность (P_1=27) Вт, а при разомкнутом ключе на резисторе (R_1) выделяется мощность (P_2=3) Вт. Какая мощность выделяется на резисторе (R_2) при разомкнутом ключе. Ответ дайте в Вт.

Сила тока при замкнутом ключе равна по закону Ома для полной цепи [I_1=dfrac{xi}{R_1}] Значит, мощность на первом резисторе при замкнутом ключе равна [P_1=I_1^2 R_1dfrac{xi^2}{R_1}quad (1)] где (xi) – ЭДС источника.
При разомкнутом ключе сила тока равна [I_2=dfrac{xi}{R_1+R_2}] При разомкнутом ключе мощности на первом и втором резисторах равны соответственно [P_1’=I_2^2R_1=dfrac{xi^2R_1}{(R_1+R_2)^2} quad (2)] [P_2’=I_2^2R_2=dfrac{xi^2R_2}{(R_1+R_2)^2} quad (3)] Поделим (1) на (2), с учетом условия [dfrac{(R_1+R_2)^2}{R_1^2}=dfrac{27text{ Вт}}{3text{ Вт}}] Извлечём квадрат [dfrac{R_1+R_2}{R_1}=3 Rightarrow R_2=2R_1 quad (4)] Подставим (4) в (3) с учетом (1) [P_2’=dfrac{2xi^2 R_1 }{9R^2_1}=dfrac{2}{9}P_1=dfrac{2}{9}27text{ Вт}=6text{ Вт}]

Ответ: 6

При коротком замыкании клемм источника тока сила тока в цепи равна (I_text{кз}=12 А). При подключении к клеммам электрической лампы электрическим сопротивлением (R_1=5) Ом сила тока в цепи равна (I_1=2) А. Определите ЭДС источника тока.

Ток в замкнутой цепи определяется по закону Ома для полной цепи. [I=dfrac{xi}{R+r},] где (xi) – ЭДС источника, (r) – внутреннее сопротивление источника. При коротком замыкании (R=0), а значит внутреннее сопротивление равно [r=dfrac{xi}{I_text{ кз}}] Для второго случая, когда лампа подключена в цепь имеем [I_1=dfrac{xi}{R_1+r}=dfrac{xi}{R_1+dfrac{xi}{I_text{ кз}}}=2] Выразим подставим данные из условия [xi=I_1R_1+I_1dfrac{xi}{r}Rightarrow xi=2text{ А}cdot 5text{ Ом}+ 2text{ A}dfrac{xi}{12text{ А}}] Выразим ЭДС [5xi=60text{ В}Rightarrow xi=12text{ В}]

Ответ: 12

В лаборатории имеется однородный медный цилиндрический проводник длиной (l=10) м, в опыте к нему приложили разность потенциалов 20 В. Каким будет изменение температуры проводника через 15с? Изменением сопротивления проводника и рассеянием тепла при его нагревании пренебречь. (Удельное сопротивление меди (1,7cdot 10^{-8}) Ом(cdot)м), ответ дайте в градусах Цельсия.

По закону Джоуля –Ленца не проводнике будет выделяться тепло:

(Q=dfrac{U^2 cdot t}{R}, quad (1)) где (U) – разность потенциалов(напряжение), (t) – время, (R) – сопротивление проводника, оно находится по формуле: [R=dfrac{rho l}{S}quad (2)]

(rho)-Удельное сопротивление меди, (S) – площадь сечения проводника

Так как изменением сопротивления проводника и рассеянием тепла при его нагревании пренебречь, то все тепло пойдет на нагревание проводника

[Q=cmDelta t, (2)]

(c)-удельная теплоемкость меди=385 (Дж/кг(cdot)К), (m) – масса проводника, ее мы найдем по формуле:

(m=rho_0 V=rho_0 lS quad (3))

(V) – объем, (rho_0=8930) кг/м(^3)-плотность меди

приравняем (1) и (3) с учетом (2) и (4)

[dfrac{U^2 cdot t}{dfrac{rho l}{S}}=crho_0 lSDelta t] Выразим изменение температуры [Delta t=dfrac{U^2 cdot t}{crho_0 rho l^2}] Найдем изменение температуры [Delta t=dfrac{400text{ В$^2$}cdot 15text{ с}}{385text{ Дж/(кг$cdot$К)}cdot8930text{ кг/м$^3$}cdot1,7cdot 10^{-8}text{ Ом$cdot$м}cdot 100text{ м$^2$}}=1026,57^circ C]

Ответ: 1026,57

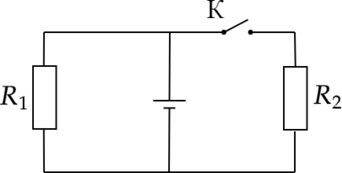
В схеме, показанной на рисунке, резисторы имеют сопротивления (R_1 = 1) Ом, (R_2 = 2) Ом. Определить внутреннее сопротивление батареи (r) , если известно, что при разомкнутом ключе К через резистор (R_1) течет ток (I_1 = 2,8) А, а при замкнутом ключе К через резистор (R_2) течет ток (I_2 = 1) А. Ответ дайте в Ом.

Закон Ома для полной цепи (при разомкнутом ключе): [I_1=frac{xi}{R_1+r}] (I) – сила тока, (xi) – ЭДС источника, (R) – внешнее сопротивление, (r) – внутреннее сопротивление. При замкнутом ключе (R_1) и (R_2) подключены параллельно, их общее сопротивление: [R_{12}=frac{R_1R_2}{R_1+R_2}=frac{2}{3} text{ Ом}] Напряжение на втором резисторе: [U_2=I_2R_2=2 text{ В}] Напряжение на втором резисторе: [U_1=U_2=2 text{ В}] Ток через первый резистор: [I_3=frac{U_1}{R_1}=2 text{ А}] Следовательно, общий ток в цепи во втором случае: [I_4=I_2+I_3=3 text{ А}]
Закон Ома для полной цепи (при замкнутом ключе): [I_4=frac{xi}{R_{12}+r}] [I_1(R_1+r)=I_4(R_{12}+r)] [r=frac{I_1R_1-I_4R_{12}}{I_4-I_1}=frac{2,8text{ А}cdot1text{ Ом}-2text{ В}}{3text{ А}-2,8text{ А}}=4 text{ Ом}]

Ответ: 4

При коротком замыкании выводов аккумулятора сила тока в цепи равна 12 А. При подключении к выводам аккумулятора электрической лампы электрическим сопротивлением 5 Ом сила тока в цепи равна 2 А. По результатам этих экспериментов определите внутреннее сопротивление аккумулятора. Ответ дайте в Ом.

Короткое замыкание: [I_{text{ к.з.}}=I_1=frac{xi}{r},] где (I_{text{ к.з.}}) – сила тока короткого замыкания, (I_1) – сила тока в цепи, (xi) – ЭДС источника, (r) – внутреннее сопротивление
Закон Ома для полной цепи во втором случае: [I_2=frac{xi}{R+r}] [I_2(R+r)=I_1r] (R) – сопротивление лампы, выразим внутреннее сопротивление аккумулятора: [r=frac{I_2R}{I_1-I_2}=frac{2text{ А}cdot5text{ Ом} }{12text{ А}-2text{ А}}=1 text{ Ом}]

Ответ: 1

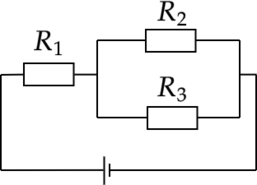
В схеме, показанной на рисунке, (R_1 =1) Ом, (R_2 = 2) Ом, (R_3 = 3) Ом. Известно, что на резисторе с сопротивлением (R_1) выделяется мощность (N_1 = 25) Вт. Какая мощность (N_2) выделяется на резисторе с сопротивлением (R_2)? Ответ дайте в Вт.

Мощность: [N_1=I^2R_1,] где (I) – сила тока, тогда [I_1=sqrt{frac{N_1}{R_1}}=sqrt{dfrac{25text{ Вт}}{1text{ Ом}}}=5 text{ А}] Резисторы (R_2) и (R_3) соединены параллельно, значит сила тока распределится обратно пропорционально сопротивлениям ((I_1=I_2+I_3) (I_2R_2=I_3R_3)): [I_2=3 text{ А}] [I_3=2 text{ А}] Мощность на втором резисторе: [N_2=I_2^2R_2=3^2text{ А$^2$}cdot2text{ Ом}=18 text{ Вт}]

Ответ: 18

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Закон Ома для всей цепи. ЗАДАЧИ на ЕГЭ

Закон Ома для всей цепи. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

ЭДС. Закон Ома для полной цепи

Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.

Сторонняя сила

Закон Ома для полной цепи

КПД электрической цепи

Закон Ома для неоднородного участка

Закон Ома для всей цепи.
ЗАДАЧИ на ЕГЭ

Закон Ома для всей цепи.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ