Поиск
в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 60 1–20 | 21–40 | 41–60
Добавить в вариант
Тип 11 № 549378
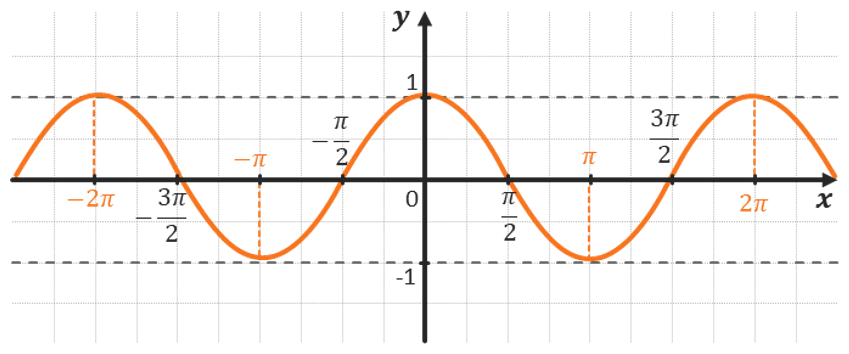
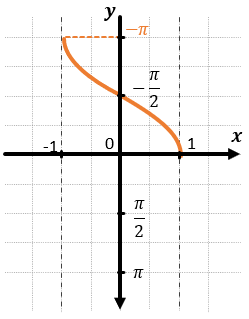
Найдите точку максимума функции принадлежащую промежутку
Кодификатор ФИПИ/Решу ЕГЭ: 3.2.6 Наибольшее и наименьшее значения функции, 3.3.5 Тригонометрические функции, их графики, 4.2.1 Применение производной к исследованию функций и построению графиков
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Тип 10 № 564531
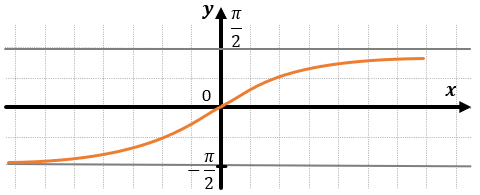
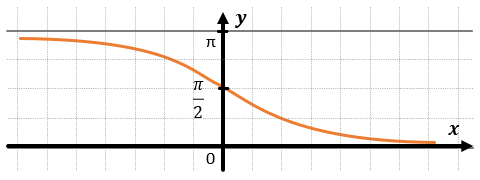
На рисунке изображён график функции вида где числа a, b, c и d — целые. Найдите
Аналоги к заданию № 564531: 564543 564555 564542 564551 564552 564553 564554 564556 564578 564579 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.2.3 Периодичность функции, 3.3.5 Тригонометрические функции, их графики
Решение
·
·
1 комментарий · Сообщить об ошибке · Помощь
Тип 10 № 564542
На рисунке изображён график функции вида
где числа a, b, c и d — целые. Найдите
Аналоги к заданию № 564531: 564543 564555 564542 564551 564552 564553 564554 564556 564578 564579 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.2.3 Периодичность функции, 3.3.5 Тригонометрические функции, их графики
Решение
·
Прототип задания
·
·
Сообщить об ошибке · Помощь
Тип 10 № 564543
На рисунке изображён график функции вида
где числа a, b, c и d — целые. Найдите
Аналоги к заданию № 564531: 564543 564555 564542 564551 564552 564553 564554 564556 564578 564579 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.2.3 Периодичность функции, 3.3.5 Тригонометрические функции, их графики
Решение
·
Прототип задания
·
·
Сообщить об ошибке · Помощь
Тип 10 № 564553
На рисунке изображён график функции вида
где числа a, b, c и d — целые. Найдите
Аналоги к заданию № 564531: 564543 564555 564542 564551 564552 564553 564554 564556 564578 564579 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.2.3 Периодичность функции, 3.3.5 Тригонометрические функции, их графики
Решение
·
Прототип задания
·
·
Сообщить об ошибке · Помощь
Тип 10 № 564554
На рисунке изображён график функции вида
где числа a, b, c и d — целые. Найдите
Аналоги к заданию № 564531: 564543 564555 564542 564551 564552 564553 564554 564556 564578 564579 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.2.3 Периодичность функции, 3.3.5 Тригонометрические функции, их графики
Решение
·
Прототип задания
·
·
Сообщить об ошибке · Помощь
Тип 10 № 564555
На рисунке изображён график функции вида
где числа a, b, c и d — целые. Найдите
Аналоги к заданию № 564531: 564543 564555 564542 564551 564552 564553 564554 564556 564578 564579 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.2.3 Периодичность функции, 3.3.5 Тригонометрические функции, их графики
Решение
·
Прототип задания
·
·
Сообщить об ошибке · Помощь
Тип 10 № 564556
На рисунке изображён график функции вида
где числа a, b, c и d — целые. Найдите
Аналоги к заданию № 564531: 564543 564555 564542 564551 564552 564553 564554 564556 564578 564579 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.2.3 Периодичность функции, 3.3.5 Тригонометрические функции, их графики
Решение
·
Прототип задания
·
·
Сообщить об ошибке · Помощь
Тип 10 № 564578
На рисунке изображён график функции вида
где числа a, b, c и d — целые. Найдите
Аналоги к заданию № 564531: 564543 564555 564542 564551 564552 564553 564554 564556 564578 564579 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.2.3 Периодичность функции, 3.3.5 Тригонометрические функции, их графики
Решение
·
Прототип задания
·
·
Сообщить об ошибке · Помощь
Тип 10 № 564579
На рисунке изображён график функции вида
где числа a, b, c и d — целые. Найдите
Аналоги к заданию № 564531: 564543 564555 564542 564551 564552 564553 564554 564556 564578 564579 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.2.3 Периодичность функции, 3.3.5 Тригонометрические функции, их графики
Решение
·
Прототип задания
·
·
Сообщить об ошибке · Помощь
Тип 10 № 564580
На рисунке изображён график функции вида
где числа a, b, c и d — целые. Найдите
Аналоги к заданию № 564531: 564543 564555 564542 564551 564552 564553 564554 564556 564578 564579 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.2.3 Периодичность функции, 3.3.5 Тригонометрические функции, их графики
Решение
·
Прототип задания
·
·
Сообщить об ошибке · Помощь
Тип 10 № 564584
На рисунке изображён график функции вида
где числа a, b, c и d — целые. Найдите
Аналоги к заданию № 564531: 564543 564555 564542 564551 564552 564553 564554 564556 564578 564579 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.2.3 Периодичность функции, 3.3.5 Тригонометрические функции, их графики
Решение
·
Прототип задания
·
·
Сообщить об ошибке · Помощь
Тип 10 № 564585
На рисунке изображён график функции вида
где числа a, b, c и d — целые. Найдите
Аналоги к заданию № 564531: 564543 564555 564542 564551 564552 564553 564554 564556 564578 564579 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.2.3 Периодичность функции, 3.3.5 Тригонометрические функции, их графики
Решение
·
Прототип задания
·
·
Сообщить об ошибке · Помощь
Тип 10 № 564589
На рисунке изображён график функции вида
где числа a, b, c и d — целые. Найдите
Аналоги к заданию № 564531: 564543 564555 564542 564551 564552 564553 564554 564556 564578 564579 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.2.3 Периодичность функции, 3.3.5 Тригонометрические функции, их графики
Решение
·
Прототип задания
·
·
Сообщить об ошибке · Помощь
Тип 10 № 564551
На рисунке изображён график функции вида
где числа a, b, c и d — целые. Найдите
Аналоги к заданию № 564531: 564543 564555 564542 564551 564552 564553 564554 564556 564578 564579 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.2.3 Периодичность функции, 3.3.5 Тригонометрические функции, их графики
Решение
·
Прототип задания
·
·
Сообщить об ошибке · Помощь
Тип 10 № 564552
На рисунке изображён график функции вида
где числа a, b, c и d — целые. Найдите
Аналоги к заданию № 564531: 564543 564555 564542 564551 564552 564553 564554 564556 564578 564579 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.2.3 Периодичность функции, 3.3.5 Тригонометрические функции, их графики
Решение
·
Прототип задания
·
·
Сообщить об ошибке · Помощь
Тип 10 № 564586
На рисунке изображён график функции вида
где числа a, b, c и d — целые. Найдите
Аналоги к заданию № 564531: 564543 564555 564542 564551 564552 564553 564554 564556 564578 564579 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.2.3 Периодичность функции, 3.3.5 Тригонометрические функции, их графики
Решение
·
Прототип задания
·
·
Сообщить об ошибке · Помощь
Тип 10 № 564587
На рисунке изображён график функции вида
где числа a, b, c и d — целые. Найдите
Аналоги к заданию № 564531: 564543 564555 564542 564551 564552 564553 564554 564556 564578 564579 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.2.3 Периодичность функции, 3.3.5 Тригонометрические функции, их графики
Решение
·
Прототип задания
·
·
Сообщить об ошибке · Помощь
Тип 10 № 564588
На рисунке изображён график функции вида
где числа a, b, c и d — целые. Найдите
Аналоги к заданию № 564531: 564543 564555 564542 564551 564552 564553 564554 564556 564578 564579 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.2.3 Периодичность функции, 3.3.5 Тригонометрические функции, их графики
Решение
·
Прототип задания
·
·
Сообщить об ошибке · Помощь
Тип 10 № 509123
На рисунке изображён график функции
Найдите a.
Аналоги к заданию № 509123: 509131 509124 509125 509126 509127 509128 509129 509130 509132 509133 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.5 Тригонометрические функции, их графики
Решение
·
·
Сообщить об ошибке · Помощь
Всего: 60 1–20 | 21–40 | 41–60
Тема 10.
Задачи на свойства графиков функций
10
.
08
Графики синуса и косинуса
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
задачи на свойства графиков функций
10.01График линейной функции (прямая)
10.02График квадратичной функции (парабола)
10.03График корня
10.04График обратной пропорциональности (гипербола)
10.05График показательной функции (экспонента)
10.06График логарифмической функции
10.07График модуля
10.08Графики синуса и косинуса
10.09Комбинации нескольких графиков
Решаем задачи
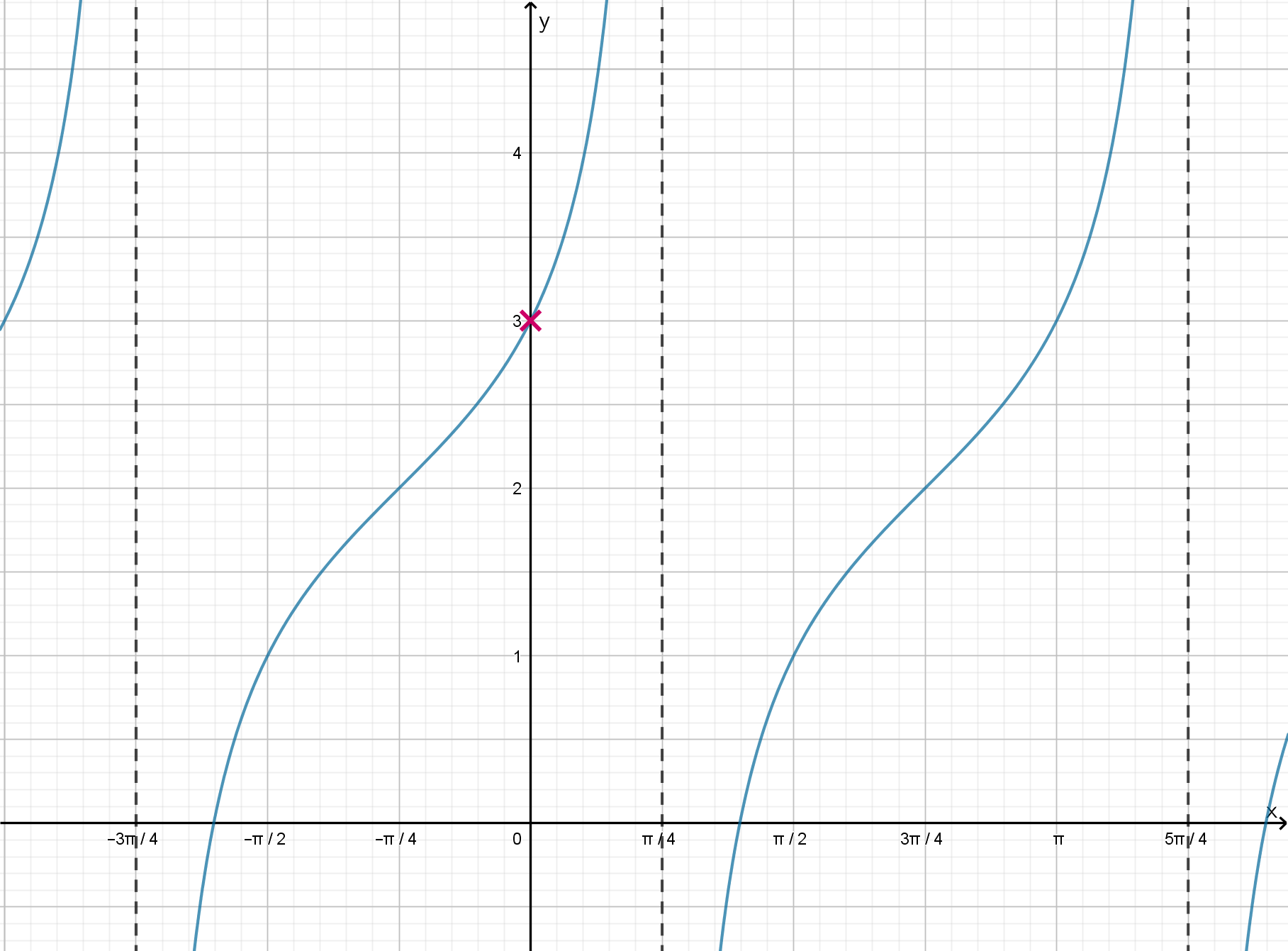
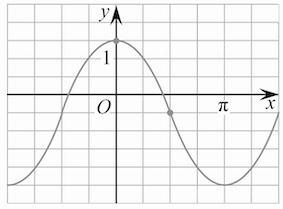
На рисунке изображен график функции ,
Найдите
На рисунке изображен график функции . Найдите
Показать ответ и решение
График функции проходит через точки и
, следовательно,
где
Ответ:
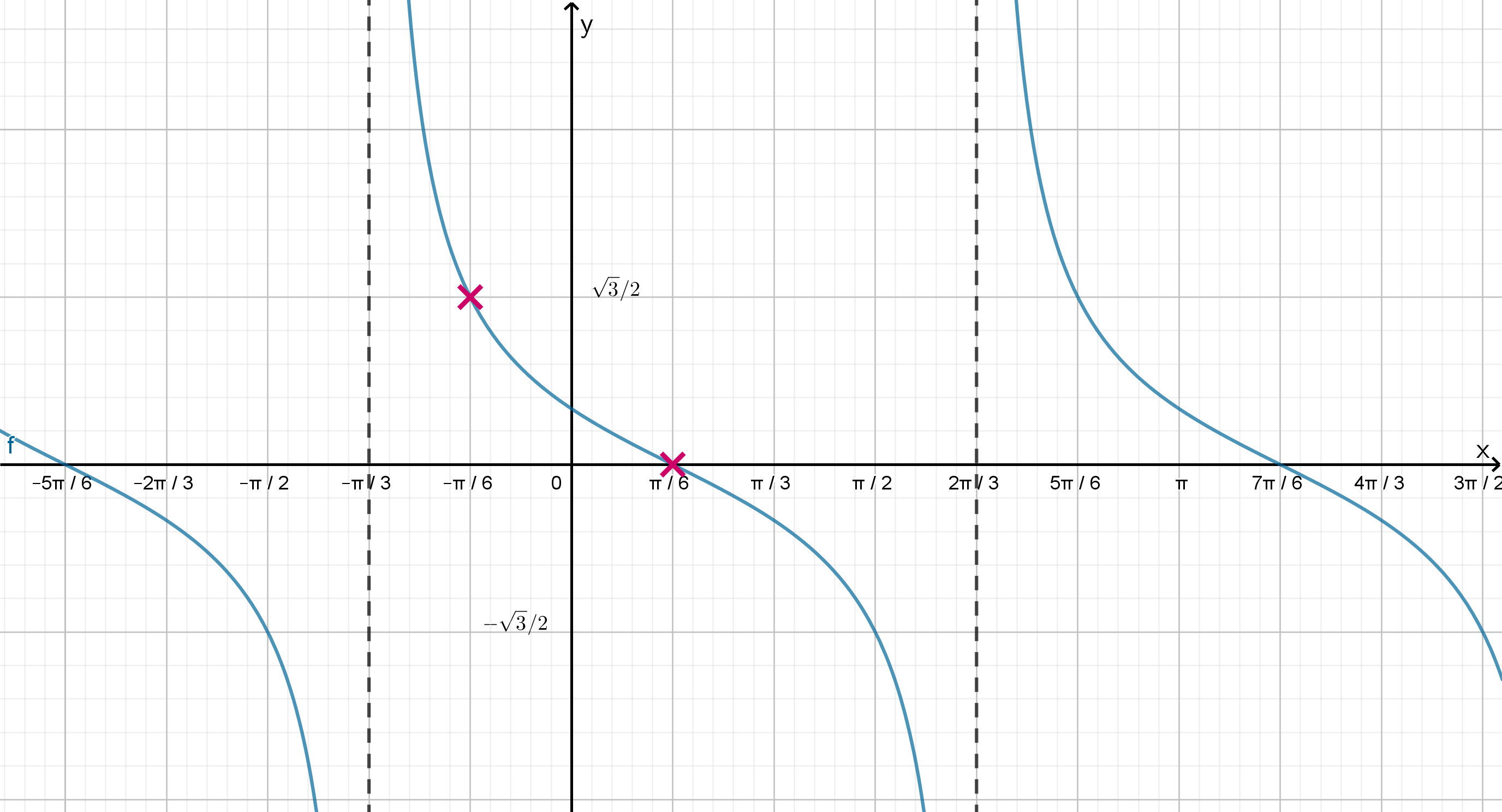
На рисунке изображен график функции . Найдите
Показать ответ и решение
График функции проходит через точки и
, следовательно,
Ответ:
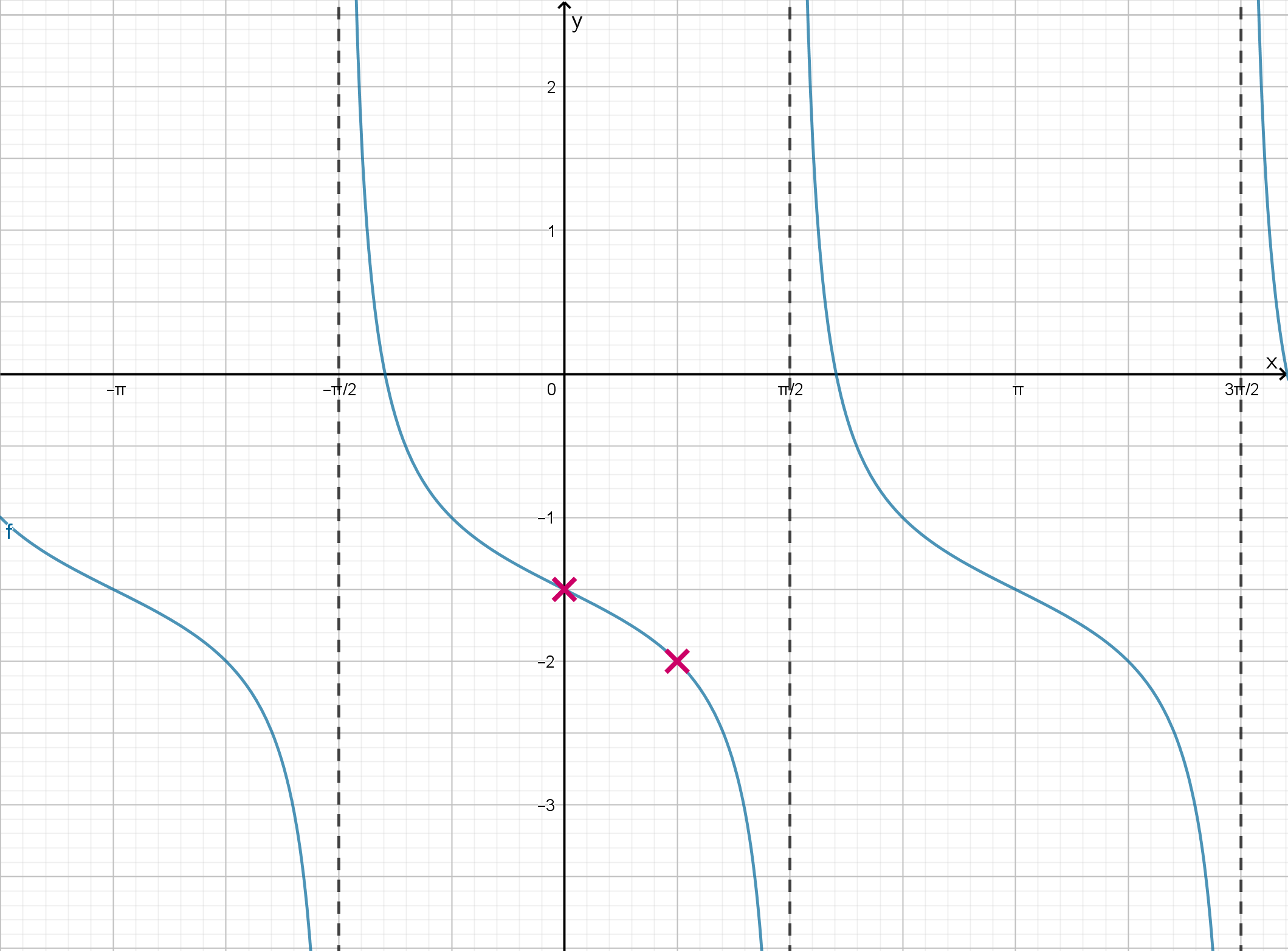
На рисунке изображен график функции . Найдите
Показать ответ и решение
График функции проходит через точки и
, следовательно,
Ответ:
На рисунке изображён график функции Найдите
Показать ответ и решение
С самого начала определим знак коэффициента Так как нам дана функция
вида а в окрестности точки
ее график выглядит как
мы можем сделать вывод, что
Определим величину «коридора», в котором меняется функция. Наименьшее
значение, которое принимает функция, равно а наибольшее значение
равно Тогда величина коридора равна
У классического графика косинуса величина коридора равна 2. После
домножения функции на коэффициент величина коридора изменяется в
раз, то есть
Найдем также Рассмотрим вспомогательную функцию
Она лежит в коридоре от до
При этом функция
лежит в
коридоре от до
Это значит, что если мы сдвинем коридор функции
на 1 вверх, то получим коридор функции
Все точки графиков также
совпадут, тогда
На рисунке изображён график функции Найдите
Показать ответ и решение
С самого начала определим знак коэффициента Так как нам дана функция вида
а в окрестности точки
ее график выглядит как
мы можем сделать вывод, что
Определим величину «коридора», в котором меняется функция. Наименьшее значение, которое принимает функция, равно
а наибольшее значение равно 0,5. Тогда величина коридора равна
У классического графика косинуса величина коридора равна 2. После домножения функции на коэффициент величина
коридора изменяется в раз, то есть
Теперь найдем Рассмотрим вспомогательную функцию
Она лежит в коридоре от до
При этом функция
лежит в коридоре от
до
Это значит, что
если мы сдвинем коридор функции на
вниз, то получим коридор функции
Все точки графиков также
совпадут, тогда
На рисунке изображен график функции Найдите
Показать ответ и решение
Заметим, что максимальное значение функции равно 1, а минимальное
—
Тогда при максимальное значение
равно
минимальное
равно
Если то наоборот, максимальное значение
равно
а
минимальное равно
Сложив максимальное и минимальное значения мы получим
По картинке видно, что максимальное значение равно 1, а минимальное
равно
Тогда окончательно имеем:
На рисунке изображен график функции Найдите
Показать ответ и решение
Мы знаем, что и
С другой стороны, по картинке видно, что
и
Тогда
имеем систему:
На рисунке изображён график функции
Найдите
Показать ответ и решение
Заметим, что — среднее значение между наибольшим и наименьшим значением функции. Наибольшее значение функции
равно 3, наименьшее — Тогда
- Развертка абсциссы движения точки по числовой окружности в функцию от угла
- Свойства функции y=cosx
- Примеры
п.1. Развертка ординаты движения точки по числовой окружности в функцию от угла
Развертка абсциссы движения точки по числовой окружности в функцию от угла (см. §2 данного справочника).
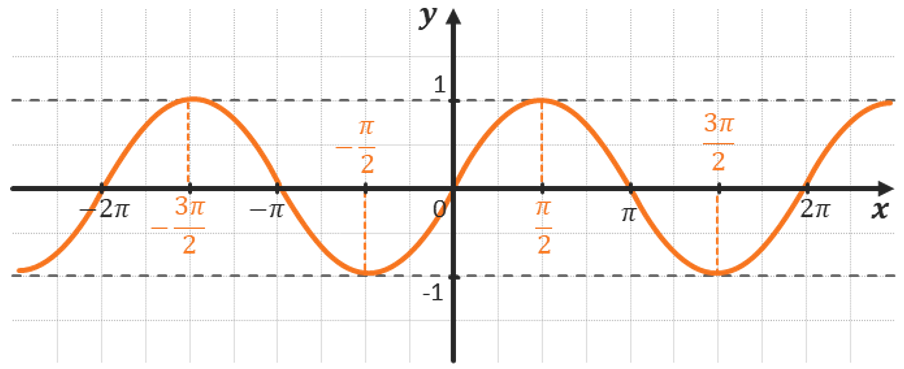
Рассмотрим, как изменяется косинус, если точка описывает полный круг, и угол x изменяется в пределах: 0≤x≤2π и построим график y=cosx на этом отрезке.
Если мы продолжим движение по окружности для углов x > 2π, кривая продолжится вправо; если будем обходить числовую окружность в отрицательном направлении (по часовой стрелке) для углов x<0, кривая продолжится влево.
В результате получаем график y=cosx для любого (xinmathbb{R}).
График y=cosx называют косинусоидой.
Часть косинусоиды для –π≤x≤π называют волной косинусоиды.
Часть косинусоиды для (-fracpi2leq xleqfracpi2) называют полуволной или аркой косинусоиды.
Заметим, что термин «косинусоида» используется достаточно редко. Обычно, и в случае косинуса, говорят о «синусоиде».
п.2. Свойства функции y=cosx
1. Область определения (xinmathbb{R}) — множество действительных чисел.
2. Функция ограничена сверху и снизу $$ -1leq cosxleq 1 $$ Область значений (yin[-1;1])
3. Функция чётная $$ cos(-x)=cosx $$
4. Функция периодическая с периодом 2π $$ cos(x+2pi k)=cosx $$
5. Максимальные значения (y_{max}=1) достигаются в точках $$ x=2pi k $$ Минимальные значения (y_{min}=-1) достигаются в точках $$ x=pi+2pi k $$ Нули функции (y_{0}=cosx_0=0) достигаются в точках (x=fracpi2 +pi k)
6. Функция возрастает на отрезках $$ -pi+2pi kleq xleq 2pi k $$ Функция убывает на отрезках $$ 2pi kleq xleqpi+2pi k $$
7. Функция непрерывна.
п.3. Примеры
Пример 1.Найдите наименьшее и наибольшее значение функции y=cosx на отрезке:
a) (left[fracpi6; frac{3pi}{4}right]) $$ y_{min}=cosleft(frac{3pi}{4}right)=-frac{sqrt{2}}{2}, y_{max}=cosleft(fracpi6right)=frac{sqrt{3}}{2} $$ б) (left[frac{5pi}{6}; frac{5pi}{3}right]) $$ y_{min}=cos(pi)=-1, y_{max}=cosleft(frac{5pi}{3}right)=frac12 $$
Пример 2. Решите уравнение графически:
a) (cosx=fracpi2-x)
Один корень: (x=fracpi2)
б) (cosx-x=1)
(cosx=x+1)
Один корень: x = 0
в) (cosx-x^2=1)
(cosx=x^2+1) 
Один корень: x = 0
г*) (cosx-x^2+frac{pi^2}{4}=0)
(cosx=x^2-frac{pi^2}{4})
(y=x^2-frac{pi^2}{4}) – парабола ветками вверх, с осью симметрии (x_0=0) (ось OY) и вершиной (left(0; -frac{pi^2}{4}right)) (см. §29 справочника для 8 класса)
Два корня: (x_{1,2}=pmfracpi2)
Пример 3. Постройте в одной системе координат графики функций $$ y=cosx, y=-cosx, y=2cosx, y=cosx-2 $$ 
(y=-cosx) – отражение исходной функции (y=cosx) относительно оси OX. Область значений (yin[-1;1]).
(y=2cosx) – исходная функция растягивается в 2 раза по оси OY. Область значений (yin[-2;2]).
(y=cosx-2) — исходная функция опускается вниз на 2. Область значений (yin[-3;-1]).
Пример 4. Постройте в одной системе координат графики функций $$ y=cosx, y=cos2x, y=cosfrac{x}{2} $$ 
Амплитуда колебаний у всех трёх функций одинакова, область значений (yin[-1;1]).
Множитель под косинусом изменяет период колебаний.
(y=cosx) – главная арка косинуса соответствует отрезку (-fracpi2leq xleqfracpi2)
(y=cos2x) — период уменьшается в 2 раза, главная арка укладывается в отрезок (-fracpi4leq xleqfracpi4).
(y=cosfrac{x}{2}) — период увеличивается в 2 раза, главная арка растягивается в отрезок (-pi leq xleq pi).
Графики тригонометрических функций
Рассмотрим графики и свойства тригонометрических функций и обратных им.
СИНУС:
Синус – функция вида (y = sin x.)
Графиком этой функции является синусоида.
ХАРАКТЕРИСТИКИ СИНУСА:
| 1. Область определения: | (D(ymathbb{) = R}) |
|---|---|
| 2. Область значения: | (E(y) = lbrack–1; 1rbrack) |
| 3. Ограниченность и непрерывность: | Ограничена сверху и снизу; непрерывна |
| 4. Наибольшее и наименьшее значение функции: |
(y_{наиб.}) при: (x in frac{pi}{2} + 2pi k), (k in mathbb{Z}) (y_{наим.}) при: (x in frac{3pi}{2} + 2pi k), (k in mathbb{Z}) |
| 5. Промежутки знакопостоянства: |
(y > 0) при: (x in (0; pi) + 2pi k), (k in mathbb{Z}) (y < 0) при: (x in (pi;2pi) + 2pi k), (k in mathbb{Z}) |
| 6. Монотонность: |
Возрастает при: (x in left( –frac{pi}{2};frac{pi}{2} right) + 2pi k), (k in mathbb{Z}) Убывает при: (x in left( frac{pi}{2}; frac{3pi}{2} right) + 2pi k, k in mathbb{Z}) |
| 7. Экстремумы: |
(y_{max}) при: (x in frac{pi}{2} + 2pi k, k in mathbb{Z}) (y_{min}) при: (x in frac{3pi}{2} + 2pi k), (k in mathbb{Z}) |
| 8. Четность: | Нечетная |
| 9. Периодичность: | (Период = 2pi) |
| 10. Пересекает ось Ох | В точках (x = text{πk}, k in mathbb{Z}) |
| 11. Пересекает ось Оу | В точке ((0;0)) |
КОСИНУС:
Косинус – функция вида (y = cos x).
Графиком этой функции является косинусоида.
ХАРАКТЕРИСТИКИ КОСИНУСА:
| 1. Область определения: | (D(ymathbb{) = R}) |
|---|---|
| 2. Область значения: | (E(y) = lbrack–1; 1rbrack) |
| 3. Ограниченность и непрерывность: | Ограничена сверху и снизу; непрерывна |
| 4. Наибольшее и наименьшее значение функции: |
(y_{наиб.} )при: (x in 2pi k, k in mathbb{Z}) (y_{наим.}) при: (x in pi + pi k), k(in)ℤ |
| 5. Промежутки знакопостоянства: |
(y > 0) при: (x in (–frac{pi}{2}; frac{pi}{2}) + 2pi k, k in mathbb{Z}) (y < 0) при: (x in (frac{pi}{2};frac{3pi}{2}) + 2pi k, k in mathbb{Z}) |
| 6. Монотонность: |
Возрастает при: (x in (pi; 2pi) + 2pi k, k in mathbb{Z}) Убывает при: (x in left( 0;pi right) + 2pi k, k in mathbb{Z}) |
| 7. Экстремумы: |
(y_{max}) при: (x in 2pi k, k in mathbb{Z}) (y_{min}) при: (x in pi + pi k, k in mathbb{Z}) |
| 8. Четность: | Четная |
| 9. Периодичность: | (Период = 2pi) |
| 10. Пересекает ось Ох | В точках (x = frac{pi}{2} + text{πk}, k in mathbb{Z}) |
| 11. Пересекает ось Оу | В точке ((0;1)) |
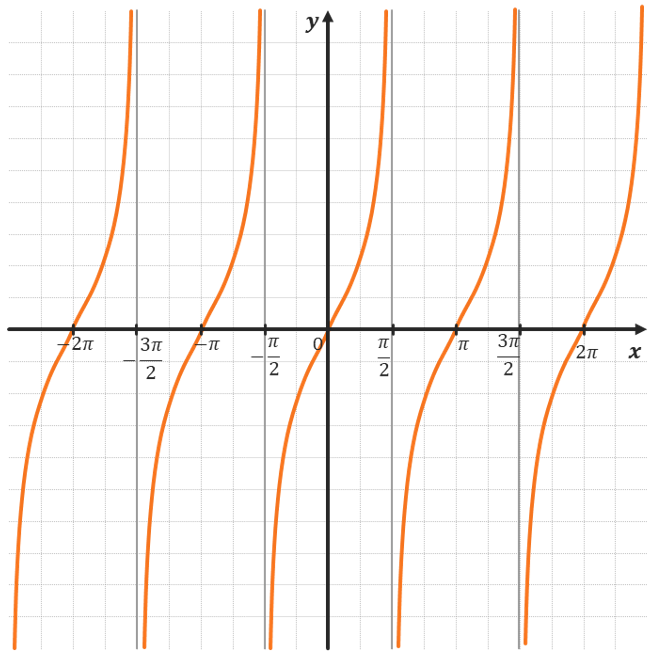
ТАНГЕНС:
Тангенс – функция (вида y = text{tg} x ).
ХАРАКТЕРИСТИКИ ТАНГЕНСА:
| 1. Область определения: | (D(y): x neq frac{pi}{2} + pi k, kmathbb{in Z}) |
|---|---|
| 2. Область значения: | (E(y) = lbrack–1; 1rbrack) |
| 3. Ограниченность и непрерывность: |
Неограничена; Имеет асимптоты точках ( x = frac{pi}{2} + text{πk}, kmathbb{in Z}) |
| 4. Наибольшее и наименьшее значение функции: | Нет |
| 5. Промежутки знакопостоянства: |
(y > 0 )при: (x in (0;frac{pi}{2}) + pi k, k in mathbb{Z}) (y < 0) при: (x in (–frac{pi}{2}; 0) + pi k, k in mathbb{Z}) |
| 6. Монотонность: | Возрастает между всеми асимптотами |
| 7. Экстремумы: | нет |
| 8. Четность: | Нечетная |
| 9. Периодичность: | (Период = pi) |
| 10. Пересекает ось Ох | В точках (x = text{πk}, k in mathbb{Z}) |
| 11. Пересекает ось Оу | В точке ((0;0)) |
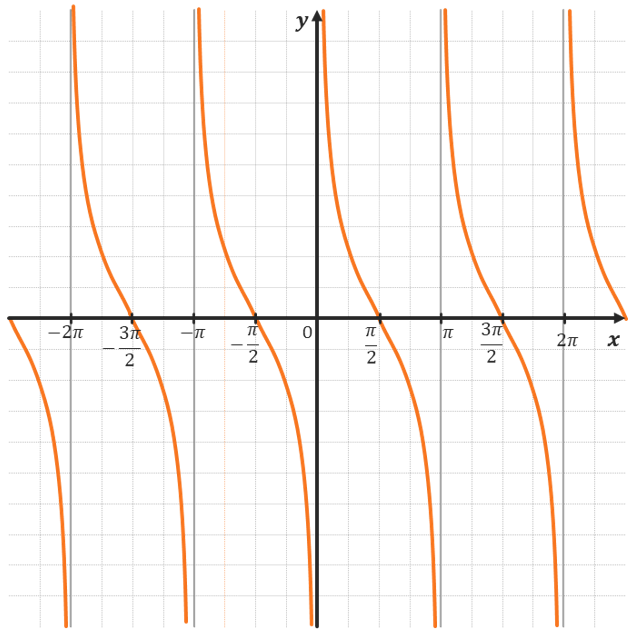
КОТАНГЕНС:
Котангенс – функция вида (y = text{ctg} x.)
ХАРАКТЕРИСТИКИ КОТАНГЕНСА:
| 1. Область определения: | (D(y): x neq pi k, kmathbb{in Z}) |
|---|---|
| 2. Область значения: | (E(y) = lbrack–1; 1rbrack) |
| 3. Ограниченность и непрерывность: |
Неограничена; Имеет асимптоты в точках ( x = text{πk}, kmathbb{in Z}) |
| 4. Наибольшее и наименьшее значение функции: | Нет |
| 5. Промежутки знакопостоянства: |
(y > 0) при: (x in (0;frac{pi}{2}) + pi k, k in mathbb{Z}) (y < 0) при: (x in (frac{pi}{2};pi) + pi k, k in mathbb{Z}) |
| 4. Монотонность: | Убывает между всеми асимптотами |
| 7. Экстремумы: | нет |
| 5. Четность: | Нечетная |
| 6. Периодичность: | (Период = pi) |
| 7. Пересекает ось Ох | В точках ( x = frac{pi}{2} + text{πk}, kmathbb{in Z}) |
| 8. Пересекает ось Оу | Не пересекает ось |
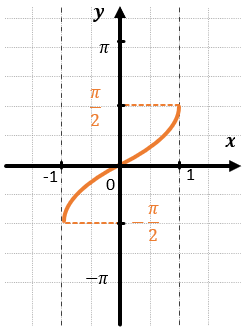
АРКСИНУС:
Арксинус – функция вида (y = arcsin x).
ХАРАКТЕРИСТИКИ АРКСИНУСА:
| 1. Область определения: | (D(y) = lbrack–1; 1rbrack) |
|---|---|
| 2. Область значения: | (E(y) = leftlbrack –frac{pi}{2};frac{pi}{2} rightrbrack) |
| 3. Ограниченность и непрерывность: | Ограничена со всех сторон; непрерывна |
| 4. Наибольшее и наименьшее значение функции: |
(y_{наиб.}) при: (x = 1) (y_{наим.}) при: (x = –1) |
| 5. Промежутки знакопостоянства: |
(y > 0) при: (x in (0;1)) (y < 0) при: (x in (–1;0) ) |
| 6. Монотонность: | Возрастает |
| 7. Экстремумы: | нет |
| 8. Четность: | Нечетная |
| 9. Периодичность: | Не периодична |
| 10. Пересекает ось Ох | В точке( (0;0)) |
| 11. Пересекает ось Оу | В точке ((0;0)) |
АРККОСИНУС:
Арккосинус – функция (вида y = arccos x).
ХАРАКТЕРИСТИКИ АРККОСИНУСА:
| 1. Область определения: | (D(y) = lbrack–1; 1rbrack) |
|---|---|
| 2. Область значения: | (E(y) = (0; pi)) |
| 3. Ограниченность и непрерывность: | Ограничена со всех сторон |
| 4. Наибольшее и наименьшее значение функции: |
(y_{наиб. }) при: (x = –1) (y_{наим.}) при: (x = 1) |
| 5. Промежутки знакопостоянства: | (y > 0) при: (x in (–1;1)) |
| 6. Монотонность: | Убывает |
| 7. Экстремумы: | нет |
| 8. Четность: | Ни четная, ни нечетная |
| 9. Периодичность: | Не периодична |
| 10. Пересекает ось Ох | В точке ((1;0)) |
| 11. Пересекает ось Оу | В точке ((0;frac{pi}{2})) |
АРКТАНГЕНС:
Арктангенс – функция вида (y = text{arctg} x.)
ХАРАКТЕРИСТИКИ АРКТАНГЕНСА:
| 1. Область определения: | (D(y): mathbb{R}) |
|---|---|
| 2. Область значения: | (E(y) = leftlbrack –frac{pi}{2};frac{pi}{2} rightrbrack) |
| 3. Ограниченность и непрерывность: | Ограничена сверху и снизу; непрерывна |
| 4. Наибольшее и наименьшее значение функции: | Нет |
| 5. Промежутки знакопостоянства: |
(y > 0 )при: (x in (0; + infty)) (y < 0) при: (x in (–infty;0) ) |
| 6. Монотонность: | Возрастает |
| 7. Экстремумы: | нет |
| 8. Четность: | Нечетная |
| 9. Периодичность: | Не периодична |
| 10. Пересекает ось Ох | В точке ((0;0)) |
| 11. Пересекает ось Оу | В точке ((0;0)) |
АРККОТАНГЕНС:
Арккотангенс – функция вида (y = text{arcctg} x).
ХАРАКТЕРИСТИКИ АРККОТАНГЕНСА:
| 1. Область определения: | (D(y): mathbb{R}) |
|---|---|
| 2. Область значения: | (E(y) = (0; pi)) |
| 3. Ограниченность и непрерывность: | Ограничена сверху и снизу; непрерывна |
| 4. Наибольшее и наименьшее значение функции: | Нет |
| 5. Промежутки знакопостоянства: | (y > 0) при: (x in mathbb{R}) |
| 6. Монотонность: | Убывает |
| 7. Экстремумы: | нет |
| 8. Четность: | Ни четная, ни нечетная |
| 9. Периодичность: | Не периодична |
| 10. Пересекает ось Ох | Не пересекает ось |
| 11. Пересекает ось Оу | В точке ((0; frac{pi}{2})) |
На этой странице вы узнаете
- Как найти углы у апельсина?
- Кто сказал “Ты как хочешь, а я уехала!”
Люди пользуются тригонометрией с древнейших времен. Добывая еду с помощью лука и стрел, человек уже применял знания, которые мы разберем в этой статье.
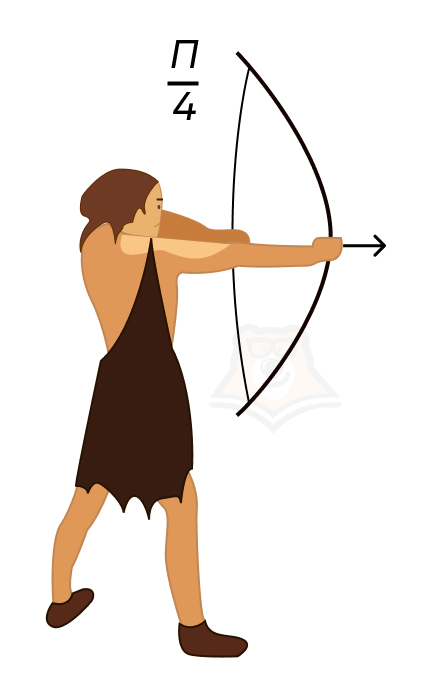
Единичная тригонометрическая окружность
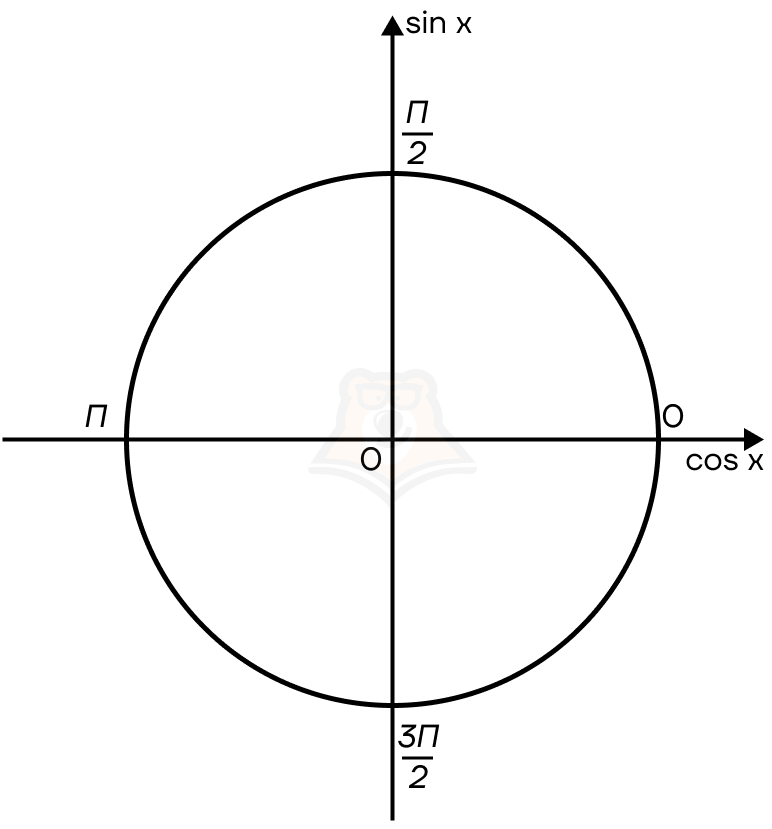
Единичная тригонометрическая окружность — это окружность с центром в точке (0; 0) на координатной плоскости, радиус которой равен 1
Так как длина всей окружности равна 2π, сделаем вывод, что половина окружности — это π, а четверть — это π2.
Теперь разделим окружность сначала на восемь частей, а потом ту же окружность на двенадцать частей. Рассчитаем значения полученных точек.
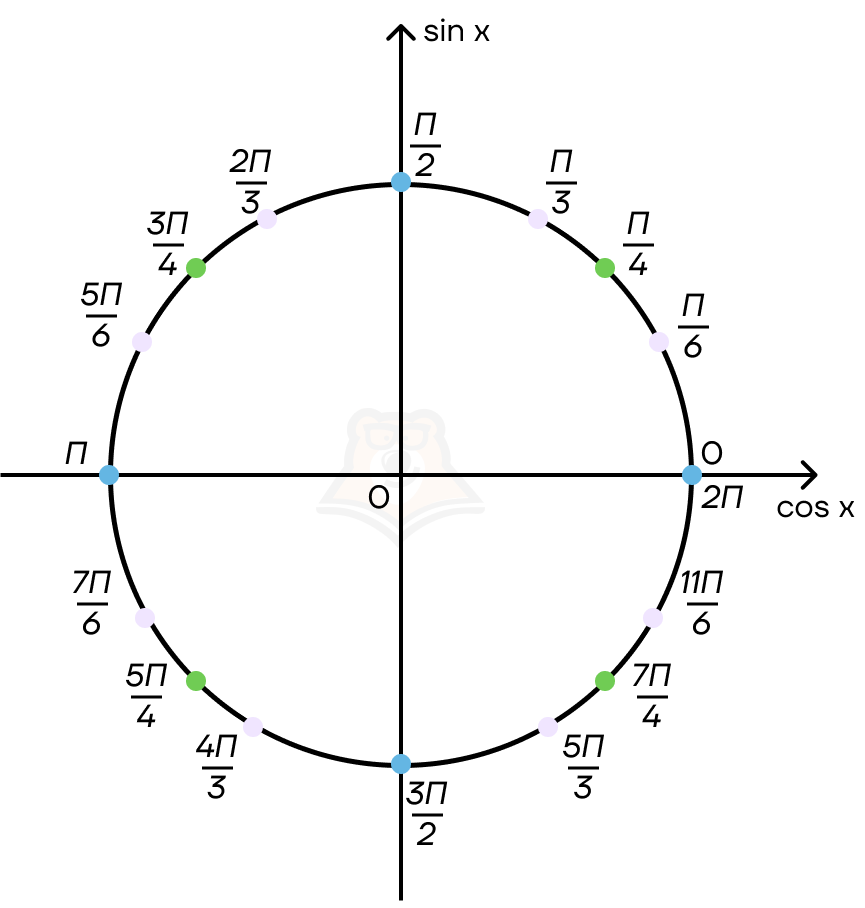
Заметим, что точка 0 совпадает с точкой 2π. Это означает, что мы сделали один оборот по окружности. Но мы можем продолжать идти так и дальше: тогда эта же точка будет принимать значения 4π, 6π, 8π.
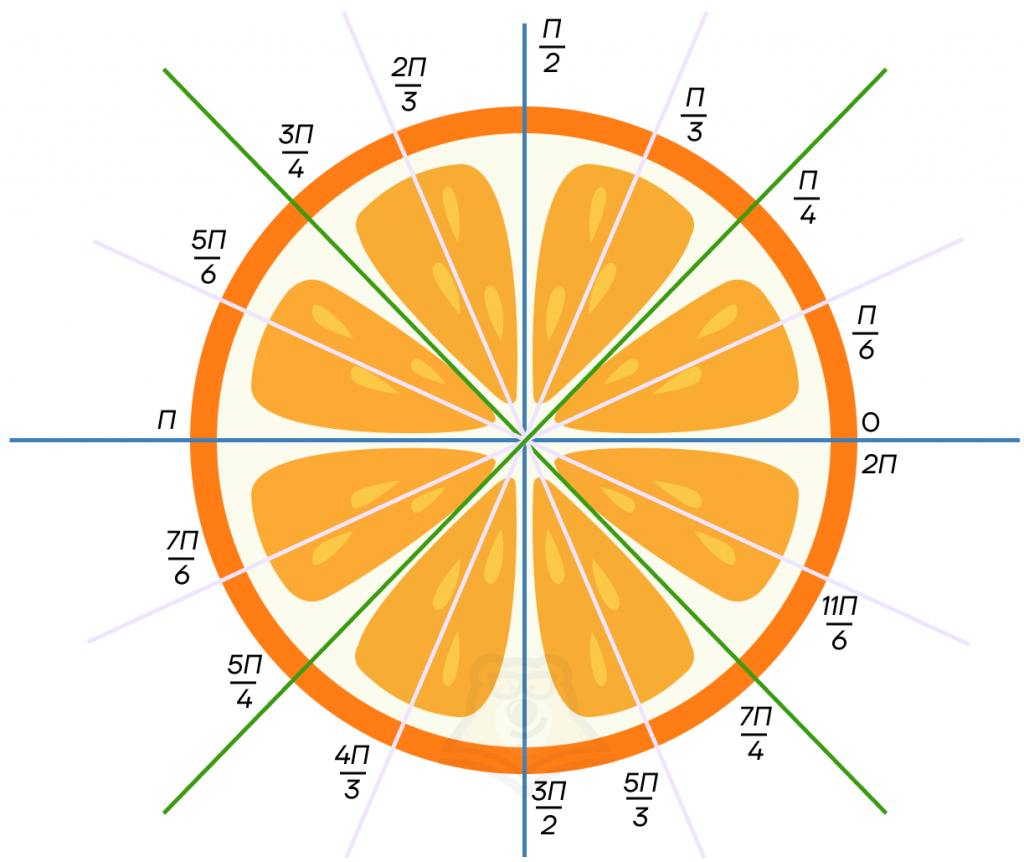
Для удобства представим, что окружность — это половинка апельсина. Длина корочки апельсина равна 2π. А теперь будем делить 2π на 4, 8 и 12. Таким образом, получившиеся кусочки апельсина будут являться углами на тригонометрической окружности.
Движение по тригонометрической окружности можно сравнить с движением по числовой прямой, закрученной в спираль.
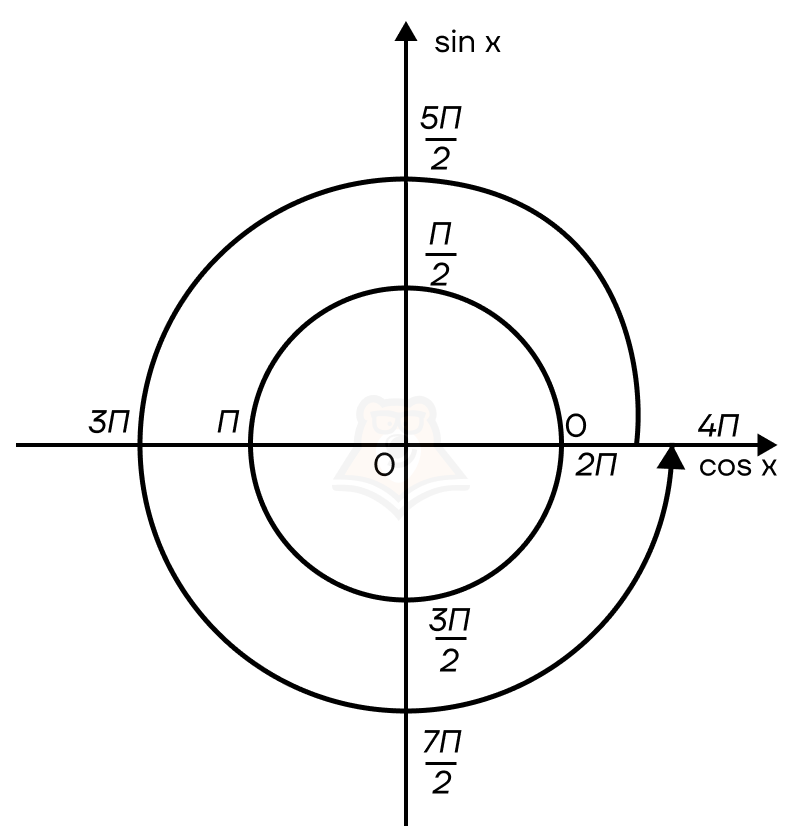
Аналогично можно двигаться и против движения часовой стрелки, но это уже будет отрицательная спираль.
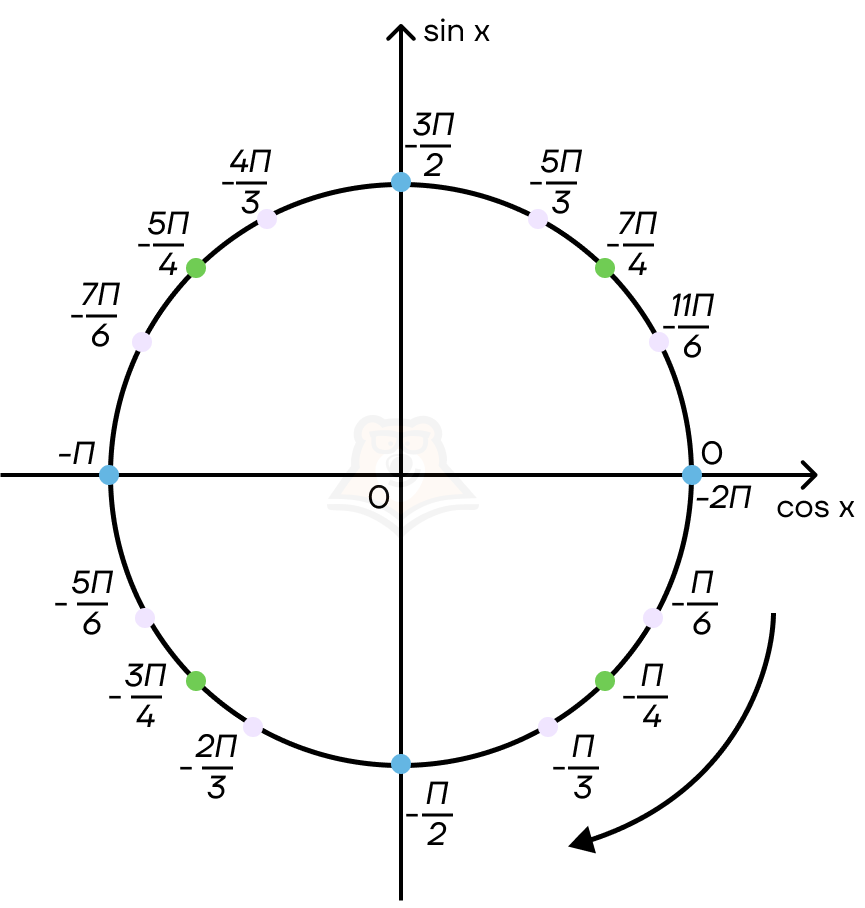
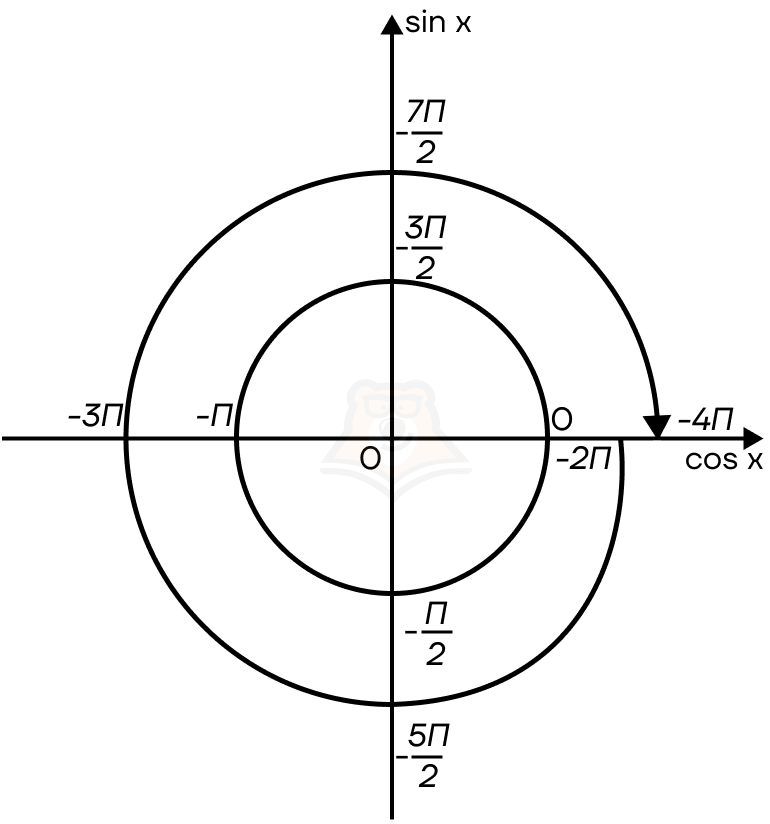
Как записать множество точек, находящихся в одной точке окружности, но на разных витках спирали?
Так как тригонометрические функции — это периодические функции, то и значения в точках будут повторяться с определенным интервалом: то есть с интервалом 2πk, где k принадлежит множеству целых чисел.
Пример: π + 2πk, k ∈ Z
Теперь рассмотрим значения синусов и косинусов, определенных на окружности точек.
На положительных частях осей они представлены как (frac{1}{2}), (frac{sqrt{2}}{2}), (frac{sqrt{3}}{2}), а на отрицательных — (-frac{1}{2}), (-frac{sqrt{2}}{2}), (-frac{sqrt{3}}{2}).
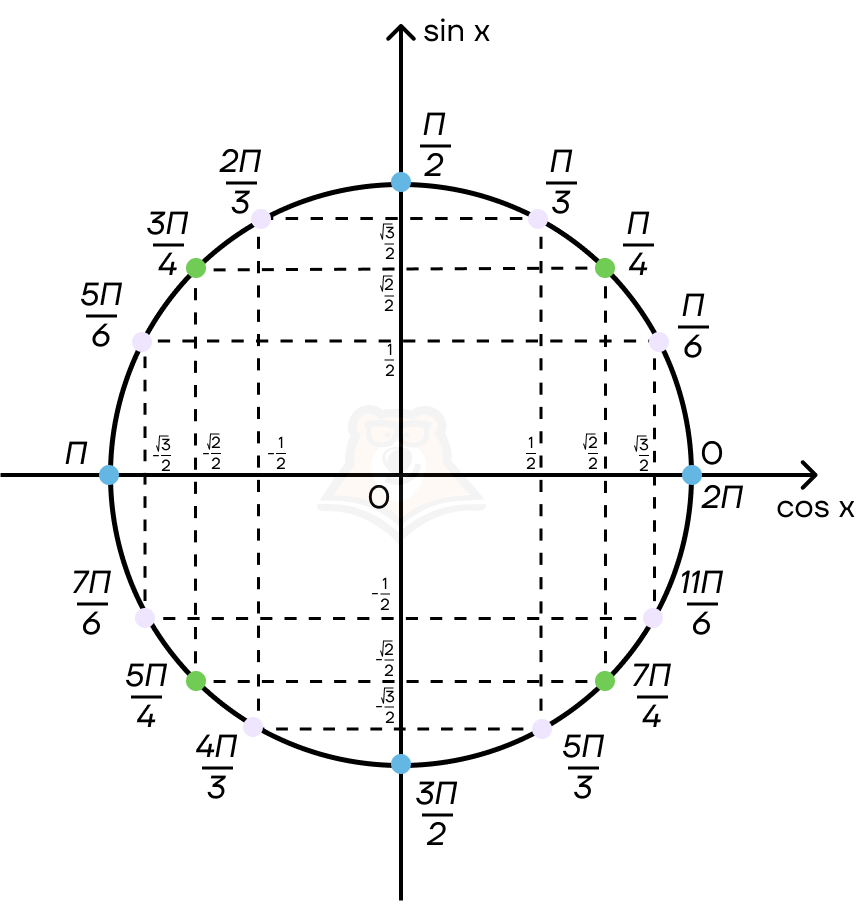
Для нахождения значения синуса или косинуса известного угла нужно провести перпендикулярную прямую к прямой, предназначенной этой функции. Значение, в котором она пересечет прямую функции будет являться значением этой тригонометрической функции от известного числа.
Пример:
Нужно узнать чему равно (sin frac{pi}{3})
Сначала найдем (frac{pi}{3}) на окружности, затем проведем перпендикулярную прямую к прямой синусов. Ответом является значение в точки пересечения.
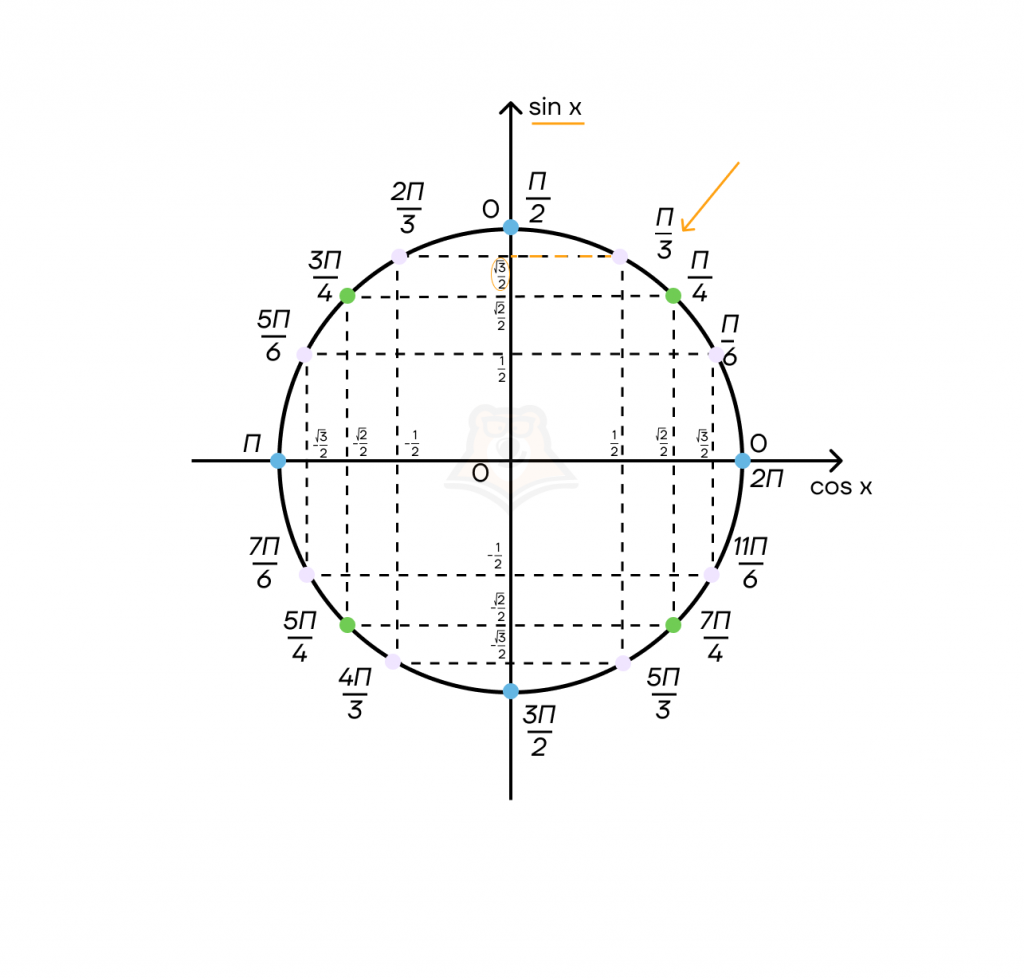
(sin frac{pi}{3} = frac{sqrt{3}}{2})
Теперь проведём ещё две прямые для обозначения прямых тангенса и котангенса. Отметим на них значения для точек окружности.
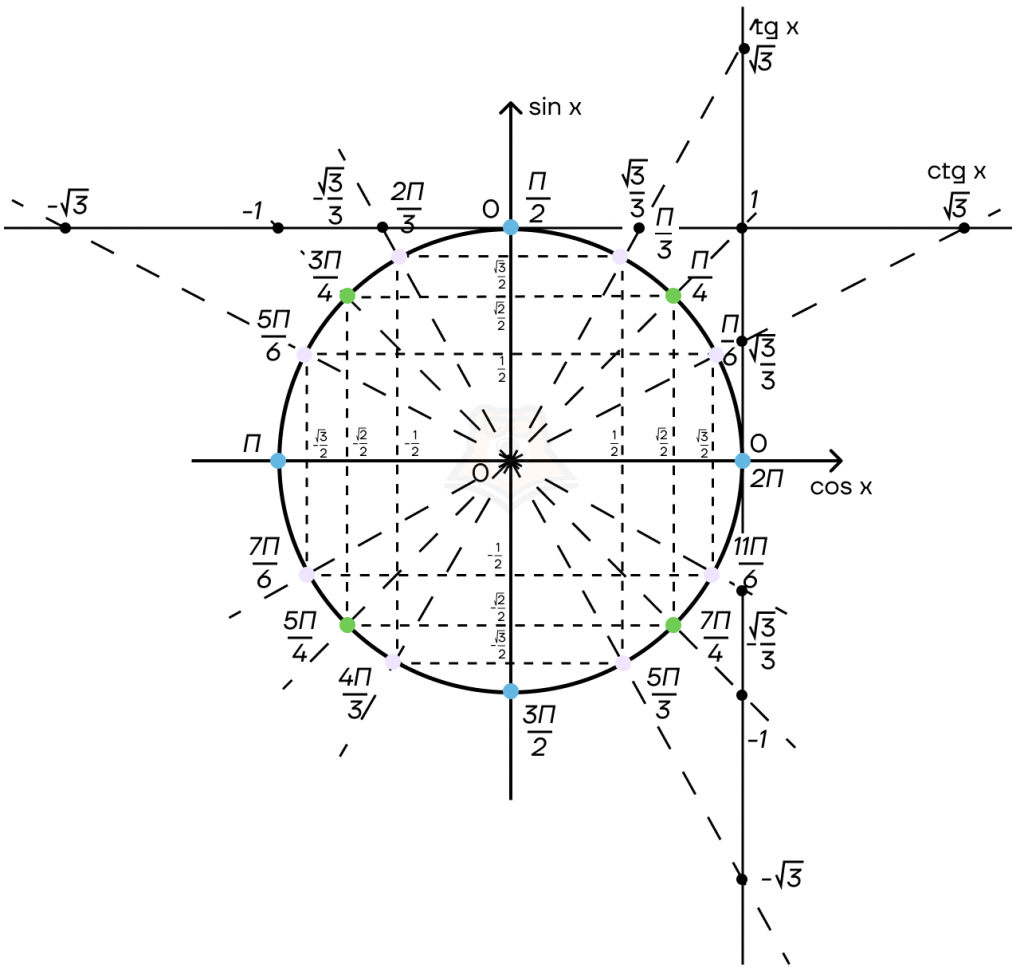
Для нахождения значения тангенса или котангенса известного угла нужно провести прямую через точку (0; 0) и это число на окружности. Значение, в котором она пересечет прямую данной функции, будет являться значением этой тригонометрической функции от известного числа.
Пример:
Нужно узнать чему равно (ctg frac{2 pi}{3})
Сначала найдем (frac{2 pi}{3}) на окружности, затем проведём прямую через (0; 0) и эту точку на окружности. Ответом является значение в точки пересечения проведенной прямой и прямой котангенсов.
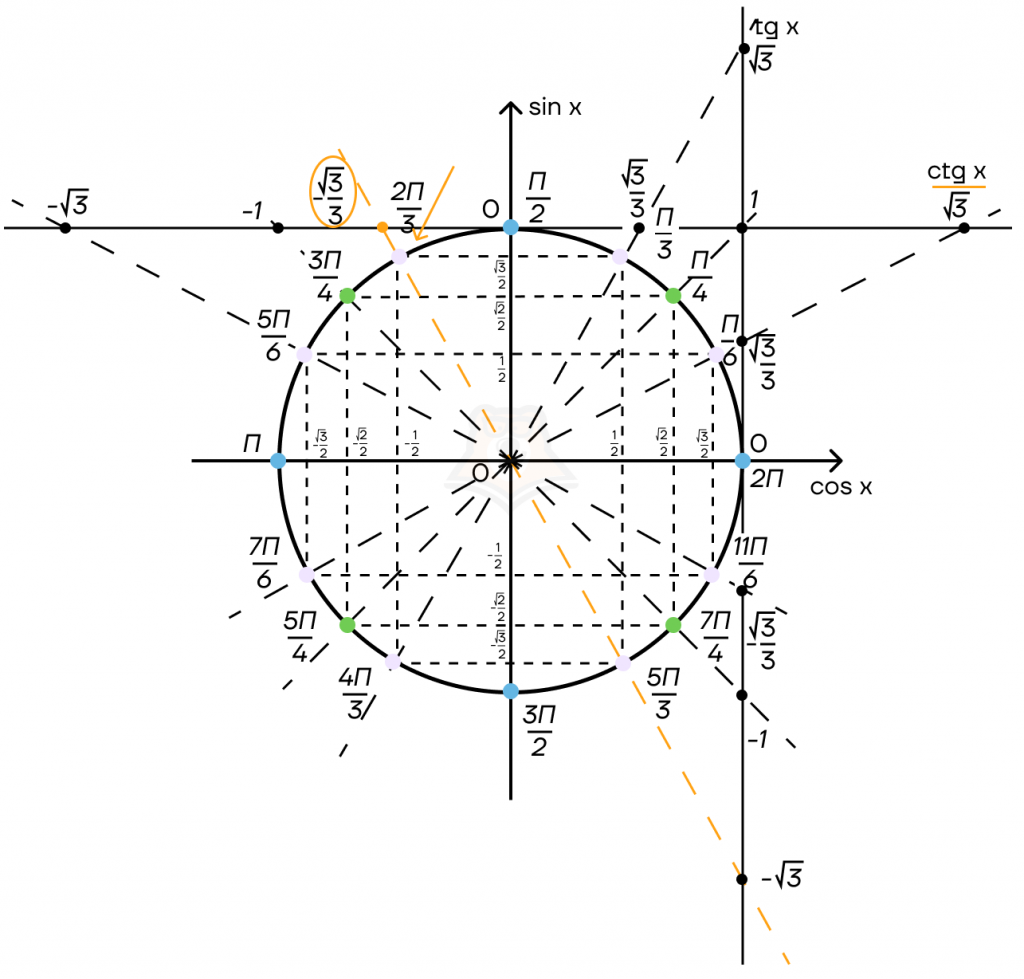
(ctg frac{2 pi}{3} = -frac{sqrt{3}}{3})
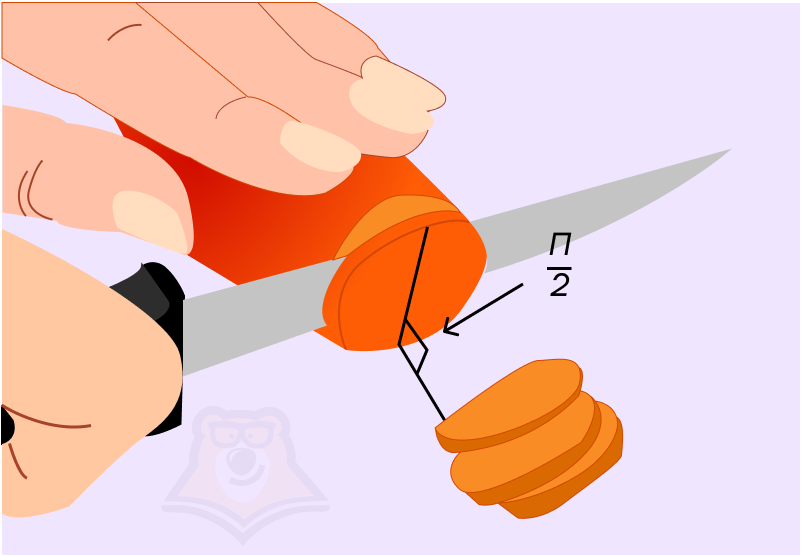
Примеры тригонометрии можно найти и в жизни. Например: когда мы режем морковку, нож находится под углом (frac{pi}{2}) к поверхности доски.
Графики тригонометрических функций
Как уже было сказано ранее, тригонометрические функции — это периодические функции.
То есть, значения этих функций повторяются через определенный период. Теперь рассмотрим подробнее графики таких функций.
Находя значения у для разных значений х и соединяя точки, можно получить следующие графики функций.
График y = sin x — синусоида.
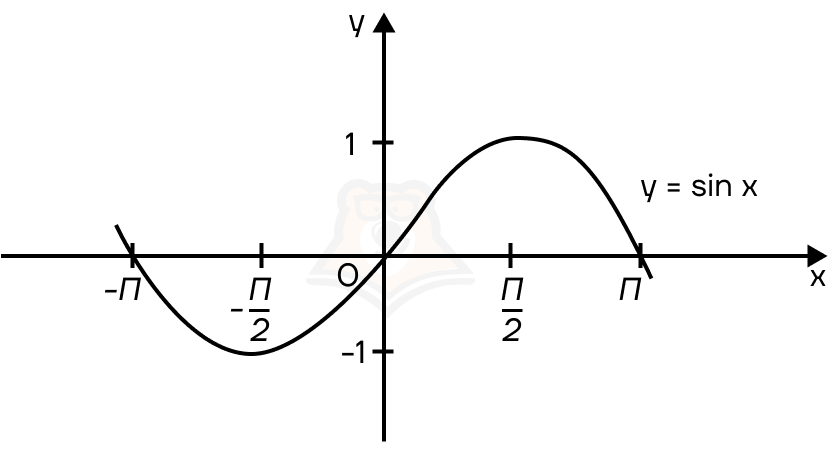
График y = cos x — косинусоида.
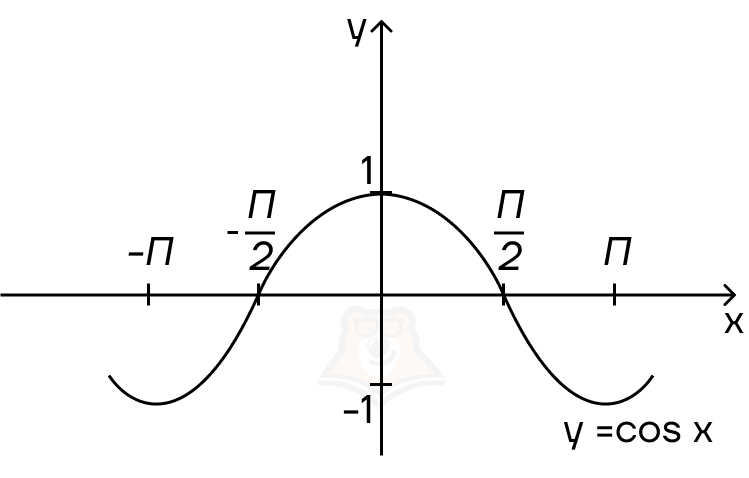
График y = tgx — тангенсоида.
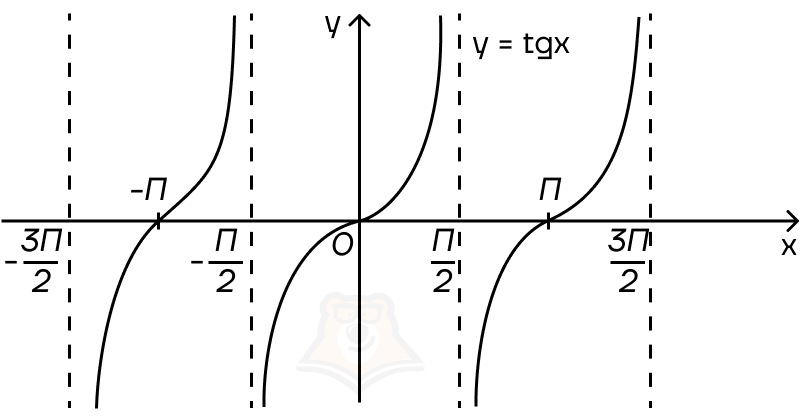
Важно: тангенсоида никогда не может принимать значения (frac{pi}{2}); (frac{3 pi}{2}); (frac{5 pi}{2}) и т. д. Так как тангенс — это синус делить на косинус, а делить на ноль нельзя, следовательно, косинус не равен нулю. Данные значения отмечены на графике пунктирными линиями.
График y = ctgx — котангенсоида.
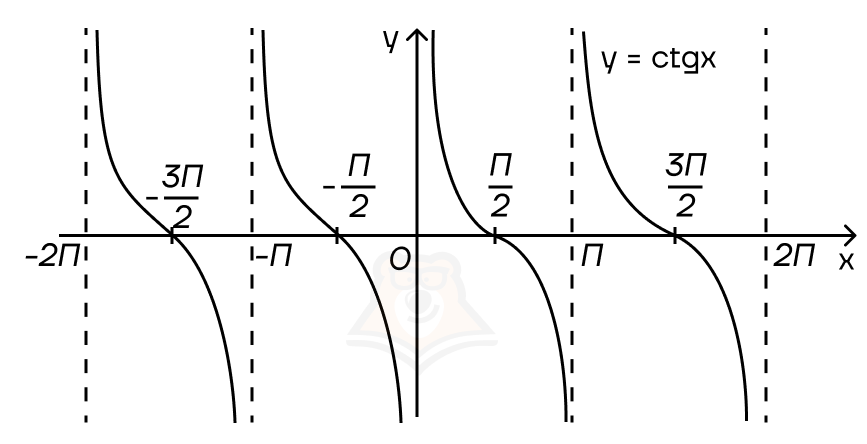
Важно: котангенсоида никогда не может принимать значения 0; π; 2π и т. д., так как котангенс — это косинус делить на синус. Делить на ноль нельзя, значит синус не равен нулю. Данные значения отмечены на графике пунктирными линиями.
Каждую из рассмотренных выше функций можно сдвигать по осям Х и Y и растягивать по оси Y. Давайте рассмотрим такие растяжения и сдвиги.
Коэффициент перед тригонометрической функцией
Чем больше коэффициент перед тригонометрической функцией, тем сильнее она вытягивается по вертикали.
Рассмотрим на примере синусоиды и тангенсоиды. Косинусоида и котангенсоида растягиваются по аналогии.
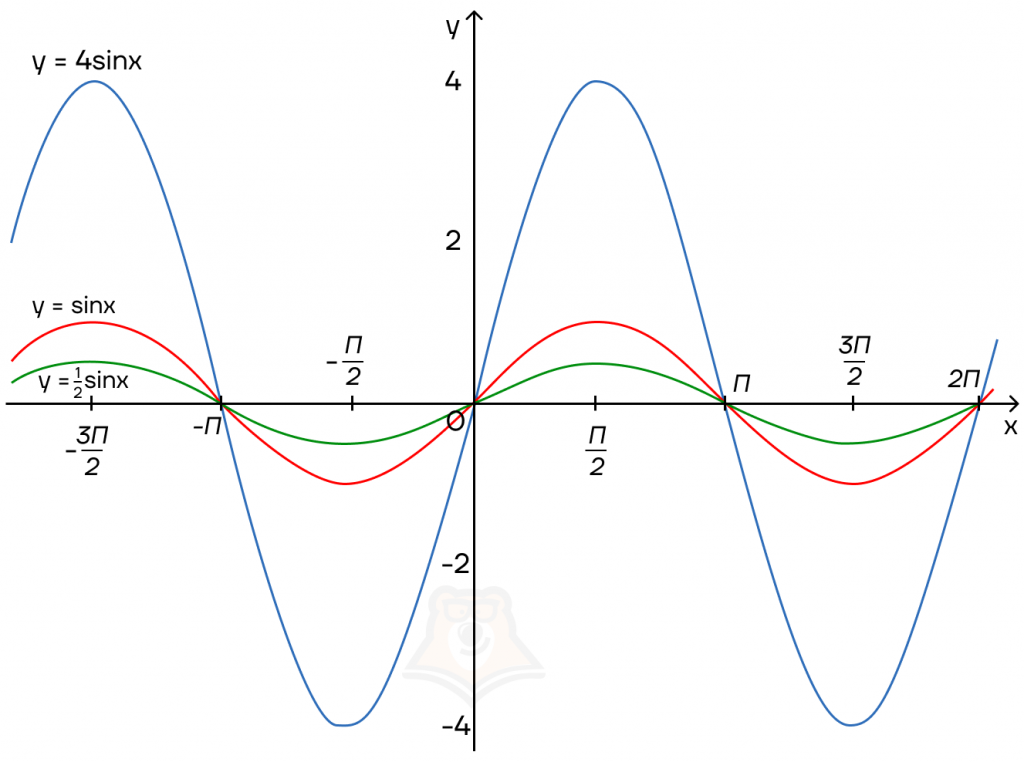
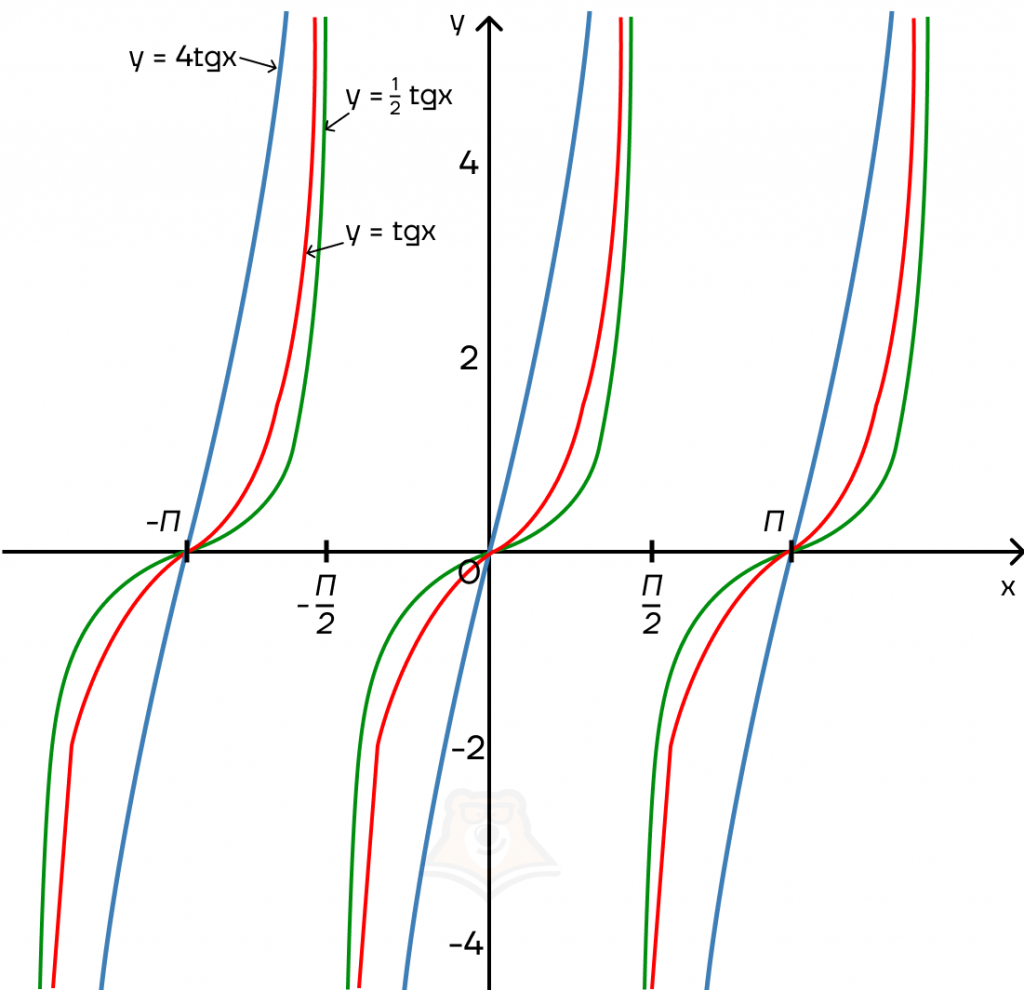
Сдвиг по оси Y
График тригонометрической функции сдвигается по оси Y на прибавленную к значению y константу.
Рассмотрим на примере синусоиды и тангенсоиды. Косинусоида и котангенсоида сдвигаются по аналогии.
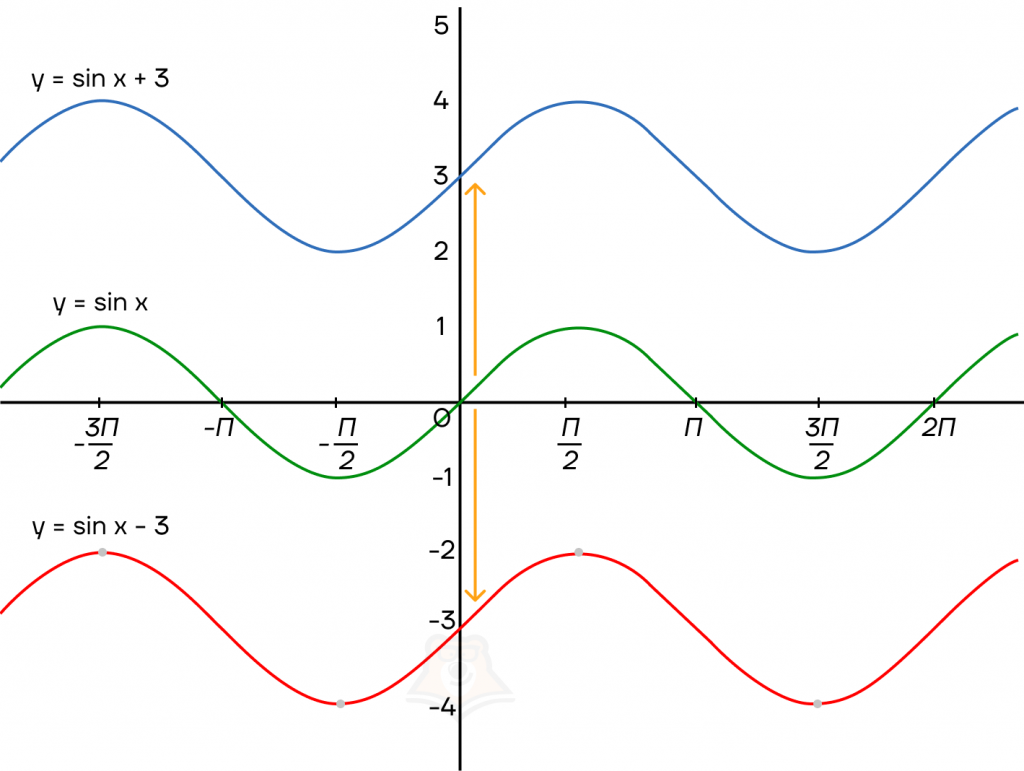
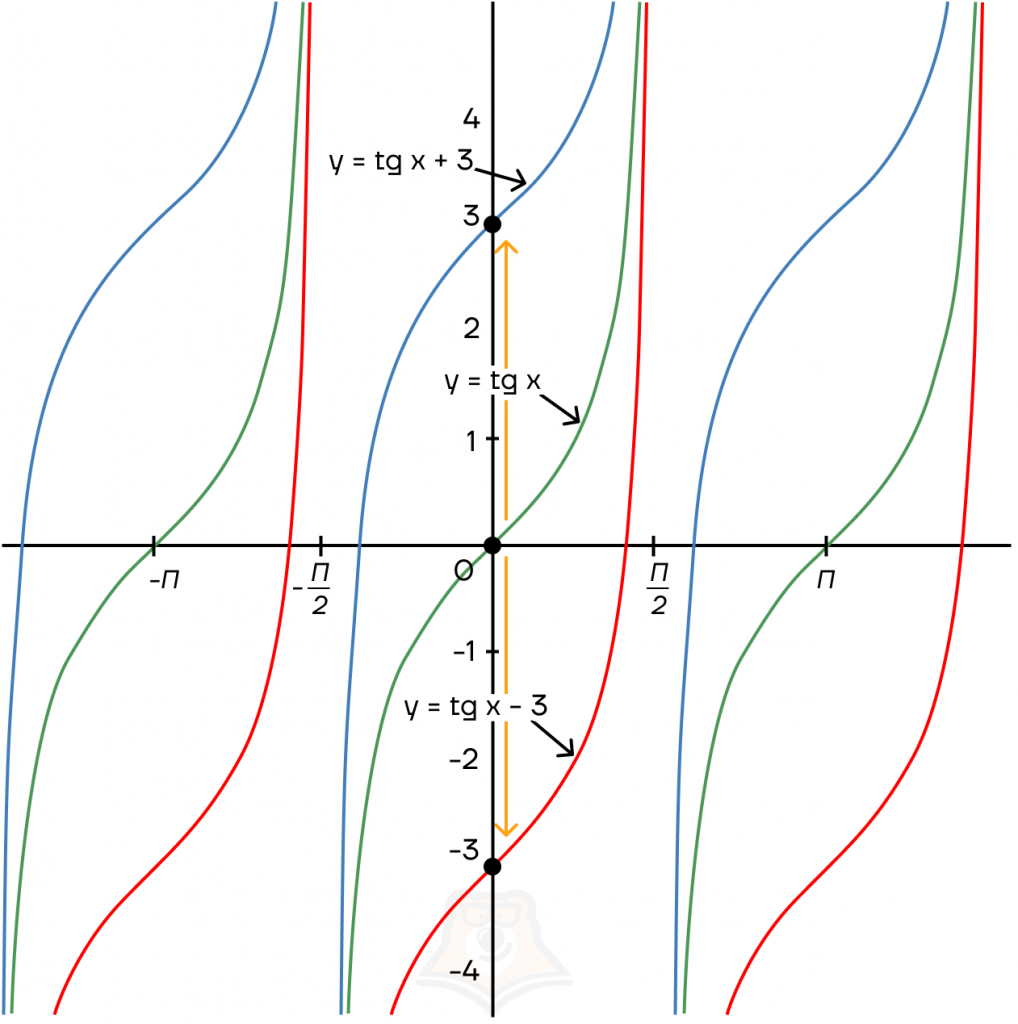
Сдвиг по оси Х
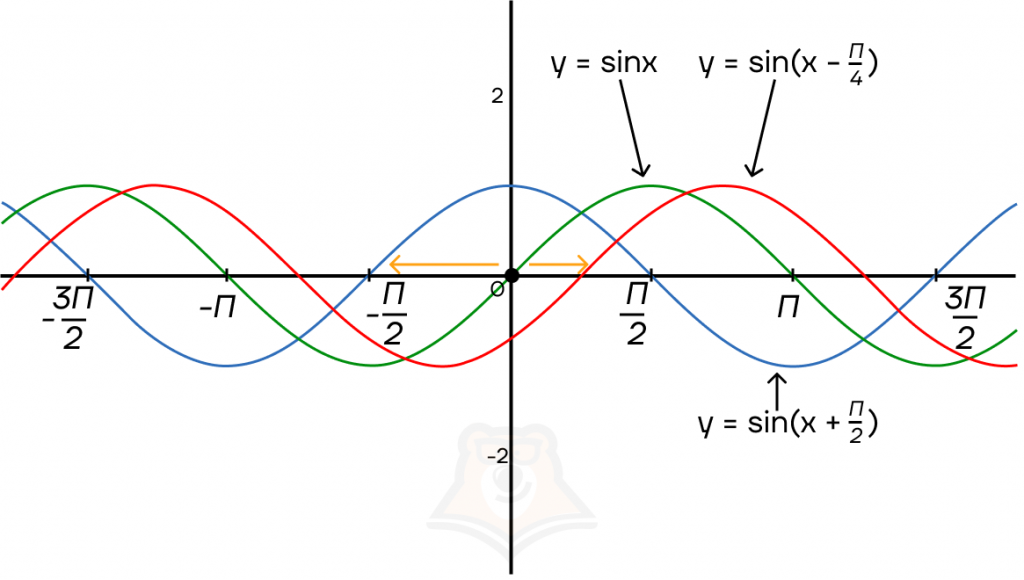
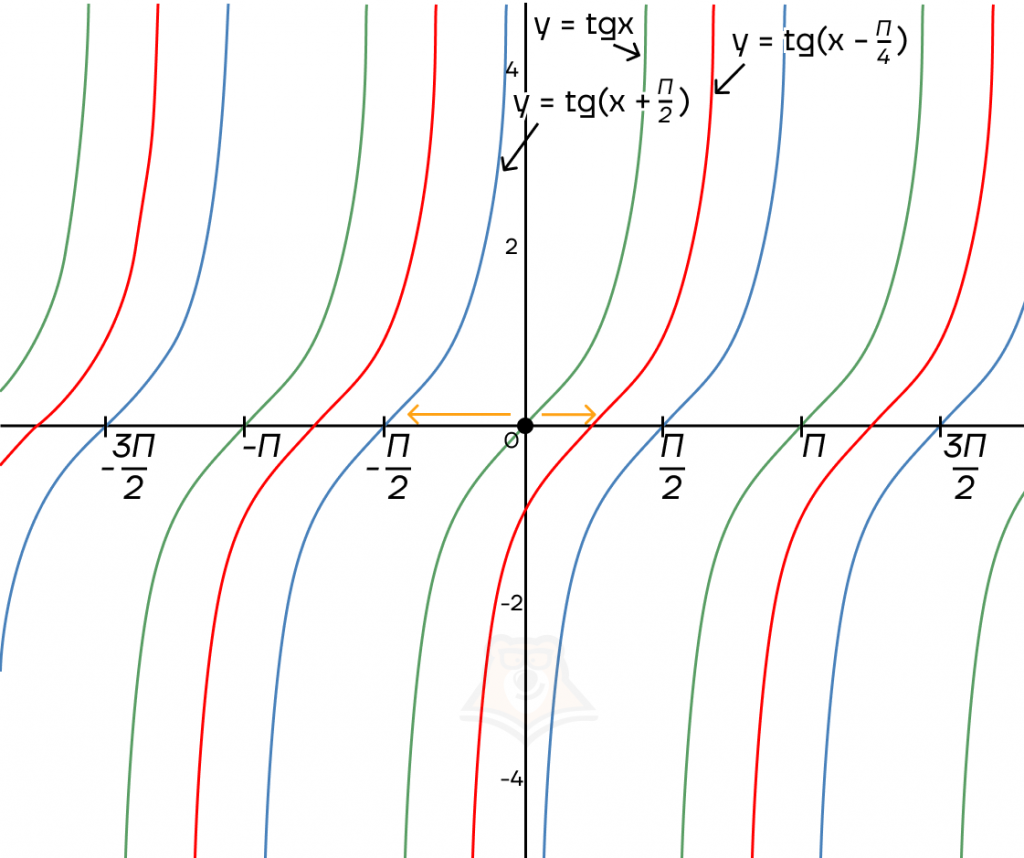
График тригонометрической функции сдвигается по оси Х на прибавленную к значению х константу.
Рассмотрим на примере синусоиды и тангенсоиды. Косинусоида и котангенсоида сдвигаются по аналогии.
Важно: при прибавлении положительной константы — сдвиг влево, при вычитании положительной константы — сдвиг вправо.
Косинусоида, она такая. Сказала — и подвинулась на 2 вверх и вправо. Как она это сделала?
Рассмотрим сдвиг косинусоиды по двум осям сразу
Изначальный вид функции: y=cos x
Сдвиг на 2 вверх: y = cos x + 2
Сдвиг на вправо: y = cos(x — π) + 2
Получилось, что функция косинусоиды после сдвигов — это y=cos(x — π) + 2
Фактчек
- Единичная тригонометрическая окружность — это окружность с центром в точке (0; 0) на координатной плоскости, радиус которой равен 1.
- Один проход по окружности — это 2π.
- Двигаться по окружности можно как в положительную, так и в отрицательную сторону.
- График функции — это представление функции на координатной плоскости.
- Коэффициент перед функцией отвечает за растяжение графика функции вдоль оси Y.
- Константа, прибавляемая к х или y, отвечает за сдвиг функции относительно изначального значения.
Проверь себя
Задание 1.
Чему равно (sin frac{5 pi}{4})?
- (frac{sqrt{3}}{2})
- (frac{sqrt{2}}{2})
- (-frac{sqrt{2}}{2})
- 1
Задание 2.
Чему равно (cos frac{pi}{3})?
- 1
- (frac{1}{2})
- (-frac{1}{2})
- (frac{sqrt{3}}{2})
Задание 3.
Чему равно (ctg frac{pi}{2})?
- 0
- 1
- (sqrt{3})
- (frac{sqrt{2}}{2})
Задание 4.
Куда будет сдвиг (sin(x + frac{4 pi}{3}))?
- Вправо
- Влево
- Вверх
- Вниз
Задание 5.
Куда будет сдвиг ctg x + 2?
- Вправо
- Влево
- Вниз
- Вверх
Ответы: 1. — 3; 2. — 2; 3. — 1; 4. — 2; 5. — 4.
16
Сен 2022
Категория: 10 Графики функций
2022-09-16
2022-09-16
Задача 1. На рисунке изображён график функции Найдите
Решение: + показать
Задача 2. На рисунке изображён график функции Найдите
Решение: + показать
Задача 3. На рисунке изображён график функции Найдите
Решение: + показать
Задача 4. На рисунке изображён график функции Найдите
Решение: + показать
Задача 5. На рисунке изображён график функции Найдите
Решение: + показать
Задача 6. На рисунке изображён график функции где
и
– целые. Найдите
Решение: + показать
Задача 7. На рисунке изображён график функции где
и
– целые. Найдите
Решение: + показать
Пройти тест
Автор: egeMax |
Нет комментариев
Виктория Кос – Кос Константин
Репетиторы по математике
Подготовка к профильному ЕГЭ
Записаться
Математику:
Любить
Сдавать
Понимать
Зубрить
- ЕГЭ
- Графики — мы их ждали 10 лет
Задание
10
Графики функций
Как найти k и b по графику линейной функции?
Преобразование графиков функций
Как определить a, b и c по графику параболы
- Задачи с параболами из 9 задания ЕГЭ
3 способа решить любую 10 задачу ЕГЭ с графиком функций
Присоединяйтесь к нашей группе ВКонтакте
Смотрите нас в YouTube
© 2017-2019. Кос Константин и Кос Виктория
Все выложенные на сайте материалы принадлежат их авторам. Любое коммерческое или иное использование, кроме ознакомления — запрещено
Благодарности и пожелания
E-mail:
cos.victoriya@mail.ru
Об авторах сайта
Дизайн и разработка сайта
Благодарим за комментарий
Он будет опубликован после того, как пройдет модерацию. Ожидайте ответ, на указанный вами e-mail.