Крамор в с готовимся к экзамену по математике учебное пособие - Помощь в подготовке к экзаменам и поступлению

В. С.Крамор

Готовимся к экзамену

по МАТЕМАТИКЕ

Учебное пособие

Москва

ОНИКС Мир и Образование

ÓÄÊ 51(075.3) ÁÁÊ 22.1ÿ721 Ê78

Крамор В. С.

К78 Готовимся к экзамену по математике: Учебное пособие / В. С. Крамор. — М.: ООО «Издательство Оникс»: ООО

«Издательство «Мир и Образование», 2008. — 544 с.: ил.

ISBN 978-5-488-01543-2 (ООО «Издательство Оникс»)

ISBN 978-5-94666-454-7 (ООО «Издательство «Мир и Образование»)

Пособие может быть использовано при подготовке к выпускным экзаменам в средней школе, сдаче ЕГЭ и вступительным экзаменам в вуз. Оно будет полезно школьникам, абитуриентам и преподавателям.

ÓÄÊ 51(075.3) ÁÁÊ 22.1ÿ721

ISBN 978-5-488-01543-2 (ООО «Издательство Оникс»)

ISBN 978-5-94666-454-7 (ООО «Издательство «Мир и Образование»)

ООО «Издательство Оникс», 2008

ПРЕДИСЛОВИЕ

Данная ни а предназначена для самостоятельно о повторения ш ольно о урса ал ебры и начал анализа, а та же для под отов и выпус ным э заменам в средней ш оле и вступительным э заменам в высшее учебное заведение.

Весь учебный материал разбит на 22 темы, оторые имеют одну и ту же стру туру. Каждая тема содержит: теоретичес ие сведения; онтрольные вопросы; упражнения (в лючая задания для повторения); ответы, решения и методичес ие у азания упражнениям.

Вразделе «Теоретичес ие сведения» приводятся формулиров и правил, определений, теорем и т. д. Весь учебный материал изложен онспе тивно в той же последовательности, что

ипри изучении е о в ш оле. В этом разделе имеются та же подробно разобранные примеры, позволяющие частично за репить усвоение теории. У азанный раздел является узловым, пос оль у в случае затруднений при ответах на онтрольные вопросы или при решении упражнений учащийся может получить необходимые онсультации, обращаясь справочному материалу.

Раздел «Контрольные вопросы» призван обеспечить онтроль за усвоением теоретичес о о материала. Отвечая на поставленные вопросы, учащийся сможет за репить полученные им теоретичес ие знания.

Вразделе «Упражнения» содержатся разнообразные примеры и задачи, относящиеся данной теме. Ко всем упражнениям даны ответы. Значительная часть упражнений сопровождается подробными решениями и методичес ими у азаниями. Каждый этап решения в лючает необходимую информацию о правомерности то о или ино о ша а. Среди упражнений имеются примеры и задачи довольно высо о о уровня сложности, взятые из вариантов, предла авшихся на вступительных э заменах в различные вузы. Наличие именно та их упражнений

позволяет приобрести необходимые умения и навы и, усвоить мно очисленные стандартные и нестандартные приемы решения математичес их задач.

Начиная с темы 3 раздел «Упражнения» содержит та же задания для повторения. Эти задания в лючают не толь о примеры и задачи та о о же типа, что и в предыдущих темах, но и упражнения, оторые по тем или иным причинам в предыдущие темы не вошли. Кроме то о, здесь приводится большоеоличество те стовых задач, решение оторых, а по азывает пра ти а, вызывает у учащихся определенные трудности. Подробные решения та их задач, приведенные в ни е, позволяют учащемуся устранить имеющиеся у не о пробелы.

Кни а завершается разделом «Приложение», оторый содержит 30 вариантов билетов, предла авшихся на вступительных письменных э заменах по математи е ( 20 вариантам даны ответы) в различных вузах страны. Самостоятельное решение та их задач поможет о ончательно за репить знания

иумения, приобретенные в процессе изучения данной ни и,

иа можно лучше под отовиться выпус ным и вступительным э заменам по математи е.

Успехов вам, настоящие и будущие абитуриенты!

Автор

Т е м а 1

Натуральные числа и действия над ними. Сложение и законы сложения. Вычитание. Умножение и законы умножения. Деление.

Признаки делимости чисел. Понятие множества. Операции над множествами.

Взаимно однозначное соответствие.

Простые и составные числа. Наибольший общий делитель. Наименьшее общее кратное

Теоретичес ие сведения

1. Натуральные числа и действия над ними

1°. Понятие натурально о числа относится простейшим, первоначальным понятиям математи и и не подлежит определению через дру ие, более простые понятия.

2°. Натуральные числа получаются в результате счета предметов, например 1, 3, 100 и т. д.

3°. Та им образом, натуральные числа в поряд е возрастания можно написать а ряд чисел 1, 2, 3, 4, … .

4°. Для натуральных чисел определены следующие действия: сложение, вычитание, умножение, деление, возведение в степень и извлечение орня.

Заметим, что сложение и умножение выполнимы все да, т. е. в результате этих действий получаются та же натуральные числа.

2. Сложение и законы сложения

1°. Результат сложения двух или нес оль их чисел называют их с ммой, а сами числа — сла аемыми.

Например, a + b + c + … + k = P. Здесь P — сумма; a, b, c, …, k — сла аемые.

2°. Для любых натуральных чисел a и b верно равенство a + b = b + a. Это свойство называют переместительным ( ом-

мутативным) за оном сложения, оторый формулируется та : от перестанов и сла аемых значение суммы не изменится.

3°. Для любых натуральных чисел a, b и c верно равенство a + b + c = (a + b) + c = a + (b + c). Это свойство называют сочетательным (ассоциативным) за оном сложения, оторый формулируется та : значение суммы не изменится, если а уюлибо руппу сла аемых заменить их суммой.

3. Вычитание

1°. Вычесть из числа a число b — значит найти та ое число x,оторое в сумме с числом b дает a, т. е. b + x = a.

2°. Число x называют разностью чисел a и b и обозначают a – b; число a называют меньшаемым, число b — вычитаемым.

3°. Для натуральных чисел вычитание не все да выполнимо. Например, 4 – 4; 2 – 7; 17 – 30, т. е. в результате мы не получим натуральное число.

4. Умножение и законы умножения

1°. Умножить число a на число b — значит найти сумму b сла аемых, аждое из оторых равно a. Выражение ab называют произведением, а числа a и b — множителями.

Например, a · 3 = a + a + a; b · 5 = b + b + b + b + b.

2°. Для любых натуральных чисел a и b верно равенство ab = ba. Это свойство называют переместительным за оном умножения, оторый формулируется та : от перестанов и множителей значение произведения не изменится.

3°. Для любых натуральных чисел a, b и c верно равенство abc = (ab)c = a(bc). Это свойство называют сочетательным за-оном умножения, оторый формулируется та : значение произведения не изменится, если а ую-либо руппу множителей заменить их произведением.

4°. При любых значениях a, b и c верно равенство (a + b)c = = ac + bc. Это свойство называют распределительным (дистрибутивным) за оном умножения (относительно сложения), о- торый формулируется та : чтобы умножить сумму на число, достаточно умножить аждое сла аемое на это число и сложить полученные произведения.

Анало ично можно записать: (a – b)c = ac – bc.

5. Деление

1°. Разделить число a на число b — значит найти та ое число x, при умножении оторо о на число b получается число a, т. е. a : b = x, если x · b = a.

2°. Число a называют делимым (или ратным) числа b, число b — делителем числа a, число x — частным чисел a и b.

3°. Для натуральных чисел деление нацело не все да выполнимо, т. е. результат деления двух натуральных чисел не все да является натуральным числом.

4°. Призна делимости суммы. Если аждое из сла аемых x и y делится на не оторое число c, то и сумма x + y делится на это число c.

6. Признаки делимости чисел

1°. На 2 и на 5 делятся те и толь о те числа, в записи оторых последняя цифра либо 0, либо выражает число, делящееся соответственно на 2 или на 5.

2°. На 4 или на 25 делятся те и толь о те числа, у оторых две последние цифры — нули или выражают число, делящееся соответственно на 4 или на 25.

3°. На 3 (или на 9) делятся те и толь о те числа, сумма цифроторых делится на 3 (или на 9).

4°. На 10 делятся числа, о анчивающиеся нулем.

5°. Числа, делящиеся на 2, называют четными, а остальные — нечетными.

7. Понятие множества

1°. Одним из фундаментальных понятий математи и является понятие множества. Множество можно представить себеа сово упность (собрание) не оторых объе тов, объединенных по а ому-либо призна у. Множество — понятие неопределяемое.

2°. Множество может состоять из чисел (предметов) и т. п. Каждое число (предмет), входящее в множество, называют элементом множества. Та , множество однозначных чисел состоит из элементов 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

3°. Для записи множества с любыми элементами используют фи урные с об и. Элементы множества можно записать в лю-

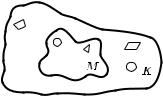
Рис. 1

бом поряд е; например, {2; 3; 1} и {1; 3; 2} — это одно и то же множество, состоящее из чисел 1, 2, 3.

4°. Множества обозначают прописными бу вами латинс о-о алфавита. Например, A = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9} — множество однозначных чисел; число 4 принадлежит множеству A (4 Ý A); число 20 множеству A не принадлежит (20 Ô A).

5°. Множество, оторое не содержит элементов, называют п стым и обозначают символом ¾.

6°. Из рис. 1 видно, что аждый элемент множества M принадлежит та же и множеству K. Еслиаждый элемент одно о множества M является элементом дру о о

множества K, то оворят, что множество M является подмножеством множества K. Это выражается записью M ô K.

7°. Пустое множество ¾ и само множество та же считают подмножествами данно о множества. Та , множество {1; 2; 3} имеет 8 подмножеств: ¾, {1}, {2}, {3}, {1; 2}, {1; 3}, {2; 3}, {1; 2; 3}.

8°. Если аждый элемент множества A является одновременно элементом множества B (т. е. A ô B) и аждый элемент множества B — элементом множества A (т. е. B ô A), то множества A и B называют равными и пишут A = B.

9°. Различают онечные и бес онечные множества. Например, множество всех трехзначных чисел — онечное, а множество N натуральных чисел — бес онечное.

8. Операции над множествами

1°. Пересечением множеств A и B называют множество, состоящее из элементов, оторые принадлежат аждому из данных множеств A и B (рис. 2, а). Пересечение множеств обозначают символом ∩ и пишут C = A ∩ B = {x | x Ý A и x Ý B}.

Пусть, например, A = {1; 2; 5; 7}, B = {3; 5; 7; 8}; то да пересечением этих множеств служит множество C = {5; 7}.

2°. Если множества A и B не имеют общих элементов, то пересечением та их множеств является пустое множество (рис. 2, б).

3°. Объединением множеств A и B называют множество, состоящее из всех элементов множеств A и B и толь о из них. Объединение множеств обозначают символом и пишут

Рис. 2

C = A B = {x | x Ý A или x Ý B} (рис. 2, в). При этом если множества A и B имеют общие элементы, то аждый из этих общих элементов в объединение входит толь о один раз.

Пусть, например, A = {1; 2; 5; 7}, B = {3; 5; 7; 8}; то да объединением этих множеств служит множество D = {1; 2; 3; 5; 7; 8}.

9. Взаимно однозначное соответствие

1°. Если аждому элементу множества A можно поставить в соответствие один и толь о один элемент множества B и, наоборот, аждому элементу множества B можно поставить в соответствие один и толь о один элемент множества A, то та ое соответствие между множествами A и B называют взаимно однозначным.

2°. Если между множествами A и B можно установить взаимно однозначное соответствие, то та ие множества называют

э вивалентными (равносильными).

3°. Установление взаимно однозначно о соответствия дает возможность сравнивать множества с бес онечным числом элементов. Например, между множеством N натуральных чисел и множеством всех четных натуральных чисел можно установить взаимно однозначное соответствие:

1	2	3	4	5	…	n	…
J	J	J	J	J		J
2	4	6	8	10	…	2n …

Та им образом, эти два множества равносильны.

10. Простые и составные числа

1°. Число a называют простым, если е о делителями являются толь о единица и само число a. Например, числа 2, 3, 5, 13, 29 — простые.

2°. Число a, имеющее дру ие делители ( роме 1 и а), называют составным. Например, числа 4, 6, 15 — составные.

Заметим, что число 1 не относят ни простым, ни составным числам.

3°. ОСНОВНАЯ ТЕОРЕМА АРИФМЕТИКИ. Любое составное натуральное число можно представить в виде произведения простых чисел. Например, 12 = 2 · 2 · 3. Говорят та же, что число 12 разложено на простые множители.

Пример. Разложить на простые множители число 525. Р е ш е н и е. Имеем

525	3

175	5
35	5	525 = 3 · 5 · 5 · 7.
7	7
1

11. Наибольший общий делитель

1°. Рассмотрим множество A делителей числа 45 и множество B делителей числа 60, т. е. A = {1; 3; 5; 9; 15; 45}; B = {1; 2; 3; 4; 5; 6; 10; 12; 15; 20; 30; 60}. Общими делителями чисел 45 и 60 называют числа, являющиеся элементами а множества A, та и множества B, т. е. элементы пересечения этих множеств: A ∩ B = {1; 3; 5; 15}.

2°. Наибольший из этих элементов (число 15) называют наибольшим общим делителем и обозначают та : НОД(45, 60) = 15.

3°. Если наибольший общий делитель чисел равен 1, то та-ие числа называют взаимно простыми. Например, числа 16 и 25 — взаимно простые, та а НОД(16, 25) = 1.

Пример. Найти НОД(126, 540, 630). Р е ш е н и е. Имеем

126	2	540	2	630	2	A = (2; 3; 3; 7};

63	3	270	2	315	3	B = {2; 2; 3; 3; 3; 5};
21	3	135	3	105	3	C = {2; 3; 3; 5; 7};
7	7	45	3	35	5	A ∩ B ∩ C = {2; 3; 3};
1		15	3	7	7	НОД = 2 · 3 · 3 = 18.
		5	5	1
		1

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Готовимся к экзамену по математике, Крамор В.С., 2008.

Пособие может быть использовано при подготовке к выпускным экзаменам в средней школе, сдаче ЕГЭ и вступительным экзаменам в ВУЗ. Оно будет полезно школьникам, абитуриентам и преподавателям.

СОДЕРЖАНИЕ
Тема 1
Теоретические сведения
1. Натуральные числа и действия над ними 5
2. Сложение и законы сложения 5
4. Умножение и законы умножения 6
6. Признаки делимости чисел 7
7. Понятие множества 7
8. Операции над множествами 8
9. Взаимно однозначное соответствие 9
10. Простые и составные числа 9
11. Наибольший общий делитель 10
12. Наименьшее общее кратное 11
Контрольные вопросы 11
Решения и методические указания 13
Тема 2
Теоретические сведения
1. Обыкновенные дроби 16
2. Правильные и неправильные дроби 17
3. Основное свойство дроби 17
4. Сравнение дробей. Сокращение дроби 18
5. Сложение и вычитание дробей 18
6. Умножение дробей 19
7. Деление дробей 19
8. Десятичные дроби 20
9. Обращение десятичной дроби в обыкновенную и обыкновенной в десятичную. Периодические дроби 21
10. Отношение. Пропорция 22
11. Свойства пропорций 23
12. Свойства отношений 23
13. Процент. Основные задачи на проценты 24
14. Деление числа на части, прямо и обратно пропорциональные данным числам 25
Контрольные вопросы 25
Решения и методические указания 27
Тема 3
Теоретические сведения
1. Координатная прямая 29
2. Множество целых чисел 29
3. Положительные и отрицательные числа 30
4. Множество рациональных чисел 30
5. Модуль числа 30
6. Сравнение рациональных чисел 31
7. Сложение и вычитание рациональных чисел 31
8. Умножение и деление рациональных чисел 31
9. Возведение рациональных чисел в степень с натуральным показателем 32
Контрольные вопросы 32
Задания для повторения 34
Решения и методические указания 34
Тема 4
Теоретические сведения
1. Свойства степени с натуральным показателем 37
2. Числовые выражения 38
3. Выражения с переменными 38
4. Тождественно равные выражения 39
5. Одночлены 39
6. Многочлены 39
7. Преобразование суммы и разности многочленов 40
8. Умножение многочлена на одночлен и многочлена
9. Разложение многочлена на множители способом вынесения общего множителя за скобки 41
10. Разложение многочлена на множители способом
11. Тождества сокращенного умножения 42
12. Выделение квадрата двучлена из квадратного трехчлена. 43
13. Примеры использования различных способов разложения на множители 43
Контрольные вопросы 44
Задания для повторения 47
Решения и методические указания 48
Тема 5
Теоретические сведения
1. Понятие об иррациональном числе 54
2. Множество действительных чисел 54
3. Арифметические действия с действительными числами . 55
4. Корень к-& степени из действительного числа 56
5. Преобразования арифметических корней 57
6. Степени с целыми и дробными показателями 59
7. Примеры применения тождеств сокращенного умножения к действиям над степенями 59
Контрольные вопросы 60
Задания для повторения 63
Решения и методические указания 63
Тема 6
Теоретические сведения
1. Понятие функции 73
2. Способы задания функции 74
3. Монотонность функции 74
4. Четные и нечетные функции 75
5. Периодические функции 76
6. Промежутки знакопостоянства и корни функции 76
7. Уравнения с одной переменной 76
8. Понятие о равносильности уравнений 77
9. Свойства числовых равенств и теоремы о равносильности
10. Примеры решения уравнений с одной переменной 78
Контрольные вопросы 79
Задания для повторения 81
Решения и методические указания 82
Тема 7
Теоретические сведения
1. Линейная функция и ее график 87
2. Квадратичная функция и ее график 88
3. Функция у = — и ее график 89
4. Дробно-линейная функция и ее график 90
5. Квадратные уравнения 91
6. Теорема Виета 92
7. Графический способ решения квадратных уравнений 92
8. Уравнения с несколькими переменными 93
9. Системы уравнений 93
Контрольные вопросы 95
Задания для повторения 100
Решения и методические указания 101
Тема 8
Теоретические сведения
1. Неравенства 122
2. Основные свойства неравенств 123
3. Действия с неравенствами 124
4. Доказательство неравенств 124
5. Неравенства, содержащие переменную 126
6. Решение линейных и квадратных неравенств 127
Контрольные вопросы 129
Задания для повторения 131
Решения и методические указания 131
Тема 9
Теоретические сведения
1. Системы и совокупности неравенств 135
2. Неравенства и системы неравенств с двумя переменными 137
3. Решение неравенств, содержащих переменную под знаком модуля 139
4. Решение рациональных неравенств методом интервалов 140
5. Расположение корней квадратного трехчлена 142
Контрольные вопросы 146
Задания для повторения 148
Решения и методические указания 149
Тема 10
Теоретические сведения
1. Обратная функция 159
2. Степенная функция с целым показателем 160
3. Функция y =hJx 162
4. Иррациональные уравнения 162
5. Иррациональные неравенства 163
Контрольные вопросы 164
Задания для повторения 167
Решения и методические указания 168
Тема 11
Теоретические сведения
1. Понятие о степени положительного числа с иррациональным показателем 187
2. Показательная функция, ее свойства и график 188
3. Показательные уравнения 189
4. Показательные неравенства 190
5. Системы показательных уравнений и неравенств 190
Контрольные вопросы 192
Задания для повторения 195
Решения и методические указания 196
Тема 12
Теоретические сведения
1. Понятие логарифма 210
2. Свойства логарифмов 210
3. Логарифмическая функция, ее свойства и график 211
4. Теоремы о логарифме произведения, частного и степени. Формула перехода к новому основанию 212
5. Десятичные логарифмы и их свойства 214
6. Логарифмирование и потенцирование 215
7. Логарифмические уравнения 215
8. Логарифмические неравенства 217
9. Системы логарифмических уравнений и неравенств 219
Контрольные вопросы 221
Задания для повторения 223
Решения и методические указания 225
Тема 13
Теоретические сведения
1. Арифметическая прогрессия 238
2. Геометрическая прогрессия 240
3. Сумма бесконечной геометрической прогрессии при |д| < 1 242
Контрольные вопросы 243
Задания для повторения 247
Решения и методические указания 248
Тема 14
Теоретические сведения
1. Поворот точки вокруг начала координат 258
2. Градусное и радианное измерение угловых величин 259
3. Тригонометрические функции числового аргумента 260
4. Знаки тригонометрических функций 261
5. Зависимость между тригонометрическими функциями одного и того же аргумента 262
6. Вычисление значений тригонометрических функций некоторых углов 264
7. Четность и нечетность тригонометрических функций 266
8. Периодичность тригонометрических функций 266
9. Свойства тригонометрических функций 267
10. Формулы сложения 269
11. Формулы приведения 270
Контрольные вопросы 271
Задания для повторения 273
Решения и методические указания 275
Тема 15
Теоретические сведения
1. Тригонометрические функции двойного аргумента 282
2. Тригонометрические функции половинного аргумента 284
3. Выражение тригонометрических функций через тангенс половинного аргумента 285
4. Преобразование произведения тригонометрических функций в сумму 286
5. Формулы суммы и разности одноименных тригонометрических функций 288
Контрольные вопросы 290
Задания для повторения 292
Решения и методические указания 294
Тема 16
Теоретические сведения
1. Свойства функции y = sin x и ее график 303
2. Функция y = arcsin x и ее график 304
3. Решение уравнения sin x = a 305
4. Свойства функции y = cos x и ее график 306
5. Функция y = arccos x и ее график 307
6. Решение уравнения cos x = a 308
7. Свойства функции у = tg х и ее график 309
8. Функция у = arctg х и ее график 310
9. Решение уравнения tg х = а 311
10. Свойства функции у = ctg x и ее график 311
11. Функция у = arcctg x и ее график 312
12. Решение уравнения ctg x = a 313
13. Некоторые соотношения для аркфункций 314
Контрольные вопросы 316
Задания для повторения 321
Решения и методические указания 323
Тема 17
Теоретические сведения
1. Решение тригонометрических уравнений методом разложения на множители 351
2. Решение тригонометрических уравнений методом введения новой переменной 352
3. Решение тригонометрических уравнений, однородных относительно синуса и косинуса 353
4. Решение тригонометрических уравнений вида a cos х + Ь sin x = с 354
5. Решение простейших тригонометрических неравенств 356
Контрольные вопросы 357
Задания для повторения 361
Решения и методические указания 364
Тема 18
Теоретические сведения
1. Приращение аргумента и приращение функции 389
2. Предел функции 390
3. Непрерывность функции 392
4. Определение производной 393
5. Производная суммы 394
6. Производная произведения 395
7. Производная частного 395
8. Производная степенной функции 396
9. Производная сложной функции 396
Контрольные вопросы 396
Задания для повторения 398
Решения и методические указания 400
Тема 19
Теоретические сведения
1. Касательная к графику функции 407
2. Скорость и ускорение в данный момент времени 409
3. Применение производной к нахождению промежутков монотонности функции 411
4. Критические точки функции, ее максимумы и минимумы 412
5. Общая схема исследования функции 414
6. Задачи на отыскание наименьшего и наибольшего значений функции 417
Контрольные вопросы 418
Задания для повторения 423
Решения и методические указания 425
Тема 20
Теоретические сведения
1. Непрерывность тригонометрических функций 441
2. Первый замечательный предел 441
3. Производные тригонометрических функций 442
4. Производные логарифмической и показательной функций.
Контрольные вопросы 445
Задания для повторения 448
Решения и методические указания 449
Тема 21
Теоретические сведения
1. Первообразная 462
2. Основное свойство первообразной 463
3. Правила нахождения первообразных 463
4. Площадь криволинейной трапеции 464
Контрольные вопросы 465
Задания для повторения 467
Решения и методические указания 469
Тема 22
Теоретические сведения
1. Формула Ньютона-Лейбница 483
2. Основные правила интегрирования 485
3. Вычисление площадей с помощью интеграла 486
4. Физические приложения интеграла 488
Контрольные вопросы 491
Задания для повторения 492
Решения и методические указания 493
ПРИЛОЖЕНИЕ
Варианты билетов для вступительных письменных экзаменов. 503

ПРЕДИСЛОВИЕ.
Данная книга предназначена для самостоятельного повторения школьного курса алгебры и начал анализа, а также для подготовки к выпускным экзаменам в средней школе и вступительным экзаменам в высшее учебное заведение.

Весь учебный материал разбит на 22 темы, которые имеют одну и ту же структуру. Каждая тема содержит: теоретические сведения; контрольные вопросы; упражнения (включая задания для повторения); ответы, решения и методические указания к упражнениям.

В разделе «Теоретические сведения» приводятся формулировки правил, определений, теорем и т. д. Весь учебный материал изложен конспективно в той же последовательности, что и при изучении его в школе. В этом разделе имеются также подробно разобранные примеры, позволяющие частично закрепить усвоение теории. Указанный раздел является узловым, поскольку в случае затруднений при ответах на контрольные вопросы или при решении упражнений учащийся может получить необходимые консультации, обращаясь к справочному материалу.

Раздел «Контрольные вопросы» призван обеспечить контроль за усвоением теоретического материала. Отвечая на поставленные вопросы, учащийся сможет закрепить полученные им теоретические знания.

Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:

Скачать книгу Готовимся к экзамену по математике, Крамор В.С., 2008 — fileskachat.com, быстрое и бесплатное скачивание.

Скачать pdf
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России.Купить эту книгу

Скачать книгу — Готовимся к экзамену по математике, Крамор В.С., 2008.
— Яндекс Народ Диск.

Скачать книгу — Готовимся к экзамену по математике, Крамор В.С., 2008. — depositfiles.

Дата публикации: 22.05.2012 10:33 UTC

Теги:

ЕГЭ по математике :: Крамор :: 2008

Следующие учебники и книги:

ЕГЭ, Математика, Тематическая рабочая тетрадь, Ященко И.В., Шестаков С.А., Трепалин А.С., 2012
ЕГЭ, Математика, Решение задач типа В, Глазков Ю.А., Варшавский И.К., Гаиашвили М.Я., 2012
Математика, Базовый уровень ЕГЭ 2012, В7-В14, Коннова Е.Г., Лысенко Ф.Ф., Кулабухов С.Ю., 2011
Математика, Базовый уровень ЕГЭ 2012, В1-В6, Коннова Е.Г., Лысенко Ф.Ф., Кулабухов С.Ю., 2011

Предыдущие статьи:

Математика, Базовый уровень ЕГЭ 2012 (В7-В14), Пособие для чайников, Коннова Е.Г., Лысенко Ф.Ф., Кулабухов С.Ю., 2011
Математика, Базовый уровень ЕГЭ 2012 (В1-В6), Пособие для чайников, Коннова Е.Г., Лысенко Ф.Ф., Кулабухов С.Ю., 2011
ЕГЭ 2012, Математика, Самое полное издание типовых вариантов заданий, Высоцкий И.Р., Гущин Д.Д., Захаров П.И., 2011
Подготовка к ЕГЭ по математике в 2012, Методические указания, Ященко И.В., Шестаков С.А., Трепалин А.С., Захаров П.И., 2012

Источник

Крамор В. С. Готовимся к экзамену по математике: Учебное пособие / В. С. Крамор. — М., 2008. — 544 с.: ил.
Книга предназначена для самостоятельного повторения школьного курса математики. Она поможет учащимся систематизировать имеющиеся знания и ликвидировать в них пробелы. Весь материал разбит на 22 темы, которые содержат: теоретические сведения; контрольные вопросы; упражнения (включая задачи для повторения); методические указания, решения и ответы.
Пособие может быть использовано при подготовке к выпускным экзаменам в средней школе, сдаче ЕГЭ и вступительным экзаменам в вуз. Оно будет полезно школьникам, абитуриентам и преподавателям.
Содержание
Предисловие……………………………………………………………………..3
Тема 1. Теоретические сведения
1. Натуральные числа и действия над ними……………………..5
2. Сложение и законы сложения……………………………………..5
3. Вычитание………………………………………………………………..6
4. Умножение и законы умножения………………………………..6
5. Деление……………………………………………………………………7
6. Признаки делимости чисел…………………………………………7
7. Понятие множества……………………………………………………7
8. Операции над множествами……………………………………….8
9. Взаимно однозначное соответствие………………………………9
10. Простые и составные числа…………………………………………9
11. Наибольший общий делитель……………………………………..10
12. Наименьшее общее кратное…………………………………………11
Контрольные вопросы…………………………………………………………11
Упражнения……………………………………………………………………..12
Ответы………………………………………………………………………………13
Решения и методические указания……………………………………..13
Тема 2. Теоретические сведения
1. Обыкновенные дроби………………………………………………….16
2. Правильные и неправильные дроби…………………………….17
3. Основное свойство дроби…………………………………………….17
4. Сравнение дробей. Сокращение дроби…………………………..18
5. Сложение и вычитание дробей……………………………………18
6. Умножение дробей……………………………………………………..19
7. Деление дробей…………………………………………………………19
8. Десятичные дроби……………………………………………………..20
9. Обращение десятичной дроби в обыкновенную и обыкновенной в десятичную. Периодические дроби … 21
10. Отношение. Пропорция………………………………………………22
11. Свойства пропорций………………………………………………….23
12. Свойства отношений………………………………………………….23
13. Процент. Основные задачи на проценты……………………….24
14. Деление числа на части, прямо и обратно пропорциональные данным числам…………….25
Контрольные вопросы…………………………………………………………25
Упражнения……………………………………………………………………..26
Ответы………………………………………………………………………………27
Решения и методические указания……………………………………..27
Тема 3. Теоретические сведения
1. Координатная прямая………………………………………………..29
2. Множество целых чисел…………………………………………….29
3. Положительные и отрицательные числа……………………….30
4. Множество рациональных чисел………………………………….30
5. Модуль числа…………………………………………………………….30
6. Сравнение рациональных чисел………………………………….31
7. Сложение и вычитание рациональных чисел………………..31
8. Умножение и деление рациональных чисел………………….31
9. Возведение рациональных чисел в степень с натуральным показателем……32
Контрольные вопросы…………………………………………………………32
Упражнения……………………………………………………………………..33
Задания для повторения……………………………………………………..34
Ответы………………………………………………………………………………34
Решения и методические указания……………………………………..34
Тема 4
Теоретические сведения
1. Свойства степени с натуральным показателем………………37
2. Числовые выражения………………………………………………..38
3. Выражения с переменными…………………………………………38
4. Тождественно равные выражения………………………………..39
5. Одночлены………………………………………………………………..39
6. Многочлены………………………………………………………………39
7. Преобразование суммы и разности многочленов…………….40
8. Умножение многочлена на одночлен и многочлена на многочлен………40
9. Разложение многочлена на множители способом вынесения общего множителя за скобки…….41
10. Разложение многочлена на множители способом группировки………41
11. Тождества сокращенного умножения…………………………..42
12. Выделение квадрата двучлена из квадратного трехчлена. 43
13. Примеры использования различных способов разложения на множители……..43
14. Дробь……………………………………………………………………….44
Контрольные вопросы…………………………………………………………44
Упражнения……………………………………………………………………..45
Задания для повторения……………………………………………………..47
Ответы………………………………………………………………………………47
Решения и методические указания……………………………………..48
Тема 5
Теоретические сведения
1. Понятие об иррациональном числе………………………………54
2. Множество действительных чисел………………………………54
3. Арифметические действия с действительными числами . 55
4. Корень к-й степени из действительного числа………………56
5. Преобразования арифметических корней……………………..57
6. Степени с целыми и дробными показателями………………..59
7. Примеры применения тождеств сокращенного
умножения к действиям над степенями……………………….59
Контрольные вопросы…………………………………………………………60
Упражнения……………………………………………………………………..61
Задания для повторения……………………………………………………..63
Ответы………………………………………………………………………………63
Решения и методические указания……………………………………..63
Тема 6. Теоретические сведения
1. Понятие функции……………………………………………………..73
2. Способы задания функции…………………………………………..74
3. Монотонность функции………………………………………………74
4. Четные и нечетные функции……………………………………….75
5. Периодические функции…………………….. 76
6. Промежутки знакопостоянства и корни функции…………76
7. Уравнения с одной переменной……………………………………76
8. Понятие о равносильности уравнений…………………………..77
9. Свойства числовых равенств и теоремы о равносильности уравнений………77
10. Примеры решения уравнений с одной переменной…………78
Контрольные вопросы…………………………………………………………79
Упражнения……………………………………………………………………..80
Задания для повторения……………………………………………………..81
Ответы………………………………………………………………………………82
Решения и методические указания……………………………………..82
Тема 7. Теоретические сведения
1. Линейная функция и ее график………………………………….87
2. Квадратичная функция и ее график…………………………….88
3. Функция у = k/x и ее график…………………………………………89
4. Дробно-линейная функция и ее график……………………….90
5. Квадратные уравнения………………………………………………91
6. Теорема Виета…………………………………………………………..92
7. Графический способ решения квадратных уравнений … 92
8. Уравнения с несколькими переменными……………………..93
9. Системы уравнений……………………………………………………93
Контрольные вопросы…………………………………………………………95
Упражнения……………………………………………………………………..97
Задания для повторения……………………………………………………..100
Ответы………………………………………………………………………………100
Решения и методические указания……………………………………..101
Тема 8. Теоретические сведения
1. Неравенства………………………………………………………………122
2. Основные свойства неравенств……………………………………123
3. Действия с неравенствами…………………………………………..124
4. Доказательство неравенств…………………………………………124
5. Неравенства, содержащие переменную…………………………126
6. Решение линейных и квадратных неравенств………………..127
Контрольные вопросы…………………………………………………………129
Упражнения……………………………………………………………………..130
Задания для повторения……………………………………………………..131
Ответы………………………………………………………………………………131
Решения и методические указания……………………………………..131
Тема 9. Теоретические сведения
1. Системы и совокупности неравенств…………………………….135
2. Неравенства и системы неравенств с двумя переменными 137
3. Решение неравенств, содержащих переменную под знаком модуля……139
4. Решение рациональных неравенств методом интервалов … 140
5. Расположение корней квадратного трехчлена………………142
Контрольные вопросы…………………………………………………………146
Упражнения……………………………………………………………………..147
Задания для повторения……………………………………………………..148
Ответы………………………………………………………………………………149
Решения и методические указания……………………………………..149
Тема 10. Теоретические сведения
1. Обратная функция……………………………………………………..159
2. Степенная функция с целым показателем……………………..160
3. Функция у = ……………………………………………………….162
4. Иррациональные уравнения……………………………………….162
5. Иррациональные неравенства……………………………………..163
Контрольные вопросы…………………………………………………………164
Упражнения……………………………………………………………………..165
Задания для повторения……………………………………………………..167
Ответы………………………………………………………………………………168
Решения и методические указания……………………………………..168
Тема 11. Теоретические сведения
1. Понятие о степени положительного числа с иррациональным показателем………187
2. Показательная функция, ее свойства и график………………188
3. Показательные уравнения…………………………………………..189
4. Показательные неравенства……………………………………….190
5. Системы показательных уравнений и неравенств…………..190
Контрольные вопросы…………………………………………………………192
Упражнения……………………………………………………………………..193
Задания для повторения……………………………………………………..195
Ответы………………………………………………………………………………196
Решения и методические указания……………………………………..196
Тема 12. Теоретические сведения
1. Понятие логарифма……………………………………………………210
2. Свойства логарифмов………………………………………………….210
3. Логарифмическая функция, ее свойства и график…………211
4. Теоремы о логарифме произведения, частного и степени. Формула перехода к новому основанию………212
5. Десятичные логарифмы и их свойства…………………………214
6. Логарифмирование и потенцирование…………………………215
7. Логарифмические уравнения……………………………………..215
8. Логарифмические неравенства……………………………………217
9. Системы логарифмических уравнений и неравенств …. 219
Контрольные вопросы…………………………………………………………221
Упражнения……………………………………………………………………..222
Задания для повторения……………………………………………………..223
Ответы………………………………………………………………………………224
Решения и методические указания……………………………………..225
Тема 13. Теоретические сведения
1. Арифметическая прогрессия……………………………………….238
2. Геометрическая прогрессия…………………………………………240
3. Сумма бесконечной геометрической прогрессии при |g| меньше 1…..242
Контрольные вопросы…………………………………………………………243
Упражнения……………………………………………………………………..244
Задания для повторения……………………………………………………..247
Ответы………………………………………………………………………………248
Решения и методические указания……………………………………..248
Тема 14. Теоретические сведения
1. Поворот точки вокруг начала координат……………………….258
2. Градусное и радианное измерение угловых величин……….259
3. Тригонометрические функции числового аргумента …. 260
4. Знаки тригонометрических функций…………………………..261
5. Зависимость между тригонометрическими функциями одного и того же аргумента…………………..262
6. Вычисление значений тригонометрических функций некоторых углов…………………..264
7. Четность и нечетность тригонометрических функций . . . 266
8. Периодичность тригонометрических функций………………266
9. Свойства тригонометрических функций……………………….267
10. Формулы сложения……………………………………………………269
11. Формулы приведения………………………………………………..270
Контрольные вопросы…………………………………………………………271
Упражнения……………………………………………………………………..272
Задания для повторения……………………………………………………..273
Ответы………………………………………………………………………………274
Решения и методические указания……………………………………..275
Тема 15. Теоретические сведения
1. Тригонометрические функции двойного аргумента……….282
2. Тригонометрические функции половинного аргумента …….284
3. Выражение тригонометрических функций через тангенс половинного аргумента……….285
4. Преобразование произведения тригонометрических функций в сумму………….286
5. Формулы суммы и разности одноименных тригонометрических функций………….288
Контрольные вопросы…………………………………………………………290
Упражнения……………………………………………………………………..291
Задания для повторения……………………………………………………..292
Ответы………………………………………………………………………………293
Решения и методические указания……………………………………..294

Часть 1

Тема 16. Теоретические сведения
1. Свойства функции у = sin х и ее график……………………….303
2. Функция у = arcsin х и ее график………………………………..304
3. Решение уравнения sin х = а……………………………………….305
4. Свойства функции у = cos х и ее график……………………….306
5. Функция у = arccos х и ее график………………………………..307
6. Решение уравнения cos х = а……………………………………….308
7. Свойства функции у = tg х и ее график…………………………309
8. Функция у = arctg х и ее график………………………………….310
9. Решение уравнения tg х = а……………………………………….311
10. Свойства функции у = ctg х и ее график……………………….311
11. Функция у = arcctg х и ее график………………………………..312
12. Решение уравнения ctg х = а……………………………………….313
13. Некоторые соотношения для аркфункций……………………314
Контрольные вопросы…………………………………………………………316
Упражнения……………………………………………………………………..317
Задания для повторения……………………………………………………..321
Ответы………………………………………………………………………………322
Решения и методические указания……………………………………..323
Тема 17. Теоретические сведения
1. Решение тригонометрических уравнений методом разложения на множители………….351
2. Решение тригонометрических уравнений методом введения новой переменной…….352
3. Решение тригонометрических уравнений, однородных относительно синуса и косинуса………..353
4. Решение тригонометрических уравнений вида a cos х + Ь sin х = с……….354
5. Решение простейших тригонометрических неравенств ……356
Контрольные вопросы…………………………………………………………357
Упражнения……………………………………………………………………..358
Задания для повторения……………………………………………………..361
Ответы………………………………………………………………………………362
Решения и методические указания……………………………………..364
Тема 18. Теоретические сведения
1. Приращение аргумента и приращение функции…………….389
2. Предел функции……………………………………………………….390
3. Непрерывность функции…………………………………………….392
4. Определение производной…………………………………………..393
5. Производная суммы………………………………………………….394
6. Производная произведения…………………………………………395
7. Производная частного………………………………………………..395
8. Производная степенной функции………………………………..396
9. Производная сложной функции………………………………….396
Контрольные вопросы…………………………………………………………396
Упражнения……………………………………………………………………..398
Задания для повторения……………………………………………………..398
Ответы………………………………………………………………………………400
Решения и методические указания……………………………………..400
Тема 19. Теоретические сведения
1. Касательная к графику функции………………………………..407
2. Скорость и ускорение в данный момент времени…………..409
3. Применение производной к нахождению промежутков монотонности функции………………….411
4. Критические точки функции, ее максимумы и минимумы…….412
5. Общая схема исследования функции…………………………..414
6. Задачи на отыскание наименьшего и наибольшего значений функции…………….417
Контрольные вопросы…………………………………………………………418
Упражнения……………………………………………………………………..419
Задания для повторения……………………………………………………..423
Ответы………………………………………………………………………………424
Решения и методические указания……………………………………..425
Тема 20. Теоретические сведения
1. Непрерывность тригонометрических функций………………441
2. Первый замечательный предел……………………………………441
3. Производные тригонометрических функций………………..442
4. Производные логарифмической и показательной функций. Число е……………………444
Контрольные вопросы…………………………………………………………445
Упражнения……………………………………………………………………..446
Задания для повторения……………………………………………………..448
Ответы………………………………………………………………………………448
Решения и методические указания……………………………………..449
Тема 21. Теоретические сведения
1. Первообразная…………………………………………………………..462
2. Основное свойство первообразной………………………………..463
3. Правила нахождения первообразных…………………………..463
4. Площадь криволинейной трапеции………………………………464
Контрольные вопросы…………………………… 465
Упражнения…………………………………. 466
Задания для повторения…………………………. 467
Ответы……………………………………… 469
Решения и методические указания…………………. 469
Тема 22. Теоретические сведения
1. Формула Ньютона—Лейбница………………… 483.
2. Основные правила интегрирования……………… 485
3. Вычисление площадей с помощью интеграла………. 486
4. Физические приложения интеграла…………….. 488
Контрольные вопросы…………………………… 491
Упражнения…………………………………. 491
Задания для повторения…………………………. 492
Ответы……………………………………… 493
Решения и методические указания…………………. 493
ПРИЛОЖЕНИЕ
Варианты билетов для вступительных письменных экзаменов …. 503

Часть 2

Источник

Файлы
Абитуриентам и школьникам
Математика
Подготовка к экзамену по математике

Крамор В.С. Готовимся к экзамену по математике

Файл формата
rar
размером 5,64 МБ
содержит документ формата
pdf

Добавлен пользователем Елена, дата добавления неизвестна
Описание отредактировано 21.01.2023 22:40

М.: Оникс, 2008. — 544 с.

Книга предназначена для самостоятельного повторения школьного курса математики. Она поможет учащимся систематизировать имеющиеся знания и ликвидировать в них пробелы. Весь материал разбит на 22 темы, которые содержат: теоретические сведения; контрольные вопросы; упражнения (включая задачи для повторения); методические указания, решения и ответы.
Пособие может быть использовано при подготовке к выпускным экзаменам в средней школе, сдаче ЕГЭ и вступительным экзаменам в вуз.
Оно будет полезно школьникам, абитуриентам и преподавателям.

Чтобы скачать этот файл зарегистрируйтесь и/или войдите на сайт используя форму сверху.
Регистрация

Узнайте сколько стоит уникальная работа конкретно по Вашей теме:
Сколько стоит заказать работу?

Источник

2008

Читать онлайн

Готовимся к экзамену по математике — Крамор В.С.:

Рубрика: Математика / Дополнительно Математика / Дополнительно Математика
Автор: Крамор В.С.
Язык: Русский
Год: 2008
Класс: —
Просмотров: 141

Источник

Переплёт: Твердый |

Вес: 0.376 кг. |

Страниц: 544 |

Размер: 140 х 210 x 22 мм

ISBN 978-5-488-01543-2
Последний тираж: 18.04.2008 г.

Недовольны качеством издания?

Дайте жалобную книгу

Аннотация

Книга предназначена для самостоятельного повторения школьного курса математики. Она поможет учащимся систематизировать имеющиеся знания и ликвидировать в них пробелы. Весь материал разбит на 22 темы, которые содержат: теоретические сведения; контрольные вопросы; упражнения (включая задачи для повторения); методические указания, решения и ответы.
Пособие может быть использовано при подготовке к выпускным экзаменам в средней школе, сдаче ЕГЭ и вступительным экзаменам в вуз. Оно будет полезно школьникам, абитуриентам и преподавателям.

Отзывы читателей

Отзывы могут оставлять только авторизованные пользователи.
Для этого войдите или зарегистрируйтесь на нашем сайте.

Вход
/
Регистрация

Недовольны качеством издания?

Дайте жалобную книгу

Характеристики

Ниша:

ЛИТЕРАТУРА ДЛЯ СТАРШЕКЛАССНИКОВ И АБИТУРИЕНТОВ (10-11 КЛ)

Дата последнего тиража:

18.04.2008 г.

Знак информационной продукции:

12+

Недовольны качеством издания?

Дайте жалобную книгу

Источник