Образовательный портал для подготовки к экзаменам
Математика базового уровня
Математика базового уровня
Сайты, меню, вход, новости
Задания
Версия для печати и копирования в MS Word
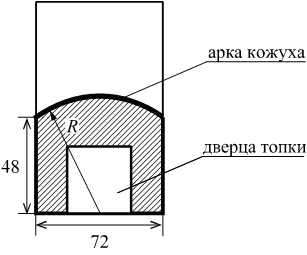
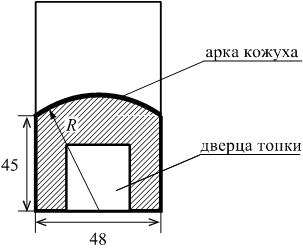
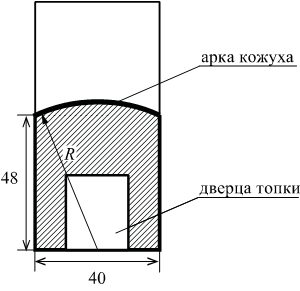
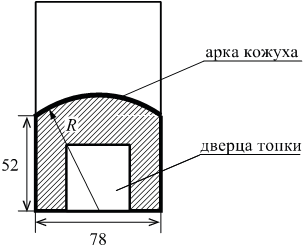
В магазине вся мебель продаётся в разобранном виде. Покупатель может заказать сборку мебели на дому, стоимость которой составляет 5% от стоимости купленной мебели. Шкаф стоит 4200 рублей. Во сколько рублей обойдётся покупка этого шкафа вместе со сборкой?
Спрятать решение
Решение.
По условию задачи шкаф стоит рублей. Вычислим, сколько будет стоить сборка данного шкафа:
рублей. Шкаф вместе со сборкой будет стоить:
рублей.
Ответ: 4410
Главная
-
- 0
-
За стиральную машину и ее установку заплатили 28350р. Стоимость установки составляет 5% от стоимости машины. Сколько стоит стиральная машина?
Дамир Заволдаев
Вопрос задан 21 июля 2019 в
5 — 9 классы,
Математика.
-
Комментариев (0)
Добавить
Отмена
1 Ответ (-а, -ов)
- По голосам
- По дате
-
- 0
-
х — стоит стиральная машина
0,5 х — стоит установка стиральной машины
х + 0,5 х = 28350
1,05 х = 28350
х = 28350 / 1,05
х = 27000 руб — стоит стиральная машина
Отмена
Вероника Ранеткина
Отвечено 21 июля 2019
-
Комментариев (0)
Добавить
Отмена
Ваш ответ
Кроссовки стоили 3100 рублей. После снижения цены они стали стоить 2914 рублей.…
Разбор сложных заданий в тг-канале:
Сложность:
Среднее время решения: 2 мин. 4 сек.
ЕГЭ по математике (база) 2023 задание 15: номер 5 | 062zj | Кроссовки стоили 3100 рублей.…
25
Кроссовки стоили 3100 рублей. После снижения цены они стали стоить 2914 рублей. На сколько процентов была снижена цена на кроссовки?
Объект авторского права ООО «Легион»
Вместе с этой задачей также решают:
Для приготовления хлеба взяли смесь пшеничной и ржаной муки в соотношении 4 : 1. Какой процент в смеси составляет пшеничная мука?
Для приготовления хлеба взяли смесь пшеничной и ржаной муки в соотношении 3 : 1. Какой процент в смеси составляет пшеничная мука?
Плитка шоколада стоит 56 рублей. Сколько рублей заплатит покупатель за 20 плиток шоколада, если при покупке более 10 плиток шоколада магазин делает скидку 5% ?
Стул на распродаже уценили на 40%, при этом он стал стоить 480 рублей. Сколько рублей стоил стул до распродажи?
Педсовет — сообщество для тех, кто учит и учится. С нами растут профессионалы.
Хотите успевать за миром и трендами, первыми узнавать о новых подходах, методиках, научиться применять их на практике или вообще пройти переквалификацию и освоить новую специальность? Всё возможно в нашем Учебном Центре.
На нашей платформе уже более 40 онлайн-курсов переквалификации и дополнительного образования.
Смотрите
Введение
Слово процент от латинского слова pro centum, что буквально означает «за сотню» или «со ста». Идея выражения частей целого постоянно в одних и тех же долях, вызванная практическими соображениями, родилась еще в древности у вавилонян. Ряд задач клинописных табличек посвящен исчислению процентов, однако вавилонские ростовщики считали не «со ста», а «с шестидесяти».
Проценты были особенно распространены в Древнем Риме. Римляне называли процентами деньги, которые платил должник заимодавцу за каждую сотню. От римлян проценты перешли к другим народам Европы. Долгое время под процентами понимались исключительно прибыль или убыток на каждые сто рублей. Они применялись только в торговых и денежных сделках. Затем область их применения расширилась, проценты встречаются в хозяйственных и финансовых расчетах, статистике, науке и технике.
Ныне процент — это частный вид десятичных дробей, сотая доля целого (принимаемого за единицу). Знак % происходит, как полагают, от итальянского слова cento (сто), которое в процентных расчетах часто писалось сокращенно cto. Отсюда путем дальнейшего упрощения в скорописи буква t превратилась в наклонную черту (/), возник современный символ для обозначения процента. В школьном учебнике «Математика, 5«,авторов Н.Я. Виленкина и др. дана еще одна любопытная версия возникновения знака %. Там, в частности, говорится, что этот знак произошел в результате нелепой опечатки, совершенной наборщиком. В 1685 г. в Париже была опубликована книга-руководство по коммерческой арифметике, где по ошибке наборщик вместо cto напечатал %.
Еще больше полезных материалов — в Телеграм-канале Педсовета. Подписывайтесь, чтобы не пропускать свежие статьи и новости.
Подписаться
Современная жизнь делает задачи на проценты актуальными, так как сфера практического приложения процентных расчетов расширяется. Вопросы инфляции, повышение цен, рост стоимости акций, снижение покупательской способности касаются каждого человека в нашем обществе. Планирование семейного бюджета, выгодного вложения денег в банки, невозможны без умения производить несложные процентные вычисления.
Сами проценты не дают экономического развития, но их знание помогает в развитии практических способностей, а также умение решать экономические задачи. Обдуманное изучение процентов может способствовать развитию таких навыков как экономичность, расчетливость.
В вариантах вступительных экзаменов встречаются задачи на проценты, и эти задачи часто вызывают затруднения у школьников. Причина в том, что тема «Проценты» изучается в младших 5-6 классах, причем непродолжительно, закрепляется в 7 классе при решении задач на повторение, а в старших классах к этой теме совсем не возвращаются.
Так, пересмотрев школьные учебники по математике, по которым обучаются ученики нашей гимназии, я выяснила, что в учебнике «Алгебра, 9», под ред. Теляковского, задач, в которых упоминается слово «процент», всего три. В учебнике «Алгебра и начала анализа, 10-11» под ред Колмогорова А.Н задач на проценты и процентную концентрацию черыре. Но, задачи на проценты уже встречались в вариантах единого государственного экзамена в 2003, 2004, 2005 годах. Предлагается такая задача и в демонстрационном варианте 2007 года. Поэтому, изучение наиболее часто встречающихся типов задач на проценты, считаю актуальным.
Объектом исследования является изучение различных типов задач по теме «Проценты».
Изучая эту тему по сборникам для поступающих в вузы[5], я пришла к мнению, что многие задачи авторы сборников предлагают решать с использованием специальных формул, которых в школьных учебниках 5-6 классов, когда и изучаются эти темы, нет.
Предмет исследования: решение задач на проценты и процентное содержание, концентрацию, смеси и сплавы с преимущественным использованием основных правил действия с десятичными и обыкновенными дробями.
Цель работы. Составить практическое пособие по решению задач на проценты для школьников.
Задачи исследования:
1) Изучить исторический и теоретический материал по интересующему вопросу.
2) Систематизировать задачи на проценты по типам.
3) Составить практические рекомендации по решению задач на проценты.
4) Выявить практическое применение таких задач.
5) Определить план дальнейшей работы над темой.
Практическая значимость работы. Данное пособие по решению задач на проценты будет интересно не только школьникам 5-6 класса, которым интересна математика. Здесь найдут много полезного и выпускники школ, и абитуриенты при подготовке к выпускным и вступительным экзаменам.
Глава 1.Основные типы задач по теме «Проценты»
В данной главе приводятся примеры задач, которые решаются с применением определения, что такое один процент, как выразить дробь в процентах и правилам нахождения части (дроби) от числа, и числа по значению его части (дроби), т.е. это те темы и задачи, которые рассматриваются в школе.
Обращаем внимание, что существуют и другие способы решения простейших задач на проценты, например, составляют пропорции на каждом шаге, но в этом случае решение становится на несколько шагов длиннее. Мы же видим свою задачу в нахождении более быстрых способов решения таких задач, в связи с тем, что в настоящее время редкий тест по математике для абитуриентов, обходится без задач, в которых не упоминались бы проценты.
1.1. Решение задач на применение основных понятий о процентах.
Сотая часть метра — это сантиметр, сотая часть рубля — копейка, сотая часть центнера — килограмм. Люди давно замети, что сотые доли величин удобны в тактической деятельности. Потому для них было придумано специальное название — процент. Значит одна копейка — один процент от одного рубля, а один сантиметр — один процент от одного метра.
Один процент — это одна сотая доля числа. Математическими знаками один процент записывается так: 1%.
Определение одного процента можно записать равенством: 1 % = 0,01 * а
5%=0,05, 23%=0,23, 130%=1,3 и т. д
Как найти 1% от числа? Раз 1% это одна сотая часть, надо число разделить на 100. Деление на 100 можно заменить умножением на 0,01. Поэтому, чтобы найти 1% от данного числа, нужно умножить его на 0,01. А если нужно найти 5% от числа, то умножаем данное число на 0,05 и т.д.
Пример. Найти: 25% от 120.
Решение:
1) 25% = 0,25;
2) 120 . 0,25 = 30.
Ответ: 30.
Правило 1. Чтобы найти данное число процентов от числа, нужно проценты записать десятичной дробью, а затем число умножить на эту десятичную дробь
Пример. Токарь вытачивал за час 40 деталей. Применив резец из более прочной стали, он стал вытачивать на 10 деталей в час больше. На сколько процентов повысилась производительность труда токаря?
Решение: Чтобы решить эту задачу, надо узнать, сколько, процентов составляют 10 деталей от 40. Для этого найдем сначала, какую часть составляет число 10 от числа 40. Мы знаем, что нужно разделить 10 на 40. Получится 0,25. А теперь запишем в процентах — 25%. Получаем ответ: производительность труда токаря повысилась на 25%.
Правило 2. Чтобы найти, сколько процентов одно число составляет от другого, нужно разделить первое число на второе и полученную дробь записать в виде процентов.
Пример. При плановом задании 60 автомобилей в день завод выпустил 66 автомобилей. На сколько процентов завод выполнил план?
Решение: — такую часть составляют изготовленные автомобили от количества автомобилей по плану. Запишем в процентах =110%
Ответ: 110%
Пример.
На сколько процентов 10 больше 6? 2. На сколько процентов 6 меньше 10?
Решение:
1. ((10 — 6).100%)/6 = 66 2/3 %
2. ((10 — 6).100%)/10 = 40%
Ответ: 66 2/3 %, 40 %.
Пример. Бронза является сплавом олова и меди. Сколько процентов сплава составляет медь в куске бронзы, состоящем из 6 кг олова и 34 кг меди?
Решение: 1) 6+ 34 =40 (кг) масса всего сплава.
2) = 85% сплава составляет медь.
Ответ. 85%.
Пример. Что произойдет с ценой товара, если сначала ее повысить на 25%, а потом понизить на 25%?
Решение: Пусть цена товара х руб, тогда после повышения товар стоит 125% прежней цены, т.е. 1,25х;, а после понижения на 25% , его стоимость составляет 75% или 0, 75 от повышенной цены, т.е. 0,75 *1,25х= 0,9375х, тогда цена товара понизилась на 6, 25 %, т.к. х — 0,9375х = 0,0625х ; 0,0625х/х . 100% = 6,25%
Ответ: первоначальная цена товара снизилась на 6,25%.
Правило 3. Чтобы найти процентное отношение двух чисел А и В, надо отношение этих чисел умножить на 100%, то есть вычислить (а/в)*100%.
Пример. Найти число, если 15% его равны 30.
Решение:
1) 15% = 0,15;
2) 30 : 0,15 = 200.
или: х — данное число; 0,15.х = 300; х = 200.
Ответ: 200.
Пример. Из хлопка-сырца получается 24% волокна. Сколько надо взять хлопка-сырца, чтобы получить 480кг волокна.?
Решение. Запишем 24% десятичной дробью 0,24 и получим задачу о нахождении числа по известной ему части (дроби). 480 : 0,24= 2000 кг = 2 т
Ответ: 2 т
Пример. Сколько кг белых грибов надо собрать для получения 1 кг сушеных, если при обработке свежих грибов остается 50% их массы, а при сушке остается 10% массы обработанных грибов?
Решение. 1кг сушеных грибов — это 10% или 0, 01 часть обработанных, т.е. 1 кг : 0,1=10 кг обработанных грибов, что составляет 50% или 0,5 собранных грибов, т.е. 10 кг : 0,05=20 кг
Ответ: 20 кг
Пример. Свежие грибы содержали по массе 90% воды, а сухие 12%. Сколько получится сухих грибов из 22 кг свежих?
Решение:
1) 22 . 0,1 = 2,2 (кг) — грибов по массе в свежих грибах; (0,1 это 10% сухого вещества)
2) 2,2 : 0,88 = 2,5 (кг) — сухих грибов, получаемых из свежих (количество сухого вещества не изменилось, но изменилось его процентное содержание в грибах и теперь 2,2 кг это 88% или 0,88 сухих грибов).
Ответ: 2,5 кг.
Правило 4. Чтобы найти число по данным его процентам, надо выразить проценты в виде дроби, а затем значение процентов разделить на эту дробь.
1.2. Решение задач на понятия «процентное содержание», «концентрация», «%-й раствор».
Процентное содержание. Процентный раствор.
Пример. Сколько кг соли в 10 кг соленой воды, если процентное содержание соли 15%.
Решение. 10 . 0,15 = 1,5 (кг) соли.
Ответ: 1,5 кг.
Процентное содержание вещества в растворе (например, 15%), иногда называют %-м раствором, например, 15%-й раствор соли.
Пример. Сплав содержит 10 кг олова и 15 кг цинка. Каково процентное содержание олова и цинка в сплаве?
Решение: Процентное содержание вещества в сплаве — это часть, которую составляет вес данного вещества от веса всего сплава.
1) 10 + 15 = 25 (кг) — сплав;
2) 10/25 . 100% = 40% — процентное содержание олова в сплаве;
3) 15/25 . 100% = 60% — процентное содержание цинка в сплаве;
Ответ: 40%, 60%.
Концентрация.
Если концентрация вещества в соединении по массе составляет р%, то это означает, что масса этого вещества составляет р% от массы всего соединения.
Пример. Концентрация серебра в сплаве 300 г составляет 87%. Это означает, что чистого серебра в сплаве 261 г.
Решение. 300 . 0,87 = 261 (г).
В этом примере концентрация вещества выражена в процентах.
Отношения объема чистой компоненты в растворе ко всему объему смеси называется объемной концентрацией этой компоненты.
Сумма концентраций всех компонент, составляющих смесь, равна 1.
Если известно процентное содержание вещества, то его концентрация находится по формуле: К=р/100% к — концентрация вещества; р — процентное содержание вещества (в процентах).
Пример. Имеется 2 сплава, в одном из которых, содержится 40%, а в другом 20% серебра. Сколько кг второго сплава нужно добавить к 20 кг первого, чтобы после сплавления вместе получить сплав, содержащий 32% серебра?
Решение: Пусть к 20 кг первого сплава нужно добавить х кг второго сплава. Тогда получим (20 + х) кг нового сплава. В 20 кг первого сплава содержится 0,4 . 20 = 8 (кг) серебра, в х кг второго сплава содержится 0,2х кг серебра, а в (20+х) кг нового сплава содержится 0,32 . (20+х) кг серебра. Составим уравнение:
8 + 0,2х = 0,32 . (20 +х); х = 13 1/3.
Ответ: 13 1/3 кг второго сплава нужно добавить к 20 кг первого, чтобы получить сплав, содержащий 32% серебра.
Пример. К 15 л 10%-ного раствора соли добавили 5%-ный раствор соли и получили 8%-ный раствор. Какое количество литров 5%-ного раствора добавили?
Решение. Пусть добавили х л 5%-ного раствора соли. Тогда нового раствора стало (15 + х) л, в котором содержаться 0,8 . (15 + х) л соли. В 15 л 10%-ного раствора содержится 15 . 0,1 = 1,5 (л) соли, в х л 5%-ного раствора содержится 0,05х (л) соли.
Составим уравнение.
1,5 + 0,05х = 0,08 . (15 + х);
х = 10.
Ответ: добавили 10 л 5%-ного раствора
1.3. Решение задач с использованием понятия коэффициента увеличения.
Чтобы увеличить положительное число а на р процентов, следует умножить число а на коэффициент увеличения к=(1+0,01р).
Чтобы уменьшить положительное число а на р процентов, следует умножить число а на коэффициент уменьшения к= (1-0,01р).
Пример. Вклад, вложенный в сбербанк два года назад, достиг суммы, равной 13125 руб. Каков был первоначальный вклад при 25% годовых?
Решение. Если а (рублей) — размер первоначального вклада, то в конце первого года вклад составит 1,25а а в конце второго года размер вклада составит 1,25 *1,25а. Решая уравнение 1,25* 1,25а=13125, находим а=8400.
Ответ: 8400 руб.
Пример. В феврале цена на нефть увеличилась на 12% по сравнению с январской. В марте цена нефти упала на 25%. На сколько процентов мартовская цена изменилась по сравнению с январской?
Решение. Если х — январская цена нефти, то февральская цена нефти равна
(1 +0,01*12)х = 1,12х. Чтобы вычислить мартовскую цену у на нефть, следует умножить февральскую цену 1,12х на (1-0,01*25)=0,75, т.е. у=0,75 1,12х=0,84х , мартовская цена отличается от январской на (0,84х)/х100 —100=84-100= −16(%), т.е. цена упала на 16 %
Ответ: цена упала на 16%.
Правило 5. Чтобы найти, на сколько % положительное число у отличается от положительного числа а , следует вычислить, сколько % у составляет от а, а затем от полученного числа отнять а.
Глава 2. Разные задачи на проценты ( с решениями)
В данной главе рассматривается выборка задач из различных источников, которые охватывают весь теоретический материал, который излагался выше, предлагаем свои решения. Отметим, что предложенный способ решения не является единственным.
2.1 Тестовые задания на проценты.
Задача 1.Товар стоил тысячу рублей. Продавец поднял цену на 10%, а через месяц снизил её на 10%.Сколько стал стоить товар?
Решение. Пусть товар стоил 1000руб., после повышения цены на 10% он стал стоить 1,1*1000 руб. После понижения этой цены на 10%, он стал стоить 0,9*1,1*1000=990 руб.
Ответ. 990 руб.
Задача 2.Собрали 100 кг грибов. Оказалось, что их влажность 99%. Когда грибы подсушили, влажность снизилась до 98%. Какой стала масса этих грибов после подсушивания?
Решение. Так как влажность грибов составляет 99%, это означает, что на так называемое «сухое вещество приходится 1% грибов, т.е 1 кг, после сушки влажность составляет 98%, т.е. на «сухое вещество» приходится 2%, т.е 1кг это 0,02 подсушенных грибов, 1 кг : 0,02=50 кг.
Ответ. 50 кг.
Задача 3. Цена входного билета на стадион была 1 рубль 80 копеек. После снижения входной платы число зрителей увеличилось на 50% , а выручка выросла на 25% .Сколько стал стоить билет после снижения?
Решение. Пусть зрителей, до понижения цены, на стадион приходило А чел. и выручка составляла 1,8А руб. После понижения цены, цена 1,8*р, зрителей стало 1,5А, выручка составляет 1,8*р*1,5*А руб. С другой стороны, выручка повысилась на 25%, т.е. составляет 1,25*1,8А. Получаем 1,8*р*1,5*А=1,25*1,8А., откуда р=12,5/15, тогда билет стоит 1,8*12,5/15=1,5 руб.
Ответ. 1руб. 50 коп
Задача 4. По дороге идут два туриста. Первый из них делает шаги на 10% короче и в то же время на 10% чаще, чем второй. Кто из туристов идет быстрее и почему?
Решение. Пусть второй турист делает а шагов, каждый из которых равен в, тогда ав это длина пройденного пути. А первый турист тогда прошел1,1*а*0,9*в=0,99*ав, что меньше ав.
Ответ. Второй турист идет быстрее.
Задача 5. Цену за товар уменьшили на 10%, а затем еще на 10%. Стоит ли он дешевле, если цену сразу снизить на 20%?
Решение. Если товар стоил А руб, после двух понижений он стал стоить 0,9*0,9*А=0,81А. А цену товара сразу понизить на 20%, то он станет стоить 0,8*А , что дешевле.
Ответ. Да.
Задача 6. Числитель дроби увеличили на 20%. На сколько процентов надо уменьшить её знаменатель, чтобы в итоге дробь возросла вдвое?
Решение. Пусть данная дробь, новая дробь. , откуда К=0,6, что означает, что знаменатель нужно уменьшить на 40%
Ответ. 40%
Задача 7. Матроскин продает молоко через магазин и хочет получать за него 25 рублей за литр. Магазин удерживает 20% стоимости проданного товара. По какой цене будет продаваться молоко в магазине?
Решение. Пусть молоко продает магазин по А руб, тогда после удержания 20% стоимости товара, Матроскину остается 0,8*А=25, откуда А=31, 25 руб.
Ответ. 31 руб. 25 коп.
Задача 8. Один покупатель купил 25% имевшегося куска полотна, второй покупатель 30% остатка, а третий — 40% нового остатка. Сколько (в процентах) полотна осталось непроданным?
Решение. Пусть полотна было р . Первый купил 0,25р,, осталось (1-0,25)р полотна, второй покупатель купил 0,3*0,75р=0,225р, осталось 0,75р —0,225р=0,525р, третий купил 0,4*0,525р=0,21р, осталось 0,525р-0,21р=0,315р, что составляет 31,5% от р.
Ответ. 31,5%
Задача 9. Бригада косарей в первый день скосила половину луга и еще 2 га, а во второй день 25% оставшейся части и последние 6 га. Найти площадь луга.
Решение. 6 га составляют 75% или0,75=3/4 от оставшейся части после 1 дня работы, т.е.6: 0,75=6 га 8+2=10 га — это половина луга, весь луг 20 га
Ответ. 20 га
Задача 10. Как изменится в процентах площадь прямоугольника, если его длина увеличится на 30%, а ширина уменьшится на 30%?
Решение. АВ- площадь исходного прямоугольника, 1,3*А*0,7*В=0,91АВ — площадь нового прямоугольника, что составляет 91% исходного.
Ответ. Уменьшится на 9%
Задача 11. В драматическом кружке число мальчиков составляет 80% от числа девочек. Сколько процентов составляет число девочек в этом кружке от числа мальчиков?
Решение. Девочек А чел, мальчиков 0,8*А, девочки составляют от мальчиков А/(0,8А)= 1,25, т.е. 125 % от числа мальчиков
Ответ. 125%
Задача 12. В бассейн проведена труба. Вследствие засорения её приток воды уменьшился на 60%. На сколько процентов вследствие этого увеличится время, необходимое для заполнения бассейна
Решение. Пусть Х — объем воды, который должен поступить за время Т при притоке А в ед времени., т.е. Х=АТ. Так как приток уменьшился на 60%, т.е. стал составлять 0,4А, тогда время стало ТК. Получим АТ=0,4А*КТ, откуда К = 2,5, что составляет 250% от времени, необходимого на заполнение бассейна до засорения, т.е. время увеличилось на 150%
Ответ. 150%
Задача 13. 5 литров сливок с содержанием жира 35% смешали с 4 литрами 20%-ных сливок и к смеси добавили 1 литр чистой воды. Какой жирности получилась смесь?
Решение. 0,35*5+0,2*4=р*(5+4+1), откуда р=0,255, что составляет 25,5%
Ответ. 25,5%
2.2. Избранные задачи вариантов единого государственного экзамена.
Впервые в вариантах единого государственного экзамена по математике задача на проценты появились в 2003 году в заданиях группы В, в 2004 и в 2005 годах такие задачи также были представлены в вариантах единого экзамена. В вариантах 2006 года были задачи на работу, но в демонстрационном варианте 2007 года снова появляется задача на проценты, что говорит о необходимости серьезной работы над этой темой. Следует отметить, что для решения всех задач, которые предлагались, достаточно знания тех методов, которые рассматриваются в данной работе.
2003. Тренировочный вариант. Задание В7
Банк предлагает вклад «студенческий». По этому вкладу, сумма, имеющаяся на 1 января, ежегодно увеличивается на одно и то же число процентов. Вкладчик положил 1 января 1000 руб. и в течение 2 лет не производил со своим вкладом никаких операций. В результате вложенная им сумма увеличилась до 1210 руб. На сколько процентов ежегодно увеличивалась сумма денег, положенная на этот вклад?
Решение. Используя формулу увеличения положительного число на p%, получим, что через год сумма вклада составит 1000*(1+0,01р), а через два года 1000*(1+0,01р)2=1210, т.е. (1+0,01р)2=1,21, 1+0,01р=1,1, 0,01р=0,1, откуда р=10%
Ответ: сумма ежегодно увеличивалась на 10%.
2003. Демонстрационный вариант. Задание В7
Владелец дискотеки имел стабильный доход. В погоне за увеличением прибыли он повысил цену на билеты на 25%. Количество посетителей резко уменьшилось, и он стал нести убытки. Тогда он вернулся к первоначальной цене билетов. На сколько процентов, владелец дискотеки снизил новую цену билетов, чтобы она стала равна первоначальной?
Решение. Пусть цена билета была А руб. После повышения на 25% цена стала 1,25А, после понижения цена билета стала р*1,25А. Т.к. цена билета вернулась к первоначальной, то получим р*1,25А=А, откуда р=1/1,25 = 0,8, что означает, что новая цена составляет 80% цены после повышения., значит владелец дискотеки снизил цену на 20%.
Ответ: 20%
2003. ЕГЭ
Предприятие уменьшило выпуск продукции на 20%. На сколько процентов, необходимо теперь увеличить выпуск продукции, чтобы достигнуть его первоначального уровня?
Решение. Пусть А количество продукции, выпускаемое предприятием, 0,8А-количество продукции, которое стало выпускать предприятия после уменьшения на 20%. Из условия задачи следует уравнение р*0,8А=А, где р —коэффициент увеличения, откуда р=1/0,8=1,25, что означает, что необходимо увеличить выпуск продукции на 25%.
Ответ: 25%
2003. ЕГЭ
К 120 г раствора, содержащего 80% соли, добавили 480 г раствора, содержащего 20 % той же соли. Сколько процентов соли содержится в получившемся растворе?
Решение. 1) 0,8*120=96(г)-соли в первоначальном растворе;
2) 480*0,2=96(г) соли во втором растворе;
3) ((96+96)/(120+480))*100%=32%-процентное содержание соли в получившемся растворе.
Ответ: 32%
2003. ЕГЭ
За год стипендия студента увеличилась на 32%. В первом полугодии стипендия увеличилась на 10%. Определить, на сколько процентов увеличилась стипендия во втором полугодии?
Решение. Пусть А- первоначальный размер стипендии, 1,1А — размер стипендии после повышения в 1 полугодии, р*1,1А- размер стипендии после увеличения во 2 полугодии, где р- коэффициент увеличения. Так как за год стипендия увеличилась на 32%, получим уравнение р*1,1А=1,32А, р=132/110=1,2, что означает , что стипендия во 2 полугодии составляет 120% стипендии 1 полугодия., т.е. стипендия во 2 полугодии увеличилась на 20%
Ответ: на 20%.
2004. ЕГЭ
Имеются два слитка сплава золота с медью. Первый слиток содержит 230 г золота и 20 г меди, а второй слиток — 240 г золота и 60 г меди. От каждого слитка взяли по куску, сплавили их и получили 300 г сплава, в котором оказалось 84 % золота. Определить массу ( в граммах) куска, взятого от первого слитка.
Решение. Определим процентное содержание золота в обоих слитках. 1) 230+20=250(г)-масса 1 слитка, 230/250=0,92 (92%)процентное содержание золота в 1 слитке.
2) 240+60=300(г) —масса 2 слитка, 240/300=0,8 (80%)- процентное содержание золота во 2 слитке. Пусть х масса куска, взятого от 1 слитка, (300-х)- масса куска, взятого от 2 слитка, получим уравнение 0,92х+0,8(300-х)=0,84*300, откуда х=100
Ответ: 100г.
2004 ЕГЭ
Первый сплав серебра и меди содержит 70 г меди, а второй сплав — 210 г серебра и 90 г меди. Взяли 225 г первого сплава и кусок второго сплава, сплавили их и получили 300 г сплава, который содержит 82 % серебра. Сколько граммов серебра содержалось в первом сплаве?
Решение. Пусть х г серебра содержится в 1 сплаве., тогда 70/(х+70)-какую часть 1 сплава составляет медь, 90/(210+90)-такую часть составляет медь во 2 сплаве., кусок второго сплава 300-225=75г, тогда получаем уравнение.
225*(70/(х+70))+75*(90/300)=(1-0,82)*300, откуда х=430г
Ответ: 430г
ЕГЭ 2004
В колбе было 200 г 80% -го спирта. Провизор отлил из колбы некоторое количество этого спирта и затем добавил в нее столько же воды, чтобы получить 60% — ый спирт. Сколько граммов воды добавил провизор?.
Решение. 200*0,8=160(г)-масса чистого спирта в колбе, их колбы отлили х г раствора, осталось (200-х)г раствора, в котором чистого спирта 0,8*(200-х). Когда к раствору добавили х г воды, то масса раствора снова стала 200 г, а концентрация
[(0,8*(200-х))/200]*100%=60%, откуда х=50(г).
Ответ: провизор добавил 50г воды.
ЕГЭ 2004
В колбе было 800 г 80% -ного спирта. Провизор отлил из колбы 200 г этого спирта и добавил в нее 200 г воды. Определить концентрацию ( в процентах) полученного спирта.
Решение. После того, как провизор отлил 200 г раствора, стало 600г, в котором чистого спирта 0,8*600=480г, когда добавили200г воды, то раствор снова 800г, а концентрация чистого спирта в растворе (480/800)*100%=60%
Ответ: 60%
ЕГЭ 2005
Численность населения в городе Таганроге в течение двух лет возрастала на 2 процента ежегодно. В результате число жителей возросло на 11312 человек. Сколько жителей было в Таганроге первоначально?
Решение. А- первоначальное количество жителей Таганрога. Используя формулу коэффициента увеличения, получаем
А(1+0,02)2=А+11312, откуда А=280000
Ответ: 280000 чел
ЕГЭ 2005
Из сосуда, доверху наполненного 94% -м раствором кислоты, отлили 1,5 л жидкости и долили 1,5 л 70% -го раствора этой же кислоты. После этого в сосуде получился 86% раствор кислоты. Сколько л раствора вмещает сосуд?
Решение. Пусть х л вмещает сосуд, тогда из условий задачи следует уравнение 0,94(х-1,5)+0,7*1,5=0,86х, откуда х=4,5 л.
Ответ: 4,5 л
Демонстрационный вариант 2007
Денежный вклад в банк за год увеличивается на 11 %. Вкладчик внес в банк 7000 рублей. В конце первого года он решил увеличить сумму вклада и продлить срок действия договора еще на год, чтобы в конце второго года иметь на счету не менее 10000 рублей. Какую наименьшую сумму необходимо дополнительно положить на счет по окончании первого года, чтобы при той же процентной ставке (11 %) реализовать этот план? (Ответ округлите до целых.)
Решение. 1,11* 7000=7770руб-будет на счете в конце 1 года. Пусть х руб. положили дополнительно на счет, из условия задачи получаем неравенство 1,11(7770+х)> 10000, получим х>1239, 1/111, что означает, чтобы на счету было не менее 10000 руб, нужно положить не менее12 40руб.
Ответ: 1240 руб.
Заключение
Данное практическое пособие позволит развить и закрепить навыки решения задач по теме: «Проценты» у учащихся 5-6 классов, может быть интересно учащимся, увлеченным математикой, а также полезно выпускникам школ и абитуриентам при подготовке к экзаменам. В дальнейшем на факультативных и кружковых занятиях возможны изучение вопроса применения процентов в экономике, в банковском деле. Можно провести сравнительный анализ банковских процентных ставок по потребительским кредитам и ипотечному кредитованию населения.
Литература
1. .Быков А.А. и др В помощь поступающим в ГУ — ВШЭ, Математика, М: ГУ-ВШЭ, 2004
2.Денищева Л.О., Глазков Ю.А. и др., Учебно-тренировочные материалы для подготовки к ЕГЭ. Математика, М: Интеллект- Центр, 2003.
3. Потапов М.К., Олехник С.Н., Нестеренко Ю.В., Конкурсные задачи по математикеМ: Наука, 1992.
4. Семенко Е.А. и др., Готовимся к ЕГЭ по математике, Краснодар, Просвещение-Юг, 2005.
5. Алгебра, 9, под ред. Теляковского С.А., М: Просвещение, 2001
6. Алгебра и начала анализа, 10-11, под ред. Колмогорова А.Н., М: Просвещение, 2003.
7. Математика. Контрольные измерительные материалы единого государственного экзамена в 2004 г. М: Центр тестирования, 2004.
8. Экзаменационные материалы для подготовки к единому государственному экзамену. ЕГЭ 2006, М: Центр тестирования, 2005.
[1] «Математика, 5», Виленкин Н.Я. и др., «Мнемозина», 2003, с. 337
[2] «Алгебра, 9», под ред. Теляковского С.А., М: Просвещение, 2001, с.215, 223
[3] «Алгебра и начала анализа, 10-11», под ред. Колмогорова А.Н., М: Просвещение, 2003, с.306,330.
[4] «Учебно-тренировочные материалы для подготовки к ЕГЭ. Математика», Денищева Л.О., Гдазков Ю.А. и др., М: Интеллект- Центр, 2003.
«Математика. Контрольные измерительные материалы единого государственного экзамена в 2004 г.» М: Центр тестирования, 2004.
«Экзаменационные материалы для подготовки к единому государственному экзамену. ЕГЭ 2006», М: Центр тестирования, 2005.
[5] «Конкурсные задачи по математике», Потапов М.К., Олехник С.Н., Нестеренко Ю.В., М: Наука, 1992, с330-332.
«В помощь поступающим в ГУ — ВШЭ, Математика», Быков А.А. и дрМ: ГУ-ВШЭ, 2004, с 53-64
«Готовимся к ЕГЭ по математике», Семенко Е.А. и др., Краснодар, Просвещение-Юг, 2005, с. 46-51
Автор: Валентина Молибоженко
Материалы по мотивации на Педсовете
- Как вовлечь ребёнка в учебу. Основы эмоциональной и когнитивной вовлеченности
- Как удержать внимание в классе. Идеи из книг по мотивации взрослых
- Учусь по собственному желанию! Как повысить мотивацию у школьников?
- Как вовлечь детей в учебу: 7 простых приемов от выпускников Центра опережающей педагогики
- Как удержать внимание на уроке-лекции. Как сделать лекцию интересной и запоминающейся?
- Как заинтересовать ребёнка в учёбе? Опыт выпускницы с красным дипломом
- Чудеса мотивации: на урок как в театр. Занятия по химии в антураже вселенной Гарри Поттера
- Как мотивировать к учебе и повысить успешность «слабых» учащихся?
- Мотивация к учебе. Где ее раздают?
- 7 проверенных способов мотивировать ребенка в начальной школе
- Как повысить мотивацию к обучению у современных школьников
- 8 стратегий развития мотивации школьников при изучении математики
На рисунке изображён план двухкомнатной квартиры в многоэтажном жилом доме. Сторона одной клетки на плане соответствует 0,4 м, а условные обозначения двери и окна приведены в правой части рисунка.
Вход в квартиру находится в коридоре. Слева от входа в квартиру находится санузел, а в противоположном конце коридора – дверь в кладовую.
Рядом с кладовой находится спальня, из которой можно пройти на одну из застеклённых лоджий. Самое большое по площади помещение – гостиная, откуда можно попасть в коридор и на кухню. Из кухни также можно попасть на застеклённую лоджию.
Задание 1: Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк перенесите последовательность четырёх цифр без пробелов, запятых и других дополнительных символов.
Задание 2: Найдите ширину окна в спальне. Ответ дайте в сантиметрах.
Задание 3: Найдите площадь гостиной. Ответ дайте в квадратных метрах.
Задание 6 про план квартиры: Плитка для пола размером 20 см на 40 см продаётся в упаковках по 8 штук. Сколько упаковок плитки понадобилось, чтобы выложить пол санузла?
Задание 7 про квартиру: Паркетная доска размером 20 см на 80 см продаётся в упаковках по 16 штук. Сколько упаковок паркетной доски понадобилось, чтобы выложить пол в спальне?
Задание 8: В квартире планируется подключить интернет. Предполагается, что трафик составит 850 Мб в месяц, и исходя из этого выбирается наиболее дешёвый вариант. Провайдер предлагает три тарифных плана.
Сколько рублей нужно будет заплатить за интернет за месяц, если трафик действительно будет равен 850 Мб?
Задание 9 про план квартиры: В квартире планируется заменить электрическую плиту. Характеристики электроплит, условия подключения и доставки приведены в таблице. Планируется купить электрическую плиту глубиной 60 см с духовкой объёмом не менее 54 л.
Сколько рублей будет стоить наиболее дешёвый подходящий вариант вместе с подключением и доставкой?
Задание 10: В квартире планируется установить стиральную машину. Характеристики стиральных машин, условия подключения и доставки приведены в таблице. Планируется купить стиральную машину с вертикальной загрузкой вместимостью не менее 6 кг.
Сколько рублей будет стоить наиболее дешёвый подходящий вариант вместе с подключением и доставкой?
Решения задач про квартиру.
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
Решение.
Поскольку гостиная занимает наибольшую площадь в квартире, можно заключить, что она обозначена на схеме цифрой 4. Слева от гостиной находится кухня, следовательно, она обозначена цифрой 2. Ванная комната находится напротив санузла, значит, ванная обозначена на схеме цифрой 7. Кладовая комната расположена справа от коридора, следовательно, она обозначена цифрой 3.
Ответ: 4273.
Плитка продаётся в упаковках по 5 штук. Сколько упаковок плитки понадобилось, чтобы выложить пол в ванной комнате и санузле?
На плане изображена схема квартиры (сторона каждой клетки на схеме равна 1 м). Квартира имеет прямоугольную форму. Вход и выход осуществляются через единственную дверь.
При входе в квартиру расположен коридор, отмеченный цифрой 1, а справа находится кладовая комната, которая занимает площадь в 20 кв. м.
Гостиная занимает наибольшую площадь в квартире, а слева от неё находится кухня. Прямо перед гостиной находится детская.
В верхнем правом углу схемы находится санузел, отмеченный цифрой 6. Прямо напротив него располагается ванная комната.
В санузле и ванной комнате пол выложен плиткой, которая имеет размер 0,5 м × 0,5 м.
В квартире стоит однотарифный счётчик электроэнергии. Имеется возможность установить двухтарифный счётчик.
Решение.
Заметим, что, поскольку одна плитка имеет площадь 0,25 м2, чтобы выложить 1 м2 пола плиткой, понадобится 4 плитки. Площадь санузла равна 6 4 = 24 м2. Площадь ванной равна 4 5 = 20 м2. Теперь найдём, сколько упаковок плитки понадобилось: Следовательно, чтобы выложить пол в ванной комнате и санузле понадобится 36 упаковок плитки.
Ответ: 36.
Найдите площадь, которую занимает гостиная. Ответ дайте в квадратных метрах.
Решение.
Сторона одной клетки равна 1 м. Значит, площадь гостиной равна:
Ответ: 42.
Найдите расстояние от верхнего левого угла квартиры до нижнего правого угла квартиры (расстояние между двумя ближайшими точками по прямой) в метрах.
Решение.
Найдём расстояние между двумя ближайшими точками по прямой верхнего левого угла квартиры и нижнего правого угла квартиры по теореме Пифагора:
Ответ: 20.
Хозяин квартиры планирует заменить в квартире счётчик. Он рассматривает два варианта: однотарифный или двухтарифный счётчики. Цены на оборудование и стоимость его установки, данные о тарифах оплаты, и их стоимости даны в таблице.
Обдумав оба варианта, хозяин решил установить двухтарифный электросчётчик. Через сколько дней непрерывного использования электричества экономия от использования двухтарифного счётчика вместо однотарифного компенсирует разность в стоимости установки двухтарифного счётчика и однотарифного?
Решение.
Заметим, что, поскольку одна плитка имеет площадь 0,25 м2, чтобы выложить 1 м2 пола плиткой, понадобится 4 плитки. Площадь санузла равна 6 4 = 24 м2. Площадь ванной равна 4 5 = 20 м2. Теперь найдём, сколько упаковок плитки понадобилось: Следовательно, чтобы выложить пол в ванной комнате и санузле понадобится 36 упаковок плитки.
Ответ: 36.
Плитка для пола продаётся в упаковках по 5 штук. Сколько упаковок плитки нужно купить, чтобы покрыть пол кухни?
Владелец собирается провести ремонт своей квартиры. На плане изображена предполагаемая расстановка мебели и бытовой техники на кухне после ремонта. Сторона каждой клетки равна 0,3 м. Кухня имеет квадратную форму. Единственная дверь кухни деревянная, в стене напротив двери расположено окно. Справа от двери будут поставлены полки для посуды, слева от двери будет смонтирована раковина для мытья посуды. В углу слева от окна предполагается разместить газовую плиту. Между раковиной и плитой будет собран буфет, отмеченный цифрой 3. Площадь, занятая буфетом, по плану будет равна 0,72 м2. В центре кухни планируется поставить обеденный стол. Кроме того, в угол кухни будет поставлен холодильник, занимающий 0,36 м2 пола. Пол кухни (в том числе там, где будет стоять мебель и бытовая техника) планируется покрыть плиткой размером 30 см × 30 см. Кроме того, владелец квартиры планирует смонтировать на кухне электрический подогрев пола. Чтобы сэкономить, владелец не станет подводить обогрев под холодильник, плиту, буфет, раковину и полки для посуды, а также на участок площадью 0,18 м2 между буфетом и плитой.
Решение.
Заметим, что, поскольку одна плитка имеет площадь 0,09 м2, чтобы выложить пол в кухне понадобится столько плитки, сколько площади занимает кухня. Сторона одной клетки равна 0,3 м, значит, площадь кухни равна 9 0,3 9 0,3 = 7,29 м2. Теперь найдём, сколько плитки понадобится: Следовательно, чтобы выложить пол в кухне, понадобится
упаковок плитки. Значит, необходимо купить 17 упаковок плитки.
Ответ: 17.
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
Решение.
Стол планируется поставить в центре кухни, значит, стол отмечен на плане цифрой 4. Раковина будет смонтирована слева от двери, значит, раковина отмечена цифрой 5. В углу слева от окна планируется поставить плиту, она отмечена на плане цифрой 1. Известно, что холодильник планируется поставить в угол кухни. В углах левой части кухни будут стоять плита и раковина, в угле справа от двери будут стоять полки для посуды. Значит, холодильник отмечен на плане цифрой 2.
Ответ: 4215.
Найдите площадь той части кухни, на которой будет смонтирован электрический подогрев пола. Ответ дайте в м2.
Решение.
Сторона одной клетки равна 0,3 м. Значит, площадь кухни равна:
Владелец не станет подводить обогрев под холодильник, плиту, буфет, раковину и полки для посуды, а также на участок между буфетом и плитой, который имеет площадь 0,18 м2. Холодильник занимает площадь 0,36 м2. На плане видно, что раковина и плита также занимают 0,36 м2. Буфет занимает 0,72 м2. Полки для посуды занимают участок площадью м2. Значит, площадь той части кухни, на которой будет смонтирован электрический подогрев пола, равна
Ответ: 5,13.
Приведем другое решение.
Владелец не станет подводить подогрев под раковину, плиту и буфет, а также на участок между буфетом и плитой. По рисунку видно, что все эти участки расположены вдоль левой стены кухни и занимают общую площадь 2 0,3 9 0,3 = 1,62 м2. Кроме того, владелец не будет подводить подогрев под холодильник площадью 0,36 м2 и полки для посуды площадью 0,18 м2. Значит, площадь той части кухни, на которой будет смонтирован электрический подогрев пола, равна 7,29 − 1,62 − 0,36 − 0,18 = 5,13 м2.
Найдите расстояние (по прямой) между противоположными углами обеденного стола. Ответ дайте в метрах.
Решение.
Найдём расстояние между противоположными углами обеденного стола по теореме Пифагора:
Ответ: 1,5.
Задание 10
Владелец квартиры выбирает холодильник из двух моделей А и Б. Цена холодильников и их среднее суточное потребление электроэнергии указаны в таблице. Цена электроэнергии составляет 4 рубля за кВт ч.
| Модель | Цена холодильника (руб) |
Среднее потребление электроэнергии в сутки, кВт ч |
|---|---|---|
| А | 30 000 | 0,7 |
| Б | 28 000 | 0,9 |
Обдумав оба варианта, владелец квартиры выбрал модель А. Через сколько лет непрерывной работы экономия от меньшего расхода электроэнергии окупит разницу в цене этих холодильников? Ответ округлите до целого числа.
Решение.
Заметим, что, поскольку одна плитка имеет площадь 0,09 м2, чтобы выложить пол в кухне понадобится столько плитки, сколько площади занимает кухня. Сторона одной клетки равна 0,3 м, значит, площадь кухни равна 9 0,3 9 0,3 = 7,29 м2. Теперь найдём, сколько плитки понадобится: Следовательно, чтобы выложить пол в кухне, понадобится
упаковок плитки. Значит, необходимо купить 17 упаковок плитки.
Ответ: 17.
* * * * *
Задание 11
Краска продаётся в банках по 3 л. Сколько банок краски требуется купить, чтобы покрасить потолок в гостиной?
На плане изображена схема квартиры (сторона каждой клетки на схеме равна 1 м). Вход и выход осуществляются через единственную дверь.
При входе в квартиру расположен коридор, отмеченный цифрой 1. Напротив входа расположена туалетная комната, а справа от нее — ванная комната.
Гостиная занимает наибольшую площадь в квартире, а справа от неё находится кухня. Прямо перед гостиной находится детская. Из детской можно попасть на балкон, отмеченный цифрой 6.
Потолок в гостиной планируется покрасить в красный цвет. Для покраски одного 1 м2 потолка требуется 0,25 л краски.
В квартире планируется установить счётчик электроэнергии. Имеется возможность установить однотарифный или двухтарифный счётчик.
Решение.
Площадь гостиной равна 5 9 = 45 м2. Для покраски одного 1 м2 потолка требуется 0,25 л краски. Значит, чтобы покрасить потолок в гостиной понадобится
0,25 45 = 11,25 л
краски. Таким образом, требуется купить 4 банки краски.
Ответ: 4.
Задание 12
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | Туалет | Детская | Гостиная | Кухня |
|---|---|---|---|---|
| Цифры |
Решение.
Туалет расположен напротив входа в квартиру, следовательно, он отмечен цифрой 2. Из детской можно попасть на балкон, отмеченный цифрой 6, значит, детская отмечена на схеме цифрой 4. Гостиная занимает наибольшую площадь в квартире, поэтому гостиная отмечена цифрой 5. Кухня находится справа от гостиной, следовательно, кухня отмечена цифрой 7.
Ответ: 2457.
Задание 13
Найдите площадь, которую занимают детская и балкон. Ответ дайте в квадратных метрах.
Решение.
Сторона одной клетки равна 1 м. Значит, площадь детской и балкона равна:
м2.
Ответ: 48.
Задание 14
Найдите расстояние между противоположными углами детской комнаты в метрах. Ответ запишите в виде
Решение.
Найдём расстояние между противоположными углами детской комнаты по теореме Пифагора:
Таким образом, получаем ответ:
Ответ: 6.
Задание 15
Хозяин квартиры планирует установить в квартире счётчик. Он рассматривает два варианта: однотарифный или двухтарифный счётчики. Цены на оборудование и стоимость его установки, данные о потребляемой мощности, и тарифах оплаты даны в таблице.
| Оборудование и монтаж |
Сред. потребл. мощность в час |
Стоимость оплаты | |
|---|---|---|---|
| Двухтарифный | 8 675 руб. | 3,5 кВт | 3 руб./(кВт ч) днём |
| 1,5 руб./(кВт ч ) ночью (с 23:00 до 6:00) |
Обдумав оба варианта, хозяин решил установить двухтарифный электросчётчик. Через сколько дней непрерывного использования электричества экономия от использования двухтарифного счётчика вместо однотарифного компенсирует разность в стоимости установки двухтарифного счётчика и однотарифного?
Решение.
Разница в стоимости установки двухтарифного и однотарифного счётчиков равна 8 675 − 5 000 = 3 675 руб. День использования электроэнергии с однотарифным счётчиком стоит 3 3,5 24 = 252 руб./(кВт ч). День использования электроэнергии с двухтарифным счётчиком стоит 3,5 3 17 + 3,5 1,5 7 = 215,25 руб./(кВт ч). Разница в стоимости составляет 252 − 215,25 = 36,75 руб./(кВт ч). Значит, экономия от использования двухтарифного счётчика вместо однотарифного компенсирует разность в стоимости установки двухтарифного и однотарифного счётчиков через дней.
Ответ: 100.
* * * * *
Задание 16
Краска продаётся в банках по 2 л. Сколько банок краски требуется купить, чтобы покрасить потолок в ванной комнате и санузле?
На плане изображена схема квартиры (сторона каждой клетки на схеме равна 1 м). Вход и выход осуществляются через единственную дверь.
При входе в квартиру расположен коридор, отмеченный цифрой 1. Перед входом в квартиру располагается ванная комната, а справа от неё — санузел.
Гостиная занимает наибольшую площадь в квартире, из гостиной можно попасть в детскую комнату. Также в квартире есть кухня, из которой можно попасть на балкон, отмеченный цифрой 6. В конце коридора находится кладовая комната, имеющая площадь 10 м2.
Потолок в ванной комнате и санузле планируется покрасить в белый цвет. Для покраски одного 1 м2 потолка требуется 0,2 л краски.
В квартире стоит однотарифный счётчик электроэнергии. Имеется возможность установить двухтарифный счётчик.
Решение.
Площадь ванной комнаты и санузла равна
м2.
Для покраски одного 1 м2 потолка требуется 0,2 л краски. Значит, чтобы покрасить потолок в ванной комнате и санузле понадобится
0,2 24 = 4,8 л
краски. Таким образом, требуется купить 3 банки краски.
Ответ: 3.
Задание 17
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | Ванная комната | Детская комната | Кухня | Кладовая комната |
|---|---|---|---|---|
| Цифры |
Решение.
Перед входом в квартиру располагается ванная комната, следовательно, ванная комната отмечена цифрой 2. Гостиная занимает наибольшую площадь в квартире, из гостиной можно попасть в детскую комнату, поэтому детская комната отмечена цифрой 7. Также в квартире есть кухня, из которой можно попасть на балкон, отмеченный цифрой 6, значит, кухня отмечена на схеме цифрой 4. В конце коридора находится кладовая комната, имеющая площадь 10 м2, следовательно, кладовая комната отмечена цифрой 8.
Ответ: 2748.
Задание 18
Найдите площадь, которую занимают кухня и балкон. Ответ дайте в квадратных метрах.
Решение.
Сторона одной клетки равна 1 м. Значит, площадь кухни и балкона равна:
м2.
Ответ: 28.
Задание 19
Найдите расстояние между противоположными углами (диагональ) ванной комнаты в метрах.
Решение.
Найдём расстояние между противоположными углами ванной комнаты по теореме Пифагора:
Ответ: 5.
Задание 20
Хозяин квартиры планирует установить в квартире счётчик. Он рассматривает два варианта: однотарифный или двухтарифный счётчики. Цены на оборудование и стоимость его установки, данные о потребляемой мощности, и тарифах оплаты даны в таблице.
| Оборудование и монтаж |
Сред. потребл. мощность (в час) |
Стоимость оплаты | |
|---|---|---|---|
| Двухтарифный | 8 200 руб. | 6 кВт | 5 руб./(кВт ч) днём |
| 3 руб./(кВт ч ) ночью (с 23:00 до 6:00) |
Обдумав оба варианта, хозяин решил установить двухтарифный электросчётчик. Через сколько дней непрерывного использования электричества экономия от использования двухтарифного счётчика вместо однотарифного компенсирует разность в стоимости установки двухтарифного счётчика и однотарифного?
Решение.
Разница в стоимости установки двухтарифного и однотарифного счётчиков равна 8 200 − 4 000 = 4 200 руб. День использования электроэнергии с однотарифным счётчиком стоит 5 6 24 = 720 руб./(кВт ч). День использования электроэнергии с двухтарифным счётчиком стоит 6 5 17 + 6 3 7 = 636 руб./(кВт ч). Разница в стоимости составляет 720 − 636 = 84 руб./(кВт ч). Значит, экономия от использования двухтарифного счётчика вместо однотарифного компенсирует разность в стоимости установки двухтарифного и однотарифного счётчиков через дней.
Ответ: 50.
* * * * *
Задание 21
Паркетная доска продаётся в упаковках по 8 шт. Сколько упаковок с паркетной доской требуется купить, чтобы покрыть пол в гостиной?
На плане изображена схема квартиры (сторона каждой клетки на схеме равна 1 м). Вход и выход осуществляются через единственную дверь.
При входе в квартиру расположен коридор, отмеченный цифрой 2. Слева от него расположен балкон. Перед входом в квартиру располагается совмещённый санузел, а справа от него — детская комната.
Гостиная занимает наибольшую площадь в квартире, из гостиной можно попасть в кабинет. В конце коридора находится кухня площадью 20 м2.
Пол в гостиной планируется покрыть паркетной доской длиной 1 м и шириной 0,25 м.
В квартире проведены газопровод и электричество.
Решение.
Заметим, что чтобы покрыть паркетной доской 1 м2 пола, требуется 4 доски. Найдём площадь гостиной:
м2.
Значит, требуется 35 4 = 140 досок. Следовательно, требуется упаковок с паркетной доской. Таким образом, необходимо купить 18 упаковок.
Ответ: 18.
Задание 22
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | Балкон | Детская комната | Кабинет | Кухня |
|---|---|---|---|---|
| Цифры |
Решение.
При входе в квартиру расположен коридор, отмеченный цифрой 2. Слева от него расположен балкон. Значит, балкон отмечен цифрой 1. Перед входом в квартиру располагается совмещённый санузел, а справа от него — детская комната, следовательно, детская комната отмечена на схеме цифрой 4. Гостиная занимает наибольшую площадь в квартире, из гостиной можно попасть в кабинет, поэтому кабинет отмечен цифрой 7. В конце коридора находится кухня площадью 20 м2, значит, кухня отмечена цифрой 5.
Ответ: 1475.
Задание 23
Найдите площадь коридора (коридором считается площадь квартиры, незанятая комнатами или балконом). Ответ дайте в квадратных метрах.
Решение.
Сторона одной клетки равна 1 м. Значит, площадь коридора равна:
м2.
Ответ: 25.
Задание 24
Найдите расстояние между противоположными углами детской комнаты в метрах. Ответ запишите в виде
Решение.
Найдём расстояние между противоположными углами детской комнаты по теореме Пифагора:
Таким образом, получаем ответ:
Ответ: 4.
Задание 25
Хозяин квартиры планирует установить в квартире плиту для готовки. Он рассматривает два варианта: газовая плита или электроплитка. Цены на плиты, данные о потреблении и тарифах оплаты даны в таблице.
| Цена | Сред. расход газа / сред. потребл. мощность |
Стоимость газа / электро-энергии |
|
|---|---|---|---|
| Газовая плита | 44 680 руб. | 1,4 куб. м/ч | 6 руб./куб. м |
| Электроплитка | 21 000 руб. | 5,8 кВт | 4 руб./(кВт ч ) |
Обдумав оба варианта, хозяин решил установить газовую плиту. Через сколько часов непрерывного использования экономия от использования газовой плиты вместо электрической компенсирует разность в стоимости установки газовой плиты и электроплитки?
Решение.
Разница в стоимости покупки газовой плиты и электроплитки равна 44 680 − 21 000 = 23 680 руб. Час использования газовой плиты стоит 1,4 6 = 8,4 руб. Час использования электроплитки стоит 5,8 4 = 23,2 руб. Разница в стоимости составляет 23,2 − 8,4 = 14,8 руб. Значит, экономия от использования газовой плиты вместо электроплитки компенсирует разность в стоимости установки газовой и электрической плит через часов.
Ответ: 1600.
* * * * *
Задание 26
Паркетная доска продаётся в упаковках по 16 шт. Сколько упаковок с паркетной доской требуется купить, чтобы покрыть пол в гостиной?
На плане изображена схема квартиры (сторона каждой клетки на схеме равна 1 м). Вход и выход осуществляются через единственную дверь.
При входе в квартиру расположена прихожая, отмеченная цифрой 6. Из прихожей можно попасть в гостиную, расположенную справа от неё. В квартире есть балкон, занимающий наименьшую площадь. Перед входом в прихожую располагается спальня, а справа от неё — детская комната, в которую можно попасть только из спальни. Рядом со спальней расположен совмещенный санузел площадью 12 м2. Кроме того, в квартире есть кухня.
Пол в гостиной планируется покрыть паркетной доской длиной 1 м и шириной 0,25 м.
В квартире проведены газопровод и электричество.
Решение.
Заметим, что чтобы покрыть паркетной доской 1 м2 пола, требуется 4 доски. Найдём площадь гостиной:
м2.
Значит, требуется 30 4 = 120 досок. Следовательно, требуется упаковок с паркетной доской. Таким образом, необходимо купить 8 упаковок.
Ответ: 8.
Задание 27
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | Балкон | Детская комната | Гостиная | Кухня |
|---|---|---|---|---|
| Цифры |
Решение.
В квартире есть балкон, занимающий наименьшую площадь, следовательно, балкон отмечен на схеме цифрой 1. Перед входом в прихожую располагается спальня, а справа от неё — детская комната, в которую можно попасть только из спальни, значит, детская комната отмечена цифрой 5. Из прихожей можно попасть в гостиную, расположенную справа от неё, поэтому гостиная отмечена цифрой 7. Рядом со спальней расположен совмещенный санузел площадью 12 м2, он отмечен цифрой 3. Значит, кухня отмечена цифрой 2.
Ответ: 1572.
Задание 28
Найдите площадь, которую занимают спальная комната и детская. Ответ дайте в квадратных метрах.
Решение.
Сторона одной клетки равна 1 м. Значит, площадь спальной комнаты и детской равна:
м2.
Ответ: 36.
Задание 29
Найдите расстояние d между противоположными углами кухни в метрах. В ответ запишите
Решение.
Найдём расстояние между противоположными углами кухни по теореме Пифагора:
Таким образом, получаем ответ:
Ответ: 5.
Задание 30
Хозяин квартиры планирует установить в квартире плиту для готовки. Он рассматривает два варианта: газовая плита или электроплитка. Цены на плиты, данные о потреблении и тарифах оплаты даны в таблице.
| Цена | Сред. расход газа / сред. потребл. мощность |
Стоимость газа / электро-энергии |
|
|---|---|---|---|
| Газовая плита | 43 730 руб. | 1,2 куб. м/ч | 5,3 руб./куб. м |
| Электроплитка | 17 000 руб. | 6,2 кВт | 3,9 руб./(кВт ч ) |
Обдумав оба варианта, хозяин решил установить газовую плиту. Через сколько часов непрерывного использования экономия от использования газовой плиты вместо электрической компенсирует разность в стоимости установки газовой плиты и электроплитки?
Решение.
Разница в стоимости покупки газовой плиты и электроплитки равна 43 730 − 17 000 = 26 730 руб. Час использования газовой плиты стоит 1,2 5,3 = 6,36 руб. Час использования электроплитки стоит 6,2 3,9 = 24,18 руб. Разница в стоимости составляет 24,18 − 6,36 = 17,82 руб. Значит, экономия от использования газовой плиты вместо электроплитки компенсирует разность в стоимости установки газовой и электрической плит через часов.
Ответ: 1500.
* * * * *
Задание 31
Паркетная доска продаётся в упаковках по 15 штук. Сколько упаковок с паркетной доской нужно купить, чтобы покрыть пол гостиной?
Владелец собирается провести ремонт своей квартиры. На плане изображена предполагаемая расстановка мебели в гостиной после ремонта. Сторона каждой клетки равна 0,4 м. Гостиная имеет прямоугольную форму. Единственная дверь гостиной деревянная, в стене напротив двери расположено окно. Справа от двери будет поставлен комод, слева от двери у стены будет собран книжный шкаф. В глубине комнаты у стены планируется поставить диван. Перед книжным шкафом будет поставлено кресло. Справа от дивана будет стоять торшер. Площадь, занятая диваном, по плану будет равна 1,28 м2. У стены справа от двери планируется поставить письменный стол, а перед ним поставить стул. Пол гостиной (в том числе там, где будет стоять мебель) планируется покрыть паркетной доской размером 40 см × 20 см. Кроме того, владелец квартиры планирует смонтировать в гостиной электрический подогрев пола. Чтобы сэкономить, владелец не станет подводить обогрев под книжный шкаф, кресло, диван и комод, а также на участок площадью 0,16 м2 между диваном и торшером.
Решение.
Заметим, что чтобы покрыть паркетной доской 0,16 м2 пола, требуется 2 доски. Найдём площадь гостиной:
м2.
Значит, требуется доски. Следовательно, требуется
упаковок с паркетной доской. Таким образом, необходимо купить 13 упаковок.
Ответ: 13.
Задание 32
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | Книжный шкаф | Диван | Торшер | Стул |
|---|---|---|---|---|
| Цифры |
Решение.
Слева от двери у стены будет собран книжный шкаф, значит, книжный шкаф отмечен цифрой 1. В глубине комнаты у стены планируется поставить диван, поэтому диван отмечен на плане цифрой 3. Справа от дивана будет стоять торшер, следовательно, торшер отмечен цифрой 7. У стены справа от двери планируется поставить письменный стол, а перед ним поставить стул, значит, стул отмечен цифрой 5.
Ответ: 1375.
Задание 33
Найдите площадь той части гостиной, на которой будет смонтирован электрический подогрев пола. Ответ дайте в м2.
Решение.
Сторона одной клетки равна 0,4 м. Значит, площадь гостиной равна:
м2.
Владелец не станет подводить обогрев под книжный шкаф, кресло, диван и комод, а также на участок площадью 0,16 м2 между диваном и торшером. Книжный шкаф занимает площадь м2. Диван занимает 1,28 м2. Кресло занимает участок площадью
м2. Комод занимает участок площадью
м2. Значит, площадь той части гостиной, на которой будет смонтирован электрический подогрев пола, равна
м2.
Ответ: 12.
Задание 34
Найдите расстояние d между противоположными углами кресла (диагональ). Ответ дайте в метрах в формате
Решение.
Найдём расстояние между противоположными углами кресла по теореме Пифагора:
Таким образом, получаем ответ:
Ответ: 0,8.
Задание 35
Владелец квартиры выбирает торшер из двух моделей А и Б. Цена торшеров и их среднее суточное потребление электроэнергии указаны в таблице. Цена электроэнергии составляет 4 рубля за кВт ч.
| Модель | Цена торшера (руб) |
Среднее потребление электроэнергии в сутки, кВт ч |
|---|---|---|
| А | 2 000 | 0,2 |
| Б | 1 200 | 0,3 |
Обдумав оба варианта, владелец квартиры выбрал модель А. Через сколько лет непрерывной работы экономия от меньшего расхода электроэнергии окупит разницу в цене этих торшеров? Ответ округлите до целого числа в большую сторону.
Решение.
Разница в стоимости торшеров равна руб. Стоимость электроэнергии за сутки работы первого торшера равна
руб. Стоимость электроэнергии за сутки работы второго торшера равна
руб. Значит, при установке первого торшера владелец квартиры за сутки экономит
руб. Следовательно, в год владелец квартиры экономит
руб. Таким образом, экономия от меньшего расхода электроэнергии окупит разницу в цене этих торшеров через
лет. Округлив, получаем ответ: через 6 лет.
Ответ: 6.
* * * * *
Задание 36
Паркетная доска продаётся в упаковках по 25 штук. Сколько упаковок с паркетной доской нужно купить, чтобы покрыть пол гостиной?
Владелец собирается провести ремонт своей квартиры. На плане изображена предполагаемая расстановка мебели в гостиной после ремонта. Сторона каждой клетки равна 0,4 м. Гостиная имеет прямоугольную форму. Единственная дверь гостиной деревянная, в стене напротив двери расположено окно. Справа от двери будет поставлен письменный стол, а к нему приставлен стул, слева от двери у стены будет собран книжный шкаф. В глубине комнаты у стены планируется поставить диван, а перед ним — журнальный столик. Слева от дивана будет стоять торшер. Площадь, занятая диваном, по плану будет равна 1,6 м2. В оставшемся свободным углу планируется поставить кресло. Пол гостиной (в том числе там, где будет стоять мебель) планируется покрыть паркетной доской размером 40 см × 10 см. Кроме того, владелец квартиры планирует смонтировать в гостиной электрический подогрев пола. Чтобы сэкономить, владелец не станет подводить обогрев под книжный шкаф, кресло и диван.
Решение.
Заметим, что чтобы покрыть паркетной доской 0,16 м2 пола, требуется 4 доски. Найдём площадь гостиной:
м2.
Значит, требуется доски. Следовательно, требуется
упаковок с паркетной доской. Таким образом, необходимо купить 18 упаковок.
Ответ: 18.
Задание 37
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответ запишите последовательность четырёх цифр без пробелов и других дополнительных символов.
| Объекты | Стул | Диван | Журнальный столик | Кресло |
|---|---|---|---|---|
| Цифры |
Решение.
Справа от двери будет поставлен письменный стол, а к нему приставлен стул, значит, стул отмечен цифрой 6. В глубине комнаты у стены планируется поставить диван, а перед ним — журнальный столик, следовательно, диван отмечен цифрой 2, а журнальный столик отмечен цифрой 4. В оставшемся свободным углу планируется поставить кресло, поэтому кресло отмечено цифрой 3.
Ответ: 6243.
Задание 38
Найдите площадь той части гостиной, на которой будет смонтирован электрический подогрев пола. Ответ дайте в м2.
Решение.
Сторона одной клетки равна 0,4 м. Значит, площадь гостиной равна:
м2.
Владелец не станет подводить обогрев под книжный шкаф, кресло и диван. Книжный шкаф занимает площадь м2. Диван занимает 1,6 м2. Кресло занимает участок площадью
м2. Значит, площадь той части гостиной, на которой будет смонтирован электрический подогрев пола, равна
м2.
Ответ: 14,56.
Задание 39
Найдите расстояние от дивана до письменного стола (расстояние между двумя ближайшими точками по прямой) в метрах.
Решение.
Найдём расстояние между двумя ближайшими точками по прямой дивана и письменного стола по теореме Пифагора:
Ответ: 2.
Задание 40
Владелец квартиры выбирает торшер из двух моделей А и Б. Цена торшеров и их среднее суточное потребление электроэнергии указаны в таблице. Цена электроэнергии составляет 5 рублей за кВт ч.
| Модель | Цена торшера (руб) |
Среднее потребление электроэнергии в сутки, кВт ч |
|---|---|---|
| А | 2 100 | 0,3 |
| Б | 1 370 | 0,4 |
Обдумав оба варианта, владелец квартиры выбрал модель А. Через сколько лет непрерывной работы экономия от меньшего расхода электроэнергии окупит разницу в цене этих торшеров? Ответ округлите до целого числа.
Решение.
Разница в стоимости торшеров равна руб. Стоимость электроэнергии за сутки работы первого торшера равна
руб. Стоимость электроэнергии за сутки работы второго торшера равна
руб. Значит, при установке первого торшера владелец квартиры за сутки экономит
руб. Следовательно, в год владелец квартиры экономит
руб. Таким образом, экономия от меньшего расхода электроэнергии окупит разницу в цене этих торшеров через
года.
Ответ: 4.
* * * * *
Задание 41
Паркетная доска продаётся в упаковках по 32 штуки. Сколько упаковок с паркетной доской нужно купить, чтобы покрыть пол в гостиной?
Владелец собирается провести ремонт своей квартиры. На плане изображена предполагаемая расстановка мебели в гостиной после ремонта. Сторона каждой клетки равна 0,4 м. Гостиная имеет прямоугольную форму. Единственная дверь гостиной деревянная, в стене напротив двери расположено окно. Справа от двери будет поставлен письменный стол, а к нему приставлен стул, слева от двери у стены будет собран книжный шкаф. В глубине комнаты у стены планируется поставить диван, а перед ним — журнальный столик. Площадь, занятая диваном, по плану будет равна 1,6 м2. В оставшемся свободным углу планируется поставить кресло. Слева от кресла будет стоять торшер. Пол гостиной (в том числе там, где будет стоять мебель) планируется покрыть паркетной доской размером 40 см × 5 см. Кроме того, владелец квартиры планирует смонтировать в гостиной электрический подогрев пола. Чтобы сэкономить, владелец не станет подводить обогрев под книжный шкаф, кресло и диван.
Решение.
Заметим, что чтобы покрыть паркетной доской 0,16 м2 пола, требуется 8 досок. Найдём площадь гостиной:
м2.
Значит, требуется доски. Следовательно, требуется
упаковок с паркетной доской.
Приведем другое решение.
Найдем площадь гостиной: м2.
Найдем площадь одной паркетной доски: м2.
Значит, требуется доски, или
упаковок с паркетной доской.
Ответ: 27.
Задание 42
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответ запишите последовательность четырёх цифр без пробелов и других дополнительных символов.
| Объекты | Письменный стол | Диван | Журнальный столик | Торшер |
|---|---|---|---|---|
| Цифры |
Решение.
Справа от двери будет поставлен письменный стол, значит, письменный стол отмечен цифрой 7. В глубине комнаты у стены планируется поставить диван, а перед ним — журнальный столик, следовательно, диван отмечен цифрой 2, а журнальный столик отмечен цифрой 4. В оставшемся свободным углу планируется поставить кресло. Слева от кресла будет стоять торшер, поэтому торшер отмечен цифрой 1.
Ответ: 7241.
Задание 43
Найдите площадь той части гостиной, на которой не будет смонтирован электрический подогрев пола. Ответ дайте в м2.
Решение.
Сторона одной клетки равна 0,4 м. Владелец не станет подводить обогрев под книжный шкаф, кресло и диван. Книжный шкаф занимает площадь м2. Диван занимает 1,6 м2. Кресло занимает участок площадью
м2. Значит, площадь той части гостиной, на которой не будет смонтирован электрический подогрев пола, равна
м2.
Ответ: 3,36.
Задание 44
Найдите расстояние от журнального столика до стула (расстояние между двумя ближайшими точками по прямой) в метрах.
Решение.
Найдём расстояние между двумя ближайшими точками по прямой журнального столика и стула по теореме Пифагора:
Ответ: 2.
Задание 45
В гостиной предполагалось класть ламинат, но решили не экономить и покрыть пол паркетной доской. Ламинат и паркетная доска продаются только в упаковках. Каждая упаковка содержит одинаковое количество м2материала. Сколько рублей можно было бы сэкономить, если бы владелец решил покрыть пол ламинатом?
| Тип покрытия | Стоимость 0,16 м2 материала (руб.) |
Стоимость укладки 0,16 м2 материала (руб.) |
Количество материала в упаковке (м2) |
|---|---|---|---|
| Паркетная доска | 1400 | 500 | 0,64 |
| Ламинат | 440 | 160 | 0,48 |
Решение.
Найдём площадь гостиной:
м2.
Для того, чтобы покрыть пол в гостиной паркетной доской, требуется купить 27 упаковок материала. Стоимость 27 упаковок паркетной доски равна
рублей.
Стоимость укладки паркетной доски равна
рублей.
Всего на укладку пола в гостиной паркетной доской требуется
рублей.
Для того, чтобы покрыть пол в гостиной ламинатом, требуется купить 36 упаковок материала. Стоимость 36 упаковок ламината равна
рублей.
Стоимость укладки ламината равна
рублей.
Всего на укладку пола в гостиной ламинатом требуется
рублей.
Таким образом, удалось сэкономить
рублей.
Ответ: 140400.
При оплате услуг через платежный терминал
Дата: 2015-04-28
6765
Категория: ОкруглениеПроценты
Метка: №15-БАЗА
77352. При оплате услуг через платежный терминал взимается комиссия 5%. Терминал принимает суммы кратные 10 рублям. Аня хочет положить на счет своего мобильного телефона не меньше 300 рублей. Какую минимальную сумму она должна положить в приемное устройство данного терминала?
Определим, какую сумму необходимо внести, чтобы после списывания 5%, осталось 300 рублей. Учитываем, что 5% отнимается от вносимой суммы. Таким образом, вносимую сумму примем за х и она соответствует 100%. Сказано, что сумма после списывания пяти процентов составляет 300 рублей, то есть она соответствует 95%. Составляем пропорцию:
х рублей — 100%
300 рублей — 95%
То есть, необходимо внести минимум 315,78 рубля.
Данную сумму Аня внести не сможет, так как сказано, что терминал принимает суммы кратные 10 рублям. Значит минимальная сумма, которую Ане необходимо внести, чтобы поставленное условие было выполнено – это 320 рублей.
Действительно, 5% от 320 рублей это
То есть, комиссия составит 16 рублей и на счету у Ани будет 320–16=304 рубля, а это более 300. Условие выполняется.
Ответ: 320
Используя этот сайт, Вы соглашаетесь с тем, что мы сохраняем и используем файлы cookies, а также используем похожие технологии для улучшения работы сайта.
Ok
Страница 5 из 7
Практические задачи №1-5 к ОГЭ по математике
Прочитайте внимательно текст и выполните задания 1–5.
Хозяин дачного участка строит баню с парным отделением. Парное отделение имеет размеры: длина 3,5 м, ширина 2,2 м, высота 2 м. Окон в парном отделении нет, для доступа внутрь планируется дверь шириной 60 см, высота дверного проёма 1,8 м. Для прогрева парного отделения можно использовать электрическую или дровяную печь. В таблице представлены характеристики трёх печей.
|
Номер печи |
Тип |
Объём помещения (куб. м) |
Масса (кг) |
Стоимость (руб.) |
|
1 |
дровяная |
8–12 |
40 |
18 000 |
|
2 |
дровяная |
10–16 |
48 |
19 500 |
|
3 |
электрическая |
9–15,5 |
15 |
15 000 |
Для установки дровяной печи дополнительных затрат не потребуется. Установка электрической печи потребует подведения специального кабеля, что обойдётся в 6500 руб.
Задание 1.
Установите соответствие между массами и номерами печей.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Масса (кг) |
15 |
40 |
48 |
|
Номер печи |
Решение:
Ответ: 312
Задание 1.
Установите соответствие между стоимостями и номерами печей.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Стоимость (руб.) |
15 000 |
19 500 |
18 000 |
|
Номер печи |
Решение:
Ответ: 321
Задание 1.
Установите соответствие между объёмами помещения и номерами печей, для которых данный объём является наибольшим для отопления помещений.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Объём (куб. м) |
12 |
15,5 |
16 |
|
Номер печи |
Решение:
Ответ: 132
Задание 1.
Установите соответствие между объёмами помещения и номерами печей, для которых данный объём является наименьшим для отопления помещений.
Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.
|
Объём (куб. м) |
8 |
9 |
10 |
|
Номер печи |
Решение:
Ответ: 132
Задание 2.
Найдите объём парного отделения строящейся бани. Ответ дайте в кубических метрах.
Решение:
Парное отделение имеет размеры: длина 3,5 м, ширина 2,2 м, высота 2 м.
Объем парного отделения может быть вычислен по формуле: V=a * b * c, где a — ширина, b — длина, с — высота. Имеем: V=3,5 * 2,2 * 2 = 15,4м3.
Ответ: 15,4
Задание 2.
Найдите суммарную площадь стен парного отделения строящейся бани (без площади двери). Ответ дайте в квадратных метрах.
Решение:
Найдём площадь всех 4-х стен (2 длинных и 2 широких) парного отделения:
Sстен = 3,5·2 + 3,5·2 + 2,2·2 + 2,2·2 = 3,5·4 + 2,2·4 = 22,8 м
Окон нет, есть дверь, найдём её площадь:
Sдвери = 60 см·1,8 м = 0,6 м·1,8 м = 1,08 м
Вычтем от площади стен площадь двери:
S = Sстен – Sдвери = 22,8 – 1,08 = 21,72 м
Ответ: 21,72
Задание 2.
Найдите площадь потолка парного отделения строящейся бани. Ответ дайте в квадратных метрах.
Решение:
S=3,5*2,2=7,7м2
Ответ: 7,7
Задание 2.
Найдите площадь пола парного отделения строящейся бани. Ответ дайте в квадратных метрах.
Решение:
S=3,5*2,2=7,7м2
Ответ: 7,7
Задание 3.
На сколько рублей покупка дровяной печи, подходящей по объёму парного отделения, обойдётся дешевле электрической с учётом установки?
Решение:
Парное отделение имеет размеры: длина 3,5 м, ширина 2,2 м, высота 2 м.
Объем парного отделения может быть вычислен по формуле: V=a * b * c, где a — ширина, b — длина, с — высота. Имеем: V=3,5 * 2,2 * 2 = 15,4м3.
То есть надо брать печку за 19 500. А электрическая обойдется 15000 печка + потребует подведения специального кабеля, что обойдётся в 6500 руб. 21 500 руб.
21 500 — 19 500=2 000
Ответ: 2000
Задание 3.
На сколько рублей покупка дровяной печи, подходящей по объёму парного отделения, обойдётся дороже электрической без учёта установки?
Решение:
Парное отделение имеет размеры: длина 3,5 м, ширина 2,2 м, высота 2 м.
Объем парного отделения может быть вычислен по формуле: V= a * b * c, где a — ширина, b — длина, с — высота. Имеем: V=3,5 * 2,2 * 2 = 15,4м3.
То есть надо брать печку за 19 500. А электрическая обойдется 15000 печка.
19 500 — 15 000=4500
Ответ: 4500
Задание 3.
Во сколько рублей обойдётся покупка дровяной печи, подходящей по объёму парного отделения, с доставкой, если доставка печи до дачного участка будет стоить 1400 рублей?
Решение:
Парное отделение имеет размеры: длина 3,5 м, ширина 2,2 м, высота 2 м.
Объем парного отделения может быть вычислен по формуле: V= a * b * c, где a — ширина, b — длина, с — высота. Имеем: V=3,5 * 2,2 * 2 = 15,4м3.
То есть надо брать печку за 19 500. Доставка 1400. 19500+1400=20900
Ответ: 20900
Задание 3.
Во сколько рублей обойдётся покупка дровяной печи, подходящей по объёму парного отделения, с доставкой, если доставка печи до дачного участка будет стоить 1200 рублей?
Решение:
Парное отделение имеет размеры: длина 3,5 м, ширина 2,2 м, высота 2 м.
Объем парного отделения может быть вычислен по формуле: V= a * b * c, где a — ширина, b — длина, с — высота. Имеем: V=3,5 * 2,2 * 2 = 15,4м3.
То есть надо брать печку за 19 500. Доставка 1400. 19500+1200=20700
Ответ: 20700
Задание 3.
Во сколько рублей обойдётся покупка электрической печи с установкой и доставкой, если доставка печи до дачного участка будет стоить 1000 рублей?
Решение:
Парное отделение имеет размеры: длина 3,5 м, ширина 2,2 м, высота 2 м.
Объем парного отделения может быть вычислен по формуле: V= a * b * c, где a — ширина, b — длина, с — высота. Имеем: V=3,5 * 2,2 * 2 = 15,4м3.
То есть электрическая печка подойдет. 1500+1000=16 000
Ответ: 16 000
Задание 3.
Во сколько рублей обойдётся покупка электрической печи с установкой и доставкой, если доставка печи до дачного участка будет стоить 800 рублей?
Решение:
Парное отделение имеет размеры: длина 3,5 м, ширина 2,2 м, высота 2 м.
Объем парного отделения может быть вычислен по формуле: V= a * b * c, где a — ширина, b — длина, с — высота. Имеем: V=3,5 * 2,2 * 2 = 15,4м3.
То есть электрическая печка подойдет. 1500+8000=15 800
Ответ: 15800
Задание 4.
На дровяную печь, масса которой 40 кг, сделали скидку 10%. Сколько рублей стала стоить печь?
Решение:
18000-(18000*10)/100= 18000-1800=16 200
Ответ: 16200
Задание 4.
На дровяную печь, масса которой 48 кг, сделали скидку 10%. Сколько рублей стала стоить печь?
Решение:
19 500-(19 500*10)/100= 19500-1950=17550
Ответ: 17550
Задание 4.
На электрическую печь сделали скидку 15%. Сколько рублей стала стоить печь?
Решение:
15000-(15000*15)/100=15000-2250=12750 р.
Ответ: 12750
Задание 4.
В прошлом году печи, указанные в таблице, стоили дороже. На них были сделаны скидки: на печь номер 1 скидка составила 10%, на печь номер 2 — 35%, на печь номер 3 — 25%.
Сколько рублей стоила печь номер 1 в прошлом году?
Решение:
1-18000 18000-18000*10/100=16200
2-19500
3-15000
Ответ: 16200
Задание 4.
В прошлом году печи, указанные в таблице, стоили дороже. На них были сделаны скидки: на печь номер 1 скидка составила 10%, на печь номер 2 — 35%, на печь номер 3 — 25%.
Сколько рублей стоила печь номер 2 в прошлом году?
Решение:
1-18000
2-19500 19500-19500*35/100=19000-6650=12350
3-15000
Ответ: 12350
Задание 4.
В прошлом году печи, указанные в таблице, стоили дороже. На них были сделаны скидки: на печь номер 1 скидка составила 10%, на печь номер 2 — 35%, на печь номер 3 — 25%.
Сколько рублей стоила печь номер 3 в прошлом году?
Решение:
1-18000
2-19500
3-15000 15000-15000*25/100=15000-3750=11250
Ответ: 11250
Задание 4.
Доставка любой печи из магазина до участка стоит 1000 рублей. При покупке печи стоимостью больше 19 000 рублей магазин делает скидку 5% на товар
и 30% на доставку. Сколько рублей будет стоить покупка печи номер 2
с доставкой на этих условиях?
Решение:
2-19500
19500-19500*5/100+1000*70/100=18025+700=18725Ответ: 18725
Задание 4.
Доставка любой печи из магазина до участка стоит 1000 рублей. При покупке печи стоимостью больше 19 000 рублей магазин делает скидку 10% на товар и 25% на доставку. Сколько рублей будет стоить покупка печи номер 2 с доставкой на этих условиях?
Решение:
2-19500
19500-19500*10/100+1000*75/100=17550+750=18300
Ответ: 18300
Задание 4.
Доставка любой печи из магазина до участка стоит 1000 рублей. При покупке печи стоимостью больше 17 000 рублей магазин делает скидку 15% на товар и 20% на доставку. Сколько рублей будет стоить покупка печи номер 1
с доставкой на этих условиях?
Решение:
1-18000
18000-18000*15/100+1000*(100-20)/100=15300+800=16100
Ответ: 16100
Задание 4.
Доставка любой печи из магазина до участка стоит 1000 рублей. При покупке печи стоимостью больше 17 000 рублей магазин делает скидки 5% на товар
и 25% на доставку. Сколько рублей будет стоить покупка печи номер 1 с доставкой на этих условиях?
Решение:
1-18000
18000-18000*5/100+1000*(100-25)/100=17100+750=17850 р.
Ответ: 17850
8889B9
Задание 5.
Хозяин выбрал дровяную печь (рис. 1). Чертёж передней панели печи показан на рисунке 2.
Рис. 1
Рис. 2
Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке печки по дуге окружности с центром в середине нижней части кожуха (рис. 2).
Для установки печки хозяину понадобилось узнать радиус закругления арки R. Размеры кожуха в сантиметрах показаны на рисунке. Найдите радиус закругления арки в сантиметрах.
Решение:
Проведем радиус как показано на рисунке, но проведем его из центра нижней стороны в угол радиуса и боковой стороны. Получим прямоугольный треугольник, где гипотенуза будет нашим радиусом. По теореме Пифагора найдем радиус:
√ (442+332)=√ (1936+1089)=√ 3025=55
Ответ: 55
09D7F4
Задание 5.
Хозяин выбрал дровяную печь (рис. 1). Чертёж передней панели печи показан на рисунке 2.
Рис. 1
Рис. 2
Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке печки по дуге окружности с центром в середине нижней части кожуха (рис. 2).
Для установки печки хозяину понадобилось узнать радиус закругления арки R. Размеры кожуха в сантиметрах показаны на рисунке. Найдите радиус закругления арки в сантиметрах.
Решение:
Проведем радиус как показано на рисунке, но проведем его из центра нижней стороны в угол радиуса и боковой стороны. Получим прямоугольный треугольник, где гипотенуза будет нашим радиусом. По теореме Пифагора найдем радиус:
√ (402+302)=√ (1600+900)=√ 2500=50
Ответ: 50
59DCD0
Задание 5.
Хозяин выбрал дровяную печь (рис. 1). Чертёж передней панели печи показан на рисунке 2.
Рис. 1
Рис. 2
Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке печки по дуге окружности с центром в середине нижней части кожуха (рис. 2).
Для установки печки хозяину понадобилось узнать радиус закругления арки R. Размеры кожуха в сантиметрах показаны на рисунке. Найдите радиус закругления арки в сантиметрах.
Решение:
Проведем радиус как показано на рисунке, но проведем его из центра нижней стороны в угол радиуса и боковой стороны. Получим прямоугольный треугольник, где гипотенуза будет нашим радиусом. По теореме Пифагора найдем радиус:
√ (602+252)=√ (3600+625)=√ 4225=65
Ответ: 65
BE99C7
Задание 5.
Хозяин выбрал дровяную печь (рис. 1). Чертёж передней панели печи показан на рисунке 2.
Рис. 1
Рис. 2
Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке печки по дуге окружности с центром в середине нижней части кожуха (рис. 2).
Для установки печки хозяину понадобилось узнать радиус закругления арки R. Размеры кожуха в сантиметрах показаны на рисунке. Найдите радиус закругления арки в сантиметрах.
Решение:
Проведем радиус как показано на рисунке, но проведем его из центра нижней стороны в угол радиуса и боковой стороны. Получим прямоугольный треугольник, где гипотенуза будет нашим радиусом. По теореме Пифагора найдем радиус:
√ (602+322)=√ (3600+1024)=√ 4624=68
Ответ: 68
EF4A79
Задание 5.
Хозяин выбрал дровяную печь (рис. 1). Чертёж передней панели печи показан на рисунке 2.
Рис. 1
Рис. 2
Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке печки по дуге окружности с центром в середине нижней части кожуха (рис. 2).
Для установки печки хозяину понадобилось узнать радиус закругления арки R. Размеры кожуха в сантиметрах показаны на рисунке. Найдите радиус закругления арки в сантиметрах.
Решение:
Проведем радиус как показано на рисунке, но проведем его из центра нижней стороны в угол радиуса и боковой стороны. Получим прямоугольный треугольник, где гипотенуза будет нашим радиусом. По теореме Пифагора найдем радиус:
√ (602+322)=√ (3600+1024)=√ 4624=68
Ответ: 68
B65DB1
Задание 5.
Хозяин выбрал дровяную печь (рис. 1). Чертёж передней панели печи показан на рисунке 2.
Рис. 1
Рис. 2
Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке печки по дуге окружности с центром в середине нижней части кожуха (рис. 2).
Для установки печки хозяину понадобилось узнать радиус закругления арки R. Размеры кожуха в сантиметрах показаны на рисунке. Найдите радиус закругления арки в сантиметрах.
Решение:
Проведем радиус как показано на рисунке, но проведем его из центра нижней стороны в угол радиуса и боковой стороны. Получим прямоугольный треугольник, где гипотенуза будет нашим радиусом. По теореме Пифагора найдем радиус:
√ (452+242)=√ (2025+576)=√ 2601=51
Ответ: 51
4B7C1D
Задание 5.
Хозяин выбрал дровяную печь (рис. 1). Чертёж передней панели печи показан на рисунке 2.
Рис. 1
Рис. 2
Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке печки по дуге окружности с центром в середине нижней части кожуха (рис. 2).
Для установки печки хозяину понадобилось узнать радиус закругления арки R. Размеры кожуха в сантиметрах показаны на рисунке. Найдите радиус закругления арки в сантиметрах.
Решение:
Проведем радиус как показано на рисунке, но проведем его из центра нижней стороны в угол радиуса и боковой стороны. Получим прямоугольный треугольник, где гипотенуза будет нашим радиусом. По теореме Пифагора найдем радиус:
√ (482+202)=√ (2304+400)=√ 2704=52
Ответ: 52
D58214
Задание 5.
Хозяин выбрал дровяную печь (рис. 1). Чертёж передней панели печи показан на рисунке 2.
Рис. 1
Рис. 2
Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке печки по дуге окружности с центром в середине нижней части кожуха (рис. 2).
Для установки печки хозяину понадобилось узнать радиус закругления арки R. Размеры кожуха в сантиметрах показаны на рисунке. Найдите радиус закругления арки в сантиметрах.
Решение:
Проведем радиус как показано на рисунке, но проведем его из центра нижней стороны в угол радиуса и боковой стороны. Получим прямоугольный треугольник, где гипотенуза будет нашим радиусом. По теореме Пифагора найдем радиус:
√ (522+392) =√ (2704+1521) =√ 4225=65
Ответ: 65
BEAF28
Задание 5.
Хозяин выбрал дровяную печь (рис. 1). Чертёж передней панели печи показан на рисунке 2.
Рис. 1
Рис. 2
Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке печки по дуге окружности с центром в середине нижней части кожуха (рис. 2).
Для установки печки хозяину понадобилось узнать радиус закругления арки R. Размеры кожуха в сантиметрах показаны на рисунке. Найдите радиус закругления арки в сантиметрах.
Решение:
Проведем радиус как показано на рисунке, но проведем его из центра нижней стороны в угол радиуса и боковой стороны. Получим прямоугольный треугольник, где гипотенуза будет нашим радиусом. По теореме Пифагора найдем радиус:
√ (362+272)=√ (1296+729)=√ 2025=45
Ответ: 45
9825C3
Задание 5.
Хозяин выбрал дровяную печь (рис. 1). Чертёж передней панели печи показан на рисунке 2.
Рис. 1
Рис. 2
Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке печки по дуге окружности с центром в середине нижней части кожуха (рис. 2).
Для установки печки хозяину понадобилось узнать радиус закругления арки R. Размеры кожуха в сантиметрах показаны на рисунке. Найдите радиус закругления арки в сантиметрах.
Решение:
Проведем радиус как показано на рисунке, но проведем его из центра нижней стороны в угол радиуса и боковой стороны. Получим прямоугольный треугольник, где гипотенуза будет нашим радиусом. По теореме Пифагора найдем радиус:
√ (722+212)=√ (5184+441)=√ 5625=75
Ответ: 75
8EF36E