Кредит на 21 месяц егэ

В 2018 году на ЕГЭ по математике появились задачи, напугавшие многих выпускников. «Это страшно, — говорили они после экзамена. — Никогда такого не было. Решить невозможно».

Конечно же, я сочувствую абитуриентам, для которых ЕГЭ – все-таки большой стресс. Экзамен – это испытание не только знаний, но и хладнокровия, и способности действовать в сложной ситуации. И может быть, сказать себе: «Да, задача необычная, но я знаю общий подход к решению таких задач – справлюсь и на этот раз».

Действительно ли настолько страшны были «банковские» задачи на ЕГЭ по математике 2018 года? Они своеобразны. Их невозможно решить без подготовки, без знания того, как вообще устроены задачи ЕГЭ на кредиты.

Запомним: есть всего два характерных типа «банковских» задач, или задач на кредиты.

1 тип. Выплаты кредита производятся равными платежами. Эта схема еще называется «аннуитет». К первому типу относятся также все задачи, где известны платежи (или дана закономерность именно для платежей).

2 тип. Выплаты кредита подбираются так, что сумма долга уменьшается равномерно. Это так называемая «схема с дифференцированными платежами». Ко второму типу относятся также задачи, где известна закономерность уменьшения суммы долга.

О двух схемах решения задач на кредиты – мой краткий теоретический материал.

Более подробно я рассказываю теорию и решаю такие задачи на своих мастер-классах и интенсивах. Чтобы узнать о них, подпишись на нашу рассылку.

Посмотрим с этой точки зрения на «банковские» задачи ЕГЭ-2018.

1.

15-го декабря планируется взять кредит в банке на 21 месяц. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 20-й долг должен быть на 30 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 21-го месяца кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1604 тысяч рублей?

Прежде всего, введем переменные. Расчеты будем вести в тысячах рублей.

Пусть S – сумма, которую планируется взять в кредит,

Z – общая сумма выплат, Z = 1604 (тыс. рублей),

Х — ежемесячное уменьшение суммы долга, Х = 30 (тысяч рублей),

p=3% — процент, начисляемый банком ежемесячно.

После первого начисления процентов сумма долга равна После каждого начисления процентов сумма долга увеличивается в раза. В нашей задаче k = 1,03.

Определим, к какому типу относится задача. Долг уменьшается равномерно (по условию, 15-го числа каждого месяца с 1-го по 20-й долг должен быть на 30 тысяч рублей меньше долга на 15-е число предыдущего месяца). Значит, это задача второго типа. А в задачах второго типа мы рисуем следующую схему:

После первого начисления процентов сумма долга равна kS. Затем, после первой выплаты, сумма долга равна S – X, где Х = 30 (тысяч рублей).

Значит, первая выплата равна kS – (S – X) (смотри схему).

Вторая выплата: k (S – X ) – ( S – 2X).
…

Последняя выплата: k ( S – 20 X).

Найдем общую сумму выплат Z:

Z = kS – (S – X) + k (S – X ) – ( S – 2X) + … + k ( S – 20X) =
= k ( S + S – X + S – 2X + … + S – 20 X) – ( S – X + S – 2X + … + S – 20X).

Мы сгруппировали слагаемые, содержащие множитель k, и те, в которых нет k.

Упростим выражения в скобках:

k (21S – X (1 + 2 + 3+ … + 20)) – (20S – X (1 + 2 + 3+ … + 20)) = Z.

В задачах этого типа (когда сумма долга уменьшается равномерно) применяется формула для суммы арифметической прогрессии:

В этой задаче мы тоже ее используем:

Получим:

k (21 S – 210X ) – 20 S + 210 k = S (21k – 20) – 210 X (k-1) = Z.

Осталось подставить числовые значения:

S ( 21⋅ 1,03 – 20) – 210 ⋅ 30 ⋅ 0,03 = 1604.

Отсюда S = 1100 тысяч рублей = 1 100 000 рублей.

Следующая задача относится к тому же типу. Математическая модель та же самая. Только найти нужно другую величину – процент, начисляемый банком. К тому же количество месяцев, на которое взят кредит, неизвестно.

2.

15-го декабря планируется взять кредит в банке на 1 000 000 рублей на (n+1) месяц. Условия его возврата таковы:
—1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
— cо 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по n-й долг должен быть на 40 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— 15-го числа n-го месяца долг составит 200 тысяч рублей;
— к 15-му числу (n + 1)-го месяца кредит должен быть полностью погашен.
Найдите r, если известно, что общая сумма выплат после полного погашения кредита составит 1378 тысяч рублей.

Как всегда, введем обозначения. Для удобства ведем расчеты в тысячах рублей.

S = 1000000 рублей = 1000 (тыс. рублей) – сумма кредита,

Х = 40 (тыс. рублей) – ежемесячное уменьшение суммы долга,

Z = 1378 (тыс. рублей) – общая сумма выплат,

— коэффициент, показывающий, во сколько раз увеличилась сумма долга после начисления процентов.

Рисуем уже знакомую схему погашения кредита.

Первая выплата: kS – (S – X).

Вторая выплата: k (S – X ) – ( S – 2X).

…

Последняя выплата: k ( S – n X).

По условию, 15-го числа n-го месяца долг составит 200 тысяч рублей.

Значит, S – nX = 200. Подставим числовые данные:

1000 – 40 n = 200; тогда n = 20, n + 1 = 21, то есть кредит был взят на 21 месяц. Очень удобно – количество месяцев в этой задаче оказалось таким же, как в предыдущей. Поэтому очень кратко повторим основные моменты решения

Общая сумма выплат Z:

Z = kS – (S – X) + k (S – X ) – ( S – 2X) + … + k ( S – X) =
= k ( S + S – X + S – 2X + … + S – 20 X) – ( S – X + S – 2X + … + S – 20X) =
= k (21S – X (1 + 2 + 3+ … + 20)) – (20S – X (1 + 2 + 3+ … + 20)) =
= k (21 S – 210X ) – 20 S + 210 k = S (21k – 20) – 210 X (k-1).

Мы снова использовали ту же формулу для суммы арифметической прогрессии:

По условию, Z = 1378 (тыс. рублей).

Выразим k из формулы S (21k – 20) – 210 X (k-1) = Z:

Подставим данные из условия задачи.

Ответ: r = 3%.

Третья задача из числа «кошмаров» ЕГЭ-2018 по математике. Та же схема!

3.

15-го декабря планируется взять кредит в банке на сумму 300 тысяч рублей на 21 месяц. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 20-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;
— 15-го числа 20-го месяца долг составит 100 тысяч рублей;
— к 15-му числу 21-го месяца кредит должен быть полностью погашен.
Найдите общую сумму выплат после полного погашения кредита.

Тоже задача второго типа – есть информация об уменьшении суммы долга. Точно также будем вести расчеты в тысячах рублей.

Как всегда, введем обозначения. Для удобства ведем расчеты в тысячах рублей.

S = 300 (тыс. рублей) – сумма кредита,

n = 21 – количество месяцев,

r = 2%; ,

Х – ежемесячное уменьшение суммы долга,

Z – общая сумма выплат.

Рисуем ту же схему, что и в предыдущей задаче. По условию, 15-го числа 20-го месяца долг составит 100 тысяч рублей.

Значит, S – 20 X = 100. Подставив данные из условия, найдем, что Х = 10.

Точно так же считаем сумму выплат (смотри задачи 1 и 2).

Z = S (21k – 20) – 210 X (k-1).

Подставляем данные из условия: Z = 300 (21 ⋅ 1,02 – 20) – 210 ⋅ 10 ⋅ 0,02 = 384 (тыс. рублей).

Ответ: 384000 рублей.

Хочешь узнать решения всех сложных задач ЕГЭ? Подпишись на нашу рассылку.

4 июня 2018

В закладки

Обсудить

Разбор экономической задачи, которая вызвала затруднения у многих выпускников.

15 января планируется взять кредит в банке на некоторую сумму на 21 месяц. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на 1% по сравнению с концом предыдущего месяца;
— с 2-го по 14-е число каждого месяца необходимо выплатить одним платежом часть долга;
— на 15-е число каждого с 1-го по 20-й месяц долг должен уменьшаться на 50 тыс. руб.;
— за двадцать первый месяц долг должен быть погашен полностью.
Сколько тысяч рублей составляет долг на 15-е число 20-го месяца, если банку всего было выплачено 2073 тыс. рублей?

а) Долг на 1-е число месяца без учета процентной ставки:
1. S.
2. S-50.
3. S-100.
…
20. S-19⋅50.
21. S-20⋅50.

б) Выплачено до 15-го числа месяца:
1. (50 + S cdot frac{1}{{100}}).
2. (50 + left( {S — 50} right) cdot frac{1}{{100}}).
3. (50 + left( {S — 100} right) cdot frac{1}{{100}}).
…
20. (50 + left( {S — 19 cdot 50} right) cdot frac{1}{{100}}).
21. (left( {S — 1000} right) + left( {S — 1000} right) cdot frac{1}{{100}}).

в) Долг после 14-го числа месяца:
1. (S — 50).
2. (S — 100).
3. (S — 150).
…
20. (S — 20 cdot 50).
21. (0).

г) Складывая выплаты, получим:
(1000 + S — 1000 + frac{{21S}}{{100}} — frac{{left( {50 + 100 + ldots + 20 cdot 50} right)}}{{100}} = 2073.)
(121S = 207300 + 50 cdot frac{{1 + 20}}{2} cdot 20 = 217800,;;S = 1800.)

Требуется найти (S — 1000 = 800).

Ответ: 800 тыс. рублей.

Условие

Решение

Написать комментарий

варианты егэ 2018 математика профиль 1 июня Задание 17 (17.1)

1 июня Задача 17 (прототип 17.1) № задачи в базе 1124

15 января планируется взять кредит в банке на некоторую сумму на 21 месяц. Условия его возврата таковы: 1 числа каждого месяца долг увеличивается на 1% по сравнению с концом предыдущего месяца; с 2 по 14 число каждого месяца необходимо выплатить одним платежом часть долга; на 15 число каждого с 1 по 20 месяц долг должен уменьшаться на 40 тыс.руб.; за 21-й месяц долг должен быть погашен полностью.
Сколько тысяч рублей составляет долг на 15 число 20-го месяца, если банку всего было выплачено 1852 тыс. рублей?

Ответ: 800

ФИПИ 2023 🔥 …

Примечание: варианты егэ 2018 математика профиль 1 июня Задание 17 (17.1)! 1 июня Задача 17 (прототип 17.1)

Рейтинг сложности задачи:

Задача 1

15 января планируется взять кредит в банке на 16 месяцев. Условия возврата таковы:

• 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
• со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
• 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.

Какую сумму следует взять в кредит, чтобы общая сумма выплат после полного погашения равнялась 2,34 млн рублей?

Дано:

S — кредит

n = 16 месяцев

r = 2%

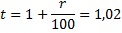
2,34 млн рублей — общая сумма выплат

Найти:

S — ?

Решение:

Долг	Долг с %	Выплаты
	St
…	…	…
	—	—

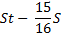
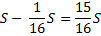
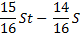
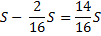
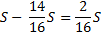
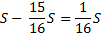
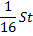
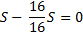
По условиям задачи, общая сумма выплат после полного погашения кредита равна 2,34 млн рублей.

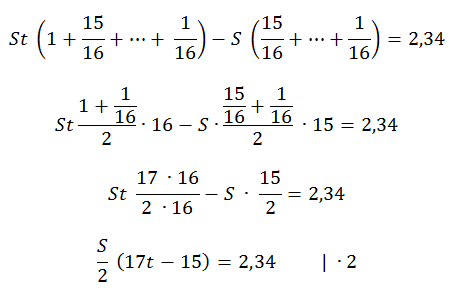
S (17t — 15) = 4,68

Подставим в полученное выражение известное значение t.

S (17 • 1,02 — 15) = 4,68

2,34 S = 4,68

S = 2 (млн рублей)

Ответ: 2 млн рублей

Задача 2

15-го января планируется взять кредит в банке на сумму 2,4 млн рублей на 24 месяца. Условия возврата таковы:

• 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
• со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
• 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.

Какую сумму нужно выплатить банку в первые 12 месяцев?

Дано:

S = 2,4 млн рублей

n = 24 месяца

r = 3%

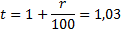
Найти:

Общую сумму выплат за первые 12 месяцев.

Решение:

Долг	Долг с %	Выплаты
	St
…	…	…
…	…	…
	—	—

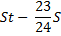
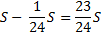
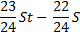
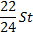
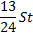
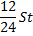
Найдем общую сумму выплат за первые 12 месяцев.

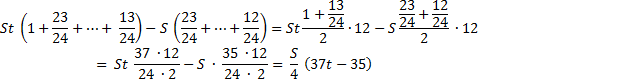
Подставим в полученное выражение значения известных переменных.

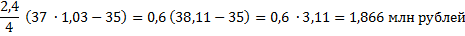
Ответ: 1,866 млн рублей

Задача 3

15-го декабря планируется взять кредит в банке на 21 месяц. Условия возврата таковы:

• 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
• со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
• 15-го числа каждого месяца с 1-го по 20-й долг должен быть на 30 тысяч рублей меньше долга на 15-е число предыдущего месяца;
• к 15-му числу 21-го месяца кредит должен быть полностью погашен.

Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1604 тысяч рублей?

Дано:

S тыс. рублей: кредит

n = 21 месяц

r = 3%

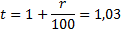
Общая сумма выплат равна 1604 тыс. руб.

Найти:

S — ?

Решение:

Долг	Долг с %	Выплаты
S — 0 • 30	tS	1) tS — (S — 1 • 30)
S — 1 • 30	t (S — 1 • 30)	2) t(S — 1 • 30) — (S — 2 • 30)
S — 2 • 30	t (S — 2 • 30)	3) t(S — 2 • 30) — (S — 3 • 30)
S — 3 • 30	t (S — 3 • 30)	4) t(S — 3 • 30) — (S — 4 • 30)
…	…	…
S — 18 • 30	t (S — 18 • 30)	19) t(S — 18 • 30) — (S — 19 • 30)
S — 19 • 30	t (S — 19 • 30)	20) t(S — 19 • 30) — (S — 20 • 30)
S — 20 • 30	t (S — 20 • 30)	21) t(S — 20 • 30) — 0
0

По условию задачи известно, что общая сумма выплат равна 1604 тыс. рублей.

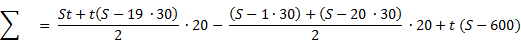
1) (St + St — 570t) • 10 — (2S — 630) • 10 + St — 600t = 20St — 5700t — 20S +6300 + St — 600t = 21St — 20S + 6300 — 5700t = 21 • 1,03S — 20S + 6300 — 5700 • 1,03 = 21,63S — 20S +6300 — 6489 = 1,63S — 189

2) Выплаты составили 1604 тыс. рублей:

1,63S — 189 = 1604

1,63S = 1793

S = 1100 тыс. рублей

Ответ: 1100 тыс. рублей.

Задача 4

15-го декабря планируется взять кредит в банке на 1200 тысяч рублей на (n + 1) месяц. Условия возврата таковы:

• 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
• cо 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
• 15-го числа каждого месяца с 1-го по n-й долг должен быть на 80 тысяч рублей меньше долга на 15-е число предыдущего месяца;
• 15-го числа n-го месяца долг составит 400 тысяч рублей;
• к 15-му числу (n+1)-го месяца кредит должен быть полностью погашен.

Найдите r, если известно, что общая сумма выплат после полного погашения кредита составит 1288 тысяч рублей.

Дано:

S = 1200 тыс. рублей (кредит)

n + 1 месяц — срок кредитования

r%

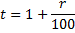
С 1-го по n-ный месяц долг уменьшается на 80 тыс. рублей.

15-го числа n-го месяца долг составит 400 тыс. рублей.

Общая сумма выплат составляет 1288 тыс. рублей (после полного погашения кредита).

Найти:

r — ?

Решение:

Долг	Долг с %	Выплаты
S — 0 • 80	t • S	1) tS — (S — 1 • 80)
S — 1 • 80	t (S — 1 • 80)	2) t(S — 1 • 80) — (S — 2 • 80)
S — 2 • 80	t (S — 2 • 80)	3) t(S — 2 • 80) — (S — 3 • 80)
S — 3 • 80	t (S — 3 • 80)
…	…	…
S — (n — 1) • 80	t (S — (n — 1) • 80)	n) t(S — (n — 1) • 80) — (S — n • 80)
S — n • 80	t (S — n • 80)	n + 1) t(S — n • 80) — 0
0

1) 15 числа n-го месяца долг составляет 400 тыс. рублей:

S — n • 80 = 400

1200 — n • 80 = 400

n • 80 = 800

n = 10

2) Общая сумма выплат составляет 1288 тыс. рублей.

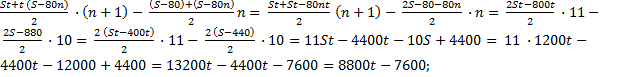
8800t — 7600 = 1288

8800t = 8888

t = 1,01

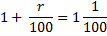
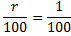
r = 1%

Ответ: 1%

Задача 5

В июле планируется взять кредит в банке на сумму 5 млн рублей на некоторый срок (целое число лет). Условия возврата таковы:

• каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
• с февраля по июнь каждого года необходимо выплатить часть долга;
• в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.

На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 7,5 млн рублей?

Дано:

S = 5 млн руб. (кредит)

r = 20%,

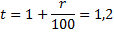
Общая сумма выплат после полного погашения кредита составит 7,5 млн. руб.

Найти:

n — ? (число лет)

Решение:

1)

Долг	Долг с %	Выплаты
	St
…	…	…
	—	—

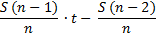
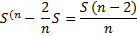
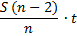
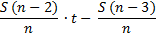
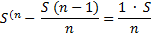
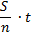
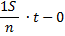
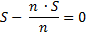
По формуле суммы арифметической прогрессии получим:

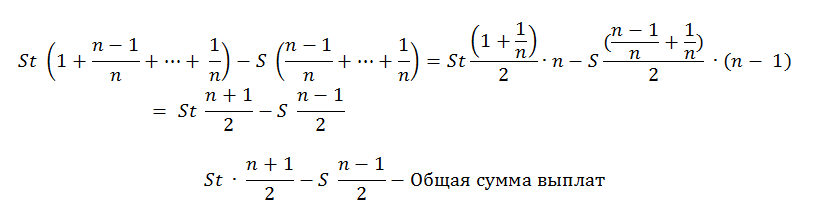
2) По условию задачи известно, что общая сумма выплат после полного погашения кредита составит 7,5 млн рублей, тогда:

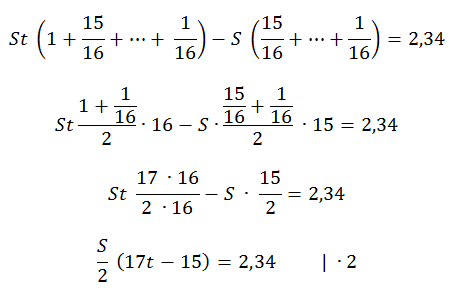
0,2n + 2,2 = 3

0,2n = 0,8

n = 4

4 года — на столько лет планируется взять кредит.

Ответ: 4

Задача 6

15-го января планируется взять кредит в банке на девять месяцев. Условия возврата таковы:

• 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;
• со 2-го по 14-е число месяца необходимо выплатить часть долга;
• 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.

Известно, что общая сумма выплат после полного погашения кредита на 25% больше суммы, взятой в кредит. Найдите r.

Дано:

S — кредит

n = 9 месяцев

r = r%

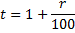
Со 2-го по 14-е число месяца необходимо выплатить часть долга.

15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.

Общая сумма выплат по кредиту на 25% больше суммы, взятой в кредит.

Найти:

r — ?

Решение:

Долг	Долг с %	Выплаты
	St
…	…	…
	—	—

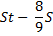
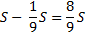
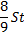
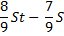
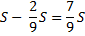
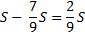
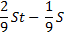
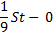
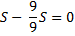
1) Найдем общую сумму выплат:

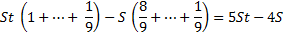
2) По условию задачи известно, что общая сумма выплат на 25% больше суммы, взятой в кредит:

S — 100%

(5St — 4S) — 125%

100 (5St — 4S) = 125S

500St — 400S = 125S

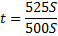
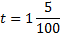
3)

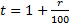
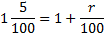
r = 5%

Ответ: 5%

Задача 7

15-го января планируется взять кредит в банке на 18 месяцев. Условия возврата таковы:

• 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
• со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
• 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.

Сколько процентов от суммы кредита составляет общая сумма денег, которую нужно выплатить банку за весь срок кредитования?

Дано:

S — кредит

n = 18 месяцев

r = 2%

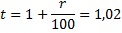
Долг уменьшается на одну и ту же сумму.

Сколько процентов от суммы кредита составляет общая сумма денег, которую нужно выплатить банку за весь срок кредитования?

Решение:

Долг	Долг с %	Выплаты
	St
		…
…	…	…

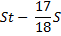
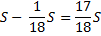
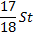
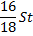
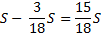
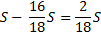
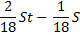
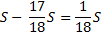
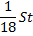
1) По формуле суммы арифметической прогрессии получим:

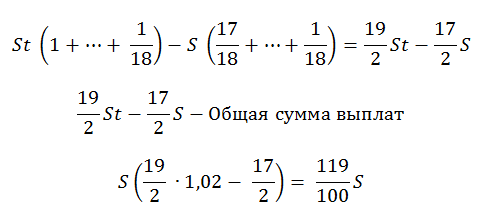
2) S — 100%

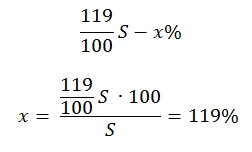
— столько процентов от суммы кредита составляет общая сумма денег, которую нужно выплатить банку за весь срок кредитования.

Ответ: 119%

Задача 8

15-го декабря планируется взять кредит в банке на 1 млн рублей на 6 месяцев. Условия возврата таковы:

• 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца, где r — целое число;
• со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
• 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.

Найдите наибольшее значение r, при котором общая сумма выплат будет составлять менее 1,7 млн рублей.

Дано:

S = 1 млн рублей (кредит)

n = 6 месяцев

Дата	15.01	15.02	15.03	15.04	15.05	15.06	15.07
Долг	1	0,7	0,6	0,4	0,2	0,1	0

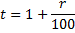
Найти:

Наибольшее значение r, при котором общая сумма выплат будет составлять менее 1,7 млн рублей.

Решение:

1)

Долг	Долг с %	Выплаты
1	1t	1t — 0,7
0,7	0,7t	0,7t — 0,6
0,6	0,6t	0,6t — 0,4
0,4	0,4t	0,4t — 0,2
0,2	0,2t	0,2t — 0,1
0,1	0,1t	0,1t — 0
0	—	—

Найдем общую сумму выплат:

t (1 + 0,7 + 0,6 + 0,4 + 0,2 + 0,1) — (0,7 + 0,6 + 0,4 + 0,2 + 0,1) = 3t — 2

3t — 2 — общая сумма выплат.

2) По условию задачи известно, что общая сумма выплат будет меньше 1,7 млн рублей:

3t — 2 < 1,7

3t < 3,7

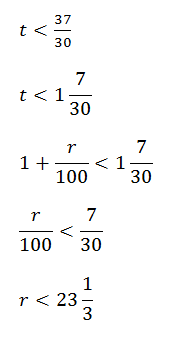
Наибольшее целое число этого неравенства r = 23%

Ответ: 23%

Задача 9

15 декабря планируется взять кредит в банке на сумму 300 тысяч рублей на 21 месяц. Условия возврата таковы:

• 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
• со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
• 15-го числа каждого месяца с 1-го по 20-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;
• 15-го числа 20-го месяца долг составит 100 тысяч рублей;
• к 15-му числу 21-го месяца кредит должен быть полностью погашен.

Найдите общую сумму выплат после полного погашения кредита.

Дано:

S = 300 тыс. руб. (кредит)

n = 21 месяц

r = 2%

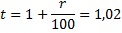
15-го числа 20-го месяца долг составит 100 тыс. рублей.

Найти:

Общую сумму выплат.

Решение:

Пусть х тыс. рублей — ежемесячный равный платеж.

Долг	Долг с %	Выплаты
S — 0 • x	t (S — 0 • x)	1) t (S — 0 • x) — (S — 1x)
S — 1 • x	t (S — 1 • x)	2) t (S — 1 • x) — (S — 2x)
S — 2 • x	t (S — 2 • x)	3) t (S — 2 • x) — (S — 3x)
S — 3 • x	t (S — 3 • x)
…	…	…
18) S — 18x	t (S — 18 • x)	19) t (S — 18 • x) — (S — 19x)
19) S — 19x	t (S — 19 • x)	20) t (S — 19 • x) — (S — 20x)
20) S — 20x	t (S — 20 • x)	21) t (S — 20 • x) — 0
0

1) По условиям задачи известно, что 15-го числа 20-го месяца долг составит 100 тыс. рублей:

S — 20x = 100

300 — 20x = 100

20x = 200

X = 10 тыс. рублей

2) Найдем общую сумму выплат:

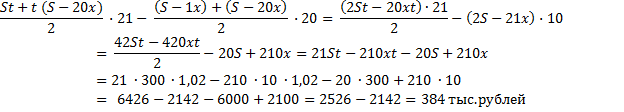
Ответ: 384 тыс. рублей.

---

#ADVERTISING_INSERT#