Под
криптографической
защитой информации
понимается такое преобразование исходной
информации, в результате которого она
становится недоступной для ознакомления
и использования лицами, не имеющими на
это полномочий.
Методы криптографического
преобразования информации:
— шифрование;
— стеганография;
— кодирование;
— сжатие.
Шифрование
– проведение
обратимых математических, логических,
комбинаторных и других преобразований
исходной информации, в результате
которых зашифрованная информация
представляет собой хаотический набор
букв, цифр, других символов и двоичных
кодов.
Для
шифрования используются алгоритм
преобразования и ключ. Как правило,
алгоритм преобразования для определенного
метода шифрования является неизменным.
Ключ содержит управляющую информацию,
которая определяет выбор преобразования
на определенных шагах алгоритма и
величины операндов, используемые при
реализации алгоритма шифрования.
Методы
стеганографии
позволяют
скрыть не только смысл хранящейся или
передаваемой информации, но и сам факт
хранения или передачи закрытой информации
(в КС этот метод только начинает
реализовываться). В основе всех методов
стеганографии лежит маскирование
закрытой информации среди открытых
файлов.
Современные методы
шифрования должны отвечать следующим
требованиям:
— стойкость шифра
противостоять криптоанализу
(криптостойкость) должна быть такой,
чтобы вскрытие его могло быть осуществлено
только путем решения задачи полного
перебора ключей;
—
криптостойкость обеспечивается не
секретностью алгоритмов шифрования, а
секретностью ключа;
—
шифротекст не должен существенно
превосходить по объему исходную
информацию;
— ошибки, возникающие
при шифровании, не должны приводить к
искажениям и потерям информации;
— время шифрования
не должно быть большим;
—
стоимость шифрования должна быть
согласована со стоимостью закрываемой
информации.
Методы
шифрования с симметричным ключом:
— методы замены;
— методы перестановки;
— аналитические
методы шифрования;
— аддитивные методы
шифрования.
Системы
шифрования с открытым ключом
– используют два ключа. Информация
шифруется с помощью открытого ключа, а
расшифровывается с использованием
секретного ключа.
Кодирование
– замена смысловых конструкций исходной
информации (слов, предложений) кодами.
В качестве кодов могут использоваться
сочетания букв, цифр, букв и цифр. При
кодировании и обратном преобразовании
используются специальные таблицы или
словари.
Кодирование
информации целесообразно применять в
системах с ограниченным набором смысловых
конструкций. Недостаток – необходимость
хранения и распространения кодировочных
таблиц, которые необходимо часто менять,
чтобы избежать раскрытия кодов
статистическими методами обработки
перехваченных сообщений.
Сжатие
– представляет сокращение объема
информации (с определенными оговорками
может быть отнесено к криптографическим
методам). Сжатая информация не может
быть прочитана или использована без
обратного преобразования (учитывая
доступность средств сжатия и обратного
преобразования, эти методы нельзя
рассматривать как надежные средства
криптографического преобразования
информации).
Сжатые
файлы конфиденциальной информации
подвергаются последующему шифрованию.
Для сокращения времени целесообразно
совмещать процесс сжатия и шифрования
информации.
Перспективным
направлением развития криптозащиты
информации является стеганография.
Комплексное использование стеганографии
и шифрования намного повышает
криптостойкость закрытой информации.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Форма обучения:
дистанционная
Стоимость самостоятельного обучения:
бесплатно
В курсе дан необходимый теоретический минимум по основным вопросам современной криптографии.
Дополнительные курсы
Основы теории чисел
В первой лекции мы приводим основные понятия теории чисел. Вводим определение сравнимости по модулю и формулируем основные свойства сравнений. Таким образом мы подготавливаем учащегося к освоению собственно криптографических тем.
—
Алгоритмы тестирования на простоту и факторизации
Для построения многих систем защиты информации требуются простые числа большой разрядности. В связи с этим актуальной является задача тестирования на простоту натуральных чисел. В лекции 2 рассматриваются тесты техника компьютерных вычислений с многоразрядными числами.
—
Алгебраические системы
Изложены основные понятия современной алгебры. Этот материал нужен для понимания алгоритмов шифрования, представленных в следующих лекциях.
—
Эллиптические кривые
Теория эллиптических кривых в настоящее время развивается во многих направлениях. Одновременно такие кривые получают все большее применение в защите информации. Так, действующий в Российской Федерации стандарт электронной подписи основан на свойствах группы точек эллиптической кривой над конечным полем. В лекции 4 вводится операция над точками такой кривой, примеры вычислений суммы точек.
—
Классические шифры
Рассматриваются исторические шифры: перестановка строк текста, простая замена, шифр Виженера. Приведены примеры композиционных шифров. Этот материал полезен тем, что иллюстрирует основные идеи криптографии. Современные сложные шифры так или иначе используют те же идеи, что и исторические (классические) шифры.
—
Современные симметричные алгоритмы шифрования
Из большого множества современных алгоритмов шифрования мы выбрали такие, которые иллюстрируют применение различных математических конструкций. В лекции представлены алгоритмы: DES, ГОСТ 28147-89, AES, IDEA. Алгоритм DES был первым, открыто опубликованным алгоритмом, послужил основой для разработки методов криптоанализа. Алгоритм ГОСТ 28147-89 и в настоящее время используется в России. Алгоритм AES интересен тем, что построен на своеобразной, весьма нетривиальной математике полей Галуа. Наконец, IDEA примечателен тем, что соединяет в себе разные алгебраические конструкции.
—
Алгоритмы с открытыми ключами
Рассмотрены наиболее популярные алгоритмы с открытым ключом. В частности, алгоритм RSA, применяемый в банковской сфере, интересен своими особенностями, обусловленными результатами теории чисел. Рюкзачное шифрование и вероятностное шифрование также основаны на достаточно тонких теоретико-числовых фактах. Приведена криптосистема на эллиптических кривых(одна из возможных).
—
Хэш-функции и электронная подпись
Рассмотрены хэш-функции и алгоритмы подписи. Реально действующие в настоящее время хэш-функции являются сложными для первоначального ознакомления, вместе с тем, идейная сторона таких функций довольна прозрачна. Для введения учащегося в круг идей и методов построения хэш-функций и подписи приводим учебные алгоритмы хэширования. Далее достаточно подробно представлен алгоритм подписи на основе эллиптических кривых. Изучение этого алгоритма будет полезно для подготовки к использованию подписи по действующему стандарту РФ.
—
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
ВЕЧЕРОК
или
ШАШЛЫКИ
— устойчивее к действию этой программы?
Определить, является ли число 5618014398241046527 простым с вероятностью не меньше 0,999.
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1101000001101110011110000.
, построить контрольную сумму для сообщения 1101000001101110011110000.
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=43, n2=29, x=10.
Чей компьютер он взломает быстрее?
Определить, является ли число 36413321723440003717 простым с вероятностью не меньше 0,999.
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1011110001000101010010111.
, построить контрольную сумму для сообщения 1011110001000101010010111.
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=23, n2=41, x=20.
Чей компьютер он взломает быстрее?
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
КОШКА
или
МЫШКА
— устойчивее к действию этой программы?
Найти корреляционную матрицу блока замен 5 11 13 14 2 1 10 0 6 15 8 12 7 4 3 9 размерностью  бит
бит
Зашифруйте открытый текст УВЕРОВАТЬ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(425, 663), значения случайных чисел для букв открытого текста k: 6, 14, 5, 7, 12, 11, 4, 9, 19, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 5431. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 39, значения цифровой подписи: r = 50; s = 42. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 8832. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 31, значения цифровой подписи: r = 47; s = 41. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Проверьте подлинность ЭЦП (11, 11) для сообщения с известным значением хэш-свертки 7, зная открытый ключ проверки подписи (455, 368). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Проверить действительность подписей (224, 158), (11, 133) для сообщения с известным значением хэш-свертки 63 и открытым ключом проверки (110,50). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Проверьте подлинность ЭЦП (11, 6) для сообщения с известным значением хэш-свертки 10, зная открытый ключ проверки подписи (455, 368). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Найти корреляционную матрицу блока замен 5 10 4 7 12 3 2 8 6 1 9 11 0 14 13 15 размерностью  бит
бит
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1101001101101010111011101.
, построить контрольную сумму для сообщения 1101001101101010111011101.
Вычислить динамическое расстояние порядка 1 булевой функции 00000011 от 3 переменных
С помощью  -алгоритма Полларда найти наибольший нетривиальный делитель числа 3007.
-алгоритма Полларда найти наибольший нетривиальный делитель числа 3007.
Вычислить нелинейность булевой функции 01011110 от 3 переменных
Найти произвольный квадратичный невычет по модулю 293
Решить сравнение  с помощью цепных дробей.
с помощью цепных дробей.
Зашифровать биграмму ЛИ с помощью матрицы  ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=24 и k=5 системы цифровой подписи и подписываемый текст РОД. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст ДЕНЬГИ.
Расшифровать сообщение на английском языке 6-4.txt, зашифрованное шифром Виженера, Длина ключа равна 3.
В ответ введите ключ.
.
Решить сравнение  с помощью индексов.
с помощью индексов.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=8, зная секретный ключ подписи d=2 при данном значении выбираемого случайным образом числа k=5. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Расшифровать сообщение 5-14.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Вычислить динамическое расстояние порядка (2,2) блока замен 5 10 4 7 12 3 2 8 6 1 9 11 0 14 13 15 размерностью  бит
бит
Найти остаток от деления  на 45.
на 45.
Решить систему сравнений:
Найти наибольший квадратный корень из 169 по модулю 269.
Найти наибольший квадратный корень из 10 по примарному модулю 81.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=28 и k=7 системы цифровой подписи и подписываемый текст ОВАЛ. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Шифртекст (671410783, 10111110100000010011) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=99439, q=98327. Найти открытый текст и введите его заглавными буквами.
Расшифровать текст 3-13.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите второе слово заглавными буквами.
Решить следующее сравнение  .
.
Применением цепных дробей найти секретный ключ d и разложение модуля 95841214023781 (экспонента — 2005229) на множители. В ответе укажите секретный ключ.
Шифротекст УПК_ИАКМРАНЫОХ_ЕБЛИ_СО_ЬЛ получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Решить в целых числах уравнение  . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)
Решить следующее сравнение  .
.
Решить сравнение  с помощью цепных дробей.
с помощью цепных дробей.
Решить систему сравнений:
Решить сравнение  с помощью индексов. (В качестве ответа введите наименьшее значение x.)
с помощью индексов. (В качестве ответа введите наименьшее значение x.)
Найти остаток от деления  на 13.
на 13.
Вычислить значение  при a = 5124; b = 129; c = 59466.
при a = 5124; b = 129; c = 59466.
С помощью  -алгоритма Полларда найти наибольший нетривиальный делитель числа 3649.
-алгоритма Полларда найти наибольший нетривиальный делитель числа 3649.
Найти произвольный квадратичный невычет по модулю 337
Найти наименьший квадратный корень из 186 по модулю 239.
Найти наименьший квадратный корень из 24 по примарному модулю 25.
Найти количество квадратных корней из 120 по непримарному составному модулю 4199.
Найти число элементов порядка 495 в циклической группе порядка 5545.
Найти дискретный логарифм числа 30 по основанию 6 по модулю 103951.
Вычислить порядок точки (24, 14) кривой  порядка 25.
порядка 25.
Шифротекст ТОЮКЛИЧ_ТЕТОЕ_СИТО_МИНРТО получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Расшифровать фразу ИМНЕ_ЯВСТ_СОБЩО_РЕМВРЧИ_Е, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Расшифровать текст 3-3.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите третье слово заглавными буквами.
Расшифровать сообщение 4-19.txt, зашифрованное шифром Виженера, Длина ключа равна 4, пробел является частью алфавита.
В ответ введите ключ.
.
Расшифровать сообщение 5-6.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Расшифровать сообщение на английском языке 6-17.txt, зашифрованное шифром Виженера, Длина ключа равна 5.
В ответ введите ключ.
.
Зашифровать биграмму БЕ с помощью матрицы  ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст НЕПТУН.
Вычислить нелинейность булевой функции 00101101 от 3 переменных
Вычислить динамическое расстояние порядка 1 булевой функции 01011110 от 3 переменных
Вычислить нелинейность блока замен 5 2 14 10 8 7 15 11 13 4 3 9 12 6 1 0 размерностью  бит
бит
Вычислить динамическое расстояние порядка (2,2) блока замен 1 9 12 14 2 11 13 10 8 6 15 5 0 7 4 3 размерностью  бит
бит
Провести операцию SubBytes алгоритма AES со значением байта BA.
Провести операцию MixColumns над приведенным ниже столбцом состояния
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
Провести первый раунд зашифрования открытого текста D352 FEAC D98D AC8E шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Дано: модуль шифрования N = 4559, открытый ключ e = 17. Найти значение шифртекста, полученного при зашифровании открытого текста 946 на открытом ключе (N, e) по алгоритму RSA.
Даны значения модуля шифрования N = 323 и открытого ключа e = 131. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 321.
Даны значения модуля шифрования N = 3713 и открытого ключа e = 3359. Используя метод факторизации Ферма, найти значение закрытого ключа.
Дан шифртекст 117, а также значения модуля шифрования N = 143 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Сообщение 762 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {3,6,11,21,43,85,171}, m=343 и n=43. В ответе укажите исходное сообщение.
Шифртекст (5978393092, 10001100110111000010) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=92779, q=90127. Найти открытый текст и введите его заглавными буквами.
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(618, 206), (294, 595)}; {(188, 93), (13, 617)}; |
| {(188, 93), (206, 106)}; {(188, 93), (67, 667)}; |
| {(56, 419), (350, 184)}; {(440, 539), (275, 456)}; |
| {(745, 210), (301, 17)}; {(346, 242), (588, 707)}; |
| {(188, 93), (256, 121)}; {(425, 663), (209, 82)}; |
| {(16, 416), (687, 660)} |
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=55 и k=19 системы цифровой подписи и подписываемый текст РУЛЬ. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=18 и k=37 системы цифровой подписи и подписываемый текст СХОД. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=11, зная секретный ключ подписи d=2 при данном значении выбираемого случайным образом числа k=8. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=10, зная секретный ключ подписи d=9 при данном значении выбираемого случайным образом числа k=11. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=6, зная секретный ключ подписи d=10 при данном значении выбираемого случайным образом числа k=2. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Дано: модуль шифрования N = 4087, открытый ключ e = 13. Найти значение шифртекста, полученного при зашифровании открытого текста 146 на открытом ключе (N, e) по алгоритму RSA.
Вычислить динамическое расстояние порядка 1 булевой функции 00011010 от 3 переменных
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=8 и k=35 системы цифровой подписи и подписываемый текст МЕЧ. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Вычислить нелинейность булевой функции 00110001 от 3 переменных
Провести операцию MixColumns над приведенным ниже столбцом состояния
Даны значения модуля шифрования N = 319 и открытого ключа e = 33. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 198.
Решить следующее сравнение  .
.
С помощью  -алгоритма Полларда найти наибольший нетривиальный делитель числа 2573.
-алгоритма Полларда найти наибольший нетривиальный делитель числа 2573.
Применением цепных дробей найти секретный ключ d и разложение модуля 89318473363897 (экспонента — 2227661) на множители. В ответе укажите секретный ключ.
Зашифровать биграмму ША с помощью матрицы  ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.
Найти наибольший квадратный корень из 156 по модулю 277.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=9 и k=25 системы цифровой подписи и подписываемый текст ХОД. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Сообщение 553 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {4,7,12,25,49,98,197}, m=395 и n=61. В ответе укажите исходное сообщение.
Расшифровать сообщение 5-9.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Решить систему сравнений:
Решить следующее сравнение  . (В качестве ответа введите наименьшее значение x.)
. (В качестве ответа введите наименьшее значение x.)
Найти наименьший квадратный корень из 155 по модулю 307.
Шифротекст ИРЕМЗЬО_ЕТСНВОНУАЧ_ЮСУТОТ получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Определить, является ли число 29497513910652490397 простым с вероятностью не меньше 0,999.
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
Вычислить динамическое расстояние порядка 1 булевой функции 00000001 от 3 переменных
Вычислить порядок точки (31, 15) кривой  порядка 38.
порядка 38.
Даны значения модуля шифрования N = 391 и открытого ключа e = 145. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 173.
Найти количество квадратных корней из 7226 по непримарному составному модулю 7429.
Применением цепных дробей найти секретный ключ d и разложение модуля 74701165267919 (экспонента — 3145553) на множители. В ответе укажите секретный ключ.
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(16, 416), (128, 672)}; {(56, 419), (59, 386)}; |
| {(425, 663), (106, 24)}; {(568, 355), (145, 608)}; |
| {(188, 93), (279, 398)}; {(425, 663), (99, 295)}; |
| {(179, 275), (269, 187)}; {(188, 93), (395, 337)}; |
| {(188, 93), (311, 68)}; {(135, 82), (556, 484)}; |
| {(56, 419), (106, 727)}; {(16, 416), (307, 693)} |
Провести первый раунд зашифрования открытого текста D12F 992B B2AD C9BA шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Вычислить значение  при a = 8727; b = 948; c = 46329.
при a = 8727; b = 948; c = 46329.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 7256. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 51, значения цифровой подписи: r = 41; s = 44. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Решить сравнение  с помощью индексов.
с помощью индексов.
Шифртекст (7764435203, 10010100111100010011) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=93151, q=94483. Найти открытый текст и введите его заглавными буквами.
Дан шифртекст 86, а также значения модуля шифрования N = 323 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Проверить действительность подписей (106, 108), (35, 44) для сообщения с известным значением хэш-свертки 166 и открытым ключом проверки (436,660). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Провести операцию SubBytes алгоритма AES со значением байта D0.
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст КРИКЕТ.
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=31, n2=37, x=10.
Чей компьютер он взломает быстрее?
Провести операцию MixColumns над приведенным ниже столбцом состояния
Найти остаток от деления  на 60.
на 60.
Решить в целых числах уравнение  . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)
Решить следующее сравнение  .
.
Решить сравнение  с помощью цепных дробей.
с помощью цепных дробей.
Решить систему сравнений:
Решить сравнение  с помощью индексов. (В качестве ответа введите наименьшее значение x.)
с помощью индексов. (В качестве ответа введите наименьшее значение x.)
Найти остаток от деления  на 100.
на 100.
Вычислить значение  при a = 3568; b = 229; c = 63339.
при a = 3568; b = 229; c = 63339.
Определить, является ли число 40206835204840513073 простым с вероятностью не меньше 0,999.
С помощью  -алгоритма Полларда найти наибольший нетривиальный делитель числа 4189.
-алгоритма Полларда найти наибольший нетривиальный делитель числа 4189.
Найти наибольший квадратный корень из 316 по модулю 331.
Найти наибольший квадратный корень из 128 по примарному модулю 343.
Найти количество квадратных корней из 70 по непримарному составному модулю 105.
Найти число элементов порядка 3328 в циклической группе порядка 6656.
Найти дискретный логарифм числа 3 по основанию 2 по модулю 102061.
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1111001110011000110000001.
, построить контрольную сумму для сообщения 1111001110011000110000001.
Вычислить порядок точки (27, 15) кривой  порядка 55.
порядка 55.
Шифротекст УЛОЧПЛЭ_ЕИОРТНК_ЮУПНУТЧ_О получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Расшифровать фразу ИРТЙООИИЛББ__ОД_ТИКЕПК_КА, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Расшифровать текст 3-8.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите последнее слово заглавными буквами.
Расшифровать сообщение 4-6.txt, зашифрованное шифром Виженера, Длина ключа равна 6, пробел является частью алфавита.
В ответ введите ключ.
.
Расшифровать сообщение 5-5.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Зашифровать биграмму ДО с помощью матрицы  ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст ПРЯМАЯ.
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=29, n2=31, x=7.
Чей компьютер он взломает быстрее?
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
МЯЧИК
или
ШАРИК
— устойчивее к действию этой программы?
Вычислить нелинейность булевой функции 01010100 от 3 переменных
Вычислить динамическое расстояние порядка 1 булевой функции 00101101 от 3 переменных
Вычислить нелинейность блока замен 12 9 10 6 5 0 3 15 14 8 2 11 1 13 4 7 размерностью  бит
бит
Вычислить динамическое расстояние порядка (2,2) блока замен 7 9 3 10 13 11 4 14 8 1 12 5 6 0 15 2 размерностью  бит
бит
Найти корреляционную матрицу блока замен 12 9 10 6 5 0 3 15 14 8 2 11 1 13 4 7 размерностью  бит
бит
Провести операцию SubBytes алгоритма AES со значением байта 61.
Провести операцию MixColumns над приведенным ниже столбцом состояния
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
Провести первый раунд зашифрования открытого текста 8966 FB62 A4AA FAD9 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Дано: модуль шифрования N = 3149, открытый ключ e = 13. Найти значение шифртекста, полученного при зашифровании открытого текста 2027 на открытом ключе (N, e) по алгоритму RSA.
Даны значения модуля шифрования N = 377 и открытого ключа e = 283. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 261.
Даны значения модуля шифрования N = 5723 и открытого ключа e = 301. Используя метод факторизации Ферма, найти значение закрытого ключа.
Применением цепных дробей найти секретный ключ d и разложение модуля 72903890242273 (экспонента — 3261683) на множители. В ответе укажите секретный ключ.
Дан шифртекст 311, а также значения модуля шифрования N = 323 и открытого ключа e = 5. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Сообщение 561 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {1,6,8,17,35,69,137}, m=275 и n=107. В ответе укажите исходное сообщение.
Шифртекст (3466465879, 01111000011000111101) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=99023, q=92479. Найти открытый текст и введите его заглавными буквами.
Зашифруйте открытый текст НИЗМЕННЫЙ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(286, 136), значения случайных чисел для букв открытого текста k: 12, 5, 7, 17, 18, 2, 12, 10, 11, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(188, 93), (623, 166)}; {(725, 195), (513, 414)}; |
| {(346, 242), (461, 4)}; {(489, 468), (739, 574)}; |
| {(725, 195), (663, 476)}; {(745, 210), (724, 522)}; |
| {(725, 195), (663, 476)}; {(618, 206), (438, 40)}; |
| {(286, 136), (546, 670)}; {(179, 275), (73, 72)} |
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=19 и k=37 системы цифровой подписи и подписываемый текст ВОСК. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=52 и k=41 системы цифровой подписи и подписываемый текст ГОД. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 7327. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 20, значения цифровой подписи: r = 42; s = 47. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=8, зная секретный ключ подписи d=5 при данном значении выбираемого случайным образом числа k=3. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=2, зная секретный ключ подписи d=11 при данном значении выбираемого случайным образом числа k=5. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Проверьте подлинность ЭЦП (3, 7) для сообщения с известным значением хэш-свертки 5, зная открытый ключ проверки подписи (455, 368). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Проверить действительность подписей (31, 171), (211,141) для сообщения с известным значением хэш-свертки 182 и открытым ключом проверки (239,329). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Зашифровать биграмму ОП с помощью матрицы  ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=6, зная секретный ключ подписи d=7 при данном значении выбираемого случайным образом числа k=11. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Даны значения модуля шифрования N = 221 и открытого ключа e = 35. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 80.
Сообщение 305 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {1,2,6,10,21,41,85}, m=167 и n=48. В ответе укажите исходное сообщение.
Определить, является ли число 71755440315342536873 простым с вероятностью не меньше 0,999.
Решить в целых числах уравнение  . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)
Провести операцию MixColumns над приведенным ниже столбцом состояния
Решить сравнение  с помощью цепных дробей.
с помощью цепных дробей.
Найти наибольший квадратный корень из 10 по примарному модулю 27.
Решить систему сравнений:
С помощью  -алгоритма Полларда найти наибольший нетривиальный делитель числа 2419.
-алгоритма Полларда найти наибольший нетривиальный делитель числа 2419.
Вычислить динамическое расстояние порядка 1 булевой функции 01010100 от 3 переменных
Дано: модуль шифрования N = 2491, открытый ключ e = 19. Найти значение шифртекста, полученного при зашифровании открытого текста 388 на открытом ключе (N, e) по алгоритму RSA.
Найти корреляционную матрицу блока замен 2 0 13 7 9 11 14 3 1 10 5 15 4 12 6 размерностью  бит
бит
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст МИНУТА.
Провести первый раунд зашифрования открытого текста BDD3 AE17 C12A F70A шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Найти наименьший квадратный корень из 316 по примарному модулю 343.
Расшифровать сообщение на английском языке 6-13.txt, зашифрованное шифром Виженера, Длина ключа равна 3.
В ответ введите ключ.
.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=10, зная секретный ключ подписи d=5 при данном значении выбираемого случайным образом числа k=11. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Вычислить порядок точки (21, 2) кривой  порядка 28.
порядка 28.
Вычислить нелинейность булевой функции 00101000 от 3 переменных
Найти произвольный квадратичный невычет по модулю 331
Зашифровать биграмму ПИ с помощью матрицы  ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.
Зашифруйте открытый текст ОТСЛУЖИТЬ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(16, 416), значения случайных чисел для букв открытого текста k: 2, 8, 4, 2, 6, 10, 3, 3, 18, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(377, 456), (367, 360)}; {(425, 663), (715, 398)}; |
| {(188, 93), (279, 353)}; {(179, 275), (128, 79)}; |
| {(568, 355), (515, 67)}; {(568, 355), (482, 230)}; |
| {(377, 456), (206, 645)}; {(188, 93), (300, 455)}; |
| {(489, 468), (362, 446)}; {(16, 416), (69, 510)}; |
| {(425, 663), (218, 601)} |
Найти количество квадратных корней из 16 по непримарному составному модулю 385.
Расшифровать сообщение 5-7.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Вычислить значение  при a = 6122; b = 225; c = 42649.
при a = 6122; b = 225; c = 42649.
Решить в целых числах уравнение  . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)
Шифротекст РВЕПИИЕ_ДТРМЕПИ_ИАРДРМЫГА получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Провести операцию SubBytes алгоритма AES со значением байта C5.
Сообщение 180 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {2,5,8,16,34,67,136}, m=270 и n=139. В ответе укажите исходное сообщение.
Проверить действительность подписей (71, 65), (127, 230) для сообщения с известным значением хэш-свертки 52 и открытым ключом проверки (10,275). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Даны значения модуля шифрования N = 4183 и открытого ключа e = 519. Используя метод факторизации Ферма, найти значение закрытого ключа.
Вычислить динамическое расстояние порядка (2,2) блока замен 6 15 12 4 14 2 3 9 1 7 11 10 13 5 8 0 размерностью  бит
бит
Проверьте подлинность ЭЦП (11, 6) для сообщения с известным значением хэш-свертки 8, зная открытый ключ проверки подписи (596, 318). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Найти наименьший квадратный корень из 2 по модулю 271.
Определить, является ли число 11111111111111111111 простым с вероятностью не меньше 0,999.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=15 и k=17 системы цифровой подписи и подписываемый текст КОД. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст УРАГАН.
Найти произвольный квадратичный невычет по модулю 229
Проверьте подлинность ЭЦП (7, 4) для сообщения с известным значением хэш-свертки 5, зная открытый ключ проверки подписи (596, 318). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Найти количество квадратных корней из 3025 по непримарному составному модулю 4199.
Найти дискретный логарифм числа 15 по основанию 10 по модулю 98011.
Найти остаток от деления  на 35.
на 35.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=3, зная секретный ключ подписи d=4 при данном значении выбираемого случайным образом числа k=7. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Найти наименьший квадратный корень из 31 по примарному модулю 125.
Зашифровать биграмму БЫ с помощью матрицы  ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.
Найти корреляционную матрицу блока замен 6 15 12 4 14 2 3 9 1 7 11 10 13 5 8 0 размерностью  бит
бит
Найти наименьший квадратный корень из 14 по модулю 337.
Вычислить нелинейность блока замен 8 14 3 7 4 11 12 6 5 1 10 15 0 9 2 13 размерностью  бит
бит
Шифртекст (8611143873, 01001110000001100000) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=98207, q=90679. Найти открытый текст и введите его заглавными буквами.
Определить, является ли число 45095080578985454453 простым с вероятностью не меньше 0,999.
Вычислить порядок точки (35, 1) кривой  порядка 44.
порядка 44.
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
ОКОШКО
или
ДВЕРЦА
— устойчивее к действию этой программы?
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 2764. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 8, значения цифровой подписи: r = 47; s = 42. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Расшифровать сообщение на английском языке 6-7.txt, зашифрованное шифром Виженера, Длина ключа равна 3.
В ответ введите ключ.
.
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=29, n2=37, x=11.
Чей компьютер он взломает быстрее?
Даны значения модуля шифрования N = 299 и открытого ключа e = 139. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 87.
Вычислить значение  при a = 6627; b = 313; c = 66999.
при a = 6627; b = 313; c = 66999.
Проверить действительность подписей (3, 85), (195, 216) для сообщения с известным значением хэш-свертки 215 и открытым ключом проверки (104,30). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Расшифровать фразу ИПССАДП_ЕРЕЕДИНЖПУЕРАОБЗ_, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Проверьте подлинность ЭЦП (7, 10) для сообщения с известным значением хэш-свертки 6, зная открытый ключ проверки подписи (562, 662). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Решить сравнение  с помощью цепных дробей.
с помощью цепных дробей.
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
Расшифровать сообщение 5-17.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Провести первый раунд зашифрования открытого текста AC2B EECD DA96 989D шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Найти корреляционную матрицу блока замен 15 10 4 2 0 13 9 1 12 6 7 5 3 8 14 11 размерностью  бит
бит
Сообщение 1309 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {4,6,11,22,45,90,181}, m=360 и n=79. В ответе укажите исходное сообщение.
Шифртекст (978847044, 10011100011011001101) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=99971, q=98143. Найти открытый текст и введите его заглавными буквами.
Определить, является ли число 66405897020462343733 простым с вероятностью не меньше 0,999.
Расшифровать сообщение 4-18.txt, зашифрованное шифром Виженера, Длина ключа равна 6, пробел является частью алфавита.
В ответ введите ключ.
.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 1746. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 47, значения цифровой подписи: r = 31; s = 56. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=12, зная секретный ключ подписи d=9 при данном значении выбираемого случайным образом числа k=2. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Найти наибольший квадратный корень из 86 по примарному модулю 125.
Дан шифртекст 75, а также значения модуля шифрования N = 221 и открытого ключа e = 5. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 8806. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 29, значения цифровой подписи: r = 50; s = 24. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Зашифровать биграмму ВО с помощью матрицы  ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.
Проверьте подлинность ЭЦП (5, 7) для сообщения с известным значением хэш-свертки 6, зная открытый ключ проверки подписи (135, 669). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Провести операцию SubBytes алгоритма AES со значением байта FB.
Решить сравнение  с помощью индексов. (В качестве ответа введите наименьшее значение x.)
с помощью индексов. (В качестве ответа введите наименьшее значение x.)
Проверить действительность подписей (11, 133), (35, 48) для сообщения с известным значением хэш-свертки 148 и открытым ключом проверки (166,741). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(56, 419), (739, 177)}; {(16, 416), (282, 410)}; |
| {(425, 663), (221, 138)}; {(188, 93), (329, 447)}; |
| {(286, 136), (235, 19)}; {(725, 195), (496, 31)}; |
| {(56, 419), (236, 712)}; {(440, 539), (514, 662)}; |
| {(377, 456), (323, 94)}; {(179, 275), (203, 324)}; |
| {(568, 355), (197, 606)} |
Сообщение 212 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {1,2,4,8,17,34,68}, m=135 и n=103. В ответе укажите исходное сообщение.
Найти наименьший квадратный корень из 173 по модулю 263.
С помощью  -алгоритма Полларда найти наибольший нетривиальный делитель числа 3763.
-алгоритма Полларда найти наибольший нетривиальный делитель числа 3763.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=3, зная секретный ключ подписи d=9 при данном значении выбираемого случайным образом числа k=6. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Даны значения модуля шифрования N = 299 и открытого ключа e = 139. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 285.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=11 и k=55 системы цифровой подписи и подписываемый текст СЛОЙ. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Применением цепных дробей найти секретный ключ d и разложение модуля 84032429242009 (экспонента — 2581907) на множители. В ответе укажите секретный ключ.
Шифротекст ЮВЧКЛ_ИКТЕЬОЮМП_ТВЕРТ_ЬСЕ получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Найти дискретный логарифм числа 10 по основанию 11 по модулю 103681.
Провести первый раунд зашифрования открытого текста BDC6 FF70 AC32 B3A6 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Вычислить динамическое расстояние порядка (2,2) блока замен 9 4 15 11 7 0 5 6 13 14 1 8 10 2 3 12 размерностью  бит
бит
Вычислить значение  при a = 8398; b = 895; c = 38124.
при a = 8398; b = 895; c = 38124.
Вычислить порядок точки (12,  кривой
кривой  порядка 28.
порядка 28.
Расшифровать сообщение 5-16.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Расшифровать сообщение на английском языке 6-22.txt, зашифрованное шифром Виженера, Длина ключа равна 4.
В ответ введите ключ.
.
Решить следующее сравнение  .
.
Найти произвольный квадратичный невычет по модулю 367
Расшифровать сообщение 4-20.txt, зашифрованное шифром Виженера, Длина ключа равна 6, пробел является частью алфавита.
В ответ введите ключ.
.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=13 и k=23 системы цифровой подписи и подписываемый текст ТРЕП. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Применением цепных дробей найти секретный ключ d и разложение модуля 77027476849549 (экспонента — 2936957) на множители. В ответе укажите секретный ключ.
Найти остаток от деления  на 7.
на 7.
Найти корреляционную матрицу блока замен 3 10 4 2 6 9 14 8 11 5 13 1 7 0 15 12 размерностью  бит
бит
Даны значения модуля шифрования N = 221 и открытого ключа e = 91. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 79.
Расшифровать фразу ВЕОИТ_ЛЕФИСНУТАНЫ_ОВТ_ЬРЫ, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Найти произвольный квадратичный невычет по модулю 211
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
Вычислить нелинейность булевой функции 01010100 от 3 переменных
Провести операцию MixColumns над приведенным ниже столбцом состояния
Зашифровать биграмму НО с помощью матрицы  ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.
Вычислить динамическое расстояние порядка 1 булевой функции 01001001 от 3 переменных
Расшифровать сообщение 4-16.txt, зашифрованное шифром Виженера, Длина ключа равна 7, пробел является частью алфавита.
В ответ введите ключ.
.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=5, зная секретный ключ подписи d=12 при данном значении выбираемого случайным образом числа k=6. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
ПРОБИРКА
или
МЕНЗУРКА
— устойчивее к действию этой программы?
Найти наибольший квадратный корень из 46 по примарному модулю 625.
Проверить действительность подписей (3, 220), (10, 171) для сообщения с известным значением хэш-свертки 152 и открытым ключом проверки (195, 321). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Расшифровать текст 3-20.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите второе слово заглавными буквами.
Расшифровать сообщение на английском языке 6-18.txt, зашифрованное шифром Виженера, Длина ключа равна 4.
В ответ введите ключ.
.
Дан шифртекст 47, а также значения модуля шифрования N = 77 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Провести первый раунд зашифрования открытого текста 97F4 C6AD D65F A8A2 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Вычислить нелинейность блока замен 15 10 4 2 0 13 9 1 12 6 7 5 3 8 14 11 размерностью  бит
бит
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
ТОВАР
или
РЫНОК
— устойчивее к действию этой программы?
Шифртекст (438845908, 10101000101000000100) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=93131, q=90247. Найти открытый текст и введите его заглавными буквами.
Даны значения модуля шифрования N = 253 и открытого ключа e = 139. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 106.
Проверьте подлинность ЭЦП (5, 11) для сообщения с известным значением хэш-свертки 12, зная открытый ключ проверки подписи (135, 669). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Провести операцию SubBytes алгоритма AES со значением байта 22.
Провести первый раунд зашифрования открытого текста BF55 E71E 8CD6 9001 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Шифротекст СИЫЧВТ_ИЛЛЕОЧНООЛПО_ЕИЕНЖ получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Расшифровать фразу А__ФНРЕПДЕТЕА_ЙРУВСИШКЛЕЕ, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 8190. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 10, значения цифровой подписи: r = 56; s = 48. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Найти количество квадратных корней из 212 по непримарному составному модулю 1001.
Сообщение 557 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {3,5,9,19,37,77,151}, m=302 и n=59. В ответе укажите исходное сообщение.
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=31, n2=23, x=17.
Чей компьютер он взломает быстрее?
Решить систему сравнений:
Найти произвольный квадратичный невычет по модулю 229
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=8, зная секретный ключ подписи d=5 при данном значении выбираемого случайным образом числа k=5. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Вычислить динамическое расстояние порядка 1 булевой функции 01101011 от 3 переменных
Вычислить динамическое расстояние порядка (2,2) блока замен 15 9 4 6 12 1 0 8 10 11 2 7 13 14 3 5 размерностью  бит
бит
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(179, 275), (326, 675)}; {(725, 195), (83, 378)}; |
| {(440, 539), (340, 78)}; {(425, 663), (67, 84)}; |
| {(425, 663), (620, 71)}; {(72, 254), (251, 245)}; |
| {(568, 355), (75, 318)}; {(725, 195), (228, 271)}; |
| {(188, 93), (734, 170)}; {(188, 93), (704, 705)}; |
| {(286, 136), (235, 732)} |
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст САТУРН.
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1111111111010001011001100.
, построить контрольную сумму для сообщения 1111111111010001011001100.
Зашифруйте открытый текст РЕМОНТНЫЙ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(188, 93), значения случайных чисел для букв открытого текста k: 2, 2, 4, 18, 15, 19, 11, 2, 15, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Проверить действительность подписей (3, 208), (166, 235) для сообщения с известным значением хэш-свертки 14 и открытым ключом проверки (286, 213). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
КРЫСА
или
ХОРЕК
— устойчивее к действию этой программы?
Вычислить нелинейность блока замен 13 6 3 14 12 11 4 1 15 5 10 7 0 9 2 8 размерностью  бит
бит
Найти количество квадратных корней из 653 по непримарному составному модулю 1001.
Вычислить нелинейность булевой функции 01001001 от 3 переменных
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 1892. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 37, значения цифровой подписи: r = 56; s = 26. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Провести первый раунд зашифрования открытого текста A267 8C95 8111 B0B7 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Дано: модуль шифрования N = 4331, открытый ключ e = 11. Найти значение шифртекста, полученного при зашифровании открытого текста 632 на открытом ключе (N, e) по алгоритму RSA.
Решить сравнение  с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)
с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)
Найти произвольный квадратичный невычет по модулю 271
Даны значения модуля шифрования N = 3713 и открытого ключа e = 2455. Используя метод факторизации Ферма, найти значение закрытого ключа.
Расшифровать сообщение 5-20.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Найти наибольший квадратный корень из 139 по модулю 313.
Решить в целых числах уравнение  . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)
Решить следующее сравнение  .
.
Решить сравнение  с помощью цепных дробей.
с помощью цепных дробей.
Найти остаток от деления  на 2.
на 2.
Вычислить значение  при a = 1811; b = 576; c = 62147.
при a = 1811; b = 576; c = 62147.
С помощью  -алгоритма Полларда найти наибольший нетривиальный делитель числа 1147.
-алгоритма Полларда найти наибольший нетривиальный делитель числа 1147.
Найти наибольший квадратный корень из 271 по модулю 293.
Найти количество квадратных корней из 291 по непримарному составному модулю 385.
Найти число элементов порядка 1734 в циклической группе порядка 5202.
Найти дискретный логарифм числа 17 по основанию 5 по модулю 95257.
Вычислить порядок точки (46, 18) кривой  порядка 38.
порядка 38.
Шифротекст ЫТБСРЕПЕ_ОВДДОИЕВТ_ОСАЙК_ получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Расшифровать текст 3-5.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите третье слово заглавными буквами.
Расшифровать сообщение 4-11.txt, зашифрованное шифром Виженера, Длина ключа равна 5, пробел является частью алфавита.
В ответ введите ключ.
.
Зашифровать биграмму МА с помощью матрицы  ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.
Вычислить динамическое расстояние порядка 1 булевой функции 01110111 от 3 переменных
Вычислить нелинейность блока замен 12 2 8 3 9 1 11 15 14 6 4 5 13 0 10 7 размерностью  бит
бит
Вычислить динамическое расстояние порядка (2,2) блока замен 11 3 14 5 12 6 13 1 10 2 8 4 15 0 9 7 размерностью  бит
бит
Найти корреляционную матрицу блока замен 13 6 3 14 12 11 4 1 15 5 10 7 0 9 2 8 размерностью  бит
бит
Провести операцию MixColumns над приведенным ниже столбцом состояния
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
Дано: модуль шифрования N = 3403, открытый ключ e = 11. Найти значение шифртекста, полученного при зашифровании открытого текста 855 на открытом ключе (N, e) по алгоритму RSA.
Дан шифртекст 96, а также значения модуля шифрования N = 187 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Сообщение 295 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {1,5,8,16,31,63,125}, m=251 и n=56. В ответе укажите исходное сообщение.
Шифртекст (942315396, 10100111100011100111) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=100019, q=94903. Найти открытый текст и введите его заглавными буквами.
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(188, 93), (573, 583)}; {(188, 93), (128, 79)}; |
| {(425, 663), (703, 125)}; {(489, 468), (109, 200)}; |
| {(568, 355), (348, 27)}; {(377, 456), (323, 657)}; |
| {(72, 254), (399, 65)}; {(16, 416), (660, 275)}; |
| {(179, 275), (267, 670)}; {(568, 355), (642, 53)} |
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=5 и k=31 системы цифровой подписи и подписываемый текст ШАР. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=11, зная секретный ключ подписи d=5 при данном значении выбираемого случайным образом числа k=6. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Проверьте подлинность ЭЦП (5, 7) для сообщения с известным значением хэш-свертки 6, зная открытый ключ проверки подписи (562, 662). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Определить, является ли число 59713968361666935769 простым с вероятностью не меньше 0,999.
Зашифровать биграмму КУ с помощью матрицы  ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(179, 275), (712, 186)}; {(725, 195), (395, 414)}; |
| {(72, 254), (434, 136)}; {(425, 663), (251, 506)}; |
| {(16, 416), (383, 340)}; {(745, 210), (102, 484)}; |
| {(346, 242), (78, 271)}; {(179, 275), (712, 186)}; |
| {(725, 195), (739, 574)}; {(346, 242), (78, 271)} |
Вычислить динамическое расстояние порядка (2,2) блока замен 2 10 7 6 3 5 15 4 12 8 14 0 9 11 13 1 размерностью  бит
бит
Вычислить динамическое расстояние порядка 1 булевой функции 01001010 от 3 переменных
Найти корреляционную матрицу блока замен 2 10 7 6 3 5 15 4 12 8 14 0 9 11 13 1 размерностью  бит
бит
Сообщение 855 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {4,5,11,21,43,85,170}, m=340 и n=101. В ответе укажите исходное сообщение.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=7, зная секретный ключ подписи d=3 при данном значении выбираемого случайным образом числа k=7. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Решить сравнение  с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)
с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)
Решить сравнение  с помощью индексов.
с помощью индексов.
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=43, n2=23, x=9.
Чей компьютер он взломает быстрее?
Проверить действительность подписей (201, 7), (195, 143) для сообщения с известным значением хэш-свертки 20 и открытым ключом проверки (87,716). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Даны значения модуля шифрования N = 3901 и открытого ключа e = 2375. Используя метод факторизации Ферма, найти значение закрытого ключа.
Расшифровать сообщение 5-8.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Дано: модуль шифрования N = 1739, открытый ключ e = 17. Найти значение шифртекста, полученного при зашифровании открытого текста 132 на открытом ключе (N, e) по алгоритму RSA.
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=29, n2=47, x=12.
Чей компьютер он взломает быстрее?
Провести первый раунд зашифрования открытого текста F7C1 A026 AB48 9F0F шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=8, зная секретный ключ подписи d=12 при данном значении выбираемого случайным образом числа k=8. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
Зашифруйте открытый текст ПРОКРУТКА с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(618, 206), значения случайных чисел для букв открытого текста k: 10, 15, 16, 2, 3, 4, 2, 11, 16, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Найти корреляционную матрицу блока замен 14 7 13 2 0 10 8 9 4 3 15 5 12 11 1 6 размерностью  бит
бит
Найти дискретный логарифм числа 13 по основанию 11 по модулю 100801.
Найти наименьший квадратный корень из 114 по примарному модулю 125.
Проверьте подлинность ЭЦП (11, 10) для сообщения с известным значением хэш-свертки 8, зная открытый ключ проверки подписи (135, 82). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
С помощью  -алгоритма Полларда найти наибольший нетривиальный делитель числа 2201.
-алгоритма Полларда найти наибольший нетривиальный делитель числа 2201.
Найти остаток от деления  на 5.
на 5.
Даны значения модуля шифрования N = 5917 и открытого ключа e = 1571. Используя метод факторизации Ферма, найти значение закрытого ключа.
Вычислить динамическое расстояние порядка 1 булевой функции 01011000 от 3 переменных
Вычислить динамическое расстояние порядка (2,2) блока замен 15 4 14 0 8 13 7 5 1 12 3 10 2 6 11 9 размерностью  бит
бит
Найти наименьший квадратный корень из 61 по модулю 229.
Вычислить значение  при a = 9928; b = 413; c = 82224.
при a = 9928; b = 413; c = 82224.
Расшифровать текст 3-15.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите предпоследнее слово заглавными буквами.
Решить следующее сравнение  .
.
Решить сравнение  с помощью цепных дробей.
с помощью цепных дробей.
Решить систему сравнений:
Найти остаток от деления  на 100.
на 100.
Вычислить значение  при a = 5065; b = 413; c = 61564.
при a = 5065; b = 413; c = 61564.
Определить, является ли число 54673257461630679457 простым с вероятностью не меньше 0,999.
С помощью  -алгоритма Полларда найти наибольший нетривиальный делитель числа 3977.
-алгоритма Полларда найти наибольший нетривиальный делитель числа 3977.
Найти произвольный квадратичный невычет по модулю 347
Найти дискретный логарифм числа 25 по основанию 22 по модулю 96769.
Вычислить порядок точки (9, 14) кривой  порядка 42.
порядка 42.
Шифротекст АМО_ЛЕРУРСОС_ДВЯЛЗА_УПКАС получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Расшифровать фразу ТСАНУОБЛЬ_ИВТЕО_ЕРОШТЕОКЗ, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Расшифровать сообщение 4-13.txt, зашифрованное шифром Виженера, Длина ключа равна 5, пробел является частью алфавита.
В ответ введите ключ.
.
Расшифровать сообщение на английском языке 6-14.txt, зашифрованное шифром Виженера, Длина ключа равна 5.
В ответ введите ключ.
.
Зашифровать биграмму МЫ с помощью матрицы  ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст ПОБЕДА.
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=37, n2=47, x=13.
Чей компьютер он взломает быстрее?
Вычислить динамическое расстояние порядка 1 булевой функции 00101000 от 3 переменных
Найти корреляционную матрицу блока замен 9 13 0 10 12 2 15 11 3 6 8 7 14 4 5 1 размерностью  бит
бит
Провести операцию SubBytes алгоритма AES со значением байта F0.
Провести операцию MixColumns над приведенным ниже столбцом состояния
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
Провести первый раунд зашифрования открытого текста A7BE CFBC F166 AB89 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Дано: модуль шифрования N = 2923, открытый ключ e = 19. Найти значение шифртекста, полученного при зашифровании открытого текста 678 на открытом ключе (N, e) по алгоритму RSA.
Даны значения модуля шифрования N = 4717 и открытого ключа e = 4205. Используя метод факторизации Ферма, найти значение закрытого ключа.
Применением цепных дробей найти секретный ключ d и разложение модуля 60902079700513 (экспонента — 3914857) на множители. В ответе укажите секретный ключ.
Дан шифртекст 45, а также значения модуля шифрования N = 323 и открытого ключа e = 5. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(283, 493), (314, 127)}; {(425, 663), (561, 140)}; |
| {(568, 355), (75, 433)}; {(440, 539), (602, 627)}; |
| {(188, 93), (395, 414)}; {(179, 275), (25, 604)}; |
| {(72, 254), (47, 349)}; {(72, 254), (417, 137)}; |
| {(188, 93), (298, 225)}; {(56, 419), (79, 111)} |
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=25 и k=17 системы цифровой подписи и подписываемый текст СТОП. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=21 и k=5 системы цифровой подписи и подписываемый текст ГИД. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=11, зная секретный ключ подписи d=5 при данном значении выбираемого случайным образом числа k=7. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Проверьте подлинность ЭЦП (11, 4) для сообщения с известным значением хэш-свертки 4, зная открытый ключ проверки подписи (596, 318). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Проверить действительность подписей (195, 216), (9, 85) для сообщения с известным значением хэш-свертки 7 и открытым ключом проверки (245,637). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Расшифровать фразу ЕМОТНББСУОЙИТН_СЙРЕ_СТЯЕЯ, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Какая наибольшая степень элемента a порядка 50 порождает группу  ?
?
Решить систему сравнений:
Даны значения модуля шифрования N = 3713 и открытого ключа e = 2929. Используя метод факторизации Ферма, найти значение закрытого ключа.
Применением цепных дробей найти секретный ключ d и разложение модуля 78908333904637 (экспонента — 2821057) на множители. В ответе укажите секретный ключ.
Проверьте подлинность ЭЦП (3, 1) для сообщения с известным значением хэш-свертки 6, зная открытый ключ проверки подписи (455, 383). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=6 и k=29 системы цифровой подписи и подписываемый текст БАР. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Найти дискретный логарифм числа 12 по основанию 17 по модулю 105601.
Шифротекст САЕДЛТА_ЬЗМ_НЕУПМРЕЕЕЙННО получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=4 и k=41 системы цифровой подписи и подписываемый текст ШУМ. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Вычислить динамическое расстояние порядка 1 булевой функции 01100011 от 3 переменных
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 3057. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 58, значения цифровой подписи: r = 11; s = 2. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Провести первый раунд зашифрования открытого текста CBD9 93EC CB0F F839 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
ПРОСТУДА
или
СКВОЗНЯК
— устойчивее к действию этой программы?
Дано: модуль шифрования N = 5561, открытый ключ e = 19. Найти значение шифртекста, полученного при зашифровании открытого текста 2718 на открытом ключе (N, e) по алгоритму RSA.
Вычислить динамическое расстояние порядка (2,2) блока замен 14 7 13 2 0 10 8 9 4 3 15 5 12 11 1 6 размерностью  бит
бит
Расшифровать фразу НУАСТРИОДЕРРОАТТЕСГИВО_ВИ, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Проверьте подлинность ЭЦП (11, 1) для сообщения с известным значением хэш-свертки 7, зная открытый ключ проверки подписи (596, 433). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Провести операцию SubBytes алгоритма AES со значением байта 15.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=5, зная секретный ключ подписи d=12 при данном значении выбираемого случайным образом числа k=8. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Вычислить нелинейность блока замен 4 2 0 10 11 9 6 1 13 8 15 14 12 5 7 3 размерностью  бит
бит
Найти корреляционную матрицу блока замен 12 9 0 15 6 13 1 5 14 7 11 2 4 8 10 3 размерностью  бит
бит
Решить следующее сравнение  . (В качестве ответа введите наименьшее значение x.)
. (В качестве ответа введите наименьшее значение x.)
Решить следующее сравнение  . (В качестве ответа введите наименьшее значение x.)
. (В качестве ответа введите наименьшее значение x.)
Решить систему сравнений:
Найти остаток от деления  на 14.
на 14.
Вычислить значение  при a = 4831; b = 504; c = 69596.
при a = 4831; b = 504; c = 69596.
Определить, является ли число 909090909090909091 простым с вероятностью не меньше 0,999.
С помощью  -алгоритма Полларда найти наибольший нетривиальный делитель числа 3139.
-алгоритма Полларда найти наибольший нетривиальный делитель числа 3139.
Найти произвольный квадратичный невычет по модулю 307
Найти количество квадратных корней из 7155 по непримарному составному модулю 7429.
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1110101101110110010110101.
, построить контрольную сумму для сообщения 1110101101110110010110101.
Вычислить порядок точки (37, 11) кривой  порядка 54.
порядка 54.
Шифротекст РОВПЕ_ИТНЕЛЕГРУ_ТОЯРОЛЕВВ получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Расшифровать сообщение 4-3.txt, зашифрованное шифром Виженера, Длина ключа равна 6, пробел является частью алфавита.
В ответ введите ключ.
.
Расшифровать сообщение на английском языке 6-11.txt, зашифрованное шифром Виженера, Длина ключа равна 3.
В ответ введите ключ.
.
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст ПРОРЫВ.
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=31, n2=43, x=7.
Чей компьютер он взломает быстрее?
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
ДОКЛАД
или
ТЕЗИСЫ
— устойчивее к действию этой программы?
Вычислить нелинейность булевой функции 00000011 от 3 переменных
Вычислить динамическое расстояние порядка 1 булевой функции 00101110 от 3 переменных
Вычислить динамическое расстояние порядка (2,2) блока замен 2 0 13 7 9 11 14 3 1 10 5 15 4 12 6 размерностью  бит
бит
Провести операцию SubBytes алгоритма AES со значением байта 0E.
Провести операцию MixColumns над приведенным ниже столбцом состояния
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
Провести первый раунд зашифрования открытого текста C95A B90A 8B3D EB0 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Дано: модуль шифрования N = 1927, открытый ключ e = 19. Найти значение шифртекста, полученного при зашифровании открытого текста 1260 на открытом ключе (N, e) по алгоритму RSA.
Даны значения модуля шифрования N = 187 и открытого ключа e = 59. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 114.
Даны значения модуля шифрования N = 2479 и открытого ключа e = 2251. Используя метод факторизации Ферма, найти значение закрытого ключа.
Зашифруйте открытый текст БЕЛИБЕРДА с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(286, 136), значения случайных чисел для букв открытого текста k: 2, 9, 18, 2, 19, 4, 5, 11, 9, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(16, 416), (150, 355)}; {(188, 93), (394, 20)}; |
| {(725, 195), (13, 134)}; {(377, 456), (209, 669)}; |
| {(56, 419), (514, 662)}; {(56, 419), (243, 87)}; |
| {(618, 206), (719, 538)}; {(618, 206), (159, 13)}; |
| {(618, 206), (326, 76)}; {(188, 93), (557, 28)} |
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 6549. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 11, значения цифровой подписи: r = 38; s = 43. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Проверьте подлинность ЭЦП (7,  для сообщения с известным значением хэш-свертки 12, зная открытый ключ проверки подписи (135, 82). Используйте кривую
для сообщения с известным значением хэш-свертки 12, зная открытый ключ проверки подписи (135, 82). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Проверить действительность подписей (166, 242), (3, 9) для сообщения с известным значением хэш-свертки 84 и открытым ключом проверки (286, 213). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=41, n2=37, x=5.
Чей компьютер он взломает быстрее?
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст ЮПИТЕР.
Зашифровать биграмму ВЫ с помощью матрицы  ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.
Шифротекст ЫОЧНТО_КОЕАДИНР_Ы_ВТЕУПЛД получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Зашифруйте открытый текст СИММЕТРИЯ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(179, 275), значения случайных чисел для букв открытого текста k: 11, 17, 18, 19, 16, 6, 12, 8, 2, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Провести операцию SubBytes алгоритма AES со значением байта 6C.
Дан шифртекст 64, а также значения модуля шифрования N = 187 и открытого ключа e = 3. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Даны значения модуля шифрования N = 2911 и открытого ключа e = 1697. Используя метод факторизации Ферма, найти значение закрытого ключа.
Дано: модуль шифрования N = 5609, открытый ключ e = 17. Найти значение шифртекста, полученного при зашифровании открытого текста 4425 на открытом ключе (N, e) по алгоритму RSA.
Вычислить значение  при a = 8271; b = 845; c = 15241.
при a = 8271; b = 845; c = 15241.
Решить сравнение  с помощью индексов.
с помощью индексов.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=44 и k=11 системы цифровой подписи и подписываемый текст СВОД. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Вычислить нелинейность булевой функции 00110010 от 3 переменных
Решить в целых числах уравнение  . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)
Расшифровать фразу К_ЙАО__ЕУНОМЕПЧН_ЮЗАТТ_КО, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(425, 663), (273, 481)}; {(188, 93), (85, 716)}; |
| {(16, 416), (422, 162)}; {(283, 493), (36, 87)}; |
| {(179, 275), (100, 364)}; {(188, 93), (298, 225)}; |
| {(56, 419), (555, 303)}; {(745, 210), (100, 387)}; |
| {(377, 456), (526, 412)}; {(286, 136), (316, 228)}; |
| {(745, 210), (49, 183)}; {(179, 275), (428, 247)} |
Дан шифртекст 163, а также значения модуля шифрования N = 187 и открытого ключа e = 3. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 2563. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 33, значения цифровой подписи: r = 11; s = 34. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
В скольких подгруппах группы  порядка 6656 содержится фиксированный элемент порядка 2?
порядка 6656 содержится фиксированный элемент порядка 2?
Применением цепных дробей найти секретный ключ d и разложение модуля 70109121369029 (экспонента — 3401467) на множители. В ответе укажите секретный ключ.
Вычислить нелинейность блока замен 5 10 4 7 12 3 2 8 6 1 9 11 0 14 13 15 размерностью  бит
бит
Вычислить динамическое расстояние порядка 1 булевой функции 00100010 от 3 переменных
Вычислить порядок точки (13, 4) кривой  порядка 32.
порядка 32.
Найти произвольный квадратичный невычет по модулю 241
Проверьте подлинность ЭЦП (11, 9) для сообщения с известным значением хэш-свертки 4, зная открытый ключ проверки подписи (384, 475). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст РАЗБОР.
Провести операцию SubBytes алгоритма AES со значением байта D0.
Зашифруйте открытый текст РЕНЕССАНС с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(725, 195), значения случайных чисел для букв открытого текста k: 2, 19, 4, 8, 2, 2, 16, 10, 2, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Найти дискретный логарифм числа 71 по основанию 5 по модулю 101377.
Решить следующее сравнение  . (В качестве ответа введите наименьшее значение x.)
. (В качестве ответа введите наименьшее значение x.)
Решить сравнение  с помощью цепных дробей.
с помощью цепных дробей.
Решить систему сравнений:
Вычислить значение  при a = 4520; b = 762; c = 55807.
при a = 4520; b = 762; c = 55807.
Определить, является ли число 12764787846358441471 простым с вероятностью не меньше 0,999.
Найти наименьший квадратный корень из 99 по примарному модулю 125.
Найти количество квадратных корней из 86 по непримарному составному модулю 385.
Найти дискретный логарифм числа 18 по основанию 7 по модулю 110251.
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1111111100000111001000110.
, построить контрольную сумму для сообщения 1111111100000111001000110.
Вычислить порядок точки (27, 5) кривой  порядка 32.
порядка 32.
Шифротекст ША_УНППРААУТУРААЗЕМ_ЛИ_ИТ получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Расшифровать фразу _ААЛВРАТЗВД_УАББТОЕ__ЕИБГ, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Расшифровать сообщение 4-5.txt, зашифрованное шифром Виженера, Длина ключа равна 7, пробел является частью алфавита.
В ответ введите ключ.
.
Расшифровать сообщение 5-18.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Расшифровать сообщение на английском языке 6-24.txt, зашифрованное шифром Виженера, Длина ключа равна 3.
В ответ введите ключ.
.
Зашифровать биграмму ЛА с помощью матрицы  ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
ТАЙМЕР
или
ЗВОНОК
— устойчивее к действию этой программы?
Вычислить нелинейность булевой функции 00101110 от 3 переменных
Вычислить динамическое расстояние порядка 1 булевой функции 01101000 от 3 переменных
Вычислить динамическое расстояние порядка (2,2) блока замен 13 11 7 4 12 14 6 8 9 10 3 1 0 2 5 15 размерностью  бит
бит
Найти корреляционную матрицу блока замен 7 9 3 10 13 11 4 14 8 1 12 5 6 0 15 2 размерностью  бит
бит
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
Провести первый раунд зашифрования открытого текста B05F A79E CEF6 AA22 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Даны значения модуля шифрования N = 3397 и открытого ключа e = 113. Используя метод факторизации Ферма, найти значение закрытого ключа.
Применением цепных дробей найти секретный ключ d и разложение модуля 47050437355283 (экспонента — 4674517) на множители. В ответе укажите секретный ключ.
Дан шифртекст 13, а также значения модуля шифрования N = 143 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Сообщение 1018 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {5,6,13,25,54,107,211}, m=423 и n=167. В ответе укажите исходное сообщение.
Зашифруйте открытый текст ТЕРНОВНИК с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(188, 93), значения случайных чисел для букв открытого текста k: 8, 14, 17, 17, 2, 10, 8, 2, 2, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(745, 210), (259, 401)}; {(568, 355), (606, 147)}; |
| {(188, 93), (407, 82)}; {(56, 419), (739, 574)}; |
| {(286, 136), (329, 447)}; {(425, 663), (520, 749)}; |
| {(72, 254), (374, 315)}; {(188, 93), (149, 97)}; |
| {(745, 210), (13, 134)}; {(440, 539), (235, 19)}; |
| {(425, 663), (128, 79)} |
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=6, зная секретный ключ подписи d=5 при данном значении выбираемого случайным образом числа k=6. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Проверьте подлинность ЭЦП (3, 1) для сообщения с известным значением хэш-свертки 8, зная открытый ключ проверки подписи (384, 276). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Проверить действительность подписей (3, 49), (3, 85) для сообщения с известным значением хэш-свертки 31 и открытым ключом проверки (318,109). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Найти наименьший квадратный корень из 11 по примарному модулю 25.
Вычислить нелинейность блока замен 14 12 7 3 0 11 1 15 8 10 9 6 5 13 2 4 размерностью  бит
бит
Сообщение 782 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {4,5,10,21,45,88,174}, m=349 и n=80. В ответе укажите исходное сообщение.
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=41, n2=31, x=12.
Чей компьютер он взломает быстрее?
Решить в целых числах уравнение  . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)
Вычислить динамическое расстояние порядка 1 булевой функции 01010111 от 3 переменных
Расшифровать текст 3-17.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите второе слово заглавными буквами.
Вычислить нелинейность булевой функции 01111000 от 3 переменных
Проверьте подлинность ЭЦП (7, 5) для сообщения с известным значением хэш-свертки 6, зная открытый ключ проверки подписи (596, 318). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
Зашифруйте открытый текст МУШТРОВКА с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(618, 206), значения случайных чисел для букв открытого текста k: 5, 19, 8, 2, 5, 8, 15, 19, 6, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=43, n2=47, x=16.
Чей компьютер он взломает быстрее?
Вычислить значение  при a = 5834; b = 998; c = 57238.
при a = 5834; b = 998; c = 57238.
Найти корреляционную матрицу блока замен 8 14 3 7 4 11 12 6 5 1 10 15 0 9 2 13 размерностью  бит
бит
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1110101100010111101110010.
, построить контрольную сумму для сообщения 1110101100010111101110010.
Вычислить порядок точки (36, 5) кривой  порядка 36.
порядка 36.
Вычислить нелинейность блока замен 12 0 7 10 6 4 15 9 3 8 1 5 14 13 11 2 размерностью  бит
бит
Расшифровать сообщение на английском языке 6-15.txt, зашифрованное шифром Виженера, Длина ключа равна 4.
В ответ введите ключ.
.
Найти число всех подгрупп (не включая единичную) группы  порядка 5202, не содержащих элемент порядка 18.
порядка 5202, не содержащих элемент порядка 18.
Расшифровать текст 3-7.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите третье с конца слово заглавными буквами.
Решить сравнение  с помощью индексов.
с помощью индексов.
Зашифровать биграмму ОН с помощью матрицы  ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=9, зная секретный ключ подписи d=3 при данном значении выбираемого случайным образом числа k=5. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Дано: модуль шифрования N = 3713, открытый ключ e = 11. Найти значение шифртекста, полученного при зашифровании открытого текста 3415 на открытом ключе (N, e) по алгоритму RSA.
Найти наименьший квадратный корень из 161 по модулю 251.
С помощью  -алгоритма Полларда найти наибольший нетривиальный делитель числа 3233.
-алгоритма Полларда найти наибольший нетривиальный делитель числа 3233.
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
ДОЛЛАР
или
ФАНТИК
— устойчивее к действию этой программы?
Решить в целых числах уравнение  . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)
Решить систему сравнений:
Решить сравнение  с помощью индексов.
с помощью индексов.
Определить, является ли число 3489133282872437279 простым с вероятностью не меньше 0,999.
Найти наибольший квадратный корень из 189 по модулю 227.
Найти наименьший квадратный корень из 18 по примарному модулю 343.
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1100001010011100001100010.
, построить контрольную сумму для сообщения 1100001010011100001100010.
Расшифровать текст 3-16.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите последнее слово заглавными буквами.
Расшифровать сообщение на английском языке 6-1.txt, зашифрованное шифром Виженера, Длина ключа равна 3.
В ответ введите ключ.
.
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст РАКЕТА.
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=31, n2=47, x=8.
Чей компьютер он взломает быстрее?
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
ЗРНТИК
или
ДОЖДИК
— устойчивее к действию этой программы?
Вычислить нелинейность блока замен 5 11 13 14 2 1 10 0 6 15 8 12 7 4 3 9 размерностью  бит
бит
Вычислить динамическое расстояние порядка (2,2) блока замен 5 2 14 10 8 7 15 11 13 4 3 9 12 6 1 0 размерностью  бит
бит
Найти корреляционную матрицу блока замен 15 0 1 6 8 3 4 14 5 9 11 7 10 13 2 12 размерностью  бит
бит
Провести операцию MixColumns над приведенным ниже столбцом состояния
Провести первый раунд зашифрования открытого текста A64E D30C E720 E3E8 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Дано: модуль шифрования N = 6319, открытый ключ e = 17. Найти значение шифртекста, полученного при зашифровании открытого текста 2741 на открытом ключе (N, e) по алгоритму RSA.
Даны значения модуля шифрования N = 391 и открытого ключа e = 145. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 386.
Шифртекст (9775365428, 11010000001111001000) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=101987, q=101267. Найти открытый текст и введите его заглавными буквами.
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(725, 195), (651, 560)}; {(425, 663), (147, 361)}; |
| {(286, 136), (109, 551)}; {(440, 539), (90, 730)}; |
| {(618, 206), (668, 342)}; {(745, 210), (109, 200)}; |
| {(425, 663), (147, 361)}; {(72, 254), (228, 480)}; |
| {(346, 242), (530, 22)} |
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=10 и k=35 системы цифровой подписи и подписываемый текст БОЙ. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Проверьте подлинность ЭЦП (7, 6) для сообщения с известным значением хэш-свертки 10, зная открытый ключ проверки подписи (384, 276). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Проверить действительность подписей (127, 230), (71, 65) для сообщения с известным значением хэш-свертки 165 и открытым ключом проверки (624,469). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Проверьте подлинность ЭЦП (11, 4) для сообщения с известным значением хэш-свертки 2, зная открытый ключ проверки подписи (596, 433). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Вычислить динамическое расстояние порядка 1 булевой функции 00100011 от 3 переменных
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 2205. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 27, значения цифровой подписи: r = 13; s = 29. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Дан шифртекст 185, а также значения модуля шифрования N = 247 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Вычислить значение  при a = 4618; b = 285; c = 24748.
при a = 4618; b = 285; c = 24748.
Вычислить порядок точки (20,  кривой
кривой  порядка 40.
порядка 40.
Даны значения модуля шифрования N = 221 и открытого ключа e = 35. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 172.
Найти произвольный квадратичный невычет по модулю 317
Дано: модуль шифрования N = 4891, открытый ключ e = 17. Найти значение шифртекста, полученного при зашифровании открытого текста 4654 на открытом ключе (N, e) по алгоритму RSA.
Вычислить нелинейность блока замен 3 10 4 2 6 9 14 8 11 5 13 1 7 0 15 12 размерностью  бит
бит
Шифротекст КАЛЗААК_ДЗИШТАА_ВЯ_Д_ООРС получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Найти остаток от деления  на 22.
на 22.
Вычислить динамическое расстояние порядка (2,2) блока замен 15 8 11 3 1 5 0 12 6 9 7 10 14 13 4 2 размерностью  бит
бит
Решить сравнение  с помощью цепных дробей.
с помощью цепных дробей.
Дан шифртекст 96, а также значения модуля шифрования N = 143 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Провести операцию MixColumns над приведенным ниже столбцом состояния
Расшифровать сообщение 4-4.txt, зашифрованное шифром Виженера, Длина ключа равна 4, пробел является частью алфавита.
В ответ введите ключ.
.
Определить, является ли число 27542476619900900873 простым с вероятностью не меньше 0,999.
Решить в целых числах уравнение  . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)
Найти дискретный логарифм числа 2 по основанию 69 по модулю 110881.
Решить в целых числах уравнение  . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)
Решить сравнение  с помощью цепных дробей.
с помощью цепных дробей.
Решить систему сравнений:
Решить сравнение  с помощью индексов. (В качестве ответа введите наименьшее значение x.)
с помощью индексов. (В качестве ответа введите наименьшее значение x.)
С помощью  -алгоритма Полларда найти наибольший нетривиальный делитель числа 1517.
-алгоритма Полларда найти наибольший нетривиальный делитель числа 1517.
Найти наименьший квадратный корень из 153 по модулю 281.
Расшифровать фразу АЗАДЙАЧЬЛНОЛИВЯЕЫУ_СЕТН_А, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Расшифровать текст 3-22.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите последнее слово заглавными буквами.
Расшифровать сообщение 4-17.txt, зашифрованное шифром Виженера, Длина ключа равна 4, пробел является частью алфавита.
В ответ введите ключ.
.
Расшифровать сообщение 5-2.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Зашифровать биграмму СУ с помощью матрицы  ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.
Вычислить нелинейность булевой функции 00000001 от 3 переменных
Вычислить динамическое расстояние порядка (2,2) блока замен 14 12 7 3 0 11 1 15 8 10 9 6 5 13 2 4 размерностью  бит
бит
Провести операцию SubBytes алгоритма AES со значением байта 3A.
Провести операцию MixColumns над приведенным ниже столбцом состояния
Даны значения модуля шифрования N = 299 и открытого ключа e = 61. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 178.
Применением цепных дробей найти секретный ключ d и разложение модуля 81177745546021 (экспонента — 2711039) на множители. В ответе укажите секретный ключ.
Дан шифртекст 58, а также значения модуля шифрования N = 187 и открытого ключа e = 3. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Сообщение 480 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {2,6,9,19,38,75,151}, m=301 и n=113. В ответе укажите исходное сообщение.
Зашифруйте открытый текст ОТСЛЕДИТЬ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(188, 93), значения случайных чисел для букв открытого текста k: 19, 2, 13, 5, 19, 5, 7, 8, 5, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(16, 416), (93, 484)}; {(489, 468), (531, 397)}; |
| {(188, 93), (654, 102)}; {(489, 468), (218, 150)}; |
| {(16, 416), (530, 729)}; {(425, 663), (295, 219)}; |
| {(725, 195), (742, 299)}; {(188, 93), (367, 360)}; |
| {(188, 93), (235, 732)}; {(618, 206), (251, 245)}; |
| {(425, 663), (688, 10)} |
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 1989. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 42, значения цифровой подписи: r = 34; s = 13. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 4381. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 32, значения цифровой подписи: r = 24; s = 45. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Вычислить порядок точки (2, 16) кривой  порядка 48.
порядка 48.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 7144. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 22, значения цифровой подписи: r = 47; s = 52. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Провести операцию SubBytes алгоритма AES со значением байта DD.
Вычислить динамическое расстояние порядка (2,2) блока замен 5 11 13 14 2 1 10 0 6 15 8 12 7 4 3 9 размерностью  бит
бит
Даны значения модуля шифрования N = 3403 и открытого ключа e = 2439. Используя метод факторизации Ферма, найти значение закрытого ключа.
Решить следующее сравнение  . (В качестве ответа введите наименьшее значение x.)
. (В качестве ответа введите наименьшее значение x.)
Дан шифртекст 152, а также значения модуля шифрования N = 187 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Найти количество квадратных корней из 595 по непримарному составному модулю 2431.
Найти произвольный квадратичный невычет по модулю 313
Расшифровать сообщение 5-15.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
В скольких подгруппах группы  порядка 5202 содержится фиксированный элемент порядка 3?
порядка 5202 содержится фиксированный элемент порядка 3?
Вычислить значение  при a = 5642; b = 272; c = 49989.
при a = 5642; b = 272; c = 49989.
Дано: модуль шифрования N = 5063, открытый ключ e = 11. Найти значение шифртекста, полученного при зашифровании открытого текста 4679 на открытом ключе (N, e) по алгоритму RSA.
Даны значения модуля шифрования N = 493 и открытого ключа e = 369. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 300.
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст пробел.
Расшифровать сообщение 4-7.txt, зашифрованное шифром Виженера, Длина ключа равна 6, пробел является частью алфавита.
В ответ введите ключ.
.
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(16, 416), (724, 522)}; {(489, 468), (719, 538)}; |
| {(56, 419), (205, 372)}; {(72, 254), (628, 293)}; |
| {(188, 93), (594, 337)}; {(440, 539), (588, 707)}; |
| {(568, 355), (707, 556)}; {(489, 468), (719, 538)}; |
| {(16, 416), (590, 376)}; {(56, 419), (612, 329)}; |
| {(188, 93), (594, 337)} |
Вычислить динамическое расстояние порядка (2,2) блока замен 9 13 0 10 12 2 15 11 3 6 8 7 14 4 5 1 размерностью  бит
бит
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=29, n2=41, x=7.
Чей компьютер он взломает быстрее?
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1011110100111110001011011.
, построить контрольную сумму для сообщения 1011110100111110001011011.
Найти корреляционную матрицу блока замен 2 12 1 4 13 7 9 6 8 14 0 15 3 5 11 10 размерностью  бит
бит
Даны значения модуля шифрования N = 3569 и открытого ключа e = 265. Используя метод факторизации Ферма, найти значение закрытого ключа.
Решить следующее сравнение  .
.
Расшифровать фразу РСГЕИЯ_Н_ЕТИАРЦСОСОТИ_СТЯ, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Дан шифртекст 28, а также значения модуля шифрования N = 187 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Решить в целых числах уравнение  . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)
Решить сравнение  с помощью цепных дробей.
с помощью цепных дробей.
Решить сравнение  с помощью индексов.
с помощью индексов.
Найти остаток от деления  на 11.
на 11.
Найти произвольный квадратичный невычет по модулю 257
Найти количество квадратных корней из 478 по непримарному составному модулю 1001.
Какая наибольшая степень элемента a порядка 66 порождает группу  ?
?
Расшифровать текст 3-23.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите предпоследнее слово заглавными буквами.
Расшифровать сообщение 4-14.txt, зашифрованное шифром Виженера, Длина ключа равна 6, пробел является частью алфавита.
В ответ введите ключ.
.
Расшифровать сообщение 5-10.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Расшифровать сообщение на английском языке 6-23.txt, зашифрованное шифром Виженера, Длина ключа равна 3.
В ответ введите ключ.
.
Зашифровать биграмму БУ с помощью матрицы  ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
ВОЛК
или
ЗАЯЦ
— устойчивее к действию этой программы?
Вычислить динамическое расстояние порядка 1 булевой функции 00001001 от 3 переменных
Вычислить нелинейность блока замен 2 10 7 6 3 5 15 4 12 8 14 0 9 11 13 1 размерностью  бит
бит
Найти корреляционную матрицу блока замен 15 4 14 0 8 13 7 5 1 12 3 10 2 6 11 9 размерностью  бит
бит
Провести операцию MixColumns над приведенным ниже столбцом состояния
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
Даны значения модуля шифрования N = 209 и открытого ключа e = 53. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 85.
Даны значения модуля шифрования N = 4183 и открытого ключа e = 2099. Используя метод факторизации Ферма, найти значение закрытого ключа.
Зашифруйте открытый текст ПРОКОПАТЬ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(489, 468), значения случайных чисел для букв открытого текста k: 3, 16, 17, 5, 16, 18, 3, 7, 15, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(618, 206), (426, 662)}; {(72, 254), (67, 667)}; |
| {(286, 136), (739, 574)}; {(16, 416), (143, 602)}; |
| {(618, 206), (313, 203)}; {(618, 206), (114, 607)}; |
| {(618, 206), (438, 711)}; {(188, 93), (573, 168)} |
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 3629. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 54, значения цифровой подписи: r = 56; s = 41. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=4, зная секретный ключ подписи d=6 при данном значении выбираемого случайным образом числа k=11. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Проверьте подлинность ЭЦП (7, 7) для сообщения с известным значением хэш-свертки 9, зная открытый ключ проверки подписи (135, 82). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=47, n2=41, x=9.
Чей компьютер он взломает быстрее?
Решить сравнение  с помощью индексов.
с помощью индексов.
Зашифруйте открытый текст НИКЕЛЕВЫЙ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=,(568, 355) значения случайных чисел для букв открытого текста k: 9, 9, 2, 3, 8, 19, 6, 18, 9, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Вычислить нелинейность булевой функции 01101000 от 3 переменных
Шифротекст ПКЕРЕЛТИЧЮЕМУТ_Б_РЕЛВХРЕВ получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Решить сравнение  с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)
с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)
Проверить действительность подписей (10, 163), (10, 153) для сообщения с известным значением хэш-свертки 169 и открытым ключом проверки (671,267). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Провести первый раунд зашифрования открытого текста F1FE EF23 8B38 B3BF шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
ГОРШОК
или
ЦВЕТОК
— устойчивее к действию этой программы?
Решить в целых числах уравнение  . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)
Расшифровать сообщение 5-4.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Вычислить нелинейность блока замен 7 9 3 10 13 11 4 14 8 1 12 5 6 0 15 2 размерностью  бит
бит
Найти остаток от деления  на 11.
на 11.
Расшифровать текст 3-4.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите второе слово заглавными буквами.
Зашифруйте открытый текст ОТСТУПИТЬ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(188, 93), значения случайных чисел для букв открытого текста k: 7, 9, 3, 8, 18, 18, 8, 11, 16, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст КРИВАЯ.
Вычислить значение  при a = 2794; b = 509; c = 12876.
при a = 2794; b = 509; c = 12876.
Решить в целых числах уравнение  . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)
Решить сравнение  с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)
с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)
Решить систему сравнений:
Найти остаток от деления  на 10.
на 10.
Вычислить значение  при a = 6259; b = 580; c = 50861.
при a = 6259; b = 580; c = 50861.
С помощью  -алгоритма Полларда найти наибольший нетривиальный делитель числа 3239.
-алгоритма Полларда найти наибольший нетривиальный делитель числа 3239.
Найти наименьший квадратный корень из 233 по примарному модулю 343.
Найти количество квадратных корней из 914 по непримарному составному модулю 2431.
Какая наибольшая степень элемента a порядка 54 порождает группу  ?
?
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1100010010010001001001100.
, построить контрольную сумму для сообщения 1100010010010001001001100.
Расшифровать фразу П_КИУУТОРГ.ЙЕ_Щ_О_КИАУЛСБ, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Расшифровать текст 3-18.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите последнее слово заглавными буквами.
Расшифровать сообщение на английском языке 6-8.txt, зашифрованное шифром Виженера, Длина ключа равна 5.
В ответ введите ключ.
.
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст МАСТЕР.
Найти корреляционную матрицу блока замен 15 8 11 3 1 5 0 12 6 9 7 10 14 13 4 2 размерностью  бит
бит
Провести операцию SubBytes алгоритма AES со значением байта 53.
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
Даны значения модуля шифрования N = 437 и открытого ключа e = 233. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 381.
Даны значения модуля шифрования N = 1891 и открытого ключа e = 277. Используя метод факторизации Ферма, найти значение закрытого ключа.
Сообщение 302 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {1,4,6,12,25,49,100}, m=199 и n=78. В ответе укажите исходное сообщение.
Зашифруйте открытый текст МЫСЛЕННЫЙ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(346, 242), значения случайных чисел для букв открытого текста k: 6, 17, 18, 11, 18, 2, 4, 2, 12, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 3271. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 21, значения цифровой подписи: r = 2; s = 47. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=9, зная секретный ключ подписи d=6 при данном значении выбираемого случайным образом числа k=6. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Даны значения модуля шифрования N = 143 и открытого ключа e = 19. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 115.
Провести первый раунд зашифрования открытого текста E90A F652 CD88 F9EC шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
С помощью  -алгоритма Полларда найти наибольший нетривиальный делитель числа 4819.
-алгоритма Полларда найти наибольший нетривиальный делитель числа 4819.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=33 и k=35 системы цифровой подписи и подписываемый текст СКАЧ. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Применением цепных дробей найти секретный ключ d и разложение модуля 54296750879837 (экспонента — 4282063) на множители. В ответе укажите секретный ключ.
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
Провести операцию MixColumns над приведенным ниже столбцом состояния
Провести первый раунд зашифрования открытого текста C20A 8A8E A533 C2AB шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Проверьте подлинность ЭЦП (7, 6) для сообщения с известным значением хэш-свертки 2, зная открытый ключ проверки подписи (135, 669). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Даны значения модуля шифрования N = 3239 и открытого ключа e = 2467. Используя метод факторизации Ферма, найти значение закрытого ключа.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 8948. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 30, значения цифровой подписи: r = 38; s = 16. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Вычислить порядок точки (28, 17) кривой  порядка 40.
порядка 40.
Решить в целых числах уравнение  . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)
Найти число всех подгрупп (не включая единичную) группы  порядка 5545, не содержащих элемент порядка 5.
порядка 5545, не содержащих элемент порядка 5.
Шифртекст (3928629409, 01011110010001001001) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=96263, q=98479. Найти открытый текст и введите его заглавными буквами.
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(745, 210), (185, 105)}; {(188, 93), (681, 385)}; |
| {(377, 456), (576, 465)}; {(440, 539), (138, 298)}; |
| {(745, 210), (520, 2)}; {(188, 93), (681, 385)}; |
| {(286, 136), (282, 410)}; {(72, 254), (200, 721)}; |
| {(72, 254), (643, 94)}; {(745, 210), (476, 315)}; |
| {(440, 539), (724, 229)} |
Решить в целых числах уравнение  . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)
Решить следующее сравнение  .
.
Решить систему сравнений:
Найти количество квадратных корней из 399 по непримарному составному модулю 2431.
Найти дискретный логарифм числа 3 по основанию 10 по модулю 112501.
Расшифровать текст 3-9.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите третье слово заглавными буквами.
Расшифровать сообщение 4-1.txt, зашифрованное шифром Виженера, Длина ключа равна 6, пробел является частью алфавита.
В ответ введите ключ.
.
Вычислить динамическое расстояние порядка (2,2) блока замен 15 6 5 9 2 13 14 12 7 3 11 0 10 8 1 4 размерностью  бит
бит
Найти корреляционную матрицу блока замен 15 6 5 9 2 13 14 12 7 3 11 0 10 8 1 4 размерностью  бит
бит
Провести операцию MixColumns над приведенным ниже столбцом состояния
Провести первый раунд зашифрования открытого текста C485 FB04 B366 E288 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Применением цепных дробей найти секретный ключ d и разложение модуля 59046883376179 (экспонента — 4044583) на множители. В ответе укажите секретный ключ.
Шифртекст (8978530064, 11010000110111010111) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=95747, q=95327. Найти открытый текст и введите его заглавными буквами.
Зашифруйте открытый текст ТЕРПЕЛИВО с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(725, 195), значения случайных чисел для букв открытого текста k: 17, 5, 4, 17, 13, 2, 17, 14, 19, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(618, 206), (99, 456)}; {(425, 663), (31, 136)}; |
| {(377, 456), (688, 741)}; {(425, 663), (636, 747)}; |
| {(16, 416), (298, 526)}; {(188, 93), (356, 175)}; |
| {(489, 468), (147, 390)}; {(346, 242), (546, 670)}; |
| {(72, 254), (114, 144)}; {(377, 456), (25, 147)} |
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 1867. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 20, значения цифровой подписи: r = 36; s = 57. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Расшифровать фразу РЕТИ_АУКС_РКСАРГФАРАРБЗАЕ, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=29, n2=23, x=19.
Чей компьютер он взломает быстрее?
Вычислить нелинейность блока замен 9 13 0 10 12 2 15 11 3 6 8 7 14 4 5 1 размерностью  бит
бит
В скольких подгруппах группы  порядка 5545 содержится фиксированный элемент порядка 5?
порядка 5545 содержится фиксированный элемент порядка 5?
Провести операцию MixColumns над приведенным ниже столбцом состояния
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=17 и k=11 системы цифровой подписи и подписываемый текст ЩИТ. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Найти остаток от деления  на 12.
на 12.
Зашифруйте открытый текст ОТСТАВНОЙ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(286, 136), значения случайных чисел для букв открытого текста k: 5, 3, 3, 2, 4, 19, 2, 4, 10, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Вычислить динамическое расстояние порядка (2,2) блока замен 12 9 10 6 5 0 3 15 14 8 2 11 1 13 4 7 размерностью  бит
бит
Проверьте подлинность ЭЦП (11, 1) для сообщения с известным значением хэш-свертки 5, зная открытый ключ проверки подписи (384, 475). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(179, 275), (269, 564)}; {(179, 275), (73, 72)}; |
| {(440, 539), (189, 454)}; {(618, 206), (628, 458)}; |
| {(568, 355), (660, 275)}; {(72, 254), (709, 595)}; |
| {(745, 210), (12, 314)}; {(188, 93), (36, 664)}; |
| {(618, 206), (530, 22)}; {(286, 136), (532, 50)}; |
| {(425, 663), (660, 275)}; {(725, 195), (482, 230)} |
Решить следующее сравнение  .
.
Дано: модуль шифрования N = 8633, открытый ключ e = 13. Найти значение шифртекста, полученного при зашифровании открытого текста 688 на открытом ключе (N, e) по алгоритму RSA.
Найти число всех подгрупп (не включая единичную) группы  порядка 6656, не содержащих элемент порядка 26.
порядка 6656, не содержащих элемент порядка 26.
Расшифровать сообщение 5-12.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Шифртекст (102131499, 11010111001111111000) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=95891, q=90007. Найти открытый текст и введите его заглавными буквами.
Решить сравнение  с помощью индексов.
с помощью индексов.
Зашифруйте открытый текст ИЗЛЕЧИМЫЙ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(179, 275), значения случайных чисел для букв открытого текста k: 10, 14, 2, 2, 10, 10, 14, 3, 7, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Решить систему сравнений:
Определить, является ли число 9418352160768000001 простым с вероятностью не меньше 0,999.
С помощью  -алгоритма Полларда найти наибольший нетривиальный делитель числа 2279.
-алгоритма Полларда найти наибольший нетривиальный делитель числа 2279.
Найти произвольный квадратичный невычет по модулю 283
Найти дискретный логарифм числа 18 по основанию 2 по модулю 97021.
Расшифровать сообщение на английском языке 6-2.txt, зашифрованное шифром Виженера, Длина ключа равна 5.
В ответ введите ключ.
.
Зашифровать биграмму ДУ с помощью матрицы  ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
ВОРОНА
или
ЛИСИЦА
— устойчивее к действию этой программы?
Вычислить нелинейность булевой функции 01001010 от 3 переменных
Вычислить динамическое расстояние порядка 1 булевой функции 01001100 от 3 переменных
Вычислить нелинейность блока замен 2 0 13 7 9 11 14 3 1 10 5 15 4 12 6 размерностью  бит
бит
Найти корреляционную матрицу блока замен 13 11 7 4 12 14 6 8 9 10 3 1 0 2 5 15 размерностью  бит
бит
Провести операцию SubBytes алгоритма AES со значением байта 95.
Провести операцию MixColumns над приведенным ниже столбцом состояния
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
Даны значения модуля шифрования N = 2911 и открытого ключа e = 487. Используя метод факторизации Ферма, найти значение закрытого ключа.
Дан шифртекст 13, а также значения модуля шифрования N = 77 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Сообщение 812 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {5,6,12,24,48,98,195}, m=389 и n=111. В ответе укажите исходное сообщение.
Шифртекст (5538085341, 11011101111000111001) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=90059, q=91199. Найти открытый текст и введите его заглавными буквами.
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(725, 195), (9, 150)}; {(745, 210), (138, 453)}; |
| {(56, 419), (36, 87)}; {(283, 493), (39, 580)}; |
| {(377, 456), (515, 684)}; {(346, 242), (458, 261)}; |
| {(283, 493), (105, 369)}; {(568, 355), (326, 675)}; |
| {(425, 663), (529, 358)}; {(283, 493), (668, 409)} |
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 3669. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 15, значения цифровой подписи: r = 6; s = 29. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Проверьте подлинность ЭЦП (11, 10) для сообщения с известным значением хэш-свертки 10, зная открытый ключ проверки подписи (455, 383). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Проверить действительность подписей (150,17), (195, 167) для сообщения с известным значением хэш-свертки 59 и открытым ключом проверки (60,74). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Сообщение 595 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {2,5,9,17,35,77,146}, m=292 и n=109. В ответе укажите исходное сообщение.
Даны значения модуля шифрования N = 1891 и открытого ключа e = 1487. Используя метод факторизации Ферма, найти значение закрытого ключа.
Вычислить динамическое расстояние порядка (2,2) блока замен 3 10 4 2 6 9 14 8 11 5 13 1 7 0 15 12 размерностью  бит
бит
Шифротекст ПРГРОА_АММНАЗЕ_ПАКУСЕ_ЯТС получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Расшифровать текст 3-14.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите последнее слово заглавными буквами.
Решить систему сравнений:
Провести операцию MixColumns над приведенным ниже столбцом состояния
Провести операцию SubBytes алгоритма AES со значением байта 1D.
С помощью  -алгоритма Полларда найти наибольший нетривиальный делитель числа 2449.
-алгоритма Полларда найти наибольший нетривиальный делитель числа 2449.
Дан шифртекст 82, а также значения модуля шифрования N = 119 и открытого ключа e = 5. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Найти произвольный квадратичный невычет по модулю 359
Решить сравнение  с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)
с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)
Дано: модуль шифрования N = 5767, открытый ключ e = 17. Найти значение шифртекста, полученного при зашифровании открытого текста 3063 на открытом ключе (N, e) по алгоритму RSA.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=3, зная секретный ключ подписи d=3 при данном значении выбираемого случайным образом числа k=11. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Сообщение 442 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {2,4,8,15,30,60,122}, m=244 и n=83. В ответе укажите исходное сообщение.
Найти наибольший квадратный корень из 336 по примарному модулю 625.
Найти количество квадратных корней из 781 по непримарному составному модулю 1001.
Найти корреляционную матрицу блока замен 4 2 0 10 11 9 6 1 13 8 15 14 12 5 7 3 размерностью  бит
бит
Провести операцию MixColumns над приведенным ниже столбцом состояния
Решить следующее сравнение  .
.
Решить сравнение  с помощью цепных дробей.
с помощью цепных дробей.
Найти остаток от деления  на 1000.
на 1000.
Вычислить значение  при a = 3825; b = 701; c = 32551.
при a = 3825; b = 701; c = 32551.
Определить, является ли число 14532464368718952447 простым с вероятностью не меньше 0,999.
Найти наибольший квадратный корень из 350 по примарному модулю 625.
Найти дискретный логарифм числа 31 по основанию 3 по модулю 114689.
Расшифровать сообщение 4-8.txt, зашифрованное шифром Виженера, Длина ключа равна 6, пробел является частью алфавита.
В ответ введите ключ.
.
Расшифровать сообщение на английском языке 6-10.txt, зашифрованное шифром Виженера, Длина ключа равна 4.
В ответ введите ключ.
.
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст ЧАЙНИК.
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
ЧАЙНИК
или
МАСТЕР
— устойчивее к действию этой программы?
Вычислить нелинейность булевой функции 01001010 от 3 переменных
Вычислить динамическое расстояние порядка 1 булевой функции 00011001 от 3 переменных
Провести операцию SubBytes алгоритма AES со значением байта 9B.
Провести операцию MixColumns над приведенным ниже столбцом состояния
Провести первый раунд зашифрования открытого текста 8DAA 8960 C100 DFD3 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Даны значения модуля шифрования N = 209 и открытого ключа e = 131. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 92.
Даны значения модуля шифрования N = 5917 и открытого ключа e = 1103. Используя метод факторизации Ферма, найти значение закрытого ключа.
Применением цепных дробей найти секретный ключ d и разложение модуля 67510894259489 (экспонента — 3543923) на множители. В ответе укажите секретный ключ.
Шифртекст (8137015367, 01101001111001011111) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=98899, q=101531. Найти открытый текст и введите его заглавными буквами.
Зашифруйте открытый текст КУПАЛЬЩИК с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(188, 93), значения случайных чисел для букв открытого текста k: 17, 17, 9, 12, 17, 7, 15, 7, 16, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(72, 254), (397, 184)}; {(188, 93), (526, 412)}; |
| {(188, 93), (328, 290)}; {(135, 82), (433, 47)}; |
| {(179, 275), (711, 341)}; {(568, 355), (546, 670)}; |
| {(16, 416), (734, 170)}; {(568, 355), (371, 14)}; |
| {(596, 433), (604, 610)}; {(16, 416), (734, 170)} |
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=12 и k=47 системы цифровой подписи и подписываемый текст ЛУЧ. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Проверьте подлинность ЭЦП (3, 10) для сообщения с известным значением хэш-свертки 2, зная открытый ключ проверки подписи (596, 433). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Дано: модуль шифрования N = 1763, открытый ключ e = 11. Найти значение шифртекста, полученного при зашифровании открытого текста 436 на открытом ключе (N, e) по алгоритму RSA.
С помощью  -алгоритма Полларда найти наибольший нетривиальный делитель числа 5063.
-алгоритма Полларда найти наибольший нетривиальный делитель числа 5063.
Применением цепных дробей найти секретный ключ d и разложение модуля 93767386321457 (экспонента — 2091619) на множители. В ответе укажите секретный ключ.
Найти количество квадратных корней из 900 по непримарному составному модулю 1001.
Вычислить значение  при a = 3823; b = 788; c = 50508.
при a = 3823; b = 788; c = 50508.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=6, зная секретный ключ подписи d=12 при данном значении выбираемого случайным образом числа k=7. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Проверьте подлинность ЭЦП (11, 12) для сообщения с известным значением хэш-свертки 5, зная открытый ключ проверки подписи (596, 433). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст ПЛУТОН.
Зашифруйте открытый текст АБЕРРАЦИЯ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(56, 419), значения случайных чисел для букв открытого текста k: 16, 2, 17, 19, 8, 4, 3, 2, 8, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Вычислить значение  при a = 2473; b = 382; c = 59825.
при a = 2473; b = 382; c = 59825.
Вычислить нелинейность булевой функции 00100010 от 3 переменных
Вычислить порядок точки (9, 11) кривой  порядка 33.
порядка 33.
Найти наибольший квадратный корень из 17 по модулю 257.
Расшифровать текст 3-24.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите последнее слово заглавными буквами.
Найти остаток от деления  на 48.
на 48.
Найти произвольный квадратичный невычет по модулю 383
Найти количество квадратных корней из 324 по непримарному составному модулю 7429.
Решить следующее сравнение  . (В качестве ответа введите наименьшее значение x.)
. (В качестве ответа введите наименьшее значение x.)
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1100000110010011010000011.
, построить контрольную сумму для сообщения 1100000110010011010000011.
Шифротекст СЗАУПРТИС_РЕД_УБАЗАР_ОТИК получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Расшифровать текст 3-1.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число. (Примечание: знак _ обозначает пробел между словами.)
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите предпоследнее слово заглавными буквами.
Вычислить нелинейность булевой функции 01011000 от 3 переменных
Вычислить динамическое расстояние порядка (2,2) блока замен 2 12 1 4 13 7 9 6 8 14 0 15 3 5 11 10 размерностью  бит
бит
Провести операцию SubBytes алгоритма AES со значением байта 18.
Провести операцию MixColumns над приведенным ниже столбцом состояния
Провести первый раунд зашифрования открытого текста E26A 945F BE59 B5CC шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Применением цепных дробей найти секретный ключ d и разложение модуля 87046121832829 (экспонента — 2342047) на множители. В ответе укажите секретный ключ.
Шифртекст (901439779, 10110110111111110111) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=101839, q=98867. Найти открытый текст и введите его заглавными буквами.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 6686. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 53, значения цифровой подписи: r = 22; s = 30. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 7135. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 46, значения цифровой подписи: r = 50; s = 52. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Проверьте подлинность ЭЦП (5, 2) для сообщения с известным значением хэш-свертки 7, зная открытый ключ проверки подписи (384, 276). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
Вычислить значение  при a = 8484; b = 621; c = 25106.
при a = 8484; b = 621; c = 25106.
Решить сравнение  с помощью индексов.
с помощью индексов.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=6, зная секретный ключ подписи d=10 при данном значении выбираемого случайным образом числа k=7. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Расшифровать фразу _ТОЬВО_ВМЫОПРГИИСУ_ПЛЙ_ОП, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Найти дискретный логарифм числа 31 по основанию 5 по модулю 118273.
Вычислить динамическое расстояние порядка (2,2) блока замен 13 6 3 14 12 11 4 1 15 5 10 7 0 9 2 8 размерностью  бит
бит
Найти остаток от деления  на 13.
на 13.
Даны значения модуля шифрования N = 3901 и открытого ключа e = 343. Используя метод факторизации Ферма, найти значение закрытого ключа.
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1110101000011100000001111.
, построить контрольную сумму для сообщения 1110101000011100000001111.
Дан шифртекст 10, а также значения модуля шифрования N = 221 и открытого ключа e = 5. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Расшифровать сообщение 4-12.txt, зашифрованное шифром Виженера, Длина ключа равна 5, пробел является частью алфавита.
В ответ введите ключ.
.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=10, зная секретный ключ подписи d=9 при данном значении выбираемого случайным образом числа k=2. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Решить систему сравнений:
Найти остаток от деления  на 11.
на 11.
С помощью  -алгоритма Полларда найти наибольший нетривиальный делитель числа 2263.
-алгоритма Полларда найти наибольший нетривиальный делитель числа 2263.
Найти наименьший квадратный корень из 70 по примарному модулю 81.
Расшифровать сообщение 5-3.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Расшифровать сообщение на английском языке 6-20.txt, зашифрованное шифром Виженера, Длина ключа равна 4.
В ответ введите ключ.
.
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст СИНТЕЗ.
Вычислить динамическое расстояние порядка 1 булевой функции 00110010 от 3 переменных
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
Сообщение 1097 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {4,6,11,23,45,92,186}, m=369 и n=31. В ответе укажите исходное сообщение.
Шифртекст (8446011652, 10111001000000000000) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=101603, q=99871. Найти открытый текст и введите его заглавными буквами.
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(16, 416), (726, 608)}; {(188, 93), (395, 337)}; |
| {(440, 539), (163, 513)}; {(188, 93), (269, 187)}; |
| {(725, 195), (177, 562)}; {(188, 93), (115, 509)}; |
| {(188, 93), (734, 170)}; {(745, 210), (110, 622)}; |
| {(179, 275), (576, 286)}; {(188, 93), (325, 297)} |
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=6, зная секретный ключ подписи d=12 при данном значении выбираемого случайным образом числа k=11. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Проверить действительность подписей (10, 153), (11, 133) для сообщения с известным значением хэш-свертки 141 и открытым ключом проверки (35,374). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 3521. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 28, значения цифровой подписи: r = 18; s = 31. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Применением цепных дробей найти секретный ключ d и разложение модуля 42982346145803 (экспонента — 4777621) на множители. В ответе укажите секретный ключ.
Провести операцию MixColumns над приведенным ниже столбцом состояния
Провести первый раунд зашифрования открытого текста 991C 9E65 9A45 BD8C шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Сообщение 516 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {2,3,7,13,27,55,109}, m=218 и n=131. В ответе укажите исходное сообщение.
Решить в целых числах уравнение  . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1101111101111101101100100.
, построить контрольную сумму для сообщения 1101111101111101101100100.
Определить, является ли число 1243354398042316799 простым с вероятностью не меньше 0,999.
Найти наибольший квадратный корень из 29 по примарному модулю 625.
Найти дискретный логарифм числа 12 по основанию 17 по модулю 118801.
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1111011100110110000001001.
, построить контрольную сумму для сообщения 1111011100110110000001001.
Шифротекст ЭЕМЕФРДЫ_ИЗГРУАЖНЫ_ЕВОЗУ_ получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Расшифровать текст 3-21.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите первое слово заглавными буквами.
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=23, n2=47, x=16.
Чей компьютер он взломает быстрее?
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
ОВАЛ
или
КРУГ
— устойчивее к действию этой программы?
Вычислить нелинейность булевой функции 01101011 от 3 переменных
Вычислить нелинейность блока замен 6 15 12 4 14 2 3 9 1 7 11 10 13 5 8 0 размерностью  бит
бит
Провести операцию SubBytes алгоритма AES со значением байта 47.
Провести операцию MixColumns над приведенным ниже столбцом состояния
Применением цепных дробей найти секретный ключ d и разложение модуля 85609460573249 (экспонента — 2448539) на множители. В ответе укажите секретный ключ.
Найти корреляционную матрицу блока замен 14 12 7 3 0 11 1 15 8 10 9 6 5 13 2 4 размерностью  бит
бит
Зашифровать биграмму МУ с помощью матрицы  ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.
Расшифровать текст 3-19.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите второе слово заглавными буквами.
Вычислить значение  при a = 1611; b = 857; c = 47199.
при a = 1611; b = 857; c = 47199.
Решить следующее сравнение  . (В качестве ответа введите наименьшее значение x.)
. (В качестве ответа введите наименьшее значение x.)
Вычислить динамическое расстояние порядка 1 булевой функции 00110001 от 3 переменных
Вычислить порядок точки (11, 3) кривой  порядка 30.
порядка 30.
Дано: модуль шифрования N = 3953, открытый ключ e = 17. Найти значение шифртекста, полученного при зашифровании открытого текста 2402 на открытом ключе (N, e) по алгоритму RSA.
Провести операцию SubBytes алгоритма AES со значением байта E8.
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст ТАЙМЕР.
Решить сравнение  с помощью цепных дробей.
с помощью цепных дробей.
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=37, n2=43, x=12.
Чей компьютер он взломает быстрее?
Вычислить нелинейность булевой функции 00011001 от 3 переменных
Вычислить нелинейность блока замен 12 9 0 15 6 13 1 5 14 7 11 2 4 8 10 3 размерностью  бит
бит
Найти корреляционную матрицу блока замен 5 2 14 10 8 7 15 11 13 4 3 9 12 6 1 0 размерностью  бит
бит
Провести операцию SubBytes алгоритма AES со значением байта 6B
Провести операцию MixColumns над приведенным ниже столбцом состояния
Провести первый раунд зашифрования открытого текста FAAA A9D9 D006 8DC3 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Дано: модуль шифрования N = 4087, открытый ключ e = 13. Найти значение шифртекста, полученного при зашифровании открытого текста 3474 на открытом ключе (N, e) по алгоритму RSA.
Применением цепных дробей найти секретный ключ d и разложение модуля 55925060669503 (экспонента — 4156793) на множители. В ответе укажите секретный ключ.
Дан шифртекст 117, а также значения модуля шифрования N = 187 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=3, зная секретный ключ подписи d=1 при данном значении выбираемого случайным образом числа k=8. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Вычислить нелинейность булевой функции 01111111 от 3 переменных
Найти наибольший квадратный корень из 13 по примарному модулю 27.
Найти наибольший квадратный корень из 60 по модулю 241.
Вычислить нелинейность булевой функции 00011010 от 3 переменных
Проверить действительность подписей (166, 213), (3, 188) для сообщения с известным значением хэш-свертки 45 и открытым ключом проверки (286, 213). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Провести операцию MixColumns над приведенным ниже столбцом состояния
Решить в целых числах уравнение  . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)
Решить следующее сравнение  . (В качестве ответа введите наименьшее значение x.)
. (В качестве ответа введите наименьшее значение x.)
Найти остаток от деления  на 5.
на 5.
С помощью  -алгоритма Полларда найти наибольший нетривиальный делитель числа 2479.
-алгоритма Полларда найти наибольший нетривиальный делитель числа 2479.
Найти наименьший квадратный корень из 340 по примарному модулю 343.
Расшифровать текст 3-2.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите последнее слово заглавными буквами.
Расшифровать сообщение на английском языке 6-21.txt, зашифрованное шифром Виженера, Длина ключа равна 5.
В ответ введите ключ.
.
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст ЛОГИКА.
Вычислить нелинейность блока замен 14 7 13 2 0 10 8 9 4 3 15 5 12 11 1 6 размерностью  бит
бит
Вычислить динамическое расстояние порядка (2,2) блока замен 8 14 3 7 4 11 12 6 5 1 10 15 0 9 2 13 размерностью  бит
бит
Провести операцию MixColumns над приведенным ниже столбцом состояния
Даны значения модуля шифрования N = 3569 и открытого ключа e = 1013. Используя метод факторизации Ферма, найти значение закрытого ключа.
Применением цепных дробей найти секретный ключ d и разложение модуля 62781628076903 (экспонента — 3804071) на множители. В ответе укажите секретный ключ.
Зашифруйте открытый текст НЕЭТИЧНЫЙ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(489, 468), значения случайных чисел для букв открытого текста k: 14, 18, 11, 11, 6, 6, 17, 2, 5, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Проверьте подлинность ЭЦП (11, 11) для сообщения с известным значением хэш-свертки 9, зная открытый ключ проверки подписи (416, 696). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Проверить действительность подписей (10, 163), (31, 79) для сообщения с известным значением хэш-свертки 214 и открытым ключом проверки (73,63). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Вычислить значение  при a = 9018; b = 435; c = 73171.
при a = 9018; b = 435; c = 73171.
Вычислить динамическое расстояние порядка 1 булевой функции 01110111 от 3 переменных
Проверьте подлинность ЭЦП (3, 2) для сообщения с известным значением хэш-свертки 12, зная открытый ключ проверки подписи (562, 89). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Вычислить нелинейность булевой функции 01110111 от 3 переменных
Провести операцию MixColumns над приведенным ниже столбцом состояния
Зашифровать биграмму ТЫ с помощью матрицы  ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.
Решить сравнение  с помощью индексов.
с помощью индексов.
Вычислить динамическое расстояние порядка 1 булевой функции 00000001 от 3 переменных
Решить следующее сравнение  .
.
Решить систему сравнений:
Найти остаток от деления  на 18.
на 18.
Вычислить порядок точки (13, 7) кривой  порядка 36.
порядка 36.
Расшифровать фразу _ЕТИЕИ_ЛО_АКАЗЖС_.ЩТЛУТС_, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Расшифровать сообщение 4-10.txt, зашифрованное шифром Виженера, Длина ключа равна 6, пробел является частью алфавита.
В ответ введите ключ.
.
Вычислить нелинейность блока замен 15 0 1 6 8 3 4 14 5 9 11 7 10 13 2 12 размерностью  бит
бит
Провести операцию SubBytes алгоритма AES со значением байта 69.
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
Сообщение 505 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {1,3,5,13,23,49,99}, m=195 и n=127. В ответе укажите исходное сообщение.
Зашифровать биграмму АН с помощью матрицы  ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.
Определить, является ли число 2332134563018038201 простым с вероятностью не меньше 0,999.
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
Найти наименьший квадратный корень из 49 по модулю 317.
Решить сравнение  с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)
с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)
С помощью  -алгоритма Полларда найти наибольший нетривиальный делитель числа 1927.
-алгоритма Полларда найти наибольший нетривиальный делитель числа 1927.
С помощью  -алгоритма Полларда найти наибольший нетривиальный делитель числа 5141.
-алгоритма Полларда найти наибольший нетривиальный делитель числа 5141.
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1101100000111111010001011.
, построить контрольную сумму для сообщения 1101100000111111010001011.
Провести операцию SubBytes алгоритма AES со значением байта 1E.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=22 и k=25 системы цифровой подписи и подписываемый текст РОЙ. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Решить в целых числах уравнение  . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)
Определить, является ли число 2305843009213693951 простым с вероятностью не меньше 0,999.
Расшифровать фразу _ПАЕНЕ_ВИ_ЯНЕРЖЕ_ИСТИОКНЗ, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Вычислить динамическое расстояние порядка 1 булевой функции 01100100 от 3 переменных
Вычислить нелинейность блока замен 15 9 4 6 12 1 0 8 10 11 2 7 13 14 3 5 размерностью  бит
бит
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
Даны значения модуля шифрования N = 143 и открытого ключа e = 113. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 64.
Сообщение 945 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {2,4,7,14,29,57,116}, m=233 и n=64. В ответе укажите исходное сообщение.
Зашифруйте открытый текст ПРОЛЕЖЕНЬ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(179, 275), значения случайных чисел для букв открытого текста k: 9, 5, 17, 2, 2, 2, 3, 17, 15, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Проверить действительность подписей (35, 236), (57, 230) для сообщения с известным значением хэш-свертки 10 и открытым ключом проверки (177,531). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
ПИЛЮЛЯ
или
БОЛЮСЫ
— устойчивее к действию этой программы?
Решить в целых числах уравнение  . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)
Решить сравнение  с помощью цепных дробей.
с помощью цепных дробей.
Какая наибольшая степень элемента a порядка 60 порождает группу  ?
?
Вычислить нелинейность булевой функции 00001001 от 3 переменных
Дано: модуль шифрования N = 2257, открытый ключ e = 17. Найти значение шифртекста, полученного при зашифровании открытого текста 539 на открытом ключе (N, e) по алгоритму RSA.
Расшифровать сообщение 5-13.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Расшифровать текст 3-25.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите последнее слово заглавными буквами.
Решить сравнение  с помощью индексов.
с помощью индексов.
С помощью  -алгоритма Полларда найти наибольший нетривиальный делитель числа 2501.
-алгоритма Полларда найти наибольший нетривиальный делитель числа 2501.
Найти количество квадратных корней из 2278 по непримарному составному модулю 2431.
Зашифровать биграмму РО с помощью матрицы  ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.
Вычислить динамическое расстояние порядка 1 булевой функции 01010100 от 3 переменных
Вычислить динамическое расстояние порядка (2,2) блока замен 15 14 7 10 4 8 1 12 13 2 11 3 9 5 0 6 размерностью  бит
бит
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
Провести первый раунд зашифрования открытого текста E37F C8BC F84A DFA3 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Даны значения модуля шифрования N = 377 и открытого ключа e = 283. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 66.
Дан шифртекст 117, а также значения модуля шифрования N = 133 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Шифртекст (1439738115, 11000111110111010001) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=100847, q=96331. Найти открытый текст и введите его заглавными буквами.
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(425, 663), (651, 191)}; {(188, 93), (177, 562)}; |
| {(286, 136), (603, 562)}; {(440, 539), (588, 707)}; |
| {(72, 254), (269, 187)}; {(56, 419), (49, 568)}; |
| {(16, 416), (426, 662)}; {(425, 663), (557, 28)}; |
| {(188, 93), (149, 97)}; {(179, 275), (711, 341)} |
Проверьте подлинность ЭЦП (11, 10) для сообщения с известным значением хэш-свертки 3, зная открытый ключ проверки подписи (135, 669). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст ТАЙФУН.
Даны значения модуля шифрования N = 143 и открытого ключа e = 37. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 100.
С помощью  -алгоритма Полларда найти нетривиальный делитель числа 5251.
-алгоритма Полларда найти нетривиальный делитель числа 5251.
Решить сравнение  с помощью индексов.
с помощью индексов.
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
ПЛАЦЕБО
или
СПАСИБО
— устойчивее к действию этой программы?
Найти остаток от деления  на 1000.
на 1000.
Найти дискретный логарифм числа 21 по основанию 7 по модулю 96001.
Шифротекст ПООВРД_ЕРИБНАКЕ__ЕДВТА_ДС получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Зашифровать биграмму АД с помощью матрицы  ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.
Вычислить нелинейность булевой функции 01100011 от 3 переменных
Найти корреляционную матрицу блока замен 15 14 7 10 4 8 1 12 13 2 11 3 9 5 0 6 размерностью  бит
бит
Провести операцию SubBytes алгоритма AES со значением байта CB.
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=37 и k=25 системы цифровой подписи и подписываемый текст ВВОД. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Вычислить нелинейность блока замен 11 3 14 5 12 6 13 1 10 2 8 4 15 0 9 7 размерностью  бит
бит
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
ПЛИТА
или
ПЛАТО
— устойчивее к действию этой программы?
Провести операцию MixColumns над приведенным ниже столбцом состояния
Решить систему сравнений:
(В качестве ответа введите наименьшее значение x.)
Решить сравнение  с помощью индексов. (В качестве ответа введите наименьшее значение x.)
с помощью индексов. (В качестве ответа введите наименьшее значение x.)
Вычислить нелинейность булевой функции 01001100 от 3 переменных
Найти произвольный квадратичный невычет по модулю 227
Расшифровать сообщение на английском языке 6-9.txt, зашифрованное шифром Виженера, Длина ключа равна 3.
В ответ введите ключ.
.
Найти наибольший квадратный корень из 188 по модулю 211.
Вычислить порядок точки (3, 5) кривой  порядка 32.
порядка 32.
Расшифровать сообщение на английском языке 6-12.txt, зашифрованное шифром Виженера, Длина ключа равна 5.
В ответ введите ключ.
.
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
ШУБА
или
СНЕГ
— устойчивее к действию этой программы?
Вычислить нелинейность блока замен 15 4 14 0 8 13 7 5 1 12 3 10 2 6 11 9 размерностью  бит
бит
Вычислить динамическое расстояние порядка (2,2) блока замен 12 9 0 15 6 13 1 5 14 7 11 2 4 8 10 3 размерностью  бит
бит
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
Шифртекст (3441665394, 10010010000100110110) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=92051, q=94651. Найти открытый текст и введите его заглавными буквами.
Найти наименьший квадратный корень из 18 по модулю 223.
Даны значения модуля шифрования N = 667 и открытого ключа e = 575. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 593.
Вычислить нелинейность булевой функции 00000001 от 3 переменных
Зашифруйте открытый текст РЕГРЕССОР с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(425, 663), значения случайных чисел для букв открытого текста k: 6, 12, 16, 4, 9, 4, 19, 9, 18, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(725, 195), (329, 304)}; {(440, 539), (59, 386)}; |
| {(618, 206), (543, 357)}; {(188, 93), (520, 749)}; |
| {(489, 468), (585, 211)}; {(179, 275), (707, 556)}; |
| {(596, 433), (419, 38)}; {(377, 456), (643, 94)}; |
| {(188, 93), (385, 749)}; {(725, 195), (150, 355)}; |
| {(725, 195), (197, 606)} |
Провести операцию SubBytes алгоритма AES со значением байта 43.
Решить сравнение  с помощью индексов. (В качестве ответа введите наименьшее значение x.)
с помощью индексов. (В качестве ответа введите наименьшее значение x.)
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1111110111100101001010100.
, построить контрольную сумму для сообщения 1111110111100101001010100.
Расшифровать фразу О_ДАВВРСТЕТСИМЯ_ВУ_Х_РПАК, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Расшифровать сообщение 4-9.txt, зашифрованное шифром Виженера, Длина ключа равна 7, пробел является частью алфавита.
В ответ введите ключ.
.
Провести операцию MixColumns над приведенным ниже столбцом состояния
Даны значения модуля шифрования N = 2911 и открытого ключа e = 359. Используя метод факторизации Ферма, найти значение закрытого ключа.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=7 и k=23 системы цифровой подписи и подписываемый текст ТОР. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Решить сравнение  с помощью индексов.
с помощью индексов.
Найти произвольный квадратичный невычет по модулю 353
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
СТАТУС
или
ЗОЛОТО
— устойчивее к действию этой программы?
Найти корреляционную матрицу блока замен 12 2 8 3 9 1 11 15 14 6 4 5 13 0 10 7 размерностью  бит
бит
Решить следующее сравнение  .
.
Решить сравнение  с помощью цепных дробей.
с помощью цепных дробей.
Решить систему сравнений:
Дано: модуль шифрования N = 1961, открытый ключ e = 11. Найти значение шифртекста, полученного при зашифровании открытого текста 1382 на открытом ключе (N, e) по алгоритму RSA.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=48 и k=23 системы цифровой подписи и подписываемый текст РЫБА. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Решить в целых числах уравнение  . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)
Найти корреляционную матрицу блока замен 15 9 4 6 12 1 0 8 10 11 2 7 13 14 3 5 размерностью  бит
бит
Расшифровать текст 3-11.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите четвертое слово заглавными буквами.
Дано: модуль шифрования N = 8051, открытый ключ e = 11. Найти значение шифртекста, полученного при зашифровании открытого текста 6206 на открытом ключе (N, e) по алгоритму RSA.
Зашифруйте открытый текст ЛАТЫШСКИЙ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(179,275), значения случайных чисел для букв открытого текста k: 15, 17, 12, 2, 2, 4, 8, 6, 17, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Проверьте подлинность ЭЦП (5, 5) для сообщения с известным значением хэш-свертки 7, зная открытый ключ проверки подписи (384, 475). Используйте кривую  и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13
Вычислить порядок точки (35, 4) кривой  порядка 44.
порядка 44.
Найти остаток от деления  на 7.
на 7.
Расшифровать текст 3-6.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите последнее слово заглавными буквами.
Провести первый раунд зашифрования открытого текста B89F F9A1 C5A5 8C39 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Применением цепных дробей найти секретный ключ d и разложение модуля 48992988576733 (экспонента — 4545733) на множители. В ответе укажите секретный ключ.
Сообщение 518 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {1,3,5,10,21,42,88}, m=171 и n=23. В ответе укажите исходное сообщение.
Проверить действительность подписей (166, 186), (104, 103) для сообщения с известным значением хэш-свертки 115 и открытым ключом проверки (126,463). Используется кривая  и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251.
Вычислить нелинейность блока замен 9 4 15 11 7 0 5 6 13 14 1 8 10 2 3 12 размерностью  бит
бит
Сообщение 518 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {1,4,7,15,28,57,114}, m=227 и n=51. В ответе укажите исходное сообщение.
С помощью  -алгоритма Полларда найти наибольший нетривиальный делитель числа 4559.
-алгоритма Полларда найти наибольший нетривиальный делитель числа 4559.
Провести операцию SubBytes алгоритма AES со значением байта 35.
Вычислить динамическое расстояние порядка 1 булевой функции 01100100 от 3 переменных
Решить систему сравнений:
Найти наибольший квадратный корень из 195 по модулю 233.
Даны значения модуля шифрования N = 2701 и открытого ключа e = 1507. Используя метод факторизации Ферма, найти значение закрытого ключа.
Дан шифртекст 52, а также значения модуля шифрования N = 133 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Сообщение 249 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {1,2,7,11,23,47,92}, m=185 и n=29. В ответе укажите исходное сообщение.
Сообщение 390 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {3,4,9,17,34,69,137}, m=277 и n=99. В ответе укажите исходное сообщение.
Применением цепных дробей найти секретный ключ d и разложение модуля 64806601923671 (экспонента — 3676721) на множители. В ответе укажите секретный ключ.
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(725, 195), (538, 325)}; {(725, 195), (176, 413)}; |
| {(425, 663), (689, 670)}; {(346, 242), (652, 315)}; |
| {(283, 493), (463, 736)}; {(16, 416), (744, 133)}; |
| {(179, 275), (542, 351)}; {(56, 419), (298, 225)}; |
| {(286, 136), (719, 538)}; {(568, 355), (319, 518)}; |
| {(16, 416), (704, 46)} |
Найти количество квадратных корней из 1820 по непримарному составному модулю 2431.
Расшифровать сообщение 4-15.txt, зашифрованное шифром Виженера, Длина ключа равна 5, пробел является частью алфавита.
В ответ введите ключ.
.
Расшифровать сообщение на английском языке 6-6.txt, зашифрованное шифром Виженера, Длина ключа равна 3.
В ответ введите ключ.
.
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
МАКАКИ
или
ЖИРАФЫ
— устойчивее к действию этой программы?
Даны значения модуля шифрования N = 3397 и открытого ключа e = 2477. Используя метод факторизации Ферма, найти значение закрытого ключа.
Применением цепных дробей найти секретный ключ d и разложение модуля 34542035262313 (экспонента — 4727621) на множители. В ответе укажите секретный ключ.
Шифртекст (432159239, 01101010010011011001) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=93503, q=97007. Найти открытый текст и введите его заглавными буквами.
Зашифруйте открытый текст НОВЕНЬКИЙ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(425,663), значения случайных чисел для букв открытого текста k: 19, 12, 13, 2, 12, 14, 19, 18, 12, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(440, 539), (279, 398)}; {(568, 355), (295, 219)}; |
| {(16, 416), (724, 229)}; {(346, 242), (730, 240)}; |
| {(72, 254), (334, 226)}; {(188, 93), (310, 169)}; |
| {(72, 254), (36, 664)}; {(179, 275), (481, 369)}; |
| {(188, 93), (236, 39)}; {(377, 456), (438, 711)}; |
| {(377, 456), (307, 58)} |
Решить систему сравнений:
Решить в целых числах уравнение  . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)
Дан шифртекст 90, а также значения модуля шифрования N = 247 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Расшифровать сообщение 5-1.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Найти остаток от деления  на 7.
на 7.
Определить, является ли число 1111111111111111111 простым с вероятностью не меньше 0,999.
Найти дискретный логарифм числа 23 по основанию 13 по модулю 90001.
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
Провести первый раунд зашифрования открытого текста 97A0 9BD3 DF10 C86A шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Применением цепных дробей найти секретный ключ d и разложение модуля 50824793010569 (экспонента — 4440901) на множители. В ответе укажите секретный ключ.
Решить сравнение  с помощью цепных дробей.
с помощью цепных дробей.
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(16, 416), (675, 505)}; {(72, 254), (611, 579)}; |
| {(72, 254), (727, 686)}; {(489, 468), (39, 171)}; |
| {(72, 254), (531, 354)}; {(568, 355), (36, 87)}; |
| {(188, 93), (588, 44)}; {(618, 206), (70, 195)}; |
| {(568, 355), (267, 81)}; {(56, 419), (525, 674)} |
Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=37, n2=23, x=14.
Чей компьютер он взломает быстрее?
С помощью  -алгоритма Полларда найти наибольший нетривиальный делитель числа 3869.
-алгоритма Полларда найти наибольший нетривиальный делитель числа 3869.
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1010001111010000011110000.
, построить контрольную сумму для сообщения 1010001111010000011110000.
Расшифровать сообщение на английском языке 6-3.txt, зашифрованное шифром Виженера, Длина ключа равна 5.
В ответ введите ключ.
.
Сообщение 537 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {2,3,7,15,29,57,115}, m=230 и n=43. В ответе укажите исходное сообщение.
Решить сравнение  с помощью индексов. (В качестве ответа введите наименьшее значение x.)
с помощью индексов. (В качестве ответа введите наименьшее значение x.)
Вычислить динамическое расстояние порядка (2,2) блока замен 12 0 7 10 6 4 15 9 3 8 1 5 14 13 11 2 размерностью  бит
бит
Провести операцию MixColumns над приведенным ниже столбцом состояния
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
РАБОТА
или
ОТПУСК
— устойчивее к действию этой программы?
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 7707. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 46, значения цифровой подписи: r = 11; s = 43. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
Расшифровать фразу МДЕ_Ж__ВТАЕТВТОНЧЕИЕН_ДЯЕ, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Вычислить нелинейность булевой функции 00100011 от 3 переменных
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст РАЗДЕЛ.
Решить систему сравнений:
С помощью  -алгоритма Полларда найти наибольший нетривиальный делитель числа 2773.
-алгоритма Полларда найти наибольший нетривиальный делитель числа 2773.
Расшифровать сообщение 4-2.txt, зашифрованное шифром Виженера, Длина ключа равна 6, пробел является частью алфавита.
В ответ введите ключ.
.
Зашифровать биграмму НЕ с помощью матрицы  ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.
Вычислить динамическое расстояние порядка 1 булевой функции 01111000 от 3 переменных
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=9, зная секретный ключ подписи d=11 при данном значении выбираемого случайным образом числа k=2. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Найти остаток от деления  на 14.
на 14.
Вычислить значение  при a = 5105; b = 414; c = 89303.
при a = 5105; b = 414; c = 89303.
Найти количество квадратных корней из 1598 по непримарному составному модулю 2431.
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1110000001000000101010101.
, построить контрольную сумму для сообщения 1110000001000000101010101.
Расшифровать текст 3-12.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите первое слово заглавными буквами.
Вычислить динамическое расстояние порядка (2,2) блока замен 15 0 1 6 8 3 4 14 5 9 11 7 10 13 2 12 размерностью  бит
бит
Решить сравнение  с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)
с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)
Даны значения модуля шифрования N = 391 и открытого ключа e = 47. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 262.
Решить следующее сравнение  .
.
Применением цепных дробей найти секретный ключ d и разложение модуля 99595193774911 (экспонента — 1908299) на множители. В ответе укажите секретный ключ.
Определить, является ли число 4108888687178291199 простым с вероятностью не меньше 0,999.
С помощью  -алгоритма Полларда найти наибольший нетривиальный делитель числа 4661.
-алгоритма Полларда найти наибольший нетривиальный делитель числа 4661.
Вычислить нелинейность блока замен 15 6 5 9 2 13 14 12 7 3 11 0 10 8 1 4 размерностью  бит
бит
Найти корреляционную матрицу блока замен 9 4 15 11 7 0 5 6 13 14 1 8 10 2 3 12 размерностью  бит
бит
С помощью  -алгоритма Полларда найти наибольший нетривиальный делитель числа 3127.
-алгоритма Полларда найти наибольший нетривиальный делитель числа 3127.
Дан шифртекст 49, а также значения модуля шифрования N = 187 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Решить в целых числах уравнение  . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)
Расшифровать сообщение 5-19.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Определить, является ли число 4653425899839733759 простым с вероятностью не меньше 0,999.
Найти дискретный логарифм числа 53 по основанию 23 по модулю 115201.
Вычислить динамическое расстояние порядка (2,2) блока замен 15 10 4 2 0 13 9 1 12 6 7 5 3 8 14 11 размерностью  бит
бит
Провести операцию SubBytes алгоритма AES со значением байта 72.
Дано: модуль шифрования N = 3071, открытый ключ e = 11. Найти значение шифртекста, полученного при зашифровании открытого текста 1058 на открытом ключе (N, e) по алгоритму RSA.
Найти дискретный логарифм числа 10 по основанию 14 по модулю 106921.
Определить, является ли число 99599500573849980909 простым с вероятностью не меньше 0,999.
Используя порождающий полином для CRC  , построить контрольную сумму для сообщения 1111000110001000100101001.
, построить контрольную сумму для сообщения 1111000110001000100101001.
Провести первый раунд зашифрования открытого текста FE2D FEEA B158 BE38 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Даны значения модуля шифрования N = 143 и открытого ключа e = 113. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 124.
Даны значения модуля шифрования N = 4717 и открытого ключа e = 523. Используя метод факторизации Ферма, найти значение закрытого ключа.
Решить следующее сравнение  .
.
Дан шифртекст 84, а также значения модуля шифрования N = 187 и открытого ключа e = 3. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Найти наибольший квадратный корень из 524 по примарному модулю 625.
Зашифруйте открытый текст РЕПАРАЦИЯ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(435, 663), значения случайных чисел для букв открытого текста k: 12, 11, 18, 7, 16, 18, 17, 2, 3, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
Сообщение 792 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {1,7,9,19,37,75,152}, m=307 и n=63. В ответе укажите исходное сообщение.
Определить, является ли число 9642690137449562111 простым с вероятностью не меньше 0,999.
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст ЭЛЛИПС.
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
Провести операцию SubBytes алгоритма AES со значением байта D6.
Решить следующее сравнение  . (В качестве ответа введите наименьшее значение x.)
. (В качестве ответа введите наименьшее значение x.)
Даны значения модуля шифрования N = 319 и открытого ключа e = 51. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 209.
Зашифруйте открытый текст НИЩЕНСКИЙ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(489, 468), значения случайных чисел для букв открытого текста k: 2, 2, 7, 11, 19, 4, 2, 15, 6, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Провести первый раунд зашифрования открытого текста CF85 F7CE F928 C262 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Вычислить динамическое расстояние порядка (2,2) блока замен 13 11 7 4 12 14 6 8 9 10 3 1 0 2 5 15 размерностью  бит
бит
Найти произвольный квадратичный невычет по модулю 281
Найти корреляционную матрицу блока замен 12 0 7 10 6 4 15 9 3 8 1 5 14 13 11 2 размерностью  бит
бит
Зашифруйте открытый текст ЗВЕЗДОЧКА с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(725, 195), значения случайных чисел для букв открытого текста k: 11, 17, 10, 10, 5, 2, 10, 19, 4, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(188, 93), (295, 219)}; {(618, 206), (646, 706)}; |
| {(440, 539), (573, 583)}; {(16, 416), (694, 581)}; |
| {(179, 275), (585, 540)}; {(377, 456), (701, 570)}; |
| {(618, 206), (67, 667)}; {(286, 136), (36, 664)}; |
| {(72, 254), (727, 65)}; {(568, 355), (438, 40)} |
Провести операцию SubBytes алгоритма AES со значением байта EF.
Провести первый раунд зашифрования открытого текста D14E C9C9 F441 8039 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок  .
.
Вычислить нелинейность булевой функции 01110111 от 3 переменных
Решить сравнение  с помощью индексов. (В качестве ответа введите наименьшее значение x.)
с помощью индексов. (В качестве ответа введите наименьшее значение x.)
Расшифровать фразу МИКСО_ВЫ_ЕУБ_АДПЛДЕУОНСНИ, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
Вычислить динамическое расстояние порядка 1 булевой функции 01111111 от 3 переменных
Вычислить нелинейность блока замен 2 12 1 4 13 7 9 6 8 14 0 15 3 5 11 10 размерностью  бит
бит
Вычислить значение  при a = 8105; b = 405; c = 25261.
при a = 8105; b = 405; c = 25261.
Вычислить нелинейность блока замен 15 14 7 10 4 8 1 12 13 2 11 3 9 5 0 6 размерностью  бит
бит
Сообщение 429 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {1,4,6,14,27,55,109}, m=217 и n=73. В ответе укажите исходное сообщение.
Решить следующее сравнение  .
.
Решить систему сравнений:
Расшифровать сообщение на английском языке 6-16.txt, зашифрованное шифром Виженера, Длина ключа равна 4.
В ответ введите ключ.
.
Шифротекст КУАМКЛТУОЯ_ЖРЕУРЗ_РАЖНЯ_Е получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
Дан шифртекст 107, а также значения модуля шифрования N = 209 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Зашифруйте открытый текст ЛАТЕНТНЫЙ с помощью алфавита, приведенного в таблице, используйте открытый ключ B=(725, 195), значения случайных чисел для букв открытого текста k: 9, 10, 13, 2, 2, 12, 12, 5, 7, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
Вычислить динамическое расстояние порядка (2,2) блока замен 4 2 0 10 11 9 6 1 13 8 15 14 12 5 7 3 размерностью  бит
бит
Сообщение 492 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {3,4,8,17,33,67,138}, m=271 и n=65. В ответе укажите исходное сообщение.
Расшифровать текст 3-10.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите третье слово заглавными буквами.
Провести операцию MixColumns над приведенным ниже столбцом состояния
Зашифровать биграмму ДА с помощью матрицы  ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.
Шифртекст (6737479610, 00010100110100110110) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=93763, q=90011. Найти открытый текст и введите его заглавными буквами.
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(745, 210), (268, 597)}; {(725, 195), (310, 582)}; |
| {(618, 206), (59, 365)}; {(440, 539), (371, 14)}; |
| {(188, 93), (348, 27)}; {(72, 254), (434, 136)}; |
| {(16, 416), (623, 166)}; {(188, 93), (235, 19)}; |
| {(440, 539), (660, 275)}; {(188, 93), (434, 615)}; |
| {(725, 195), (73, 679)}; {(188, 93), (642, 53)} |
Расшифровать сообщение 5-11.txt, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Расшифровать сообщение на английском языке 6-5.txt, зашифрованное шифром Виженера, Длина ключа равна 4.
В ответ введите ключ.
.
Вычислить динамическое расстояние порядка (2,2) блока замен 12 2 8 3 9 1 11 15 14 6 4 5 13 0 10 7 размерностью  бит
бит
Дано: модуль шифрования N = 4307, открытый ключ e = 17. Найти значение шифртекста, полученного при зашифровании открытого текста 983 на открытом ключе (N, e) по алгоритму RSA.
Решить сравнение  с помощью цепных дробей.
с помощью цепных дробей.
Провести операцию MixColumns над приведенным ниже столбцом состояния
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3Д 4 Е 5 Ё 6 Ж 7З 8 И 9 Й 10 К 11Л 12 М 13 Н 14 О 15П 16 Р 17 С 18 Т 19У 20 Ф 21 Х 22 Ц 23Ч 24 Ш 25 Щ 26 Ъ 27Ы 28 Ь 29 Э 30 Ю 31 Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст АНАЛИЗ.
Вычислить нелинейность блока замен 15 8 11 3 1 5 0 12 6 9 7 10 14 13 4 2 размерностью  бит
бит
Сообщение 402 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {6,7,14,29,57,114,229}, m=457 и n=150. В ответе укажите исходное сообщение.
Расшифровать сообщение на английском языке 6-19.txt, зашифрованное шифром Виженера, Длина ключа равна 4.
В ответ введите ключ.
.
Вычислить динамическое расстояние порядка 1 булевой функции 01001010 от 3 переменных
Решить сравнение  с помощью индексов.
с помощью индексов.
Определить, является ли число 48112959837082048697 простым с вероятностью не меньше 0,999.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=3, зная секретный ключ подписи d=10 при данном значении выбираемого случайным образом числа k=6. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
С помощью  -алгоритма Полларда найти наибольший нетривиальный делитель числа 4399.
-алгоритма Полларда найти наибольший нетривиальный делитель числа 4399.
С помощью  -алгоритма Полларда найти наибольший нетривиальный делитель числа 4331.
-алгоритма Полларда найти наибольший нетривиальный делитель числа 4331.
Дан шифртекст, показанный ниже. Зная секретный ключ  , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  и генерирующая точка G = (-1, 1)).
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(440, 539), (128, 672)}; {(489, 468), (282, 341)}; |
| {(489, 468), (45, 720)}; {(72, 254), (227, 299)}; |
| {(188, 93), (251, 506)}; {(72, 254), (319, 518)}; |
| {(745, 210), (129, 659)}; {(286, 136), (515, 684)}; |
| {(568, 355), (395, 414)} |
Найти корреляционную матрицу блока замен 11 3 14 5 12 6 13 1 10 2 8 4 15 0 9 7 размерностью  бит
бит
Провести операцию SubBytes алгоритма AES со значением байта D9.
Вычислить нелинейность булевой функции 01010111 от 3 переменных
Найти корреляционную матрицу блока замен 1 9 12 14 2 11 13 10 8 6 15 5 0 7 4 3 размерностью  бит
бит
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
РУБАХА
или
ПОРТКИ
— устойчивее к действию этой программы?
Михаил Витер
Эксперт по предмету «Информационная безопасность»
Задать вопрос автору статьи
Определение 1
Криптографическая защита информации – это механизм защиты посредством шифрования данных для обеспечения информационной безопасности общества.
Криптографические методы защиты информации активно используются в современной жизни для хранения, обработки и передачи информации по сетям связи и на различных носителях.
Сущность и цели криптографической защиты информации
Сегодня самым надежным способом шифрования при передаче информационных данных на большие расстояния является именно криптографическая защита информации.
Криптография – это наука, изучающая и описывающая модели информационной безопасности (далее – ИБ) данных. Она позволяет разрешить многие проблемы, что присущи информационной безопасности сети: конфиденциальность, аутентификация, контроль и целостность взаимодействующих участников.

Тренируй мозг с удовольствием
Развивай память, внимание и мышление c помощью онлайн-тренажеров
Выбрать программу
Определение 2
Шифрование – это преобразование информационных данных в форму, которая будет не читабельной для программных комплексов и человека без ключа шифрования-расшифровки. Благодаря криптографическим методам защиты информации обеспечиваются средства информационной безопасности, поэтому они являются основной частью концепции ИБ.
Замечание 1
Ключевой целью криптографической защиты информации является обеспечение конфиденциальности и защиты информационных данных компьютерных сетей в процессе передачи ее по сети между пользователями системы.
Защита конфиденциальной информации, которая основана на криптографической защите, зашифровывает информационные данные посредством обратимых преобразований, каждое из которых описывается ключом и порядком, что определяет очередность их применения.
«Криптографическая защита информации» 👇
Важным компонентом криптографической защиты информации является ключ, отвечающий за выбор преобразования и порядок его реализации.
Определение 3
Ключ – это определенная последовательность символов, которая настраивает шифрующий и дешифрующий алгоритм системы криптозащиты информации. Каждое преобразование определяется ключом, задающим криптографический алгоритм, который обеспечивает безопасность информационной системы и информации в целом.
Каждый алгоритм криптозащиты информации работает в разных режимах, которые обладают, как рядом преимуществ, так и рядом недостатков, что влияют на надежность информационной безопасности государства и средства ИБ.
Средства и методы криптографической защиты информации
К основным средствам криптозащиты информации можно отнести программные, аппаратные и программно-аппаратные средства, которые реализуют криптографические алгоритмы информации с целью:
- защиты информационных данных при их обработке, использовании и передаче;
- обеспечения целостности и достоверности обеспечения информации при ее хранении, обработке и передаче (в том числе с применением алгоритмов цифровой подписи);
- выработки информации, которая используется для аутентификации и идентификации субъектов, пользователей и устройств;
- выработки информации, которая используется для защиты аутентифицирующих элементов при их хранении, выработке, обработке и передаче.
В настоящее время криптографические методы защиты информации для обеспечения надежной аутентификации сторон информационного обмена являются базовыми. Они предусматривают шифрование и кодирование информации.
Различают два основных метода криптографической защиты информации:
- симметричный, в котором один и тот же ключ, что хранится в секрете, применяется и для шифровки, и для расшифровки данных;
- ассиметричный.
Кроме этого существуют весьма эффективные методы симметричного шифрования – быстрый и надежный. На подобные методы в Российской Федерации предусмотрен государственный стандарт «Системы обработки информации. Криптографическая защита информации. Алгоритм криптографического преобразования» — ГОСТ 28147-89.
В ассиметричных методах криптографической защиты информации используются два ключа:
- Несекретный, который может публиковаться вместе с другими сведениями о пользователе, что являются открытыми. Этот ключ применяется для шифрования.
- Секретный, который известен только получателю, используется для расшифровки.
Из ассиметричных наиболее известным методом криптографической защиты информации является метод RSA, который основан на операциях с большими (100-значными) простыми числами, а также их произведениями.
Благодаря применению криптографических методов можно надежно контролировать целостность отдельных порций информационных данных и их наборов, гарантировать невозможность отказаться от совершенных действий, а также определять подлинность источников данных.
Основу криптографического контроля целостности составляют два понятия:
- Электронная подпись.
- Хэш-функция.
Определение 4
Хэш-функция – это одностороння функция или преобразование данных, которое сложно обратить, реализуемое средствами симметричного шифрования посредством связывания блоков. Результат шифрования последнего блока, который зависит от всех предыдущих, и служит результатом хэш-функции.
В коммерческой деятельности криптографическая защита информации приобретает все большее значение. Для того чтобы преобразовать информацию, используются разнообразные шифровальные средства: средства шифрования документации (в том числе для портативного исполнения), средства шифрования телефонных разговоров и радиопереговоров, а также средства шифрования передачи данных и телеграфных сообщений.
Для того чтобы защитить коммерческую тайну на отечественном и международном рынке, используются комплекты профессиональной аппаратуры шифрования и технические устройства криптозащиты телефонных и радиопереговоров, а также деловой переписки.
Кроме этого широкое распространение получили также маскираторы и скремблеры, которые заменяют речевой сигнал цифровой передачей данных. Производятся криптографические средства защиты факсов, телексов и телетайпов. Для этих же целей применяются и шифраторы, которые выполняются в виде приставок к аппаратам, в виде отдельных устройств, а также в виде устройств, которые встраиваются в конструкцию факс-модемов, телефонов и других аппаратов связи. Электронная цифровая подпись широкое применяется для того, чтобы обеспечить достоверность передаваемых электронных сообщений.
Криптографическая защита информации в РФ решает вопрос целостности посредством добавления определенной контрольной суммы или проверочной комбинации для того, чтобы вычислить целостность данных. Модель информационной безопасности является криптографической, то есть она зависит от ключа. По оценкам информационной безопасности, которая основана на криптографии, зависимость вероятности прочтения данных от секретного ключа является самым надежным инструментом и даже используется в системах государственной информационной безопасности.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Правильные ответы выделены зелёным цветом.
Все ответы: В курсе дан необходимый теоретический минимум по основным вопросам современной криптографии.
Решить в целых числах уравнение 
Определить, является ли число 2305843009213693951 простым с вероятностью не меньше 0,999.
Шифротекст РВЕПИИЕ_ДТРМЕПИ_ИАРДРМЫГА получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
ПРИВЕДИТЕ_ПРИМЕР_ДИАГРАМЫ
Вычислить нелинейность булевой функции 01010100 от 3 переменных
Дано: модуль шифрования N = 3149, открытый ключ e = 13. Найти значение шифртекста, полученного при зашифровании открытого текста 2027 на открытом ключе (N, e) по алгоритму RSA.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=5 и k=31 системы цифровой подписи и подписываемый текст ШАР. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Решить следующее сравнение 
С помощью 
Расшифровать фразу НУАСТРИОДЕРРОАТТЕСГИВО_ВИ, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
УСТАНОВИ_ВИДЕОРЕГИСТРАТОР
Вычислить динамическое расстояние порядка 1 булевой функции 01010100 от 3 переменных
Даны значения модуля шифрования N = 437 и открытого ключа e = 233. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 381.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=6 и k=29 системы цифровой подписи и подписываемый текст БАР. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Решить сравнение 
Найти произвольный квадратичный невычет по модулю 337
Расшифровать текст 3-1.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число. (Примечание: знак _ обозначает пробел между словами.)
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите предпоследнее слово заглавными буквами.
Вычислить нелинейность блока замен 15 4 14 0 8 13 7 5 1 12 3 10 2 6 11 9 размерностью 
Даны значения модуля шифрования N = 2911 и открытого ключа e = 487. Используя метод факторизации Ферма, найти значение закрытого ключа.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 3521. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 28, значения цифровой подписи: r = 18; s = 31. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
(1) подпись действительна
(2) подпись недействительна
Решить систему сравнений:

Найти наибольший квадратный корень из 188 по модулю 211.
Расшифровать сообщение
4-1.txt
, зашифрованное шифром Виженера, Длина ключа равна 6, пробел является частью алфавита.
В ответ введите ключ.
.
Вычислить динамическое расстояние порядка (2,2) блока замен 15 4 14 0 8 13 7 5 1 12 3 10 2 6 11 9 размерностью 
Применением цепных дробей найти секретный ключ d и разложение модуля 99595193774911 (экспонента — 1908299) на множители. В ответе укажите секретный ключ.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 7135. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 46, значения цифровой подписи: r = 50; s = 52. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
(1) подпись действительна
(2) подпись недействительна
Решить сравнение 
Найти наибольший квадратный корень из 29 по примарному модулю 625.
Расшифровать сообщение
5-1.txt
, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Найти корреляционную матрицу блока замен 15 4 14 0 8 13 7 5 1 12 3 10 2 6 11 9 размерностью 
(1)
begin{matrix}
0.25 & -0.5 & 0.25 & 0
0.25 & 0.25 & -0.25 & 0
0.25 & 0 & 0 & 0
0 & 0.25 & -0.5 & 0
end{matrix}
(2)
begin{matrix}
-0.25 & -0.5 & 0.25 & 0
0.25 & 0.25 & -0.25 & 0
0.25 & 0 & 0 & 0
0 & 0.25 & -0.5 & 0end{matrix}
(3)
begin{matrix}
0.25 & -0.5 & 0.25 & 0
0.25 & 0.25 & 0.25 & 0
0.25 & 0 & 0 & 0
0 & 0.25 & -0.5 & 0end{matrix}
(4)
begin{matrix}
0.25 & -0.5 & 0.25 & 0
0.25 & 0.25 & -0.25 & 0
0.25 & 0 & 0 & 0
0 & 0.25 & 0.5 & 0end{matrix}
Дан шифртекст 82, а также значения модуля шифрования N = 119 и открытого ключа e = 5. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=9, зная секретный ключ подписи d=3 при данном значении выбираемого случайным образом числа k=5. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Найти остаток от деления 
Найти количество квадратных корней из 291 по непримарному составному модулю 385.
Расшифровать сообщение на английском языке
6-1.txt
, зашифрованное шифром Виженера, Длина ключа равна 3.
В ответ введите ключ.
.
Провести операцию SubBytes алгоритма AES со значением байта 3A.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=6, зная секретный ключ подписи d=12 при данном значении выбираемого случайным образом числа k=11. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Вычислить значение 
Найти число элементов порядка 1734 в циклической группе порядка 5202.
Провести операцию MixColumns над приведенным ниже столбцом состояния
Проверьте подлинность ЭЦП (11, 4) для сообщения с известным значением хэш-свертки 4, зная открытый ключ проверки подписи (596, 318). Используйте кривую 
(1) подпись действительна
(2) подпись недействительна
Найти дискретный логарифм числа 23 по основанию 13 по модулю 90001.
Зашифровать биграмму ОН с помощью матрицы 
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
5A11FBA5474A9F8EC5B1B01B7FC389CC
Сообщение 295 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {1,5,8,16,31,63,125}, m=251 и n=56. В ответе укажите исходное сообщение.
Проверить действительность подписей (10, 153), (11, 133) для сообщения с известным значением хэш-свертки 141 и открытым ключом проверки (35,374). Используется кривая 
(1) обе подписи действительны
(2) первая подпись действительна, вторая — недействительна
(3) первая подпись недействительна, вторая — действительна
(4) обе подписи недействительны
Используя порождающий полином для CRC 
(1) {0,1,0,0,0}
(2) {1,1,0,0,0}
(3) {0,0,0,1,0}
(4) {1,1,0,0,1}
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3
Д 4 Е 5 Ё 6 Ж 7
З 8 И 9 Й 10 К 11
Л 12 М 13 Н 14 О 15
П 16 Р 17 С 18 Т 19
У 20 Ф 21 Х 22 Ц 23
Ч 24 Ш 25 Щ 26 Ъ 27
Ы 28 Ь 29 Э 30 Ю 31
Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст АНАЛИЗ.
Провести первый раунд зашифрования открытого текста 97F4 C6AD D65F A8A2 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок 
Шифртекст (9775365428, 11010000001111001000) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=101987, q=101267. Найти открытый текст и введите его заглавными буквами.
С помощью алгоритма Берлекемпа проверить, является ли приводимым многочлен 

Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=29, n2=23, x=19.
Чей компьютер он взломает быстрее?
Зашифруйте открытый текст ПЕРЕДРЯГА с помощью алфавита, приведенного в
таблице
, используйте открытый ключ B=(489, 468), значения случайных чисел
для букв открытого текста k: 18, 15, 14, 18, 5, 10, 19, 14, 19, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
(1) {(618, 206),(253, 211)}; {(745, 210),(318, 429)}; {(596, 433),(85, 716)};
{(618, 206),(90, 730)}; {(425, 663),(43, 527)}; {(377, 456),(652, 315)}; {(568, 355),(675, 505)}; {(596, 433),(376, 686)}; {(568, 355),(85, 35)}
(2) {(745, 210),(318, 429)}; {(596, 433),(85, 716)}; {(618, 206),(253, 211)};
{(618, 206),(90, 730)}; {(425, 663),(43, 527)}; {(377, 456),(652, 315)}; {(568, 355),(675, 505)}; {(596, 433),(376, 686)}; {(568, 355),(85, 35)}
(3) {(425, 663),(43, 527)}; {(618, 206),(253, 211)}; {(745, 210),(318, 429)}; {(596, 433),(85, 716)};
{(618, 206),(90, 730)}; {(377, 456),(652, 315)}; {(568, 355),(675, 505)}; {(596, 433),(376, 686)}; {(568, 355),(85, 35)}
(4) {(377, 456),(652, 315)}; {(618, 206),(253, 211)}; {(745, 210),(318, 429)}; {(596, 433),(85, 716)};
{(618, 206),(90, 730)}; {(425, 663),(43, 527)}; {(568, 355),(675, 505)}; {(596, 433),(376, 686)}; {(568, 355),(85, 35)}
Даны точки P(58, 139), Q(67, 667), R(82, 481) на кривой 

Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
ВОРОНА
или
ЛИСИЦА
— устойчивее к действию этой программы?
(1) Первый пароль надежнее
(2) Второй пароль надежнее
(3) Пароли одинаково ненадежные
Дан шифртекст, показанный ниже. Зная секретный ключ 
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(440, 539), (128, 672)}; {(489, 468), (282, 341)}; |
| {(489, 468), (45, 720)}; {(72, 254), (227, 299)}; |
| {(188, 93), (251, 506)}; {(72, 254), (319, 518)}; |
| {(745, 210), (129, 659)}; {(286, 136), (515, 684)}; |
| {(568, 355), (395, 414)} |
Дана точка P(62, 372) на кривой 

Вычислить порядок точки (2, 16) кривой 
Решить в целых числах уравнение 
Определить, является ли число 9642690137449562111 простым с вероятностью не меньше 0,999.
Шифротекст РОВПЕ_ИТНЕЛЕГРУ_ТОЯРОЛЕВВ получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
ПОВЕРНИТЕ_РЕГУЛЯТОР_ВЛЕВО
Вычислить нелинейность булевой функции 01001010 от 3 переменных
Дано: модуль шифрования N = 5767, открытый ключ e = 17. Найти значение шифртекста, полученного при зашифровании открытого текста 3063 на открытом ключе (N, e) по алгоритму RSA.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=12 и k=47 системы цифровой подписи и подписываемый текст ЛУЧ. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Решить следующее сравнение 
С помощью 
Расшифровать фразу ИРТЙООИИЛББ__ОД_ТИКЕПК_КА, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
КАК_ПРОЙТИ_ДО_БИБЛИОТЕКИ_
Вычислить динамическое расстояние порядка 1 булевой функции 01001010 от 3 переменных
Даны значения модуля шифрования N = 253 и открытого ключа e = 139. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 106.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=21 и k=5 системы цифровой подписи и подписываемый текст ГИД. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Решить сравнение 
Найти произвольный квадратичный невычет по модулю 307
Расшифровать текст 3-2.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите последнее слово заглавными буквами.
Вычислить нелинейность блока замен 14 12 7 3 0 11 1 15 8 10 9 6 5 13 2 4 размерностью 
Даны значения модуля шифрования N = 2701 и открытого ключа e = 1507. Используя метод факторизации Ферма, найти значение закрытого ключа.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 6686. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 53, значения цифровой подписи: r = 22; s = 30. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
(1) подпись действительна
(2) подпись недействительна
Решить систему сравнений:

Найти наименьший квадратный корень из 18 по модулю 223.
Расшифровать сообщение
4-2.txt
, зашифрованное шифром Виженера, Длина ключа равна 6, пробел является частью алфавита.
В ответ введите ключ.
.
Вычислить динамическое расстояние порядка (2,2) блока замен 14 12 7 3 0 11 1 15 8 10 9 6 5 13 2 4 размерностью 
Применением цепных дробей найти секретный ключ d и разложение модуля 95841214023781 (экспонента — 2005229) на множители. В ответе укажите секретный ключ.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 7256. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 51, значения цифровой подписи: r = 41; s = 44. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
(1) подпись действительна
(2) подпись недействительна
Решить сравнение 
Найти наименьший квадратный корень из 31 по примарному модулю 125.
Расшифровать сообщение
5-2.txt
, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Найти корреляционную матрицу блока замен 14 12 7 3 0 11 1 15 8 10 9 6 5 13 2 4 размерностью 
(1)
begin{matrix}
0 & 0.25 & 0.25 & 0.25 &
0.25 & 0.25 & 0 & -0.5 &
0.25 & -0.25 & 0 & -0.25 &
0.25 & -0.25 & 0 & 0 &
end{matrix}
(2)
begin{matrix}
0 & 0.25 & 0.25 & 0.25 &
0.25 & 0.25 & 0 & -0.5 &
0.25 & -0.25 & 0 & -0.25 &
-0.25 & -0.25 & 0 & 0 &
end{matrix}
(3)
begin{matrix}
0 & 0.25 & 0.25 & 0.25 &
0.25 & 0.25 & 0 & -0.5 &
0.25 & 0.25 & 0 & -0.25 &
-0.25 & -0.25 & 0 & 0 &
end{matrix}
(4)
begin{matrix}
0 & 0.25 & 0.25 & 0.25 &
0.25 & 0.25 & 0 & 0.5 &
0.25 & -0.25 & 0 & -0.25 &
-0.25 & -0.25 & 0 & 0 &
end{matrix}
Дан шифртекст 28, а также значения модуля шифрования N = 187 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=3, зная секретный ключ подписи d=9 при данном значении выбираемого случайным образом числа k=6. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Найти остаток от деления 
Найти количество квадратных корней из 1820 по непримарному составному модулю 2431.
Расшифровать сообщение на английском языке
6-2.txt
, зашифрованное шифром Виженера, Длина ключа равна 5.
В ответ введите ключ.
.
Провести операцию SubBytes алгоритма AES со значением байта 9B.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=2, зная секретный ключ подписи d=11 при данном значении выбираемого случайным образом числа k=5. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Вычислить значение 
Найти число элементов порядка 3328 в циклической группе порядка 6656.
Провести операцию MixColumns над приведенным ниже столбцом состояния
Проверьте подлинность ЭЦП (3, 7) для сообщения с известным значением хэш-свертки 5, зная открытый ключ проверки подписи (455, 368). Используйте кривую 
(1) подпись действительна
(2) подпись недействительна
Найти дискретный логарифм числа 17 по основанию 5 по модулю 95257.
Зашифровать биграмму АД с помощью матрицы 
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
42DBBABD6BB5B6763B93BCEECD01FE78
Сообщение 537 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {2,3,7,15,29,57,115}, m=230 и n=43. В ответе укажите исходное сообщение.
Проверить действительность подписей (150,17), (195, 167) для сообщения с известным значением хэш-свертки 59 и открытым ключом проверки (60,74). Используется кривая 
(1) обе подписи действительны
(2) первая подпись действительна, вторая — недействительна
(3) первая подпись недействительна, вторая — действительна
(4) обе подписи недействительны
Используя порождающий полином для CRC 
(1) {0,1,0,0,0}
(2) {1,1,0,0,0}
(3) {0,0,0,1,0}
(4) {1,1,0,0,1}
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3
Д 4 Е 5 Ё 6 Ж 7
З 8 И 9 Й 10 К 11
Л 12 М 13 Н 14 О 15
П 16 Р 17 С 18 Т 19
У 20 Ф 21 Х 22 Ц 23
Ч 24 Ш 25 Щ 26 Ъ 27
Ы 28 Ь 29 Э 30 Ю 31
Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст СИНТЕЗ.
Провести первый раунд зашифрования открытого текста F1FE EF23 8B38 B3BF шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок 
Шифртекст (3441665394, 10010010000100110110) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=92051, q=94651. Найти открытый текст и введите его заглавными буквами.
С помощью алгоритма Берлекемпа проверить, является ли приводимым многочлен 

Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=31, n2=23, x=17.
Чей компьютер он взломает быстрее?
Зашифруйте открытый текст ЛАТЫШСКИЙ с помощью алфавита, приведенного в
таблице
, используйте открытый ключ B=(179,275), значения случайных чисел
для букв открытого текста k: 15, 17, 12, 2, 2, 4, 8, 6, 17, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
(1) {(745, 210), (434, 136)}; {(440, 539), (229, 600)}; {(286, 136), (520, 2)};
{(188, 93), (642, 698)}; {(188, 93), (45, 720)}; {(16, 416), (719, 538)};
{(346, 242), (45, 31)}; {(725, 195), (438, 711)}; {(440, 539), (395, 414)}.
(2) {(286, 136), (520, 2)}; {(745, 210), (434, 136)}; {(440, 539), (229, 600)};
{(188, 93), (642, 698)}; {(188, 93), (45, 720)}; {(16, 416), (719, 538)};
{(346, 242), (45, 31)}; {(725, 195), (438, 711)}; {(440, 539), (395, 414)}.
(3) {(745, 210), (434, 136)}; {(440, 539), (229, 600)}; {(286, 136), (520, 2)};
{(16, 416), (719, 538)}; {(188, 93), (642, 698)}; {(188, 93), (45, 720)};
{(346, 242), (45, 31)}; {(725, 195), (438, 711)}; {(440, 539), (395, 414)}.
(4) {(286, 136), (520, 2)}; {(745, 210), (434, 136)}; {(440, 539), (229, 600)};
{(188, 93), (642, 698)}; {(188, 93), (45, 720)}; {(16, 416), (719, 538)};
{(346, 242), (45, 31)}; {(725, 195), (438, 711)}; {(440, 539), (395, 414)}.
Даны точки P(61, 129), Q(59, 365), R(105, 369) на кривой 

Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
КОШКА
или
МЫШКА
— устойчивее к действию этой программы?
(1) Первый пароль надежнее
(2) Второй пароль надежнее
(3) Пароли одинаково ненадежные
Дан шифртекст, показанный ниже. Зная секретный ключ 
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(72, 254), (397, 184)}; {(188, 93), (526, 412)}; |
| {(188, 93), (328, 290)}; {(135, 82), (433, 47)}; |
| {(179, 275), (711, 341)}; {(568, 355), (546, 670)}; |
| {(16, 416), (734, 170)}; {(568, 355), (371, 14)}; |
| {(596, 433), (604, 610)}; {(16, 416), (734, 170)} |
Дана точка P(43, 527) на кривой 

Вычислить порядок точки (31, 15) кривой 
Решить в целых числах уравнение 
Определить, является ли число 4108888687178291199 простым с вероятностью не меньше 0,999.
Шифротекст ЮВЧКЛ_ИКТЕЬОЮМП_ТВЕРТ_ЬСЕ получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
ВКЛЮЧИТЕ_КОМПЬЮТЕР_В_СЕТЬ
Вычислить нелинейность булевой функции 01010111 от 3 переменных
Дано: модуль шифрования N = 5609, открытый ключ e = 17. Найти значение шифртекста, полученного при зашифровании открытого текста 4425 на открытом ключе (N, e) по алгоритму RSA.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=28 и k=7 системы цифровой подписи и подписываемый текст ОВАЛ. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Решить следующее сравнение 
С помощью 
Расшифровать фразу П_КИУУТОРГ.ЙЕ_Щ_О_КИАУЛСБ, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
КУПИ_ЕЩЁ_ЙОГУРТ_И_КОЛБАСУ
Вычислить динамическое расстояние порядка 1 булевой функции 01010111 от 3 переменных
Даны значения модуля шифрования N = 143 и открытого ключа e = 19. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 115.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=13 и k=23 системы цифровой подписи и подписываемый текст ТРЕП. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Решить сравнение 
Найти произвольный квадратичный невычет по модулю 227
Расшифровать текст 3-3.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите третье слово заглавными буквами.
Вычислить нелинейность блока замен 6 15 12 4 14 2 3 9 1 7 11 10 13 5 8 0 размерностью 
Даны значения модуля шифрования N = 1891 и открытого ключа e = 1487. Используя метод факторизации Ферма, найти значение закрытого ключа.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 2205. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 27, значения цифровой подписи: r = 13; s = 29. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
(1) подпись действительна
(2) подпись недействительна
Решить систему сравнений:

Найти наибольший квадратный корень из 189 по модулю 227.
Расшифровать сообщение
4-3.txt
, зашифрованное шифром Виженера, Длина ключа равна 6, пробел является частью алфавита.
В ответ введите ключ.
.
Вычислить динамическое расстояние порядка (2,2) блока замен 6 15 12 4 14 2 3 9 1 7 11 10 13 5 8 0 размерностью 
Применением цепных дробей найти секретный ключ d и разложение модуля 93767386321457 (экспонента — 2091619) на множители. В ответе укажите секретный ключ.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 6549. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 11, значения цифровой подписи: r = 38; s = 43. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
(1) подпись действительна
(2) подпись недействительна
Решить сравнение 
Найти наибольший квадратный корень из 13 по примарному модулю 27.
Расшифровать сообщение
5-3.txt
, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Найти корреляционную матрицу блока замен 6 15 12 4 14 2 3 9 1 7 11 10 13 5 8 0 размерностью 
(1)
begin{matrix}
0 & 0 & 0 & -0.25 &
0.25 & -0.25 & -0.5 & 0.25 &
0 & -0.25 & -0.25 & 0 &
0.25 & -0.25 & -0.25 & 0 &
end{matrix}
(2)
begin{matrix}
0 & 0 & 0 & -0.25 &
-0.25 & -0.25 & -0.5 & 0.25 &
0 & -0.25 & -0.25 & 0 &
0.25 & -0.25 & -0.25 & 0 &
end{matrix}
(3)
begin{matrix}
0 & 0 & 0 & -0.25 &
-0.25 & -0.25 & 0.5 & 0.25 &
0 & -0.25 & -0.25 & 0 &
0.25 & -0.25 & -0.25 & 0 &
end{matrix}
(4)
begin{matrix}
0 & 0 & 0 & -0.25 &
-0.25 & -0.25 & -0.5 & 0.25 &
0 & -0.25 & -0.25 & 0 &
0.25 & -0.25 & 0.25 & 0 &
end{matrix}
Дан шифртекст 45, а также значения модуля шифрования N = 323 и открытого ключа e = 5. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=12, зная секретный ключ подписи d=9 при данном значении выбираемого случайным образом числа k=2. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Найти остаток от деления 
Найти количество квадратных корней из 86 по непримарному составному модулю 385.
Расшифровать сообщение на английском языке
6-3.txt
, зашифрованное шифром Виженера, Длина ключа равна 5.
В ответ введите ключ.
.
Провести операцию SubBytes алгоритма AES со значением байта D6.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=10, зная секретный ключ подписи d=5 при данном значении выбираемого случайным образом числа k=11. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Вычислить значение 
Найти число элементов порядка 495 в циклической группе порядка 5545.
Провести операцию MixColumns над приведенным ниже столбцом состояния
Проверьте подлинность ЭЦП (5, 7) для сообщения с известным значением хэш-свертки 6, зная открытый ключ проверки подписи (135, 669). Используйте кривую 
(1) подпись действительна
(2) подпись недействительна
Найти дискретный логарифм числа 21 по основанию 7 по модулю 96001.
Зашифровать биграмму БЕ с помощью матрицы 
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
F65E28E126885442A986D8C4DCD7F3A4
Сообщение 442 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {2,4,8,15,30,60,122}, m=244 и n=83. В ответе укажите исходное сообщение.
Проверить действительность подписей (3, 220), (10, 171) для сообщения с известным значением хэш-свертки 152 и открытым ключом проверки (195, 321). Используется кривая 
(1) обе подписи действительны
(2) первая подпись действительна, вторая — недействительна
(3) первая подпись недействительна, вторая — действительна
(4) обе подписи недействительны
Используя порождающий полином для CRC 
(1) {0,1,0,0,0}
(2) {1,1,0,0,0}
(3) {0,0,0,1,0}
(4) {1,1,0,0,1}
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3
Д 4 Е 5 Ё 6 Ж 7
З 8 И 9 Й 10 К 11
Л 12 М 13 Н 14 О 15
П 16 Р 17 С 18 Т 19
У 20 Ф 21 Х 22 Ц 23
Ч 24 Ш 25 Щ 26 Ъ 27
Ы 28 Ь 29 Э 30 Ю 31
Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст РАЗБОР.
Провести первый раунд зашифрования открытого текста E90A F652 CD88 F9EC шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок 
Шифртекст (942315396, 10100111100011100111) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=100019, q=94903. Найти открытый текст и введите его заглавными буквами.
С помощью алгоритма Берлекемпа проверить, является ли приводимым многочлен 

Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=37, n2=23, x=14.
Чей компьютер он взломает быстрее?
Зашифруйте открытый текст РЕГРЕССОР с помощью алфавита, приведенного в
таблице
, используйте открытый ключ B=(425, 663), значения случайных чисел
для букв открытого текста k: 6, 12, 16, 4, 9, 4, 19, 9, 18, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
(1) {(725, 195), (86, 726)}; {(286, 136), (681, 366)}; {(72, 254), (86, 25)};
{(16, 416), (138, 453)}; {(489, 468), (157, 175)}; {(16, 416), (31, 136)};
{(568, 355), (109, 551)}; {(489, 468), (143, 602)}; {(618, 206), (652, 315)}.
(2) {(725, 195), (86, 726)}; {(286, 136), (681, 366)}; {(72, 254), (86, 25)};
{(16, 416), (138, 453)}; {(489, 468), (157, 175)}; {(16, 416), (31, 136)};
{(489, 468), (143, 602)}; {(568, 355), (109, 551)}; {(618, 206), (652, 315)}.
(3) {(286, 136), (681, 366)}; {(725, 195), (86, 726)}; {(72, 254), (86, 25)};
{(16, 416), (138, 453)}; {(489, 468), (157, 175)}; {(16, 416), (31, 136)};
{(568, 355), (109, 551)}; {(489, 468), (143, 602)}; {(618, 206), (652, 315)}.
(4) {(72, 254), (86, 25)}; {(725, 195), (86, 726)}; {(286, 136), (681, 366)};
{(16, 416), (138, 453)}; {(489, 468), (157, 175)}; {(16, 416), (31, 136)};
{(568, 355), (109, 551)}; {(489, 468), (143, 602)}; {(618, 206), (652, 315)}.
Даны точки P(62, 372), Q(70, 195), R(67, 84) на кривой 

Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
ОВАЛ
или
КРУГ
— устойчивее к действию этой программы?
(1) Первый пароль надежнее
(2) Второй пароль надежнее
(3) Пароли одинаково ненадежные
Дан шифртекст, показанный ниже. Зная секретный ключ 
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(188, 93), (573, 583)}; {(188, 93), (128, 79)}; |
| {(425, 663), (703, 125)}; {(489, 468), (109, 200)}; |
| {(568, 355), (348, 27)}; {(377, 456), (323, 657)}; |
| {(72, 254), (399, 65)}; {(16, 416), (660, 275)}; |
| {(179, 275), (267, 670)}; {(568, 355), (642, 53)} |
Дана точка P(39, 171) на кривой 

Вычислить порядок точки (37, 11) кривой 
Решить в целых числах уравнение 
Определить, является ли число 9418352160768000001 простым с вероятностью не меньше 0,999.
Шифротекст САЕДЛТА_ЬЗМ_НЕУПМРЕЕЕЙННО получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
СДЕЛАТЬ_ЗАМЕНУ_ПЕРЕМЕННОЙ
Вычислить нелинейность булевой функции 00000011 от 3 переменных
Дано: модуль шифрования N = 2491, открытый ключ e = 19. Найти значение шифртекста, полученного при зашифровании открытого текста 388 на открытом ключе (N, e) по алгоритму RSA.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=7 и k=23 системы цифровой подписи и подписываемый текст ТОР. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Решить следующее сравнение 
С помощью 
Расшифровать фразу ВЕОИТ_ЛЕФИСНУТАНЫ_ОВТ_ЬРЫ, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
УСТАНОВИТЕ_НОВЫЕ_ФИЛЬТРЫ_
Вычислить динамическое расстояние порядка 1 булевой функции 00000011 от 3 переменных
Даны значения модуля шифрования N = 221 и открытого ключа e = 91. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 79.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=11 и k=55 системы цифровой подписи и подписываемый текст СЛОЙ. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Решить сравнение 
Найти произвольный квадратичный невычет по модулю 367
Расшифровать текст 3-4.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите второе слово заглавными буквами.
Вычислить динамическое расстояние порядка (2,2) блока замен 13 11 7 4 12 14 6 8 9 10 3 1 0 2 5 15 размерностью 
Даны значения модуля шифрования N = 3239 и открытого ключа e = 2467. Используя метод факторизации Ферма, найти значение закрытого ключа.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 7707. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 46, значения цифровой подписи: r = 11; s = 43. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
(1) подпись действительна
(2) подпись недействительна
Решить систему сравнений:

Найти наименьший квадратный корень из 61 по модулю 229.
Расшифровать сообщение
4-4.txt
, зашифрованное шифром Виженера, Длина ключа равна 4, пробел является частью алфавита.
В ответ введите ключ.
.
Вычислить динамическое расстояние порядка (2,2) блока замен 13 11 7 4 12 14 6 8 9 10 3 1 0 2 5 15 размерностью 
Применением цепных дробей найти секретный ключ d и разложение модуля 89318473363897 (экспонента — 2227661) на множители. В ответе укажите секретный ключ.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 4381. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 32, значения цифровой подписи: r = 24; s = 45. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
(1) подпись действительна
(2) подпись недействительна
Решить сравнение 
Найти наименьший квадратный корень из 114 по примарному модулю 125.
Расшифровать сообщение
5-4.txt
, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Найти корреляционную матрицу блока замен 13 11 7 4 12 14 6 8 9 10 3 1 0 2 5 15 размерностью 
(1)
begin{matrix}
-0.25 & 0.25 & -0.25 & 0.25 &
0.25 & 0 & 0.25 & -0.5 &
-0.5 & 0 & 0.25 & 0 &
-0.25 & 0 & -0.5 & -0.25 &
end{matrix}
(2)
begin{matrix}
-0.25 & 0.25 & -0.25 & 0.25 &
0.25 & 0 & 0.25 & -0.5 &
-0.5 & 0 & 0.25 & 0 &
0.25 & 0 & -0.5 & -0.25 &
end{matrix}
(3)
begin{matrix}
-0.25 & 0.25 & -0.25 & 0.25 &
0.25 & 0 & 0.25 & -0.5 &
-0.5 & 0 & 0.25 & 0 &
0.25 & 0 & 0.5 & -0.25 &
end{matrix}
(4)
begin{matrix}
-0.25 & 0.25 & -0.25 & 0.25 &
0.25 & 0 & 0.25 & 0.5 &
-0.5 & 0 & 0.25 & 0 &
0.25 & 0 & -0.5 & -0.25 &
end{matrix}
Дан шифртекст 90, а также значения модуля шифрования N = 247 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=3, зная секретный ключ подписи d=4 при данном значении выбираемого случайным образом числа k=7. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Найти остаток от деления 
Найти количество квадратных корней из 914 по непримарному составному модулю 2431.
Расшифровать сообщение на английском языке
6-4.txt
, зашифрованное шифром Виженера, Длина ключа равна 3.
В ответ введите ключ.
.
Провести операцию SubBytes алгоритма AES со значением байта 6B
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=11, зная секретный ключ подписи d=5 при данном значении выбираемого случайным образом числа k=7. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Вычислить значение 
В скольких подгруппах группы 
Провести операцию MixColumns над приведенным ниже столбцом состояния
Проверьте подлинность ЭЦП (5, 7) для сообщения с известным значением хэш-свертки 6, зная открытый ключ проверки подписи (562, 662). Используйте кривую 
(1) подпись действительна
(2) подпись недействительна
Найти дискретный логарифм числа 25 по основанию 22 по модулю 96769.
Зашифровать биграмму МУ с помощью матрицы 
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
704B343512FD911C043C31181157D80B
Сообщение 505 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {1,3,5,13,23,49,99}, m=195 и n=127. В ответе укажите исходное сообщение.
Проверить действительность подписей (201, 7), (195, 143) для сообщения с известным значением хэш-свертки 20 и открытым ключом проверки (87,716). Используется кривая 
(1) обе подписи действительны
(2) первая подпись действительна, вторая — недействительна
(3) первая подпись недействительна, вторая — действительна
(4) обе подписи недействительны
Используя порождающий полином для CRC 
(1) {0,1,0,0,0}
(2) {1,1,0,0,0}
(3) {0,0,0,1,0}
(4) {1,1,0,0,1}
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3
Д 4 Е 5 Ё 6 Ж 7
З 8 И 9 Й 10 К 11
Л 12 М 13 Н 14 О 15
П 16 Р 17 С 18 Т 19
У 20 Ф 21 Х 22 Ц 23
Ч 24 Ш 25 Щ 26 Ъ 27
Ы 28 Ь 29 Э 30 Ю 31
Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст НЕПТУН.
Провести первый раунд зашифрования открытого текста 97A0 9BD3 DF10 C86A шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок 
Шифртекст (3466465879, 01111000011000111101) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=99023, q=92479. Найти открытый текст и введите его заглавными буквами.
С помощью алгоритма Берлекемпа проверить, является ли приводимым многочлен 

Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=43, n2=23, x=9.
Чей компьютер он взломает быстрее?
Зашифруйте открытый текст СИММЕТРИЯ с помощью алфавита, приведенного в
таблице
, используйте открытый ключ B=(179, 275), значения случайных чисел
для букв открытого текста k: 11, 17, 18, 19, 16, 6, 12, 8, 2, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
(1) {(179, 275), (383, 411)}; {(440, 539), (229, 151)}; {(618, 206), (466, 214)};
{(568, 355), (156, 704)}; {(72, 254), (564, 38)}; {(725, 195), (145, 143)};
{(286, 136), (176, 413)}; {(346, 242), (12, 314)}; {(188, 93), (275, 456)}.
(2) {(440, 539), (229, 151)}; {(179, 275), (383, 411)}; {(618, 206), (466, 214)};
{(568, 355), (156, 704)}; {(72, 254), (564, 38)}; {(725, 195), (145, 143)};
{(286, 136), (176, 413)}; {(346, 242), (12, 314)}; {(188, 93), (275, 456)}.
(3) {(179, 275), (383, 411)}; {(440, 539), (229, 151)}; {(618, 206), (466, 214)};
{(725, 195), (145, 143)}; {(568, 355), (156, 704)}; {(72, 254), (564, 38)};
{(286, 136), (176, 413)}; {(346, 242), (12, 314)}; {(188, 93), (275, 456)}.
(4) {(618, 206), (466, 214)}; {(179, 275), (383, 411)}; {(440, 539), (229, 151)};
{(568, 355), (156, 704)}; {(72, 254), (564, 38)}; {(725, 195), (145, 143)};
{(286, 136), (176, 413)}; {(346, 242), (12, 314)}; {(188, 93), (275, 456)}.
Даны точки P(56, 332), Q(69, 241), R(83, 373) на кривой 

Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
РАБОТА
или
ОТПУСК
— устойчивее к действию этой программы?
(1) Первый пароль надежнее
(2) Второй пароль надежнее
(3) Пароли одинаково ненадежные
Дан шифртекст, показанный ниже. Зная секретный ключ 
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(618, 206), (426, 662)}; {(72, 254), (67, 667)}; |
| {(286, 136), (739, 574)}; {(16, 416), (143, 602)}; |
| {(618, 206), (313, 203)}; {(618, 206), (114, 607)}; |
| {(618, 206), (438, 711)}; {(188, 93), (573, 168)} |
Дана точка P(43, 527) на кривой 

Вычислить порядок точки (27, 15) кривой 
Решить в целых числах уравнение 
Определить, является ли число 909090909090909091 простым с вероятностью не меньше 0,999.
Шифротекст ПКЕРЕЛТИЧЮЕМУТ_Б_РЕЛВХРЕВ получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
ПЕРЕКЛЮЧИТЕ_ТУМБЛЕР_ВВЕРХ
Вычислить нелинейность булевой функции 00000001 от 3 переменных
Дано: модуль шифрования N = 5063, открытый ключ e = 11. Найти значение шифртекста, полученного при зашифровании открытого текста 4679 на открытом ключе (N, e) по алгоритму RSA.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=8 и k=35 системы цифровой подписи и подписываемый текст МЕЧ. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Решить следующее сравнение 
С помощью 
Расшифровать фразу _ААЛВРАТЗВД_УАББТОЕ__ЕИБГ, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
ЗАВТРА_БУДЕТ_ОБЛАВА_БЕГИ_
Вычислить динамическое расстояние порядка 1 булевой функции 00000001 от 3 переменных
Даны значения модуля шифрования N = 493 и открытого ключа e = 369. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 300.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=48 и k=23 системы цифровой подписи и подписываемый текст РЫБА. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Решить сравнение 
Найти произвольный квадратичный невычет по модулю 229
Расшифровать текст 3-5.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите третье слово заглавными буквами.
Вычислить нелинейность блока замен 4 2 0 10 11 9 6 1 13 8 15 14 12 5 7 3 размерностью 
Даны значения модуля шифрования N = 3713 и открытого ключа e = 3359. Используя метод факторизации Ферма, найти значение закрытого ключа.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 7144. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 22, значения цифровой подписи: r = 47; s = 52. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
(1) подпись действительна
(2) подпись недействительна
Решить систему сравнений:

Найти наибольший квадратный корень из 195 по модулю 233.
Расшифровать сообщение
4-5.txt
, зашифрованное шифром Виженера, Длина ключа равна 7, пробел является частью алфавита.
В ответ введите ключ.
.
Вычислить динамическое расстояние порядка (2,2) блока замен 4 2 0 10 11 9 6 1 13 8 15 14 12 5 7 3 размерностью 
Применением цепных дробей найти секретный ключ d и разложение модуля 87046121832829 (экспонента — 2342047) на множители. В ответе укажите секретный ключ.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 1746. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 47, значения цифровой подписи: r = 31; s = 56. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
(1) подпись действительна
(2) подпись недействительна
Решить сравнение 
Найти наибольший квадратный корень из 128 по примарному модулю 343.
Расшифровать сообщение
5-5.txt
, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Найти корреляционную матрицу блока замен 4 2 0 10 11 9 6 1 13 8 15 14 12 5 7 3 размерностью 
(1)
begin{matrix}
0 & 0 & -0.5 & 0 &
0 & 0.5 & 0 & -0.25 &
0.5 & 0 & 0 & -0.25 &
-0.25 & 0 & 0.5 & 0.25 &
end{matrix}
(2)
begin{matrix}
0 & 0 & -0.5 & 0 &
0 & 0.5 & 0 & -0.25 &
0.5 & 0 & 0 & -0.25 &
0.25 & 0 & 0.5 & 0.25 &
end{matrix}
(3)
begin{matrix}
0 & 0 & -0.5 & 0 &
0 & 0.5 & 0 & -0.25 &
0.5 & 0 & 0 & 0.25 &
0.25 & 0 & 0.5 & 0.25 &
end{matrix}
(4)
begin{matrix}
0 & 0 & -0.5 & 0 &
0 & 0.5 & 0 & 0.25 &
0.5 & 0 & 0 & -0.25 &
0.25 & 0 & 0.5 & 0.25 &
end{matrix}
Дан шифртекст 84, а также значения модуля шифрования N = 187 и открытого ключа e = 3. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=5, зная секретный ключ подписи d=12 при данном значении выбираемого случайным образом числа k=6. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Найти остаток от деления 
Найти количество квадратных корней из 478 по непримарному составному модулю 1001.
Расшифровать сообщение на английском языке
6-5.txt
, зашифрованное шифром Виженера, Длина ключа равна 4.
В ответ введите ключ.
.
Провести операцию SubBytes алгоритма AES со значением байта 72.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=6, зная секретный ключ подписи d=10 при данном значении выбираемого случайным образом числа k=7. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Вычислить значение 
В скольких подгруппах группы 
Провести операцию MixColumns над приведенным ниже столбцом состояния
Проверьте подлинность ЭЦП (7, 6) для сообщения с известным значением хэш-свертки 2, зная открытый ключ проверки подписи (135, 669). Используйте кривую 
(1) подпись действительна
(2) подпись недействительна
Найти дискретный логарифм числа 13 по основанию 11 по модулю 100801.
Зашифровать биграмму ПИ с помощью матрицы 
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
851A741395DCD1B2705B5A932A3D8E82
Сообщение 595 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {2,5,9,17,35,77,146}, m=292 и n=109. В ответе укажите исходное сообщение.
Проверить действительность подписей (31, 171), (211,141) для сообщения с известным значением хэш-свертки 182 и открытым ключом проверки (239,329). Используется кривая 
(1) обе подписи действительны
(2) первая подпись действительна, вторая — недействительна
(3) первая подпись недействительна, вторая — действительна
(4) обе подписи недействительны
Используя порождающий полином для CRC 
(1) {1,0,0,0,1}
(2) {0,1,1,0,0}
(3) {1,1,0,0,0}
(4) {0,1,0,1,0}
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3
Д 4 Е 5 Ё 6 Ж 7
З 8 И 9 Й 10 К 11
Л 12 М 13 Н 14 О 15
П 16 Р 17 С 18 Т 19
У 20 Ф 21 Х 22 Ц 23
Ч 24 Ш 25 Щ 26 Ъ 27
Ы 28 Ь 29 Э 30 Ю 31
Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст ФЕНИКС.
Провести первый раунд зашифрования открытого текста C94E F93C D340 8C98 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок 
Шифртекст (8446011652, 10111001000000000000) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=101603, q=99871. Найти открытый текст и введите его заглавными буквами.
С помощью алгоритма Берлекемпа проверить, является ли приводимым многочлен 

Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=23, n2=41, x=20.
Чей компьютер он взломает быстрее?
Зашифруйте открытый текст УВЕРОВАТЬ с помощью алфавита, приведенного в
таблице
, используйте открытый ключ B=(425, 663), значения случайных чисел
для букв открытого текста k: 6, 14, 5, 7, 12, 11, 4, 9, 19, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
(1) {(725, 195), (620, 680)}; {(596, 433), (39, 171)}; {(425, 663), (654, 102)};
{(135, 82), (85, 716)}; {(286, 136), (99, 295)}; {(179, 275), (526, 412)}; {(16, 416), (458, 490)}; {(489, 468), (140, 115)}; {(568, 355), (400, 56)}.
(2) {(596, 433), (39, 171)}; {(725, 195), (620, 680)}; {(425, 663), (654, 102)};
{(135, 82), (85, 716)}; {(286, 136), (99, 295)}; {(179, 275), (526, 412)}; {(16, 416), (458, 490)}; {(489, 468), (140, 115)}; {(568, 355), (400, 56)}.
(3) {(425, 663), (654, 102)}; {(725, 195), (620, 680)}; {(596, 433), (39, 171)};
{(135, 82), (85, 716)}; {(286, 136), (99, 295)}; {(179, 275), (526, 412)}; {(16, 416), (458, 490)}; {(489, 468), (140, 115)}; {(568, 355), (400, 56)}.
(4) {(179, 275), (526, 412)}; {(725, 195), (620, 680)}; {(596, 433), (39, 171)}; {(425, 663), (654, 102)};
{(135, 82), (85, 716)}; {(286, 136), (99, 295)}; {(16, 416), (458, 490)}; {(489, 468), (140, 115)}; {(568, 355), (400, 56)}.
Даны точки P(59, 386), Q(70, 195), R(72, 254) на кривой 

Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
ВОЛК
или
ЗАЯЦ
— устойчивее к действию этой программы?
(1) Первый пароль надежнее
(2) Второй пароль надежнее
(3) Пароли одинаково ненадежные
Дан шифртекст, показанный ниже. Зная секретный ключ 
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(283, 493), (314, 127)}; {(425, 663), (561, 140)}; |
| {(568, 355), (75, 433)}; {(440, 539), (602, 627)}; |
| {(188, 93), (395, 414)}; {(179, 275), (25, 604)}; |
| {(72, 254), (47, 349)}; {(72, 254), (417, 137)}; |
| {(188, 93), (298, 225)}; {(56, 419), (79, 111)} |
Дана точка P(36, 87) на кривой 

Вычислить порядок точки (46, 18) кривой 
Решить в целых числах уравнение 
Определить, является ли число 4653425899839733759 простым с вероятностью не меньше 0,999.
Шифротекст ЫТБСРЕПЕ_ОВДДОИЕВТ_ОСАЙК_ получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
БЫСТРЕЕ_ПОДВОДИТЕ_ВОЙСКА_
Вычислить нелинейность булевой функции 01110111 от 3 переменных
Дано: модуль шифрования N = 6319, открытый ключ e = 17. Найти значение шифртекста, полученного при зашифровании открытого текста 2741 на открытом ключе (N, e) по алгоритму RSA.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=17 и k=11 системы цифровой подписи и подписываемый текст ЩИТ. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Решить следующее сравнение 
С помощью 
Расшифровать фразу ИПССАДП_ЕРЕЕДИНЖПУЕРАОБЗ_, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
СПАСИБО_ЗА_ПРЕДУПРЕЖДЕНИЕ
Вычислить динамическое расстояние порядка 1 булевой функции 01110111 от 3 переменных
Даны значения модуля шифрования N = 299 и открытого ключа e = 61. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 178.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=37 и k=25 системы цифровой подписи и подписываемый текст ВВОД. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Решить сравнение 
Найти произвольный квадратичный невычет по модулю 317
Расшифровать текст 3-6.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите последнее слово заглавными буквами.
Вычислить нелинейность блока замен 12 0 7 10 6 4 15 9 3 8 1 5 14 13 11 2 размерностью 
Даны значения модуля шифрования N = 4717 и открытого ключа e = 523. Используя метод факторизации Ферма, найти значение закрытого ключа.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 5431. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 39, значения цифровой подписи: r = 50; s = 42. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
(1) подпись действительна
(2) подпись недействительна
Решить систему сравнений:

Найти наименьший квадратный корень из 186 по модулю 239.
Расшифровать сообщение
4-6.txt
, зашифрованное шифром Виженера, Длина ключа равна 6, пробел является частью алфавита.
В ответ введите ключ.
.
Вычислить динамическое расстояние порядка (2,2) блока замен 12 0 7 10 6 4 15 9 3 8 1 5 14 13 11 2 размерностью 
Применением цепных дробей найти секретный ключ d и разложение модуля 85609460573249 (экспонента — 2448539) на множители. В ответе укажите секретный ключ.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 8832. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 31, значения цифровой подписи: r = 47; s = 41. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
(1) подпись действительна
(2) подпись недействительна
Решить сравнение 
Найти наименьший квадратный корень из 24 по примарному модулю 25.
Расшифровать сообщение
5-6.txt
, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Найти корреляционную матрицу блока замен 12 0 7 10 6 4 15 9 3 8 1 5 14 13 11 2 размерностью 
(1)
begin{matrix}
-0.25 & -0.5 & -0.25 & 0 &
0.5 & 0.25 & -0.25 & 0 &
0 & 0.25 & 0.25 & -0.25 &
0.25 & 0 & -0.25 & 0 &
end{matrix}
(2)
begin{matrix}
-0.25 & -0.5 & -0.25 & 0 &
0.5 & 0.25 & -0.25 & 0 &
0 & 0.25 & 0.25 & 0.25 &
0.25 & 0 & -0.25 & 0 &
end{matrix}
(3)
begin{matrix}
-0.25 & -0.5 & -0.25 & 0 &
0.5 & 0.25 & -0.25 & 0 &
0 & 0.25 & 0.25 & 0.25 &
-0.25 & 0 & -0.25 & 0 &
end{matrix}
(4)
begin{matrix}
-0.25 & -0.5 & -0.25 & 0 &
0.5 & 0.25 & -0.25 & 0 &
0 & 0.25 & 0.25 & 0.25 &
0.25 & 0 & 0.25 & 0 &
end{matrix}
Дан шифртекст 13, а также значения модуля шифрования N = 77 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=6, зная секретный ключ подписи d=12 при данном значении выбираемого случайным образом числа k=7. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Найти остаток от деления 
Найти количество квадратных корней из 7155 по непримарному составному модулю 7429.
Расшифровать сообщение на английском языке
6-6.txt
, зашифрованное шифром Виженера, Длина ключа равна 3.
В ответ введите ключ.
.
Провести операцию SubBytes алгоритма AES со значением байта E8.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=10, зная секретный ключ подписи d=9 при данном значении выбираемого случайным образом числа k=11. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Вычислить значение 
В скольких подгруппах группы 
Провести операцию MixColumns над приведенным ниже столбцом состояния
Проверьте подлинность ЭЦП (11, 10) для сообщения с известным значением хэш-свертки 8, зная открытый ключ проверки подписи (135, 82). Используйте кривую 
(1) подпись действительна
(2) подпись недействительна
Найти дискретный логарифм числа 3 по основанию 2 по модулю 102061.
Зашифровать биграмму ЛА с помощью матрицы 
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
E4A2CF62B960D6B4674BEC1836A333E8
Сообщение 492 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {3,4,8,17,33,67,138}, m=271 и n=65. В ответе укажите исходное сообщение.
Проверить действительность подписей (106, 108), (35, 44) для сообщения с известным значением хэш-свертки 166 и открытым ключом проверки (436,660). Используется кривая 
(1) обе подписи действительны
(2) первая подпись действительна, вторая — недействительна
(3) первая подпись недействительна, вторая — действительна
(4) обе подписи недействительны
Используя порождающий полином для CRC 
(1) {1,0,0,0,1}
(2) {0,1,1,0,0}
(3) {1,1,0,0,0}
(4) {0,1,0,1,0}
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3
Д 4 Е 5 Ё 6 Ж 7
З 8 И 9 Й 10 К 11
Л 12 М 13 Н 14 О 15
П 16 Р 17 С 18 Т 19
У 20 Ф 21 Х 22 Ц 23
Ч 24 Ш 25 Щ 26 Ъ 27
Ы 28 Ь 29 Э 30 Ю 31
Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст ЧАЙНИК.
Провести первый раунд зашифрования открытого текста D352 FEAC D98D AC8E шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок 
Шифртекст (8978530064, 11010000110111010111) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=95747, q=95327. Найти открытый текст и введите его заглавными буквами.
С помощью алгоритма Берлекемпа проверить, является ли приводимым многочлен 

Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=23, n2=47, x=16.
Чей компьютер он взломает быстрее?
Зашифруйте открытый текст ТЕРНОВНИК с помощью алфавита, приведенного в
таблице
, используйте открытый ключ B=(188, 93), значения случайных чисел
для букв открытого текста k: 8, 14, 17, 17, 2, 10, 8, 2, 2, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
(1) {(346, 242), (594, 414)}; {(596, 433), (34, 677)}; {(440, 539), (546, 670)};
{(440, 539), (694, 581)}; {(188, 93), (515, 684)}; {(377, 456), (517, 573)};
{(346, 242), (288, 639)}; {(188, 93), (209, 82)}; {(188, 93), (205, 379)}.
(2) {(596, 433), (34, 677)}; {(346, 242), (594, 414)}; {(440, 539), (546, 670)};
{(440, 539), (694, 581)}; {(188, 93), (515, 684)}; {(377, 456), (517, 573)};
{(346, 242), (288, 639)}; {(188, 93), (209, 82)}; {(188, 93), (205, 379)}.
(3) {(440, 539), (546, 670)}; {(346, 242), (594, 414)}; {(596, 433), (34, 677)};
{(440, 539), (694, 581)}; {(188, 93), (515, 684)}; {(377, 456), (517, 573)};
{(346, 242), (288, 639)}; {(188, 93), (209, 82)}; {(188, 93), (205, 379)}.
(4) {(440, 539), (694, 581)}; {(346, 242), (594, 414)}; {(596, 433), (34, 677)};
{(440, 539), (546, 670)}; {(188, 93), (515, 684)}; {(377, 456), (517, 573)};
{(346, 242), (288, 639)}; {(188, 93), (209, 82)}; {(188, 93), (205, 379)}.
Даны точки P(72, 497), Q(61, 622), R(70, 556) на кривой 

Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
МАКАКИ
или
ЖИРАФЫ
— устойчивее к действию этой программы?
(1) Первый пароль надежнее
(2) Второй пароль надежнее
(3) Пароли одинаково ненадежные
Дан шифртекст, показанный ниже. Зная секретный ключ 
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(377, 456), (367, 360)}; {(425, 663), (715, 398)}; |
| {(188, 93), (279, 353)}; {(179, 275), (128, 79)}; |
| {(568, 355), (515, 67)}; {(568, 355), (482, 230)}; |
| {(377, 456), (206, 645)}; {(188, 93), (300, 455)}; |
| {(489, 468), (362, 446)}; {(16, 416), (69, 510)}; |
| {(425, 663), (218, 601)} |
Дана точка P(49, 568) на кривой 

Вычислить порядок точки (9, 11) кривой 
Решить в целых числах уравнение 
Определить, является ли число 5618014398241046527 простым с вероятностью не меньше 0,999.
Шифротекст УПК_ИАКМРАНЫОХ_ЕБЛИ_СО_ЬЛ получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
КУПИ_МАКАРОНЫ_ХЛЕБ_И_СОЛЬ
Вычислить нелинейность булевой функции 01001100 от 3 переменных
Дано: модуль шифрования N = 2923, открытый ключ e = 19. Найти значение шифртекста, полученного при зашифровании открытого текста 678 на открытом ключе (N, e) по алгоритму RSA.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=22 и k=25 системы цифровой подписи и подписываемый текст РОЙ. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Решить следующее сравнение 
С помощью 
Расшифровать фразу РЕТИ_АУКС_РКСАРГФАРАРБЗАЕ, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
РАЗБЕРИТЕ_РАСКРАСКУ_ГРАФА
Вычислить динамическое расстояние порядка 1 булевой функции 01001100 от 3 переменных
Даны значения модуля шифрования N = 209 и открытого ключа e = 53. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 85.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=9 и k=25 системы цифровой подписи и подписываемый текст ХОД. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Решить сравнение 
Найти произвольный квадратичный невычет по модулю 281
Расшифровать текст 3-7.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите третье с конца слово заглавными буквами.
Вычислить нелинейность блока замен 9 13 0 10 12 2 15 11 3 6 8 7 14 4 5 1 размерностью 
Даны значения модуля шифрования N = 3569 и открытого ключа e = 1013. Используя метод факторизации Ферма, найти значение закрытого ключа.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 8806. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 29, значения цифровой подписи: r = 50; s = 24. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
(1) подпись действительна
(2) подпись недействительна
Решить систему сравнений:

Найти наибольший квадратный корень из 60 по модулю 241.
Расшифровать сообщение
4-7.txt
, зашифрованное шифром Виженера, Длина ключа равна 6, пробел является частью алфавита.
В ответ введите ключ.
.
Вычислить динамическое расстояние порядка (2,2) блока замен 9 13 0 10 12 2 15 11 3 6 8 7 14 4 5 1 размерностью 
Применением цепных дробей найти секретный ключ d и разложение модуля 84032429242009 (экспонента — 2581907) на множители. В ответе укажите секретный ключ.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 3629. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 54, значения цифровой подписи: r = 56; s = 41. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
(1) подпись действительна
(2) подпись недействительна
Решить сравнение 
Найти наибольший квадратный корень из 46 по примарному модулю 625.
Расшифровать сообщение
5-7.txt
, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Найти корреляционную матрицу блока замен 9 13 0 10 12 2 15 11 3 6 8 7 14 4 5 1 размерностью 
(1)
begin{matrix}
0 & 0.25 & 0 & -0.25 &
-0.25 & 0 & -0.25 & 0 &
0 & 0 & 0.25 & 0 &
0 & 0 & 0.25 & -0.5 &
end{matrix}
(2)
begin{matrix}
0 & 0.25 & 0 & -0.25 &
0.25 & 0 & -0.25 & 0 &
0 & 0 & 0.25 & 0 &
0 & 0 & 0.25 & -0.5 &
end{matrix}
(3)
begin{matrix}
0 & 0.25 & 0 & -0.25 &
0.25 & 0 & -0.25 & 0 &
0 & 0 & 0.25 & 0 &
0 & 0 & 0.25 & 0.5 &
end{matrix}
(4)
begin{matrix}
0 & 0.25 & 0 & 0.25 &
0.25 & 0 & -0.25 & 0 &
0 & 0 & 0.25 & 0 &
0 & 0 & 0.25 & -0.5 &
end{matrix}
Дан шифртекст 117, а также значения модуля шифрования N = 187 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=8, зная секретный ключ подписи d=5 при данном значении выбираемого случайным образом числа k=5. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Найти остаток от деления 
Найти количество квадратных корней из 653 по непримарному составному модулю 1001.
Расшифровать сообщение на английском языке
6-7.txt
, зашифрованное шифром Виженера, Длина ключа равна 3.
В ответ введите ключ.
.
Провести операцию SubBytes алгоритма AES со значением байта 6C.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=6, зная секретный ключ подписи d=10 при данном значении выбираемого случайным образом числа k=2. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Вычислить значение 
Какая наибольшая степень элемента a порядка 54 порождает группу 
Провести операцию MixColumns над приведенным ниже столбцом состояния
Проверьте подлинность ЭЦП (11, 9) для сообщения с известным значением хэш-свертки 4, зная открытый ключ проверки подписи (384, 475). Используйте кривую 
(1) подпись действительна
(2) подпись недействительна
Найти дискретный логарифм числа 10 по основанию 11 по модулю 103681.
Зашифровать биграмму ВЫ с помощью матрицы 
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
DC0A90413D046B9B7F0B2E6C68AF97A4
Сообщение 429 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {1,4,6,14,27,55,109}, m=217 и n=73. В ответе укажите исходное сообщение.
Проверить действительность подписей (166, 186), (104, 103) для сообщения с известным значением хэш-свертки 115 и открытым ключом проверки (126,463). Используется кривая 
(1) обе подписи действительны
(2) первая подпись действительна, вторая — недействительна
(3) первая подпись недействительна, вторая — действительна
(4) обе подписи недействительны
Используя порождающий полином для CRC 
(1) {1,0,0,0,1}
(2) {0,1,1,0,0}
(3) {1,1,0,0,0}
(4) {0,1,0,1,0}
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3
Д 4 Е 5 Ё 6 Ж 7
З 8 И 9 Й 10 К 11
Л 12 М 13 Н 14 О 15
П 16 Р 17 С 18 Т 19
У 20 Ф 21 Х 22 Ц 23
Ч 24 Ш 25 Щ 26 Ъ 27
Ы 28 Ь 29 Э 30 Ю 31
Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст МАСТЕР.
Провести первый раунд зашифрования открытого текста C95A B90A 8B3D EB0 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок 
Шифртекст (5538085341, 11011101111000111001) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=90059, q=91199. Найти открытый текст и введите его заглавными буквами.
С помощью алгоритма Берлекемпа проверить, является ли приводимым многочлен 

Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=29, n2=31, x=7.
Чей компьютер он взломает быстрее?
Зашифруйте открытый текст ТЕРПЕЛИВО с помощью алфавита, приведенного в
таблице
, используйте открытый ключ B=(725, 195), значения случайных чисел
для букв открытого текста k: 17, 5, 4, 17, 13, 2, 17, 14, 19, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
(1) {(440, 539), (663, 275)}; {(425, 663), (638, 131)}; {(16, 416), (228, 480)};
{(440, 539), (329, 447)}; {(283, 493), (463, 736)}; {(188, 93), (688, 741)};
{(440, 539), (407, 669)}; {(596, 433), (6, 218)}; {(568, 355), (561, 140)}.
(2) {(16, 416), (228, 480)}; {(440, 539), (663, 275)}; {(425, 663), (638, 131)};
{(440, 539), (329, 447)}; {(283, 493), (463, 736)}; {(188, 93), (688, 741)};
{(440, 539), (407, 669)}; {(596, 433), (6, 218)}; {(568, 355), (561, 140)}.
(3) {(425, 663), (638, 131)}; {(16, 416), (228, 480)}; {(440, 539), (329, 447)};
{(283, 493), (463, 736)}; {(188, 93), (688, 741)}; {(440, 539), (663, 275)};
{(440, 539), (407, 669)}; {(596, 433), (6, 218)}; {(568, 355), (561, 140)}.
(4) {(440, 539), (329, 447)}; {(425, 663), (638, 131)}; {(16, 416), (228, 480)};
{(283, 493), (463, 736)}; {(188, 93), (688, 741)}; {(440, 539), (663, 275)};
{(440, 539), (407, 669)}; {(596, 433), (6, 218)}; {(568, 355), (561, 140)}.
Даны точки P(74, 170), Q(53, 277), R(86, 25) на кривой 

Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
ОКОШКО
или
ДВЕРЦА
— устойчивее к действию этой программы?
(1) Первый пароль надежнее
(2) Второй пароль надежнее
(3) Пароли одинаково ненадежные
Дан шифртекст, показанный ниже. Зная секретный ключ 
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(16, 416), (128, 672)}; {(56, 419), (59, 386)}; |
| {(425, 663), (106, 24)}; {(568, 355), (145, 608)}; |
| {(188, 93), (279, 398)}; {(425, 663), (99, 295)}; |
| {(179, 275), (269, 187)}; {(188, 93), (395, 337)}; |
| {(188, 93), (311, 68)}; {(135, 82), (556, 484)}; |
| {(56, 419), (106, 727)}; {(16, 416), (307, 693)} |
Дана точка P(39, 580) на кривой 

Вычислить порядок точки (9, 14) кривой 
Решить в целых числах уравнение 
Определить, является ли число 3489133282872437279 простым с вероятностью не меньше 0,999.
Шифротекст ЫОЧНТО_КОЕАДИНР_Ы_ВТЕУПЛД получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
ТОЧНЫЕ_КООРДИНАТЫ_В_ДУПЛЕ
Вычислить нелинейность булевой функции 01011000 от 3 переменных
Дано: модуль шифрования N = 4087, открытый ключ e = 13. Найти значение шифртекста, полученного при зашифровании открытого текста 146 на открытом ключе (N, e) по алгоритму RSA.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=10 и k=35 системы цифровой подписи и подписываемый текст БОЙ. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Решить следующее сравнение 
С помощью 
Расшифровать фразу РСГЕИЯ_Н_ЕТИАРЦСОСОТИ_СТЯ, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
РЕГИСТРАЦИЯ_НЕ_СОСТОИТСЯ_
Вычислить динамическое расстояние порядка 1 булевой функции 01011000 от 3 переменных
Даны значения модуля шифрования N = 319 и открытого ключа e = 51. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 209.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=15 и k=17 системы цифровой подписи и подписываемый текст КОД. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Решить сравнение 
Найти произвольный квадратичный невычет по модулю 313
Расшифровать текст 3-8.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите последнее слово заглавными буквами.
Вычислить нелинейность блока замен 5 2 14 10 8 7 15 11 13 4 3 9 12 6 1 0 размерностью 
Даны значения модуля шифрования N = 2911 и открытого ключа e = 1697. Используя метод факторизации Ферма, найти значение закрытого ключа.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 2563. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 33, значения цифровой подписи: r = 11; s = 34. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
(1) подпись действительна
(2) подпись недействительна
Решить систему сравнений:

Найти наименьший квадратный корень из 161 по модулю 251.
Расшифровать сообщение
4-8.txt
, зашифрованное шифром Виженера, Длина ключа равна 6, пробел является частью алфавита.
В ответ введите ключ.
.
Вычислить динамическое расстояние порядка (2,2) блока замен 5 2 14 10 8 7 15 11 13 4 3 9 12 6 1 0 размерностью 
Применением цепных дробей найти секретный ключ d и разложение модуля 81177745546021 (экспонента — 2711039) на множители. В ответе укажите секретный ключ.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 7327. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 20, значения цифровой подписи: r = 42; s = 47. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
(1) подпись действительна
(2) подпись недействительна
Решить сравнение 
Найти наименьший квадратный корень из 233 по примарному модулю 343.
Расшифровать сообщение
5-8.txt
, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Найти корреляционную матрицу блока замен 5 2 14 10 8 7 15 11 13 4 3 9 12 6 1 0 размерностью 
(1)
begin{matrix}
0.25 & 0.25 & -0.25 & -0.25 &
0.25 & 0.25 & -0.5 & 0.25 &
0 & 0 & 0 & 0 &
0 & -0.5 & 0 & -0.25 &
end{matrix}
(2)
begin{matrix}
-0.25 & 0.25 & -0.25 & -0.25 &
0.25 & 0.25 & -0.5 & 0.25 &
0 & 0 & 0 & 0 &
0 & -0.5 & 0 & -0.25 &
end{matrix}
(3)
begin{matrix}
-0.25 & 0.25 & -0.25 & -0.25 &
0.25 & 0.25 & -0.5 & 0.25 &
0 & 0 & 0 & 0 &
0 & 0.5 & 0 & -0.25 &
end{matrix}
(4)
begin{matrix}
-0.25 & 0.25 & -0.25 & -0.25 &
0.25 & 0.25 & -0.5 & 0.25 &
0 & 0 & 0 & 0 &
0 & -0.5 & 0 & 0.25 &
end{matrix}
Дан шифртекст 52, а также значения модуля шифрования N = 133 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=8, зная секретный ключ подписи d=2 при данном значении выбираемого случайным образом числа k=5. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Найти остаток от деления 
Найти количество квадратных корней из 70 по непримарному составному модулю 105.
Расшифровать сообщение на английском языке
6-8.txt
, зашифрованное шифром Виженера, Длина ключа равна 5.
В ответ введите ключ.
.
Провести операцию SubBytes алгоритма AES со значением байта C5.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=9, зная секретный ключ подписи d=6 при данном значении выбираемого случайным образом числа k=6. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Вычислить значение 
Какая наибольшая степень элемента a порядка 50 порождает группу 
Провести операцию MixColumns над приведенным ниже столбцом состояния
Проверьте подлинность ЭЦП (11, 1) для сообщения с известным значением хэш-свертки 7, зная открытый ключ проверки подписи (596, 433). Используйте кривую 
(1) подпись действительна
(2) подпись недействительна
Найти дискретный логарифм числа 18 по основанию 7 по модулю 110251.
Зашифровать биграмму ДО с помощью матрицы 
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
95F807FAA21EFF3FA27842CE7DE372FA
Сообщение 305 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {1,2,6,10,21,41,85}, m=167 и n=48. В ответе укажите исходное сообщение.
Проверить действительность подписей (10, 163), (31, 79) для сообщения с известным значением хэш-свертки 214 и открытым ключом проверки (73,63). Используется кривая 
(1) обе подписи действительны
(2) первая подпись действительна, вторая — недействительна
(3) первая подпись недействительна, вторая — действительна
(4) обе подписи недействительны
Используя порождающий полином для CRC 
(1) {1,0,0,0,1}
(2) {0,1,1,0,0}
(3) {1,1,0,0,0}
(4) {0,1,0,1,0}
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3
Д 4 Е 5 Ё 6 Ж 7
З 8 И 9 Й 10 К 11
Л 12 М 13 Н 14 О 15
П 16 Р 17 С 18 Т 19
У 20 Ф 21 Х 22 Ц 23
Ч 24 Ш 25 Щ 26 Ъ 27
Ы 28 Ь 29 Э 30 Ю 31
Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст ПРОРЫВ.
Провести первый раунд зашифрования открытого текста 8DAA 8960 C100 DFD3 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок 
Шифртекст (671410783, 10111110100000010011) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=99439, q=98327. Найти открытый текст и введите его заглавными буквами.
С помощью алгоритма Берлекемпа проверить, является ли приводимым многочлен 

Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=29, n2=37, x=11.
Чей компьютер он взломает быстрее?
Зашифруйте открытый текст РЕМОНТНЫЙ с помощью алфавита, приведенного в
таблице
, используйте открытый ключ B=(188, 93), значения случайных чисел
для букв открытого текста k: 2, 2, 4, 18, 15, 19, 11, 2, 15, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
(1) {(188, 93), (458, 261)}; {(188, 93), (184, 217)}; {(16, 416), (374, 436)};
{(618, 206), (267, 81)}; {(745, 210), (506, 92)}; {(568, 355), (256, 121)};
{(179, 275), (110, 622)}; {(188, 93), (576, 286)}; {(745, 210), (376, 686)}
(2) {(16, 416), (374, 436)}; {(188, 93), (458, 261)}; {(188, 93), (184, 217)};
{(618, 206), (267, 81)}; {(745, 210), (506, 92)}; {(568, 355), (256, 121)};
{(179, 275), (110, 622)}; {(188, 93), (576, 286)}; {(745, 210), (376, 686)}
(3) {(16, 416), (374, 436)}; {(188, 93), (458, 261)}; {(188, 93), (184, 217)}; {(16, 416), (374, 436)};
{(618, 206), (267, 81)}; {(745, 210), (506, 92)}; {(179, 275), (110, 622)}; {(188, 93), (576, 286)}; {(745, 210), (376, 686)}
(4) {(188, 93), (458, 261)}; {(618, 206), (267, 81)}; {(188, 93), (184, 217)}; {(16, 416), (374, 436)};
{(745, 210), (506, 92)}; {(568, 355), (256, 121)}; {(179, 275), (110, 622)}; {(188, 93), (576, 286)}; {(745, 210), (376, 686)}
Даны точки P(48, 702), Q(69, 241), R(98, 338) на кривой 

Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
РУБАХА
или
ПОРТКИ
— устойчивее к действию этой программы?
(1) Первый пароль надежнее
(2) Второй пароль надежнее
(3) Пароли одинаково ненадежные
Дан шифртекст, показанный ниже. Зная секретный ключ 
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(745, 210), (259, 401)}; {(568, 355), (606, 147)}; |
| {(188, 93), (407, 82)}; {(56, 419), (739, 574)}; |
| {(286, 136), (329, 447)}; {(425, 663), (520, 749)}; |
| {(72, 254), (374, 315)}; {(188, 93), (149, 97)}; |
| {(745, 210), (13, 134)}; {(440, 539), (235, 19)}; |
| {(425, 663), (128, 79)} |
Дана точка P(75, 318) на кривой 

Вычислить порядок точки (3, 5) кривой 
Решить в целых числах уравнение 
Определить, является ли число 2332134563018038201 простым с вероятностью не меньше 0,999.
Шифротекст ША_УНППРААУТУРААЗЕМ_ЛИ_ИТ получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
НАШУ_АППАРАТУРУ_ЗАМЕТИЛИ_
Вычислить нелинейность булевой функции 01111111 от 3 переменных
Дано: модуль шифрования N = 4331, открытый ключ e = 11. Найти значение шифртекста, полученного при зашифровании открытого текста 632 на открытом ключе (N, e) по алгоритму RSA.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=4 и k=41 системы цифровой подписи и подписываемый текст ШУМ. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Решить следующее сравнение 
С помощью 
Расшифровать фразу ИМНЕ_ЯВСТ_СОБЩО_РЕМВРЧИ_Е, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
СООБЩИ_МНЕ_ВРЕМЯ_ВСТРЕЧИ_
Вычислить динамическое расстояние порядка 1 булевой функции 01111111 от 3 переменных
Даны значения модуля шифрования N = 299 и открытого ключа e = 139. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 285.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=52 и k=41 системы цифровой подписи и подписываемый текст ГОД. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Решить сравнение 
Найти произвольный квадратичный невычет по модулю 359
Расшифровать текст 3-9.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите третье слово заглавными буквами.
Вычислить нелинейность блока замен 1 9 12 14 2 11 13 10 8 6 15 5 0 7 4 3 размерностью 
Даны значения модуля шифрования N = 1891 и открытого ключа e = 277. Используя метод факторизации Ферма, найти значение закрытого ключа.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 1867. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 20, значения цифровой подписи: r = 36; s = 57. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
(1) подпись действительна
(2) подпись недействительна
Решить систему сравнений:

Найти наибольший квадратный корень из 17 по модулю 257.
Расшифровать сообщение
4-9.txt
, зашифрованное шифром Виженера, Длина ключа равна 7, пробел является частью алфавита.
В ответ введите ключ.
.
Вычислить динамическое расстояние порядка (2,2) блока замен 1 9 12 14 2 11 13 10 8 6 15 5 0 7 4 3 размерностью 
Применением цепных дробей найти секретный ключ d и разложение модуля 78908333904637 (экспонента — 2821057) на множители. В ответе укажите секретный ключ.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 8948. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 30, значения цифровой подписи: r = 38; s = 16. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
(1) подпись действительна
(2) подпись недействительна
Решить сравнение 
Найти наибольший квадратный корень из 524 по примарному модулю 625.
Расшифровать сообщение
5-9.txt
, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Найти корреляционную матрицу блока замен 1 9 12 14 2 11 13 10 8 6 15 5 0 7 4 3 размерностью 
(1)
begin{matrix}
0.25 & 0.5 & 0 & 0 &
0 & 0 & 0.5 & 0.25 &
0 & 0.25 & -0.25 & -0.25 &
0 & 0 & -0.25 & -0.5 &
end{matrix}
(2)
begin{matrix}
0.25 & 0.5 & 0 & 0 &
0 & 0 & 0.5 & 0.25 &
0 & 0.25 & -0.25 & -0.25 &
0 & 0 & 0.25 & -0.5 &
end{matrix}
(3)
begin{matrix}
0.25 & 0.5 & 0 & 0 &
0 & 0 & 0.5 & 0.25 &
0 & 0.25 & -0.25 & 0.25 &
0 & 0 & 0.25 & -0.5 &
end{matrix}
(4)
begin{matrix}
0.25 & 0.5 & 0 & 0 &
0 & 0 & 0.5 & 0.25 &
0 & 0.25 & -0.25 & -0.25 &
0 & 0 & 0.25 & 0.5 &
end{matrix}
Дан шифртекст 10, а также значения модуля шифрования N = 221 и открытого ключа e = 5. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=11, зная секретный ключ подписи d=5 при данном значении выбираемого случайным образом числа k=6. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Найти остаток от деления 
Найти количество квадратных корней из 16 по непримарному составному модулю 385.
Расшифровать сообщение на английском языке
6-9.txt
, зашифрованное шифром Виженера, Длина ключа равна 3.
В ответ введите ключ.
.
Провести операцию SubBytes алгоритма AES со значением байта 95.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=8, зная секретный ключ подписи d=12 при данном значении выбираемого случайным образом числа k=8. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Вычислить значение 
Какая наибольшая степень элемента a порядка 60 порождает группу 
Провести операцию MixColumns над приведенным ниже столбцом состояния
Проверьте подлинность ЭЦП (11, 11) для сообщения с известным значением хэш-свертки 7, зная открытый ключ проверки подписи (455, 368). Используйте кривую 
(1) подпись действительна
(2) подпись недействительна
Найти дискретный логарифм числа 3 по основанию 10 по модулю 112501.
Зашифровать биграмму ТЫ с помощью матрицы 
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
FAE90C06815B5D846AA23056E470AB27
Сообщение 480 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {2,6,9,19,38,75,151}, m=301 и n=113. В ответе укажите исходное сообщение.
Проверить действительность подписей (3, 49), (3, 85) для сообщения с известным значением хэш-свертки 31 и открытым ключом проверки (318,109). Используется кривая 
(1) обе подписи действительны
(2) первая подпись действительна, вторая — недействительна
(3) первая подпись недействительна, вторая — действительна
(4) обе подписи недействительны
Используя порождающий полином для CRC 
(1) {1,1,0,0,1}
(2) {1,1,0,0,0}
(3) {0,1,0,0,1}
(4) {1,0,0,0,1}
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3
Д 4 Е 5 Ё 6 Ж 7
З 8 И 9 Й 10 К 11
Л 12 М 13 Н 14 О 15
П 16 Р 17 С 18 Т 19
У 20 Ф 21 Х 22 Ц 23
Ч 24 Ш 25 Щ 26 Ъ 27
Ы 28 Ь 29 Э 30 Ю 31
Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст МИНУТА.
Провести первый раунд зашифрования открытого текста A64E D30C E720 E3E8 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок 
Шифртекст (3928629409, 01011110010001001001) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=96263, q=98479. Найти открытый текст и введите его заглавными буквами.
С помощью алгоритма Берлекемпа проверить, является ли приводимым многочлен 

Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=29, n2=41, x=7.
Чей компьютер он взломает быстрее?
Зашифруйте открытый текст РЕНЕССАНС с помощью алфавита, приведенного в
таблице
, используйте открытый ключ B=(725, 195), значения случайных чисел
для букв открытого текста k: 2, 19, 4, 8, 2, 2, 16, 10, 2, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
(1) {(188, 93), (6, 218)}; {(568, 355), (234, 164)}; {(16, 416), (390, 603)};
{(346, 242), (307, 693)}; {(188, 93), (45, 31)}; {(188, 93), (45, 31)};
{(72, 254), (229, 600)}; {(377, 456), (685, 655)}; {(188, 93), (45, 31)}
(2) {(16, 416), (390, 603)}; {(188, 93), (6, 218)}; {(568, 355), (234, 164)};
{(346, 242), (307, 693)}; {(188, 93), (45, 31)}; {(188, 93), (45, 31)};
{(72, 254), (229, 600)}; {(377, 456), (685, 655)}; {(188, 93), (45, 31)}
(3) {(188, 93), (45, 31)}; {(568, 355), (234, 164)}; {(16, 416), (390, 603)};
{(346, 242), (307, 693)}; {(188, 93), (45, 31)}; {(188, 93), (6, 218)};
{(72, 254), (229, 600)}; {(377, 456), (685, 655)}; {(188, 93), (45, 31)}
(4) {(568, 355), (234, 164)}; {(188, 93), (6, 218)}; {(16, 416), (390, 603)};
{(346, 242), (307, 693)}; {(188, 93), (45, 31)}; {(188, 93), (45, 31)};
{(72, 254), (229, 600)}; {(377, 456), (685, 655)}; {(188, 93), (45, 31)}
Даны точки P(59, 386), Q(61, 129), R(100, 364) на кривой 

Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
ДОКЛАД
или
ТЕЗИСЫ
— устойчивее к действию этой программы?
(1) Первый пароль надежнее
(2) Второй пароль надежнее
(3) Пароли одинаково ненадежные
Дан шифртекст, показанный ниже. Зная секретный ключ 
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(188, 93), (623, 166)}; {(725, 195), (513, 414)}; |
| {(346, 242), (461, 4)}; {(489, 468), (739, 574)}; |
| {(725, 195), (663, 476)}; {(745, 210), (724, 522)}; |
| {(725, 195), (663, 476)}; {(618, 206), (438, 40)}; |
| {(286, 136), (546, 670)}; {(179, 275), (73, 72)} |
Дана точка P(45, 720) на кривой 

Вычислить порядок точки (28, 17) кривой 
Решить в целых числах уравнение 
Определить, является ли число 1243354398042316799 простым с вероятностью не меньше 0,999.
Шифротекст ПРГРОА_АММНАЗЕ_ПАКУСЕ_ЯТС получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
ПРОГРАММА_НЕ_ЗАПУСКАЕТСЯ_
Вычислить нелинейность булевой функции 00011001 от 3 переменных
Дано: модуль шифрования N = 8633, открытый ключ e = 13. Найти значение шифртекста, полученного при зашифровании открытого текста 688 на открытом ключе (N, e) по алгоритму RSA.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=19 и k=37 системы цифровой подписи и подписываемый текст ВОСК. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Решить следующее сравнение 
С помощью 
Расшифровать фразу А__ФНРЕПДЕТЕА_ЙРУВСИШКЛЕЕ, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
ПЕРЕДАЙТЕ_ВИРУС_НА_ФЛЕШКЕ
Вычислить динамическое расстояние порядка 1 булевой функции 00011001 от 3 переменных
Даны значения модуля шифрования N = 209 и открытого ключа e = 131. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 92.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=24 и k=5 системы цифровой подписи и подписываемый текст РОД. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Решить сравнение 
Найти произвольный квадратичный невычет по модулю 353
Расшифровать текст 3-10.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите третье слово заглавными буквами.
Вычислить нелинейность блока замен 12 9 10 6 5 0 3 15 14 8 2 11 1 13 4 7 размерностью 
Даны значения модуля шифрования N = 5917 и открытого ключа e = 1103. Используя метод факторизации Ферма, найти значение закрытого ключа.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 3669. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 15, значения цифровой подписи: r = 6; s = 29. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
(1) подпись действительна
(2) подпись недействительна
Решить систему сравнений:

Найти наименьший квадратный корень из 173 по модулю 263.
Расшифровать сообщение
4-10.txt
, зашифрованное шифром Виженера, Длина ключа равна 6, пробел является частью алфавита.
В ответ введите ключ.
.
Вычислить динамическое расстояние порядка (2,2) блока замен 12 9 10 6 5 0 3 15 14 8 2 11 1 13 4 7 размерностью 
Применением цепных дробей найти секретный ключ d и разложение модуля 77027476849549 (экспонента — 2936957) на множители. В ответе укажите секретный ключ.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 1892. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 37, значения цифровой подписи: r = 56; s = 26. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
(1) подпись действительна
(2) подпись недействительна
Решить сравнение 
Найти наименьший квадратный корень из 316 по примарному модулю 343.
Расшифровать сообщение
5-10.txt
, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Найти корреляционную матрицу блока замен 12 9 10 6 5 0 3 15 14 8 2 11 1 13 4 7 размерностью 
(1)
begin{matrix}
0.25 & 0 & 0 & 0.25 &
0 & 0.75 & 0 & -0.25 &
0.5 & -0.25 & 0.25 & 0.5 &
0 & 0 & 0 & 0 &
end{matrix}
(2)
begin{matrix}
0.25 & 0 & 0 & 0.25 &
0 & 0.75 & 0 & -0.25 &
0.5 & -0.25 & 0.25 & -0.5 &
0 & 0 & 0 & 0 &
end{matrix}
(3)
begin{matrix}
0.25 & 0 & 0 & 0.25 &
0 & 0.75 & 0 & -0.25 &
0.5 & -0.25 & -0.25 & -0.5 &
0 & 0 & 0 & 0 &
end{matrix}
(4)
begin{matrix}
0.25 & 0 & 0 & 0.25 &
0 & 0.75 & 0 & -0.25 &
0.5 & 0.25 & 0.25 & -0.5 &
0 & 0 & 0 & 0 &
end{matrix}
Дан шифртекст 86, а также значения модуля шифрования N = 323 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=3, зная секретный ключ подписи d=3 при данном значении выбираемого случайным образом числа k=11. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Найти остаток от деления 
Найти количество квадратных корней из 900 по непримарному составному модулю 1001.
Расшифровать сообщение на английском языке
6-10.txt
, зашифрованное шифром Виженера, Длина ключа равна 4.
В ответ введите ключ.
.
Провести операцию SubBytes алгоритма AES со значением байта 69.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=3, зная секретный ключ подписи d=1 при данном значении выбираемого случайным образом числа k=8. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Вычислить значение 
Какая наибольшая степень элемента a порядка 66 порождает группу 
Провести операцию MixColumns над приведенным ниже столбцом состояния
Проверьте подлинность ЭЦП (5, 5) для сообщения с известным значением хэш-свертки 7, зная открытый ключ проверки подписи (384, 475). Используйте кривую 
(1) подпись действительна
(2) подпись недействительна
Найти дискретный логарифм числа 31 по основанию 3 по модулю 114689.
Зашифровать биграмму АН с помощью матрицы 
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
2A1E96F3986D3980D76C0E548D3BE59B
Сообщение 561 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {1,6,8,17,35,69,137}, m=275 и n=107. В ответе укажите исходное сообщение.
Проверить действительность подписей (35, 236), (57, 230) для сообщения с известным значением хэш-свертки 10 и открытым ключом проверки (177,531). Используется кривая 
(1) обе подписи действительны
(2) первая подпись действительна, вторая — недействительна
(3) первая подпись недействительна, вторая — действительна
(4) обе подписи недействительны
Используя порождающий полином для CRC 
(1) {1,1,0,0,1}
(2) {1,1,0,0,0}
(3) {0,1,0,0,1}
(4) {1,0,0,0,1}
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3
Д 4 Е 5 Ё 6 Ж 7
З 8 И 9 Й 10 К 11
Л 12 М 13 Н 14 О 15
П 16 Р 17 С 18 Т 19
У 20 Ф 21 Х 22 Ц 23
Ч 24 Ш 25 Щ 26 Ъ 27
Ы 28 Ь 29 Э 30 Ю 31
Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст ЛОГИКА.
Провести первый раунд зашифрования открытого текста E37F C8BC F84A DFA3 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок 
Шифртекст (978847044, 10011100011011001101) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=99971, q=98143. Найти открытый текст и введите его заглавными буквами.
С помощью алгоритма Берлекемпа проверить, является ли приводимым многочлен 

Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=43, n2=29, x=10.
Чей компьютер он взломает быстрее?
Зашифруйте открытый текст РЕПАРАЦИЯ с помощью алфавита, приведенного в
таблице
, используйте открытый ключ B=(435, 663), значения случайных чисел
для букв открытого текста k: 12, 11, 18, 7, 16, 18, 17, 2, 3, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
(1) {(286, 136), (269, 187)}; {(179, 275), (490, 434)}; {(618, 206), (371, 14)};
{(135, 82), (438, 40)}; {(72, 254), (438, 711)}; {(618, 206), (407, 82)};
{(440, 539), (532, 50)}; {(188, 93), (228, 480)}; {(56, 419), (538, 325)}
(2) {(618, 206), (371, 14)}; {(286, 136), (269, 187)}; {(179, 275), (490, 434)};
{(135, 82), (438, 40)}; {(72, 254), (438, 711)}; {(618, 206), (407, 82)};
{(440, 539), (532, 50)}; {(188, 93), (228, 480)}; {(56, 419), (538, 325)}
(3) {(179, 275), (490, 434)}; {(286, 136), (269, 187)}; {(618, 206), (371, 14)};
{(135, 82), (438, 40)}; {(72, 254), (438, 711)}; {(618, 206), (407, 82)};
{(440, 539), (532, 50)}; {(188, 93), (228, 480)}; {(56, 419), (538, 325)}
(4) {(618, 206), (407, 82)}; {(179, 275), (490, 434)}; {(618, 206), (371, 14)};
{(135, 82), (438, 40)}; {(72, 254), (438, 711)}; {(286, 136), (269, 187)};
{(440, 539), (532, 50)}; {(188, 93), (228, 480)}; {(56, 419), (538, 325)}
Даны точки P(72, 497), Q(53, 474), R(90, 730) на кривой 

Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
ДОЛЛАР
или
ФАНТИК
— устойчивее к действию этой программы?
(1) Первый пароль надежнее
(2) Второй пароль надежнее
(3) Пароли одинаково ненадежные
Дан шифртекст, показанный ниже. Зная секретный ключ 
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(179, 275), (269, 564)}; {(179, 275), (73, 72)}; |
| {(440, 539), (189, 454)}; {(618, 206), (628, 458)}; |
| {(568, 355), (660, 275)}; {(72, 254), (709, 595)}; |
| {(745, 210), (12, 314)}; {(188, 93), (36, 664)}; |
| {(618, 206), (530, 22)}; {(286, 136), (532, 50)}; |
| {(425, 663), (660, 275)}; {(725, 195), (482, 230)} |
Дана точка P(78, 480) на кривой 

Вычислить порядок точки (36, 5) кривой 
Решить в целых числах уравнение 
Определить, является ли число 1111111111111111111 простым с вероятностью не меньше 0,999.
Шифротекст ПООВРД_ЕРИБНАКЕ__ЕДВТА_ДС получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
ПРОВОДИ_РЕБЕНКА_В_ДЕТСАД_
Вычислить нелинейность булевой функции 01110111 от 3 переменных
Дано: модуль шифрования N = 3713, открытый ключ e = 11. Найти значение шифртекста, полученного при зашифровании открытого текста 3415 на открытом ключе (N, e) по алгоритму RSA.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=33 и k=35 системы цифровой подписи и подписываемый текст СКАЧ. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Решить следующее сравнение 
С помощью 
Расшифровать фразу _ПАЕНЕ_ВИ_ЯНЕРЖЕ_ИСТИОКНЗ, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
НИЗКОЕ_НАПРЯЖЕНИЕ_В_СЕТИ_
Вычислить динамическое расстояние порядка 1 булевой функции 01110111 от 3 переменных
Даны значения модуля шифрования N = 377 и открытого ключа e = 283. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 261.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=18 и k=37 системы цифровой подписи и подписываемый текст СХОД. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Решить сравнение 
Найти произвольный квадратичный невычет по модулю 383
Расшифровать текст 3-11.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите четвертое слово заглавными буквами.
Вычислить нелинейность блока замен 2 12 1 4 13 7 9 6 8 14 0 15 3 5 11 10 размерностью 
Даны значения модуля шифрования N = 3901 и открытого ключа e = 343. Используя метод факторизации Ферма, найти значение закрытого ключа.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 3057. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 58, значения цифровой подписи: r = 11; s = 2. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
(1) подпись действительна
(2) подпись недействительна
Решить систему сравнений:

Найти наибольший квадратный корень из 169 по модулю 269.
Расшифровать сообщение
4-11.txt
, зашифрованное шифром Виженера, Длина ключа равна 5, пробел является частью алфавита.
В ответ введите ключ.
.
Вычислить динамическое расстояние порядка (2,2) блока замен 2 12 1 4 13 7 9 6 8 14 0 15 3 5 11 10 размерностью 
Применением цепных дробей найти секретный ключ d и разложение модуля 34542035262313 (экспонента — 4727621) на множители. В ответе укажите секретный ключ.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 2764. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 8, значения цифровой подписи: r = 47; s = 42. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
(1) подпись действительна
(2) подпись недействительна
Решить сравнение 
Найти наибольший квадратный корень из 350 по примарному модулю 625.
Расшифровать сообщение
5-11.txt
, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Найти корреляционную матрицу блока замен 2 12 1 4 13 7 9 6 8 14 0 15 3 5 11 10 размерностью 
(1)
begin{matrix}
-0.25 & 0.25 & 0.75 & 0 &
0 & 0 & -0.25 & 0 &
0.5 & 0.25 & 0 & 0 &
0 & 0.25 & 0.25 & 0.25 &
end{matrix}
(2)
begin{matrix}
-0.25 & 0.25 & 0.75 & 0 &
0 & 0 & -0.25 & 0 &
0.5 & 0.25 & 0 & 0 &
0 & 0.25 & -0.25 & 0.25 &
end{matrix}
(3)
begin{matrix}
-0.25 & 0.25 & 0.75 & 0 &
0 & 0 & -0.25 & 0 &
0.5 & 0.25 & 0 & 0 &
0 & 0.25 & 0.25 & 0.25 &
end{matrix}
(4)
begin{matrix}
-0.25 & 0.25 & 0.75 & 0 &
0 & 0 & -0.25 & 0 &
0.5 & 0.25 & 0 & 0 &
0 & 0.25 & -0.25 & -0.25 &
end{matrix}
Дан шифртекст 75, а также значения модуля шифрования N = 221 и открытого ключа e = 5. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=10, зная секретный ключ подписи d=9 при данном значении выбираемого случайным образом числа k=2. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Найти остаток от деления 
Найти количество квадратных корней из 2278 по непримарному составному модулю 2431.
Расшифровать сообщение на английском языке
6-11.txt
, зашифрованное шифром Виженера, Длина ключа равна 3.
В ответ введите ключ.
.
Провести операцию SubBytes алгоритма AES со значением байта BA.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=6, зная секретный ключ подписи d=5 при данном значении выбираемого случайным образом числа k=6. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Вычислить значение 
Провести операцию MixColumns над приведенным ниже столбцом состояния
Проверьте подлинность ЭЦП (11, 1) для сообщения с известным значением хэш-свертки 5, зная открытый ключ проверки подписи (384, 475). Используйте кривую 
(1) подпись действительна
(2) подпись недействительна
Найти дискретный логарифм числа 53 по основанию 23 по модулю 115201.
Зашифровать биграмму ДУ с помощью матрицы 
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
E5488FFAD767A6533D55BDE4809DEC18
Сообщение 782 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {4,5,10,21,45,88,174}, m=349 и n=80. В ответе укажите исходное сообщение.
Проверить действительность подписей (224, 158), (11, 133) для сообщения с известным значением хэш-свертки 63 и открытым ключом проверки (110,50). Используется кривая 
(1) обе подписи действительны
(2) первая подпись действительна, вторая — недействительна
(3) первая подпись недействительна, вторая — действительна
(4) обе подписи недействительны
Используя порождающий полином для CRC 
(1) {1,1,0,0,1}
(2) {1,1,0,0,0}
(3) {0,1,0,0,1}
(4) {1,0,0,0,1}
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3
Д 4 Е 5 Ё 6 Ж 7
З 8 И 9 Й 10 К 11
Л 12 М 13 Н 14 О 15
П 16 Р 17 С 18 Т 19
У 20 Ф 21 Х 22 Ц 23
Ч 24 Ш 25 Щ 26 Ъ 27
Ы 28 Ь 29 Э 30 Ю 31
Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст РАКЕТА.
Провести первый раунд зашифрования открытого текста BDC6 FF70 AC32 B3A6 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок 
Шифртекст (432159239, 01101010010011011001) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=93503, q=97007. Найти открытый текст и введите его заглавными буквами.
С помощью алгоритма Берлекемпа проверить, является ли приводимым многочлен 

Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=29, n2=47, x=12.
Чей компьютер он взломает быстрее?
Зашифруйте открытый текст ПРОЛЕЖЕНЬ с помощью алфавита, приведенного в
таблице
, используйте открытый ключ B=(179, 275), значения случайных чисел
для букв открытого текста k: 9, 5, 17, 2, 2, 2, 3, 17, 15, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
(1) {(489, 468), (210, 720)}; {(425, 663), (151, 518)}; {(440, 539), (594, 337)};
{(188, 93), (422, 162)}; {(188, 93), (290, 509)}; {(188, 93), (79, 640)};
{(56, 419), (496, 31)}; {(440, 539), (26, 366)}; {(745, 210), (240, 442)}
(2) {(425, 663), (151, 518)}; {(489, 468), (210, 720)}; {(440, 539), (594, 337)};
{(188, 93), (422, 162)}; {(188, 93), (290, 509)}; {(188, 93), (79, 640)};
{(56, 419), (496, 31)}; {(440, 539), (26, 366)}; {(745, 210), (240, 442)}
(3) {(440, 539), (594, 337)}; {(489, 468), (210, 720)}; {(425, 663), (151, 518)};
{(188, 93), (422, 162)}; {(188, 93), (290, 509)}; {(188, 93), (79, 640)};
{(56, 419), (496, 31)}; {(440, 539), (26, 366)}; {(745, 210), (240, 442)}
(4) {(188, 93), (79, 640)}; {(425, 663), (151, 518)}; {(440, 539), (594, 337)};
{(188, 93), (422, 162)}; {(188, 93), (290, 509)}; {(489, 468), (210, 720)};
{(56, 419), (496, 31)}; {(440, 539), (26, 366)}; {(745, 210), (240, 442)}
Даны точки P(59, 365), Q(59, 386), R(105, 382) на кривой 

Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
ПЛИТА
или
ПЛАТО
— устойчивее к действию этой программы?
(1) Первый пароль надежнее
(2) Второй пароль надежнее
(3) Пароли одинаково ненадежные
Дан шифртекст, показанный ниже. Зная секретный ключ 
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(745, 210), (185, 105)}; {(188, 93), (681, 385)}; |
| {(377, 456), (576, 465)}; {(440, 539), (138, 298)}; |
| {(745, 210), (520, 2)}; {(188, 93), (681, 385)}; |
| {(286, 136), (282, 410)}; {(72, 254), (200, 721)}; |
| {(72, 254), (643, 94)}; {(745, 210), (476, 315)}; |
| {(440, 539), (724, 229)} |
Дана точка P(53, 474) на кривой 

Вычислить порядок точки (35, 4) кривой 
Решить в целых числах уравнение 
Определить, является ли число 11111111111111111111 простым с вероятностью не меньше 0,999.
Шифротекст ИРЕМЗЬО_ЕТСНВОНУАЧ_ЮСУТОТ получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
ИЗМЕРЬТЕ_ОСНОВНУЮ_ЧАСТОТУ
Вычислить динамическое расстояние порядка 1 булевой функции 01100100 от 3 переменных
Дано: модуль шифрования N = 3953, открытый ключ e = 17. Найти значение шифртекста, полученного при зашифровании открытого текста 2402 на открытом ключе (N, e) по алгоритму RSA.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=25 и k=17 системы цифровой подписи и подписываемый текст СТОП. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Решить следующее сравнение 
С помощью 
Расшифровать фразу АЗАДЙАЧЬЛНОЛИВЯЕЫУ_СЕТН_А, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
ЗАДАЙТЕ_НАЧАЛЬНЫЕ_УСЛОВИЯ
Вычислить динамическое расстояние порядка 1 булевой функции 01100100 от 3 переменных
Даны значения модуля шифрования N = 391 и открытого ключа e = 145. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 386.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=44 и k=11 системы цифровой подписи и подписываемый текст СВОД. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Решить сравнение 
Найти произвольный квадратичный невычет по модулю 211
Расшифровать текст 3-12.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите первое слово заглавными буквами.
Вычислить нелинейность блока замен 15 14 7 10 4 8 1 12 13 2 11 3 9 5 0 6 размерностью 
Даны значения модуля шифрования N = 3713 и открытого ключа e = 2929. Используя метод факторизации Ферма, найти значение закрытого ключа.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 1989. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 42, значения цифровой подписи: r = 34; s = 13. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
(1) подпись действительна
(2) подпись недействительна
Решить систему сравнений:

Найти наименьший квадратный корень из 2 по модулю 271.
Расшифровать сообщение
4-12.txt
, зашифрованное шифром Виженера, Длина ключа равна 5, пробел является частью алфавита.
В ответ введите ключ.
.
Вычислить динамическое расстояние порядка (2,2) блока замен 15 14 7 10 4 8 1 12 13 2 11 3 9 5 0 6 размерностью 
Применением цепных дробей найти секретный ключ d и разложение модуля 74701165267919 (экспонента — 3145553) на множители. В ответе укажите секретный ключ.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 8190. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 10, значения цифровой подписи: r = 56; s = 48. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
(1) подпись действительна
(2) подпись недействительна
Решить сравнение 
Найти наименьший квадратный корень из 70 по примарному модулю 81.
Расшифровать сообщение
5-12.txt
, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Найти корреляционную матрицу блока замен 15 14 7 10 4 8 1 12 13 2 11 3 9 5 0 6 размерностью 
(1)
begin{matrix}
-0.5 & 0.25 & 0 & 0 &
0 & 0.25 & -0.25 & -0.25 &
-0.25 & 0.75 & 0 & -0.25 &
0.25 & 0 & -0.25 & -0.25 &
end{matrix}
(2)
begin{matrix}
-0.5 & 0.25 & 0 & 0 &
0 & 0.25 & -0.25 & -0.25 &
-0.25 & -0.75 & 0 & -0.25 &
0.25 & 0 & -0.25 & -0.25 &
end{matrix}
(3)
begin{matrix}
-0.5 & 0.25 & 0 & 0 &
0 & 0.25 & -0.25 & -0.25 &
0.25 & -0.75 & 0 & -0.25 &
0.25 & 0 & -0.25 & -0.25 &
end{matrix}
(4)
begin{matrix}
-0.5 & 0.25 & 0 & 0 &
0 & 0.25 & -0.25 & -0.25 &
-0.25 & -0.75 & 0 & -0.25 &
0.25 & 0 & -0.25 & 0.25 &
end{matrix}
Дан шифртекст 96, а также значения модуля шифрования N = 187 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=11, зная секретный ключ подписи d=2 при данном значении выбираемого случайным образом числа k=8. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Найти остаток от деления 
Найти количество квадратных корней из 399 по непримарному составному модулю 2431.
Расшифровать сообщение на английском языке
6-12.txt
, зашифрованное шифром Виженера, Длина ключа равна 5.
В ответ введите ключ.
.
Провести операцию SubBytes алгоритма AES со значением байта DD.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=6, зная секретный ключ подписи d=7 при данном значении выбираемого случайным образом числа k=11. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Вычислить значение 
Провести операцию MixColumns над приведенным ниже столбцом состояния
Проверьте подлинность ЭЦП (11, 10) для сообщения с известным значением хэш-свертки 10, зная открытый ключ проверки подписи (455, 383). Используйте кривую 
(1) подпись действительна
(2) подпись недействительна
Найти дискретный логарифм числа 31 по основанию 5 по модулю 118273.
Зашифровать биграмму ША с помощью матрицы 
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
36FA9452068CB3472388A76CC6FC9E59
Сообщение 180 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {2,5,8,16,34,67,136}, m=270 и n=139. В ответе укажите исходное сообщение.
Проверить действительность подписей (166, 213), (3, 188) для сообщения с известным значением хэш-свертки 45 и открытым ключом проверки (286, 213). Используется кривая 
(1) обе подписи действительны
(2) первая подпись действительна, вторая — недействительна
(3) первая подпись недействительна, вторая — действительна
(4) обе подписи недействительны
Используя порождающий полином для CRC 
(1) {1,1,0,0,1}
(2) {1,1,0,0,0}
(3) {0,1,0,0,1}
(4) {1,0,0,0,1}
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3
Д 4 Е 5 Ё 6 Ж 7
З 8 И 9 Й 10 К 11
Л 12 М 13 Н 14 О 15
П 16 Р 17 С 18 Т 19
У 20 Ф 21 Х 22 Ц 23
Ч 24 Ш 25 Щ 26 Ъ 27
Ы 28 Ь 29 Э 30 Ю 31
Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст УРАГАН.
Провести первый раунд зашифрования открытого текста E26A 945F BE59 B5CC шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок 
Шифртекст (901439779, 10110110111111110111) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=101839, q=98867. Найти открытый текст и введите его заглавными буквами.
С помощью алгоритма Берлекемпа проверить, является ли приводимым многочлен 

Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=31, n2=37, x=10.
Чей компьютер он взломает быстрее?
Зашифруйте открытый текст ПРОКРУТКА с помощью алфавита, приведенного в
таблице
, используйте открытый ключ B=(618, 206), значения случайных чисел
для букв открытого текста k: 10, 15, 16, 2, 3, 4, 2, 11, 16, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
(1) {(377, 456), (558, 359)}; {(745, 210), (688, 741)}; {(72, 254), (679, 73)};
{(188, 93), (36, 664)}; {(56, 419), (588, 44)}; {(16, 416), (558, 392)};
{(188, 93), (606, 147)}; {(179, 275), (269, 564)}; {(72, 254), (395, 414)}
(2) {(72, 254), (679, 73)}; {(377, 456), (558, 359)}; {(745, 210), (688, 741)};
{(188, 93), (36, 664)}; {(56, 419), (588, 44)}; {(16, 416), (558, 392)};
{(188, 93), (606, 147)}; {(179, 275), (269, 564)}; {(72, 254), (395, 414)}
(3) {(745, 210), (688, 741)}; {(377, 456), (558, 359)}; {(72, 254), (679, 73)};
{(188, 93), (36, 664)}; {(56, 419), (588, 44)}; {(16, 416), (558, 392)};
{(188, 93), (606, 147)}; {(179, 275), (269, 564)}; {(72, 254), (395, 414)}
(4) {(16, 416), (558, 392)}; {(745, 210), (688, 741)}; {(72, 254), (679, 73)};
{(188, 93), (36, 664)}; {(56, 419), (588, 44)}; {(377, 456), (558, 359)};
{(188, 93), (606, 147)}; {(179, 275), (269, 564)}; {(72, 254), (395, 414)}
Даны точки P(61, 622), Q(61, 622), R(90, 730) на кривой 

Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
СТАТУС
или
ЗОЛОТО
— устойчивее к действию этой программы?
(1) Первый пароль надежнее
(2) Второй пароль надежнее
(3) Пароли одинаково ненадежные
Дан шифртекст, показанный ниже. Зная секретный ключ 
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(425, 663), (651, 191)}; {(188, 93), (177, 562)}; |
| {(286, 136), (603, 562)}; {(440, 539), (588, 707)}; |
| {(72, 254), (269, 187)}; {(56, 419), (49, 568)}; |
| {(16, 416), (426, 662)}; {(425, 663), (557, 28)}; |
| {(188, 93), (149, 97)}; {(179, 275), (711, 341)} |
Дана точка P(43, 527) на кривой 

Вычислить порядок точки (35, 1) кривой 
Решить в целых числах уравнение 
Определить, является ли число 14532464368718952447 простым с вероятностью не меньше 0,999.
Шифротекст ТОЮКЛИЧ_ТЕТОЕ_СИТО_МИНРТО получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
ОТКЛЮЧИТЕ_ОТ_СЕТИ_МОНИТОР
Вычислить нелинейность булевой функции 01101011 от 3 переменных
Дано: модуль шифрования N = 1961, открытый ключ e = 11. Найти значение шифртекста, полученного при зашифровании открытого текста 1382 на открытом ключе (N, e) по алгоритму RSA.
Вычислить подпись Эль-Гамаля для сообщения. Использовать параметры p=79, g=15, параметры x=55 и k=19 системы цифровой подписи и подписываемый текст РУЛЬ. Использовать первый учебный алгоритм хэширования. Ответ введите в формате (N1,N2), например, (23,12) или (33,5) — в скобках и без пробелов.
Решить следующее сравнение 
С помощью 
Расшифровать фразу МДЕ_Ж__ВТАЕТВТОНЧЕИЕН_ДЯЕ, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
ЖДЕМ_ОТВЕТА_В_ТЕЧЕНИЕ_ДНЯ
Вычислить динамическое расстояние порядка 1 булевой функции 01101011 от 3 переменных
Даны значения модуля шифрования N = 143 и открытого ключа e = 113. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 64.
Решить сравнение 
Найти произвольный квадратичный невычет по модулю 241
Расшифровать текст 3-13.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите второе слово заглавными буквами.
Вычислить нелинейность блока замен 15 9 4 6 12 1 0 8 10 11 2 7 13 14 3 5 размерностью 
Даны значения модуля шифрования N = 3397 и открытого ключа e = 2477. Используя метод факторизации Ферма, найти значение закрытого ключа.
Проверить подлинность цифровой подписи Эль-Гамаля для полученного сообщения M = 3271. Параметры подписи: p = 59, g = 14, открытый ключ отправителя y = 21, значения цифровой подписи: r = 2; s = 47. Для получения хэш-суммы использовался второй учебный алгоритм хэширования.
(1) подпись действительна
(2) подпись недействительна
Решить систему сравнений:

Найти наибольший квадратный корень из 156 по модулю 277.
Расшифровать сообщение
4-13.txt
, зашифрованное шифром Виженера, Длина ключа равна 5, пробел является частью алфавита.
В ответ введите ключ.
.
Вычислить динамическое расстояние порядка (2,2) блока замен 15 9 4 6 12 1 0 8 10 11 2 7 13 14 3 5 размерностью 
Применением цепных дробей найти секретный ключ d и разложение модуля 72903890242273 (экспонента — 3261683) на множители. В ответе укажите секретный ключ.
Решить сравнение 
Найти наибольший квадратный корень из 86 по примарному модулю 125.
Расшифровать сообщение
5-13.txt
, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Найти корреляционную матрицу блока замен 15 9 4 6 12 1 0 8 10 11 2 7 13 14 3 5 размерностью 
(1)
begin{matrix}
0.25 & 0 & 0 & 0 &
-0.25 & 0 & 0 & -0.75 &
0 & 0.5 & 0 & 0 &
0.25 & 0.5 & 0 & 0 &
end{matrix}
(2)
begin{matrix}
0.25 & 0 & 0 & 0 &
-0.25 & 0 & 0 & -0.75 &
0 & -0.5 & 0 & 0 &
0.25 & 0.5 & 0 & 0 &
end{matrix}
(3)
begin{matrix}
0.25 & 0 & 0 & 0 &
-0.25 & 0 & 0 & -0.75 &
0 & -0.5 & 0 & 0 &
-0.25 & 0.5 & 0 & 0 &
end{matrix}
(4)
begin{matrix}
0.25 & 0 & 0 & 0 &
-0.25 & 0 & 0 & -0.75 &
0 & -0.5 & 0 & 0 &
0.25 & -0.5 & 0 & 0 &
end{matrix}
Дан шифртекст 58, а также значения модуля шифрования N = 187 и открытого ключа e = 3. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=8, зная секретный ключ подписи d=5 при данном значении выбираемого случайным образом числа k=3. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Найти остаток от деления 
Найти количество квадратных корней из 1598 по непримарному составному модулю 2431.
Расшифровать сообщение на английском языке
6-13.txt
, зашифрованное шифром Виженера, Длина ключа равна 3.
В ответ введите ключ.
.
Провести операцию SubBytes алгоритма AES со значением байта 22.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=7, зная секретный ключ подписи d=3 при данном значении выбираемого случайным образом числа k=7. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Вычислить значение 
Провести операцию MixColumns над приведенным ниже столбцом состояния
Проверьте подлинность ЭЦП (3, 1) для сообщения с известным значением хэш-свертки 8, зная открытый ключ проверки подписи (384, 276). Используйте кривую 
(1) подпись действительна
(2) подпись недействительна
Найти дискретный логарифм числа 12 по основанию 17 по модулю 118801.
Зашифровать биграмму ВО с помощью матрицы 
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
00F96C92BDC986BEB5B3678AB02DC63A
Сообщение 518 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {1,4,7,15,28,57,114}, m=227 и n=51. В ответе укажите исходное сообщение.
Проверить действительность подписей (3, 208), (166, 235) для сообщения с известным значением хэш-свертки 14 и открытым ключом проверки (286, 213). Используется кривая 
(1) обе подписи действительны
(2) первая подпись действительна, вторая — недействительна
(3) первая подпись недействительна, вторая — действительна
(4) обе подписи недействительны
Используя порождающий полином для CRC 
(1) {1,1,0,0,0}
(2) {1,0,1,0,0}
(3) {1,1,0,1,1}
(4) {1,1,1,0,1}
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3
Д 4 Е 5 Ё 6 Ж 7
З 8 И 9 Й 10 К 11
Л 12 М 13 Н 14 О 15
П 16 Р 17 С 18 Т 19
У 20 Ф 21 Х 22 Ц 23
Ч 24 Ш 25 Щ 26 Ъ 27
Ы 28 Ь 29 Э 30 Ю 31
Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст ТАЙФУН.
Провести первый раунд зашифрования открытого текста A7BE CFBC F166 AB89 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок 
Шифртекст (7764435203, 10010100111100010011) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=93151, q=94483. Найти открытый текст и введите его заглавными буквами.
С помощью алгоритма Берлекемпа проверить, является ли приводимым многочлен 

Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=41, n2=31, x=12.
Чей компьютер он взломает быстрее?
Зашифруйте открытый текст ПРОКОПАТЬ с помощью алфавита, приведенного в
таблице
, используйте открытый ключ B=(489, 468), значения случайных чисел
для букв открытого текста k: 3, 16, 17, 5, 16, 18, 3, 7, 15, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
(1) {(56, 419), (454, 628)}; {(72, 254), (67, 84)}; {(440, 539), (397, 567)};
{(425, 663), (53, 474)}; {(72, 254), (414, 563)}; {(618, 206), (253, 211)};
{(56, 419), (688, 10)}; {(135, 82), (160, 142)}; {(745, 210), (48, 49)}
(2) {(72, 254), (67, 84)}; {(440, 539), (397, 567)}; {(56, 419), (454, 628)};
{(425, 663), (53, 474)}; {(72, 254), (414, 563)}; {(618, 206), (253, 211)};
{(56, 419), (688, 10)}; {(135, 82), (160, 142)}; {(745, 210), (48, 49)}
(3) {(618, 206), (253, 211)}; {(72, 254), (67, 84)}; {(440, 539), (397, 567)};
{(425, 663), (53, 474)}; {(72, 254), (414, 563)}; {(56, 419), (454, 628)};
{(56, 419), (688, 10)}; {(135, 82), (160, 142)}; {(745, 210), (48, 49)}
(4) {(440, 539), (397, 567)}; {(56, 419), (454, 628)}; {(72, 254), (67, 84)};
{(425, 663), (53, 474)}; {(72, 254), (414, 563)}; {(618, 206), (253, 211)};
{(56, 419), (688, 10)}; {(135, 82), (160, 142)}; {(745, 210), (48, 49)}
Даны точки P(61, 129), Q(69, 510), R(72, 497) на кривой 

Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
ПИЛЮЛЯ
или
БОЛЮСЫ
— устойчивее к действию этой программы?
(1) Первый пароль надежнее
(2) Второй пароль надежнее
(3) Пароли одинаково ненадежные
Дан шифртекст, показанный ниже. Зная секретный ключ 
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(179, 275), (712, 186)}; {(725, 195), (395, 414)}; |
| {(72, 254), (434, 136)}; {(425, 663), (251, 506)}; |
| {(16, 416), (383, 340)}; {(745, 210), (102, 484)}; |
| {(346, 242), (78, 271)}; {(179, 275), (712, 186)}; |
| {(725, 195), (739, 574)}; {(346, 242), (78, 271)} |
Дана точка P(49, 568) на кривой 

Вычислить порядок точки (12, 

Решить в целых числах уравнение 
Определить, является ли число 48112959837082048697 простым с вероятностью не меньше 0,999.
Шифротекст КУАМКЛТУОЯ_ЖРЕУРЗ_РАЖНЯ_Е получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
АККУМУЛЯТОР_УЖЕ_РАЗРЯЖЕН_
Вычислить нелинейность булевой функции 00101101 от 3 переменных
Дано: модуль шифрования N = 1763, открытый ключ e = 11. Найти значение шифртекста, полученного при зашифровании открытого текста 436 на открытом ключе (N, e) по алгоритму RSA.
Решить следующее сравнение 
С помощью 
Расшифровать фразу _ЕТИЕИ_ЛО_АКАЗЖС_.ЩТЛУТС_, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
ЗАКАЖИТЕ_ЕЩЁ_СТОЛ_И_СТУЛ_
Вычислить динамическое расстояние порядка 1 булевой функции 00101101 от 3 переменных
Даны значения модуля шифрования N = 667 и открытого ключа e = 575. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 593.
Решить сравнение 
Найти произвольный квадратичный невычет по модулю 257
Расшифровать текст 3-14.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите последнее слово заглавными буквами.
Вычислить нелинейность блока замен 7 9 3 10 13 11 4 14 8 1 12 5 6 0 15 2 размерностью 
Даны значения модуля шифрования N = 2911 и открытого ключа e = 359. Используя метод факторизации Ферма, найти значение закрытого ключа.
Решить систему сравнений:

Найти наименьший квадратный корень из 153 по модулю 281.
Расшифровать сообщение
4-14.txt
, зашифрованное шифром Виженера, Длина ключа равна 6, пробел является частью алфавита.
В ответ введите ключ.
.
Вычислить динамическое расстояние порядка (2,2) блока замен 7 9 3 10 13 11 4 14 8 1 12 5 6 0 15 2 размерностью 
Применением цепных дробей найти секретный ключ d и разложение модуля 70109121369029 (экспонента — 3401467) на множители. В ответе укажите секретный ключ.
Решить сравнение 
Найти наименьший квадратный корень из 340 по примарному модулю 343.
Расшифровать сообщение
5-14.txt
, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Найти корреляционную матрицу блока замен 7 9 3 10 13 11 4 14 8 1 12 5 6 0 15 2 размерностью 
(1)
begin{matrix}
0 & 0 & -0.5 & 0 &
-0.25 & 0.25 & 0.25 & 0 &
-0.25 & 0.25 & 0.25 & 0 &
0.25 & -0.25 & 0 & -0.25 &
end{matrix}
(2)
begin{matrix}
0 & 0 & -0.5 & 0 &
-0.25 & 0.25 & 0.25 & 0 &
-0.25 & 0.25 & 0.25 & 0 &
-0.25 & -0.25 & 0 & -0.25 &
end{matrix}
(3)
begin{matrix}
0 & 0 & -0.5 & 0 &
-0.25 & 0.25 & 0.25 & 0 &
-0.25 & 0.25 & 0.25 & 0 &
-0.25 & 0.25 & 0 & -0.25 &
end{matrix}
(4)
begin{matrix}
0 & 0 & -0.5 & 0 &
-0.25 & 0.25 & 0.25 & 0 &
-0.25 & 0.25 & 0.25 & 0 &
-0.25 & -0.25 & 0 & 0.25 &
end{matrix}
Дан шифртекст 49, а также значения модуля шифрования N = 187 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=3, зная секретный ключ подписи d=10 при данном значении выбираемого случайным образом числа k=6. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Найти остаток от деления 
Найти количество квадратных корней из 212 по непримарному составному модулю 1001.
Расшифровать сообщение на английском языке
6-14.txt
, зашифрованное шифром Виженера, Длина ключа равна 5.
В ответ введите ключ.
.
Провести операцию SubBytes алгоритма AES со значением байта 0E.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=9, зная секретный ключ подписи d=11 при данном значении выбираемого случайным образом числа k=2. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Вычислить значение 
Провести операцию MixColumns над приведенным ниже столбцом состояния
Проверьте подлинность ЭЦП (11, 10) для сообщения с известным значением хэш-свертки 3, зная открытый ключ проверки подписи (135, 669). Используйте кривую 
(1) подпись действительна
(2) подпись недействительна
Найти дискретный логарифм числа 18 по основанию 2 по модулю 97021.
Зашифровать биграмму НЕ с помощью матрицы 
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
759E4BC1BCC1BB22C43022BEFDF64120
Сообщение 557 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {3,5,9,19,37,77,151}, m=302 и n=59. В ответе укажите исходное сообщение.
Проверить действительность подписей (71, 65), (127, 230) для сообщения с известным значением хэш-свертки 52 и открытым ключом проверки (10,275). Используется кривая 
(1) обе подписи действительны
(2) первая подпись действительна, вторая — недействительна
(3) первая подпись недействительна, вторая — действительна
(4) обе подписи недействительны
Используя порождающий полином для CRC 
(1) {1,1,0,0,0}
(2) {1,0,1,0,0}
(3) {1,1,0,1,1}
(4) {1,1,1,0,1}
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3
Д 4 Е 5 Ё 6 Ж 7
З 8 И 9 Й 10 К 11
Л 12 М 13 Н 14 О 15
П 16 Р 17 С 18 Т 19
У 20 Ф 21 Х 22 Ц 23
Ч 24 Ш 25 Щ 26 Ъ 27
Ы 28 Ь 29 Э 30 Ю 31
Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст ПОБЕДА.
Провести первый раунд зашифрования открытого текста A267 8C95 8111 B0B7 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок 
Шифртекст (5978393092, 10001100110111000010) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=92779, q=90127. Найти открытый текст и введите его заглавными буквами.
С помощью алгоритма Берлекемпа проверить, является ли приводимым многочлен 

Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=31, n2=43, x=7.
Чей компьютер он взломает быстрее?
Зашифруйте открытый текст ОТСТУПИТЬ с помощью алфавита, приведенного в
таблице
, используйте открытый ключ B=(188, 93), значения случайных чисел
для букв открытого текста k: 7, 9, 3, 8, 18, 18, 8, 11, 16, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
(1) {(135, 82), (69, 510)}; {(489, 468), (481, 369)}; {(56, 419), (426, 89)};
{(346, 242), (594, 414)}; {(618, 206), (100, 387)}; {(618, 206), (350, 184)};
{(346, 242), (86, 726)}; {(179, 275), (660, 476)}; {(72, 254), (642, 53)}
(2) {(56, 419), (426, 89)}; {(135, 82), (69, 510)}; {(489, 468), (481, 369)};
{(346, 242), (594, 414)}; {(618, 206), (100, 387)}; {(618, 206), (350, 184)};
{(346, 242), (86, 726)}; {(179, 275), (660, 476)}; {(72, 254), (642, 53)}
(3) {(618, 206), (350, 184)}; {(135, 82), (69, 510)}; {(489, 468), (481, 369)};
{(346, 242), (594, 414)}; {(618, 206), (100, 387)}; {(56, 419), (426, 89)};
{(346, 242), (86, 726)}; {(179, 275), (660, 476)}; {(72, 254), (642, 53)}
(4) {(489, 468), (481, 369)}; {(135, 82), (69, 510)}; {(56, 419), (426, 89)};
{(346, 242), (594, 414)}; {(618, 206), (100, 387)}; {(618, 206), (350, 184)};
{(346, 242), (86, 726)}; {(179, 275), (660, 476)}; {(72, 254), (642, 53)}
Даны точки P(70, 556), Q(56, 419), R(86, 726) на кривой 

Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
ПЛАЦЕБО
или
СПАСИБО
— устойчивее к действию этой программы?
(1) Первый пароль надежнее
(2) Второй пароль надежнее
(3) Пароли одинаково ненадежные
Дан шифртекст, показанный ниже. Зная секретный ключ 
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(425, 663), (273, 481)}; {(188, 93), (85, 716)}; |
| {(16, 416), (422, 162)}; {(283, 493), (36, 87)}; |
| {(179, 275), (100, 364)}; {(188, 93), (298, 225)}; |
| {(56, 419), (555, 303)}; {(745, 210), (100, 387)}; |
| {(377, 456), (526, 412)}; {(286, 136), (316, 228)}; |
| {(745, 210), (49, 183)}; {(179, 275), (428, 247)} |
Дана точка P(39, 171) на кривой 

Вычислить порядок точки (13, 4) кривой 
Решить в целых числах уравнение 
Определить, является ли число 54673257461630679457 простым с вероятностью не меньше 0,999.
Шифротекст СЗАУПРТИС_РЕД_УБАЗАР_ОТИК получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
ЗАПУСТИ_СРЕДУ_РАЗРАБОТКИ_
Вычислить нелинейность булевой функции 01011110 от 3 переменных
Дано: модуль шифрования N = 4307, открытый ключ e = 17. Найти значение шифртекста, полученного при зашифровании открытого текста 983 на открытом ключе (N, e) по алгоритму RSA.
Решить следующее сравнение 
С помощью 
Расшифровать фразу ЕМОТНББСУОЙИТН_СЙРЕ_СТЯЕЯ, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
СУББОТНИЙ_РЕЙС_ОТМЕНЯЕТСЯ
Вычислить динамическое расстояние порядка 1 булевой функции 01011110 от 3 переменных
Даны значения модуля шифрования N = 187 и открытого ключа e = 59. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 114.
Решить сравнение 
Найти произвольный квадратичный невычет по модулю 331
Расшифровать текст 3-15.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите предпоследнее слово заглавными буквами.
Вычислить нелинейность блока замен 5 11 13 14 2 1 10 0 6 15 8 12 7 4 3 9 размерностью 
Даны значения модуля шифрования N = 4717 и открытого ключа e = 4205. Используя метод факторизации Ферма, найти значение закрытого ключа.
Решить систему сравнений:

Найти наибольший квадратный корень из 271 по модулю 293.
Расшифровать сообщение
4-15.txt
, зашифрованное шифром Виженера, Длина ключа равна 5, пробел является частью алфавита.
В ответ введите ключ.
.
Вычислить динамическое расстояние порядка (2,2) блока замен 5 11 13 14 2 1 10 0 6 15 8 12 7 4 3 9 размерностью 
Применением цепных дробей найти секретный ключ d и разложение модуля 67510894259489 (экспонента — 3543923) на множители. В ответе укажите секретный ключ.
Решить сравнение 
Найти наибольший квадратный корень из 10 по примарному модулю 27.
Расшифровать сообщение
5-15.txt
, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Найти корреляционную матрицу блока замен 5 11 13 14 2 1 10 0 6 15 8 12 7 4 3 9 размерностью 
(1)
begin{matrix}
0 & -0.25 & 0 & 0.25 &
-0.25 & -0.25 & -0.25 & 0.5 &
0 & 0 & -0.5 & -0.5 &
0 & 0 & -0.25 & 0 &
end{matrix}
(2)
begin{matrix}
0 & -0.25 & 0 & 0.25 &
-0.25 & -0.25 & -0.25 & 0.5 &
0 & 0 & -0.5 & -0.5 &
0 & 0 & 0.25 & 0 &
end{matrix}
(3)
begin{matrix}
0 & -0.25 & 0 & 0.25 &
-0.25 & -0.25 & -0.25 & 0.5 &
0 & 0 & -0.5 & 0.5 &
0 & 0 & 0.25 & 0 &
end{matrix}
(4)
begin{matrix}
0 & -0.25 & 0 & 0.25 &
-0.25 & -0.25 & -0.25 & 0.5 &
0 & 0 & -0.5 & -0.5 &
0 & 0 & -0.25 & 0 &
end{matrix}
Дан шифртекст 64, а также значения модуля шифрования N = 187 и открытого ключа e = 3. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=4, зная секретный ключ подписи d=6 при данном значении выбираемого случайным образом числа k=11. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Найти остаток от деления 
Найти количество квадратных корней из 120 по непримарному составному модулю 4199.
Расшифровать сообщение на английском языке
6-15.txt
, зашифрованное шифром Виженера, Длина ключа равна 4.
В ответ введите ключ.
.
Провести операцию SubBytes алгоритма AES со значением байта 53.
Сгенерируйте ЭЦП для сообщения с известным значением хэш-свертки e=5, зная секретный ключ подписи d=12 при данном значении выбираемого случайным образом числа k=8. Используйте кривую E751(-1,1) и генерирующую точку G = (416, 55) порядка n = 13. Ответ введите в формате (N1,N2), например: (12,3) или (14,11) — в сокбках и без пробелов.
Вычислить значение 
Найти число всех подгрупп (не включая единичную) группы 
Провести операцию MixColumns над приведенным ниже столбцом состояния
Проверьте подлинность ЭЦП (3, 1) для сообщения с известным значением хэш-свертки 6, зная открытый ключ проверки подписи (455, 383). Используйте кривую 
(1) подпись действительна
(2) подпись недействительна
Найти дискретный логарифм числа 30 по основанию 6 по модулю 103951.
Зашифровать биграмму МА с помощью матрицы 
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
228DB633C4D65EE857C589F4A59BB1B7
Сообщение 1018 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {5,6,13,25,54,107,211}, m=423 и n=167. В ответе укажите исходное сообщение.
Проверить действительность подписей (127, 230), (71, 65) для сообщения с известным значением хэш-свертки 165 и открытым ключом проверки (624,469). Используется кривая 
(1) обе подписи действительны
(2) первая подпись действительна, вторая — недействительна
(3) первая подпись недействительна, вторая — действительна
(4) обе подписи недействительны
Используя порождающий полином для CRC 
(1) {1,1,0,0,0}
(2) {1,0,1,0,0}
(3) {1,1,0,1,1}
(4) {1,1,1,0,1}
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3
Д 4 Е 5 Ё 6 Ж 7
З 8 И 9 Й 10 К 11
Л 12 М 13 Н 14 О 15
П 16 Р 17 С 18 Т 19
У 20 Ф 21 Х 22 Ц 23
Ч 24 Ш 25 Щ 26 Ъ 27
Ы 28 Ь 29 Э 30 Ю 31
Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст ПЛУТОН.
Провести первый раунд зашифрования открытого текста 8966 FB62 A4AA FAD9 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок 
Шифртекст (102131499, 11010111001111111000) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=95891, q=90007. Найти открытый текст и введите его заглавными буквами.
С помощью алгоритма Берлекемпа проверить, является ли приводимым многочлен 

Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=31, n2=47, x=8.
Чей компьютер он взломает быстрее?
Зашифруйте открытый текст ОТСТАВНОЙ с помощью алфавита, приведенного в
таблице
, используйте открытый ключ B=(286, 136), значения случайных чисел
для букв открытого текста k: 5, 3, 3, 2, 4, 19, 2, 4, 10, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
(1) {(425, 663), (99, 295)}; {(56, 419), (606, 147)}; {(56, 419), (151, 233)};
{(188, 93), (279, 398)}; {(16, 416), (218, 601)}; {(568, 355), (328, 461)};
{(188, 93), (390, 603)}; {(16, 416), (585, 540)}; {(377, 456), (237, 297)}
(2) {(56, 419), (151, 233)}; {(425, 663), (99, 295)}; {(56, 419), (606, 147)};
{(188, 93), (279, 398)}; {(16, 416), (218, 601)}; {(568, 355), (328, 461)};
{(188, 93), (390, 603)}; {(16, 416), (585, 540)}; {(377, 456), (237, 297)}
(3) {(56, 419), (606, 147)}; {(56, 419), (151, 233)}; {(425, 663), (99, 295)};
{(188, 93), (279, 398)}; {(16, 416), (218, 601)}; {(568, 355), (328, 461)};
{(188, 93), (390, 603)}; {(16, 416), (585, 540)}; {(377, 456), (237, 297)}
(4) {(568, 355), (328, 461)}; {(56, 419), (606, 147)}; {(56, 419), (151, 233)};
{(188, 93), (279, 398)}; {(16, 416), (218, 601)}; {(425, 663), (99, 295)};
{(188, 93), (390, 603)}; {(16, 416), (585, 540)}; {(377, 456), (237, 297)}
Даны точки P(67, 84), Q(69, 241), R(66, 199) на кривой 

Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
КРЫСА
или
ХОРЕК
— устойчивее к действию этой программы?
(1) Первый пароль надежнее
(2) Второй пароль надежнее
(3) Пароли одинаково ненадежные
Дан шифртекст, показанный ниже. Зная секретный ключ 
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(618, 206), (99, 456)}; {(425, 663), (31, 136)}; |
| {(377, 456), (688, 741)}; {(425, 663), (636, 747)}; |
| {(16, 416), (298, 526)}; {(188, 93), (356, 175)}; |
| {(489, 468), (147, 390)}; {(346, 242), (546, 670)}; |
| {(72, 254), (114, 144)}; {(377, 456), (25, 147)} |
Дана точка P(49, 183) на кривой 

Вычислить порядок точки (21, 2) кривой 
Решить в целых числах уравнение 
Определить, является ли число 29497513910652490397 простым с вероятностью не меньше 0,999.
Шифротекст КАЛЗААК_ДЗИШТАА_ВЯ_Д_ООРС получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
ЗАКЛАДКА_ЗАШИТА_В_ЯДРО_ОС
Вычислить нелинейность булевой функции 00101110 от 3 переменных
Дано: модуль шифрования N = 1739, открытый ключ e = 17. Найти значение шифртекста, полученного при зашифровании открытого текста 132 на открытом ключе (N, e) по алгоритму RSA.
Решить следующее сравнение 
С помощью 
Расшифровать фразу МИКСО_ВЫ_ЕУБ_АДПЛДЕУОНСНИ, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
КОМИССИОННЫЕ_В_ДУПЛЕ_ДУБА
Вычислить динамическое расстояние порядка 1 булевой функции 00101110 от 3 переменных
Даны значения модуля шифрования N = 377 и открытого ключа e = 283. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 66.
Решить сравнение 
Найти произвольный квадратичный невычет по модулю 347
Расшифровать текст 3-16.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите последнее слово заглавными буквами.
Вычислить нелинейность блока замен 2 0 13 7 9 11 14 3 1 10 5 15 4 12 6 размерностью 
Даны значения модуля шифрования N = 4183 и открытого ключа e = 519. Используя метод факторизации Ферма, найти значение закрытого ключа.
Решить систему сравнений:

Найти наименьший квадратный корень из 155 по модулю 307.
Расшифровать сообщение
4-16.txt
, зашифрованное шифром Виженера, Длина ключа равна 7, пробел является частью алфавита.
В ответ введите ключ.
.
Вычислить динамическое расстояние порядка (2,2) блока замен 2 0 13 7 9 11 14 3 1 10 5 15 4 12 6 размерностью 
Применением цепных дробей найти секретный ключ d и разложение модуля 64806601923671 (экспонента — 3676721) на множители. В ответе укажите секретный ключ.
Решить сравнение 
Найти наименьший квадратный корень из 18 по примарному модулю 343.
Расшифровать сообщение
5-16.txt
, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Найти корреляционную матрицу блока замен 2 0 13 7 9 11 14 3 1 10 5 15 4 12 6 размерностью 
(1)
begin{matrix}
0 & 0.25 & -0.25 & 0.25 &
0.25 & 0.25 & 0.5 & 0 &
-0.25 & 0 & 0 & 0.25 &
-0.25 & 0.25 & 0.25 & 0 &
end{matrix}
(2)
begin{matrix}
0 & 0.25 & -0.25 & 0.25 &
0.25 & 0.25 & 0.5 & 0 &
-0.25 & 0 & 0 & 0.25 &
-0.25 & -0.25 & 0.25 & 0 &
end{matrix}
(3)
begin{matrix}
0 & 0.25 & -0.25 & 0.25 &
0.25 & 0.25 & 0.5 & 0 &
-0.25 & 0 & 0 & 0.25 &
0.25 & -0.25 & 0.25 & 0 &
end{matrix}
(4)
begin{matrix}
0 & 0.25 & -0.25 & 0.25 &
0.25 & 0.25 & 0.5 & 0 &
-0.25 & 0 & 0 & -0.25 &
-0.25 & -0.25 & 0.25 & 0 &
end{matrix}
Дан шифртекст 13, а также значения модуля шифрования N = 143 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Найти остаток от деления 
Найти количество квадратных корней из 3025 по непримарному составному модулю 4199.
Расшифровать сообщение на английском языке
6-16.txt
, зашифрованное шифром Виженера, Длина ключа равна 4.
В ответ введите ключ.
.
Провести операцию SubBytes алгоритма AES со значением байта 43.
Вычислить значение 
Найти число всех подгрупп (не включая единичную) группы 
Провести операцию MixColumns над приведенным ниже столбцом состояния
Проверьте подлинность ЭЦП (3, 10) для сообщения с известным значением хэш-свертки 2, зная открытый ключ проверки подписи (596, 433). Используйте кривую 
(1) подпись действительна
(2) подпись недействительна
Найти дискретный логарифм числа 12 по основанию 17 по модулю 105601.
Зашифровать биграмму СУ с помощью матрицы 
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
A41E5D56149D16FC4A1C5A00D954ED31
Сообщение 1097 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {4,6,11,23,45,92,186}, m=369 и n=31. В ответе укажите исходное сообщение.
Проверить действительность подписей (10, 163), (10, 153) для сообщения с известным значением хэш-свертки 169 и открытым ключом проверки (671,267). Используется кривая 
(1) обе подписи действительны
(2) первая подпись действительна, вторая — недействительна
(3) первая подпись недействительна, вторая — действительна
(4) обе подписи недействительны
Используя порождающий полином для CRC 
(1) {1,1,0,0,0}
(2) {1,0,1,0,0}
(3) {1,1,0,1,1}
(4) {1,1,1,0,1}
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3
Д 4 Е 5 Ё 6 Ж 7
З 8 И 9 Й 10 К 11
Л 12 М 13 Н 14 О 15
П 16 Р 17 С 18 Т 19
У 20 Ф 21 Х 22 Ц 23
Ч 24 Ш 25 Щ 26 Ъ 27
Ы 28 Ь 29 Э 30 Ю 31
Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст САТУРН.
Провести первый раунд зашифрования открытого текста F7C1 A026 AB48 9F0F шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок 
Шифртекст (6737479610, 00010100110100110110) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=93763, q=90011. Найти открытый текст и введите его заглавными буквами.
С помощью алгоритма Берлекемпа проверить, является ли приводимым многочлен 

Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=37, n2=47, x=13.
Чей компьютер он взломает быстрее?
Зашифруйте открытый текст ОТСЛУЖИТЬ с помощью алфавита, приведенного в
таблице
, используйте открытый ключ B=(16, 416), значения случайных чисел
для букв открытого текста k: 2, 8, 4, 2, 6, 10, 3, 3, 18, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
(1) {(188, 93), (62, 372)}; {(346, 242), (329, 447)}; {(16, 416), (376, 686)};
{(188, 93), (358, 491)}; {(725, 195), (143, 602)}; {(377, 456), (243, 87)};
{(56, 419), (185, 105)}; {(56, 419), (396, 481)}; {(618, 206), (558, 359)}
(2) {(16, 416), (376, 686)}; {(188, 93), (62, 372)}; {(346, 242), (329, 447)};
{(188, 93), (358, 491)}; {(725, 195), (143, 602)}; {(377, 456), (243, 87)};
{(56, 419), (185, 105)}; {(56, 419), (396, 481)}; {(618, 206), (558, 359)}
(3) {(188, 93), (62, 372)}; {(16, 416), (376, 686)}; {(346, 242), (329, 447)};
{(188, 93), (358, 491)}; {(725, 195), (143, 602)}; {(377, 456), (243, 87)};
{(56, 419), (185, 105)}; {(56, 419), (396, 481)}; {(618, 206), (558, 359)}
(4) {(346, 242), (329, 447)}; {(16, 416), (376, 686)}; {(188, 93), (62, 372)};
{(188, 93), (358, 491)}; {(725, 195), (143, 602)}; {(377, 456), (243, 87)};
{(56, 419), (185, 105)}; {(56, 419), (396, 481)}; {(618, 206), (558, 359)}
Даны точки P(73, 72), Q(56, 332), R(85, 35) на кривой 

Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
МЯЧИК
или
ШАРИК
— устойчивее к действию этой программы?
(1) Первый пароль надежнее
(2) Второй пароль надежнее
(3) Пароли одинаково ненадежные
Дан шифртекст, показанный ниже. Зная секретный ключ 
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(16, 416), (724, 522)}; {(489, 468), (719, 538)}; |
| {(56, 419), (205, 372)}; {(72, 254), (628, 293)}; |
| {(188, 93), (594, 337)}; {(440, 539), (588, 707)}; |
| {(568, 355), (707, 556)}; {(489, 468), (719, 538)}; |
| {(16, 416), (590, 376)}; {(56, 419), (612, 329)}; |
| {(188, 93), (594, 337)} |
Дана точка P(58, 139) на кривой 

Вычислить порядок точки (24, 14) кривой 
Решить в целых числах уравнение 
Определить, является ли число 40206835204840513073 простым с вероятностью не меньше 0,999.
Шифротекст УЛОЧПЛЭ_ЕИОРТНК_ЮУПНУТЧ_О получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
ПОЛУЧИ_ЭЛЕКТРОННУЮ_ПОЧТУ_
Вычислить нелинейность булевой функции 01111000 от 3 переменных
Дано: модуль шифрования N = 1927, открытый ключ e = 19. Найти значение шифртекста, полученного при зашифровании открытого текста 1260 на открытом ключе (N, e) по алгоритму RSA.
Решить следующее сравнение 
С помощью 
Расшифровать фразу К_ЙАО__ЕУНОМЕПЧН_ЮЗАТТ_КО, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
КТО_ТАКОЙ_ПОЧЕМУ_НЕ_ЗНАЮ_
Вычислить динамическое расстояние порядка 1 булевой функции 01111000 от 3 переменных
Даны значения модуля шифрования N = 221 и открытого ключа e = 35. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 80.
Решить сравнение 
Найти произвольный квадратичный невычет по модулю 229
Расшифровать текст 3-17.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите второе слово заглавными буквами.
Вычислить нелинейность блока замен 13 6 3 14 12 11 4 1 15 5 10 7 0 9 2 8 размерностью 
Даны значения модуля шифрования N = 3569 и открытого ключа e = 265. Используя метод факторизации Ферма, найти значение закрытого ключа.
Решить систему сравнений:

Найти наибольший квадратный корень из 139 по модулю 313.
Расшифровать сообщение
4-17.txt
, зашифрованное шифром Виженера, Длина ключа равна 4, пробел является частью алфавита.
В ответ введите ключ.
.
Вычислить динамическое расстояние порядка (2,2) блока замен 13 6 3 14 12 11 4 1 15 5 10 7 0 9 2 8 размерностью 
Применением цепных дробей найти секретный ключ d и разложение модуля 62781628076903 (экспонента — 3804071) на множители. В ответе укажите секретный ключ.
Решить сравнение 
Найти наибольший квадратный корень из 10 по примарному модулю 81.
Расшифровать сообщение
5-17.txt
, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Найти корреляционную матрицу блока замен 13 6 3 14 12 11 4 1 15 5 10 7 0 9 2 8 размерностью 
(1)
begin{matrix}
0.25 & 0 & 0 & 0 &
-0.25 & 0.25 & -0.25 & -0.25 &
0.25 & -0.5 & -0.5 & 0 &
0 & 0 & -0.25 & 0 &
end{matrix}
(2)
begin{matrix}
0.25 & 0 & 0 & 0 &
-0.25 & 0.25 & -0.25 & -0.25 &
-0.25 & -0.5 & -0.5 & 0 &
0 & 0 & -0.25 & 0 &
end{matrix}
(3)
begin{matrix}
0.25 & 0 & 0 & 0 &
-0.25 & 0.25 & -0.25 & -0.25 &
-0.25 & -0.5 & -0.5 & 0 &
0 & 0 & 0.25 & 0 &
end{matrix}
(4)
begin{matrix}
0.25 & 0 & 0 & 0 &
-0.25 & 0.25 & -0.25 & 0.25 &
-0.25 & -0.5 & -0.5 & 0 &
0 & 0 & -0.25 & 0 &
end{matrix}
Дан шифртекст 311, а также значения модуля шифрования N = 323 и открытого ключа e = 5. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Найти остаток от деления 
Найти количество квадратных корней из 781 по непримарному составному модулю 1001.
Расшифровать сообщение на английском языке
6-17.txt
, зашифрованное шифром Виженера, Длина ключа равна 5.
В ответ введите ключ.
.
Провести операцию SubBytes алгоритма AES со значением байта 15.
Вычислить значение 
Найти число всех подгрупп (не включая единичную) группы 
Провести операцию MixColumns над приведенным ниже столбцом состояния
Проверьте подлинность ЭЦП (11, 6) для сообщения с известным значением хэш-свертки 10, зная открытый ключ проверки подписи (455, 368). Используйте кривую 
(1) подпись действительна
(2) подпись недействительна
Найти дискретный логарифм числа 15 по основанию 10 по модулю 98011.
Зашифровать биграмму БУ с помощью матрицы 
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
67F85A1DE0C49C62EC291416F690DD76
Сообщение 553 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {4,7,12,25,49,98,197}, m=395 и n=61. В ответе укажите исходное сообщение.
Проверить действительность подписей (11, 133), (35, 48) для сообщения с известным значением хэш-свертки 148 и открытым ключом проверки (166,741). Используется кривая 
(1) обе подписи действительны
(2) первая подпись действительна, вторая — недействительна
(3) первая подпись недействительна, вторая — действительна
(4) обе подписи недействительны
Используя порождающий полином для CRC 
(1) {1,0,1,0,0}
(2) {1,1,1,1,1}
(3) {0,0,1,1,0}
(4) {1,0,1,1,0}
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3
Д 4 Е 5 Ё 6 Ж 7
З 8 И 9 Й 10 К 11
Л 12 М 13 Н 14 О 15
П 16 Р 17 С 18 Т 19
У 20 Ф 21 Х 22 Ц 23
Ч 24 Ш 25 Щ 26 Ъ 27
Ы 28 Ь 29 Э 30 Ю 31
Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст ЮПИТЕР.
Провести первый раунд зашифрования открытого текста FE2D FEEA B158 BE38 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок 
Шифртекст (1439738115, 11000111110111010001) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=100847, q=96331. Найти открытый текст и введите его заглавными буквами.
С помощью алгоритма Берлекемпа проверить, является ли приводимым многочлен 

Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=37, n2=43, x=12.
Чей компьютер он взломает быстрее?
Зашифруйте открытый текст ОТСЛЕДИТЬ с помощью алфавита, приведенного в
таблице
, используйте открытый ключ B=(188, 93), значения случайных чисел
для букв открытого текста k: 19, 2, 13, 5, 19, 5, 7, 8, 5, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
(1) {(568, 355), (461, 747)}; {(188, 93), (675, 246)}; {(283, 493), (328, 290)};
{(425, 663), (543, 357)}; {(568, 355), (206, 106)}; {(425, 663), (496, 31)};
{(135, 82), (394, 731)}; {(346, 242), (594, 414)}; {(425, 663), (454, 628)}
(2) {(425, 663), (496, 31)}; {(188, 93), (675, 246)}; {(283, 493), (328, 290)};
{(425, 663), (543, 357)}; {(568, 355), (206, 106)}; {(568, 355), (461, 747)};
{(135, 82), (394, 731)}; {(346, 242), (594, 414)}; {(425, 663), (454, 628)}
(3) {(283, 493), (328, 290)}; {(568, 355), (461, 747)}; {(188, 93), (675, 246)};
{(425, 663), (543, 357)}; {(568, 355), (206, 106)}; {(425, 663), (496, 31)};
{(135, 82), (394, 731)}; {(346, 242), (594, 414)}; {(425, 663), (454, 628)}
(4) (188, 93), (675, 246)}; {(568, 355), (461, 747)}; {{(283, 493), (328, 290)};
{(425, 663), (543, 357)}; {(568, 355), (206, 106)}; {(425, 663), (496, 31)};
{(135, 82), (394, 731)}; {(346, 242), (594, 414)}; {(425, 663), (454, 628)}
Даны точки P(69, 241), Q(53, 277), R(106, 24) на кривой 

Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
ЗРНТИК
или
ДОЖДИК
— устойчивее к действию этой программы?
(1) Первый пароль надежнее
(2) Второй пароль надежнее
(3) Пароли одинаково ненадежные
Дан шифртекст, показанный ниже. Зная секретный ключ 
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(56, 419), (739, 177)}; {(16, 416), (282, 410)}; |
| {(425, 663), (221, 138)}; {(188, 93), (329, 447)}; |
| {(286, 136), (235, 19)}; {(725, 195), (496, 31)}; |
| {(56, 419), (236, 712)}; {(440, 539), (514, 662)}; |
| {(377, 456), (323, 94)}; {(179, 275), (203, 324)}; |
| {(568, 355), (197, 606)} |
Дана точка P(33, 355) на кривой 

Вычислить порядок точки (27, 5) кривой 
Решить в целых числах уравнение 
Определить, является ли число 12764787846358441471 простым с вероятностью не меньше 0,999.
Шифротекст СИЫЧВТ_ИЛЛЕОЧНООЛПО_ЕИЕНЖ получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
ВЫЧИСЛИЛ_ТОЧНОЕ_ПОЛОЖЕНИЕ
Вычислить нелинейность булевой функции 01001010 от 3 переменных
Дано: модуль шифрования N = 2257, открытый ключ e = 17. Найти значение шифртекста, полученного при зашифровании открытого текста 539 на открытом ключе (N, e) по алгоритму RSA.
Решить следующее сравнение 
С помощью 
Расшифровать фразу ТСАНУОБЛЬ_ИВТЕО_ЕРОШТЕОКЗ, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
УСТАНОВИТЕ_БОЛЬШЕ_РОЗЕТОК
Вычислить динамическое расстояние порядка 1 булевой функции 01001010 от 3 переменных
Даны значения модуля шифрования N = 391 и открытого ключа e = 47. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 262.
Решить сравнение 
Найти произвольный квадратичный невычет по модулю 271
Расшифровать текст 3-18.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите последнее слово заглавными буквами.
Вычислить нелинейность блока замен 15 6 5 9 2 13 14 12 7 3 11 0 10 8 1 4 размерностью 
Даны значения модуля шифрования N = 3403 и открытого ключа e = 2439. Используя метод факторизации Ферма, найти значение закрытого ключа.
Решить систему сравнений:

Найти наименьший квадратный корень из 49 по модулю 317.
Расшифровать сообщение
4-18.txt
, зашифрованное шифром Виженера, Длина ключа равна 6, пробел является частью алфавита.
В ответ введите ключ.
.
Вычислить динамическое расстояние порядка (2,2) блока замен 15 6 5 9 2 13 14 12 7 3 11 0 10 8 1 4 размерностью 
Применением цепных дробей найти секретный ключ d и разложение модуля 60902079700513 (экспонента — 3914857) на множители. В ответе укажите секретный ключ.
Решить сравнение 
Найти наименьший квадратный корень из 99 по примарному модулю 125.
Расшифровать сообщение
5-18.txt
, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Найти корреляционную матрицу блока замен 15 6 5 9 2 13 14 12 7 3 11 0 10 8 1 4 размерностью 
(1)
begin{matrix}
-0.25 & -0.5 & 0 & 0 &
0 & -0.5 & 0 & 0 &
-0.5 & -0.25 & 0 & 0.25 &
0 & 0 & -0.5 & 0.25 &
end{matrix}
(2)
begin{matrix}
-0.25 & -0.5 & 0 & 0 &
0 & -0.5 & 0 & 0 &
-0.5 & -0.25 & 0 & 0.25 &
0 & 0 & -0.5 & -0.25 &
end{matrix}
(3)
begin{matrix}
-0.25 & -0.5 & 0 & 0 &
0 & -0.5 & 0 & 0 &
-0.5 & -0.25 & 0 & 0.25 &
0 & 0 & -0.5 & 0.25 &
end{matrix}
(4)
begin{matrix}
-0.25 & -0.5 & 0 & 0 &
0 & -0.5 & 0 & 0 &
-0.5 & -0.25 & 0 & 0.25 &
0 & 0 & 0.5 & -0.25 &
end{matrix}
Дан шифртекст 47, а также значения модуля шифрования N = 77 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Найти остаток от деления 
Найти количество квадратных корней из 7226 по непримарному составному модулю 7429.
Расшифровать сообщение на английском языке
6-18.txt
, зашифрованное шифром Виженера, Длина ключа равна 4.
В ответ введите ключ.
.
Провести операцию SubBytes алгоритма AES со значением байта CB.
Вычислить значение 
Провести операцию MixColumns над приведенным ниже столбцом состояния
Проверьте подлинность ЭЦП (11, 12) для сообщения с известным значением хэш-свертки 5, зная открытый ключ проверки подписи (596, 433). Используйте кривую 
(1) подпись действительна
(2) подпись недействительна
Найти дискретный логарифм числа 71 по основанию 5 по модулю 101377.
Зашифровать биграмму МЫ с помощью матрицы 
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
C020455D1CE7BF15A4DD89C18A7E5C0D
Сообщение 212 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {1,2,4,8,17,34,68}, m=135 и n=103. В ответе укажите исходное сообщение.
Проверить действительность подписей (166, 242), (3, 9) для сообщения с известным значением хэш-свертки 84 и открытым ключом проверки (286, 213). Используется кривая 
(1) обе подписи действительны
(2) первая подпись действительна, вторая — недействительна
(3) первая подпись недействительна, вторая — действительна
(4) обе подписи недействительны
Используя порождающий полином для CRC 
(1) {1,0,1,0,0}
(2) {1,1,1,1,1}
(3) {0,0,1,1,0}
(4) {1,0,1,1,0}
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3
Д 4 Е 5 Ё 6 Ж 7
З 8 И 9 Й 10 К 11
Л 12 М 13 Н 14 О 15
П 16 Р 17 С 18 Т 19
У 20 Ф 21 Х 22 Ц 23
Ч 24 Ш 25 Щ 26 Ъ 27
Ы 28 Ь 29 Э 30 Ю 31
Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст ПРЯМАЯ.
Провести первый раунд зашифрования открытого текста C20A 8A8E A533 C2AB шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок 
Шифртекст (8611143873, 01001110000001100000) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=98207, q=90679. Найти открытый текст и введите его заглавными буквами.
С помощью алгоритма Берлекемпа проверить, является ли приводимым многочлен 

Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=41, n2=37, x=5.
Чей компьютер он взломает быстрее?
Зашифруйте открытый текст НОВЕНЬКИЙ с помощью алфавита, приведенного в
таблице
, используйте открытый ключ B=(425,663), значения случайных чисел
для букв открытого текста k: 19, 12, 13, 2, 12, 14, 19, 18, 12, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
(1) {(568, 355), (321, 467)}; {(286, 136), (99, 295)}; {(283, 493), (358, 491)};
{(188, 93), (314, 127)}; {(286, 136), (685, 655)}; {(596, 433), (515, 67)};
{(568, 355), (205, 379)}; {(618, 206), (405, 747)}; {(286, 136), (525, 674)}
(2) {(283, 493), (358, 491)}; {(568, 355), (321, 467)}; {(286, 136), (99, 295)};
{(188, 93), (314, 127)}; {(286, 136), (685, 655)}; {(596, 433), (515, 67)};
{(568, 355), (205, 379)}; {(618, 206), (405, 747)}; {(286, 136), (525, 674)}
(3) {(286, 136), (99, 295)}; {(568, 355), (321, 467)}; {(283, 493), (358, 491)};
{(188, 93), (314, 127)}; {(286, 136), (685, 655)}; {(596, 433), (515, 67)};
{(568, 355), (205, 379)}; {(618, 206), (405, 747)}; {(286, 136), (525, 674)}
(4) {(286, 136), (99, 295)}; {(283, 493), (358, 491)}; {(568, 355), (321, 467)};
{(188, 93), (314, 127)}; {(286, 136), (685, 655)}; {(596, 433), (515, 67)};
{(568, 355), (205, 379)}; {(618, 206), (405, 747)}; {(286, 136), (525, 674)}
Даны точки P(74, 581), Q(53, 277), R(85, 35) на кривой 

Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
ШУБА
или
СНЕГ
— устойчивее к действию этой программы?
(1) Первый пароль надежнее
(2) Второй пароль надежнее
(3) Пароли одинаково ненадежные
Дан шифртекст, показанный ниже. Зная секретный ключ 
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(745, 210), (268, 597)}; {(725, 195), (310, 582)}; |
| {(618, 206), (59, 365)}; {(440, 539), (371, 14)}; |
| {(188, 93), (348, 27)}; {(72, 254), (434, 136)}; |
| {(16, 416), (623, 166)}; {(188, 93), (235, 19)}; |
| {(440, 539), (660, 275)}; {(188, 93), (434, 615)}; |
| {(725, 195), (73, 679)}; {(188, 93), (642, 53)} |
Дана точка P(39, 580) на кривой 

Вычислить порядок точки (13, 7) кривой 
Решить в целых числах уравнение 
Определить, является ли число 71755440315342536873 простым с вероятностью не меньше 0,999.
Шифротекст ЭЕМЕФРДЫ_ИЗГРУАЖНЫ_ЕВОЗУ_ получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
ЭФЕМЕРИДЫ_ЗАГРУЖЕНЫ_В_ОЗУ
Вычислить нелинейность булевой функции 01101000 от 3 переменных
Дано: модуль шифрования N = 4087, открытый ключ e = 13. Найти значение шифртекста, полученного при зашифровании открытого текста 3474 на открытом ключе (N, e) по алгоритму RSA.
Решить следующее сравнение 
С помощью 
Расшифровать фразу _ТОЬВО_ВМЫОПРГИИСУ_ПЛЙ_ОП, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
ПРИГОТОВЬ_СУП_И_ВЫМОЙ_ПОЛ
Вычислить динамическое расстояние порядка 1 булевой функции 01101000 от 3 переменных
Даны значения модуля шифрования N = 323 и открытого ключа e = 131. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 321.
Решить сравнение 
Найти произвольный квадратичный невычет по модулю 283
Расшифровать текст 3-19.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите второе слово заглавными буквами.
Вычислить нелинейность блока замен 11 3 14 5 12 6 13 1 10 2 8 4 15 0 9 7 размерностью 
Даны значения модуля шифрования N = 2479 и открытого ключа e = 2251. Используя метод факторизации Ферма, найти значение закрытого ключа.
Решить систему сравнений:

Найти наибольший квадратный корень из 316 по модулю 331.
Расшифровать сообщение
4-19.txt
, зашифрованное шифром Виженера, Длина ключа равна 4, пробел является частью алфавита.
В ответ введите ключ.
.
Вычислить динамическое расстояние порядка (2,2) блока замен 11 3 14 5 12 6 13 1 10 2 8 4 15 0 9 7 размерностью 
Применением цепных дробей найти секретный ключ d и разложение модуля 59046883376179 (экспонента — 4044583) на множители. В ответе укажите секретный ключ.
Решить сравнение 
Найти наибольший квадратный корень из 336 по примарному модулю 625.
Расшифровать сообщение
5-19.txt
, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Найти корреляционную матрицу блока замен 11 3 14 5 12 6 13 1 10 2 8 4 15 0 9 7 размерностью 
(1)
begin{matrix}
0 & 0 & 0 & -1 &
0.25 & -0.5 & 0.25 & 0 &
0.25 & -0.25 & 0.25 & 0 &
-0.25 & 0 & 0.25 & 0 &
end{matrix}
(2)
begin{matrix}
0 & 0 & 0 & -1 &
0.25 & -0.5 & 0.25 & 0 &
0.25 & -0.25 & 0.25 & 0 &
-0.25 & 0 & -0.25 & 0 &
end{matrix}
(3)
begin{matrix}
0 & 0 & 0 & -1 &
0.25 & -0.5 & 0.25 & 0 &
0.25 & -0.25 & 0.25 & 0 &
0.25 & 0 & -0.25 & 0 &
end{matrix}
(4)
begin{matrix}
0 & 0 & 0 & -1 &
0.25 & -0.5 & 0.25 & 0 &
0.25 & -0.25 & -0.25 & 0 &
-0.25 & 0 & -0.25 & 0 &
end{matrix}
Дан шифртекст 107, а также значения модуля шифрования N = 209 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Найти остаток от деления 
Найти количество квадратных корней из 324 по непримарному составному модулю 7429.
Расшифровать сообщение на английском языке
6-19.txt
, зашифрованное шифром Виженера, Длина ключа равна 4.
В ответ введите ключ.
.
Провести операцию SubBytes алгоритма AES со значением байта 47.
Вычислить значение 
Провести операцию MixColumns над приведенным ниже столбцом состояния
Проверьте подлинность ЭЦП (7, 7) для сообщения с известным значением хэш-свертки 9, зная открытый ключ проверки подписи (135, 82). Используйте кривую 
(1) подпись действительна
(2) подпись недействительна
Найти дискретный логарифм числа 2 по основанию 69 по модулю 110881.
Зашифровать биграмму ОП с помощью матрицы 
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
112BE2CDB64C311DCC8C6F8F0065D715
Сообщение 518 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {1,3,5,10,21,42,88}, m=171 и n=23. В ответе укажите исходное сообщение.
Проверить действительность подписей (195, 216), (9, 85) для сообщения с известным значением хэш-свертки 7 и открытым ключом проверки (245,637). Используется кривая 
(1) обе подписи действительны
(2) первая подпись действительна, вторая — недействительна
(3) первая подпись недействительна, вторая — действительна
(4) обе подписи недействительны
Используя порождающий полином для CRC 
(1) {1,0,1,0,0}
(2) {1,1,1,1,1}
(3) {0,0,1,1,0}
(4) {1,0,1,1,0}
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3
Д 4 Е 5 Ё 6 Ж 7
З 8 И 9 Й 10 К 11
Л 12 М 13 Н 14 О 15
П 16 Р 17 С 18 Т 19
У 20 Ф 21 Х 22 Ц 23
Ч 24 Ш 25 Щ 26 Ъ 27
Ы 28 Ь 29 Э 30 Ю 31
Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст КРИВАЯ.
Провести первый раунд зашифрования открытого текста BF55 E71E 8CD6 9001 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок 
Шифртекст (8137015367, 01101001111001011111) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=98899, q=101531. Найти открытый текст и введите его заглавными буквами.
С помощью алгоритма Берлекемпа проверить, является ли приводимым многочлен 

Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=47, n2=41, x=9.
Чей компьютер он взломает быстрее?
Зашифруйте открытый текст НИЩЕНСКИЙ с помощью алфавита, приведенного в
таблице
, используйте открытый ключ B=(489, 468), значения случайных чисел
для букв открытого текста k: 2, 2, 7, 11, 19, 4, 2, 15, 6, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
(1) {(188, 93), (221, 613)}; {(188, 93), (446, 227)}; {(135, 82), (426, 89)};
{(179, 275), (102, 267)}; {(568, 355), (599, 696)}; {(16, 416), (151, 233)};
{(188, 93), (27, 120)}; {(745, 210), (27, 631)}; {(725, 195), (235, 732)}
(2) {(135, 82), (426, 89)}; {(188, 93), (221, 613)}; {(188, 93), (446, 227)};
{(179, 275), (102, 267)}; {(568, 355), (599, 696)}; {(16, 416), (151, 233)};
{(188, 93), (27, 120)}; {(745, 210), (27, 631)}; {(725, 195), (235, 732)}
(3) {(188, 93), (446, 227)}; {(188, 93), (221, 613)}; {(135, 82), (426, 89)};
{(179, 275), (102, 267)}; {(568, 355), (599, 696)}; {(16, 416), (151, 233)};
{(188, 93), (27, 120)}; {(745, 210), (27, 631)}; {(725, 195), (235, 732)}
(4) {(188, 93), (27, 120)}; {(188, 93), (446, 227)}; {(135, 82), (426, 89)};
{(179, 275), (102, 267)}; {(568, 355), (599, 696)}; {(16, 416), (151, 233)};
{(188, 93), (221, 613)}; {(745, 210), (27, 631)}; {(725, 195), (235, 732)}
Даны точки P(56, 419), Q(69, 510), R(79, 640) на кривой 

Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
ТАЙМЕР
или
ЗВОНОК
— устойчивее к действию этой программы?
(1) Первый пароль надежнее
(2) Второй пароль надежнее
(3) Пароли одинаково ненадежные
Дан шифртекст, показанный ниже. Зная секретный ключ 
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(725, 195), (538, 325)}; {(725, 195), (176, 413)}; |
| {(425, 663), (689, 670)}; {(346, 242), (652, 315)}; |
| {(283, 493), (463, 736)}; {(16, 416), (744, 133)}; |
| {(179, 275), (542, 351)}; {(56, 419), (298, 225)}; |
| {(286, 136), (719, 538)}; {(568, 355), (319, 518)}; |
| {(16, 416), (704, 46)} |
Дана точка P(44, 366) на кривой 

Вычислить порядок точки (11, 3) кривой 
Решить в целых числах уравнение 
Определить, является ли число 45095080578985454453 простым с вероятностью не меньше 0,999.
Шифротекст АМО_ЛЕРУРСОС_ДВЯЛЗА_УПКАС получен в результате следующего алгоритма шифрования: открытый текст был записан в таблицу по строкам, после чего переставлены столбцы. Найти открытый текст.
МАЛО_РЕСУРСОВ_ДЛЯ_ЗАПУСКА
Вычислить нелинейность булевой функции 00100010 от 3 переменных
Дано: модуль шифрования N = 3403, открытый ключ e = 11. Найти значение шифртекста, полученного при зашифровании открытого текста 855 на открытом ключе (N, e) по алгоритму RSA.
Решить следующее сравнение 
С помощью 
Расшифровать фразу О_ДАВВРСТЕТСИМЯ_ВУ_Х_РПАК, зашифрованную двойной перестановкой (сначала были переставлены столбцы, затем строки)
ВСТРЕТИМСЯ_У_ВХОДА_В_ПАРК
Вычислить динамическое расстояние порядка 1 булевой функции 00100010 от 3 переменных
Даны значения модуля шифрования N = 319 и открытого ключа e = 33. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 198.
Решить сравнение 
Найти произвольный квадратичный невычет по модулю 293
Расшифровать текст 3-20.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите второе слово заглавными буквами.
Вычислить нелинейность блока замен 5 10 4 7 12 3 2 8 6 1 9 11 0 14 13 15 размерностью 
Даны значения модуля шифрования N = 5723 и открытого ключа e = 301. Используя метод факторизации Ферма, найти значение закрытого ключа.
Решить систему сравнений:
(В качестве ответа введите наименьшее значение x.)
Найти наименьший квадратный корень из 14 по модулю 337.
Расшифровать сообщение
4-20.txt
, зашифрованное шифром Виженера, Длина ключа равна 6, пробел является частью алфавита.
В ответ введите ключ.
.
Вычислить динамическое расстояние порядка (2,2) блока замен 5 10 4 7 12 3 2 8 6 1 9 11 0 14 13 15 размерностью 
Применением цепных дробей найти секретный ключ d и разложение модуля 55925060669503 (экспонента — 4156793) на множители. В ответе укажите секретный ключ.
Решить сравнение 
Найти наименьший квадратный корень из 11 по примарному модулю 25.
Расшифровать сообщение
5-20.txt
, зашифрованное шифром Виженера, Длина ключа неизвестна, пробел является частью алфавита.
В ответ введите ключ.
.
Найти корреляционную матрицу блока замен 5 10 4 7 12 3 2 8 6 1 9 11 0 14 13 15 размерностью 
(1)
begin{matrix}
0.25 & 0.5 & -0.25 & 0.25 &
0.25 & 0 & 0 & 0.25 &
-0.25 & 0 & 0 & 0.25 &
0.25 & 0 & 0 & -0.25 &
end{matrix}
(2)
begin{matrix}
0.25 & 0.5 & -0.25 & 0.25 &
0.25 & 0 & 0 & 0.25 &
-0.25 & 0 & 0 & 0.25 &
0.25 & 0 & 0 & 0.25 &
end{matrix}
(3)
begin{matrix}
0.25 & 0.5 & -0.25 & 0.25 &
0.25 & 0 & 0 & 0.25 &
-0.25 & 0 & 0 & -0.25 &
0.25 & 0 & 0 & 0.25 &
end{matrix}
(4)
begin{matrix}
0.25 & 0.5 & -0.25 & -0.25 &
0.25 & 0 & 0 & 0.25 &
-0.25 & 0 & 0 & 0.25 &
0.25 & 0 & 0 & 0.25 &
end{matrix}
Дан шифртекст 117, а также значения модуля шифрования N = 133 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Найти остаток от деления 
Найти количество квадратных корней из 595 по непримарному составному модулю 2431.
Расшифровать сообщение на английском языке
6-20.txt
, зашифрованное шифром Виженера, Длина ключа равна 4.
В ответ введите ключ.
.
Провести операцию SubBytes алгоритма AES со значением байта D0.
Вычислить значение 
Провести операцию MixColumns над приведенным ниже столбцом состояния
Проверьте подлинность ЭЦП (11, 4) для сообщения с известным значением хэш-свертки 2, зная открытый ключ проверки подписи (596, 433). Используйте кривую 
(1) подпись действительна
(2) подпись недействительна
Найти дискретный логарифм числа 10 по основанию 14 по модулю 106921.
Зашифровать биграмму БЫ с помощью матрицы 
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
43151A44C095AA684C2255301A73955D
Сообщение 390 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {3,4,9,17,34,69,137}, m=277 и n=99. В ответе укажите исходное сообщение.
Проверить действительность подписей (3, 85), (195, 216) для сообщения с известным значением хэш-свертки 215 и открытым ключом проверки (104,30). Используется кривая 
(1) обе подписи действительны
(2) первая подпись действительна, вторая — недействительна
(3) первая подпись недействительна, вторая — действительна
(4) обе подписи недействительны
Используя порождающий полином для CRC 
(1) {1,0,1,0,0}
(2) {1,1,1,1,1}
(3) {0,0,1,1,0}
(4) {1,0,1,1,0}
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3
Д 4 Е 5 Ё 6 Ж 7
З 8 И 9 Й 10 К 11
Л 12 М 13 Н 14 О 15
П 16 Р 17 С 18 Т 19
У 20 Ф 21 Х 22 Ц 23
Ч 24 Ш 25 Щ 26 Ъ 27
Ы 28 Ь 29 Э 30 Ю 31
Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст ЭЛЛИПС.
Провести первый раунд зашифрования открытого текста AC2B EECD DA96 989D шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок 
Шифртекст (438845908, 10101000101000000100) получен из слова в алфавите {А, Б, …, Я} по схеме вероятностного шифрования с использованием открытого ключа n=pq, p=93131, q=90247. Найти открытый текст и введите его заглавными буквами.
С помощью алгоритма Берлекемпа проверить, является ли приводимым многочлен 

Специалист по защите информации А разработал собственную систему авторизации на компьютере. Пользователь вводит пароль — трехзначное натуральное число. Компьютер делит это число на n1, полученный при этом остаток M умножает на 2 и получает число K. После этого число K делит на n2 и полученный остаток A сохраняет на жестком диске. Если пользователь ввел пароль P, и после указанных вычислений получилось число, совпадающее с числом, хранящимся в памяти компьютера, то он получает доступ.
Пользователь Б решил использовать на своем компьютере такую же систему. Но чтобы А не подал на него в суд за кражу интеллектуальной собственности, решил поменять местами числа n1 и n2. То есть сначала стал делить на n1, а потом на n1.
Известно, что в компьютере А и в компьютере Б хранится число x. Злоумышленник не знает паролей А и Б и поэтому перебирает их все подряд в случайном порядке.
Известно, что n1=43, n2=47, x=16.
Чей компьютер он взломает быстрее?
Зашифруйте открытый текст НИКЕЛЕВЫЙ с помощью алфавита, приведенного в
таблице
, используйте открытый ключ B=,(568, 355) значения случайных чисел
для букв открытого текста k: 9, 9, 2, 3, 8, 19, 6, 18, 9, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
(1) {(489, 468), (599, 696)}; {(489, 468), (61, 622)}; {(188, 93), (13, 134)};
{(56, 419), (447, 0)}; {(346, 242), (197, 145)}; {(568, 355), (554, 330)};
{(725, 195), (705, 687)}; {(618, 206), (295, 219)}; {(489, 468), (407, 82)}
(2) {(188, 93), (13, 134)}; {(489, 468), (599, 696)}; {(489, 468), (61, 622)};
{(56, 419), (447, 0)}; {(346, 242), (197, 145)}; {(568, 355), (554, 330)};
{(725, 195), (705, 687)}; {(618, 206), (295, 219)}; {(489, 468), (407, 82)}
(3) {(568, 355), (554, 330)}; {(489, 468), (61, 622)}; {(188, 93), (13, 134)};
{(56, 419), (447, 0)}; {(346, 242), (197, 145)}; {(489, 468), (599, 696)};
{(725, 195), (705, 687)}; {(618, 206), (295, 219)}; {(489, 468), (407, 82)}
(4) {(489, 468), (61, 622)}; {(489, 468), (599, 696)}; {(188, 93), (13, 134)};
{(56, 419), (447, 0)}; {(346, 242), (197, 145)}; {(568, 355), (554, 330)};
{(725, 195), (705, 687)}; {(618, 206), (295, 219)}; {(489, 468), (407, 82)}
Даны точки P(58, 612), Q(67, 84), R(83, 373) на кривой 

Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
ВЕЧЕРОК
или
ШАШЛЫКИ
— устойчивее к действию этой программы?
(1) Первый пароль надежнее
(2) Второй пароль надежнее
(3) Пароли одинаково ненадежные
Дан шифртекст, показанный ниже. Зная секретный ключ 
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(725, 195), (329, 304)}; {(440, 539), (59, 386)}; |
| {(618, 206), (543, 357)}; {(188, 93), (520, 749)}; |
| {(489, 468), (585, 211)}; {(179, 275), (707, 556)}; |
| {(596, 433), (419, 38)}; {(377, 456), (643, 94)}; |
| {(188, 93), (385, 749)}; {(725, 195), (150, 355)}; |
| {(725, 195), (197, 606)} |
Дана точка P(73, 72) на кривой 

Вычислить порядок точки (20, 

Решить в целых числах уравнение 
Определить, является ли число 27542476619900900873 простым с вероятностью не меньше 0,999.
Вычислить нелинейность булевой функции 00100011 от 3 переменных
Дано: модуль шифрования N = 3071, открытый ключ e = 11. Найти значение шифртекста, полученного при зашифровании открытого текста 1058 на открытом ключе (N, e) по алгоритму RSA.
Решить следующее сравнение 
С помощью 
Вычислить динамическое расстояние порядка 1 булевой функции 00100011 от 3 переменных
Даны значения модуля шифрования N = 143 и открытого ключа e = 37. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 100.
Решить сравнение 
Расшифровать текст 3-21.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите первое слово заглавными буквами.
Вычислить нелинейность блока замен 15 10 4 2 0 13 9 1 12 6 7 5 3 8 14 11 размерностью 
Даны значения модуля шифрования N = 5917 и открытого ключа e = 1571. Используя метод факторизации Ферма, найти значение закрытого ключа.
Решить систему сравнений:

Вычислить динамическое расстояние порядка (2,2) блока замен 15 10 4 2 0 13 9 1 12 6 7 5 3 8 14 11 размерностью 
Применением цепных дробей найти секретный ключ d и разложение модуля 54296750879837 (экспонента — 4282063) на множители. В ответе укажите секретный ключ.
Решить сравнение 
Найти корреляционную матрицу блока замен 15 10 4 2 0 13 9 1 12 6 7 5 3 8 14 11 размерностью 
(1)
begin{matrix}
0 & 0 & -0.25 & 0 &
0.25 & 0 & 0 & -0.25 &
0.25 & -0.25 & -0.5 & 0.25 &
0 & 0.25 & -0.25 & 0 &
end{matrix}
(2)
begin{matrix}
0 & 0 & -0.25 & 0 &
0.25 & 0 & 0 & -0.25 &
0.25 & -0.25 & -0.5 & 0.25 &
0 & 0.25 & 0.25 & 0 &
end{matrix}
(3)
begin{matrix}
0 & 0 & -0.25 & 0 &
0.25 & 0 & 0 & -0.25 &
0.25 & -0.25 & -0.5 & 0.25 &
0 & -0.25 & 0.25 & 0 &
end{matrix}
(4)
begin{matrix}
0 & 0 & -0.25 & 0 &
0.25 & 0 & 0 & -0.25 &
0.25 & -0.25 & -0.5 & -0.25 &
0 & 0.25 & 0.25 & 0 &
end{matrix}
Дан шифртекст 152, а также значения модуля шифрования N = 187 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Найти остаток от деления 
Расшифровать сообщение на английском языке
6-21.txt
, зашифрованное шифром Виженера, Длина ключа равна 5.
В ответ введите ключ.
.
Провести операцию SubBytes алгоритма AES со значением байта 35.
Вычислить значение 
Провести операцию MixColumns над приведенным ниже столбцом состояния
Проверьте подлинность ЭЦП (7, 5) для сообщения с известным значением хэш-свертки 6, зная открытый ключ проверки подписи (596, 318). Используйте кривую 
(1) подпись действительна
(2) подпись недействительна
Даны точки P(62, 379), Q(53, 474), R(110, 622) на кривой 

Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
ПРОБИРКА
или
МЕНЗУРКА
— устойчивее к действию этой программы?
(1) Первый пароль надежнее
(2) Второй пароль надежнее
(3) Пароли одинаково ненадежные
Дан шифртекст, показанный ниже. Зная секретный ключ 
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(16, 416), (93, 484)}; {(489, 468), (531, 397)}; |
| {(188, 93), (654, 102)}; {(489, 468), (218, 150)}; |
| {(16, 416), (530, 729)}; {(425, 663), (295, 219)}; |
| {(725, 195), (742, 299)}; {(188, 93), (367, 360)}; |
| {(188, 93), (235, 732)}; {(618, 206), (251, 245)}; |
| {(425, 663), (688, 10)} |
Дана точка P(85, 716) на кривой 

Зашифровать биграмму ДА с помощью матрицы 
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
D24E3A7E2A03DD05B41C3C5F41E73D2B
Сообщение 945 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {2,4,7,14,29,57,116}, m=233 и n=64. В ответе укажите исходное сообщение.
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3
Д 4 Е 5 Ё 6 Ж 7
З 8 И 9 Й 10 К 11
Л 12 М 13 Н 14 О 15
П 16 Р 17 С 18 Т 19
У 20 Ф 21 Х 22 Ц 23
Ч 24 Ш 25 Щ 26 Ъ 27
Ы 28 Ь 29 Э 30 Ю 31
Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст РАЗДЕЛ.
Провести первый раунд зашифрования открытого текста CBD9 93EC CB0F F839 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок 
Зашифруйте открытый текст НИЗМЕННЫЙ с помощью алфавита, приведенного в
таблице
, используйте открытый ключ B=(286, 136), значения случайных чисел
для букв открытого текста k: 12, 5, 7, 17, 18, 2, 12, 10, 11, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
(1) {(286, 136), (612, 329)}; {(425, 663), (526, 412)}; {(135, 82), (27, 120)};
{(745, 210), (707, 195)}; {(618, 206), (281, 518)}; {(188, 93), (390, 603)};
{(286, 136), (612, 329)}; {(377, 456), (160, 609)}; {(179, 275), (530, 22)}
(2) {(135, 82), (27, 120)}; {(286, 136), (612, 329)}; {(425, 663), (526, 412)};
{(745, 210), (707, 195)}; {(618, 206), (281, 518)}; {(188, 93), (390, 603)};
{(286, 136), (612, 329)}; {(377, 456), (160, 609)}; {(179, 275), (530, 22)}
(3) {(425, 663), (526, 412)}; {(286, 136), (612, 329)}; {(135, 82), (27, 120)};
{(745, 210), (707, 195)}; {(618, 206), (281, 518)}; {(188, 93), (390, 603)};
{(286, 136), (612, 329)}; {(377, 456), (160, 609)}; {(179, 275), (530, 22)}
(4) {(188, 93), (390, 603)}; {(425, 663), (526, 412)}; {(135, 82), (27, 120)};
{(745, 210), (707, 195)}; {(618, 206), (281, 518)}; {(286, 136), (612, 329)};
{(286, 136), (612, 329)}; {(377, 456), (160, 609)}; {(179, 275), (530, 22)}
Решить в целых числах уравнение 
Определить, является ли число 66405897020462343733 простым с вероятностью не меньше 0,999.
Вычислить нелинейность булевой функции 00000001 от 3 переменных
Дано: модуль шифрования N = 4891, открытый ключ e = 17. Найти значение шифртекста, полученного при зашифровании открытого текста 4654 на открытом ключе (N, e) по алгоритму RSA.
Решить следующее сравнение 
С помощью 
Вычислить динамическое расстояние порядка 1 булевой функции 00000001 от 3 переменных
Даны значения модуля шифрования N = 143 и открытого ключа e = 113. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 124.
Решить сравнение 
Расшифровать текст 3-22.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите последнее слово заглавными буквами.
Вычислить нелинейность блока замен 14 7 13 2 0 10 8 9 4 3 15 5 12 11 1 6 размерностью 
Даны значения модуля шифрования N = 3901 и открытого ключа e = 2375. Используя метод факторизации Ферма, найти значение закрытого ключа.
Решить систему сравнений:

Вычислить динамическое расстояние порядка (2,2) блока замен 14 7 13 2 0 10 8 9 4 3 15 5 12 11 1 6 размерностью 
Применением цепных дробей найти секретный ключ d и разложение модуля 50824793010569 (экспонента — 4440901) на множители. В ответе укажите секретный ключ.
Решить сравнение 
Найти корреляционную матрицу блока замен 14 7 13 2 0 10 8 9 4 3 15 5 12 11 1 6 размерностью 
(1)
begin{matrix}
0.25 & 0.5 & -0.25 & -0.25 &
0.25 & -0.25 & 0 & 0 &
-0.25 & -0.25 & -0.5 & 0.25 &
0.25 & 0 & 0.25 & 0.25 &
end{matrix}
(2)
begin{matrix}
0.25 & 0.5 & -0.25 & -0.25 &
0.25 & -0.25 & 0 & 0 &
-0.25 & -0.25 & -0.5 & 0.25 &
0.25 & 0 & 0.25 & -0.25 &
end{matrix}
(3)
begin{matrix}
0.25 & 0.5 & -0.25 & -0.25 &
0.25 & -0.25 & 0 & 0 &
-0.25 & -0.25 & -0.5 & 0.25 &
0.25 & 0 & -0.25 & -0.25 &
end{matrix}
(4)
begin{matrix}
0.25 & 0.5 & -0.25 & 0.25 &
0.25 & -0.25 & 0 & 0 &
-0.25 & -0.25 & -0.5 & 0.25 &
0.25 & 0 & 0.25 & -0.25 &
end{matrix}
Дан шифртекст 117, а также значения модуля шифрования N = 143 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Найти остаток от деления 
Расшифровать сообщение на английском языке
6-22.txt
, зашифрованное шифром Виженера, Длина ключа равна 4.
В ответ введите ключ.
.
Провести операцию SubBytes алгоритма AES со значением байта D9.
Вычислить значение 
Провести операцию MixColumns над приведенным ниже столбцом состояния
Проверьте подлинность ЭЦП (7, 4) для сообщения с известным значением хэш-свертки 5, зная открытый ключ проверки подписи (596, 318). Используйте кривую 
(1) подпись действительна
(2) подпись недействительна
Даны точки P(53, 277), Q(66, 552), R(99, 456) на кривой 

Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
ПРОСТУДА
или
СКВОЗНЯК
— устойчивее к действию этой программы?
(1) Первый пароль надежнее
(2) Второй пароль надежнее
(3) Пароли одинаково ненадежные
Дан шифртекст, показанный ниже. Зная секретный ключ 
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(179, 275), (326, 675)}; {(725, 195), (83, 378)}; |
| {(440, 539), (340, 78)}; {(425, 663), (67, 84)}; |
| {(425, 663), (620, 71)}; {(72, 254), (251, 245)}; |
| {(568, 355), (75, 318)}; {(725, 195), (228, 271)}; |
| {(188, 93), (734, 170)}; {(188, 93), (704, 705)}; |
| {(286, 136), (235, 732)} |
Дана точка P(66, 199) на кривой 

Зашифровать биграмму ЛИ с помощью матрицы 
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
AE5AC5EACE6AAB4577105DE2CB202675
Сообщение 812 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {5,6,12,24,48,98,195}, m=389 и n=111. В ответе укажите исходное сообщение.
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3
Д 4 Е 5 Ё 6 Ж 7
З 8 И 9 Й 10 К 11
Л 12 М 13 Н 14 О 15
П 16 Р 17 С 18 Т 19
У 20 Ф 21 Х 22 Ц 23
Ч 24 Ш 25 Щ 26 Ъ 27
Ы 28 Ь 29 Э 30 Ю 31
Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст пробел.
Провести первый раунд зашифрования открытого текста D14E C9C9 F441 8039 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок 
Зашифруйте открытый текст НЕЭТИЧНЫЙ с помощью алфавита, приведенного в
таблице
, используйте открытый ключ B=(489, 468), значения случайных чисел
для букв открытого текста k: 14, 18, 11, 11, 6, 6, 17, 2, 5, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
(1) {(596, 433), (66, 552)}; {(618, 206), (90, 730)}; {(179, 275), (590, 376)};
{(179, 275), (687, 91)}; {(725, 195), (535, 374)}; {(725, 195), (203, 324)};
{(440, 539), (344, 400)}; {(188, 93), (461, 747)}; {(425, 663), (269, 564)}
(2) {(179, 275), (590, 376)}; {(596, 433), (66, 552)}; {(618, 206), (90, 730)};
{(179, 275), (687, 91)}; {(725, 195), (535, 374)}; {(725, 195), (203, 324)};
{(440, 539), (344, 400)}; {(188, 93), (461, 747)}; {(425, 663), (269, 564)}
(3) {(618, 206), (90, 730)}; {(596, 433), (66, 552)}; {(179, 275), (590, 376)};
{(179, 275), (687, 91)}; {(725, 195), (535, 374)}; {(725, 195), (203, 324)};
{(440, 539), (344, 400)}; {(188, 93), (461, 747)}; {(425, 663), (269, 564)}
(4) {(725, 195), (203, 324)}; {(618, 206), (90, 730)}; {(179, 275), (590, 376)};
{(179, 275), (687, 91)}; {(725, 195), (535, 374)}; {(596, 433), (66, 552)};
{(440, 539), (344, 400)}; {(188, 93), (461, 747)}; {(425, 663), (269, 564)}
Решить следующее сравнение 
С помощью 
Вычислить динамическое расстояние порядка 1 булевой функции 00101000 от 3 переменных
Даны значения модуля шифрования N = 299 и открытого ключа e = 139. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 87.
Решить сравнение 
Расшифровать текст 3-23.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите предпоследнее слово заглавными буквами.
Вычислить нелинейность блока замен 12 9 0 15 6 13 1 5 14 7 11 2 4 8 10 3 размерностью 
Даны значения модуля шифрования N = 3397 и открытого ключа e = 113. Используя метод факторизации Ферма, найти значение закрытого ключа.
Решить систему сравнений:

Вычислить динамическое расстояние порядка (2,2) блока замен 12 9 0 15 6 13 1 5 14 7 11 2 4 8 10 3 размерностью 
Применением цепных дробей найти секретный ключ d и разложение модуля 48992988576733 (экспонента — 4545733) на множители. В ответе укажите секретный ключ.
Решить сравнение 
Найти корреляционную матрицу блока замен 12 9 0 15 6 13 1 5 14 7 11 2 4 8 10 3 размерностью 
(1)
begin{matrix}
0.5 & 0 & 0 & 0 &
0.25 & 0.25 & -0.5 & -0.25 &
0 & -0.25 & 0 & -0.25 &
-0.25 & 0.5 & 0.25 & 0 &
end{matrix}
(2)
begin{matrix}
0.5 & 0 & 0 & 0 &
0.25 & 0.25 & -0.5 & -0.25 &
0 & -0.25 & 0 & -0.25 &
-0.25 & 0.5 & -0.25 & 0 &
end{matrix}
(3)
begin{matrix}
0.5 & 0 & 0 & 0 &
0.25 & 0.25 & -0.5 & -0.25 &
0 & -0.25 & 0 & 0.25 &
-0.25 & 0.5 & -0.25 & 0 &
end{matrix}
(4)
begin{matrix}
0.5 & 0 & 0 & 0 &
0.25 & 0.25 & -0.5 & -0.25 &
0 & -0.25 & 0 & -0.25 &
-0.25 & -0.5 & -0.25 & 0 &
end{matrix}
Дан шифртекст 185, а также значения модуля шифрования N = 247 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Найти остаток от деления 
Расшифровать сообщение на английском языке
6-23.txt
, зашифрованное шифром Виженера, Длина ключа равна 3.
В ответ введите ключ.
.
Провести операцию SubBytes алгоритма AES со значением байта 61.
Вычислить значение 
Провести операцию MixColumns над приведенным ниже столбцом состояния
Проверьте подлинность ЭЦП (5, 11) для сообщения с известным значением хэш-свертки 12, зная открытый ключ проверки подписи (135, 669). Используйте кривую 
(1) подпись действительна
(2) подпись недействительна
Определить, является ли число 36413321723440003717 простым с вероятностью не меньше 0,999.
Вычислить нелинейность булевой функции 00101000 от 3 переменных
Дано: модуль шифрования N = 4559, открытый ключ e = 17. Найти значение шифртекста, полученного при зашифровании открытого текста 946 на открытом ключе (N, e) по алгоритму RSA.
Даны точки P(67, 667), Q(53, 474), R(105, 382) на кривой 

Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
ТОВАР
или
РЫНОК
— устойчивее к действию этой программы?
(1) Первый пароль надежнее
(2) Второй пароль надежнее
(3) Пароли одинаково ненадежные
Дан шифртекст, показанный ниже. Зная секретный ключ 
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(618, 206), (294, 595)}; {(188, 93), (13, 617)}; |
| {(188, 93), (206, 106)}; {(188, 93), (67, 667)}; |
| {(56, 419), (350, 184)}; {(440, 539), (275, 456)}; |
| {(745, 210), (301, 17)}; {(346, 242), (588, 707)}; |
| {(188, 93), (256, 121)}; {(425, 663), (209, 82)}; |
| {(16, 416), (687, 660)} |
Дана точка P(44, 385) на кривой 

Зашифровать биграмму НО с помощью матрицы 
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
1D3AABA253AF64341E3E9E36EAB76F6F
Сообщение 302 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {1,4,6,12,25,49,100}, m=199 и n=78. В ответе укажите исходное сообщение.
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3
Д 4 Е 5 Ё 6 Ж 7
З 8 И 9 Й 10 К 11
Л 12 М 13 Н 14 О 15
П 16 Р 17 С 18 Т 19
У 20 Ф 21 Х 22 Ц 23
Ч 24 Ш 25 Щ 26 Ъ 27
Ы 28 Ь 29 Э 30 Ю 31
Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст ДЕНЬГИ.
Провести первый раунд зашифрования открытого текста CF85 F7CE F928 C262 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок 
Зашифруйте открытый текст МЫСЛЕННЫЙ с помощью алфавита, приведенного в
таблице
, используйте открытый ключ B=(346, 242), значения случайных чисел
для букв открытого текста k: 6, 17, 18, 11, 18, 2, 4, 2, 12, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
(1) {(725, 195), (4, 567)}; {(440, 539), (727, 65)}; {(618, 206), (13, 134)};
{(179, 275), (79, 640)}; {(618, 206), (147, 361)}; {(188, 93), (288, 639)};
{(16, 416), (362, 446)}; {(188, 93), (267, 81)}; {(286, 136), (395, 414)}
(2) {(440, 539), (727, 65)}; {(725, 195), (4, 567)}; {(618, 206), (13, 134)};
{(179, 275), (79, 640)}; {(618, 206), (147, 361)}; {(188, 93), (288, 639)};
{(16, 416), (362, 446)}; {(188, 93), (267, 81)}; {(286, 136), (395, 414)}
(3) {(618, 206), (13, 134)}; {(725, 195), (4, 567)}; {(440, 539), (727, 65)};
{(179, 275), (79, 640)}; {(618, 206), (147, 361)}; {(188, 93), (288, 639)};
{(16, 416), (362, 446)}; {(188, 93), (267, 81)}; {(286, 136), (395, 414)}
(4) {(16, 416), (362, 446)}; {(440, 539), (727, 65)}; {(618, 206), (13, 134)};
{(179, 275), (79, 640)}; {(618, 206), (147, 361)}; {(188, 93), (288, 639)};
{(725, 195), (4, 567)}; {(188, 93), (267, 81)}; {(286, 136), (395, 414)}
Решить следующее сравнение 
С помощью 
Вычислить динамическое расстояние порядка 1 булевой функции 00011010 от 3 переменных
Даны значения модуля шифрования N = 221 и открытого ключа e = 35. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 172.
Решить сравнение 
Расшифровать текст 3-24.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите последнее слово заглавными буквами.
Вычислить нелинейность блока замен 12 2 8 3 9 1 11 15 14 6 4 5 13 0 10 7 размерностью 
Даны значения модуля шифрования N = 3713 и открытого ключа e = 2455. Используя метод факторизации Ферма, найти значение закрытого ключа.
Решить систему сравнений:

Вычислить динамическое расстояние порядка (2,2) блока замен 12 2 8 3 9 1 11 15 14 6 4 5 13 0 10 7 размерностью 
Применением цепных дробей найти секретный ключ d и разложение модуля 47050437355283 (экспонента — 4674517) на множители. В ответе укажите секретный ключ.
Решить сравнение 
Найти корреляционную матрицу блока замен 12 2 8 3 9 1 11 15 14 6 4 5 13 0 10 7 размерностью 
(1)
begin{matrix}
0.25 & 0.25 & 0 & -0.75 &
0.25 & 0.25 & 0 & 0 &
0.5 & 0 & -0.25 & 0.25 &
-0.25 & 0 & 0.5 & 0.25 &
end{matrix}
(2)
begin{matrix}
0.25 & 0.25 & 0 & -0.75 &
0.25 & 0.25 & 0 & 0 &
0.5 & 0 & -0.25 & 0.25 &
-0.25 & 0 & 0.5 & -0.25 &
end{matrix}
(3)
begin{matrix}
0.25 & 0.25 & 0 & -0.75 &
0.25 & 0.25 & 0 & 0 &
0.5 & 0 & -0.25 & 0.25 &
0.25 & 0 & 0.5 & -0.25 &
end{matrix}
(4)
begin{matrix}
0.25 & 0.25 & 0 & 0.75 &
0.25 & 0.25 & 0 & 0 &
0.5 & 0 & -0.25 & 0.25 &
-0.25 & 0 & 0.5 & -0.25 &
end{matrix}
Дан шифртекст 96, а также значения модуля шифрования N = 143 и открытого ключа e = 7. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Найти остаток от деления 
Расшифровать сообщение на английском языке
6-24.txt
, зашифрованное шифром Виженера, Длина ключа равна 3.
В ответ введите ключ.
.
Провести операцию SubBytes алгоритма AES со значением байта EF.
Вычислить значение 
Провести операцию MixColumns над приведенным ниже столбцом состояния
Проверьте подлинность ЭЦП (3, 2) для сообщения с известным значением хэш-свертки 12, зная открытый ключ проверки подписи (562, 89). Используйте кривую 
(1) подпись действительна
(2) подпись недействительна
Определить, является ли число 59713968361666935769 простым с вероятностью не меньше 0,999.
Вычислить нелинейность булевой функции 00011010 от 3 переменных
Дано: модуль шифрования N = 5561, открытый ключ e = 19. Найти значение шифртекста, полученного при зашифровании открытого текста 2718 на открытом ключе (N, e) по алгоритму RSA.
Даны точки P(69, 241), Q(66, 552), R(69, 510) на кривой 

Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
ГОРШОК
или
ЦВЕТОК
— устойчивее к действию этой программы?
(1) Первый пароль надежнее
(2) Второй пароль надежнее
(3) Пароли одинаково ненадежные
Дан шифртекст, показанный ниже. Зная секретный ключ 
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(188, 93), (295, 219)}; {(618, 206), (646, 706)}; |
| {(440, 539), (573, 583)}; {(16, 416), (694, 581)}; |
| {(179, 275), (585, 540)}; {(377, 456), (701, 570)}; |
| {(618, 206), (67, 667)}; {(286, 136), (36, 664)}; |
| {(72, 254), (727, 65)}; {(568, 355), (438, 40)} |
Дана точка P(45, 720) на кривой 

Зашифровать биграмму КУ с помощью матрицы 
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
D19BBD490CE4871C18A8DBF20152A3E4
Сообщение 855 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {4,5,11,21,43,85,170}, m=340 и n=101. В ответе укажите исходное сообщение.
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3
Д 4 Е 5 Ё 6 Ж 7
З 8 И 9 Й 10 К 11
Л 12 М 13 Н 14 О 15
П 16 Р 17 С 18 Т 19
У 20 Ф 21 Х 22 Ц 23
Ч 24 Ш 25 Щ 26 Ъ 27
Ы 28 Ь 29 Э 30 Ю 31
Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст КРИКЕТ.
Провести первый раунд зашифрования открытого текста FAAA A9D9 D006 8DC3 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок 
Зашифруйте открытый текст МУШТРОВКА с помощью алфавита, приведенного в
таблице
, используйте открытый ключ B=(618, 206), значения случайных чисел
для букв открытого текста k: 5, 19, 8, 2, 5, 8, 15, 19, 6, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
(1) {(425, 663), (636, 4)}; {(568, 355), (660, 275)}; {(346, 242), (229, 151)};
{(188, 93), (606, 147)}; {(425, 663), (652, 315)}; {(346, 242), (414, 563)};
{(745, 210), (340, 78)}; {(568, 355), (422, 589)}; {(725, 195), (422, 589)}
(2) {(346, 242), (229, 151)}; {(425, 663), (636, 4)}; {(568, 355), (660, 275)};
{(188, 93), (606, 147)}; {(425, 663), (652, 315)}; {(346, 242), (414, 563)};
{(745, 210), (340, 78)}; {(568, 355), (422, 589)}; {(725, 195), (422, 589)}
(3) {(568, 355), (660, 275)}; {(425, 663), (636, 4)}; {(346, 242), (229, 151)};
{(188, 93), (606, 147)}; {(425, 663), (652, 315)}; {(346, 242), (414, 563)};
{(745, 210), (340, 78)}; {(568, 355), (422, 589)}; {(725, 195), (422, 589)}
(4) {(346, 242), (414, 563)}; {(568, 355), (660, 275)}; {(346, 242), (229, 151)};
{(188, 93), (606, 147)}; {(425, 663), (652, 315)}; {(425, 663), (636, 4)};
{(745, 210), (340, 78)}; {(568, 355), (422, 589)}; {(725, 195), (422, 589)}
Решить следующее сравнение 
С помощью 
Вычислить динамическое расстояние порядка 1 булевой функции 00001001 от 3 переменных
Даны значения модуля шифрования N = 391 и открытого ключа e = 145. Найти значение открытого текста, который при зашифровании на открытом ключе (N, e) по алгоритму RSA дает 173.
Найти остаток от деления 
Провести операцию SubBytes алгоритма AES со значением байта D0.
Вычислить значение 
Провести операцию MixColumns над приведенным ниже столбцом состояния
Проверьте подлинность ЭЦП (7, 10) для сообщения с известным значением хэш-свертки 6, зная открытый ключ проверки подписи (562, 662). Используйте кривую 
(1) подпись действительна
(2) подпись недействительна
Определить, является ли число 99599500573849980909 простым с вероятностью не меньше 0,999.
Вычислить нелинейность булевой функции 00001001 от 3 переменных
Дано: модуль шифрования N = 8051, открытый ключ e = 11. Найти значение шифртекста, полученного при зашифровании открытого текста 6206 на открытом ключе (N, e) по алгоритму RSA.
Даны точки P(69, 510), Q(53, 277), R(105, 369) на кривой 

Для подтверждения своих полномочий в компьютерной системе пользователь должен ввести свое имя и пароль, состоящий из 30 букв русского алфавита с исключенными Ё и Ь. Файл с паролями пользователей хранится на сервере в зашифрованном виде. Для их зашифровывания использовался следующий способ. Буквам алфавита поставлены в соответствие числа от 0 до 30: А — 0, Б -1, …, Я — 30. При зашифровывании пароля каждую его букву заменяют остатком от деления на 31 значения выражения (6a3 + 5a2 + 6a + 20), где a — число, соответствующее заменяемой букве. В начале каждого сеанса работы введенный пользователем пароль зашифровывается и сравнивается с соответствующей записью в файле. При совпадении сеанс продолжается, а при расхождении пароль запрашивается снова. Злоумышленник хочет войти в систему под чужим именем, а соответствующий этому имени пароль не знает. Он написал программу, которая в случайном порядке перебирает пароли. Какой из двух паролей —
ЧАЙНИК
или
МАСТЕР
— устойчивее к действию этой программы?
(1) Первый пароль надежнее
(2) Второй пароль надежнее
(3) Пароли одинаково ненадежные
Дан шифртекст, показанный ниже. Зная секретный ключ 
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(725, 195), (9, 150)}; {(745, 210), (138, 453)}; |
| {(56, 419), (36, 87)}; {(283, 493), (39, 580)}; |
| {(377, 456), (515, 684)}; {(346, 242), (458, 261)}; |
| {(283, 493), (105, 369)}; {(568, 355), (326, 675)}; |
| {(425, 663), (529, 358)}; {(283, 493), (668, 409)} |
Дана точка P(39, 171) на кривой 

Расшифровать текст 3-25.txt, зашифрованный алгоримом простой замены, каждой букве алфавита соответствует двузначное число.
Это задание достаточно легко и за небольшое время выполняется, если использовать программный комплекс «Classic», специально разработанный авторами для таких задач и представленный в лекции. В качестве ответа введите последнее слово заглавными буквами.
Вычислить нелинейность блока замен 15 0 1 6 8 3 4 14 5 9 11 7 10 13 2 12 размерностью 
Даны значения модуля шифрования N = 4183 и открытого ключа e = 2099. Используя метод факторизации Ферма, найти значение закрытого ключа.
Зашифровать биграмму РО с помощью матрицы 
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
8EC5D16B5AE720389D4C21207A257241
Сообщение 249 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {1,2,7,11,23,47,92}, m=185 и n=29. В ответе укажите исходное сообщение.
Для демонстрации качества алгоритма выберем два открытых текста, различающихся лишь одной перестановкой соседних букв, пусть это будут слова АТЛАНТ и ТАЛАНТ.
А 0 Б 1 В 2 Г 3
Д 4 Е 5 Ё 6 Ж 7
З 8 И 9 Й 10 К 11
Л 12 М 13 Н 14 О 15
П 16 Р 17 С 18 Т 19
У 20 Ф 21 Х 22 Ц 23
Ч 24 Ш 25 Щ 26 Ъ 27
Ы 28 Ь 29 Э 30 Ю 31
Я 32
Первое преобразование: 

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы 




Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.
Зашифровать по данной схеме с теми же параметрами текст ТАЙМЕР.
Провести первый раунд зашифрования открытого текста B05F A79E CEF6 AA22 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок 
Вычислить динамическое расстояние порядка (2,2) блока замен 15 0 1 6 8 3 4 14 5 9 11 7 10 13 2 12 размерностью 
Применением цепных дробей найти секретный ключ d и разложение модуля 42982346145803 (экспонента — 4777621) на множители. В ответе укажите секретный ключ.
Найти корреляционную матрицу блока замен 15 0 1 6 8 3 4 14 5 9 11 7 10 13 2 12 размерностью 
(1)
begin{matrix}
0 & 0 & 0.25 & 0 &
-0.25 & 0.25 & 0.25 & -0.25 &
-0.5 & 0 & 0 & 0.25 &
0.25 & 0 & 0 & -0.25 &
end{matrix}
(2)
begin{matrix}
0 & 0 & 0.25 & 0 &
-0.25 & 0.25 & 0.25 & -0.25 &
-0.5 & 0 & 0 & 0.25 &
0.25 & 0 & 0 & 0.25 &
end{matrix}
(3)
begin{matrix}
0 & 0 & 0.25 & 0 &
0.25 & 0.25 & 0.25 & -0.25 &
-0.5 & 0 & 0 & 0.25 &
0.25 & 0 & 0 & 0.25 &
end{matrix}
(4)
begin{matrix}
0 & 0 & 0.25 & 0 &
-0.25 & 0.25 & 0.25 & -0.25 &
-0.5 & 0 & 0 & -0.25 &
0.25 & 0 & 0 & 0.25 &
end{matrix}
Дан шифртекст 163, а также значения модуля шифрования N = 187 и открытого ключа e = 3. Используя метод перешифрования, найти значение открытого текста, не находя значения секретного ключа.
Зашифруйте открытый текст ЛАТЕНТНЫЙ с помощью алфавита, приведенного в
таблице
, используйте открытый ключ B=(725, 195), значения случайных чисел
для букв открытого текста k: 9, 10, 13, 2, 2, 12, 12, 5, 7, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
(1) {(489, 468), (517, 573)}; {(377, 456), (151, 233)}; {(283, 493), (629, 403)};
{(188, 93), (682, 179)}; {(188, 93), (165, 382)}; {(286, 136), (75, 433)};
{(286, 136), (417, 614)}; {(425, 663), (275, 456)}; {(135, 82), (729, 578)}
(2) {(377, 456), (151, 233)}; {(489, 468), (517, 573)}; {(283, 493), (629, 403)};
{(188, 93), (682, 179)}; {(188, 93), (165, 382)}; {(286, 136), (75, 433)};
{(286, 136), (417, 614)}; {(425, 663), (275, 456)}; {(135, 82), (729, 578)}
(3) {(188, 93), (165, 382)}; {(377, 456), (151, 233)}; {(283, 493), (629, 403)};
{(188, 93), (682, 179)}; {(286, 136), (75, 433)}; {(489, 468), (517, 573)};
{(286, 136), (417, 614)}; {(425, 663), (275, 456)}; {(135, 82), (729, 578)}
(4) {(283, 493), (629, 403)}; {(489, 468), (517, 573)}; {(377, 456), (151, 233)};
{(188, 93), (682, 179)}; {(188, 93), (165, 382)}; {(286, 136), (75, 433)};
{(286, 136), (417, 614)}; {(425, 663), (275, 456)}; {(135, 82), (729, 578)}
С помощью 
Вычислить динамическое расстояние порядка 1 булевой функции 01001001 от 3 переменных
Даны точки P(72, 497), Q(62, 372), R(69, 241) на кривой 

Дан шифртекст, показанный ниже. Зная секретный ключ 
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(16, 416), (150, 355)}; {(188, 93), (394, 20)}; |
| {(725, 195), (13, 134)}; {(377, 456), (209, 669)}; |
| {(56, 419), (514, 662)}; {(56, 419), (243, 87)}; |
| {(618, 206), (719, 538)}; {(618, 206), (159, 13)}; |
| {(618, 206), (326, 76)}; {(188, 93), (557, 28)} |
Дана точка P(34, 677) на кривой 

Вычислить нелинейность булевой функции 01001001 от 3 переменных
Вычислить нелинейность блока замен 8 14 3 7 4 11 12 6 5 1 10 15 0 9 2 13 размерностью 
Вычислить динамическое расстояние порядка (2,2) блока замен 8 14 3 7 4 11 12 6 5 1 10 15 0 9 2 13 размерностью 
Найти корреляционную матрицу блока замен 8 14 3 7 4 11 12 6 5 1 10 15 0 9 2 13 размерностью 
(1)
begin{matrix}
0.5 & 0.25 & 0.25 & 0.25 &
0 & 0.5 & 0.25 & 0 &
-0.25 & -0.25 & 0 & 0 &
0.25 & -0.25 & 0.25 & 0 &
end{matrix}
(2)
begin{matrix}
0.5 & 0.25 & 0.25 & 0.25 &
0 & 0.5 & 0.25 & 0 &
-0.25 & -0.25 & 0 & 0 &
0.25 & -0.25 & -0.25 & 0 &
end{matrix}
(3)
begin{matrix}
0.5 & 0.25 & 0.25 & 0.25 &
0 & 0.5 & 0.25 & 0 &
-0.25 & -0.25 & 0 & 0 &
0.25 & 0.25 & -0.25 & 0 &
end{matrix}
(4)
begin{matrix}
0.5 & 0.25 & 0.25 & 0.25 &
0 & 0.5 & 0.25 & 0 &
-0.25 & 0.25 & 0 & 0 &
0.25 & -0.25 & -0.25 & 0 &
end{matrix}
Провести операцию SubBytes алгоритма AES со значением байта 1E.
Провести операцию MixColumns над приведенным ниже столбцом состояния
Проверьте подлинность ЭЦП (7, 

(1) подпись действительна
(2) подпись недействительна
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
276D036078486A4BAED723B5A6632DCF
Сообщение 762 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {3,6,11,21,43,85,171}, m=343 и n=43. В ответе укажите исходное сообщение.
Провести первый раунд зашифрования открытого текста BDD3 AE17 C12A F70A шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок 
Зашифруйте открытый текст КУПАЛЬЩИК с помощью алфавита, приведенного в
таблице
, используйте открытый ключ B=(188, 93), значения случайных чисел
для букв открытого текста k: 17, 17, 9, 12, 17, 7, 15, 7, 16, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
(1) {(440, 539), (705, 64)}; {(440, 539), (350, 567)}; {(489, 468), (273, 270)};
{(286, 136), (243, 664)}; {(440, 539), (229, 151)}; {(135, 82), (99, 456)};
{(745, 210), (668, 409)}; {(135, 82), (394, 731)}; {(72, 254), (611, 579)}
(2) {(489, 468), (273, 270)}; {(440, 539), (705, 64)}; {(440, 539), (350, 567)};
{(286, 136), (243, 664)}; {(440, 539), (229, 151)}; {(135, 82), (99, 456)};
{(745, 210), (668, 409)}; {(135, 82), (394, 731)}; {(72, 254), (611, 579)}
(3) {(440, 539), (350, 567)}; {(440, 539), (705, 64)}; {(489, 468), (273, 270)};
{(286, 136), (243, 664)}; {(440, 539), (229, 151)}; {(135, 82), (99, 456)};
{(745, 210), (668, 409)}; {(135, 82), (394, 731)}; {(72, 254), (611, 579)}
(4) {(440, 539), (229, 151)}; {(440, 539), (350, 567)}; {(489, 468), (273, 270)};
{(286, 136), (243, 664)}; {(135, 82), (99, 456)}; {(440, 539), (705, 64)};
{(745, 210), (668, 409)}; {(135, 82), (394, 731)}; {(72, 254), (611, 579)}
С помощью 
Вычислить динамическое расстояние порядка 1 булевой функции 00110010 от 3 переменных
Даны точки P(61, 129), Q(59, 365), R(105, 369) на кривой 

Дан шифртекст, показанный ниже. Зная секретный ключ 
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(440, 539), (279, 398)}; {(568, 355), (295, 219)}; |
| {(16, 416), (724, 229)}; {(346, 242), (730, 240)}; |
| {(72, 254), (334, 226)}; {(188, 93), (310, 169)}; |
| {(72, 254), (36, 664)}; {(179, 275), (481, 369)}; |
| {(188, 93), (236, 39)}; {(377, 456), (438, 711)}; |
| {(377, 456), (307, 58)} |
Дана точка P(34, 74) на кривой 

Вычислить нелинейность булевой функции 00110010 от 3 переменных
Вычислить нелинейность блока замен 15 8 11 3 1 5 0 12 6 9 7 10 14 13 4 2 размерностью 
Вычислить динамическое расстояние порядка (2,2) блока замен 15 8 11 3 1 5 0 12 6 9 7 10 14 13 4 2 размерностью 
Найти корреляционную матрицу блока замен 15 8 11 3 1 5 0 12 6 9 7 10 14 13 4 2 размерностью 
(1)
begin{matrix}
0 & -0.25 & -0.25 & 0.25 &
-0.25 & 0.25 & -0.25 & -0.25 &
-0.25 & -0.5 & 0.25 & -0.25 &
0.25 & 0.25 & 0.25 & 0 &
end{matrix}
(2)
begin{matrix}
0 & -0.25 & -0.25 & 0.25 &
-0.25 & 0.25 & -0.25 & -0.25 &
-0.25 & -0.5 & 0.25 & -0.25 &
-0.25 & 0.25 & 0.25 & 0 &
end{matrix}
(3)
begin{matrix}
0 & -0.25 & -0.25 & 0.25 &
-0.25 & 0.25 & -0.25 & -0.25 &
-0.25 & -0.5 & 0.25 & -0.25 &
-0.25 & 0.25 & -0.25 & 0 &
end{matrix}
(4)
begin{matrix}
0 & -0.25 & -0.25 & 0.25 &
-0.25 & 0.25 & 0.25 & -0.25 &
-0.25 & -0.5 & 0.25 & -0.25 &
-0.25 & 0.25 & 0.25 & 0 &
end{matrix}
Провести операцию SubBytes алгоритма AES со значением байта 18.
Провести операцию MixColumns над приведенным ниже столбцом состояния
Проверьте подлинность ЭЦП (5, 2) для сообщения с известным значением хэш-свертки 7, зная открытый ключ проверки подписи (384, 276). Используйте кривую 
(1) подпись действительна
(2) подпись недействительна
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
853C0BE633A9C211751A2714F76BA8D4
Сообщение 516 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {2,3,7,13,27,55,109}, m=218 и n=131. В ответе укажите исходное сообщение.
Провести первый раунд зашифрования открытого текста 991C 9E65 9A45 BD8C шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок 
Зашифруйте открытый текст ИЗЛЕЧИМЫЙ с помощью алфавита, приведенного в
таблице
, используйте открытый ключ B=(179, 275), значения случайных чисел
для букв открытого текста k: 10, 14, 2, 2, 10, 10, 14, 3, 7, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
(1) {(377, 456), (47, 349)}; {(596, 433), (45, 31)}; {(188, 93), (422, 162)};
{(188, 93), (290, 509)}; {(377, 456), (240, 309)}; {(377, 456), (47, 349)};
{(596, 433), (533, 299)}; {(56, 419), (414, 563)}; {(135, 82), (394, 20)}
(2) {(188, 93), (422, 162)}; {(377, 456), (47, 349)}; {(596, 433), (45, 31)};
{(188, 93), (290, 509)}; {(377, 456), (240, 309)}; {(377, 456), (47, 349)};
{(596, 433), (533, 299)}; {(56, 419), (414, 563)}; {(135, 82), (394, 20)}
(3) {(596, 433), (45, 31)}; {(377, 456), (47, 349)}; {(188, 93), (422, 162)};
{(188, 93), (290, 509)}; {(377, 456), (240, 309)}; {(377, 456), (47, 349)};
{(596, 433), (533, 299)}; {(56, 419), (414, 563)}; {(135, 82), (394, 20)}
(4) {(56, 419), (414, 563)}; {(596, 433), (45, 31)}; {(188, 93), (422, 162)};
{(188, 93), (290, 509)}; {(377, 456), (240, 309)}; {(377, 456), (47, 349)};
{(377, 456), (47, 349)}; {(596, 433), (533, 299)}; {(135, 82), (394, 20)}
С помощью 
Вычислить динамическое расстояние порядка 1 булевой функции 00110001 от 3 переменных
Даны точки P(61, 622), Q(59, 365), R(102, 267) на кривой 

Дан шифртекст, показанный ниже. Зная секретный ключ 
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(16, 416), (675, 505)}; {(72, 254), (611, 579)}; |
| {(72, 254), (727, 686)}; {(489, 468), (39, 171)}; |
| {(72, 254), (531, 354)}; {(568, 355), (36, 87)}; |
| {(188, 93), (588, 44)}; {(618, 206), (70, 195)}; |
| {(568, 355), (267, 81)}; {(56, 419), (525, 674)} |
Дана точка P(34, 677) на кривой 

Вычислить нелинейность булевой функции 00110001 от 3 переменных
Вычислить нелинейность блока замен 3 10 4 2 6 9 14 8 11 5 13 1 7 0 15 12 размерностью 
Вычислить динамическое расстояние порядка (2,2) блока замен 3 10 4 2 6 9 14 8 11 5 13 1 7 0 15 12 размерностью 
Найти корреляционную матрицу блока замен 3 10 4 2 6 9 14 8 11 5 13 1 7 0 15 12 размерностью 
(1)
begin{matrix}
-0.25 & -0.5 & -0.5 & 0 &
-0.25 & -0.25 & 0.25 & 0.25 &
-0.25 & 0 & 0.25 & 0.25 &
0.5 & 0.25 & 0.25 & 0 &
end{matrix}
(2)
begin{matrix}
-0.25 & -0.5 & -0.5 & 0 &
-0.25 & -0.25 & 0.25 & 0.25 &
-0.25 & 0 & 0.25 & 0.25 &
0.5 & -0.25 & 0.25 & 0 &
end{matrix}
(3)
begin{matrix}
-0.25 & -0.5 & -0.5 & 0 &
-0.25 & -0.25 & 0.25 & 0.25 &
-0.25 & 0 & 0.25 & -0.25 &
0.5 & -0.25 & 0.25 & 0 &
end{matrix}
(4)
begin{matrix}
-0.25 & -0.5 & -0.5 & 0 &
-0.25 & -0.25 & 0.25 & 0.25 &
-0.25 & 0 & 0.25 & 0.25 &
0.5 & -0.25 & -0.25 & 0 &
end{matrix}
Провести операцию SubBytes алгоритма AES со значением байта 1D.
Провести операцию MixColumns над приведенным ниже столбцом состояния
Проверьте подлинность ЭЦП (11, 6) для сообщения с известным значением хэш-свертки 8, зная открытый ключ проверки подписи (596, 318). Используйте кривую 
(1) подпись действительна
(2) подпись недействительна
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
17D93B6A32CA702ADB04A0180F0FDD3B
Сообщение 402 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {6,7,14,29,57,114,229}, m=457 и n=150. В ответе укажите исходное сообщение.
Провести первый раунд зашифрования открытого текста C485 FB04 B366 E288 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок 
Зашифруйте открытый текст ЗВЕЗДОЧКА с помощью алфавита, приведенного в
таблице
, используйте открытый ключ B=(725, 195), значения случайных чисел
для букв открытого текста k: 11, 17, 10, 10, 5, 2, 10, 19, 4, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
(1) {(179, 275), (237, 297)}; {(440, 539), (86, 726)}; {(377, 456), (681, 366)};
{(377, 456), (114, 607)}; {(425, 663), (147, 361)}; {(188, 93), (319, 233)};
{(377, 456), (445, 271)}; {(568, 355), (67, 667)}; {(16, 416), (243, 664)}
(2) {(377, 456), (681, 366)}; {(179, 275), (237, 297)}; {(440, 539), (86, 726)};
{(377, 456), (114, 607)}; {(425, 663), (147, 361)}; {(188, 93), (319, 233)};
{(377, 456), (445, 271)}; {(568, 355), (67, 667)}; {(16, 416), (243, 664)}
(3) {(440, 539), (86, 726)}; {(377, 456), (681, 366)}; {(179, 275), (237, 297)};
{(377, 456), (114, 607)}; {(425, 663), (147, 361)}; {(188, 93), (319, 233)};
{(377, 456), (445, 271)}; {(568, 355), (67, 667)}; {(16, 416), (243, 664)}
(4) {(188, 93), (319, 233)}; {(440, 539), (86, 726)}; {(377, 456), (681, 366)};
{(377, 456), (114, 607)}; {(425, 663), (147, 361)}; {(179, 275), (237, 297)};
{(377, 456), (445, 271)}; {(568, 355), (67, 667)}; {(16, 416), (243, 664)}
С помощью 
Вычислить динамическое расстояние порядка 1 булевой функции 01100011 от 3 переменных
Даны точки P(58, 139), Q(67, 84), R(85, 35) на кривой 

Дан шифртекст, показанный ниже. Зная секретный ключ 
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(725, 195), (651, 560)}; {(425, 663), (147, 361)}; |
| {(286, 136), (109, 551)}; {(440, 539), (90, 730)}; |
| {(618, 206), (668, 342)}; {(745, 210), (109, 200)}; |
| {(425, 663), (147, 361)}; {(72, 254), (228, 480)}; |
| {(346, 242), (530, 22)} |
Дана точка P(79, 640) на кривой 

Вычислить нелинейность булевой функции 01100011 от 3 переменных
Вычислить нелинейность блока замен 9 4 15 11 7 0 5 6 13 14 1 8 10 2 3 12 размерностью 
Вычислить динамическое расстояние порядка (2,2) блока замен 9 4 15 11 7 0 5 6 13 14 1 8 10 2 3 12 размерностью 
Найти корреляционную матрицу блока замен 9 4 15 11 7 0 5 6 13 14 1 8 10 2 3 12 размерностью 
(1)
begin{matrix}
-0.75 & 0 & 0 & 0 &
0.25 & 0 & 0 & 0 &
-0.25 & 0.25 & 0 & 0.5 &
-0.25 & 0 & -0.25 & 0.25 &
end{matrix}
(2)
begin{matrix}
-0.75 & 0 & 0 & 0 &
0.25 & 0 & 0 & 0 &
-0.25 & 0.25 & 0 & -0.5 &
-0.25 & 0 & -0.25 & 0.25 &
end{matrix}
(3)
begin{matrix}
-0.75 & 0 & 0 & 0 &
0.25 & 0 & 0 & 0 &
-0.25 & 0.25 & 0 & -0.5 &
-0.25 & 0 & 0.25 & 0.25 &
end{matrix}
(4)
begin{matrix}
-0.75 & 0 & 0 & 0 &
0.25 & 0 & 0 & 0 &
-0.25 & 0.25 & 0 & -0.5 &
-0.25 & 0 & -0.25 & -0.25 &
end{matrix}
Провести операцию SubBytes алгоритма AES со значением байта FB.
Провести операцию MixColumns над приведенным ниже столбцом состояния
Проверьте подлинность ЭЦП (7, 6) для сообщения с известным значением хэш-свертки 10, зная открытый ключ проверки подписи (384, 276). Используйте кривую 
(1) подпись действительна
(2) подпись недействительна
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
57E919643132A2087C3FA94CABBA62D3
Сообщение 1309 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {4,6,11,22,45,90,181}, m=360 и n=79. В ответе укажите исходное сообщение.
Провести первый раунд зашифрования открытого текста B89F F9A1 C5A5 8C39 шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок 
Зашифруйте открытый текст АБЕРРАЦИЯ с помощью алфавита, приведенного в
таблице
, используйте открытый ключ B=(56, 419), значения случайных чисел
для букв открытого текста k: 16, 2, 17, 19, 8, 4, 3, 2, 8, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
(1) {(72, 254), (218, 601)}; {(188, 93), (86, 726)}; {(440, 539), (334, 226)};
{(568, 355), (251, 245)}; {(346, 242), (228, 480)}; {(16, 416), (6, 533)};
{(56, 419), (320, 7)}; {(188, 93), (138, 453)}; {(346, 242), (192, 719)}
(2) {(440, 539), (334, 226)}; {(72, 254), (218, 601)}; {(188, 93), (86, 726)};
{(568, 355), (251, 245)}; {(346, 242), (228, 480)}; {(16, 416), (6, 533)};
{(56, 419), (320, 7)}; {(188, 93), (138, 453)}; {(346, 242), (192, 719)}
(3) {(188, 93), (86, 726)}; {(440, 539), (334, 226)}; {(72, 254), (218, 601)};
{(568, 355), (251, 245)}; {(346, 242), (228, 480)}; {(16, 416), (6, 533)};
{(56, 419), (320, 7)}; {(188, 93), (138, 453)}; {(346, 242), (192, 719)}
(4) {(16, 416), (6, 533)}; {(72, 254), (218, 601)}; {(188, 93), (86, 726)};
{(568, 355), (251, 245)}; {(346, 242), (228, 480)}; {(440, 539), (334, 226)};
{(56, 419), (320, 7)}; {(188, 93), (138, 453)}; {(346, 242), (192, 719)}
С помощью 
Вычислить динамическое расстояние порядка 1 булевой функции 01010100 от 3 переменных
Даны точки P(69, 510), Q(62, 372), R(74, 170) на кривой 

Дан шифртекст, показанный ниже. Зная секретный ключ 
и генерирующая точка G = (-1, 1)).
| Шифртекст |
|---|
| {(16, 416), (726, 608)}; {(188, 93), (395, 337)}; |
| {(440, 539), (163, 513)}; {(188, 93), (269, 187)}; |
| {(725, 195), (177, 562)}; {(188, 93), (115, 509)}; |
| {(188, 93), (734, 170)}; {(745, 210), (110, 622)}; |
| {(179, 275), (576, 286)}; {(188, 93), (325, 297)} |
Дана точка P(58, 139) на кривой 

Вычислить нелинейность булевой функции 01010100 от 3 переменных
Вычислить нелинейность блока замен 2 10 7 6 3 5 15 4 12 8 14 0 9 11 13 1 размерностью 
Вычислить динамическое расстояние порядка (2,2) блока замен 2 10 7 6 3 5 15 4 12 8 14 0 9 11 13 1 размерностью 
Найти корреляционную матрицу блока замен 2 10 7 6 3 5 15 4 12 8 14 0 9 11 13 1 размерностью 
(1)
begin{matrix}
-0.25 & -0.25 & -0.25 & 0.25 &
0 & 0 & 0.5 & -0.25 &
0.75 & -0.25 & 0 & 0 &
0 & -0.5 & -0.25 & 0.5 &
end{matrix}
(2)
begin{matrix}
-0.25 & -0.25 & -0.25 & -0.25 &
0 & 0 & 0.5 & -0.25 &
0.75 & -0.25 & 0 & 0 &
0 & -0.5 & -0.25 & 0.5 &
end{matrix}
(3)
begin{matrix}
-0.25 & -0.25 & -0.25 & -0.25 &
0 & 0 & 0.5 & -0.25 &
0.75 & -0.25 & 0 & 0 &
0 & -0.5 & -0.25 & -0.5 &
end{matrix}
(4)
begin{matrix}
-0.25 & -0.25 & -0.25 & -0.25 &
0 & 0 & 0.5 & -0.25 &
0.75 & -0.25 & 0 & 0 &
0 & -0.5 & 0.25 & 0.5 &
end{matrix}
Провести операцию SubBytes алгоритма AES со значением байта F0.
Провести операцию MixColumns над приведенным ниже столбцом состояния
Проверьте подлинность ЭЦП (11, 11) для сообщения с известным значением хэш-свертки 9, зная открытый ключ проверки подписи (416, 696). Используйте кривую 
(1) подпись действительна
(2) подпись недействительна
Провести один раунд зашифрования AES над входным состоянием S с помощью раундового ключа K, после чего расшфровать и получить открытый текст.
| S: |
|
K: |
|
BAF83884CBF1188C4BB1807E5B99C3B7
Сообщение 792 (шифротекст) зашифровано с помощью шифра на основе проблемы рюкзака. Расшифровать его с помощью закрытого ключа — {1,7,9,19,37,75,152}, m=307 и n=63. В ответе укажите исходное сообщение.
Провести первый раунд зашифрования открытого текста D12F 992B B2AD C9BA шифром IDEA с заданным ключом K = 6B43 28AB 8F99 3E1E 4363 1CDB 362C 5C1F. Ключ и открытый текст задаются шестнадцатеричными последовательностями. Каждые четыре последовательных шестнадцатеричных разряда WXYZ обозначают 16-битный блок 
Зашифруйте открытый текст БЕЛИБЕРДА с помощью алфавита, приведенного в
таблице
, используйте открытый ключ B=(286, 136), значения случайных чисел
для букв открытого текста k: 2, 9, 18, 2, 19, 4, 5, 11, 9, кривую E751(-1,1) и генерирующую точку G = (0, 1)).
(1) {(188, 93), (557, 28)}; {(489, 468), (589, 429)}; {(618, 206), (229, 151)};
{(188, 93), (13, 617)}; {(568, 355), (324, 128)}; {(16, 416), (307, 693)};
{(425, 663), (269, 187)}; {(179, 275), (177, 189)}; {(568, 355), (266, 91)}
(2) {(618, 206), (229, 151)}; {(188, 93), (557, 28)}; {(489, 468), (589, 429)};
{(188, 93), (13, 617)}; {(568, 355), (324, 128)}; {(16, 416), (307, 693)};
{(425, 663), (269, 187)}; {(179, 275), (177, 189)}; {(568, 355), (266, 91)}
(3) {(489, 468), (589, 429)}; {(188, 93), (557, 28)}; {(618, 206), (229, 151)};
{(188, 93), (13, 617)}; {(568, 355), (324, 128)}; {(16, 416), (307, 693)};
{(425, 663), (269, 187)}; {(179, 275), (177, 189)}; {(568, 355), (266, 91)}
(4) {(16, 416), (307, 693)}; {(489, 468), (589, 429)}; {(618, 206), (229, 151)};
{(188, 93), (13, 617)}; {(568, 355), (324, 128)}; {(188, 93), (557, 28)};
{(425, 663), (269, 187)}; {(179, 275), (177, 189)}; {(568, 355), (266, 91)}
Провести операцию MixColumns над приведенным ниже столбцом состояния
Провести операцию MixColumns над приведенным ниже столбцом состояния
Что такое криптографические методы защиты информации
Определение
Криптография — это наука о способах конфиденциальности и подлинности информации.
Криптографические методы преобразования данных являются самыми надежными в сфере информационной безопасности.
Криптография составляет целую систему методов, которые направлены на видоизменение персональных данных, чтобы сделать их бесполезными для злоумышленников.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Способы криптографического шифрования позволяют решить две ключевые задачи:
- обеспечение секретности;
- защита целостности информации.
Виды криптографической защиты информации
Классификация криптографических методов преобразования информации по типу воздействия на исходные данные включает следующие виды:
- шифрование;
- стенография;
- кодирование;
- сжатие.
Шифрование
Шифрование предполагает видоизменение исходника посредством логических, математических, комбинаторных и других операций. В итоге таких преобразований первоначальные данные приобретают вид хаотически расположенных символов (цифр, букв и т.д.) и кодов двоичной системы.
Инструментами создания шифра служат алгоритм преобразования и ключ.
В определенных методах шифрования применяется постоянная преобразовательная последовательность. Ключ включает управляющие данные, определяющие выбор видоизменения на конкретных пунктах алгоритма и размер используемых в ходе шифрования операндов.
Шифрование является основным криптографическим способом видоизменения данных в компьютерах. Чтобы обеспечить эффективную борьбу против криптоатак (атак на шифр, криптоанализа), методы шифрования должны отвечать ряду требований:
- Криптостойкость (стойкость перед криптоанализом), позволяющая вскрыть шифр лишь через полный перебор ключей.
- Стойкость шифра благодаря конфиденциальности ключа, а не алгоритма преобразования.
- Соразмерность объемов исходного текста и шифротекста.
- Исключение искажений и потерь данных, последовавших за ошибками в ходе шифрования.
- Небольшое время шифрования.
- Согласованность стоимости шифрования и стоимости исходной информации.
Примечание
Эффективность шифрования определяется криптостойкостью шифра. Единицей измерения этого показателя могут быть: время; стоимость инструментов, необходимых криптоаналитику на расшифровку без знания ключа.
На схеме изображен механизм работы простейшей криптосистемы:
В данной модели отправитель создает открытое исходное сообщение (М), передаваемое законному адресату по незащищённому каналу. Канал находится под контролем злоумышленника, который стремится перехватить сообщение и рассекретить его. Чтобы перехватчик не смог расшифровать передаваемые данные, отправитель защищает его посредством обратимого преобразования (Ек(С)), после чего получает шифротекст (С). Его он отправляет получателю. Адресат принимает зашифрованный текст, раскрывает засекреченное сообщение с помощью дешифровщика (Dк(С)) и получает исходный текст (М).
Ек — один из алгоритмов преобразования, К — это критпографический ключ, который определяет выбор алгоритма, подходящего для конкретного шифрования.
Выделяют два вида шифрования:
- Симметричное: с использованием одного криптографического ключа.
- Асимметричное: с открытым ключом.
Стенография
Этот метод, единственный среди криптографических способов, позволяет скрыть не только информацию, но и сам факт ее хранения и передачи. В основе стенографии лежит маскирование секретных данных среди общедоступных файлов. Иными словами, закрытая информация скрывается, а вместо нее создаются дубликаты.
Кодирование
Преобразование данных по этой методике происходит по принципу замещения слов и предложений исходника кодами. Закодированные данные могут выглядеть как буквенные, цифровые или буквенно-цифровые комбинации. Для кодирования и раскодирования применяют специальные словари или таблицы.
Рассматриваемый метод удобно использовать в системах с небольшим набором смысловых конструкций. Недостаток кодирования заключается в том, что необходимо хранить и распространять кодировочные таблица, а также достаточно часто их менять во избежание нежелательного рассекречивания информации.
Сжатие
Данный способ представляет собой сокращение объема исходной информации. Понятие сжатия относят к криптографическим с некоторыми оговорками. С одной стороны, сжатые данные требуют обратного преобразования для возможности их прочтения. С другой стороны, средства сжатия и обратного преобразования общедоступны, поэтому этот способ не является надежным в части защиты информации.
Используемые методы технологии
На сегодняшний день широкое применение получили следующие алгоритмы шифрования: Data Encryption Standard (DES), 3DES и International Data Encryption Algorithm (IDEA).
Характерной чертой данных преобразовательных стандартов является блочная шифровка информации по 64 бита. В случае, когда объем передаваемого сообщения больше 64 бит, его нужно разбить на блоки, каждый из которых содержит 64 бита. Далее все образовавшиеся блоки сводятся воедино одним из следующих способов:
- электронная кодовая книга (ECB);
- цепочка из зашифрованных блоков (CBC);
- x-битовая зашифрованная обратная связь (CFB-x);
- выходная обратная связь (OFB).
Алгоритм 3DES создан на базе DES, чтобы устранить основной недостаток последнего — возможность взлома ключа посредством перебора из-за его малой длины в 54 бит. Несмотря на то, что 3DES в три раза менее производителен, чем его предшественник, криптостойкость первого значительно выше DES.
Преобразовательный стандарт Advanced Encryption Standard (AES) или Rijndael использует в процессе создания шифров 128-битные, 192-битные или 256-битные ключи. Информационные сообщения шифруются блоками по 128 бит.
Сертифицированные криптографические средства защиты информации в России
Сертификацией средств защиты информации занимается Федеральная служба безопасности России. Криптографические СЗИ определены в следующие классы:
- КС1;
- КС2;
- КС3;
- КВ;
- КА.
Класс КС1
Средства этого класса могут оказывать сопротивление внешним атакам, которые реализуются методами, неизвестными криптоаналитикам. Данные о системах, использующих средства класса КС1 находятся в общем доступе.
Класс КС2
К рассматриваемой категории относятся криптографические инструменты защиты данных, способные препятствовать атакам за пределами зоны контроля, блокируемым СЗИ класса КС1. При этом атакующие могли получить информацию о физических мерах безопасности данных и пр.
Класс КС3
Средства этой категории могут противодействовать атакам, имея физический доступ к компьютерным системам с установленными криптографическими методами защиты.
КВ1 и КВ2
Средства группы КВ обладают свойством сопротивления атакам, созданным криптоаналитиками и прошедшим лабораторные испытания.
Класс КА
Инструменты данного класса способны защитить от атак, которые разрабатывались с применением знаний о недокументированных возможностях вычислительных систем и конструкторской документацией, а также с доступом к любым компонентам СЗИ.


 , построить контрольную сумму для сообщения 1101000001101110011110000.
, построить контрольную сумму для сообщения 1101000001101110011110000. бит
бит и генерирующую точку G = (562, 89) порядка n = 13
и генерирующую точку G = (562, 89) порядка n = 13 и генерирующая точку G = (318, 660) порядка n = 251.
и генерирующая точку G = (318, 660) порядка n = 251. -алгоритма Полларда найти наибольший нетривиальный делитель числа 3007.
-алгоритма Полларда найти наибольший нетривиальный делитель числа 3007.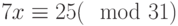 с помощью цепных дробей.
с помощью цепных дробей. ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.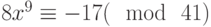 с помощью индексов.
с помощью индексов. на 45.
на 45.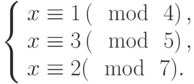
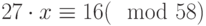 .
.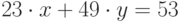 . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)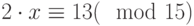 .
.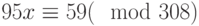 с помощью цепных дробей.
с помощью цепных дробей.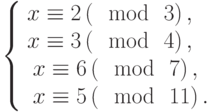
 с помощью индексов. (В качестве ответа введите наименьшее значение x.)
с помощью индексов. (В качестве ответа введите наименьшее значение x.) на 13.
на 13. при a = 5124; b = 129; c = 59466.
при a = 5124; b = 129; c = 59466.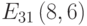 порядка 25.
порядка 25.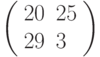 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33. .
. , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая 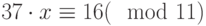 .
.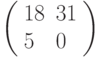 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.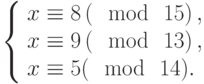
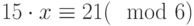 . (В качестве ответа введите наименьшее значение x.)
. (В качестве ответа введите наименьшее значение x.) порядка 38.
порядка 38. , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая 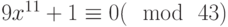 с помощью индексов.
с помощью индексов.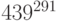 на 60.
на 60. . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)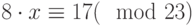 .
.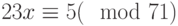 с помощью цепных дробей.
с помощью цепных дробей.
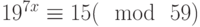 с помощью индексов. (В качестве ответа введите наименьшее значение x.)
с помощью индексов. (В качестве ответа введите наименьшее значение x.) на 100.
на 100.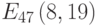 порядка 55.
порядка 55. ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33. , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая 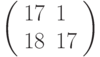 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.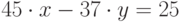 . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)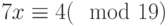 с помощью цепных дробей.
с помощью цепных дробей.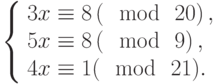
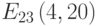 порядка 28.
порядка 28. ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33. , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая 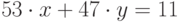 . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.) на 35.
на 35.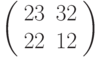 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.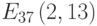 порядка 44.
порядка 44.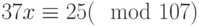 с помощью цепных дробей.
с помощью цепных дробей.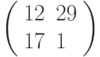 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.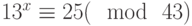 с помощью индексов. (В качестве ответа введите наименьшее значение x.)
с помощью индексов. (В качестве ответа введите наименьшее значение x.) , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  порядка 28.
порядка 28. .
. на 7.
на 7.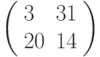 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.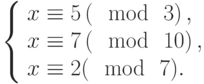
 , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая 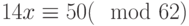 с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)
с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)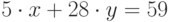 . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.) .
.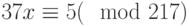 с помощью цепных дробей.
с помощью цепных дробей.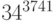 на 2.
на 2. порядка 38.
порядка 38.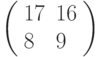 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33. , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая 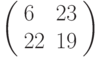 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33. , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая 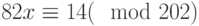 с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)
с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.) с помощью индексов.
с помощью индексов.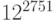 на 5.
на 5. .
.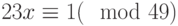 с помощью цепных дробей.
с помощью цепных дробей.
 на 100.
на 100.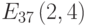 порядка 42.
порядка 42.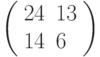 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33. , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая 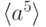 ?
?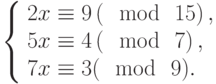
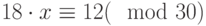 . (В качестве ответа введите наименьшее значение x.)
. (В качестве ответа введите наименьшее значение x.)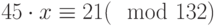 . (В качестве ответа введите наименьшее значение x.)
. (В качестве ответа введите наименьшее значение x.)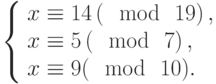
 на 14.
на 14.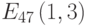 порядка 54.
порядка 54. , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая 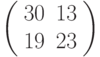 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.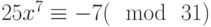 с помощью индексов.
с помощью индексов.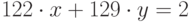 . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)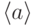 порядка 6656 содержится фиксированный элемент порядка 2?
порядка 6656 содержится фиксированный элемент порядка 2?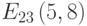 порядка 32.
порядка 32. . (В качестве ответа введите наименьшее значение x.)
. (В качестве ответа введите наименьшее значение x.) с помощью цепных дробей.
с помощью цепных дробей.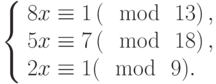
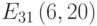 порядка 32.
порядка 32.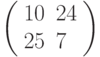 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33. , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая 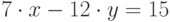 . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)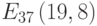 порядка 36.
порядка 36.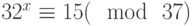 с помощью индексов.
с помощью индексов.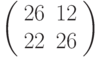 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33. . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)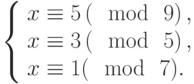
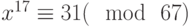 с помощью индексов.
с помощью индексов. , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  порядка 40.
порядка 40.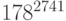 на 22.
на 22.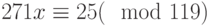 с помощью цепных дробей.
с помощью цепных дробей.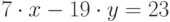 . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)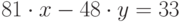 . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)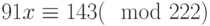 с помощью цепных дробей.
с помощью цепных дробей.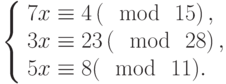
 с помощью индексов. (В качестве ответа введите наименьшее значение x.)
с помощью индексов. (В качестве ответа введите наименьшее значение x.)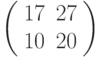 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33. , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая 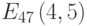 порядка 48.
порядка 48.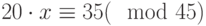 . (В качестве ответа введите наименьшее значение x.)
. (В качестве ответа введите наименьшее значение x.)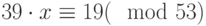 .
.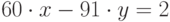 . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)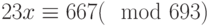 с помощью цепных дробей.
с помощью цепных дробей.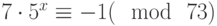 с помощью индексов.
с помощью индексов. на 11.
на 11.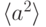 ?
?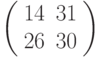 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33. , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  с помощью индексов.
с помощью индексов.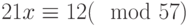 с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)
с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)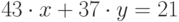 . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.) на 11.
на 11.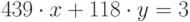 . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)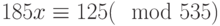 с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)
с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)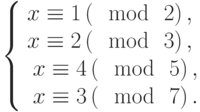
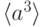 ?
?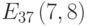 порядка 40.
порядка 40.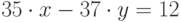 . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.) , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая 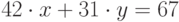 . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)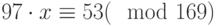 .
.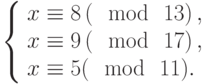
 на 12.
на 12. , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая 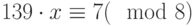 .
.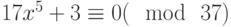 с помощью индексов.
с помощью индексов.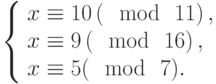
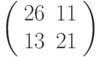 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33. , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая 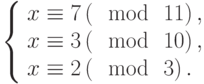
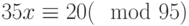 с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)
с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)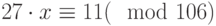 .
.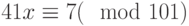 с помощью цепных дробей.
с помощью цепных дробей. на 1000.
на 1000. , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая  порядка 33.
порядка 33.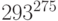 на 48.
на 48. . (В качестве ответа введите наименьшее значение x.)
. (В качестве ответа введите наименьшее значение x.)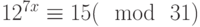 с помощью индексов.
с помощью индексов. на 13.
на 13.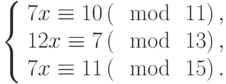
 на 11.
на 11.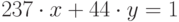 . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)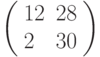 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.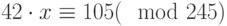 . (В качестве ответа введите наименьшее значение x.)
. (В качестве ответа введите наименьшее значение x.)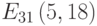 порядка 30.
порядка 30.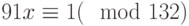 с помощью цепных дробей.
с помощью цепных дробей.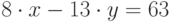 . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)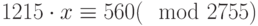 . (В качестве ответа введите наименьшее значение x.)
. (В качестве ответа введите наименьшее значение x.) на 5.
на 5.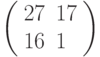 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.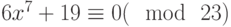 с помощью индексов.
с помощью индексов. .
.
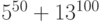 на 18.
на 18.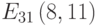 порядка 36.
порядка 36.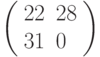 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.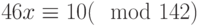 с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)
с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)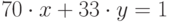 . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.) . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.) с помощью цепных дробей.
с помощью цепных дробей. с помощью индексов.
с помощью индексов.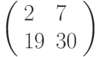 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33. с помощью индексов.
с помощью индексов.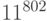 на 1000.
на 1000.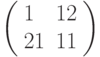 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33.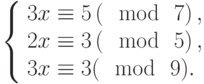
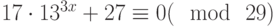 с помощью индексов. (В качестве ответа введите наименьшее значение x.)
с помощью индексов. (В качестве ответа введите наименьшее значение x.)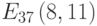 порядка 32.
порядка 32.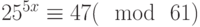 с помощью индексов. (В качестве ответа введите наименьшее значение x.)
с помощью индексов. (В качестве ответа введите наименьшее значение x.) с помощью индексов.
с помощью индексов.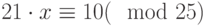 .
.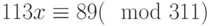 с помощью цепных дробей.
с помощью цепных дробей.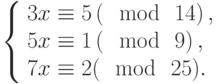
 . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)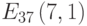 порядка 44.
порядка 44. на 7.
на 7.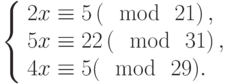
 , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая 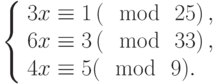
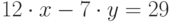 . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.) на 7.
на 7.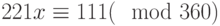 с помощью цепных дробей.
с помощью цепных дробей. , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая 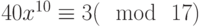 с помощью индексов. (В качестве ответа введите наименьшее значение x.)
с помощью индексов. (В качестве ответа введите наименьшее значение x.)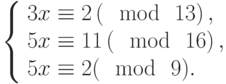
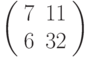 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33. на 14.
на 14.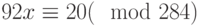 с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)
с помощью цепных дробей. (В качестве ответа введите наименьшее значение x.)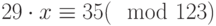 .
.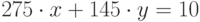 . (В качестве ответа введите значение x.)
. (В качестве ответа введите значение x.)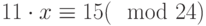 .
.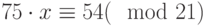 . (В качестве ответа введите наименьшее значение x.)
. (В качестве ответа введите наименьшее значение x.) , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая 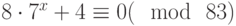 с помощью индексов. (В качестве ответа введите наименьшее значение x.)
с помощью индексов. (В качестве ответа введите наименьшее значение x.) .
.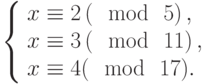
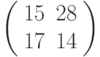 ; вычисления проводить по модулю 33.
; вычисления проводить по модулю 33. , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая 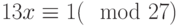 с помощью цепных дробей.
с помощью цепных дробей.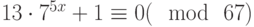 с помощью индексов.
с помощью индексов. , найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая
, найдите открытый текст с помощью алфавита, приведенного в таблице (используется кривая 