Л2ш примеры вступительных экзаменов - Помощь в подготовке к экзаменам и поступлению

Лицей «Вторая школа» — Главная страница

Примеры вступительных испытаний

: Создано: 03 января 2008

Для успешной сдачи письменного зачета по математике необходимо освоить следующие темы в рамках обычной школьной программы

в 6 класс – темы
в 7 класс – темы
в 8 класс – темы

Устные задания по математике

вариант прошлых лет (в формате PDF)
задачи устного зачёта в конкурсе ВМШ

Письменные задания прошлых лет (в формате Microsoft Word).

По математике

в 6 класс и ещё один в 6 класс
в 7 класс
в 8 класс
в 9 класс
в 10 класс

По русскому языку

в 6 класс
в 7 класс
в 8 и 9 классы

По физике

Программы по физике

в 8 класс
в 9 класс
в 10 класс

Источник

Примеры вступительных испытаний

Печать
E-mail

Информация о материале: Создано: 03 января 2008

в 6 класс – темы
в 7 класс – темы
в 8 класс – темы

Устные задания по математике

вариант прошлых лет (в формате PDF)
задачи устного зачёта в конкурсе ВМШ

Письменные задания прошлых лет (в формате Microsoft Word).

По математике

в 6 класс и ещё один в 6 класс
в 7 класс
в 8 класс
в 9 класс
в 10 класс

По русскому языку

в 6 класс
в 7 класс
в 8 и 9 классы

По физике

Программы по физике

в 8 класс
в 9 класс
в 10 класс

Источник

Поступление в Лицей «Вторая Школа»

№1. Сумма. Найдите число, равное сумме сорока одной тысячи, сорока одной сотни, сорока одного десятка и сорока одной единицы.
№2. Масштаб. На карте указан масштаб: в 1 см на карте 150000 см на местности. Расстояние между пунктами 6 см. Сколько это километров на местности?
№3. Пенсия. У бабушки в запасе 20 тысяч рублей. Каждый месяц она тратит 15 тысяч рублей и получает пенсию 13 тысяч рублей. Сколько месяцев бабушка сможет тратить по 15 тысяч рублей?
№4. Папа. Сыну 13 лет. Папа говорит ему: «Когда ты дорастешь до моего нынешнего возраста, мне будет 69 лет». Сколько сейчас лет папе?
№5. Коробка. Коробка имеет форму прямоугольного параллелепипеда, длина. Ширина и высота которой – 8 дм, 5 дм и 6 дм. Найдите площадь поверхности коробки (все 6 граней) в дм2.
№6. Покупка. Миша купил 6 йогуртов и 5 сырков. Йогурт дороже сырка на 5 рублей. Миша заплатил за покупку 250 рублей. Сколько стоит 1 сырок?
№7. Уголком. Число 11…1 (двести единиц) поделили на число 11…11 (десять единиц). Сколько цифр получилось в частном?
№8. Площади. Квадрат со стороной 6 см и прямоугольник со стороной 1 мм имеют равные площади. Найдите вторую сторону прямоугольника в см.
№9. Домашка. Ученик потратил на домашнее задание по математике в 2 раза больше времени, чем на д/з по географии, а на д/з по географии в 2 раза больше времени, чем на д/з по литературе. Всего он потратил на эти предметы 2 часа и 20 минут. Сколько минут он потратил на домашнее задание по географии?
№10. Шаги: Тима и Леша шли рядом. Пока Тима делал 5 шагов, Леша делал 4 шага. Шагомеры показали, что Тима сделал на 600 шагов больше Леши. Сколько шагов сделал Тима?
№11. Кубик. Кубик с ребром 8 см сложили из кубиков с ребром 2 см, его поверхность покрасили (все грани). Сколько маленьких кубиков, у которых окрашена ровно одна грань?
№12. Роботы. 3 робота за 3 дня собирают 16 компьютеров. Сколько компьютеров соберут 6 роботов за 6 дней?
№13. Этаж. Саша живет на 12-этажном доме в квартире № 753. Все подъезды одинаковые, на каждом этаже, начиная с первого, по 6 квартир. В каком подъезде живет Саша?
№14. Поля. Чтобы засеять поле размером 50 м на 60 м нужно 90 кг семян. Сколько понадобится семян (кг), чтобы засеять поле размером 140 м на 60 м?
№15. Проценты. В классе девочек 20 %. Каждой девочке дали 4 конфеты, а каждому мальчику – 3 конфеты. Сколько процентов от всех конфет получили девочки?
№16. Гномы. За круглым столом сидят 12 гномов. Каждый из них сказал: «Справа от меня среди ближайших двоих соседей один правдивый и один лжец». Сколько лжецов сидит за столом , если не все гномы – лжецы?

Источник

Поступление во Вторую школу

Примеры и задачи из школьной программы30%

Олимпиадная математика80%

В 2019-2020 году лицей Вторая школа (или Л2Ш) набирал 3 шестых класса и 2 седьмых класса. В старшие классы был только добор на освободившиеся места. Специализации классов нет – они все математические. Конкурс при поступлении в Вторую школу оценить сложно, списки участников не публикуются. По некоторым оценкам речь идет о 9 – 12 человек на место. Такой относительно «небольшой» конкурс объясняется тем, что много соискателей отказываются от поступления еще на этапе подготовки, когда понимают, что задачи устного экзамена им не по плечу. Отличительная особенность Л2Ш – близкое соотношение в наборе девочек и мальчиков, что нетипично для физматшкол.

3 вступительных экзамена: математика письменно, математика устно и диктант. Письменная математика состоит из 16 – 20 коротких задач, не требующих развернутого решения. Задачи по школьной программе, но с «изюминками». Зачет получат те, у кого не более двух серьезных проблем. Серьезная проблема – не решил задачу или совсем неправильно решил. Легкая проблема – ошибка в вычислениях при правильном решении, не правильно записал ответ, 2 легких проблемы равно 1 серьезная. На экзамен дается полтора часа.

Устная математика – 10 олимпиадных задач возрастающей сложности, задачи во второй пятерке – высокого уровня. Продолжительность экзамена – два часа. В 2019 году действовало правило – если не сдал три задачи за первый час, то до свидания.

По русскому проводится диктант средней сложности на 45 минут.

Поступление во Вторую школу организовано так (в 2020 году все иначе по понятным причинам): где-то с середины марта каждую неделю – все три экзамена, и так до конца мая. Сдавать можно в разные недели, но только в определенном порядке – письменная математика, потом устная математика, и наконец диктант. Такой порядок проведения вступительных испытаний удобен для соискателей, позволяет разнести экзамены во времени, не переживать в случае болезни или других форс-мажоров.

За каждый экзамен ставится не оценка и не баллы, а просто зачет или не зачет, зачет дает допуск к следующему этапу. При незачете дается еще одна попытка, но критерии на зачет будут жестче. Для письменной математики и диктанта критерии зачета известны заранее, с устной математикой не все так прозрачно, результат зависит от сложности решаемых задач. В один день кто-то может получить зачет с 4 задачами, а в другой – остаться без зачета с 6. Поступающих, решивших более 8 задач на устном – единицы. Результаты объявляют в течение 2-3 дней.

Интересно, что задачи по устной математике для 6 и 7 класса одинаковые. В 7 класс может быть (а может и не быть) более высокий балл для зачета.

После получения всех зачетов остается только пройти тест психологов (не влияет на поступление) и томительно ждать результатов до июня, так как поступят не все зачетники. Кто именно – решает приемная комиссия в закрытом режиме. Наибольший вес имеют результаты устного экзамена.

Вторая школа – бесспорный гранд физмат образования Москвы. Поступить во Вторую школу – мечта многих.

Удобное расписание приемных экзаменов

Устная олимпиадная математика – главный критерий

Варианты вступительных экзаменов во Вторую школу

Только реальные варианты прошлых лет, никаких пробников

Вступительный экзамен Вторая школа — математика письменно 6 класс — 2019 — 2

Вступительный экзамен Вторая школа — математика письменно 6 класс — 2019 — 1

Вступительный экзамен Вторая школа — математика устно 6 класс — 2019 — 1

Вступительный экзамен Вторая школа — математика устно 6 класс — 2018 — 1

Источник

Канал в Telegram (главные объявления): https://telegram.me/matolimp
Канал в Telegram с архивом рекламных объявлений Ярмарок: https://telegram.me/matolimp_market
Группы (чаты) matolimp в Telegram (там можно задавать вопросы, отвечать на вопросы, читать ответы других):
Чат про начальную школу (кроме вопроса поступления в 5 класс): https://t.me/matolimp04
Чат matolimp для поступающих в 5 класс: https://t.me/matolimp5
Чат matolimp для 5-7 классов: https://t.me/matolimp57
Чат matolimp для 8-11 классов: https://t.me/matolimp811
Чат matolimp про математику на английском: https://t.me/matolimp_eng
Чат matolimp для прочих вопросов: https://t.me/matolimp_chat
Матолимп в Инстаграме: https://www.instagram.com/matolimp/
Матолимп в Facebook: https://www.facebook.com/matolimp

Актуальную информацию 2022 года можно найти на сайте школы:
Официальный сайт: https://lycuz2.mskobr.ru/
Неофициальный сайт: https://sch2.ru/
Положение о приёме в 2022 году: https://t.me/matolimp/1205

Итоги приёмной кампании в 2020 году

Для подготовки к письменному экзамену может быть полезно ознакомиться с реальными вариантами экзаменов прошлых лет, но ещё полезнее занятия.

Варианты экзаменов (письменная математика) 2021 года в 6-7 классы:
https://t.me/matolimp/640
https://t.me/matolimp/671
https://t.me/matolimp/758
https://t.me/matolimp/751
https://t.me/matolimp/736
Варианты экзаменов (письменная математика) 2021 года в 8 класс:
https://t.me/matolimp/645
https://t.me/matolimp/775
Варианты экзаменов (устная математика) 2021 года в 6-7 классы:
https://t.me/matolimp/763
https://t.me/matolimp/715

Вступительные испытания в 6-7 класс лицея «Вторая школа» в 2020 году.
https://t.me/matolimp/306 27 марта 2020
https://t.me/matolimp/308 3 апреля 2020
https://t.me/matolimp/313 14 апреля 2020
https://t.me/matolimp/321 8 мая 2020

Задания прошлых лет, в т.ч. варианты письменного зачёта и архив задач конкурса ВМШ:
https://t.me/matolimp/216

Задания устного зачёта в 2020 году:
27 марта 2020 года
3 апреля 2020 года
14 апреля 2020 года
8 мая 2020 года

Варианты письменного зачёта:

—

Кроме того для подготовки к устному зачёту полезно порешать задачи конкурса ВМШ текущего года https://sch2.ru/vmsh/3023-2018-10-24-konkurs-vmsh

и задачи прошлых лет (с сайта их удалили, можно воспользоваться сервисом archive.org или аналогичными):

 http://sch2.ru/content/view/2205/81/2014-2015 для 3-4 и 5-9 классов

http://sch2.ru/content/view/1764/9/

2013-2014 для 3-4 и 5-7 классов

http://sch2.ru/content/view/1345/9/

И обязательно приходите на занятия!

Источник

Физико-математический лицей «Вторая школа» — это достаточно сильное образовательное учреждение г. Москвы. Поток желающих обучаться в этом лицее традиционно очень высок. Но поступить в него удаётся далеко не каждому абитуриенту, поскольку для этого требуется сдать вступительные экзамены. На сайте учебного заведения приведены примеры заданий вступительного экзамена по математике для 10 класса (устной и письменной части). В данной статье предлагаю вашему вниманию разбор предложенных заданий. Оцените их сложность, чтобы узнать, насколько вы готовы к сдаче вступительного экзамена в Московскую физико-математическую школу №2 (Государственный лицей «Вторая школа»).

Задания письменной части вступительного экзамена в лицей «Вторая школа»

1. Упростите выражение:

$[ left(frac{sqrt{a}}{sqrt{a}-2}-frac{a-4sqrt{a}+2}{3sqrt{a}-a-2}right)cdot frac{1-a}{2-sqrt{16a}}. ]$

Введём замену и представим выражение в виде:

$[ left(frac{x}{x-2}+frac{x^2-4x+2}{(x-2)(x-1)}right)cdotfrac{(1-x)(1+x)}{2(1-2x)}. ]$

Далее, используя стандартные правила преобразования выражений, получаем:

$[ frac{(x-2)(2x-1)}{(x-2)(x-3)}cdotfrac{(x-1)(1+x)}{2(2x-1)} = frac{1+x}{2}. ]$

Итак, окончательный ответ: $frac{1}{2}left(1+sqrt{a}right)$ .

2. Решите неравенство:

a) Заметим сразу, что для неравенство не выполняется.

б) Для оно равносильно следующему:

$[ x^2-11x+30>0Leftrightarrow left[ begin{array}{l} x > 6 \ x < 5. end{array} ]$

То есть с учётом условия в данном случае получаем: .

в) Для неравенство равносильно следующему:

То есть с учётом условия получаем в этом случае: .

Итак, окончательно получаем: .

3. Решить уравнение:

$[ frac{3x^2-|2x+3|+2}{3|x|-1} = 0. ]$

Область допустимых решений уравнения составляют все действительные числа, кроме тех, что удовлетворяют уравнению:

$[ 3|x|-1 = 0Leftrightarrow x = pmfrac{1}{3}. ]$

В области допустимых значений данное уравнение равносильно следующему:

а) Для $xgeqslant -frac{3}{2}$ получаем:

$[ 3x^2-2x-1 = 0Leftrightarrow left[begin{array}{l} x = -frac{1}{3} \ x = 1 end{array} ]$

Оба значения входят в указанный промежуток. Однако, корень $x = -frac{1}{3}$ не входит в область допустимых значений исходного уравнения.

б) Для $x<-frac{3}{2}$ получаем:

У последнего уравнения решений нет, поскольку его дискриминант отрицателен.

Итак, .

4. Решить графически систему уравнений:

$[ begin{cases} xy = 4 \ y^2 = x+2. end{cases} ]$

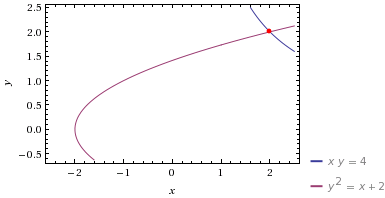
Геометрическим местом точек, удовлетворяющих условию , является гипербола. Геометрическим местом точек, удовлетворяющих условию , — парабола с вершиной в точке и ветвями, направленными вправо. Изобразим их на одном координатном поле:

Видно, что решением предложенной системы уравнений является пара .

а) Упростим первое выражение, воспользовавшись формулой преобразования произведения косинусов в сумму:

$[ cosleft(frac{pi}{4}-2alpharight)cosleft(frac{5pi}{4}+2alpharight) = ]$

$[ = frac{1}{2}left(cosfrac{3pi}{2}+cos(pi+4alpha)right) = -frac{1}{2}cos 4alpha. ]$

б) Второе выражение преобразуем, используя формулы приведения и понижения степени:

$[ -cos^22alpha - frac{-1-cos 4alpha}{2} = aLeftrightarrow cos 4alpha = -2a-1. ]$

в) Итак, окончательно получаем: $-frac{1}{2}(-2a-1)=a+frac{1}{2}$ .

6. В геометрической прогрессии первый, третий и пятый члены равны соответственно первому, четвёртому и шестнадцатому члену некоторой арифметической прогрессии. Найти пятый член арифметической прогрессии, если первый её член равен 5.

Пусть разность арифметической прогрессии равна , а знаменатель геометрической прогрессии равен . Тогда первый, третий и пятый члены геометрической прогрессии, а также первый, четвёртый и шестнадцатый члены арифметической прогрессии будут равны соответственно:

$[ begin{array}{l} 5,, 5q^2,, 5q^4 \ 5,, 5+3d,, 5+15d end{array} ]$

Тогда имеет место следующая система уравнений:

$[ begin{cases} 5q^2 = 5+3d \ 5q^4 = 5+15 d end{cases}Rightarrow q^4-5q^2+4=0Leftrightarrow ]$

$[ left[ begin{array}{l} begin{cases} d = 0 \ q^2 = 1 end{cases}\ begin{cases} d = 5 \ q^2 = 4 end{cases} end{array} ]$

В первом тривиальном случае пятый член арифметической прогрессии равен её первому члену, то есть 5. Во втором случае пятый член арифметической прогрессии равен 25.

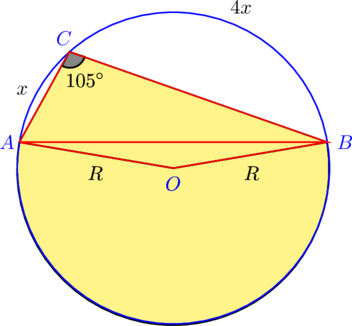
7. Из точки C окружности проведены две хорды CA и CB так, что $angle ACB=105^{circ}$ , а дуга CB, не содержащая точки A, в четыре раза длиннее, чем дуга AC, не содержащая точки B. Найти площадь фигуры, ограниченной этими хордами и дугой AB, не содержащей точки C, если радиус круга равен R.

Искомая фигура состоит из трёх частей: треугольника ABC, треугольника ABO и сектора с вершиной O и дугой AB, не содержащей точки C. Найдём последовательно площади всех трёх фигур и сложим их, чтобы получить ответ.

а) Ищем площадь сектора. Вписанный угол ACB опирается на дугу AB, не содержащую точку C, градусная мера которой равна, соответственно, $2angle ACB = 210^{circ}$ . Центральный угол AOB, опирающийся на эту дугу также равен $210^{circ}$ . Тогда искомая площадь сектора равна:

$[ S_1 = pi R^2cdot {frac{210^{circ}}{360^{circ}}} = frac{7}{12}pi R^2. ]$

б) Ищем площадь треугольника AOB. Меньший угол AOB равен $150^{circ}$ . Треугольник равнобедренный с боковым сторонами, которые равны радиусу окружности. Следовательно, его площадь равна:

$[ S_2 = frac{1}{2}R^2sin 150^{circ} = frac{1}{4}R^2. ]$

в) Ищем площадь треугольника ACB. По условию дуга CB, не содержащая точки A, в четыре раза длиннее, чем дуга AC, не содержащая точки B. Градусная мера полной окружности равна $360^{circ}$ . Поэтому имеет место уравнение:

Отсюда градусные меры малых дуг AC, CB и AB равны $30^{circ}$ , $120^{circ}$ и $150^{circ}$ соответственно.

Ищем неизвестные углы треугольника ABC. Вписанный угол CAB опирается на дугу BC и равен половине её градусной меры, то есть $60^{circ}$ . Аналогично, угол CBA равен $15^{circ}$ .

Сторону AB находим из треугольника AOB по теореме косинусов:

$[ AB = sqrt{2R^2-2R^2cos 150^{circ}} = Rsqrt{2+sqrt{3}}. ]$

С помощью формулы понижения степени можно показать также, что:

$[ sin 15^{circ} = frac{sqrt{2-sqrt{3}}}{2},, cos 15^{circ} = frac{sqrt{2+sqrt{3}}}{2}. ]$

Тогда из теоремы синусов для треугольника ABC получаем:

$[ frac{AB}{sin 105^{circ}} = frac{AC}{sin 15^{circ}}Leftrightarrow AC = ABcdotfrac{sin 15^{circ}}{cos 15^{circ}}. ]$

В последнем преобразовании воспользовались формулой приведения:

$[ sin 105^{circ} = sin(90^{circ}+15^{circ}) = cos 15^{circ}. ]$

То есть получаем:

$[ AC = Rsqrt{2+sqrt{3}}cdotfrac{sqrt{2-sqrt{3}}}{sqrt{2+sqrt{3}}} = = Rsqrt{2-sqrt{3}}. ]$

То есть площадь треугольника ABC равна:

$[ S_3 = frac{1}{2} ACcdot ABsin 60^{circ} = ]$

$[ =frac{sqrt{3}}{4}R^2sqrt{2-sqrt{3}}sqrt{2+sqrt{3}} =frac{sqrt{3}}{4}R^2. ]$

Тогда искомая площадь равна:

$[ S = S_1+S_2+S_3 = frac{(3+3sqrt{3}+7pi)R^2}{12}. ]$

Примечание. Есть способ чуть более короткий и изящный, основанный на использовании формулы площади треугольника через радиус описанной окружности: $S = frac{abc}{4R}$ . Однако, здесь я сознательно его не использовал, поскольку далеко не все школьные учителя знакомят учеников на своих уроках с этой формулой.

Решение некоторых заданий устной части вступительного экзамена в лицей «Вторая школа»

Из школьного курса математики известно, что $frac{22}{7}>pi$ . Поэтому сравним сперва и $frac{22}{7}$ .

Возводим обе части в квадрат и получаем: и $frac{484}{49}$ . Сравниваем тогда и $frac{1}{2}left(frac{484}{49}-5right) = frac{239}{98}$ .

Вновь возводим обе части в квадрат и получаем: и $frac{57121}{9604} = 5frac{9101}{9604}$ . То есть $sqrt{2}+sqrt{3}>frac{22}{7}$ , а значит и .

2. Найдите последнюю цифру числа: $2^{1996}$ .

Ищем закономерность:

, , , , , , , , , $2^{10} = 1024$ и т. д.

Закономерность такова: идут группы по 4 числа, в конце которых в указанном порядке стоят цифры: , , и . Замечаем, что .

Следовательно, будет таких групп чисел. Поэтому последняя цифра последнего числа будет равна .

3. Доказать, что для всех чётных натуральных чисел n число делится на 48.

Поскольку n — четное натуральное число, его можно представить в виде , где k — натуральное число. Тогда представленное выражение принимает вид: . Оно делится на 8. Следовательно, осталось доказать, что выражение делится на 6. Для этого нужно доказать, что оно делится на 2 и на 3.

а) Доказываем делимость на 2. Если k — чётное, то выражение делится на 2. Если k — нечётное, то его можно представить в виде , где Тогда выражение для k принимает вид: . Это выражение также делится на 2.

б) Докажем делимость на 3. Если k делится на 3, то выражение делится на 3. Если k не делится на 3, то его можно представить в виде или , где В первом случае выражение для k принимает вид: . Последнее выражение делится на 3. Во втором случае выражение для k принимает вид: . Последнее выражение также делится на 3.

4. Найдите максимальное и минимальное значение выражения:

$[ frac{2x+1}{x^2+x+1}. ]$

Задача легко решается с помощью такого мощного понятия, как производная функции. Однако, поступающие в 10 класс школьники с этим понятием, к сожалению, не знакомы. Поэтому придётся «изобретать» другое решение.

Заметим сразу, что выражение, стоящее в знаменателе всегда положительно, поскольку коэффициент при положителен, а дискриминант соответствующего квадратного уравнения отрицателен. Заметим также, что выражение принимает отрицательные значения при $x<-frac{1}{2}$ и положительные значения при $x>-frac{1}{2}$ . То есть минимальное значение будет отрицательным, а максимальное значение будет положительным.

а) Ищем максимальное значение. Рассмотрим следующее неравенство с параметром :

$[ frac{2x+1}{x^2+x+1}leqslant a. ]$

Будем искать минимальное значение a, при котором это неравенство выполняется для любых x. Это значение и будет являться максимальным значением данного выражения. Поскольку , то неравенство можно представить в виде:

При последнее неравенство будет выполняться для всех x в том случае, если дискриминант соответствующего квадратного уравнения будет меньше или равен нулю. То есть при . Наименьшее из возможных значений значений a, которое удовлетворяет всем требуемым условиям, является число $dfrac{2}{sqrt{3}}$ . Это значение достигается в вершине соответствующей квадратичной функции, то есть при $x = dfrac{sqrt{3}-1}{2}$ .

б) Рассуждая аналогично, находим, что наименьшее значение выражения равно $-dfrac{2}{sqrt{3}}$ .

Разбор заданий вступительного экзамена по математике в лицей «Вторая школа» представлен репетитором по математике в Москве, Сергеем Валерьевичем.

Источник

В этой статье я делюсь информацией о поступлении и вариантами вступительных экзаменов в лучшие школы Москвы, такие как Лицей №1535, 57 школа, Лицей «Вторая школа», 179 школа, Гимназия на Юго-Западе №1543, Гимназия №1567, Гимназия №1514, Физико-математическая школа №2007, Курчатовская школа 2077, Школа «Интеллектуал», и другие школы.

АКТУАЛЬНЫЕ ДАННЫЕ 2021 года на сайте http://matolimp.ru/школы/вступительные-экзамены

Вся актуальная информация появляется на страницах matolimp в соцсетях. Подписывайтесь:
Telegram: https://telegram.me/matolimp
Инстаграм: https://www.instagram.com/matolimp/
Facebook: https://www.facebook.com/matolimp

Лицей №1535
Сайт школы
Правила поступления
Примеры вступительных испытаний
Вступительные задания в 7 класс:
Математика: программа вариант работы
Русский язык: программа вариант работы
Английский язык: программа вариант работы

Центр образования №57 (Пятьдесят седьмая школа)
Сайт школы
Информация о приёме в школу

Школа «Интеллектуал»
Вступительные испытания проходит в три тура
1 тур:
тест по математике и по руссокому языку
два задания по выбору
2 тур:
Защита самостоятельной исследовательской работы
3 тур:
Уроки с учителями школы

Средняя общеобразовательная школа №179
Сайт школы №179
Информация о наборе
Задание при поступлении в 7 класс

Гимназия №1567
Сайт школы
Информация о приёме
Экзаменационные материалы для поступающих в 5 класс 8 класс

Гимназия на Юго-Западе №1543
Сайт школы
Информация о приёме в 5 класс
Требования к знаниям поступающих в 5 класс
Вариант вступительных заданий в 5 класс
Информация о приёме в 8 класс
Требования к знаниям поступающих в 8 класс

Гимназия №1514
Сайт школы
Информация для поступающих в 5 класс 7 класс 8 класс
Вариант олимпиады для 4 классов с решениями
Вариант экзамена в 7 класс по математике
Вариант зкзамена в 7 класс по русскому языку
Экзаменационная работа по алгебре для поступающих в 8 класс
Билеты по геометрии для поступающих в 8 класс

Лицей «Вторая Школа»
Сайт школы
Подробная информация о поступлении
Задания прошлых лет на официальном сайте школы
Задания по математике в 6 класс 7 класс 8 класс
Задания по русскому языку в 6 класс 7 класс 8 класс

Курчатовская школа 2077
Курчатовская школа 2077 официальный сайт
Подробнее о поступлении в Курчатовскую школу 2077

Физико-математическая школа №2007
Сайт школы
Варианты заданий, предлагаемые на вступительных испытаниях в
5 класс устное задание письменное задание письменное задание 2
6 класс устное задание письменное задание письменное задание 2
7 класс устное задание письменное задание письменное задание 2

Олимпиады по математике для школьников 5, 6, 7 классов
Олимпиады по математике для начальных классов
Занятия по математике

Источник