Log3 x 3 1 неравенство егэ

Условие

Решение

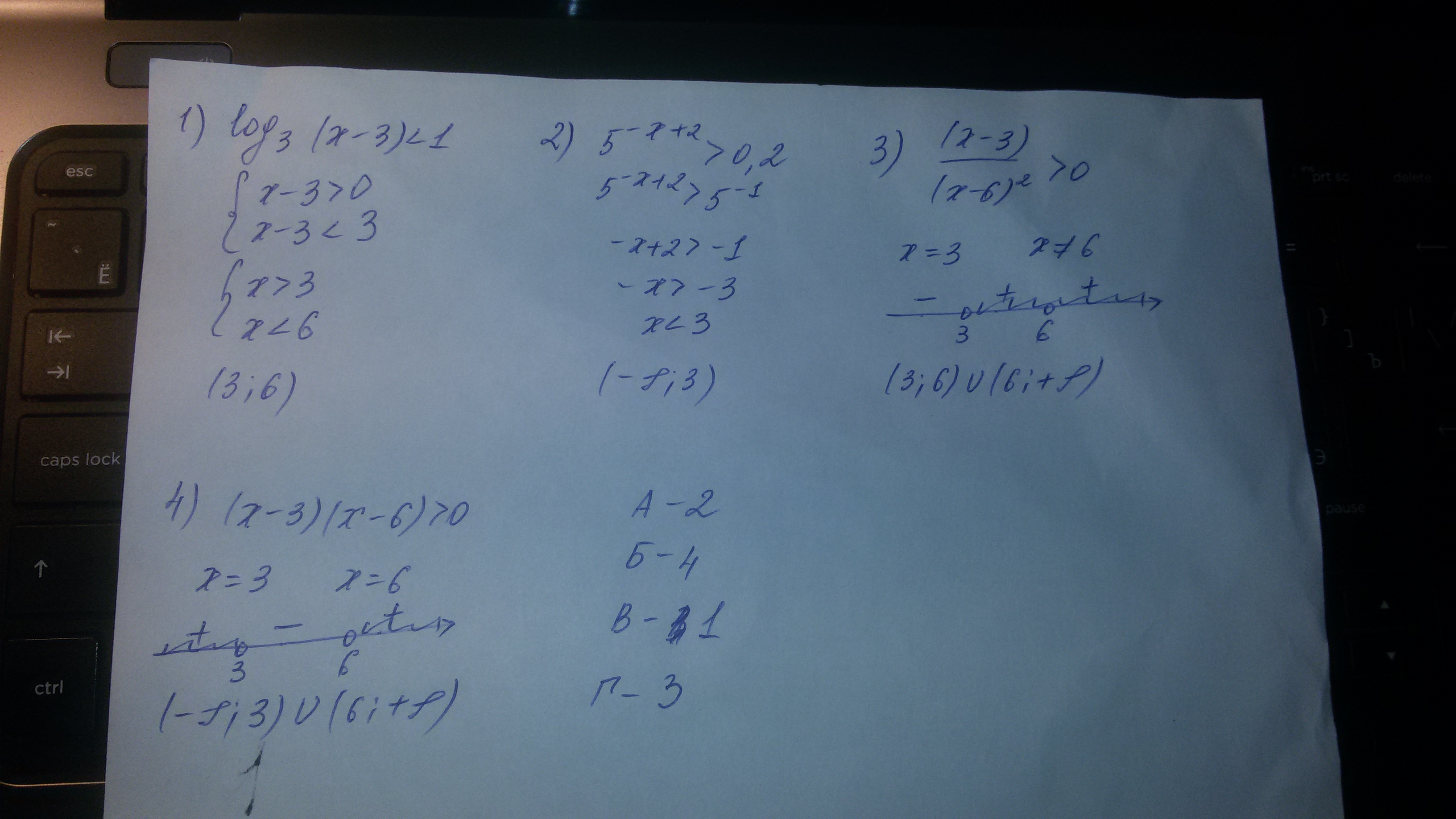
Все решения

Написать комментарий

Как решать логарифмические неравенства?

Решение неравенств с логарифмами похоже на решение обычных логарифмических уравнений. Но есть несколько моментов, которые необходимо учитывать.

Для начала вспомним, что такое логарифм (log_{a}b) — это в какую степень нужно возвести число (a), чтобы получить (b). Кстати, число (a) называют основанием логарифма, а число (b) — аргументом. Например:
$$log_{3}(27)=3;$$
$$log_{frac{1}{3}}(9)=log_{frac{1}{3}}((frac{1}{3})^{-2})=-2;$$
$$log_{2}(sqrt{2})=log_{2}(2^{frac{1}{2}})=frac{1}{2};$$

Если у вас возникают сложности с вычислением логарифмов настоятельно рекомендую сначала почитать про логарифмы и их свойства.

При этом нужно помнить про ограничения, которые накладываются на логарифм (log_{a}b):
$$ begin{cases}
b>0, \
a>0, \
a neq 1.
end{cases}$$

Начнем изучение неравенств с небольшого примера:
$$log_{2}x>log_{2}4;$$
Сравниваются два логарифма с ОДИНАКОВЫМ основанием, значит вполне логично предположить, что (log_{2}x) будет больше (log_{2}4), при условии, что (x>4). Это и будет решением нашего простого неравенства.

Действительно, согласно определению логарифма, чем больше (х), тем в бОльшую степень нужно возвести (2-ку) в основании логарифма, а значит, и тем больше будет сам логарифм. Подставим в неравенство (х=16) — число большее (4):
$$log_{2}16>log_{2}4;$$
Посчитаем получившиеся логарифмы:
$$4>2;$$
Получили верное неравенство.

И подставляя любые числа большие (4), вы всегда будете получать верное неравенство. Некоторые логарифмы мы не можем посчитать, как например (log_{2}15), но логика сохраняется, если подставлять (x>4), неравенство будет верным. Кстати, калькулятор вам любезно подскажет, что (log_{2}15=3,907>log_{2}4), что нас устраивает.

Ответ: (x>4).

Теперь рассмотрим другой пример:
$$log_{frac{1}{2}}(x)>log_{frac{1}{2}}(4);$$
Обратите внимание, я поменял основания на (frac{1}{2}). Интересно, изменится ли логика рассуждений? Подставим (х=16>4):
$$log_{frac{1}{2}}(16)>log_{frac{1}{2}}(4);$$
$$log_{frac{1}{2}}(2^4)>log_{frac{1}{2}}(2^2);$$
$$log_{frac{1}{2}}((frac{1}{2})^{-4})>log_{frac{1}{2}}((frac{1}{2})^{-2});$$
Посчитаем логарифмы слева и справа:
$$-4>-2;$$

Опа! Получилось неверное неравенство! (-4) конечно же не больше (-2). Мы подставили под левый логарифм число большее, чем у правого, но получили, что значение логарифма меньше.
Другими словами, если основание логарифма будет меньше единицы, то чем бОльший аргумент мы подставляем, тем меньший логарифм будем получать.

Оказывается, если основание у логарифма больше единицы, то логарифм будет возрастающей функцией: чем БОЛЬШЕЕ значение аргумента, тем БОЛЬШЕ сам логарифм. Если основание логарифма меньше единицы, то логарифм будет убывающей функцией: чем БОЛЬШЕЕ значение аргумента, тем МЕНЬШЕ значение логарифма.

Для примера на рисунке показан график логарифмов (log_{2}(x)) с основанием 2 (красным цветом) — возрастающая функция. И (log_{frac{1}{2}}(x)) с основанием 0,5 — синим цветом (убывающая функция).

Находим пересечение указанных областей. И видим, что все (x>8) удовлетворяют ОДЗ, записываем ответ.

Ответ: (x>8.)

Пример 2
$$log_{3}(x+3)>log_{3}(2x-4);$$

Любой пример начинаем с ОДЗ:
$$ begin{cases}
x+3>0, \
2x-4>0. \
end{cases}$$
$$ begin{cases}
x>-3, \
x>2. \
end{cases}$$
Итого ОДЗ получается (x>2).
Теперь приступаем к решению самого неравенства. Слева и справа стоят логарифмы с одинаковыми основаниями большими единицы. Значит просто избавляемся от логарифмов:
$$x+3>2x-4;$$
$$x-2x>-4-3;$$
$$-x>-7;$$
$$x lt 7.$$
Сверяем с ОДЗ ((x>2)) — получается (хin(2;7)).

Ответ: (xin(2;7)).

В примере 2 был важный момент в ОДЗ, на который стоит отдельно обратить внимание. Мы накладывали условия, что оба выражения под логарифмами должны быть больше нуля:
$$ begin{cases}
x+3>0, \
2x-4>0. \
end{cases}$$
Но на самом деле, в этом случае в ОДЗ можно рассмотреть только (2x-4>0). А условие (x+3>0) необязательно! Это следует из простой логики, что если (2x-4>0), то (x+3>0) выполняется автоматически, так как, когда при решении примера избавляемся от логарифмов, мы ищем такие значения (х), при которых (x+3>2x-4>0).

Конкретно в этом примере это не критично, но дальше, когда будут гораздо более сложные примеры, решение дополнительных неравенств в ОДЗ может существенно усложнить жизнь. Особенно это касается заданий с параметром. Настоятельно рекомендую думать, а не просто по схеме накладывать ОДЗ на все подряд.

Пример 3
$$ log_{0,1}(x^2-x-2)>log_{0,1}(3-x);$$
ОДЗ:
$$ begin{cases}
x^2-x-2>0, \
3-x>0. \
end{cases}$$

Для того, чтобы решить первое неравенство в ОДЗ, необходим метод интервалов. Через дискриминант или по теореме Виета (как кому удобно) находим корни квадратного многочлена:
$$D=1-4*(-2)=9;$$
$$x_1=frac{1+3}{2}=2;$$
$$x_2=frac{1-3}{2}=-1;$$
Раскладываем на множители по формуле:
$$ax^2+bx+c=a(x-x_1)(x-x_2);$$
$$x^2-x-2=(x-2)(x+1);$$
$$(x-2)(x+1)>0;$$
Рисуем ось (х), расставляем знаки, отмечаем подходящие промежутки и на этой же оси отмечаем решение второго неравенства в ОДЗ:
$$3-х>0;$$
$$x lt 3;$$

Метод замены переменной в неравенствах с логарифмом

Еще один очень популярный тип неравенств — это неравенства, которые решаются при помощи замены переменной. Как всегда, проще разобраться с этим на примерах:

Пример 5
$$log_{3}^{2}(x)+2>3log_{3}(x);$$
Сперва найдем ОДЗ, здесь оно крайне простое:
$$x>0.$$
Очень легкий пример, который решается при помощи замены. Действительно, обратите внимание, что логарифмы в неравенстве абсолютно одинаковые. Заменим их на какую-нибудь переменную (t):
$$Пусть t=log_{3}(x)$$
Тогда неравенство примет вид:
$$t^2+2>3t;$$
$$t^2-3t+2>0;$$
Получили обыкновенное квадратное неравенство, только относительно переменной не (х), а (t).
Находим корни (t), раскладываем на множители и решаем методом интервалов:
$$(t-1)(t-2)>0;$$
$$tin(-infty;1)cup(2;+infty);$$
То же самое можно переписать в виде совокупности неравенств, смысл остается такой же:
$$left[
begin{gathered}
t lt 1, \
t gt 2. \
end{gathered}
right.$$
Не путайте совокупность и систему! Знак системы используется, когда нужно найти значения (х), удовлетворяющие ОДНОВРЕМЕННО всем неравенствам, входящим в систему.

А знак совокупности используется, когда нужно объединить решение каждого неравенства — то есть решением совокупности будут все корни, полученные в каждом неравенстве по отдельности.

В данном примере мы используем совокупность, так как нас устраивают и (t<1), и (t>2). И то, и то является решением нашего неравенства.

Понимание разницы между совокупностью и системой — принципиальный момент при решении логарифмических и показательных неравенств. С совокупностью мы познакомились в этом примере, а когда используется система, поговорим чуть позже.

Итак, у нас совокупность из двух неравенств относительно переменной (t). Время сделать обратную замену — вместо (t) подставляем выражение, на которое мы его заменяли. Напоминаю (t=log_{3}(x)):
$$left[
begin{gathered}
log_{3}(x) lt 1, \
log_{3}(x) gt 2. \
end{gathered}
right.$$
Ну вот, перед нами два простеньких логарифмических неравенства, которые мы уже научились решать выше:
$$log_{3}(x)<1;$$
$$log_{3}(x)<log_{3}(3);$$
$$x<3.$$

$$log_{3}(x)>2;$$
$$log_{3}(x)>log_{3}(3^2);$$
$$x>9.$$
С учетом ОДЗ ((x>0)), и не забыв про совокупность, получаем:
Ответ: (xin(0;3),cup ,(9;+infty)).

Пример 6
$$frac{log_{4}(64x)}{log_{4}(x)-3}+frac{log_{4}(x)-3}{log_{4}(64x)}geqfrac{log_{4}(x^4)+16}{log_{4}^{2}(x)-9}.$$
Неравенство, на первый взгляд, выглядит немного страшно. Но именно такой пример был на ЕГЭ 2017 года, да и на самом деле оно совсем не страшное.

Запишем ОДЗ:
$$ begin{cases}
x>0, \
log_{4}(x)-3neq 0, \
log_{4}(64x)neq 0, \
log_{4}^{2}(x)-9 neq 0.
end{cases}$$

$$ begin{cases}
x>0, \
log_{4}(x)neq log_{4}(4^3), \
log_{4}(64x)neq log_{4}(4^0), \
(log_{4}(x)-3)(log_{4}(x)+3) neq 0.
end{cases}$$

$$ begin{cases}
x>0, \
log_{4}(x)neq log_{4}(4^3), \
log_{4}(64x)neq log_{4}(4^0), \
log_{4}(x)neq log_{4}({4}^{-3}).
end{cases}$$

В итоге, ОДЗ получается: (xin (0;frac{1}{64}) , cup , (frac{1}{64};64) , cup , (64;+infty).)

Главное помнить про правило: мы должны стараться сделать так, чтобы все логарифмы были с одинаковым основанием, и, по возможности, привести их к одинаковым аргументам.
Здесь у каждого логарифма основание (4) — с этим тут все в порядке. А вот подлогарифмические функции постараемся сделать одинаковыми, воспользовавшись свойствами логарифмов. А именно, нам понадобятся следующие формулы:

$$a=log_{b}(b^a);$$
$$log_{a}(bc)=log_{a}(b)+log_{a}(c);$$
$$log_{a}(b^n)=n*log_{a}(b);$$

Воспользуемся ими для преобразования логарифмов в неравенстве:
$$frac{log_{4}(64)+log_{4}(x)}{log_{4}(x)-3}+frac{log_{4}(x)-3}{log_{4}(64)+log_{4}(x)}geqfrac{4*log_{4}(x)+16}{log_{4}^{2}(x)-9};$$

Заметим, что (log_{4}(64)=3)
$$frac{3+log_{4}(x)}{log_{4}(x)-3}+frac{log_{4}(x)-3}{3+log_{4}(x)}geqfrac{4*log_{4}(x)+16}{log_{4}^{2}(x)-9};$$
Теперь у нас везде одинаковые логарифмы, можно сделать замену. Пусть (t=log_{4}(x):)
$$frac{3+t}{t-3}+frac{t-3}{3+t}geqfrac{4*t+16}{t^2-9};$$
Получилось обыкновенное неравенство из 9-го класса, которое решается методом интервалов. Для этого перекинем все налево, приведем к общему знаменателю, приведем подобные и разложим на множители:
$$frac{3+t}{t-3}+frac{t-3}{3+t}geqfrac{4*t+16}{(t-3)(t+3)};$$
$$frac{(3+t)(t+3)}{(t-3)(t+3)}+frac{(t-3)(t-3)}{(t+3)(t-3)}-frac{4*t+16}{(t-3)(t+3)}geq0;$$
$$frac{9+6t+t^2+t^2-6t+9-4t-16}{(t-3)(t+3)}geq 0;$$
$$frac{2*t^2-4t+2}{(t-3)(t+3)}geq 0;$$
$$frac{2(t-1)^2}{(t-3)(t+3)}geq 0;$$
Воспользуемся методом интервалов, для этого нарисуем ось (х) и расставим знаки:

Обратите внимание, на точку (t=1), она нас устраивает, ведь при этом значении (t) все выражение равно нулю. В ЕГЭ очень часто попадаются отдельные точки, про которые надо не забыть.

$$left[
begin{gathered}
t lt -3, \
t=1, \
t gt 3.\
end{gathered}
right.$$

Сделаем обратную замену (t=log_{4}(x)):
$$left[
begin{gathered}
log_{4}(x)<-3, \
log_{4}(x)=1, \
log_{4}(x)>3. \
end{gathered}
right.$$
Решаем получившиеся простенькие логарифмические неравенства и, неожиданно, одно уравнение. Обратите внимание, что мы решаем опять не систему, а совокупность. Нас устраивают все решения, полученные в каждом уравнениинеравенстве по отдельности.

$$log_{4}(x)<log_{4}({4}^{-3});$$
$$x<{4}^{-3};$$
$$x<frac{1}{64}.$$

$$log_{4}(x)=1;$$
$$log_{4}(x)=log_{4}(4^1);$$
$$x=4.$$

$$log_{4}(x)>3;$$
$$log_{4}(x)>log_{4}(4^3);$$
$$x>64.$$

C учетом ОДЗ записываем ответ:
Ответ: (xin(-infty;frac{1}{64}) , cup , [1] , cup , (64;+infty).)

С основными стандартными типами логарифмических неравенств мы познакомились. Теперь обсудим «подводные камни», которые часто встречаются при решении логарифмических неравенств.

ОДЗ в логарифмических неравенствах. Как сделать проще?

Иногда можно немного упростить себе жизнь при поиске ОДЗ в неравенствах. Для этого нам понадобится немного логики. Разберем на примере:

Пример 7
$$1+log_{6}(4-x)leqlog_{6}(16-x^2).$$
Выпишем ОДЗ, но не будем его решать — да, так можно делать!

ОДЗ:
$$ begin{cases}
4-x>0, \
16-x^2>0.
end{cases}$$

ОДЗ выписали, теперь преобразуем исходное неравенство. Для этого (1) представим в виде логарифма с основанием (6): (1=log_{6}(6)). И воспользуемся формулой:
$$log_{a}(bc)=log_{a}(b)+log_{a}(c).$$
$$log_{6}(6)+log_{6}(4-x)leqlog_{6}(16-x^2).$$
$$log_{6}(6*(4-x))leqlog_{6}(16-x^2).$$
Сравниваются два логарифма с одинаковым основанием, можем смело избавляться от логарифмов, сохраняя знак неравенства:
$$6*(4-x)leq16-x^2;$$

И вот здесь остановимся и поговорим.
Согласно ОДЗ
$$begin{cases}
4-x>0, \
16-x^2>0.
end{cases}$$
Обратите внимание! Что если: (6*(4-x)geq0), то и (16-x^2) будем больше (0) автоматически, так как мы решаем неравенство (6*(4-x)leq16-x^2).

Для нас это означает радостную новость — оказывается необязательно решать все ОДЗ. В данном примере достаточно соблюдать условие (6*(4-x)geq0), а все остальное ОДЗ будет выполняться автоматически, исходя из логики примера. Таким образом, наш пример сводится к решению системы:
$$ begin{cases}
6*(4-x)leq16-x^2, \
6*(4-x)>0.
end{cases}$$

Что избавляет нас от необходимости решать (16-x^2>0), это будет лишним действием.
Конкретно в этом примере нет большой трудности решить все условия из ОДЗ и не думать. Но часто встречаются примеры, в которых выше представленная логика поможет вам не запутаться, ведь иногда это спасает от необходимости решения очень сложных неравенств. Особенно это касается решения заданий с параметрами в профильном ЕГЭ по математике. Вот там каждое лишнее условие в разы увеличивает объем работы.

Дорешаем пример:
$$ begin{cases}
6*(4-x)leq16-x^2, \
6*(4-x)>0.
end{cases}$$

$$ begin{cases}
24-6xleq16-x^2, \
4-x>0.
end{cases}$$

$$ begin{cases}
x^2-6x+8leq0, \
x>4.
end{cases}$$

$$ begin{cases}
2 leq x leq 4, \
4-x>0.
end{cases}$$

Ответ: (x in [2;4).)

Запишем эти правила в общем виде:

$$log_{a}(f(x)>log_{a}(g(x));$$
Эквивалентно
При (a>1):

$$ begin{cases}
f(x)>g(x), \
g(x)>0.
end{cases}$$

При (0 lt a lt 1:)

$$ begin{cases}
f(x) lt g(x), \
f(x) gt 0.
end{cases}$$

Неравенства с логарифмами по переменному основанию

Что, если в основании логарифма будет стоять не положительное число, а некоторое выражение, зависящее от (х — log_{g(x)}(f(x)))? Такие логарифмы называются логарифмами с переменным основанием.

Разберемся, как решать, на примере:

Пример 8
$$ log_{frac{x}{3}}(3x^2-2x+1) ge 0);$$

Начнем решение с ОДЗ. Обратите внимание, что условия накладываются еще и на основание логарифма — оно должно быть больше нуля и не равно единице:
$$ begin{cases}
3x^2-2x+1>0;, \
frac{х}{3}>0; ,\
frac{x}{3}neq1.
end{cases}$$

Заметим, что данный квадратный многочлен больше нуля при любых значениях (х). Второе неравенство имеет решения при (х>0). А третье дает нам (xneq 1).
Объединяя все решения, получаем итоговое ОДЗ:
$$xin(0;3)cup(3;+infty);$$

Приступим к решению.
Мы знаем, чтобы решить неравенство, нужно представить (0) справа в виде логарифма с таким же основанием. Но проблема в том, что основание логарифма слева не число, а выражение, зависящее от (х). Нас не должно это смущать, продолжаем решать точно так же, как если бы в основании было число, то есть, приводим к одинаковому основанию:
$$ log_{frac{x}{3}}(3x^2-2x+1) ge log_{frac{x}{3}}((frac{x}{3})^0);$$
$$ log_{frac{x}{3}}(3x^2-2x+1) ge log_{frac{x}{3}}(1);$$

Получилось, что сравниваются два логарифма с одинаковым основанием. Вот только это основание может быть совершенно любым. Это важно, если вспомнить, как решать классические логарифмические неравенства: знак неравенства должен меняться, если в основании логарифмов стоит число от нуля до единицы, и оставаться таким же, если основание больше единицы. У нас в основании стоит (frac{x}{3}) — выражение, зависящее от (х). Оно может принимать значения, как больше единицы, так и меньше. Поэтому логично было бы рассмотреть два случая, когда основание больше (1), и когда от (0) до (1).

Рассмотрим первый случай:

$$ frac{x}{3}>1;$$
$$ frac{x}{3}-1>0;$$
$$frac{x-3}{3}>0;$$
$$x>3.$$

То есть при (х>3) основание будет больше (1) и знак неравенства должен сохраняться:

$$ begin{cases}
3x^2-2x+1 ge 1, \
х>3.
end{cases}$$

$$ begin{cases}
3x^2-2x ge 0, \
х>3.
end{cases}$$

$$ begin{cases}
x(3x-2) ge 0, \
х>3.
end{cases}$$

Решаем методом интервалов первое неравенство в системе и находим пересечения с условием (x>3):

Метод сужения ОДЗ в логарифмических неравенствах

Эта неприятная штука часто встречается в ЕГЭ по профильной математике и приводит к множеству ошибок и потерянным баллам.

Оказывается, при решении логарифмических неравенств не всегда можно применять формулы из свойств логарифмов (вынесение степени, логарифм от произведения или частного и т.д.). Это связано с изменением области определения логарифмов.

Что это все значит? Проще обсудить на примерах. Рассмотрим простое неравенство с логарифмом:

Пример 11
$$log_{3}(x^2)>4;$$

Как обычно, начинаем с ОДЗ:
$$x^2>0;$$
$$x neq 0.$$

Решаем сам пример, для этого представим (4)-ку справа в виде логарифма с основанием (3).
$$log_{3}(x^2)>log_{3}(3^4);$$
$$x^2>3^4;$$
Разложим в разность квадратов и методом интервалов решим:
$$(x-9)(x+9)>0;$$
$$xin(-infty;-9)cup(9;+infty);$$

А теперь обратите внимание, что этот же самый пример можно было решить по-другому. Согласно формуле вынесения степени из-под логарифма (log_{a}(b^n)=n*log_{a}(b)), можно вынести 2-ю степень. Сделаем это и посмотрим, к чему все это приведет.

$$log_{3}(x^2)>4;$$
$$2*log_{3}(x)>4;$$
Сократим на (2):
$$log_{3}(x)>2;$$
Отдельно обратим внимание на то, как изменилось ОДЗ неравенства после вынесения степени.
$$ОДЗ: x>0;$$
Продолжаем решать неравенство:
$$log_{3}(x)>log_{3}(3^2);$$
$$x>9;$$

Итак, мы решили одно и то же неравенство двумя способами, но ответ получился разный. Как вы думаете, почему? Какое из решений будет верным?

На самом деле, все очень просто. Напоминаю, что логарифм существует только от положительных чисел. Значит, когда под логарифмом стоит (x^2), то вместо (x) можно подставлять любые значения, кроме 0. Вторая степень будет превращать подлогарифмическое выражение в положительное, что нас устраивает. Поэтому могут существовать отрицательные значения (x), при подстановке которых ничего не нарушается. Собственно говоря, у нас так и получилось в первом случае: (xin(-infty;-9)cup(9;+infty)). Есть отрицательные корни, которые удовлетворяют ОДЗ.

А во втором случае, как только мы вынесли из-под логарифма четную степень, отрицательные корни (x) больше не подходят, ведь логарифм не будет существовать, и положительные корни — единственные, которые могут получиться. Другими словами, наше ОДЗ СУЗИЛОСЬ!
И, как мы увидели, ответ получился другой, без отрицательных промежутков. Что, разумеется, неправильно.

Очень важное общее правило. Нельзя с логарифмами производить такие преобразования, при которых происходит сужение области допустимых значений ВСЕГО ПРИМЕРА. Если ОДЗ после преобразования остается прежним или увеличивается, то такое преобразование разрешено.

Отдельная очень важная оговорка про то, что ОДЗ не должно сужаться у всего примера. Посмотрите еще раз на разобранный выше пример 6. Там в одном из логарифмов была четная четвертая степень, которую мы не постеснялись вынести, и ни про какое сужение ОДЗ даже речи не было. Неужели неправильно решили пример? Нет, все абсолютно верно, ведь ОДЗ всего неравенства не сузилось, а значит, можно было пользоваться формулой.

Кстати, все эти размышления касаются не только формул вынесения степени, а всех свойств логарифма (суммы, разности и т.д.), нужно быть внимательными! Но чаще всего встречаются ловушки, связанные с вынесением четной степени.

Пример 12
$$9*log_{7}(x^2+x-2)leq10+log_{7}left(frac{(x-1)^9}{x+2}right).$$
Найдем ОДЗ:
$$ begin{cases}
x^2+x-2>0, \
frac{(x-1)^9}{x+2}>0.
end{cases}$$

$$ begin{cases}
(x+2)(x-1)>0, \
frac{(x-1)^9}{x+2}>0.
end{cases}$$

Решаем методом интервалов:

Блок 1. Логарифмические неравенства. Равносильные преобразования (схемы) для простых неравенств

Блок 2. Логарифмические неравенства. Равносильные преобразования (схемы) для более сложных неравенств

Блок 3. Логарифмические неравенства. Метод замены множителей (метод рационализации)

Блок 4. Логарифмические неравенства. Метод замены множителей (метод рационализации) и замена переменных

Блок 5. Логарифмические неравенства. Закрепление метода замены множителей (метода рационализации) и метода замены переменных

Блок 6. Логарифмические неравенства. Использование свойств логарифмической функции

Решая логарифмические неравенства, мы пользуемся свойством монотонности логарифмической функции. Также мы используем определение логарифма и основные логарифмические формулы.

Давайте повторим, что такое логарифмы:

Логарифм положительного числа по основанию — это показатель степени, в которую надо возвести , чтобы получить .

При этом

Основное логарифмическое тождество:

Основные формулы для логарифмов:

(Логарифм произведения равен сумме логарифмов)

(Логарифм частного равен разности логарифмов)

(Формула для логарифма степени)

Формула перехода к новому основанию:

Алгоритм решения логарифмических неравенств

Можно сказать, что логарифмические неравенства решаются по определенному алгоритму. Нам нужно записать область допустимых значений (ОДЗ) неравенства. Привести неравенство к виду Знак здесь может быть любой: Важно, чтобы слева и справа в неравенстве находились логарифмы по одному и тому же основанию.

И после этого «отбрасываем» логарифмы! При этом, если основание степени , знак неравенства остается тем же. Если основание такое, что знак неравенства меняется на противоположный.

Конечно, мы не просто «отбрасываем» логарифмы. Мы пользуемся свойством монотонности логарифмической функции. Если основание логарифма больше единицы, логарифмическая функция монотонно возрастает, и тогда большему значению х соответствует большее значение выражения .

Если основание больше нуля и меньше единицы, логарифмическая функция монотонно убывает. Большему значению аргумента х будет соответствовать меньшее значение

Важное замечание: лучше всего записывать решение в виде цепочки равносильных переходов.

Перейдем к практике. Как всегда, начнем с самых простых неравенств.

1. Рассмотрим неравенство log₃x > log₃5.
Поскольку логарифмы определены только для положительных чисел, необходимо, чтобы x был положительным. Условие x > 0 называется областью допустимых значений (ОДЗ) данного неравенства. Только при таких x неравенство имеет смысл.

Что делать дальше? Стандартный ответ, который дают школьники, — «Отбросить логарифмы!»

Что ж, эта формулировка лихо звучит и легко запоминается. Но почему мы все-таки можем это сделать?

Мы люди, мы обладаем интеллектом. Наш разум устроен так, что все логичное, понятное, имеющее внутреннюю структуру запоминается и применяется намного лучше, чем случайные и не связанные между собой факты. Вот почему важно не механически вызубрить правила, как дрессированная собачка-математик, а действовать осознанно.

Так почему же мы все-таки «отбрасываем логарифмы»?

Ответ простой: если основание больше единицы (как в нашем случае), логарифмическая функция монотонно возрастает, значит, большему значению x соответствует большее значение y и из неравенства log₃x₁ > log₃x₂ следует, что x₁ > x₂.

Обратите внимание, мы перешли к алгебраическому неравенству, и знак неравенства при этом — сохраняется.

Итак, x > 5.

Следующее логарифмическое неравенство тоже простое.

2. log₅(15 + 3x) > log₅2x

Начнём с области допустимых значений. Логарифмы определены только для положительных чисел, поэтому

Решая эту систему, получим: x > 0.

Теперь от логарифмического неравенства перейдем к алгебраическому — «отбросим» логарифмы. Поскольку основание логарифма больше единицы, знак неравенства при этом сохраняется.

15 + 3x > 2x.

Получаем: x > −15.

Итак,

Ответ: x > 0.

А что же будет, если основание логарифма меньше единицы? Легко догадаться, что в этом случае при переходе к алгебраическому неравенству знак неравенства будет меняться.

Приведем пример.

3.

Запишем ОДЗ. Выражения, от которых берутся логарифмы, должны быть положительно, то есть

Решая эту систему, получим: x > 4,5.

Поскольку , логарифмическая функция с основанием монотонно убывает. А это значит, что большему значению функции отвечает меньшее значение аргумента:

И если , то
2x − 9 ≤ x.

Получим, что x ≤ 9.

Учитывая, что x > 4,5, запишем ответ:

x ∈ (4,5; 9].

В следующей задаче логарифмическое неравенство сводится к квадратному. Так что тему «квадратные неравенства» рекомендуем повторить.

Теперь более сложные неравенства:

4. Решите неравенство

Ответ:

5. Решите неравенство

ОДЗ:

Если , то . Нам повезло! Мы знаем, что основание логарифма больше единицы для всех значений х, входящих в ОДЗ.

Сделаем замену

Обратите внимание, что сначала мы полностью решаем неравенство относительно новой переменной t. И только после этого возвращаемся к переменной x. Запомните это и не ошибайтесь на экзамене!

Ответ:

6.

Запомним правило: если в уравнении или неравенстве присутствуют корни, дроби или логарифмы — решение надо начинать с области допустимых значений. Поскольку основание логарифма должно быть положительно и не равно единице, получим систему условий:

Упростим эту систему:

Это область допустимых значений неравенства.

Мы видим, что переменная содержится в основании логарифма. Перейдем к постоянному основанию. Напомним, что

В данном случае удобно перейти к основанию 4.

Сделаем замену

Упростим неравенство и решим его методом интервалов:

Итак,

Вернемся к переменной x:

Мы добавили условие x > 0 (из ОДЗ).

Ответ:

7. Следующая задача тоже решается с помощью метода интервалов

Как всегда, решение логарифмического неравенства начинаем с области допустимых значений. В данном случае

Это условие обязательно должно выполняться, и к нему мы вернемся. Рассмотрим пока само неравенство. Запишем левую часть как логарифм по основанию 3:

Правую часть тоже можно записать как логарифм по основанию 3, а затем перейти к алгебраическому неравенству:

Видим, что условие (то есть ОДЗ) теперь выполняется автоматически. Что ж, это упрощает решение неравенства.

Решаем неравенство методом интервалов:

Ответ:

Получилось? Что же, повышаем уровень сложности:

8. Решите неравенство:

Неравенство равносильно системе:

Ответ:

9. Решите неравенство:

Выражение 5^—x2навязчиво повторяется в условии задачи. А это значит, что можно сделать замену:

Поскольку показательная функция принимает только положительные значения, t > 0. Тогда

Неравенство примет вид:

Уже лучше. Найдем область допустимых значений неравенства. Мы уже сказали, что t > 0. Кроме того, (t − 3) (5⁹ · t − 1) > 0

Если это условие выполнено, то и частное будет положительным.

А еще выражение под логарифмом в правой части неравенства должно быть положительно, то есть (625t − 2)².

Это означает, что 625t − 2 ≠ 0, то есть

Аккуратно запишем ОДЗ

и решим получившуюся систему, применяя метод интервалов.

Итак,

Ну что ж, полдела сделано — разобрались с ОДЗ. Решаем само неравенство. Сумму логарифмов в левой части представим как логарифм произведения:

«Отбросим» логарифмы. Знак неравенства сохраняется.

Перенесем все в левую часть и разложим по известной формуле разности квадратов:

Вспомним, что (это ОДЗ неравенства) и найдем пересечение полученных промежутков.

Получим, что

Вернемся к переменной x

Поскольку

Ответ:

10. Еще один прием, упрощающий решение логарифмических неравенств, — переход к постоянному основанию. Покажем, как использовать переход к другому основанию и обобщенный метод интервалов.

Запишем ОДЗ:

Воспользуемся формулой и перейдем к основанию 10:

Применим обобщенный метод интервалов. Выражение в левой части неравенства можно записать как функцию

Эта функция может менять знак в точках, где она равна нулю или не существует.

Выражение lg |x − 3| равно нулю, если |x − 3| = 1, то есть x = 4 или x = 2.

Выражение lg (|x| − 2) равно нулю, если |x| = 3, то есть в точках 3 и −3.

Отметим эти точки на числовой прямой, с учетом ОДЗ неравенства.

Найдем знак функции g(x) на каждом из промежутков, на которые эти точки разбивают область допустимых значений. Точно так же мы решали методом интервалов обычные рациональные неравенства.

Ответ:

11. А в следующей задаче спрятаны целых две ловушки для невнимательных абитуриентов.

Запишем ОДЗ:

Итак, Это ОДЗ.

Обратите внимание, что .

Это пригодится вам при решении неравенства.

Упростим исходное неравенство:

Теперь главное – не спешить. Мы уже говорили, что задача непростая – в ней расставлены ловушки. В первую вы попадете, если напишете, что Ведь выражение в данном случае не имеет смысла, поскольку x < 18.

Как же быть? Вспомним, что (x — 18)²=(18 — x)². Тогда:

Вторая ловушка – попроще. Запись означает, что сначала надо вычислить логарифм, а потом возвести полученное выражение в квадрат. Поэтому:

Дальше – всё просто. Сделаем замену

Выражение в левой части этого неравенства не может быть отрицательным, поэтому t = 2. Тогда

— не удовлетворяет ОДЗ;

Ответ: 2.

Мы рассмотрели основные приемы решения логарифмических неравенств — от простейших до сложных, которые решаются с помощью обобщенного метода интервалов. Однако есть еще один интересный метод, помогающий справиться и показательными, и с логарифмическими, и с многими другими видами неравенств. Это метод рационализации (замены множителя). О нем — в следующей статье.

Читайте также: Неравенства. Метод замены множителя (метод рационализации)

Логарифмические неравенства повышенной сложности

ЕГЭ Профиль №14. Логарифмические неравенства с переменным основаниемadmin2022-11-03T16:31:55+03:00

Скачать файл в формате pdf.

ЕГЭ Профиль №14. Логарифмические неравенства с переменным основанием

Задача 1. Решите неравенство    ({log _x}left( {4 — x} right) cdot {log _x}left( {x + 1} right) geqslant 0) Ответ ОТВЕТ: (left( {0;;1} right) cup left( {1;;3} right].)

Задача 2. Решите неравенство    ({log _{x — 1}}left( {5 — x} right) cdot {log _{x — 1}}x geqslant 0) Ответ ОТВЕТ: (left( {1;;2} right) cup left( {2;;4} right].)

Задача 3. Решите неравенство    (left( {{x^2} + 3x + 2} right) cdot {log _{x + 3}}left( {x + 2} right) cdot {log _3}{left( {x — 1} right)^2} leqslant 0) Ответ ОТВЕТ: (left{ { — 1} right} cup left[ {0;;1} right) cup left( {1;;2} right].)

Задача 4. Решите неравенство    (left( {{x^2} + 7x + 12} right) cdot {log _{x + 5}}left( {x + 4} right) cdot {log _5}{left( {x + 1} right)^2} leqslant 0) Ответ ОТВЕТ: (left{ { — 3} right} cup left[ { — 2;; — 1} right) cup left( { — 1;,0} right].)

Задача 5. Решите неравенство    (frac{{left( {{x^2} + 9x + 20} right) cdot {{log }_{x + 6}}left( {x + 5} right) cdot lg {{left( {x + 2} right)}^2}}}{{2{x^2} + 21x + 54}} leqslant 0) Ответ ОТВЕТ: (left( { — 5;; — 4,5} right) cup left{ { — 4} right} cup left[ { — 3;; — 2} right) cup left( { — 2;; — 1} right].)

Задача 6. Решите неравенство    (frac{{left( {{x^2} — 7x + 12} right) cdot {{log }_{x — 2}}left( {x — 3} right) cdot ln {{left( {x — 6} right)}^2}}}{{2{x^2} — 11x + 14}} leqslant 0) Ответ ОТВЕТ: (left( {3;;3,5} right) cup left{ 4 right} cup left[ {5;;6} right) cup left( {6;;7} right].)

Задача 7. Решите неравенство    (left( {4x — 7} right) cdot {log _{{x^2} — 4x + 5}}left( {3x — 5} right) geqslant 0) Ответ ОТВЕТ: (left( {frac{5}{3};;frac{7}{4}} right] cup left( {2;;infty } right).)

Задача 8. Решите неравенство    (left( {4x + 13} right) cdot {log _{{x^2} + 6x + 10}}left( {3x + 10} right) geqslant 0) Ответ ОТВЕТ: (left( { — frac{{10}}{3};; — frac{{13}}{4}} right] cup left( { — 3;;infty } right).)

Задача 9. Решите неравенство    ({log _{{{left( {sqrt 5 } right)}^{x + frac{1}{3}}}}}{5^{frac{4}{{{x^2} + 3x}}}} leqslant frac{6}{{3x + 1}}) Ответ ОТВЕТ: (left[ { — 4;; — 3} right) cup left( { — frac{1}{3};;0} right) cup left[ {1;;infty } right).)

Задача 10. Решите неравенство    ({log _{{{left( {sqrt 7 } right)}^{x + frac{1}{2}}}}}{7^{frac{2}{{{x^2} + x}}}} leqslant frac{4}{{2x + 1}}) Ответ ОТВЕТ: (left[ { — 2;; — 1} right) cup left( { — frac{1}{2};;0} right) cup left[ {1;;infty } right).)

Задача 11. Решите неравенство    ({log _{5 — x}}left( {x + 3} right) leqslant 0) Ответ ОТВЕТ: (left( { — 3;; — 2} right] cup left( {4;;5} right).)

Задача 12. Решите неравенство    ({log _{7 — x}}left( {2x + 9} right) leqslant 0) Ответ ОТВЕТ: (left( { — frac{9}{2};; — 4} right] cup left( {6;;7} right).)

Задача 13. Решите неравенство    ({log _{frac{x}{3}}}left( {3{x^2} — 2x + 1} right) geqslant 0) Ответ ОТВЕТ: (left( {0;;frac{2}{3}} right] cup left( {3;;infty } right).)

Задача 14. Решите неравенство    ({log _{frac{x}{2}}}left( {4{x^2} — 3x + 1} right) geqslant 0) Ответ ОТВЕТ: (left( {0;;frac{3}{4}} right] cup left( {2;;infty } right).)

Задача 15. Решите неравенство    ({log _{{x^2}}}left( {frac{1}{x} + frac{2}{{{x^2}}}} right) leqslant 0) Ответ ОТВЕТ: (left( { — 2;; — 1} right) cup left( { — 1;;0} right) cup left( {0;;1} right) cup left[ {2;;infty } right).)

Задача 16. Решите неравенство    ({log _{{x^2}}}left( {frac{2}{{{x^2}}} — frac{1}{x}} right) leqslant 0) Ответ ОТВЕТ: (left( { — infty ;; — 2} right] cup left( { — 1;;0} right) cup left( {0;;1} right) cup left( {1;;2} right).)

Задача 17. Решите неравенство    ({log _{6{x^2} — x — 1}}left( {2{x^2} — 5x + 3} right) geqslant 0) Ответ ОТВЕТ: (left( { — infty ;; — frac{1}{2}} right) cup left( {frac{1}{2};;frac{2}{3}} right) cup left[ {2;;infty } right).)

Задача 18. Решите неравенство    ({log _{6{x^2} + 5x}}left( {2{x^2} — 3x + 1} right) geqslant 0) Ответ ОТВЕТ: (left( { — infty ;; — 1} right) cup left( {0;;frac{1}{6}} right) cup left[ {frac{3}{2};;infty } right).)

Задача 19. Решите неравенство    ({log _{5x}}left( {{x^2} — 14x + 48} right) < 1) Ответ ОТВЕТ: (left( {0;;0,2} right) cup left( {3;;6} right) cup left( {8;;16} right).)

Задача 20. Решите неравенство    ({log _{7x}}left( {{x^2} — 13x + 36} right) < 1) Ответ ОТВЕТ: (left( {0;;frac{1}{7}} right) cup left( {2;;4} right) cup left( {9;;18} right).)

Задача 21. Решите неравенство    ({2^{lg left( {cos left( { — 6pi } right)} right)}} geqslant {log _{{x^2}}}left( {2{x^2} — 6x + 9} right)) Ответ ОТВЕТ: (left( { — 1;;0} right) cup left( {0;;1} right) cup left{ 3 right}.)

Задача 22. Решите неравенство    ({7^{ln left( {cos left( { — 2pi } right)} right)}} geqslant {log _{{x^2}}}left( {2{x^2} — 10x + 25} right)) Ответ ОТВЕТ: (left( { — 1;;0} right) cup left( {0;;1} right) cup left{ 5 right}.)

Задача 23. Решите неравенство    ({log _{x + 2}}left( {7{x^2} + 11x — 6} right) < 2) Ответ ОТВЕТ: (left( {frac{3}{7};;frac{5}{6}} right).)

Задача 24. Решите неравенство    ({log _{x + 1}}left( {6{x^2} + x — 5} right) < 2) Ответ ОТВЕТ: (left( {frac{5}{6};;frac{6}{5}} right).)

Задача 25. Решите неравенство    ({log _{{{left( {x — 1} right)}^2}}}{left( {x — 2} right)^2} leqslant 1) Ответ ОТВЕТ: (left( {0;;1} right) cup left( {1;;1,5} right] cup left( {2;;infty } right).)

Задача 26. Решите неравенство    ({log _{{{left( {x — 2} right)}^2}}}{left( {x — 3} right)^2} leqslant 1) Ответ ОТВЕТ: (left( {1;;2} right) cup left( {2;;2,5} right] cup left( {3;;infty } right).)

Задача 27. Решите неравенство    ({log _{x + 2}}left( {{x^2} — 5x + 1} right) leqslant {log _{frac{{4x + 5}}{{5x + 6}}}}1) Ответ ОТВЕТ: (left( { — 2;; — frac{5}{4}} right) cup left( { — frac{6}{5};; — 1} right) cup left[ {0;;frac{{5 — sqrt {21} }}{2}} right) cup left( {frac{{5 + sqrt {21} }}{2};;5} right].)

Задача 28. Решите неравенство    ({log _{x + 3}}left( {{x^2} — 3x + 1} right) leqslant {log _{frac{{2x + 5}}{{3x + 7}}}}1) Ответ ОТВЕТ: (left( { — 3;; — frac{5}{2}} right) cup left( { — frac{7}{3};; — 2} right) cup left[ {0;;frac{{3 — sqrt 5 }}{2}} right) cup left( {frac{{3 + sqrt 5 }}{2};;3} right].)

Задача 29. Решите неравенство    ({log _{2x + 4}}{left( {2x — 3} right)^2} leqslant 2{log _{2x + 4}}left( {x + 2} right)) Ответ ОТВЕТ: (left( { — 2;; — frac{3}{2}} right) cup left[ {frac{1}{3};;frac{3}{2}} right) cup left( {frac{3}{2};;5} right].)

Задача 30. Решите неравенство    ({log _{2x + 2}}{left( {2x — 5} right)^2} leqslant 2{log _{2x + 2}}left( {x + 1} right)) Ответ ОТВЕТ: (left( { — 1;; — frac{1}{2}} right) cup left[ {frac{4}{3};;frac{5}{2}} right) cup left( {frac{5}{2};;6} right].)

Задача 31. Решите неравенство    ({log _x}left( {x + 4} right) cdot {log _{x + 4}}left( {x + 8} right) cdot {log _{x + 8}}left( {x + 12} right) leqslant 2) Ответ ОТВЕТ: (left( {0;;1} right) cup left[ {4;;infty } right).)

Задача 32. Решите неравенство    ({log _x}left( {x + 10} right) cdot {log _{x + 10}}left( {x + 20} right) cdot {log _{x + 20}}left( {x + 30} right) leqslant 2) Ответ ОТВЕТ: (left( {0;;1} right) cup left[ {6;;infty } right).)

Задача 33. Решите неравенство    ({log _x}left( {{x^3} — 8} right) leqslant {log _x}left( {{x^3} + 2x — 13} right)) Ответ ОТВЕТ: (left[ {2,5;;infty } right).)

Задача 34. Решите неравенство    ({log _x}left( {{x^3} — 1} right) leqslant {log _x}left( {{x^3} + 2x — 4} right)) Ответ ОТВЕТ: (left[ {1,5;;infty } right).)

Задача 35. Решите неравенство    (frac{{{{log }_{x + 3}}left( {{x^2} — x + 30} right)}}{{{{log }_{x + 3}}left( {{x^2} — x — 1} right)}} geqslant frac{{lg left( {{x^4} — 2{x^3} + {x^2}} right)}}{{lg left( {{x^2} — x — 1} right)}}) Ответ ОТВЕТ: (left( { — 2;; — 1} right) cup left( {2;;3} right].)

Задача 36. Решите неравенство    (frac{{{{log }_{x + 5}}left( {{x^2} + 2x + 56} right)}}{{{{log }_{x + 5}}left( {{x^2} + 2x — 2} right)}} geqslant frac{{{{log }_2}left( {{x^4} + 4{x^3} + 4{x^2}} right)}}{{{{log }_2}left( {{x^2} + 2x — 2} right)}}) Ответ ОТВЕТ: (left( { — 4;; — 3} right) cup left( {1;;2} right].)

Задача 37. Решите неравенство    ({log _{4 — x}}frac{{{{left( {x — 4} right)}^8}}}{{x + 5}} geqslant Ответ ОТВЕТ: (left( { — 5;; — 4} right] cup left( {3;;4} right).)

Задача 38. Решите неравенство    ({log _{5 — x}}frac{{x + 2}}{{{{left( {x — 5} right)}^4}}} geqslant  — 4) Ответ ОТВЕТ: (left[ { — 1;;4} right).)

Задача 39. Решите неравенство    ({log _{x + 6}}{left( {frac{{x — 4}}{x}} right)^2} + {log _{x + 6}}frac{x}{{x — 4}} leqslant 1) Ответ ОТВЕТ: (left( { — 6;; — 5} right) cup left[ { — 4;; — 1} right] cup left( {4;;infty } right).)

Задача 40. Решите неравенство    ({log _{x + 7}}{left( {frac{{3 — x}}{{x + 1}}} right)^2} leqslant 1 — {log _{x + 7}}frac{{x + 1}}{{x — 3}}) Ответ ОТВЕТ: (left( { — 7;; — 6} right) cup left[ { — 5;; — 2} right] cup left( {3;;infty } right).)

Задача 41. Решите неравенство    ({log _{5x + 7}}left( {{{log }_{7 — x}}left( {x + 3} right)} right) geqslant 0) Ответ ОТВЕТ: (left( { — 1,4;; — 1,2} right) cup left[ {2;;6} right).)

Задача 42. Решите неравенство    ({log _{5x + 12}}left( {{{log }_{6 — x}}left( {x + 4} right)} right) geqslant 0) Ответ ОТВЕТ: (left( { — 2,4;; — 2,2} right) cup left[ {1;;5} right).)

Задача 43. Решите неравенство    ({log _{x + 3}}6 + {log _{ — 13 — 6x}}6 leqslant 0) Ответ ОТВЕТ: (left[ { — frac{8}{3};; — frac{5}{2}} right] cup left( { — frac{7}{3};; — frac{{13}}{6}} right).)

Задача 44. Решите неравенство    ({log _{x — 2}}3 + {log _{31 — 12x}}3 leqslant 0) Ответ ОТВЕТ: (left[ {frac{9}{4};;frac{7}{3}} right] cup left( {frac{5}{2};;frac{{31}}{{12}}} right).)

Задача 45. Решите неравенство    ({log _{6 — 8{x^2}}}left( {36 — 64{x^4}} right) leqslant 2 + frac{1}{{{{log }_2}left( {6 — 8{x^2}} right)}}) Ответ ОТВЕТ: (left( { — frac{{sqrt 3 }}{2};; — sqrt {frac{5}{8}} } right) cup left[ { — 0,5;;0,5} right] cup left( {sqrt {frac{5}{8}} ;;frac{{sqrt 3 }}{2}} right).)

Задача 46. Решите неравенство    ({log _{3 — 9{x^2}}}left( {9 — 81{x^4}} right) leqslant 2 + frac{1}{{{{log }_2}left( {3 — 9{x^2}} right)}}) Ответ ОТВЕТ: (left( { — frac{{sqrt 3 }}{3};; — frac{{sqrt 2 }}{3}} right) cup left[ { — frac{1}{3};;frac{1}{3}} right] cup left( {frac{{sqrt 2 }}{3};;frac{{sqrt 3 }}{3}} right).)

Задача 47. Решите неравенство    ({log _{x + 1}}2 leqslant {log _{3 — x}}2) Ответ ОТВЕТ: (left( { — 1;;0} right) cup left[ {1;;2} right).)

Задача 48. Решите неравенство    ({log _{frac{x}{{x — 1}}}}5 leqslant {log _{frac{x}{2}}}5) Ответ ОТВЕТ: (left( {2;;3} right].)

Задача 49. Решите неравенство    ({log _{{{log }_x}2x}}left( {6x — 2} right) geqslant 0) Ответ ОТВЕТ: (left( {frac{1}{3};;frac{1}{2}} right) cup left( {1;;infty } right).)

Задача 50. Решите неравенство    ({log _{{{log }_x}2x}}left( {9x — 4} right) geqslant 0) Ответ ОТВЕТ: (left( {frac{4}{9};;frac{1}{2}} right) cup left( {1;;infty } right).)

Задача 51. Решите неравенство    ({log _{{x^2} + 1}}frac{{2 cdot {4^x} — 15 cdot {2^x} + 23}}{{{4^x} — 9 cdot {2^x} + 14}} geqslant 0) Ответ ОТВЕТ: (left( { — infty ;;0} right) cup left( {0;;1} right) cup left{ {{{log }_2}3} right} cup left( {{{log }_2}7;;infty } right).)

Задача 52. Решите неравенство    ({log _{{x^2} + 1}}frac{{2 cdot {9^x} — 19 cdot {3^x} + 40}}{{{9^x} — 11 cdot {3^x} + 24}} geqslant 0) Ответ ОТВЕТ: (left( { — infty ;;0} right) cup left( {0;;1} right) cup left{ {{{log }_3}4} right} cup left( {{{log }_3}8;;infty } right).)

Задача 53. Решите неравенство    ({log _{x + 1}}left( {2x — 5} right) + {log _{2x — 5}}left( {x + 1} right) leqslant 2) Ответ ОТВЕТ: (left( {frac{5}{2};;3} right) cup left{ 6 right}.)

Задача 54. Решите неравенство    ({log _{2x — 1}}left( {4x — 5} right) + {log _{4x — 5}}left( {2x — 1} right) leqslant 2) Ответ ОТВЕТ: (left( {frac{5}{4};;frac{3}{2}} right) cup left{ 2 right}.)

Задача 55. Решите неравенство    (0,5{log _{x — 2}}left( {{x^2} — 10x + 25} right) + {log _{5 — x}}left( {7x — {x^2} — 10} right) geqslant 3) Ответ ОТВЕТ: (left( {3;;4} right).)

Задача 56. Решите неравенство    (0,5{log _{x — 1}}left( {{x^2} — 8x + 16} right) + {log _{4 — x}}left( {5x — {x^2} — 4} right) geqslant 3) Ответ ОТВЕТ: (left( {2;;3} right).)

Задача 57. Решите неравенство    (frac{{{{log }_2}left( {2x} right) cdot {{log }_{0,5x}}2}}{{{{log }_{0,125x}}8}} leqslant 1) Ответ ОТВЕТ: (left( {0;;1} right] cup left( {2;;8} right) cup left( {8;;32} right].)

Задача 58. Решите неравенство    (frac{{{{log }_2}left( {8x} right) cdot {{log }_{0,125x}}2}}{{{{log }_{0,5x}}16}} leqslant frac{1}{4}) Ответ ОТВЕТ: (left( {0;;0,5} right] cup left[ {1;;2} right) cup left( {2;;8} right).)

Задача 59. Решите неравенство    ({log _2}left( {16x} right) geqslant {log _{0,5x}}2 cdot {log _4}left( {16{x^4}} right)) Ответ ОТВЕТ: (left[ {frac{1}{8};;2} right) cup left[ {4;;infty } right).)

Задача 60. Решите неравенство    ({log _2}left( {0,5x} right) geqslant {log _{16x}}2 cdot {log _4}left( {16{x^4}} right)) Ответ ОТВЕТ: (left( {frac{1}{{16}};;frac{1}{8}} right] cup left[ {4;;infty } right).)

Задача 61. Решите неравенство    ({log _x}3 + 2{log _{3x}}3 — 6{log _{9x}}3 leqslant 0) Ответ ОТВЕТ: (left( {frac{1}{9};;frac{1}{3}} right) cup left[ {{3^{ — frac{2}{3}}};;1} right) cup left[ {3;;infty } right).)

Задача 62. Решите неравенство    ({log _x}2 + 3{log _{2x}}2 — 6{log _{4x}}2 leqslant 0) Ответ ОТВЕТ: (left( {frac{1}{4};;frac{1}{2}} right) cup left[ {frac{{sqrt 2 }}{2};;1} right) cup left[ {4;;infty } right).)

Задача 63. Решите неравенство (log _2^2left( {3x — 1} right) + log _{3x — 1}^22 — {log _2}{left( {3x — 1} right)^2} — {log _{3x — 1}}4 + 2 leqslant 0) Ответ ОТВЕТ: 1.

Задача 64. Решите неравенство (log _2^2left( {3x + 1} right) + log _{3x + 1}^22 — {log _2}{left( {3x + 1} right)^4} — {log _{3x + 1}}16 + 6 leqslant 0) Ответ ОТВЕТ: 1/3.

Задача 65. Решите неравенство    ({log _{3x}}frac{1}{{27}} cdot {log _3}left( {27x} right) + 9 geqslant 0) Ответ ОТВЕТ: (left( {0;;frac{1}{3}} right) cup left[ {1;;infty } right).)

Задача 66. Решите неравенство    ({log _{2x}}0,25 leqslant {log _2}left( {32x} right) — 1) Ответ ОТВЕТ: (left[ {frac{1}{8};;frac{1}{4}} right] cup left( {frac{1}{2};;infty } right).)

Задача 67. Решите неравенство    (frac{{{{log }_{1 — 2x}}left( {left( {x + 1} right)left( {1 — 4x + 4{x^2}} right)} right)}}{{{{log }_{x + 1}}left( {1 — 2x} right)}} leqslant  — 1) Ответ ОТВЕТ: -0,5.

Задача 68. Решите неравенство    (frac{{{{log }_{1 — x}}left( {left( {3x + 1} right)left( {1 — 2x + {x^2}} right)} right)}}{{{{log }_{3x + 1}}left( {1 — x} right)}} leqslant  — 1) Ответ ОТВЕТ: 2/3.

Задача 69. Решите неравенство    (left| {{{log }_x}frac{x}{4}} right| cdot {log _{4x}}left( {2{x^2}} right) leqslant left| {{{log }_x}frac{x}{4}} right|) Ответ ОТВЕТ: (left( {frac{1}{4};;1} right) cup left( {1;;2} right] cup left{ 4 right}.)

Задача 70. Решите неравенство    (frac{{{{log }_{{7^{x + 3}}}}49}}{{{{log }_{{7^{x + 3}}}}left( { — 49x} right)}} leqslant frac{1}{{{{log }_7}{{log }_{frac{1}{7}}}{7^x}}}) Ответ ОТВЕТ: (left[ { — 49;; — 3} right) cup left( { — 3;; — 1} right) cup left( { — frac{1}{{49}};;0} right).)

Задача 71. Решите неравенство    ({log _x}left( {sqrt {{x^2} + x — 2}  + 1} right) cdot {log _7}left( {{x^2} + x + 1} right) leqslant {log _x}3) Ответ ОТВЕТ: (left( {1;;2} right].)

Задача 72. Решите неравенство ({log _x}left( {sqrt {{x^2} + 2x — 3}  + 2} right) cdot {log _5}left( {{x^2} + 2x — 2} right) geqslant {log _x}4) Ответ ОТВЕТ: (left[ {2sqrt 2  — 1;;infty } right).)

Задача 73. Решите неравенство ({log _{left| {,3x — 3,} right|}}left( {{{25}^x} — {9^x}} right) < {log _{left| {,3x — 3,} right|}}left( {{5^x} + {3^x}} right) + {log _{left| {,3x — 3,} right|}}left( {{5^{x — 1}} + {3^{x — 1}}} right)) Ответ ОТВЕТ: (left( {0;,,frac{2}{3}} right) cup left( {1;,,frac{4}{3}} right).)

Задача 74. Решите неравенство  (left( {{{log }_{left| {,x + 0,5,} right|}}left( {0,25 — x} right) — 1} right) cdot {log _{16}}left( {0,25 — x} right) > {log _4}frac{{0,25 — x}}{{left| {,x + 0,5,} right|}}) Ответ ОТВЕТ: (left( { — 2;,, — 1,5} right) cup left( { — 0,125;,,0} right).)

Задача 75. Решите неравенство    ({log _x}3 cdot {log _9}frac{{5 — 12x}}{{12x — 8}} leqslant frac{1}{2}) Ответ ОТВЕТ: (left[ {frac{1}{2};,,frac{2}{3}} right).)

Текстовое решение задач:

1B	2B	3B	4B	5B	6B	7B	8B	9B	10B
11B	12B	13B	14B	15B	16B	17B	18B	19B	20B
21B	22B	23B	24B	25B	26B	27B	28B	29B	30B
31B	32B	33B	34B	35B	36B	37B	38B	39B	40B
41B	42B	43B	44B	45B	46B	47B	48B	49B	50B
51B	52B	53B	54B	55B	56B	57B	58B	59B	60B
61B	62B	63B	64B	65B	66B	67B	68B	69B	70B
71B	72B	73B	74B	75B