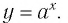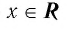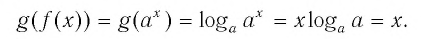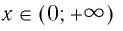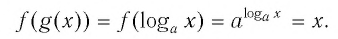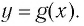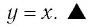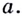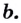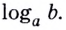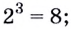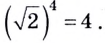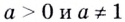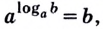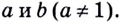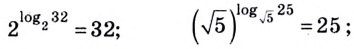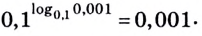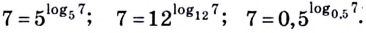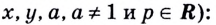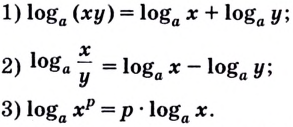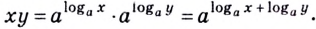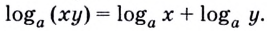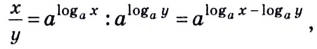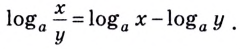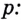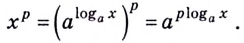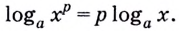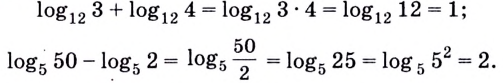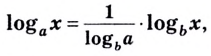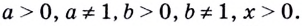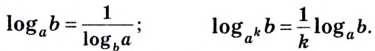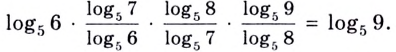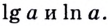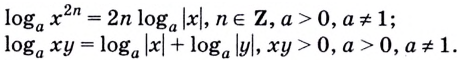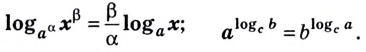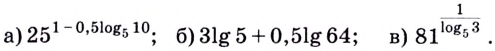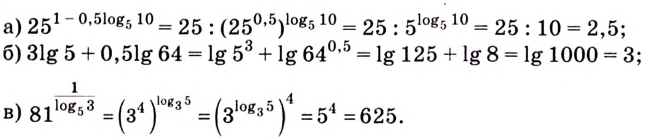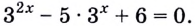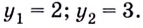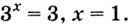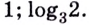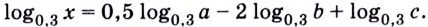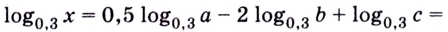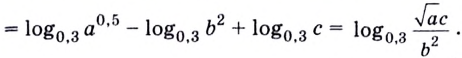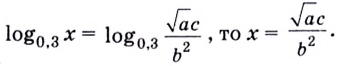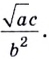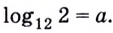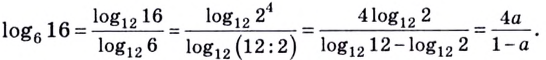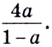Логарифмы
Предыдущую статью о показательных уравнениях мы начали с уравнения 2x = 8. Там всё было ясно: x = 3.
А теперь рассмотрим уравнение 2x = 7.
По графику функции y = 2x мы видим, что это уравнение имеет корень, и притом единственный.
Ясно, что этот корень — не целое число (так как 22 = 4, 23 = 8). Более того, оказывается, что он не является даже рациональным числом, т. е. не представляется в виде обыкновенной дроби. Интуитивно мы чувствуем лишь, что он меньше 3, но не намного.
Этот корень обозначается log27 (читается: «логарифм семи по основанию два»). Он является иррациональным числом, т. е. бесконечной непериодической десятичной дробью. Калькулятор даёт: log27 = 2,807354922057604107…
Итак, наше число log27 — это показатель степени, в которую надо возвести 2, чтобы получить 7.
Теперь дадим общее определение логарифма. Пусть a > 0 и a ≠ 1 (условия те же, что и для основания показательной функции).
Определение. Логарифм положительного числа b по основанию a (обозначается logab) — это показатель степени, в которую надо возвести a, чтобы получить b.
Иными словами,
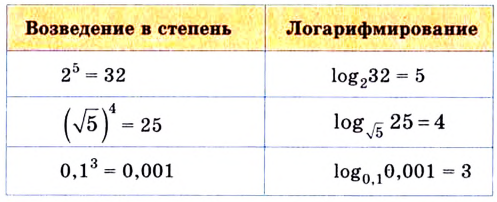
Например:








Логарифм с основанием 10 называется десятичным и обозначается lg. Например, lg 100 = 2, lg 1000 = 3, lg 0,01 = −2.
Логарифм с основанием e называется натуральным и обозначается ln.
Обратите внимание: логарифм определён только для положительных чисел. Причина заключается в том, что показательная функция может принимать лишь положительные значения. Например, число log2(−4) не существует: в какую бы степень мы ни возводили 2, мы никогда не получим −4.
Не забывайте также про ограничения на основание логарифма: 0 < a < 1 или a > 1.
Основные формулы
По определению, logab — это показатель степени, в которую надо возвести число a, чтобы получить число b:
Формула (1) называется основным логарифмическим тождеством.
Вот еще один вариант записи основного логарифмического тождества:
logaax=x.
Перечислим свойства логарифмов. Они являются простыми следствиями правил действия со степенями. Все логарифмы ниже считаются определёнными.
Логарифм произведения — это сумма логарифмов:
| loga(bc) = logab + logac. | (2) |
Логарифм частного — это разность логарифмов:
| (3) |
Показатель степени логарифмируемого числа «спрыгивает» перед логарифмом:
| (4) |
Показатель степени основания логарифма тоже «спрыгивает», но в виде обратного числа:
| (5) |
Формулы (4) и (5) вместе дают:
 . . |
(6) |
В частности, если m = n, мы получаем формулу:
 . . |
(7) |
Например, 
Наконец, важнейшая формула перехода к новому основанию:
 . . |
(8) |
В частности, если c = b, то logbb = 1, и тогда:
 . . |
(9) |
Приведём несколько примеров из банка заданий.
1. 
2. 
3. (применили формулу (4)).
4. (применили формулу (9), перейдя к новому основанию 0,8).
5. (применили формулу (3) разности логарифмов).
Немного истории
Теперь вы поняли, что такое логарифмы и как ими пользоваться. Но для чего они всё-таки нужны? Или это просто такая математическая игрушка с хитрой инструкцией по применению?
Понятие логарифма и логарифмические таблицы появились в 17 веке, и значение их было огромно.
Это в наши дни вычисления не представляют труда — у каждого есть калькулятор. А как считали в «докомпьютерные» времена?
Складывать и вычитать можно было на счётах, а вот умножать и делить приходилось «в столбик» — медленно и трудно.
В 15–17 веках, в эпоху великих географических открытий, стали бурно развиваться торговля, экономика и наука. Требования к математике росли: расчёты становились более сложными, а точность — например, для решения навигационных задач — нужна была всё более высокая.
Необходим был инструмент, позволяющий упростить и ускорить расчёты, и таким инструментом явились логарифмы.
Предположим, что b и c — большие числа, которые надо перемножить. Появление таблиц логарифмов (например, с основанием 10) существенно упростило эту задачу. Теперь вычислителю достаточно было найти по таблицам десятичные логарифмы чисел b и c, сложить их (на счётах) и получить логарифм произведения: lgb + lgc = lg(bc).
А затем по таблице логарифмов найти само произведение чисел b и c.
Недаром французский математик и астроном Лаплас сказал, что изобретение логарифмов удлинило жизнь вычислителей. Логарифмическая линейка (которой инженеры пользовались до 70-х годов двадцатого века) была не менее прогрессивным изобретением, чем современный калькулятор.
Но это еще не всё! Мы не занимались бы логарифмами, если бы они имели лишь историческую, «музейную» ценность. О неожиданных применениях логарифмов мы расскажем в следующей статье, посвящённой логарифмической функции.
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Логарифмы» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
09.03.2023
Логарифм числа b (b > 0) по основанию a (a > 0, a ≠ 1) – показатель степени, в которую нужно возвести число a, чтобы получить b.
ax = b ⇔ logab = x
Логарифм числа b по основанию 10 можно записать как lg(b), а логарифм по основанию e (натуральный логарифм) – ln(b).
Основное логарифмическое тождество
Основное логарифмическое тождество часто используется при решении задач с логарифмами:
alogab = b
Свойства логарифмов
Существует четыре основных свойства логарифмов.
Пусть a > 0, a ≠ 1, x > 0 и y > 0.
Свойство 1. Логарифм произведения
Логарифм произведения равен сумме логарифмов:
loga(x ⋅ y) = logax + logay
Свойство 2. Логарифм частного
Логарифм частного равен разности логарифмов:
loga(x / y) = logax – logay
Свойство 3. Логарифм степени
Логарифм степени равен произведению степени на логарифм:
logaxk = k ⋅ logax
Если в степени находится основание логарифма, то действует другая формула:
logakx = 1/k ⋅ logax
Свойство 4. Логарифм корня
Данной свойство можно получить из свойства логарифм степени, так как корень n-ой степени равен степени 1/n:
loga(x)1/n = 1/n ⋅ logax
Формула перехода от логарифма в одном основании к логарифму при другом основании
Данная формула также часто применяется при решении различных заданий на логарифмы:
logab = logcb / logca
Частный случай:
logab = 1 / logba
Сравнение логарифмов (неравенства)
Пусть у нас есть 2 функции f(x) и g(x) под логарифмами с одинаковыми основаниями и между ними стоит знак неравенства:
logaf(x) > logag(x)
Чтобы их сравнить, нужно сначала посмотреть на основание логарифмов a:
- Если a > 0, то f(x) > g(x) > 0
- Если 0 < a < 1, то 0 < f(x) < g(x)
Как решать задачи с логарифмами: примеры
Задания с логарифмами включены в состав ЕГЭ по математике для 11 класса в задании 5 и задании 7, вы можете найти задания с решениями на нашем сайте в соответствующих разделах. Также задания с логарифмами встречаются в банке заданий по математике. Все примеры вы можете найти через поиск по сайту.
Повторяем логарифмы
Формулы и свойства логарифмов
Определение
Логарифмом числа по основанию ( ) называется такое число , что , то есть записи и равносильны. Логарифм имеет смысл, если .
Если немного перефразировать — Логарифм числа по основанию определяется как показатель степени, в которую надо возвести число , чтобы получить число (Логарифм существует только у положительных чисел).
Логарифм в переводе с греческого языка буквально означает «число, изменяющее отношение».
Специальные обозначения:1. Натуральный логарифм — логарифм по основанию , где — число Эйлера.
- 2. Десятичный логарифм — логарифм по основанию 10.
Свойства логарифмов:
1° — основное логарифмическое тождество.
2°
3°
Логарифм единицы по любому положительному, отличному от 1, основанию равен нулю. Это возможно потому, что из любого действительного числа можно получить 1, только возведя его в нулевую степень.
4° — логарифм произведения.
Логарифм произведения равен сумме логарифмов сомножителей.
5° — логарифм частного.
Логарифм частного (дроби) равен разности логарифмов сомножителей.
6° — логарифм степени.
Логарифм степени равен произведению показателя степени на логарифм ее основания.
7°
8°
9° — переход к новому основанию.
Примеры решения задач
Пример
Задание. Вычислить , если
Решение. Перепишем данное выражение, используя свойство логарифма степени и логарифма произведения:
Решение логарифмических уравнений.
Логарифмическим называется уравнение, в котором неизвестное (х) и выражения с ним находятся под знаком логарифмической функции.
Самое простое логарифмическое уравнение имеет вид logax = b, где a и b -некоторые числа, x — неизвестное.
Решением данного уравнения является x = a b при условии: a > 0, a 1.
Следует отметить, что если x будет находиться где-нибудь вне логарифма, например log2х = х-2, то такое уравнение уже называется смешанным и для его решения нужен особый подход.
Идеальным случаем является ситуация, когда Вам попадется уравнение, в котором под знаком логарифма находятся только числа, например х+2 = log22. Здесь достаточно знать свойства логарифмов для его решения. Но такая удача случается не часто, поэтому приготовьтесь к более сложным вещам.
Но сначала, все-таки, начнём с простых уравнений. Для их решения желательно иметь самое общее представление о логарифме.
Простейшие логарифмические уравнения
К таковым относятся уравнения типа log2х = log216. Невооруженным глазом видно, что опустив знак логарифма получим x = 16.
Для того, чтобы решить более сложное логарифмическое уравнение, его обычно приводят к решению обычного алгебраического уравнения или к решению простейшего логарифмического уравнения logax = b. В простейших уравнениях это происходит в одно движение, поэтому они и носят название простейших.
Выше использованный метод опускания логарифмов является одним из основных способов решения логарифмических уравнений и неравенств. В математике эта операция носит название потенцирования. Существуют определенные правила или ограничения для подобного рода операций:
- одинаковые числовые основания у логарифмов
- логарифмы в обеих частях уравнения находятся свободно, т.е. без каких бы то ни было коэффициентов и других разного рода выражений.
Скажем в уравнении log2х = 2log2 (1- х) потенцирование неприменимо — коэффициент 2 справа не позволяет. В следующем примере log2х+log2 (1 — х) = log2 (1+х) также не выполняется одно из ограничений — слева логарифма два. Вот был бы один – совсем другое дело!
Вообще, убирать логарифмы можно только при условии, что уравнение имеет вид:
loga (…) = loga (…)
В скобках могут находиться совершенно любые выражения, на операцию потенцирования это абсолютно никак не влияет. И уже после ликвидации логарифмов останется более простое уравнение – линейное, квадратное, показательное и т.п., которое Вы уже, надеюсь, умеете решать. Возьмем другой пример:
log3 (2х-5) = log3х
Применяем потенцирование, получаем:
2х-5 = x
х=5
Пойдем дальше. Решим следующий пример:
log3 (2х-1) = 2
Исходя из определения логарифма, а именно, что логарифм — это число, в которое надо возвести основание, чтобы получить выражение, которое находится под знаком логарифма, т.е. (4х-1), получаем:
3 2 = 2х-1
Дальше уже дело техники:
2х-1 = 9
x =5
Опять получили красивый ответ. Здесь мы обошлись без ликвидации логарифмов, но потенцирование применимо и здесь, потому как логарифм можно сделать из любого числа, причем именно такой, который нам надо. Этот способ очень помогает при решении логарифмических уравнений и особенно неравенств.
Решим наше уравнение log3 (2х-1) = 2 с помощью потенцирования:
Представим число 2 в виде логарифма, например, такого log39, ведь 3 2=9.
Тогда log3 (2х-1) = log39 и опять получаем все то же уравнение 2х-1 = 9. Надеюсь, все понятно.
Вот мы и рассмотрели простейшие логарифмические уравнения, которые на самом деле очень важны, ведь решение логарифмических уравнений, даже самых страшных и закрученных, в итоге всегда сводится к решению простейших уравнений.
Во всем, что мы делали выше, мы упускали из виду один очень важный момент, который в последующем будет иметь большое значение. Дело в том, что решение любого логарифмического уравнения, даже самого элементарного, состоит из двух равноценных частей. Первая – это само решение уравнения, вторая — работа с областью допустимых значений (ОДЗ). Вот как раз первую часть мы и освоили. В вышеприведенных примерах ОДЗ на ответ никак не влияет, поэтому мы ее и не рассматривали.
А вот возьмем другой пример:
log3 (x 2-3) = log3 (2х)
Внешне это уравнение ничем не отличается от простейшего уравнения, которое весьма успешно решается. Но это не совсем так. Нет, мы, конечно же его решим, но скорее всего неправильно, потому что в нем кроется небольшая засада, в которую сходу попадаются и троечники, и отличники. Давайте рассмотрим его поближе.
Допустим, необходимо найти корень уравнения или сумму корней, если их несколько:
log3 (x 2-3) = log3 (2х)
Применяем потенцирование, здесь оно допустимо. В итоге получаем обычное квадратное уравнение.
x 2-3 = 2х
x 2-2х-3 = 0
Находим корни уравнения:
х1= 3
х2= -1
Получилось два корня, поэтому находим их сумму:
3+(-1) = 2 Ответ 2.
С первого взгляда все правильно. Но давайте проверим результат и подставим его в исходное уравнение.
Начнем с х1= 3:
log36 = log36
Проверка прошла успешно, теперь очередь х2= -1:
log3 (-2) = log3 (-2)
Так, стоп! Внешне всё идеально. Один момент — логарифмов от отрицательных чисел не бывает! А это значит, что корень x = -1 не подходит для решения нашего уравнения. И поэтому правильный ответ будет 3, а не 2, как мы написали.
Вот тут-то и сыграла свою роковую роль ОДЗ, о которой мы позабыли.
Напомню, что под областью допустимых значений принимаются такие значения х, которые разрешены или имеют смысл для исходного примера.
Без ОДЗ любое решение, даже абсолютно правильное, любого уравнения превращается в лотерею — 50/50.
Как же мы смогли попасться при решении, казалось бы, элементарного примера? А вот именно в момент потенцирования. Логарифмы пропали, а с ними и все ограничения.
Что же в таком случае делать? Отказываться от ликвидации логарифмов? И напрочь отказаться от решения этого уравнения?
Нет, мы просто, как настоящие герои из одной известной песни, пойдем в обход!
Перед тем, как приступать к решению любого логарифмического уравнения, будем записывать ОДЗ. А вот уж после этого можно делать с нашим уравнением все, что душа пожелает. Получив ответ, мы просто выбрасываем те корни, которые не входят в наше ОДЗ, и записываем окончательный вариант.
Теперь определимся, как же записывать ОДЗ. Для этого внимательно осматриваем исходное уравнение и ищем в нем подозрительные места, вроде деления на х, корня четной степени и т.п. Пока мы не решили уравнение, мы не знаем – чему равно х, но твердо знаем, что такие х, которые при подстановке дадут деление на 0 или извлечение квадратного корня из отрицательного числа, заведомо в ответ не годятся. Поэтому такие х неприемлемы, остальные же и будут составлять ОДЗ.
Воспользуемся опять тем же уравнением:
log3 (x 2-3) = log3 (2х)
log3 (x 2-3) = log3 (2х)
Как видим, деления на 0 нет, квадратных корней также нет, но есть выражения с х в теле логарифма. Тут же вспоминаем, что выражение, находящееся внутри логарифма, всегда должно быть >0. Это условие и записываем в виде ОДЗ:
Т.е. мы еще ничего не решали, но уже записали обязательное условие на всё подлогарифмическое выражение. Фигурная скобка означает, что эти условия должны выполняться одновременно.
ОДЗ записано, но необходимо еще и решить полученную систему неравенств, чем и займемся. Получаем ответ x > v3. Теперь точно известно – какие из значений x нам не подойдут. А дальше уже приступаем к решению самого логарифмического уравнения, что мы и сделали выше.
Получив ответы х1= 3 и х2= -1, легко увидеть, что нам подходит лишь х1= 3, его и записываем, как окончательный ответ.
На будущее очень важно запомнить следующее: решение любого логарифмического уравнения делаем в 2 этапа. Первый — решаем само уравнение, второй – решаем условие ОДЗ. Оба этапа выполняются независимо друг от друга и только лишь при написании ответа сопоставляются, т.е. отбрасываем все лишнее и записываем правильный ответ.
Логарифмы в заданиях ЕГЭ
Логарифмы в заданиях ЕГЭ
Борисова Елена Леонидовна,
учитель математики
высшей квалификационной категории
МОУ Левобережная средняя школа
г.Тутаева ярославской области.
Большая часть заданий, включенных в ЕГЭ, представляет собой задания на вычисление
значений числовых логарифмических выражений. При подготовке следует обратить внимание на
формулу перехода к новому основанию логарифма и следствия из нее. Задачи на использование
этих формул в школьных учебниках практически не встречаются.
Проверяемые элементы:
Владение понятием логарифм
Знание основных свойств логарифмов
Умение выполнять тождественные преобразования логарифмических выражений.
Вариант 1.
Найдите значение выражения:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Вариант 2.
Найдите значение выражения:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Вариант 3.
Найдите значение выражения:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Вариант 4.
Найдите значение выражения:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Вариант 5.
Найдите значение выражения:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Вариант 6.
Найдите значение выражения:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Вариант 7.
Найдите значение выражения:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Вариант 8.
Найдите значение выражения:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Вариант 9.
Найдите значение выражения:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Вариант 10.
Найдите значение выражения:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Вариант 11.
Найдите значение выражения:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Вариант 12.
Найдите значение выражения:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Вариант 13.
Найдите значение выражения:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Вариант 14.
Найдите значение выражения:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Вариант15.
Найдите значение выражения:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Используемые источники:
1. ЕГЭ: 4000 задач с ответами по математике. Все задания «Закрытый сегмент». Базовый и
профильный уровни /И.В.Ященко, И.Р.Высоцкий, А.В.Забелин и др.; под редакцией И.В.Ященко. –
М.: Издательство «Экзамен», 2016. – 640 с. (Серия «Банк заданий ЕГЭ»)
2. http://reshuege.ru/
3. http://www.yaklass.ru/materiali?mode=lsntheme&themeid=10
4. http://nsportal.ru/shkola/algebra/library/2012/01/09/svoystva-logarifmov-trenirovochnye-zadaniya
Логарифмические уравнения
Прежде чем решать логарифмические уравнения, повторим еще раз определение логарифма и основные формулы.
Логарифм положительного числа b по основанию a — это показатель степени, в которую надо возвести a, чтобы получить b.
При этом 0,;a> 0,;aneq 1′ alt=’b> 0,;a> 0,;aneq 1′ />.
Обратим внимание на область допустимых значений логарифма:
Основное логарифмическое тождество:
Основные формулы для логарифмов:
(Логарифм произведения равен сумме логарифмов)
(Логарифм частного равен разности логарифмов)
(Формула для логарифма степени)
Формула перехода к новому основанию:
Мы знаем, как выглядит график логарифмической функции. Эта функция монотонна. Если основание логарифма больше единицы, логарифмическая функция монотонно возрастает. Если основание больше нуля и меньше единицы, логарифмическая функция монотонно убывает. И в любом случае каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, то равны и сами числа.
Все это пригодится нам в решении логарифмических уравнений.
Простейшие логарифмические уравнения
Основания логарифмов равны, сами логарифмы тоже равны – значит, равны и числа, от которых они берутся.
Обычно ученики запоминают это правило в краткой жаргонной формулировке: «Отбросим логарифмы!» Конечно, мы «отбрасываем» их не просто так, а пользуясь свойством монотонности логарифмической функции.
Решая логарифмические уравнения, не забываем про область допустимых значений логарифма. Помним, что выражение определено при 0,;a> 0,;aneq 1′ alt=’b> 0,;a> 0,;aneq 1′ />.
Очень хорошо, если вы, найдя корень уравнения, просто подставите его в уравнение. Если после такой подстановки левая или правая часть уравнения не имеют смысла – значит, найденное число не является корнем уравнения и не может быть ответом задачи. Это хороший способ проверки на ЕГЭ.
2. Решите уравнение:
В левой части уравнения – логарифм, в правой – число 7. Применив основное логарифмическое тождество, представим число 7 в виде . Дальше все просто.
3. Решите уравнение:
Видите число 2 перед логарифмом в правой части уравнения? Сейчас оно мешает вам «отбросить логарифмы». Что с ним сделать, чтобы в левой и правой частях были просто логарифмы по основанию 5? Конечно же, поможет формула для логарифма степени.
4. Решите уравнение:
Область допустимых значений: 0.’ alt=’4+x> 0.’ /> Значит, -4.’ alt=’x> -4.’ />
Представим 2 в правой части уравнения как — чтобы слева и справа в уравнении были логарифмы по основанию 5.
Функция монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом -4′ alt=’x> -4′ />.
5. Решите уравнение:
Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:
0\ x^<2>-4> 0\ x^<2>+x=x^<2>-4 endright.Leftrightarrow left <beginx^<2>+x> 0\ x^<2>-4> 0\ x=-4 endright.Leftrightarrow x=-4′ alt=’log _<8>left ( x^<2>+x right )=log _<8>left ( x^<2>-4 right )Leftrightarrow left <beginx^<2>+x> 0\ x^<2>-4> 0\ x^<2>+x=x^<2>-4 endright.Leftrightarrow left <beginx^<2>+x> 0\ x^<2>-4> 0\ x=-4 endright.Leftrightarrow x=-4′ />
Ответ: –4.
Заметим, что решения логарифмических уравнений лучше всего записывать в виде цепочки равносильных переходов. Это поможет нам не забыть про область допустимых значений.
Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2. Мы делаем это по формуле перехода к другому основанию:
Запишем решение как цепочку равносильных переходов.
0 endright.Leftrightarrow left <beginleft (2^<log _<2>left ( 4x+5 right )> right )^<frac<1><2>>=9\ x> -1frac<1> <4>endright.Leftrightarrow left <beginleft ( 4x+5 right )^<frac<1><2>>=9\ x> -1frac<1> <4>endright.Leftrightarrow left <beginsqrt<4x+5>=9\ x> -1frac<1> <4>endright.Leftrightarrow left <begin4x+5=81\ x> -1frac<1> <4>endright.Leftrightarrow left <beginx=19\ x> -1frac<1> <4>endright.’ alt=’2^<log _<4>left ( 4x+5 right )>=9Leftrightarrow left <begin2^frac<<log _<2>left ( 4x+5 right )>><2>=9\ 4x+5> 0 endright.Leftrightarrow left <beginleft (2^<log _<2>left ( 4x+5 right )> right )^<frac<1><2>>=9\ x> -1frac<1> <4>endright.Leftrightarrow left <beginleft ( 4x+5 right )^<frac<1><2>>=9\ x> -1frac<1> <4>endright.Leftrightarrow left <beginsqrt<4x+5>=9\ x> -1frac<1> <4>endright.Leftrightarrow left <begin4x+5=81\ x> -1frac<1> <4>endright.Leftrightarrow left <beginx=19\ x> -1frac<1> <4>endright.’ />
Обратите внимание: переменная х и под логарифмом, и в основании логарифма. Мы помним, что основание логарифма должно быть положительно и не равно 1.
ОДЗ:
0\ x> 0\ xneq 1 endright.’ alt=’left <begin12-x> 0\ x> 0\ xneq 1 endright.’ />
Теперь можно «убрать» логарифмы.
— посторонний корень, поскольку должно выполняться условие 0′ alt=’x> 0′ />.
8. Решите уравнение .
ОДЗ уравнения: 0′ alt=’x> 0′ />
Сделаем замену . Как и в алгебраических уравнениях, мы делаем замену переменной всегда, когда только возможно.
Вернемся к переменной х:
Выражение под логарифмом всегда положительно – поскольку к неотрицательной величине прибавляем 25. Выражение под корнем в правой части также положительно. Значит, х может быть любым действительным числом.
Представим сумму логарифмов в левой части как логарифм произведения. В правой части – перейдем к логарифму по основанию 3. И используем формулу логарифма степени.
Такое уравнение называется биквадратным. В него входят выражения и . Сделаем замену
Вернемся к переменной х. Получим:
. Мы нашли все корни исходного уравнения.
Логарифмические уравнения могут встретиться вам и в задании №1 Профильного ЕГЭ по математике, и в задании №12. И если в задании №1 нужно решить простейшее уравнение, то в задаче 12 решение состоит из двух пунктов. Второй пункт – отбор корней на заданном отрезке или интервале.
Логарифмические уравнения
Логарифмом положительного числа $b$ по основанию $а$, где $a>0, a ≠ 1$, называется показатель степени, в которую надо возвести число $а$, чтобы получить $b$.
$log_<2>8 = 3$, т.к. $2^3 = 8;$
Особенно можно выделить три формулы:
Основное логарифмическое тождество:
Это равенство справедливо при $b> 0, a> 0, a≠ 1$
Некоторые свойства логарифмов
Все свойства логарифмов мы будем рассматривать для $a> 0, a≠ 1, b> 0, c> 0, m$ – любое действительное число.
1. Для любого действительного числа $m$ справедливы равенства:
2. Для решения задач иногда полезно следующее свойство: Если числа $а$ и $b$ на числовой оси расположены по одну сторону от единицы, то $log_b>0$, а если по разные, то $log_b 0$
Представим обе части уравнения в виде логарифма по основанию 2
Если логарифмы по одинаковому основанию равны, то подлогарифмические выражения тоже равны.
Т.к. основания одинаковые, то приравниваем подлогарифмические выражения
Перенесем все слагаемые в левую часть уравнения и приводим подобные слагаемые
Проверим найденные корни по условиям: $<table x^2-3x-5>0; 7-2x>0;$
При подстановке во второе неравенство корень $х=4$ не удовлетворяет условию, следовательно, он посторонний корень
4. Уравнения вида $a^x=b$. Решаются логарифмированием обеих частей по основанию $а$.
Решить уравнение $log_5log_2(x+1)=1$
Сделаем в обеих частях уравнения логарифмы по основанию $5$
Т.к. основания одинаковые, то приравниваем подлогарифмические выражения
Далее представим обе части уравнения в виде логарифма по основанию $2$
ОДЗ данного уравнения $x+1>0$
Подставим вместо х в неравенство $31$ и проверим, получиться ли верное условие $32>0$, следовательно, $31$ корень уравнения.
Логарифмические уравнения.Прототипы В 5
материал для подготовки к егэ (гиа) по алгебре (11 класс) по теме
Подготовка к ЕГЭ
Скачать:
| Вложение | Размер |
|---|---|
| 42626_yu_5.docx | 104.35 КБ |
Предварительный просмотр:
Проверочная работа по математике.
Тема: «Решение логарифмических уравнений». Задания В5 из открытого банка заданий ЕГЭ(http://mathege.ru/)
Задание В5 в ЕГЭ проверяет умение решать простейшие уравнения. Данная разработка посвящена одному из разделов задания В5 – это решение логарифмических уравнений.
Основной задачей является:
— проверка качества знаний и умений учащихся;
-повышение вычислительной культуры учащихся
Представленная проверочная работа состоит из 4вариантов, в каждом из которых по 13 заданий. Задания данной работы соответствуют прототипам заданий В5 из открытого банка заданий ЕГЭ по математике. Данный материал можно использовать при подготовке к ЕГЭ. Для удобства проверки приведены ответы
Тест по логарифмическим уравнениям, задания В5 из открытого банка заданий ЕГЭ вариант1
Тест по логарифмическим уравнениям, задания В5из открытого банка заданий ЕГЭ вариант2
Тест по логарифмическим уравнениям, задания В5 из открытого банка заданий ЕГЭ вариант3.
Тест по логарифмическим уравнениям, задания В5 из открытого банка заданий ЕГЭ вариант4
источники:
http://examer.ru/ege_po_matematike/teoriya/logarifmicheskie_uravneniya
http://nsportal.ru/shkola/algebra/library/2013/11/10/logarifmicheskie-uravneniyaprototipy-v-5
ЕГЭ Профиль №11. Логарифмические функции
Содержание:
Множеством (областью) значений показательной функции
Такое значение аргумента единственное, так как если 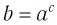
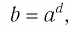
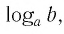
Таким образом, равенство 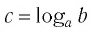
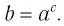
Определение:
Пусть 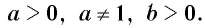
Приведем несколько примеров:
Нахождение логарифма числа называется логарифмированием.
Обозначим 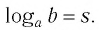
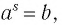
Это равенство называется основным логарифмическим тождеством.
Согласно этому тождеству, например, имеем: 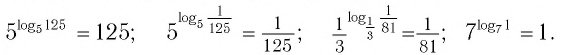
Например:
История логарифма
Логарифмы были изобретены в 1614 г. шотландским математиком Д. Непером (1550—1617) и независимо от него на 6 лет позднее швейцарским механиком и математиком И. Бюрги (1552—1632).
Оба исследователя хотели найти новое удобное средство арифметических вычислений, но их определения логарифма различны и у обоих не похожи на современные. Понимание логарифма как показателя степени с данным основанием впервые появилось в XVIII в. в работах английского математика В. Гардинера (1742). Широкому распространению этого определения логарифма более других содействовал Jl. Эйлер, который впервые применил в этой связи и термин «основание».
Термин «логарифм» принадлежит Неперу. Он возник из сочетания греческих слов логос — отношение и аритмос — число. Слово «логарифм», таким образом, означало «число отношения».
Пример:
а) Записать число 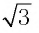
б) Записать число -5 в виде логарифмов по основанию 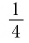
Решение:
а) По определению логарифма имеем:
б) По определению логарифма имеем:
Пример:
Между какими целыми числами находится число
Решение:
Пусть 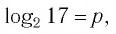
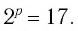
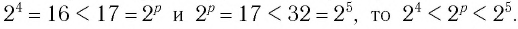
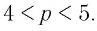
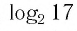
Ответ:
Пример:
Решить уравнение:
Решение:
а) Поскольку 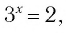
б)
Ответ:
Логарифмы по основанию 10 имеют особое название — десятичные логарифмы. Десятичный логарифм числа b обозначается 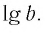
▲ Особое обозначение и название имеют не только десятичные логарифмы, но и логарифмы, основанием которых является число е:
Такие логарифмы называются натуральными.
Логарифмы по основанию е позволяют выражать математическую зависимость, которая характеризует многие биологические, химические, физические, социальные и другие процессы. По-видимому, этим объясняется и название «натуральные логарифмы», т. е. естественные (этот термин ввел в 1659 г. итальянский математик П. Менголи). Натуральные и десятичные логарифмы имели большое значение для облегчения вычислений в XVII—XX вв. до создания мощных современных вычислительных средств. Натуральные логарифмы имеют и большое теоретическое значение.▲
Основные свойства логарифмов
Теорема:
При любых положительных значениях b и с верно равенство:
Доказательство:
Докажем утверждение (1).
По основному логарифмическому тождеству
Таким образом, имеем:
Отсюда по следствию из п. 2.3 получаем равенство (1).
Докажем утверждение (2). Преобразуем левую часть равенства (2):
Заметим, что равенство (2) можно доказать тем же способом, что и равенство (1), — сделайте это самостоятельно.
Равенство (1) означает, что логарифм произведения двух положительных чисел равен сумме логарифмов этих чисел.
Равенство (2) означает, что логарифм дроби с положительными. числителем и знаменателем равен разности логарифмов числителя и знаменателя.
Замечание. Равенства, доказанные в теореме 1 (как и другие равенства этого пункта), являются тождествами. Действительно, каждое из них превращается в верное числовое равенство при любых значениях a, b и с, для которых входящие в равенство выражения имеют смысл.
Теорема:
При любых значениях s и положительных значениях b верно равенство
Доказательство:
По основному логарифмическому тождеству
Таким образом, имеем
Отсюда по следствию из п. 2.3 получаем равенство (3).
Следствие 1. Если числа 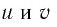
Следствие 2. При любом целом 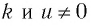
Пример №1
Найти значение выражения:
Решение:
Ответ:
Теорема:
При любых значениях 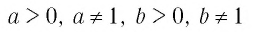
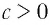
Доказательство:
Способ 1. По основному логарифмическому тождеству имеем
Прологарифмировав левую и правую части этого тождества по основанию а, получим
Применив тождество (3), имеем
Так как 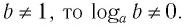
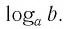
Способ 2. Пусть 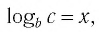
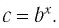
Откуда имеем
Итак,
Тождество (6) называется формулой перехода от логарифма по одному основанию к логарифму по другому основанию.
Обычно в таблицах, калькуляторах даются значения логарифмов по основанию 10, а когда нужно найти значение логарифма по другому основанию, пользуются формулой перехода от логарифма по одному основанию к логарифму по другому основанию.
Следствием из тождества (6) при основании а = с является формула
(убедитесь в этом самостоятельно).
Пример №2
Найти значение выражения, если
Решение:




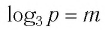
6)


Ответ:
Следствие 3. Имеют место тождества:
Тождества (8) и (9) можно доказать, используя уже доказанные тождества из этого пункта.
Пример №3
Упростить выражение
Решение:
Используя определение логарифма, представим числа 1 и 3 в виде логарифмов по основанию 2:
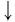
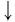
Ответ:
Развитие науки, прежде всего астрономии, уже в XVI в. привело к необходимости громоздких вычислений при умножении и делении многозначных чисел. Эти вычислительные проблемы были в некоторой степени решены с открытием логарифмов и созданием таблиц логарифмов.
Логарифмическая функция
Рассмотрим выражение 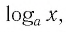
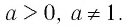
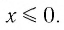
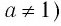
Определение:
Логарифмической функцией называется функция вида 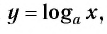
Область определения логарифмической функции — это естественная область определения выражения 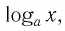
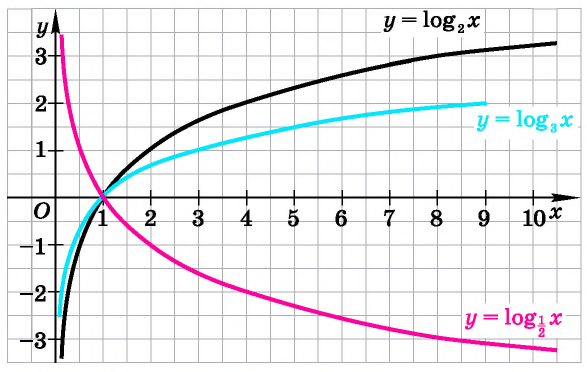
Графики некоторых логарифмических функций изображены на рисунке 34. Эти изображения (как и для графиков других функций) можно было получить, строя их по точкам. Отметим некоторые особенности изображенных графиков.
График функции 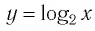
Когда значения аргумента х уменьшаются, т. е. приближаются к нулю, то график этой функции «приближается» к оси Оу и при этом «круто» опускается вниз. А когда значения аргумента х увеличиваются, то график «медленно» поднимается вверх (ем. рис. 34). Аналогично для любой функции 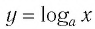
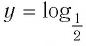
Заметим, что когда значения аргумента х уменьшаются, т. е. приближаются к нулю, то график этой функции «приближается» к оси Оу и при этом «круто» поднимается вверх. А когда значения аргумента х увеличиваются, то график «медленно» опускается вниз. Аналогично для любой функции 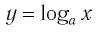
Теорема (о свойствах логарифмической функции 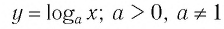
- Областью определения логарифмической функции является интервал
- Множеством (областью) значений логарифмической функции является множество R всех действительных чисел.
- Логарифмическая функция не имеет ни наименьшего, ни наибольшего значений.
- График логарифмической функции пересекается с осью абсцисс в точке (1; 0) и не пересекается с осью ординат.
- Значение аргумента х = 1 является нулем логарифмической функции.
- 6. При а > 1 логарифмическая функция принимает отрицательные значения на интервале (0; 1) и принимает положительные значения на интервале
И при 0 < а < 1 логарифмическая функция принимает отрицательные значения на интервале
и принимает положительные значения на интервале (0; 1).
- Логарифмическая функция не является ни четной, ни нечетной.
- При а > 1 логарифмическая функция возрастает на всей области определения. При 0 < а < 1 логарифмическая функция убывает на всей области определения.
- Логарифмическая функция не является периодической.
Изображение графика логарифмической функции позволяет наглядно представить эти свойства.
Множество (область) значений логарифмической функции — проекция ее графика на ось Оу, а на рисунках 35 и 36 видно, что эта проекция есть ось Оу. Это значит, что для любой точки 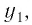
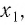
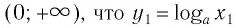
Множество (область) значений логарифмической функции — это множество всех действительных чисел, а в нем нет ни наименьшего числа, ни наибольшего (свойство 3).
График логарифмической функции проходит через точку (1; 0) и лежит в правой полуплоскости (свойства 4, 5).
При а > 1 график логарифмической функции лежит в IV координатном угле, когда 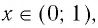
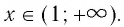
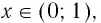
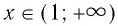
Область определения логарифмической функции — интервал 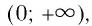
На рисунке 35 видно, что при а > 1 логарифмическая функция возрастает на области определения, а на рисунке 36 видно, что при 0 < а < 1 логарифмическая функция убывает на области определения (свойство 8).
Пусть точка 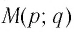
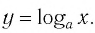
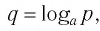
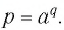
Заметим, что точки 
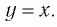
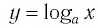
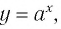
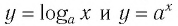
Последнее утверждение дает возможность, зная график функции 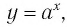
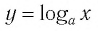
▲ Симметричность графиков функций 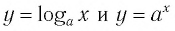
Функции 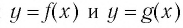
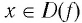
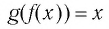
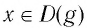
Покажем, что показательная и логарифмическая функции с одним, и тем же основанием а взаимно обратны.
Пусть 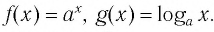
Для любого
Для любого
Покажем, что графики взаимно обратных функций 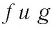
Пусть точка 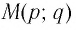
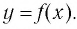
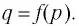
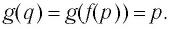
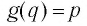
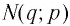
Таким образом, каждой точке М на графике функции 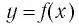
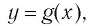
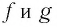
- Заказать решение задач по высшей математике
Логарифмы и их свойства
В предыдущем параграфе вы находили корни уравнения вида 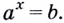
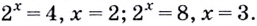
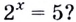
Для записи корней показательного уравнения используют понятие «логарифм» и соответствующий символ. Корнем уравнения 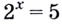
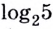
Рассмотрим общий случай-.
Пусть 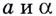
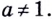
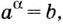
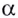
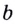
Логарифмом числа 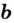
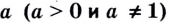
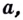
Логарифм числа 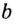
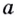
Примеры:
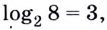
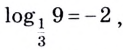
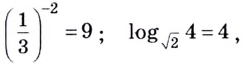
Основанием логарифма может быть произвольное положительное число, кроме единицы. Как известно, если 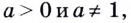
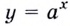
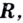
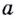
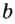
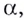
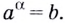
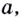
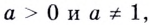
Полезно помнить, что для каждого
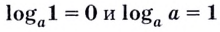
Нахождение логарифма числа называют логарифмированием. Эта операция обратная к операции возведения в степень с соответствующим основанием.
Согласно определению логарифма, если 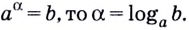
которое называют основным логарифмическим тождеством. Оно правильное для любых положительных
Например:
С помощью основного логарифмического тождества любое положительное число можно представить в виде степени, имеющей заданное основание.
Например:
Докажем ещё несколько важных свойств логарифмов (для положительных
1) По основному логарифмическому тождеству и основному свойству степени
Итак, 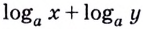
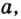
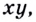
Эту формулу можно обобщить на три и более множителя:
Кратко говорят: логарифм произведения равен сумме логарифмов множителей.
2) Доказательство аналогичное предыдущему:
отсюда
Кратко говорят: логарифм частного равен разности логарифмов делимого и делителя.
3) Возведём обе части тождества 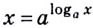
Итак,
Доказанные формулы можно использовать и справа налево, например:
В логарифмах переходить от одного основания к другому можно при помощи формулы перехода
где
Докажем эту формулу. Поскольку положительные числа 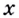
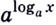
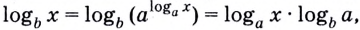
Обратите внимание! Как следствия из формулы перехода можно получить следующие формулы:
Докажите их самостоятельно.
Пример №4
Упростите выражение 
Решение:
Сведём все логарифмы к основанию 5. Имеем:
Особенно часто используют логарифмы по основаниям 10 и 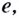
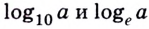
Рассмотренные в параграфе свойства логарифмов правиль-1 ные при условии, что переменные принимают положительные значения. С помощью модуля можно расширить использование некоторых формул. Например:
Для преобразования выражений, решения уравнений и неравенств используют и другие формулы, содержащие логарифмы:
Докажите их самостоятельно.
Пример №5
Вычислите:
Решение:
Пример №6
Решите уравнение:
Решение:
Пусть 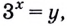
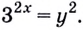
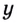
Получим: 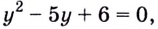
Поскольку 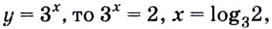
Ответ.
Пример №7
Найдите 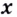
Решение:
Поскольку
Ответ.
Пример №8
Вычислите 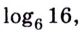
Решение:
Ответ.
- Корень из числа — нахождение и вычисление
- Теория множеств — виды, операции и примеры
- Числовые множества
- Вектор — определение и основные понятия
- Бесконечно убывающая геометрическая прогрессия
- Периодические дроби
- Степень с рациональным показателем
- Степень с действительным показателем



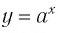
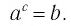
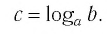
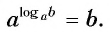
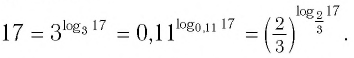
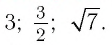
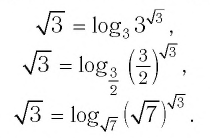
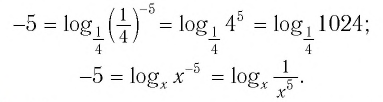
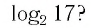
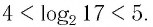
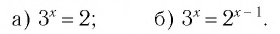
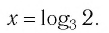
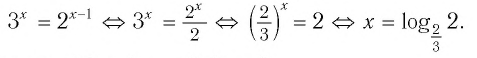
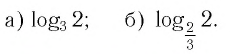
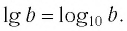
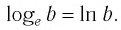
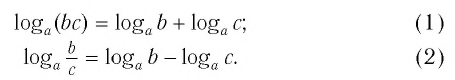
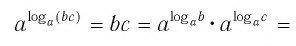
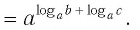
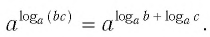
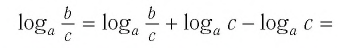
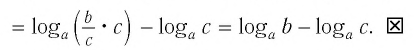

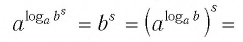
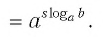
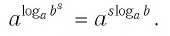

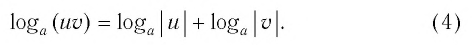
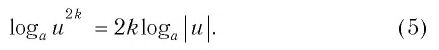
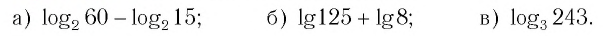
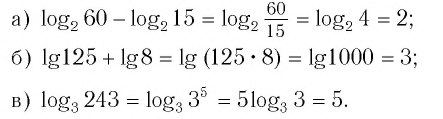
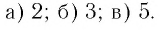

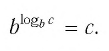
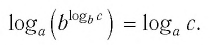
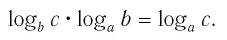

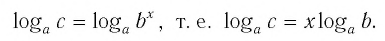
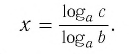
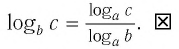

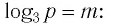
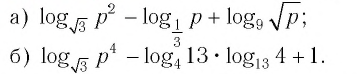
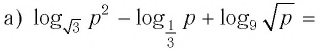
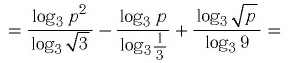
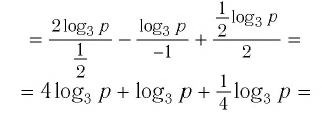
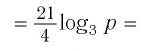
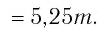
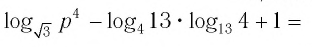
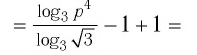
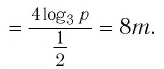

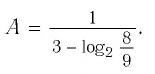
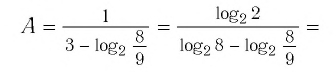
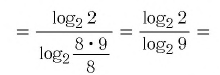
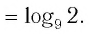
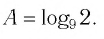
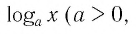
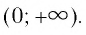
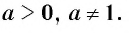
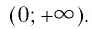
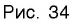
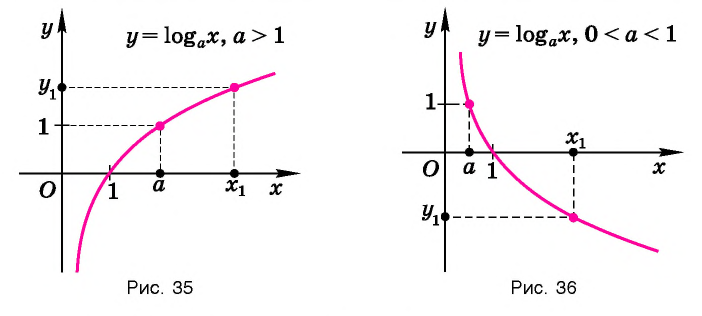
 И при 0 < а < 1 логарифмическая функция принимает отрицательные значения на интервале
И при 0 < а < 1 логарифмическая функция принимает отрицательные значения на интервале 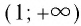 и принимает положительные значения на интервале (0; 1).
и принимает положительные значения на интервале (0; 1).