Логарифмические функции 9 задание егэ - Помощь в подготовке к экзаменам и поступлению

Поиск

Всего: 27 1–20 | 21–27

Добавить в вариант

Источник: Пробный экзамен по математике Кировского района Санкт-Петербурга, 2015. Вариант 2.

Найдите наименьшее значение функции

Найдите наибольшее значение функции

Найдите наименьшее значение функции

Найдите точку максимума функции

Найдите наибольшее значение функции

Найдите наименьшее значение функции

Найдите наибольшее значение функции на отрезке

Найдите наименьшее значение функции

Найдите точку максимума функции

Всего: 27 1–20 | 21–27

Источник

Главная
Новости
ЕГЭ
- ЕГЭ Профиль 2023
- ЕГЭ Профиль 2022
- ЕГЭ Профиль 2016-2021
- Варианты профильного ЕГЭ
- ЕГЭ База 2023
- ЕГЭ База 2022
- ЕГЭ База 2016-2021
ОГЭ
- ОГЭ 2019
- ОГЭ 2023
ГВЭ
- ГВЭ 11 класс
ВПР
- ВПР 4 класс
- ВПР 5 класс
- ВПР 6 класс
- ВПР 7 класс
- ВПР 8 класс
Алгебра
- Алгебра 7-9
- Алгебра 10-11
Геометрия
- Геометрия 7-9
- Геометрия 10-11
YouTube
Прочее
- Class100
- Разработки
- Обо мне
- Репетитор

ЕГЭ Профиль №9. Логарифмическая и показательная функции

ЕГЭ Профиль №9. Логарифмическая и показательная функцииadmin2022-08-22T14:16:20+03:00

Скачать файл в формате pdf.

ЕГЭ Профиль №9. Логарифмическая и показательная функции

Задача 1. На рисунке изображён график функции (fleft( x right) = b + {log _a}x.) Найдите (fleft( {27} right).) Ответ ОТВЕТ: 1.
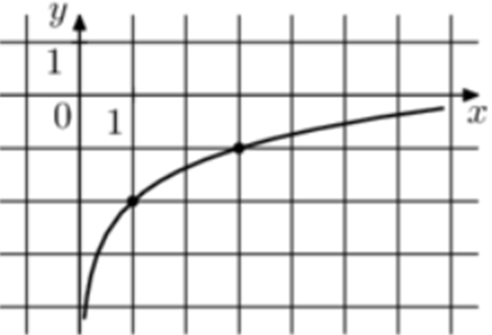Задача 2. На рисунке изображён график функции (fleft( x right) = b + {log _a}x.) Найдите (fleft( {16} right).) Ответ ОТВЕТ: 7.
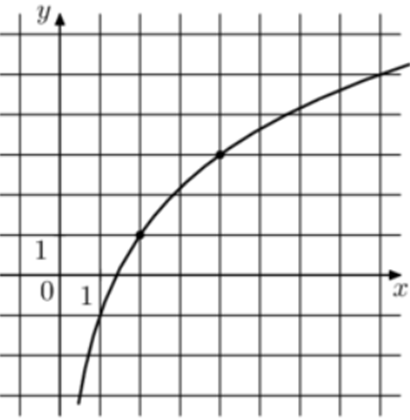Задача 3. На рисунке изображён график функции (fleft( x right) = b + {log _a}x.) Найдите (fleft( {128} right).) Ответ ОТВЕТ: — 5.
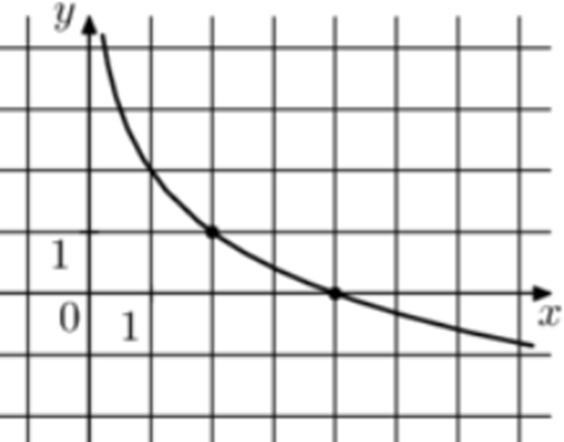Задача 4. На рисунке изображён график функции (fleft( x right) = b + {log _a}x.) Найдите (fleft( {0,125} right).) Ответ ОТВЕТ: 5.
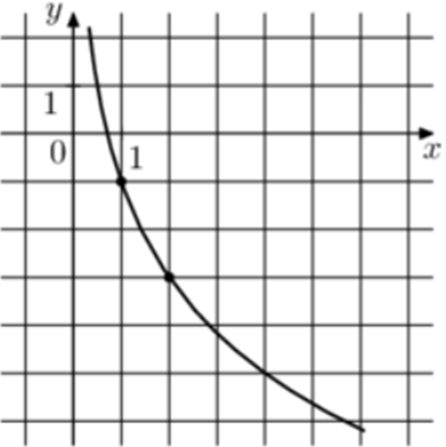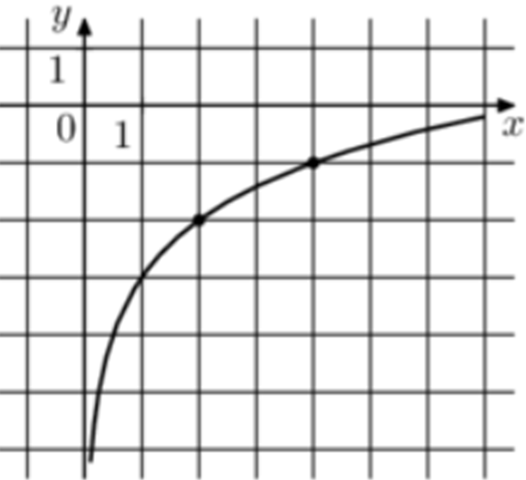
Задача 5. На рисунке изображён график функции (fleft( x right) = b + {log _a}x.) Найдите значение x при котором (fleft( x right) = 3.) Ответ ОТВЕТ: 64.
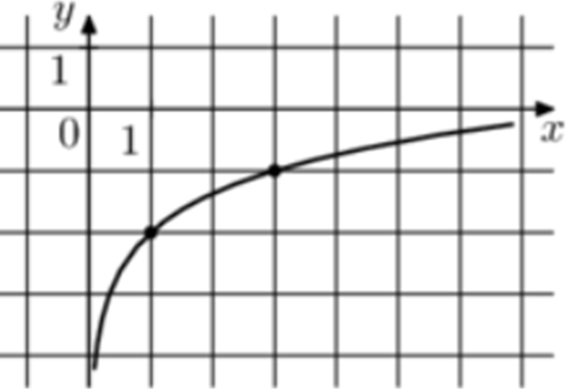
Задача 6. На рисунке изображён график функции (fleft( x right) = b + {log _a}x.) Найдите значение x при котором (fleft( x right) = 2.) Ответ ОТВЕТ: 81.
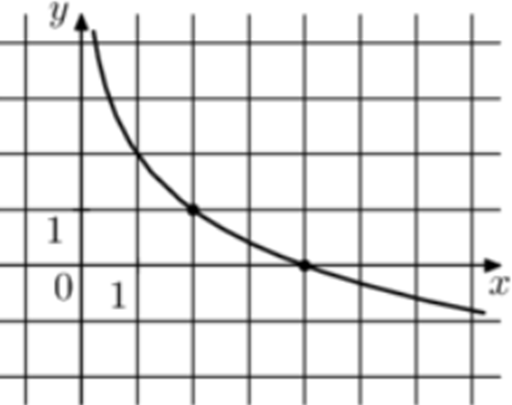
Задача 7. На рисунке изображён график функции (fleft( x right) = b + {log _a}x.) Найдите значение x при котором (fleft( x right) = — 3.) Ответ ОТВЕТ: 32.
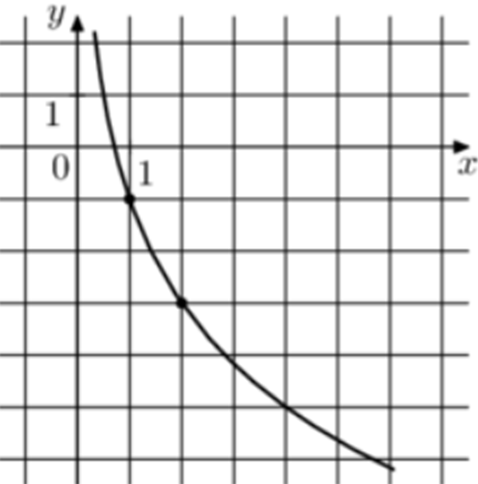
Задача 8. На рисунке изображён график функции (fleft( x right) = b + {log _a}x.) Найдите значение x при котором (fleft( x right) = 3.) Ответ ОТВЕТ: 0,25.
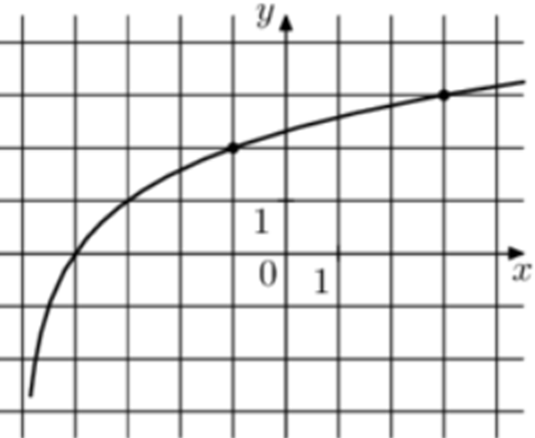
Задача 9. На рисунке изображён график функции (fleft( x right) = {log _a}left( {x + b} right).) Найдите (fleft( {27} right).) Ответ ОТВЕТ: 5.
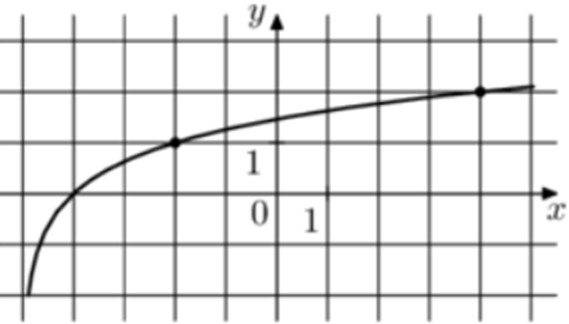
Задача 10. На рисунке изображён график функции (fleft( x right) = {log _a}left( {x + b} right).) Найдите (fleft( {238} right).) Ответ ОТВЕТ: 5.
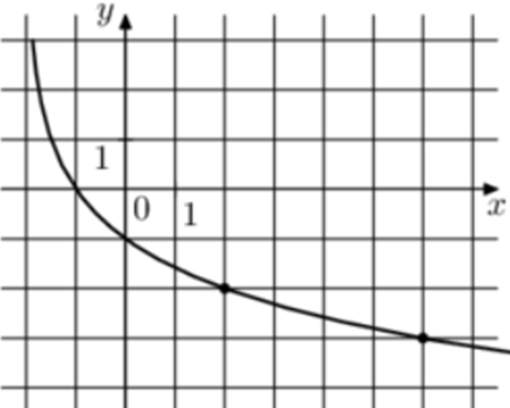
Задача 11. На рисунке изображён график функции (fleft( x right) = {log _a}left( {x + b} right).) Найдите (fleft( {30} right).) Ответ ОТВЕТ: — 5.
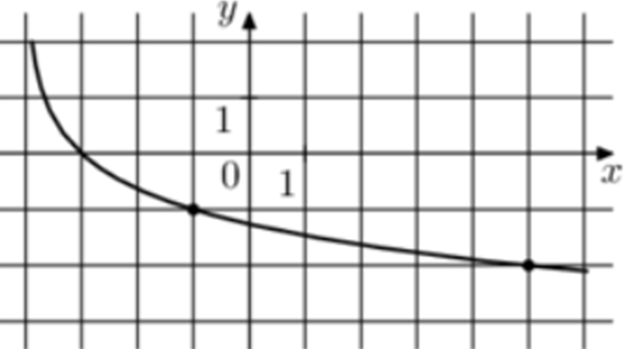
Задача 12. На рисунке изображён график функции (fleft( x right) = {log _a}left( {x + b} right).) Найдите (fleft( {77} right).) Ответ ОТВЕТ: — 4.
Задача 13. На рисунке изображён график функции (fleft( x right) = {log _a}left( {x + b} right).) Найдите значение x, при котором (fleft( x right) = 6.) Ответ ОТВЕТ: 59.
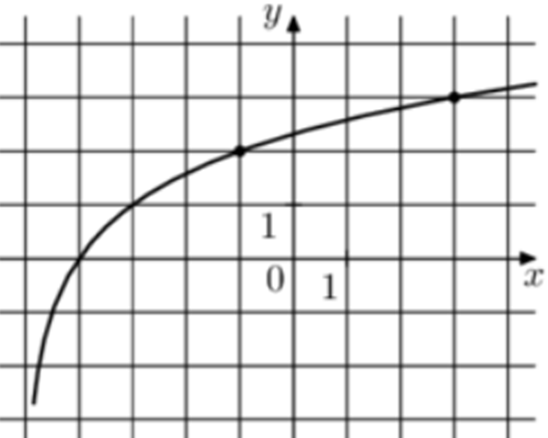Задача 14. На рисунке изображён график функции (fleft( x right) = {log _a}left( {x + b} right).) Найдите значение x, при котором (fleft( x right) = 5.) Ответ ОТВЕТ: 31.
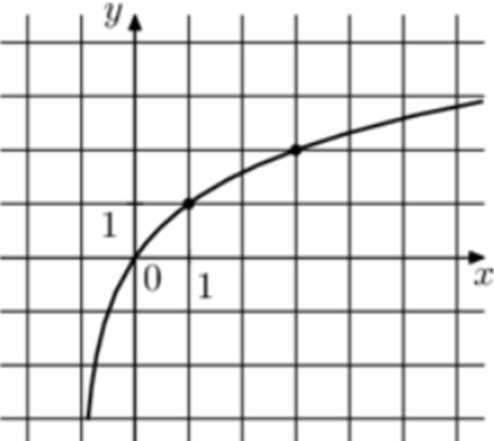Задача 15. На рисунке изображён график функции (fleft( x right) = {log _a}left( {x + b} right).) Найдите значение x, при котором (fleft( x right) = — 8.) Ответ ОТВЕТ: 79.
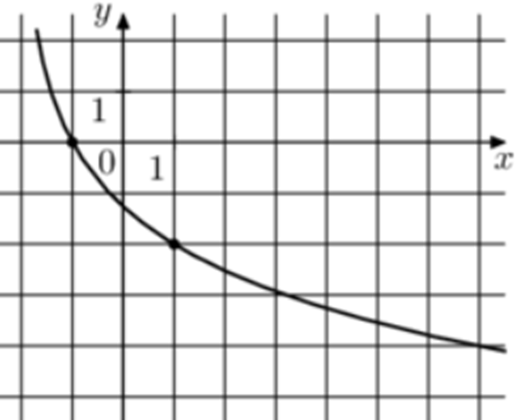Задача 16. На рисунке изображён график функции (fleft( x right) = {log _a}left( {x + b} right).) Найдите значение x, при котором (fleft( x right) = — 5.) Ответ ОТВЕТ: 239.

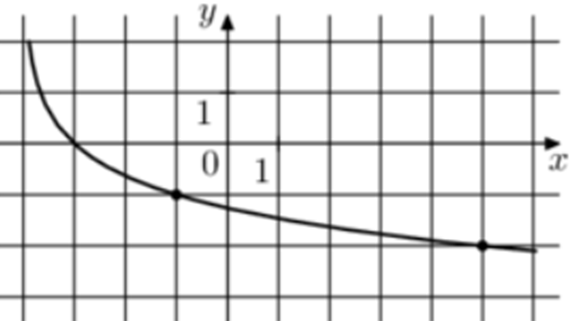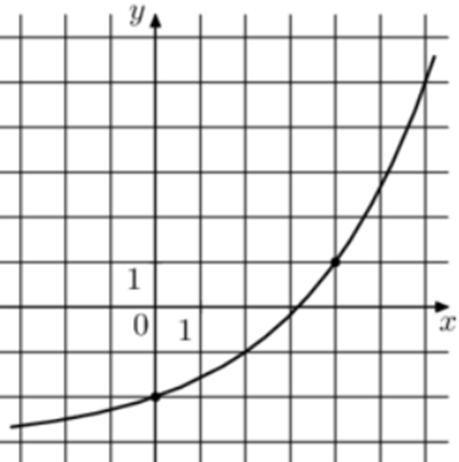
Задача 17. На рисунке изображён график функции (fleft( x right) = {a^x} + b.) Найдите (fleft( {10} right).) Ответ ОТВЕТ: 29.
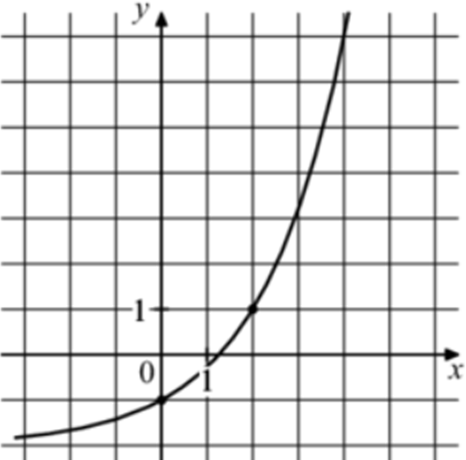
Задача 18. На рисунке изображён график функции (fleft( x right) = {a^x} + b.) Найдите (fleft( 8 right).) Ответ ОТВЕТ: 79.
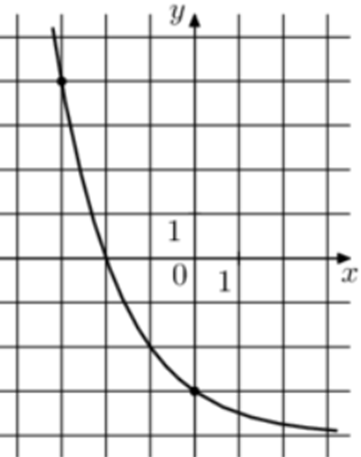
Задача 19. На рисунке изображён график функции (fleft( x right) = {a^x} + b.) Найдите (fleft( { — 5} right).) Ответ ОТВЕТ: 28.
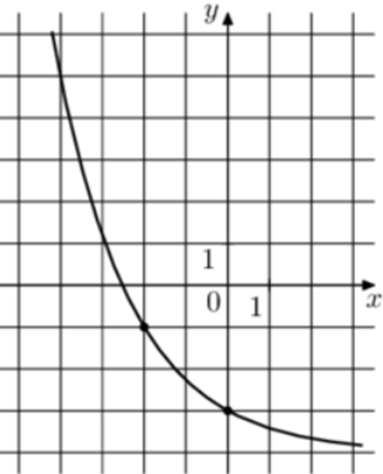
Задача 20. На рисунке изображён график функции (fleft( x right) = {a^x} + b.) Найдите (fleft( { — 8} right).) Ответ ОТВЕТ: 77.
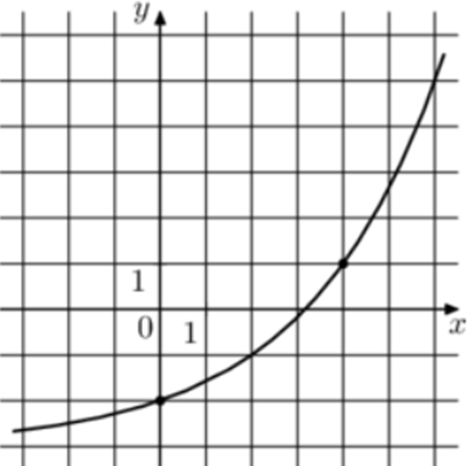
Задача 21. На рисунке изображён график функции (fleft( x right) = {a^x} + b.) Найдите значение x, при котором (fleft( x right) = 13.) Ответ ОТВЕТ: 8.
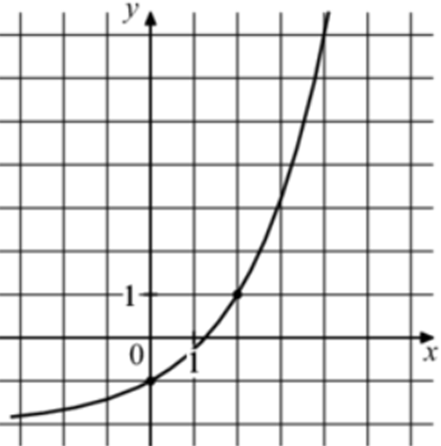
Задача 22. На рисунке изображён график функции (fleft( x right) = {a^x} + b.) Найдите значение x, при котором (fleft( x right) = 25.) Ответ ОТВЕТ: 6.
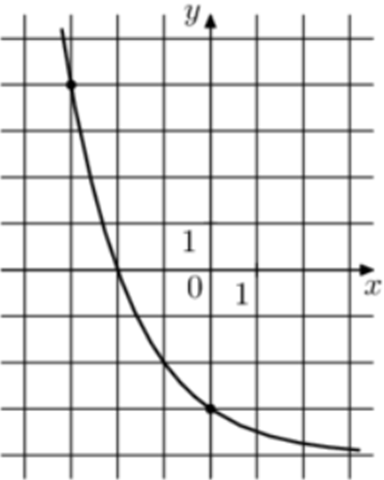
Задача 23. На рисунке изображён график функции (fleft( x right) = {a^x} + b.) Найдите значение x, при котором (fleft( x right) = 12.) Ответ ОТВЕТ: — 4.
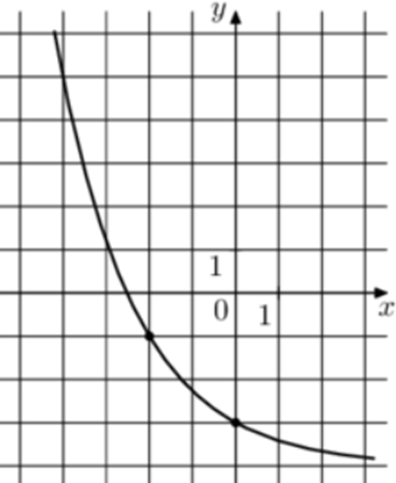
Задача 24. На рисунке изображён график функции (fleft( x right) = {a^x} + b.) Найдите значение x, при котором (fleft( x right) = 23.) Ответ ОТВЕТ: — 6.
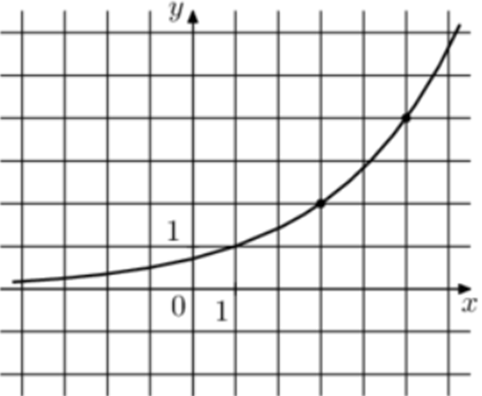
Задача 25. На рисунке изображён график функции (fleft( x right) = {a^{x + b}}.) Найдите (fleft( { — 5} right).) Ответ ОТВЕТ: 0,125.
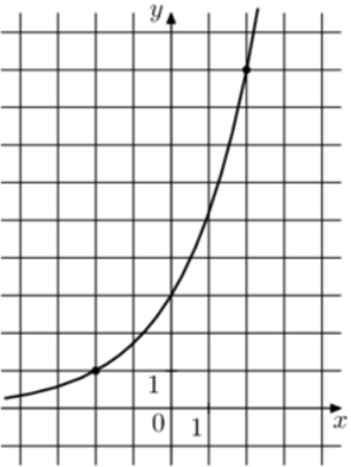
Задача 26. На рисунке изображён график функции (fleft( x right) = {a^{x + b}}.) Найдите (fleft( 6 right).) Ответ ОТВЕТ: 81.
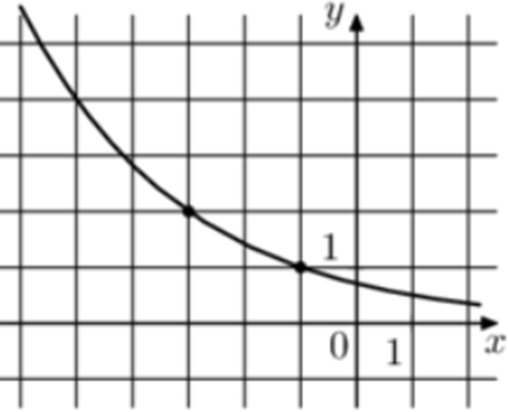
Задача 27. На рисунке изображён график функции (fleft( x right) = {a^{x + b}}.) Найдите (fleft( { — 9} right).) Ответ ОТВЕТ: 16.
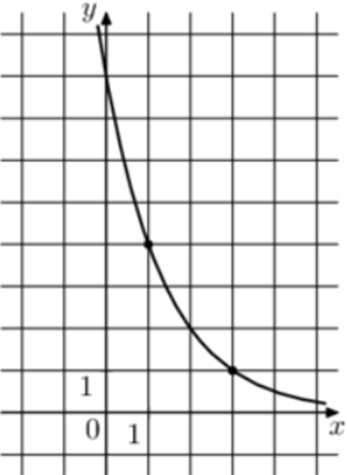
Задача 28. На рисунке изображён график функции (fleft( x right) = {a^{x + b}}.) Найдите (fleft( { — 2} right).) Ответ ОТВЕТ: 32.
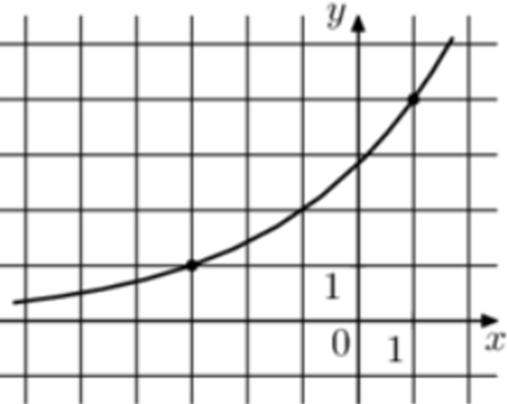
Задача 29. На рисунке изображён график функции (fleft( x right) = {a^{x + b}}.) Найдите значение x, при котором (fleft( x right) = 16.) Ответ ОТВЕТ: 5.
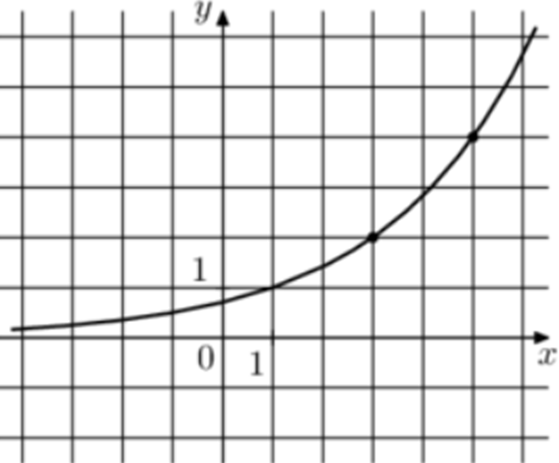
Задача 30. На рисунке изображён график функции (fleft( x right) = {a^{x + b}}.) Найдите значение x, при котором (fleft( x right) = 0,125.) Ответ ОТВЕТ: — 5.
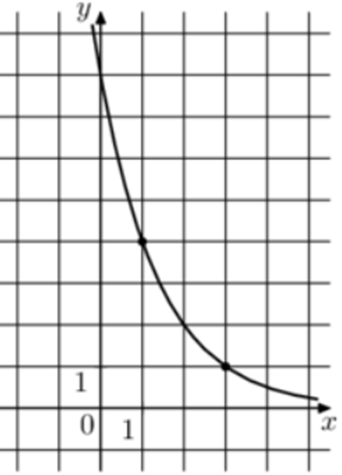
Задача 31. На рисунке изображён график функции (fleft( x right) = {a^{x + b}}.) Найдите значение x, при котором (fleft( x right) = 64.) Ответ ОТВЕТ: — 3.
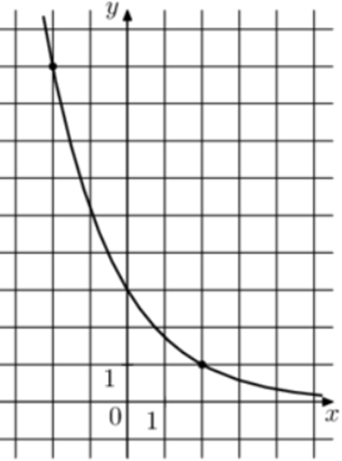
Задача 32. На рисунке изображён график функции (fleft( x right) = {a^{x + b}}.) Найдите значение x, при котором (fleft( x right) = 81.) Ответ ОТВЕТ: — 6.

Источник

В 2022 году в вариантах ЕГЭ Профильного уровня появилась задание №10 по теме «Графики функций». Можно считать его подготовительным для освоения задач с параметрами.

Как формулируется задание 10 ЕГЭ по математике? По графику функции, который дается в условии, вам нужно определить неизвестные параметры в ее формуле. Возможно — найти значение функции в некоторой точке или координаты точки пересечения графиков функций.

Чтобы выполнить это задание, надо знать, как выглядят и какими свойствами обладают графики элементарных функций. Надо уметь читать графики, то есть получать из них необходимую информацию. Например, определять формулу функции по ее графику.

Вот необходимая теория для решения задания №10 ЕГЭ.

Что такое функция

Чтение графика функции

Четные и нечетные функции

Периодическая функция

Обратная функция

5 типов элементарных функций и их графики

Преобразование графиков функций

Построение графиков функций

Да, теоретического материала здесь много. Но он необходим — и для решения задания 10 ЕГЭ, и для понимания темы «Задачи с параметрами», а также для дальнейшего изучения математики на первом курсе вуза.

Рекомендации:

Запоминай, как выглядят графики основных элементарных функций. Замечай особенности графиков, чтобы не перепутать параболу с синусоидой : -)

Проверь себя: какие действия нужно сделать с формулой функции, чтобы сдвинуть ее график по горизонтали или по вертикали, растянуть, перевернуть?

Разбирая решения задач, обращай внимание на то, как мы ищем точки пересечения графиков или неизвестные переменные в формуле функции. Такие элементы оформления встречаются также в задачах с параметрами.

Задание 10 в формате ЕГЭ-2021

Линейная функция

Необходимая теория

1. На рисунке изображён график функции . Найдите значение , при котором

Решение:

Найдем, чему равны k и b. График функции проходит через точки (3; 4) и (-1; -3). Подставив по очереди координаты этих точек в уравнение прямой y = kx + b, получим систему:

$left{ begin{array}{c}3k+b=4 \-k+b=-3 end{array}right..$

Вычтем из первого уравнения второе:

$left{ begin{array}{c}4k=7 \-k+b=-3 end{array};right. left{ begin{array}{c}k=frac{7}{4} \b=-frac{5}{4} end{array}right. .$

Уравнение прямой имеет вид:

$displaystyle y=frac{7}{4}x-frac{5}{4}.$

Найдем, при каком значение функции равно -13,5.

$displaystyle frac{7}{4}x-frac{5}{4}=-13,5;$

7x=-49;

x=-7.

Ответ: -7.

2. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

Решение:

Запишем формулы функций.

Одна из них проходит через точку (0; 1) и ее угловой коэффициент равен -1. Это линейная функция y=-x+1.

Другая проходит через точки (-1; -1) и (-2; 4). Подставим по очереди координаты этих точек в формулу линейной функции y=kx+b.

$left{ begin{array}{c}-k+b=-1 \-2k+b=4 end{array}right. .$

Вычтем из первого уравнения второе.

k=-5; тогда b=-6.

Прямая задается формулой:

Найдем абсциссу точки пересечения прямых. Эта точка лежит на обеих прямых, поэтому:

$left{ begin{array}{c}y=-x+1 \y=-5x-6 end{array} ;right. begin{array}{c}-x+1=-5x-6 ; \x=-frac{7}{4}=-1,75. end{array}$

Ответ: -1,75.

3. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

Решение:

Прямая, расположенная на рисунке ниже, задается формулой y=x+1, так как ее угловой коэффициент равен 1 и она проходит через точку (-3; -2).

Для прямой, расположенной выше, угловой коэффициент равен $displaystyle frac{3}{2}=1,5.$

Эта прямая проходит через точку (-2; 4), поэтому: b=7, эта прямая задается формулой

Для точки пересечения прямых:

x=-12.

Ответ: -12.

Квадратичная функция. Необходимая теория

4. На рисунке изображен график функции Найдите b.

Решение:

На рисунке — квадратичная парабола $y={left(x-aright)}^2,$ полученная из графика функции y=x^2 сдвигом на 1 вправо, то есть a=1.

Получим: $fleft(xright)={left(x-1right)}^2=x^2-2x+1;$

b=-2.

Ответ: -2.

5. На рисунке изображен график функции $y={left(x-cright)}^2$ . Найдите с.

Решение:

На рисунке изображена парабола, ветви которой направлены вверх, значит, коэффициент при x^2 положительный. График сдвинут относительно графика функции y=x^2 на 1 единицу вправо вдоль оси Ох. Формула функции имеет вид $y={left(x-1right)}^2$ .

Значит, с = 1.

Ответ: 1

6. На рисунке изображён график функции Найдите

Решение:

График функции проходит через точки с координатами (1; 1) и (-2; -2). Подставляя координаты этих точек в формулу функции, получим:

$left{ begin{array}{c}2+b+c=1 \2cdot 4-2b+c=-2 end{array}right. .$

$left{ begin{array}{c}b+c=-1 \-2b+c=-10 end{array};right.$ отсюда b=3, c=-4.

Формула функции имеет вид:

Ответ: 31.

7. На рисунке изображены графики функций и которые пересекаются в точках А и В. Найдите абсциссу точки В.

Решение:

Найдем a, b и c в формуле функции . График этой функции пересекает ось ординат в точке (0; -3), поэтому c=-3.

График функции g(x) проходит через точки (-1; -3) и (2; 3). Подставим по очереди координаты этих точек в формулу функции:

$left{ begin{array}{c}a-b-3=-3 \4a+2b-3=3 end{array};right.$ отсюда a=b=1;

Найдем абсциссу точки B. Для точек A и B:

x=-2 (это абсцисса точки A) или x=6 (это абсцисса точки B).

Ответ: 6.

Степенные функции. Необходимая теория

8. На рисунке изображены графики функций $displaystyle fleft(xright)=frac{k}{x}$ и , которые пересекаются в точках А и В. Найдите абсциссу точки В.

Решение:

График функции $displaystyle y=frac{k}{x}$ проходит через точку (2; 1); значит, $displaystyle frac{k}{2}=1;$

$displaystyle k=2, ; fleft(xright)=frac{2}{x}.$

График функции проходит через точки (2; 1) и (1; -4), a=5 — угловой коэффициент прямой; (находим как тангенс угла наклона прямой и положительному направлению оси X); тогда b=-9.

Для точек A и B имеем:

$displaystyle frac{2}{x}=5x-9;$

Отсюда x=2 (абсцисса точки A) или x=-0,2 (абсцисса точки B).

Ответ: -0,2.

9. На рисунке изображён график функции . Найдите f (6,76).

Решение:

Функция задана формулой:

Ее график проходит через точку (4; 5); значит, k=2,5;

Тогда

Ответ: 6,5.

10. На рисунке изображен график функции . Найдите .

Решение:

График функции на рисунке симметричен графику функции относительно оси Y. Он проходит через точку (-1; 1). Значит, формула изображенной на рисунке функции: , а = — 1. Тогда = 5.

Ответ: 5.

Показательная функция. Необходимая теория

11. На рисунке изображён график функции $fleft(xright)=a^{x+b}.$ Найдите

Решение:

График функции проходит через точки (-3; 1) и (1; 4). Подставив по очереди координаты этих точек в формулу функции $fleft(xright)=a^{x+b},$ получим:

$left{ begin{array}{c}a^{-3+b}=1 \a^{1+b}=4 end{array}.right.$

Поделим второе уравнение на первое:

$a^{1+b+3-b}=4; ; a^4=4;; a=sqrt{2}.$

Подставим во второе уравнение:

$displaystyle {sqrt{2}}^{1+b}=4;; 2^{frac{1+b}{2}}=2^2;; 1+b=4;; b=3.$

$displaystyle fleft(xright)={left(sqrt{2}right)}^{x+3};; fleft(-7right)={left(sqrt{2}right)}^{-7+3}={left(sqrt{2}right)}^{-4}=frac{1}{4}=0,25.$

Ответ: 0,25.

12. На рисунке изображен график функции . Найдите

Решение:

График функции проходит через точку Это значит, что

a=2, формула функции имеет вид: .

Ответ: 2.

Логарифмическая функция. Необходимая теория

13. На рисунке изображён график функции $fleft(xright)={{log}_a left(x+bright)}.$ Найдите

Решение:

График функции $y={{log}_a left(x+bright) }$ проходит через точки (-3; 1) и (-1; 2). Подставим по очереди эти точки в формулу функции.

$left{ begin{array}{c}{{log}_a left(-3+bright)=1 } \{{log}_a left(-1+bright) }=2 end{array}.right.$

Отсюда: $left{ begin{array}{c}b-3=a \b-1=a^2 end{array}.right.$

Вычтем из второго уравнения первое:

a=2 или a=-1 — не подходит, так как (как основание логарифма).

Тогда $fleft(xright)={{log}_2 left(x+5right) };$

$fleft(11right)={{log}_2 16=4.}$

Ответ: 4.

14. На рисунке изображен график функции $fleft(xright)=a{{log}_5 x }-c$ .

Найдите f(0,2).

Решение:

График логарифмической функции на рисунке проходит через точки и . Подставив по очереди координаты этих точек в формулу функции, получим систему уравнений:

$left{ begin{array}{c}a{{log}_5 1 }-c=-2 \a{{log}_5 5 }-c=3 end{array};right.$

$left{ begin{array}{c}-c=-2 \a-c=3 end{array};right.$

$left{ begin{array}{c}c=2 \a=5 end{array}.right.$

Формула функции: $fleft(xright)=5{{log}_5 x }-2.$

Найдем $displaystyle fleft(0,2right)=fleft(frac{1}{5}right)$ :

$displaystyle 5cdot {{log}_5 frac{1}{5} }-2=-5-2=-7.$

Ответ: -7.

Тригонометрические функции. Необходимая теория

15. На рисунке изображён график функции Найдите

Решение:

График функции сдвинут на 1,5 вверх; Значит, b=1,5. Амплитуда a=2 (наибольшее отклонение от среднего значения).

Это график функции Он получен из графика функции растяжением в 2 раза по вертикали и сдвигом вверх на 1,5 .

Ответ: b=1,5.

16. На рисунке изображён график функции

Найдите .

Решение:

На рисунке — график функции Так как b=-1,5.

График функции проходит через точку A $displaystyle (frac{pi}{4}; ; frac{1}{2}).$ Подставим и координаты точки А в формулу функции.

$displaystyle a tg frac{pi}{4}-1,5=frac{1}{2}.$

Так как $displaystyle tg frac{pi}{4}=1,$ получим: a = 2.

Ответ: 2.

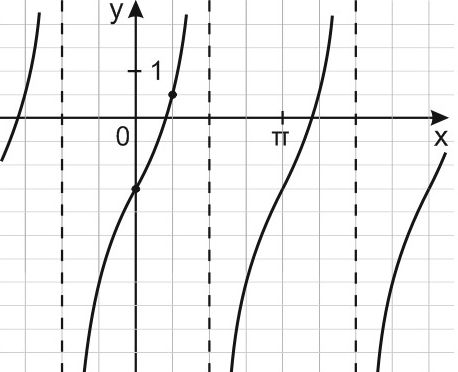
17. На рисунке изображен график периодической функции у = f(x). Найдите значение выражения

Решение:

Функция, график которой изображен на рисунке, не только периодическая, но и нечетная, и если то

Пользуясь периодичностью функции , период которой T = 4, получим:

Ответ: 5.

Друзья, мы надеемся, что на уроках математики в школе вы решаете такие задачи. Для углубленного изучения темы «Функции и графики» (задание 10 ЕГЭ по математике), а также задач с параметрами и других тем ЕГЭ — рекомендуем Онлайн-курс для подготовки к ЕГЭ на 100 баллов.

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 10 ЕГЭ по математике. Графики функций» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник

: ЕГЭ по математике профиль

Новые задания №9 ЕГЭ 2022 по профильной математике — графики функций.

Для успешного результата необходимо уметь выполнять действия с функциями.

Задание №9 ЕГЭ 2022 математика профильный уровень Прототипы

Скачать задания	Источник
Новые задания 9	ФИПИ
Прототипы задания №9	vk.com/mathegeexam
Скачать задания	vk.com/ekaterina_chekmareva
→ Теория → Задачи → Шпаргалка	vk.com/abel_mat
Линейная функция	math100.ru
Парабола
Гипербола
Логарифмическая и показательная функции
Иррациональные функции
Тригонометрические функции

Из кодификатора 2022 года для выполнения 9 задания нужно изучить основные элементарные функции, их свойства и графики:

3.3.1 Линейная функция, её график

3.3.2 Функция, описывающая обратную пропорциональную зависимость, её график

3.3.3 Квадратичная функция, её график

3.3.4 Степенная функция с натуральным показателем, её график

3.3.5 Тригонометрические функции, их графики

3.3.6 Показательная функция, её график

3.3.7 Логарифмическая функция, её график

Уметь выполнять действия с функциями: определять значение функции по значению аргумента при различных способах задания функции; описывать по графику поведение и свойства функции, находить по графику функции наибольшее и наименьшее значения; строить графики изученных функций:

При отработке данного задания будут полезны книги:

Купить ЕГЭ. Математика. Графики функций, уравнения и неравенства, содержащие переменную под знаком модуля

Купить Задачи с параметрами. Применение свойств функций, преобразование неравенств

Связанные страницы:

Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи в разделе контакты

Источник

Лучшие репетиторы для сдачи ЕГЭ

Задания по теме «Логарифмические функции»

Открытый банк заданий по теме логарифмические функции. Задания B12 из ЕГЭ по математике (профильный уровень)

Тригонометрические уравнения

Задание №1132

Тип задания: 12
Тема:
Логарифмические функции

Условие

Найдите наименьшее значение функции y=5x^2-12x+2ln x+37 на отрезке left[frac35; frac75right].

Показать решение

Решение

ОДЗ: x>0.

Найдём производную исходной функции:

y'(x)= 10x-12+frac{2}{x}= frac{10x^2-12x+2}{x}.

Определим нули производной: y'(x)=0;

frac{10x^2-12x+2}{x}=0,

5x^2-6x+1=0,

x_{1,2}= frac{3pmsqrt{3^2-5cdot1}}{5}= frac{3pm2}{5},

x_1=frac15notinleft[frac35; frac75right],

x_2=1inleft[frac35; frac75right].

Расставим знаки производной и определим промежутки монотонности исходной функции на рассматриваемом промежутке.

Из рисунка видно, что на отрезке left[frac35; 1right]исходная функция убывает, а на отрезке left[1; frac75right]возрастает. Таким образом, наименьшее значение на отрезке left[frac35; frac75right]достигается при x=1 и равно y(1)= 5cdot 1^2-12cdot 1+2 ln 1+37= 30.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1124

Тип задания: 12
Тема:
Логарифмические функции

Условие

Найдите наибольшее значение функции y=4x^2-19x+11ln x+715 на отрезке left[frac34; frac54right].

Показать решение

Решение

ОДЗ: x>0.

Найдём производную исходной функции:

y'(x)= 8x-19+frac{11}{x}= frac{8x^2-19x+11}{x}.

Определим нули производной: y'(x)=0;

frac{8x^2-19x+11}{x}=0,

8x^2-19x+11=0,

x_{1,2}= frac{19pmsqrt{19^2-4cdot8cdot11}}{2cdot8}= frac{19pm3}{16},

x_1=1,

x_1in left[frac34; frac54right],

x_2=frac{22}{16}=frac{11}{8}>frac{10}{8}=frac{5}{4},

x_2notin left[frac34; frac54right].

Расставим знаки производной и определим промежутки монотонности исходной функции.

Из рисунка видно, что на отрезке left[frac34; 1right] исходная функция возрастает, а на отрезке left[1; frac54right] убывает. Таким образом, наибольшее значение на отрезке left[frac34; frac54right] достигается при x=1 и равно y(1)= 4cdot 1^2-19cdot 1+11 ln 1+715= 700.

Ответ

700

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1116

Тип задания: 12
Тема:
Логарифмические функции

Условие

Найдите наименьшее значение функции y=7x-ln(x+11)^7 на отрезке [-10,5;,,0].

Показать решение

Решение

ОДЗ: (x+11)^7>0, x+11>0, x>-11. На ОДЗ исходная функция примет вид:y=7x-7 ln (x+11).

Найдём производную: y’=7-frac{7}{x+11}. Определим нули производной: 7-frac{7}{x+11}=0,

frac{1}{x+11}=1,

x=-10.

Расставим знаки производной и определим промежутки монотонности исходной функции.

Из рисунка видно, что на отрезке [-10,5; -10] исходная функция убывает, а на отрезке [-10; 0] возрастает. Таким образом, наименьшее значение на отрезке [-10,5; 0] достигается при x=-10 и равно y(-10)= 7cdot (-10)-ln (-10+11)^7= -70.

Ответ

-70

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №952

Тип задания: 12
Тема:
Логарифмические функции

Условие

Найдите наибольшее значение функции y=ln(x+7)^9-9x на отрезке [-6,5; 0].

Показать решение

Решение

ОДЗ. (x+7)^9>0, x+7>0, x>-7.

Так как на ОДЗ ln(x+7)^9=9ln(x+7), то исходная функция примет вид: y=9ln(x+7)-9x. Найдём производную: y’=frac{9}{x+7}-9.

Определим нули производной

frac{9}{x+7}-9=0,

frac{1}{x+7}=1,

x=-6.

Расставим знаки производной и определим промежутки монотонности исходной функции

Из рисунка видно, что на отрезке [-6,5; -6] исходная функция возрастает, а на отрезке [-6; 0] — убывает. Таким образом, наибольшее значение на отрезке [-6,5; 0] достигается при x=-6 и равно y(-6)=ln(-6+7)^9-9cdot(-6)=54.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №336

Тип задания: 12
Тема:
Логарифмические функции

Условие

Найдите наименьшее значение функции y=12x-ln(12x)+100 на отрезке left [frac{1}{36}; frac34 right ].

Показать решение

Решение

y’=(12x-ln(12x)+100)’=12-frac{12}{12x}=frac{12x-1}{x}.

y’=0 при x=frac{1}{12}, причем y’ меняет знак в этой точке с «−» на «+». Это означает, что x=frac{1}{12} является точкой минимума.

yleft ( frac{1}{12} right )=12cdotfrac{1}{12}-lnleft ( 12cdotfrac{1}{12} right )+100=1-0+100=101.

Ответ

101

Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №125

Тип задания: 12
Тема:
Логарифмические функции

Условие

Найдите наибольшее значение функции y=ln(x+8)^3-3x на отрезке [−7,5; 0]

Показать решение

Решение

Выполним преобразования и вычислим производную.

y=3ln(x+8)-3x

y’=frac{3}{x+8}-3

Найдем точки экстремума, в которых производная функции обращается в нуль.

frac{3}{x+8}=3

x+8=1

x=-7

На числовой оси расставим знаки производной и посмотрим как ведет себя функция.

При переходе через точку x = −7 производная меняет знак с плюса на минус. Значит x = −7 – точка максимума функции.

Найдем наибольшее значение функции в точке x = −7.

y(-7)=3ln1+21=21

Наибольшее значение функции равно 21.

Ответ

Задание №124

Тип задания: 12
Тема:
Логарифмические функции

Условие

Найдите точку максимума функции y=log_2(4+10x-x^2)-71.

Показать решение

Решение

Определим область допустимых значений функции.

4+10x-x^2>0

x^2-10x-4<0

5-sqrt{29}<x<5+sqrt{29}

Вычислим производную функции.

y’=frac{10-2x}{(4+10x-x^2)ln2}

Найдем точки экстремума, в которых производная функции обращается в нуль.

10-2x=0

x = 5

На числовой оси отложим граничные точки ОДЗ и точку экстремума и посмотрим как ведет себя функция.

При переходе через точку x = 5 производная меняет знак с плюса на минус. Значит x = 5 – точка максимума функции.

Ответ

Задание №123

Тип задания: 12
Тема:
Логарифмические функции

Условие

Найдите наибольшее значение функции y=ln(x+5)^4-4x на отрезке [−4,5; 0].

Показать решение

Решение

Выполним преобразования и вычислим производную.

y=4ln(x+5)-4x

y’=frac{4}{x+5}-4

Найдем точки экстремума, в которых производная функции обращается в нуль.

frac{4}{x+5}=4

x+5=1

x=-4

На числовой оси отложим граничные точки отрезка и точку экстремума и посмотрим как ведет себя функция.

При переходе через точку x = −4 производная меняет знак с плюса на минус. Значит x = −4 – точка максимума функции.

Найдем наибольшее значение функции в точке x = −4.

y(-4)=ln(-4+5)^4-4cdot(-4)=16

Наибольшее значение функции равно 16.

Ответ

Лучшие репетиторы для сдачи ЕГЭ

Сложно со сдачей ЕГЭ?

Звоните, и подберем для вас репетитора: 78007750928

Источник