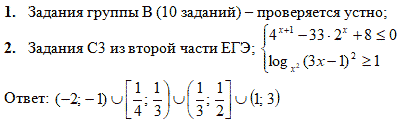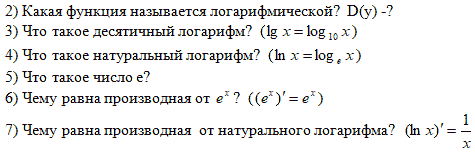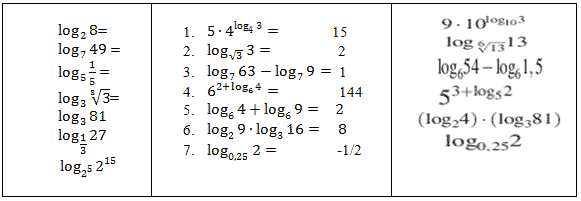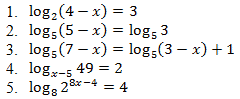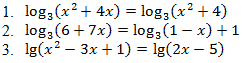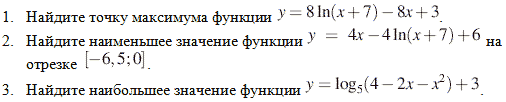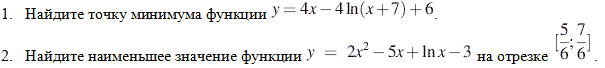Логарифмы конспект егэ

Логарифмы

Предыдущую статью о показательных уравнениях мы начали с уравнения 2^x = 8. Там всё было ясно: x = 3.

А теперь рассмотрим уравнение 2^x = 7.

По графику функции y = 2^x мы видим, что это уравнение имеет корень, и притом единственный.

Ясно, что этот корень — не целое число (так как 2² = 4, 2³ = 8). Более того, оказывается, что он не является даже рациональным числом, т. е. не представляется в виде обыкновенной дроби. Интуитивно мы чувствуем лишь, что он меньше 3, но не намного.

Этот корень обозначается log₂7 (читается: «логарифм семи по основанию два»). Он является иррациональным числом, т. е. бесконечной непериодической десятичной дробью. Калькулятор даёт: log₂7 = 2,807354922057604107…

Итак, наше число log₂7 — это показатель степени, в которую надо возвести 2, чтобы получить 7.

Теперь дадим общее определение логарифма. Пусть a > 0 и a ≠ 1 (условия те же, что и для основания показательной функции).

Определение. Логарифм положительного числа b по основанию a (обозначается log_ab) — это показатель степени, в которую надо возвести a, чтобы получить b.

Иными словами,

Например:

  так как  ;

, так как  ;

  так как  ;

, так как  .

Логарифм с основанием 10 называется десятичным и обозначается lg. Например, lg 100 = 2, lg 1000 = 3, lg 0,01 = −2.

Логарифм с основанием e называется натуральным и обозначается ln.

Обратите внимание: логарифм определён только для положительных чисел. Причина заключается в том, что показательная функция может принимать лишь положительные значения. Например, число log₂(−4) не существует: в какую бы степень мы ни возводили 2, мы никогда не получим −4.

Не забывайте также про ограничения на основание логарифма: 0 < a < 1 или a > 1.

Основные формулы

По определению, log_ab — это показатель степени, в которую надо возвести число a, чтобы получить число b:

Формула (1) называется основным логарифмическим тождеством.
Вот еще один вариант записи основного логарифмического тождества:

log_aa^x=x.

Перечислим свойства логарифмов. Они являются простыми следствиями правил действия со степенями. Все логарифмы ниже считаются определёнными.

Логарифм произведения — это сумма логарифмов:

loga(bc) = logab + logac.

(2)

Логарифм частного — это разность логарифмов:

.

(3)

Показатель степени логарифмируемого числа «спрыгивает» перед логарифмом:

(4)

Показатель степени основания логарифма тоже «спрыгивает», но в виде обратного числа:

(5)

Формулы (4) и (5) вместе дают:

.

(6)

В частности, если m = n, мы получаем формулу:

.

(7)

Например, .

Наконец, важнейшая формула перехода к новому основанию:

.

(8)

В частности, если c = b, то log_bb = 1, и тогда:

.

(9)

Приведём несколько примеров из банка заданий.
1. (применили формулу (2) суммы логарифмов).

2. (применили основное логарифмическое тождество(1)).

3. (применили формулу (4)).

4. (применили формулу (9), перейдя к новому основанию 0,8).

5. (применили формулу (3) разности логарифмов).

Немного истории

Теперь вы поняли, что такое логарифмы и как ими пользоваться. Но для чего они всё-таки нужны? Или это просто такая математическая игрушка с хитрой инструкцией по применению?

Понятие логарифма и логарифмические таблицы появились в 17 веке, и значение их было огромно.

Это в наши дни вычисления не представляют труда — у каждого есть калькулятор. А как считали в «докомпьютерные» времена?

Складывать и вычитать можно было на счётах, а вот умножать и делить приходилось «в столбик» — медленно и трудно.

В 15–17 веках, в эпоху великих географических открытий, стали бурно развиваться торговля, экономика и наука. Требования к математике росли: расчёты становились более сложными, а точность — например, для решения навигационных задач — нужна была всё более высокая.

Необходим был инструмент, позволяющий упростить и ускорить расчёты, и таким инструментом явились логарифмы.

Предположим, что b и c — большие числа, которые надо перемножить. Появление таблиц логарифмов (например, с основанием 10) существенно упростило эту задачу. Теперь вычислителю достаточно было найти по таблицам десятичные логарифмы чисел b и c, сложить их (на счётах) и получить логарифм произведения: lgb + lgc = lg(bc).

А затем по таблице логарифмов найти само произведение чисел b и c.

Недаром французский математик и астроном Лаплас сказал, что изобретение логарифмов удлинило жизнь вычислителей. Логарифмическая линейка (которой инженеры пользовались до 70-х годов двадцатого века) была не менее прогрессивным изобретением, чем современный калькулятор.

Но это еще не всё! Мы не занимались бы логарифмами, если бы они имели лишь историческую, «музейную» ценность. О неожиданных применениях логарифмов мы расскажем в следующей статье, посвящённой логарифмической функции.

Слайд 1

Логарифмическая линия в ЕГЭ «Счет и вычисления – основа порядка в голове». Песталоцци В7 В10 В3 С1 С3

Слайд 2

Повторить и закрепить: свойства логарифма ; решение логарифмических уравнений ; навыки и умения применения знаний по теме к решению упражнений. Задачи урока:

Слайд 3

Логарифмом положительного числа b по положительному и отличному от 1 основанию а называют показатель степени, в которую нужно возвести число а, чтобы получить число b . В7 В10 С1 С3 В3 Логарифмическая линия

Слайд 4

В7 В10 С1 С3 В3 Логарифмическая линия 1 1 2 2 3 3 4 4 5 5 6 6

Слайд 5

В7 В10 С1 С3 В3 Устный счет Логарифмическая линия

Слайд 6

В7 В12 С1 С3 В3 Ответ: 35 Ответ: -71 Логарифмическая линия Найти значение выражения 1 2

Слайд 7

В7 В10 С1 С3 В3 Простейшее логарифмическое уравнение log a x=b, a > 0; a = 1 . Оно имеет единственное решение х =a b при любом b Логарифмическая линия

Слайд 8

Решите уравнение: 1. 2. 3. В7 В10 С1 С3 В3 Логарифмическая линия Решение уравнений

Слайд 9

Емкость высоковольтного конденсатора в телевизоре Ф. Параллельно с конденсатором подключен резистор с сопротивлением Ом. Во время работы телевизора напряжение на конденсаторе кВ. После выключения телевизора напряжение на конденсаторе убывает до значения U (кВ) за время, определяемое выражением (с), где — постоянная. Определите (в киловольтах), наибольшее возможное напряжение на конденсаторе, если после выключения телевизора прошло не менее 28 с? В7 В10 С1 С3 В3 Логарифмическая линия задача

Слайд 10

В7 В10 С1 С3 В3 Задание B12 (№ 28463) Найти U наиб =? при t ≥ 28c Ответ : 6 Логарифмическая линия задача

Слайд 11

Самостоятельная работа 1 вариант 2 вариант 1. 1. 2. 2. 3. 3. 4.Решите уравнение 4.Решите уравнение 5.Решите уравнение . Если уравнение имеет более одного корня, в ответе укажите меньший из них. 5.Решите уравнение . Если уравнение имеет более одного корня, в ответе укажите меньший из них. Знания должны не только ум наполнять. Их надо применять . А. Эйнштейн

Слайд 12

Ответы 1 вариант 2 вариант 1 12 27 2 3 0 3 4 9 4 0 8 5 -1 -2 Шкала оценок: 5 баллов – «5» 4балла – «4» 3 балла — «3» 0-2 балла- «2»

Слайд 13

В7 В10 С1 С3 В3 Логарифмическая линия Решение уравнений Решение неравенств Преобразование логарифмических выражений Нахождение значения логарифмического выражения Решение логарифмических уравнений Решение задач

Слайд 14

Знания должны не только ум наполнять. Их надо применять . А. Эйнштейн Желаю удачи!!!

Логарифмом положительного числа $b$ по основанию а, где $a>0$, $a≠1$, называется показатель степени, в которую надо возвести число $а$, чтобы получить $b$.

Особенно можно выделить три формулы:

$log_{a}a=1;$

$log_{a}1=0;$

$log_{a}a^b=b.$

Десятичным логарифмом числа называют логарифм этого числа по основанию $10$ и пишут $lg⁡b$ вместо $log_{10}b$.

Натуральным логарифмом числа называют логарифм этого числа по основанию $е$, где $е$ – иррациональное число, приближенно равное $2.7$. При этом пишут $lnb$, вместо $log_{e}b$

Свойства логарифмов.

Все свойства логарифмов мы будем рассматривать для $a>0, a≠1, b>0, c>0, m$ – любое действительное число.

1. Для любых действительных чисел $m$ и $n$ справедливы равенства:

$log{_а}b^m=mlog_{a}b;$

$log_{a^m}b={1}/{m}log_{a}b.$

$log_{a^n}b^m={m}/{n}log_{a}b$

2. Логарифм произведения равен сумме логарифмов по тому же основанию от каждого множителя.

$log_{a}(bc)=log_{a}b+log_{a}c$

3. Логарифм частного равен разности логарифмов от числителя и знаменателя по тему же основанию

$log_{a}{b}/{c}=log_{a}b-log_{a}c$

4. При умножении двух логарифмов можно поменять местами их основания

$log_{a}b·log_{c}d=log_{c}b·log_{a}d$, если $a$, $b$, $c$, $d>0$, $a≠1$, $b≠1.$

5. $c^{log_{a}b}=b^{log_{a}c}$, где $а, b, c>0, a≠1$

6. Формула перехода к новому основанию

$log_{a}b={log_{c}b}/{log_{c}a}$

7. В частности, если необходимо поменять местами основание и подлогарифмическое выражение

$log_{a}b={1}/{log_{b}a}$

Тема урока: Свойства логарифмов. Решение заданий ЕГЭ.

Тип урока: закрепление полученных знаний.

Цели урока.

Образовательные:

• Отработка понятий: логарифм, логарифмическая функция.

• Закрепление свойств логарифма и логарифмической функции.

• Сформировать умение упрощать выражение, используя основное логарифмическое тождество и свойства логарифмов.

• Отработка навыка решения простейших логарифмических уравнений.

• Ознакомление с решением логарифмических уравнений, неравенств и систем с помощью применения свойств логарифмов.

Развивающие:

• способствовать развитию внимания, логического, аналитического мышления, памяти.

• развитие умения работать в заданном темпе.

Воспитательные:

• Формировать навыки общения, умения работать в коллективе.

• Способствовать воспитанию познавательного интереса к математике.

Оборудование:

• Персональный компьютер у учителя.

• Мультимедийный проектор, экран.

• Презентация к уроку.

• Ноутбуки для учащихся с возможностью выхода в интернет.

• Раздаточный материал: сопроводительный лист с заданиями и оценочной таблицей, справочный материал.

Учебно-методический комплект:

• Учебник: Алгебра и начала анализа 10-11 ( под редакцией А.Г. Мордковича ), М., «Мнемозина», 2011 г., 12-е издание

• Задачник: Алгебра и начала анализа 10-11 ( под редакцией А.Г. Мордковича ), М., «Мнемозина», 2011 г., 12-е издание

Основные этапы урока:

1. Организационный момент.

2. Актуализация.

3. Формулирование темы урока, постановка целей и задач урока.

4. Закрепление знаний.

5. Физкультминутка.

6. Усвоение знаний.

7. Подведение итогов урока.

8. Инструктаж по домашнему заданию.

9. Рефлексия.

Ход урока:

1. Организационный момент (приветствие, перекличка организация внимания).

Наш урок я хочу начать со слов американского математика Айвена Нивена:

“Нельзя изучать математику, наблюдая за тем, как это делаем сосед…” (слайд 1)

Чтобы оценить свою работу на уроке у вас на сопроводительных листах есть оценочная таблица (слайд 2). Отмечайте, количество баллов, которое вы себе поставите после каждого этапа урока.

1. Актуализация.

Повторим свойства логарифмов, которые мы с вами изучили на предыдущих уроках (слайд 3):

Устная работа «Своя игра» (слайд 4)

Называйте координаты ячейки, открываем её и вычисляем логарифмы. Открытые буквы дают нам фамилию английского учёного Джона Непера – математик и астронома, изобретатель логарифмов (слайд 5).

Итак, мы повторили необходимый материал. На что вы опирались при решении заданий? (Ответ: На свойства логарифмов).

1. Формулирование темы урока, постановка целей и задач урока.

Задания такого типа представлены в Едином Государственном Экзамене в номере 10. Кроме этого в задание 6 – простейшие логарифмические уравнения. (слайд 6) В КИМах экзамена есть задания повышенной трудности – решение логарифмических уравнений с опорой на свойства логарифмов. Какова тема урока?

(Ответ: Свойства логарифмов. Подготовка в ЕГЭ) (слайд 7).

Какова цель урока?

(Ответ: Подготовиться к ЕГЭ) (слайд 7).

Какие задачи для этого нам нужно выполнить?

(Ответ: 1. Вспомнить свойства логарифмов, свойства степеней, решение простейших логарифмических уравнений

2. Научиться решать лог. уравнения повышенной сложности)

3. Развитие внимания, мышления, памяти.

4. Воспитание познавательного интереса к математике. (слайд 8).

1. Закрепление знаний.

1. Рассмотрим преобразование буквенного логарифмического выражения. (Слайд 9)

Слайд 9 Слайд 10

Работа в группах: задания на сопроводительных листах. Результат на слайде 10.

1. Рассмотрим два способа решения простейшего логарифмического уравнения. (Слайд 11)

Слайд 11 Слайд 12

Работа в парах: решение простейших логарифмических уравнений с самопроверкой (слайд 12-13).

1. Физкультминутка. Динамическая пауза «Изобрази и угадай график». (Слайд 14)

Слайд 14 Слайд 15

1. Усвоение знаний. Решение уравнения повышенной трудности.

(Слайд 15)

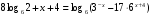
Составление плана решения, выявление трудных моментов в решении, возможность использования ИК-технологий для нахождения приёмов решения (запрос в яндексе: решение логарифмических уравнений повышенной сложности; сайт — http://festival.1september.ru/articles/576163)

1. Блиц-опрос.

И напоследок проверим себя, насколько каждый владеет определением и свойствами логарифмов (слайд 16). В сопроводительных листах необходимо ответить только «да» или «нет».

Подлогарифмическое выражение всегда должно быть больше нуля.

да
Основание логарифма всегда строго больше нуля.	нет
Логарифм частного равен разности логарифмов.	да
Логарифм произведения равен произведению логарифмов.	нет
Если подлогарифмическое выражение записано в виде степени, то показатель можно вынести вперед и умножить на логарифм основания.	да

Не забудьте оценить свою работу в оценочной таблице.

1. Рефлексия. Посчитайте количество баллов за урок.

Этапы урока

Устная работа	Работа в группах	Работа в парах	Инд. работа	Блиц-опрос	Общее количество баллов за урок
Числовые выражения	Буквенные выражения	Уравнения	Уравнение повышенной сложности
3 балла	Сразу понятен ход решения	Мне понятен ход решения	Решено верно 2 уравнения, каждое своим способом	Смог(ла) найти приём решения и применить его	5 правил. ответов
2 балла	Понятно только после объяснения	Мне помогли (подсказали) в группе	Решено верно 1 уравнение	Смог(ла) найти подобное уравнение, но не могу применить приём	3-4 правил. ответов
1 балл	Решение многих примеров непонятно	Я наблюдаю как решают остальные	Нет верно решенных	Не смог(ла) найти подобное уравнение	0-2 правил. ответов
Баллы по этапам урока

Согласно полученным баллам прочитайте, на каком уровне вы находитесь и рекомендации к дальнейшему изучению темы.

Баллы

Уровень	Рекомендации	Оценка
13-15 баллов	Я хорошо ориентируюсь в этой теме: знаю все определения и свойства; могу свободно применять полученные знания при решении заданий ЕГЭ; знаю, где можно найти приёмы решения сложных заданий.	В дальнейшем мне можно рассматривать решение заданий повышенной трудности.	5
10-12 баллов	Я ориентируюсь в свойствах, но не всегда могу применить их на практике при решении заданий ЕГЭ; знаю, где можно найти решение сложных заданий, но не всегда понятны приёмы, используемые в процессе решения.	Мне нужно отрабатывать решение заданий базовой части ЕГЭ и рассматривать решение заданий повышенной трудности.	4
7-9 баллов	Я слабо ориентируюсь в свойствах и не могу применить их на практике самостоятельно; решение многих заданий мне понятно только после обсуждения/объяснения	Мне необходимо учить определение логарифма числа и свойства логарифмов; нужно отрабатывать решение заданий базовой части ЕГЭ.	3
5-6 баллов	Мне сложно ориентироваться в заданиях, непонятно какие свойства нужно применять для решения заданий базового уровня.	Мне нужно начать учить свойства и отрабатывать решение простейших заданий.	2

Какую оценку вы поставите себе за урок? (слайд 17)

1. Подведение итогов урока.

Пожалуйста, подведите итог урока. Реализовали ли мы поставленные задачи? Каким образом?

(Ответ: 1. Вспомнили свойства логарифмов,

1. решали задания на преобразования лог.выражений,

2. решали простейшие лог.уравнения,

3. рассмотрели преобразование на примере решения лог.уравнения повышенной сложности) (Слайд 18)

Можно ли сделать вывод, что мы справились с поставленной целью?

(Ответ: мы готовились к ЕГЭ по теме «Логарифмы»)

1. Инструктаж по домашнему заданию (Слайд 19).

Основное: § 40-43 повторить, № 43.17, 43,26, 43.31.

Дополнительное: С помощью Интернет-ресурсов найдите уравнения и неравенства повышенной трудности, принцип решения которых вам непонятен.

Алгебра и начала математического анализа, 10 класс

Урок № 24. Логарифм. Свойства логарифмов.

Перечень вопросов, рассматриваемых в теме

1. Определение логарифма.

2. Основное логарифмическое тождество.

3. Свойства логарифмов.

Глоссарий по теме

Логарифмом положительного числа по основанию , называется показатель степени, в которую надо возвести чтобы получить .

Логарифмирование – это действие нахождения логарифма числа.

Основное логарифмическое тождество:

Свойства логарифмов. При , справедливы равенства:

— логарифм произведения: ;

— логарифм частного: ;

— логарифм степени: .

Основная литература:

Колягин Ю. М., Ткачева М. В., Фёдорова Н.Е. и др. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс. Базовый и углублённый уровни. – М.: Просвещение, 2014. – 384 с.

Открытые электронные ресурсы:

http://fipi.ru/

Теоретический материал для самостоятельного изучения

При решении простейших показательных уравнений не всегда можно найти точный ответ. Например, уравнение имеет корень 5, т. к. значит , В уравнении число 5 не является степенью 2, значит предыдущий способ решения не подходит. Нам известно, что уравнение имеет единственный корень. Посмотрим это на графике.

Абсцисса точки пересечения – единственное решение данного уравнения. Это число и называют логарифмом 5 по основанию 2.

Дадим определение логарифма.

Логарифмом положительного числа по основанию , называется показатель степени, в которую надо возвести чтобы получить .

Т. е. логарифм числа по основанию , есть некоторое число такое, что .

Пример 1.

, т. к. выполнены все условия определения:

1) 216 > 0; 2) 6 > 0, 6 ≠ 1; 3) .

Пример 2.

, т. к. выполнены все условия определения:

1) ; 2) 2 > 0, 2 ≠ 1; 3) .

Это действие называется логарифмированием.

Логарифмирование – это действие нахождения логарифма числа.

Существует краткая запись определения логарифма:

так называемое основное логарифмическое тождество. Его используют при вычислениях.

Пример 3.

(Читают: 4 в степени логарифм 5 по основанию 4 равен 5)

Пример 4.

(Читают: одна треть в степени логарифм 6 по основанию одна треть равен 6)

Решим несколько задач с использованием определения логарифма.

Задача 1. Вычислить .

Решение. Пусть тогда по определению логарифма Приведем левую и правую части к одному основанию. 27 = 3³, 81 = 3⁴, значит . Отсюда следует, что

Задача 2. Вычислить .

Решение. Для вычисления воспользуемся свойствами степеней: 1) , 2) и основным логарифмическим тождеством: .

.

Для решения более сложных задач потребуется знание свойств логарифмов. Рассмотрим их.

1. Логарифм произведения.

Логарифм произведения чисел по основанию равен сумме логарифма по основанию и логарифма по основанию .

Пример 5.

2. Логарифм частного.

Логарифм частного чисел по основанию равен разности логарифма по основанию и логарифма по основанию .

Пример 6.

3. Логарифм степени.

Логарифм числа по основанию равен произведению показателя и логарифма по основанию .

Пример 7.

Важно! Свойства выполняются при ,

Примеры и разбор решения заданий тренировочного модуля

№ 1. Вычислите: .

Решение:

Чтобы выполнить это задание нам понадобятся следующие определения и свойства:

1. 
2. ;
3. .

Представим в виде степени с рациональным показателем: . Далее воспользуемся свойством нахождения логарифма степени: . Вспоминаем таблицу квадратов: , значит , . Ответ: .

№ 2. Вычислите

1. 
2. 
3. 
4. 

Решение:

Чтобы выполнить это задание нам понадобятся следующие определения и свойства:

1. ;
2. ;
3. ;
4. 
5. .
6. 

.

1. 
2. 

Метод решения хорош, если с самого начала мы можем предвидеть –
и в последствии подтвердить это, — что, следуя этому методу, мы достигнем цели.
Г.Лейбниц

ТИП УРОКА: Закрепление и совершенствование знаний.

ЦЕЛИ:

• Дидактическая — Повторить и закрепить свойства  логарифмов; логарифмические уравнения; закрепить методы решения наибольшего и наименьшего значения функции; совершенствовать применение полученных знаний при решении задач ЕГЭ С1 и С3;
• Развивающая — Развитие логического мышления, памяти, познавательного интереса, продолжить формирование математической речи и графической культуры, вырабатывать умение анализировать;
• Воспитательная — Приучать к эстетическому оформлению записи в тетради, умению общаться, прививать аккуратность.

Оборудование: классная доска, компьютер, проектор, экран,  карточки с заданиями теста, с заданиями для работы всех обучающихся.
Формы работы: фронтальная, индивидуальная, коллективная.

ХОД УРОКА

1. ОРГАНИЗАЦИОННЫЙ МОМЕНТ

2. ПОСТАНОВКА ЦЕЛИ

3. ПРОВЕРКА ДОМАШНЕГО ЗАДАНИЯ

3. работа личных кабинетов в Интернет (просмотр результатов)

4. АКТУАЛИЗАЦИЯ ЗНАНИЙ

Проанализировать: в каких заданиях ЕГЭ встречаются логарифмы.

(В-7-простейшие логарифмические уравнения
В-11-преобразование логарифмических выражений
В-12- задачи физического содержания, связанные с логарифмами
В-15- нахождение наибольшего и наименьшего значения функции
С-1- тригонометрические уравнения, содержащие логарифм
С-3 – система неравенств, содержащая логарифмическое неравенство)

На данном этапе проводится устная работа, в ходе которой учащиеся не только вспоминают свойства логарифмов, но и выполняют простейшие задания ЕГЭ.

1) Определение логарифма. Какие вы знаете свойства логарифма? (и условия ?)

 

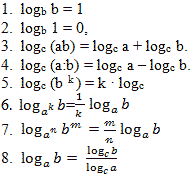
5. УСТНАЯ РАБОТА для всех обучающихся.

Вычислить устно: (задания В-11)

6. Самостоятельная деятельность учащихся по решению заданий.

В-7 с последующей проверкой

Решите уравнения (первые два уравнения проговаривают устно, а остальные решает самостоятельно  весь класс и записывает решение в тетрадь):

После проверки с места 3-5 уравнений, ребятам предлагается доказать, что уравнение не имеет решения (устно)

7. Решение В-12 (задачи физического содержания, связанные с логарифмами).

Весь класс решает задачу (у доски 2 человека: 1-й решает вместе с классом, 2-й решает аналогичную задачу самостоятельно)

8. УСТНАЯ РАБОТА (вопросы)

Вспомнить алгоритм нахождения наибольшего и наименьшего значения функции на отрезке и на промежутке.

Работа на доске и в тетради.

(прототип В15 — ЕГЭ)

(Пока ученики работают у доски, 4-м учащимся даются карточки с аналогичными заданиями)

9. Мини-тест с самоконтролем.

Тест

Ключи к тесту:

	№1	№2	№3	№4	№5	№6
Вариант №1	250	49	4	-8	3	8
Вариант №2	63	144	13	-22	7	3

Ребята меняются друг с другом работами и выступают в роли экспертов.

10. Решение заданий С1

Учащиеся выполняют задание, 1 человек работает у доски.

Подробный разбор предложенного задания на доске.

11. Выступление учащихся в роли экспертов.

Ребятам предлагается оценить работу ученика – задание С-1, выполненную на экзаменационном бланке – 0,1,2 баллами (см.презентацию)

12. ДОМАШНЕЕ ЗАДАНИЕ.

Учитель поясняет домашнее задание, обращая внимание на то, что аналогичные задания были рассмотрены на уроке. Учащиеся внимательно прослушав пояснения учителя, записывают домашнее задание.

1. ФИПИ (открытый банк заданий: раздел геометрия, 6-я страница)
2. uztest.ru (преобразование логарифмов)
3. С3 – задание второй части ЕГЭ

13. ПОДВЕДЕНИЕ  ИТОГОВ.

Сегодня на уроке мы повторили свойства логарифмов; логарифмические уравнения; закрепили методы нахождения  наибольшего и наименьшего значения функции; рассмотрели задачи физического содержания, связанные с логарифмами; решали задачи С1 и С3, которые  предлагаются на ЕГЭ по математике.

Выставление оценок.
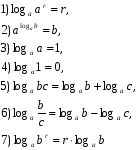