ЕГЭ 2023, Математика, Профильный уровень, 40 тренировочных вариантов, Лысенко Ф.Ф., Кулабухова С.Ю.
Фрагмент из книги.
Геометрическое место точек, равноудалённых от вершим треугольника, есть прямая, проходящая через центр описанной окружности треугольника перпендикулярно его плоскости.
Примеры.
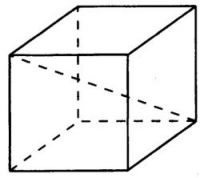
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 6. Объём параллелепипеда равен 720. Найдите высоту цилиндра.
В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 15 см. На какой высоте будет находиться уровень воды, если её перелить в другой такой же сосуд, у которого сторона основания в 3 раза меньше, чем у первого? Ответ выразите в см.
Объём конуса равен 54. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объём меньшего конуса.
Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:
Скачать книгу ЕГЭ 2023, Математика, Профильный уровень, 40 тренировочных вариантов, Лысенко Ф.Ф., Кулабухова С.Ю. — fileskachat.com, быстрое и бесплатное скачивание.
Скачать pdf
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России.Купить эту книгу
Скачать
— pdf — Яндекс.Диск.
Дата публикации: 05.12.2022 07:23 UTC
Теги:
ЕГЭ по математике :: математика :: Лысенко :: Кулабухова
Следующие учебники и книги:
- ЕГЭ 2023, Математика, 11 класс, Тренировочная работа №1, Профильный уровень, Вариант МА2210109-110
- Задачник по алгебре, Уравнения и выражения
- ЕГЭ 2023, Математика, 11 класс, Тренировочная работа №1
- ЕГЭ 2023, Математика, Вариант 2, Ященко И.В.
Предыдущие статьи:
- ЕГЭ 2023, Математика, Базовый уровень, Типовые экзаменационные варианты, 30 вариантов, Ященко И.В.
- ЕГЭ 2023, Математика, Профильный уровень, 36 вариантов, Ященко И.В.
- ЕГЭ 2023, Математика, 11 класс, Кодификатор
- ЕГЭ 2023, Математика, 11 класс, Спецификация, Профильный уровень
Укажите регион, чтобы мы точнее рассчитали условия доставки
Начните вводить название города, страны, индекс, а мы подскажем
Например:
Москва,
Санкт-Петербург,
Новосибирск,
Екатеринбург,
Нижний Новгород,
Краснодар,
Челябинск,
Кемерово,
Тюмень,
Красноярск,
Казань,
Пермь,
Ростов-на-Дону,
Самара,
Омск
Решений пока нет, можете прикрепить свои. Для этого сперва надо завершить тест, а потом нажать на синий знак вопроса на задаче и там выбрать «Предложить своё решение»
Найдите корень уравнения ( left(dfrac{1}{6} right)^{x+5}=6^x )
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 5 очков. Ответ округлите до сотых.
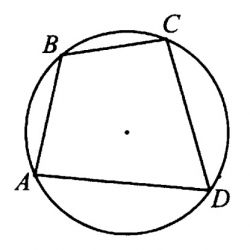
Стороны AB, BC, CD и AD четырёхугольника ABCD стягивают дуги описанной окружности, градусные величины которых равны соответственно 75°, 63°, 93°, 129°. Найдите угол BCD. Ответ дайте в градусах.
Найдите значение выражения (11sqrt{3} mathrm{tgdfrac{7pi}{6}}cdotcos{dfrac{4pi}{3}} )
Площадь поверхности куба равна 72. Найдите его диагональ.
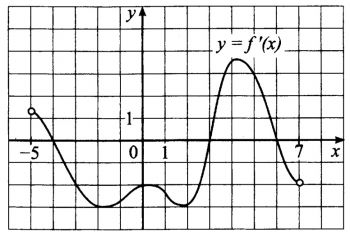
На рисунке изображен график y=f'(x) — производной f(x), определённой на интервале (-5;7). В какой точке отрезка [-3;2] функция f(x) принимает наименьшее значение?
При температуре (0^circ) (C) рельс имеет длину (l_{0}=10)м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону (l(t_{0}) = l_{0}(1+alphacdot t^{circ})), где (alpha=1{,}2 cdot10^{-5}(^{circ}C)^{-1}) — коэффициент теплового расширения, (t^circ) — температура (в градусах Цельсия). При какой температуре рельс удлинится на 3 мм? Ответ дайте в градусах Цельсия.
Из двух городов A и B, расстояние между которыми равно 360 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 3 часа на расстоянии 135 км от города B. За сколько часов автомобиль, выехавший из города A, доедет до города B?
График функции (y=dfrac{k}{x}+b) проходит через точки (left (6;8right)) и (left (-2;12right)). Найдите (b).
Телефон передаёт SMS-сообщение. В случае неудачи он делает следующую попытку. Вероятность того, что SMS-сообщение удастся передать без ошибок, в ходе каждой отдельной попытки равна 0,5. Найдите вероятность того, что для передачи собщения потребуется не больше трёх попыток.
Найдите точку максимума функции (y=ln({x+6})-4x+11).
а) Решите уравнение (2cosleft({dfrac{3pi}{2}-x}right)cdotsinleft({dfrac{pi}{2}-x}right)=sqrt{3}sin({2pi+x}))
б) Найдите корни данного уравнения, принадлежашие отрезку (left[-dfrac{11pi}{2};-3piright])
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. -11π/2 | 18. -16π/3 | 19. -21π/4 | 20. -31π/6 |
| 21. -5π | 22. -29π/6 | 23. -19π/4 | 24. -14π/3 |
| 25. -9π/2 | 26. -13π/3 | 27. -17π/4 | 28. -25π/6 |
| 29. -4π | 30. -23π/6 | 31. -15π/4 | 32. -11π/3 |
| 33. -7π/2 | 34. -10π/3 | 35. -13π/4 | 36. -19π/6 |
| 37. -3π |
В правильной четырёхугольной пирамиде SABCD сторона основания AB = 10, а боковое ребро SA = 15. На рёбрах AB и SB отмечены точки M и K соответственно, причём AM = 40/7, SK = 6.
а) Докажите, что плоскость CKM перпендикулярна плоскости ABC.
б) Найдите объём пирамиды BCKM.
Решите неравенство (7log_{12}({x^2-2x-8})leqslant 8+log_{12}{dfrac{(x+2)^7}{x-4}})
В сентябре планируется взять кредит в банке на сумму 3 млн рублей на некоторый срок. Условия его возврата таковы:
— каждый январь долг возрастает на 15% по сравнению с концом предыдущего года;
— с февраля по август каждого года нужно выплачивать часть долга;
— в сентябре каждого года долг должен быть на одну и ту же величину меньше долга на сентябрь предыдущего года.
На какой минимальный срок (целое число лет) следует брать кредит, чтобы наибольший годовой платёж по кредиту не превысил 0,96 млн рублей?
В прямоугольном треугольнике ABC точка D лежит на катете AC, а точка F — на продолжении катета BC за точку C, причём CD = BC и CF = AC. Отрезки CM и CN — высоты треугольников ABC и FCD соответственно.
а) Докажите, что CM и CN перпендикулярны.
б) Прямые AF и BD пересекаются в точке K. Найдите DK, если BC = 3, AC = 9.
Найдите все значения параметра (a), при каждом из которых уравнение ( dfrac{x^2-8x-2a}{11x^2-8ax-3a^2}=0 ) имеет ровно два различных решения.
Костя написал на доске несколько различных натуральных чисел, каждое из которых делится нацело на 7 и оканчивается на 8.
а) Может ли их сумма равняться 644?
б) Может ли среднее арифметическое равняться 200?
в) Какое набольшее количество чисел может быть выписано на доску, если их среднее арифметическое является чётным натуральным числом и не превышает 500?
Введите ответ в форме строки «да;да;1234». Где ответы на пункты разделены «;», и первые два ответа с маленькой буквы.

ID товара
2871013
Год издания
2021
ISBN
978-5-9966-1553-7
Количество страниц
336
Размер
20×14.5×1.5
Тип обложки
Мягкий переплет
Тираж
35000
Вес, г
219
Наше пособие предназначено для качественной подготовки к профильному уровню ЕГЭ по математике в 2022 году. Книга содержит:
•40 новых тренировочных вариантов, составленных в соответствии с проектами демоверсии и спецификации 2022 года профильного уровня ЕГЭ по математике, опубликованными на сайте ФИПИ 25.08.2021 г.;
•подробное решение 10 вариантов;
•краткий теоретический справочник;
•ответы ко всем вариантам.
Материал пособия позволит выпускникам и абитуриентам получить на ЕГЭ желаемый результат — от минимального количества баллов до 100 баллов.
Книга адресована выпускникам общеобразовательных учреждений и учителям. Она может использоваться также и при дистанционном обучении.
Наше пособие предназначено для качественной подготовки к профильному уровню ЕГЭ по математике в 2022 году. Книга содержит:
•40 новых тренировочных вариантов, составленных в соответствии с проектами демоверсии и спецификации 2022 года профильного уровня ЕГЭ по математике, опубликованными на сайте ФИПИ 25.08.2021 г.;
•подробное решение 10 вариантов;
•краткий теоретический справочник;
•ответы ко всем вариантам.
Материал пособия позволит выпускникам и абитуриентам получить на ЕГЭ желаемый результат — от минимального количества баллов до 100 баллов.
Книга адресована выпускникам общеобразовательных учреждений и учителям. Она может использоваться также и при дистанционном обучении.
Легион
Как получить бонусы за отзыв о товаре
1
Сделайте заказ в интернет-магазине
2
Напишите развёрнутый отзыв от 300 символов только на то, что вы купили
3
Дождитесь, пока отзыв опубликуют.
Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать
неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в
первой десятке.
Правила начисления бонусов
Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать
неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в
первой десятке.
Правила начисления бонусов
Профиль
Плюсы
В процессе решения ты сразу понимаешь так ли тебе нужен профиль, или же можно сдавать базу и идти на гуманитарное направление(так я и сделала)
Книга «Математика. Подготовка к ЕГЭ-2022. Профильный уровень. 40 тренировочных вариантов по демоверсии 2022 года. Учебно-методическое пособие» есть в наличии в интернет-магазине «Читай-город» по привлекательной цене.
Если вы находитесь в Москве, Санкт-Петербурге, Нижнем Новгороде, Казани, Екатеринбурге, Ростове-на-Дону или любом
другом регионе России, вы можете оформить заказ на книгу
Федор Лысенко
«Математика. Подготовка к ЕГЭ-2022. Профильный уровень. 40 тренировочных вариантов по демоверсии 2022 года. Учебно-методическое пособие» и выбрать удобный способ его получения: самовывоз, доставка курьером или отправка
почтой. Чтобы покупать книги вам было ещё приятнее, мы регулярно проводим акции и конкурсы.