Диагностический вариант СтатГрад ЕГЭ Профиль по математике 2110310-16.02.2022 с ответами
Новая тренировочная работа №3 статград по математике 11 класс ЕГЭ 2022, тренировочные варианты базового и профильного уровня МА2110301-МА2110312 с ответами и решением на все задания, официальная дата проведения работы 16 февраля 2022 года.
Скачать варианты базового уровня
Скачать варианты профильного уровня
Скачать ответы и решения для вариантов
Решать варианты МА2110301-МА2110308 базового уровня статград ЕГЭ 2022 по математике 11 класс задания и ответы:
Решать варианты МА2110309-МА2110312 профильного уровня статград ЕГЭ 2022 задания и ответы:
Сложные задания с варианта МА2110301 (ответы выше):
2)Для покраски 1 кв. м потолка требуется 150 г краски. Краска продаётся в банках по 2,5 кг. Какое наименьшее количество банок краски нужно для покраски потолка площадью 41 кв. м?
4)В таблице приведены размеры штрафов за превышение максимальной разрешённой скорости, зафиксированное с помощью средств автоматической фиксации, установленных на территории России с 1 сентября 2013 года. Какой штраф должен заплатить владелец автомобиля, зафиксированная скорость которого составила 77 км/ч на участке дороги с максимальной разрешённой скоростью 40 км/ч? Ответ дайте в рублях.
5)План местности разбит на клетки. Каждая клетка обозначает квадрат 1м×1м. Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах.
6)Держатели дисконтной карты книжного магазина получают при покупке скидку 5 %. Книга стоит 240 рублей. Сколько рублей заплатит держатель дисконтной карты за эту книгу?
10)Дачный участок имеет форму прямоугольника, стороны которого равны 40 м и 50 м. Дом, расположенный на участке, имеет на плане форму квадрата со стороной 9 м. Найдите площадь оставшейся части участка, не занятой домом. Ответ дайте в квадратных метрах.
11)В чемпионате по гимнастике участвуют 65 спортсменок: 18 из Аргентины, 21 из Бразилии, остальные — из Парагвая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Парагвая.
12)На соревнованиях по прыжкам в воду судьи выставили оценки от 0 до 10 трём спортсменам. Результаты приведены в таблице. Итоговый балл вычисляется следующим образом: две наибольшие и две наименьшие оценки отбрасываются, а три оставшиеся складываются, и их сумма умножается на коэффициент сложности. В ответе укажите номера спортсменов, итоговый балл которых больше 170, без пробелов, запятых и других дополнительных символов.
13)Высота бака цилиндрической формы равна 40 см, а площадь его основания равна 150 квадратным сантиметрам. Чему равен объём этого бака (в литрах)? В одном литре 1000 кубических сантиметров.
16)Объём конуса равен 48π , а его высота равна 9. Найдите радиус основания конуса.
18)Каждый раз, когда Надя приезжает в деревню к бабушке в гости, бабушка заплетает ей косички. Также Надя заплетает себе косички всегда, когда идёт на физкультуру. Выберите утверждения, которые верны при приведённых условиях. 1) Каждый раз, когда у Нади заплетены косички, она находится в деревне. 2) Если Надя без косичек, значит, она не у бабушки в гостях. 3) Если Надя без косичек, значит, сегодня физкультура. 4) Когда Надя сдаёт норматив по бегу на физкультуре, она с косичками.
19)Найдите пятизначное число, кратное 18, любые две соседние цифры которого отличаются на 2. В ответе укажите какое-нибудь одно такое число.
20)Из двух городов, расстояние между которыми равно 270 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 55 км/ч и 80 км/ч?
21)Взяли несколько досок и распилили их. Всего сделали 9 поперечных распилов, в итоге получилось 17 кусков. Сколько досок взяли?
Сложные задания с варианта МА2110302 (ответы выше):
1)Для покраски 1 кв. м потолка требуется 230 г краски. Краска продаётся в банках по 2 кг. Какое наименьшее количество банок краски нужно для покраски потолка площадью 44 кв. м?
4)В таблице приведены размеры штрафов за превышение максимальной разрешённой скорости, зафиксированное с помощью средств автоматической фиксации, установленных на территории России с 1 сентября 2013 года. Какой штраф должен заплатить владелец автомобиля, зафиксированная скорость которого составила 182 км/ч на участке дороги с максимальной разрешённой скоростью 100 км/ч? Ответ дайте в рублях.
6)Держатели дисконтной карты книжного магазина получают при покупке скидку 10 %. Книга стоит 210 рублей. Сколько рублей заплатит держатель дисконтной карты за эту книгу?
7)Найдите значение выражения − ° 15cos630 .
10)Дачный участок имеет форму квадрата, сторона которого равна 40 м. Дом, расположенный на участке, имеет на плане форму прямоугольника, стороны которого равны 9 м и 8 м. Найдите площадь оставшейся части участка, не занятой домом. Ответ дайте в квадратных метрах.
11)В чемпионате по гимнастике участвуют 50 спортсменок: 21 из Сербии, 14 из Хорватии, остальные — из Словении. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Словении.
13)Высота бака цилиндрической формы равна 50 см, а площадь его основания равна 140 квадратным сантиметрам. Чему равен объём этого бака (в литрах)? В одном литре 1000 кубических сантиметров.
16)Объём конуса равен 84π , а его высота равна 7. Найдите радиус основания конуса.
18)В 9 «Б» классе география по расписанию по средам и пятницам. Каждый ученик должен приносить атлас на каждый урок географии. На других уроках атлас не требуется. Выберите утверждения, которые верны при приведённых условиях. 1) Всякий день, когда ученик 9 «Б» класса берёт с собой в школу атлас, является пятницей. 2) В среду Маше из 9 «Б» класса надо принести в школу атлас. 3) По четвергам ученикам 9 «Б» класса не надо брать в школу географический атлас. 4) В каждый день, отличный от среды, ученикам 9 «Б» класса атлас можно в школу не брать.
19)Найдите пятизначное число, кратное 25, любые две соседние цифры которого отличаются на 2. В ответе укажите какое-нибудь одно такое число.
20)Из двух городов, расстояние между которыми равно 420 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 65 км/ч и 75 км/ч?
21)Взяли несколько досок и распилили их. Всего сделали 6 поперечных распилов, в итоге получилось 15 кусков. Сколько досок взяли?
Сложные задания с варианта МА2110305 (ответы выше):
2)Установка двух счётчиков воды (холодной и горячей) стоит 3400 рублей. До установки счётчиков за воду платили 2100 рублей ежемесячно. После установки счётчиков ежемесячная оплата воды стала составлять 1400 рублей. Через какое наименьшее количество месяцев экономия по оплате воды превысит затраты на установку счётчиков, если тарифы на воду не изменятся?
4)На рисунке показано изменение атмосферного давления в течение трёх суток. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Определите по рисунку наименьшее значение атмосферного давления (в миллиметрах ртутного столба) в четверг.
6)Магазин детских товаров закупает погремушки по оптовой цене 240 рублей за одну штуку и продаёт с наценкой 35 %. Сколько рублей будут стоить 2 такие погремушки, купленные в этом магазине?
10)От столба высотой 12 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба равно 12 м. Найдите длину провода. Ответ дайте в метрах.
11)Помещение освещается двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,2. Найдите вероятность того, что в течение года обе лампы перегорят.
13)Даны две коробки, имеющие форму правильной четырёхугольной призмы, стоящей на основании. Первая коробка в четыре раза выше второй, а вторая в полтора раза ýже первой. Во сколько раз объём второй коробки меньше объёма первой?
15)На окружности отмечена точка C. Отрезок AB — диаметр окружности, AC = 8, BC =15 . Найдите радиус окружности.
16)Объём конуса равен 32π , а его высота равна 6. Найдите радиус основания конуса.
18)Маша младше Алисы на год, но старше Кати на два года. Выберите утверждения, которые верны при указанных условиях. 1) Любая девочка, помимо указанных, которая старше Кати, также старше Маши. 2) Среди указанных девочек нет никого младше Кати. 3) Любая девочка, помимо указанных, которая старше Маши, также старше Кати. 4) Алиса и Катя одного возраста.
19)Найдите четырёхзначное число, кратное 55, все цифры которого различны и чётны. В ответе укажите какое-нибудь одно такое число.
20)Двое рабочих, работая вместе, могут выполнить работу за 6 дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за 1 день выполняет такую же часть работы, какую второй — за 2 дня?
21)В конце четверти Петя выписал подряд все свои отметки по одному из предметов, их оказалось 5, и поставил между некоторыми из них знаки умножения. Произведение получившихся чисел оказалось равным 3345. Какая отметка выходит у Пети в четверти по этому предмету, если учитель ставит только отметки «2», «3», «4» или «5» и итоговая отметка в четверти является средним арифметическим всех текущих отметок, округлённым по правилам округления? (Например, 3,2 округляется до 3; 4,5 — до 5; 2,8 — до 3.)
Сложные задания с варианта МА2110306 (ответы выше):
2)Установка двух счётчиков воды (холодной и горячей) стоит 3500 рублей. До установки счётчиков за воду платили 2400 рублей ежемесячно. После установки счётчиков ежемесячная оплата воды стала составлять 1500 рублей. Через какое наименьшее количество месяцев экономия по оплате воды превысит затраты на установку счётчиков, если тарифы на воду не изменятся?
6)Магазин детских товаров закупает погремушки по оптовой цене 120 рублей за одну штуку и продаёт с наценкой 25 %. Сколько рублей будут стоить 3 такие погремушки, купленные в этом магазине?
10)От столба высотой 12 м к дому натянут провод, который крепится на высоте 4 м от земли (см. рисунок). Расстояние от дома до столба равно 15 м. Найдите длину провода. Ответ дайте в метрах.
11)Помещение освещается двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,3. Найдите вероятность того, что в течение года обе лампы перегорят.
13)Даны две коробки, имеющие форму правильной четырёхугольной призмы, стоящей на основании. Первая коробка в полтора раза выше второй, а вторая втрое шире первой. Во сколько раз объём первой коробки меньше объёма второй?
15)На окружности отмечена точка C. Отрезок AB — диаметр окружности, AC = 7 , BC = 24. Найдите радиус окружности.
16)Объём конуса равен 75π , а его высота равна 9. Найдите радиус основания конуса.
18)Кошка Китти весит на 3 килограмма больше кошки Машки, а кошка Лада на полтора килограмма легче кошки Машки. Выберите утверждения, которые верны при указанных условиях. 1) Любая кошка, помимо указанных, которая весит меньше Лады, весит также меньше Китти. 2) Любая кошка, помимо указанных, которая весит меньше Китти, весит также меньше Лады. 3) Среди указанных кошек нет кошек тяжелее Китти. 4) Машка весит меньше Лады.
19)Найдите четырёхзначное число, кратное 88, все цифры которого различны и чётны. В ответе укажите какое-нибудь одно такое число.
20)Двое рабочих, работая вместе, могут выполнить работу за 6 дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за 5 дней выполняет такую же часть работы, какую второй — за 3 дня?
21)В конце четверти Петя выписал подряд все свои отметки по одному из предметов, их оказалось 5, и поставил между некоторыми из них знаки умножения. Произведение получившихся чисел оказалось равным 2097. Какая отметка выходит у Пети в четверти по этому предмету, если учитель ставит только отметки «2», «3», «4» или «5» и итоговая отметка в четверти является средним арифметическим всех текущих отметок, округлённым по правилам округления? (Например, 3,2 округляется до 3; 4,5 — до 5; 2,8 — до 3.)
Сложные задания с варианта МА2110309 (ответы выше):
2)Перед началом первого тура чемпионата по теннису участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 36 теннисистов, среди которых 8 спортсменов из России, в том числе Юрий Молчанов. Найдите вероятность того, что в первом туре Юрий Молчанов будет играть с каким-либо теннисистом из России.
3)В треугольнике ABC угол C равен 62° , AD и BE — биссектрисы, пересекающиеся в точке O . Найдите угол AOB. Ответ дайте в градусах.
5)Стороны основания правильной шестиугольной пирамиды равны 24, боковые рёбра равны 37. Найдите площадь боковой поверхности этой пирамиды.
6)На рисунке изображён график функции y f’ x = ( ) — производной функции f x( ), определённой на интервале ( −2; 9). В какой точке отрезка [−1; 3] функция f x( ) принимает наибольшее значение?
8)Первый и второй насосы, работая совместно, наполняют бассейн за 24 минуты, второй и третий — за 35 минут, а первый и третий — за 40 минут. За сколько минут эти три насоса, работая совместно, заполнят бассейн?
10)Платежный терминал в течение рабочего дня может выйти из строя. Вероятность этого события 0,07. В торговом центре независимо друг от друга работают два таких платёжных терминала. Найдите вероятность того, что хотя бы один из них в течение рабочего дня будет исправен.
13)Основанием пирамиды SABCD является квадрат ABCD . Высота пирамиды проходит через точку D , М — середина бокового ребра SC . Угол между прямыми АМ и ВС равен 60° . а) Докажите, что SD CD : 11 = . б) Найдите расстояние от точки D до плоскости ABS , если сторона основания пирамиды равна 2 33 .
15)По вкладу «А» банк в конце каждого года планирует увеличивать на 7 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивать эту сумму на 6 % в первый год и на целое число n процентов во второй год. Найдите наименьшее значение n , при котором за два года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных вкладов.
18)На доске написали несколько не обязательно различных двузначных натуральных чисел без нулей в десятичной записи. Сумма этих чисел оказалась равной 264. Затем в каждом числе поменяли местами первую и вторую цифры (например, число 17 заменили на число 71). а) Могла ли сумма получившихся чисел быть ровно в 4 раза больше, чем сумма исходных чисел? б) Могла ли сумма получившихся чисел быть ровно в 3 раза больше, чем сумма исходных чисел? в) Найдите наибольшее возможное значение суммы получившихся чисел.
Сложные задания с варианта МА2110310 (ответы выше):
2)Перед началом первого тура чемпионата по шахматам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 76 шахматистов, среди которых 10 спортсменов из России, в том числе Александр Ефимов. Найдите вероятность того, что в первом туре Александр Ефимов будет играть с каким-либо шахматистом из России.
3)В треугольнике ABC угол C равен 138° , AD и BE — биссектрисы, пересекающиеся в точке O . Найдите угол AOB. Ответ дайте в градусах.
5)Стороны основания правильной шестиугольной пирамиды равны 18, боковые рёбра равны 41. Найдите площадь боковой поверхности этой пирамиды.
8)Первый и второй насосы, работая совместно, наполняют бассейн за 180 минут, второй и третий — за 210 минут, а первый и третий — за 280 минут. За сколько минут эти три насоса, работая совместно, заполнят бассейн?
10)Платежный терминал в течение рабочего дня может выйти из строя. Вероятность этого события 0,04. В торговом центре независимо друг от друга работают два таких платёжных терминала. Найдите вероятность того, что хотя бы один из них в течение рабочего дня будет исправен.
15)По вкладу «А» банк в конце каждого года планирует увеличивать на 9 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивать эту сумму на 7 % в первый год и на целое число n процентов во второй год. Найдите наименьшее значение n , при котором за два года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных вкладов.
18)На доске написали несколько не обязательно различных двузначных натуральных чисел без нулей в десятичной записи. Сумма этих чисел оказалась равной 165. Затем в каждом числе поменяли местами первую и вторую цифры (например, число 17 заменили на число 71). а) Могла ли сумма получившихся чисел быть ровно в 4 раза больше, чем сумма исходных чисел? б) Могла ли сумма получившихся чисел быть ровно в 5 раз больше, чем сумма исходных чисел? в) Найдите наибольшее возможное значение суммы получившихся чисел.
Сложные задания с варианта МА2110311 (ответы выше):
2)Конкурс исполнителей проводится в 4 дня. Всего заявлено 60 выступлений: по одному от каждой страны, участвующей в конкурсе. Исполнитель из России участвует в конкурсе. В первый день запланировано 6 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность того, что выступление исполнителя из России состоится в третий день конкурса?
3)Найдите угол ACB , если вписанные углы ADB и DAE опираются на дуги окружности, градусные меры которых равны соответственно 98° и 32° . Ответ дайте в градусах.
5)Диагональ куба равна 13. Найдите площадь полной поверхности куба.
6)На рисунке изображён график функции y f’ x = ( ) — производной функции f x( ), определённой на интервале ( −10;12). Найдите количество точек минимума функции f x( ), принадлежащих отрезку [−9;10].
8)Первый велосипедист выехал из посёлка по шоссе со скоростью 15 км/ч. Через час после него со скоростью 14 км/ч из того же посёлка в том же направлении выехал второй велосипедист, а ещё через час после этого — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 3 часа после этого догнал первого. Ответ дайте в км/ч.
10)Две фабрики выпускают одинаковые стёкла для автомобильных фар. Первая фабрика выпускает 45 % этих стёкол, вторая –– 55 %. Среди стекол, произведенных на первой фабрике, 3 % имеют дефекты. Вторая фабрика выпускает 1 % дефектных стекол. Все стекла поступают в продажу в магазины запчастей. Найдите вероятность того, что случайно выбранное стекло окажется с дефектом.
13)Основанием пирамиды SABCD является квадрат ABCD . Высота пирамиды проходит через точку D , М — середина бокового ребра SC . Угол между прямыми АМ и ВС равен 30° . а) Докажите, что CD SD : 3 = . б) Найдите расстояние от точки D до плоскости ABS , если сторона основания пирамиды равна 6.
15)По вкладу «А» банк в конце каждого года планирует увеличивать на 8 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивать эту сумму на 6 % в первый год и на целое число n процентов во второй год. Найдите наименьшее значение n , при котором за два года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных вкладов.
18)На доске написали несколько не обязательно различных двузначных натуральных чисел без нулей в десятичной записи. Сумма этих чисел оказалась равной 429. Затем в каждом числе поменяли местами первую и вторую цифры (например, число 17 заменили на число 71). а) Могла ли сумма получившихся чисел быть ровно в 4 раза больше, чем сумма исходных чисел? б) Могла ли сумма получившихся чисел быть ровно в 3 раза больше, чем сумма исходных чисел? в) Найдите наибольшее возможное значение суммы получившихся чисел.
Другие тренировочные варианты статград ЕГЭ 2022 по математике 11 класс:
-
Варианты МА2100101-МА2100110 ЕГЭ 2022 математика 10-11 класс статград с ответами
-
Математика 11 класс пробный ЕГЭ 2022 статград 12 вариантов МА2110201-МА2110212 с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
- 29.09.2021
Первая тренировочная работа от Статграда по математике профильного уровня в формате ЕГЭ 2022 года для 11 класса. С учетом всех изменений 2022 года от ФИПИ (смотрите изменения по профилю + демоверсию).
Работа проходила 28 сентября 2021 года.
Другие работы Статграда 2022
Тренировочные варианты по математике профиль
Все задания + ответы и решения к ним изложены в формате видеоразбора ниже.
Есть вопросы? Пишите в комментариях ниже!
Вариант целиком
Разбор заданий с 1 по 15
Вариант целиком — разбор с Анной Малковой
| 3318 | Найдите угол ACB, если вписанные углы ADB и DAE опираются на дуги окружности, градусные меры которых равны 98^@ и 32^@ соответственно. Ответ дайте в градусах
|
Найдите угол ACB, если вписанные углы ADB и DAE опираются на дуги окружности ! Тренировочная работа №3 по Математике 11 класс 16.02.2022 Вариант МА2110311 Задание 3 | |
| 3317 | Диагональ куба равна 13. Найдите площадь полной поверхности куба |
Диагональ куба равна 13. Найдите площадь полной поверхности куба ! Тренировочная работа №3 по Математике 11 класс 16.02.2022 Вариант МА2110311 Задание 5 |
|
| 3316 | Первый велосипедист выехал из посёлка по шоссе со скоростью 15 км/ч. Через час после него со скоростью 14 км/ч из того же посёлка в том же направлении выехал второй велосипедист, а ещё через час после этого — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 3 часа после этого догнал первого. Ответ дайте в км/ч |
Первый велосипедист выехал из посёлка по шоссе со скоростью 15 км/ч ! Тренировочная работа №3 по Математике 11 класс 16.02.2022 Вариант МА2110311 Задание 8 # Задача-Аналог 1930 | |
| 3315 | Две фабрики выпускают одинаковые стёкла для автомобильных фар. Первая фабрика выпускает 45 % этих стёкол, вторая — 55 %. Среди стекол, произведенных на первой фабрике, 3 % имеют дефекты. Вторая фабрика выпускает 1 % дефектных стекол. Все стекла поступают в продажу в магазины запчастей. Найдите вероятность того, что случайно выбранное стекло окажется с дефектом |
Среди стекол, произведенных на первой фабрике, 3 % имеют дефекты ! Тренировочная работа №3 по Математике 11 класс 16.02.2022 Вариант МА2110311 Задание 10 | |
| 3314 | Найдите точку максимума функции y=(x^2-4x+9)/(3x^2+6) |
Найдите точку максимума функции y= x2 -4x +9 / 3×2 +6 ! Тренировочная работа №3 по Математике 11 класс 16.02.2022 Вариант МА2110311 Задание 11 | |
| 3313 | а) Решите уравнение sin(x)+cos(x)-tan(x)=1 б) Укажите корни этого уравнения, принадлежащие отрезку[-(5pi)/2; -pi]. |
а) Решите уравнение sinx +cosx -tgx =1 ! Тренировочная работа №3 по Математике 11 класс 16.02.2022 Вариант МА2110311 Задание 12 | |
| 3312 | Основанием пирамиды SABCD является квадрат ABCD. Высота пирамиды проходит через точку D, М — середина бокового ребра SC. Угол между прямыми АМ и ВС равен 30°. а) Докажите, что CD:SD = sqrt3. б) Найдите расстояние от точки D до плоскости ABS, если сторона основания пирамиды равна 6 |
Основанием пирамиды SABCD является квадрат ABCD. Высота пирамиды проходит через точку D ! Тренировочная работа №3 по Математике 11 класс 16.02.2022 Вариант МА2110311 Задание 13 | |
| 3311 | Решите неравенство (1/(x^2-9x+14)-(x-2)/(7-x)). sqrt(x^3-10x^2+21x) <= 0. |
Решите неравенство (1 / x2 — 9x+ 14 — x-2 / 7 -x ) корень из x3 -10×2 + 21x <= 0 ! Тренировочная работа №3 по Математике 11 класс 16.02.2022 Вариант МА2110311 Задание 14 | |
| 3310 | Прямая, проходящая через середину M стороны BC треугольника ABC, пересекает сторону AC в точке K, причём /_CMK =/_BAC. а) Докажите, что /_BAM=/_BKM. б) Найдите медиану MN треугольника CKM, если BC=6, AB=sqrt35, CK=2 |
Прямая, проходящая через середину M стороны BC треугольника ABC, пересекает сторону AC в точке K ! Тренировочная работа №3 по Математике 11 класс 16.02.2022 Вариант МА2110311 Задание 16 | |
Главная страница » Работы статград март 2023 год варианты ответы и решения
Автор admin На чтение 2 мин Просмотров 3.1к. Опубликовано 2 марта, 2023
Вам также может понравиться
Сценарий внеклассного мероприятия » Экологическая
09
Урок-игра: «Формула здоровья» Решение и ответы
05
ИСПОЛЬЗОВАНИЕ ЭЛЕКТРОННОГО ПРИЛОЖЕНИЯ НА УРОКАХ БИОЛОГИИ
06
ПРИМЕНЕНИЕ ЭЛЕКТРОННОЙ ФОРМЫ УЧЕБНИКА НА УРОКАХ БИОЛОГИИ
012
Тест по теме: «Общие закономерности биологической эволюции»
07
Үрчү һәм организмнарның индивидуаль үсеше Решение и
08
Технологическая карта бинарного урока биология-физика «
08
Технологическая карта урока биологии в 6 классе по
08
Математика, 11 класс, Тренировочная работа №3, Вариант МА2110301-308, 2022.
Работа по математике включает в себя 21 задание.
На выполнение работы отводится 3 часа (180 минут).
Ответы к заданиям записываются в виде числа или последовательности цифр в поле ответа в тексте работы.
При выполнении заданий можно пользоваться черновиком. Записи в черновике не учитываются при оценивании работы. Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
Примеры.
Для покраски 1 кв. м потолка требуется 150 г краски. Краска продаётся в банках по 2,5 кг. Какое наименьшее количество банок краски нужно для покраски потолка площадью 41 кв. м?
В чемпионате по гимнастике участвуют 65 спортсменок: 18 из Аргентины, 21 из Бразилии, остальные — из Парагвая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Парагвая.
Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:
Скачать книгу Математика, 11 класс, Тренировочная работа №3, Вариант МА2110301-308, 2022 — fileskachat.com, быстрое и бесплатное скачивание.
Скачать pdf
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России.Купить эту книгу
Скачать
— pdf — Яндекс.Диск.
Дата публикации: 13.06.2022 08:03 UTC
Теги:
тесты по математике :: математика :: 11 класс
Следующие учебники и книги:
- Математика, 11 класс, Тренировочная работа №5, Вариант МА2110501-508, 2022
- Математика, 11 класс, Тренировочная работа №4, Профильный уровень, Вариант МА2110409-412, 2022
- Математика, 11 класс, Тренировочная работа №4, Вариант МА2110401-408, 2022
- Математика, 11 класс, Тренировочная работа №3, Профильный уровень, Вариант МА2110309-312, 2022
Предыдущие статьи:
- Математика, 11 класс, Тренировочная работа №2, Профильный уровень, Вариант МА2110209-212, 2021
- Математика, 11 класс, Тренировочная работа №2, Вариант МА2110201-208, 2021
- Математика, 10-11 классы, Тренировочная работа №1, Профильный уровень, Вариант МА2100109-110, 2022
- Математика, 10-11 класс, Тренировочная работа №1, Вариант МА2100101-108, 2022
Решение и ответы заданий варианта МА2210101 СтатГрад 28 сентября ЕГЭ 2023 по математике (базовый уровень). Тренировочная работа №1. ГДЗ профиль для 11 класса. Полный разбор.

Задание 1.
В школе есть двухместные туристические палатки. Какое наименьшее число палаток нужно взять в поход, в котором участвует 21 человек?
Задание 2.
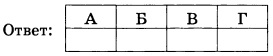
Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
| ВЕЛИЧИНЫ | ВОЗМОЖНЫЕ ЗНАЧЕНИЯ |
| А) рост новорождённого ребёнка Б) длина реки Енисей В) толщина лезвия бритвы Г) высота горы Эльбрус |
1) 4300 км |
В таблице под каждой буквой укажите соответствующий номер.
Задание 3.
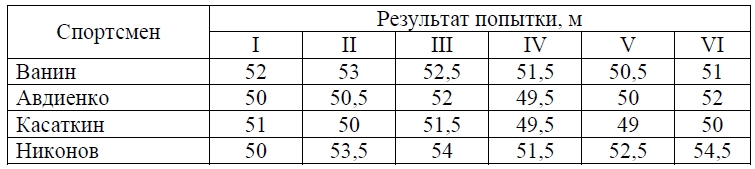
Результаты соревнований по метанию молота представлены в таблице.
Места распределяются по результату лучшей попытки каждого спортсмена: чем дальше он метнул молот, тем лучше. Каков результат лучшей попытки (в метрах) спортсмена, занявшего третье место?
Задание 4.
Скорость камня (в м/с), падающего с высоты h (в м), в момент удара о землю можно найти по формуле v = sqrt{2gh}. Найдите скорость (в м/с), с которой ударится о землю камень, падающий с высоты 0,9 м. Считайте, что ускорение свободного падения g равно 9,8 м/с2 .
Задание 5.
Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд будет владеть мячом в начале матча. Команда «Физик» играет два матча с разными командами. Найдите вероятность того, что «Физик» хотя бы один раз выиграет мяч.
Задание 6.
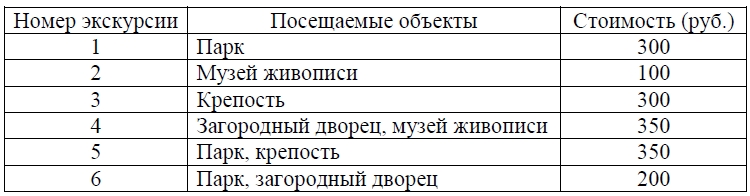
Турист подбирает экскурсии. Сведения об экскурсиях представлены в таблице.
Пользуясь таблицей, подберите набор экскурсий так, чтобы турист посетил четыре объекта: крепость, загородный дворец, парк и музей живописи, а суммарная стоимость экскурсий не превышала 650 рублей. В ответе укажите какой-нибудь один набор номеров экскурсий без пробелов, запятых и других дополнительных символов.
Задание 7.
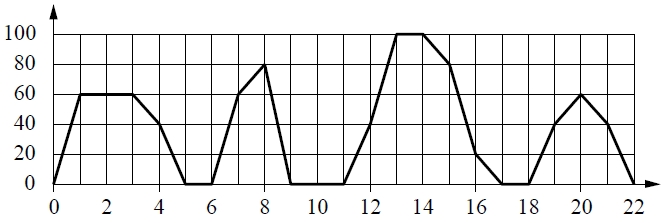
На графике изображена зависимость скорости движения рейсового автобуса от времени. На вертикальной оси отмечена скорость автобуса в км/ч, на горизонтальной – время в минутах, прошедшее с начала движения автобуса.
Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику движения автобуса на этом интервале.
| ИНТЕРВАЛЫ ВРЕМЕНИ | ХАРАКТЕРИСТИКИ |
| А) 0–4 мин. Б) 4–8 мин. В) 8–12 мин. Г) 12–16 мин. |
1) Автобус сделал остановку длительностью ровно 1 минута. 2) Скорость автобуса достигла максимума за всё время движения. 3) Две минуты автобус двигался с постоянной ненулевой скоростью. 4) Автобус сделал остановку длительностью 2 минуты. |
В таблице под каждой буквой укажите соответствующий номер.
Задание 8.
Во дворе школы растут всего три дерева: берёза, клён и дуб. Берёза выше клёна на 1 метр, но ниже дуба на 3 метра. Выберите утверждения, которые верны при указанных условиях.
1) Среди указанных деревьев не найдётся двух одной высоты.
2) Берёза, растущая во дворе школы, выше дуба, растущего там же.
3) Любое дерево, помимо указанных, которое ниже берёзы, растущей во дворе школы, также ниже клёна, растущего там же.
4) Любое дерево, помимо указанных, которое ниже клёна, растущего во дворе школы, также ниже берёзы, растущей там же.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Задание 9.
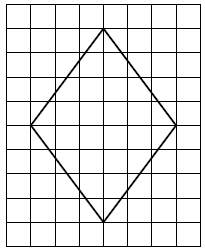
План местности разбит на клетки. Каждая клетка обозначает квадрат 1м ×1м. Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах.
Задание 10.
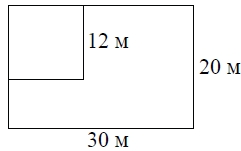
Дачный участок имеет форму прямоугольника со сторонами 30 метров и 20 метров. Хозяин планирует обнести его изгородью и отгородить такой же изгородью квадратный участок со стороной 12 метров (см. рисунок). Найдите суммарную длину изгороди в метрах.
Задание 11.
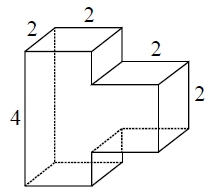
Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Цифры на рисунке обозначают длины рёбер в сантиметрах. Найдите площадь поверхности этой детали. Ответ дайте в квадратных сантиметрах.
Задание 12.
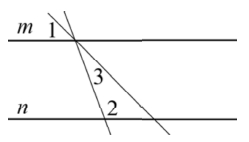
Прямые m и n параллельны (см. рисунок). Найдите ∠3, если ∠1 = 22°, ∠2 = 138°. Ответ дайте в градусах.
Задание 13.
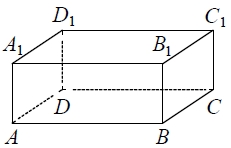
В прямоугольном параллелепипеде ABCDA1B1C1D1 рёбра CD, CB и диагональ CD1 боковой грани равны соответственно 2, 4 и 2√10. Найдите объём параллелепипеда ABCDA1B1C1D1.
Задание 14.
Найдите значение выражения 28cdot (frac{2}{7}-frac{3}{14}-frac{5}{28}).
Задание 15.
Тетрадь стоит 21 рубль. Сколько рублей заплатит покупатель за 70 тетрадей, если при покупке больше 50 тетрадей магазин делает скидку 10% от стоимости всей покупки?
Задание 16.
Найдите значение выражения frac{(8sqrt{3})^{2}}{48}.
Задание 17.
Найдите корень уравнения 32х–4 : 3х–3 = 1.
Задание 18.
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
Впишите в приведённую в ответе таблицу под каждой буквой соответствующий решению номер.
Задание 19.
Четырёхзначное число A состоит из цифр 3, 4, 8, 9, а четырёхзначное число B – из цифр 6, 7, 8, 9. Известно, что B = 2A. Найдите число A. В ответе укажите какое-нибудь одно такое число, большее 3500.
Задание 20.
Расстояние между городами A и B равно 500 км. Из города A в город B выехал первый автомобиль, а через час после этого навстречу ему из городе B выехал со скоростью 80 км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 260 км от города A. Ответ дайте в км/ч.
Задание 21.
Клетки таблицы 6х5 раскрашены в чёрный и белый цвета так, что получилось 26 пар соседних клеток разного цвета и 6 пар соседних клеток чёрного цвета. (Клетки считаются соседними, если у них есть общая сторона.) Сколько пар соседних клеток белого цвета?
Источник варианта: СтатГрад/statgrad.org.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 4
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.