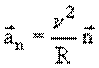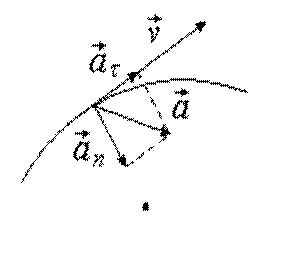Ставлю 10/10
Все нравится, очень удобный сайт, помогает в учебе. Кроме этого, можно заработать самому, выставляя готовые учебные материалы на продажу здесь. Рейтинги и отзывы на преподавателей очень помогают сориентироваться в начале нового семестра. Спасибо за такую функцию. Ставлю максимальную оценку.
Отлично
Лучшая платформа для успешной сдачи сессии
Познакомился со СтудИзбой благодаря своему другу, очень нравится интерфейс, количество доступных файлов, цена, в общем, все прекрасно. Даже сам продаю какие-то свои работы.
Отлично
Студизба ван лав ❤
Очень офигенный сайт для студентов. Много полезных учебных материалов. Пользуюсь студизбой с октября 2021 года. Серьёзных нареканий нет. Хотелось бы, что бы ввели подписочную модель и сделали материалы дешевле 300 рублей в рамках подписки бесплатными.
Отлично
Отличный сайт
Лично меня всё устраивает — и покупка, и продажа; и цены, и возможность предпросмотра куска файла, и обилие бесплатных файлов (в подборках по авторам, читай, ВУЗам и факультетам). Есть определённые баги, но всё решаемо, да и администраторы реагируют в течение суток.
Отлично
Маленький отзыв о большом помощнике!
Студизба спасает в те моменты, когда сроки горят, а работ накопилось достаточно. Довольно удобный сайт с простой навигацией и огромным количеством материалов.
Хорошо
Студ. Изба как крупнейший сборник работ для студентов
Тут дофига бывает всего полезного. Печально, что бывают предметы по которым даже одного бесплатного решения нет, но это скорее вопрос к студентам. В остальном всё здорово.
Отлично
Спасательный островок
Если уже не успеваешь разобраться или застрял на каком-то задание поможет тебе быстро и недорого решить твою проблему.
Отлично
Всё и так отлично
Всё очень удобно. Особенно круто, что есть система бонусов и можно выводить остатки денег. Очень много качественных бесплатных файлов.
Отлично
Отзыв о системе «Студизба»
Отличная платформа для распространения работ, востребованных студентами. Хорошо налаженная и качественная работа сайта, огромная база заданий и аудитория.
Хорошо
Отличный помощник
Отличный сайт с кучей полезных файлов, позволяющий найти много методичек / учебников / отзывов о вузах и преподователях.
Отлично
Отлично помогает студентам в любой момент для решения трудных и незамедлительных задач
Хотелось бы больше конкретной информации о преподавателях. А так в принципе хороший сайт, всегда им пользуюсь и ни разу не было желания прекратить. Хороший сайт для помощи студентам, удобный и приятный интерфейс. Из недостатков можно выделить только отсутствия небольшого количества файлов.
Отлично
Спасибо за шикарный сайт
Великолепный сайт на котором студент за не большие деньги может найти помощь с дз, проектами курсовыми, лабораторными, а также узнать отзывы на преподавателей и бесплатно скачать пособия.
Отлично
Помогите рассортировать файлы. К какому предмету относится данный файл?
Ненужные и мусорные файлы можно перемещать в предмет [НА УДАЛЕНИЕ].
Помогите дать файлам осмысленные названия
Примеры:
lab1 => Лабораторная работа №1. Фотоэффект.
Savelev_molekulyarnaya_fizika => Савельев. Молекулярная физика
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вопросы к экзамену по первой части курса
«Физика»
1.
Кинематика материальной точки.
Координатная и векторная формы описания движения. Перемещение, скорость и
ускорение материальной точки.
2.
Виды движения материальной точки.
Прямолинейное (равномерное и равноускоренное) движение. Движение по окружности.
Криволинейное движение. Скорость и ускорение (нормальное, тангенциальное) при
криволинейном движении.
3.
Законы Ньютона. Их взаимосвязь и
границы применимости.
4.
Закон инерции. Инерциальные
системы отсчета. Принцип относительности Галилея.
5.
Второй закон Ньютона. Силы: сила
тяжести, сила упругости, сила трения. Движение под действием этих сил.
6.
Третий закон Ньютона. Импульс.
Закон сохранения импульса.
7.
Центр масс. Теорема о движении
центра масс.
8.
Движение в центральном поле сил.
Закон всемирного тяготения.
9.
Соударение двух тел. Абсолютно
упругий и абсолютно неупругий удар.
10.
Консервативные силы и
потенциальное поле. Работа в потенциальном поле. Кинетическая и потенциальная
энергия. Закон сохранения энергии в механике.
11.
Момент импульса и момент силы
относительно неподвижного начала. Уравнение моментов. Закон сохранения момента
импульса.
12.
Момент импульса и момент сил
относительно неподвижной оси. Уравнение динамики вращательного движения
относительно неподвижной оси.
13.
Момент инерции. Теорема Штейнера.
Кинетическая энергия вращающегося твердого тела.
14.
Гармонические колебания и их
характеристики. Комплексная форма представления гармонических колебаний.
Сложение гармонических колебаний одинаковых и близких частот. Биения.
15.
Гармонический осциллятор.
Уравнение динамики гармонических колебаний. Примеры гармонических осцилляторов:
пружинный, физический и математический маятники.
16.
Затухающие колебания. Время
релаксации. Коэффициент затухания. Логарифмический декремент затухания.
17.
Вынужденные колебания. Амплитуда и
фаза вынужденных колебаний. Резонанс.
18.
Волны. Продольные и поперечные
волны. Одномерное волновое уравнение. Интерференция волн. Стоячие волны.
19.
Состояние равновесия.
Макроскопические параметры. Уравнения состояния.
20.
Законы идеальных газов: закон
Бойля-Мариотта, закон Гей-Люссака, закон Авогадро, закон Дальтона.
21.
Уравнение состояния и внутренняя
энергия идеального газа. Степени свободы. Теорема о равнораспределении энергии
по степеням свободы.
22.
Давление газа с точки зрения молекулярно-кинетической
теории. Молекулярно-кинетический смысл температуры.
23.
Функция распределения молекул по
скоростям. Распределение Максвелла.
24.
Барометрическая формула.
Распределение Больцмана.
25.
Изопроцессы. Изопроцессы
идеального газа.
26.
Теплоемкость. Теплоемкость
идеальных газов. Уравнение Майера.
27.
Первое начало термодинамики.
Макроскопическая работа, количество тепла.
28.
Второе начало термодинамики.
Равенство Клаузиуса. Энтропия.
29.
Явления переноса. Распределение
молекул по длинам свободного пробега. Средняя длина свободного пробега.
30.
Уравнение Ван-дер-Ваальса.
Критическое состояние вещества.
31.
Фазы. Условия равновесия фаз.
Уравнение Клапейрона-Клаузиуса.
Ответы
1 Кинематика материальной точки- изучает законы перемещения
материальной точки в зависимости от времени без учета причин, вызывающих это
перемещение. Материальная точка- тело, размерами которого в условиях данной
задачи можно пренебречь.
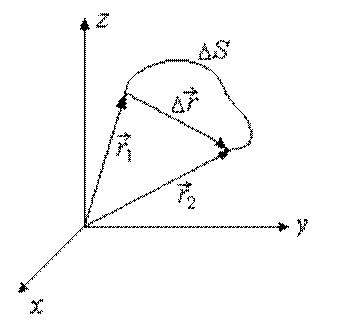
Мгновенное положение материальной точки (Р) в
пространстве можно описать при помощи радиуса-вектора этой точки, начало которого связано с
началом координат (рис. 1.1). Радиус- вектор в данный момент времени является
функцией координат (x, y, z). Разложим вектор на сумму векторов, направленных по осям
координат :
Рис. 1.1
,
где (x, y, z) – проекции вектора на координатные оси (координаты
точки), – орты
соответствующих осей.
В векторной форме радиус-вектор записывается:
,
длина вектора (модуль вектора):
.
При движении материальной точки конец ее радиуса-вектора
описывает в пространстве некоторую линию (годограф), называемую траекторией.
Форма траектории определяет характер движения – прямолинейное или
криволинейное. Длина траектории называется длиной пути (). Путь – скалярная функция
времени и всегда положительная величина.
Разность радиусов-векторов, определяющих два положения
материальной точки в моменты времени t1 и t2, называется
вектором перемещения (рис.
1.2).
Рис. 1.2
При прямолинейном движении модуль вектора перемещения равен длине пути
.
В общем случае криволинейного движения это равенство возможно
лишь для бесконечно малого отрезка времени (рис. 1.3):
Рис. 1.3
Запишем вектор перемещения и модуль вектора перемещения
в координатной форме.
Так как:
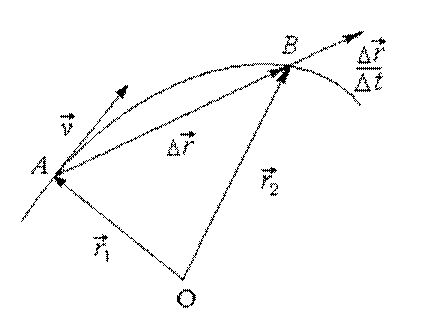
Пусть материальная точка движется по криволинейной траектории из
точки А, положение которой задается радиусом-вектором (рис. 1.4).
Рис. 1.4
Через некоторое время она будет находиться в точке В,
радиус-вектор которой .
Перемещение точки равно вектору , пройденный путь
равен длине дуги AB. Вектором
средней скорости движения
материальной точки называется отношение перемещения ко времени
, за которое это перемещение
произошло
Средней путевой скоростью называется отношение:
Уменьшим время наблюдения, при этом перемещение также уменьшится. Отношение
при
стремится к определенному пределу,
называемому вектором мгновенной скорости. Мгновенная скорость – вектор,
направленный по касательной к кривой в точке А, так как, по
определению, касательная – это предельное положение секущей при бесконечно
малом перемещении.
|
|
(1.1) |
Единица измерения скорости – [м/с].
Вектор скорости – первая производная радиуса–вектора по времени.
Модуль вектора скорости – первая производная пути по времени. Так как
то
т. е.
|
|
(1.2) |
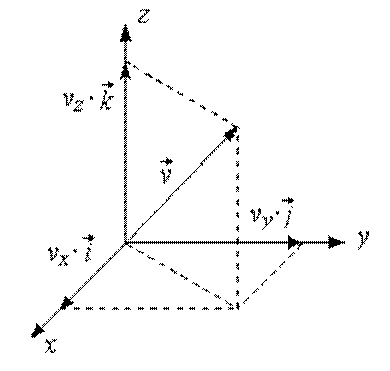
Запишем вектор скорости в координатной форме
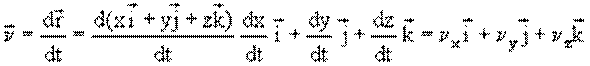
где –
проекции вектора скорости на соответствующие оси координат
(рис. 1.5).
Рис. 1.5
Модуль вектора скорости равен:
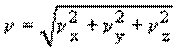
В случае, если тело за сколь угодно малые равные промежутки
времени проходит
одинаковые отрезки пути , то тело движется равномерно , с
постоянной скоростью. При этом мгновенная скорость в разные моменты времени по
модулю остается постоянной.
Так, движение точки по окружности с постоянной по величине
скоростью является равномерным, но криволинейным.
1. 3. Ускорение. Тангенциальное, нормальное и
полное ускорение
В общем случае, при движении материальной точки по криволинейной
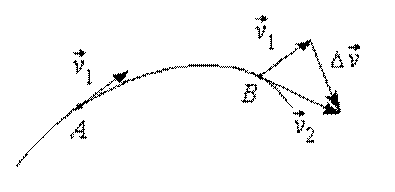
траектории вектор скорости может меняться по величине и направлению.
Пусть за малый промежуток времени точка переместилась из положения А
в положение В и при этом скорость ее изменилась от до
(рис. 1.6).
Перенесем вектор скорости в точку В методом параллельного
переноса, тогда –
изменение вектора скорости за время движения тела из А в В.
Рис. 1.6
Векторная величина, равная пределу, к которому стремится
отношение при
неограниченном уменьшении промежутка времени называется ускорением.
Вектор ускорения равен первой производной вектора скорости по времени:
|
|
(1.3) |
Как всякий вектор, ускорение можно представить в виде суммы
проекций на оси (x, y, z):
Модуль вектора ускорения
Единица измерения ускорения – [м/c2].
Вектор ускорения сонаправлен с вектором изменения скорости
.
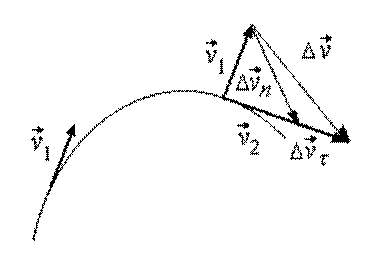
Пусть за время скорость материальной точки изменилась по
величине и по направлению. Тогда вектор изменения скорости можно представить в виде суммы
двух векторов, один из которых характеризует изменение скорости по
направлению, другой –
изменение скорости по величине (рис. 1.7)
Рис. 1.7
В этом случае вектор ускорения также можно представить в виде суммы двух
векторов ( и
)
|
|
(1.4) |
где – нормальное
ускорение, характеризующее быстроту изменения скорости по направлению, а
– тангенциальное
ускорение, характеризующее быстроту изменения скорости по величине.
Тангенциальное ускорение удобно рассмотреть на примере
неравномерного прямолинейного движения. При этом скорость изменяется только по
величине , поэтому
:
т. е.
|
|
(1.5) |
В векторной форме 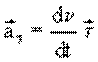
– единичный вектор, сонаправленный с
вектором скорости.
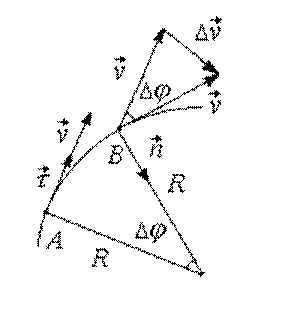
Нормальное ускорение удобно рассмотреть на примере
равномерного движения по окружности. При этом .
Перенесем вектор скорости из точки А в точку В
методом параллельного переноса (рис. 1.8).
Рис. 1.8
Если время перемещения точки из А в В мало, то
малый угол поворота радиуса-вектора точки может быть записан следующим образом:
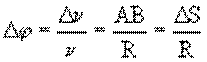
где АВ – длина дуги окружности радиуса R, – угол в радианах.
Тогда
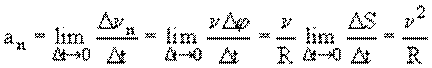
т. е.
|
|
(1.6) |
В векторной форме:
где –
единичный вектор, направленный по радиусу к центру кривизны траектории в данной
точке, т.е. перпендикулярно вектору скорости (рис. 1.8).
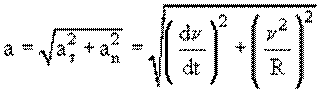
Таким образом, вектор полного ускорения материальной точки равен
|
|
(1.7) |
а модуль вектора полного ускорения :
|
|
(1.7′) |
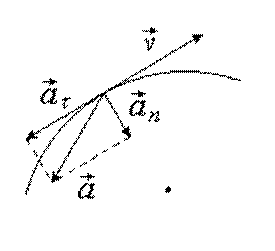
|
Рис. 1.9, a |
Рис. 1.9, б |
На рис. 1.9 показано направление векторов при ускоренном и
замедленном движении. Модуль вектора тангенциального ускорения
положителен 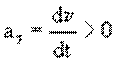
ускоренном движении (рис. 1.9, а) и отрицателен 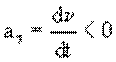
1.9, б). Модуль вектора нормального ускорения всегда положителен.
2
ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ (МАДИ)
«УТВЕРЖДАЮ»
Проректор по УВР
__________________
Ушаков В.В.
«______» ___________2013г.
П Р О Г Р А М М А
ПИСЬМЕННОГО ЭКЗАМЕНА ПО ДИСЦИПЛИНЕ
«ФИЗИКА»
- Настоящая программа разработана в соответствии с «Положением о курсовых экзаменах и зачетах в Московском автомобильно-дорожном государственном техническом университете (МАДИ)» от 11 декабря 2012 г. и « Положением о балльно-рейтинговой системе оценки знаний студентов на кафедре физики МАДИ» от 13 февраля 2013 г.
- Критерии допуска к экзамену. К экзамену допускаются студенты, получившие зачет по лабораторному практикуму и набравшие необходимое количество баллов (45% от нормативного рейтинга) по результатам работы в семестре. В соответствии с «Положением о балльно-рейтинговой системе оценки знаний студентов на кафедре физики МАДИ» студенты, набравшие по результатам контроля учебной работы в семестре 85% от максимально возможного количества баллов, освобождаются от сдачи экзамена и получают оценку «отлично», 75% — «хорошо», 65% — «удовлетворительно». Оценка проставляется в ведомость в день экзамена. Студенты, отказавшиеся от оценки, соответствующей набранным баллам, оцениваются по результатам экзамена.
- Единство требований на экзамене. Для всех специальностей (направлений подготовки) всех форм обучения (очной, очно-заочной и заочной) экзамен по физике проводится в письменной форме по единым требованиям.
Лектор потока обязан своевременно подготовить экзаменационные билеты в соответствии с утвержденной рабочей программой курса физики текущего семестра. Перечень вопросов и экзаменационные билеты утверждаются на заседании кафедры и подписываются заведующей кафедрой. Перечень вопросов и типовые задачи передаются студенческой группе не позднее, чем за 14 дней до начала сессии. Количество билетов должно превышать число студентов в группе.
- Продолжительность экзамена и методика его проведения. Экзаменационные билеты должны содержать два теоретических вопроса и одну качественную или тестовую задачу. Трудоемкость выполнения экзаменационных заданий рассчитывается, исходя из следующих норм: ответ на каждый теоретический вопрос – 30 минут, решение задачи – 20 минут, уяснение заданий и оформление работы -10 минут. Продолжительность письменного экзамена 1 час 30 минут.
При получении студентом билета преподаватель, проводящий экзамен, проставляет на бланке номер билета и время его выдачи.
- Порядок и критерии выставления оценки. Проверку работ осуществляет лектор потока. К проверке экзаменационных работ могут быть также привлечены другие преподаватели кафедры, назначенные заведующей кафедры. Полностью раскрытый теоретический вопрос оценивается в 20 баллов, задача — 10 баллов. Оценка «удовлетворительно» выставляется студенту, набравшему от 20 до 29 баллов, «хорошо» от 30 до 39 баллов, «отлично» от 40 до 50 баллов.
В исключительных случаях для уточнения оценки экзаменатор может задавать студентам дополнительные вопросы по программе курса.
- Условия пересдачи экзамена. Условия пересдачи экзамена определяются действующими «Положением о курсовых экзаменах и зачетах в Московском автомобильно-дорожном государственном техническом университете (МАДИ)» и «Инструкцией о порядке проведения письменных экзаменов по дисциплинам учебных планов и подведении их итогов».
Заведующая кафедрой физики / Смык А.Ф./





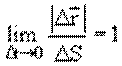
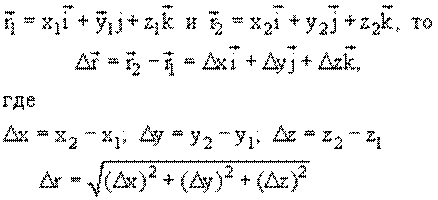
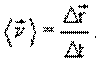
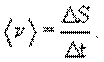
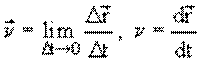
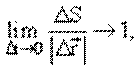
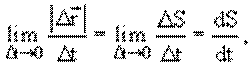
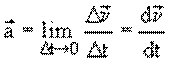


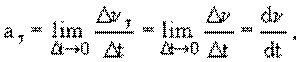
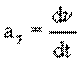
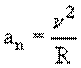 .
.