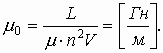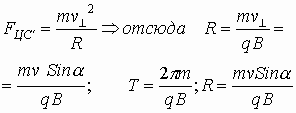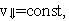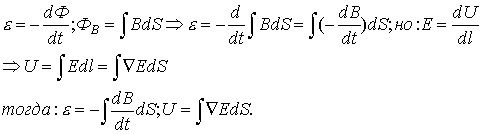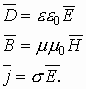Оглавление:
- Основные теоретические сведения
- Сила Ампера
- Сила Лоренца
- Теория о магнитном поле
- Магнитный поток. Электромагнитная индукция
- Движение проводника в магнитном поле
- Индуктивность. Самоиндукция. Энергия магнитного поля
- Правило Ленца
Основные теоретические сведения
Сила Ампера
К оглавлению…
Заряженные тела способны создавать кроме электрического еще один вид поля. Если заряды движутся, то в пространстве вокруг них создается особый вид материи, называемый магнитным полем. Следовательно, электрический ток, представляющий собой упорядоченное движение зарядов, тоже создает магнитное поле. Как и электрическое поле, магнитное поле не ограничено в пространстве, распространяется очень быстро, но все же с конечной скоростью. Его можно обнаружить только по действию на движущиеся заряженные тела (и, как следствие, токи).
Для описания магнитного поля необходимо ввести силовую характеристику поля, аналогичную вектору напряженности E электрического поля. Такой характеристикой является вектор B магнитной индукции. В системе единиц СИ за единицу магнитной индукции принят 1 Тесла (Тл). Если в магнитное поле с индукцией B поместить проводник длиной l с током I, то на него будет действовать сила, называемая силой Ампера, которая вычисляется по формуле:
где: В – индукция магнитного поля, I – сила тока в проводнике, l – его длина. Сила Ампера направлена перпендикулярно вектору магнитной индукции и направлению тока, текущего по проводнику.
Для определения направления силы Ампера обычно используют правило «Левой руки»: если расположить левую руку так, чтобы линии индукции входили в ладонь, а вытянутые пальцы были направлены вдоль тока, то отведенный большой палец укажет направление силы Ампера, действующей на проводник (см. рисунок).
Если угол α между направлениями вектора магнитной индукции и тока в проводнике отличен от 90°, то для определения направления силы Ампера надо взять составляющую магнитного поля, которая перпендикулярна направлению тока. Решать задачи этой темы нужно так же как и в динамике или статике, т.е. расписав силы по осям координат или складывая силы по правилам сложения векторов.
Момент сил, действующих на рамку с током
Пусть рамка с током находится в магнитном поле, причём плоскость рамки перпендикулярна полю. Силы Ампера будут сжимать рамку, а их равнодействующая будет равна нулю. Если поменять направление тока, то силы Ампера поменяют своё направление, и рамка будет не сжиматься, а растягиваться. Если линии магнитной индукции лежат в плоскости рамки, то возникает вращательный момент сил Ампера. Вращательный момент сил Ампера равен:
где: S — площадь рамки, α — угол между нормалью к рамке и вектором магнитной индукции (нормаль — вектор, перпендикулярный плоскости рамки), N – количество витков, B – индукция магнитного поля, I – сила тока в рамке.
Сила Лоренца
К оглавлению…
Сила Ампера, действующая на отрезок проводника длиной Δl с силой тока I, находящийся в магнитном поле B может быть выражена через силы, действующие на отдельные носители заряда. Эти силы называют силами Лоренца. Сила Лоренца, действующая на частицу с зарядом q в магнитном поле B, двигающуюся со скоростью v, вычисляется по следующей формуле:
Угол α в этом выражении равен углу между скоростью и вектором магнитной индукции. Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки или по правилу буравчика (как и сила Ампера). Вектор магнитной индукции нужно мысленно воткнуть в ладонь левой руки, четыре сомкнутых пальца направить по скорости движения заряженной частицы, а отогнутый большой палец покажет направление силы Лоренца. Если частица имеет отрицательный заряд, то направление силы Лоренца, найденное по правилу левой руки, надо будет заменить на противоположное.
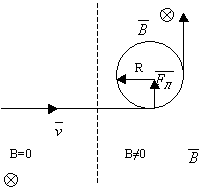
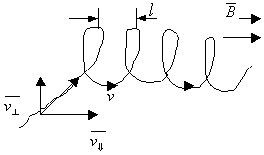
Сила Лоренца направлена перпендикулярно векторам скорости и индукции магнитного поля. При движении заряженной частицы в магнитном поле сила Лоренца работы не совершает. Поэтому модуль вектора скорости при движении частицы не изменяется. Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость лежит в плоскости, перпендикулярной вектору индукции магнитного поля, то частица будет двигаться по окружности, радиус которой можно вычислить по следующей формуле:
Сила Лоренца в этом случае играет роль центростремительной силы. Период обращения частицы в однородном магнитном поле равен:
Последнее выражение показывает, что для заряженных частиц заданной массы m период обращения (а значит и частота, и угловая скорость) не зависит от скорости (следовательно, и от кинетической энергии) и радиуса траектории R.
Теория о магнитном поле
К оглавлению…
Магнитное взаимодействие токов
Если по двум параллельным проводам идёт ток в одном направлении, то они притягиваются; если в противоположных направлениях, то отталкиваются. Закономерности этого явления были экспериментально установлены Ампером. Взаимодействие токов вызывается их магнитными полями: магнитное поле одного тока действует силой Ампера на другой ток и наоборот. Опыты показали, что модуль силы, действующей на отрезок длиной Δl каждого из проводников, прямо пропорционален силам тока I1 и I2 в проводниках, длине отрезка Δl и обратно пропорционален расстоянию R между ними:
где: μ0 – постоянная величина, которую называют магнитной постоянной. Введение магнитной постоянной в СИ упрощает запись ряда формул. Ее численное значение равно:
μ0 = 4π·10–7 H/A2 ≈ 1,26·10–6 H/A2.
Сравнивая приведенное только что выражение для силы взаимодействия двух проводников с током и выражение для силы Ампера нетрудно получить выражение для индукции магнитного поля создаваемого каждым из прямолинейных проводников с током на расстоянии R от него:
где: μ – магнитная проницаемость вещества (об этом чуть ниже). Если ток протекает по круговому витку, то в центре витка индукция магнитного поля определяется по формуле:
Силовыми линиями магнитного поля называют линии, по касательным к которым располагаются магнитные стрелки. Магнитной стрелкой называют длинный и тонкий магнит, его полюса точечны. Подвешенная на нити магнитная стрелка всегда поворачивается в одну сторону. При этом один её конец направлен в сторону севера, второй — на юг. Отсюда название полюсов: северный (N) и южный (S). Магниты всегда имеют два полюса: северный (обозначается синим цветом или буквой N) и южный (красным цветом или буквой S). Магниты взаимодействуют так же, как и заряды: одноименные полюса отталкиваются, а разноименные – притягиваются. Невозможно получить магнит с одним полюсом. Даже если магнит разломать, то у каждой части будет по два разных полюса.
Вектор магнитной индукции
Вектор магнитной индукции — векторная физическая величина, являющаяся характеристикой магнитного поля, численно равная силе, действующей на элемент тока в 1 А и длиной 1 м, если направление силовой линии перпендикулярно проводнику. Обозначается В, единица измерения — 1 Тесла. 1 Тл — очень большая величина, поэтому в реальных магнитных полях магнитную индукцию измеряют в мТл.
Вектор магнитной индукции направлен по касательной к силовым линиям, т.е. совпадает с направлением северного полюса магнитной стрелки, помещённой в данное магнитное поле. Направление вектора магнитной индукции не совпадает с направлением силы, действующей на проводник, поэтому силовые линии магнитного поля, строго говоря, силовыми не являются.
Силовая линия магнитного поля постоянных магнитов направлена по отношению к самим магнитам так, как показано на рисунке:
В случае магнитного поля электрического тока для определения направления силовых линий используют правило «Правой руки»: если взять проводник в правую руку так, чтобы большой палец был направлен по току, то четыре пальца, обхватывающие проводник, показывают направление силовых линий вокруг проводника:
В случае прямого тока линии магнитной индукции — окружности, плоскости которых перпендикулярны току. Вектора магнитной индукции направлены по касательной к окружности.
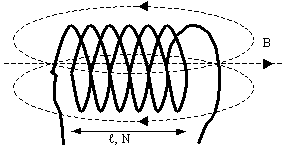
Соленоид — намотанный на цилиндрическую поверхность проводник, по которому течёт электрический ток I. Магнитное поле соленоида подобно полю прямого постоянного магнита. Внутри соленоида длиной l и количеством витков N создается однородное магнитное поле с индукцией (его направление также определяется правилом правой руки):
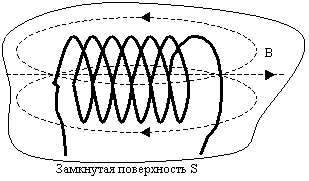
Линии магнитного поля имеют вид замкнутых линий — это общее свойство всех магнитных линий. Такое поле называют вихревым. В случае постоянных магнитов линии не оканчиваются на поверхности, а проникают внутрь магнита и замыкаются внутри. Это различие электрического и магнитного полей объясняется тем, что, в отличие от электрических, магнитных зарядов не существует.
Магнитные свойства вещества
Все вещества обладают магнитными свойствами. Магнитные свойства вещества характеризуются относительной магнитной проницаемостью μ, для которой верно следующее:
Данная формула выражает соответствие вектора магнитной индукции поля в вакууме и в данной среде. В отличие от электрического, при магнитном взаимодействии в среде можно наблюдать и усиление, и ослабление взаимодействия по сравнению с вакуумом, у которого магнитная проницаемость μ = 1. У диамагнетиков магнитная проницаемость μ немного меньше единицы. Примеры: вода, азот, серебро, медь, золото. Эти вещества несколько ослабляют магнитное поле. Парамагнетики — кислород, платина, магний — несколько усиливают поле, имея μ немного больше единицы. У ферромагнетиков — железо, никель, кобальт — μ >> 1. Например, у железа μ ≈ 25000.
Магнитный поток. Электромагнитная индукция
К оглавлению…
Явление электромагнитной индукции было открыто выдающимся английским физиком М.Фарадеем в 1831 году. Оно заключается в возникновении электрического тока в замкнутом проводящем контуре при изменении во времени магнитного потока, пронизывающего контур. Магнитным потоком Φ через площадь S контура называют величину:
где: B – модуль вектора магнитной индукции, α – угол между вектором магнитной индукции B и нормалью (перпендикуляром) к плоскости контура, S – площадь контура, N – количество витком в контуре. Единица магнитного потока в системе СИ называется Вебером (Вб).
Фарадей экспериментально установил, что при изменении магнитного потока в проводящем контуре возникает ЭДС индукции εинд, равная скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус:
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум возможным причинам.
- Магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле. Возникновение ЭДС индукции объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
- Вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре.
При решении задач важно сразу определить за счет чего меняется магнитный поток. Возможно три варианта:
- Меняется магнитное поле.
- Меняется площадь контура.
- Меняется ориентация рамки относительно поля.
При этом при решении задач обычно считают ЭДС по модулю. Обратим внимание также внимание на один частный случай, в котором происходит явление электромагнитной индукции. Итак, максимальное значение ЭДС индукции в контуре состоящем из N витков, площадью S, вращающемся с угловой скоростью ω в магнитном поле с индукцией В:
Движение проводника в магнитном поле
К оглавлению…
При движении проводника длиной l в магнитном поле B со скоростью v на его концах возникает разность потенциалов, вызванная действием силы Лоренца на свободные электроны в проводнике. Эту разность потенциалов (строго говоря, ЭДС) находят по формуле:
где: α — угол, который измеряется между направлением скорости и вектора магнитной индукции. В неподвижных частях контура ЭДС не возникает.
Если стержень длиной L вращается в магнитном поле В вокруг одного из своих концов с угловой скоростью ω, то на его концах возникнет разность потенциалов (ЭДС), которую можно рассчитать по формуле:
Индуктивность. Самоиндукция. Энергия магнитного поля
К оглавлению…
Самоиндукция является важным частным случаем электромагнитной индукции, когда изменяющийся магнитный поток, вызывающий ЭДС индукции, создается током в самом контуре. Если ток в рассматриваемом контуре по каким-то причинам изменяется, то изменяется и магнитное поле этого тока, а, следовательно, и собственный магнитный поток, пронизывающий контур. В контуре возникает ЭДС самоиндукции, которая согласно правилу Ленца препятствует изменению тока в контуре. Собственный магнитный поток Φ, пронизывающий контур или катушку с током, пропорционален силе тока I:
Коэффициент пропорциональности L в этой формуле называется коэффициентом самоиндукции или индуктивностью катушки. Единица индуктивности в СИ называется Генри (Гн).
Запомните: индуктивность контура не зависит ни от магнитного потока, ни от силы тока в нем, а определяется только формой и размерами контура, а также свойствами окружающей среды. Поэтому при изменении силы тока в контуре индуктивность остается неизменной. Индуктивность катушки можно рассчитать по формуле:
где: n — концентрация витков на единицу длины катушки:
ЭДС самоиндукции, возникающая в катушке с постоянным значением индуктивности, согласно формуле Фарадея равна:
Итак ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в ней.
Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии. Энергия Wм магнитного поля катушки с индуктивностью L, создаваемого током I, может быть рассчитана по одной из формул (они следуют друг из друга с учётом формулы Φ = LI):
Соотнеся формулу для энергии магнитного поля катушки с её геометрическими размерами можно получить формулу для объемной плотности энергии магнитного поля (или энергии единицы объёма):
Правило Ленца
К оглавлению…
Инерция – явление, происходящее и в механике (при разгоне автомобиля мы отклоняемся назад, противодействуя увеличению скорости, а при торможении отклоняемся вперёд, противодействуя уменьшению скорости), и в молекулярной физике (при нагревании жидкости увеличивается скорость испарения, самые быстрые молекулы покидают жидкость, уменьшая скорость нагревания) и так далее. В электромагнетизме инерция проявляется в противодействии изменению магнитного потока, пронизывающего контур. Если магнитный поток нарастает, то возникающий в контуре индукционный ток направлен так, чтобы препятствовать нарастанию магнитного потока, а если магнитный поток убывает, то возникающий в контуре индукционный ток направлен так, чтобы препятствовать убыванию магнитного потока.
Правило Ленца для определения направления индукционного тока: возникающий в контуре индукционный ток имеет такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, которое вызывало этот ток.
МАГНИТНОЕ ПОЛЕ
Подобно тому, как покоящийся электрический заряд действует на другой заряд посредством электрического поля, электрический ток действует на другой ток посредством магнитного поля. Действие магнитного поля на постоянные магниты сводится к действию его на заряды, движущиеся в атомах вещества и создающие микроскопические круговые токи.
Учение об электромагнетизме основано на двух положениях:
- магнитное поле действует на движущиеся заряды и токи;
- магнитное поле возникает вокруг токов и движущихся зарядов.
Взаимодействие магнитов
Постоянный магнит (или магнитная стрелка) ориентируется вдоль магнитного меридиана Земли. Тот его конец, который указывает на север, называется северным полюсом (N), а противоположный конец — южным полюсом (S). Приближая два магнита друг к другу, заметим, что одноименные их полюсы отталкиваются, а разноименные — притягиваются (рис. 1).
Если разделить полюса, разрезав постоянный магнит на две части, то мы обнаружим, что каждая из них тоже будет иметь два полюса, т. е. будет постоянным магнитом (рис. 2). Оба полюса — северный и южный, — неотделимые друг от друга, равноправны.
Магнитное поле, создаваемое Землей или постоянными магнитами, изображается, подобно электрическому полю, магнитными силовыми линиями. Картину силовых линий магнитного поля какого-либо магнита можно получить, помещая над ним лист бумаги, на котором насыпаны равномерным слоем железные опилки. Попадая в магнитное поле, опилки намагничиваются — у каждой из них появляется северный и южный полюсы. Противоположные полюсы стремятся сблизиться друг с другом, но этому мешает трение опилок о бумагу. Если постучать по бумаге пальцем, трение уменьшится и опилки притянутся друг к другу, образуя цепочки, изображающие линии магнитного поля.
На рис. 3 показано расположение в поле прямого магнита опилок и маленьких магнитных стрелок, указывающих направление линий магнитного поля. За это направление принято направление северного полюса магнитной стрелки.
Опыт Эрстэда. Магнитное поле тока
В начале XIX в. датский ученый Эрстэд сделал важное открытие, обнаружив действие электрического тока на постоянные магниты. Он поместил длинный провод вблизи магнитной стрелки. При пропускании по проводу тока стрелка поворачивалась, стремясь расположиться перпендикулярно ему (рис. 4). Это можно было объяснить возникновением вокруг проводника магнитного поля.
Магнитные силовые линии поля, созданного прямым проводником с током, представляют собой концентрические окружности, расположенные в перпендикулярной к нему плоскости, с центрами в точке, через которую проходит ток (рис. 5). Направление линий определяется правилом правого винта:
Если винт вращать по направлению линий поля, он будет двигаться в направлении тока в проводнике.
Силовой характеристикой магнитного поля является вектор магнитной индукции B. В каждой точке он направлен по касательной к линии поля. Линии электрического поля начинаются на положительных зарядах и оканчиваются на отрицательных, а сила, действующая в этом поле на заряд, направлена по касательной к линии в каждой ее точке. В отличие от электрического, линии магнитного поля замкнуты, что связано с отсутствием в природе «магнитных зарядов».
Магнитное поле тока принципиально ничем не отличается от поля, созданного постоянным магнитом. В этом смысле аналогом плоского магнита является длинный соленоид — катушка из провода, длина которой значительно больше ее диаметра. Схема линий созданного им магнитного поля, изображенная на рис. 6, аналогична таковой для плоского магнита (рис. 3). Кружочками обозначены сечения провода, образующего обмотку соленоида. Токи, текущие по проводу от наблюдателя, обозначены крестиками, а токи противоположного направления — к наблюдателю — обозначены точками. Такие же обозначения приняты и для линий магнитного поля, когда они перпендикулярны плоскости чертежа (рис. 7 а, б).
Направление тока в обмотке соленоида и направление линий магнитного поля внутри него также связаны правилом правого винта, которое в этом случае формулируется так:
Если смотреть вдоль оси соленоида, то текущий по направлению часовой стрелки ток создает в нем магнитное поле, направление которого совпадает с направлением движения правого винта (рис. 8)
Исходя из этого правила, легко сообразить, что у соленоида, изображенного на рис. 6, северным полюсом служит правый его конец, а южным — левый.
Магнитное поле внутри соленоида является однородным — вектор магнитной индукции имеет там постоянное значение (B = const). В этом отношении соленоид подобен плоскому конденсатору, внутри которого создается однородное электрическое поле.
Сила, действующая в магнитном поле на проводник с током
Опытным путем было установлено, что на проводник с током в магнитном поле действует сила. В однородном поле прямолинейный проводник длиной l, по которому течет ток I, расположенный перпендикулярно вектору поля B, испытывает действие силы: F = I l B.
Направление силы определяется правилом левой руки:
Если четыре вытянутых пальца левой руки расположить по направлению тока в проводнике, а ладонь — перпендикулярно вектору B, то отставленный большой палец укажет направление силы, действующей на проводник (рис. 9).
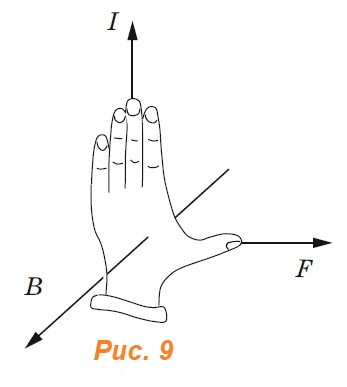
Уравнение F = IlB позволяет дать количественную характеристику индукции магнитного поля.
Отношение 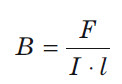
Модуль вектора магнитной индукции B численно равен силе, действующей на расположенный перпендикулярно к нему проводник единичной длины, по которому течет ток силой один ампер.
В системе СИ единицей индукции магнитного поля служит тесла (Тл):
Магнитное поле. Таблицы, схемы, формулы
(Взаимодействие магнитов, опыт Эрстеда, вектор магнитной индукции, направление вектора, принцип суперпозиции. Графическое изображение магнитных полей, линии магнитной индукции. Магнитный поток, энергетическая характеристика поля. Магнитные силы, сила Ампера, сила Лоренца. Движение заряженных частиц в магнитном поле. Магнитные свойства вещества, гипотеза Ампера)
Дополнительные материалы по теме: Электромагнитные явления
Конспект по теме «Магнитное поле. Теория, формулы, схемы».
Следующая тема «Электромагнитная индукция»
Теория по физике на тему «Магнетизм»
- 14.12.2016
Теория по физике на тему «Магнетизм»
- вектор магнитной индукции
- модуль вектора магнитной индукции
- способы определения вектора магнитной индукции
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.
Сохранить ссылку:
Комментарии (0)
Добавить комментарий
Добавить комментарий
Комментарии без регистрации. Несодержательные сообщения удаляются.
Имя (обязательное)
E-Mail
Подписаться на уведомления о новых комментариях
Отправить
Часто бывает, что задачу не удается решить из-за того, что под рукой нет нужной формулы. Выводить формулу с самого начала – дело не самое быстрое, а у нас на счету каждая минута.
Ниже мы собрали вместе основные формулы по теме «Электричество и Магнетизм». Теперь, решая задачи, вы сможете пользоваться этим материалом как справочником, чтобы не терять время на поиски нужной информации.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Магнетизм: определение
Магнетизм – это взаимодействие движущихся электрических зарядов, происходящее посредством магнитного поля.
Поле – особая форма материи. В рамках стандартной модели существует электрическое, магнитное, электромагнитные поля, поле ядерных сил, гравитационное поле и поле Хиггса. Возможно, есть и другие гипотетические поля, о которых мы пока что можем только догадываться или не догадываться вовсе. Сегодня нас интересует магнитное поле.
Магнитная индукция
Так же, как заряженные тела создают вокруг себя электрическое поле, движущиеся заряженные тела порождают магнитное поле. Магнитное поле не только создается движущимися зарядами (электрическим током), но еще и действует на них. По сути магнитное поле можно обнаружить только по действию на движущиеся заряды. А действует оно на них с силой, называемой силой Ампера, о которой речь пойдет позже.
Прежде чем мы начнем приводить конкретные формулы, нужно рассказать про магнитную индукцию.
Магнитная индукция – это силовая векторная характеристика магнитного поля.
Она обозначается буквой B и измеряется в Тесла (Тл). По аналогии с напряженностью для электрического поля Е магнитная индукция показывает, с какой силой магнитное поле действует на заряд.
Кстати, вы найдете много интересных фактов на эту тему в нашей статье про теорию магнитного поля и интересные факты о магнитном поле Земли.
Как определять направление вектора магнитной индукции? Здесь нас интересует практическая сторона вопроса. Самый частый случай в задачах – это магнитное поле, создаваемое проводником с током, который может быть либо прямым, либо в форме окружности или витка.
Для определения направления вектора магнитной индукции существует правило правой руки. Приготовьтесь задействовать абстрактное и пространственное мышление!
Если взять проводник в правую руку так, что большой палец будет указывать на направление тока, то загнутые вокруг проводника пальцы покажут направление силовых линий магнитного поля вокруг проводника. Вектор магнитной индукции в каждой точке будет направлен по касательной к силовым линиям.
Сила Ампера
Представим, что есть магнитное поле с индукцией B. Если мы поместим в него проводник длиной l, по которому течет ток силой I, то поле будет действовать на проводник с силой:
Это и есть сила Ампера. Угол альфа – угол между направлением вектора магнитной индукции и направлением тока в проводнике.
Направление силы Ампера определяется по правилу левой руки: если расположить левую руку так, чтобы в ладонь входили линии магнитной индукции, а вытянутые пальцы указывали бы направление тока, отставленный большой палец укажет направление силы Ампера.
Сила Лоренца
Мы выяснили, что поле действует на проводник с током. Но если это так, то изначально оно действует отдельно на каждый движущийся заряд. Сила, с которой магнитное поле действует на движущийся в нем электрический заряд, называется силой Лоренца. Здесь важно отметить слово «движущийся», так на неподвижные заряды магнитное поле не действует.
Итак, частица с зарядом q движется в магнитном поле с индукцией В со скоростью v, а альфа – это угол между вектором скорости частицы и вектором магнитной индукции. Тогда сила, которая действует на частицу:
Как определить направление силы Лоренца? По правилу левой руки. Если вектор индукции входит в ладонь, а пальцы указывают на направление скорости, то отогнутый большой палец покажет направление силы Лоренца. Отметим, что так направление определяется для положительно заряженных частиц. Для отрицательных зарядов полученное направление нужно поменять на противоположное.
Если частица массы m влетает в поле перпендикулярно линиям индукции, то она будет двигаться по окружности, а сила Лоренца будет играть роль центростремительной силы. Радиус окружности и период обращения частицы в однородном магнитном поле можно найти по формулам:
Взаимодействие токов
Рассмотрим два случая. Первый – ток течет по прямому проводу. Второй – по круговому витку. Как мы знаем, ток создает магнитное поле.
В первом случае магнитная индукция провода с током I на расстоянии R от него считается по формуле:
Мю – магнитная проницаемость вещества, мю с индексом ноль – магнитная постоянная.
Во втором случае магнитная индукция в центре кругового витка с током равна:
Также при решении задач может пригодиться формула для магнитного поля внутри соленоида. Соленоид – это катушка, то есть множество круговых витков с током.
Пусть их количество – N, а длина самого соленоилда – l. Тогда поле внутри соленоида вычисляется по формуле:
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Магнитный поток и ЭДС
Если магнитная индукция – векторная характеристика магнитного поля, то магнитный поток – скалярная величина, которая также является одной из самых важных характеристик поля. Представим, что у нас есть какая-то рамка или контур, имеющий определенную площадь. Магнитный поток показывает, какое количество силовых линий проходит через единицу площади, то есть характеризует интенсивность поля. Измеряется в Веберах (Вб) и обозначается Ф.
S – площадь контура, альфа – угол между нормалью (перпендикуляром) к плоскости контура и вектором В.
При изменении магнитного потока через контур в контуре индуцируется ЭДС, равная скорости изменения магнитного потока через контур. Кстати, подробнее о том, что такое электродвижущая сила, вы можете почитать в еще одной нашей статье.
По сути формула выше – это формула для закона электромагнитной индукции Фарадея. Напоминаем, что скорость изменения какой-либо величины есть не что иное, как ее производная по времени.
Для магнитного потока и ЭДС индукции также справедливо обратное. Изменение тока в контуре приводит к изменению магнитного поля и, соответственно, к изменению магнитного потока. При этом возникает ЭДС самоиндукции, которая препятствует изменению тока в контуре. Магнитный поток, который пронизывает контур с током, называется собственным магнитным потоком, пропорционален силе тока в контуре и вычисляется по формуле:
L – коэффициент пропорциональности, называемый индуктивностью, который измеряется в Генри (Гн). На индуктивность влияют форма контура и свойства среды. Для катушки с длиной l и с числом витков N индуктивность рассчитывается по формуле:
Формула для ЭДС самоиндукции:
Энергия магнитного поля
Электроэнергия, ядерная энергия, кинетическая энергия. Магнитная энергия – одна из форм энергии. В физических задачах чаще всего нужно рассчитывать энергию магнитного поля катушки. Магнитная энергия катушки с током I и индуктивностью L равна:
Объемная плотность энергии поля:
Конечно, это не все основные формулы раздела физики «электричество и магнетизм», однако они часто могут помочь при решении стандартных задач и расчетах. Если же вам попалась задача со звездочкой, и вы никак не можете подобрать к ней ключ, упростите себе жизнь и обратитесь за решением в сервис студенческой помощи.
Магнитное поле. Силы
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: сила Ампера, сила Лоренца.
В отличие от электрического поля, которое действует на любой заряд, магнитное поле действует только на движущиеся заряженные частицы. При этом оказывается, что сила зависит не только от величины, но и от направления скорости заряда.
Сила Лоренца
Сила, с которой магнитное поле действует на заряженную частицу, называется силой Лоренца. Опыт показывает, что вектор силы Лоренца находится следующим образом.
1. Абсолютная величина силы Лоренца равна:
(1)
Здесь — абсолютная величина заряда,
— скорость заряда,
— индукция магнитного поля,
— угол между векторами
и
.
2. Сила Лоренца перпендикулярна обоим векторам и
. Иными словами, вектор
перпендикулярен плоскости, в которой лежат векторы скорости заряда и индукции магнитного поля.
Остаётся выяснить, в какое полупространство относительно данной плоскости направлена сила Лоренца.
3. Взаимное расположение векторов ,
и
для положительного заряда
показано на рис. 1.
Рис. 1. Сила Лоренца
Направление силы Лоренца определяется в данном случае по одному из двух альтернативных правил.
Правило часовой стрелки. Сила Лоренца направлена туда, глядя откуда кратчайший поворот вектора скорости частицы v к вектору магнитной индукции B виден против часовой стрелки.
Правило левой руки . Располагаем левую руку так, чтобы четыре пальца указывали направление скорости частицы, а линии поля входили в ладонь. Тогда оттопыренный большой палец укажет направление силы Лоренца.
Для отрицательного заряда направление силы Лоренца меняется на противоположное.
Всё вышеперечисленное является обобщением опытных фактов. Формула (1) позволяет связать размерность индукции магнитного поля с размерностями других физических величин:
Сила Ампера
Если металлический проводник с током поместить в магнитное поле, то на этот проводник со стороны магнитного поля будет действовать сила, которая называется силой Ампера.
Происхождение силы Ампера легко понять. Ведь ток в металле является направленным движением электронов, а на каждый электрон действует сила Лоренца. Все эти силы Лоренца, действующие на свободные электроны, имеют одинаковое направление и одинаковую величину; они складываются друг с другом и дают результирующую силу Ампера.
Направление силы Ампера определяется по тем же двум правилам, сформулированным выше.
Правило часовой стрелки . Сила Ампера направлена туда, глядя откуда кратчайший поворот тока к полю виден против часовой стрелки .
Правило левой руки . Располагаем левую руку так, чтобы четыре пальца указывали направление тока, а линии поля входили в ладонь. Тогда оттопыренный большой палец укажет направление силы Ампера .
Взаимное расположение тока, поля и силы Ампера указано на рис. 2.
Рис. 2. Сила Ампера
На этом рисунке проводник имеет длину , а угол между направлениями тока и поля равен
. Мы сейчас выведем выражение для абсолютной величины силы Ампера.
На каждый свободный электрон действует сила Лоренца:
где — скорость направленного движения свободных электронов в проводнике.
Пусть — число свободных электронов в данном проводнике,
— их концентрация (число в единице объёма). Тогда:
где — объём проводника,
— площадь его поперечного сечения. Получаем:
Мы не случайно выделили скобками четыре сомножителя. Ведь это есть не что иное, как сила тока: (вспомните выражение силы тока через скорость направленного движения свободных зарядов!). В результате приходим к окончательной формуле для силы Ампера:
(2)
Хорошую возможность поупражняться в нахождении направлений магнитного поля и силы Ампера даёт взаимодействие параллельных токов. Оказывается, два параллельных провода отталкиваются, если направления токов в них противоположны, и притягиваются, если направления токов совпадают (рис. 3).
Рис. 3. Взаимодействие параллельных токов
Обязательно убедитесь в этом самостоятельно! Делаем так. Сначала берём произвольную точку на первом проводе и определяем направление магнитного поля, создаваемого в этой точке вторым проводом (правило вам известно — см. предыдущий листок>). Ну а затем находим направление силы Ампера, действующей на первый провод со стороны магнитного поля второго провода.
Рамка с током в магнитном поле
В листках по термодинамике мы говорили о важности циклически работающих машин: они снабжают нас энергией. Понимание законов термодинамики позволило сконструировать тепловые двигатели, которые исправно служат нам и по сей день.
Понимание же законов электромагнетизма дало возможность создать циклическую машину другого типа — электродвигатель.
Мы рассмотрим один из элементов электродвигателя — рамку с током в магнитном поле. Разобравшись в её поведении, мы сможем уловить основную идею функционирования электродвигателя.
Пусть прямоугольная рамка может вращаться вокруг горизонтальной оси (рис. 4, слева). Рамка находится в вертикальном однородном магнитном поле
. Ток течёт по рамке в направлении
; это направление показано соответствующими стрелками.
Рис. 4. Рамка с током в магнитном поле
Вектор называется вектором нормали; он перпендикулярен плоскости рамки и направлен туда, глядя откуда ток кажется циркулирующим против часовой стрелки. (Иными словами, вектор
сонаправлен с вектором индукции магнитного поля, которое создаётся током в рамке.) Поворот рамки измеряется углом
между векторами
и
.
Теперь определим направления сил Ампера, которые действуют на рамку со стороны магнитного поля. Эти силы расставлены на рисунке; вот вам ещё одно упражнение на правило часовой стрелки (левой руки) — обязательно проверьте правильность указанных направлений!
Силы и
, приложенные к сторонам
и
, действуют вдоль оси вращения. Они лишь растягивают рамку и не вызывают её вращение.
Куда более интересны силы и
, приложеные соответственно к сторонам
и
. Они лежат в горизонтальной плоскости и перпендикулярны оси вращения. Эти силы вращают рамку в направлении по часовой стрелке, если смотреть справа (рис. 4, правая часть). Вычислим момент этой пары сил относительно оси
вращения рамки.
Пусть длина стороны равна
. Тогда
Пусть длина стороны равна
. Плечо
силы
, как видно из рис. 4 (справа) равно:
Таким же будет плечо силы . Отсюда получаем момент сил, вращающий рамку:
Теперь заметим, что — площадь рамки. Окончательно имеем:
(3)
В этой формуле площадь служит единственной геометрической характеристикой рамки.Это наводит на мысль, что только площадь рамки и существенна в выражении для вращающего момента. И действительно, можно доказать (разбивая рамку на бесконечно узкие полоски, неотличимые от прямоугольников), что формула (3) справедлива для рамки любой формы с площадью .
Как видно из формулы (3), максимальный вращающий момент равен:
Эта максимальная величина момента достигается при , то есть когда плоскость рамки параллельна магнитному полю.
Вращающий момент становится равным нулю при и
. Оба этих положения по-своему интересны.
При плоскость рамки перпендикулярна полю, а векторы
и
направлены в разные стороны. Данное положение является положением неустойчивого равновенсия: стоит хоть немного шевельнуть рамку, как силы Ампера начнут её вращать в том же направлении, поворачивая вектор
к вектору
(убедитесь!).
При плоскость рамки также перпендикулярна полю, а векторы
и
сонаправлены. Это — положение устойчивого равновенсия: при отклонении рамки возникает вращающий момент, стремящийся вернуть рамку назад (убедитесь!). Начнутся колебания рамки, постепенно затухающие из-за трения. В конце концов рамка остановится в положении
; в этом положении вектор индукции магнитного поля рамки сонаправлен с вектором
индукции внешнего магнитного поля (вот почему при намагничивании вещества элементарные токи ориентируются так, что их поля направлены в сторону внешнего магнитного поля). Полезное сопоставление: рамка занимает такое положение, что её положительная нормаль ориентируется в том же направлении, что и северный конец стрелки компаса, помещённой в это магнитное поле.
Таким образом, поведение рамки в магнитном поле становится ясным: если отклонить рамку от положения устойчивого равновесия и отпустить, то рамка будет совершать колебания. С точки зрения совершения механической работы это не очень хорошо: если намотать нить на ось вращения и подвесить к нити груз, то груз будет то подниматься, то опускаться.
Но вот если исхитриться и заставить ток менять направление в нужные моменты, то вместо колебаний рамки начнётся её непрерывное вращение и, соответственно, непрерывный подъём подвешенного груза. Тогда-то и получится полноценный электродвигатель; идея с переменой направления тока реализуется с помощью коллектора и щёток.
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Магнитное поле. Силы» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.03.2023
Магнитное поле
Магнитное поле – особая форма материи, существующая вокруг движущихся электрических зарядов – токов.
Источниками магнитного поля являются постоянные магниты, проводники с током. Обнаружить магнитное поле можно по действию на магнитную стрелку, проводник с током и движущиеся заряженные частицы.
Для исследования магнитного поля используют замкнутый плоский контур с током (рамку с током).
Впервые поворот магнитной стрелки около проводника, по которому протекает ток, обнаружил в 1820 году Эрстед. Ампер наблюдал взаимодействие проводников, по которым протекал ток: если токи в проводниках текут в одном направлении, то проводники притягиваются, если токи в проводниках текут в противоположных направлениях, то они отталкиваются.
Свойства магнитного поля:
- магнитное поле материально;
- источник и индикатор поля – электрический ток;
- магнитное поле является вихревым – его силовые линии (линии магнитной индукции) замкнутые;
- величина поля убывает с расстоянием от источника поля.
Важно!
Магнитное поле не является потенциальным. Его работа на замкнутой траектории может быть не равна нулю.
Магнитным взаимодействием называют притяжение или отталкивание электрически нейтральных проводников при пропускании через них электрического тока.
Магнитное взаимодействие движущихся электрических зарядов объясняется так: всякий движущийся электрический заряд создает в пространстве магнитное поле, которое действует на движущиеся заряженные частицы.
Силовая характеристика магнитного поля – вектор магнитной индукции ( vec{B} ). Модуль вектора магнитной индукции равен отношению максимального значения силы, действующей со стороны магнитного поля на проводник с током, к силе тока в проводнике ( I ) и его длине ( l ):
Обозначение – ( vec{B} ), единица измерения в СИ – тесла (Тл).
1 Тл – это индукция такого магнитного поля, в котором на каждый метр длины проводника при силе тока 1 А действует максимальная сила 1 Н.
Направление вектора магнитной индукции совпадает с направлением от южного полюса к северному полюсу магнитной стрелки (направление, которое указывает северный полюс магнитной стрелки), свободно установившейся в магнитном поле.
Направление вектора магнитной индукции можно определить по правилу буравчика:
если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением вектора магнитной индукции.
Для определения магнитной индукции нескольких полей используется принцип суперпозиции:
магнитная индукция результирующего поля, созданного несколькими источниками, равна векторной сумме магнитных индукций полей, создаваемых каждым источником в отдельности:
Поле, в каждой точке которого вектор магнитной индукции одинаков по величине и направлению, называется однородным.
Наглядно магнитное поле изображают в виде магнитных линий или линий магнитной индукции. Линия магнитной индукции – это воображаемая линия, в любой точке которой вектор магнитной индукции направлен по касательной к ней.
Свойства магнитных линий:
- магнитные линии непрерывны;
- магнитные линии замкнуты (т.е. в природе не существует магнитных зарядов, аналогичных электрическим зарядам);
- магнитные линии имеют направление, связанное с направлением тока.
Густота расположения позволяет судить о величине поля: чем гуще расположены линии, тем сильнее поле.
На плоский замкнутый контур с током, помещенный в однородное магнитное поле, действует момент сил ( M ):
где ( I ) – сила тока в проводнике, ( S ) – площадь поверхности, охватываемая контуром, ( B ) – модуль вектора магнитной индукции, ( alpha ) – угол между перпендикуляром к плоскости контура и вектором магнитной индукции.
Тогда для модуля вектора магнитной индукции можно записать формулу:
где максимальный момент сил соответствует углу ( alpha ) = 90°.
В этом случае линии магнитной индукции лежат в плоскости рамки, и ее положение равновесия является неустойчивым. Устойчивым будет положение рамки с током в случае, когда плоскость рамки перпендикулярна линиям магнитной индукции.
Содержание
- Взаимодействие магнитов
- Магнитное поле проводника с током
- Сила Ампера
- Сила Лоренца
- Основные формулы раздела «Магнитное поле»
Взаимодействие магнитов
Постоянные магниты – это тела, длительное время сохраняющие намагниченность, то есть создающие магнитное поле.
Основное свойство магнитов: притягивать тела из железа или его сплавов (например стали). Магниты бывают естественные (из магнитного железняка) и искусственные, представляющие собой намагниченные железные полосы. Области магнита, где его магнитные свойства выражены наиболее сильно, называют полюсами. У магнита два полюса: северный ( N ) и южный ( S ).
Важно!
Вне магнита магнитные линии выходят из северного полюса и входят в южный полюс.
Разделить полюса магнита нельзя.
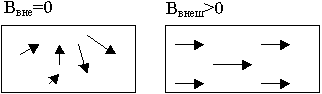
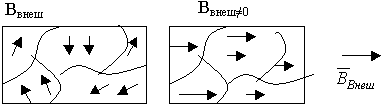
Объяснил существование магнитного поля у постоянных магнитов Ампер. Согласно его гипотезе внутри молекул, из которых состоит магнит, циркулируют элементарные электрические токи. Если эти токи ориентированы определенным образом, то их действия складываются и тело проявляет магнитные свойства. Если эти токи расположены беспорядочно, то их действие взаимно компенсируется и тело не проявляет магнитных свойств.
Магниты взаимодействуют: одноименные магнитные полюса отталкиваются, разноименные – притягиваются.
Магнитное поле проводника с током
Электрический ток, протекающий по проводнику с током, создает в окружающем его пространстве магнитное поле. Чем больше ток, проходящий по проводнику, тем сильнее возникающее вокруг него магнитное поле.
Магнитные силовые линии этого поля располагаются по концентрическим окружностям, в центре которых находится проводник с током.
Направление линий магнитного поля вокруг проводника с током всегда находится в строгом соответствии с направлением тока, проходящего по проводнику.
Направление магнитных силовых линий можно определить по правилу буравчика: если поступательное движение буравчика (1) совпадает с направлением тока (2) в проводнике, то вращение его рукоятки укажет направление силовых линий (4) магнитного поля вокруг проводника.
При изменении направления тока линии магнитного поля также изменяют свое направление.
По мере удаления от проводника магнитные силовые линии располагаются реже. Следовательно, индукция магнитного поля уменьшается.
Направление тока в проводнике принято изображать точкой, если ток идет к нам, и крестиком, если ток направлен от нас.
Для получения сильных магнитных полей при небольших токах обычно увеличивают число проводников с током и выполняют их в виде ряда витков; такое устройство называют катушкой.
В проводнике, согнутом в виде витка, магнитные поля, образованные всеми участками этого проводника, будут внутри витка иметь одинаковое направление. Поэтому интенсивность магнитного поля внутри витка будет больше, чем вокруг прямолинейного проводника. При объединении витков в катушку магнитные поля, созданные отдельными витками, складываются. При этом концентрация силовых линий внутри катушки возрастает, т. е. магнитное поле внутри нее усиливается.
Чем больше ток, проходящий через катушку, и чем больше в ней витков, тем сильнее создаваемое катушкой магнитное поле. Магнитное поле снаружи катушки также складывается из магнитных полей отдельных витков, однако магнитные силовые линии располагаются не так густо, вследствие чего интенсивность магнитного поля там не столь велика, как внутри катушки.
Магнитное поле катушки с током имеет такую же форму, как и поле прямолинейного постоянного магнита: силовые магнитные линии выходят из одного конца катушки и входят в другой ее конец. Поэтому катушка с током представляет собой искусственный электрический магнит. Обычно для усиления магнитного поля внутрь катушки вставляют стальной сердечник; такую катушку называют электромагнитом.
Направление линий магнитной индукции катушки с током находят по правилу правой руки:
если мысленно обхватить катушку с током ладонью правой руки так, чтобы четыре пальца указывали направление тока в ее витках, тогда большой палец укажет направление вектора магнитной индукции.
Для определения направления линий магнитного поля, создаваемого витком или катушкой, можно использовать также правило буравчика:
если вращать ручку буравчика по направлению тока в витке или катушке, то поступательное движение буравчика укажет направление вектора магнитной индукции.
Электромагниты нашли чрезвычайно широкое применение в технике. Полярность электромагнита (направление магнитного поля) можно определить и с помощью правила правой руки.
Сила Ампера
Сила Ампера – сила, которая действует на проводник с током, находящийся в магнитном поле.
Закон Ампера: на проводник c током силой ( I ) длиной ( l ), помещенный в магнитное поле с индукцией ( vec{B} ), действует сила, модуль которой равен:
где ( alpha ) – угол между проводником с током и вектором магнитной индукции ( vec{B} ).
Направление силы Ампера определяют по правилу левой руки: если ладонь левой руки расположить так, чтобы перпендикулярная к проводнику составляющая вектора магнитной индукции ( B_perp ) входила в ладонь, а четыре вытянутых пальца указывали направление тока в проводнике, то отогнутый на 90° большой палец покажет направление силы Ампера.
Сила Ампера не является центральной. Она направлена перпендикулярно линиям магнитной индукции.
Сила Ампера широко используется. В технических устройствах создают магнитное поле с помощью проводников, по которым течет электрический ток. Электромагниты используют в электромеханическом реле для дистанционного выключения электрических цепей, магнитном подъемном кране, жестком диске компьютера, записывающей головке видеомагнитофона, в кинескопе телевизора, мониторе компьютера. В быту, на транспорте и в промышленности широко применяют электрические двигатели. Взаимодействие электромагнита с полем постоянного магнита позволило создать электроизмерительные приборы (амперметр, вольтметр).
Простейшей моделью электродвигателя служит рамка с током, помещенная в магнитное поле постоянного магнита. В реальных электродвигателях вместо постоянных магнитов используют электромагниты, вместо рамки – обмотки с большим числом витков провода.
Коэффициент полезного действия электродвигателя:
где ( N ) – механическая мощность, развиваемая двигателем.
Коэффициент полезного действия электродвигателя очень высок.
Алгоритм решения задач о действии магнитного поля на проводники с током:
- сделать схематический чертеж, на котором указать проводник или контур с током и направление силовых линий поля;
- отметить углы между направлением поля и отдельными элементами контура;
- используя правило левой руки, определить направление силы Ампера, действующей на проводник с током или на каждый элемент контура, и показать эти силы на чертеже;
- указать все остальные силы, действующие на проводник или контур;
- записать формулы для остальных сил, упоминаемых в задаче. Выразить силы через величины, от которых они зависят. Если проводник находится в равновесии, то необходимо записать условие его равновесия (равенство нулю суммы сил и моментов сил);
- записать второй закон Ньютона в векторном виде и в проекциях;
- решить полученную систему уравнений относительно неизвестной величины;
- решение проверить.
Сила Лоренца
Сила Лоренца – сила, действующая на движущуюся заряженную частицу со стороны магнитного поля.
Формула для нахождения силы Лоренца:
где ( q ) – заряд частицы, ( v ) – скорость частицы, ( B ) – модуль вектора магнитной индукции, ( alpha ) – угол между вектором скорости частицы и вектором магнитной индукции.
Направление силы Лоренца определяют по правилу левой руки: если ладонь левой руки расположить так, чтобы перпендикулярная к проводнику составляющая вектора магнитной индукции ( B_perp ) входила в ладонь, а четыре вытянутых пальца указывали направление скорости положительно заряженной частицы, то отогнутый на 90° большой палец покажет направление силы Лоренца.
Если заряд частицы отрицательный, то направление силы изменяется на противоположное.
Важно!
Если вектор скорости сонаправлен с вектором магнитной индукции, то частица движется равномерно и прямолинейно.
В однородном магнитном поле сила Лоренца искривляет траекторию движения частицы.
Если вектор скорости перпендикулярен вектору магнитной индукции, то частица движется по окружности, радиус которой равен:
где ( m ) – масса частицы, ( v ) – скорость частицы, ( B ) – модуль вектора магнитной индукции, ( q ) – заряд частицы.
В этом случае сила Лоренца играет роль центростремительной и ее работа равна нулю. Период (частота) обращения частицы не зависит от радиуса окружности и скорости частицы. Формула для вычисления периода обращения частицы:
Угловая скорость движения заряженной частицы:
Важно!
Сила Лоренца не меняет кинетическую энергию частицы и модуль ее скорости. Под действием силы Лоренца изменяется направление скорости частицы.
Если вектор скорости направлен под углом ( alpha ) (0° < ( alpha ) < 90°) к вектору магнитной индукции, то частица движется по винтовой линии.
В этом случае вектор скорости частицы можно представить как сумму двух векторов скорости, один из которых, ( vec{v}_2 ), параллелен вектору ( vec{B} ), а другой, ( vec{v}_1 ), – перпендикулярен ему. Вектор ( vec{v}_1 ) не меняется ни по модулю, ни по направлению. Вектор ( vec{v}_2 ) меняется по направлению. Сила Лоренца будет сообщать движущейся частице ускорение, перпендикулярное вектору скорости ( vec{v}_1 ). Частица будет двигаться по окружности. Период обращения частицы по окружности – ( T ).
Таким образом, на равномерное движение вдоль линии индукции будет накладываться движение по окружности в плоскости, перпендикулярной вектору ( vec{B} ). Частица движется по винтовой линии с шагом ( h=v_2T ).
Важно!
Если частица движется в электрическом и магнитном полях, то полная сила Лоренца равна:
Особенности движения заряженной частицы в магнитном поле используются в масс-спектрометрах – устройствах для измерения масс заряженных частиц; ускорителях частиц; для термоизоляции плазмы в установках «Токамак».
Алгоритм решения задач о действии магнитного (и электрического) поля на заряженные частицы:
- сделать чертеж, указать на нем силовые линии магнитного (и электрического) поля, нарисовать вектор начальной скорости частицы и отметить знак ее заряда;
- изобразить силы, действующие на заряженную частицу;
- определить вид траектории частицы;
- разложить силы, действующие на заряженную частицу, вдоль направления магнитного поля и по направлению, ему перпендикулярному;
- составить основное уравнение динамики материальной точки по каждому из направлений разложения сил;
- выразить силы через величины, от которых они зависят;
- решить полученную систему уравнений относительно неизвестной величины;
- решение проверить.
Основные формулы раздела «Магнитное поле»
Магнитное поле
3.2 (64%) 120 votes
1. Электростатика
1.1. Электростатика
1.2. Закон сохранения заряда
1.3. Закон Кулона
1.4. Характеристики электрического поля
1.5. Разность потенциалов или напряжение
1.6. Закон суперпозиции для потенциала
1.7. Связь между напряженностью и потенциалом
1.8. Эквипотенциальные поверхности
1.9. Теорема Остроградского-Гаусса
1.10. Теорема Гаусса
1.10.1. Теорема Гаусса для системы точечных зарядов
1.10.2. Применение теоремы Гаусса к расчетам электростатических полей
1.11. Проводник в электрическом поле
1.12. Свойства проводников
1.13. Индуцирование заряда
1.14. Проводник во внешнем электрическом поле
1.15. Электроемкость проводника
1.16. Соединение конденсаторов
1.17. Энергия электростатического поля
1.17.1. Энергия плоского конденсатора
1.18. Диэлектрики
1.18.1. Свойства диэлектриков
1.18.2. Поведение диэлектриков во внешнем электрическом поле
1.19. Поток вектора электрического смещения
1.20. Сегнетоэлектрики и их свойства
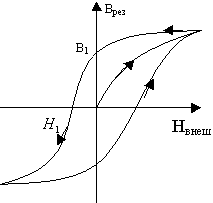
1.20.1. Электрический гистерезис в сегнетоэлектриках
2. Постоянный электрический ток
2.1. Плотность тока носителей заряда разных знаков
2.2. ЭДС. Источник тока. Напряжение
2.3. Законы Ома в интегральной форме
2.3.1. Закон Ома в дифференциальной форме
2.4. Закон Джоуля-Ленца
2.5. Законы Кирхгофа
2.6. Эмиссия электронов с поверхности
2.6.1. Работа выхода
2.6.2. Способы выбивания (отрыва) электронов с поверхности
2.6.3. Электрический ток в вакууме
2.7. Заряженная частица в плоском конденсаторе
3. Электромагнетизм
3.1. Электромагнетизм
3.2. Взаимодействие токов
3.3. Принцип суперпозиции
3.4. Закон Био-Савара-Лапласа
3.4.1. Магнитное поле проводника с током
3.4.2. Применение закона Био-Савара-Лапласа для анализа магнитных полей проводников с током различной конфигурации. Конечный и бесконечный прямолинейный проводник с током
3.4.3. Магнитное поле кругового проводника с током
3.4.4. Магнитное поле вдали от центра контура с током
3.4.5. Магнитное поле соленоида
3.5. Магнитный поток
3.6. Напряженность магнитного поля
3.7. Силы, действующие в магнитном поле
3.7.1. Сравнение электрической и магнитной сил
3.8. Взаимодействие параллельных проводников с током
3.9. Закон Ампера
3.10. Работа по перемещению проводника стоком в магнитном поле
3.11. Действие магнитного поля на контур с током
3.12. Магнитный момент контура с током
3.13. Явление электромагнитной индукции. ЭДС электромагнитной индукции
3.14. Явление взаимоиндукции
3.15. Явление самоиндукции
3.16. Вихревые токи. Токи Фуко
3.17. Энергия магнитного поля
3.18. Плотность энергии магнитного поля
3.19. Единицы измерения магнитных величин
3.20. Магнетики. Вещества в магнитном поле
3.21. Движение зарядов в магнитном поле
3.22. Уравнения Максвелла. Обобщение теории магнитного поля
3.23. Анализ массово-зарядового состояния элементарных частиц
3.24. Приложение к теореме Остроградского-Гаусса
3.25. Первое уравнение Максвелла
3.26. Второе уравнение Максвелла
3.27. Третье уравнение Максвелла
3.28. Четвертое уравнение Максвелла
3.29. Анализ III и IV уравнений
1. Электростатика
1.1. Электростатика
Электростатика — раздел физики, изучающий взаимодействие неподвижных зарядов; или взаимодействие зарядов в начале перемещения (если оно есть) и в конце него.
Заряд — особое свойство материи, заключающееся в притяжении или отталкивании тел друг от друга вне зависимости от гравитационных свойств.
Элементарный заряд:
qэ=1,6· 10-19 Кл, = > заряд электрона, обозначается e, исторически принято считать отрицательным.
e = -1,6· 10-19 Кл — это наименьшее количество заряда, которое может иметь материальное тело. Масса электрона, как материального тела:
mэ=9,1· 10 -31 кг — масса электрона.
[q]=1 Кл численное значение в международной системе единиц – СИ.
Принято исторически заряд электрона считать со знаком «-» . То есть тело считается «+» заряженным, если в нем наблюдается недостаток электронов, и «-» заряженным, если в нем имеется избыток электронов. Вблизи зарядов наблюдают электрическое поле.
Электрическое поле указывает на наличие зарядовых свойств у физических тел. Принято электрическое поле характеризовать силовыми линиями и линиями потенциалов. Силовые линии указывают действие со стороны электрического поля на испытываемый заряд. Силовые линии указывают на силу, действующую на «+» пробный qпр точечный заряд (точечный — пренебрегают размерами, пробный – для проверки наличия поля).
Силовые линии, сформированные у » +» заряда, направлены по радиусу от заряда в ¥. Для отрицательно заряженного тела силовые линии направлены по радиусу от ¥ к заряду.
1.2. Закон сохранения заряда
При исследовании взаимодействия зарядов установлено, что одноименно заряженные тела — отталкиваются, а разноименно заряженные — притягиваются. Известно, что в замкнутой системе количество массы вещества остается неизменным. А так как свойство заряда несут тела, обладающие массой, то также можно сказать: для замкнутой системы количество заряда остается величиной постоянной.
Если в замкнутой системе существует несколько зарядов разных знаков, то силовые линии начинаются на положительном заряде и оканчиваются на отрицательном.
1.3. Закон Кулона (1785 г.)
Сила взаимодействия между заряженными телами прямо пропорциональна зарядам этих тел и обратно пропорциональна квадрату расстояния между ними:
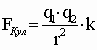
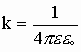
eо=8,85· 10-12 [Ф/м] — электрическая постоянная.
e — характеристика среды, называется — диэлектрическая проницаемость.
e — имеет электрический характер и определяет во сколько раз взаимодействие между одинаковыми зарядами, расположенными на одинаковом расстоянии друг от друга в среде меньше, чем аналогичное взаимодействие в вакууме.
e в-х = 1,00013 — в воздухе.
e вак = 1 — в вакууме, соответственно:
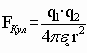
Во всех остальных средах e ср >1.
1.4. Характеристики электрического поля
Напряженность поля точечного заряда.
Поле, создаваемое зарядом Q, действует на q’пр с силой
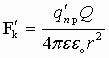
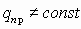
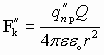
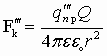
Е — величина напряженности электрического поля, создаваемого зарядом Q на расстоянии r. Чтобы рассчитать напряженность Е от нескольких зарядов применяют принцип суперпозиции.
Суперпозиция — воздействие однородных объектов на исследуемый или пробный объект (касается любых взаимодействий). Суть принципа суперпозиции — исследуется влияние одного изолированного объекта q1 на искомый qпр независимо от других зарядов, затем влияние второго изолированного объекта q2 на искомый qпр и т.д. Затем результат суммируется векторно (см. рис) или скалярно (см. формулы), пока не задействуются все заряды.
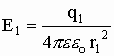
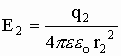
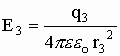
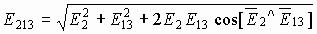
Силы рассчитываются аналогично.
Пример: Определить напряженность поля, созданного зарядами, расположенными в вершинах квадрата, в одной из вершин квадрата. Q=q1=q2=q3, a — сторона квадрата.
В векторной форме имеем:
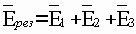
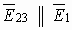
Если напряженности от каждого заряда
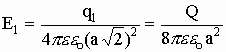
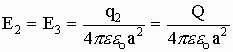
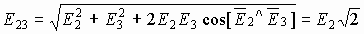
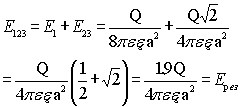
Потенциал — энергетическая характеристика электрического поля, указывающая на способность поля перемещать заряды в пространстве. Если траектория перемещения заряда (от точки 1 к точке 2) носит произвольный характер, то разбиваем ее на малые участки 
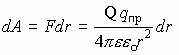
Работа на участке (1-2):
Это численное значение работы по переносу пробного заряда из (1) в (2). Если пробный заряд перемещается из данной точки поля r1 в ¥ , то
А если менять величину пробного переносимого заряда, то получаем отношение работы к величине переносимого заряда как величину постоянную, не зависящую от пробного заряда:
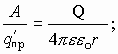
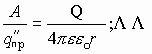
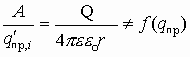
Для данного заряда, формулирующего поле, отношение работы к величине переносимого заряда из данной точки поля в бесконечность является характеристикой заряда, формирующего поле, и есть величина постоянная. Это отношение и есть энергетическая характеристика электрического поля и называется потенциалом данной точки поля, созданного зарядом Q.
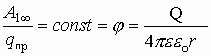
1.5. Разность потенциалов или напряжение
Если в выражении работы по переносу заряда r2 ¹ ¥ , то, выполняя последовательные преобразования, получим: 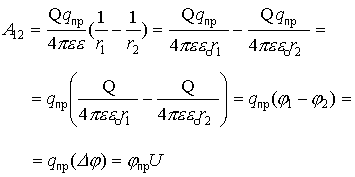
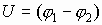
1.6. Закон суперпозиции для потенциала
Если система зарядов замкнута, то работа по перемещению пробного заряда в бесконечность со стороны каждого заряда системы: 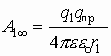
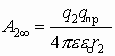
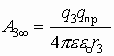
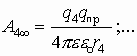
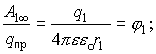
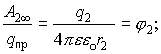
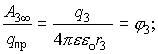
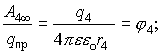
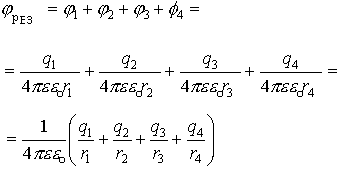
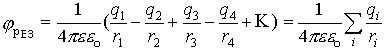
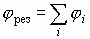
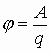
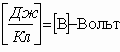
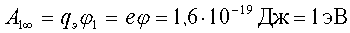
1.7. Связь между напряженностью и потенциалом
Если закон перемещения пробного заряда неизвестен, то для определения работы разбиваем траекторию на участки 


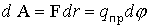
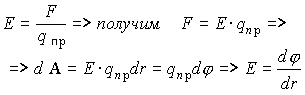
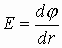
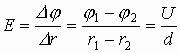
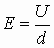
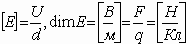
1.8. Эквипотенциальные поверхности
Вблизи любого геометрического тела (заряженного) всегда можно определить совокупность точек, потенциалы которых одинаковы. Естественно, основной такой совокупностью точек является поверхность заряженного тела. Вдали от поверхности тела совокупностей точек с равным потенциалом может быть сколь угодно много. В трехмерном пространстве такая совокупность точек называется эквипотенциальной поверхностью. Но на плоскости это отобразить сложно. Поэтому на практике ограничиваются отображением сечений эквипотенциальной поверхности на рисунке.
Эти сечения называются эквипотенциальными линиями или линиями равного потенциала. Очевидно, что вблизи точечного заряда эквипотенциальная поверхность (линия) есть сфера (окружность). А работа электрических сил по перемещению заряда вдоль эквипотенциальной поверхности (линии)

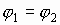
Работа по перемещению заряда вдоль эквипотенциальной линии численно равна 0.
Ориентация векторов напряженности относительно эквипотенциальной поверхности:
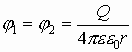
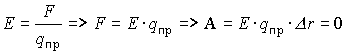
Так как Е¹ 0, qпр ¹ 0, 
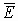
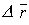
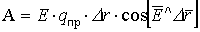
Проведём анализ вариантов:
а) если принять, что 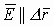
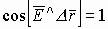
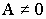
б) если же 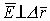
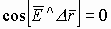
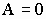
Т.е. 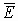
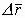
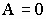
1.9. Теорема Остроградского–Гаусса
Теорема Остроградского-Гаусса касается расчета векторных полей, пересекающих различные поверхности. Лучше эту проблему решить через пример истечения жидкости через поперечное сечение трубы. Чтобы определить количество истекшей жидкости, разбиваем пространство поперечного сечения на маленькие участки 
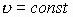
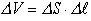
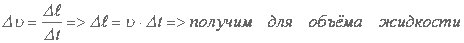
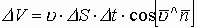
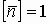
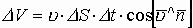
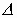
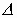
Поток вектора скоростей — количество или объем истекающей жидкости в единицу времени (можно назвать это мощностью):
В качестве площади, через которую истекает жидкость, берут её составляющую, перпендикулярную потоку жидкости, т.е. 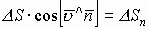
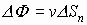
Это выражение для потока скоростей жидкости. На этом примере можно анализировать потоки любых векторов, проходящих через поверхность. Поведение любых векторов в пространстве аналогично поведению вектора 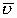
Приложения к теореме Остроградского-Гаусса:
Если потоком векторов считать просто количество векторов, проходящих через площадку, пусть есть источник векторов 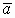
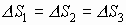
1) Поток векторов 
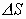
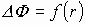
Для определения полного потока (общего количества 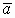
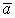
2) Полный поток через замкнутую поверхность есть величина постоянная, т.е.
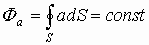
1.10. Теорема Гаусса
Вектор Е (вектор напряженности электрического поля), проходящий через поверхность, можно рассматривать как любой другой вектор в пространстве, поэтому к нему применима вышеизложенная теорема. Тогда для расчета количества векторов Е можно записать:
Если источник поля — положительный заряд, то напряженность электрического поля от него:
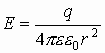
Если замкнутая поверхность сфера, то напряженность на ее точках есть величина постоянная. Тогда поток вектора Е через замкнутую поверхность от точечного заряда запишется как:
Это есть теорема Гаусса, говорящая, что поток вектора Е через замкнутую поверхность численно равен величине заряда, формирующего электрическое поле, деленного на электрическую постоянную и диэлектрическую проницаемость.
1.10.1. Теорема Гаусса для системы точечных зарядов
Полный поток, через замкнутую поверхность: 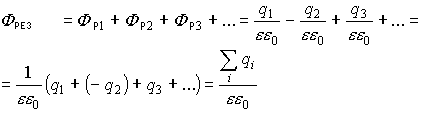
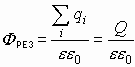
1.10.2. Применение теоремы Гаусса к расчетам электростатических полей
Пусть в качестве заряда есть бесконечная заряженная нить.
Если r<<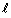
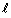
Ограничим замкнутую поверхность вокруг dl цилиндром с основанием r. Через основание цилиндра количество векторов Е=0, т.к. 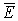
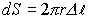
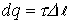
Подставив все выражения, получим:
Это выражение определяет напряженность поля бесконечной заряженной нити в любой точке пространства.
Расчет напряженностей для заряженной сферы (поле заряженной сферы).
Пусть имеется:
а) Полая сфера 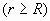
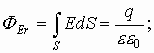
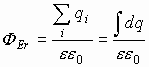
Приравняем интегралы
Аналогичным способом рассуждая, полный поток вектора 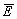
Окончательно получаем напряженность в любой точке пространства, расположенной вдали от заряженной полой сферы:
б) Если
Каждый отдельно взятый заряд на поверхности сферы дает силовую линию, которая пересекает сферу радиуса r дважды (со знаком “+” и со знаком “-”, т.е. входящий и выходящий), таким образом результирующее количество векторов Е, пересекающих эту сферу, равно нулю. То есть электрическое поле внутри полой сферы отсутствует.
в) Поле сферы с зарядом, равномерно распределенным по объему.
По закону Кулона (взаимное отталкивание зарядов) в однородном проводящем теле заряды распределяются по поверхности. Поэтому возьмем искусственный случай смеси проводящих элементов в непроводящей массе.
Рассмотрим случай (r > R): Аналогично рассуждая, поток вектора Е через сферу радиуса r определится как:
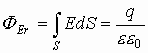
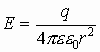
Рассмотрим случай (r < R):
По теореме Гаусса поток вектора Е состоит из двух потоков 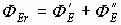
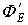
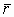
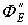
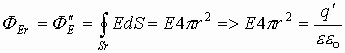
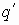
Вводится понятие объемной плотности заряда r , т.е. количество заряда в единице объёма, тогда количество заряда внутри сферы r определится как:
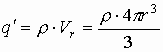
По определению:
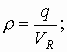
Окончательно получаем, что величина напряженности в любой точке пространства внутри однородно заряженной сферы:
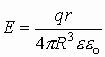
Поле бесконечной заряженной плоскости.
Определим напряженность в точке А, находящейся на расстоянии r, много меньшем чем любой геометрический размер плоскости (r < <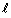
Каждый элементарный заряд на заряженной плоскости дает две силовые линии, пересекающие замыкающие поверхности. Используя положения о перпендикулярности силовых линий к поверхности заряженных тел, получим систему параллельных силовых линий, расположенных по обе стороны от заряженной плоскости.
Поле, характеризующееся параллельными силовыми линиями, называется однородным (так же силовые линии должны быть равными между собой). Тогда по теореме Гаусса поток вектора Е через замкнутую поверхность равен:
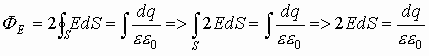
Введем понятие поверхностной плотности заряда:
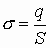
Тогда количество заряда:
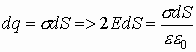
Окончательно имеем напряженность вблизи бесконечно заряженной плотности (величина напряженности вблизи бесконечно заряженной плотности не зависит от расстояния):
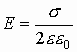
Поле двух бесконечно заряженных плоскостей.
Пусть имеем
1) разноименно заряженные бесконечные плоскости (понятие бесконечности см. предыдущий раздел).
По принципу суперпозиции определим напряженность от каждой плоскости и сложим:
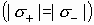
Поле между плоскостями:
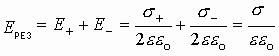
Аналогично рассмотрим ситуацию вне плоскостей. По принципу суперпозиции:
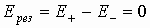
Поле для разноименно заряженных пластин между ними присутствует и однородно. Поле вне пластин отсутствует. Такое образование (конструкция) используется в электротехники, как накопитель электрической энергии, называемый конденсатором или электроемкостью.
2) Одинаково заряженные бесконечные пластины:
Если пластины заряжены одним знаком заряда, аналогично рассуждая, получим, что поле между пластинами отсутствует, а вне пластин неоднородно, т.к. распределено во всем окружающем пространстве. Практического применения не имеет.
1.11. Проводник в электрическом поле
Проводник — материальный объект, в котором в естественных условиях имеется множество свободных носителей заряда. Проводником может стать любой объект, если его подвергнуть внешнему воздействию, вызывающему появление свободных носителей заряда.
Любое вещество состоит из атомов, в составе которых находятся заряженные и не заряженные частицы, это электроны, протоны, нейтроны и т.д. Под действием внешних термодинамических условий (температура, облучение) электроны из атома могут вырываться и становиться свободными. Т.е. существует ряд веществ, обладающих избытком свободных электронов (например, металлы), как правило, знак избыточных зарядов в таких проводниках «-» . На практике всегда работают со свободными носителями заряда — электронами.
«Свободные носители заряда» — значит, что при воздействии на физическое тело сколь угодно малой электрической силы свободные носители заряда движутся направленно вдоль направления движущей силы.
1.12. Свойства проводников
1) есть свободные заряды (металлы). 2) напряженность поля внутри проводника равна нулю (см. выше). 3) напряженность поля у поверхности всегда перпендикулярна поверхности. 4) если внутри проводника: 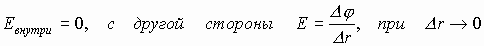
Отсюда последовательно можно получить:
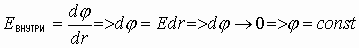
Математически, если производная от величины (j ) равна нулю по параметру дифференцирования — расстоянию, тогда выражение под знаком дифференциала есть величина постоянная, не зависящая от параметра дифференцирования — от расстояния, т.е. любая точка внутри проводника обладает одинаковым потенциалом. Отсюда следствия:
а) объем проводника эквипотенциальный, 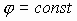
б) проводник в целом нейтрален, но под воздействием внешних сил двигаются только электроны поскольку атомы, во-первых, обладают много большей массой, а, во-вторых, атомы могут быть закреплены между собой (кристаллическая решетка).
1.13. Индуцирование заряда
Если проводник находится в замкнутой системе, то свободные носители заряда первоначально располагаются хаотично по объему проводника, а затем по закону Кулона расталкиваются и распределяются по всей поверхности проводника.
Чем больше расстояние от центра тела, тем больше скопление заряда. Если проводнику сообщить избыточный заряд, то с наиболее удаленных от центра частей проводника может наблюдаться срыв заряда, если вблизи находится другой проводник (по этому принципу работают молниеотводы).
Если к незаряженному проводнику поднести заряженное тело, то в проводнике произойдет перераспределение заряда в соответствие со знаком поднесенного тела.
В этом заключается принцип индуцирования заряда.
1.14. Проводник во внешнем электрическом поле
По закону Кулона происходит индуцирование заряда на частях поверхности, близких к пластинам конденсатора. Такое перераспределение свободных зарядов по проводнику происходит до тех пор пока величина напряженности внешнего поля (создаваемого пластинами конденсатора), не выровняется величиной напряженности поля, создаваемого перераспределенным зарядом в проводнике.
Перераспределение закончится, когда по первому закону Ньютона результирующая сила равна нулю: при F ¹ 0 заряд перераспределяется; при F = 0 перераспределение прекращается, т.к. / Eвнешнее /=/ Евнутреннее/.
Таким образом, в проводнике, помещенном во внешнее поле, собственно поле как таковое отсутствует. Если внешнее поле увеличить или уменьшить, то перераспределение заряда соответственно усилит или уменьшит величину внутреннего электрического поля, чтобы скомпенсировать внешнее. Т.е. создается ситуация изолированного пространства внутри проводника от внешних воздействий. Этот принцип используется в технике как электростатическая защита для высокоточных приборов, которые нужно изолировать от внешних полей.
1.15. Электроемкость проводника
Если проводнику сообщать избыточный заряд, то величина потенциала на проводнике будет прямо соответствовать величине избыточного заряда (j ~ q).
Величина избыточного заряда зависит от формы проводника. Величина, связывающая заряд и потенциал называется электроемкостью — способностью проводника принимать избыточные заряды.
Если изменять заряды:
Соответственно 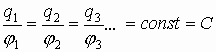
Величина отношения заряда к потенциалу для проводника данной геометрической формы есть величина постоянная (но зависит от формы проводника), это и есть электроемкость:
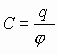
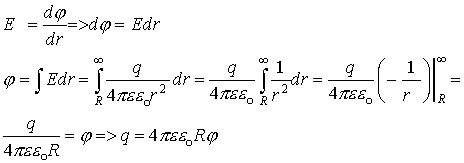
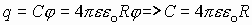
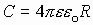
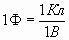
Поле между обкладками конденсатора однородное, т.е. 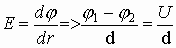
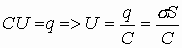
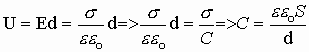
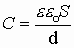
1.16. Соединение конденсаторов
Часто необходимо использовать набор конденсаторов, чтобы создать электроемкость нужного номинала. Для увеличения или уменьшения номинала электрической емкости используют параллельное и последовательное соединение конденсаторов.
Батарея конденсаторов — совокупность соединенных каким-либо образом конденсаторов.
а) параллельное соединение.
При параллельном соединении все обкладки, соединенные металлическим проводником, имеют одинаковый потенциал и представляют собой эквипотенциальную поверхность.
Разность потенциалов между обкладками конденсатора — есть напряжение:
По принципу индуцирования зарядов на противоположной обкладке появится избыток заряда, численно равный по величине первому заряду, но противоположный ему по знаку.
А заряд на каждой из левых обкладок конденсатора составляет сумму зарядов, распределенных от общего заряда q+ как поток (электронов) распределяется по ручейкам (проводникам).
Таким образом, при параллельном соединении конденсаторов общая электроемкость равна сумме емкостей батареи конденсаторов.
б) последовательное соединение.
Величина заряда, переносимая на первую обкладку, индуцирует такой же по величине, но противоположный по знаку заряд на второй обкладке:
| q1+ | = | q2— | = | q3+ | = | q4— | =¼=| qi | ¼ и т.д.
Разность потенциалов на каждой из этих обкладок разная. Известно, что по закону Кирхгофа, сумма падений потенциала (j1 — j2) на элементах замкнутой цепи численно равна напряжению элементов, питающих эту цепь. А падение напряжения на концах не замкнутой цепи численно равно сумме падения напряжения на элементах этой цепи:
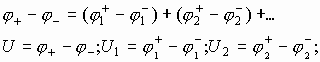
При последовательном соединении обратная величина результирующей емкости численно равна сумме обратных величин емкостей, составляющих батарею конденсаторов.
Приложение:
Как правило, в технике используется соединение двух конденсаторов, и чем их больше — тем реже.
а) при параллельном.
б) при последовательном.
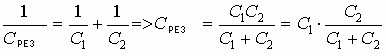
Обобщение: Если требуется увеличить электроемкость, то исходные емкости включаются параллельно, если уменьшить — то последовательно.
1.17. Энергия электростатического поля
Так как электрическое поле способно переносить заряженные тела в пространстве, т.е. совершать работу, значит, можно сказать, что оно обладает энергией.
Wэл=Ar¥ => W — характеристика q, формирующего электрического поля.
Принято за способность заряда совершать работу считать работу по переносу одной половины заряда другой половинной этого же заряда, формирующего поле:
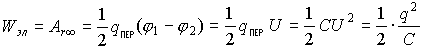
Итак 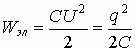
Сравни с кинетической энергией:
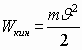
1.17.1. Энергия плоского конденсатора
Используя выражение электроёмкости конденсатора 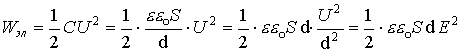
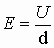
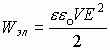
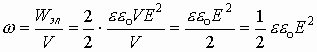
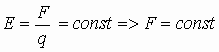
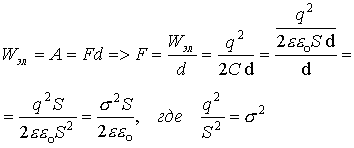
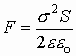
Поскольку между обкладками конденсатора действует сила притяжения, то во избежании нарушения геометрического пространства между обкладками помещают твердое непроводящее тело, так называемый диэлектрик.
1.18. Диэлектрики
В силу строения атомы некоторых элементов в нормальных термодинамических условиях могут отдавать в межатомное пространство валентные электроны, т.е. энергия связи электронов с атомами так слаба, что тепловая энергия отрывает их от атома. Количество свободных электронов в таком веществе может составлять nсв» 1023 эл/см3. Такие вещества называются проводниками или металлами.
У других элементов валентная связь электронов с атомами может быть сильнее Wсвязи > 3кТ/2 . Тогда в межатомном пространстве число свободных электронов очень мало. Некоторая часть свободных электронов в этих веществах обуславливается термодинамическими функциями (отклонения, обусловленные нестандартными причинами, от нормальной ситуации). Процесс отрыва электронов от атомов носит вероятностный характер. Вероятность отрыва электрона от атома тем больше, чем больше энергия внешнего воздействия.
Поэтому в большинстве диэлектриков количество свободных электронов составляет nсв» 1011 эл/см3. Такого количество электронов мало, чтобы вызвать в электрических цепях, включающих диэлектрик ощутимое протекание электрического тока, которое можно зарегистрировать реальными приборами.
Но в целом в таком веществе суммарное количество заряда остается таким же как и в проводящем веществе. Принято вещество с концентрацией носителей заряда 10-21см-3 — 10 -23 см-3 называется проводящим (проводником), а вещество с концентрацией носителей заряда 10 9 — 1012см -3 называется диэлектриком, но это понятие относительно, т.е. если сопряжены два вещества с концентрациями носителей заряда 1018см-3 и 1014 см-3, то первое вещество называется проводником относительно второго, второе — изолятором (диэлектриком) относительно другого (первого).
Любой физический объект материального мира в нормальных термодинамических условиях всегда имеет как минимум 109 см-3 свободных носителей заряда.
Заряды, которые не свободны в диэлектриках, называются связанными, и под действием внешнего электрического поля они также изменяют свое поведение. Диэлектрики бывают полярные и неполярные.
1.18.1. Свойства диэлектриков
Связанные заряды проявляют в диэлектрике свои свойства под действием внешнего электрического поля соблюдая правила:
- связанные заряды не перемещаются по веществу под действием внешнего поля.
- связанные заряды не могут передаваться с одного тела на другое.
В исходном состоянии связанные заряды могут перераспределяться двумя способами:
- общий центр » -» зарядов может совпадать с центром » +» зарядов (например, в атоме центр » +» зарядов (ядро) может совпадать с центром » -» зарядов (центр окружностей вращающихся электронов));
- общий центр » +» зарядов не совпадает с общим центром » -» зарядов.
Тогда первые называются неполярные диэлектрики, а вторые называются полярные диэлектрики: например, Н2, N2, ССl4, CO2, O2, … , неполярные NaCl, и другие соли — полярные.
1.18.2. Поведение диэлектриков во внешнем электрическом поле
При внесении в электрическое поле диэлектрика его объем приобретает электрический дипольный момент. Это явление называется поляризацией диэлектрика. Дипольный момент характеризуется вектором поляризации — электрическим дипольным моментом единицы объема:
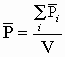
Электрическим диполем называется совокупность положительных и отрицательных зарядов, связанных между собой, но разнесенных в пространстве. Расстояние между центрами » +» и » -» зарядов называется плечом диполя. Характеристикой диполя является электрический момент диполя:
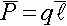
Направление принято считать 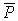
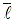
Модель полярного диэлектрика
Объем полярного диэлектрика состоит из хаотически ориентированных дипольных моментов в пространстве так, что в целом диэлектрик нейтрален с точки зрения зарядового состояния. Если задать внешнее поле, т.е. поместить диэлектрик между обкладками конденсатора, тогда во внешнем электрическом поле дипольные моменты (диполи) развернутся вдоль силовых линий, т.е. диэлектрик электризуется. Степень поворота диполей вдоль силовых линий зависит от величины внешнего электрического поля. Такие диэлектрики называются содержащими жесткие диполи.
Модель неполярного диэлектрика
В этом состоянии (исходном) диполи нейтральны. При внесении во внешнее электрическое поле центры » +» и » -» зарядов растягиваются в пространстве.
Появляется дипольный момент (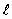
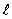
После снятия внешнего поля у неполярных — центры » +» и » -» зарядов сомкнутся, у полярных восстановится хаотическая ориентация диполей. Способность диэлектриков электризоваться под действием внешнего электрического поля называется диэлектрической восприимчивостью 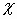
Можно провести качественный анализ реакции диэлектрика на внешнее поле. Любой диэлектрик отзывается под действием внешнего электрического поля носителями заряда. Удельное количество всех зарядов, задающих электризацию диэлектрика, состоит из отзывающихся свободных и связанных носителей заряда: r = 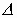
Очевидно, что nсвоб » 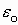
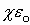
Тогда r =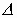
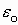
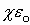
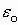
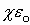
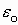
1+ c = 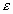
Тогда P=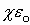
Для обычных диэлектриков c не превышает единиц и десятков единиц. У неполярных c =соnst. У полярных c ~ f(T), где Т — абсолютная температура. (в градусах Кельвина).
1.19. Поток вектора электрического смещения
Исходя из общего правила по теореме Остроградского-Гаусса:
можно записать:
А из предыдущего раздела следует:
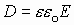
Если один любой вектор электрического смещения связан с аналогичным вектором напряженности по формуле (*), то можно предположить, что и любой другой вектор электрического смещения связан с вектором Е. И соответственно, множество векторов электрического смещения связано аналогично с соответствующими векторами напряженности.
Множество векторов — поток векторов. Тогда можно записать:
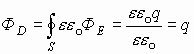
Поскольку выражение для потока вектора Е численно определенно для замкнутой поверхности, то потоком вектора электрического смещения называется количество заряда, сосредоточенное внутри замкнутой поверхности. Таким образом, частные формулы силовых характеристик электрического поля можно записать:
1.20. Сегнетоэлектрики и их свойства
Сегнетоэлектрики — класс диэлектриков, обладающий электризованностью в отсутствии внешнего электрического поля.
Если стрелками указать вектора поляризованности, то схематически можно представить
Если в обычных диэлектриках диполи ориентированны хаотично, то сегнетоэлектриках эти диполи могут группироваться по десять, сто и более штук с параллельно ориентированными диполями. Сегнетоэлектрики — только полярные диэлектрики. Области сегнетоэлектрика с параллельно ориентированными дипольными моментами называется доменами.
При внесении во внешнее электрическое поле сегнетоэлектрик в целом переориентируется в пространстве блоками дипольных моментов и если первоначально при малых напряженностях электрического поля разворот доменов затруднен, то при дальнейшем увеличении Е домены разворачиваются вдоль силовых линий Е как единое целое, а дальнейшее увеличение Е уже не вызывает переориентации диполей, если все домены выстроились вдоль поля.
Сегнетоэлектрик во внешнем электрическом поле.
При снятии внешнего электрического поля многие домены не возвращаются в исходное состояние. Таким образом, сегнетоэлектрик приобретает преимущественную поляризацию в отсутствии внешнего поля.
Свойства сегнетоэлектриков:
а) у обычных диэлектриков e составляет единицы, десятки единиц (c = 1 + e ), у сегнетоэлектриков сотни, тысячи единиц.
б) зависимость поляризованности от внешнего электрического поля нелинейна (тогда, как Р=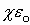
Вид зависимости, представленный на следующем рисунке, для поляризованности диэлектрика от внешнего электрического поля, носит название гистерезиса.
1.20.1. Электрический гистерезис в сегнетоэлектриках
Анализируем схему гистерезиса. Точка (1) характеризуется тем, что последовательное увеличение напряженности внешнего электрического поля Е приводит все к меньшему увеличению поляризованности, дальше после (2) происходит насыщение, т.е. поляризованность не изменяется при увеличении внешнего поля.
Если электрическое поле снимать (уменьшать), то поляризованность уменьшается не так как увеличивалось (3), а при полном снятии электрического поля Е=0 поляризованность сохраняется (P1) — это есть остаточная поляризованность.
Для того, чтобы снять остаточную поляризованность, следует приложить электрическое поле обратной полярности и величина напряженности, при которой поляризованность полностью снимается, численно равна Ес- коэрцитивная сила, возвращающая исходное положение (Р=0). Если увеличивать обратную напряженность (4), то домены переориентируются противоположным образом и при достижении (5) дальнейшее увеличение обратного поля также не приводит к увеличению поляризованности. Снятие обратного поля оставляет в диэлектрике поляризованность (P2), для ее снятия прикладывают силу Е’с и т.д.
Остаточную поляризованность, кроме внешнего поля можно снять нагревом. При нагреве тепловая энергия Q=3кТ/2 сообщается доменами, через них диполям и домены могут разрушатся, т.е. сегнетоэлектрик переходит в обычный диэлектрик с хаотичной ориентацией диполей. Если нагрев снять, то диполи опять, как правило, формируются в домены.
Температуры, при которой домены разрушаются (теряются сегнетоэлектрические свойства) называются температурой Кюри (точкой Кюри). Температура Кюри симметрична относительно нагрева и охлаждения. Потеря и восстановление сегнетоэлектрических свойств происходит при одной температуре. Причиной заставляющей отдельные диполи объединяться в домены, является энергетический выигрыш, т.е. при объединении отдельных диполей при создании доменов высвобождается энергия, что приводит к понижению собственной энергии сегнетоэлектрика.
2. Постоянный электрический ток
Электрический ток — направленное движение зарядов.
Направление тока — направление движения «+» зарядов. Так исторически принято, хотя основными носителями заряда в подавляющем большинстве случаев являются электроны, т.е. отрицательно заряженные частицы.
Условия возникновения электрического тока:
1. наличие свободных носителей электрических зарядов. 2. электрическое поле (внешнее).
Характеристики электрического поля:
Сила тока — количество заряда, протекающего по проводнику в единицу времени. Для постоянного тока:
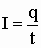
Если количество заряда меняется со временем, то:
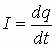
Плотность тока — численно равна величине тока, протекающего через единичную площадку, расположенную перпендикулярно направлению движения заряда.
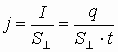
Если сила тока величина скалярная, то плотность тока – вектор, направленный вдоль нормали к поверхности, через которую протекает заряд. Если поперечное сечение проводника, по которому протекает ток, неоднородно, тогда плотность тока в разных частях проводника выражается дифференцированием, т.е. величина силы тока есть поток векторов j, через поперечное сечение проводника (см. т.Гаусса).
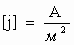
Электропроводность — физическая величина, количественно характеризующая способность тела пропускать электрический ток под действием электрического поля (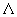
Величина, обратная электропроводности, называется сопротивлением.
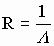
Сопротивление протеканию тока есть величина, характеризующаяся структурными и химическими особенностями среды, по которой протекает заряд. Структурные особенности — взаимное расположение атомов в проводнике, химическая особенность — разного рода молекулярная связь атомов и молекул вещества.
Эти особенности, как правило табличные, и называются удельным сопротивлением 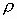
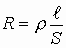
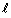
Поскольку сопротивление определяется особенностями строения проводника, то температура окружающей среды, искажающая состояние структуры химических связей атомов вещества, оказывает решающее влияние на это сопротивление. Из общих соображений можно сказать, что повышение температуры повышает сопротивление.
Rt=Ro+(1+a t) где Rо- сопротивление при комнатной температуре, t — температура в градусах Цельсия, α — температурный коэффициент сопротивления.
Изменение температуры на десятки градусов изменяет сопротивление на несколько процентов, на сотни градусов — на десятки процентов. (α ~ 10-3 К-1).
2.1. Плотность тока носителей заряда разных знаков
В общем случае для разных типов носителей заряда: 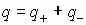
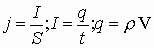
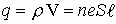
Аналогичное математическое рассмотрение можно провести, как для “+” так и для “-” зарядов. Предполагается, что “+” и “-” заряды при протекании не взаимодействуют друг с другом, тогда общие потоки зарядов движутся навстречу друг другу и результирующий поток равен:
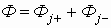
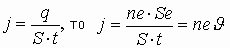
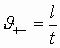
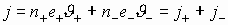
2.2. ЭДС. Источник тока. Напряжение
Чтобы в проводнике протекал постоянный электрический ток: 1) подают на один конец заряды, а на другом их снимают; и 2) нужны некоторые силы, чтобы заряд перемещался, т.е. нужны силы неэлектрического происхождения, их называют сторонние силы.
Сторонние силы не должны быть электрическими, а должны быть химическими, ядерными, механическими и т.д. для совершения работы по перемещению заряда по участку цепи. Участок цепи, в который включается источник сторонних сил обозначается двумя перпендикулярными линиями: тонкая длинная — источник «+» зарядов, толстая короткая — источник «-» .
Устройство, в котором возникают сторонние силы, называются источником тока. Если потенциалы φ1, φ2 в точках 1 и 2 создаются так же электрическими силами, тогда полная сила, вынуждающая заряды двигаться, F=Fстор+FK , а работа по перемещению заряда из точки (1) в точку (2) А12=Fr, если ток протекает в цепи постоянный:
А12=Fr=Fстор · r+FK· r =Eстор·qr+Eкул·qr
Введем понятие силовой характеристики сторонних сил, заставляющих заряды q двигаться, такое как, напряженность поля сторонних сил, тогда:
Fстор =Eстор·q
Зная связь между напряженностью и разностью потенциалов, можем записать, что:
Тогда полная работа:
А12=Eстор·qr + (φ1-φ2 )·q.
Разделив это уравнение на величину переносимого заряда q, получим: 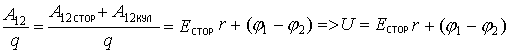
Это напряжение, получаемое на концах участка цепи 1-2, содержащего сторонние силы. Согласно определению силовой характеристики сторонних сил можно записать:
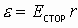
ЭДС (e) — электродвижущая сила источника сторонних сил; тогда выражение напряжения на концах участка цепи, содержащего сторонние силы, численно определяется с “+” , если э.д.с. помогает протеканию тока; и с “-” , если э.д.с. препятствует протеканию тока.
2.3. Законы Ома в интегральной форме
Закон Ома в интегральной форме подразумевает, что рассматривается полный ток, протекающий в цепи и величина тока со временем не меняется. Очевидно, что количество заряда, протекающее по проводнику, обратно пропорционально сопротивлению проводника. Количество заряда протекающее в проводнике, прямо пропорционально напряженности или разности потенциалов, создающих внешнее электрическое поле.
1) 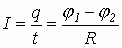
Суммарное сопротивление проводников и элементов цепи без э.д.с. обозначается на схеме.
2) Если участок цепи включает в себя э.д.с, то собственное сопротивление источника тока выделяется и обозначается r.
Тогда закон Ома для участка цепи, содержащей э.д.с., будет иметь вид:
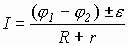
3) Если замкнутый участок цепи, содержит э.д.с., тогда φ1 = φ2, и получаем:
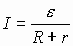
В целом участок цепи, содержащей множество э.д.с. и разных деталей представлен законом Ома в виде:
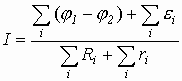
Если при напряжении на концах участка цепи в 1В по цепи протекает ток в 1А, то говорят, что сопротивление цепи равно одному Ому.
Из закона Ома следует:
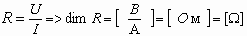
2.3.1. Закон Ома в дифференциальной форме
Сечение проводника или элементов цепи, как правило, неоднородно, и сопротивляемость в разных участках цепи протеканию тока также различная. Тогда разбивают участки цепи на элементы (дифференцируют) и определяют закон Ома в каждом отдельном участке.
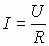
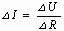
Учитывая, что для участка цепи
и 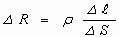
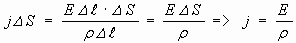
Это закон Ома в дифференциальной форме. Зная, что удельная электропроводность σ и удельное сопротивление ρ связаны, как:
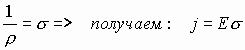
σ — удельная электропроводность,
ρ — удельная сопротивление,
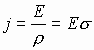
2.4. Закон Джоуля-Ленца
В интегральной форме
Закон Джоуля-Ленца касается закона сохранения энергии; если считать, что система электрической цепи замкнутая, то работа по перемещению заряда в проводнике, если сам проводник не перемещается в пространстве, полностью преобразуется в тепловую энергию Q на участке (1-2).
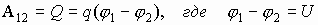
Q=IU· t (1) 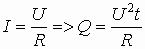
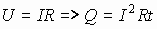
Вид формулы для Q определяется условием задачи по определению выделившегося тепла. Формулы (1), (2), (3) есть закон Джоуля-Ленца в интегральной форме (определение полного тепла, выделившегося в цепи за все время протекания тока).
Тепловая мощность тока.
Для определения количества теплоты, выделившегося в единицу времени, вводят понятие тепловой мощности тока:
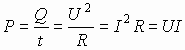
Единицей мощности тока считают 1Вт=1Дж/1с.
В дифференциальной форме
Если электрическая цепь состоит из элементов различного сопротивления и геометрии, то цепь разбивают на отдельные участки и определяют закон Джоуля-Ленца для каждого участка. Последовательно расписывая
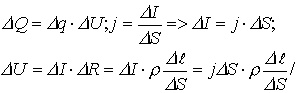
Из закона Ома в дифференциальной форме следует:
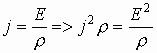
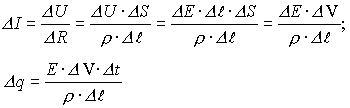
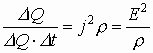
2.5. Законы Кирхгофа
I Закон Кирхгофа — закон токов (для узлов цепей).
В участке электрических цепей очень часто содержатся узлы, в которых сходятся множество элементов, проводящих ток.
Если цепь работающая, то по разным участкам будут протекать различные токи. По закону сохранения заряда, как материального объекта, можно предположить, что количество заряда, приходящего в узел, должно быть численно равно количеству заряда, выходящего из узла:
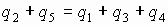
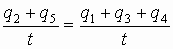
Окончательно имеем:
Сумма электрических токов, сходящихся в узле работающих цепей, всегда равна нулю.
II Закон Кирхгофа — закон напряжений (закон замкнутых цепей).
Величина электрического тока в последовательных цепях есть величина постоянная и по закону сохранения заряда 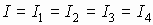
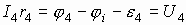
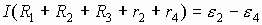
Окончательно получаем 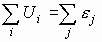
В любом замкнутом контуре сумма падений напряжений на всех участках цепи равна алгебраической сумме э.д.с., включенных в цепь.
2.6. Эмиссия (испускание) электронов с поверхности
Так как любое вещество имеет в своем объеме свободные электроны, то любое внешнее электрическое воздействие на вещество может привести к отрыву электронов с поверхности вещества (эмиссия).
Итак, для того, чтобы удалить электрон с поверхности вещества, требуется совершить работу. Принципиально свободные электроны могут испускаться поверхностями любых веществ, где есть граница раздела (воздух-вода, дерево-вакуум).
Но наибольшее количество испускаемых электронов наблюдается у металлов в связи с наибольшим количеством свободных электронов у этого класса веществ. Эмиссия электронов характеризуется работой выхода — минимальной энергией, которую необходимо затратить для удаления электрона с поверхности твердого или жидкого вещества в вакуум.
2.6.1. Работа выхода
Энергетический разрыв между энергиями электронов в атоме и энергиями электронов в свободном состоянии (в кристалле) называется энергией отрыва электрона от атома. Значит энергетическое состояние свободного электрона больше, чем энергия электрона в атоме. Точно также для отрыва свободного электрона с поверхности вещества требуется совершить работу. Значит, энергетическое состояние электрона вне вещества выше, чем энергия электрона в кристалле.
Для чистых веществ работа выхода зависит только от особенностей атома вещества и взаимосвязей атомов между собой.
Для разных веществ Авых не превышает нескольких эВ, например:
| Металл | Pt | W | Mo | Fe | Mg | Na |
| Авых (эВ) | 5,29 | 4,5 | 4,27 | 4,36 | 3,45 | 2,27 |
2.6.2. Способы выбивания (отрыва) электронов с поверхности
Фотоэлектронная эмиссия — выбивание электронов с поверхности под действием электромагнитного излучения (свет — это часть диапазона электромагнитных волн).
И — источник электромагнитных волн (света).
а) окошко для света закрыто, тока нет, т.е. I=0;
б) окошко для света открыто, ток есть, то есть I≠0, т.к. свет падает на поверхность электрода, выбивает электроны, которые и создают ток между анодом и катодом.
Вторичная электронная эмиссия — испускание электронов с поверхности вещества под действием бомбардировки внешних электронов.
Если энергия внешних электронов достаточна для совершения работы выхода (отрыва) электронов с поверхности, то общий поток электронов между анодом и катодом возрастает.
Это устройство называют электронным умножителем.
Автоэлектронная эмиссия — вырывание электронов с поверхности вещества под действием внешнего электрического поля (холодная эмиссия).
Острие катода является концентратором электрического поля. При повышении напряжения между электродами возникает ситуация, когда энергия электрического поля превышает Авых электрона с поверхности.
Задавая напряжение 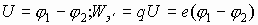
Если 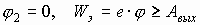
Термоэлектронная эмиссия — явление вырывания электрона с поверхности вещества под действием тепла. При этом тепло или энергия, подводимая к поверхности вещества, превышает работу выхода Q = I2· Rt 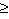
2.6.3. Электрический ток в вакууме
Электрод, на который подается “+” потенциал, называется анод, а “-” потенциал — катод. Эти электроды помещены в замкнутую вакуумированную среду, а все устройство называют вакуумным диодом.
Пропуская по катоду регулируемый электрический ток по закону Джоуля-Ленца мы вызываем его нагрев. В результате нагрева с поверхности катода испускаются термоэлектроны. Под действием электрического поля между катодом и анодом электроны летят на анод, цепь замыкается, приборы фиксируют наличие тока.
Анализ зависимости тока от напряжения называется вольтамперной характеристикой. ВАХ вакуумного диода имеет сложный характер насыщения.
Проанализируем характерные точки:
1) При отсутствии напряжения между анодом и катодом, электроны вылетают с катода хаотично и часть электронов может попасть на анод; эта величина тока очень мала, но физически имеет место.
2) При увеличении напряжения между анодом и катодом электроны, вылетающие с катода, вытягиваются электрическим полем к аноду и величина тока возрастает; зависимость тока от напряжения на этом участке происходит по закону Богуславского — Ленгмюра (закон 3/2): 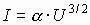
3) участок называется током насыщения; при дальнейшем увеличении напряжения между анодом и катодом наступает момент, когда все электроны, вылетающие с катода, вытягиваются электрическим полем на анод, и дальнейшее увеличение напряжения не приводит к увеличению тока, т.к. количество электронов, вылетающих с катода, ограничено.
4) для того, чтобы полностью подавить анодный ток, необходимо между электродами подать обратное напряжение, и величина напряжения, при котором анодный ток равен 0, называется Uзап — запирающим напряжением.
Поскольку электроны, вылетающие с поверхности, как правило, обладают кинетической энергией, то по данным точки (4) по закону сохранения энергии можно рассчитать скорость вылета электронов, если запирающее напряжение — несколько вольт:
Это среднее значение скорости электронов, летящих от катода к аноду. Величину тока насыщения вакуумного диода можно изменять, изменив нагрев катода, т.е. T3> T2> T1 и, соответственно, изменяется количество электронов, вылетающих с поверхности, как следствие, изменяется Iнас3> Iнас2> Iнас1 .
Зависимость тока насыщения от температуры — закон Риичардсона-Дэшмана и имеет вид:
2.7. Заряженная частица в плоском конденсаторе
Рассмотрим два случая поведения заряженной частицы в конденсаторе.
а) частица движется перпендикулярно пластинам.
Напишем уравнение для отдельного электрона. По закону сохранения энергии работа по переносу заряда от пластины до пластины:
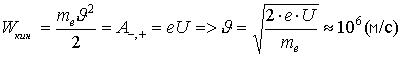
б) частица движется параллельно пластинам.
Также рассмотрим действие поля конденсатора на электрон. По 2-му закону Ньютона сила Кулона вызывает ускорение в направлении, перпендикулярном пластинам, и отклоняет электрон к “+” пластине:
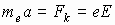
Зная, 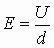
Разложим скорость электрона на две составляющие: параллельную и перпендикулярную пластинам. 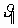

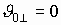
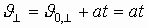
Тогда путь, пройденный электроном в направлении, перпендикулярном пластинам:
Тогда время пролета электрона в конденсаторе параллельно пластинам:
В результате этого анализа можно сказать, что электрон может выйти из конденсатора, если 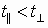
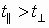
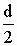
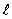
3. Электромагнетизм
3.1. Электромагнетизм
Электромагнетизм — это раздел электричества, рассматривающий воздействие движущихся зарядов на движущиеся заряды.
Движение заряда может быть равномерным (I закон Ньютона). Если к такому заряду привязать систему отсчета, то в этой системе заряд не движется. Таким образом, если другая заряженная частица движется параллельно первой с той же скоростью и в том же направлении, то между ними не будет магнитного взаимодействия, а только кулоновское взаимодействие. Итак, чтобы магнитное взаимодействие проявилось, частицы должны двигаться или с разной скоростью или в разном направлении.
Связь характеристик магнитного поля:
B = µ0*H; где B — индукция магнитного поля; H — напряженность магнитного поля; µ0 = 1,16 * 10-6
Для того, чтобы заряды направленно двигались в пространстве, необходимо наличие проводящей среды, специально ориентированной в пространстве.
3.2. Взаимодействие параллельных токов
Закон Фарадея:
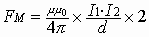
Направление токов влияет на силу взаимодействия.
По аналогии с электростатикой, где сила определяет напряженность, а напряженность — индукцию, в магнетизме напряженность и индукция — силовые характеристики. Принято в электростатике основной силовой характеристикой считать напряженность, а в магнетизме — индукцию.
Правило буравчика:
Если ток направлен по закрутке буравчика, то шляпка вращается по силовой линии. В каждой точке пространства направление силовых линий совпадает с направление касательной. Таким образом, силовые линии магнитного поля являются замкнутыми.
3.3. Принцип суперпозиции
Примем на рисунке направление токов перпендикулярно плоскости рисунка. Тогда в точках:
A:Bрез = B1 + B2 D:Bрез = B1 — B2 C:Bрез=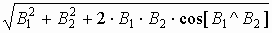

3.4. Закон Био-Савара–Лапласа
3.4.1. Магнитное поле проводника с током
В общем случае для определения магнитного поля от произвольного проводника с произвольным знаком протекания тока проводим дифференцирование. Определяем полную индукцию, как сумму элементарных индукций от элементов тока dl, содержащих dq движущегося заряда.
Согласно последнему утверждению, совпадает с перпендикуляром к плоскости, образованной векторами cкорости
и радиус- вектора
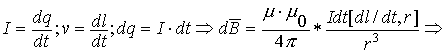
Последняя формула и есть закон Био-Савара-Лапласа для определения магнитной индукции для проводника с током.
3.4.2. Применение закона Био-Савара-Лапласа для анализа магнитных полей проводников с током различной конфигурации. Конечный и бесконечный прямолинейный проводник с током
Примем условиями: 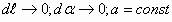
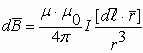
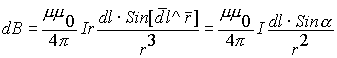
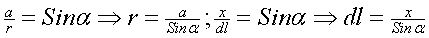
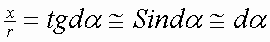
Подставляя полученное в формулу для dB, получаем:
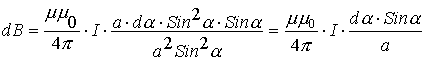
Это выражение для составляющей магнитного поля в точке p элемента проводника с током dl. Тогда полное магнитное поле проводника с током в искомой точке принимает вид:
Назовем предельные углы α1 и α2 как углы, под которыми из искомой точки видны концы проводника, создающего магнитное поле. Тогда для конечного проводника с током это будет выглядеть так:
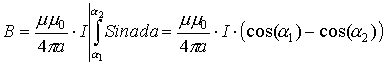
, то:
;
. Тогда
.
3.4.3. Магнитное поле кругового проводника с током
Направление магнитного поля (B) внутри кругового проводника с током также подчиняется правилу буравчика (шляпка как ток, буравчик как индукция). Магнитное поле элемента dl кругового проводника с током:
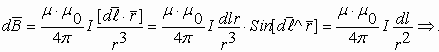
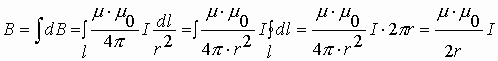
— Магнитная индукция кругового проводника (контура) с током в центре контура.
3.4.4. Магнитное поле вдали от центра контура с током
Элементы контура с током dl создают в точке А элементарные индукции dB, являющиеся трехмерным образованием в виде конуса, который дает результирующую B, равную:
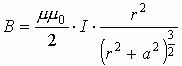
:
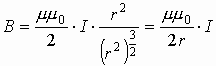
3.4.5. Магнитное поле соленоида
Если контура с током последовательно соединить в одном месте пространства, то такое образование называется соленоидом.
В таком соленоиде магнитные потоки от последовательно соединенных контуров суммируются. Так как магнитные силовые линии замкнутые, то внутри соленоида число силовых линий равно числу силовых линий всего соленоида.
А раз объем внутри соленоида ограничен, то можно сказать, что магнитное поле сконцентрировано внутри соленоида, снаружи рассеяно, и магнитные силовые линии внутри соленоида параллельны между собой и поле внутри соленоида считается однородным, вне соленоида — неоднородным. Величина магнитной индукции внутри соленоида записывается так:
, где μ — среда внутри соленоида, N — число витков соленоида, l — длина соленоида. Если обозначить
— удельное число витков
3.5. Магнитный поток
По теореме Остроградского-Гаусса в общем случае поток любого вектора через поверхность S численно равен
Индукция — вектор в пространстве, поэтому можно применить понятие потока индукции
. Если площадь фигуры, пересекающей силовые линии магнитного поля — площадь контура, по которому протекает ток, тогда
— магнитный поток контура с током. Если имеется множество последовательно соединенных контуров, то есть соленоид, то общее количество магнитных силовых линий равно сумме силовых линий, образованных каждым контуром.
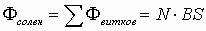
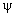
.
3.6. Напряженность магнитного поля
Зная, что , а магнитная индукция для бесконечного прямолинейного проводника с током равна
. Аналогично: Для конечного проводника:
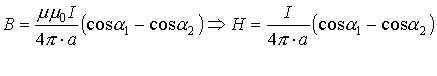
. На оси кругового витка:
3.7. Силы, действующие в магнитном поле
Сила Лоренца — сила, действующая со стороны магнитного поля на движущийся заряд. Эмпирически получаем F В векторной форме F
, а в скалярной форме
.
Принято правило левой руки (для “+” заряда для нахождения направления силы Лоренца): если вектор входит в ладонь, вектор
направлен по отогнутым пальцам, то
направлена, как показывает большой палец. Правило правой руки для отрицательного заряда аналогично. Если на заряд действуют и электрическая и магнитная силы, то в этом случае сила Лоренца равна в векторной форме:
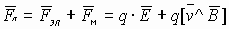
3.7.1. Сравнение электрической и магнитной сил
Сравним взаимодействие зарядов (сила Кулона) и токов, образованных этими зарядами (сила ампера) в параллельных проводниках.
Магнитное поле, действующее на заряд, создается другим зарядом, движущимся относительно первого. Предположим, что ν1=ν2, заряды находятся на расстоянии r друг от друга. Возьмем перпендикулярно
, то есть
, тогда по закону Био-Савара-Лапласа выражаем
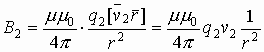
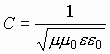
Получим 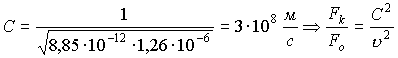
Следствия:
- Электрическая сила больше магнитной
- Магнитная сила принимает существенные значения, когда скорости зарядов близки к скорости света. Если бы С
- Поскольку скорость света конечна, магнитная сила релятивистская, то есть проявляет себя при скоростях, близких к скорости света.
3.8. Взаимодействие параллельных проводников с током
Вблизи каждого проводника с током формируется магнитное поле (сила, действующая на проводник с током, определяется по правилу левой руки: магнитные силовые линии входят в ладонь, ток по вытянутым пальцам, тогда сила направлена по отогнутому большому пальцу)
Два близко расположенных проводника с током притягиваются, с противоположным направлением токов — отталкиваются. Силы магнитного и электрического взаимодействия между движущимися зарядами противоположны.
3.9. Закон Ампера
Касается действия силы на проводник с током со стороны магнитного поля. Ориентируем проводник в соответствии с направлением тока.
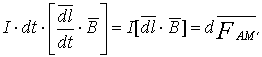
— закон Ампера в интегральной форме.
— закон Ампера в скалярной форме.
Сила Ампера указывает величину и направление силы, действующей на проводник с током I, длиной l помещенный в однородное магнитное поле. Направление задается правилом левой руки (
— в ладонь,
— вдоль пальцев,
— вдоль большого пальца).
3.10. Работа по перемещению проводника с током в магнитном поле
Длина проводника l, и перемещается он слева направо. Тогда работа по перемещению элемента проводника с током на расстояние dr равна:
.
Условия перемещения:
- магнитное поле и проводник в пространстве взаимно перпендикулярны,
.
- Направление перемещения проводника параллельно силе, вдоль которой мы совершаем работу по перемещению. То есть
— площадочка, заметаемая элементом проводника с током dl при его перемещении на dr. Тогда поток векторов B, проходящих через эту площадку:
Работа по перемещению проводника с током в магнитном поле определяется величиной тока, величиной магнитной индукции и площадью закрываемой (заметаемой) проводником при движении. Она также определяется величиной тока и магнитным потоком, проходящим через площадь, закрываемую проводником при движении.
3.11. Действие магнитного поля на контур с током
Для удобства предположим, что контур имеет прямоугольную форму.
1) Пусть dl перпендикулярен B, т. е. любой элемент контура перпендикулярен силовым линиям. Cилы Ампера, действующие на каждый прямолинейный участок контура, указаны на рисунке.
Если контур с током расположен перпендикулярно силовым линиям, то действие поля выражается в сжимании и разжимании контура. Если же контур состоит из упругого проводника, то внешнего изменения положения в пространстве не будет.
2) площадь контура с током параллельна силовым линиям. То есть нормаль плоскости контура перпендикулярна вектору магнитной индукции.
Тогда силы Ампера на каждом участке:
I. Sin=1, FA≠0, сила направлена от нас.
II, IV. Sin=0, FA=0, То есть на элемент контура с током лежащим вдоль силовых линий FA не действует.
III Sin=1, FA≠0, сила направлена к нам. Тогда если контур с током закрепить в точках A и B ,то при таком расположении его в магнитном поле он будет вращаться, то есть на него действует момент силы.
3.12. Магнитный момент контура с током
Пусть r — плечо силы. (См. предыдущий рисунок) .
. Если FA перпендикулярна r, тогда Sin=1. Это момент силы, действующий на I или III участок контура. Площадь S — между линией A B и участком тока I или III.
Поскольку в каждой из противоположных сторон контура действует самостоятельная сила Ампера, то за площадь для суммарного момента сил принимается не половина, а вся площадь контура. Тогда вводится понятие магнитного момента контура с током как собственной характеристики контура, которая численно равна произведению P=IS, где S это вся площадь контура. Направление магнитного момента задается нормалью контура с током
Тогда полный момент силы, действующий на контур с током в магнитном поле, численно равен: .
3.13. Явление электромагнитной индукции. ЭДС электромагнитной индукции
Проводник, по которому не пропускают ток, помещаем в магнитное поле. Будем перемещать проводник перпендикулярно вектору магнитного поля. По закону Лоренца так как
. Мы получили, что свободные заряды, которые, по определению, имеются в проводнике, будут перемещаться вдоль проводника. В результате перераспределения зарядов в проводнике при их движении на концах проводника возникает разность потенциалов, которая создает электрическое поле в проводнике:
. Тогда напряженность электрического поля в проводнике
Если подключим гальванометр, то можно выразить напряженность через напряжение . В равновесии Fл=Fк. То есть:
. Если закон перемещения проводника в магнитном поле произволен, то разбиваем все перемещение на отрезки dr:
, где dS=drℓ — площадь, заметаемая проводником при перемещении. Правило Фарадея: величина разности потенциалов, возникающих на концах проводника при его перемещении в магнитном поле прямо пропорциональна скорости изменения магнитного потока.
Если концы проводника замкнуты между собой, то в цепи протекает ток так, если бы проводник являлся источником тока. Тогда по закону Ампера сила, действующая на проводник с током в магнитном поле (правило левой руки) направлена в сторону, противоположную перемещению проводника в магнитном поле, то есть эта сила препятствует перемещению. Тогда:
- разность потенциалов, возникающих на концах проводника, называют ЭДС магнитной индукции.
- поскольку ЭДС вызывает силы, препятствующие движению проводника, то в законе Фарадея ставят знак “минус” (правило Ленца):
3.14. Явление электромагнитной индукции (взаимоиндукции)
В 1831 году Фарадей установил, что если изменять магнитный поток, проходящий через контур, то в этом контуре возникает ЭДС, препятствующая изменению внешнего магнитного поля. Пусть есть контур I, к которому подключен гальванометр, и контур II, к которому подключен резистор, и источник ЭДС.
- силовые линии II проводника пересекают первый контур. Если менять величину тока во II контуре, то меняется B2 , то есть магнитный поток, создаваемый вторым контуром также меняется. И по закону Фарадея в первом контуре возникает ЭДС.
- Удаление или приближение второго контура также вызывает ЭДС в первом.
- Можно поворачивать контура относительно друг друга, чтобы вызвать ЭДС в I контуре.
- Вызвать ЭДС можно также изменением магнитной среды, которая находится между контурами.
Приложение:
- Контуры с током, близко расположенные друг с другом называют связанными.
- Влияние одного контура на другой возможно только, если ток в контурах переменный (принцип трансформатора). Для усиления взаимодействия используют последовательно соединенные контура – соленоиды.
Пусть:
Соленоид 1 содержит N витков, а соленоид, II: N2 витков. S — поперечное сечение соленоида.
Если в соленоиде I изменить величину тока, то в соленоиде II возникает ЭДС, равная:
Если в каждом из контуров соленоида возникает ЭДС, то результирующая ЭДС соленоида будет равна произведению числа витков соленоида на ЭДС одного витка:
то есть: , где L12 — коэффициент взаимной индукции первого соленоида относительно второго.
Если источник неэлектрических сил подключить ко второму соленоиду, а гальванометр к первому, то ЭДС, возникающую в первом соленоиде можно будет рассчитать аналогично:
, где
— коэффициент взаимоиндукции II-ого соленоида относительно первого. Таким образом L21=L12
3.15. Явление самоиндукции
Возьмем один соленоид. Если в таком соленоиде изменять величину тока, то в контуре соленоида возникает ЭДС, стимулирующая магнитное поле, и препятствующая изменению тока в соленоиде.
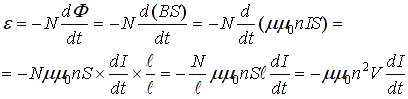
— коэффициент самоиндукции, связывающий ЭДС электромагнитной индукции и ток. Его называют индуктивностью соленоида.
Индуктивность — характеристика соленоида, связывающая скорость изменения тока в соленоиде с препятствующей ей ЭДС и определяемая только геометрическим устройством соленоида.
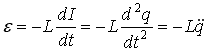
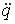
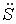
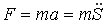
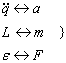
3.16. Вихревые токи или токи Фуко
В связанных контурах для передачи энергии переменного электрического тока из одного участка цепи в другой, часто используются магнитопроводящие среды.
При подаче переменного напряжения (тока) на первый 1 соленоид со второго 2 можно снять переменное напряжение (ток) противоположного направления (закон Фарадея-Ленца) Так как магнитное поле замкнутое, то сердечники делаются сплошными, чтобы избежать потери магнитного поля. Тогда сам сердечник создает замкнутый контур, по которому может протекать электрический ток. Если сопротивление сердечника мало, то по закону Джоуля-Ленца количество теплоты, выделившейся на этом сердечнике, будет велико. То есть . Эта теплота отбирается от энергии переменного электрического тока, подаваемого на соленоид. Для того, чтобы избежать паразитных тепловых потерь, магнитнопроводящие сердечники делаются из специального металла, обладающего большим сопротивлением (углеродистая сталь — пермаллой, ферритовые сплавы).
Если в связанных между собой механических частях какой- либо установки присутствуют электрические цепи с переменным током, то для предотвращения перемещения одной механической части относительно другой( когда их невозможно закрепить жестко) подвижные части делают в виде электрической цепи. ЭДС препятствует изменению магнитного поля, вызываемого движением. Возникающая ЭДС создает собственное магнитное поле, препятствующее движению механической детали. Таким образом, её движение ограничено. Это явление называют током Фуко.
Индуцирование переменного тока и напряжения используется для создания переменных токов и напряжений в местах, недоступных человеку (в вакуумных устройствах, где требуется разогреть какую-либо деталь).
Пропуская переменный ток по наружному соленоиду мы индуцируем электрический ток внутри вакуумного объема и так как соленоид внутри замкнут сам на себя, то энергия тока второго соленоида переходит в тепловую энергию. Такие устройства называют индукционными печами (температура достигает в них ≈1000С).
3.17. Энергия магнитного поля
Как любое поле, магнитное поле обладает энергией. Легче всего исследуется однородное магнитное поле, которое находится в соленоиде.
При замкнутом ключе внутри соленоида накапливается магнитная энергия. Если величину тока не менять в стационарных условиях, то часть тока идет через нагрузку, например, лампочку Л, другая часть через соленоид L.
При выключении ЭДС батареи в момент времени ток, протекающий в соленоиде, уменьшается и вызывает ЭДС электромагнитной индукции, препятствующую этому уменьшению. Эта ЭДС стремиться поддержать ток на нагрузке.
Поэтому величина тока на приборе плавно уменьшиться. Это происходит за счет энергии магнитного поля, накопленной в соленоиде.
Можно записать работу по переносу заряда для поддержания тока в цепи при выключении ключа, которая происходит за счет энергии магнитного поля, запасенной в соленоиде.
а так, как
(Закон Фарадея-Ленца) и dq=Idt,
то — закон сохранения энергии.
Тогда полная энергия магнитного поля:
— полная магнитная энергия, запасенная в соленоиде с индуктивностью L. Аналогична ситуация с включением.
Схема включения цепи с соленоидом. Время релаксации τ — время, необходимое для установления в рабочих цепях режима равновесной (стационарной) работы.
3.18. Плотность энергии магнитного поля
Плотность энергии магнитного поля – количество магнитной энергии в единице объема соленоида: 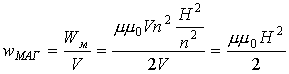
Итак:
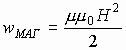
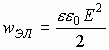
3.19. Единицы измерения магнитных величин
-
- Магнитный момент:
, где
— единичный вектор, нормаль к площади контура, определяющий ее ориентацию в пространстве.
- Магнитная индукция: так как
(см. § 12), то
— тесла.
- Магнитный поток Ф:
.
- Потокосцепление
- Индуктивность — коэффициент, зависящий от геометрических размеров соленоида.
- Магнитный момент:
- Напряженность магнитного поля для витка с током
или для соленоида
.
- Магнитная проницаемость m — показывает, во сколько раз магнитное поле в среде отличается от магнитного поля в вакууме.
— для среды.
— безразмерная.
- Магнитная постоянная
Аналогия: магнитное поле ↔ механика
Аналогия между силой и ЭДС заключается в том, что сила есть вектор и направление его действия в пространстве легко установить, а ЭДС — скаляр, и направление его действия на изменение тока в цепи указывается знаком “-”
3.20. Магнетики. Вещества в магнитном поле
Вещества, способные намагничиваться и влиять на направление вектора магнитной индукции внешнего поля B, называются магнетиками.
Способность намагничиваться — создание собственного магнитного поля в веществе, которое или усиливает, или уменьшает внешнее магнитное поле.
Собственные магнитные свойства вещества определяются электронами, связанными с атомами. Строение атома подразумевает наличие электрона e, вращающегося вокруг ядра. Магнитный момент электрона , то есть каждая орбита электрона в атоме обладает собственным магнитным моментом и создает собственное магнитное поле. В целом в веществе суммарные магнитные моменты электронов в атоме расположены хаотично и их сумма зачастую равна нулю.
Под действием внешнего магнитного поля собственные магнитные поля, созданные электронами, упорядочиваются. Это и есть явление намагниченности. Оно может сохраняться после снятия магнитного поля, а может и исчезать. У ферромагнетиков оно сохраняется, а у диа и парамагнетиков исчезает.
В результате поле равно:
, где каппа
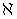
и
— магнитные моменты электронных орбит.
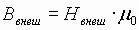
— магнитная проницаемость.
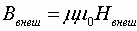
Для разных веществ значение может принимать как положительные, так и отрицательные значения. В большинстве веществ собственные магнитные моменты атомов (молекул) не зависят друг от друга и хаотично расположены в пространстве. Если к такому веществу приложить внешнее поле, то собственный магнитный момент каждого атома стремится, как волчок, выровнять положение оси вращения вдоль силовых линий внешнего поля.
Bвне — индукция внешнего магнитного поля, Pm- собственный магнитный момент атома.
Изменение собственной оси вращения (собственного магнитного момента) относительно вектора магнитной индукции (внешнего поля) называется прецессией.
Собственный механический момент или количество движения Ls (спин)
Механические моменты электронов в атоме могут отличаться только направлением движения по орбите (вдоль и против часовой стрелки).
- Если внешнее магнитное поле затрачивает энергию на прецессию, то её результирующее магнитное поле ослабляется. Такие вещества называют диа–магнетиками:
.
- В некоторых веществах внешнее магнитное поле не затрачивает энергию на прецессию, а разворачивает весь атом так, чтобы его собственное магнитное поле совпадало с внешним магнитным полем. Эти вещества -парамагнетики. Для них
.
Парамагнетики
Стрелками укажем магнитные моменты отдельных атомов.
Ферромагнетики.
Для объяснения ферромагнетизма вводим понятие доменов. Домен — совокупность атомов с одинаковым направлением собственных магнитных полей. Подобные совокупности атомов требуют меньше энергии для образования доменов, т.е. энергетически более выгодны по сравнению с разрозненными атомами. В целом собственное магнитное поле вещества равно нулю. Под действием внешнего магнитного поля домены могут увеличиваться за счет других доменов вплоть до поглощения неориентированных доменов, то есть все пространство вещества заполняется доменами, ориентированными вдоль поля. При снятии внешнего поля обратной переориентации не происходит, так как это энергетически не выгодно. В этом случае магнитная восприимчивость составляет тысячи и десятки тысяч единиц. Оказывается, реакция вещества на воздействие внешнего магнитного поля носит нелинейный характер. Это определяется способностью собственных магнитных моментов переориентироваться во внешнем магнитном поле. Сначала идёт резкое изменение ориентации во внешнем магнитном поле, магнитные моменты ориентируются вдоль силовых линий магнитного поля. Дальнейшее увеличение магнитного поля не изменяет намагниченность, так как все магнитные моменты уже ориентированы вдоль поля. Зависимость результирующего магнитного поля в веществе в целом в зависимости от внешнего поля носит характер гистерезиса.
B1 — остаточная индукция. H1 — коэрцетивная сила.
B1 — в веществе остается собственное магнитное поле без внешнего магнитного поля H1 = 0, (так создаются постоянные магниты).
H1 — внешнее поле, необходимое для снятия собственной намагниченности, B1=0. Эта величина называется коэрцетивная сила.
Анализ петли гистерезиса см. в разделе “Сегнетоэлектрики”. Если коэрцетивная сила велика, то говорят, что ферромагнетик жёсткий, если мала — то мягкий.
3.21. Движение зарядов в магнитном поле
1) Вектор скорости перпендикулярен силовым линиям.
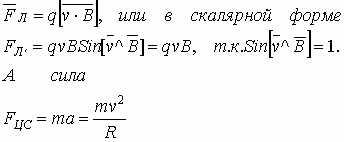
Скорость изменяется только по направлению, но не по величине. Сила Лоренца, действующая на движущуюся частицу в магнитном поле, закручивает траекторию движения в окружность, то есть появляется центростремительное ускорение: значит v изменяется только по направлению, но не по величине. Тогда приравняем
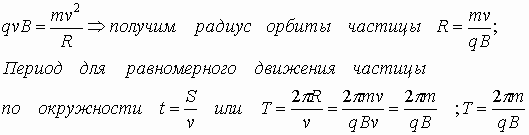
где Т – период обращения заряда по орбите
2) угол между направлением скорости и силовыми линиями не равен 90 градусам.
, 0<α<90
Дальнейший анализ траектории движения частицы относительно вектора скорости аналогичен пункту 1).
Здесь сила Лоренца
. Новой характеристикой здесь является l — шаг спирали.
Приложение:
- если частица движется вдоль силовых линий магнитного поля, то сила Лоренца равна нулю.
- Если частица неподвижна в магнитном поле, то сила Лоренца также равна нулю.
3.22. Уравнение Максвелла. Обобщение теории магнитного поля (обобщение электродинамики)
Имеется замкнутый контур и внешнее магнитное поле, меняющееся во времени. Если внешнее магнитное поле создается соленоидом с током, то изменение магнитного поля через контур произойдет, если
- в соленоид вносим сердечник,
- меняем ток в этом соленоиде,
- изменяем положение соленоида относительно контура.
Тогда в контуре появляется ЭДС по закону Фарадея-Ленца, препятствующая изменению внешнего магнитного поля, то есть стрелка прибора, который можно подключить к контуру, отклоняется, в контуре идет движении зарядов, то есть появляется электрический ток. Так как до включения магнитного поля заряды в проводнике находились в неподвижности, значит после включения поля сила Лоренца не должно действовать на заряды. Откуда же берется ЭДС? Единственным объяснением появления ЭДС в контуре, то есть движения зарядов, является появление электрического поля, сила Кулона которого заставляет заряды двигаться. Напряженность такого поля
Не зная источника внешнего магнитного поля можно записать для ЭДС в контуре
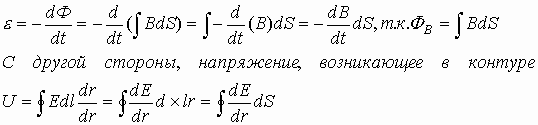
— оператор дифференцирования по координатам (декартовым или полярным). Аналогично
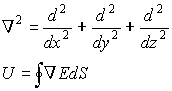
Напряжение, выраженное через законы электростатики, и ЭДС, возникшее в контуре, есть одно и то же. Тогда интегралы равны между собой, а, следовательно, и подинтегральные выражения равны.
. Здесь отображена связь между неоднородным электрическим полем и переменным магнитным.
3.23. Анализ массово-зарядового состояния (q/m) элементарных частиц
С поверхности вещества испаряют часть атомов или молекул. Как правило, при этом такие атомы обладают зарядовыми свойствами. Далее эти атомы ускоряются в электрическом поле E, и движущийся поток атомов пропускают через магнитное поле B. По закону Лоренца эти заряды в магнитном поле отклоняются. Тогда на экране за магнитным полем в разных местах оседают атомы разных зарядов. По степени отклонения атомов от прямолинейного распространения можно судить о заряде атома.
Частицы в магнитном поле отклоняются. Тогда на экране за магнитным полем в разных местах, например:
Заряд q= 1e – в точке 2 на экране.
Заряд q=2e – в точке 1 на экране.
Процесс разделения частиц по зарядам называется сепарированием, а прибор, анализирующий состав этих пучков — масспектрограф.
3.24. Приложение к теореме Остроградского-Гаусса
Для любого вектора a можно записать его поток:
Так как интегрирование и дифференцирование по сути своей противоположные операции, то можно записать, например:
Интегрирование и дифференцирование по одному и тому же параметру по сути взаимно компенсирующие операции. Тогда можно записать для вектора а:
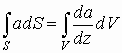
А так же:
Таким образом, можно связать линейный, поверхностный и объемный интегралы, т.е. можно переходить от линейного к поверхностному, и от поверхностного к объёмному интегралу.
Приложение к теореме Остроградского-Гаусса мы используем при рассмотрении уравнений Максвелла.
3.25. I-ое уравнение Максвелла
Итак, мы из предыдущих параграфов (§ 22, 24) получаем закон Фарадея-Ленца:
ЭДС, возникающая в контуре при изменении магнитного поля, регистрируется гальванометром как напряжение на концах проводника контура. Тогда приравняем подинтегральные выражения.
.
Переменное магнитное поле породило неоднородное электрическое поле, которое создало электрический ток, создающий собственное поле, препятствующее (знак “-“) изменению внешнего магнитного поля (закон сохранения энергии). Это и есть I-ое уравнение Максвелла.
3.26. II-ое уравнение Максвелла
Используем соленоид для создания магнитного поля. r- радиус соленоида, l — его длина, N — число витков, n — удельное число витков соленоида. Запишем напряженность соленоида
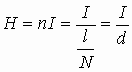
Если предположим, что соленоид намотан в один слой и витки плотно прилегают друг к другу, то — толщина одного витка. Тогда можно считать d, как элемент l, или d=dl.
Продифференцируем левую и правую часть по координатам.
— площадь сечения проводника, из которого сделан соленоид. По определению
, плотность тока
Если внутри соленоида находится среда с μ>1, то магнитное поле в соленоиде усиливается за счет электрического поля, обусловленного протекающим по проводнику током. Так как среда в соленоиде непроводящая, то электрическое поле вызывает в этой среде только смещение зарядов (смотри раздел “диэлектрики”). Тогда плотность тока зарядов проводимости и смещенных зарядов в самом общем случае, когда есть и свободные и связанные заряды
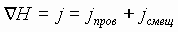
Как и в диэлектриках смещение зарядов вызывается электрической индукцией, а именно . Тогда имеем
— второе уравнение Максвелла, которое говорит, что электрическое поле, которое вызывало в проводнике электрический ток проиндуцировало в среде усиление магнитного поля, то есть сформировало его.
В I уравнении знак “-” означает, что переменное магнитное поле вызывает электрический ток, который генерирует магнитное поле, препятствующее изменению внешнего магнитного поля. Это связанно с законом сохранения энергии. Во II уравнении минус не ставится, так как за направление электрического тока принято движение положительных зарядов, а реально движутся отрицательные.
3.27. III-e уравнение Максвелла
В системе зарядов поток векторов напряженности по теореме Остроградского-Гаусса равен Если заряды распределены произвольно в пространстве, то введем понятие объемная плотность заряда:
Тогда по теореме Гаусса
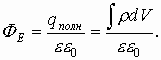
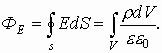
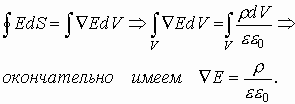
3.28. IV уравнение Максвелла
Если есть соленоид, по которому течет ток, то соленоид формирует магнитное поле. Принцип силовых линий магнитного поля B — замкнутость. Найдем поток векторов B, который по теореме Остроградского есть . Полный поток векторов найдем, замкнув соленоид поверхностью S.
Чтобы посчитать этот поток, мы должны учесть как входящие, так и выходящие через поверхность S силовые линии B магнитного поля. Результатом является компенсация этих линий, то есть общий поток равен нулю, т.к. количество входящих и выходящих линий B через поверхность S одинаково из-за замкнутости линий. Используя приложение к теореме перейдем от поверхностного интеграла к объемному
Отсюда следует, что в объеме, в котором находится соленоид, как источник магнитного поля, нет зарядов. Это IV уравнение Максвелла.
3.29. Анализ III и IV уравнений
Из III уравнения Максвелла следует, что в объеме, из которого исходят силовые линии электрического поля, находятся электрические заряды, а из IV следует, что объем, из которого исходят силовые линии магнитного поля не содержит зарядов магнитного поля.
Это доказательство того, что в природе не существует магнитных зарядов, соответственно, нет потенциала магнитного поля.
Итак, рассмотренные 4 уравнения Максвелла считаются основными, но есть еще три дополнительных.
Эти уравнения соединяют свойства электрических и магнитных полей в вакууме и средах.
Первые два уравнения Максвелла получены из поверхностных интегралов, для которых важно задать направление силовых линий, значит, в уравнениях обязательно отмечается векторность полей.
(I).
(II)
А III и IV уравнения – количественные, то есть скалярные уравнения.
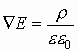
получим
(III).
И наконец (IV).
Система уравнений Максвелла отображает единую теорию электромагнитного поля и показывает, что оно есть единое поле, то есть электрического поля не существует без магнитного, а магнитное поле не существует без электрического. Можно ещё сказать, что переменное магнитное поле порождает неоднородное электрическое, а переменное электрическое поле порождает неоднородное магнитное поле.













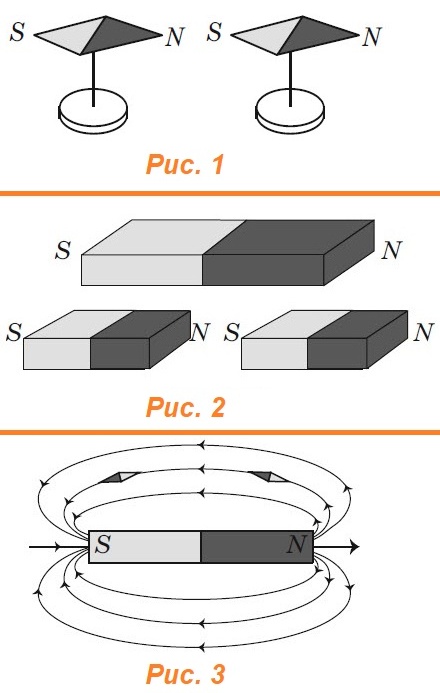
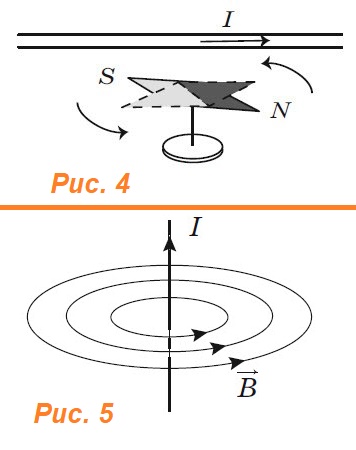
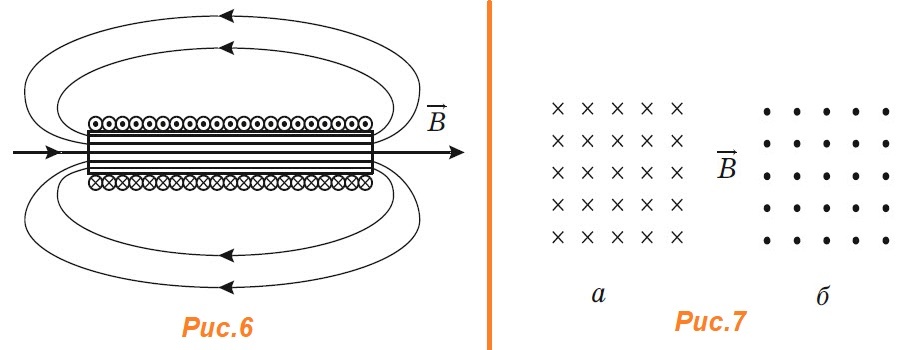
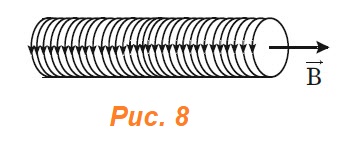
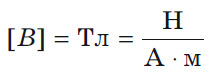
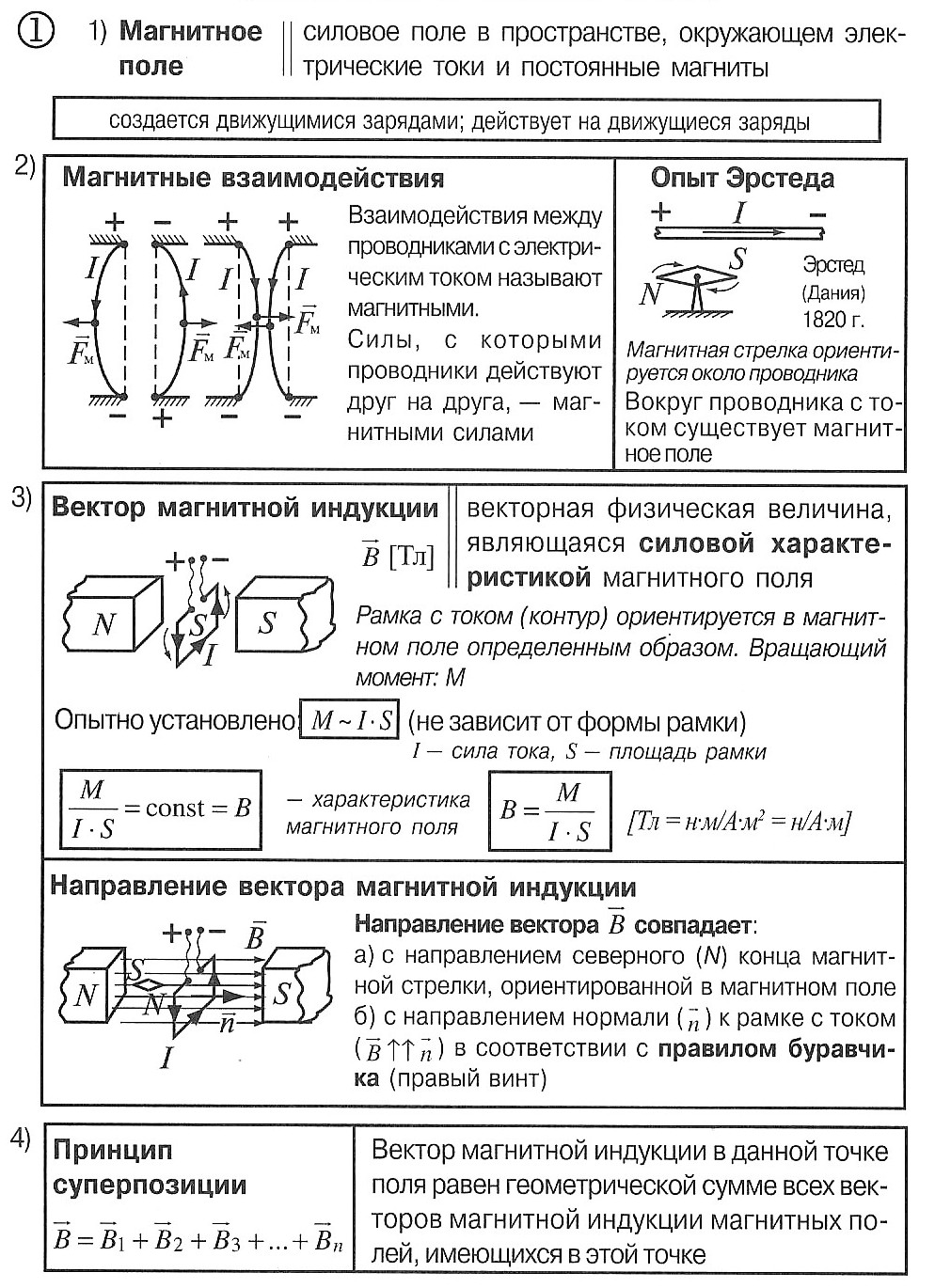
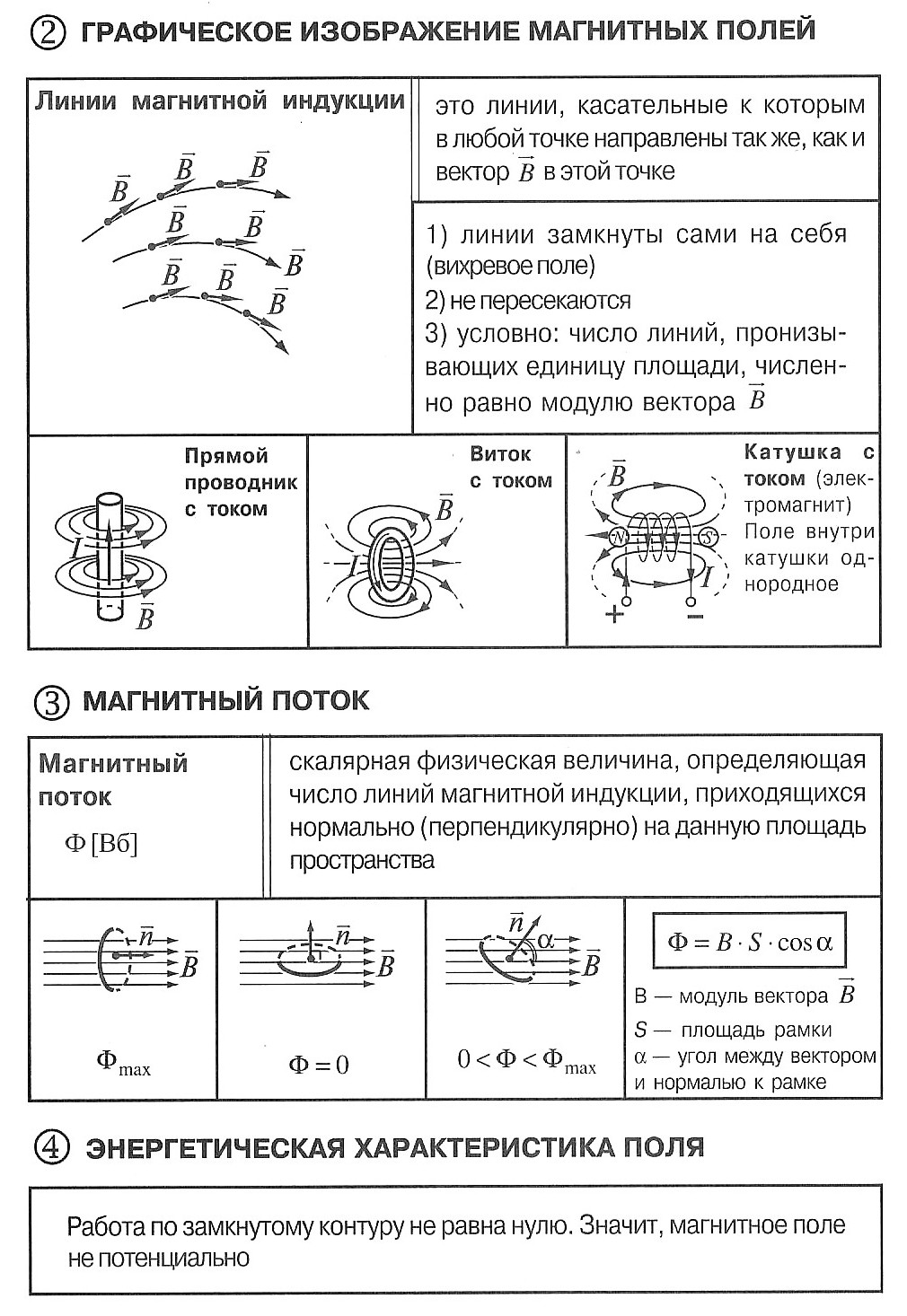
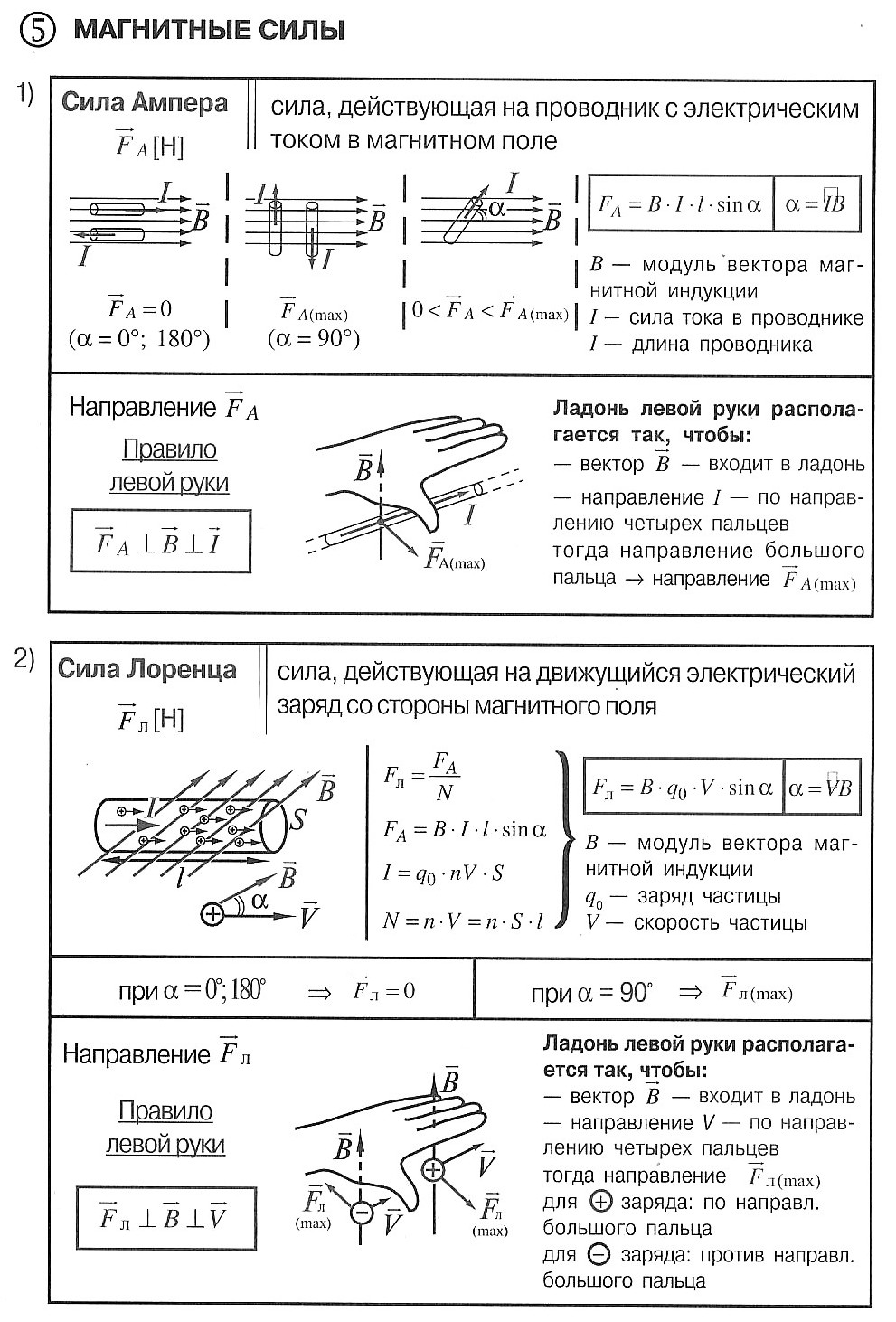

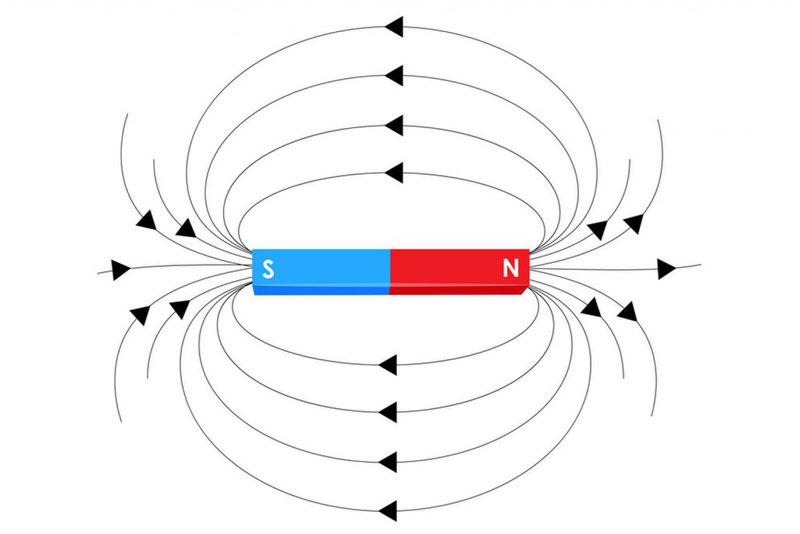
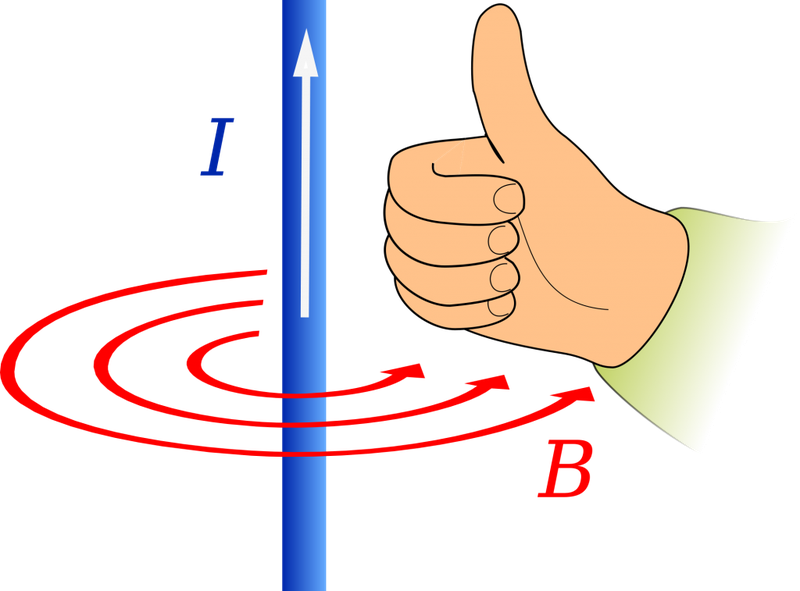
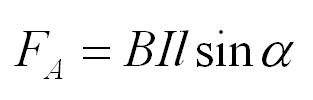
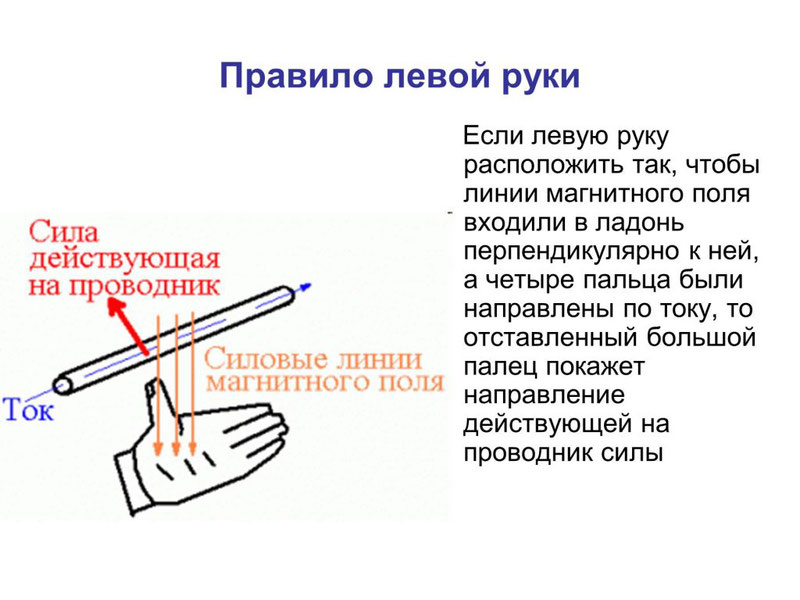
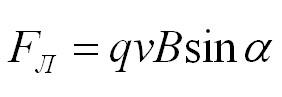
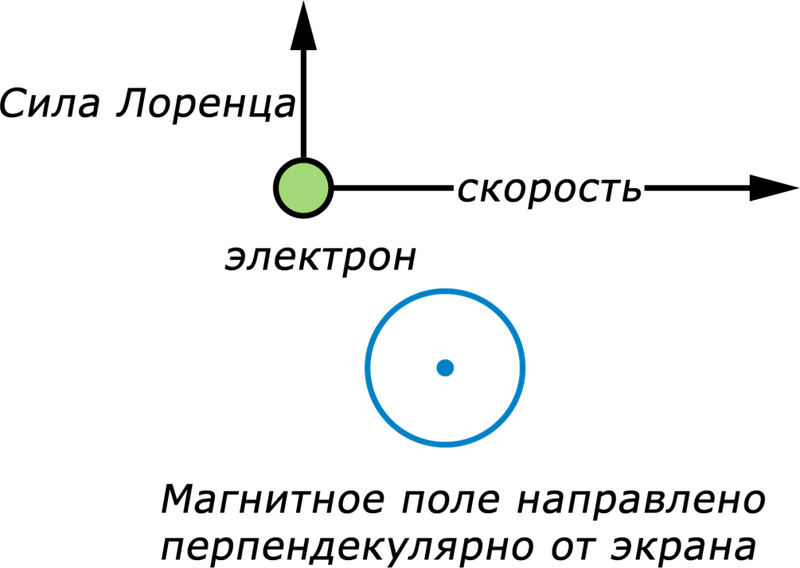
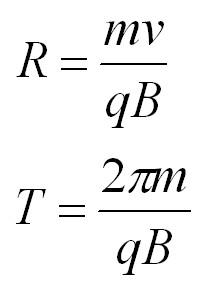
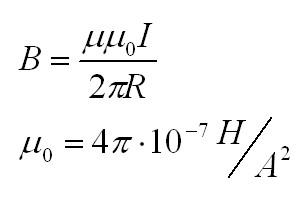
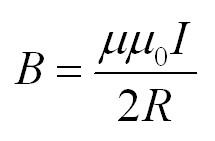
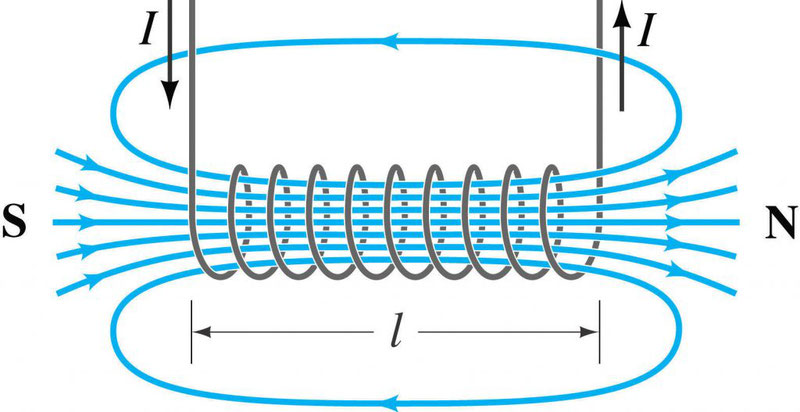
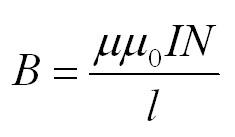
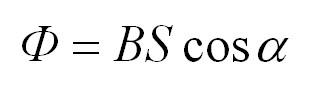
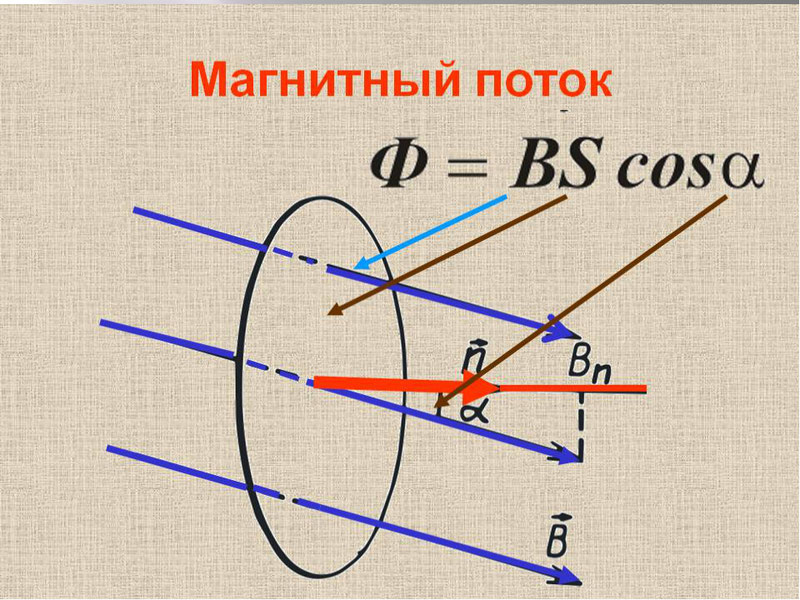
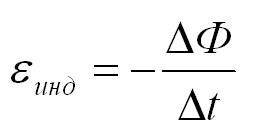
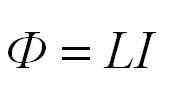
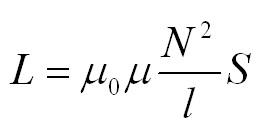
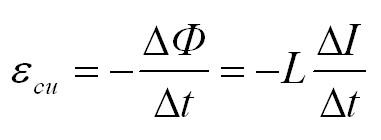
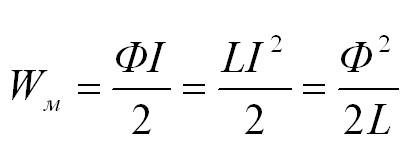
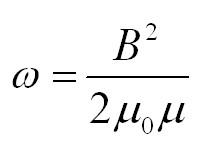






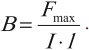
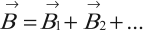
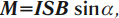
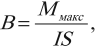
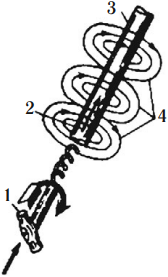
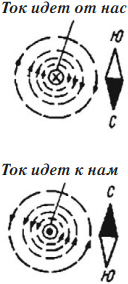
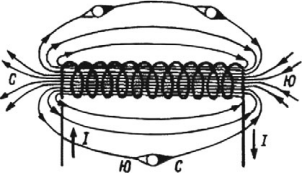
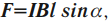
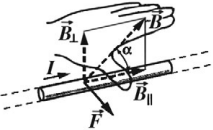
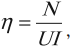
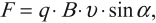
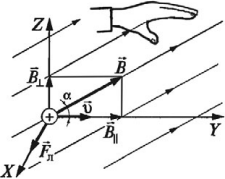
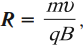
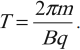
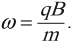
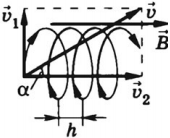

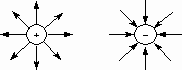
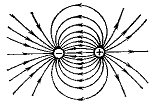
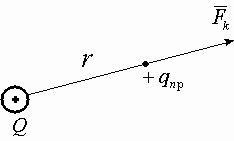
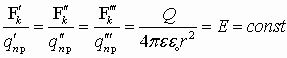
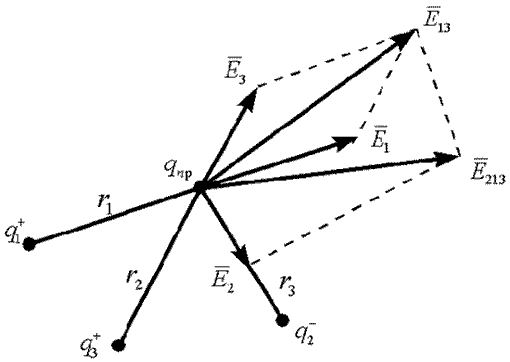
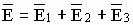
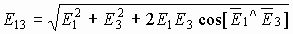
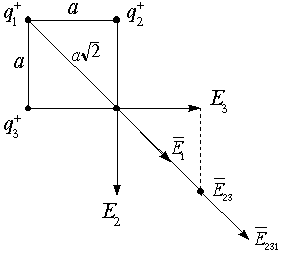
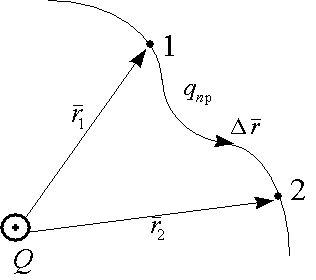
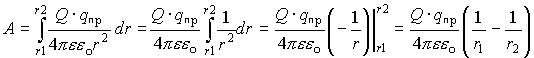
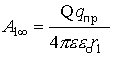
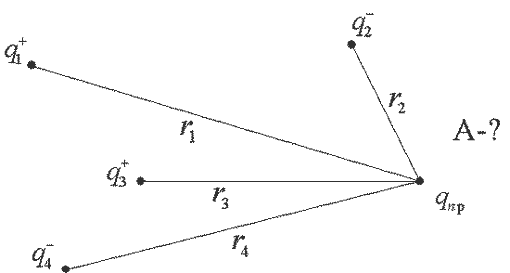
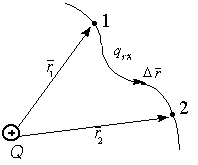
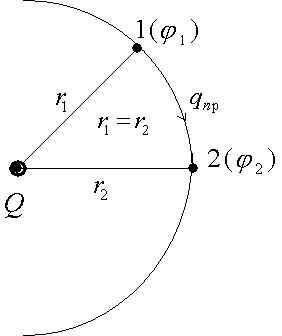
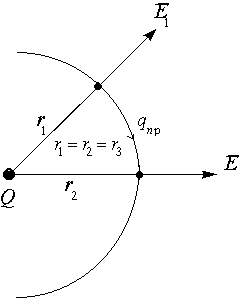
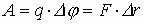
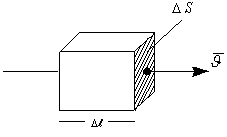
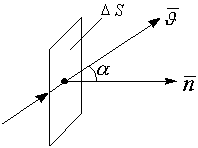
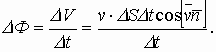
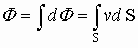
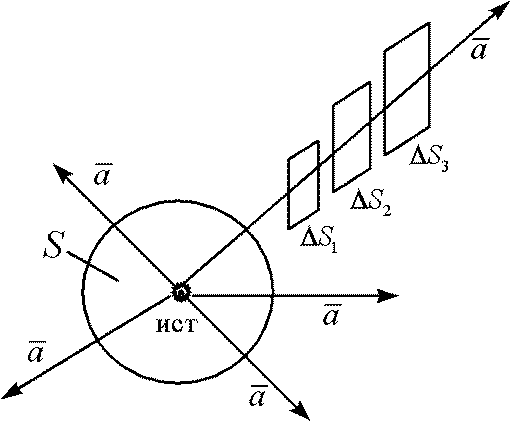
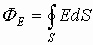
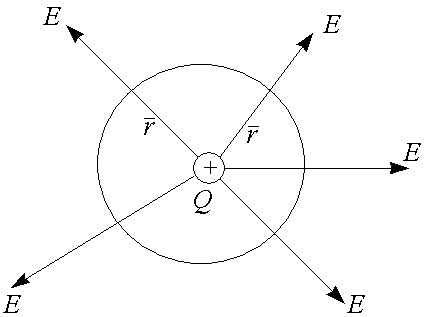
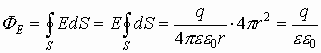
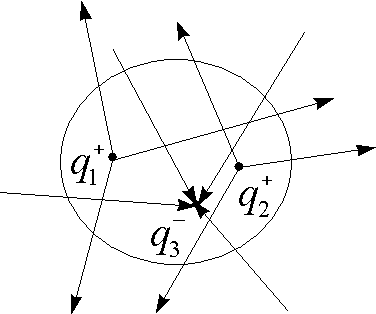
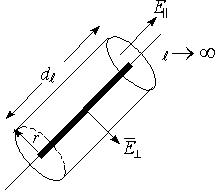
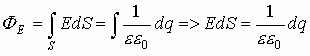
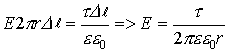
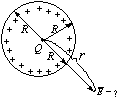
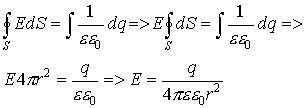
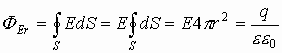
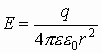
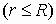
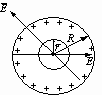
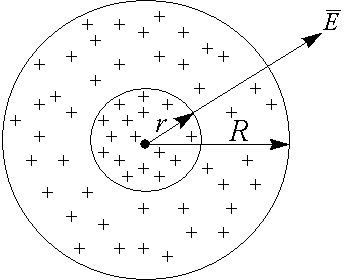
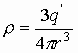
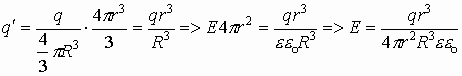
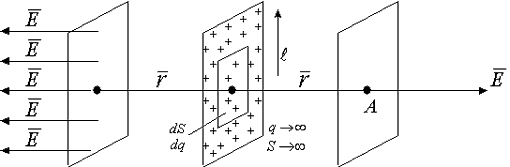
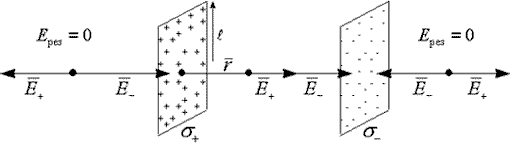
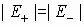
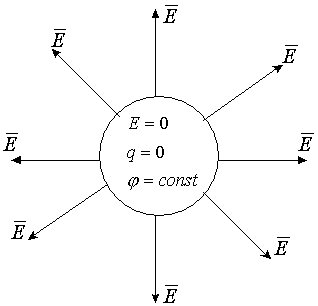
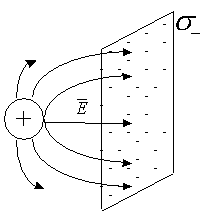
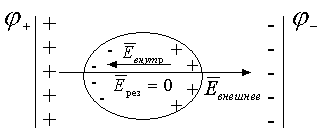

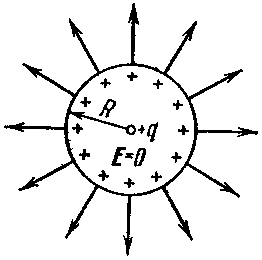
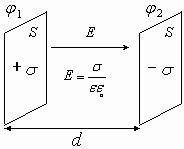
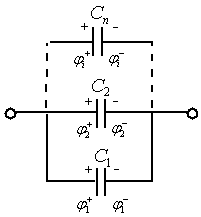
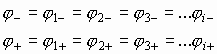
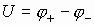
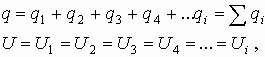
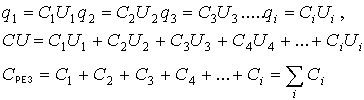
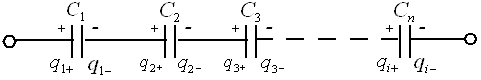
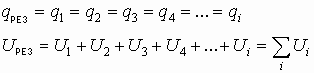
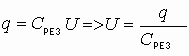
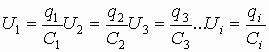
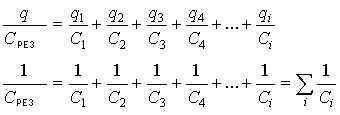
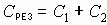
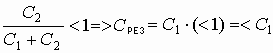

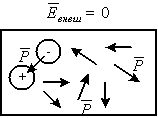
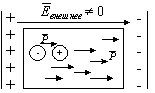
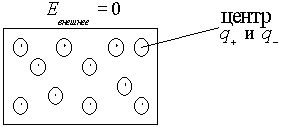
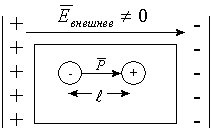
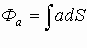
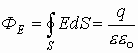
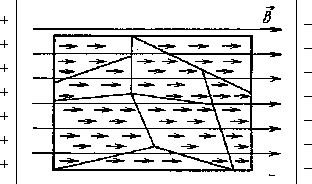
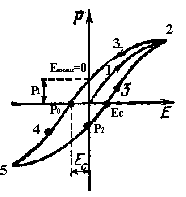
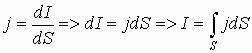
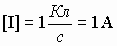
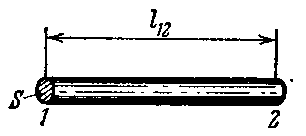
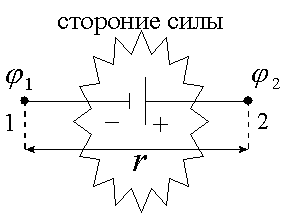
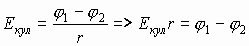
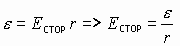

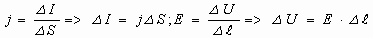
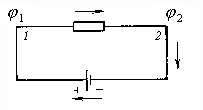
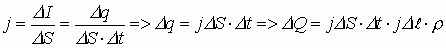
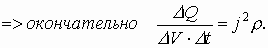
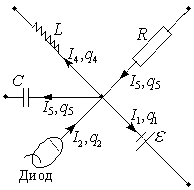
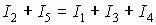
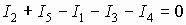
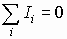
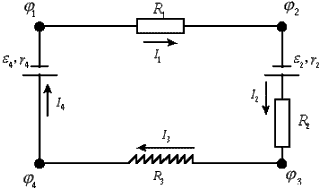
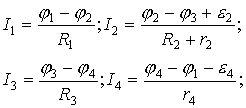
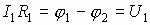
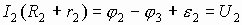
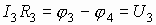
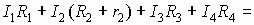
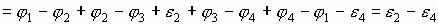
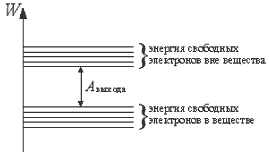
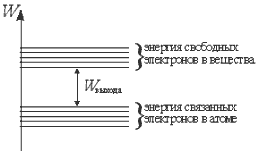
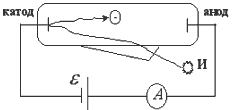
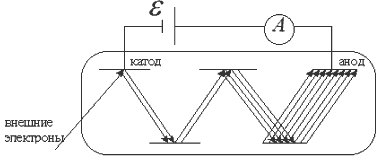
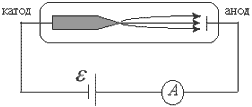
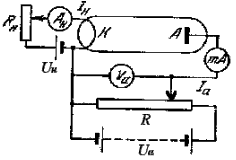
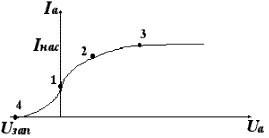
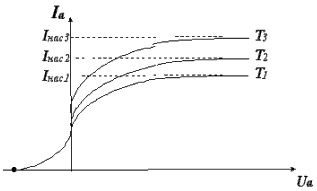
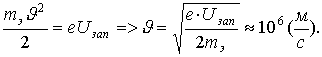
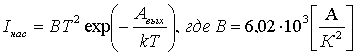
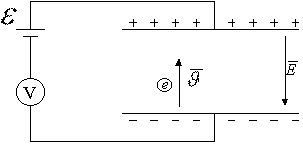
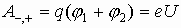
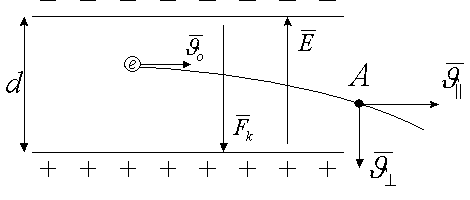
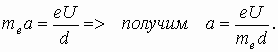
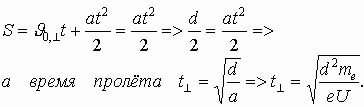
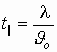
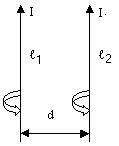
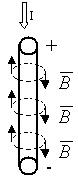
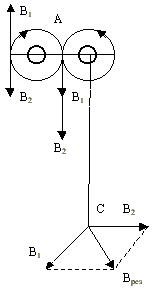
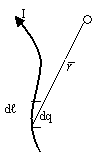
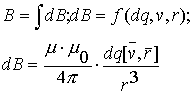
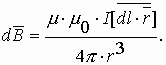
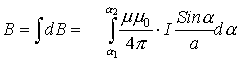
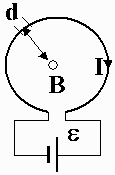
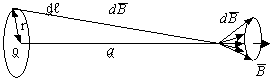
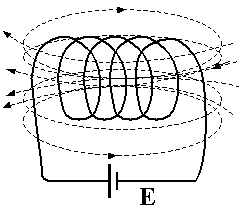
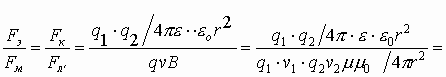
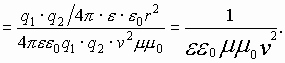
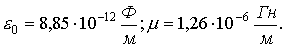
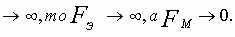
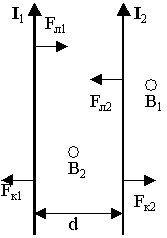
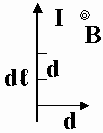
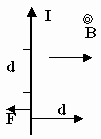
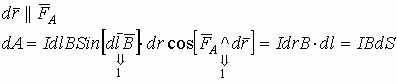
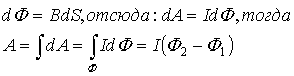
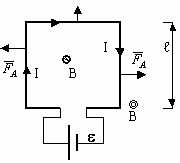
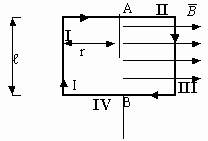
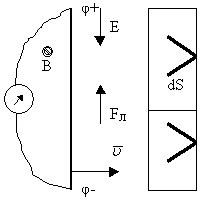
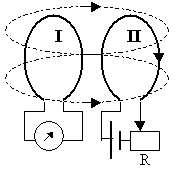
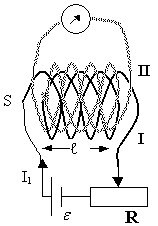
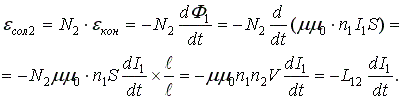
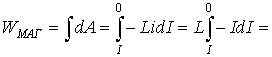
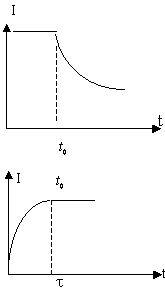
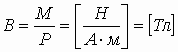 — тесла.
— тесла.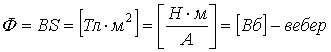 .
.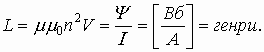
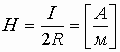 или для соленоида
или для соленоида 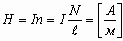 .
.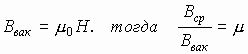 — безразмерная.
— безразмерная.