Места в соревнованиях оценки за экзамен измеряются в шкале - Помощь в подготовке к экзаменам и поступлению

Шкалы измерений

В
спортивной практике наибольшее
распространение получили четыре шкалы
измерений: шкала
наименований, шкала порядка, шкала
интервалов, шкала отношений.
Каждая из них специфична, имеет свое
практическое приложение, способ и
принцип измерения, свой набор математических
процедур. В общем представлении это
показано в таблице.

Шкалы
измерений

Шкала	Основные принципы	Методы статистики	Примеры
Наименований	Установление равенства	Число случаев Мода Корреляция	Нумерация спортсменов в команде Результаты жеребьевки
Порядка	Установление соотношений “больше” или “меньше”	Медиана Ранговая корреляция Ранговые критерии Проверка гипотез	Место, занятое на соревнованиях Результаты ранжирования спортсменов группой экспертов
Интервалов	Установление равенства интервалов	Среднее Стандартное отклонение Корреляция	Календарные даты Суставной угол
Отношений	Установление равенства отношений	Коэффициент вариации Среднее геометрическое	Длина, сила, масса, скорость и т.п.

Шкала
наименований служит
для обнаружения и различения изучаемых
объектов за счет введения и присвоения
ярлыков. Ярлыки, для удобства контроля
за объектами, выражаются через числа.
Например, нумерация игроков в баскетболе,
футболе и т.п. Здесь цифровые значения
не имеют строго порядка и могут меняться
местами. В шкале наименований нет
отношений типа “больше – меньше”, но
это не значит, что ее нельзя считать
шкалой измерения. Имея некоторые
ограничения в использовании, шкала
наименований незаменима, например, при
подсчете частоты технических (или
других) действий каждым спортсменом за
период соревнования (тайма, матча и
т.п.).

Шкала
порядка
называется ранговой или неметрической.
Шкала измерения может не иметь одинаковых
интервалов между рангами. Эта шкала
позволяет установить равенство или
неравенство измеряемых объектов, а
также определить характер неравенства
в виде суждений: “больше-меньше”,
“лучше-хуже” и т.п. С помощь шкалы
порядка можно измерять не только
количественные, но и качественные
показатели. Наибольшее распространение
эти шкалы получили распространение в
педагогике, психологии, социологии. В
спортивной практике шкала порядка
применяется для установления занятого
места в соревнованиях, при оценке
физической подготовленности, предпочтений
технических и тактических действий
спортсменом, используя ранговые критерии.

Шкала
интервалов отличается
строгой упорядоченностью чисел и
определенными интервалами между рангами.
В этой шкале нулевая точка выбирается
произвольно. Например, при измерении
угла в суставе точной отсчета может
быть нуль или любое начальное значение
в градусах, также как при измерении
температуры, потенциальной энергии
поднятого груза может произвольно
определяться начальная точка. Использование
шкалы интервалов дает ответ на вопрос
“на сколько больше или меньше?”.

Шкала
отношений отличается
строгой определенностью нулевой точки.
В спорте по этой шкале измеряют расстояние,
силу, скорость и многие другие переменные.
Универсальность шкалы отношений
заключается в возможности измерения
разности чисел, отсчитанных по шкале
интервалов. Измеряя какую-либо величину
можно определить ее отношение к
соответствующей единице измерения
(например, отношение массы штанги к
массе тела, длина прыжка к длине сегмента
тела и т.п.).

1 Укажите пример для шкалы наименований?	Результаты жеребьевки Результаты ранжирования спортсменов группой экспертовСуставной уголДлина, сила, масса, скорость и т.п.
2 Укажите пример для шкалы порядка?	Результаты жеребьевки Результаты ранжирования спортсменов группой экспертовСуставной уголДлина, сила, масса, скорость и т.п.
3 Укажите пример для шкалы интервалов?	Результаты жеребьевки Результаты ранжирования спортсменов группой экспертовСуставной уголДлина, сила, масса, скорость и т.п.
4 Укажите пример для шкалы отношений?	Результаты жеребьевки Результаты ранжирования спортсменов группой экспертовСуставной уголДлина, сила, масса, скорость и т.п.

ЕДИНИЦЫ
ИЗМЕРЕНИЙ

Для
сравнения результатов измерения, они
должны быть выражены в одних и тех же
единицах. Первая единая метрическая
система мер (иначе называют, десятичная
система мер) разработана в конце XVIII в.
В последующем, более совершенная, была
принята Международная система единиц
– СИ
(от начальных слов System International). СИ
в настоящее время включает семь не
зависимых друг от друга основных
единиц, из которых в качестве производных
выводят (путем арифметических действий)
единицы остальных физических величин.
Например, единица длины (метр) и единица
времени (секунда) -– основные единицы,
а единицы скорости (метр в секунду) –
производная.

Основные
и некоторые производные единицы СИ

Наименование величин	Единицы измерения	Сокращенные обозначения	Размер единицы
русские	международные

Основные
единицы

Длина	Метр	м	m
Масса	Килограмм	кг	kg
Время	Секунда	с	s
Сила электрического тока	Ампер	а	A
Термодинамическая температура	градус Кельвина	^оК	^оК
Количество вещества	моль	моль	mol
Сила света	кандела	св	cd

Производные
единицы

Площадь	Квадратный метр	м²	m²	(1 м²)
Частота	Герц	гц	Hz	1 : (1 с)
Ускорение	метр на секунду в квадрате	м/с²	m/s²	(1м) : (1/с²)
Энергия	джоуль	дж	J	(1 н) * (1 м)
Мощность	ватт	вт	W	(1 дж) : (1 с)

Все
производные величины имеют свои
размерности. Размерностью
называется выражение, связывающее
производную величину с основными
величинами системы при коэффициенте
пропорциональности равном единице.
Например, размерность длины – L,
размерность времени – T; отсюда размерность
скорости равна L/T = L * T^-1,
а размерность ускорения равна L * T^-2.

Помимо
единиц измерения, входящих в систему
СИ, есть также внесистемные
единицы
(час, минута, лошадиная сила, калория и
др.), которые часто применяются для
удобства. Эти единицы измерения могут
быть построены из основных единиц
системы (построенных по десятичному
принципу) или вообще не иметь связей с
единицами установленных систем (например,
калория, миллиметры ртутного столба и
др.)

1 Единицы измерения, величины которых равны специальным образцам-эталонам?	Внесистемные единицы Основные единицыПроизводные единицы
2 Единицы измерения, полученные в результате арифметических преобразований?	Внесистемные единицы Основные единицыПроизводные единицы
3 Какие это единицы измерения: м, кГ, с, а ?	Внесистемные единицы Основные единицыПроизводные единицы
4 Какие это единицы измерения: см/с², кГм, дж, в, м³ ?	Внесистемные единицы Основные единицыПроизводные единицы
5 Какие это единицы измерения: кал, час, л.с. ?	Внесистемные единицы Основные единицыПроизводные единицы
6 Какая система единиц в настоящее время является общепринятой?	СГС МКСССИ
7 Единицы измерения массы?	Дж ВткГкГмН
8 Единицы измерения силы?	Дж ВткГкГмН
9 Единицы измерения работы?	Дж ВткГкГмН
10 Единицы измерения мощности?	Дж ВткГкГмН
11 Единицы измерения энергии?	Дж ВткГкГмН

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Любая система содержит очень много различной информации. Конечно же, не вся она нам нужна, но ту, которая нам нужна, надо как-то измерить и преобразовать. Для этого информации нужно предать какую-нибудь форму, то есть перевести её в данные. Например, общую информацию о том, что потребителям нравится наша продукция, и они согласны покупать её в большем количестве, можно формализовать, проведя исследования и дав оценку удовлетворённости покупателей. В результате этого мы получим данные, с которыми можно уже работать и на основе которых можно принимать решение.

Во время такого преобразования исследователь явно или неявно выбирает шкалу, в которой он будет измерять данные. Существует много различных классификаций шкал, и даже есть специальный раздел математики, изучающий шкалы и операции с ними — теория измерений. Не вдаваясь в детали это дисциплины, рассмотрим то, что может нам пригодиться в прогнозировании.

Принято считать, что любая шкала может обладать следующими характеристиками:

описание,
порядок,
расстояние,
естественная точка отсчёта,
естественная единица измерения.

Последняя характеристика обычно опускается, так как для целей исследования особо полезной информации не несёт. С точки зрения прогнозирования выделение следующих четырёх видов шкал (упорядоченных по уровню) на основе первых четырёх характеристик вполне достаточно для использования по максимуму различных математических и не математических методов:

1. Номинальная шкала

Шкала, в которой есть только характеристика «описание». В ней нет естественного упорядочения, нет расстояния между элементами и тем более нет естественной точки отсчёта. С данными, измеренными в номинальной шкале возможна только одна операция — сравнение в форме «равно» или «неравно». То есть обладает ли объект указанным свойством или нет.

Пример (шутливый). Туристы бывают:

белые,
китайцы,
русские,
женщины,
другие.

Из-за ограниченности номинальной шкалы, практически всё, что можно сделать с данными, измеренными в ней — это посмотреть на количество объектов, имеющих указанные признаки. Например, мы можем понять, сколько в нашем распоряжении оказалось китайских туристов, какой процент от всех туристов они составляют. Если в нашем распоряжении несколько величин, измеренных в номинальной шкале, мы можем, например, использовать коэффициент сопряжённости, для того, чтобы оценить, есть ли связь в выборе признака в одной шкале с выбором признака в другой.

Для целей анализа номинальную шкалу бывает удобно трансформировать в бинарную, в которой «1» соответствует наличию, а «0» — отсутствию свойства. В случае с нашими туристами мы получим соответственно 5 новых переменных, измеренных в такой бинарной шкале.

2. Порядковая (ранговая) шкала

Это уже более сложная шкала, в ней появляется вторая характеристика — «порядок». Данные, измеренные в этой шкале можно сравнить и упорядочить, однако сказать насколько (и уж тем более во сколько раз) одна величина больше другой нельзя. То есть к операциям с данными, в этой шкале добавляется «больше» и «меньше».

Пример. Туристы бывают:

грустные,
нейтральные,
весёлые.

В этом примере, как видим, туристы упорядочены по настроению, но при этом нет возможности сказать, насколько один может быть веселее другого. К порядковой шкале будет относиться даже шкала, которая на первый взгляд не выглядит как порядковая.

Пример. Туристы бывают:

от 10 до 15 килограмм,
от 15 до 20 килограмм,
от 20 до 100 килограмм,
больше 100 килограмм.

Измерить расстояние между элементами в такой шкале не представляется возможным, поэтому она порядковая.

Точно так же оценки за экзамен измеряются в порядковой шкале: разница между 5 и 3 формально равна двум, но при этом не имеет смысла, так как в этой шкале двойка — это просто ещё одна оценка. Если по курсу вначале получить 3,а потом — 2, то пятёрки не получится.

В порядковой шкале можно уже использовать некоторые базовые статистические инструменты. Например, можно оценить моду, для того, чтобы понять, туристы какого веса чаще встречаются в выборке. Можно так же рассчитать ранговый коэффициент корреляции (Спирмена либо Кендалла), который может показать, есть ли статистическая линейная связь между весом туристов и их настроением. Расчёт средней величины (а так же медианы и стандартного отклонения) в порядковой шкале возможен, но в этом случае получаемое значение будет просто добавлять в нашу шкалу новые значения, но не более того. Например, если в шкале оценок за экзамены появилась «4.5» (как средняя между «4» и «5»), то это значение просто расширяет нашу шкалу, которая теперь будет содержать: «2», «3», «4», «4.5» и «5». Расстояние между «4» и «4.5», а так же «4.5» и «5» всё так же невозможно адекватно измерить.

3. Интервальная шкала

В интервальной шкале добавляется ещё одна характеристика — расстояние, но в ней всё так же отсутствует естественная точка отсчёта. Приемлемые операции в этой шкале (плюс к тем, которые уже были) — сложение и вычитание. Однако операции деления и умножения в этой шкале бессмысленны.

Пример. Температура туриста.

Если температура одного туриста — 36.6ºC, а другого — 18.3ºC, то мы можем сказать, что второй турист холоднее первого на 18.3ºC, но сказать, что первый турист горячее второго в два раза нельзя — это не имеет смысла. А всё потому что 0ºC — это не естественная точка отсчёта, а искусственная, привязанная к температуре замерзания воды. Если в качестве точки отсчёта в этой шкале взять, например, абсолютный ноль, то этот бессмысленный эффект «первый в два раза горячее второго» пропадёт.

В интервальной шкале имеют смысл и средняя величина, и медиана, и стандартное отклонение, и квантили распределения. Если очень хочется, то можно рассчитать и коэффициент корреляции Пирсона, который покажет, есть ли линейная связь между показателями.

4. Абсолютная шкала.

Это последний тип шкалы, и он имеет все рассмотренные нами характеристики. Наличие естественной точки отсчёта означает, что когда показатель принимает значение «0», то это говорит о том, что исследуемое свойство у объекта просто отсутствует. В этой шкале возможны все математические операции.

Пример. Количество туристов в комнате.

Думаю, комментарии к этому примеру излишни.

У шкал есть одно удобное свойство: любые данные, измеренные в шкале более высокого уровня, можно легко преобразовать в данные, измеренные в шкале более низкого уровня.
Например, количество туристов в комнате можно перевести в интервальную шкалу, если это количество центрировать относительно какой-нибудь величины (то есть фактически избавиться от естественной точки отсчёта). В таком случае положительное число будет означать превышение установленного лимита, а отрицательные — занижение. Ноль в таком случае будет соответствовать искусственной точке, в которой количество соответствует выбранному нами эталону.

Если провести ещё одну свёртку данных и избавиться от расстояний между значениями, то можно получить порядковую шкалу, например, следующего вида:

менее 5 туристов,
от 5 до 10 туристов,
более 10 туристов.

Продолжая упрощения, избавляясь от порядка, можно предложить простейшую номинальную шкалу:

5 туристов,
не 5 туристов.

Очевидно, что обратное преобразование невозможно. Если мы изначально собирали данные в номинальной шкале, то получить из них данные, измеренные в шкале более высокого уровня, в принципе невозможно.

И последнее. В случае, если оказывается нужно оценить связь между показателями, измеренными в разных шкалах, нужно использовать коэффициенты, предназначенные для шкал более низкого уровня. Например, для определения связи настроения туриста с его температурой стоит обратиться к ранговому коэффициенту корреляции.

Источник

Шкала отношений. Есть виды спорта, где результат спортсмена определяется только местом, занятым на соревнованиях (например

Шкала интервалов

Шкала порядка

Есть виды спорта, где результат спортсмена определяется только местом, занятым на соревнованиях (например, единоборства). После таких соревнований ясно, кто из спортсменов сильнее, а кто слабее. Но насколько сильнее или слабее, сказать нельзя. Если три спортсмена заняли соответственно первое, второе и третье места, то каковы их различия в спортивном мастерстве, остается неясным: второй спортсмен может быть почти равен первому, а может быть существенно слабее его и быть почти одинаковым с третьим. Места, занимаемые в шкале порядка, называются рангами, а сама шкала называется ранговой или неметрической. В такой шкале составляющие ее числа упорядочены по рангам (т.е. занимаемым местам), но интервалы между ними точно измерить нельзя. В отличие от шкалы наименований шкала порядка позволяет не только установить факт равенства или неравенства измеряемых объектов, но и определить характер неравенства в виде суждений: «больше — меньше», «лучше — хуже» и т.п.

С помощью шкал порядка можно измерять качественные, не имеющие строгой количественной меры, показатели. Особенно широко эти шкалы используются в гуманитарных науках: педагогике, психологии, социологии. К рангам шкалы порядка можно применять большее число математических операций, чем к числам шкалы наименований.

Это такая шкала, в которой числа не только упорядочены по рангам, но и разделены определенными интервалами. Особенность, отличающая ее от описываемой дальше шкалы отношений, состоит в том, что нулевая точка выбирается произвольно. Примерами могут быть календарное время (начало летоисчисления в разных календарях устанавливалось по случайным причинам), суставной угол (угол в локтевом суставе при полном разгибании предплечья может приниматься равным либо нулю, либо 180о), температура, потенциальная энергия поднятого груза, потенциал электрического поля и др.
Результаты измерений по шкале интервалов можно обрабатывать всеми математическими методами, кроме вычисления отношений. Данные шкалы интервалов дают ответ на вопрос «на сколько больше?», но не позволяют утверждать, что одно значение измеренной величины во столько-то раз больше или меньше другого. Например, если температура повысилась с 10о до 20о по Цельсию, то нельзя сказать, что стало в два раза теплее.

В спорте по шкале отношений измеряют расстояние, силу, скорость и десятки других переменных. По шкале отношений измеряют и те величины, которые образуются как разности чисел, отсчитанных по шкале интервалов. Так, календарное время отсчитывается по шкале интервалов, а интервалы времени — по шкале отношений.

При использовании шкалы отношений (и только в этом случае!) измерение какой-либо величины сводится к экспериментальному определению отношения этой величины к другой подобной, принятой за единицу. Измеряя длину прыжка, мы узнаем во сколько раз эта длина больше длины другого тела, принятого за единицу длины (метровой линейки в частном случае); взвешивая штангу, определяем отношение ее массы к массе другого тела — единичной гири «килограмма» и т.п. Если ограничиться только применением шкал отношений, то можно дать другое (более узкое, частное) определение измерению: измерить какую-либо величину — значит найти опытным путем ее отношение к соответствующей единице измерения.

В таблице 3 приведены сводные сведения о шкалах измерения.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Ранговая корреляция

Наряду с линейным коэффициентом корреляции для измерения тесноты связи между двумя коррелируемыми признаками часто используются менее точные, но более простые по расчету коэффициенты корреляции рангов (или ранговые коэффициенты корреляции) Спирмена и Кендалла. Оба показателя, названные именами английских ученых, предложивших эти коэффициенты, основаны на корреляции не самих значений коррелируемых признаков, а их рангов.

Пусть объекты генеральной совокупности обладают двумя качественными признаками, и выборка объема п содержит независимые объекты, которые будем располагать (ранжировать) в порядке ухудшения качества. Для оценки степени связи признаков вводят коэффициенты ранговой корреляции Спирмена и Кендалла.

Коэффициент корреляции Кендалла (/*) вычисляется по формуле:

где R = R_f +r₂ + „. + д_и_₁ и R:.— ЧИСЛО у_м у. У„, больших у., /7— объем выборки, а выборка X расположена в порядке возрастания рангов.

Определим степень связи итогов чемпионата России по баскетболу для 8 команд в суперлиге по итогам сезонов 2008 и 2009 гг.

и между итогами чемпионатов двух последних лет существует сильная прямая связь.

Рассмотрим теперь выборочный коэффициент корреляции Спирмена, вычисляемый по формуле:

где dj = Xj — y_t (разность соответствующих рангов). Предпочтение в дальнейшем отдаем коэффициенту Спирмена, поскольку он дает более точный результат.

Заметим, что при равных показателях у нескольких участников им присваивается один общий ранг, равный среднему арифметическому соответствующих возможных мест.

При наличии одинаковых рангов рассчитываются поправки:

где а, b — объем каждой группы одинаковых рангов в ранговых рядах А и В; и в этом случае коэффициент ранговой корреляции Спирмена рассчитывается по формуле

Для проверки значимости отличия коэффициента корреляции г_х от нуля находится г_Хкр(а) и проводится его сравнение с г,.

Установим степень связи между стоимостью сборных команд мира и их спортивными достижениями.

Сколько стоят сборные-участницы ЕВРО-2008

Ранг — место на ЧЕ- 2008

По данным сайта transfcrmarkt.de; Советский спорт. Футбол. № 23 (210). С. 39.

и существует средняя связь между стоимостью сборных команд и местами, занятыми ими на ЧЕ-2008. Проверим на значимость коэффициент корреляции:

|#; | = 0,55 >0,47 = ^, то есть в нашем случае коэффициент значим, и корреляция достоверно отличается от 0.

Удобным и наглядным способом представления информации при наличии более двух переменных служат корреляционные матрицы. Покажем это на следующем примере. По результатам соревнований три арбитра оценили мастерство 10 фигуристов, получивших три последовательности рангов:

Найдем двух арбитров, оценки которых наиболее согласуются, и построим матрицу ранговой корреляции Спирмена.

рангов арбитров А и В.

аналогично находим, что r_n = 1—= 0,61 и /• = 1—= 0,15

13 9 10 1 1 23 9 10 1 1

Представим полученный результат в виде матрицы ранговой корреляции Спирмена, которая выглядит следующим образом

Из корреляционной матрицы видно, что коэффициент Г|з = 0,61 является максимальным и, следовательно, оценки арбитров А и С наиболее согласуются.

При числе ранжируемых признаков более двух для тесноты связи можно применить множественный коэффициент ранговой корреляции или, иначе говоря, коэффициент конкордации, предложенный М. Кендэлом и Б. Смитом. Он вычисляется по формуле:

где S — сумма квадратов отклонений суммы т рангов от их средней величины,

т — число ранжируемых признаков, п — число наблюдений (количество команд).

Эта формула применяется в тех случаях, когда ранги по каждому признаку не повторяются. Если имеются связанные ранги, то коэффициент конкордации рассчитывается с учетом числа таких повторяющихся (связанных) рангов по каждому фактору:

где t — число одинаковых рангов по каждому признаку.

В обозначенных формулах главное вычисление сводится к нахождению 5, которую можно найти двумя способами. Обозначив через R,j ранг /-ого фактора у j-й единицы, ранжируем каждый из w-факторов, а затем находим сумму рангов по каждой строке и общую сумму.

Коэффициент конкордации W принимает значения от О до 1. Считаем, что если 0 1

Аргументы и факты. № 24 (1441). Июнь. 2008. С. 34.

Таким образом, число футболистов сборных разных стран стабильно и не зависит от выступления их в каком-то определенном чемпионате.

=- (при отсутствии связанных рангов)

или Хфвкт =-=;—з-( П Р И наличии связанных рангов).

Фактическое значение сравнивается с табличным,

соответствующим принятому уровню значимости а (0,01 или 0,05, или 0,1) и числу степеней свободы k = n-1.

1 то коэффициент W существенен на уровне значимости а.

Коэффициент конкордации особенно часто используется в экспертных оценках, чтобы определить степень согласованности мнений экспертов о важности того или иного оцениваемого показателя. Сложные задачи приходится решать и при комплектовании команд в спортивных играх. Здесь наряду с индивидуальными возможностями игроков на отбор в команду влияет принятый командой тактический вариант, особенности тактики и техники противника. Не менее важным является умение каждого игрока реально оценивать свои возможности и возможности партнеров, подчинять стремление к достижению личного успеха интересам команды. Согласованность общих усилий предлагается оценивать через коэффициент конкордации, который будет полезен и при нахождении связи сразу между несколькими спортивными показателями или по одному показателю за несколько лет.

Источник

Спортивная метрология: тесты и методы измерений

Содержание

ОСНОВЫ СПОРТИВНОЙ МЕТРОЛОГИИ [ править | править код ]

Введение в предмет спортивной метрологии [ править | править код ]

Основы метрологии комплексного контроля [ править | править код ]

Подготовка спортсмена представляет собой управляемый процесс. Важнейшим ее атрибутом является обратная связь. Основу её содержания составляет комплексный контроль, который даёт тренерам возможность получать объективную информацию о проделанной работе и тех функциональных сдвигах, которые она вызвала. Это позволяет вносить необходимые коррективы в тренировочный процесс.

Комплексный контроль включает педагогический, медико-биологический и психологический разделы. Эффективный процесс подготовки возможен лишь при комплексном использовании всех разделов контроля.

Управление процессом подготовки спортсменов [ править | править код ]

Управление процессом подготовки спортсменов включает пять этапов [1] [2] :

Специалисты в области хоккея получают большой объём субъективной информации о подготовленности игроков в ходе тренировочной и соревновательной деятельности. Несомненно, тренерский штаб нуждается и в объективной информации об отдельных сторонах подготовленности, которую можно получить только в специально созданных стандартных условиях.

Эта задача может быть решена применением программы тестирования, состоящей из минимально возможного количества тестов, позволяющих получить максимум полезной и всесторонней информации.

Виды контроля [ править | править код ]

Основными видами педагогического контроля являются [1] [2] [3] [4] [5] :

«По содержанию и направленности различают следующие виды контроля:

Основы теории измерений [ править | править код ]

Шкалы измерений [ править | править код ]

Существует четыре основные шкалы измерений:

Таблица 1. Характеристики и примеры шкал измерений [1]

Объекты сгруппированы, а группы обозначены номерами. То, что номер одной группы больше или меньше другой, еще ничего не говорит об их свойствах, за исключением того, что они различаются

Тетрахорические и полихорические коэффициенты корреляции

Номер спортсмена Амплуа и т.д.

Числа, присвоенные объектам, отражают количество свойства, принадлежащего им. Возможно установление соотношения «больше» или «меньше»

Ранговая корреляция Ранговые критерии Проверка гипотез непараметрической статистики

Результаты ранжирования спортсменов в тесте

Существует единица измерений, при помощи которой объекты можно не только упорядочить, но и приписать им числа так, чтобы разные разности отражали разные различия в количестве измеряемого свойства. Нулевая точка произвольна и не указывает на отсутствие свойства

Все методы статистики кроме определения отношений

Температура тела, суставные углы и т.д.

Числа, присвоенные предметам, обладают всеми свойствами интервальной шкалы. На шкале существует абсолютный нуль, который указывает на полное отсутствие данного свойства у объекта. Отношение чисел, присвоенных объектам после измерений, отражают количественные отношения измеряемого свойства.

Все методы статистики

Длина и масса тела Сила движений Ускорение и т.п.

Точность измерений [ править | править код ]

В спорте наиболее часто применяются два типа измерений: прямое (искомое значение находится из опытных данных) и косвенное (искомое выводится на основании зависимости одной величины от других, подвергаемых измерению). К примеру, в тесте Купера дистанцию измеряют (прямой метод), а МПК получают методом расчёта (косвенный метод).

Согласно законам метрологии, любые измерения имеют погрешность. Задача свести её к минимуму. От точности измерения зависит объективность оценки; исходя из этого, знание точности измерений является обязательным условием.

Систематические и случайные ошибки измерений [ править | править код ]

Согласно теории ошибок, их подразделяют на систематические и случайные.

Величина первых всегда одинакова, если измерения проводятся одним и тем же методом с использованием одних и тех же приборов. Выделяют следующие группы систематических ошибок [1] :

Для устранения систематической погрешности измерительные устройства предварительно проверяют и сравнивают с показателями эталонов либо калибруют (определяется погрешность и величина поправок).

Случайными называются такие ошибки, которые предсказать заранее попросту невозможно. Их выявляют и учитывают с помощью теории вероятностей и математического аппарата.

Абсолютные и относительные ошибки измерений [ править | править код ]

Различие, равное разности между показателями измерительного устройства и истинным значением, является абсолютной погрешностью измерения (выражается в тех же единицах, что и измеряемая величина) [1] :

где х — абсолютная погрешность.

При проведении тестирования часто возникает необходимость в определении не абсолютной, а относительной погрешности:

Основные требования к тестам [ править | править код ]

Все тесты подразделяются на группы в зависимости от цели:

1) показатели, измеряемые в покое (длина и масса тела, ЧСС и т.д.);

2) стандартные тесты с использованием немаксимальной нагрузки (например, бег на тредбане 6 м/с в течение 10 минут). Отличительной чертой данных тестов является отсутствие мотивации на достижение максимально возможного результата. Результат зависит от способа задания нагрузки: к примеру, если она задаётся по величине сдвигов медико-биологических показателей (например, бег при ЧСС 160 уд/мин), то измеряются физические величины нагрузки (расстояние, время и т.п.) [9] и наоборот.

Стандартизация измерительных процедур [ править | править код ]

1) режим дня, предшествующий тестированию, должен протекать по одной схеме. Допускается проведение занятий исключительно восстановительной направленности;

2) разминка непосредственно перед тестированием должна быть идентичной;

3) желательно, чтобы тестирование проводили одни и те же специалисты, обладающие необходимыми знаниями, навыками и опытом;

5) схема выполнения теста должна быть неизменной от тестирования к тестированию. При использовании батареи тестов, направленной на оценку различных способностей, уместно использовать следующую последовательность:

а) тесты, не вызывающие утомление (антропометрия, состав тела, психологический контроль и т.д.);

б) координационные способности;

в) абсолютные силовые, скоростно-силовые способности, мощность (анаэробно-алактатный механизм энергообеспечения);

г) скоростные способности (анаэробно-алактатный механизм энергообеспечения);

д) скоростная и скоростно-силовая выносливость (анаэробно-гликолитический механизм энергообеспечения);

е) общая выносливость (аэробный механизм энергообеспечения);

6) интервалы отдыха между попытками и испытаниями обязаны быть до полного восстановления испытуемого:

а) между повторениями упражнений, не требующих максимальных усилий — не менее 2-3 минут;

б) между повторениями упражнений с максимальными усилиями — не менее 3-5 минут;

7) мотивация на достижение максимального результата. Достижение данного условия бывает достаточно затруднительным, особенно когда речь идёт о профессиональных спортсменах. Здесь всё во многом зависит от харизмы, лидерских качеств наставника и умения мотивировать своих подопечных.

Достижение перечисленных условий далеко не всегда возможно в реальной жизни. Однако, не смотря на это, специалисты, ответственные за проведение тестирования, должны приложить максимум усилий для их достижения.

Надёжность тестов [ править | править код ]

1) дисперсионный анализ — позволяет рассчитать коэффициент надёжности, а также определить степень влияния различных факторов на изменчивость результатов. Данный подход является довольно сложным;

2) второй метод определения надёжности тестов значительно проще. Здесь достаточно рассчитать коэффициент корреляции.

Таблица 2. Градация уровней надёжности [1]

Необходимо исключить из практики применение малонадёжных тестов, так как они приводят к ошибочной оценке измеряемого параметра.

Стабильность тестов [ править | править код ]

На стабильность измерений влияет содержание учебно-тренировочного процесса и динамика нагрузки. Кроме этого, определенное влияние оказывают: сложность теста, а также временной интервал между тестированиями.

Согласованность тестов [ править | править код ]

Эквивалентность тестов [ править | править код ]

Информативность тестов [ править | править код ]

1) Логический метод определения информативности тестов

Суть данного метода определения информативности тестов состоит в логическом (качественном) сопоставлении физиологических, биомеханических и других характеристик критерия и тестов.

2a) Эмпирический метод определения информативности тестов при наличии единичного измеряемого критерия

2б) Эмпирический метод определения информативности тестов при отсутствии единичного критерия

Такая ситуация может возникнуть, если поставлена задача составить батарею тестов для юных хоккеистов 11-13 лет. С учётом того, что такой контроль должен быть массовым, тесты должны отвечать следующим параметрам:

Под данные требования подходит множество тестов, но необходимо отобрать наиболее информативные:

Безопасность [ править | править код ]

Любое контрольное испытание должно проводиться в безопасных условиях. Площадка для тестирования и используемое оборудование должны быть заблаговременно проверены на исправность. Во время выполнения теста всё используемое пространство должно быть свободно от посторонних предметов.

Тестирование в полевых условиях должно проводиться в установленных температурных диапазонах [8] [42] (Таблица 3).

Таблица 3. Допустимые погодные условия при выполнении интенсивных

Основы теории оценок [ править | править код ]

Оценка — унифицированная мера успеха в каком-либо тесте или задании. Процесс оценивания состоит из следующих стадий [1] :

Основными задачами, решаемыми в ходе оценивания, являются [1] :

Самым популярным и простым способом «трансформации» результатов тестирования в оценки является метод ранжирования (Таблица 4):

Таблица 4. Ранжирование результатов тестов профессиональных хоккеистов

Лучший результат в тесте оценивается в 1 балл, каждый последующий на 1 балл больше. Несмотря на повсеместное использование данной методики оценки, её существенным минусом является несправедливость — так, в нашем примере в тесте «Становая тяга» различие между первым и вторым местом равняется 29 килограммам, а между вторым и третьим — 5.

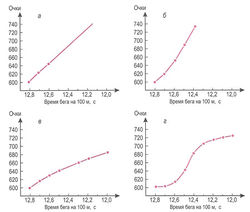
Поэтому для того, чтобы процесс оценивания был более справедливым, разработаны специальные шкалы. На рисунке 1 в качестве примера представлены четыре вида шкал:

«Первая (рисунок 1, а) — пропорциональная шкала. При ее использовании равные приросты результатов в тесте поощряются равными приростами в баллах. Так, в этой шкале, как это видно из рисунка, уменьшение времени бега на 0,1 секунды оценивается в 20 очков. Их получит спортсмен, бежавший 100 м за 12,8 секунд и пробежавший эту дистанцию за 12,7 секунд, и спортсмен, улучшивший свой результат с 12,1 до 12 секунд.

Второй тип — прогрессирующая шкала (рисунок 1, б). Здесь, как это видно из рисунка, равные приросты результатов оцениваются по-разному. Чем выше абсолютные приросты, тем больше прибавка в оценке. Так, за улучшение результата в беге на 100 м с 12,8 до 12,7 секунд дается 20 очков, с 12,7 до 12,6 секунд — 30 очков.

Перечисленные шкалы применяются в соответствии с поставленными задачами. Так, к примеру, можно использовать регрессирующую шкалу, если стоит задача поддержать и мотивировать отстающих спортсменов. Сигмовидная же подойдёт для тренера, считающего, что атлет должен быть гармонично развит. Однако бытует и иной взгляд. Так, во многих видах спорта издавна ведутся споры, что приоритетнее — подтягивать отстающие качества или развивать свои «коронные» способности. Если тренер приверженец второго мнения, то ему больше подойдёт прогрессирующая шкала оценок.

Применение шкал оценки в практике [ править | править код ]

Стандартная шкала [ править | править код ]

«В основе ее лежит пропорциональная шкала (см. рисунок 1, а), а свое название она получила потому, что масштабом в ней служит стандартное (среднеквадратическое) отклонение. Наиболее распространена Т-шкала.

При ее использовании средний результат приравнивается к 50 очкам, а вся формула выглядит следующим образом:

Пересчитаем данные таблицы 4, применив эту формулу (Таблица 5).

Сравнение таблиц 4 и 5 подтверждает большую справедливость оценки по Т-шкале в сравнении с ранжированием. Так, два хоккеиста сменили прежнее место в группе (выделены). Если раньше разрыв между 1 и 2 местом составлял 1 балл, между 8 и 9 местом тоже 1 балл, то по новым оценкам — 9 и 5 баллов, соответственно.

Перцентильная шкала [ править | править код ]

Суть данной шкалы в том, что каждый испытуемый из команды (группы) получает за свой результат столько очков, сколько процентов спортсменов он опередил. Как следует из вышесказанного, оценка победителя всегда будет равнятся 100 баллам, а последнего — 0 баллов. Преимуществом использования данной шкалы является её простота и отсутствие формул, что несёт важное значение для тренеров-практиков. Единственное,

Таблица 5. Оценка результатов тестирования профессиональных хоккеистов

что здесь нужно считать — какое количество испытуемых укладывается в один интервал шкалы (перцентиль).

Шкала ГЦОЛИФКа [ править | править код ]

Все вышеперечисленные шкалы хороши для тестирования всей команды и сравнения её представителей в отдельности между собой. Однако, когда стоит задача оценить прогресс спортсмена при повторных тестированиях на разных этапах (например, перед началом этапа предсезонной подготовки и по его окончании), наилучшим образом подойдёт шкала ГЦОЛИФКа [1] :

Оценка в баллах= 100 • (1- (Лучший результат-Оцениваемый результат)/ (Лучший результат-Худший результат)) (1.4)

Суть данного подхода в том, что результат теста оценивается не сам по себе, а в тесной взаимосвязи с лучшим и худшим результатами спортсмена, которым присваивается 100 и 0 очков, соответственно.

Пример: лучший результат в прыжке в длину с места равен 279 см, худший 265 см. Сегодня в ходе тестирования испытуемый показал результат 275 см.

Его оценка = 100-(1-(279-275)/(279-265))= 71 балл (1.5)

Оценка батареи (комплекса) тестов [ править | править код ]

Существует два подхода для того, чтобы дать обобщенную характеристику спортсмену по итогам комплексного тестирования:

1) Выведение обобщенной оценки. Если все тесты равнозначны, то подойдёт обычное суммирование баллов за каждый тест. Однако в спорте часто встречается ситуация, когда главный тренер считает не все тесты равнозначными. В данном случае можно поступить следующим образом [1] :

1. Даётся экспертная оценка. К примеру, тренерский штаб считает, что тест «Бег на коньках 5×54 метра» более важен, нежели остальные. В таком случае специалисты могут назначить ему коэффициент 2. Тогда очки, полученные за результат в этом тесте, будут удваиваться и затем суммироваться с баллами, начисленными по итогам остальных тестов.

2. Произвести факторный анализ, что позволит выделить более и менее «весомые» показатели, на основе чего каждому тесту установить индивидуальный коэффициент.

3. Произвести корреляционный анализ между результатом теста и достижением в соревнованиях, что и будет являться количественной мерой «весомости» теста. Однако данный вариант больше подходит для цикличных видов спорта, нежели к хоккею.

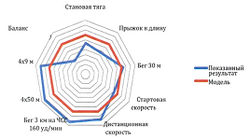
2) Второй подход заключается в создании «профиля» хоккеиста по итогам комплексного тестирования (рис. 2)

Нормы [ править | править код ]

«Нормой в спортивной метрологии называется граничная величина результата теста, на основе которой производится классификация спортсменов [1] ».

Разновидности норм [ править | править код ]

Б) Индивидуальные нормы выводятся за счёт сравнения показателей одного и того же хоккеиста на разных этапах, что играет крайне важную роль для эффективной индивидуализации тренировочного процесса. Причиной их создания стала существенная разница в структуре тренированности игроков (даже в рамках одной команды). Убедиться в этом можно на реальном примере двух нападающих, выступающих в одной тройке нападения (Таблица 7):

Таблица 6. Шкалы оценок хоккеистов КХЛ [6] [45]

Тесты (контрольные нормативы)

Уровень подготовленности, баллы

Тест Слаломный бег на коньках без шайбы (сек)

Считать пригодными можно только те нормы, которые отвечают следующим условиям: релевантность, репрезентативность и современность.

Методы количественной оценки качественных показателей [ править | править код ]

«Качественными называются показатели, не имеющие определённых единиц измерения. Для количественной оценки таких показателей используются методы квалиметрии.

Метод экспертных оценок [ править | править код ]

Отбор экспертов [ править | править код ]

Объективная оценка пригодности эксперта определяется по формуле:

где М_ист — истинная оценка; М — оценка эксперта.

Желательно иметь однородную группу экспертов, но если это не удается, то для каждого из них вводится ранг.

Согласованность мнений экспертов определяется по величине коэффициента конкордации:

где S — сумма квадратов отклонений сумм рангов, приписанных каждому объекту оценки, от средней суммы рангов; т — количество экспертов; п — количество объектов оценки.

Достоверность экспертизы зависит не только от качественных особенностей экспертов, но и от их числа. Оно определяется по формуле:

Подготовка и проведение экспертизы [ править | править код ]

Таблица 8. Экспертная оценка игроков по итогам матчам регулярного чемпионата КХЛ

Оценка экспертов в баллах

Анкетирование [ править | править код ]

Грамотная формулировка вопроса — ключевой аспект при составлении анкеты. При составлении вопросов необходимо следовать следующим рекомендациям [52] :

По характеру вопросы могут предполагать различные формы ответа [1] :

1) при ответе требуется выбрать одно из заранее сформулированных утверждений (или несколько, с количественной оценкой в шкале порядка). Пример:

Пожалуйста, распределите, с Вашей точки зрения, значимость (1.2.3.4.5) следующих видов подготовки хоккеиста:

A) Физическая
Б) Техническая
B) Тактическая
Г) Теоретическая
Д) Психологическая

2) какое решение респондент принял бы в определенной ситуации (или несколько, с количественной оценкой в шкале порядка). Пример:

Какие тесты для оценки ОФП Вы предпочитаете использовать?

3) требующая количественной оценки какой-либо величины. Пример:

Конкретизируйте, пожалуйста, в процентном соотношении количество игроков, приступающих к предсезонному сбору:

A) С отличной физической подготовленностью (%)
Б) Средней физической подготовленностью (%)
B) Неудовлетворительной физической подготовленностью (%)

В соответствии с решаемыми задачами, встречаются следующие виды вопросов [52] :

1. Закрытые — открытые

Ваше игровое амплуа в прошлом (специализация)?

А) Нападающий
Б) Защитник
В)Вратарь
Г) Иное (укажите)

Какие тесты для оценки СФП Вы предпочитаете использовать?

2. Субъективные — проективные

Кто, с Вашей точки зрения, должен отвечать за осуществление педагогического контроля?

A) Главный тренер
Б) Тренер по физической подготовке
B) Врач
Г) Научный сотрудник
Д) Научная группа
Е) Иное (желательно указать)

В каком физическом состоянии игроки команды приступают к предсезонным сборам?

A) Отличном
Б) Среднем
B) Неудовлетворительном

Периодизация комплексного контроля [ править | править код ]

Исходя из современных тенденций проведения чемпионатов в игровых видах спорта, где график игр выстроен максимально плотно, минимально приемлемым вариантом проведения тестирования является:

1) начало предсезонной подготовки — позволяет определить, в каком состоянии спортсмены вернулись после отпуска;

2) окончание предсезонной подготовки — даёт возможность оценить степень прогресса игроков и эффективность предложенной тренировочной программы. Данный момент является щепетильным для тренеров, так как служит прямой оценкой их работы. Вместе с тем, это является жизненно необходимым, поскольку способствует совершенствованию системы подготовки;

3) середина соревновательного периода (игрового сезона) — позволяет оценить, насколько удаётся поддерживать достигнутый в предсезонном периоде уровень подготовленности;

4) окончание сезона — характеризует уровень подготовленности в период наиболее ответственных игр.

Заключение [ править | править код ]

Комплексный контроль является важнейшим атрибутом процесса управления подготовкой спортсмена. Его результаты дают тренерам информацию об эффективности тренировочного процесса, возможность совершенствовать программу подготовки, а также обеспечить индивидуальное планирование нагрузки в соответствии с поставленными задачами. Получение объективной информации возможно при условии знания и соблюдения метрологических основ комплексного контроля, таких как: требования к точности, стандартизации и безопасности измерительных процедур; использование надёжных, стабильных и информативных тестов; оценка результатов согласно научно обоснованным шкалам. Важнейшим итогом систематического применения комплексного контроля в работе тренера будет рост его профессиональных навыков и, следовательно, результативности работы.

Источник

Тема: Краткий конспект по всему курсу спортивной метрологии — файл n1.doc

приобрести
Тема: Краткий конспект по всему курсу спортивной метрологии
скачать (905 kb.)
Доступные файлы (1):

Лекции — Конспект лекций по всему курсу (Лекция)
Обществознание. Краткий конспект (Документ)
Алексеев В.В. Краткий конспект лекций по курсу Электрический привод. Часть 1 (Документ)
Алексеев В.В. Краткий конспект лекций по курсу Электрические машины. Машины постоянного тока. Трансформаторы (Документ)
Лапчик Д.Р. Лекции по метрологии в телекоммуникации (Документ)
Программа спортивной подготовки (Документ)
Диплом — Методика обучения профилирующим прыжкам спортивной аэробики (на примере прыжка согнувшись, согнув одну ногу — Cossack jump) (Дипломная работа)
Шпаргалка по курсу Демография (Шпаргалка)
Кузнецов В.А., Ялунина Г.В. Основы метрологии: Учеб. пособие (Документ)
Пронкин Н.С. Основы метрологии: практикум по метрологии и измерениям (Документ)
Евдокимов А.И. и др. Учебно-методическая разработка по курсу Мировая экономика (Документ)
Основы метрологии и электрические измерения (Документ)

n1.doc

КОНТРОЛЬНАЯ РАБОТА ПО СПОРТИВНОЙ МЕТРОЛОГИИ

для студентов заочного отделения

2009-2010 уч.год

Теория: составить краткий конспект по предлагаемому плану
Расчетная часть
1. Разработать тест (описание теста)
2. Проверить надёжность теста
3. Оценить информативность теста
4. Рассчитать шкалы оценок для теста

Выполнил:

Студент 1 гр. З/ф
Часть I. Теория

Раздел I. Основы метрологии.

Основы теории измерений

1. Измерением (в широком смысле) называют установление соответствия между изучаемыми явлениями с одной стороны, и числами, с другой.

Шкалы измерений

Шкала наименований (номинальная шкала)

Это самая простая из всех шкал. В ней числа выполняют роль ярлыков и служат для обнаружения и различения изучаемых объектов (например, нумерация игроков футбольной команды). Числа, составляющие шкалу наименований, разрешается менять местами. В этой шкале нет отношений типа «больше — меньше», поэтому некоторые полагают, что применение шкалы наименований не стоит считать измерением. При использовании шкалы наименований могут проводится только некоторые математические операции. Например, ее числа нельзя складывать и вычитать, но можно подсчитывать, сколько раз (как часто) встречается то или иное число.

Шкала порядка

Шкала интервалов

Это такая шкала, в которой числа не только упорядочены по рангам, но и разделены определенными интервалами. Особенность, отличающая ее от описываемой дальше шкалы отношений, состоит в том, что нулевая точка выбирается произвольно. Примерами могут быть календарное время (начало летоисчисления в разных календарях устанавливалось по случайным причинам), суставной угол (угол в локтевом суставе при полном разгибании предплечья может приниматься равным либо нулю, либо 180о), температура, потенциальная энергия поднятого груза, потенциал электрического поля и др.
Результаты измерений по шкале интервалов можно обрабатывать всеми математическими методами, кроме вычисления отношений. Данные шкалы интервалов дают ответ на вопрос «на сколько больше?», но не позволяют утверждать, что одно значение измеренной величины во столько-то раз больше или меньше другого. Например, если температура повысилась с 10^◦ до 20^◦ по Цельсию, то нельзя сказать, что стало в два раза теплее.

Шкала отношений

Эта шкала отличается от шкалы интервалов только тем, что в ней строго определено положение нулевой точки. Благодаря этому шкала отношений не накладывает никаких ограничений на математический аппарат, используемый для обработки результатов наблюдений.
В спорте по шкале отношений измеряют расстояние, силу, скорость и десятки других переменных. По шкале отношений измеряют и те величины, которые образуются как разности чисел, отсчитанных по шкале интервалов. Так, календарное время отсчитывается по шкале интервалов, а интервалы времени — по шкале отношений.
При использовании шкалы отношений (и только в этом случае!) измерение какой-либо величины сводится к экспериментальному определению отношения этой величины к другой подобной, принятой за единицу. Измеряя длину прыжка, мы узнаем во сколько раз эта длина больше длины другого тела, принятого за единицу длины (метровой линейки в частном случае); взвешивая штангу, определяем отношение ее массы к массе другого тела — единичной гири «килограмма» и т.п. Если ограничиться только применением шкал отношений, то можно дать другое (более узкое, частное) определение измерению: измерить какую-либо величину — значит найти опытным путем ее отношение к соответствующей единице измерения.
Сводные сведения по шкалам

Шкала	Основные операции	Допустимые математические процедуры (статистика)	Примеры
наименований	Установление равенства	Число случаев Мод Корреляция случайных событий (тетра- и полихорические коэффициенты корреляции)	Нумерация спортсменов в команде Результаты жеребьёвки
порядка	Установление соотношений «больше» или «меньше»	Медиана Ранговая корреляция Ранговые критерии Проверка гипотез	Место занятое на соревнованиях. Результаты ранжирования спортсменов группой экспертов
интервалов	Установление равенства интервалов	Среднее Среднее квадратическое (стандартное) отклонение Корреляция	Календарные даты (время) Суставной угол
отношений	Установление равенства отношений	Коэффициент вариации Среднее геометрическое	Длина, сила, масса, скорость и т.п.

Пример использования шкал измерения в своем виде спорта.

В виндсерфинге в гоночных дисциплинах используется шкала отношений, а во фристайле и вэйврайдинге – шкала порядка.

2. Шкалы измерений и точность измерений:

— какую точность измерений обеспечивают разные шкалы;

— погрешности измерений:

Основная и дополнительная погрешности

Основная погрешность – это погрешность метода измерения или измерительного прибора, которая имеет место в нормальных условиях их применения.

Дополнительная погрешность – это погрешность измерительного прибора, вызванная отклонением условий его работы от нормальных.

Абсолютная и относительная погрешности

Абсолютная погрешность – это величина ∆А = А — А_о, равная разности между показанием измерительного прибора (А) и истинным значением измеряемой величины (А_о).

Относительная погрешность измерения бывает двух видов.

Действительная относительная погрешность – это отношение абсолютной погрешности к истинному значению измеряемой величины:

∆А_д = ∙ 100%

Приведённая относительная погрешность – это отношение абсолютной погрешности к максимально возможному значению измеряемой величины:

∆А_п = ∙ 100%

В тех случаях, когда оценивается не погрешность измерения, а погрешность измерительного прибора, за максимальное значение измеряемой величины принимают предельное значение шкалы прибора.

Систематическая и случайная погрешности

Систематическая погрешность – её величина не меняется от измерения к измерению.

Случайная погрешность возникает под воздействием разнообразных факторов, которые ни предсказать заранее, ни точно учесть не удаётся.

II. Основы теории оценок

1. Оценка спортивных достижений:

— проблема эквивалентности оценок;

— оценка в многоборье;

Нормы

Нормой в спортивной метрологии называется граничная величина результата теста, на основе которой производится классификация спортсмена.

Существует три вида норм:

а) индивидуальные;

б) должные;

в) сопоставительные.

Индивидуальные нормы основаны на сравнении показателей одного и того же спортсмена в разных состояниях.

Должные нормы устанавливаются на основании требований, которые предъявляют человеку условия жизни. Примером могут служить нормы выполнения заданий в различных видах производственной деятельности.

Сопоставительные нормы устанавливаются после сравнения достижений людей, принадлежащих к одной и той же совокупности. Сопоставительные нормы ранжируют людей внутри совокупности, но ничего не говорят о совокупности в целом. Эти нормы можно разрабатывать непосредственно на основе показателей средних величин и стандартов. Например, в таблице 11 приведены 7 классификационных групп, границы которых определяются средним квадратическим отклонением. Нормы такого рода удобны тем, что сразу ясно, какому проценту исследуемых лиц они посильны.

Таблица

Возможные градации оценок и норм

В практике физического воспитания широко распространены возрастные нормы. Эти нормы относятся к сопоставительным нормам.

Требования к пригодности норм:

1. Если нормы пригодны только для той совокупности, для которой разработаны, такая пригодность называется релевантностью, а нормы — релевантными.
2. Если нормы установлены при обследовании типичной выборки исследуемых, т.е. пригодны для всей генеральной совокупности, они называются репрезентативными.
3. Нормы должны быть современными, т.е. пересматриваться один раз в 4 года.
Таблица норм

Пример

Используя данные таблицы (нормы для результатов прыжков в длину с места), определить в какой зоне находится результат 10-го спортсмена, если данные выборки таковы:

xi , см ~ 180; 185; 190; 190; 195; 200; 200; 185; 205; 200.

Решение:

1. Занесем результаты тестирования в таблицу:

2. Определим среднее арифметическое по формуле:

см.

3. Определим среднее квадратическое отклонение по формуле:

? = = см

4. Используя стандартное отклонение, определим границы групповых норм результатов прыжков в длину с места и охарактеризуем их словесно:

Вывод: Результат 10-го спортсмена, равный 200 см, соответствует словесной оценке «хорошая».
2. Шкалы оценок
Разновидности шкал

Шкала оценок может быть представлена:

таблицей;
графиком функции;
математической формулой.

Все шкалы можно разделить на две группы:

1. Пропорциональные (линейные) шкалы.

2. Нелинейные шкалы.

Принято выделять четыре основных типа шкал оценок

I — пропорциональная шкала,

II — регрессирующая,

III — прогрессирующая,

IV — сигмовидная.

Первый тип — пропорциональные шкалы. Этот тип шкал предполагает начисление одинакового числа очков за равный прирост результатов (например, за каждые 0,1с улучшения результата в беге на 100м начисляется 20 очков).

Второй тип — регрессирующие шкалы. В этом случае за один и тот же прирост результата начисляются по мере возрастания спортивных достижений все меньшее число очков (например, за улучшение результата в беге на 100 м с 15,0 с до 14,9 с добавляются 20 очков, а за 0,1 с в диапазоне 10,0–9,9 с — только 15 очков).

Третий тип — прогрессирующие шкалы. Здесь, чем выше спортивный результат, тем большей прибавкой очков оценивается его улучшение (например, за улучшение времени в беге от 15,0 с до 14,9 с добавляются 10 очков, а от 10,0–9,9 с — 100 очков).

Четвертый тип — комбинированные, сигмовидные (или S-образные). В этих шкалах улучшение результатов в зонах очень низких и очень высоких достижений поощряется скупо; больше всего очков приносит прирост результатов в средней зоне достижений, т.е. в этих шкалах за равный прирост результата дается меняющаяся сумма баллов.

В спортивной практике наиболее часто применяются шкалы, для которых эквивалентными принято считать результаты в различных видах спорта, в равной степени доступные одинаковому проценту спортсменов одного возраста и пола. Исходя из этого, считают все мировые рекорды эквивалентными, независимо от вида спорта, и оценивают их одинаковым числом очков, например 100. Составив список сильнейших спортсменов по каждому виду спорта, считают эквивалентными также сотые результаты, т.е. всем таким спортсменам начисляют один балл.

Стандартные шкалы

Относятся к группе пропорциональных шкал. Названы они стандартными потому, что масштабом в них служат стандартные отклонения. Наиболее популярна среди стандартных шкал Т-шкала. Здесь средняя величина приравнивается к 50 очкам, а стандарт — к 10 очкам, и расчет суммы баллов ведется по формуле:

Например, если средняя величина в прыжках в длину с места равнялась 224 см, а стандартное отклонение составило ± 20 см, то за результат 222 см начисляется 49 очков:

При массовых обследованиях спортсменов или групп здоровья можно использовать так называемую С-шкалу, описываемую формулой:

Достоинством этой шкалы является простота подсчетов, что достигается за счет меньшей точности.

Перцентильная шкала

Основана на мере преимущества каждого спортсмена по сравнению с более слабыми участниками соревнования. Если, например, проводится кросс с общим стартом, спортсмену можно начислять столько очков, сколько участников (в процентах) он обогнал. Если спортсмен опередил всех участников (99%), то он получает 99 очков, если опередил 72% — 72 очка и т.д. Тот же принцип можно использовать и в других тестах: число начисляемых очков приравнивается к проценту лиц, которых опередил (по результату) данный участник.

Шкала, построенная таким образом, называется перцентильной, а интервал этой шкалы — перцентилем.

Один перцентиль включает 1% всех испытуемых. 50%-ный перцентиль называется медианой.

Шкалы выбранных точек

Описанные шкалы можно построить, если известно статистическое распределение результатов теста: средняя, стандарты и другие параметры распределения. Такие данные не всегда удается получить. Это достижимо, например, при разработке таких шкал, как комплекс ГТО, нормы по физическому воспитанию в школе и т.п., и недостижимо при разработке таблиц по видам спорта.

В последнем случае обычно поступают так: берут какой-нибудь высокий спортивный результат (например, мировой рекорд или 10-й результат в истории данного вида спорта) и приравнивают его, скажем, к 1000 очкам. Затем на основе результатов массовых испытаний определяют среднее достижение группы слабо подготовленных лиц и приравнивают его, скажем, к 100 очкам. После этого, если используется пропорциональная шкала, остается выполнить лишь арифметические вычисления — ведь две точки однозначно определяют прямую линию. Шкала, построенная таким образом, называется шкалой выбранных точек.

Для примера рассмотрим построение шкалы выбранных точек на основе данных мирового табеля о рангах спортсменов по итогам выступления в течение года. В нем мировым рекордам во всех видах спорта дается наивысшая сумма баллов — 1000 очков, а худшие результаты оцениваются 100 очками. Используя принцип построения пропорциональных шкал, строится график шкалы выбранных точек, представленный на рисунке.

График шкалы выбранных точек

Далее производится расчет уравнения прямой для данной шкалы оценок по формуле:

K = ax + b — уравнение прямой,

где: K — сумма баллов или очков;

x — результат;

a — коэффициент пропорциональности;

b — свободный член уравнения.

Подставив в данное уравнение значение x₁и соответствующее ему значение K₁=100 и x₂, которому соответствует K₂=1000(x₁ – худший, x₂ – лучший результаты), составим систему уравнений:

Решая систему относительно a , получим:

Подставляя a в уравнение (1) получим b:

Подставив полученные числовые значения a и b в уравнение прямой, получим формулу для расчета оценок по шкале выбранных точек:

Таким образом, конечный вид уравнения прямой для расчета оценок по шкале выбранных точек будет следующим:

Например, лучший результат в беге на 100 м в группе исследуемых спортсменов, равный 11,0 с, оценивался 100 очками, а худший (14,0 с) — 10 очками. Тогда сумма очков спортсмена, показавшего время забега, равное 12,5 с, по формуле уравнения прямой для расчета оценок по шкале выбранных точек равна:

Шкала ГЦОЛИФК

При периодических обследованиях состав и общая численность тестируемой команды по разным причинам не остаются постоянными: кто-то заболел, кто-то отозван для участия в других соревнованиях т.п.

Предположим, что в ноябре тестирование проводилось на 10, а в феврале на 20 спортсменах. Конечно, занять 10 место при 10 или при 20 участниках — ни одно и то же (во втором случае спортсмен опередил девятерых, а в первом — никого). Кроме того, ранговая шкала (шкала порядка), например, перцентильная, неудобна тем, что она однозначно не определяет интервалы между исследуемыми.

Для случаев, когда условия тестирования не остаются постоянными, в ГЦОЛИФКе была разработана шкала, в основе которой лежит следующее математическое выражение:

где: К — оценка результата в баллах или очках.

Например, лучший результат в ударе ногой по мячу на дальность (в метрах) для подростков 10-11 лет равнялся 30,5м, худший — 8,5м. Очки, начисляемые спортсмену за результат 19,5м, рассчитываются по следующей формуле:

Спортсмен, показавший лучший результат, по шкале ГЦОЛИФКа всегда получает 100 очков, занявший же последнее место очков не получает.

Шкала ГЦОЛИФК относится к сигмовидным шкалам оценок, в то время как стандартные, перцентильные и шкалы выбранных точек — это пропорциональные шкалы.

3. Оценка результатов комплексного контроля

Если спортсмены проходят испытания в комплексе (батарее) тестов, то оценивание можно проводить двумя основными способами.

При первом общая оценка по всему тесту не выводится, а в процессе последующего анализа используются оценки, полученные отдельно по каждому тесту. Очень часто в таких случаях применяют графическую форму представления результатов тестирования – так называемые профили. Результаты показанные спортсменом или группой, сравниваются со средними результатами и стандартными отклонениями результатов, продемонстрированными до этого большой группой спортсменов.

При втором способе выводится итоговая оценка по всему комплексу тестов. Здесь возможны два варианта: 1) суммируют оценки, полученные по отдельным тестам, входящим в комплекс, как выводят итоговые оценки на соревнованиях по многоборьям; 2) оценки, полученные за отдельные виды, сначала умножают на коэффициенты («веса»), различные для каждого теста, а потом уже складывают. Такая итоговая оценка по комплексу тестов называется взвешенной оценкой. Её используют, когда надо усилить значение отдельных видов. Для более важных тестов «веса» делают высокими.

4. Методы экспертных оценок

Под экспертными методиками понимают комплекс логических и математико-статистических процедур, направленных на получение от специалистов информации, ее анализ и обобщение с целью подготовки и выбора рациональных решений.

Экспертные методы применимы в том случае, когда выбор и обоснование оценки результата не могут быть выполнены на основании точных измерений и расчетов.

Экспертной называется оценка, получаемая путем опроса мнений специалистов.

Экспертиза бывает индивидуальной и групповой. Существует несколько видов информации, используемой при работе с экспертной группой:

1. Эксперт высказывает мнение в виде соответствующего числа в предложенных рамках, т.е. дает оценку.
2. Эксперт может проранжировать участников, т.е. расставить их по местам.
3. Эксперт может разбить участников всей совокупности на отдельные подклассы.
4. Эксперт может попарно сравнивать оцениваемые объекты и сообщает какой из них лучше.

Требования, предъявляемые к экспертам: эксперт должен быть высококвалифицированным, компетентным, беспристрастным специалистом с хорошо развитой интуицией, имеющим широкие взгляды и независимость суждений.

Существует 2 подхода к выбору экспертов:

1. Проводятся специальные экзамены, применяется самооценка экспертов.
2. Определяется эффективность деятельности экспертов.

Различают абсолютную и относительную эффективность.

Абсолютная — отношение правильно высказанных мнений к общему числу высказываний эксперта.

Относительная — отношение абсолютной эффективности к средней абсолютной эффективности группы экспертов.

Проведение экспертизы включает в себя следующие этапы:

1. Формирование цели экспертизы.
2. Подбор экспертов.
3. Выбор методики проведения опроса.
4. Обработка полученной информации, в том числе проверка согласованности достоверности индивидуальных экспертных оценок.

Пример

Определить методом предпочтения места спортсменок в показательных выступлениях по художественной гимнастике (10-ти балльная система).

Решение:

С у д ь и

№	Ф.И.О.	1	2	3	4	5	е	Место
1	Иванова Г.И.	10	9	10	10	10	49	II
2	. . .	8	7	8	7	7	37	IV
3	. . .	6	6	5	5	6	28	V
4	. . .	9	9	9	8	8	43	III
5	. . .	10	10	10	10	10	50	I
6	. . .	5	5	4	4	3	21	VII
7	. . .	6	4	5	7	5	27	VI

Пример

Определить методом попарного сравнения места спортсменок-гимнасток (этот метод основан на попарном сравнении всех факторов). При этом устанавливается в каждой сравниваемой паре объектов наиболее лучший спортсмен (он оценивается 1 баллом, а второй, наиболее худший — 0 баллов).

Решение:

5. Метод анкетирования

Анкетированием называется метод сбора мнений посредством заполнения анкет. Анкетирование наряду с интервью и беседой относится к методам опроса. Методы опроса позволяют получать информацию о мнениях людей, мотивах поведения, намерениях и т.д., то есть обо всем, что пока еще не может быть установлено при помощи инструментальных методов измерения. По отношению к методу экспертных оценок анкетирование играет служебную роль, но имеет и самостоятельное значение, если речь идет о сборе массовых мнений. В отличие от интервью и беседы анкетирование предполагает письменные ответы лица, заполняющего анкету — респондента (англ. respondent — отвечающий), на систему стандартизированных вопросов.

Применяется несколько вариантов анкетирования: групповое и индивидуальное, очное и заочное, персональное и анонимное.

Анкета как правило, состоит из двух частей: демографической и основной. Вопросы демографического характера рекомендуется помещать в конце анкеты. В основную часть анкеты включают следующие вопросы: открытые (свободные) и закрытые, безусловные и условные, прямые и косвенные.

От составителя анкеты требуется высокая профессиональная компетентность, безупречная грамотность, такт. Вопросы должны быть лаконичны и точны, они должны соответствовать образовательному уровню респондентов. Желательно в начале анкеты расположить нетрудные вопросы, которые могли бы заинтересовать респондентов, а основную часть вопросов «по существу» поместить в середину анкеты.

Качество анкетирования повысится, если до начала опроса подвергнуть составленную анкету экспертной оценке и усовершенствовать ее в соответствии с высказываниями экспертов.

В последнее время квалиметрические методы (экспертиза, анкетирование и др.) все чаще используются для решения оптимизационных задач (оптимизация соревновательной деятельности, тренировочного процесса). Современный подход к задачам оптимизации связан с имитационным моделированием соревновательной и тренировочной деятельности. В отличие от других видов моделирования при синтезе имитационной модели наряду с математически точными данными используется квалитативная информация, собираемая методами экспертизы, анкетирования и наблюдения. Например, при моделировании соревновательной деятельности лыжников нельзя точно предсказать коэффициент скольжения. Его вероятную величину можно оценить путем опроса специалистов по смазке лыж, знакомых с климатическими условиями и особенностями трассы, на которой будут проходить соревнования.
Раздел II. Основы теории тестов.

1. Основы теории тестов

Тест – измерение или испытание, проводимое с целью определения состояния или способностей спортсмена.

Батарея тестов. Иногда используется не один, а несколько тестов, имеющих единую конечную цель (например, оценку состояния спортсмена в соревновательном периоде тренировки). Такая группа тестов называется комплексом или батареей тестов.

Требования к тестированию:

1. стандартность (процедура и условия тестирования должны быть одинаковыми во всех случаях применения теста);
2. надежность;
3. информативность;
4. наличие системы оценок.

Добротность тестов. Тесты, удовлетворяющие требованиям надежности и информативности, называют добротными или аутентичными (греч. аутентико — достоверным образом).

Виды тестов:

Максимальный двигательный тест

Максимальный функциональный тест

Стандартная функциональная проба

Тест покоя

Таблица Разновидности двигательных тестов

Название теста	Задание спортсмену	Результат теста	Пример
Контрольные упражнения	Показать максимальный результат	Двигательные достижения	Бег 1500 м, время бега
Стандартные функциональные пробы	Одинаковое для всех, дозируется а) по величине выполненной работы либо б) по величине физиологических сдвигов	Физиологические или биохимические показатели при стандартной работе Двигательные показатели при стандартной величине физиологических сдвигов	Регистрация ЧСС при стандартной работе 1000 кГм/мин Скорость бега при ЧСС 160 уд/мин
Максимальные функциональные пробы	Показать максимальный результат	Физиологические или биохимические показатели	Определение максимального кислородного долга или МПК

Источник

С этим файлом связано 3 файл(ов). Среди них: Вопросы_спортивная метрология10 57644155.doc, Вопросы_спортивная метрология10 57644155.doc, Вопросы_спортивная метрология10 57644155.doc.
Показать все связанные файлы

Подборка по базе: Практический курс по созданию своего онлайн-курса за 3 дня. 2.pd, Примерные вопросы к дифференцированному зачету_Психология общени, методичка курсового МКСП 03.02.2017.pdf, Тестовые вопросы к разделу 5_ просмотр попытки.pdf, 12.02.2023 Курсовая Винничук Я. В..docx, Тестовые вопросы к разделу 8_ просмотр попытки.pdf, исп. Курсовая Орловский Д. В. 1 часть.docx, отчет по практике 4 курс.docx, +Ниязова Әсем курс жумысы.docx, Экзамен вопросы СП ОМ_англ_ok.docx

Спортивная метрология

вопросы для экзамена 1 курс

Дайте определение понятиям «шкала оценок». Охарактеризуйте шкалы оценок: пропорциональная шкала, прогрессирующая шкала, сигмовидная (S-образная) шкала, Т-шкала, С-шкала, перцентильная шкала, шкала выбранных точек, шкала ГЦОЛИФК. Приведите примеры применения вышеперечисленных шкал оценок в спортивной деятельности.
. Дайте определение понятиям «шкала оценок». Охарактеризуйте шкалы оценок: пропорциональная шкала, прогрессирующая шкала, сигмовидная (S-образная) шкала, Т-шкала, С-шкала, перцентильная шкала, шкала выбранных точек, шкала ГЦОЛИФК. Приведите примеры применения вышеперечисленных шкал оценок в спортивной деятельности.
Обоснуйте особенности метрологических основ и методов отбора спортсменов в зависимости от уровня комплектования команд.
Дайте определение понятию «измерение». Проведите подробную основную классификацию видов измерений в спортивной метрологии.
Дайте определение понятию «контроль». Обоснуйте особенности управления учебно-тренировочным процессом, в зависимости от вида контроля за подготовкой спортсмена. Перечислите средства и методы контроля за спортивной подготовкой.
Дайте определение понятию «стандартизация». Раскройте функции стандартизации, и ее разновидности (приведите примеры). Перечислите органы и службы стандартизации.
Дайте определение понятию «точность измерений». Охарактеризуйте разновидности ошибок измерений. Обоснуйте методы борьбы с ошибками измерений: калибровка, тарирование, рандомизация.
Дайте определение понятиям «норма», «норматив», «нормирование». Проведите подробную классификацию норм в спортивной метрологии. Охарактеризуйте критерии пригодности норм: своевременность, релевантность, репрезентативность.
Дайте определение понятиям «спортивная метрология», «объект и предмет спортивной метрологии». Охарактеризуйте задачи спортивной метрологии как учебной дисциплины. Расскажите историю возникновения и современное состояние спортивной метрологии.
Дайте определения понятию «единица измерений». Расскажите историю возникновения единиц измерений. Охарактеризуйте международную систему единиц (СИ)
Дайте подробную характеристику основных показателей спортивной метрологии. Приведите примеры производных показателей спортивной метрологии.
Дайте сравнительную характеристику видам контроля за соревновательными и тренировочными нагрузками. Обоснуйте критерии использования средств контроля за соревновательными и тренировочными нагрузками.
Дайте сравнительную характеристику типов контроля за состоянием спортсмена. Обоснуйте особенности содержания и организации контроля в зависимости от типов состояния спортсмена.
Обоснуйте особенности применения средств и методов контроля за уровнем развития ловкости. Охарактеризуйте критерии развития ловкости. Перечислите основные способы измерения ловкости.
Обоснуйте особенности применения средств и методов контроля за уровнем развития выносливости. Приведите примеры использования специфических и неспецифических тестов для определения выносливости.
Обоснуйте особенности проведения контроля за техническим и тактическим мастерством спортсмена. Охарактеризуйте основные показатели технического мастерства и методы контроля за ними.
Обоснуйте особенности проведения прогнозирования и отборе в спорте.
Обоснуйте особенности управления тренировочным процессом в спорте. Определите место спортивной метрологии в управлении процессом подготовки спортсменов.
Охарактеризуйте особенности метрологического обеспечения измерений в спорте. Обоснуйте метрологические основы разработки нормативных требований по видам спорта.
Дайте определение понятию «измерение». Проведите подробную классификацию видов измерений в зависимости от способа получения числового значения и характера изменения измеряемой величины.
Дайте определение понятию «стандартизация». Проведите подробный анализ стандартизации измерительных процедур. Расскажите о роли стандартизации в обеспечении качества учебно-тренировочного процесса.
Дайте определение понятию «экспертиза в спорте». Раскройте особенности использования метода экспертных оценок для оценки качественных показателей в спорте. Приведите примеры.
Дайте определение понятия «квалиметрия». Перечислите количественные методы оценки качества. Проведите подробный анализ использования квалиметрических методов оценки качества в практике спортивных измерений.
Дайте определение понятиям «оценка», «оценивание». Обоснуйте стадии оценивания. Приведите примеры использования учебных и квалификационных оценок в физической культуре и спорте.
Дайте определение понятиям «специализированность физических упражнений», «сложность физических упражнений», «направленность физических упражнений». Проведите сравнительный анализ контроля за специализированостью, сложностью и направленностью физических упражнений в тренировочном процессе и на соревнованиях.
Дайте определение понятиям «тест», «тестирование». Определите основные требования, предъявляемые к тестам. Приведите примеры использования тестов в физической культуре и спорте.
Дайте определения понятиям «стабильность теста», «согласованность теста», «надежность теста», «эквивалентность теста», «аутентичность теста», «информативность теста». Приведите примеры.
Дайте подробную классификацию средств измерений. Обоснуйте особенности использования средств измерений при измерении показателей пространства и углов.
Дайте характеристику основным понятиям спортивной метрологии: законодательная метрология, фундаментальная (научная) метрология, практическая (прикладная) метрология. Приведите примеры взаимосвязи спортивной метрологии с другими дисциплинами предметной подготовки.
Дайте характеристику основным понятиям спортивной метрологии: законодательная метрология, фундаментальная (научная) метрология, практическая (прикладная) метрология. Приведите примеры взаимосвязи спортивной метрологии с другими дисциплинами предметной подготовки.
Обоснуйте особенности измерения коэффициентов «запас скорости» и «индекс выносливости» в зависимости от дистанции. Вычислите «запас скорости» в беге на 100 м.
Обоснуйте особенности использования методов оценки качественных показателей: опрос, интервью, мониторинг, анкетирование, экспертиза в физической культуре и спорте.
Обоснуйте особенности использования метрологических методов отбора детей для занятий определенным видом спорта.
Обоснуйте особенности использования тестов для измерения быстроты в физической культуре и спорте. Приведите примеры использования батареи тестов для измерения быстроты.
Обоснуйте особенности использования тестов для измерения выносливости в физической культуре и спорте. Приведите примеры гетерогенных тестов для измерения выносливости.
Обоснуйте особенности использования тестов для измерения гибкости в физической культуре и спорте. Приведите примеры использования тестов для измерения гибкости в спорте.
Обоснуйте особенности использования тестов для измерения ловкости в физической культуре и спорте. Приведите примеры гомогенных тестов для измерения ловкости.
Обоснуйте особенности использования тестов для измерения силовых качеств в физической культуре и спорте. Приведите примеры двигательных тестов.
Обоснуйте особенности использования тестов для определения способностей к комплексной реакции в физической культуре и спорте. Приведите примеры батареи тестов для тестирования способностей комплексной реакции.
Обоснуйте особенности применения основ теории вероятности и математической статистики в физической культуре и спорте. Проведите подробный анализ применения метода средних величин, выборочного метода, корреляционного анализа в научных исследованиях по спорту.
Обоснуйте особенности применения средств и методов контроля за силовыми качествами спортсмена. Перечислите основные особенности регистрации силовых качеств.
Обоснуйте особенности применения средств и методов контроля за скоростными качествами спортсмена. Охарактеризуйте элементарные и комплексные формы проявления скоростных качеств. Перечислите основные способы регистрации быстроты.
Обоснуйте особенности применения средств и методов контроля за скоростными качествами спортсмена. Охарактеризуйте элементарные и комплексные формы проявления скоростных качеств. Перечислите основные способы регистрации быстроты.
Обоснуйте особенности физических величин в зависимости от уровня измеряемых параметров (интегральный, комплексный, дифференциальный, единичный).
Обоснуйте особенности физических величин в зависимости от уровня измеряемых параметров (интегральный, комплексный, дифференциальный, единичный).
Приведите подробную классификацию методов измерений. Обоснуйте особенности использования методов измерений в зависимости от вида спорта.
Проведите подробную классификацию методов измерений. Обоснуйте особенности использования методов измерений в зависимости от вида спорта.
Проведите подробную классификацию объектов измерений в спортивной метрологии. Обоснуйте особенности использования средств и методов измерения в зависимости от объекта измерений.
Проведите подробную классификацию тестов. Обоснуйте особенности использования различных видов тестов для оценки физической подготовленности. Перечислите факторы, влияющие на результат теста.
Проведите подробную классификацию типов состояния спортсмена и его разновидностей. Обоснуйте особенности использования гомогенных и гетерогенных тестов в зависимости от типа состояния спортсмена.

Источник