Метод декомпозиции на егэ - Помощь в подготовке к экзаменам и поступлению

17 января 2018

В закладки

Обсудить

Жалоба

Применение метода декомпозиции при решении неравенств

При выполнении задания №15 на решение различных неравенств целесообразно применять метод рационализации неравенств (метод декомпозиции).

Этот метод позволяет проще решать логарифмические, показательные неравенства, неравенства с модулем. В данной работе приводятся решённые неравенства методом декомпозициии.

me-d15.pdf

Источник

При выполнении задание №15 на решение различных неравенств целесообразно применять метод рационализации неравенств (метод декомпозиции). Этот метод позволяет проще решать логарифмические, показательные неравенства , неравенства с модулем. В частности, при решении логарифмических неравенств, содержащих переменную в основании логарифма, отпадает необходимость рассматривать два случая, когда единицы. Если неравенство содержит выражение с модулем , то его можно сразу преобразовать в произведение двух множителе, не выполняя операцию по раскрытию модуля. При решении показательных неравенств с одинаковыми основаниями, но разными показателями этот метод значительно упрощает решение.

Скачать:

Предварительный просмотр:

Подписи к слайдам:

Слайд 1

Применение метода декомпозиции при решении заданий на тему: «НЕРАВЕНСТВА» Автор: Лемещенко Марина Николаевна Учитель математики МОУ СОШ№ 65

Слайд 2

ВВЕДЕНИЕ При выполнении задание №15 на решение различных неравенств целесообразно применять метод рационализации неравенств (метод декомпозиции) . Этот метод позволяет проще решать логарифмические, показательные неравенства , неравенства с модулем . Так как в программе 10-11 класса для средней школы этот метод не изучается, то при выполнении задания с помощью данного метода ученик обязательно должен написать фразу: « Применим метод декомпозиции».

Слайд 3

Рационализация неравенств Рационализация неравенств, или метод декомпозиции, или метод замены множителей. Цель: упрощение решения неравенств. Суть: в замене сложного выражения F(x) на более простое выражение G (x) , при которой неравенство G(x) равносильно неравенству F(x) на области определения F(x).

Слайд 4

Таблица замены множителей

Слайд 5

Примеры решения неравенств методом декомпозиции из КИМ 2014-2017 гг. Пример 1

Слайд 6

Пример 2

Слайд 7

Пример 3

Слайд 8

Пример 5

Слайд 9

Примеры, которые лучше решить методом замены

Слайд 12

Спасибо за внимание!

По теме: методические разработки, презентации и конспекты

Применение метода оценки к решению уравнений

Применение метода оценки к решению уравненийУрок — творческая лаборатория Математика всегда была неотъемлемой и существенной составной частью человеческой культуры, она является ключом к по…

Лекция «Решение неравенств с одной переменной»

В лекции представлена и обобщены теоретические сведения о решении таких видов неравенств: показательные неравенства, иррациональные неравенства, логарифмические неравенства, неравенства, содержащие не…

Решение неравенств методом интервалов

Рассмотрим общий метод интервалов. Ян Амос Коменский говорил: «Считай несчастным тот день или тот час, в который ты не усвоил ничего нового, ничего не прибавил к своему образованию»….

Мне нравится

Источник

Инфоурок

›

Алгебра

›Другие методич. материалы›Подготовка к ЕГЭ «Метод декомпозиции»

Подготовка к ЕГЭ «Метод декомпозиции»

Скачать материал

Подготовка к ЕГЭ

метод декомпозиции

Скачать материал

Сейчас обучается 128 человек из 47 регионов

Сейчас обучается 23 человека из 17 регионов

Сейчас обучается 1081 человек из 83 регионов

Описание презентации по отдельным слайдам:

1 слайд

Подготовка к ЕГЭ

метод декомпозиции
2 слайд

Метод декомпозиции заключается
в замене сложного выражения F(x) на
более простое выражение G(x),
при которой
неравенство G(x)v0 равносильно
неравенству F(x)v0 в
области определения выражения F(x)
3 слайд

Метод декомпозиции
logab-logac (a-1)(b-c)
logab-1 (a-1)(b-a)
Logab (a-1)(b-1)
4 слайд

1. Классический способ
2. Метод декомпозиции
5 слайд

О.Д.З.

a)
b)

Нет решений
Ответ: ( ; -1

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 154 237 материалов в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Другие материалы

02.12.2021
213
6

02.12.2021
1107
94

Рабочая программа по алгебре 7-9 классы

Учебник: «Алгебра», Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. / Под ред. Теляковского С.А.
Тема: Глава 1. Выражения, тождества, уравнения

02.12.2021
134
0

02.12.2021
101
0

Вам будут интересны эти курсы:

Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Формирование компетенций межкультурной коммуникации в условиях реализации ФГОС»
Курс повышения квалификации «Специфика преподавания конституционного права с учетом реализации ФГОС»
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
Курс профессиональной переподготовки «Деятельность по хранению музейных предметов и музейных коллекций в музеях всех видов»
Курс профессиональной переподготовки «Уголовно-правовые дисциплины: теория и методика преподавания в образовательной организации»
Курс профессиональной переподготовки «Организация деятельности по водоотведению и очистке сточных вод»
Курс профессиональной переподготовки «Технический контроль и техническая подготовка сварочного процесса»

Настоящий материал опубликован пользователем Цупрун Ольга Николаевна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.

Удалить материал
- На сайте: 7 лет и 3 месяца
- Подписчики: 0
- Всего просмотров: 2218825
- Всего материалов:
  
  1921

Источник

При решении неравенств методом интервалов вычисление значений функций в промежуточных точках может вызвать трудности вычислительного характера. С другой стороны, применение свойства знакочередования рациональной функции сводит вычисления до минимума.

Чтобы расширить возможности применения метода интервалов при решении неравенств, используем идею рационализации неравенств, известную в математической литературе под другими названиями.

Метод рационализации заключается в замене сложного выражения F(x) на более простое выражение G(x) (в конечном счете, рациональное), при которой неравенство G(x)>0 (G(x)<0) равносильно неравенству F(x)>0 (F(x)<0) в области определения выражения F(x). В этом случае будем говорить, что выражение G(x) является рационализацией (или рационализирующим выражением) для выражения F(x).

Идея метода рационализации состоит в использовании свойств монотонной функции [4, с. 288].

Сначала напомним теорему о корне монотонной функции.

Теорема. Если p(x) – функция, монотонная на промежутке M, и E(p) – множество ее значений на этом промежутке, то для любого числа c∈E(p) существует и притом единственный корень x₀∈M 0x M – уравнения p(x)=c.

Следствие 1. Если p(x) – возрастающая функция на промежутке M, то для любых чисел x₁,x₂∈M неравенства p(x₁)≥p(x₂) и x₁≥x₂ равносильны, или p(x₁)-p(x₂)≥0< = >x₁-x₂≥0 (аналогично (x₁)-p(x₂)>0< = >x₁-x₂>0).

Отметим, что функции p(t)=log_at и p(t)=a^t являются монотонными на всей своей области определения, причем при a>1 они являются возрастающими, а при 0<a<1 – убывающими.

Рассмотрим знаки выражений F(x)= log_af(x)-log_ag(x), fx-g(x) и G(x)=(a-1)(f(x)-g(x)) в зависимости от a на области определения F(x), заданной системой неравенств

(1)

где f(x),g(x) функции, a основание логарифма.

Таблица 1

Зависимость основания a от логарифмических функций

a	F(x)	f(x)-g(x)	G(x)
a>1	+	+	+
a>1	–	–	–
0<a<1	+	–	+
0<a<1	–	+	–

Источник: учебное пособие «Решение показательных и логарифмических уравнений, неравенств и систем уравнений повышенного и высокого уровня сложности (Часть 2)

Из таблицы следует, что выражения F(x) и G(x) при всех допустимых значениях x имеют одинаковые знаки.

Полученный результат запишем в виде теоремы.

Теорема 1. При a>0 и a≠1 знаки выражений log_af(x)-log_ag(x) и (a-1)(f(x)-g(x)) совпадают для всех значений x таких, что f(x)>0 и g(x)>0.

Поскольку при a>0 и a≠1 и всех допустимых значениях x справедливы равенства:

то получаем следующие следствия из теоремы 1.

Следствие 1. При a>0 и a≠1 знаки выражений

совпадают для всех значений x таких, что f(x)>0.

Следствие 2. При a>0 и a≠1 знаки выражений

log_af(x) и (a-1)(f(x)-1)

совпадают для всех значений x таких, что fx>0.

Замечание. Для выражения или рационализацией является выражение при условиях (2).

Метод рационализации используют при решении неравенств вида F(x)∨0, где символ ∨ означает один из знаков неравенств ≥,≤,>,<, в которых выражение F(x) удается рационализировать, либо выражение

(2)

записано в виде произведения или частного выражений, каждое из которых можно рационализировать.

Например, при соответствующих ограничениях на переменную x:

неравенство равносильно неравенству

неравенство равносильно неравенству

Стандартные ошибки, которые допускают учащиеся при использовании метода рационализации, заключаются в следующем:

проводят рационализацию без учета области определения данного неравенства;
применяют метод рационализации к неравенствам, не приведенным к стандартному виду F(x)∨0;
формально применяют метод рационализации к выражениям вида log_af(x)+log_ag(x), заменяя на выражение f(x)+g(x) (см. выше замечание);
подменяют формулировку «о совпадении знаков выражений для каждого допустимого значения x» на неверную формулировку «о совпадении значений выражений для каждого допустимого значения x».

Рассмотрим теперь неравенства, содержащие логарифмы с переменным основанием и выражения под знаком логарифма, содержащие функции, зависящие от x.

Теорема 2. Знаки выражений

совпадают для всех значений x таких, что

Следствие 1. Знаки выражений

совпадают для всех значений x таких, что

Следствие 2. Знаки выражений

совпадают для всех значений x таких, что

Теорема 3. Знаки выражений

log _f(x)hx-log _g(x)h(x) и

совпадают для всех значений x таких, что

Теорема 4. Знаки выражений

совпадают для всех значений x таких, что h(x)>0.

Следствие 1. Знаки выражений h(x)_f(x)-1 и (hx-1)*f(x) совпадают для всех значений x таких, что h(x)>0.

Следствие 2. Для числа a>0 знаки выражений a^f(x)-a^g(x) и

(a-1)(f(x)-g(x)) совпадают для всех допустимых значений x.

Теорема 5. Знаки выражений f(x)^h(x)-g(x)^h(x) и (f(x)-g(x))h(x) совпадают для всех значений x таких, что f(x)>0, g(x)>0.

Следствие 1. Знаки выражений и f(x)-g(x) совпадают для всех допустимых значений x, где n∈N.

Следствие 2. Знаки выражений и совпадают для всех значений x таких, что f(x)>0, g(x)>0, n∈N.

Теорема 6. Знаки выражений |f(x)|-|g(x)| и (f(x)-g(x))(f(x)+g(x)) совпадают для всех допустимых значений x.

Пример 9. Решить неравенство

Решение. ОДЗ данного неравенства следующее

Представим решение ОДЗ на графике.

Рис. 1. Графическое изображение решения примера 9

Решая эту систему получаем следующее, что неравенство определено при всех значениях x∈(-∞;-4)∪(0;1)∪(1;+∞). Далее необходимо преобразовать исходное неравенство, насколько это возможно

Применим свойство степени логарифмируемого числа, то есть коэффициент 2 выразим как квадрат аргумента.

Числитель и знаменатель дроби разложим по формуле разность квадратов

Решением данного неравенства представим графическим методом.

Рис. 2. Графическое изображение решения примера 9

x∈[-5;-3]∪(-1;1)

Учитывая ранее найденное ОДЗ текущего неравенства ответ представим на графическом рисунке.

x∈[-5;-4)]∪[0;1)

Ответ. x∈[-5;-4)]∪[0;1)

Таблица 2

Основные выражения F и соответствующие им рационализирующие выражения G при соответствующих ограничениях на переменную x

№

Выражение F

Выражение G

1а

1б

log_af-log_ag

log_af-1

log_af

(a-1)(f-g)

(a-1)(f-a)

(a-1)(f-1)

2а

2б

log_hf-log_hg

log_hf-1

log_hf

(h-1)(f-g)

(h-1)(f-h)

(h-1)(f-1)

log_fh-log_gh

(f-1)(g-1)*

(h-1)(g-f)

4а

4б

h^f-h^g

h^f-1

a^f-a^g

(h-1)(f-g)

(h-1)f

(a-1)(f-g)

5а

f^h-g^h

(f-g)h

f-g

|f|-|g|

(f-g)(f+g)

Источник: Учебное пособие «Решение показательных и логарифмических уравнений, неравенств и систем уравнений повышенного и высокого уровня сложности (Часть 2).

Источник

Нестандартный способ решения логарифмического неравенства.

Метод рационализации

Составитель разработки -Бибаева А.М.

Учитель математики МБОУСОШ №3 г.Беслан

«Стандартный» метод решения логарифмических неравенств

Рассмотрим традиционный метод решения логарифмического неравенства на конкретном примере.

Пример 1. Решить логарифмическое неравенство:

Вне зависимости от того, каким методом вы решаете то или иное логарифмическое неравенство, начинать всегда нужно с области допустимых значений. Основание логарифма должно быть положительным и не равным 1, а выражение, стоящее под знаком логарифма, — положительным. То есть область допустимых значений в нашем примере определяется следующей системой:

Видно, что решением данной системы является промежуток: .

Теперь, используя свойства логарифмов, представим двойку справа в виде логарифма с основанием . Тогда неравенства примет вид:

Далее решение неравенства разбивается на два случая:

1) если . В этом случае в основаниях логарифмов стоят одинаковые числа из интервала . Значит, соответствующие логарифмические функции являются убывающими. Поэтому, опуская знаки логарифмов, нам нужно изменить знак неравенства на обратный. В результате в этом случае приходим к следующему неравенству:

Изобразим соответствующую параболу, ветви которой направлены вверх, пересекающую ось OX в двух точках: и , являющихся корнями квадратного трёхчлена :

Тогда с учётом рассматриваемого ограничения на получаем для этого случая .

2) рассмотрим теперь случай, когда . В этом случае оба логарифма будут возрастающими, поэтому после ухода от знаков логарифма, знак неравенства останется прежним. То есть в этом случае исходное логарифмическое неравенство можно заменить следующим:

В учётом ограничения на решение этого неравенства можно проиллюстрировать на числовой прямой следующим образом:

То есть решение в данном случае имеет вид: .

Объединяя решения, полученные в пунктах а) и б), приходим к окончательному ответу, который имеет вид: .

Как известно, ЕГЭ по математике длится 235 минут, и чтобы распределить это время рационально на все задания, не помешало бы узнать короткие пути решения той или иной задачи. Так, на задача №14 оцениваемое в 2 балла, рекомендовано 30 минут (при условии, что ученик намерен решать все задания). Если проводить решение согласно всем известному методу интервалов, то, возможно, вы потратите все отведенное на него время. Существует ли такой метод решения неравенств, при котором мы сможем упростить наши вычисления, тем самым сохранив время?

Вернемся к нашему неравенству. Описанный в предыдущем параграфе способ является правильным, но при этом чрезвычайно неудобным. Как видите, приходится рассматривать два отдельных случая, что существенно повышает вероятность совершения ошибки. Гораздо проще поступить следующим образом. Перепишем исходное логарифмическое неравенства в виде:

А дальше, в области допустимых значений, то есть при (это мы установили выше), данное неравенство можно заменить следующим равносильным ему неравенством:

Ну действительно, если , то первая скобка положительна, и на неё можно разделить, не меняя при этом знак неравенства. Если же , то первая скобка отрицательна, и при делении на неё, знак неравенства изменится на противоположный.

То есть мы получили ровно то же самое, что имели в предыдущем пункте. Но при этом нет необходимости рассматривать два случая. Всё решается в рамках одного единственного неравенства. И хотя этот способ не избавляет нас от необходимости определения области допустимых значений, он всё равно приводит к существенному упрощению решения задачи.

Решаем полученное неравенство методом интервалов. Для этого поменяем знаки во второй скобке, разделим обе части неравенства на -1, поменяв знак неравенства:

Теперь разложим выражение во вторых скобках на множители:

Изобразим на числовой прямой множество решений полученного неравенства (стрелкой обозначена область допустимых значений исходного логарифмического неравенства):

В результате получаем тот же результат, что и в предыдущем параграфе:

Это метод рационализации (оптимизации, декомпозиции, замены множителей, замены функций, обобщенный метод интервалов, правило знаков)

Теоретическое обоснование метода

Часто, при решении логарифмических неравенств, встречаются задачи с переменным основанием логарифма. Так, неравенство вида

является стандартным школьным неравенством. Как правило, для его решения применяется переход к равносильной совокупности систем:

Недостатком данного метода является необходимость решения семи неравенств, не считая двух систем и одной совокупности. Уже при данных квадратичных функциях решение совокупности может потребовать много времени. Можно предложить альтернативный, менее трудоемкий метод решения этого стандартного неравенства. Это метод рационализации неравенств, известный в математической литературе под названием декомпозиции.

Метод декомпозиции

Метод декомпозиции заключается в замене сложного выражения F(x) на более простое выражение G(x), при которой неравенство G(x)^0 равносильно неравенству F(x)^0 в области определения F(x).

f, g, h – выражения с переменной х, a – фиксированное число или функция ( а>0, a≠1).

	Выражение F	Выражение G
1


2


3


4


5

6

Из данных выражений можно вывести некоторые следствия (с учетом области определения):

0  0

В указанных равносильных переходах символ ^ заменяет один из знаков неравенств: >, <, ≤, ≥.

Для решения:

1) Рассмотрим пример решения логарифмического неравенства двумя методами

1. Метод интервалов

-11/6

-5/3

////////////////////////////

О.Д.З.

a) b)

-5/3

-11/6

////////////////

//////////////////

///////

//////////////////////

-1

-5/3

Нет решений

/////////////////////

-1

Ответ: ( ;

2. Метод декомпозиции (рационализации)

//////////////////////////////////////////////////////////////////

-1

Ответ: ( ;

2. Пример

2) ,

, ,

, ;

U U .

Ответ. , , .

3) Пример

Решение.

;

Ответ.

4. Пример.

2) ,

, , , ,

, .

3) U .

Ответ. , .

5)log12x2-41+35(3 – x) ≥ log2x2-5x+3(3- x).

Решение. Запишем неравенство в виде log12x2-41+35(3 – x) — log2x2-5x+3(3- x) ≥ 0 и заменим его равносильной системой, используя метод рационализации

Для решения первых трёх неравенств системы используем метод интервалов.

Ответ:

6) ≥ 0.

Решение. Заменим данное неравенство равносильной системой, используя метод рационализации

< 2.

При решении неравенства (х – 1)(х – 2) < 0 системы учтены условия x < 3, x > 0, x ≠ 1. Условие 1 < x < 2 позволяет исключить множитель x – 1 > 0 в первом неравенстве системы.

Ответ: .

Дополнительно

[0; 4]

///////////////////////////////////////////////////////////////

-1/3

-1

///////////////////////////////////////////////////////////////

Ответ: [0; 4]

-2

Ответ:

Решение:

Ответ: (-1;1) U (3;5)

10) Решите неравенство log 2x+3 x2 < 1.

Решение. Запишем неравенство в виде log2x+3x2 – 1< 0 и заменим его равносильной системой, используя метод рационализации

(2x + 2)(x2 – 2x – 3) < 0

2x + 3 > 0

x ≠ 0

(x + 1)(x + 1)(x – 3) < 0

x > 1,5

x ≠ 0

Ответ: (-1.5; -1) (-1; 0) (0; 3).

11) .

Решение. Получим следующую систему неравенств:

Решая первые четыре неравенства, практически находим ОДЗ исходного неравенства:

Откуда: .

Решим теперь пятое неравенство системы. После элементарных преобразований получим неравенство

Умножим второй сомножитель на -1 и поменяем знак неравенства:

Нетрудно заметить, что корнями второго множителя в этом неравенстве являются числа 1 и -2. Поэтому, раскладывая второй множитель на одночлены первого порядка, получаем:

Это неравенство легко решить методом интервалов: .

С учетом найденного ранее ОДЗ, получаем окончательный ответ.

Ответ: .

12)

Решение.

, , ,

, , .

, .

Ответ. , .

13)

, .

Ответ. .

Дополнительно для самостоятельного решения:

. Ответ. .

. Ответ. , .

. Ответ.

. Ответ. .

Комментарий.

а) проводят рационализацию без учета области определения данного неравенства;

б) применяют метод рационализации к неравенствам, не приведенным к стандартному виду F(x) ˅ 0;

в) формально применяют метод рационализации к выражениям вида

, заменяя на выражение ;

г) подменяют формулировку «о совпадении знаков выражений для каждого

допустимого значения х» на неверную формулировку «о совпадении значений

выражений для каждого допустимого значения х».

Для работы с учениками:

Детям нужно рекомендовать использование метода рационализации в логарифмических неравенствах, когда неизвестное находится в основании степени.

Для отработки навыка решения предлагать решение в 3действия:

Найти область определения неравенства.

Использование замены функций по формулам рационализации.

Решить систему всех полученных условий.

Список литературы:

Семенов А.Л., Ященко И.В. Математика 2021. 30 вариантов. М.: Экзамен, 2021

Методы решения неравенств с одной переменной. www.alexlarin.net

Лысенко Ф.Ф., Кулабухова С.Ю. Математика. Подготовка к ЕГЭ – 2021.

Источник

Неравенства. Метод замены множителя (метод рационализации)

Полезный прием для решения сложных неравенств на ЕГЭ по математике – метод рационализации неравенства. Другое название — метод замены множителя. Это один из тех секретов, о которых ученику рассказывает репетитор. В учебниках о таком не написано.

Суть метода в том, чтобы от неравенства, содержащего в качестве множителей сложные показательные или логарифмические выражения, перейти к равносильному ему более простому рациональному неравенству.

Давайте для начала вспомним, что такое равносильные уравнения (или неравенства). В школьной программе этот важный вопрос почти не обсуждается. Поэтому запишем определение.

Равносильными называются уравнения, множества решений которых совпадают.

Заметим, что внешне уравнения могут быть и не похожи друг на друга.

Например, уравнения (x − 3)² = 0 и x − 3 = 0 равносильны. Число 3 является единственным решением и того, и другого.

Уравнения $x^{2}=-1$ и также равносильны. Оба они не имеют решений. Другими словами, множество решений каждого из них – пусто.

Уравнения и $2x-1=(x-2)^{2}$ не являются равносильными. Решением первого уравнения является только x = 5. Решения второго – два числа: x = 5 и x = 1. Получается, что возведение обеих частей уравнения в квадрат в общем случае приводит к уравнению, неравносильному исходному.

Аналогичное определение – для неравенств.

Равносильными называются неравенства, множества решений которых совпадают.

Например, неравенства и $frac{x-1}{x-3}>0$ равносильны – ведь множества их решений совпадают. В этом легко убедиться с помощью метода интервалов.

Неравенства $log_{2}x>log_{2}5$ и x> 5 также равносильны при x> 0 . Заметим, что внешне эти неравенства не похожи – одно из них логарифмическое, другое алгебраическое.

Другими словами, при x > 0 неравенства $log_{2}x-log_{2}5>0$ и x-5>0 имеют одинаковые решения. Если какое-либо число x > 0 является решением одного из них, то оно будет и решением второго.

А это значит, что при любом x > 0 выражение $log_{2}x-log_{2}5$ будет иметь такой же знак, как и выражение x − 5. Следовательно, если в какое-либо сложное неравенство входит в качестве множителя выражение $log_{2}x-log_{2}5$ , то при выполнении условия x > 0 его можно заменить на более простое x − 5 и получить неравенство, равносильное исходному.

Вот ключевой момент. На этом и основан метод рационализации – замены множителей, содержащих сложные логарифмические или показательные выражения, на более простые алгебраические множители.

Например, выражение вида $log_{a}f-log_{a}g$ , где f и g – функции от x, a – число, можно заменить на более простое (f − g) (a − 1) – конечно, при условии, что f(x) > 0 и g(x) > 0. Доказательство легко провести самостоятельно.

А сейчас – самое главное: волшебная таблица, позволяющая заменять сложные логарифмические (или показательные) множители в неравенствах на более простые. Эта таблица является ключом к задаче С3. Вот увидите, она выручит вас на ЕГЭ по математике:

Сложный множитель	На что заменить
log_h f − log_h g	(h − 1) (f − g)
log_h f − 1	(h − 1) (f − h)
log_h f	(h − 1) (f − 1)
h^f − h^g	(h − 1) (f − g)
h^f − 1	(h − 1) · f
f^h − g^h	(f − g) · h
f, g — функции от x. h — функция или число.

Конечно же, все выражения, которые содержат логарифмы, существуют при f, g, h > 0 и h ≠ 1.

Когда на ЕГЭ по математике вы применяете метод рационализации (замены множителя), – обязательно поясните, что вы им воспользовались. И не забудьте доказать соответствующую формулу. Иначе можно потерять балл.

Обратите внимание, что мы говорим о замене множителя в неравенствах вида Знак здесь может быть любой: >, ≥, ≤. Правая часть обязательно должна быть равна нулю. И заменяем мы именно множитель (а не слагаемое, например). Иначе ничего не получится.

Перейдем к практике – к решению задач из вариантов ЕГЭ по математике Профильного уровня.

1. $log_{2-x}(x+2)cdot log_{x+3}(3-x)leq 0$ .

ОДЗ неравенства: .

Применим метод рационализации. В соответствии с нашей таблицей, множитель $log_{2-x}(x+2)$ заменим на (2 − x − 1)(x + 2 − 1). Множитель вида $log_{x+3}(3-x)$ заменим на (x + 3 − 1)(3 − x − 1). Таким образом, от логарифмического неравенства мы перешли к рациональному:

(1 − x) (x + 1) (x + 2) (2 − x) ≤ 0.

Решим его методом интервалов:

Ответ: .

2. $frac{10^{x}}{2cdot log^{2}_{2}(x+1)^{2}cdot log_{3}(x+2)}leq frac{(15cdot 3^{x})^{x}}{9cdot log^{2}_{2}(x+1)^{2}cdot log_{3}(x+2)}.$

Начнем с ОДЗ.

$left{begin{matrix} xneq 0;\ x>-2;\ xneq -1. end{matrix}right.$

Заметим, что выражение $log^{2}_{2}(x+1)^{2}$ положительно при x ∈ ОДЗ. Умножим обе части неравенства на это выражение.
Упростим числитель правой части неравенства:

$(15cdot 3^{x})^{x}=5^{x}cdot 3^{x}cdot 3^{x^{2}}=5^{x}cdot 3^{x^{2}+x}$
Поделим обе части неравенства на 5^x > 0:

$frac{2^{x}}{2log_{3}(x+2)}leq frac{3^{x^{2}+x}}{9log_{3}(x+2)}: : Leftrightarrow \ , , \ : : \ Leftrightarrow frac{2^{x-1}-3^{x^{2}+x-2}}{log_{3}(x+2)}leq 0: : Leftrightarrow \ , , \ : : \ Leftrightarrow frac{2^{x-1}-3^{(x-1)(x+2)}}{log_{3}(x+2)}leq 0.$ Неравенство уже намного проще, чем исходное. Но основания степеней разные! Чтобы применить метод рационализации, нам придется представить 2^{x − 1} в виде степени с основанием 3.

$2^{x-1}=3^{log_{3}2^{x-1}}=3^{(x-1)log_{3}2}.$ Неравенство примет вид:

$frac{3^{(x-1)log_{3}2}-3^{(x-1)(x+2)}}{log_{3}(x+2)}leq 0.$ Воспользуемся методом замены множителя. Множитель вида h^f −h^g можно заменить на (h − 1) (f − g). Да и логарифм в знаменателе можно заменить на выражение x + 1.

$frac{(x-1)(x-(log_{3}2-2))}{x+1}geq 0.$ Оценим $log_{3}2-2$ . Это необходимо сделать, чтобы правильно расставить точки на числовой прямой.

$log_{3}1<log_{3}2<log_{3}3;$ $0<log_{3}2<1$ $-2<log_{3}2-2<-1$ Ответ:

3. $frac{10^{log_{2}x}}{2x^{2}(x+1)}leq frac{(15cdot 3^{log_{2}x})^{log_{2}x}}{9x^{2}(x+1)}$ .

Постараемся упростить это неравенство. Область допустимых значений

$left{begin{matrix} x>0;\ x+1neq 0. end{matrix}right.$ Отсюда следует, что x > 0. Это хорошо, потому что при данных значениях x выражение x + 1 строго положительно, следовательно, мы можем умножить на него обе части неравенства. Да и на x² тоже можно умножить обе части неравенства, и тогда оно станет проще:

$frac{10^{log_{2}x}}{2}leq frac{15^{log_{2}x}cdot 3^{log^{2}_{2}x}}{9}$ Преобразуем числители выражений в левой и правой части и сделаем замену log₂x = t:

$frac{2^{t}cdot 5^{t}}{2}leq frac{3^{t}cdot 5^{t}cdot 3^{t^{2}}}{9}$ Теперь обе части неравенства можно сократить на 5^t > 0:

$2^{t-1}leq 3^{t^{2}+t-2};$
$2^{t-1}-3^{(t+2)(t-1)}leq 0.$

Поскольку $2=3^{log_{3}2}$ , выражение 2^t−1 можно записать как 3^{(t−1)·log₃2}:

$3^{(t-1)cdot log_{3}2}leq 3^{(t+2)(t-1)};$ $(t-1)cdot log_{3}2leq (t-1)(t+2);$ $(t-1)cdot log_{3}2-(t-1)(t+2)leq 0.$ $(t-1)(log_{3}2-t-2)leq 0;$ $(t-1)(t-(log_{3}2-2))leq 0.$ Заметим, что log₃2 − 2 < 0.

Мы получили квадратичное неравенство относительно t. Решим его:

Итак, t ≥ 1 или t ≤ log₃2 − 2.

Вернемся к переменной x:

$: \ log_{2}xgeq 1\ xgeq 2;$ или $: \ log_{2}xleq log_{3}2-2;\ 0<xleq 2^{log_{3}2-2}.$

Ответ: $x in (0;2^{log_3 2-2}]cup[2;+infty).$

4. Еще одна задача из той же серии:

$frac{14^{log_{2}(4x)}}{7cdot log^{2}_{2}(32x)cdot log_{2}(0,25x)}geq frac{(4cdot 2^{log_{2}(4x)})^{log_{2}(4x)}}{4cdot log^{2}_{2}(32x)cdot log_{2}(0,25x)}.$ Запишем ОДЗ:

$left{begin{matrix} x>0;\ 32xneq 1;\ 0,25xneq 1. end{matrix}right.$

$xin left ( 0;frac{1}{32} right )cup left ( frac{1}{32};4 right )cup left (4;+infty right ) .$

Умножим обе части неравенства на $log^{2}_{2}32x>0$ . Постараемся упростить числители выражений в левой и правой части:

$frac{7^{log_{2}(4x)}cdot 2^{log_{2}(4x)}}{7cdot log_{2}(0,25x)}geq frac{4^{log_{2}(4x)}cdot 2^{(log_{2}(4x))^{2}}}{4cdot log_{2}(0,25x)}$
Поделим обе части неравенства на $2^{log_{2}(4x)}>0.$

$frac{7^{log_{2}(4x)}}{7cdot log_{2}(0,25x)}geq frac{2^{(log_{2}(4x))^{2}+log_{2}(4x)}}{4cdot log_{2}(0,25x)};$

$frac{7^{log_{2}(4x)-1}-2^{left ((log_{2}(4x))^{2}+log_{2}(4x)-2 right )}}{ log_{2}(0,25x)} geq 0$
Хорошо бы сделать замену. Пусть log₂(4x) = t. Тогда:

$log_{2}x=t-2;$

$log_{2}(0,25x)=log_{2}left ( frac{1}{4} right )+log_{2}x=log_{2}x-2=t-4.$ Неравенство примет вид:

$frac{7^{t-1}-2^{t^{2}+t-2}}{t-4}geq 0.$
Мы уже знаем, как представить число 7 в виде степени числа 2: $7=2^{log_{2}7}.$

$frac{2^{(t-1)cdot log_{2}7}-2^{(t-1)(t+2)}}{t-4}geq 0.$ Применим метод рационализации:

$frac{(t-1)cdot log_{2}7-(t-1)(t+2)}{t-4}geq 0;$

$frac{(t-1) (log_{2}7-t-2)}{t-4}geq 0;$

Оценим $log_{2}7-2:$

4 < 7 < 8;

$log_{2}4<log_{2}7<log_{2}8;$

$2<log_{2}7<3$

$0<log_{2}7-2<1$

$tleq log_{2}7-2\ , \ log_{2}(4x)leq log_{2}7-2;\ , \ log_{2}(4x)leq log_{2}frac{7}{4};\ , \ 0<xleq frac{7}{16};$ или $1leq t<4;\ , \ 1leq log_{2}(4x)<4;\ , \ log_{2}2leq log_{2}(4x)<log_{2}16;\ , \ frac{1}{2}leq x<4;$

Ответ: $xin left ( 0;frac{1}{32} right )cup left ( frac{1}{32};frac{7}{16} right ]cup left [ frac{1}{2};4 right ).$

5. Еще одна задача-страшилка из того же сборника:

$frac{log_{2^{left ( left ( x-1 right )^{2}-1 right )}}left ( log_{(2x^{2}+10x+15)}(x^{2}+2x) right )}{log_{2^{left ( left ( x-1 right )^{2}-1 right )}}left ( x^{2}+10x+26 right )}geq 0.$ Начнем с ОДЗ. Условий будет много – все выражения под логарифмами должны быть положительны, все основания логарифмов положительны и не равны единице, и еще знаменатель не равен нулю

$left{begin{matrix} (x-1)^{2}-1neq 0;\ x(x+2)>0;\ xneq -5. end{matrix}right.$

Применим в левой части неравенства формулу перехода к другому основанию:

$frac{log_{c}b}{log_{c}a}=log_{a}b;$

$log_{x^{2}+10x+26}left ( log_{2x^{2}+10x+15} left ( x^{2}+2x right )right )geq 0.$

Последовательно применим метод замены множителя, то есть метод рационализации.

Напомним, что множитель log_h f можно заменить на (h-1)( f-1), а множитель (log_h f — 1) — на (h — 1)( f — h):

$(x^{2}+10x+25)(log_{2x^{2}+10x+15}(x^{2}+2x)-1)geq 0;$

Поскольку $(x+5)^{2}>0$ при x ∈ ОДЗ, а $2x^{2}+10x+14>0$ при всех x, получим:

С учетом ОДЗ:

Ответ: x ∈ (-5; -3].

Посмотрим, чем поможет метод замены множителя в решении сложного показательного неравенства.

6. Решите неравенство: $displaystyle frac{{rm 2}cdot {{rm 3}}^{{rm 2x+1}}{rm -}{{rm 6}}^{{rm x}}{rm -}{{rm 4}}^{{rm x+1}}{rm -}{rm 9}}{{{rm 9}}^{{rm x}}{rm -}{rm 3}}le {rm 3.}$

$displaystyle frac{{rm 2}cdot {{rm 3}cdot {rm 3}}^{{rm 2x}}{rm -}{{rm 6}}^{{rm x}}{rm -}{rm 4}cdot {{rm 2}}^{{rm 2x}}{rm -}{rm 3}cdot {{rm 3}}^{{rm 2x}}{rm -}{rm 9+9}}{{{rm 3}}^{{rm 2x}}{rm -}{rm 3}}le {rm 0}.$

$displaystyle frac{{{rm 3}cdot {rm 3}}^{{rm 2x}}{rm -}{{rm 3}}^{{rm x}}cdot {{rm 2}}^{{rm x}}{rm -}{rm 4}cdot {{rm 2}}^{{rm 2x}}}{{{rm 3}}^{{rm 2x}}{rm -}{rm 3}}le {rm 0}.$

Числитель дроби в левой части — однородное выражение, где каждое слагаемое имеет степень 2х. Поделим обе части неравенства на ${{rm 2}}^{{rm 2}{rm x}}{rm textgreater 0.}$

Получим:

$displaystyle newline frac{3 cdot left (frac{3}{2} right )^{2x}-left (frac{3}{2} right )^{x}-4}{3^{2x}-3}leq 0;$

$displaystyle newline , newline 3 cdot left (frac{3}{2} right )^{2x}-left (frac{3}{2} right )^{x}-4=0;$

$displaystyle newline , newline frac{3left ( left ( frac{3}{2} right )^x+1 right )left ( left ( frac{3}{2} right )^x-frac{4}{3} right )}{3^{2x}-3}leq 0.$

Разложим числитель на множители.

Сделаем замену:

$displaystyle newline left ( frac{3}{2} right )^x=t; , ,3t^2-t-4=0;$

$displaystyle newline , newline t=frac{1pm 7}{6}; , t_1=-1; , t_2=frac{4}{3};$

$displaystyle newline , newline 3t^2-t-4=3left ( t+1 right )left ( t-frac{4}{3} right ).$

Вернемся к неравенству:

$displaystyle frac{3left ( left ( frac{3}{2} right )^x+1 right )left ( left ( frac{3}{2} right )^x-frac{4}{3} right )}{3^{2x}-3}leq 0.$

Поскольку $displaystyle {left(frac{3}{2}right)}^x textgreater 0$ , поделим обе части неравенства на $displaystyle {left(frac{3}{2}right)}^x+1 textgreater 0.$

$displaystyle frac{{left(frac{3}{2}right)}^x-frac{4}{3}}{3^{2x}-3}le 0.$

Применяя метод рационализации, множитель вида h^f-h^g заменяем на

Получим: $displaystyle newline frac{left ( frac{3}{2} -1right )left ( x-log_{frac{3}{2}}frac{4}{3} right )}{left ( 3-1 right )left ( 2x-1 right )} leq 0;$

$displaystyle newline , newline frac{x-log_{frac{3}{2}}frac{4}{3}}{x-frac{1}{2}}leq 0.$

Остается решить неравенство методом интервалов. Но как сравнить $displaystyle frac{1}{2}$ и ${{log}_{frac{3}{2}} frac{4}{3} }$ ?

Что больше? Давайте представим $displaystyle frac{1}{2}$ как логарифм с основанием $displaystyle frac{3}{2}:$

$displaystyle frac{1}{2}={{log}_{frac{3}{2}} {left(frac{3}{2}right)}^{frac{1}{2}} }={{log}_{frac{3}{2}} sqrt{frac{3}{2}} };$

$displaystyle frac{4}{3} vee sqrt{frac{3}{2}};$

$displaystyle frac{16}{9} vee frac{3}{2};$

Значит, $displaystyle {{log}_{frac{3}{2}} frac{4}{3} } textgreater frac{1}{2}.$

Ответ: $displaystyle xin left(frac{1}{2}; {{log}_{frac{3}{2}} frac{4}{3} }right].$

7. Теперь логарифмическое неравенство. Обратите внимание, что здесь лучше всего записывать решение в виде цепочки равносильных переходов. И само неравенство, которое мы упрощаем, и область его допустимых значений мы записываем в одну систему. И решаем ее.

Решите неравенство: $displaystyle {{log}_{3-x} frac{x+4}{{left(x-3right)}^2} }ge -2.$

$displaystyle {{log}_{3-x} frac{x+4}{{left(x-3right)}^2} }ge -2 textless = textgreater left{ begin{array}{c}3-x textgreater 0 \3-xne 1 \displaystyle frac{x+4}{{left(x-3right)}^2} textgreater 0 \displaystyle {{log}_{3-x} frac{x+4}{{left(x-3right)}^2} }+2ge 0 end{array}right. .$

Мы объединили в систему и область допустимых значений, и само неравенство. Применим формулу логарифма частного, учитывая, что ${left(a-bright)}^2={left(b-aright)}^2 .$

Используем также условия

$left{ begin{array}{c}x textless 3 \xne 2 \x+4 textgreater 0 \{log}_{3-x}left(x+4right)-{log}_{3-x}{left(3-xright)}^2+2ge 0 end{array}right. textless = textgreater left{ begin{array}{c}x textless 3 \xne 2 \x textgreater -4 \{log}_{3-x}left(x+4right)ge 0 end{array}right. .$

Обратите внимание, как мы применили формулу для логарифма степени. Строго говоря, ${{log}_a {left(bleft(xright)right)}^2=2{{log}_a left|bleft(xright)right| } }.$

Поскольку $3-x textgreater 0, { log}_{3-x}{left(3-xright)}^2=2{{log}_{3-x} left|3-xright|= }2{{log}_{3-x} left(3-xright)=2. }$

Согласно методу замены множителя, выражение ${log}_{3-x}left(x+4right)$ заменим на

Получим систему:

$left{ begin{array}{c}xne 2 \-4 textless x textless 3 \left(2-xright)left(x+3right)ge 0 end{array}right. .$

Решить ее легко.

Ответ:

8. А теперь неравенство с ловушкой. Мы надеемся, что вы помните — нельзя извлекать корень из неравенства.

Решите неравенство: $displaystyle {{lg}^2 frac{{left(x+2right)}^2left(x+5right)}{5} textless {lg}^2frac{x+5}{20} }.$

Извлекать корень из неравенства нельзя! Можно перенести все в левую часть неравенства и разложить на множители как разность квадратов:

$displaystyle left ( lgfrac{left ( x+2 right )^2left ( x+5 right )}{5}-lgfrac{x+5}{20} right )left ( lgfrac{left ( x+2 right )^2left ( x+5 right )}{5}+lgfrac{x+5}{20} right ) textless 0.$

Применим формулы разности и суммы логарифмов, следя за областью допустимых значений. Все выражения под логарифмами в исходном неравенстве должны быть положительны.

$left{ begin{array}{c}displaystyle lgfrac{{left(x+2right)}^2left(x+5right)cdot 20}{5cdot left(x+5right)}cdot {lg left(frac{{left(x+2right)}^2cdot {left(x+5right)}^2}{100}right) } textless 0 \displaystyle {left(x+2right)}^2left(x+5right) textgreater 0 \x+5 textgreater 0 end{array}right. .$

Посмотрим на второе и третье неравенства системы. Поскольку х+5 положительно, то и выражение (x+2)^2 должно быть положительно.

Заметим, что решения неравенства — это все числа, кроме x= - 2.

Получим:

$left{ begin{array}{c}displaystyle lgleft ( 4cdotleft ( x+2 right )^2 right ) cdot lg left ( frac{left ( x+2 right )^2 cdot left ( x+5 right )^2}{100} right ) textless 0\x textgreater -5 \xne -2 end{array}right..$

По методу рационализации, каждый из множителей вида ${{log}_h f }$ заменяем на

$newline left{ begin{array}{c}displaystyle left(10-1right)cdot left(4{left(x+2right)}^2-1right)cdot left(10-1right)left(frac{{left(x+2right)}^2cdot {left(x+5right)}^2}{100}-1right) textless 0 \x textgreater -5 \xne -2 end{array}right.newline textless = textgreater left{ begin{array}{c}left(2x+4-1right)left(2x+4+1right)left(left(x+2right)left(x+5right)-10right)left(left(x+2right)left(x+5right)+10right) textless 0 \x textgreater -5 \xne -2 end{array}right.newlinetextless = textgreater left{ begin{array}{c}left(2x+3right)left(2x+5right)cdot xcdot left(x+7right)cdot left(x^2+7x+20right) textless 0 \x textgreater -5 \xne -2 end{array}right.newline textless = textgreater left{ begin{array}{c}left(2x+3right)left(2x+5right)cdot xcdot left(x+7right) textless 0 \x textgreater -5 \xne -2 end{array}right. .$

Просто равносильные преобразования. Выражение положительно всегда — так как в уравнении дискриминант отрицателен. Осталось применить метод интервалов.

Ответ: $displaystyle xin left(-5;-frac{5}{2}right)cup left(-frac{3}{2};0right).$

Больше неравенств: Задание 15 Профильного ЕГЭ по математике

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Неравенства. Метод замены множителя (метод рационализации)» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Неравенства, решаемые методом рационализации

(blacktriangleright) Метод рационализации для показательной функции.
Если левая часть неравенства представлена в виде произведения некоторых множителей, а справа стоит ноль, то множители вида (a^{f(x)}-a^{g(x)}) можно заменить на произведение двух скобок: ((a-1)(f(x)-g(x))).

Пример.
Неравенство ((3^x-1)(0,25^x-16)(5x^2-9x-2)leqslant0) равносильно
неравенству ((3^x-3^0)(0,25^x-0,25^{-2})(5x^2-9x-2)leqslant 0),
которое в свою очередь по методу рационализации можно переписать в виде [(3-1)(x-0)(0,25-1)(x-(-2))(5x+1)(x-2)leqslant0]

(blacktriangleright) Метод рационализации для логарифмической функции.
Так как у логарифмов уже появляются ограничения на ОДЗ, то данный метод работает только при выполнении условий ОДЗ для логарифмов! Следовательно, последовательность решения подобных неравенств такая:

1) находим ОДЗ неравенства;

2) решаем неравенство, как будто ОДЗ выполнено;

3) пересекаем полученный ответ с ОДЗ и получаем итоговый ответ.

Суть метода рационализации:
1) если левая часть неравенства представлена в виде произведения некоторых множителей, а справа стоит ноль, то множители вида ((log_{a}f(x)-log_{a}g(x))) можно заменить на произведение двух скобок: ((a-1)(f(x)-g(x))) (при условии выполнения ОДЗ!).
2) если левая часть неравенства представлена в виде произведения некоторых множителей, а справа стоит ноль, то множители вида (log_{a}f(x)) можно заменить на произведение двух скобок: ((a-1)(f(x)-1)) (при условии выполнения ОДЗ!).

Пример.
Неравенство ((3+x-2x^2)log_{x+2}{(3x+5)}geqslant 0) с помощью метода рационализации можно переписать в виде: [begin{cases}
(3+x-2x^2)(x+2-1)(3x+5-1)geqslant 0\
x+2>0qquad qquad text{(ОДЗ)}\
x+2ne 1qquad qquad text{(ОДЗ)}\
3x+5>0 qquad qquad text{(ОДЗ)}end{cases}]

Задание
1

#1595

Уровень задания: Легче ЕГЭ

Решите неравенство

[begin{aligned}
log_{x + 1} (x — 1)geqslant 0
end{aligned}]

ОДЗ: [begin{cases}
x + 1 > 0\
x + 1neq 1\
x — 1 > 0
end{cases}
qquadLeftrightarrowqquad
x > 1,.]

По методу рационализации: на ОДЗ

[begin{aligned}
log_{x + 1} (x — 1)geqslant 0qquadLeftrightarrowqquad (x + 1 — 1)cdot (x — 1 — 1)geqslant 0qquadLeftrightarrowqquad xcdot (x — 2)geqslant 0,.
end{aligned}]

Так как на ОДЗ (x > 1 > 0), то на ОДЗ последнее неравенство равносильно неравенству [x — 2geqslant 0qquadLeftrightarrowqquad x geqslant 2] C учётом ОДЗ в итоге: (xin[2; +infty).)

Ответ:

([2; +infty))

Задание
2

#1596

Уровень задания: Легче ЕГЭ

Решите неравенство

[begin{aligned}
log_{x^2} (x^2 + 1) > 0
end{aligned}]

ОДЗ: [begin{cases}
x^2 > 0\
x^2 neq 1\
x^2 + 1 > 0
end{cases}
qquadLeftrightarrowqquad
begin{cases}
x neq 0\
x neq pm 1,.
end{cases}]

По методу рационализации: на ОДЗ

[begin{aligned}
log_{x^2} (x^2 + 1) > 0qquadLeftrightarrowqquad (x^2 — 1)cdot (x^2 + 1 — 1) > 0qquadLeftrightarrowqquad (x^2 — 1)cdot x^2 > 0,.
end{aligned}]

Так как на ОДЗ (x^2 > 0), то на ОДЗ последнее неравенство равносильно неравенству [x^2 — 1 > 0qquadLeftrightarrowqquad x in(-infty; -1)cup(1; +infty),.] C учётом ОДЗ в итоге: (xin(-infty; -1)cup(1; +infty).)

Ответ:

((-infty; -1)cup(1; +infty))

Задание
3

#3144

Уровень задания: Равен ЕГЭ

Решите неравенство [(x^2+3x-10)cdot log_{0,5}(x^2-1)cdot
log_{(x^2-1)}(x+2)leqslant 0]

Выпишем ОДЗ неравенства: [begin{cases}
x^2-1>0\
x^2-1ne 1\
x+2>0 end{cases} quadLeftrightarrowquad xin
(-2;-sqrt2)cup(-sqrt2;-1)cup(1;sqrt2)cup(sqrt2;+infty).] Решим неравенство на ОДЗ. Заметим, что по формуле (log_abcdot
log_bc=log_ac) неравенство можно переписать в виде: [(x^2+3x-10)cdot log_{0,5}(x+2)leqslant 0] По методу рационализации данное неравенство равносильно: [(x^2+3x-10)cdot (0,5-1)(x+2-1)leqslant 0 quadLeftrightarrowquad
(x+5)(x-2)(x+1)geqslant 0] Решим полученное неравенство методом интервалов и получим ответ: [xin [-5;-1]cup [2;+infty)] Пересечем ответ с ОДЗ и получим окончательный ответ [xin (-2;-sqrt2)cup(-sqrt2;-1)cup[2;+infty)]

Ответ:

((-2;-sqrt2)cup(-sqrt2;-1)cup[2;+infty))

Задание
4

#1623

Уровень задания: Равен ЕГЭ

Решите неравенство

[begin{aligned}
log_{(x — 2)} (x + 3) geqslant dfrac{1}{log_{x^{2}} (x — 2)}
end{aligned}]

ОДЗ: [begin{cases}
x — 2 > 0\
x — 2neq 1\
x + 3 > 0\
x^2 > 0\
x^{2} neq 1
end{cases}
qquadLeftrightarrowqquad
begin{cases}
x > 2\
xneq 3
end{cases}]

На ОДЗ:
исходное неравенство равносильно неравенству

[begin{aligned}
&log_{(x — 2)} (x + 3) geqslant log_{(x — 2)}x^{2}qquadLeftrightarrowqquad log_{(x — 2)} (x + 3) — log_{(x — 2)}x^{2}geqslant 0qquadLeftrightarrow\
&Leftrightarrowqquad log_{(x — 2)} dfrac{(x + 3)}{x^2}geqslant 0,.
end{aligned}]

По методу рационализации: на ОДЗ

[begin{aligned}
&log_{(x — 2)} dfrac{(x + 3)}{x^2}geqslant 0 quadLeftrightarrowquad (x — 2 — 1)left(dfrac{x + 3}{x^2} — 1right)geqslant 0quadLeftrightarrow\
&Leftrightarrowquad (x — 3)cdotdfrac{x + 3 — x^2}{x^2}geqslant 0quadLeftrightarrowquad (x — 3)cdotdfrac{x^2 — x — 3}{x^2}leqslant 0
end{aligned}]

По методу интервалов на ОДЗ

Таким образом, с учётом ОДЗ исходное неравенство верно при [xinleft[dfrac{1+sqrt{13}}{2}; 3right).]

Ответ:

(left[0,5+0,5sqrt{13}; 3right))

Задание
5

#1598

Уровень задания: Равен ЕГЭ

Решите неравенство

[begin{aligned}
log_{(x + 1)} 2 geqslant dfrac{1}{log_{x} (x + 1)}
end{aligned}]

ОДЗ: [begin{cases}
x + 1 > 0\
x + 1neq 1\
x > 0\
xneq 1
end{cases}
qquadLeftrightarrowqquad
begin{cases}
x > 0\
xneq 1
end{cases}]

На ОДЗ:
исходное неравенство равносильно неравенству

[begin{aligned}
&log_{(x + 1)} 2 geqslant log_{(x + 1)} xqquadLeftrightarrowqquad log_{(x + 1)} 2 — log_{(x + 1)} xgeqslant 0qquadLeftrightarrow\
&Leftrightarrowqquad log_{(x + 1)} dfrac{2}{x}geqslant 0,.
end{aligned}]

По методу рационализации: на ОДЗ

[begin{aligned}
&log_{(x + 1)} dfrac{2}{x}geqslant 0 qquadLeftrightarrowqquad (x + 1 — 1)left(dfrac{2}{x} — 1right)geqslant 0qquadLeftrightarrowqquad xcdotdfrac{2 — x}{x}geqslant 0qquadLeftrightarrow\
&Leftrightarrowqquad 2 — xgeqslant 0qquadLeftrightarrowqquad xleqslant 2
end{aligned}]

Таким образом, с учётом ОДЗ исходное неравенство верно при [xin(0; 1)cup(1; 2].]

Ответ:

((0; 1)cup(1; 2])

Задание
6

#1602

Уровень задания: Равен ЕГЭ

Решите неравенство [log_{8-4x}(16x^2 — 8x + 1) leqslant 2.]

ОДЗ:

[begin{cases}
8 — 4x > 0\
8 — 4x neq 1\
16x^2 — 8x + 1 > 0
end{cases}
qquadLeftrightarrowqquad x in left(-infty; dfrac{1}{4}right) cup left(dfrac{1}{4}; dfrac{7}{4}right) cup left(dfrac{7}{4}; 2right).]

[log_{8-4x}(16x^2 — 8x + 1) — log_{8-4x}(8-4x)^2leqslant 0quadLeftrightarrowquad log_{8-4x}dfrac{16x^2 — 8x + 1}{(8 — 4x)^2}leqslant 0.] По методу рационализации это неравенство на ОДЗ равносильно:

[begin{aligned}
&(8 — 4x — 1)left(dfrac{16x^2 — 8x + 1}{(8 — 4x)^2} — 1right)leqslant 0 qquadLeftrightarrow\
&Leftrightarrowqquad (7 — 4x)cdotdfrac{16x^2 — 8x + 1 — (64 — 64x + 16x^2)}{(8 — 4x)^2}leqslant 0qquadLeftrightarrow\
&Leftrightarrowqquad dfrac{(7 — 4x)(56x — 63)}{(8 — 4x)^2}leqslant 0quadLeftrightarrowquaddfrac{(4x — 7)(8x — 9)}{(4x — 8)^2}geqslant 0
end{aligned}]

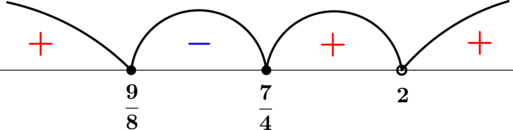
По методу интервалов:

откуда (x inleft(-infty; dfrac{9}{8}right]cupleft[dfrac{7}{4}; 2right)cup(2; +infty)).
Пересечем ответ с ОДЗ: (x inleft(-infty; dfrac{1}{4}right)cupleft(dfrac{1}{4}; dfrac{9}{8}right]cupleft(dfrac{7}{4}; 2right)).
Окончательный ответ [x inleft(-infty; dfrac{1}{4}right)cupleft(dfrac{1}{4}; dfrac{9}{8}right]cupleft(dfrac{7}{4}; 2right),.]

Ответ:

(left(-infty; dfrac{1}{4}right)cupleft(dfrac{1}{4}; dfrac{9}{8}right]cupleft(dfrac{7}{4}; 2right))

Задание
7

#2645

Уровень задания: Равен ЕГЭ

Решите неравенство [{large{left(4^{x^2-x-6}-1right)cdot
log_{0,25}left(4^{x^2+2x+2}-3right)leqslant 0}}]

(Задача от подписчиков)

Найдем ОДЗ: [4^{x^2+2x+2}-3>0quadLeftrightarrowquad 4^{x^2+2x+2}>4^{log_43}quadLeftrightarrowquad
x^2+2x+1+1>log_43quadLeftrightarrowquad (x+1)^2>log_43-1.]

Заметим, что (log_43<log_44=1), следовательно, число (log_43-1<0). Т.к. квадрат любого выражения всегда неотрицателен, то неравенство ((x+1)^2>log_43-1) выполнено при всех (x).
Следовательно, ОДЗ: (xin mathbb{R}).

Перейдем к неравенству: [{large{left(4^{x^2-x-6}-4^0right)cdot
log_{0,25}left(4^{x^2+2x+2}-3right)leqslant 0}}] Преобразуем его по методу рационализации: [begin{aligned} &(4-1)(x^2-x-6-0)cdot
(0,25-1)left(4^{x^2+2x+2}-3-1right)leqslant 0
quadLeftrightarrow\[2ex] Leftrightarrowquad &3(x^2-x-6)cdot
(-0,75)left(4^{x^2+2x+2}-4^1right)leqslant
0quadLeftrightarrow\[2ex]
Leftrightarrowquad &(x^2-x-6)cdot (4-1)(x^2+2x+2-1)geqslant
0quadLeftrightarrow\[2ex]Leftrightarrowquad &(x+2)(x-3)cdot (x+1)^2geqslant
0end{aligned}] Решая данное неравенство методом интервалов, получим ответ: [xin (-infty;-2]cup{-1}cup[3;+infty).]

Ответ:

((-infty;-2]cup{-1}cup[3;+infty))

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник