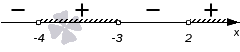Метод интервалов 11 класс егэ

Метод интервалов

Метод интервалов – простой способ решения дробно-рациональных неравенств. Так называются неравенства, содержащие рациональные (или дробно-рациональные) выражения, зависящие от переменной.

1. Рассмотрим неравенство:

Метод интервалов позволяет решить его за пару минут.

В левой части этого неравенства – дробно-рациональная функция. Рациональная, потому что не содержит ни корней, ни синусов, ни логарифмов – только рациональные выражения. В правой – нуль.

Метод интервалов основан на следующем свойстве дробно-рациональной функции.

Дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует.

Найдем нули функции в левой части нашего неравенства. Для этого разложим числитель на множители. (Если вы не помните, что такое нули функции и знак функции на промежутке – смотрите статью «Исследование графика функции»).

Напомним, как раскладывается на множители квадратный трехчлен, то есть выражение вида  .

, где  и  — корни квадратного уравнения .

Получим:

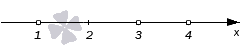
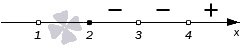
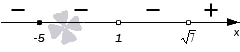
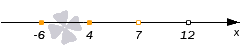
Рисуем ось X и расставляем точки, в которых числитель и знаменатель обращаются в нуль.

Нули знаменателя и  — выколотые точки, так как в этих точках функция в левой части неравенства не определена (на нуль делить нельзя).

Напомним, что мы изображаем точку на числовой прямой выколотой (пустой), если соответствующее значение переменной никак не может быть решением неравенства. В нашем примере точки и выколотые, потому что в них знаменатель обращается в ноль.

Нули числителя и  — закрашены, так как неравенство нестрогое. При  и  наше неравенство выполняется, так как обе его части равны нулю.

Эти точки разбивают ось X на 5 промежутков.

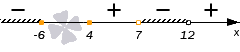
Определим знак дробно-рациональной функции в левой части нашего неравенства на каждом из этих промежутков. Мы помним, что дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует. Это значит, что на каждом из промежутков между точками, где числитель или знаменатель обращаются в нуль, знак выражения в левой части неравенства будет постоянным — либо «плюс», либо «минус».

И поэтому для определения знака функции на каждом таком промежутке мы берем любую точку, принадлежащую этому промежутку. Ту, которая нам удобна.
. Возьмем, например, и проверим знак выражения в левой части неравенства. Каждая из «скобок» отрицательная. Левая часть имеет знак .

Следующий промежуток: . Проверим знак при . Получаем, что левая часть поменяла знак на .

. Возьмем . При выражение положительно — следовательно, оно положительно на всем промежутке от до .

При  левая часть неравенства отрицательна. 

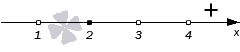
И, наконец, . Подставим и проверим знак выражения в левой части неравенства. Каждая «скобочка» положительна. Следовательно, левая часть имеет знак .

Мы нашли, на каких промежутках выражение положительно. Осталось записать ответ:

Ответ: .

Обратите внимание: знаки на промежутках чередуются. Это произошло потому, что при переходе через каждую точку ровно один из линейных множителей поменял знак, а остальные сохранили его неизменным.

Мы видим, что метод интервалов очень прост. Чтобы решить дробно-рациональное неравенство методом интервалов, приводим его к виду:

, или , или , или

(в левой части — дробно-рациональная функция, в правой — нуль).

Затем — отмечаем на числовой прямой точки, в которых числитель или знаменатель обращаются в нуль.
Эти точки разбивают всю числовую прямую на промежутки, на каждом из которых дробно-рациональная функция сохраняет свой знак.
Остается только выяснить ее знак на каждом промежутке.
Мы делаем это, проверяя знак выражения в любой точке, принадлежащей данному промежутку. После этого — записываем ответ. Вот и всё.

Но возникает вопрос: всегда ли знаки чередуются? Нет, не всегда! Надо быть внимательным и не расставлять знаки механически и бездумно.

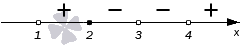
2. Рассмотрим еще одно неравенство:

Решение:

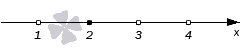
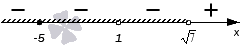
Снова расставляем точки на оси X. Точки и  — выколотые, поскольку это нули знаменателя. Точка  — тоже выколота, поскольку неравенство строгое, и значение переменной не может быть решением неравенства.

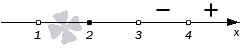
При числитель положителен, оба множителя в знаменателе отрицательны. Это легко проверить, взяв любое число с данного промежутка, например, . Левая часть имеет знак :

При числитель положителен; первый множитель в знаменателе положителен, второй множитель отрицателен. Левая часть имеет знак :

При ситуация та же! Числитель положителен, первый множитель в знаменателе положителен, второй отрицателен. Левая часть имеет знак :

Наконец, при все множители положительны, и левая часть имеет знак :

Ответ: .

Почему нарушилось чередование знаков? Потому что при переходе через точку 2 «ответственный» за неё множитель не изменил знак. Следовательно, не изменила знак и вся левая часть нашего неравенства.

Вывод: если линейный множитель  стоит в чётной степени (например, в квадрате), то при переходе через точку  знак выражения в левой части не меняется. В случае нечётной степени знак, разумеется, меняется.

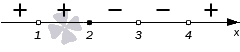
3. Рассмотрим более сложный случай. От предыдущего отличается тем, что неравенство нестрогое:

Решение:

Левая часть та же, что и в предыдущем примере. Та же будет и картина знаков:

Может, и ответ будет тем же? Нет! Добавляется решение Это происходит потому, что при и левая, и правая части неравенства равны нулю — следовательно, эта точка является решением.

Ответ: .

В задачах на ЕГЭ по математике такая ситуация встречается часто. Здесь абитуриенты попадают в ловушку и теряют баллы. Будьте внимательны!

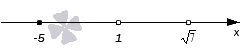
4. Что делать, если числитель или знаменатель не удается разложить на линейные множители? Рассмотрим такое неравенство:

Решение:

Квадратный трехчлен  на множители разложить нельзя: дискриминант отрицателен, корней нет. Но ведь это и хорошо! Это значит, что знак выражения при всех одинаков, а конкретно — положителен. Подробнее об этом можно прочитать в статье о свойствах квадратичной функции.

И теперь мы можем поделить обе части нашего неравенства на величину , положительную при всех .

Придём к равносильному неравенству:

Решим неравенство методом интервалов. Действуем по алгоритму: числитель левой части равен нулю при а знаменатель обращается в ноль при . Отметим эти точки на координатной прямой. Точки выколоты, потому что неравенство строгое. Эти точки разбивают числовую ось на три интервала. Найдем знаки на каждом из интервалов. На крайнем правом знак положителен, а дальше знаки чередуются.

Нам нужен «интервал со знаком минус», то есть такой, где Выпишем ответ.

Ответ:

Обратите внимание — мы поделили обе части неравенства на величину, о которой точно знали, что она положительна. Конечно, в общем случае не стоит умножать или делить неравенство на переменную величину, знак которой неизвестен.

5. Рассмотрим еще одно неравенство, на вид совсем простое:

Решение:

Так и хочется умножить его на . Но мы уже умные, и не будем этого делать. Ведь может быть как положительным, так и отрицательным. А мы знаем, что если обе части неравенства умножить на отрицательную величину — знак неравенства меняется.

Мы поступим по-другому — соберём всё в одной части и приведём к общему знаменателю. В правой части останется нуль:

Применим метод интервалов.

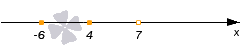
Действуем по алгоритму. Отметим на координатной прямой точки и . Они выколотые, потому что неравенство строгое. Эти точки разбивают ось Х на три интервала. Расставим знаки на каждом из них.

Ответ:

6. Решите неравенство:

Решение:

Приведем левую часть неравенства к общему знаменателю и преобразуем числитель:

Применим метод интервалов:

Числитель равен нулю при Знаменатель обращается в ноль при или . Неравенство строгое, поэтому все эти точки на числовой оси отмечаем как пустые.

Если , то . Далее знаки чередуются.

Нам нужны «интервалы со знаком минус». Выпишем их и получим ответ.

Ответ:

7. Решите неравенство

Решение:

Приведем неравенство к виду:

Для этого все перенесем в левую часть, приведем к общему знаменателю и разложим числитель и знаменатель на множители. Применяем формулу разности квадратов и формулу разложения квадратного трехчлена на множители

Получим:

Найдем нули числителя и знаменателя и отметим их на числовой оси:

Выпишем интервалы, где неравенство выполняется, и получим ответ.

Ответ:

8. Решите неравенство:

Решение:

Разложим левую часть неравенства на множители.

Для этого вынесем общий множитель за скобки, а затем воспользуемся формулой:

Получим:

Применим метод интервалов.

Левая часть неравенства обращается в ноль, если , или . Нанесем эти точки на координатную прямую. Все точки закрашенные, так как неравенство нестрогое, в нем присутствует знак «меньше или равно».

Ответ:

9. Решите неравенство:

Решение:

Разложим числитель на множители с помощью группировки:

Знаменатель тоже разложим на множители:

Неравенство примет вид:

Мы видим, что числитель равен нулю при

Знаменатель равен нулю при . Множитель стоит в числителе и в знаменателе, и он не может равняться нулю.

Отметим полученные точки на координатной прямой. Две из них закрашены (это 3 и 1), а две нет (это -1 и -2). Найдем знаки на каждом промежутке.

При переходе через точку знак не меняется, так как множитель присутствует и в числителе, и в знаменателе.

Выпишем ответ.

Ответ:

10. Решите неравенство:

Решение:

Разложим числитель и знаменатель на множители:

Напомним, что выражение мы разложили на множители, решив квадратное уравнение:

Неравенство примет вид:

Воспользуемся методом интервалов.

Числитель дроби в левой части неравенства равен нулю, если Знаменатель обращается в ноль, если или . Отметим эти точки на координатной прямой и определим знаки на интервалах.

Ответ:

11. Решите неравенство:

Решение:

Можно сразу применить метод интервалов.

Но лучше, чтобы не запутаться со знаками, умножить обе части неравенства на (-1) и не забыть поменять знак неравенства на противоположный.

Теперь применим метод интервалов.

Отметим на координатной прямой нули числителя и знаменателя и определим знаки на интервалах.

Обратите внимание, что знак не меняется при переходе через точку , так как множитель входит в выражение в левой части неравенства в четной степени.

Ответ:

12. Решите неравенство:

Решение:

Разложим числитель и знаменатель на множители:

Сократим на множитель при условии, что .

Здесь мы действуем чуть иначе, чем в задаче 9.

Неравенство равносильно системе:

Решаем второе неравенство системы методом интервалов:

Второму неравенству удовлетворяют точки .

Точка в этот промежуток не входит.

Ответ:

13. Решите неравенство:

Решение:

Разложив числитель на множители, получим:

Применим метод интервалов.

Отметим на числовой оси точки, в которых числитель и знаменатель обращаются в ноль. Обратите внимание, что точки -1 и 5 закрашены, а точки 2 и 4 пустые.

Определим знаки на интервалах.

Знак не меняется при переходе через точку , так как множитель входит в выражение в левой части неравенства в четной степени. При переходе через точку 4 знак меняется, степень соответствующего множителя нечетная.

В ответе запишем интервалы, на которых неравенство выполняется.

Ответ:

14. Решите неравенство:

Разложим числитель и знаменатель на множители, используя формулы сокращенного умножения: суммы и разности кубов, разности квадратов.

Кажется, что неравенство сложное. Попробуем разложить на множители выражения и

Оказывается, что дискриминанты соответствующих квадратных уравнений отрицательны, поэтому и при всех х.

Разделим обе части неравенства на эти положительные выражения.

Получим:

Неравенство равносильно системе:

Решим первое неравенство системы методом интервалов:

Его решением является промежуток [1;4], причем точка в этот промежуток не входит.

Ответ:

Мы показали на различных примерах, как применяется метод интервалов.

Сделаем вывод:
Метод интервалов помогает решать дробно-рациональные неравенства по алгоритму. Правила просты: приводим неравенство к такому виду, что в его левой части – произведение множителей или дробь, а в правой – ноль. Находим точки, в которых левая часть обращается в ноль или не определена. Отмечаем на числовой оси эти точки. Они разбивают числовую ось (или координатную прямую) на интервалы, на каждом из которых функция в левой части неравенства сохраняет свой знак. Определяем знаки на интервалах, помня о правилах чередования знаков. И записываем ответ.

---

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 1000    1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

Всего: 1000    1–20 | 21–40 | 41–60 | 61–80 …

На этой странице вы узнаете

• Как мы ежедневно расставляем знаки неравенства в жизни?
• Как быстро определить верное обозначение точки на прямой?
• Как правильно чередовать знаки на числовой прямой?

Решая уравнение, мы стремимся к тому, чтобы обе части были равны. Но существуют такие примеры, где мы заведомо знаем, что два выражения не могут быть равны между собой. Они называются неравенствами. 

Метод интервалов

Неравенство — это алгебраическое выражение, в котором одна сторона имеет отличное от другой значение. В неравенствах обычно одна сторона больше другой.

Для записи неравенств используют знаки > , < , ≥ , ≤ . 

При этом “>” и “<” — это строгие знаки неравенства, а “≥” и “≤” — нестрогие знаки неравенства. 

Их отличие в том, что нестрогие знаки неравенства включают граничные точки в итоговый промежуток, а строгие — нет. 

Рассмотрим пример неравенства (х — 10)(х + 21) > 0. 

Его можно решить несколькими способами. Например, вспомним, что положительным будет произведение двух положительных или двух отрицательных множителей, тогда получается совокупность из двух систем. 

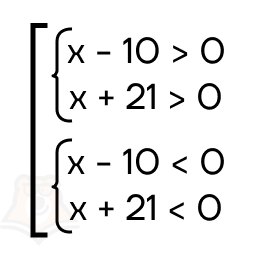
Однако этот способ решения очень трудоемкий и требует много времени. А если множителей будет больше, например, три или четыре, то время на решение в разы увеличивается. 

Небольшой секрет тайм-менеджмента: как сократить время при решении неравенств?  В таких случаях на помощь приходит метод интервалов.

Метод интервалов — специальный алгоритм решения для сложных неравенств вида f(x) > 0. При этом знак неравенства может быть любым.

Интервал — это промежуток на числовой прямой, ограниченный двумя различными числами.

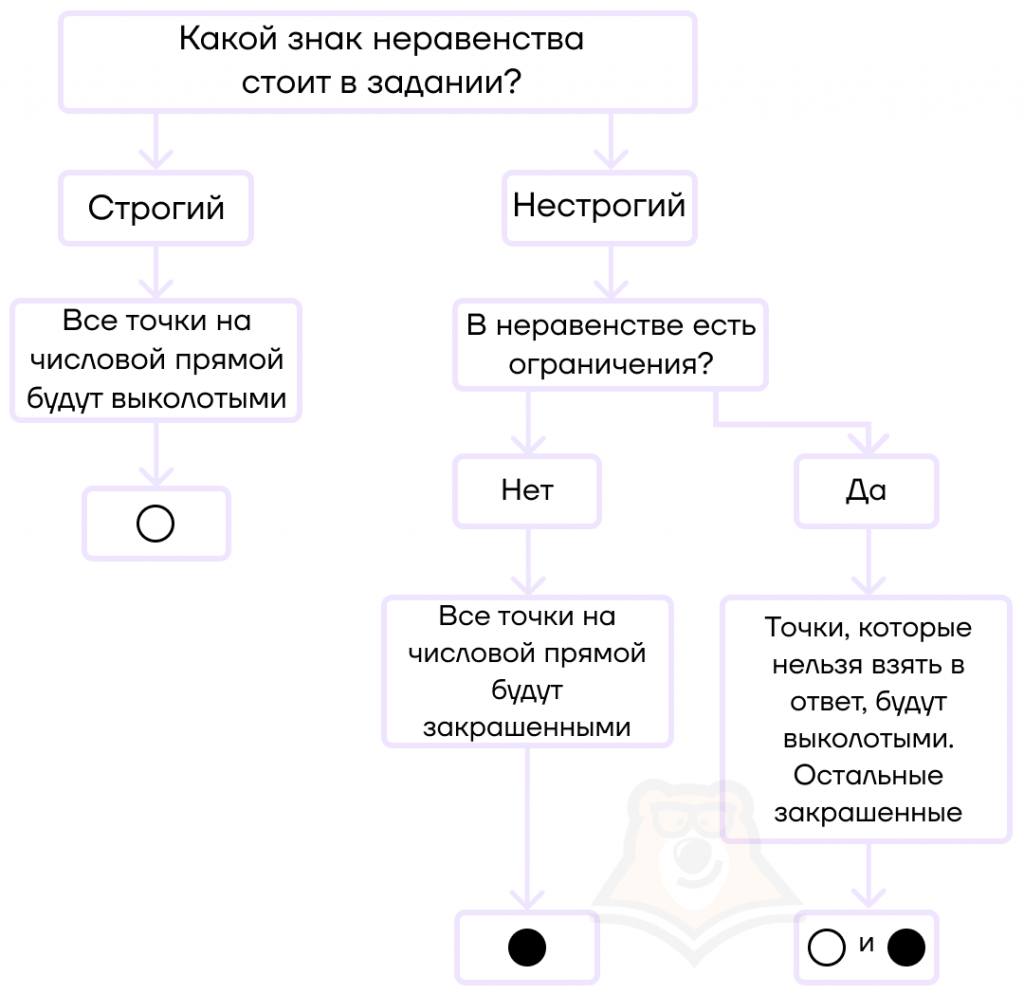
Расставляя полученные корни на прямой, необходимо отмечать их точками. При этом от того, какая отмечена точка (выколотая или закрашенная), будет зависеть ответ. 

• Если в неравенстве стоит строгий знак неравенства, то все точки на прямой должны быть выколотыми. 

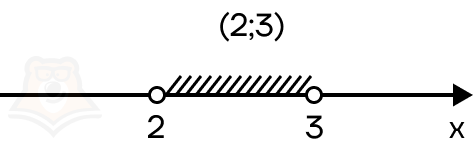
Таким образом, граничные точки не будут включены в итоговый промежуток. Для записи таких точек используют круглые скобочки. Например, в промежуток (2;3) включаются все значения от 2 до 3, но не включаются граничные точки. 

• Если в неравенстве стоит нестрогий знак неравенства, то найденные корни должны быть отмечены закрашенными точками. 

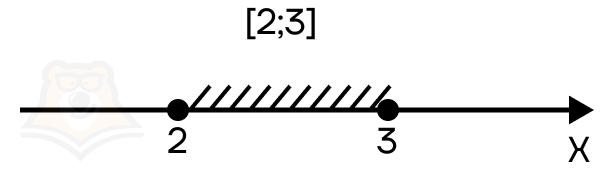
Это означает, что мы включаем их в итоговый промежуток. Для записи таких точек используют квадратные скобочки. Например, в промежуток [2;3] включаются все значения от 2 до 3, в том числе и граничные точки. 

• Если в неравенстве появляются ограничения и некоторые точки нельзя взять в ответ, то такие точки должны быть выколотыми на числовой прямой, при этом знак самого неравенства может быть как строгим, так и нестрогим. 

Например, если необходимо решить неравенство с дробью, то нули знаменателя на числовой прямой обязательно должны быть обозначены выколотыми точками. 

Стоит отметить, что непрерывная функция будет менять знак только в точках, в которых она равна 0. Подробнее узнать про смену знака функции можно в статье «Определение и график функции». Именно поэтому в методе интервалов мы ищем и отмечаем нули функции на прямой — только при переходе через них будет меняться знак функции. 

При этом существует способ, с помощью которого можно быстро расставить знаки на прямой. Достаточно определить знак на одном из интервалов, а дальше чередовать знаки при переходе через каждую точку на прямой. 

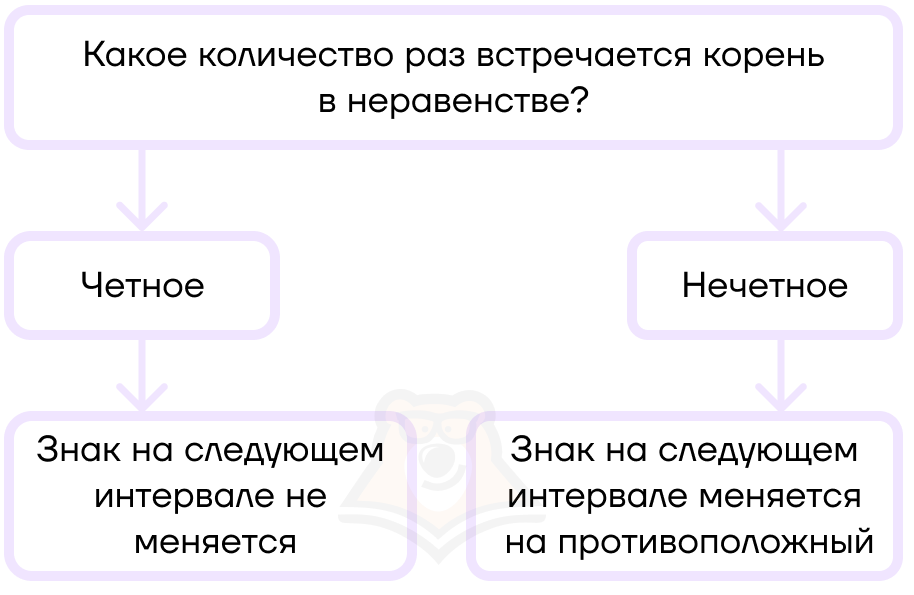
Правила чередования знаков: 

• Если корень повторяется нечетное количество раз (то есть его степень нечетная), то знак при переходе на следующий интервал меняется.

• Если корень повторяется четное количество раз (его степень четная), то знак при переходе на следующий интервал не меняется. 

Практика

Рассмотрим несколько примеров, чтобы на практике разобрать применение метода интервалов для решения неравенств.  

Пример 1. Решить неравенство x² + 8x — 33 > 0. 

Шаг 1. Первым шагом необходимо найти нули функции, для этого приравниваем выражение слева к 0: x² + 8x — 33 = 0. 

Шаг 2. Находим корни уравнения, получаем х = 3 и х = -11. 

Шаг 3. Расставляем полученные корни на числовой прямой. Поскольку знак неравенства строгий, то точки должны быть выколотыми:

Шаг 4. Дальше необходимо определить знаки на каждом интервале. Для этого подставим х = -12 в x² + 8x — 33. Получаем: 

(-12)² + 8*(-12) — 33 = 144 — 96 — 33 = 15. 

Получается положительное число, следовательно, интервал от минус бесконечности до -11 положительный. Поскольку все корни в неравенстве повторяются нечетное количество раз (по одному разу), то знаки чередуются. 

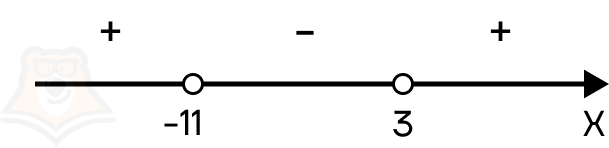
В ответ необходимо записать промежутки с положительным знаком, следовательно, ответом будет х ∈ (-∞; -11) U (3; +∞). 

Пример 2. Решить неравенство (frac{2х^2 + 22х — 204}{(х-3)(х+5)} ≤ 0). 

1. Находим нули функции. 

Нули числителя: 2х² + 22х — 204 = 0. Решая уравнение, получаем х = 6 и х = -17. 

Нули знаменателя: (х — 3)(х + 5) = 0, следовательно, х = 3 и х = -5. 

2. Расставляем полученные корни на числовой прямой. Нули числителя будут обозначены закрашенными точками, поскольку знак неравенства нестрогий. А вот нули знаменателя — выколотыми, поскольку знаменатель не может равняться 0, следовательно, и нули знаменателя не должны входить в итоговый промежуток. 

3. Определяем знак на крайнем левом промежутке, подставляя х=-20 в дробь:

(frac{2(-20)^2 + 22(-20) — 204}{(-20 -3)(-20 +5)} = frac{2 * 400 — 440 — 204}{(-23) * (-15)} = 156345. )

Следовательно, промежуток положительный. 

4. Поскольку каждый корень встречается один раз, то есть нечетное количество раз, то знаки будут чередоваться. 

В ответ необходимо включить отрицательные промежутки. Следовательно, ответом будет х ∈ [-17; -5) U (3; 6].

Пример 3. Решить неравенство (frac{1}{х^2} ≥ frac{1}{х+2})

1. Первым делом следует отметить, что знаменатели не могут быть равны 0, следовательно, х² ≠ 0 и х + 2 ≠ 0, отсюда получаем х ≠ 0 и х ≠ -2. 

2. Теперь перенесем все части неравенства влево: 

(frac{1}{х^2} — frac{1}{х+2} ≥ 0). 

Приведем к общему знаменателю:

 (frac{х + 2 — х^2}{х^2 (х + 2)} ≥ 0). 

Для решения неравенства будет удобнее, если перед х² в числителе будет стоять положительный знак, для этого умножим неравенство на -1. 

При умножении неравенства на отрицательное число знак неравенства меняется на противоположный. 

Получаем:

(frac{х^2 — х — 2}{х^2 (х + 2)} ≤ 0). 

Теперь найдем нули функции. 

Нули числителя: х² — х — 2 = 0. Тогда х = -1 и х = 2. 

Нули знаменателя: х = 0 и х = -2. 

2. Расставим корни на числовой прямой, при этом нули числителя будут обозначены закрашенными точками, а нули знаменателя — выколотыми. 

3. Определим знак на крайнем левом промежутке, подставив для этого х = -3 в дробь: 

(frac{(-3)^2 — (-3) — 2}{(-3)^2 ((-3) + 2)} = frac{9 + 3 — 2}{9 * (-1)} = frac{10}{-9})

Промежуток отрицательный. 

4. Дальше расставляем знаки, чередуя их. При этом следует заметить, что х = 0 — корень, повторяющийся четное количество раз (поскольку у х² четная степень). Следовательно, при переходе через эту точку знак функции меняться не будет. 

В ответ необходимо включить отрицательные промежутки, следовательно: х ∈ (-∞; -2) U [-1; 0) U (0; 2]. 

Фактчек

• Метод интервалов позволяет упростить решение любого  неравенства, а также экономит время, которое ограничено на экзамене. 
• Чтобы решить неравенство с помощью метода интервалов необходимо найти нули функции, расставить их на числовой прямой, а после определить знак каждого полученного интервала. 
• Нули функции на прямой обозначаются точками, при этом закрашенные точки включают граничные значения в итоговый промежуток, а незакрашенные, напротив, исключают их из промежутка. 
• Для определения знака на каждом интервале необходимо подставить любое значение из этого интервала в функцию. 
• Для упрощения расстановки знаков можно пользоваться правилами чередования, определив знак только на одном интервале, а дальше менять знаки на каждом следующем. При этом если корень встречается в функции нечетное количество раз, то знак при переходе через эту точку на следующий интервал меняется, а если корень встречается четное количество раз, то знак на следующем интервале не меняется. 

Проверь себя

Задание 1. 
Какие знаки неравенства существуют?

1. Строгие
2. Нестрогие
3. Строгие и нестрогие 
4. Больше и меньше

Задание 2. 
Какой знак неравенства может встретиться в методе интервалов?

1. Только больше или меньше. 
2. Только “больше или равно” или “меньше или равно”. 
3. Только “больше” и “больше или равно” или только “меньше” и “меньше или равно”.
4. Любой. 

Задание 3. 
Какое утверждение верное?

1. Если в неравенстве строгий знак неравенства, то точки на числовой прямой закрашены.
2. Если в неравенстве строгий знак неравенства, то точки на числовой прямой выколоты.
3. Если в неравенстве нестрогий знак неравенства, то все точки на числовой прямой закрашены, даже если в неравенстве есть ограничения.
4. Если в неравенстве нестрогий знак неравенства, то все точки на числовой прямой выколоты. 

Задание 4. 
Какое утверждение верное? 

1. При переходе на числовой прямой на следующий интервал, знак на интервале всегда будет меняться.
2. Если корень встречается в неравенстве четное количество раз, то при переходе через него на следующий интервал знак не меняется.
3. Если корень встречается в неравенстве нечетное количество раз, то при переходе через него на следующий интервал знак не меняется.
4. Невозможно определить правильное чередование знаков на прямой, не подставляя значение из каждого интервала в функцию.

Задание 5. 
Если в неравенстве строгий знак неравенства, то какие скобочки могут встретиться в ответе? 

1. Круглые
2. Квадратные
3. И круглые, и квадратные
4. Ни один из перечисленных вариантов 

Ответы: 1. — 3 2. — 4 3. — 2 4. — 2 5. — 1 

Метод
интервалов

1. Рассмотрим, например, неравенство:

В левой части этого неравенства –
дробно-рациональная функция. Рациональная, потому что не содержит ни корней, ни
синусов, ни логарифмов – только рациональные выражения. В правой – нуль.

Известно, что дробно-рациональная
функция может менять знак только в тех точках, в которых она равна нулю или не
существует.

Найдем нули функции в левой части нашего
неравенства. Для этого разложим числитель на множители.

Напомним, что если где  и  — корни квадратного уравнения , тогда ,.

Расставляем на оси Ох точки, в
которых числитель и знаменатель обращаются в нуль.

Нули знаменателя  и  — выколотые точки, так как в этих
точках функция в левой части неравенства не определена (на нуль делить нельзя).
Нули числителя  и  —
закрашены, так как неравенство нестрогое. При  и  наше неравенство выполняется, так как
обе его части равны нулю.

Эти точки разбивают ось  на  промежутков.

Определим знак дробно-рациональной функции
в левой части нашего неравенства на каждом из этих промежутков. На каждом из
промежутков между точками, где числитель или знаменатель обращаются в нуль,
знак выражения в левой части неравенства будет постоянным — либо «плюс», либо
«минус».

И поэтому для определения знака функции на каждом таком промежутке
берем любую «пробную» точку, принадлежащую этому промежутку, обычно ту, которая
удобна для вычисления.
 . Возьмем, например,  и проверим знак выражения в левой части неравенства. Левая часть
имеет знак .

 Следующий промежуток: . Проверим знак при . Получаем,
что левая часть поменяла знак на .

 . Возьмем , выражение левой части неравенства
положительно — следовательно, оно положительно на всем промежутке от  до .

 При  левая часть неравенства
отрицательна. 

 И, наконец, . Подставим  и проверим знак выражения в левой
части неравенства. Левая часть имеет знак .

Мы нашли, на каких промежутках выражение положительно. Осталось записать ответ:

Ответ: .

Мы видим, что метод интервалов очень
прост. Чтобы решить дробно-рациональное неравенство методом интервалов,
приводим его к виду:

, или , или ,
или .

(в левой части — дробно-рациональная
функция, в правой — нуль).

Затем — отмечаем на числовой прямой точки,
в которых числитель или знаменатель обращаются в нуль. Эти точки разбивают всю
числовую прямую на промежутки, на каждом из которых дробно-рациональная функция
сохраняет свой знак. Остается только выяснить ее знак на каждом промежутке.

Мы делаем это, проверяя знак выражения  в любой точке, принадлежащей данному
промежутку. После этого — записываем ответ.

В рассмотренном примере знаки выражения
чередовались, возникает вопрос: всегда ли знаки чередуются? Нет, не всегда!

2. Рассмотрим еще одно неравенство.

Снова расставляем точки на оси .
Точки  и  — выколотые, поскольку это нули
знаменателя. Точка  — тоже выколота, поскольку
неравенство строгое.

При  числитель
положителен, оба множителя в знаменателе отрицательны. Это легко проверить,
взяв любое число с данного промежутка, например, . Левая часть имеет знак :

При  числитель
положителен; первый множитель в знаменателе положителен, второй множитель отрицателен.
Левая часть имеет знак :

При  ситуация
та же! Числитель положителен, первый множитель в знаменателе положителен,
второй отрицателен. Левая часть имеет знак :

Наконец, при  все множители положительны, и левая
часть имеет знак :

Ответ: .

Почему нарушилось чередование знаков?
Потому что при переходе через точку  «ответственный»
за неё множитель  не изменил знак.
Следовательно, не изменила знак и вся левая часть нашего неравенства.

Вывод: если
линейный множитель  стоит в чётной степени
(например, в квадрате), то при переходе через точку  знак
выражения в левой части не меняется. В случае нечётной степени знак,
разумеется, меняется.

3. Рассмотрим более сложный случай.
От предыдущего отличается тем, что неравенство нестрогое:

Левая часть та же, что и в предыдущей
задаче. Та же будет и картина знаков:

Ответ будет тем же? Нет! Добавляется
решение  Это
происходит потому, что при  и
левая, и правая части неравенства равны нулю — следовательно, эта точка
является решением.

Ответ: .

В задачах на ЕГЭ по математике такая
ситуация встречается часто. Здесь абитуриенты попадают в ловушку и теряют
баллы. Будьте внимательны!

4. Что делать, если числитель или
знаменатель не удается разложить на линейные множители? Рассмотрим такое
неравенство:

Квадратный трехчлен  на
множители разложить нельзя: дискриминант отрицателен, корней нет. Это значит,
что знак выражения  при
всех  одинаков, а конкретно — положителен.

И теперь мы можем поделить обе части
нашего неравенства на величину , положительную при всех .
Придём к неравенству:

 , которое легко решается методом
интервалов.

Обратите внимание — мы поделили обе части
неравенства на величину, о которой точно знали, что она положительна. Конечно, в
общем случае не стоит умножать или делить неравенство на переменную величину,
знак которой неизвестен.

5. Рассмотрим еще одно неравенство:  
.

Хочется умножить его на .
Но мы не будем этого делать. Ведь  может
быть как положительным, так и отрицательным. Но, если обе части неравенства
умножить на отрицательную величину — знак неравенства меняется.

Мы поступим по другому — соберём всё в
одной части и приведём к общему знаменателю. В правой части останется нуль:

                

И только после этого можно применять метод интервалов…

Задания:

Задание 1	Реши неравенство  (t−8)(t+2)≤0
Задание 2	Реши неравенство (z−12)(4z+3)≤0
Задание 3	Реши неравенство (x+4)(x+7)≤0.
Задание 4	Реши неравенство x(2x + 8)(x − 3) > 0
Задание 5	Реши неравенство
Задание 6	Реши неравенство
Задание 7	Реши неравенство
Задание 8	Реши неравенство
Задание 9	Реши неравенство
Задание 10	Реши неравенство
Задание 11	Реши неравенство
Задание 12	Реши неравенство
Задание 13	Реши неравенство
Задание 14	Реши неравенство
Задание 15	Реши неравенство
Задание 16	Реши неравенство
Задание 17	Реши неравенство
Задание 18	Реши неравенство
Задание 19	Реши неравенство
Задание 20	Реши неравенство

«Решение неравенств повышенной сложности обобщённым методом интервалов»

Попова Нина Федоровна

Белых Нина Владимировна

Одной из актуальных задач, стоящей перед учителем математики в современной школе, является задача развития математических способностей учащихся, воспитание их творческой активности, а также формирование системы математических знаний, приёмов и навыков. Умение решать задачи повышенной сложности характеризуется как глубиной усвоения «базового» курса, так и овладением различными математическими приёмами и методами, выходящими за рамки основного курса.

При подборе задач школьного курса математики, безусловно, необходимы задачи, нацеленные  на отработку того или иного математического навыка, задачи иллюстративного характера, тренировочные упражнения, выполняемые по образцу. Но не менее необходимы задачи,  направленные на пробуждение у учеников устойчивого интереса к изучению математики. Осуществляя целенаправленное обучение школьников решению задач повышенной сложности, следует учить их наблюдать, пользоваться аналогией, сравнением и делать соответствующие выводы, развивать логическое  мышление.

Предлагаемый материал знакомит учащихся с  обобщённым методом интервалов, который является одним из наиболее простых и эффективных методов решения неравенств, содержащих различные функции. К сожалению, в большинстве учебников и учебных пособий этот метод рассмотрен применительно к дробно-рациональным неравенствам и не показано его использование для решения неравенств иррациональных, показательных, логарифмических, неравенств смешанного типа, а также неравенств, содержащих модули.

Метод интервалов основан на следующем свойстве непрерывных функций:

Если на интервале (a; b) функция f непрерывна и не обращается

в нуль, то она на этом интервале сохраняет постоянный знак.

Пусть функция f непрерывна на интервале I и обращается в нуль в конечном числе точек этого интервала. По сформулированному выше свойству непрерывных функций этими точками интервал I разбивается на “более мелкие” интервалы так, что на этих интервалах исходная “сложная” задача упрощается, т.к. обладает определёнными свойством, например, свойством сохранения знака.

В качестве примера решим неравенство:

Пример 1

Решение.

1. Рассмотрим функцию f(x) = и найдём значения x, при которых f(x)≤0
2. Найдём область определения функции f(x).

D(f):x≠1, следовательно, D(f)=(-∞;1) U (1;+∞)

1. Найдём нули функции:

f(x)=0, при x=2 и x=-4

1. Точки x=-4, x=1, x=2 делят числовую прямую на промежутки, в каждом из которых функция f(x) непрерывна и  сохраняет постоянный знак.

+                        —                        +                      +

x

  -4                      1                        2        

Для определения знаков, в полученных промежутках используем следующие правила:

а) т.к. внутри рассматриваемого промежутка знак неравенства не меняется, то для определения знака функции f(x) выбирается какая-либо “удобная” точка внутри этого промежутка и вычисляется значение функции в этой точке.

б) если точки неравенства (т.е. корни числителя или корни знаменателя или корни числителя и знаменателя в совокупности) имеют нечётную кратность, то при переходе через эту точку знак неравенства меняется, если указанные точки имеют чётную кратность, то при переходе через неё знак неравенства не меняется. (Для исключения ошибок желательно определить знак функции f(x) в каждом из промежутков в “удобной” точке.)  

Пусть x>2, тогда f(5)>0 (“5” – удобная точка промежутка

Пусть 10

Пусть -4

Пусть x<-4, тогда f(-5)>0

1. Таким образом, f(x) ≤0 при x є [-4; 1) U    Ответ:[-4;1)U{2}

Рассмотрим применение этого метода для решения иррациональных неравенств.

Пример 2   ≥0

1. Рассмотрим функцию f(x)=
2. D(f): x+2≥0; x≥-2; D(f)=[-2; +∞).
3. Найдём нули функции.

f(x)=0, если =0. Произведение двух множителей равно нулю, если хотя бы один из них равен нулю, а другой при этом не теряет смысла.

 или =0

x=-2

Число (-3) не является корнем, т.к. при этом подкоренное выражение отрицательно.

1. На числовую прямую наносим область определения функции
   D(f)=[-2; +∞) и нуль функции x=3, который разбивает область определения на два промежутка, в каждом из которых функциянепрерывна и  сохраняет постоянный знак.

   —             +                    

         -2                  3                                x

Если x>3, f(5)>0

Если -2

1. Таким образом, f(x)≥0 при x є [3; +∞) U {- 2}.Ответ:[3;+∞)U{-2}.

Из анализа полученного ответа следует, что особое внимание следует уделить концам промежутков и границам области определения. Такие точки могут как принадлежать множеству решений неравенства, так и не принадлежать, что надо дополнительно выяснять, подставляя их значения в неравенство.

Пример 3

или

1. Рассмотрим функцию f(x)=
2. D(f): ;   D(f)=[-2;3]
3. Нули f(x): =0

;

Проверка:  равенство неверное,

 равенство верное,

следовательно, уравнение имеет единственный корень x=2

1. Наносим область определения и нули функции на числовую прямую и определяем знак функции на каждом из промежутков с помощью удобной точки.
2. 

+

     -2                2                3                  x

Проверим знак функции на границах области определения: f(-2)<0, f(3)>0, следовательно, f(x)>0, при x є (2: 3].Следует обратить внимание на то, что x=3 является решением неравенства, хотя неравенство является строгим.Ответ:(2;3].

Пример 4(ЕГЭ 8. 12 2009 г.)

Решение

Преобразуем неравенство, разложив его на множители:

1) Рассмотрим функцию

2) D(f):

Следовательно

3)Нули

X=4 корнем не является, так как при этом знаменатель обращается в нуль.

4) Наносим на числовую прямую область определения f(x) и нули f(x) и определяем знаки f(x) в полученных интервалах, причем так как первый множитель f(x) всегда положительный, достаточно определить знаки только второго множителя.

5) Таким образом,

Ответ:(0;1]U{2}U[3;4)U(4;5]

Используем метод интервалов для решения неравенств с модулями

Пример 5

Решение

Перепишем неравенство в виде:

1) Рассмотрим функцию

2)

3) Нули f(x):

;

4)Нанесем нули f(x) на числовую прямую и определим знак функции f(x) в каждом из интервалов

1. 

Пример 6

1) Рассмотрим функцию

2)D(f)=R

3) Нули f(x):

;

4) Нанесем нули f(x) на числовую прямую и определим знаки f(x) в полученных интервалах

5)

Ответ: .

Метод интервалов представляется целесообразным и при решении показательных и логарифмических неравенств, в частности в неравенствах, в которых вводится замена переменной.

Пример 7

Решение

1) Рассмотрим функцию

2) D(f)=R

3) Нули f(x):

Пусть

Обратная замена:

 4) Наносим на числовую прямую нули f(x) и определяем знаки f(x) в полученных интервалах

5)

Ответ: (2; +  )

Пример 8

Решение

1) Рассмотрим функцию

2) D(f):;

 3)  Нули f(x):

Пусть

Обратная замена:

 4) Наносим на числовую прямую область определения и нули f(x) и определяем знаки  в полученных интервалах

5)       Ответ: (0;  ]

Пример 9

1) Рассмотрим функцию

2)

 3) Нули f(x):

4) Наносим область определения и нули функции на числовую прямую и определяем знаки f(x) в полученных интервалах.

1. Таким образом,  при

Пример  10

1. Рассмотрим функцию
2. ; .
3. Нули  ;

Пусть   , тогда ;

Обратная замена:

1. Нанесём  область определения и нули функции на числовую прямую и определим знаки , в полученных интервалах:

Если

Если

Если

Если

1. ,при .                Ответ:

               Рассмотрим применение метода интервалов к решению неравенств смешанного типа:

Пример 11  

1. Рассмотрим функцию  .
2. ;;;

 .

1. Нули

 ;  ;

Уравнение имеет единственный корень

1. Нанесём область определения и нули  на числовую прямую и определим знаки  в полученных интервалах

    +                                                +

;   ;       ;        .

1.   при

Следует обратить внимание на то, что хотя неравенство строгое, значение является решением, т. к.  .

Ответ:  

1. Метод интервалов для рациональных неравенств

        Задача (диагностическая работа № 3, 2007/2008, В6)

Сколько целочисленных решений имеет неравенство

Рассмотрим функцию

Область определения функции

Нули функции

Значит,

Таким образом, количество целочисленных решений 8.

Ответ: 8.

1. Метод интервалов для неравенств с модулями

Задача  (МГУ, геологический факультет, 2005)

Решите неравенство

1 способ (Обобщённый метод интервалов)

Рассмотрим функцию

Область определения функции

Нули функции

2 способ (Рассмотрение случаев)

1 случай. Если

Тогда неравенство принимает вид

 

Но, учитывая условие раскрытия модуля – получаем

2 случай. Если  

Тогда неравенство принимает вид

Но, учитывая условие раскрытия модуля – получаем

Объединяя полученные ответы – имеем

Ответ:

Часто обобщённый метод интервалов удобнее и короче традиционного способа решения.

1. Метод интервалов для иррациональных неравенств

Задача  (Диагностическая работа №2, 2008/2009,)

Решите неравенство

Рассмотрим функцию

Область определения

Нули функции

Учитывая область определения, получаем, что нули функции

Определим знаки функции на образовавшихся промежутках (это задача С – необходимо обосновывать!)

Знаки, принимаемые функцией , определяются значением второго множителя, так как корень неотрицателен на области определения. Так как второй множитель – квадратный трехчлен, графиком является парабола, ветви которой направлены вверх, то при  , а при  

Значит,

Ответ:

Из приведённого примера виден один из недостатков метода – может быть затруднено определение знаков на полученных интервалах, особенно, если точки расположены довольно близко друг к другу и/или когда значения нулей или границ области определения – «плохие».

В тоже время, обобщённый метод интервалов во многих случаях представляет собой хорошую альтернативу традиционным схемам решения иррациональных неравенств вида  и

Задача  (МГУ, экономический факультет, 2003)

Решить неравенство

Рассмотрим функцию

Область определения функции найдём из условия

Нули функции найдём, решив уравнение

Проверкой убеждаемся, что  является корнем уравнения, а  — корнем уравнения не является.

Определим знаки функции на полученных интервалах

Значит,

Ответ:

1. Метод интервалов для показательных и логарифмических неравенств

Задача (Демоверсия 2009 варианта ЕГЭ по версии МИОО, С10)

Решить неравенство

Рассмотрим функцию

Область определения

Нули функции

Определим знаки функции на образовавшихся промежутках

Ответ:

Обобщённый метод интервалов может быть использован и вместо традиционного способа решения логарифмических и показательных неравенств.

Задача 10 (МГУ, МГТУ)

Решить неравенство

Рассмотрим функцию

Область определения

Нули функции

С учётом области определения – ответ уравнения

Определим знаки функции на полученных интервалах

Значит,

Ответ:

1. Метод интервалов для смешанных неравенств

Наиболее полезен обобщённый метод интервалов при решении неравенств «смешанного» типа, т.е. неравенств, содержащих части различного вида.

Задача  (РЭА)

Найти наименьшее целое решение неравенства

Рассмотрим функцию

Область определения

Нули функции

Определим знаки функции на образовавшихся промежутках

Значит, . Наименьшее целое решение – число .

Ответ:

1. Метод замены множителей

В заключении рассмотрим так называемый «метод замены множителей», который может оказаться полезным при решении неравенств, содержащих части разного вида.

Например, при решении показательных неравенств, в которых неизвестное встречается и в основании, и в показателе степени, полезно использовать следующее правило (см. И.Ф. Шарыгин, В.И. Голубев «Решение задач 11»): выражение   при имеет тот же знак, что , и противоположный, если   Оба варианта можно объединить в один: выражения  и имеют один знак. При этом, конечно нельзя забывать об области определения выражения   (должно быть положительным).

Задача 12

        Решите неравенство

        Решение.

Воспользуемся утверждением

Пусть

 

Таким образом,  для всех

        +                —                +                —                +                

                -1                                0                3                        х

Ответ:

Подобные «замены множителей» могут быть (с соответствующими изменениями) произведены и при решении неравенств с модулями, иррациональных неравенств, логарифмических неравенств и т.д. Особенно данный метод полезен при решении неравенств смешанного вида.

Задача 13

Решить неравенство

Область определения данного неравенства найдём из условий

Воспользуемся методом «замены множителей».

Отсюда,

Ответ:

Задача  (МГИЭТ 2001) 

Решить неравенство

при

Отдельно следует рассмотреть случай  при этом выражения, стоящие в показателях степени должны быть положительными.

1.         

        

        Решением последней системы является

         не удовлетворяет этому условию, следовательно, не является решением неравенства.

         удовлетворяет условию, следовательно, является решением неравенства.

2.        

        

                +                —                +                                х

        

                                

        

        

        

        

                —                +                —                +        х

                                                        

        

        

        Таким образом, получаем  

Ответ:

P.S. Если в выражении  допустить отрицательные значения  то надо требовать, чтобы значение было целым числом. Тогда при  получим  то есть  Тогда  Значит,   то есть значение выражения  не является целым числом.

Метод интервалов принято считать универсальным для решения неравенств. Иногда этот метод также называют методом промежутков. Применим он как для решения рациональных неравенств с одной переменной, так и для неравенств других видов. В нашем материале мы постарались уделить внимание всем аспектам вопроса.

Что ждет вас в данном разделе? Мы разберем метод промежутков и рассмотрим алгоритмы решения неравенств с его помощью. Затронем теоретические аспекты, на которых основано применение метода.

Особое внимание мы уделяем нюансам темы, которые обычно не затрагиваются в рамках школьной программы. Например, рассмотрим правила расстановки знаков на интервалах и сам метод интервалов в общем виде без его привязки к рациональным неравенствам.

Алгоритм

Кто помнит, как происходит знакомство с методом промежутков в школьном курсе алгебры? Обычно все начинается с решения неравенств вида f(x)<0 (знак неравенства может быть использован любой другой, например, ≤, > или ≥). Здесь f(x) может быть многочленом или отношением многочленов. Многочлен, в свою очередь, может быть представлен как:

• произведение линейных двучленов с коэффициентом 1 при переменной х;
• произведение квадратных трехчленов со старшим коэффициентом 1 и с отрицательным дискриминантом их корней.

Приведем несколько примеров таких неравенств:

(x+3)·(x2−x+1)·(x+2)3≥0,

(x-2)·(x+5)x+3>0 ,

(x−5)·(x+5)≤0,

(x2+2·x+7)·(x-1)2(x2-7)5·(x-1)·(x-3)7≤0 .

Запишем алгоритм решения неравенств такого вида, как мы привели в примерах, методом промежутков:

• находим нули числителя и знаменателя, для этого числитель и знаменатель выражения в левой части неравенства приравниваем к нулю и решаем полученные уравнения;
• определяем точки, которые соответствуют найденным нулям и отмечаем их черточками на оси координат;
• определяем знаки выражения f(x) из левой части решаемого неравенства на каждом промежутке и проставляем их на графике;
• наносим штриховку над нужными участками графика, руководствуясь следующим правилом: в случае, если неравенство имеет знаки < или ≤ изображается, штрихуются «минусовые» промежутки, если же мы работаем с неравенством, имеющим знаки > или ≥, то выделяем штриховкой участки, отмеченные знаком «+».

Четреж, с которым мы будем работать, может иметь схематический вид. Излишние подробности могут перегружать рисунок и затруднять решение. Нас будет мало интересовать маштаб. Достаточно будет придерживаться правильного расположения точек по мере роста значений их координат.

При работе со строгими неравенствами мы будем использовать обозначение точки в виде круга с незакрашенным (пустым) центром. В случае нестрогих неравенств точки, которые соответствуют нулям знаменателя, мы будем изображать пустыми, а все остальные обычными черными.

Отмеченные точки разбивают координатную прямую на несколько числовых промежутков. Это позволяет нам получить геометрическое представление числового множества, которое фактически является решением данного неравенства.

Научные основы метода промежутков

Основан подход, положенный в основу метода промежутков, основан на следующем свойстве непрерывной функции: функция сохраняет постоянный знак на интервале (a, b), на котором эта функция непрерывна и не обращается в нуль. Это же свойство характерно для числовых лучей (−∞, a) и (a, +∞).

Приведенное свойство функции подтверждается теоремой Больцано-Коши, которая приведена во многих пособиях для подготовки к вступительным испытаниям.

Обосновать постоянство знака на промежутках также можно на основе свойств числовых неравенств. Например, возьмем неравенство x-5x+1>0 . Если мы найдем нули числителя и знаменателя и нанесем их на числовую прямую, то получим ряд промежутков: (−∞, −1), (−1, 5) и (5, +∞).

Возьмем любой из промежутков и покажем на нем, что на всем промежутке выражение из левой части неравенства будет иметь постоянный знак. Пусть это будет промежуток (−∞, −1). Возьмем любое число t из этого промежутка. Оно будет удовлетворять условиям t<−1, и так как −1<5, то по свойству транзитивности, оно же будет удовлетворять и неравенству t<5.

Используя оба полученных неравенства и свойство числовых неравенств, мы можем предположить, что t+1<0 и t−5<0. Это значит, что t+1 и t−5 – это отрицательные числа независимо от значения t на промежутке (−∞, −1).

Используя правило деления отрицательных чисел, мы можем утверждать, что значение выражения t-5t+1 будет положительным. Это значит, что значение выражения x-5x+1 будет положительным при любом значении x из промежутка (−∞, −1). Все это позволяет нам утверждать, что на промежутке, взятом для примера, выражение имеет постоянный знак. В нашем случае это знак «+».

Нахождение нулей числителя и знаменателя

Алгоритм нахождения нулей прост: приравниваем выражения из числителя и знаменателя к нулю и решаем полученные уравнения. При возникновении затруднений можно обратиться к теме «Решение уравнений методом разложения на множители». В этом разделе мы ограничимся лишь рассмотрением примера.

Рассмотрим дробь x·(x-0,6)x7·(x2+2·x+7)2·(x+5)3. Для того, чтобы найти нули числителя и знаменателя, приравняем их к нулю для того, чтобы получить и решить уравнения: x·(x−0,6)=0 и x7·(x2+2·x+7)2·(x+5)3=0.

В первом случае мы можем перейти к совокупности двух уравнений x=0 и x−0,6=0, что дает нам два корня 0 и 0,6. Это нули числителя.

Второе уравнение равносильно совокупности трех уравнений x7=0, (x2+2·x+7)2=0, (x+5)3=0. Проводим ряд преобразований и получаем x=0, x2+2·x+7=0, x+5=0. Корень первого уравнения 0, у второго уравнения корней нет, так как оно имеет отрицательный дискриминант, корень третьего уравнения -5. Это нули знаменателя.

0 в данном случае является одновременно и нулем числителя, и нулем знаменателя.

В общем случае, когда в левой части неравенства дробь, которая не обязательно является рациональной, числитель и знаменатель точно также приравниваются к нулю для получения уравнений. Решение уравнений позволяет найти нули числителя и знаменателя.

Определение знаков на интервалах

Определить знак интервала просто. Для этого можно найти значение выражения из левой части неравенства для любой произвольно выбранной точки из данного интервала. Полученный знак значения выражения в произвольно выбранной точке промежутка будет совпадать со знаком всего промежутка.

Рассмотрим это утверждение на примере.

Возьмем неравенство x2-x+4x+3≥0. Нулей числителя выражение, расположенное в левой части неравенства, нулей не имеет. Нулем знаменателя будет число -3. Получаем два промежутка на числовой прямой (−∞, −3) и (−3, +∞).

Для того, чтобы определить знаки промежутков, вычислим значение выражения x2-x+4x+3 для точек, взятых произвольно на каждом из промежутков.

Из первого промежутка (−∞, −3) возьмем −4. При x=−4 имеем (-4)2-(-4)+4(-4)+3=-24 . Мы получили отрицательное значение, значит весь интервал будет со знаком «-».

Для промежутка (−3, +∞) проведем вычисления с точкой, имеющей нулевую координату. При x=0 имеем 02-0+40+3=43. Получили положительное значение, что значит, что весь промежуток будет иметь знак «+».

Можно использовать еще один способ определения знаков. Для этого мы можем найти знак на одном из интервалов и сохранить его или изменить при переходе через нуль. Для того, чтобы все сделать правильно, необходимо следовать правилу: при переходе через нуль знаменателя, но не числителя, или числителя, но не знаменателя мы можем поменять знак на противоположный, если степень выражения, дающего этот нуль, нечетная, и не можем поменять знак, если степень четная. Если мы получили точку, которая является одновременно нулем числителя и знаменателя, то поменять знак на противоположный можно только в том случае, если сумма степеней выражений, дающих этот нуль, нечетная.

Если вспомнить неравенство, которое мы рассмотрели в начале первого пункта этого материала, то на крайнем правом промежутке мы можем поставить знак «+».

Теперь обратимся к примерам.

Возьмем неравенство (x-2)·(x-3)3·(x-4)2(x-1)4·(x-3)5·(x-4)≥0 и решим его методом интервалов. Для этого нам необходимо найти нули числителя и знаменателя и отметить их на координатной прямой. Нулями числителя будут точки 2, 3, 4, знаменателя точки 1, 3, 4. Отметим их на оси координат черточками.

Нули знаменателя отметим пустыми точками.

Так как мы имеем дело с нестрогим неравенством, то оставшиеся черточки заменяем обычными точками.

Теперь расставим точки на промежутках. Крайний правый промежуток (4, +∞) будет знак +.

Продвигаясь справа налево будем проставлять знаки остальных промежутков. Переходим через точку с координатой 4. Это одновременно нуль числителя и знаменателя. В сумме, эти нули дают выражения (x−4)2 и x−4. Сложим их степени 2+1=3 и получим нечетное число. Это значит, что знак при переходе в данном случае меняется на противоположный. На интервале (3, 4) будет знак минус.

Переходим к интервалу (2, 3) через точку с координатой 3. Это тоже нуль и числителя, и знаменателя. Мы его получили благодаря двум выражениям (x−3)3 и (x−3)5, сумма степеней которых равна 3+5=8. Получение четного числа позволяет нам оставить знак интервала неизменным.

Точка с координатой 2 – это нуль числителя. Степень выражения х-2 равна 1 (нечетная). Это значит, что при переходе через эту точку знак необходимо изменить на противоположный.

У нас остался последний интервал (−∞, 1). Точка с координатой 1 – это нуль знаменателя. Он был получен из выражения (x−1)4, с четной степенью 4. Следовательно, знак остается прежним. Итоговый рисунок будет иметь вот такой вид:

Применение метода интервалов особенно эффективно в случаях, когда вычисление значения выражения связано с большим объемом работы. Примером может стать необходимость вычисления значения выражения

x+3-343·x2+6·x+112·x+2-34(x-1)2·x-235·(x-12)

в любой точке интервала 3-34,3-24.

Будем считать, что с правилами определения знаков для промежутков мы разобрались. Идем дальше.

Примеры решения неравенств методом интервалов

Теперь займемся применением полученных знаний и навыков на практике.

Решение рациональных неравенств в большинстве случаев требует их предварительного преобразования к нужному виду. Только после этого появляется возможность использовать метод интервалов. Алгоритмы проведения таких преобразований рассмотрены в материале «Решение рациональных неравенств».

Рассмотрим пример преобразования квадратных трехчленов в записи неравенств.

Обобщенный метод интервалов

Обобщенный метод промежутков применяется для решения неравенств вида f(x)<0 (≤, >, ≥), где f(x) – произвольное выражение с одной переменной x.

Все действия проводятся по определенному алгоритму. При этом алгоритм решения неравенств обобщенным методом интервалов будет несколько отличаться от того, что мы разобрали ранее:

• находим область определения функции f и нули этой функции;
• отмечаем на координатной оси граничные точки;
• наносим на числовую прямую нули функции;
• определяем знаки промежутков;
• наносим штриховку;
• записываем ответ.

На числовой прямой необходимо отмечать в том числе и отдельные точки области определения. К примеру, областью определения функции служит множество (−5, 1]∪{3}∪[4, 7)∪{10}. Это значит, что нам необходимо отметить точки с координатами −5, 1, 3, 4, 7 и 10. Точки −5 и 7 изобразим пустыми, остальные можно выделить цветным карандашом для того, чтобы отличать их затем от нулей функции.

Нули функции в случае нестрогих неравенств наносятся обычными (закрашенными) точками, строгих – пустыми точками. Если нули совпадают с граничными точками или отдельными точками области определения, то их можно перекрасить в черный цвет, сделав пустыми или закрашенными в зависимости от вида неравенства.

Запись ответа представляет собой числовое множество, которое включает в себя:

• промежутки со штриховкой;
• отдельные точки области определения со знаком плюс, если мы имеем дело с неравенством, знак которого > или ≥ или со знаком минус, если в неравенстве есть знаки < или ≤.

Теперь стало понятно, что тот алгоритм, который мы привели в самом начале темы, является частным случаем алгоритма применения обобщенного метода интервалов.

Рассмотрим пример применения обобщенного метода интервалов.