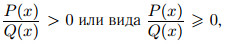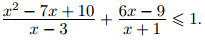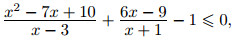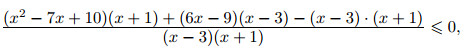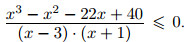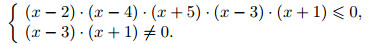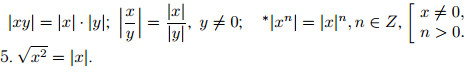в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 1000 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Решите неравенство
Решите неравенство:
Источник: А. Ларин. Тренировочный вариант № 292.
Решите неравенство:
Источник: А. Ларин. Тренировочный вариант № 384.
Решите неравенство
Источник: А. Ларин: Тренировочный вариант № 128.
Решите неравенство
Источник: А. Ларин: Тренировочный вариант № 126.
Решите неравенство
Источник: Досрочный ЕГЭ по математике (Центр) 30.03.2018
Решите неравенство:
Источник: А. Ларин. Тренировочный вариант № 382.
Решите неравенство:
Источник: А. Ларин. Тренировочный вариант № 383.
Решите неравенство:
Источник: А. Ларин. Тренировочный вариант № 401.
Решите систему неравенств
Решите неравенство
Решите неравенство
Решите неравенство
Источник: А. Ларин: Тренировочный вариант № 90.
Решите неравенство:
Решите неравенство:
Решите неравенство:
Решите неравенство:
Решите неравенство:
Решите неравенство:
Решите неравенство:
Всего: 1000 1–20 | 21–40 | 41–60 | 61–80 …
Метод интервалов
Метод интервалов – простой способ решения дробно-рациональных неравенств. Так называются неравенства, содержащие рациональные (или дробно-рациональные) выражения, зависящие от переменной.
1. Рассмотрим неравенство:
Метод интервалов позволяет решить его за пару минут.
В левой части этого неравенства – дробно-рациональная функция. Рациональная, потому что не содержит ни корней, ни синусов, ни логарифмов – только рациональные выражения. В правой – нуль.
Метод интервалов основан на следующем свойстве дробно-рациональной функции.
Дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует.
Найдем нули функции в левой части нашего неравенства. Для этого разложим числитель на множители. (Если вы не помните, что такое нули функции и знак функции на промежутке – смотрите статью «Исследование графика функции»).
Напомним, как раскладывается на множители квадратный трехчлен, то есть выражение вида .
, где
и
— корни квадратного уравнения
.
Получим:
Рисуем ось X и расставляем точки, в которых числитель и знаменатель обращаются в нуль.
Нули знаменателя и
— выколотые точки, так как в этих точках функция в левой части неравенства не определена (на нуль делить нельзя).
Напомним, что мы изображаем точку на числовой прямой выколотой (пустой), если соответствующее значение переменной никак не может быть решением неравенства. В нашем примере точки и
выколотые, потому что в них знаменатель обращается в ноль.
Нули числителя и
— закрашены, так как неравенство нестрогое. При
и
наше неравенство выполняется, так как обе его части равны нулю.
Эти точки разбивают ось X на 5 промежутков.
Определим знак дробно-рациональной функции в левой части нашего неравенства на каждом из этих промежутков. Мы помним, что дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует. Это значит, что на каждом из промежутков между точками, где числитель или знаменатель обращаются в нуль, знак выражения в левой части неравенства будет постоянным — либо «плюс», либо «минус».
И поэтому для определения знака функции на каждом таком промежутке мы берем любую точку, принадлежащую этому промежутку. Ту, которая нам удобна.
. Возьмем, например,
и проверим знак выражения
в левой части неравенства. Каждая из «скобок» отрицательная. Левая часть имеет знак
.
Следующий промежуток:
. Проверим знак при
. Получаем, что левая часть поменяла знак на
.
. Возьмем
. При
выражение положительно — следовательно, оно положительно на всем промежутке от
до
.
При
левая часть неравенства отрицательна.
И, наконец,
. Подставим
и проверим знак выражения в левой части неравенства. Каждая «скобочка» положительна. Следовательно, левая часть имеет знак
.
Мы нашли, на каких промежутках выражение положительно. Осталось записать ответ:
Ответ: .
Обратите внимание: знаки на промежутках чередуются. Это произошло потому, что при переходе через каждую точку ровно один из линейных множителей поменял знак, а остальные сохранили его неизменным.
Мы видим, что метод интервалов очень прост. Чтобы решить дробно-рациональное неравенство методом интервалов, приводим его к виду:
, или
, или
, или
(в левой части — дробно-рациональная функция, в правой — нуль).
Затем — отмечаем на числовой прямой точки, в которых числитель или знаменатель обращаются в нуль.
Эти точки разбивают всю числовую прямую на промежутки, на каждом из которых дробно-рациональная функция сохраняет свой знак.
Остается только выяснить ее знак на каждом промежутке.
Мы делаем это, проверяя знак выражения в любой точке, принадлежащей данному промежутку. После этого — записываем ответ. Вот и всё.
Но возникает вопрос: всегда ли знаки чередуются? Нет, не всегда! Надо быть внимательным и не расставлять знаки механически и бездумно.
2. Рассмотрим еще одно неравенство:
Решение:
Снова расставляем точки на оси X. Точки и
— выколотые, поскольку это нули знаменателя. Точка
— тоже выколота, поскольку неравенство строгое, и значение переменной
не может быть решением неравенства.
При числитель положителен, оба множителя в знаменателе отрицательны. Это легко проверить, взяв любое число с данного промежутка, например,
. Левая часть имеет знак
:
При числитель положителен; первый множитель в знаменателе положителен, второй множитель отрицателен. Левая часть имеет знак
:
При ситуация та же! Числитель положителен, первый множитель в знаменателе положителен, второй отрицателен. Левая часть имеет знак
:
Наконец, при все множители положительны, и левая часть имеет знак
:
Ответ: .
Почему нарушилось чередование знаков? Потому что при переходе через точку 2 «ответственный» за неё множитель не изменил знак. Следовательно, не изменила знак и вся левая часть нашего неравенства.
Вывод: если линейный множитель стоит в чётной степени (например, в квадрате), то при переходе через точку
знак выражения в левой части не меняется. В случае нечётной степени знак, разумеется, меняется.
3. Рассмотрим более сложный случай. От предыдущего отличается тем, что неравенство нестрогое:
Решение:
Левая часть та же, что и в предыдущем примере. Та же будет и картина знаков:
Может, и ответ будет тем же? Нет! Добавляется решение Это происходит потому, что при
и левая, и правая части неравенства равны нулю — следовательно, эта точка является решением.
Ответ: .
В задачах на ЕГЭ по математике такая ситуация встречается часто. Здесь абитуриенты попадают в ловушку и теряют баллы. Будьте внимательны!
4. Что делать, если числитель или знаменатель не удается разложить на линейные множители? Рассмотрим такое неравенство:
Решение:
Квадратный трехчлен на множители разложить нельзя: дискриминант отрицателен, корней нет. Но ведь это и хорошо! Это значит, что знак выражения
при всех
одинаков, а конкретно — положителен. Подробнее об этом можно прочитать в статье о свойствах квадратичной функции.
И теперь мы можем поделить обе части нашего неравенства на величину , положительную при всех
.
Придём к равносильному неравенству:
Решим неравенство методом интервалов. Действуем по алгоритму: числитель левой части равен нулю при а знаменатель обращается в ноль при
. Отметим эти точки на координатной прямой. Точки выколоты, потому что неравенство строгое. Эти точки разбивают числовую ось на три интервала. Найдем знаки на каждом из интервалов. На крайнем правом знак положителен, а дальше знаки чередуются.
Нам нужен «интервал со знаком минус», то есть такой, где Выпишем ответ.
Ответ:
Обратите внимание — мы поделили обе части неравенства на величину, о которой точно знали, что она положительна. Конечно, в общем случае не стоит умножать или делить неравенство на переменную величину, знак которой неизвестен.
5. Рассмотрим еще одно неравенство, на вид совсем простое:
Решение:
Так и хочется умножить его на . Но мы уже умные, и не будем этого делать. Ведь
может быть как положительным, так и отрицательным. А мы знаем, что если обе части неравенства умножить на отрицательную величину — знак неравенства меняется.
Мы поступим по-другому — соберём всё в одной части и приведём к общему знаменателю. В правой части останется нуль:
Применим метод интервалов.
Действуем по алгоритму. Отметим на координатной прямой точки и
. Они выколотые, потому что неравенство строгое. Эти точки разбивают ось Х на три интервала. Расставим знаки на каждом из них.
Ответ:
6. Решите неравенство:
Решение:
Приведем левую часть неравенства к общему знаменателю и преобразуем числитель:
Применим метод интервалов:
Числитель равен нулю при Знаменатель обращается в ноль при
или
. Неравенство строгое, поэтому все эти точки на числовой оси отмечаем как пустые.
Если , то
. Далее знаки чередуются.
Нам нужны «интервалы со знаком минус». Выпишем их и получим ответ.
Ответ:
7. Решите неравенство
Решение:
Приведем неравенство к виду:
Для этого все перенесем в левую часть, приведем к общему знаменателю и разложим числитель и знаменатель на множители. Применяем формулу разности квадратов и формулу разложения квадратного трехчлена на множители
Получим:
Найдем нули числителя и знаменателя и отметим их на числовой оси:
Выпишем интервалы, где неравенство выполняется, и получим ответ.
Ответ:
8. Решите неравенство:
Решение:
Разложим левую часть неравенства на множители.
Для этого вынесем общий множитель за скобки, а затем воспользуемся формулой:
Получим:
Применим метод интервалов.
Левая часть неравенства обращается в ноль, если ,
или
. Нанесем эти точки на координатную прямую. Все точки закрашенные, так как неравенство нестрогое, в нем присутствует знак «меньше или равно».
Ответ:
9. Решите неравенство:
Решение:
Разложим числитель на множители с помощью группировки:
Знаменатель тоже разложим на множители:
Неравенство примет вид:
Мы видим, что числитель равен нулю при
Знаменатель равен нулю при . Множитель
стоит в числителе и в знаменателе, и он не может равняться нулю.
Отметим полученные точки на координатной прямой. Две из них закрашены (это 3 и 1), а две нет (это -1 и -2). Найдем знаки на каждом промежутке.
При переходе через точку знак не меняется, так как множитель
присутствует и в числителе, и в знаменателе.
Выпишем ответ.
Ответ:
10. Решите неравенство:
Решение:
Разложим числитель и знаменатель на множители:
Напомним, что выражение мы разложили на множители, решив квадратное уравнение:
Неравенство примет вид:
Воспользуемся методом интервалов.
Числитель дроби в левой части неравенства равен нулю, если Знаменатель обращается в ноль, если
или
. Отметим эти точки на координатной прямой и определим знаки на интервалах.
Ответ:
11. Решите неравенство:
Решение:
Можно сразу применить метод интервалов.
Но лучше, чтобы не запутаться со знаками, умножить обе части неравенства на (-1) и не забыть поменять знак неравенства на противоположный.
Теперь применим метод интервалов.
Отметим на координатной прямой нули числителя и знаменателя и определим знаки на интервалах.
Обратите внимание, что знак не меняется при переходе через точку , так как множитель
входит в выражение в левой части неравенства в четной степени.
Ответ:
12. Решите неравенство:
Решение:
Разложим числитель и знаменатель на множители:
Сократим на множитель при условии, что
.
Здесь мы действуем чуть иначе, чем в задаче 9.
Неравенство равносильно системе:
Решаем второе неравенство системы методом интервалов:
Второму неравенству удовлетворяют точки .
Точка в этот промежуток не входит.
Ответ:
13. Решите неравенство:
Решение:
Разложив числитель на множители, получим:
Применим метод интервалов.
Отметим на числовой оси точки, в которых числитель и знаменатель обращаются в ноль. Обратите внимание, что точки -1 и 5 закрашены, а точки 2 и 4 пустые.
Определим знаки на интервалах.
Знак не меняется при переходе через точку , так как множитель
входит в выражение в левой части неравенства в четной степени. При переходе через точку 4 знак меняется, степень соответствующего множителя нечетная.
В ответе запишем интервалы, на которых неравенство выполняется.
Ответ:
14. Решите неравенство:
Разложим числитель и знаменатель на множители, используя формулы сокращенного умножения: суммы и разности кубов, разности квадратов.
Кажется, что неравенство сложное. Попробуем разложить на множители выражения и
Оказывается, что дискриминанты соответствующих квадратных уравнений отрицательны, поэтому и
при всех х.
Разделим обе части неравенства на эти положительные выражения.
Получим:
Неравенство равносильно системе:
Решим первое неравенство системы методом интервалов:
Его решением является промежуток [1;4], причем точка в этот промежуток не входит.
Ответ:
Мы показали на различных примерах, как применяется метод интервалов.
Сделаем вывод:
Метод интервалов помогает решать дробно-рациональные неравенства по алгоритму. Правила просты: приводим неравенство к такому виду, что в его левой части – произведение множителей или дробь, а в правой – ноль. Находим точки, в которых левая часть обращается в ноль или не определена. Отмечаем на числовой оси эти точки. Они разбивают числовую ось (или координатную прямую) на интервалы, на каждом из которых функция в левой части неравенства сохраняет свой знак. Определяем знаки на интервалах, помня о правилах чередования знаков. И записываем ответ.
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Метод интервалов» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
09.03.2023
Метод интервалов
Теория к заданию 14 из ЕГЭ по математике (профиль)
Разбор сложных заданий в тг-канале:
Рациональные неравенства
Рациональным называется всякое неравенство, сводящееся к неравенству вида
где P(x), Q(x) — некоторые многочлены.
| Поскольку | 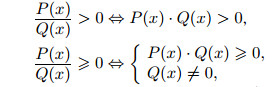 |
то для решения рациональных неравенств удобно применять метод интервалов.
Пример. Решите неравенство
Решение.
Числитель последней дроби разложим на множители. Подбором находим, что x = 2 является корнем многочлена
x3 − x2 − 22x + 40; разделив данный многочлен (уголком или по схеме Горнера) на x − 2, получаем
x3 − x2 − 22 x + 40 = (x − 2)·(x2 + x − 20) = (x − 2)·(x − 4)·(x + 5). Значит, исходное неравенство равносильно системе
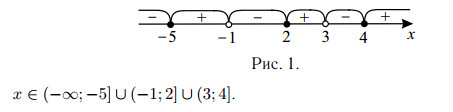
Решая первое неравенство этой системы методом интервалов (см. рис. 1)
и выкалывая точки $x = −1, x = 3$, получаем ответ
Определение модуля числа
2. Геометрически |x| есть расстояние от точки x числовой оси до начала отсчёта — точки O.
3. |x − a| есть расстояние между точками x и a числовой оси.
4. Модуль произведения, частного и степени.
На этой странице вы узнаете
- Как мы ежедневно расставляем знаки неравенства в жизни?
- Как быстро определить верное обозначение точки на прямой?
- Как правильно чередовать знаки на числовой прямой?
Решая уравнение, мы стремимся к тому, чтобы обе части были равны. Но существуют такие примеры, где мы заведомо знаем, что два выражения не могут быть равны между собой. Они называются неравенствами.
Метод интервалов
Неравенство — это алгебраическое выражение, в котором одна сторона имеет отличное от другой значение. В неравенствах обычно одна сторона больше другой.
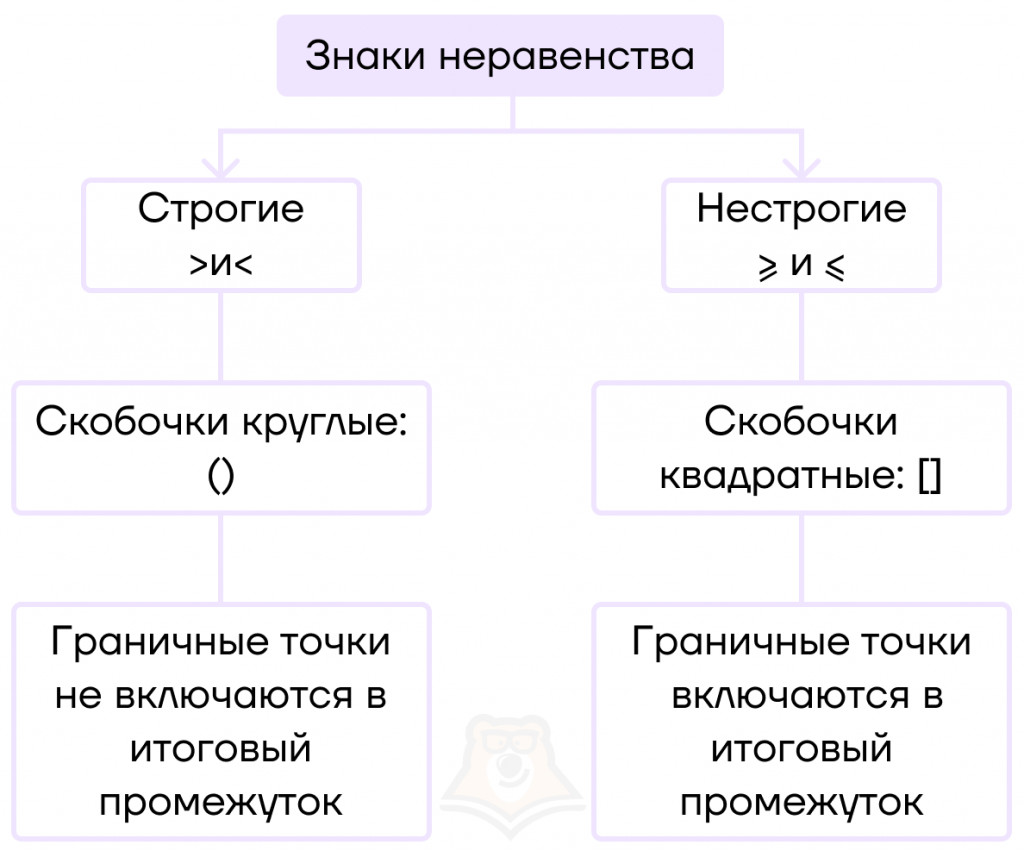
Для записи неравенств используют знаки > , < , ≥ , ≤ .
При этом “>” и “<” — это строгие знаки неравенства, а “≥” и “≤” — нестрогие знаки неравенства.
Их отличие в том, что нестрогие знаки неравенства включают граничные точки в итоговый промежуток, а строгие — нет.
Посмотрим на привычные ситуации с точки зрения строгости знаков неравенства.
Например, возьмем известную игру “Камень, ножницы, бумага”.
Правила игры говорят нам, что камень всегда побеждает ножницы, а бумага побеждает камень. Если перенести это на язык неравенства, то получится:
Теперь зайдем в магазин цифровой техники и попробуем выбрать себе новый мобильный телефон. Задачка непростая, не так ли? Две разные модели могут настолько незначительно отличаться друг от друга своими характеристиками, что будут казаться почти одинаковыми. Тогда мы можем сказать, что они практически равны между собой, то есть неравенство нестрогое. Но один из них всё-таки понравился нам больше.
И каждый наш выбор, каждый шаг – это расстановка знака неравенства в настоящей жизни. Просто по бокам от него не цифры и переменные, а существующие ситуации и вещи.
Рассмотрим пример неравенства (х — 10)(х + 21) > 0.

Его можно решить несколькими способами. Например, вспомним, что положительным будет произведение двух положительных или двух отрицательных множителей, тогда получается совокупность из двух систем.
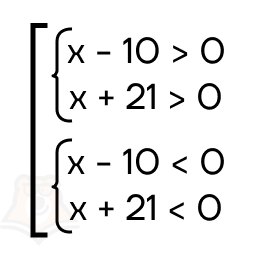
Однако этот способ решения очень трудоемкий и требует много времени. А если множителей будет больше, например, три или четыре, то время на решение в разы увеличивается.
Небольшой секрет тайм-менеджмента: как сократить время при решении неравенств? В таких случаях на помощь приходит метод интервалов.
Метод интервалов — специальный алгоритм решения для сложных неравенств вида f(x) > 0. При этом знак неравенства может быть любым.
Интервал — это промежуток на числовой прямой, ограниченный двумя различными числами.
Алгоритм решения неравенств методом интервалов
1 шаг. Перенести все части неравенства в одну сторону так, чтобы с другой остался только 0.
2 шаг. Найти нули функции, для этого необходимо решить уравнение f(x) = 0.
3 шаг. Начертить числовую прямую и отметить на ней все полученные корни. Таким образом, числовая прямая разобьется на интервалы.
4 шаг. Определить знаки на каждом интервале. Для этого необходимо подставить любое удобное значение в f(x) и определить, какой знак будет иметь функция на данном интервале.
Расставляя полученные корни на прямой, необходимо отмечать их точками. При этом от того, какая отмечена точка (выколотая или закрашенная), будет зависеть ответ.
- Если в неравенстве стоит строгий знак неравенства, то все точки на прямой должны быть выколотыми.
Таким образом, граничные точки не будут включены в итоговый промежуток. Для записи таких точек используют круглые скобочки. Например, в промежуток (2;3) включаются все значения от 2 до 3, но не включаются граничные точки.
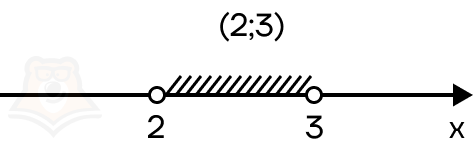
- Если в неравенстве стоит нестрогий знак неравенства, то найденные корни должны быть отмечены закрашенными точками.
Это означает, что мы включаем их в итоговый промежуток. Для записи таких точек используют квадратные скобочки. Например, в промежуток [2;3] включаются все значения от 2 до 3, в том числе и граничные точки.
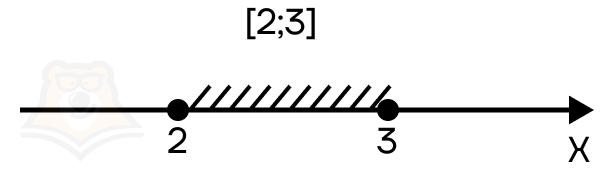
- Если в неравенстве появляются ограничения и некоторые точки нельзя взять в ответ, то такие точки должны быть выколотыми на числовой прямой, при этом знак самого неравенства может быть как строгим, так и нестрогим.
Например, если необходимо решить неравенство с дробью, то нули знаменателя на числовой прямой обязательно должны быть обозначены выколотыми точками.
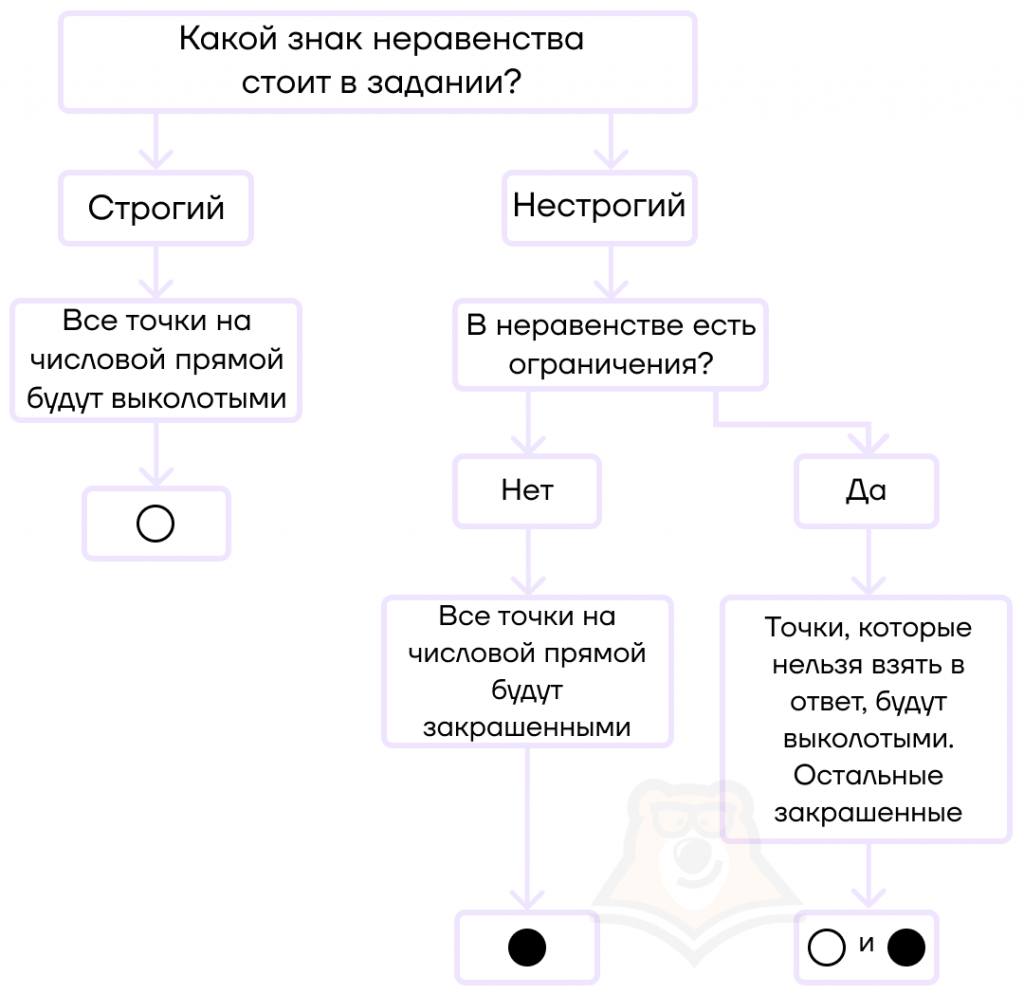
В случае сомнений мы всегда можем проверить себя по простой схеме.
Вывод:
— если знак неравенства строгий, то все точки будут выколотыми;
— если знак неравенства нестрогий, то точки будут закрашенными, кроме тех точек, которые нельзя взять в ответ (например, они не удовлетворяют ОДЗ).
Стоит отметить, что непрерывная функция будет менять знак только в точках, в которых она равна 0. Подробнее узнать про смену знака функции можно в статье «Определение и график функции». Именно поэтому в методе интервалов мы ищем и отмечаем нули функции на прямой — только при переходе через них будет меняться знак функции.
При этом существует способ, с помощью которого можно быстро расставить знаки на прямой. Достаточно определить знак на одном из интервалов, а дальше чередовать знаки при переходе через каждую точку на прямой.
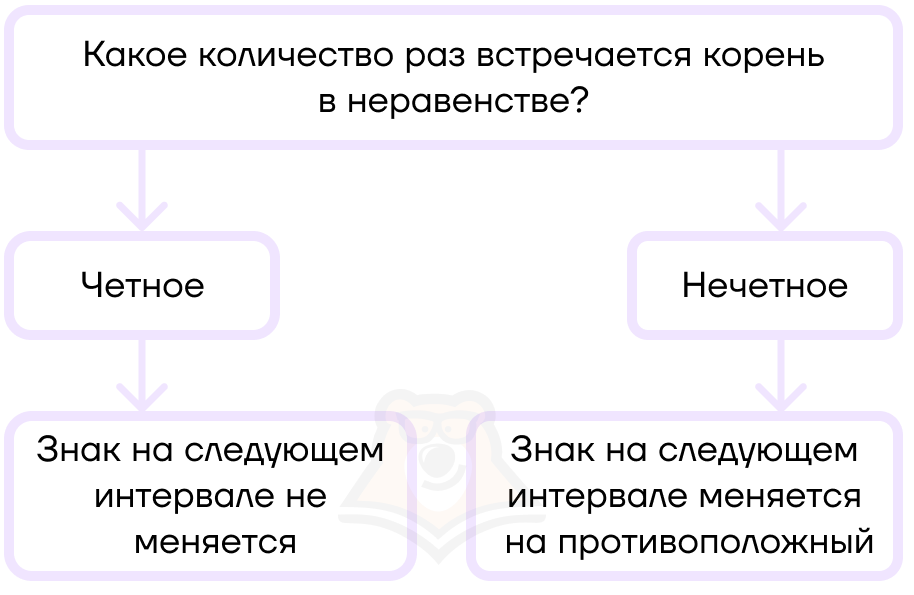
Правила чередования знаков:
- Если корень повторяется нечетное количество раз (то есть его степень нечетная), то знак при переходе на следующий интервал меняется.
- Если корень повторяется четное количество раз (его степень четная), то знак при переходе на следующий интервал не меняется.
Всегда будет нелишним перепроверить знак на каждом интервале, подставив значения в функцию, и убедиться в правильности расстановки знаков на прямой.
Но при расстановке можно пользоваться следующим алгоритмом, что значительно сократит время расстановки знаков.
Методом интервалов можно решить практически любое неравенство в задании 14 из ЕГЭ по профильной математике, также он может понадобиться в заданиях 8, 11 и 17 «профиля» или в задании 17 ЕГЭ по базовой математике.
На ОГЭ данным методом можно воспользоваться при решении неравенств из первой и второй частей — №13 и №20.
Так что осваивайте метод и 2 балла ЕГЭ или 3 балла ОГЭ будут у вас в кармане. Обязательно следуйте алгоритму решения неравенств методом интервалов, тогда вы точно решите неравенство верно.
Практика
Рассмотрим несколько примеров, чтобы на практике разобрать применение метода интервалов для решения неравенств.
Пример 1. Решить неравенство x2 + 8x — 33 > 0.
Шаг 1. Первым шагом необходимо найти нули функции, для этого приравниваем выражение слева к 0: x2 + 8x — 33 = 0.
Шаг 2. Находим корни уравнения, получаем х = 3 и х = -11.
Шаг 3. Расставляем полученные корни на числовой прямой. Поскольку знак неравенства строгий, то точки должны быть выколотыми:

Шаг 4. Дальше необходимо определить знаки на каждом интервале. Для этого подставим х = -12 в x2 + 8x — 33. Получаем:
(-12)2 + 8*(-12) — 33 = 144 — 96 — 33 = 15.
Получается положительное число, следовательно, интервал от минус бесконечности до -11 положительный. Поскольку все корни в неравенстве повторяются нечетное количество раз (по одному разу), то знаки чередуются.
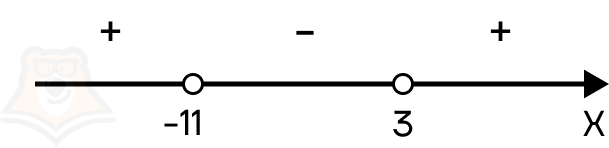
В ответ необходимо записать промежутки с положительным знаком, следовательно, ответом будет х ∈ (-∞; -11) U (3; +∞).
Пример 2. Решить неравенство (frac{2х^2 + 22х — 204}{(х-3)(х+5)} ≤ 0).
1. Находим нули функции.
Нули числителя: 2х2 + 22х — 204 = 0. Решая уравнение, получаем х = 6 и х = -17.
Нули знаменателя: (х — 3)(х + 5) = 0, следовательно, х = 3 и х = -5.
2. Расставляем полученные корни на числовой прямой. Нули числителя будут обозначены закрашенными точками, поскольку знак неравенства нестрогий. А вот нули знаменателя — выколотыми, поскольку знаменатель не может равняться 0, следовательно, и нули знаменателя не должны входить в итоговый промежуток.

3. Определяем знак на крайнем левом промежутке, подставляя х=-20 в дробь:
(frac{2(-20)^2 + 22(-20) — 204}{(-20 -3)(-20 +5)} = frac{2 * 400 — 440 — 204}{(-23) * (-15)} = 156345. )
Следовательно, промежуток положительный.
4. Поскольку каждый корень встречается один раз, то есть нечетное количество раз, то знаки будут чередоваться.

В ответ необходимо включить отрицательные промежутки. Следовательно, ответом будет х ∈ [-17; -5) U (3; 6].
Пример 3. Решить неравенство (frac{1}{х^2} ≥ frac{1}{х+2})
1. Первым делом следует отметить, что знаменатели не могут быть равны 0, следовательно, х2 ≠ 0 и х + 2 ≠ 0, отсюда получаем х ≠ 0 и х ≠ -2.
2. Теперь перенесем все части неравенства влево:
(frac{1}{х^2} — frac{1}{х+2} ≥ 0).
Приведем к общему знаменателю:
(frac{х + 2 — х^2}{х^2 (х + 2)} ≥ 0).
Для решения неравенства будет удобнее, если перед х2 в числителе будет стоять положительный знак, для этого умножим неравенство на -1.
При умножении неравенства на отрицательное число знак неравенства меняется на противоположный.
Получаем:
(frac{х^2 — х — 2}{х^2 (х + 2)} ≤ 0).
Теперь найдем нули функции.
Нули числителя: х2 — х — 2 = 0. Тогда х = -1 и х = 2.
Нули знаменателя: х = 0 и х = -2.
2. Расставим корни на числовой прямой, при этом нули числителя будут обозначены закрашенными точками, а нули знаменателя — выколотыми.

3. Определим знак на крайнем левом промежутке, подставив для этого х = -3 в дробь:
(frac{(-3)^2 — (-3) — 2}{(-3)^2 ((-3) + 2)} = frac{9 + 3 — 2}{9 * (-1)} = frac{10}{-9})
Промежуток отрицательный.
4. Дальше расставляем знаки, чередуя их. При этом следует заметить, что х = 0 — корень, повторяющийся четное количество раз (поскольку у х2 четная степень). Следовательно, при переходе через эту точку знак функции меняться не будет.

В ответ необходимо включить отрицательные промежутки, следовательно: х ∈ (-∞; -2) U [-1; 0) U (0; 2].
Давайте подведем итог. Для чего мы это изучили?
Конечно же, эти знания пригодятся на экзаменах, а также в решении школьных примеров с 8 класса по 11 класс.
Советуем после прочтения этой статьи попрактиковаться в рубрике «Проверь себя», чтобы закрепить полученные знания. После чего можете приступить к решению заданий посложнее, чтобы на экзамене у вас точно получилось решить подобные задания и набрать за них максимум баллов.
Фактчек
- Метод интервалов позволяет упростить решение любого неравенства, а также экономит время, которое ограничено на экзамене.
- Чтобы решить неравенство с помощью метода интервалов необходимо найти нули функции, расставить их на числовой прямой, а после определить знак каждого полученного интервала.
- Нули функции на прямой обозначаются точками, при этом закрашенные точки включают граничные значения в итоговый промежуток, а незакрашенные, напротив, исключают их из промежутка.
- Для определения знака на каждом интервале необходимо подставить любое значение из этого интервала в функцию.
- Для упрощения расстановки знаков можно пользоваться правилами чередования, определив знак только на одном интервале, а дальше менять знаки на каждом следующем. При этом если корень встречается в функции нечетное количество раз, то знак при переходе через эту точку на следующий интервал меняется, а если корень встречается четное количество раз, то знак на следующем интервале не меняется.
Проверь себя
Задание 1.
Какие знаки неравенства существуют?
- Строгие
- Нестрогие
- Строгие и нестрогие
- Больше и меньше
Задание 2.
Какой знак неравенства может встретиться в методе интервалов?
- Только больше или меньше.
- Только “больше или равно” или “меньше или равно”.
- Только “больше” и “больше или равно” или только “меньше” и “меньше или равно”.
- Любой.
Задание 3.
Какое утверждение верное?
- Если в неравенстве строгий знак неравенства, то точки на числовой прямой закрашены.
- Если в неравенстве строгий знак неравенства, то точки на числовой прямой выколоты.
- Если в неравенстве нестрогий знак неравенства, то все точки на числовой прямой закрашены, даже если в неравенстве есть ограничения.
- Если в неравенстве нестрогий знак неравенства, то все точки на числовой прямой выколоты.
Задание 4.
Какое утверждение верное?
- При переходе на числовой прямой на следующий интервал, знак на интервале всегда будет меняться.
- Если корень встречается в неравенстве четное количество раз, то при переходе через него на следующий интервал знак не меняется.
- Если корень встречается в неравенстве нечетное количество раз, то при переходе через него на следующий интервал знак не меняется.
- Невозможно определить правильное чередование знаков на прямой, не подставляя значение из каждого интервала в функцию.
Задание 5.
Если в неравенстве строгий знак неравенства, то какие скобочки могут встретиться в ответе?
- Круглые
- Квадратные
- И круглые, и квадратные
- Ни один из перечисленных вариантов
Ответы: 1. — 3 2. — 4 3. — 2 4. — 2 5. — 1
14 задача ЕГЭ – это всегда неравенство. На реальных ЕГЭ бывают 3 вида неравенств: показательные, логарифмические и смешанные.
Что нужно знать?
- Метод интервалов
- Как решаются дробно-рациональные неравенства
- Как делается замена и обратная замена в неравенствах
- Как решаются показательные неравенства
- Свойства логарифмов
- Как решаются логарифмические неравенства
- Метод рационализации
Задачи, которые были на экзамене за последние 7 лет с решениями на полный балл
2022:

Решение

2021:

Решение

2020:

Решение

2019:

Решение

2018:

Решение

2017:

Решение

2016:

Решение

2015:

Решение

Процент выполнения
А вот данные сколько процентов пишущих экзамен решили задачу на неравенство в разные годы:

Сколько процентов из тех, кто решал экзамен в 2021 году*, набрал в задаче хотя бы 1 балл:

* так как в 2022 году ЕГЭ был сильно скорректирован, то некоторые задачи изменили свой номер, какие-то исчезли совсем, а другие добавились. В таблице приведены данные 2021 года, приведенные к формату экзамена 2022 (поэтому, например, в задачах 9 и 10 стоят прочерки – это новые задачи)
Типичные ошибки
1. Ошибки по невнимательности
Если вы будете готовиться к 14 задаче ЕГЭ, то практически наверняка одной из главных проблем станут ошибки по невнимательности. Из всех задач профильного ЕГЭ эта задача, пожалуй, самая опасная в плане мелких ошибок. Как научиться не допускать их написано в этой статье.
Примеры таких ошибок по невнимательности выделены желтым


2. Неправильно использовать метод интервалов
Метод интервалов – это база для 14 задачи ЕГЭ. Поэтому если вы хотите научиться решать неравенства на ЕГЭ – первым делом освойте метод интервалов, чтоб ошибок не было. Вот как «косячат» в нем школьники на реальном экзамене.



3. Умножить/делить на выражение с переменной
Почему в общем случае неравенство нельзя умножать или делить на выражение с переменной? Все дело в том, что если мы неравенство умножаем (делим) на положительное число, то должны оставить знак сравнения тем же, а если на отрицательное – перевернуть его.
(2x>4) (-2x>4)
(x>2) (x<-2)
Но чаще всего мы не знаем положительно или отрицательно выражение, на которое собрались умножать (делить), потому что при разных значениях переменной знак выражения может меняться. То есть, возникает неясность — переворачивать знак сравнения или оставить тем же? Поэтому в неравенствах так не делают. В уравнении можно, в неравенстве нет.
|
Уравнение (можно и нужно умножать на икс) |
Неравенство (нужно приводить к общему знаменателю) |
| (frac{1}{x}=1) |(·x) | (frac{1}{x}>1) |
| (1=x) | (frac{1}{x}-1>0) |
| (x=1) | (frac{1-x}{x}>0) (|·(-1)) |
| (frac{x-1}{x}<0) | |
| (x∈(0;1)) |
Хотя бывают исключения, когда знак выражения с иксом определен. Например, на (2^x) умножить или разделить неравенство можно, потому что (2^x) положительно всегда, независимо от значения (x).
(frac{2^x-1}{2^x} ≥0) (|cdot2^x)
(2^x-1≥0)
Также бывает, что выражение положительно не всегда, но мы знаем, что в данном конкретном неравенстве это так, поскольку, например, таковы требования ОДЗ.
|
(log_2x+log_2frac{1}{x^2}≥0) (log_2x frac{1}{x^2} ≥log_21) (frac{1}{x}≥ 1) (|cdot x) (1≥x) (x≤1) |
Огр. (begin{cases} x>0 \ frac{1}{x^2} >0 end{cases}) |
Несколько примеров с ошибками:



4. Неправильно привести к общему знаменателю
Чаще всего такую ошибку допускают те ученики, которые ленятся написать лишнюю строчку, делают два, а то и три действия за один ход: сразу и домножаем, и раскрываем скобки, и тут же в уме приводим подобные слагаемые. Вот, например, в примере внизу пропущен шаг домножения дробей на недостающие множители и раскрытие скобок. Подозреваю, что из-за этого и возникла ошибка.

Сравните с этим бланком, где выпускник все сделал постепенно, по шагам и закономерно получил верный ответ.

5. Не сделать обратную замену
Это вообще классика – сделать замену и забыть вернуться к исходной переменной. Вот пример.

6. Неправильно снять квадрат
Такая ошибка редко совершается на самом ЕГЭ, потому что так обычно ошибаются те, кто только начал проходить неравенства. Но зато в начале пути ее делают практически все, поэтому я внесла её в список.
Скачать материал

Скачать материал


- Сейчас обучается 128 человек из 47 регионов


- Сейчас обучается 23 человека из 17 регионов


- Сейчас обучается 1081 человек из 83 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
Мурашкина И.В. Учитель высшей категории МБОУ «Гимназия №127 имени академика Е.Н.Аврорина» г.Снежинск, 2019.
-
2 слайд
Практикум по теме: «Применение метода интервалов в решении традиционно проблемных неравенств: сложно или просто?»
-
-
4 слайд
№1 Разность модулей совпадает по знаку с разностью квадратов этих величин Ответ:
-
5 слайд
№2 Ответ: Разность неотрицательных величин совпадает по знаку с разностью квадратов этих величин в их ОДЗ (3):
-
6 слайд
№3 Ответ: Красота выведенных условий равносильности состоит в том, что мы не решаем никаких неравенств с корнями и не рассматриваем решение неравенств с модулем, раскрывая модули на промежутках!
-
7 слайд
№4 Ответ: равносильно следующей системе неравенств:
-
8 слайд
№5 Ответ: равносильно следующей системе неравенств:
-
9 слайд
Работа в группах №6 №7 №8 Ответ: Ответ: Ответ:
Краткое описание документа:
«Применение метода интервалов в решении традиционно проблемных неравенств:
сложно или просто?»
Ученикам хорошо знакомы логарифмические, показательные неравенства, содержащие в основании переменную величину и способ их решения, когда рассматривают совокупность двух систем.
Я в своей работе учу ребят эффективным методам решения таких неравенств, где мы за один шаг уходим от логарифмов
Команда разработчиков КИМ не предсказуема, нельзя спрогнозировать вид задания №15. В учебно-тренировочных пособиях они представлены весьма разнообразными. Так как наши выпускники ежегодно сдают ДВИ, задания которых отличаются от ЕГЭ, поэтому мы с ребятами изучаем нестандартные методы и стараемся применять только их, потому, что именно они позволяют с помощью условий равносильности сводить решение целых классов сложных неравенств к решению простых рациональных неравенств, которые решаются классическим методом интервалов.
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 154 237 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
-
«Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (углублённый уровень)», Муравин Г.К., Муравина О.В.
Больше материалов по этому УМК
Другие материалы

Итоговая контрольная работа по математике 10 класс
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (углублённый уровень)», Муравин Г.К., Муравина О.В.
- Тема: Глава 6. Повторение
- 20.07.2019
- 1220
- 25



Рабочая программа по математике
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (углублённый уровень)», Муравин Г.К., Муравина О.В.
- 20.07.2019
- 665
- 0

Рабочая программа по алгебре 10 класс
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (углублённый уровень)», Муравин Г.К., Муравина О.В.
- 07.07.2019
- 216
- 0

Рабочая программа по алгебре 10-11 класс
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (углублённый уровень)», Муравин Г.К., Муравина О.В.
- 03.07.2019
- 351
- 0

Презентация «Сравнение тригонометрических функций»
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (углублённый уровень)», Муравин Г.К., Муравина О.В.
- Тема: Глава 4. Тригонометрические функции и их свойства
- 01.06.2019
- 527
- 7

Вам будут интересны эти курсы:
-
Курс повышения квалификации «Подростковый возраст — важнейшая фаза становления личности»
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Основы управления проектами в условиях реализации ФГОС»
-
Курс повышения квалификации «Основы построения коммуникаций в организации»
-
Курс повышения квалификации «Организация практики студентов в соответствии с требованиями ФГОС юридических направлений подготовки»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс повышения квалификации «Психодинамический подход в консультировании»
-
Курс повышения квалификации «Международные валютно-кредитные отношения»
-
Курс профессиональной переподготовки «Гражданско-правовые дисциплины: теория и методика преподавания в образовательной организации»
ЕГЭ Профиль №15. Рациональные неравенства
Нашли ошибку в заданиях? Оставьте, пожалуйста, отзыв.
15 заданием профильного ЕГЭ по математике является неравенство. Одним из видов неравенств которое может оказаться в 15 задание является рациональное неравенство. Прежде чем решать рациональные неравенства, следует научиться решать рациональные уравнения. Как правило, рациональное неравенство решается методом интервалов, который не требует каких-то специальных навыков, но при этом решение оказывается достаточно объемным и требует внимательности. Также не следует забывать про метод замен. Без умения решать рациональные неравенства невозможно будет научиться решать все остальные неравенства (показательные, логарифмические и т.д.). Поэтому изучение темы «Неравенства и системы неравенств» необходимо начинать именно с рациональных неравенств. В данном разделе представлены рациональные неравенства (всего 113) разбитые на два уровня сложности. Уровень А — это простейшие рациональные неравенства, которые являются подготовительными для решения реальных рациональных неравенств предлагаемых на экзамене. Уровень В — состоит из неравенств, которые предлагали на реальных ЕГЭ и в диагностических работах прошлых лет.